Covid-19: From Limit Cycle to Stable Focus

1. Introduction

The growing application of population models in assessing the dynamics of real biological objects necessitates greater accuracy and detail of the description. Simple models, where individuals are considered to be identical, are replaced by models with the internal structure of population, where individuals may differ in the values of various parameters [1,2]. Distributed models are of particular interest. In this case, the population structure is determined by the distribution of individuals along a continuous parameter, for example, height, weight, position in space, age, etc.

The use of models with an age structure allows a more detailed and accurate description of the behavior of a population in cases where the parameters that determine its dynamics depend significantly on age. Here, the “age” can mean various indicators that change over time: time since birth (demography and population dynamics) [1,2,3,4], time since the infection (epidemiology, including immunity dynamics) [4,5,6], time since cell division (tissue growth) [7], etc.

Population models with the age structure allow explaining phenomena such as demographic (population) waves [8], considering the dynamics of immunity [5,6], and formalizing the relationship between the rate of evolution and the rate of environmental change [9]. This enhances expressiveness of the models, increases potential accuracy in describing natural phenomena, and improves understanding of the laws of their functioning. Results obtained through this approach exemplify its efficiency. In this study, we begin by presenting some results of using the simulation model of the Covid-19 epidemic in Moscow. Subsequently, we propose a hypothesis about changing the long-term behavior of the system. Finally we introduce and explore an original mathematical model of the virus-human system explaining that behavior.

2. Materials and Methods

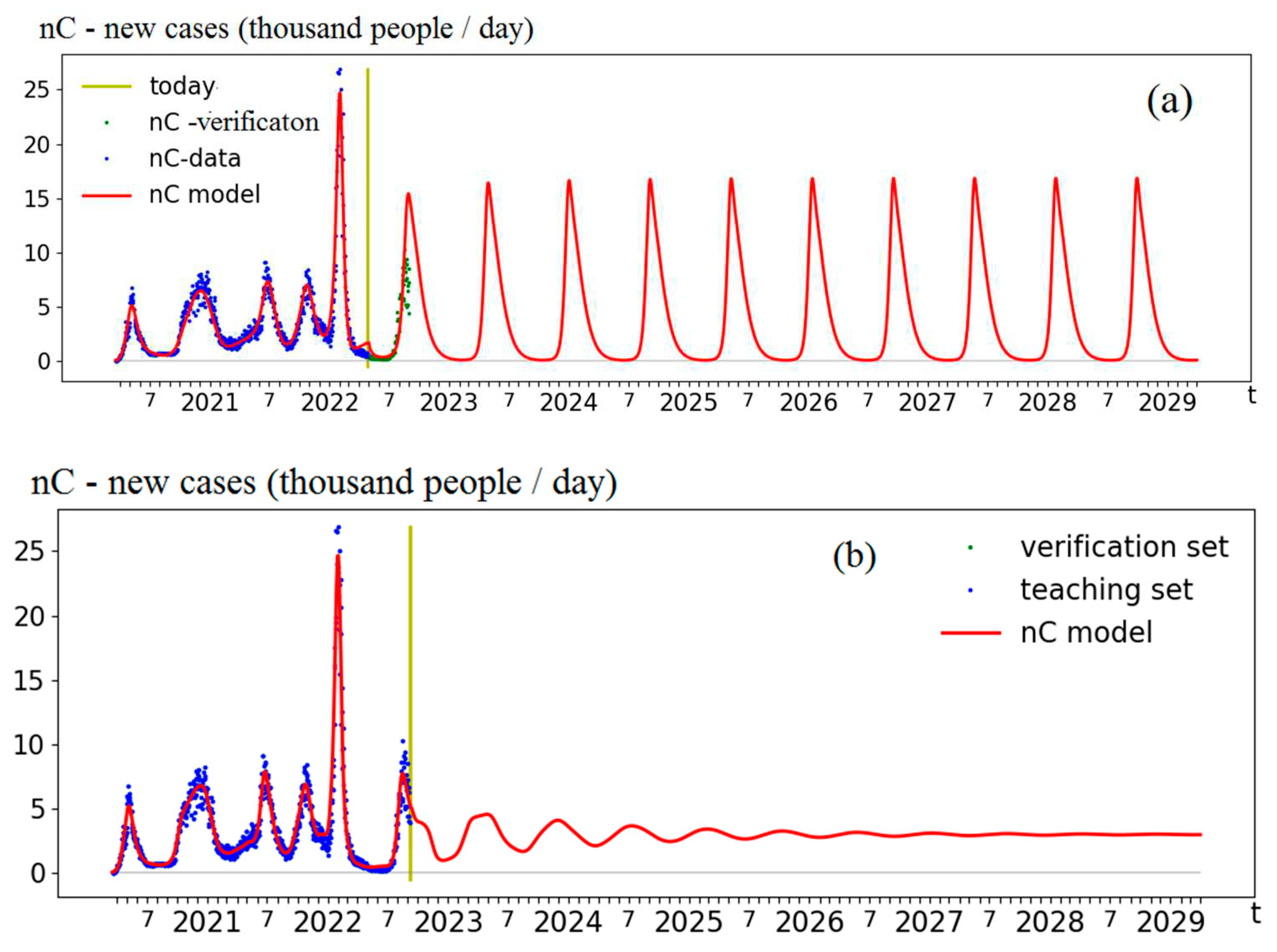
Figure 1 shows forecasts (of 04/27/22 and 09/06/22) of new detected cases (nC), obtain by the simulation model [5,6], identified by the real data collected in Moscow. In Figure 1a, the dynamics enters the mode of undamped oscillations with a period of about 8 months and with a maximum of about 15,000 cases. In Figure 1b - the dynamics display the mode of damped oscillations around a (background) value of 3,500 cases and with a period of about 7 months, the amplitude of each wave is lower by 30% than the previous one.

The main parameter determining the qualitative difference in the forecasts dynamics is the reproduction number R₀: In the first forecast R₀=2.7 and in the second one R₀=15.6.

Therefore, variations in the contagiousness of a virus result in a qualitative change in the virus-human system’s behavior.

The presented numerical experiments inspire a more complete study of the model used: the definition of stationary states and limit cycles, their stability depending on the critical (bifurcation) parameter R₀, i.e. the construction of the bifurcation diagram of the system.

The complete complex model [5,6] takes into account various factors such as testing rate, vaccination intensity, herd immunity, etc. It can be regarded as a modification of McKendrick–Von Foerster model [2,4] or Leslie model [2,3] or as a mixed Cauchy problem for the transport equation [10,11] with a specific boundary condition (representing the emergence of new infected).

To conduct a mathematical study, we use a simplified model (everything was removed, except for contagiousness and immunity, depending on the time of the infection)

$$\begin{gathered} \frac{\partial I}{\partial t}+\frac{\partial I}{\partial a}=0 \\ I\left(0,a\right)=I_0\left(a\right) \\ I\left(t,0\right)=B\left(t\right) \\ B\left(t\right)=R_0\ast \left(1-Imm\left(t\right)\right){\int }_0^{A}b\left(a^{\text{'}}\right)I\left(t,a^{\text{'}}\right)d{a}^{\text{'}} \\ {\int }_0^{A}b\left(a^{\text{'}}\right)d{a}^{\text{'}}=1 \\ Imm\left(t\right)=\frac{1}{N}{\int }_0^{I}fImm\left(t^{\text{'}}\right)B\left(t-t^{\text{'}}\right)d{t}^{\text{'}}, \end{gathered}$$

where I(t,a) is the number of infected with infection duration (the number of days since the moment of infection) a at time t, I0(a) - the number of infected people at the initial moment t=0 (initial condition), B(t) - the number of new infected (a=0) at time t (boundary condition), R₀ - the reproduction number, Imm(t) - the proportion of the population with immunity (at time t), А - the maximum duration of the disease (14 days), b(a) - the normalized (integral equal to 1) contagiousness as a function of disease duration a, N - population size, I – the maximum duration of immunity period (270 days), fImm(t) - proportion of infected who maintained immunity t days after the disease.

By integrating the first equation along the characteristic (a=t+Const), we obtain the number of infected with infection duration a at time t is the number of new infected at time t – a:

$$I\left(t,a\right)=B\left(t-a\right),$$

which leads to a modified (accounting for immunity) Euler-Lotka renewal integral equation [2,7,12]:

$$B\left(t\right)=R_0\ast \left(1-Imm\left(t\right)\right){\int }_0^{a_{max}}b\left(a^{\text{'}}\right)B\left(t-a^{\text{'}}\right)d{a}^{\text{'}}$$

(1)

$$Imm\left(t\right)=\frac{1}{N}{\int }_0^{i_{max}}fImm\left(t^{\text{'}}\right)B\left(t-t^{\text{'}}\right)d{t}^{\text{'}},$$

(2)

or by combining both equations:

$$B\left(t\right)=R_0\left(1-\frac{1}{N}{\int }_0^{I}fImm\left(t^{\text{'}}\right)B\left(t-t^{\text{'}}\right)d{t}^{\text{'}}\right){\int }_0^{A}b\left(t^{\text{'}}\right)B\left(t-t^{\text{'}}\right)d{t}^{\text{'}},$$

(3)

Equation (1) describes the emergence of new infected as the product of the reproduction number R₀ (how many people a sick person can infect) by the proportion of the population without immunity (1-Im(t)), and by the total number of infected, weighted taking into account the dependence of contagiousness on disease duration. Equation (2) describes the proportion of carriers of natural immunity as the number of infected people who have retained immunity by the time t, divided by the total population N.

To find a stationary solution (equilibrium position) we substitute B(t) = B0, Imm(t) = Imm0 in (1)-(2) and get:

$$I0=\left(1-\frac{1}{R_0}\right); B0=N\left(1-\frac{1}{R_0}\right)/{\int }_0^{I}fIm\left(t^{\text{'}}\right)d{t}^{\text{'}}.$$

(4)

To study its stability, we linearize (3) near the equilibrium point (4):

B(t) = B0 + Δ(t)

and, neglecting the values of the 2nd order and higher, we obtain a linear integral equation:

$$\Delta \left(t\right)={\int }_o^I\Phi \left(t^{\text{'}},R_0\right)\Delta \left(t-t^{\text{'}}\right)d{t}^{\text{'}},$$

(5)

where

$$\Phi \left(t^{\text{'}},R_0\right)=b\left(t^{\text{'}}\right)-\left(R_0-1\right)\frac{fImm\left(t^{\text{'}}\right)}{{\int }_0^{I}fImm\left(t^{\text{'}\text{'}}\right)d{t}^{\text{'}\text{'}}}$$

(6)

(here the function b(t) is extended by zero values for t > A).

To investigate it [2,7,12], we will look for a solution in the form of Δ(t)=Qe^rt. As a result, we obtain an eigenvalue problem - the Lotka equation:

$$1={\int }_o^I\Phi \left(t^{\text{'}},R_0\right)e^{-r{t}^{\text{'}}}d{t}^{\text{'}}.$$

(7)

The roots of equation (7) allow us to judge the stability of equilibrium (4) of equation (3). If for all solutions r of (7) Re(r) < 0, then Δ(t) tends to 0 and the equilibrium position (4) of (3) (or system (1)–(2)) is stable. Otherwise, if there exists r with Re(r) > 0, the equilibrium is unstable. Thus, we can determine the stability of stationary solutions depending on the value of the (bifurcation) parameter R₀.

The considered eigenvalue problem (7) has no analytical solutions, so it is natural to study its discrete numerical approximation:

$$1={\sum }_{t=0}^I\Phi \left(t,R_0\right)e^{-rt}.$$

(8)

Note. Equation (8) can be converted to the characteristic polynomial:

$$1={\sum }_{i=0}^I\Phi \left(i,R0\right){\lambda }^{-i},$$

where λ=e^r.

It has been established [2,3] that the obtained polynomial is the characteristic polynomial of the Leslie matrix (corresponding to problem (5)). However, unlike the classical setting, the function Φ(t, R₀) and the corresponding elements of the Leslie matrix can take negative value. Therefore, we should not expect the dominant eigenvalue to be real.

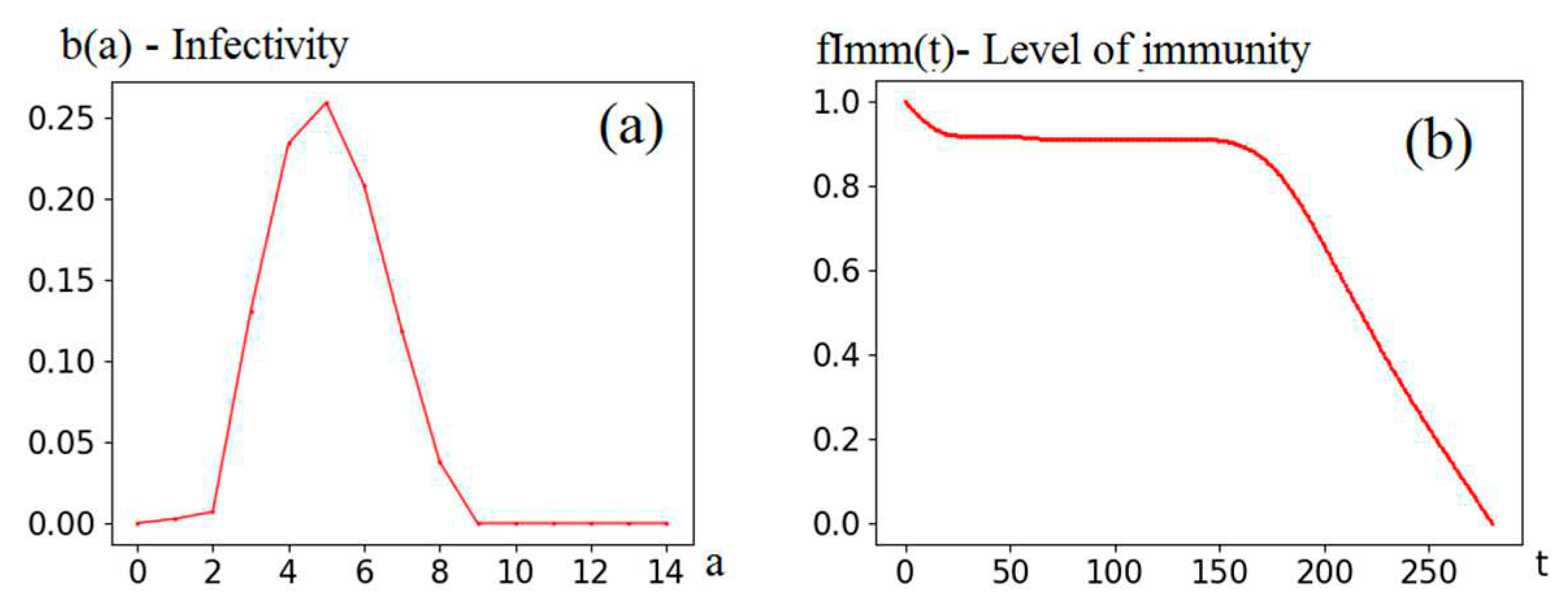
The following calculations are based on the functions (see Figure 2) that were obtained earlier when identifying the comprehensive model [5,6] for the Covid-19 epidemic in Moscow. They are used to calculate Φ(t, R₀) and corresponding elements of the numerical model (8). It is these functions, together with the parameter R₀, that determine the system behavior.

3. Numerical results and discussion

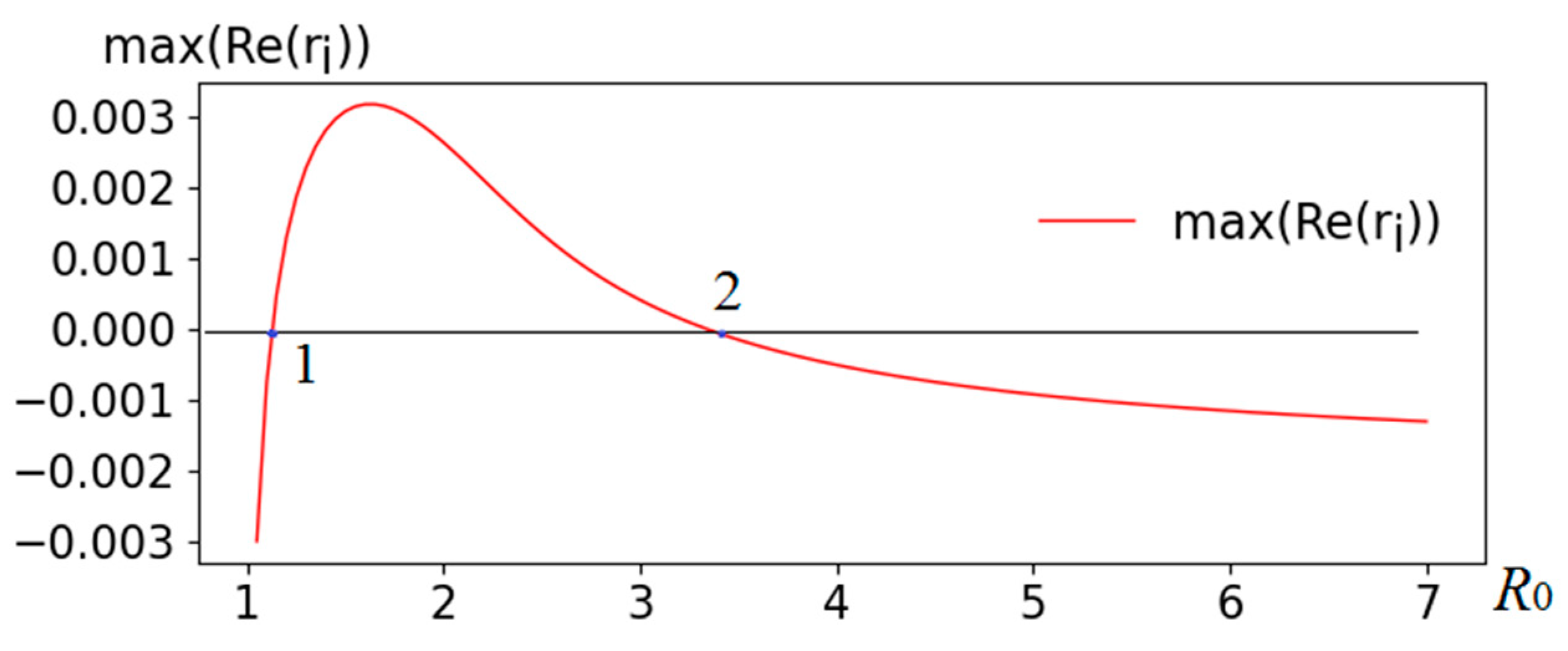
Figure 3 shows the results of a numerical study of the eigenvalue problem (8). Bifurcation points (change of sign) are marked "1" (R₀ value about 1.16) and "2" (R₀ value about 3.5). Thus, we obtain three areas: to the left of point 1 - the equilibrium (4) of system (1)-(2) is stable, between points 1 and 2 - is unstable, and to the right of 2 - the equilibrium is stable.

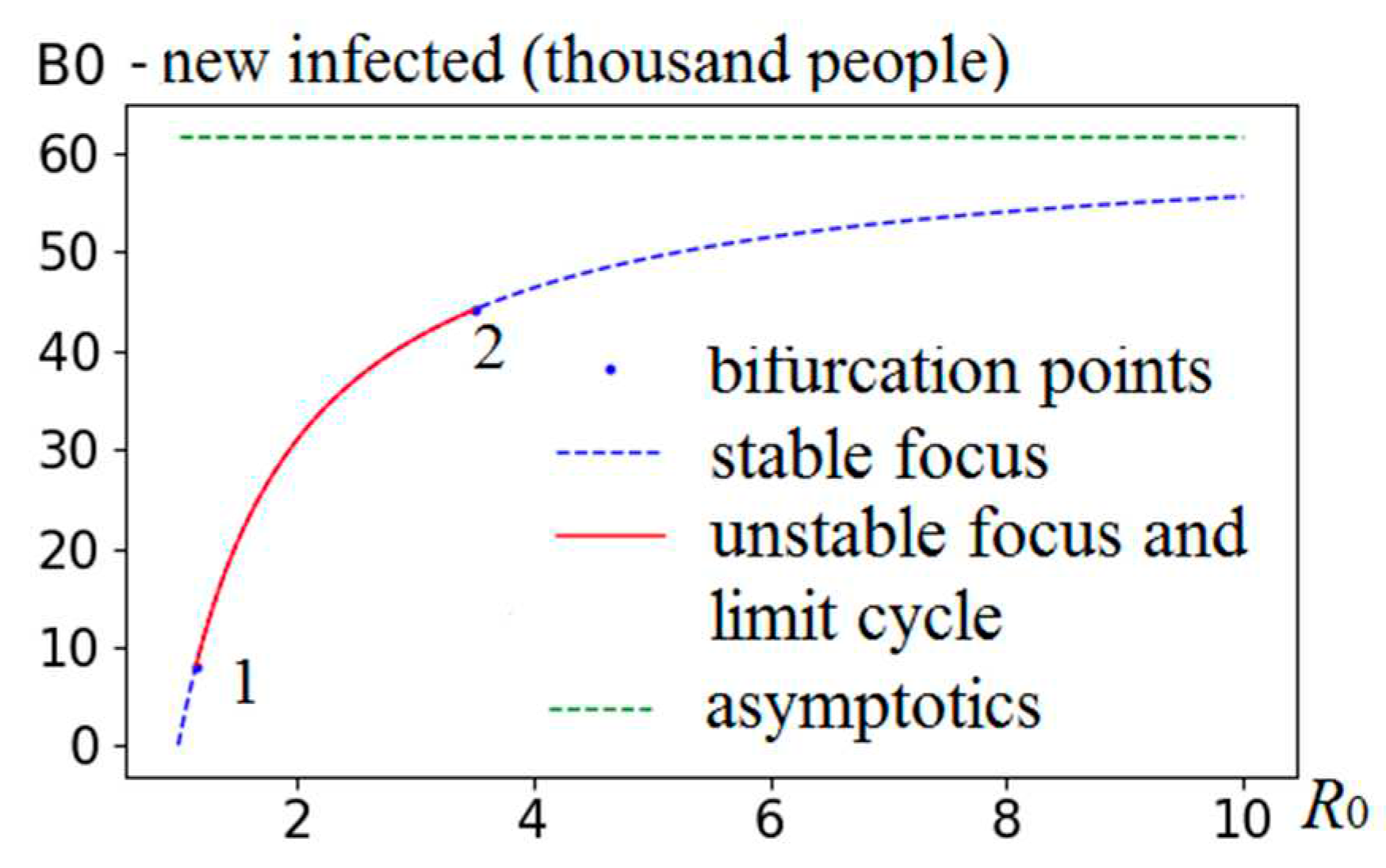
Another representation of the results in the form of a bifurcation diagram (in the space B0× R₀) is shown in Figure 4. As R₀ increases, at point 1, a stable focus is transformed into an unstable focus. At point 2, the reverse transformation occurs - an unstable focus passes into a stable focus.

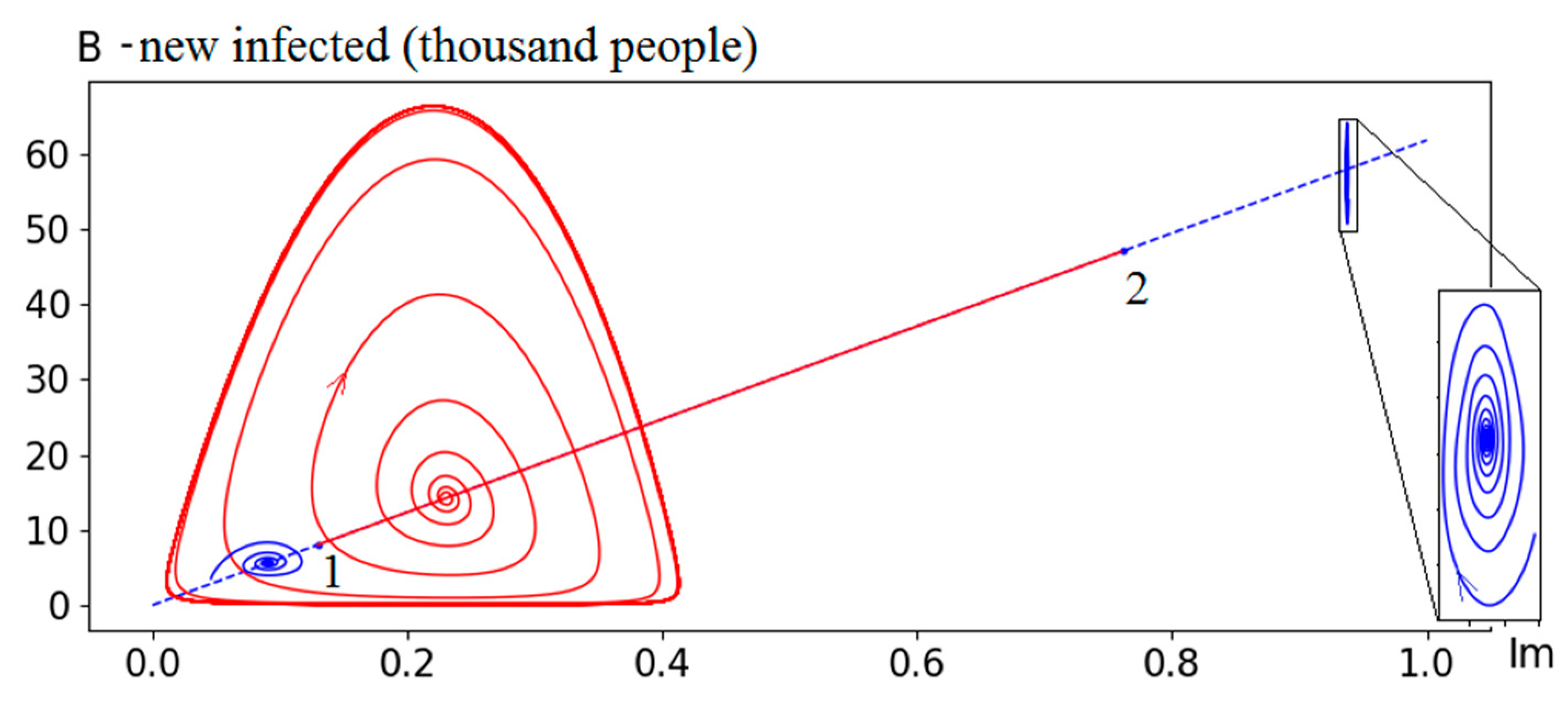
Figure 5 provides a more visual representation in the phase space B×Im. In addition to the equilibrium points (4), the figure shows some trajectories and limit cycles calculated on the basis of the numerical approximation of the model (1)-(2).

Figure 5 shows the phase portrait of system (1)-(2). The left point of the straight line with coordinates (0,0) corresponds to R₀ ≤ 1 (the epidemic ends). Further, the straight line up to bifurcation point 1 (R₀ value is about 1.16) corresponds to a stable focus. The displayed trajectory example (blue stable focus on the left part) corresponds to the value R₀=1.1. At bifurcation point 1 a qualitative change occurs in the system’s dynamic properties - the focus becomes unstable and a stable limit cycle appears (calculated on model (1)-(2), as the linearized model (5) is not sufficient). The given trajectory example (in the limit - a red stable cycle) corresponds to R₀=1.3. As we approach the point 2, the cycle amplitude initially increases (for example, at R₀=3 the amplitude B reaches 700 thousand), and then begins to decrease (at R₀=3.6 the amplitude B is about 80 thousand). The cycle also becomes more complex (with self-intersections), and closer to point 2, the system’s motion possibly becomes chaotic (this statements requires further research). After the bifurcation point 2, the system behavior is once again described by a stable focus. The example shown (blue stable focus on the right) corresponds to R₀=16.

Let’s draw some practical conclusions from this analysis.

At large values of R₀, the system tends towards a stable equilibrium point. The level of immunity at this point is determined (according to (4)) by the formula (R₀-1)/ R₀*100%. For instance, if the reproduction number R₀=10, then for zero growth, 9 of 10 people must be immune. With R₀ more than 10, stationary solutions do not differ much from each other (see Figure 4) - more than 90% of the population should have natural immunity. Therefore, according to the model considered, the emergence of more infectious strains does not significantly alter the situation.

4. Conclusions

Numerical experiments with the Covid-19 simulation model in Moscow [5,6] have led us to propose a hypothesis about a qualitative change in the behavior of the “virus-human” system as virus contagion increases. Mathematical study of the corresponding reduced model (1)-(2) confirmed this assumption. The critical value of the reproduction number R₀ is about 3.5. Below this value (observed until 2022), the forecast tends to undamped oscillations (stable limit cycle). Above this value, it is described by damped fluctuations (stable focus), with decreasing amplitudes of epidemic waves and a constant, very high background level of morbidity that maintains natural immunity slightly lower than 100%. For the current situation in Moscow (as of May 2023), according to the model, the wave period is about 7 months, the amplitude of each wave is 30% lower than the previous one. These values align with the current situation quite well.

The above calculations are approximate. They are based on functions obtained earlier in the identification of the full model [5,6] for the Covid-19 epidemic in Moscow. Similar calculations can be conduct for other populations and diseases.

The theoretical results obtained are of a fundamental (general) nature. They were obtained on a simplified model that takes into account only contagiousness and immunity retention (as functions of time since infection). The found effects are present in all epidemics of infectious diseases with natural adaptive immunity weakening over time, although they can be masked by other stronger factors, such as contact restrictions, vaccination, migration, seasonality, etc.

We can hope that our immune system will learn to "remember" the contact with the virus for a longer time (as of now, according to calculations [5,6] - about 200 days), and then the "tribute" to maintain immunity will become significantly less. Another hope for combating infectious diseases is the emergence of newer, more effective vaccines.