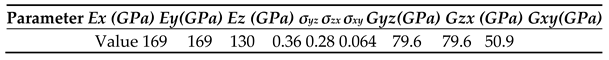Prerpints.org logo
Preprint
Article

Reem-Shape Phononic Crystal for Q anchor enhancement of TPoS MEMS Resonator

Altmetrics

Downloads

129

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts
Abstract
: This paper proposes a reem-shape phononic crystal for the performance enhancement of TPoS resonators. The proposed phononic crystal offers an ultra-wide acoustic band gap that prevents energy leakage through the supporting substrate on its placement at the anchoring boundary, resulting in significant improvements in the resonator quality factor. Simulated results show reem-shape Phononic crystals generate a band gap up to 175MHz with BG of 90% and enhance the anchor quality factor from 180,000 to 6,000,000 and unloaded quality factor from 133,000 to 160,000 representing 33.3-fold and 1.2-fold improvements respectively.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Micromachined resonators have a great possibility for integration with microelectronics at the beginning of the fabrication process at the die or package level [1,2,3,4,5]. This merit leads to reducing the cost and form factor of the system, enhancing performance, and decreasing fabrication complexity. However, before MEMS resonators widespread commercially in markets over other types of resonant devices, some loss factors such as loss in material, loss due to temperature instability, and loss due to bunch integrations and packaging with other electronics should be mitigated. Micromachined resonators are grouped into three main categories named as piezoelectric resonators, capacitive resonators, and piezoresistive resonators. Piezoelectric micromachined resonators have proven excellent performance and strong reliability to applications of timing for their incredible performance. Some of the merits of these devices include a strong electromechanical coupling coefficient [6], a large Q, better temperature stability, and the possibility of resonator implementation and fabrication on a silicon substrate at the die level [7].
Micromachined resonators with large Q are highly preferred to build oscillators with low-phase noise and filters with low insertion loss [8]. Energy dissipation in ALN micromachined resonators is caused by many sources like: thermo-elastic- damping (TED), support (anchors loss) [9,10], material loss [11], and other losses like resistive loss, surface loss, and dielectric loss [12,13]. In this regard, the quality factor of the micromachined resonator includes many items such as anchor quality factor (Qanchor), electrode quality factor (Qelectrode), TED quality factor (QTED), material quality factor (Qmaterial), and unknown quality factor (Qunknown). The equivalent Q can be expressed with the
following equation [16]:
Q = 2 π E s t o r e d E l o s s
where Estored and Eloss represent the stored and dissipated energy in the resonator, respectively. Anchor loss represents the major loss of the piezoelectric resonator's resonators with width extension mode of vibration. This loss is mainly due to the radiation of acoustic waves to the supporting substrate through tethers. One of the mechanisms used to mitigate this loss is using acoustic reflectors [14,15,16]. The shortcoming of this method is not efficient in reducing anchor loss. The other recently introduced method of improving the Q of the resonator is using energy-preserving suspended frames [17]. Even though it is reported to provide significant improvement in Q, it introduces spurious modes near the intended resonance mode. The most widely used method is to apply one-dimensional or two-dimensional phononic crystals on anchors of the resonator or on supporting tethers, which is provided by many researchers [18,19,20]. Different types of effective phononic crystals have been achieved so far. This article introduces a new phononic crystal structure with a wide acoustic band gap. With its deployment on the anchoring boundary of the resonator this newly designed Reem-PnC lends itself to achieve very high-quality factors.

2. Phononic Crystal & Theory of wave propagation

2.1. Principle of wave propagation in PnCs

The periodic structure of phononic crystals consists of two or more elastic materials with excellent mechanical properties [21,22,23]. Properly designed phononic crystals provide some range of frequencies in which acoustic waves are inhibited to propagate. This range of frequencies is defined as an acoustic band gap [24]. Bloch’s theorem can be used to characterize the propagation of waves in acoustic mediums (phononic crystals) and periodic dielectric mediums (photonic crystals) [25]. The equation of the acoustic wave propagation in material with anisotropic nature can be written as [26,27,28,29,30]:
∂ ∂ x j C i j k l ∂ u k ∂ x l = ρ v .. i
where xj represents the coordinate axes (x,y,z), Cijkl represents the tensor of elastic material and ui represents the components of displacement (ux,uy,uz), and ρ is the silicon density. To calculate the bandgap, the two boundary destinations on the unit cell (a) are adjusted to Bloch periodic boundary conditions through all the propagation directions. Bloch–Floquet theorem verifies the periodic boundary condition of displacements as defined by [24]:
ui(x,y,z+a,t)=ui(x,y,z,t)ejka
where k and a represents wave number and the lattice constants of the PnC. All frequency Eigen modes can be calculated by sweeping k through the boundaries of the first irreducible Brillouin zone (IBZ) in the single structure of the phononic crystal. The frequencies are a function of k (k=ω/c), where c represents acoustic wave velocity along the [110] direction of silicon and ω represents angular frequency, the relation among generated displacement due to stress can be expressed as [24]:
ui(x +a,t)= ejk.a ui(x, t)
σij(x, +a,t)= ejk.a σij(x, t)
The Bloch profile shows the calculations of changes in displacements, eigenfrequencies, and stress fields as k varies gradually, many curves are achieved between k and ω due to varying wave vectors through all highly symmetric edges of the first IBZ of the Reem-PnC as shown in Figure 2b. All the calculations of equations and solutions are done by using COMSOL Multiphysics through the (FE) analysis method.

2.1. PnC design

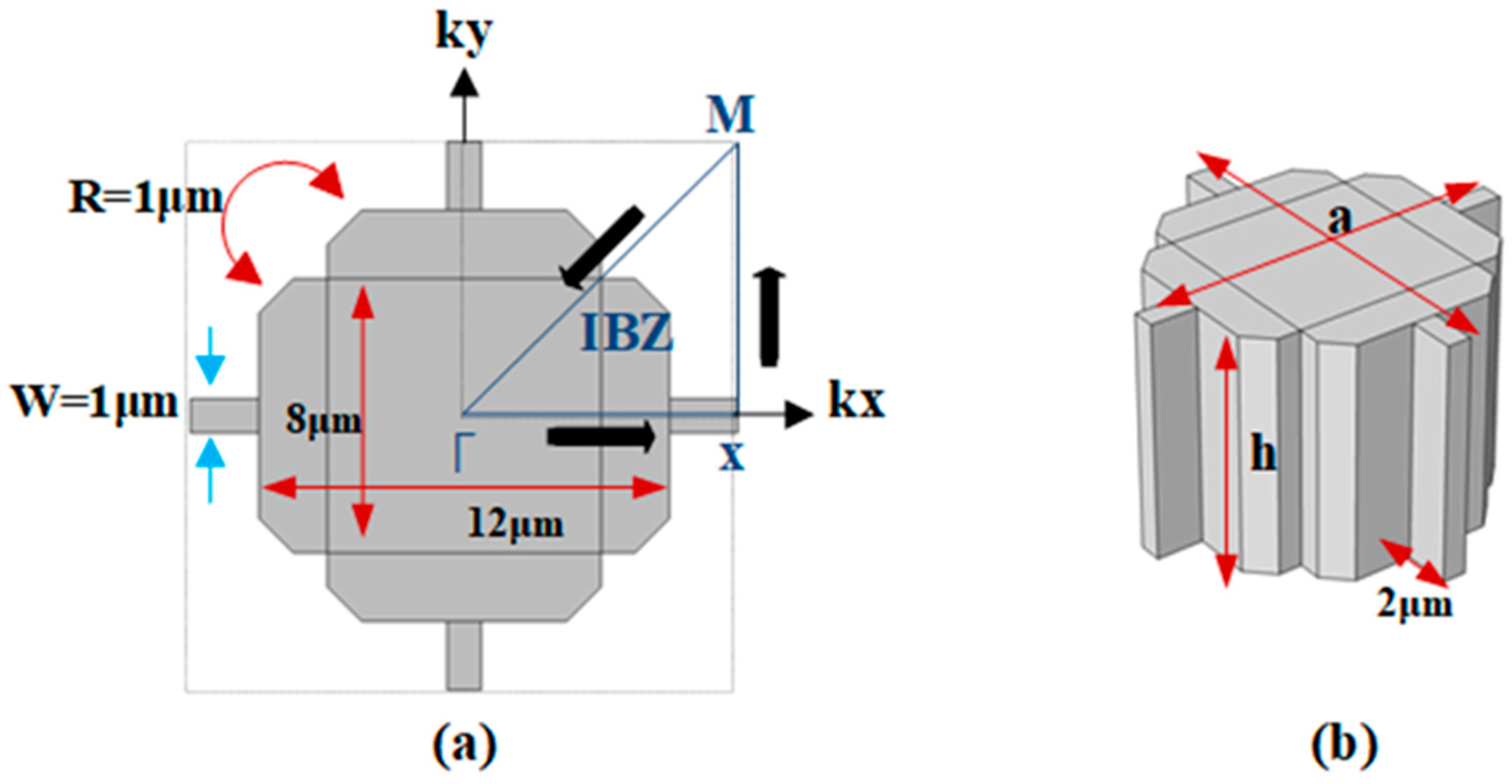
The Reem-PnC is illustrated in Figure1. Figure 1b demonstrates the structure of a single unit cell with lattice constant a=16μm and two cross blocks perpendicular to each other with width and length of 12μm,8μm, and 8μm,12μm respectively, high of h=10μm and chamfered edges of radius R= 1μm, connected by four connectors with width and length of 2μm and 1μm to array of PnCs. All the designs were constructed using single-crystal silicon, the mass density of silicon ρ = 2330 kg/m3, and the elastic constants illustrated in Table 1.
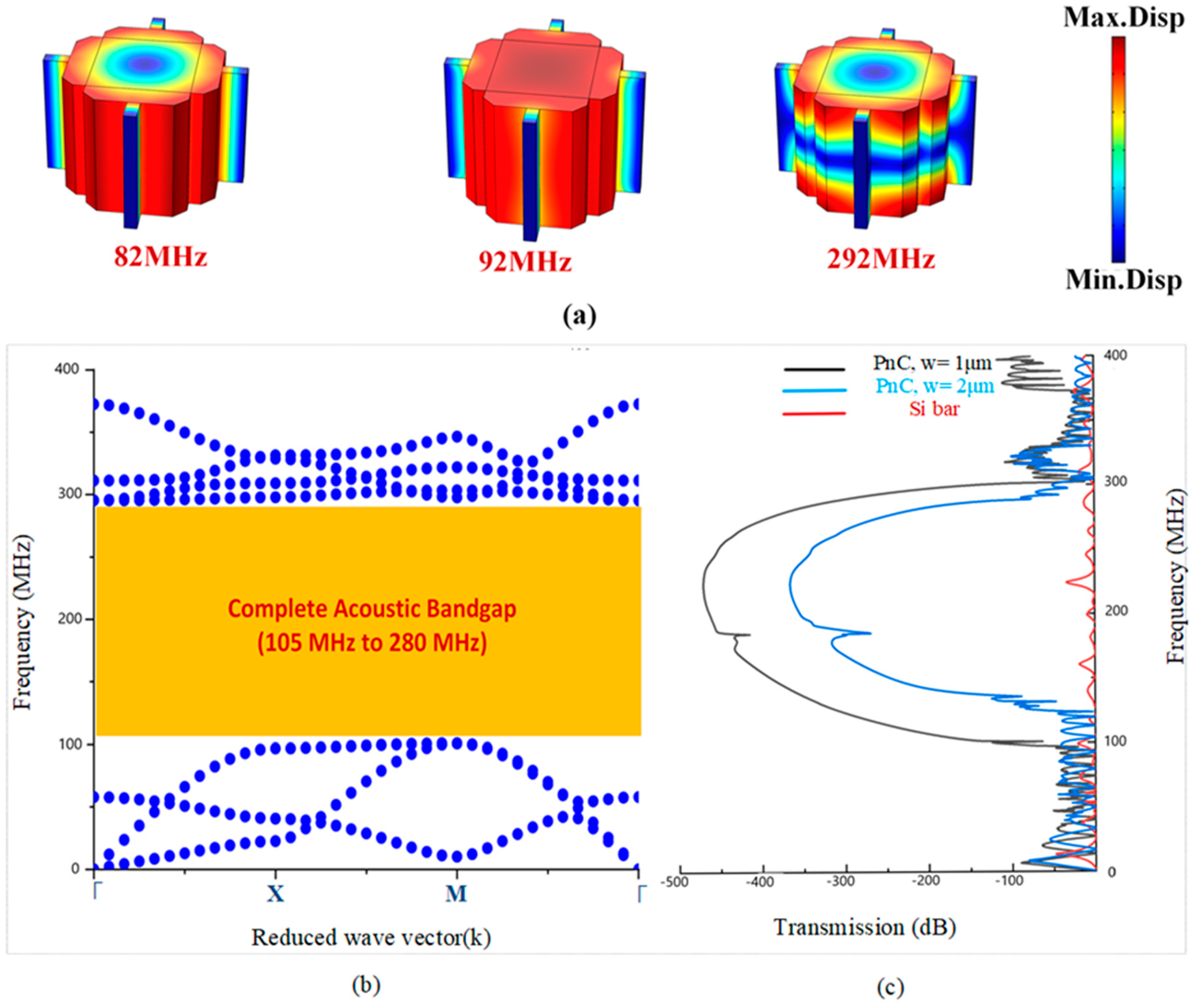
The axes (x, y, z) of the lattice synchronized with the (110), (110), and (001) direction of the original orientation silicon wafer (i.e. 100). Adding Floquet periodic boundary conditions at edges of the unit cell and sweeping the parameters of k, through the orientation of Γ-X-M-Г for the first IBZ as illustrated in Figure 1a. The first eigenfrequency modes of Reem-Shape PnC are illustrated in Figure 2a. The desired design of PnC achieves a complete bandgap of 175MHz in the frequencies range between 105–280MHz with (w) of 1μm and 135MHz in frequencies range between 125–275MHz with (w) of 2μm.
Preprints 77654 g002
Figure 2. Illustration of: (a) the first 3rd shapes of eigenmode frequencies in the band structures for Reem-PnC, (b) band structure through (Γ-X-M-Г) direction of the IBZ of Reem-PnC and (c) transmission of S21 parameters of an array of Reem-PnC unit cells.
Figure 2. Illustration of: (a) the first 3rd shapes of eigenmode frequencies in the band structures for Reem-PnC, (b) band structure through (Γ-X-M-Г) direction of the IBZ of Reem-PnC and (c) transmission of S21 parameters of an array of Reem-PnC unit cells.
Preprints 77654 g002
Reem phononic crystal generates a wide bandgap from 105 MHz to 280 MHz the ratio between gap-mid gap is determined by the equation [25]:.
B a n d g a p = f t o p − f b o t f t o p + f b o t 2
where fbot and ftop represent the open and close frequencies of the bandgap. A wide acoustic bandgap is obtained with BG of 90% from Reem-PnC dimensions as mentioned above with a connector of w=1μm, changing connector width to 2μm achieves a decrease in bandgap BG of 75% as shown in Figure 2c. The filling fraction of the Reem-PnC which represents the area of PnC to the area of the lattice is equal to 0.515 and it is calculated using the equation [25]:
f i l l i n g f r a c t i o n = a r e a   o f   P n C a r e a   o f   l a t t i c e

3. Transmission characteristics of Reem-PnC

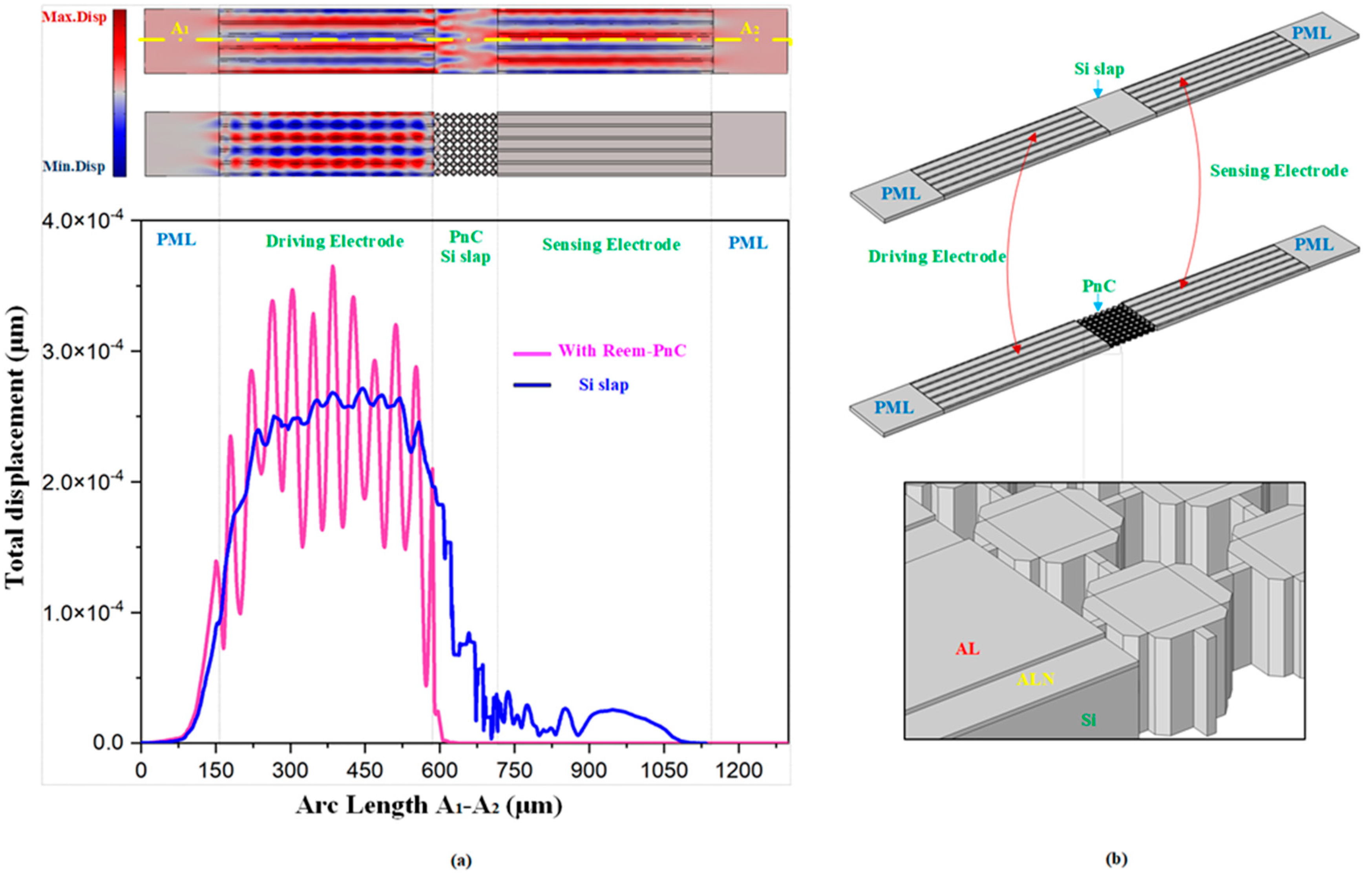
To prove the formation of the acoustic bandgap by Reem-PnC structure, the transmission characteristic is analyzed by using acoustic delay lines. As can be seen from Figure 3b, the Reem PnC plate and silicon plate line (two different transmission mediums among sense and drive electrodes) are applied to realize the transmission characteristics of the desired PnC The end of each delay line boundary in the x-direction is perfectly matched to effectively decrease the reflected wave interface. The drive electrodes are excited by 0.01-watt power and sense electrodes are terminated with set to 0.0-watt. The transmission (S21) is calculated by using the following relation [28]:
S 21 d B = 10 l o g 10 ( P o u t P i n )
where Pin and Pout are the input and output power transferred to the Reem-PnC line and solid silicon line respectively. S21 represents the transmission power coefficient between the input and output ports. Clearly from Figure 3b, the S21 transmission spectrum with an array of Reem-PnC proofs the proposed design successfully forms an acoustic bandgap. The finite element simulation results illustrate the wave is strongly attenuated in the transmission spectra at the beginning of the Reem-PnC line and continues to zero, compared to the silicon plate as shown in Figure 3a. Reem PnC satisfies there is a strong prohibition of propagation of acoustic waves.
Table 2. Comparison between various PnC shapes in simulated acoustic bandgaps with a resonance frequency in a close range.
Table 2. Comparison between various PnC shapes in simulated acoustic bandgaps with a resonance frequency in a close range.
Preprints 77654 i002

4. Resonator design

The resonator constructions can be realized as a mass-spring-damper system. Always, natural systems have energy dissipation mechanisms. This mechanism can be characterized simply as a damper. The union of the mass-spring-damper system consists the basic model for the resonator. Clearly from Figure 4b Newton’s second law of motion, realizes the linkage between the motions of mass and input force, which generally can be expressed by [1]:
m e q ∂ 2 x ∂ t 2 + c e q ∂ x ∂ t + k e q x = F
where meq represents equivalent mass, F represents applied force, keq represents equivalent stiffness, and ceq is the equivalent total losses. The relation between the input and output of the system can be expressed as [1]:
H s = X ( s ) F ( s ) = 1 m e q 2 + c e q s + k e q = 1 k e q ω n 2 s 2 + ω n Q − 1 S + ω n 2
where (s) is defined as complex frequency, Q is defined as body quality factor, and ω n defined as the natural frequency. The resonant frequency for systems of second order is given by [24]:
ω n = 2 π f n = k e q m e q
The expression which links between natural frequency ωn and the resonance frequency ωr of the system of second order is expressed by [1]:
ω r = ω n 1 − 1 2 Q 2
It clears from this relation that for high Q, like MEMS resonators, the natural frequency equals resonance frequency (i.e. ωr ≈ ωn). By applying a single frequency analysis, the resonance frequency of the MEMS resonator can be extracted from the displacement curve in the frequency response by using the general formula [21]:
Q = f r ∆ f ( − 3 d B )
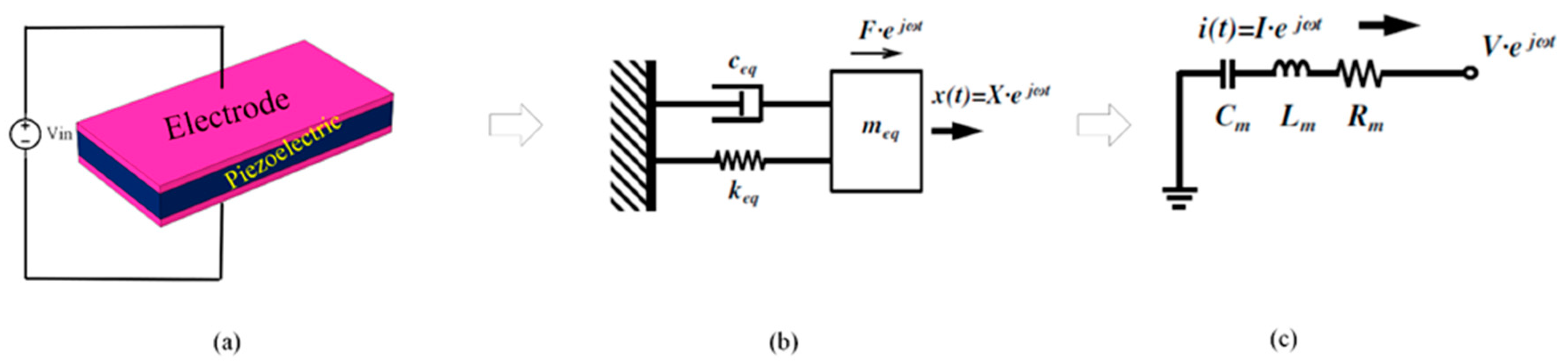
w h e r e ∆ f ( − 3 d B ) is defined as -3dB bandwidth between the resonant frequency in the frequency response curve. In all cases, the resonator is expressed as electric circuits with series R, L and C. Figure 4b,c show an equivalent mechanical and electrical model for a MEMS resonator. The input voltage represents the input force, the current represents velocity, the damping loss is represented by Rm (motional resistance), the Cm (motional capacitance) is represented by the inverse of stiffness, and the mass is represented by motional inductance Lm. The relation among Rm, Cm, Qu (unloaded quality factor), and insertion loss IL of the resonator is given by [29]:
R m = 1 R e l ( Y 11 ) , R m = 1 2 π f r C m Q u
where Y11 is the admittance curve of the resonator.
Preprints 77654 g004
Figure 4. (a) illustration of piezoelectric excitation in MEMS resonator (b) equivalent mechanical system of the resonator (c) equivalent electrical system of the resonator.
Figure 4. (a) illustration of piezoelectric excitation in MEMS resonator (b) equivalent mechanical system of the resonator (c) equivalent electrical system of the resonator.
Preprints 77654 g004
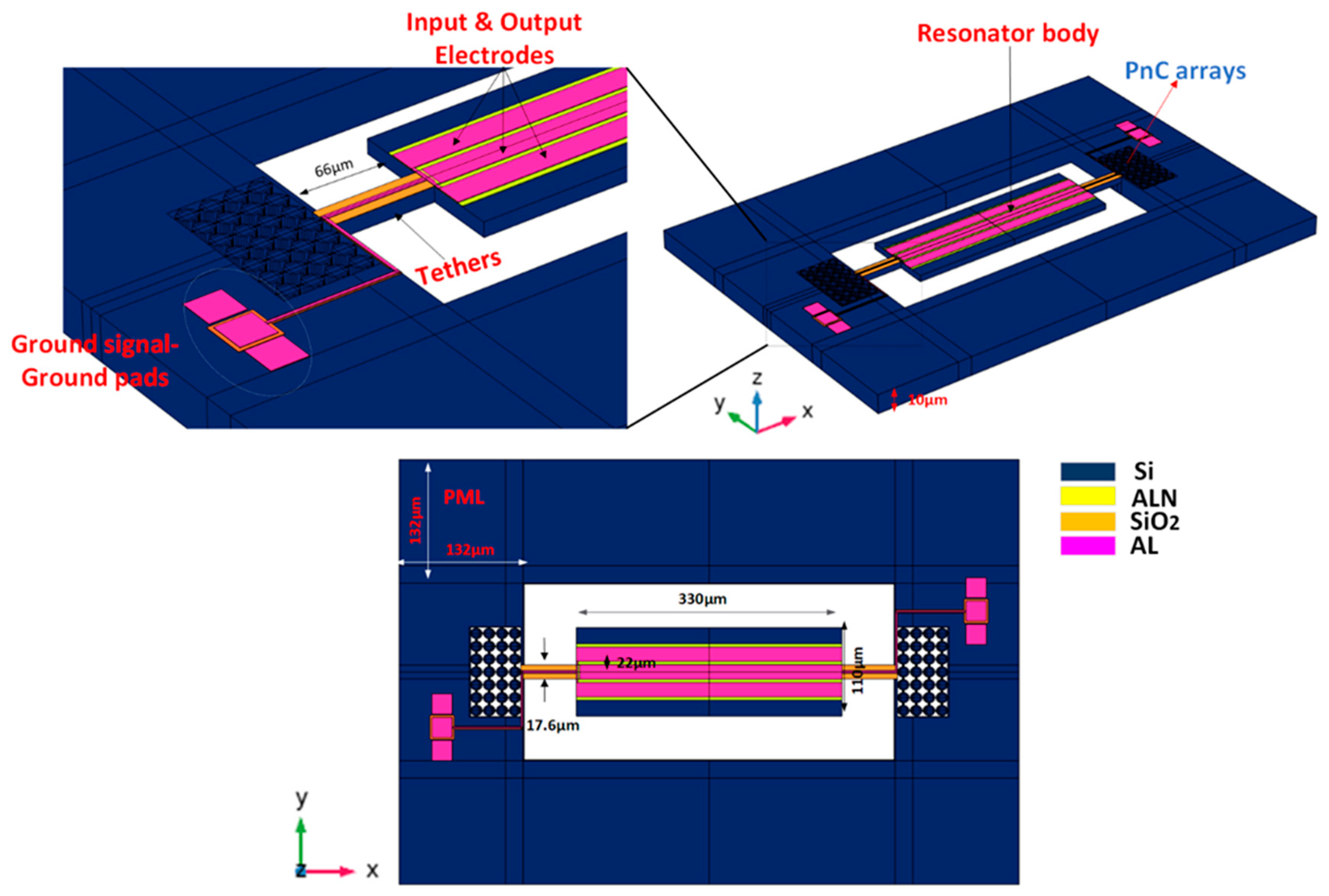
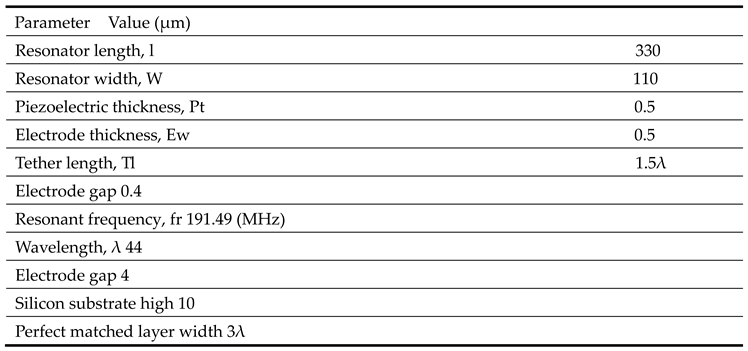
A 5th-order piezoelectric on silicon MEMS resonator was implemented, simulated, and analyzed using COMSOL Multiphysics, as demonstrated in Figure 5. A thin film of the ALN layer is bonded on a silicon substrate. The Al electrode positioned on top of piezoelectric material with a depth of 0.5μm excites vibration on the piezoelectric resonator with the application of 1 V, while the gap between the two electrodes is set to be 0.4μm. The dimensions of the resonator are 110μm width and 330μm length respectively. The wavelength of the resonator λ is equal to 44μm. The tether length and width of the desired resonator are set to be 1.5λ and 17.6μm. A Reem-PnC consists of two cross blocks perpendicular to each other with width and length of 12μm,8μm respectively, chamfering radius R at the edges of 1μm and lattice constant a=16μm. The PnC arrays are positioned externally in anchors to generate bandgap coincide with resonant frequency to prohibit the acoustic wave propagation to the device substrate and cause a loss in energy. The resonant (fr) of the resonator body can be obtained from [16]:
f r = 1 λ E ρ
where λ defined as wavelength, E is defined as Young's modulus in (110) axes, and ρ defined as the density of single crystal silicon. The fr calculated from eq (16) is around 191 MHz in the desired design λ=44μm. The resonator design parameters are fitted in Table 3.

5. Techniques for anchor loss enhancement in the resonator

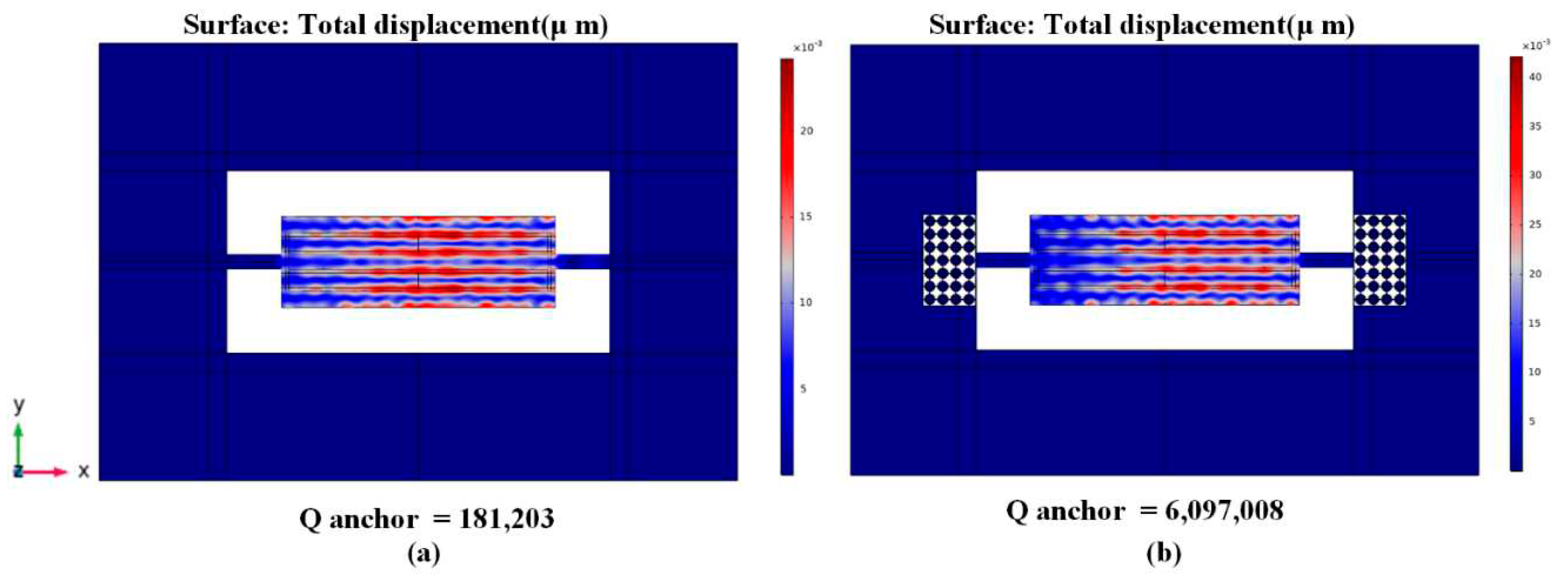
A 2-dimensional array of Reem-PnC is deployed in the anchoring boundaries of the resonator anchors to enhance the anchor quality factor and then as a result enhance the total quality factor (Qtot). From Figure 6 the Qanchor of the TPoS MEMS resonator can be obtained generally from the resonance frequency divided by the -3dB of bandwidth of the resonance maximum point in displacement profile at the frequency response as [16]:
Q a n c h o r = f r ∆ f ( − 3 d B )
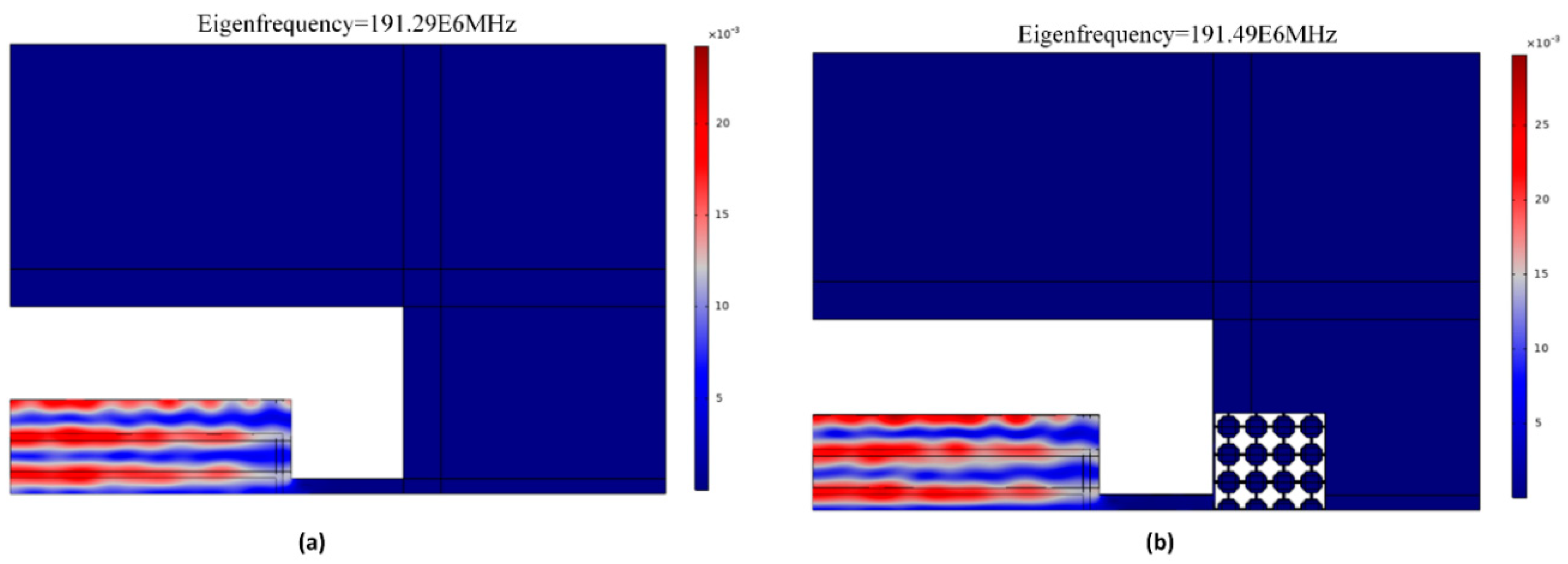
where fr is defined as resonance frequency, the resonator mode shape with and without PnC and associated anchor quality factor are shown in Figure 6.

6. Calculation of resonator performance

Simulated S21 parameters and admittance Y11 curves of a desired resonator with and without Reem-PnC were calculated by the FEA simulation at the frequency domain to obtain the insertion loss, loaded Q, unloaded Q, the figure of merit, effective electromechanical coupling coefficient (k2eff) and motional resistance Rm. The relationships of the Q, Qu, FoM, and k2eff are given by [31,32,33,34,35].
Q l = f r ∆ f ( − 3 d B ) , Q u = Q l 1 − 10 ( − I L 20 ) , k e f f 2 = π 2 8 ( f s 2 − f p 2 f p 2 ) , F o M = Q u * k e f f 2

7. Discussion

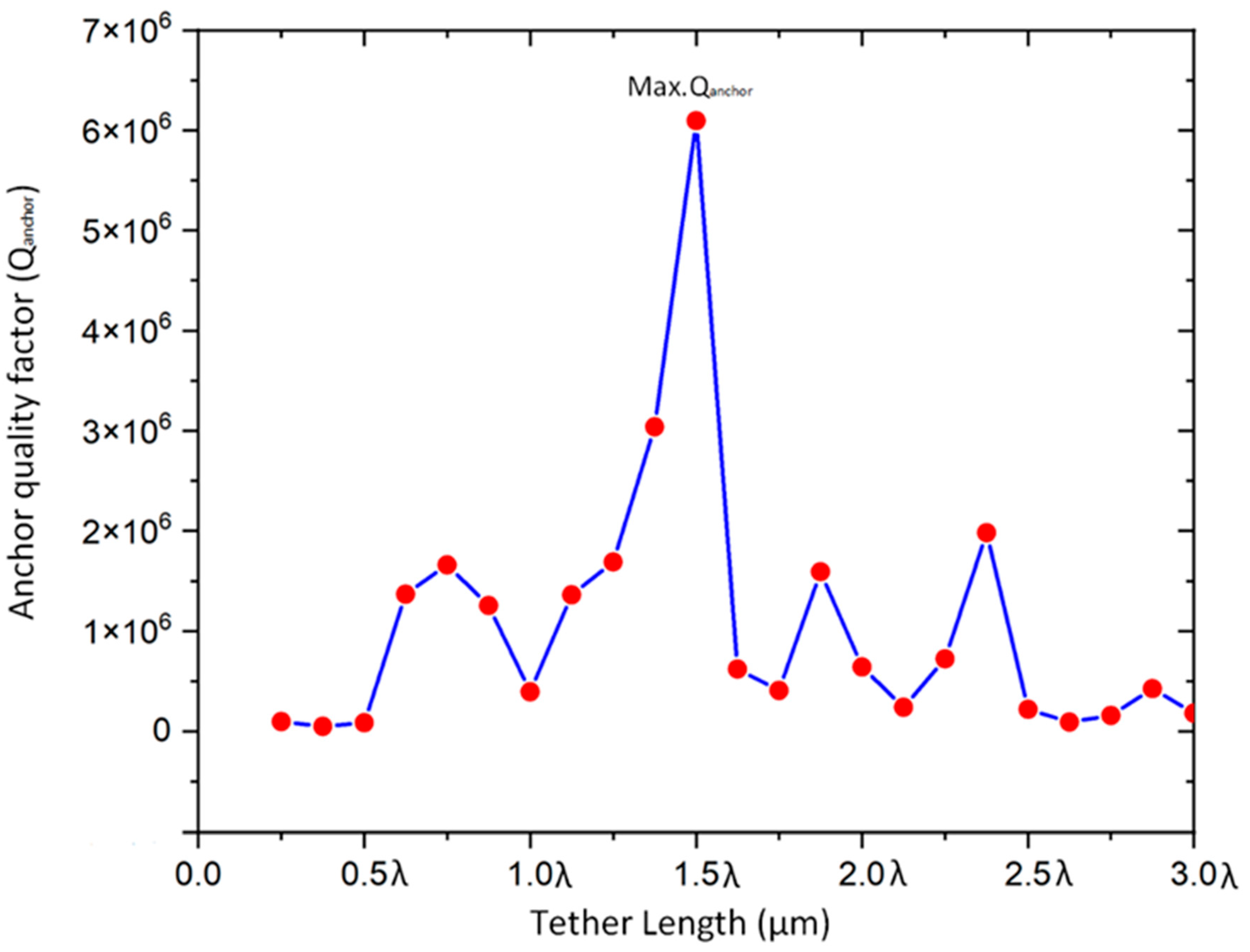
Figure 7 presents different values of anchor quality factor for multiple longitudinal wavelength (λ), the minimum value of the anchor quality factor is at the exists at the tether length equal to integer multiples of wavelength (i.e. 1*λ, 2*λ, 3*λ). The maximum points of Q are obtained at the integral multiples of quarter of the wavelength. The maximum Qanchor appears at 1.5λ.
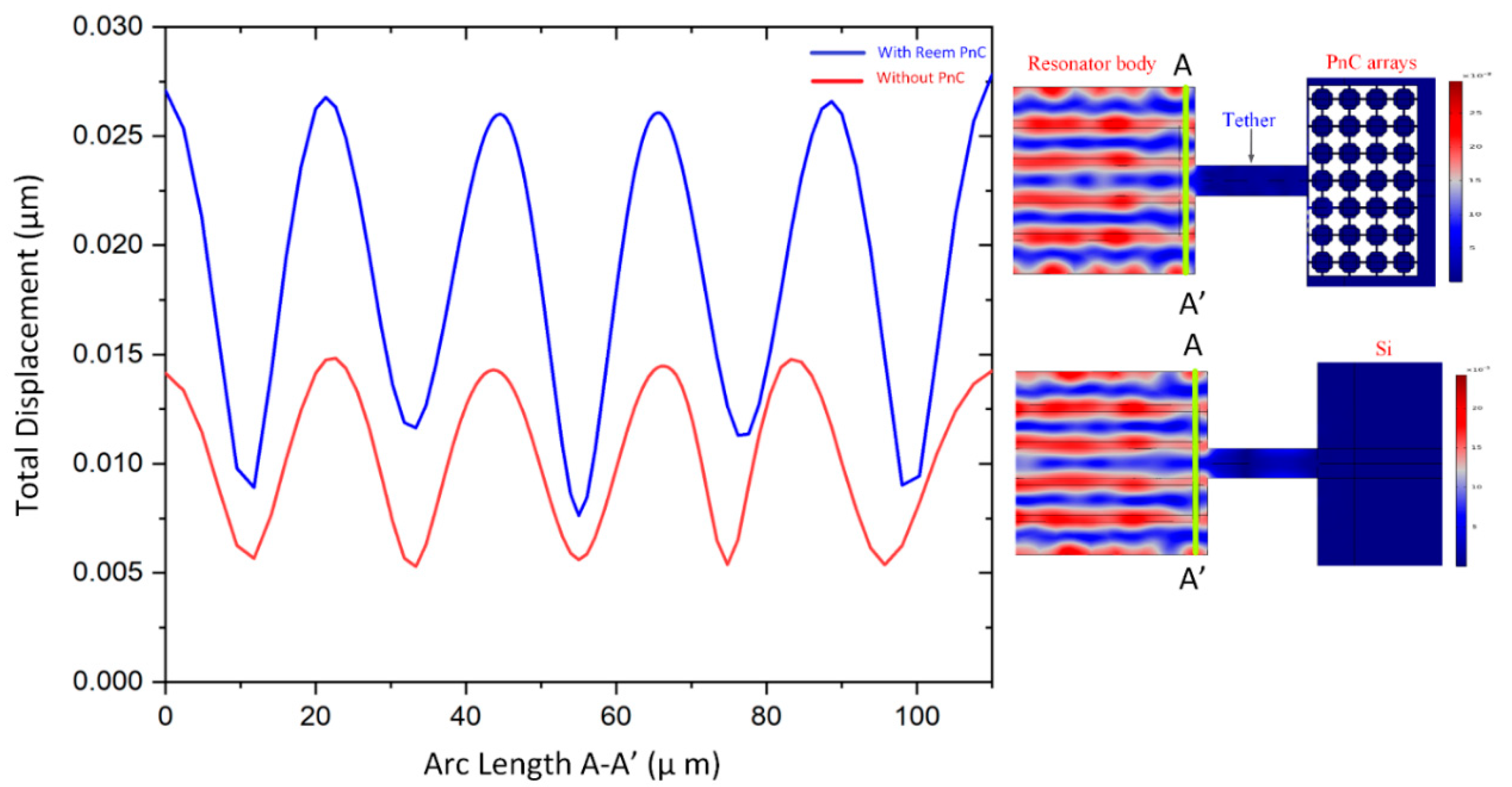
Figure 8. Illustrates the displacement plot across the line A-A′, which verifies the proposed resonator with Reem-PnC offers high enhancement in the total displacement of the resonator in comparison with resonator without PnC. This proof the amount of stored energy in the resonator with Reem-PnC is larger than the resonator without PnC.
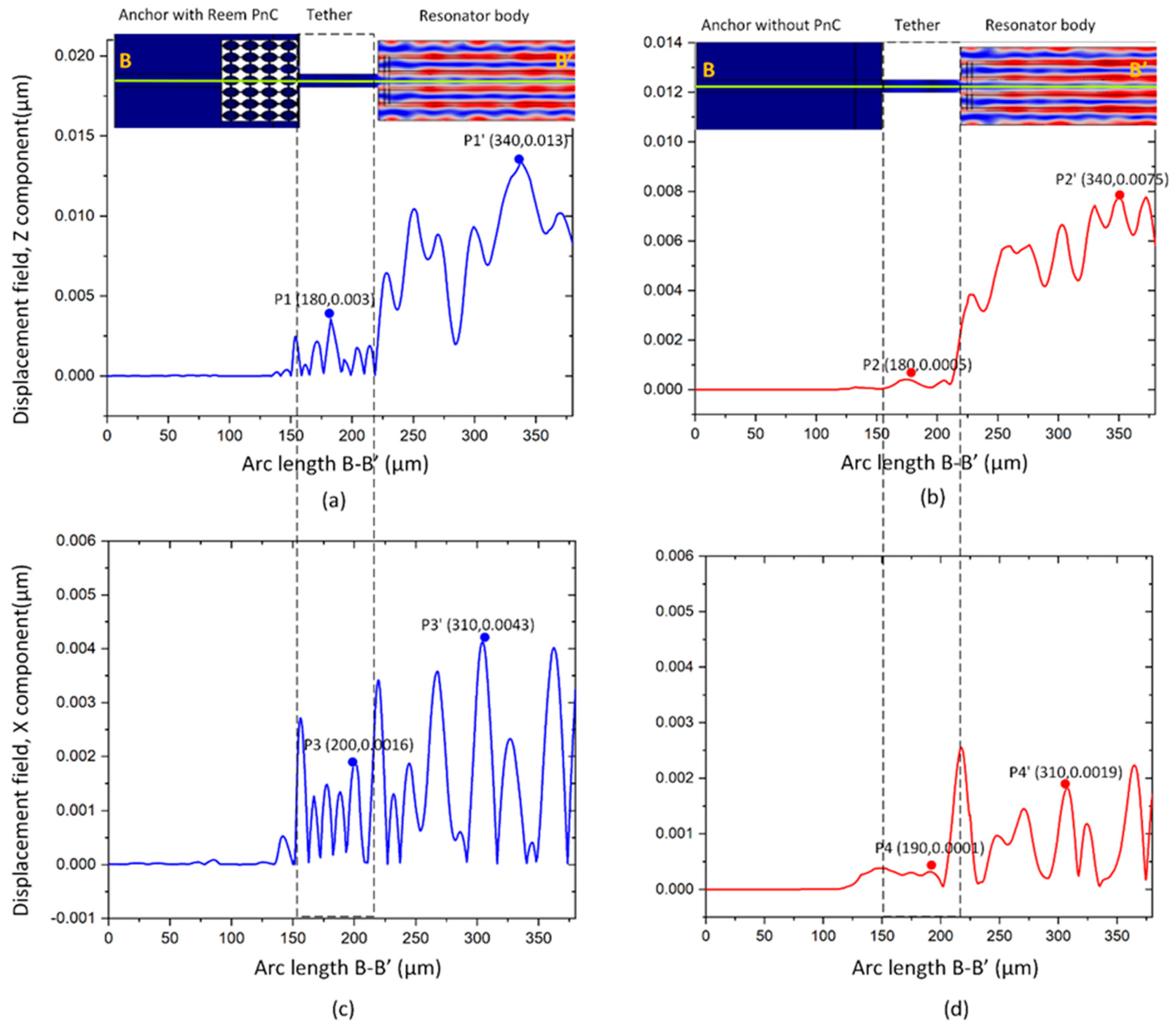
Figure 9a,b illustrate the absolute value of z components displacement field along the B–B′ line in the two resonators with and without Reem-PnC. It is clear from the plot that the peak point P1 displacement in the tether is higher than the point peak P2, continuously the displacement in the resonator is enhanced in comparison between points P′1 and P′2. Figure 9c,d illustrate the absolute value of the x components displacement field along the B–B′ line. It is clear from the plots that the displacement of the peak point P3 in the tethers is greater than the displacement in point P4, also x displacement component in the resonator is enhanced in comparison between points P′3, and P′4. The displacement component x and z in the resonator with Reem-PnC is greater than the resonator without PnC.
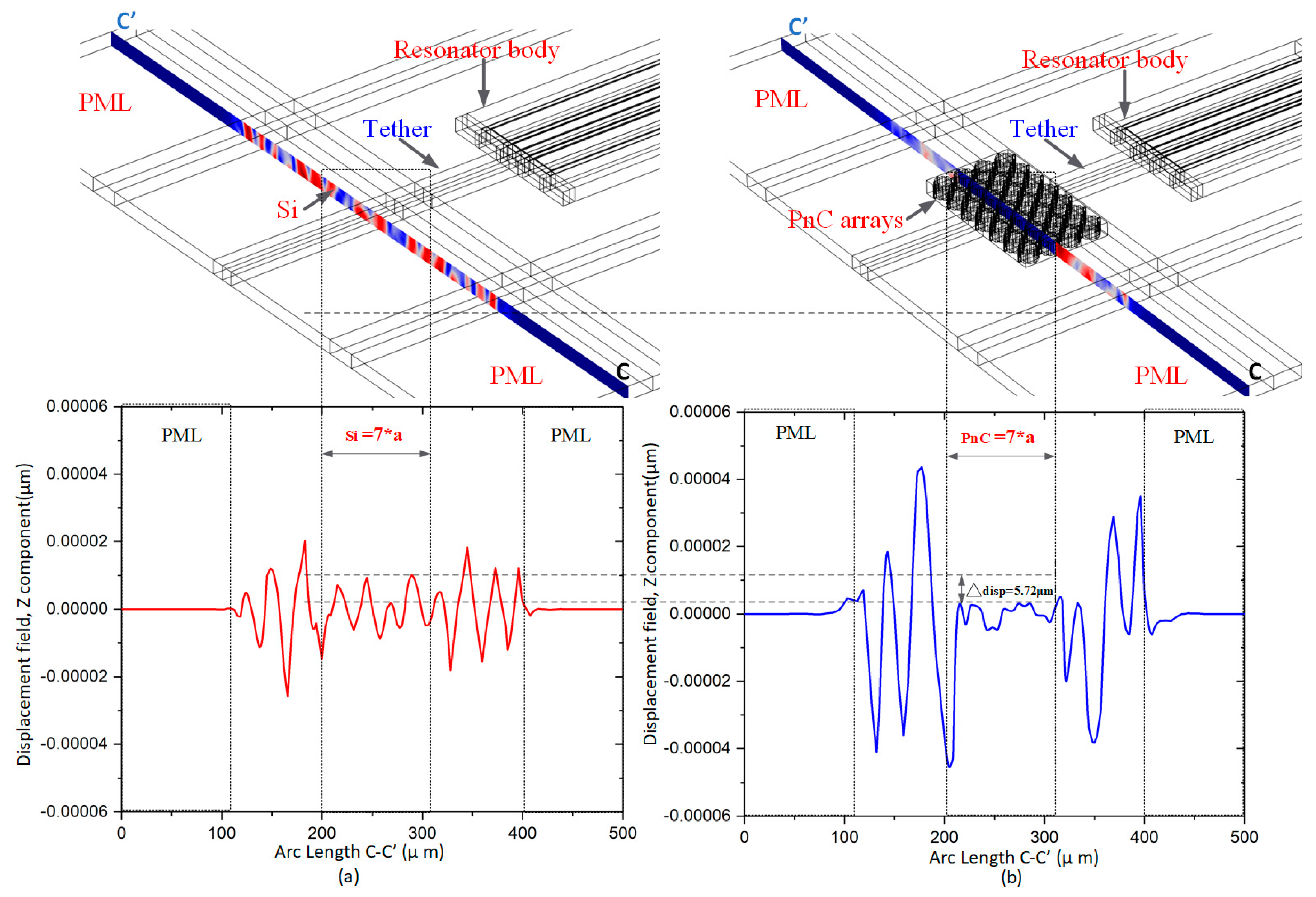
It can be clearly shown that there is no significant displacement in the PnC array in the anchor boundary of the resonator with Reem-PnC as shown in cutting plane C-C′. Also, the displacement profile in Figure 10a,b shows there is a displacement increase on the anchoring boundaries of the resonator without PnC (i.e. Δdisp=5.72μm), proofs there is energy loss due to energy transverse from the resonant body to anchors boundary through the tethers.
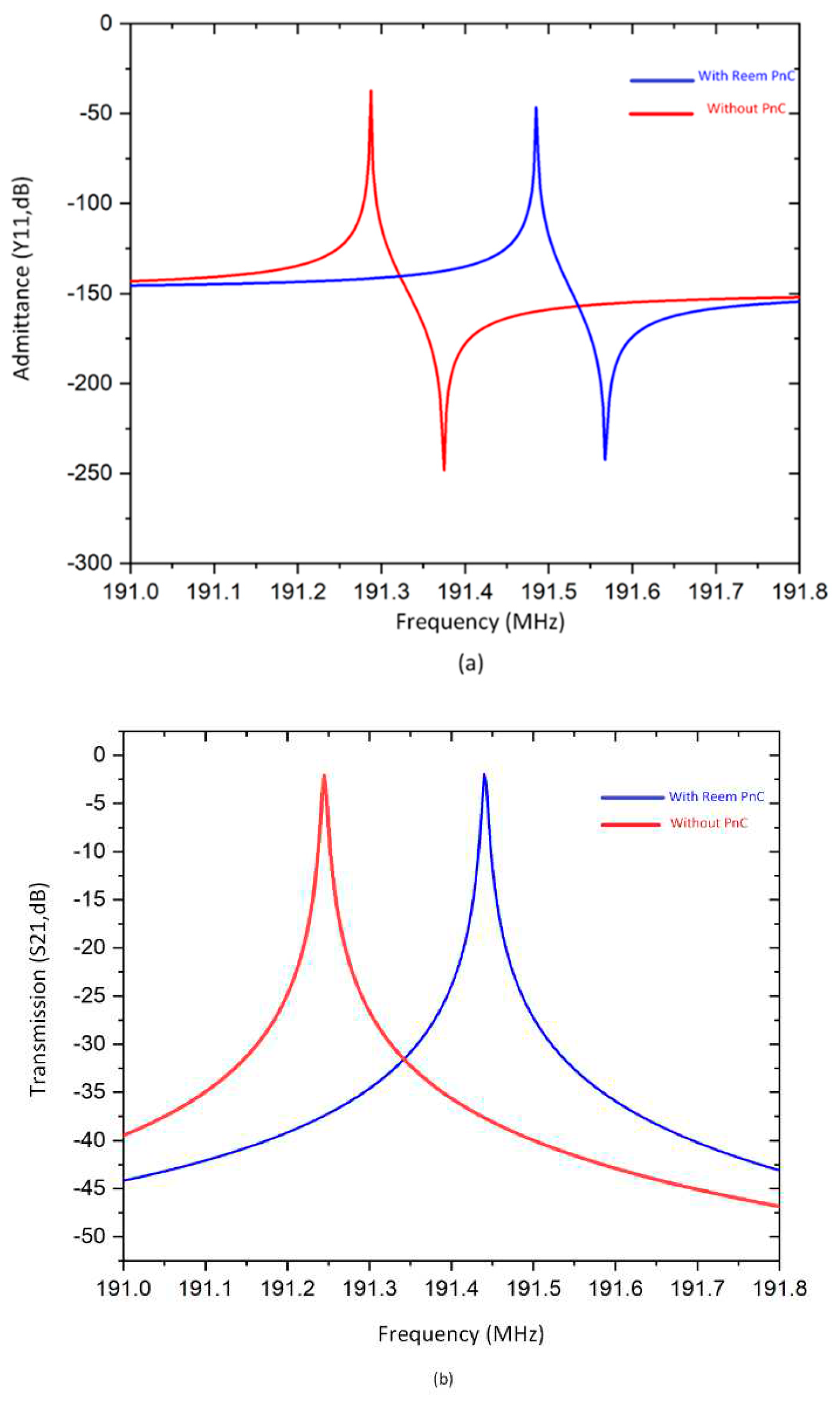
As it is clearly seen from Table 4, the simulated Qanchor and Qu of the designed resonator with Reem-shape PnC are enhanced by 13.5 folds and 1.2 folds respectively in comparison with the resonator without PnC. Remaining parameters of the resonator like insertion loss (IL) and motional resistance Rm were obtained from the transmission magnitudes (S21, dB) and admittance (Y11, dB) at the quarter of the resonator to reduce the time of the calculation as shown in Figure 11. The plots of the parameters illustrated in Figure 12a,b, respectively, these parameters clearly show enhancement due to the proposed design. While keff remains unchanged.

8. Conclusion

This work verifies Reem-PnC is effective in anchor loss reduction resulting in quality factor enhancement of thin-film-piezoelectric-on-silicon MEMS resonators. The proposed Reem-PnC lends itself to prohibit acoustic wave propagation to the supporting structure by providing a wide bandgap. Moreover, tether length and width are optimized to optimum dimensions to achieve a high anchor quality factor. With the combined effect of the two approaches, a high-quality factor is achieved. In this regard, anchor quality factor of about 6,000,000 and unloaded quality factor (Qu) of about 160,000 are obtained from the resonator with Reem-PnC which accounts to 33.3 folds and 1.2 folds enhancement in comparison with the resonator without PnC.

Author Contributions

Conceptualization, M.A. and J.B.; Formal analysis, M.A.; Funding acquisition, M.A., J.B., and K.-y.H.; Investigation, M.A. and J.B.; Methodology, M.A. and J.B.; Project administration, T.B.W., J.B., and K.-y.H.; Resources, T.B.W., J.B., and K.-y.H.; Software, M.A.; Supervision. J.B. and K.-y.H.; Validation, J.B., and K.-y.H.; Visualization, M.A.; Writing—original draft, M.A.; Writing—review and editing, J.B. and K.-y.H. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported in part by the research project under grant A1098531023601318 and in part by the grant from the National Natural Science Foundation of China and the China Academy of Engineering Physics under grant U1430102.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Abdolvand, R., Bahreyni, B., Lee, J.E.Y. and Nabki, F., 2016. Micromachined resonators: A review. Micromachines, 7(9), p.160. [CrossRef]
  2. Bao, F.H., Wu, X.Q., Zhou, X., Wu, Q.D., Zhang, X.S. and Bao, J.F., 2019. Spider web-like phononic crystals for piezoelectric MEMS resonators to reduce acoustic energy dissipation. Micromachines, 10(9), p.626. [CrossRef]. [CrossRef]
  3. Ho, G.K., Abdolvand, R., Sivapurapu, A., Humad, S. and Ayazi, F., 2008. Piezoelectric-on-silicon lateral bulk acoustic wave micromechanical resonators. Journal of microelectromechanical systems, 17(2), pp.512-520. [CrossRef]
  4. Bao, F.H., Bao, J.F., Lee, J.E.Y., Bao, L.L., Khan, M.A., Zhou, X., Wu, Q.D., Zhang, T. and Zhang, X.S., 2019. Quality factor improvement of piezoelectric MEMS resonator by the conjunction of frame structure and phononic crystals. Sensors and Actuators A: Physical, 297, p.111541. [CrossRef]
  5. Bao, F.H., Awad, M., Li, X.Y., Wu, Z.H., Bao, J.F., Zhang, X.S. and Bao, L.L., 2018, May. Suspended frame structure with phononic crystals for anchor loss reduction of MEMS resonator. In 2018 IEEE International Frequency Control Symposium (IFCS) (pp. 1-4). IEEE. [CrossRef]
  6. Zhu, H. and Lee, J.E.Y., 2015, January. AlN piezoelectric on silicon MEMS resonator with boosted Q using planar patterned phononic crystals on anchors. In 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS) (pp. 797-800). IEEE. [CrossRef]
  7. Ha, T.D. and Bao, J., 2016. Reducing anchor loss in thin-film aluminum nitride-on-diamond contour mode MEMS resonators with support tethers based on phononic crystal strip and reflector. Microsystem Technologies, 22(4), pp.791-800. [CrossRef]
  8. Van Beek, J.T.M. and Puers, R., 2011. A review of MEMS oscillators for frequency reference and timing applications. Journal of Micromechanics and Microengineering, 22(1), p.013001. [CrossRef]
  9. Jimbo, Y. and Itao, K., 1968. Energy loss of a cantilever vibrator. J Horological Institute of Japan, 47, pp.1-15.
  10. Hao, Z., Erbil, A. and Ayazi, F., 2003. An analytical model for support loss in micromachined beam resonators with in-plane flexural vibrations. Sensors and Actuators A: Physical, 109(1-2), pp.156-164. [CrossRef]
  11. 11. Nowick, A.S. and Berry, B.S., 1972. Characterization of Anelastic Behavior. Anelastic Relaxation in Crystalline Solids; Academic Press: New York, NY, USA.
  12. Jonscher, A.K., 1999. Dielectric relaxation in solids. Journal of Physics D: Applied Physics, 32(14), p. R57.
  13. 13. Seoánez, C., Guinea, F. and Neto, A.C., 2008. Surface dissipation in nanoelectromechanical systems: Unified description with the standard tunneling model and effects of metallic electrodes. Physical Review B, 77(12), p.125107. [CrossRef]
  14. Harrington, B.P. and Abdolvand, R., 2009, June. Q-enhancement through minimization of acoustic energy radiation in micromachined lateral-mode resonators. In TRANSDUCERS 2009-2009 International Solid-State Sensors, Actuators and Microsystems Conference (pp. 700-703). IEEE. [CrossRef]
  15. Harrington, B.P. and Abdolvand, R., 2011. In-plane acoustic reflectors for reducing effective anchor loss in lateral–extensional MEMS resonators. Journal of Micromechanics and Microengineering, 21(8), p.085021. [CrossRef]
  16. Liu, J., Workie, T.B., Wu, Z., Tang, P., Bao, J.F. and Hashimoto, K.Y., 2021, May. Acoustic Reflectors for Anchor Loss Reduction of Thin Film Piezoelectric on Substrate Resonators. In 2021 IEEE MTT-S International Wireless Symposium (IWS) (pp. 1-3). IEEE. [CrossRef]
  17. Workie, T.B., Wu, Z., Tang, P., Bao, J. and Hashimoto, K.Y., 2022. Figure of Merit Enhancement of Laterally Vibrating RF-MEMS Resonators via Energy-Preserving Addendum Frame. Micromachines, 13(1), p.105. [CrossRef]
  18. Bao, J., Workie, T.B. and Hashimoto, K.Y., 2022, November. Performance improvement of RF acoustic wave resonators using phononic crystals. In 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP) (pp. 1-2). IEEE.
  19. Workie, T.B., Liu, J., Wu, Z., Tang, P., Bao, J.F. and Hashimoto, K.Y., 2021, May. Swastika Hole shaped Phononic Crystal for Quality enhancement of Contour Mode Resonators. In 2021 IEEE MTT-S International Wireless Symposium (IWS) (pp. 1-3). IEEE. [CrossRef]
  20. Chen, P.J., Workie, T.B., Feng, J.J., Bao, J.F. and Hashimoto, K.Y., 2022, October. Four-Leaf Clover Shaped Phononic Crystals for Quality Factor Improvement of AlN Contour Mode Resonator. In 2022 IEEE International Ultrasonics Symposium (IUS) (pp. 1-3). IEEE. [CrossRef]
  21. Awad, M., Bao, F., Bao, J. and Zhang, X., 2018, May. Cross-shaped PnC for anchor loss reduction of thin-film ALN-on-silicon high frequency MEMS resonator. In 2018 IEEE MTT-S International Wireless Symposium (IWS) (pp. 1-3). IEEE. [CrossRef]. [CrossRef]
  22. Siddiqi, M.W.U. and Lee, J.E.Y., 2018. Wide acoustic bandgap solid disk-shaped phononic crystal anchoring boundaries for enhancing quality factor in AlN-on-Si MEMS resonators. Micromachines, 9(8), p.413. [CrossRef]. [CrossRef]
  23. Deymier, P.A. ed., 2013. Acoustic metamaterials and phononic crystals (Vol. 173). Springer Science & Business Media.
  24. Workie, T.B., Wu, T., Bao, J.F. and Hashimoto, K.Y., 2021. Design for high-quality factor of piezoelectric-on-silicon MEMS resonators using resonant plate shape and phononic crystals. Japanese Journal of Applied Physics, 60(SD), p. SDDA03. [CrossRef]
  25. Tu, C. and Lee, J.Y., 2017. Enhancing quality factor by etch holes in piezoelectric-on-silicon lateral mode resonators. Sensors and Actuators A: Physical, 259, pp.144-151. [CrossRef]
  26. Zou, J., Lin, C.M., Chen, Y.Y. and Pisano, A.P., 2014. Theoretical study of thermally stable SiO2/AlN/SiO2 Lamb wave resonators at high temperatures. Journal of Applied Physics, 115(9), p.094510.
  27. Binci, L., Tu, C., Zhu, H. and Lee, J.Y., 2016. Planar ring-shaped phononic crystal anchoring boundaries for enhancing the quality factor of Lamb mode resonators. Applied Physics Letters, 109(20), p.203501. [CrossRef]
  28. Lozzi, A., De Pastina, A., Yen, E.T.T. and Villanueva, L.G., 2019. Engineered acoustic mismatch for anchor loss control in contour mode resonators. Applied Physics Letters, 114(10), p.103502. [CrossRef]
  29. Bao, F.H., Bao, L.L., Li, X.Y., Khan, M.A., Wu, H.Y., Qin, F., Zhang, T., Zhang, Y., Bao, J.F. and Zhang, X.S., 2018. Multi-stage phononic crystal structure for anchor-loss reduction of thin-film piezoelectric-on-silicon microelectromechanical-system resonator. Applied Physics Express, 11(6), p.067201. [CrossRef]
  30. Bao, F.H., Bao, L.L., Zhang, X.S., Zhang, C., Li, X.Y., Qin, F., Zhang, T., Zhang, Y., Wu, Z.H. and Bao, J.F., 2018. Frame structure for thin-film piezoelectric-on-silicon resonator to greatly enhance quality factor and suppress spurious modes. Sensors and Actuators A: Physical, 274, pp.101-108. [CrossRef]. [CrossRef]
  31. Jiang, S., Hu, H. and Laude, V., 2018. Low-frequency band gap in cross-like holey phononic crystal strip. Journal of Physics D: Applied Physics, 51(4), p.045601. [CrossRef]. [CrossRef]
  32. Bao, F.H., Wu, X.Q., Zhou, X., Wu, Q.D., Zhang, X.S. and Bao, J.F., 2019. Spider web-like phononic crystals for piezoelectric MEMS resonators to reduce acoustic energy dissipation. Micromachines, 10(9), p.626. [CrossRef]
  33. Khelif, A., Aoubiza, B., Mohammadi, S., Adibi, A. and Laude, V., 2006. Complete band gaps in two-dimensional phononic crystal slabs. Physical Review E, 74(4), p.046610. [CrossRef]
  34. Ho, G.K., Abdolvand, R., Sivapurapu, A., Humad, S. and Ayazi, F., 2008. Piezoelectric-on-silicon lateral bulk acoustic wave micromechanical resonators. Journal of microelectromechanical systems, 17(2), pp.512-520. [CrossRef]
  35. Pennec, Y., Vasseur, J.O., Djafari-Rouhani, B., Dobrzyński, L. and Deymier, P.A., 2010. Two-dimensional phononic crystals: Examples and applications. Surface Science Reports, 65(8), pp.229-291. [CrossRef]
Preprints 77654 g001
Figure 1. (a) Reem-PnC with the first irreducible Brillouin zone (IBZ) (b) 3-D view illustration of the Reem-PnC.
Figure 1. (a) Reem-PnC with the first irreducible Brillouin zone (IBZ) (b) 3-D view illustration of the Reem-PnC.
Preprints 77654 g001
Preprints 77654 g003
Figure 3. (a) Displacement realization of the transmission medium with solid Silicon plate delay line and Reem-PnC array and resonator displacement at 191MHz on the A1–A2 line (b) 3D illustration of silicon plate and Reem-PnC.
Figure 3. (a) Displacement realization of the transmission medium with solid Silicon plate delay line and Reem-PnC array and resonator displacement at 191MHz on the A1–A2 line (b) 3D illustration of silicon plate and Reem-PnC.
Preprints 77654 g003
Preprints 77654 g005
Figure 5. Three-dimensional resonator designed body with arrays of Reem-PnC.
Figure 5. Three-dimensional resonator designed body with arrays of Reem-PnC.
Preprints 77654 g005
Preprints 77654 g006
Figure 6. 5th-order eigen mode shape and the calculated Qanchor (a) without PnC and (b) with Reem-Shape PnC.
Figure 6. 5th-order eigen mode shape and the calculated Qanchor (a) without PnC and (b) with Reem-Shape PnC.
Preprints 77654 g006
Preprints 77654 g007
Figure 7. Illustration of the relation between different quality factor values and tether length as a function of wavelength.
Figure 7. Illustration of the relation between different quality factor values and tether length as a function of wavelength.
Preprints 77654 g007
Preprints 77654 g008
Figure 8. Illustration of: A–A′ total displacement (μm) of the resonator with and without Reem-shape PnC.
Figure 8. Illustration of: A–A′ total displacement (μm) of the resonator with and without Reem-shape PnC.
Preprints 77654 g008
Preprints 77654 g009
Figure 9. Illustration of: B–B′ displacement (μm) z component of the resonator (a) with and (b) without Reem-shape PnC, B–B′ displacement (μm) x component of the resonator (c) with and (d) without Reem-shape PnC.
Figure 9. Illustration of: B–B′ displacement (μm) z component of the resonator (a) with and (b) without Reem-shape PnC, B–B′ displacement (μm) x component of the resonator (c) with and (d) without Reem-shape PnC.
Preprints 77654 g009
Preprints 77654 g010
Figure 10. Illustration of: B–B′ displacement (μm) z component of the resonator (a) with and (b) without Reem-shape PnC, B–B′ displacement (μm) x component of the resonator (c) with and (d) without Reem-shape PnC.
Figure 10. Illustration of: B–B′ displacement (μm) z component of the resonator (a) with and (b) without Reem-shape PnC, B–B′ displacement (μm) x component of the resonator (c) with and (d) without Reem-shape PnC.
Preprints 77654 g010
Preprints 77654 g011
Figure 11. The quarter of 5th order resonator (a) without PnC and (b) with Reem-PnC.
Figure 11. The quarter of 5th order resonator (a) without PnC and (b) with Reem-PnC.
Preprints 77654 g011
Preprints 77654 g012
Figure 12. (a) and (b) The admittance Y11 and transmission parameter of resonator S21 with and without Reem-PnC.
Figure 12. (a) and (b) The admittance Y11 and transmission parameter of resonator S21 with and without Reem-PnC.
Preprints 77654 g012
Table 1. Elastic constants of single crystal silicon.
Table 1. Elastic constants of single crystal silicon.
Preprints 77654 i001
Table 3. Comparison between various PnC shapes in simulated acoustic bandgaps with a resonance frequency in a close range.
Table 3. Comparison between various PnC shapes in simulated acoustic bandgaps with a resonance frequency in a close range.
Preprints 77654 i003
Table 4. Performance of the resonators with Reem-PnC and without PnC.
Table 4. Performance of the resonators with Reem-PnC and without PnC.
Preprints 77654 i004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated