Prerpints.org logo
Preprint
Article

Alternate Admissibility LMI Criteria for Descriptor Fractional Order Systems with 0 < α < 2

Altmetrics

Downloads

94

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 June 2023

Posted:

27 June 2023

You are already at the latest version

Alerts
Abstract
The paper focuses on the admissibility problem of descriptor fractional-order systems (DFOSs). The alternate admissibility criteria are addressed for DFOSs with order in (0,2) which involve a non-strict linear matrix inequality (LMI) method and a strict LMI method, respectively. The forms of non-strict and strict LMIs are brand-new and distinguished with the existing literature, which fill the gaps of studies for admissibility. These approaches are available to the order in (0,2) without separating the order ranges into (0,1) and [1,2). In addition, a method involved least real decision variables in terms of strict LMIs is derived which is more convenient to process the practical solution. Three numerical examples are given to illustrate the validity of proposed results.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

Fractional calculus has a long period of development which has been broadly applied in different areas of engineering applications, such as systems theory [1], signals processing [2] and image fusion [3]. Recently, fractional-order systems (FOSs) have aroused extensive attention of scholars because more and more practical problems based on engineering requirements are well described by fractional calculus [4,5]. Many fundamental notions and crucial research achievements on integer order systems have been expanded to FOSs sucessfully, and huge researches fruits have been published in stability analysis [6] and sliding mode control [7,8]. Besides, the special characteristics of fractional-order are broadly applied in electrical systems [9], power systems [10], economic systems [11] and fuzzy systems [12,13].
Stability analysis is a fundamental issue for all control systems, certainly including FOSs. Since the stability region of FOSs is quite different from integer order systems, exploration on stability becomes more challenging. The experts have developed a lot of researches and a quantity of theories are obtained. In [14], based on the FOS stability region, the LMI stability conditions are first proposed for fractional order 0 < α < 1 and 1 < α < 2 , respectively. However, the criterion for 0 < α < 1 contains complex numbers which is difficult to solve. In [15], the stability of FOSs with order in ( 0 , 1 ) is studied and a method for the robust asymptotical stability with real matrices is proposed, but the result is inapplicable to the system eigenvalues on positive real part. In [16], the authors provide a unified LMI formulation to ensure the stability of FOSs for a given order in ( 0 , 2 ) without separating into ( 0 , 1 ) and [ 1 , 2 ) . Those criteria are necessary and sufficient conditions with least real decision variables of LMIs. In [17], the FOSs with arbitrary real order between 0 and 2 are considered and a method to fast and robustly estimate the fractional integrals and derivatives of positions is presented. Robust stability analysis of an interval fractional-order plant with an interval time delay is investigated by a general form of fractional-order controllers in [18]. For the discrete-time systems, the finite-dimensional feedback control of FOSs with additive state disturbance is addressed in [19] and the stability regions of FOSs with interval uncertainties are analyzed in [20]. In [21], by using a boundary layer technique without any global and unknown information, the robust adaptive fault-tolerant consensus control for nonlinear fractional-order multi-agent systems is addressed.
Descriptor systems (also called singular systems, generalized state-space systems, implicit systems) are a special class of systems with a wider range of applications than normal systems, which own many good performance [22,23,24]. With the emergence of FOSs, DFOSs have aroused great attention of scholars in different research directions. A great number of attainments on admissibility have been achieved because admissibility is one of the most important properties in DFOSs. For the fractional order in [ 1 , 2 ) , the new admissibility conditions of DFOSs expressed in a set of strict LMIs are given in [25,26], and H ∞ control problem have been solved by designing a state feedback control based on bounded real lemma in [27]. For the fractional order in ( 0 , 1 ) , the authors in [28] provide necessary and sufficient conditions for admissibility of DFOSs and an observer-based controller is proposed to guarantee the system admissibility. However, the LMIs in results involve complex matrices and complex numbers which cause difficulty in solving. In [29], the admissibility and robust stabilization of DFOSs with order in ( 0 , 1 ) are investigated, and an approach with strict LMIs with real matrices is presented. In [30], a different method for admissibility is reported for order in ( 0 , 1 ) and [ 1 , 2 ) respectively, and robust stabilization problem of DFOSs with uncertain derivative matrices is solved. Although there are many papers on admissibility, most of existing theorems divide order α into ( 0 , 1 ) and [ 1 , 2 ) to analysis admissibility respectively, as shown above. A unified form of admissibility for a given fractional order interval ( 0 , 2 ) is valuable which has been considered in few studies. In [31], a unified framework for admissibility and quadratic admissibility are provided in terms of LMIs, but it is not satisfied the condition of least real decision variables which can be improved.
Motivated by the above observations, we study the admissibility of DFOSs. The main contributions of this paper are summarized as follows:
(i) The alternate admissibility criteria with order in ( 0 , 2 ) are presented with non-strict LMIs and strict LMIs, respectively. They do not involve any complex variables and are able to deal with the eigenvalues of system matrix with positive real part. The formations in the criteria are new and different from the existing achievements.
(ii) The methods are applicable to the order interval ( 0 , 2 ) directly without separating the order ranges into ( 0 , 1 ) and [ 1 , 2 ) when discuss the admissibility of DFOSs.
(iii) A strict LMI approach with only one real decision variable is provided which is easy to simulate and obtain the feasible solution.
The paper is organized as follows. Section 2 presents some preliminaries which are applicable to the rest part. In Section 3, for the fractional order α in ( 0 , 2 ) , two different methods of admissibility for DFOSs are proposed with non-strict and strict LMI formulations, respectively. Three numerical examples are given in Section 4 and a brief conclusion is provided in Section 5.
Notations: R n × m denotes the set of all n × m real matrices. P < 0 ( P ≤ 0 , respectively,) means that P is negative definite (negative semi-definite, respectively). P T represents the transpose of matrix P. sym ( P ) and asym ( P ) denote the expressions of P + P T and P − P T , respectively. I n is the identity matrix of order n. ⊗ stands for the Kronecker product of two matrices. spec ( E , A ) is the spectrum of det ( s E − A ) = 0 . arg ( z ) denotes the argument of a complex number z. Γ ( · ) indicates Euler Gamma function. α ( α ) is the floor function (ceiling function, respectively) which denotes the nearest integer less (greater) than or equal to α . The symbol * represents the symmetric part of a matrix. The symbol ★ in a matrix denotes the part which is unrelated to the discussion. For convenience, let Θ = a − b b a , a = sin ( α π 2 ) , b = cos ( α π 2 ) in the sequel.

2. Problem Formulation and Preliminaries

Consider the following DFOS
E D α x ( t ) = A x ( t ) ,
where A ∈ R n × n is a constant matrix; E ∈ R n × n is singular with rank ( E ) = r < n ; x ( t ) ∈ R n is state of the system; D α x ( t ) is the Caputo fractional order derivative with the following definition
D α x ( t ) = 1 Γ ( m − α ) ∫ 0 t x ( m ) ( τ ) ( t − τ ) α + 1 − m d τ ,
where m − 1 < α ≤ m , m is an integer. If E = I , (1) is simplified to FOS
D α x ( t ) = A x ( t ) .
Lemma 1
([29]). Assume that System (1) is regular, and two invertible matrices G and W are found such that
G E W = I r 0 0 J n − r , G A W = A ¯ 1 0 0 I n − r ,
where J n − r is nilpotent matrix, then we have:
(a) System (1) is impulse-free if J n − r = 0 .
(b) System (1) is stable if | arg ( spec ( A ¯ 1 ) ) | > α π 2 .
(c) System (1) is admissible if J n − r = 0 and | arg ( spec ( A ¯ 1 ) ) | > α π 2 .
Lemma 2
([29]). FOS (2) with 0 < α < 1 is stable iff there exist matrices X, Y ∈ R n × n such that
X Y − Y X > 0 ,
sym ( A ( a X − b Y ) ) < 0 .
Lemma 3
([14]). FOS (2) with 1 ≤ α < 2 is stable iff there exist positive matrix P such that
sym ( Θ ⊗ A P ) < 0 .

3. Main Results

In this section, for the DFOSs with order in ( 0 , 2 ) , new approaches of admissibility based on non-strict LMIs and strict LMIs are addressed, respectively.

3.1. Criteria of admissibility based on non-strict LMIs

Theorem 1.
DFOS (1) with 0 < α < 1 is admissible iff A is nonsingular and there exist matrices X, Y, Q ∈ R n × n , Q > 0 satisfying (4) and
A ( a X − b Y ) E T + E ( a X − b Y ) T A T + E Q E T ≤ 0 .
Proof 
(Sufficiency). Since A is nonsingular, det ( s α E − A ) ≠ 0 for some s ∈ C , so the system (1) is regular. Then there exist two nonsingular matrices G and W such that (3) holds.
Let
X = W X 1 X 2 X 2 T X 3 W T , X 1 = X 1 T > 0 , X 3 = X 3 T > 0 ,
Y = W Y 1 Y 2 − Y 2 T Y 3 W T , Y 1 T = − Y 1 , Y 3 T = − Y 3 ,
Q = W Q 1 Q 2 Q 2 T Q 3 W T , Q 1 = Q 1 T > 0 , Q 3 = Q 3 T > 0 .
From the condition (4)
X Y − Y X = W 0 0 W X 1 X 2 Y 1 Y 2 X 2 T X 3 − Y 2 T Y 3 − Y 1 − Y 2 X 1 X 2 Y 2 T − Y 3 X 2 T X 3 W T 0 0 W T > 0 ,
it is easy to obtain
X 1 Y 1 − Y 1 X 1 > 0 .
Substituting (3), (8), (9) and (10) into (7), we get
U = U 1 U 2 U 2 T U 3 ≤ 0 ,
where
U 1 = A ¯ 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A ¯ 1 T + Q 1 ,
U 2 = A ¯ 1 ( a X 2 − b Y 2 ) J n − r T + ( a X 2 + b Y 2 ) + Q 2 J n − r T ,
U 3 = ( a X 3 − b Y 3 ) J n − r T + J n − r ( a X 3 − b Y 3 ) T + J n − r Q 3 J n − r T .
(13) implies U 1 < 0 or U 1 ≤ 0 . Considering Q 1 > 0 , we have
A ¯ 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A ¯ 1 T < 0 .
Hence, X 1 , Y 1 satisfy (12) and (14). By Lemma 2, (1) is stable. Without loss of generality, assume that the nilpotent matrix J n − r ≠ 0 which owns the Jordan form
J n − r = 0 1 0 ⋱ ⋱ 1 0 1 0 .
Write X 3 , Y 3 , Q 3 as
X 3 = x i j t × t > 0 , x i j = x j i ,
Y 3 = y i j t × t , y i j = − y j i ( i ≠ j ) , y i i = 0 ,
Q 3 = q i j t × t > 0 , q i j = q j i ,
where t = n − r and i , j = 1 , ⋯ , n . Then U 3 is rewritten as
0 a x 11 ★ ★ a x 11 2 ( a x 12 − b y 12 ) + q 11 ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ .
Since
det ( 0 a x 11 a x 11 2 ( a x 12 − b y 12 ) + q 11 ) < 0 ,
U 3 contains two eigenvalues with different sign, so U is neither negative definite (negative semi-definite) nor positive definite (positive semi-definite) which is conflicted with U ≤ 0 . It follows that J n − r = 0 . By Lemma 1, (1) is impulse-free. This together with the regularity and stability of (1) deduces that (1) is admissible.
(Necessity). According to Lemma 1 and the admissible condition of (1), there exist nonsingular matrices G, W such that (3) holds with J n − r = 0 , and D α x 1 ( t ) = A ¯ 1 x 1 ( t ) is stable. By Lemma 2, there exist matrices X 1 , Y 1 satisfying (12) and (14) which deduces that A ¯ 1 is invertible. Then there exist a matrix Q 1 > 0 such that
A ¯ 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A ¯ 1 T + Q 1 ≤ 0 .
From the invertible matrix A ¯ 1 and (3), we get that A is also invertible. Let
X = W X 1 0 0 I n − r W T , Y = W Y 1 0 0 0 W T , Q = W Q 1 0 0 I W T .
From (12) and (20), we get
X Y − Y X = W 0 0 W X 1 0 Y 1 0 0 I n − r 0 0 − Y 1 0 X 1 0 0 0 0 I n − r W T 0 0 W T > 0 .
Substituting (3) and (20) into (7), we obtain
A ( a X − b Y ) E T + E ( a X − b Y ) T A T + E Q E T = G − 1 A 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A 1 T + Q 1 0 0 0 G − T ≤ 0 .
□
Corollary 1.
DFOS (1) with 0 < α < 1 is admissible iff A is nonsingular and there exist matrices X, Y, Q ^ ∈ R n × n , Q ^ > 0 satisfying (4) and
sym ( A ( a X − b Y ) E T ) E ∗ − Q ^ ≤ 0 .
Proof. 
Setting Q ^ = Q − 1 , by Schur complement, it is easy to get that (21) is equivalent to (7). □
Remark 1.
The formulations in Theorem 1 are new and different from the existing literature which enrich the research methods of admissibility for DFOSs. Moreover, this new approach is easy to deal with the uncertainties in singular matrix based on the special position of E in (21).
Corollary 2.
DFOS (1) with 0 < α < 1 is admissible iff A is nonsingular and there exist matrices P and Q > 0 such that
sym ( P ) asym ( P ) − asym ( P ) sym ( P ) > 0 ,
A Φ E T + E Φ T A T + E Q E T ≤ 0 ,
where Φ = a · sym ( P ) − b · asym ( P ) .
Proof. 
According to (22), we get sym ( P ) > 0 and ( asym ( P ) ) T = − asym ( P ) . Let sym ( P ) = X , asym ( P ) = Y , where X > 0 and Y T = − Y . It is easy to get
P = 1 2 ( X + Y ) , P T = 1 2 ( X − Y ) .
Therefore, (22) and (23) are equivalent to (4) and (7), respectively. By Theorem 1, (1) is admissible. □
Remark 2.
Corollary 2 provides a method to reduce the count of decision variables. Matrices X and Y are replaced by a single matrix P which simplifies the expressions in Theorem 1 and is easier to solve than the exiting approach.
Theorem 2.
DFOS (1) with 1 ≤ α < 2 is admissible iff A is nonsingular and there exist two positive matrices P, Q ∈ R n × n such that
Θ ⊗ A P E T + Θ T ⊗ E P A T + I 2 ⊗ E Q E T ≤ 0 .
Proof. 
Using the method of Theorem 1, we are easy to obtain Theorem 2. □
Corollary 3.
DFOS (1) with 1 ≤ α < 2 is admissible iff A is nonsingular and there exist two positive matrices P, Q ^ ∈ R n × n s.t.
sym ( Θ ⊗ A P E T ) I 2 ⊗ E * − I 2 ⊗ Q ^ ≤ 0 .
Proof. 
It is similar to the proof in Corollary 1. □
Remark 3.
For the order in [ 1 , 2 ) , a different criterion for admissibility is proposed in Theorem 2. Considering the special form of equation (26), this method is convenient to handle the DFOSs with uncertain singular matrix E.
Theorem 3.
DFOS (1) with 0 < α < 2 is admissible iff A is nonsingular and there exist matrices P and Q > 0 such that
sym ( P ) asym ( P ) α − 1 asym ( P ) sym ( P ) > 0 ,
sym ( Θ α ⊗ A P α E T ) + I α ⊗ E Q E T ≤ 0 ,
where Θ α = Θ ( α ) , Θ ( 1 ) = det ( Θ ) , Θ ( 2 ) = Θ , P α = a − α − 1 · sym ( P ) + b α − 1 asym ( P ) .
Proof. 
When 0 < α < 1 , it is easy to get Θ α = 1 , P α = a · sym ( P ) − b · asym ( P ) . Then, we obtain that (27) and (28) yield to (4) and (7). Thus, Theorem 3 is equivalent to Theorem 1 in this case.
When 1 ≤ α < 2 , we have Θ α = Θ , P α = sym ( P ) . From equations (27) and (28), we obtain
P α 0 0 P α > 0 ,
sym ( Θ ⊗ A P α E T ) + I 2 ⊗ E Q E T ≤ 0 .
It is easy to see that (29) and (30) are equivalent to P α > 0 and (25) in Theorem 2. □
Remark 4.
Theorem 3 is an unified form of Theorems 1 and 2, which are necessary and sufficient conditions without complex number and are able to handle eigenvalues of system matrix A with positive real part. In the case of E = I, Theorem 3 is consistent with Lemmas 2 and 3 for α in ( 0 , 1 ) and [ 1 , 2 ) , respectively. When α = 1 , Theorem 3 is the same as admissibility conditions for integer systems in [32].
Remark 5.
The inequality (28) is unable to be solved directly because it contains equality constraint. In order to tackle this issue, nonsingular matrices G, W and a column full rank matrix S which satisfies E S = 0 are introduced in the following theorems. Nonsigular matrices G and W satisfy (3) which is deduced by the nonsingular condition of A. Then a strict LMI without equality constraint is further formulated.

3.2. Criteria of admissibility based on strict LMIs

Theorem 4.
DFOS (1) with 0 < α < 1 is admissible iff A is nonsingular and there exist matrices X, Y satisfying (4) and
A ( a X − b Y ) E T + E ( a X − b Y ) T A T − ( W G ) − 1 S S T ( W G ) − T < 0 ,
where W, G satisfy (3), and S is any matrix with full column rank which satisfies E S = 0 .
Proof. 
The proof is similar to Theorem 1 and simplified as follows:
(Sufficiency) Since A is nonsingular, there exist two invertible matrices G and W satisfying (3). Set the form of X, Y as (8) and (9), respectively. Under the condition (4), it is easy to obtain (12).
Let
S = W 0 S 2 ,
which satisfies E S = 0 . Therefore J n − r S 2 = 0 . Substituting (3), (8), (9) and (32) into (31), we have
U ˜ = U ˜ 1 U ˜ 2 U ˜ 2 T U ˜ 3 < 0 ,
where
U ˜ 1 = A ¯ 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A ¯ 1 T ,
U ˜ 2 = A ¯ 1 ( a X 2 − b Y 2 ) J n − r T + ( a X 2 + b Y 2 ) ,
U ˜ 3 = ( a X 3 − b Y 3 ) J n − r T + J n − r ( a X 3 − b Y 3 ) T − S 2 S 2 T .
(33) implies U ˜ 1 < 0 . According to U ˜ 1 < 0 and (12), by Lemma 2, (1) is stable.
Without loss of generality, suppose that the nilpotent matrix J n − r ≠ 0 which owns the Jordan form (15).
Choose S 2 as
S 2 = 0 0 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 0 s 1 t s 2 t ⋯ s t t ,
where t = n − r , s i t ≠ 0 is an arbitrary real number for i = 1 , ⋯ , n , and S 2 satisfies J n − r S 2 = 0 .
Write X 3 , Y 3 as (16), (17). Then U ˜ 3 is rewritten as
0 a x 11 ★ ★ a x 11 2 ( a x 12 − b y 12 ) ★ ★ ★ ★ ★ ★ ★ ★ ★ ★ .
Since
det ( 0 a x 11 a x 11 2 ( a x 12 − b y 12 ) ) < 0 ,
U ˜ 3 contains two eigenvalues with different sign which is conflicted with U ˜ < 0 . It follows that J n − r = 0 . Applying Lemma 1, one concludes that (1) is impulse-free. This together with the regularity and stability of (1) deduces that (1) is admissible.
(Necessity) According to Lemma 1 and the admissible condition of (1), there exist nonsingular matrices G, W such that (3) holds. By Lemma 2, there exist matrices X 1 , Y 1 satisfying (12) and (14) which deduces that A is invertible. Setting the expressions of X, Y as (20), it is easy to see that (4) holds.
Choose S as
S = W 0 I ,
which satisfies E S = 0 . Substituting (3), (20) and (34) into (31), one has
A ( a X − b Y ) E T + E ( a X − b Y ) T A T − ( W G ) − 1 E ^ E ^ T ( W G ) − T = G − 1 A 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A 1 T 0 0 − I G − T < 0 . .
□
Theorem 5.
DFOS (1) with 0 < α < 1 is admissible iff A is nonsingular and there exist a matrix P satisfying (22) and
A Φ E T + E Φ T A T − ( W G ) − 1 S S T ( W G ) − T < 0 ,
where Φ = a · sym ( P ) − b · asym ( P ) .
Proof. 
The proof is similar to that in Corollary 2. □
Theorem 6.
DFOS (1) with 1 ≤ α < 2 is admissible iff A is nonsingular and there exist a matrix P > 0 such that
Θ ⊗ A P E T + Θ T ⊗ E P A T − I 2 ⊗ ( W G ) − 1 S S T ( W G ) − T < 0 ,
where W, G and S are given in Theorem 4.
Proof. 
Using the method of Theorem 4, we are easy to obtain Theorem 6. □
Theorem 7.
DFOS (1) with 0 < α < 2 is admissible iff A is nonsingular and there exist a matrix P satisfying (27) and
sym ( Θ α ⊗ A P α E T ) − I α ⊗ ( W G ) − 1 S S T ( W G ) − T < 0 ,
where Θ α and P α are given in Theorem 3.
Proof. 
The proof is similar to that in Theorem 3, so the details are omitted. □
Remark 6.
In Theorem 7, a strict LMI criterion of admissibility is proposed. This new approach is an unified form of Theorems 5 and 6, and it is easy to cope with the eigenvalues with positive real part. In addition, the LMIs in (27) and (37) only contain one real decision variable which is easy to solve. In the case of E = I, Theorem 7 is also consistent with Lemmas 2 and 3 for α in ( 0 , 1 ) and [ 1 , 2 ) , respectively.

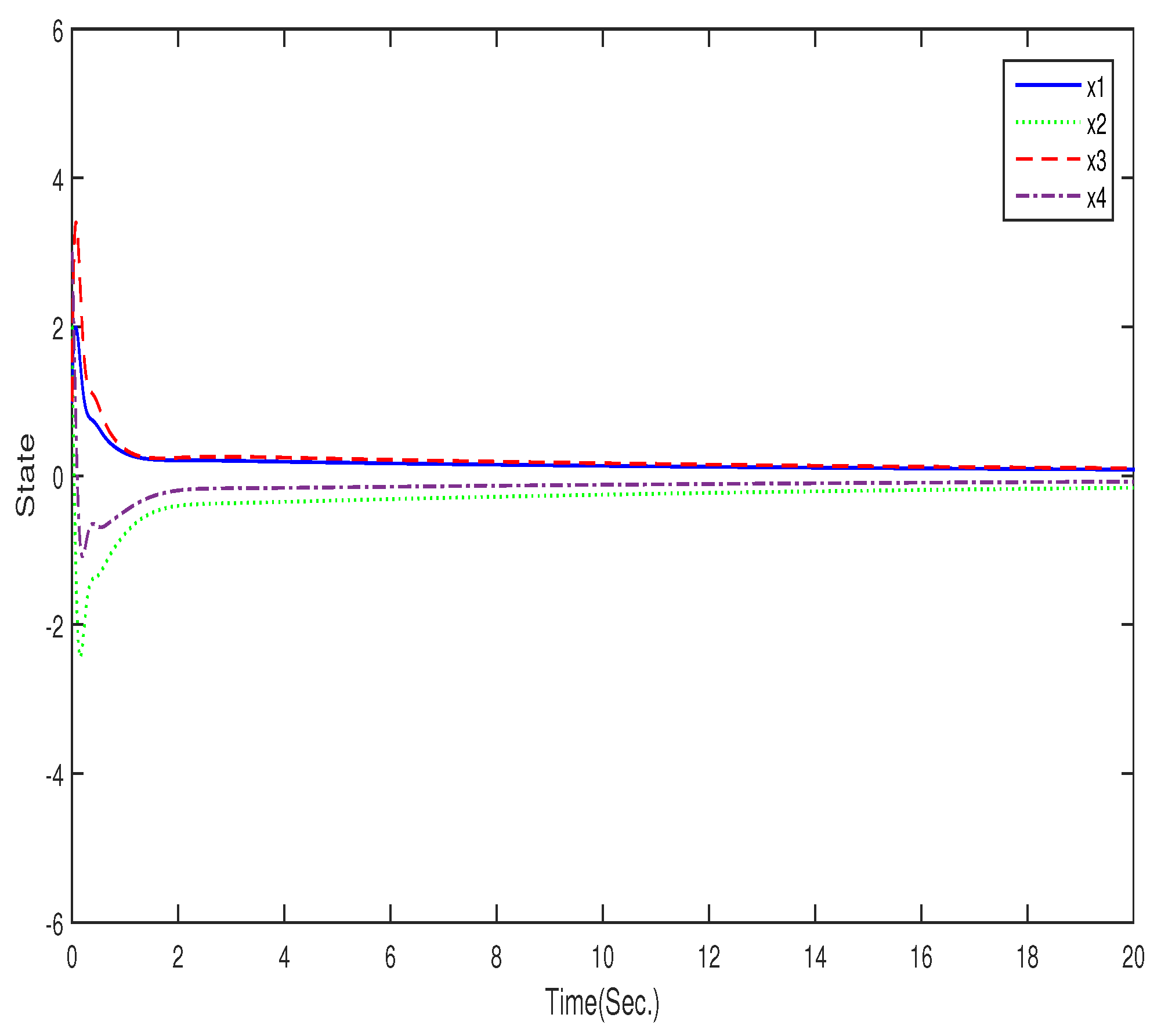
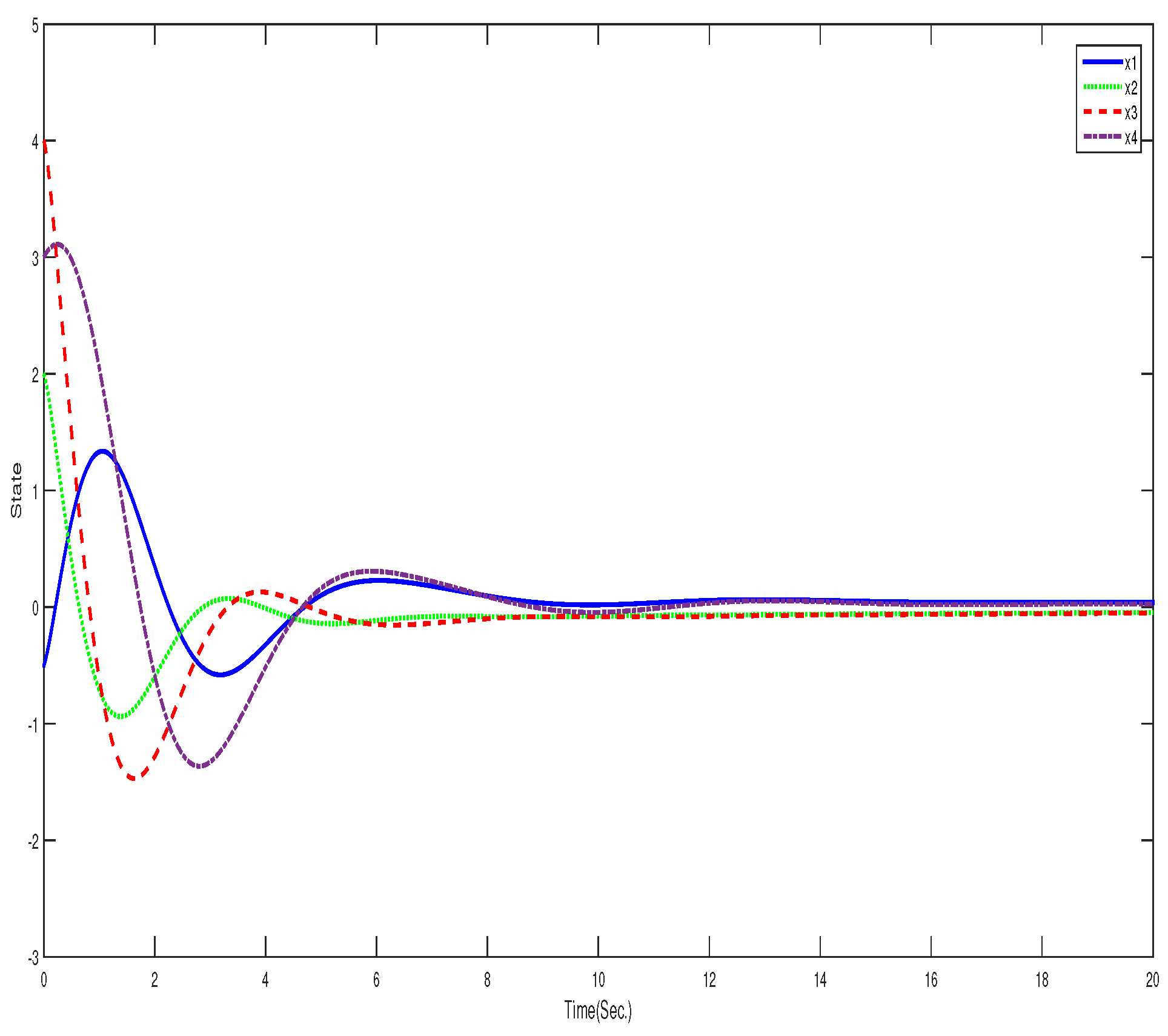
4. Numerical Examples

Three numerical examples are provided to illustrate the effectiveness of theorems based on non-strict LMIs and strict LMIs.
Example 1.
Consider system (1) with α = 0.4 , and
E = 1 0 0 0 1 0 0 0 0 , A = 1 2 0 − 2 1 0 0 0 1 .
By solving non-strict LMIs in Theorem 3, we obtain the feasible solutions as follows:
P = 0.5621 − 0.4766 0 0.4766 0.5621 0 0 0 0.5000 , Q = 0.8814 0 0 0 0.8814 0 0 0 1.0000 .
Remark 7.
The correctness of Theorem 3 is verified in Example 1 by solving equations (27) and (28). Since (28) contains equality constraint which is unable to be solved by any simulation software directly, we need to convert the matrices A and E into the form of (3). A feasible approach to get the solution is solving the following strict LMI
A ¯ 1 ( a X 1 − b Y 1 ) + ( a X 1 − b Y 1 ) T A ¯ 1 T + Q 1 < 0 .
we can get the values of X 1 , Y 1 and Q 1 . Construct matrices X, Y and Q with the form of (20). Then the feasible solutions of P and Q is obtained, where P = 1 2 ( X + Y ) .
Example 2.
Consider a DFOS in (1) with
α = 0.5 , E = − 3 − 1 2 5 1 1 − 1 − 3 − 3 1 2 3 1 1 1 1 , A = 7 2 2 1 − 3 − 2 − 4 − 5 10 1 − 7 − 16 3 4 − 2 − 7 .
Since A is nonsingular, the system (1) is regular. Due to deg ( det ( s E − A ) ) = rank ( E ) = 3 , the system (1) is impulse-free. The roots of det ( s E − A ) = 0 are − 2 and 1 ± 3 j . By Lemma 1, it is easy to verify that the DFOS with parameters in Example 2 is admissible. By solving strict LMIs (27) and (37) in Theorem 7, we get the following feasible solution of real matrix P:
P = 2.3934 − 1.7708 − 0.7703 2.3777 1.8095 8.1164 − 2.3734 2.8106 0.2597 − 0.8788 4.7747 − 2.3535 2.1066 − 1.3637 − 2.5610 3.3455 .
The state responses are displayed in Figure 1
Example 3.
Consider a DFOS in (1) with
α = 1.5 , E = 1 2 1 2 0 0 − 1 − 1 − 1 0 − 1 0 0 2 0 2 , A = − 1 − 5 − 2 − 6 2 1 4 1 1 − 1 2 0 1 − 6 1 − 7 .
By Lemma 1, it is easy to get that the DFOS in Example 3 is also admissible. By Theorem 7, we obtain the following feasible solution:
P = 12.1598 − 6.1003 − 7.1349 5.7156 − 6.1003 5.0981 3.4141 − 4.4487 − 7.1349 3.4141 5.2904 − 3.3692 5.7156 − 4.4487 − 3.3692 4.2455 .
From the state responses in Figure 2 which is simulated based on the data above, we can see that the system quickly reaches stability in 10s.
Remark 8.
The approaches reported in [33] are inapplicable to the case of matrix A with eigenvalues on positive real part, but our method has no the limitation on eigenvalues which has a wider range of applications. Compared with the necessary and sufficient criteria proposed in [25,26,27,28,29,30,31] with multiple decision variables, the Theorem 7 based on LMIs in this paper contains only one real decision variable which is easy to get the feasible solution.

5. Conclusions

In this paper, we analysis the problem concerning synthesis of DFOSs without any order interval separation. Novel and alternate admissibility approaches based on non-strict LMIs and strict LMIs are proposed, which fills the vacancy of previous achievements and have theoretical research value. For the non-strict LMI criterion, the position of singular matrix E is different of existing studies, and the validity is shown by simulation results. For the strict LMI criterion, the conditions contain only one real decision variable which can be solved by simulation software directly and more easily. When E = I or α = 1 , Theorems established in this paper are consistent with related FOSs results or descriptor integer systems results which are regarded as the extensions of Lyapunov stability. Further works will focus on the controller design for the DFOSs with uncertain derivative matrices based on the methods established above.

Author Contributions

Conceptualization, methodology, validation, Y.D., X.Z. and J.Z.; writing—original draft preparation, Y.D.; writing—review and editing, J.Z. and X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 62103093 and the Fundamental Research Funds for the Central Universities of China under Grant N2108003.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ortigueira, M.D.; Ionescu, C.M.; Machado, J.T.; Trujillo, J.J. Fractional signal processing and applications. Signal Process. 2015, 107, 197. [Google Scholar] [CrossRef]
  2. Zhang, X.F.; Dai, L.W. Image enhancement based on rough set and fractional order differentiator. Fractal Fract. 2022, 6, 214. [Google Scholar] [CrossRef]
  3. Yan, H.; Zhang, J.X.; Zhang, X.F. Injected infrared and visible image fusion via L1 decomposition model and guided filtering. IEEE Trans. Comput. Imag. 2022, 8, 162–173. [Google Scholar] [CrossRef]
  4. Liu, C.H.; Hu, M.H.; Jin, G.Q.; Xu, Y.D.; Zhai, J. State of power estimation of lithium-ion battery based on fractional-order equivalent circuit model. J. Energy Storage 2021, 41, 102954. [Google Scholar] [CrossRef]
  5. Ortigueira, M.D.; Ionescu, C.M.; Machado, J.T.; Trujillo, J.J. Fractional signal processing and applications. Signal Processing 2015, 107, 197. [Google Scholar] [CrossRef]
  6. Muresan, C.I.; Birs, I.; Ionescu, C.; Dulf, E.H.; De Keyser, R. A review of recent developments in autotuning methods for fractional-order controllers. Fractal Fract 2022, 6, 37. [Google Scholar] [CrossRef]
  7. Li, R.C.; Zhang, X.F. Adaptive sliding mode observer design for a class of T-S fuzzy descriptor fractional order systems. IEEE Trans. Fuzzy Syst. 2020, 28, 1951–1959. [Google Scholar] [CrossRef]
  8. Zhang, X.F.; Zhang, J.X.; Huang, W.K.; Shi, P. Non-fragile sliding mode observer based fault estimation for interval type-2 fuzzy singular fractional order systems. Int. J. Sysi. Sci. 2023, 1–20. [Google Scholar] [CrossRef]
  9. Radwan, A.G.; Emira, A.A.; Abdelaty, A.M.; Azar, A.T. Modeling and analysis of fractional order DC-DC converter. ISA Trans. 2018, 82, 184–199. [Google Scholar] [CrossRef]
  10. Yu, Z.M.; Sun, Y.; Dai, X. Stability and stabilization of the fractional-order power system with time delay. IEEE Trans. Circuits Syst. II, Express Briefs 2021, 68, 3446–3450. [Google Scholar] [CrossRef]
  11. Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.; Bekiros, S.; Wei, Z.C. A fractional-order hyper-chaotic economic system with transient chaos. Chaos, Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
  12. Zhang, X.F.; Zhao, Z.L. Normalization and stabilization for rectangular singular fractional order T-S fuzzy systems. Fuzzy Sets Syst. 2020, 38, 140–153. [Google Scholar] [CrossRef]
  13. Zhang, X.F.; Huang, W.K. Adaptive neural network sliding mode control for nonlinear singular fractional order systems with mismatched uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
  14. Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilisation of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
  15. Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional-order interval systems with the fractional order α : 0<α<1 case. IEEE Trans. Autom. Control 2010, 55, 152–158. [Google Scholar] [CrossRef]
  16. Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0<α<2. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 32373241. [Google Scholar] [CrossRef]
  17. Tian, Y.; Wang, Z.B.; Liu, D.Y.; Boutat, D.; Liu, H.R. Non-asymptotic estimation for fractional integrals of noisy accelerations for fractional order vibration systems. Automatica 2022, 135, 109996. [Google Scholar] [CrossRef]
  18. Ghorbani, M.; Tavakoli-Kakhki, M.; Tepljakov, A.; Petlenkov, E.; Farnam, A.; Crevecoeur, G. Robust stability analysis of interval fractional-order plants with interval time delay and general form of fractional-order controllers. IEEE Control Syst. Lett. 2021, 6, 1268–1273. [Google Scholar] [CrossRef]
  19. Alessandretti, A.; Pequito, S.; Pappas, G.J.; Aguiar, A.P. Finite-dimensional control of linear discrete-time fractional-order systems. Automatica 2020, 115, 108512. [Google Scholar] [CrossRef]
  20. Zhu, Z.; Lu, J.G. LMI-based robust stability analysis of discrete-time fractional-order systems with interval uncertainties. IEEE Trans. Circuits Syst. I-Regul. Pap. 2021, 68, 1671–1680. [Google Scholar] [CrossRef]
  21. Gong, P.; Lan, W.Y.; Han, Q.L. Robust adaptive fault-tolerant consensus control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica 2020, 117, 109011. [Google Scholar] [CrossRef]
  22. Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
  23. Zhang, J.X.; Yang, G.H. Fuzzy adaptive output feedback control of uncertain nonlinear systems with prescribed performance. IEEE Trans. Cybern. 2018, 48, 1342–1354. [Google Scholar] [CrossRef] [PubMed]
  24. Zhang, J.X.; Yang, G.H. Fault-tolerant output-constrained control of unknown Euler-Lagrange systems with prescribed tracking accuracy. Automatica 2020, 111, 108606. [Google Scholar] [CrossRef]
  25. Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. J. Frankl. Inst. 2017, 354, 752–766. [Google Scholar] [CrossRef]
  26. Marir, S.; Chadli, M. Robust admissibility and stabilization of uncertain singular fractional-order linear time-invariant systems. IEEE/CAA J. Autom. Sin. 2019, 6, 685–692. [Google Scholar] [CrossRef]
  27. Marir, S.; Chadli, M.; Basin, M.V. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
  28. Marir, S.; Chadli, M.; Bouagada, D. A novel approach of admissibility for singular linear continuous-time fractional-order systems. Int. J. Control Autom. Syst. 2017, 15, 959–964. [Google Scholar] [CrossRef]
  29. Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α : The 0<α<1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar] [CrossRef]
  30. Di, Y.; Zhang, J.X.; Zhang, X.F. Robust stabilization of descriptor fractional-order interval systems with uncertain derivative matrices. Appl. Math. Comput. 2023, 453, 128076. [Google Scholar] [CrossRef]
  31. Wang, Y.Y.; Zhang, X.F.; Boutat, D.; Shi, P. Quadratic admissibility for a class of LTI uncertain singular fractional-order systems with 0<α<2. Fractal Fract. 2022, 7, 1. [Google Scholar]
  32. Zhang, D.Q.; Zhang, Q.L. On the quadratic stability of descriptor systems with uncertainties in the derivative matrix. Int. J. Syst. Sci. 2009, 40, 695–702. [Google Scholar] [CrossRef]
  33. Zhang, Q.H.; Lu, J.G. Necessary and sufficient conditions for extended strictly positive realness of singular fractional-order systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 1997–2001. [Google Scholar] [CrossRef]
Preprints 77562 g001
Figure 1. The state responses with α = 0.5 in Example 2.
Figure 1. The state responses with α = 0.5 in Example 2.
Preprints 77562 g001
Preprints 77562 g002
Figure 2. The state responses with α = 1.5 in Example 3.
Figure 2. The state responses with α = 1.5 in Example 3.
Preprints 77562 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated