Preprint
Article
Combining Novel Integration and the DEA Technique to Compute Dredging Productivity
Altmetrics
Downloads
145
Views
17
Comments
0
This version is not peer-reviewed
Submitted:
25 June 2023
Posted:
26 June 2023
You are already at the latest version
Alerts
Abstract
Construction productivity entails a wide range of work combinations. When human resources are scarce, it is critical to replace manpower with machinery, and calculating machinery productivity is crucial. Traditional labor productivity methods, however, cannot address dredging complex multi-attribute decision-making (MADM) problems. Aiming to address the limitations of the traditional labor productivity method, this paper extends the data envelopment analysis (DEA) and proposes a new dredging productivity evaluation method. The proposed method can solve the problem of evaluating various combinations of factors (single-input, multiple-input, sin-gle-output, and multiple-output) and the problem suggesting that the efficiency of the DEA method'scalculation results is equal to 1. The effectiveness of the proposed method was verified using reservoir dredging examples. The simulation results show that the proposed method has broad applicability, can accurately evaluate the related dredging performance issues, and provide directions for construction managers to improve labor productivity.
Keywords:
Subject: Engineering - Other
1. Introduction
Completing a construction project on time, on budget, and with excellent quality is critical to a project’s success. Construction efficiency (productivity) is also a key factor determining the success or failure of a project, affecting project quality and revenue. Many factors influence construction productivity, such as construction site conditions, worker capabilities, material suitability, climatic conditions, worker motivation, and supervisory mechanisms. The emergence of such issues is referred to as a multiple-attribute decision-making (MADM) problem. Therefore, traditional methods cannot calculate actual performance or productivity.
Many scholars evaluate productivity using different methods. Some scholars used soft computing techniques to evaluate and compare labor productivity in construction [1]. Others used the Analytic Hierarchy Process (AHP) analysis to investigate the productivity losses of practitioners in concrete construction projects in Sweden and assessed the impacts of their exposure to different weather types while performing work tasks [2]. Some scholars experimented with strengthening government policy and regulatory tools to increase productivity in public works [3].
The significant increase in the frequency of natural disasters due to extreme climate change has increased the risk of natural disasters. Floods induced by heavy rainfall create reservoir sedimentation, reducing reservoir capacity by 1% per year worldwide, which has become a major problem globally. Many scholars also proposed using engineering methods to address flooding issues, such as building dams, dredging rivers, and heightening and strengthening buildings.
Dredging, a planned and systematic excavation activity, is a critical issue in water resource management. Many scholars have investigated the issues related to dredging. For example, some scholars developed a river dredging management model in South Korea using multi-criteria decision analysis techniques, which assigns weights to various dredging-related factors, such as dredging costs and social and environmental impacts, to address river dredging problems [4]. Other scholars discussed the problem definition and model formulation for optimal dredging fleet scheduling to improve the efficiency of dredging projects initiated by the United States Army Corps of Engineers (USACE) [5]. Decision-makers can use this approach to boost dredger productivity. Some scholars also asserted that proper planning and scheduling could significantly reduce waiting times and address delays, making earthworks more efficient while reducing cost overruns risks [6].
Dredging performance (productivity) is a major research area in construction engineering and management science. Dredging requires the transportation of large volumes of soil, necessitating combined transportation methods and complex machinery. Therefore, reservoir dredging is classified as a complex multi-attribute decision-making (MADM) problem.
Traditional methods for assessing dredging productivity use a labor productivity method to evaluate the issues related to dredging performance. Productivity is defined as “the work hour (WH) required to complete a unit of work.” Some researchers stated that productivity research should focus on labor-intensive, repetitive, and important crew work [7]. They used the latest version of the world’s largest corporate financial database to identify three statistical properties related to manual labor productivity [8].
To efficiently address the multiple-input and multiple-output (MIMO) problems associated with data attributes, Data Envelope Analysis (DEA) was first proposed [9]. Due to its simple calculation and ability to solve MIMO problems, many scholars employed DEA to address decision-related problems.
The proposed multifunctional DEA model for multi-activity data envelopment analysis (MADEA) can overcome data output uncertainty and share inputs, environmental variables, and inter-temporal efficiencies [10]. The model can measure the performance of prefectural/municipal departments and the entire Taiwanese. On the other hand, the integrated fuzzy data envelopment analysis (FDEA) and fuzzy-multi attribute decision-making (F-MADM) were used to evaluate and select the safest airlines in Iran [11]. Some scholars used the novel DEA-based method to evaluate the dredging productivity of the national army and found that it can effectively address the complicated MADM problem of dredging productivity [12]. A complete picture of major airlines’ operations can be achieved by exhaustively examining their efficiency in European airspace using the novel input/output parameters of the Data Envelope Analysis (DEA) [13].
Moreover, the efficiency of 3D printers can also be assessed using the DEA method [14]. Combined with multiple technologies, DEA-based interaction and expansion approach can also improve drug sales performance [15]. The application of combined goal-oriented methodology (GO methodology), integrated dynamic Bayesian networks (DBNs), and the DEA methodology can improve smart meter reliability and accuracy [16]. A certain model was developed for improving the productivity of warehouses and logistics distribution centers using the PROMETHEE II and DEA methods [17]. Since appropriate organizational changes were made in terms of infrastructure, human resources, and technology, efficiency and productivity assessments were incorporated into hospital decision-making [18].
To address complicated problems related to multiple inputs and multiple outputs of dredging productivity, this study proposes an improved method involving novel integration and DEA to establish a more reliable, objective, and accurate novel evaluation model.
The remainder of this paper is organized as follows—Section 2 reviews literature related to traditional productivity and DEA. Section 3 proposes a novel productivity evaluation method based on novel integration and DEA. Section 4 adapts the data from the case of Lai (2019) [12] to verify the effectiveness of the proposed method. Lastly, Section 5 provides conclusions and future research directions.
2. Related Works
2.1. Traditional Productivity Method
A dredging project is a complex problem requiring productivity, quality, safety, and timeliness operations of many types of work needed for project completion. However, traditional methods used in calculating productivity can only solve problems related to a single input and a single output. It cannot address problems involving multiple inputs and multiple outputs. In traditional productivity, only the completed work items and the groups’ working hours are considered; hence, productivity is defined as the ratio of “outputs” and “inputs” of an item in unit time, as shown in Equation 1. [19]. The unit of C pertains to one thousand US dollars per employee. Due to physical labor productivity, the researchers of this study denoted the number of employees (NE) as L, while the operating revenue (OR) was denoted as Y. The unit of L pertains to the employee. The unit of Y is one thousand US dollars.
Since the traditional calculation method of productivity cannot address the MIMO problem, the data must be converted before calculation. Equation (2) was used for standardization.
Dredging productivity is a complex MCDM problem. Traditional productivity methods can only address problems with single data input and output. While the DEA method can solve the MIMO problem, its results have the same efficiency (efficiency is equal to 1), making it difficult to identify which efficiency is better. This study utilized the multiple regression equation shown in Equation (3) to calculate the regression coefficient value.
2.2. DEA Method
Charnes et al. [12] initially introduced the DEA method as a mathematical programming method that can evaluate the relative efficiency of decision-making units (DMUs) (first-mode CCR model). DEA is a method that uses multiple inputs to produce multiple outputs to measure the relative efficiencies of a group of DMUs. This non-parametric technique was originally conceived to analyze a set of units. Since the DEA method can solve multiple-criteria decision analysis (MCDA) problems with single-input–single-output, single-input–multi-output, or multi-input–multiple-output, this theoretical approach can be applied to a wide range of real-world problems. The results of this study were obtained using the software “DEA.P version 2.1 for Windows” [20].
3. The Proposed Novel Construction Productivity Calculation Method
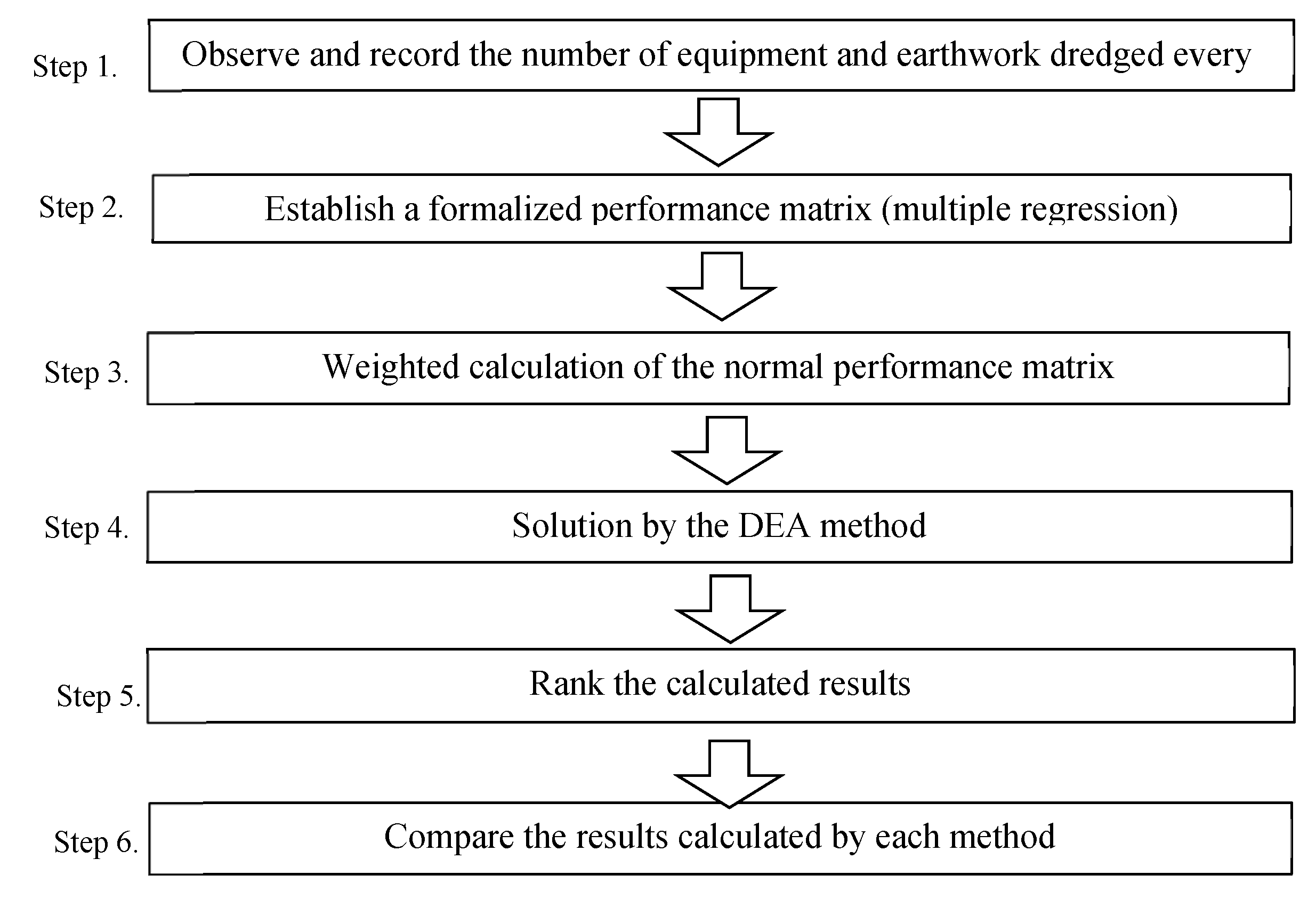
The productivity of a dredging project requires an accurate method for measuring the performance of working groups. The productivity of such working groups is a complex MADM problem. Since the traditional method can only solve productivity problems with a single input and a single output, it cannot solve construction productivity problems involving multiple inputs and outputs. While DEA can directly solve productivity problems with multiple inputs and multiple outputs, this method may generate many productivity values of 1, making it difficult to compare or rank productivities equal to 1. Therefore, this study proposes a method that can solve problems involving multiple inputs and multiple outputs and rank the calculation results where the calculation results are consistent with input and output trends. The procedures of the novel productivity calculation method proposed in this paper include the following steps:
Step 1. Observe and record the number of equipment and earthwork dredged every day.
Step 2. Establish a formalized performance matrix (multiple regression).
Step 3. Perform the weighted calculation of the normal performance matrix.
Step 4. Obtain the solution using the DEA method
Step 5. Rank the calculated results.
Step 6. Compare the results calculated using each method.
Figure 1 shows the flowchart of the novel construction productivity calculation.
4. Case Study
4.1. Overview
To verify the correctness and effectiveness of the proposed method in this study, the researchers adapted one of the case data from Lai, Chang, and Lin’s study [00] to demonstrate how the traditional method of calculating dredging productivity is a special case of the proposed method. Records from the Nanhua Reservoir dredging located in Taiwan at that time were used. The Nanhua Reservoir is about 104 square kilometers and was completed in 1994. After its completion, the water storage capacity reached about 158.05 million cubic meters. At present, it can provide domestic water for Tainan and Kaohsiung. It also serves as a reservoir for sightseeing and leisure. The collected data from the Nanhua Reservoir dredging case was for 54 working days, from April 8 to May 31, 2011. Table 1 shows the record per day for hydraulic excavators (SL-330 and 320B) and trucks as input items, including the number of dispatches, while the output is the amount of daily dredging.
4.2. Solution Using the Traditional Productivity Method
Since the traditional productivity calculation method can only solve problems involving a single input and a single output, directly calculating the problem of single input and multiple outputs, multiple inputs and single outputs, or multiple inputs and multiple outputs is quite challenging [19]. Data must be converted before calculations. To make the traditional method applicable in addressing problems involving multiple inputs and outputs, the researchers of this study used Equation 2 to standardize the input of the data in Table 1. After formalizing the conversion of all input items, the researchers proceeded to calculate the aggregated input value using the traditional method productivity (output/input) and the dredging productivity result/one-day high dredging productivity. Table 2 illustrates the calculated result.
4.3. Solution Using the DEA Method
The data envelopment analysis (DEA) method proposed by Androutsou et al. (2022) [18] is one of the critical tools for performing productivity measurements. The DEA method can deal with complex data problems involving multiple inputs and multiple outputs. This study used the CCR model of the DEAP software to calculate the daily productivity of the dredging work in the Nanhua Reservoir shown in Table 2. The calculation results are shown in Table 3.
4.4. Solution Using the Proposed Novel Productivity Calculation Method
Dredging productivity is a complex MCDM problem involving multiple data inputs and multiple data outputs. However, traditional productivity methods can only deal with a single input and output data problem. While the DEA method can solve problems involving multiple inputs and multiple outputs, its calculated results have the same efficiency (the efficiency is equal to 1), making it challenging to determine which is more efficient and which is less efficient.
Several computations with an efficiency equal to 1 can be used to solve DEA efficiently. Some scholars used the multiple regression (ML) method to adopt farming techniques that significantly impact the integration of dairy cows and goats and create smallholder employment[21]. This study proposes an integrated and novel DEA construction productivity calculation method. This method considers the objective weights in obtaining the regression coefficient and selects an input as a conversion benchmark to calculate the conversion factors for each input. The solution steps are as follows.
Step 1: Observe and record the number of equipment and earthwork dredged daily.
Observation and records of the hydraulic excavators (SL-330 and 320B) and trucks as input items include the number of dispatches. The output is the amount of daily dredging output adapted from the case data of [12], as shown in Table 1.
Step 2: Establish a formalized performance matrix (multiple regression).
The regression coefficient value was calculated based on the data recorded in Table 1 and using a multiple regression formula shown in Equation 3. The results are shown in Table 4.
Step 3: Perform the weighted calculation for the normal performance matrix.
To solve the issue concerning the efficiency is equivalent to 1, the researchers of this study used the number of trucks as the conversion benchmark, divided all the regression coefficient values by the number of trucks in the regression results to obtain the conversion factor, and summarized the total input value. Table 5 shows the calculation results.
Step 4: Obtain the solution using the DEA method
This study used the CCR model of the DEAP software to calculate the daily productivity of the dredging work in Nanhua Reservoir shown in Table 5. The calculation results are depicted in Table 6.
Step 5: Rank the calculated results.
Based on the productivity calculation method proposed in this study, the results are ranked to find the best and equivalent dates, as shown in Table 6.
Step 6: Compare the results calculated using each method.
This step involves ranking the results obtained using both productivity calculation methods. Table 7 shows the calculation results.
4.5. Comparison and Discussion
To ensure that the proposed productivity calculation method can improve the disadvantages of traditional productivity calculation, this study adapted the data from the case presented in [12]. To calculate productivity using the traditional calculation method, it is necessary to change the output items into one item after converting the formalized performance matrix. Some scholars used this regression method to identify the conversion factors and converted the output items w to one item before calculation. However, the traditional and Thomas methods can only solve problems involving single input and output [22,23]. DEA calculates the daily productivity based on the input and output coefficients entered into the DEAP software, and the values closer to 1 are deemed better. Although DEA can solve problems with multiple inputs and outputs, it cannot compare the advantages and disadvantages of the productivities when the values are all 1. The novel multi-input and multi-output productivity calculation methods proposed in this study can solve, compare, and rank the largest and equal productivity calculation results. Comparing the main differences between the above three methods, the researchers discovered that only the traditional calculation method could not solve the productivity problem of productivity involving single input and multiple outputs. The remaining two methods can deal with related problems; DEA and the proposed method can solve productivity problems with multiple inputs and outputs. As for effectively resolving performance duplication of multiple inputs and multiple outputs, only the proposed method can solve it. Table 8 summarizes the relative problems for the above three methods.
5. Conclusions and Future Work
In addition to trucks and excavators being the most expensive in dredging, other factors must be considered, such as weather, soil conditions, transportation distance, and so on. Since the productivity of different machines and tools can vary, the quality of productivity influences capital expenditure. Therefore, improving management efficiency and reducing costs through productivity measurement is particularly important initially. In addition, many items must also be considered when evaluating productivity. These include machines and tools, climate, job complexity, material supply, material stacking, and other elements constituting the MADM problem. Since the traditional method can only solve the problem of single input and single output, it cannot solve construction capacity problems with multiple inputs and outputs. Although the DEA method can solve the productivity calculation problem involving multiple inputs and multiple outputs, it cannot compare the calculation results when the efficiencies are equal.
This study combined multiple regression and regularization to solve the shortcomings of traditional methods (which can only solve the problem of single input and single output) and DEA (which cannot compare equal efficiencies) to calculate the productivity results. The researchers of this study used examples to confirm the validity and feasibility of the proposed method, and the simulation results revealed that the novel integration and the DEA technique are more suitable for the evaluation and calculation of productivity.
Future research may further explore this research topic by considering man-made and natural risk assessments, working group proficiency, and management methods. Future studies may evaluate productivity by combining a soft set and fuzzy TOPSIS for the calculation method.
References
- Mlybari, E.A. Application of soft computing techniques to predict construction labour productivity in Saudi Arabia. International Journal of Geomate, 2020, 19(71), 203-210. [CrossRef]
- Larsson, R.; Rudberg, M. Effects of weather conditions on concrete work task productivity- A questionnaire survey. Construction Innovation-England, 2021. [CrossRef]
- Ofori, G.; Zhang, Z.; Ling, F.Y.Y. Initiatives that enable Singapore contractors to improve construction productivity. Built Environment Project and Asset Management, 2021, 11(5), 785–803. [CrossRef]
- Daigneault, P.B.; Gawith, D. “Dredging versus hedging: Comparing hard infrastructure to ecosystem-based adaptation to flooding,” Ecological Economics, 2016, 122, 25–35. [CrossRef]
- Nachtmann, H.; Mitchell, K.N.; Rainwater, C.E.; Gedik, R.; Pohl, E.A. “Optimal dredge fleet scheduling within environmental work windows,” Transportation Research Record, 2014, 2426, 11–19. [CrossRef]
- Christian, J.; Xing Xie, T. “More realistic intelligence in earthmoving estimates,” in Proceedings of the 9th International Conference on Applications of Artificial Intelligence in Engineering, 1994, pp. 387–396. ISSN 1743-3517.
- Thomas, H R.; Sanders, S.R.; Bilai, S. “Comparison of labor productivity,” Journal of Construction Engineering and Management, 1992, 118, 635–650. [CrossRef]
- Ishikawa, A.; Fujimoto, S.; Mizuno, T. Statistical properties of labor productivity distributions. Front. Physics 2022, 10, 848193. [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision-making units. European Journal of Operational Research 1978, 2(6), 429–444. [CrossRef]
- Chen, C.C. Measuring departmental and overall regional performance: Applying the multi-activity DEA model to Taiwan’s cities/counties. Omega-International Journal of Management Science, 2017, 67, 60–80. [CrossRef]
- Barak, S.; Dahooei, J.H. A novel hybrid fuzzy DEA-Fuzzy MADM method for airlines safety evaluation. Journal of Air Transport Management, 2018, 73, 134–149. [CrossRef]
- Lai, H.H.; Chang, K.H.; Lin, C.L. A novel method for evaluating dredging productivity using a data envelopment analysis-based technique. Math. Probl. Eng. 2019, 5130835. [CrossRef]
- Hermoso, R.; Latorre, M.P.; Martinez-Nunez, M. Multivariate data envelopment analysis to measure airline efficiency in European airspace: A network-based approach. Appl. Sci., 2019, 9(24), 5312. [CrossRef]
- Papatheodorou, T.; Giannatsis, J.; Dedoussis, V. Evaluating 3D printers using data envelopment analysis. Appl. Sci., 2021, 11(9), 4209. [CrossRef]
- Abbasi, M.; Mozaffari, M.R.; Wanke, P.F.; Kaviani, M.A. Finding targets in non-radial FDH models- a hybrid technique based on STEM and extended ratio based approach. Appl. Sci., 2021, 11(22), 10626. [CrossRef]
- Zhou, J.; Wu, Z.H.; Yu, Z.H. Research on the reliability allocation method of smart meters based on DEA and DBN. Appl. Sci., 2021, 11(15), 6901. [CrossRef]
- Alidrisi, H. DEA-Based PROMETHEE II distribution-center productivity model -evaluation and location strategies formulation. Appl. Sci., 2021, 11(20), 9567. [CrossRef]
- Androutsou, L.; Kokkinos, M.; Latsou, D.; Geitona, M. Assessing the efficiency and productivity of the hospital clinics on the island of Rhodes during the COVID-19 pandemic. Int. J. Environ. Res. Public Health 2022, 19(23), 15640. [CrossRef]
- Ishikawa, A.; Fujimoto, S.; Mizuno, T. Statistical properties of labor productivity distributions. Front. Physics 2022, 10, 848193. [CrossRef]
- Coelli, T.J. A Guide to DEAP, Version 2.1: A Data Envelopment Analysis (Computer) Program; Working Paper, Papers No. 8/96; Center for Efficiency and Productivity Analysis, Department of Econometrics, University of New England: Armidale, NSW, Australia, 1996.
- Pathade, S.S.; Singh, B.P.; Chander, M.; Bardhan, D.; Verma, M.R.; Singh, Y.P. Potential of livestock production systems: Explaining employability and milk productivity through multivariate typology. Indian J. Anim. Sci 2022, 92(7), 902–907.
- Thomas, H.R.; Maloney, W.F.; Horner, R.M.W.; Smith, G.R.; Handa, V.K.; Sanders, S.R. Modeling construction labor productivity. Journal of Construction Engineering and Management, 1990, 116(4), 705–726. [CrossRef]
- Thomas, H.R.; Sakarcan, A.S. Forecasting labor productivity using factor model. Journal of Construction Engineering and Management, 1994, 120(1), 228–239. [CrossRef]
Figure 1.
Flowchart of the proposed novel construction productivity calculation method.
Table 1.
Data adapted from the chosen case.
| Record day | Output | Input | ||
|---|---|---|---|---|
| Daily dredging (M3) | Number of trucks | Excavator SL-330 | Excavator 320B | |
| 1 | 1668 | 98 | 1 | 5 |
| 2 | 1683 | 98 | 1 | 5 |
| 3 | 1701 | 100 | 2 | 3 |
| 4 | 1702 | 100 | 2 | 3 |
| 5 | 1700 | 100 | 1 | 4 |
| 6 | 1696 | 99 | 1 | 5 |
| 7 | 1665 | 98 | 2 | 3 |
| 8 | 1701 | 100 | 2 | 4 |
| 9 | 1716 | 101 | 1 | 5 |
| 10 | 1720 | 101 | 1 | 5 |
| 11 | 1706 | 91 | 2 | 4 |
| 12 | 1717 | 93 | 2 | 4 |
| 13 | 1729 | 94 | 1 | 5 |
| 14 | 1737 | 95 | 1 | 5 |
| 15 | 1747 | 96 | 2 | 5 |
| 16 | 1759 | 98 | 2 | 5 |
| 17 | 1770 | 99 | 1 | 6 |
| 18 | 1782 | 100 | 1 | 6 |
| 19 | 1792 | 101 | 2 | 5 |
| 20 | 1798 | 102 | 2 | 5 |
| 21 | 1826 | 104 | 1 | 6 |
| 22 | 1855 | 106 | 1 | 6 |
| 23 | 1871 | 107 | 2 | 5 |
| 24 | 1895 | 108 | 2 | 6 |
| 25 | 1925 | 110 | 2 | 6 |
| 26 | 1950 | 112 | 2 | 6 |
| 27 | 1985 | 114 | 2 | 6 |
| 28 | 2041 | 117 | 2 | 6 |
| 29 | 2093 | 120 | 2 | 6 |
| 30 | 2089 | 116 | 2 | 6 |
| 31 | 2083 | 113 | 2 | 6 |
| 32 | 2076 | 109 | 2 | 6 |
| 33 | 2067 | 106 | 2 | 6 |
| 34 | 2058 | 103 | 2 | 6 |
| 35 | 2047 | 100 | 2 | 6 |
| 36 | 2036 | 97 | 2 | 6 |
| 37 | 2024 | 94 | 2 | 6 |
| 38 | 2012 | 92 | 2 | 6 |
| 39 | 1999 | 89 | 2 | 6 |
| 40 | 1986 | 87 | 2 | 6 |
| 41 | 1973 | 85 | 2 | 6 |
| 42 | 1959 | 83 | 2 | 6 |
| 43 | 1946 | 81 | 2 | 6 |
| 44 | 1932 | 79 | 2 | 6 |
| 45 | 1918 | 78 | 2 | 6 |
| 46 | 1905 | 76 | 2 | 6 |
| 47 | 1891 | 74 | 2 | 6 |
| 48 | 1877 | 73 | 2 | 6 |
| 49 | 1863 | 71 | 2 | 6 |
| 50 | 1850 | 70 | 2 | 6 |
| 51 | 1836 | 68 | 2 | 6 |
| 52 | 1823 | 67 | 2 | 6 |
| 53 | 1809 | 66 | 2 | 6 |
| 54 | 1796 | 65 | 2 | 6 |
Table 2.
Established formalized performance matrix from the adapted case data and calculation results.
Table 2.
Established formalized performance matrix from the adapted case data and calculation results.
| Record day | Output | Input | Aggregated input value | Traditional method productivity(output/input) | Dredging productivity result/One-day high dredging productivity | ||
|---|---|---|---|---|---|---|---|
| Daily dredging | Number of trucks | Excavator SL-330 | Excavator 320B | ||||
| 1 | 1668 | 0.817 | 0.500 | 0.833 | 2.150 | 775.814 | 0.913 |
| 2 | 1683 | 0.817 | 0.500 | 0.833 | 2.150 | 782.791 | 0.921 |
| 3 | 1701 | 0.833 | 1.000 | 0.500 | 2.333 | 729.000 | 0.858 |
| 4 | 1702 | 0.833 | 1.000 | 0.500 | 2.333 | 729.429 | 0.858 |
| 5 | 1700 | 0.833 | 0.500 | 0.667 | 2.000 | 850.000 | 1.000 |
| 6 | 1696 | 0.825 | 0.500 | 0.833 | 2.158 | 785.792 | 0.924 |
| 7 | 1665 | 0.817 | 1.000 | 0.500 | 2.317 | 718.705 | 0.846 |
| 8 | 1701 | 0.833 | 1.000 | 0.667 | 2.500 | 680.400 | 0.800 |
| 9 | 1716 | 0.842 | 0.500 | 0.833 | 2.175 | 788.966 | 0.928 |
| 10 | 1720 | 0.842 | 0.500 | 0.833 | 2.175 | 790.805 | 0.930 |
| 11 | 1706 | 0.758 | 1.000 | 0.667 | 2.425 | 703.505 | 0.828 |
| 12 | 1717 | 0.775 | 1.000 | 0.667 | 2.442 | 703.208 | 0.827 |
| 13 | 1729 | 0.783 | 0.500 | 0.833 | 2.117 | 816.850 | 0.961 |
| 14 | 1737 | 0.792 | 0.500 | 0.833 | 2.125 | 817.412 | 0.962 |
| 15 | 1747 | 0.800 | 1.000 | 0.833 | 2.633 | 663.418 | 0.780 |
| 16 | 1759 | 0.817 | 1.000 | 0.833 | 2.650 | 663.774 | 0.781 |
| 17 | 1770 | 0.825 | 0.500 | 1.000 | 2.325 | 761.290 | 0.896 |
| 18 | 1782 | 0.833 | 0.500 | 1.000 | 2.333 | 763.714 | 0.898 |
| 19 | 1792 | 0.842 | 1.000 | 0.833 | 2.675 | 669.907 | 0.788 |
| 20 | 1798 | 0.850 | 1.000 | 0.833 | 2.683 | 670.062 | 0.788 |
| 21 | 1826 | 0.867 | 0.500 | 1.000 | 2.367 | 771.549 | 0.908 |
| 22 | 1855 | 0.883 | 0.500 | 1.000 | 2.383 | 778.322 | 0.916 |
| 23 | 1871 | 0.892 | 1.000 | 0.833 | 2.725 | 686.606 | 0.808 |
| 24 | 1895 | 0.900 | 1.000 | 1.000 | 2.900 | 653.448 | 0.769 |
| 25 | 1925 | 0.917 | 1.000 | 1.000 | 2.917 | 660.000 | 0.776 |
| 26 | 1950 | 0.933 | 1.000 | 1.000 | 2.933 | 664.773 | 0.782 |
| 27 | 1985 | 0.950 | 1.000 | 1.000 | 2.950 | 672.881 | 0.792 |
| 28 | 2041 | 0.975 | 1.000 | 1.000 | 2.975 | 686.050 | 0.807 |
| 29 | 2093 | 1.000 | 1.000 | 1.000 | 3.000 | 697.667 | 0.821 |
| 30 | 2089 | 0.967 | 1.000 | 1.000 | 2.967 | 704.157 | 0.828 |
| 31 | 2083 | 0.942 | 1.000 | 1.000 | 2.942 | 708.102 | 0.833 |
| 32 | 2076 | 0.908 | 1.000 | 1.000 | 2.908 | 713.811 | 0.840 |
| 33 | 2067 | 0.883 | 1.000 | 1.000 | 2.883 | 716.879 | 0.843 |
| 34 | 2058 | 0.858 | 1.000 | 1.000 | 2.858 | 720.000 | 0.847 |
| 35 | 2047 | 0.833 | 1.000 | 1.000 | 2.833 | 722.471 | 0.850 |
| 36 | 2036 | 0.808 | 1.000 | 1.000 | 2.808 | 724.985 | 0.853 |
| 37 | 2024 | 0.783 | 1.000 | 1.000 | 2.783 | 727.186 | 0.856 |
| 38 | 2012 | 0.767 | 1.000 | 1.000 | 2.767 | 727.229 | 0.856 |
| 39 | 1999 | 0.742 | 1.000 | 1.000 | 2.742 | 729.119 | 0.858 |
| 40 | 1986 | 0.725 | 1.000 | 1.000 | 2.725 | 728.807 | 0.857 |
| 41 | 1973 | 0.708 | 1.000 | 1.000 | 2.708 | 728.492 | 0.857 |
| 42 | 1959 | 0.692 | 1.000 | 1.000 | 2.692 | 727.802 | 0.856 |
| 43 | 1946 | 0.675 | 1.000 | 1.000 | 2.675 | 727.477 | 0.856 |
| 44 | 1932 | 0.658 | 1.000 | 1.000 | 2.658 | 726.771 | 0.855 |
| 45 | 1918 | 0.650 | 1.000 | 1.000 | 2.650 | 723.774 | 0.851 |
| 46 | 1905 | 0.633 | 1.000 | 1.000 | 2.633 | 723.418 | 0.851 |
| 47 | 1891 | 0.617 | 1.000 | 1.000 | 2.617 | 722.675 | 0.850 |
| 48 | 1877 | 0.608 | 1.000 | 1.000 | 2.608 | 719.617 | 0.847 |
| 49 | 1863 | 0.592 | 1.000 | 1.000 | 2.592 | 718.842 | 0.846 |
| 50 | 1850 | 0.583 | 1.000 | 1.000 | 2.583 | 716.129 | 0.843 |
| 51 | 1836 | 0.567 | 1.000 | 1.000 | 2.567 | 715.325 | 0.842 |
| 52 | 1823 | 0.558 | 1.000 | 1.000 | 2.558 | 712.573 | 0.838 |
| 53 | 1809 | 0.550 | 1.000 | 1.000 | 2.550 | 709.412 | 0.835 |
| 54 | 1796 | 0.542 | 1.000 | 1.000 | 2.542 | 706.623 | 0.831 |
Table 3.
Daily productivity calculation results using the DEA method.
| Record day | Output | Input | DEA (CCR) | ||
|---|---|---|---|---|---|
| Daily dredging | Number of trucks | Excavator SL-330 | Excavator 320B | Daily productivity | |
| 1 | 1668 | 0.817 | 0.500 | 0.833 | 0.952 |
| 2 | 1683 | 0.817 | 0.500 | 0.833 | 0.960 |
| 3 | 1701 | 0.833 | 1.000 | 0.500 | 0.999 |
| 4 | 1702 | 0.833 | 1.000 | 0.500 | 1.000 |
| 5 | 1700 | 0.833 | 0.500 | 0.667 | 1.000 |
| 6 | 1696 | 0.825 | 0.500 | 0.833 | 0.965 |
| 7 | 1665 | 0.817 | 1.000 | 0.500 | 0.992 |
| 8 | 1701 | 0.833 | 1.000 | 0.667 | 0.920 |
| 9 | 1716 | 0.842 | 0.500 | 0.833 | 0.971 |
| 10 | 1720 | 0.842 | 0.500 | 0.833 | 0.973 |
| 11 | 1706 | 0.758 | 1.000 | 0.667 | 0.968 |
| 12 | 1717 | 0.775 | 1.000 | 0.667 | 0.963 |
| 13 | 1729 | 0.783 | 0.500 | 0.833 | 1.000 |
| 14 | 1737 | 0.792 | 0.500 | 0.833 | 1.000 |
| 15 | 1747 | 0.800 | 1.000 | 0.833 | 0.892 |
| 16 | 1759 | 0.817 | 1.000 | 0.833 | 0.890 |
| 17 | 1770 | 0.825 | 0.500 | 1.000 | 0.993 |
| 18 | 1782 | 0.833 | 0.500 | 1.000 | 0.994 |
| 19 | 1792 | 0.842 | 1.000 | 0.833 | 0.893 |
| 20 | 1798 | 0.850 | 1.000 | 0.833 | 0.892 |
| 21 | 1826 | 0.867 | 0.500 | 1.000 | 0.995 |
| 22 | 1855 | 0.883 | 0.500 | 1.000 | 1.000 |
| 23 | 1871 | 0.892 | 1.000 | 0.833 | 0.906 |
| 24 | 1895 | 0.900 | 1.000 | 1.000 | 0.853 |
| 25 | 1925 | 0.917 | 1.000 | 1.000 | 0.859 |
| 26 | 1950 | 0.933 | 1.000 | 1.000 | 0.863 |
| 27 | 1985 | 0.950 | 1.000 | 1.000 | 0.871 |
| 28 | 2041 | 0.975 | 1.000 | 1.000 | 0.885 |
| 29 | 2093 | 1.000 | 1.000 | 1.000 | 0.896 |
| 30 | 2089 | 0.967 | 1.000 | 1.000 | 0.909 |
| 31 | 2083 | 0.942 | 1.000 | 1.000 | 0.918 |
| 32 | 2076 | 0.908 | 1.000 | 1.000 | 0.931 |
| 33 | 2067 | 0.883 | 1.000 | 1.000 | 0.939 |
| 34 | 2058 | 0.858 | 1.000 | 1.000 | 0.947 |
| 35 | 2047 | 0.833 | 1.000 | 1.000 | 0.955 |
| 36 | 2036 | 0.808 | 1.000 | 1.000 | 0.963 |
| 37 | 2024 | 0.783 | 1.000 | 1.000 | 0.971 |
| 38 | 2012 | 0.767 | 1.000 | 1.000 | 0.973 |
| 39 | 1999 | 0.742 | 1.000 | 1.000 | 0.981 |
| 40 | 1986 | 0.725 | 1.000 | 1.000 | 0.984 |
| 41 | 1973 | 0.708 | 1.000 | 1.000 | 0.987 |
| 42 | 1959 | 0.692 | 1.000 | 1.000 | 0.989 |
| 43 | 1946 | 0.675 | 1.000 | 1.000 | 0.992 |
| 44 | 1932 | 0.658 | 1.000 | 1.000 | 0.995 |
| 45 | 1918 | 0.650 | 1.000 | 1.000 | 0.993 |
| 46 | 1905 | 0.633 | 1.000 | 1.000 | 0.996 |
| 47 | 1891 | 0.617 | 1.000 | 1.000 | 0.999 |
| 48 | 1877 | 0.608 | 1.000 | 1.000 | 0.997 |
| 49 | 1863 | 0.592 | 1.000 | 1.000 | 0.999 |
| 50 | 1850 | 0.583 | 1.000 | 1.000 | 0.998 |
| 51 | 1836 | 0.567 | 1.000 | 1.000 | 1.000 |
| 52 | 1823 | 0.558 | 1.000 | 1.000 | 1.000 |
| 53 | 1809 | 0.550 | 1.000 | 1.000 | 1.000 |
| 54 | 1796 | 0.542 | 1.000 | 1.000 | 1.000 |
Table 4.
Established formalized performance matrix (normalization).
| Record day | Output | Input | ||
|---|---|---|---|---|
| Daily dredging | Number of trucks | Excavator SL-330 | Excavator 320B | |
| Regression coefficient | 3.767 | 156.43 | 110.981 | |
Table 5.
Calculated normal matrix weighted objective weights for input and output items.
| Record day | Output | Input | Aggregated total input value after conversion | ||
|---|---|---|---|---|---|
| Daily dredging | Number of trucks | Excavator SL-330 | Excavator 320B | ||
| Regression coefficient | 3.767 | 156.43 | 110.981 | ||
| Conversion factors | 1 | 41.523 | 29.459 | ||
| 1 | 1668 | 98.000 | 41.523 | 147.295 | 286.818 |
| 2 | 1683 | 98.000 | 41.523 | 147.295 | 286.818 |
| 3 | 1701 | 100.000 | 83.046 | 88.377 | 271.423 |
| 4 | 1702 | 100.000 | 83.046 | 88.377 | 271.423 |
| 5 | 1700 | 100.000 | 41.523 | 117.836 | 259.359 |
| 6 | 1696 | 99.000 | 41.523 | 147.295 | 287.818 |
| 7 | 1665 | 98.000 | 83.046 | 88.377 | 269.423 |
| 8 | 1701 | 100.000 | 83.046 | 117.836 | 300.882 |
| 9 | 1716 | 101.000 | 41.523 | 147.295 | 289.818 |
| 10 | 1720 | 101.000 | 41.523 | 147.295 | 289.818 |
| 11 | 1706 | 91.000 | 83.046 | 117.836 | 291.882 |
| 12 | 1717 | 93.000 | 83.046 | 117.836 | 293.882 |
| 13 | 1729 | 94.000 | 41.523 | 147.295 | 282.818 |
| 14 | 1737 | 95.000 | 41.523 | 147.295 | 283.818 |
| 15 | 1747 | 96.000 | 83.046 | 147.295 | 326.341 |
| 16 | 1759 | 98.000 | 83.046 | 147.295 | 328.341 |
| 17 | 1770 | 99.000 | 41.523 | 176.754 | 317.277 |
| 18 | 1782 | 100.000 | 41.523 | 176.754 | 318.277 |
| 19 | 1792 | 101.000 | 83.046 | 147.295 | 331.341 |
| 20 | 1798 | 102.000 | 83.046 | 147.295 | 332.341 |
| 21 | 1826 | 104.000 | 41.523 | 176.754 | 322.277 |
| 22 | 1855 | 106.000 | 41.523 | 176.754 | 324.277 |
| 23 | 1871 | 107.000 | 83.046 | 147.295 | 337.341 |
| 24 | 1895 | 108.000 | 83.046 | 176.754 | 367.800 |
| 25 | 1925 | 110.000 | 83.046 | 176.754 | 369.800 |
| 26 | 1950 | 112.000 | 83.046 | 176.754 | 371.800 |
| 27 | 1985 | 114.000 | 83.046 | 176.754 | 373.800 |
| 28 | 2041 | 117.000 | 83.046 | 176.754 | 376.800 |
| 29 | 2093 | 120.000 | 83.046 | 176.754 | 379.800 |
| 30 | 2089 | 116.000 | 83.046 | 176.754 | 375.800 |
| 31 | 2083 | 113.000 | 83.046 | 176.754 | 372.800 |
| 32 | 2076 | 109.000 | 83.046 | 176.754 | 368.800 |
| 33 | 2067 | 106.000 | 83.046 | 176.754 | 365.800 |
| 34 | 2058 | 103.000 | 83.046 | 176.754 | 362.800 |
| 35 | 2047 | 100.000 | 83.046 | 176.754 | 359.800 |
| 36 | 2036 | 97.000 | 83.046 | 176.754 | 356.800 |
| 37 | 2024 | 94.000 | 83.046 | 176.754 | 353.800 |
| 38 | 2012 | 92.000 | 83.046 | 176.754 | 351.800 |
| 39 | 1999 | 89.000 | 83.046 | 176.754 | 348.800 |
| 40 | 1986 | 87.000 | 83.046 | 176.754 | 346.800 |
| 41 | 1973 | 85.000 | 83.046 | 176.754 | 344.800 |
| 42 | 1959 | 83.000 | 83.046 | 176.754 | 342.800 |
| 43 | 1946 | 81.000 | 83.046 | 176.754 | 340.800 |
| 44 | 1932 | 79.000 | 83.046 | 176.754 | 338.800 |
| 45 | 1918 | 78.000 | 83.046 | 176.754 | 337.800 |
| 46 | 1905 | 76.000 | 83.046 | 176.754 | 335.800 |
| 47 | 1891 | 74.000 | 83.046 | 176.754 | 333.800 |
| 48 | 1877 | 73.000 | 83.046 | 176.754 | 332.800 |
| 49 | 1863 | 71.000 | 83.046 | 176.754 | 330.800 |
| 50 | 1850 | 70.000 | 83.046 | 176.754 | 329.800 |
| 51 | 1836 | 68.000 | 83.046 | 176.754 | 327.800 |
| 52 | 1823 | 67.000 | 83.046 | 176.754 | 326.800 |
| 53 | 1809 | 66.000 | 83.046 | 176.754 | 325.800 |
| 54 | 1796 | 65.000 | 83.046 | 176.754 | 324.800 |
Table 6.
Calculated daily productivity and rank.
| Record day | Output | Input | DEA(CCR) | Rank |
|---|---|---|---|---|
| Daily dredging | Total input | Daily productivity | ||
| 1 | 1668 | 286.818 | 0.887 | 13 |
| 2 | 1683 | 286.818 | 0.895 | 10 |
| 3 | 1701 | 271.423 | 0.956 | 3 |
| 4 | 1702 | 271.423 | 0.957 | 2 |
| 5 | 1700 | 259.359 | 1.000 | 1 |
| 6 | 1696 | 287.818 | 0.899 | 9 |
| 7 | 1665 | 269.423 | 0.943 | 4 |
| 8 | 1701 | 300.882 | 0.863 | 30 |
| 9 | 1716 | 289.818 | 0.903 | 8 |
| 10 | 1720 | 289.818 | 0.905 | 7 |
| 11 | 1706 | 291.882 | 0.892 | 11 |
| 12 | 1717 | 293.882 | 0.891 | 12 |
| 13 | 1729 | 282.818 | 0.933 | 6 |
| 14 | 1737 | 283.818 | 0.934 | 5 |
| 15 | 1747 | 326.341 | 0.817 | 49 |
| 16 | 1759 | 328.341 | 0.817 | 49 |
| 17 | 1770 | 317.277 | 0.851 | 39 |
| 18 | 1782 | 318.277 | 0.854 | 37 |
| 19 | 1792 | 331.341 | 0.825 | 47 |
| 20 | 1798 | 332.341 | 0.825 | 47 |
| 21 | 1826 | 322.277 | 0.864 | 28 |
| 22 | 1855 | 324.277 | 0.873 | 16 |
| 23 | 1871 | 337.341 | 0.846 | 43 |
| 24 | 1895 | 367.800 | 0.786 | 54 |
| 25 | 1925 | 369.800 | 0.794 | 53 |
| 26 | 1950 | 371.800 | 0.800 | 52 |
| 27 | 1985 | 373.800 | 0.810 | 51 |
| 28 | 2041 | 376.800 | 0.826 | 46 |
| 29 | 2093 | 379.800 | 0.841 | 45 |
| 30 | 2089 | 375.800 | 0.848 | 41 |
| 31 | 2083 | 372.800 | 0.852 | 38 |
| 32 | 2076 | 368.800 | 0.859 | 33 |
| 33 | 2067 | 365.800 | 0.862 | 31 |
| 34 | 2058 | 362.800 | 0.865 | 26 |
| 35 | 2047 | 359.800 | 0.868 | 24 |
| 36 | 2036 | 356.800 | 0.871 | 21 |
| 37 | 2024 | 353.800 | 0.873 | 16 |
| 38 | 2012 | 351.800 | 0.873 | 16 |
| 39 | 1999 | 348.800 | 0.874 | 14 |
| 40 | 1986 | 346.800 | 0.874 | 14 |
| 41 | 1973 | 344.800 | 0.873 | 16 |
| 42 | 1959 | 342.800 | 0.872 | 20 |
| 43 | 1946 | 340.800 | 0.871 | 21 |
| 44 | 1932 | 338.800 | 0.870 | 23 |
| 45 | 1918 | 337.800 | 0.866 | 25 |
| 46 | 1905 | 335.800 | 0.865 | 26 |
| 47 | 1891 | 333.800 | 0.864 | 28 |
| 48 | 1877 | 332.800 | 0.860 | 32 |
| 49 | 1863 | 330.800 | 0.859 | 33 |
| 50 | 1850 | 329.800 | 0.856 | 35 |
| 51 | 1836 | 327.800 | 0.855 | 36 |
| 52 | 1823 | 326.800 | 0.851 | 39 |
| 53 | 1809 | 325.800 | 0.847 | 42 |
| 54 | 1796 | 324.800 | 0.844 | 44 |
Table 7.
Comparison of the sorted calculated results calculated using each method
| Record day | Traditional method | DEA method | Propose method | |||
|---|---|---|---|---|---|---|
| Output/input | Ranking | Performance | Ranking | Daily productivity | Ranking | |
| 1 | 0.913 | 9 | 0.952 | 37 | 0.887 | 13 |
| 2 | 0.921 | 7 | 0.96 | 35 | 0.895 | 10 |
| 3 | 0.858 | 13 | 0.999 | 10 | 0.956 | 3 |
| 4 | 0.858 | 13 | 1 | 1 | 0.957 | 2 |
| 5 | 1 | 1 | 1 | 1 | 1.000 | 1 |
| 6 | 0.924 | 6 | 0.965 | 32 | 0.899 | 9 |
| 7 | 0.846 | 30 | 0.992 | 21 | 0.943 | 4 |
| 8 | 0.8 | 46 | 0.92 | 41 | 0.863 | 30 |
| 9 | 0.928 | 5 | 0.971 | 29 | 0.903 | 8 |
| 10 | 0.93 | 4 | 0.973 | 27 | 0.905 | 7 |
| 11 | 0.828 | 40 | 0.968 | 31 | 0.892 | 11 |
| 12 | 0.827 | 42 | 0.963 | 33 | 0.891 | 12 |
| 13 | 0.961 | 3 | 1 | 1 | 0.933 | 6 |
| 14 | 0.962 | 2 | 1 | 1 | 0.934 | 5 |
| 15 | 0.78 | 52 | 0.892 | 47 | 0.817 | 49 |
| 16 | 0.781 | 51 | 0.89 | 49 | 0.817 | 49 |
| 17 | 0.896 | 12 | 0.993 | 19 | 0.851 | 39 |
| 18 | 0.898 | 11 | 0.994 | 18 | 0.854 | 37 |
| 19 | 0.788 | 48 | 0.893 | 46 | 0.825 | 47 |
| 20 | 0.788 | 48 | 0.892 | 47 | 0.825 | 47 |
| 21 | 0.908 | 10 | 0.995 | 16 | 0.864 | 28 |
| 22 | 0.916 | 8 | 1 | 1 | 0.873 | 16 |
| 23 | 0.808 | 44 | 0.906 | 44 | 0.846 | 43 |
| 24 | 0.769 | 54 | 0.853 | 54 | 0.786 | 54 |
| 25 | 0.776 | 53 | 0.859 | 53 | 0.794 | 53 |
| 26 | 0.782 | 50 | 0.863 | 52 | 0.800 | 52 |
| 27 | 0.792 | 47 | 0.871 | 51 | 0.810 | 51 |
| 28 | 0.807 | 45 | 0.885 | 50 | 0.826 | 46 |
| 29 | 0.821 | 43 | 0.896 | 45 | 0.841 | 45 |
| 30 | 0.828 | 40 | 0.909 | 43 | 0.848 | 41 |
| 31 | 0.833 | 38 | 0.918 | 42 | 0.852 | 38 |
| 32 | 0.84 | 35 | 0.931 | 40 | 0.859 | 33 |
| 33 | 0.843 | 32 | 0.939 | 39 | 0.862 | 31 |
| 34 | 0.847 | 28 | 0.947 | 38 | 0.865 | 26 |
| 35 | 0.85 | 26 | 0.955 | 36 | 0.868 | 24 |
| 36 | 0.853 | 23 | 0.963 | 33 | 0.871 | 21 |
| 37 | 0.856 | 18 | 0.971 | 29 | 0.873 | 16 |
| 38 | 0.856 | 18 | 0.973 | 27 | 0.873 | 16 |
| 39 | 0.858 | 13 | 0.981 | 26 | 0.874 | 14 |
| 40 | 0.857 | 16 | 0.984 | 25 | 0.874 | 14 |
| 41 | 0.857 | 16 | 0.987 | 24 | 0.873 | 16 |
| 42 | 0.856 | 18 | 0.989 | 23 | 0.872 | 20 |
| 43 | 0.856 | 18 | 0.992 | 21 | 0.871 | 21 |
| 44 | 0.855 | 22 | 0.995 | 16 | 0.870 | 23 |
| 45 | 0.851 | 24 | 0.993 | 19 | 0.866 | 25 |
| 46 | 0.851 | 24 | 0.996 | 15 | 0.865 | 26 |
| 47 | 0.85 | 26 | 0.999 | 10 | 0.864 | 28 |
| 48 | 0.847 | 28 | 0.997 | 14 | 0.860 | 32 |
| 49 | 0.846 | 30 | 0.999 | 10 | 0.859 | 33 |
| 50 | 0.843 | 32 | 0.998 | 13 | 0.856 | 35 |
| 51 | 0.842 | 34 | 1 | 1 | 0.855 | 36 |
| 52 | 0.838 | 36 | 1 | 1 | 0.851 | 39 |
| 53 | 0.835 | 37 | 1 | 1 | 0.847 | 42 |
| 54 | 0.831 | 39 | 1 | 1 | 0.844 | 44 |
Table 8.
Comparison of the main differences between the above four methods.
| Method | Traditional | DEA | Proposed method | |
|---|---|---|---|---|
| Solve problem | ||||
| Multiple inputs and single outputs | No | Yes | Yes | |
| Multiple inputs and multiple outputs | No | Yes | Yes | |
| Effectively resolve performance duplication | Yes | No | Yes | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated