Properties and Maximum Likelihood Estimation of the Novel Mixture of Fréchet Distribution

Preprint

Article

Properties and Maximum Likelihood Estimation of the Novel Mixture of Fréchet Distribution

Altmetrics

Downloads

155

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 June 2023

Posted:

22 June 2023

You are already at the latest version

Alerts

Abstract

In recent decades, there have been numerous endeavors to develop a novel category of survival distributions possessing enhanced flexibility through the extension of existing distributions. This article constructs and validates the statistical properties of a novel survival distribution in order to obtain an alternative distribution that is suitable for analyzing survival data by presenting the novel mixture of the Fréchet distribution along with statistical properties such as the probability density function (PDF), cumulative distribution function (CDF), rth ordinary moment, skewness, kurtosis, moment-generating function, mean, variance, mode, survival function, hazard function, and asymptotic behavior, as well as constructing the estimators of the unknown parameter by employing the expectation-maximization (EM) algorithm, and simulated annealing. Additionally, the performance of the proposed estimators was compared with bias, mean squared errors (MSE), and simulated variances, and given an illustrative example of the proposed distribution to the survival data set in order to show that the proposed distribution is appropriate for the right-skewed data. This will be extremely advantageous in survival analysis.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

Survival analysis, a branch of statistics pertaining to death or failure, encompasses various types of statistical methods to draw conclusions. These methods include 1) nonparametric statistics, such as the Kaplan-Meier estimator and the log-rank test; 2) semi-parametric statistics, exemplified by the Cox proportional hazards model; and 3) parametric statistics, which focus on simulating survival time probabilities. Analysts may deduce that the survival function has a parametric distribution. For instance, if the survival time adheres to an exponential distribution, the hazard rate will be constant. Conversely, if the survival time conforms to a log-normal distribution, the hazard rate varies with time. Consequently, estimation of the survival function, calculation of the confidence interval, and assessment of the relative risk ensue. The utilization of a parametric survival function proves highly effective when appropriate distributions and parameter values are selected. The parametric survival distribution serves as a comprehensive representation of various types of survival data.

Hundreds of univariate continuous distributions exist. Mixture models play a crucial role in numerous applications, including survival analysis. These models involve the combination of two or more statistical distributions to create a new distribution, thereby addressing various challenges encountered in the field. Recognizing the evident necessity for mixture distributions, extensive efforts have been devoted to integrating multiple well-established distributions and utilizing them to tackle relevant issues. In the context of complete samples, Niyomdecha and Srisuradetchai [1] introduce a novel continuous three-parameter survival distribution referred to as the Complementary Gamma Zero-Truncated Poisson distribution. The traits of the maximum value in a series of independently identical gamma-distributed random variables are combined with those of zero-truncated Poisson random variables in this distribution. Abdullahi and Phaphan [2] present a mixture of Nakagami distribution, accompanied by statistical properties and a comparative analysis of the efficacy of estimators utilizing the quasi-Newton method and simulated annealing. Nanuwong et al. [3] proposed the mixture Pareto distribution by combining a Pareto distribution and a length-biased Pareto distribution. This distribution was formulated based on the concept of a weighted two-component distribution. Further investigation pertaining to the mixture models can be found in the references [4,5,6,7].

The Fréchet distribution, alternatively referred to as the inverse Weibull distribution, holds extensive application in the field of survival modeling. Fréchet [8] initially introduced the Fréchet distribution, which subsequently underwent further exploration by Fisher and Tippett [9] as well as Gumbel [10]. Furthermore, Abbas and Yincai [11] conducted a comparative analysis of the scale parameter estimation for the Fréchet distribution, employing maximum likelihood, probability-weighted moments, and Bayes estimations. Nasir and Aslam [12] utilized a Bayesian technique to estimate the parameter of the Fréchet distribution. Reyad et al. [13] established QE-Bayes and E-Bayes estimates for the scale parameters associated with the Fréchet distribution. Recent developments have introduced various extensions to the Fréchet distribution. Notably, Mead et al. [14] proposed the beta exponential Fréchet distribution.

Consequently, this article has paid special attention to developing a new survival distribution by employing the notion of a mixture distribution, which is based on the Fréchet distribution, to obtain a new alternative distribution with the value of the time-varying hazard rate and investigating the statistical properties of the new distribution, such as the probability density function, cumulative distribution function,

r^{t h}

ordinary moment, skewness, kurtosis, moment-generating function, mean, variance, mode, survival function, hazard function, asymptotic behavior, comparison of the estimators with several methods, and samples of applying to real data, which will be extremely useful in survival analysis.

2. The Fréchet Distribution

The Fréchet distribution, being a specific case of the generalized extreme value distribution, finds extensive application in the field of hydrology. This distribution is commonly employed to model extreme events, including annual maximum one-day rainfalls and river discharges. Moreover, the Fréchet distribution holds considerable significance in survival analysis utilizing experimental data from clinical research. Given its status as the inverse Weibull distribution, the Fréchet distribution exhibits properties akin to the Weibull distribution, such as time-varying hazard rates. As a result, the Fréchet distribution has been a subject of widespread discussion in the field of survival analysis.

Afify et al. [15] provides the probability density function (PDF), cumulative distribution function (CDF), and mean of the Fréchet distribution, as described by

\begin{matrix} g (x) = δ λ^{δ} x^{- (δ + 1)} e^{- {(\frac{λ}{x})}^{δ}}, x > 0 . \end{matrix}

(1)

Given that

λ > 0

represents a scale parameter and

δ > 0

represents a shape parameter, the cumulative distribution function (CDF) associated with these parameters can be expressed as follows:

\begin{matrix} G (x) = e^{- {(\frac{λ}{x})}^{δ}} . \end{matrix}

(2)

Furthermore, the mean of the distribution can be determined as follows:

\begin{matrix} E (X) = λ Γ (1 - \frac{1}{δ}) . \end{matrix}

(3)

3. The Length-biased Fréchet Distribution

Within the framework presented by Hesham et al. [16], a length-biased Fréchet distribution was introduced along with its associated CDF, PDF, and mean. The specific form of the CDF can be expressed using Equation (4).

\begin{matrix} G_{L} (x) = \frac{1}{Γ (1 - \frac{1}{δ})} Γ (1 - \frac{1}{δ}, {(\frac{λ}{x})}^{δ}), x > 0, \end{matrix}

(4)

where

λ > 0

, and

δ > 1

. The associated PDF can be expressed as follows:

\begin{matrix} g_{L} (x) = \frac{δ λ^{δ - 1}}{Γ (1 - \frac{1}{δ})} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} . \end{matrix}

(5)

Additionally, the distribution’s mean can be determined using the formula below:

\begin{matrix} E_{L} (X) = \frac{λ Γ (1 - \frac{2}{δ})}{Γ (1 - \frac{1}{δ})}, δ > 2 . \end{matrix}

(6)

4. Theoretical Result

4.1. The Probability Density Function of the Novel Mixture Fréchet (NMF) Distribution

This subsection aims to construct a novel distribution by employing the notion of a mixture distribution. The proposed distribution will be a composite of two distinct distributions, namely the Fréchet distribution and the length-biased Fréchet distribution. The probability density function (PDF) of the newly developed distribution will be derived, utilizing the function of parameter

λ

as a weighted parameter. Consequently, the PDF of the novel mixture Fréchet (NMF) distribution is defined as:

\begin{matrix} f_{N M F} (x) = \frac{1}{λ + 1} g (x) + \frac{λ}{λ + 1} g_{L} (x), x > 0, \end{matrix}

(7)

where

λ > 0

, and

δ > 1

. By substituting Equations (1) and (5) into Equation (7), the resulting expression is denoted as

\begin{matrix} f_{N M F} (x) = \frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{{- (\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})}), x > 0, λ > 0, δ > 1 . \end{matrix}

(8)

Therefore, Equation (8) represents the PDF of the NMF distribution.

4.2. Validity Check of the NMF Distribution for a Proper Density Function

A probability density function (PDF) is considered valid if it satisfies the following conditions:

\begin{matrix} \int_{- \infty}^{\infty} f (x) \partial x = 1 . \end{matrix}

(9)

In order to demonstrate the validity of the proposed NMF distribution as a PDF, the following steps are undertaken:

\begin{matrix} \int_{0}^{\infty} \frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})}) \partial x = 1, \end{matrix}

(10)

let

\begin{matrix} u = {(\frac{λ}{x})}^{δ} ⟹ x = \frac{k^{\frac{1}{β}}}{λ}, \end{matrix}

(11)

and

\begin{matrix} \partial x = \frac{\partial k}{λ β {(λ x)}^{β - 1}} . \end{matrix}

(12)

By substituting Equation (11) and (12) into Equation (10), the resulting expression can be obtained.

\begin{matrix} \int_{0}^{\infty} f_{N M F} (x) \partial x & = & \frac{1}{λ + 1} \int_{0}^{\infty} k^{α - 1 + \frac{1}{β}} e^{- k} (\frac{λ}{k^{\frac{1}{β}} Γ (α)} + \frac{1}{Γ (α + \frac{1}{β})}) \partial k \\ = & \frac{1}{λ + 1} (\frac{λ}{Γ (α)} Γ (α) + \frac{1}{Γ (α + \frac{1}{β})} Γ (α + \frac{1}{β})) \\ = & \frac{λ}{(λ + 1)} + \frac{1}{(λ + 1)} \\ = & 1 . \end{matrix}

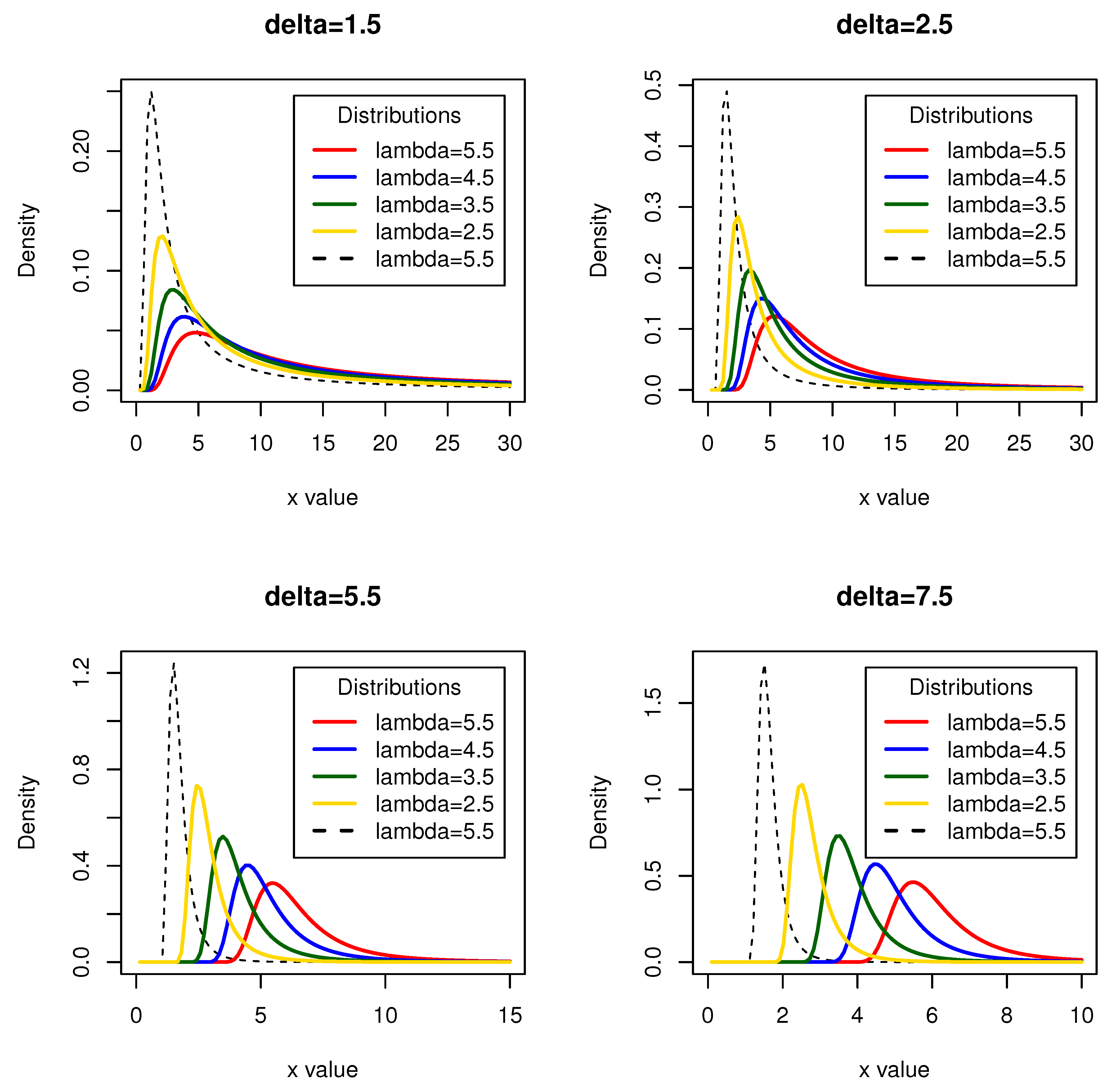
This demonstrates that the PDF defined in Equation (8) conforms to the properties of a valid probability density distribution. Figure 1 depict the PDF of the novel mixture of Fréchet distribution for different parameter values. The displayed variety of shapes demonstrates the right-skewed nature of the NMF distribution. Additionally, being a family of asymmetric distributions, the NMF distribution proves to be valuable for analyzing skewed data, particularly data with a right-skewed distribution, such as survival data.

4.3. The Cumulative Density Function of the NMF Distribution

Let

G (x)

and

G_{L} (x)

represent the cumulative density function (CDF) of the Fréchet distribution and the length-biased Fréchet distribution, respectively. Consider a random variable X following the novel mixture Fréchet (NMF) distribution. The CDF for X in this instance can be written as follows:

\begin{matrix} F_{N M F} (x) & = & \int_{0}^{x} f (t) \partial t \\ = & \int_{0}^{x} (\frac{1}{λ + 1} g (t) + \frac{λ}{λ + 1} g_{L} (t)) \partial t \end{matrix}

(13)

\begin{matrix} = & \frac{1}{λ + 1} G (x) + \frac{λ}{λ + 1} G_{L} (x) . \end{matrix}

(14)

From Equation (14), the CDF of the novel mixture of Fréchet distribution can be expressed as

\begin{matrix} F (x) & = & \frac{1}{λ + 1} [e^{- {(\frac{λ}{x})}^{δ}}] + \frac{λ}{λ + 1} [\frac{1}{Γ (1 - \frac{1}{δ})} Γ (1 - \frac{1}{δ}, {(\frac{λ}{x})}^{δ})] \\ = & \frac{1}{λ + 1} [e^{- {(\frac{λ}{x})}^{δ}} + \frac{λ}{Γ (1 - \frac{1}{δ})} Γ (1 - \frac{1}{δ}, {(\frac{λ}{x})}^{δ})] . \end{matrix}

(15)

4.4. The $r^{t h}$ Ordinary Moment of the NMF Distribution

The NMF distribution’s

r t h

ordinary moment is expressed as follows:

\begin{matrix} μ_{r}^{'} = E_{M} (X^{r}) = \int_{0}^{\infty} x^{r} f (x) \partial x . \end{matrix}

(16)

Equation (19) gives the explicit expression for the

r t h

ordinary moment of the NMF distribution upon inserting Equation (8) into Equation (16) and performing integration with respect to x.

\begin{matrix} \int_{0}^{\infty} \frac{δ λ^{δ}}{(λ + 1)} x^{- δ + r} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})}) \partial x . \end{matrix}

(17)

\begin{matrix} μ_{r}^{'} = \frac{1}{λ + 1} E (X^{r}) + \frac{λ}{λ + 1} E_{L} (X^{r}), \end{matrix}

(18)

where

\begin{matrix} E (X^{r}) = λ^{r} Γ (1 - \frac{r}{δ}), \end{matrix}

and

\begin{matrix} E_{L} (X) = \frac{λ^{r} Γ (1 - \frac{r + 1}{δ})}{Γ (1 - \frac{1}{δ})} . \end{matrix}

\begin{matrix} μ_{r}^{'} = \frac{1}{λ + 1} λ^{r} Γ (1 - \frac{r}{δ}) + \frac{1}{λ + 1} \frac{λ^{r + 1} Γ (1 - \frac{r + 1}{δ})}{Γ (1 - \frac{1}{δ})}, r = 1, 2, 3, \dots \end{matrix}

(19)

The following is the mathematical expression for the mean of the NMF distribution:

\begin{matrix} E_{N M F} (X) = \frac{λ}{(λ + 1)} [Γ (1 - \frac{1}{δ}) + \frac{λ Γ (1 - \frac{2}{δ})}{Γ (1 - \frac{1}{δ})}] . \end{matrix}

(20)

The second moment of the NMF distribution, denoted as

E (X^{2})

, can be derived from Equation (19) by setting the value of

r = 2

\begin{matrix} E_{N M F} (X^{2}) = \frac{λ^{2}}{(λ + 1)} [Γ (1 - \frac{2}{δ}) + \frac{λ Γ (1 - \frac{3}{δ})}{Γ (1 - \frac{1}{δ})}] . \end{matrix}

(21)

The third moment of the NMF distribution, denoted as

E (X^{3})

, can be obtained from Equation (19) by substituting

r = 3

\begin{matrix} E_{N M F} (X^{3}) = \frac{λ^{3}}{(λ + 1)} [Γ (1 - \frac{3}{δ}) + \frac{λ Γ (1 - \frac{4}{δ})}{Γ (1 - \frac{1}{δ})}] . \end{matrix}

(22)

The fourth moment of the NMF distribution, denoted as

E (X^{4})

, can be calculated by substituting

r = 4

in Equation (19).

\begin{matrix} E_{N M F} (X^{4}) = \frac{λ^{4}}{(λ + 1)} [Γ (1 - \frac{4}{δ}) + \frac{λ Γ (1 - \frac{5}{δ})}{Γ (1 - \frac{1}{δ})}] . \end{matrix}

(23)

Equation (19) at

r = 1

and

r = 2

and substituting into Equation (24) yields the variance of the NMF distribution.

V a r_{N M F} (X) = E_{M} (X^{2}) - {[E_{M} (X)]}^{2},

(24)

\begin{matrix} V a r_{N M F} (X) = & \frac{λ^{2}}{(λ + 1)} [Γ (1 - \frac{2}{δ}) + \frac{λ Γ (1 - \frac{3}{δ})}{Γ (1 - \frac{1}{δ})}] - \\ {\{\frac{λ}{(λ + 1)} [Γ (1 - \frac{1}{δ}) + \frac{δ Γ (1 - \frac{2}{δ})}{Γ (1 - \frac{1}{δ})}]\}}^{2} . \end{matrix}

(25)

4.5. The Skewness and Kurtosis of the NMF Distribution

The novel mixture Fréchet (NMF) distribution’s skewness and kurtosis coefficients are provided as follows, respectively:

\begin{matrix} Φ_{1} = \frac{E_{N M F} (X^{3})}{{(E_{N M F} (X^{2}))}^{\frac{3}{2}}} = \frac{\frac{λ^{3}}{(λ + 1)} [Γ (1 - \frac{3}{δ}) + \frac{λ Γ (1 - \frac{4}{δ})}{Γ (1 - \frac{1}{δ})}]}{{\{\frac{λ^{2}}{(λ + 1)} [Γ (1 - \frac{2}{δ}) + \frac{δ Γ (1 - \frac{3}{δ})}{Γ (1 - \frac{1}{δ})}]\}}^{\frac{3}{2}}}, \end{matrix}

(26)

and

\begin{matrix} Φ_{2} = \frac{E_{N M F} (X^{4})}{{(E_{N M F} (X^{2}))}^{2}} = \frac{\frac{λ^{4}}{(λ + 1)} [Γ (1 - \frac{4}{δ}) + \frac{λ Γ (1 - \frac{5}{δ})}{Γ (1 - \frac{1}{δ})}]}{{\{\frac{λ^{2}}{(λ + 1)} [Γ (1 - \frac{2}{δ}) + \frac{δ Γ (1 - \frac{3}{δ})}{Γ (1 - \frac{1}{δ})}]\}}^{2}} . \end{matrix}

(27)

4.6. The Moment Generating Function of the NMF Distribution

The NMF distribution’s moment-generating function is provided by

\begin{matrix} E_{N M F} (e^{X t}) = M_{X} (t) = \sum_{r = 0}^{\infty} \frac{t^{r} E_{N M F} (X^{r})}{r!} . \end{matrix}

(28)

By substituting Equation (19) into (28), the NMF distribution’s moment-generating function is derived as presented in Equation (29).

\begin{matrix} M_{X} (t) = \sum_{r = 0}^{\infty} \frac{t^{r}}{r!} \{\frac{1}{λ + 1} λ^{r} Γ (1 - \frac{r}{δ}) + \frac{1}{λ + 1} \frac{λ^{r + 1} Γ (1 - \frac{r + 1}{δ})}{Γ (1 - \frac{1}{δ})}\} . \end{matrix}

(29)

4.7. The Mode of the NMF Distribution

By computing the derivative of the natural logarithm of Equation (8) with respect to x, setting it equal to zero, and solving for x, one is able to determine the mode of the NMF distribution. In this subsection, a nonlinear equation is obtained in Equation ().

\begin{matrix} log f (x) = & log [\frac{δ λ^{δ}}{(λ + 1)}] - δ log (x) - {(\frac{λ}{x})}^{δ} + log (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})}), \end{matrix}

(30)

\begin{matrix} \frac{{(\frac{λ}{x})}^{δ} δ}{x} - \frac{δ}{x} - \frac{1}{x^{2} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})} = 0 . \end{matrix}

(31)

4.8. The Survival Function and the Hazard Rate Function of the NMF Distribution

Consider a continuous random variable, X, whose cumulative density function,

F (x)

, is specified on the range,

[0, \infty)

. The following is an expression for the survival function of X:

\begin{matrix} S (x) = 1 - F (x) . \end{matrix}

(32)

The survival function of the NMF distribution is obtained by inserting Equation (15) into Equation (32):

\begin{matrix} S (x) = 1 - \frac{1}{λ + 1} [e^{- {(\frac{λ}{x})}^{δ}} + \frac{λ}{Γ (1 - \frac{1}{δ})} Γ (1 - \frac{1}{δ}, {(\frac{λ}{x})}^{δ})] . \end{matrix}

(33)

Theoretically possible to define the hazard rate function of X as:

\begin{matrix} h r f (x) = \frac{f (x)}{S (x)} . \end{matrix}

Consequently, the NMF distribution’s hazard rate function is given by

\begin{matrix} h r f (x) = \frac{\frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})}{1 - \frac{1}{λ + 1} [e^{- {(\frac{λ}{x})}^{δ}} + \frac{λ}{Γ (1 - \frac{1}{δ})} Γ (1 - \frac{1}{δ} {(\frac{λ}{x})}^{δ})]} . \end{matrix}

(34)

4.9. Asymptotic Behavior of the NMF Distribution

The NMF distribution exhibits zero asymptotic behavior as x approaches infinity.

\begin{matrix} lim_{x \to \infty} f (x) = lim_{x \to \infty} [\frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})] = 0 . \end{matrix}

(35)

As x approaches

λ

\begin{matrix} lim_{x \to λ} f (x) & = & lim_{x \to \infty} [\frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})] \\ = & \frac{δ}{e (λ + 1)} (\frac{1}{λ} + \frac{1}{Γ (1 - \frac{1}{δ})}) . \end{matrix}

(36)

4.10. Maximum Likelihood Estimation of the NMF Distribution

Maximum likelihood estimators will be utilized in this subsection to estimate the NMF distribution’s parameters. The likelihood function of the NMF distribution is defined as follows if

x_{1}

, ⋯,

x_{n}

represent a random sample of size n taken from the NMF distribution:

\begin{matrix} L (x) & = & \prod_{i = 1}^{n} \{\frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})\}, \end{matrix}

(37)

\begin{matrix} ℓ (x) & = & log \prod_{i = 1}^{n} \{\frac{δ λ^{δ}}{(λ + 1)} x^{- δ} e^{- {(\frac{λ}{x})}^{δ}} (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})\} . \end{matrix}

(38)

Equation (37)’s natural logarithm has been employed to derive the log-likelihood function shown in Equation (39).

\begin{matrix} ℓ (x) & = & n log (δ) + n δ log (λ) - n log (λ + 1) - δ \sum_{i = 1}^{\infty} log (x_{i}) - \sum_{i = 1}^{\infty} {(\frac{λ}{x})}^{δ} \\ + & \sum_{i = 1}^{\infty} log (\frac{1}{x} + \frac{1}{Γ (1 + \frac{1}{δ})}) . \end{matrix}

(39)

By taking the derivative of Equation (39) with respect to

λ

and

δ

and then solving for each of those values, one can obtain the maximum likelihood estimators (MLEs).

\begin{matrix} \frac{\partial ℓ (x)}{\partial λ} & = & \frac{n δ}{λ} - \frac{n}{λ + 1} - \sum_{i = 1}^{\infty} \frac{{(\frac{λ}{x})}^{δ} δ}{λ}, \end{matrix}

(40)

\begin{matrix} \frac{\partial ℓ (x)}{\partial δ} & = & \frac{n}{δ} + n log (λ) - \sum_{i = 1}^{\infty} log (x_{i}) - \sum_{i = 1}^{\infty} {(\frac{λ}{x})}^{δ} log (\frac{λ}{x}) \\ - & \frac{Ψ (1 - \frac{1}{δ})}{δ^{2} Γ (1 - \frac{1}{δ}) (\frac{1}{x} + \frac{1}{Γ (1 - \frac{1}{δ})})} . \end{matrix}

(41)

Due to the nonlinearity of these equations, analytical solutions are not feasible, but iterative methods can be used to solve these numerically. This article proposes the utilization of the expectation-maximization (EM) algorithm and the simulated annealing to construct the MLEs for the NMF distribution.

4.10.1. Maximum Likelihood Estimation employing the Simulated Annealing Algorithm

This article examines the MLEs for the unknown parameters of the NMF distribution. Analytical solutions for the MLEs are not attainable in Section 4.10. Therefore, in this part, the R optimization function, particularly the “optim” function, is employed for maximum likelihood estimation (MLE) using the simulated annealing. The steps of the Simulated Annealing Algorithm are as follows:

Step 1: Given a initial value

x^{(k = 0)}

, temperature T, number of iterations n, and desired accuracy

ε

Step 2: Pick a random value

x^{(k + 1)}

in the vicinity of

x^{(k)}

Step 3: If

Δ E < 0

, where

Δ E = f (x^{(k + 1)}) - f (x^{(k)})

, and

f (x)

represents the objective function, then accept

x^{(k + 1)}

. Otherwise, generate a random number

α

such that

α \in (0, 1)

. If

α \leq exp (- Δ E / K T)

, where K is the Boltzmann constant, then accept

x^{(k + 1)}

. Otherwise, return to Step 2.

Step 4: If

| x^{(k + 1)} - x^{(k)} | < ε

and T is sufficiently small, terminate the iterations. Otherwise, if the number of random number generations reaches n, decrease the value of T, let

k = k + 1

, and go to Step 2. Otherwise, give

k = k + 1

and go to Step 2.

4.10.2. Maximum Likelihood Estimation employing the EM-Algorithm

An Expectation-Maximization (EM) algorithm is an iterative method employed to estimate unknown parameters in incomplete statistical models. The application of the EM algorithm encompasses two primary scenarios. The first arises when the data is incomplete due to observational process issues or limitations. The second arises when optimizing the likelihood function becomes challenging. The procedure for implementing the EM algorithm for the NMF distribution is outlined as follows:

The steps involved in the Expectation (E)-Step

1. Derive the log-likelihood function for an NMF distribution.

\begin{matrix} ln L (x) = \sum_{i = 1}^{n} ln \{\frac{1}{λ + 1} g (x) + \frac{λ}{(λ + 1)} g_{L} (x)\} . \end{matrix}

(42)

2. Compute a complete log-likelihood function by assigning a missing value

κ_{i}

in the function

ln L (x)

. The missing values

κ_{i}

can take either 0 or 1. Thus, the complete random variable is denoted as

Y = (X; K)

, where

y_{1}, y_{2}, \dots, y_{n}

represent the observations with

y_{i} = (t_{i}, κ_{i})

for

i = 1, 2, . . ., n

. Consequently, a complete log-likelihood function is written in:

\begin{matrix} l c o m p l e t e (Θ ∖ y_{1}, y_{2}, \dots, y_{n}) & = \sum_{i = 1}^{n} κ_{i} ln [\frac{1}{λ + 1} g (t)] + \sum_{i = 1}^{n} (1 - κ_{i}) ln [\frac{λ}{λ + 1} g_{L} (t)], \\ = \sum_{i = 1}^{n} κ_{i} ln [\frac{1}{λ + 1} g (t)] + \sum_{i = 1}^{n} (1 - κ_{i}) ln [\frac{x_{i}}{(λ + 1) Γ (1 - \frac{1}{δ})} g (t)], \end{matrix}

(43)

where

Θ = {λ, δ}

. The Equation (43) can be simplified by substituting Equation (1), resulting in the complete log-likelihood function, denoted as

l_{complete} (Θ ∖ y_{1}, y_{2}, \dots, y_{n})

, which is expressed as follows:

\begin{matrix} l_{complete} (Θ ∖ y_{1}, y_{2}, \dots, y_{n}) & = \sum_{i = 1}^{n} l n (x_{i}) - n l n (λ + 1) - n l n Γ (1 - \frac{1}{δ}) \\ - \sum_{i = 1}^{n} κ_{i} l n (x_{i}) + n \bar{κ} Γ (1 - \frac{1}{δ}) + n l n (δ) + n δ l n (λ) \\ - (δ + 1) \sum_{i = 1}^{n} l n (x_{i}) - \sum_{i = 1}^{n} {(\frac{λ}{x_{i}})}^{δ}, \end{matrix}

(44)

where

\bar{κ} = \frac{1}{n} \sum_{i = 1}^{n} κ_{i}

3. Formulate the new complete log-likelihood function by eliminating constant expressions, resulting in the following expression:

\begin{matrix} l_{complete} (Θ ∖ y_{1}, y_{2}, \dots, y_{n}) & = - n l n (λ + 1) - n l n Γ (1 - \frac{1}{δ}) + n \bar{κ} Γ (1 - \frac{1}{δ}) \\ + n l n (δ) + n δ l n (λ) - (δ + 1) \sum_{i = 1}^{n} l n (x_{i}) - \sum_{i = 1}^{n} {(\frac{λ}{x_{i}})}^{δ} . \end{matrix}

(45)

A pseudo-log-likelihood function is derived at an E-step of an EM algorithm by replacing missing values with their respective expectations. Hence, the pseudo-log-likelihood function at the

k^{t h}

stage can be expressed as follows:

\begin{matrix} l_{complete} (Θ ∖ y_{1}, y_{2}, \dots, y_{n}) & = - n l n (λ + 1) - n l n Γ (1 - \frac{1}{δ}) + n a^{(k)} Γ (1 - \frac{1}{δ}) \\ + n l n (δ) + n δ l n (λ) - (δ + 1) \sum_{i = 1}^{n} l n (x_{i}) - \sum_{i = 1}^{n} {(\frac{λ}{x_{i}})}^{δ}, \end{matrix}

(46)

where

a^{(k)} = \frac{1}{n} \sum_{i = 1}^{n} a_{i}^{(k)}

, and

a_{i}^{(k)}

is given by

\begin{matrix} a_{i}^{(k)} = \frac{\frac{1}{λ + 1} g (x; λ^{(k)}, δ^{(k)})}{\frac{1}{λ + 1} g (x; λ^{(k)}, δ^{(k)}) + \frac{λ}{λ + 1} g_{L} (x; λ^{(k)}, δ^{(k)})} . \end{matrix}

(47)

The steps involved in the Maximization (M)-Step

The M-step process involves iteratively increasing the number of function expressions. With each iteration, the values of

a^{(k)}

and the estimated parameters

λ^{(k + 1)},

and

δ^{(k + 1)}

will adjust. The process continues until the estimated values remain unchanged. Consequently, the MLEs for

λ,

and

δ

obtained via an EM algorithm are

λ^{(k + 1)}

, and

δ^{(k + 1)}

, respectively, achieved by maximizing Equation (46). The initial values suggested in this article for the EM algorithm are

λ^{(0)}

and

δ^{(0)}

, which are as follows:

\begin{matrix} λ^{(0)} & = {(\frac{n}{t})}^{(\frac{1}{δ})}, where t = \sum_{i = 1}^{n} {(\frac{1}{t_{i}})}^{δ}, \end{matrix}

(48)

\begin{matrix} δ^{(0)} & = 2 for sample size is small, and \end{matrix}

(49)

\begin{matrix} δ^{(0)} & = 1.5 for sample size is large . \end{matrix}

(50)

EM-Algorithm:

Step 1: Generate a random sample

t_{1}, t_{2}, \dots, t_{n}

according to the NMF distribution.

Step 2: Set

k = 0

and compute the initial values

λ^{(0)}

and

δ^{(0)}

as specified in Equation (48), (49), and (50).

Step 3: Calculate

a^{(k)} = \frac{1}{n} \sum_{i = 1}^{n} a^{(k)} i

for

i = 1, 2, \dots, n

, when

a^{(k)} i

was given by Equation (51). For example, when

k = 0

, we obtain the following:

\begin{matrix} a_{i}^{(0)} = \frac{\frac{1}{λ + 1} g (x; λ^{(0)}, δ^{(0)})}{\frac{1}{λ + 1} g (x; λ^{(0)}, δ^{(0)}) + \frac{λ}{λ + 1} g_{L} (x; λ^{(0)}, δ^{(0)})} . \end{matrix}

(51)

Step 4: Obtain the values of

λ^{(k + 1)}

and

δ^{(k + 1)}

by maximizing Equation (52). For instance, when

k = 0

, we obtain the following values:

\begin{matrix} l_{complete} (Θ ∖ y_{1}, y_{2}, \dots, y_{n}) & = - n l n (λ + 1) - n l n Γ (1 - \frac{1}{δ}) + n a^{(0)} Γ (1 - \frac{1}{δ}) \\ + n l n (δ) + n δ l n (λ) - (δ + 1) \sum_{i = 1}^{n} l n (x_{i}) - \sum_{i = 1}^{n} {(\frac{λ}{x_{i}})}^{δ} . \end{matrix}

(52)

Step 5: If

λ^{(k + 1)} = λ^{(k)}

and

δ^{(k + 1)} = δ^{(k)}

, then the algorithm stops. Otherwise, update

k = k + 1

and proceed to Step 3 and Step 4.

4.10.3. Assessment of the Efficacy of the Parameter Estimation

In this subsection, a series of simulations were performed to compare the outcomes of maximum likelihood estimators obtained using EM algorithms and simulated annealing. The utilization of Equation (48) and (49) as the initial value for the simulated annealing via “optim” function is favored in this context. The random number generator employed for generating samples from the NMF distribution followed an acceptance-rejection algorithm, utilizing a Fréchet distribution from a VGAM package in R program version 4.3.0. Each model was subjected to 500 repetitions. Sample sizes of

n = 5, 10, 30, 50

were generated for the NMF distribution with parameters

λ = 1.5, 2.5

and

δ = 2, 3, 4

. The resulting computations yielded six models for each method and sample size, as presented in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8.

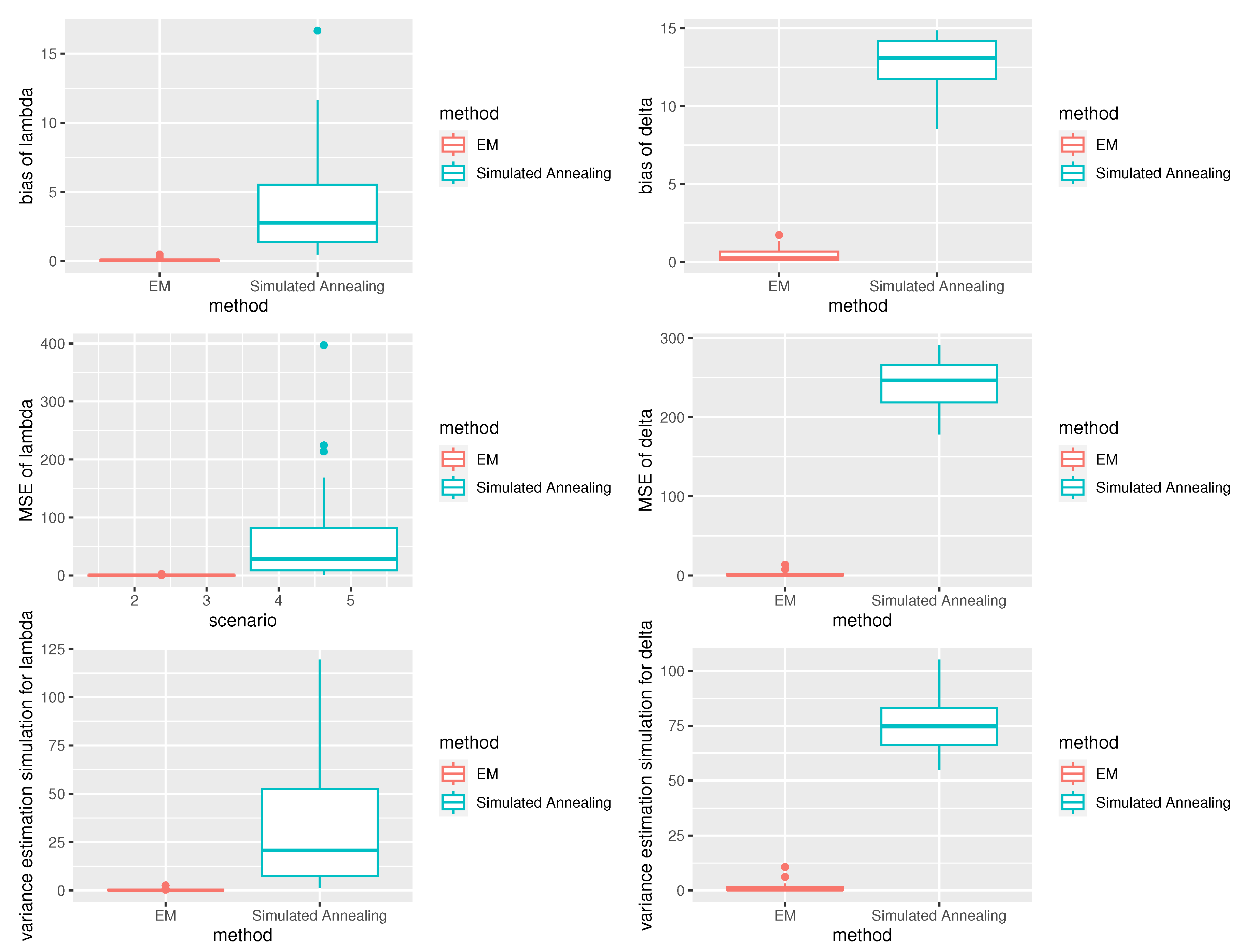
Upon reviewing all the results from Figure 2. The performance of the EM algorithm was remarkable, with estimated values for most parameters closely resembling the actual values. Moreover, the proposed EM algorithm demonstrated higher precision compared to the maximum likelihood estimates obtained through simulated annealing, as evidenced by reduced bias, lower mean squared error (MSE), and decreased variance estimation simulation.

5. Illustrative Example

The proposed distribution is applied to an actual dataset in this part. The dataset used in this analysis was collected from a clinical trial conducted by Freireich et al. [17], where patients received a placebo to evaluate the efficacy of 6-mercaptopurine (6-MP) in maintaining remission. Following the completion of the trial after a year, the following remission times were recorded and are expressed in weeks: 1, 1, 2, 2, 3, 4, 4, 5, 5, 8, 8, 8, 8, 11, 11, 12, 12, 15, 17, 22, 23.

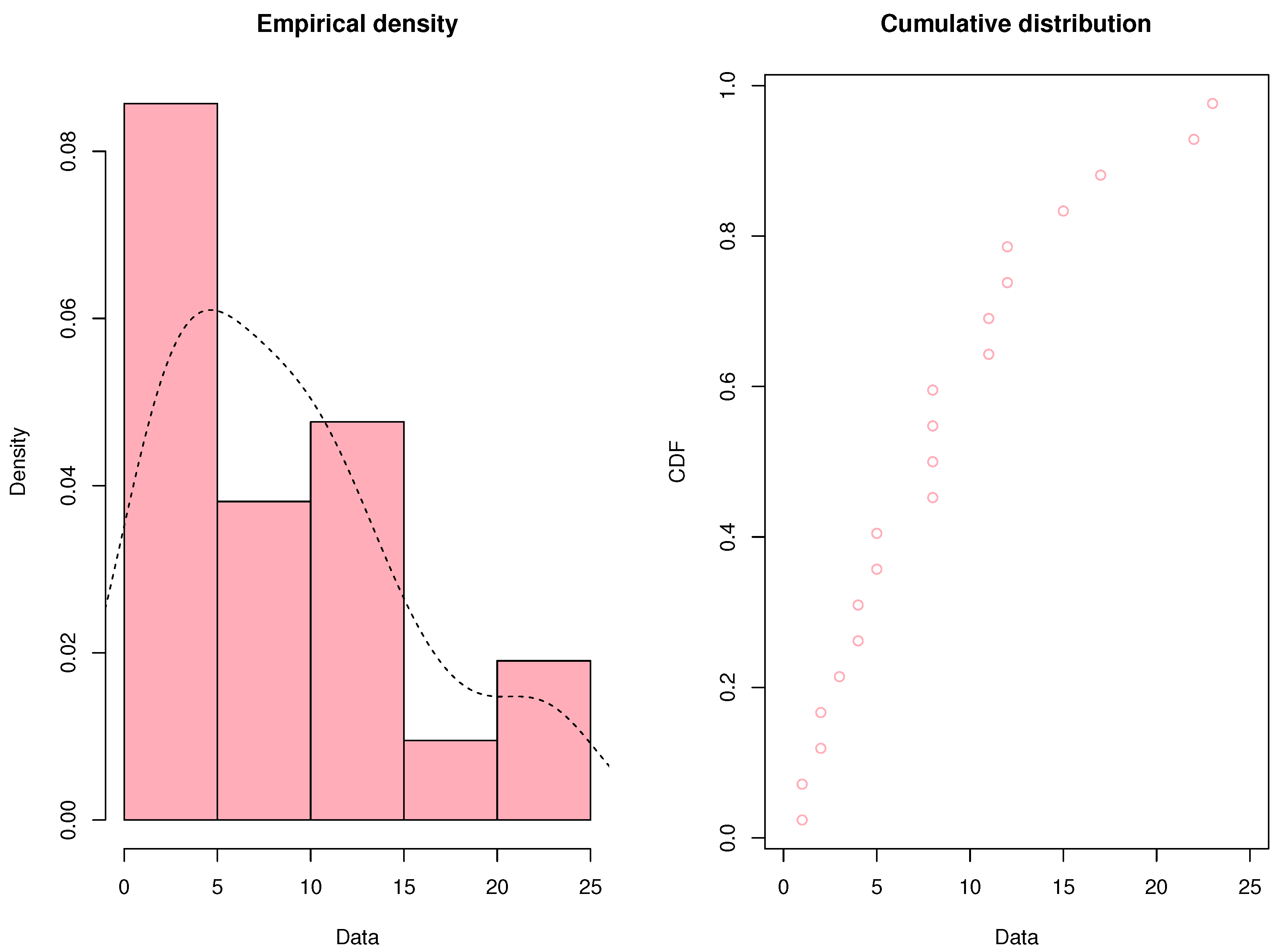
Based on the results shown in Figure 3, the remission times of patients who got a placebo had a right-skewed distribution. In order to compare the goodness of fit, three right-skewed distributions—the Fréchet distribution, the length-biased Fréchet distribution, and the proposed mixture Fréchet distribution—are chosen.

While the parameters of the other candidate distributions are determined using maximum likelihood estimation utilizing simulated annealing, the parameters of the novel mixture Fréchet (NMF) distribution are estimated using the EM algorithm. The best model is the one that provides the smallest Akaike information criterion (AIC) value, which is used as the evaluation criterion.

Based on findings presented in Table 9, it is evident that the NMF distribution yields the lowest value of the AIC. This indicates that the NMF distribution outperforms the other potential distributions when using an AIC statistic as a measure of goodness-of-fit for this example data.

6. Conclusions and Discussion

This article presents the introduction of a novel survival distribution known as the novel mixture Fréchet (NMF) distribution. This distribution is characterized by its right-skewed distribution. The study explores various statistical properties of this newly proposed distribution and estimates its two parameters using both EM algorithms and simulated annealing. To assess the performance of both methods, a simulation study is conducted, involving twenty-four different combination scenarios. The illustrative examples of the proposed distribution are implemented using patient remission times data. The results reveal that the EM estimators exhibit greater efficiency compared to the simulated annealing estimators. Additionally, the NMF distribution demonstrates a better fit when compared to other candidate distributions, as indicated by the Akaike information criterion (AIC). Consequently, this article presents a novel right-skewed distribution that holds potential application in diverse areas, including survival analysis and reliability analysis.

In future research, it is advisable to investigate interval estimation using different methods, such as [18,19], to further enhance the accuracy of the estimations.

Author Contributions

Conceptualization, W.D.P.; methodology, W.D.P., and I.A.; validation, W.D.P., I.A., and W.W.P.; formal analysis, W.D.P., I.A., and W.W.P.; investigation, I.A.; writing—original draft preparation, W.D.P., I.A., and W.W.P.; writing—review and editing, W.D.P., I.A., and W.W.P.; visualization, W.D.P.; funding acquisition, W.D.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by King Mongkut’s University of Technology North Bangkok, Thailand. Contract no.KMUTNB-66-BASIC-04.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

The authors express their gratitude to the reviewers for their invaluable insights and constructive feedback. Additionally, this research has been financially supported by King Mongkut’s University of Technology North Bangkok, Thailand, under contract number KMUTNB-66-BASIC-04.

Conflicts of Interest

The authors declare no conflict of interest.

References

Niyomdecha, A.; Srisuradetchai, P. Complementary Gamma Zero-Truncated Poisson Distribution and Its Application. Mathematics 2023, 11, 2584. [Google Scholar] [CrossRef]
Abdullahi, I.; Phaphan, W. Some Properties of the New Mixture of Nakagami Distribution. Thail. Stat. 2022, 20, 731–743. [Google Scholar]
Nanuwong, N.; Bodhisuwan, W.; Pudprommarat, C. A New Mixture Pareto Distribution and Its Application. Thail. Stat. 2015, 13, 191–207. [Google Scholar]
Aryuyuen, S.; Bodhisuwan, W.; Volodin, A. Discrete Generalized Odd Lindley–Weibull Distribution with Applications. Lobachevskii J. Math. 2020, 41, 945–955. [Google Scholar] [CrossRef]
Simmachan, T.; Phaphan, W. Generalization of Two-Sided Length Biased Inverse Gaussian Distributions and Applications. Symmetry 2022, 14, 1965. [Google Scholar] [CrossRef]
Tonggumnead, U.; Klinjan, K.; Tanprayoon, E.; Aryuyuen, S. A four-parameter negative binomial-Lindley regression model to analyze factors influencing the number of cancer deaths using Bayesian inference. Commun. Math. Biol. Neurosci. 2023, 2023, 1–20. [Google Scholar] [CrossRef]
Chananet, C.; Phaphan, W. On the new weight parameter of the mixture Pareto distribution and its application to real data. Appl. Sci. Eng. Prog. 2021, 14, 460–467. [Google Scholar] [CrossRef]
Fréchet, M. Sur la loi de probabilité de l’écart maximum. Ann. Soc. Polon. Math. 1927, 6, 93. [Google Scholar]
Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Cambridge Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, United States, 1958. [Google Scholar]
Abbas, K.; Yincai, T. Comparison of estimation methods for Frechet distribution with known shape. Casp. J. Appl. Sci. Res. 2012, 1, 58–64. [Google Scholar]
Nasir, W.; Aslam, M. Bayes approach to study shape parameter of Frechet distribution. Int. J. Basic. Appl. Sci. 2015, 4, 246–254. [Google Scholar] [CrossRef]
Reyad, H.M.; Younis, A.M.; Ahmed, S.O. QE-Bayesian and E-Bayesian estimation of the Frechet model. BJMCS 2016, 19, 62–74. [Google Scholar] [CrossRef] [PubMed]
Mead, M.E. On five-parameter Lomax distribution: properties and applications. Pak. J. Stat. Oper. Res. 2016, 1, 185–199. [Google Scholar]
Afify, A.Z.; Yousof, H.M.; Cordeiro, G.M.; Ortega, E.M.M.; Nofal, Z.M. The Weibull Fréchet distribution and its applications. J. Appl. Stat. 2016, 43, 2608–2626. [Google Scholar] [CrossRef]
Hesham, M.R.; Ahmed, M.H.; Soha, A.O.; Suzanne, A.A. The length-biased weighted Frechet distribution: Properties and estimation. Int. J. Appl. Math. Stat. 2017, 3, 189–200. [Google Scholar]
Freireich, E.J.; Gehan, E.A.; Frei, E.; et al. The Effect of 6-Mercaptopurine on the Duration of Steroid-Induced Remissions in Acute Leukemia: A Model for Evaluation of Other Potential Useful Therapy. Blood 1963, 21, 699–716. [Google Scholar]
Srisuradetchai, P.; Dangsupa, K. On Interval Estimation of the Geometric Parameter in a Zero–inflated Geometric Distribution. Thail. Stat. 2023, 21, 93–109. [Google Scholar]
Srisuradetchai, P.; Tonprasongrat, K. On Interval Estimation of the Poisson Parameter in a Zero-inflated Poisson Distribution. Thail. Stat. 2022, 20, 357–371. [Google Scholar]

Figure 1. Probability density functions for the novel mixture of Fréchet distribution at various values of

λ

(lambda) and

δ

(delta)

Figure 1. Probability density functions for the novel mixture of Fréchet distribution at various values of

λ

(lambda) and

δ

(delta)

Figure 2. Box plots display the biases, MES, and variance estimation simulation of the EM estimators and simulated annealing estimators.

Figure 3. the 21 patients who got a placebo’s times in remission.

Table 1. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 5

Table 1. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 5

$λ$	$δ$	$\hat{λ}$	$\hat{δ}$	Bias $(\hat{λ})$	Bias $(\hat{δ})$	MSE $(\hat{λ})$	MSE $(\hat{δ})$	VarSim $(\hat{λ})$	VarSim $(\hat{δ})$
1.5	2	1.7470	2.7426	0.2470	0.7426	0.4008	2.1382	0.3398	1.5867
	3	1.5637	4.0928	0.0637	1.0928	0.0814	4.3311	0.0773	3.1369
	4	1.5621	5.3009	0.0621	1.3009	0.0455	7.8207	0.0416	6.1283
2.5	2	2.9805	2.7295	0.4805	0.7295	1.2316	1.9732	1.0007	1.4410
	3	2.6579	3.9894	0.1579	0.9894	0.2846	3.6459	0.2597	2.6669
	4	2.6156	5.7329	0.1156	1.7329	0.1347	13.7042	0.1214	10.7012

Table 2. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 5

Table 2. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 5

$λ$	$δ$	$\tilde{λ}$	$\tilde{δ}$	Bias $(\tilde{λ})$	Bias $(\tilde{δ})$	MSE $(\tilde{λ})$	MSE $(\tilde{δ})$	VarSim $(\tilde{λ})$	VarSim $(\tilde{δ})$
1.5	2	3.1557	14.6394	1.6557	12.6394	16.4554	231.1034	13.7139	71.3496
	3	2.0213	15.5284	0.5213	12.5284	2.1113	225.2154	1.8395	68.2533
	4	1.9652	15.0794	0.4652	11.0794	1.4879	188.2035	1.2715	65.4498
2.5	2	5.6882	14.0020	3.1882	12.0020	36.7693	213.4220	26.6046	69.3742
	3	3.9382	14.6874	1.4382	11.6874	8.9652	220.4475	6.8969	83.8532
	4	3.7100	13.9510	1.2100	9.9510	5.6971	180.6055	4.2331	81.5837

Table 3. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 10

Table 3. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 10

$λ$	$δ$	$\hat{λ}$	$\hat{δ}$	Bias $(\hat{λ})$	Bias $(\hat{δ})$	MSE $(\hat{λ})$	MSE $(\hat{δ})$	VarSim $(\hat{λ})$	VarSim $(\hat{δ})$
1.5	2	1.5660	2.2744	0.0660	0.2744	0.0973	0.2963	0.0929	0.2210
	3	1.5444	3.4037	0.0444	0.4037	0.0381	0.9369	0.0361	0.7740
	4	1.5279	4.6493	0.0279	0.6493	0.0197	2.3606	0.0190	1.9390
2.5	2	2.6520	2.3669	0.1520	0.3669	0.3017	0.4242	0.2786	0.2896
	3	2.5847	3.3550	0.0847	0.3550	0.1212	0.9211	0.1141	0.7950
	4	2.5446	4.5805	0.0446	0.5805	0.0539	1.6688	0.0519	1.3318

Table 4. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 10

Table 4. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 10

$λ$	$δ$	$\tilde{λ}$	$\tilde{δ}$	Bias $(\tilde{λ})$	Bias $(\tilde{δ})$	MSE $(\tilde{λ})$	MSE $(\tilde{δ})$	VarSim $(\tilde{λ})$	VarSim $(\tilde{δ})$
1.5	2	3.2963	16.4428	1.7963	14.4428	18.4601	273.3670	15.2334	64.7724
	3	2.2299	16.4617	0.7299	13.4617	5.0049	240.0290	4.4722	58.8125
	4	1.9610	17.9110	0.4610	13.9110	2.0165	248.4057	1.8039	54.8905
2.5	2	7.4968	15.4376	4.9968	13.4376	75.0960	254.3734	50.1281	73.8031
	3	5.3225	16.0267	2.8225	13.0267	28.4780	252.5156	20.5112	82.8207
	4	4.3101	15.7719	1.8101	11.7719	12.9169	227.9040	9.6403	89.3260

Table 5. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 30

Table 5. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 30

$λ$	$δ$	$\hat{λ}$	$\hat{δ}$	Bias $(\hat{λ})$	Bias $(\hat{δ})$	MSE $(\hat{λ})$	MSE $(\hat{δ})$	VarSim $(\hat{λ})$	VarSim $(\hat{δ})$
1.5	2	1.5302	2.1075	0.0302	0.1075	0.0302	0.0595	0.0293	0.0479
	3	1.5117	3.1312	0.0117	0.1312	0.0108	0.1637	0.0106	0.1465
	4	1.5042	4.1778	0.0042	0.1778	0.0058	0.3782	0.0057	0.3466
2.5	2	2.5583	2.1745	0.0583	0.1745	0.0856	0.0743	0.0822	0.0439
	3	2.5240	3.1078	0.0240	0.1078	0.0309	0.1500	0.0303	0.1384
	4	2.5174	4.1438	0.0174	0.1438	0.0158	0.3076	0.0155	0.2869

Table 6. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 30

Table 6. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 30

$λ$	$δ$	$\tilde{λ}$	$\tilde{δ}$	Bias $(\tilde{λ})$	Bias $(\tilde{δ})$	MSE $(\tilde{λ})$	MSE $(\tilde{δ})$	VarSim $(\tilde{λ})$	VarSim $(\tilde{δ})$
1.5	2	5.0867	16.3140	3.5867	14.3140	45.6847	263.9548	32.8206	59.0629
	3	3.6042	17.4744	2.1042	14.4744	22.9393	272.4161	18.5115	62.9077
	4	2.6454	18.8461	1.1454	14.8461	8.7214	286.8080	7.4095	66.4026
2.5	2	13.3191	16.1026	10.8191	14.1026	213.7684	278.4768	96.7157	79.5939
	3	9.2326	15.6701	6.7326	12.6701	105.1613	244.4895	59.8331	83.9577
	4	7.6995	14.3182	5.1995	10.3182	64.7645	201.8541	37.7293	95.3889

Table 7. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 50

Table 7. The average estimations, biases, MES, and variance estimation simulation of EM estimators

\hat{λ}

and

\hat{δ}

with a sample size of

n = 50

$λ$	$δ$	$\hat{λ}$	$\hat{δ}$	Bias $(\hat{λ})$	Bias $(\hat{δ})$	MSE $(\hat{λ})$	MSE $(\hat{δ})$	VarSim $(\hat{λ})$	VarSim $(\hat{δ})$
1.5	2	1.5185	2.0694	0.0185	0.0694	0.0167	0.0293	0.0164	0.0245
	3	1.5071	3.0634	0.0071	0.0634	0.0066	0.0885	0.0065	0.0845
	4	1.5038	4.0746	0.0038	0.0746	0.0033	0.1818	0.0033	0.1763
2.5	2	2.6443	2.1385	0.1443	0.1385	2.6075	0.0505	2.5867	0.0313
	3	2.5367	3.0881	0.0367	0.0881	0.0511	0.0968	0.0497	0.0890
	4	2.5067	4.0758	0.0067	0.0758	0.0087	0.1513	0.0087	0.1456

Table 8. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 50

Table 8. The average estimations, biases, MES, and variance estimation simulation of simulated annealing estimators

\tilde{λ}

and

\tilde{δ}

with a sample size of

n = 50

$λ$	$δ$	$\tilde{λ}$	$\tilde{δ}$	Bias $(\tilde{λ})$	Bias $(\tilde{δ})$	MSE $(\tilde{λ})$	MSE $(\tilde{δ})$	VarSim $(\tilde{λ})$	VarSim $(\tilde{δ})$
1.5	2	7.9441	16.3235	6.4441	14.3235	109.6222	273.1470	68.0953	67.9839
	3	5.0498	17.6010	3.5498	14.6010	44.2769	290.7988	31.6761	77.6082
	4	4.2309	17.1473	2.7309	13.1473	28.2579	254.7019	20.8003	81.8496
2.5	2	19.1666	15.4000	16.6666	13.4000	397.1666	255.1433	119.3912	75.5836
	3	14.1514	13.6071	11.6514	10.6071	224.4617	202.7200	88.7069	90.2098
	4	12.3039	12.5652	9.8039	8.5652	168.4808	178.4291	72.3640	105.0656

Table 9. The MLE of the model’s parameters for patients who received a placebo’s times of remission.

Fitting Distribution	Estimate Parameters		Akaike Information Criterion
	$λ$	$δ$
Fréchet Distribution	15.50508	12.18451	5.58502
Length-biased Fréchet Distribution	30.18082	1.5	11.4393
NMF Distribution	2.191814	1.685673	3.662349

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Properties and Maximum Likelihood Estimation of the Novel Mixture of Fréchet Distribution

Abstract

1. Introduction

2. The Fréchet Distribution

3. The Length-biased Fréchet Distribution

4. Theoretical Result

4.1. The Probability Density Function of the Novel Mixture Fréchet (NMF) Distribution

4.2. Validity Check of the NMF Distribution for a Proper Density Function

4.3. The Cumulative Density Function of the NMF Distribution

4.4. The r t h Ordinary Moment of the NMF Distribution

4.5. The Skewness and Kurtosis of the NMF Distribution

4.6. The Moment Generating Function of the NMF Distribution

4.7. The Mode of the NMF Distribution

4.8. The Survival Function and the Hazard Rate Function of the NMF Distribution

4.9. Asymptotic Behavior of the NMF Distribution

4.10. Maximum Likelihood Estimation of the NMF Distribution

4.10.1. Maximum Likelihood Estimation employing the Simulated Annealing Algorithm

4.10.2. Maximum Likelihood Estimation employing the EM-Algorithm

4.10.3. Assessment of the Efficacy of the Parameter Estimation

5. Illustrative Example

6. Conclusions and Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.4. The $r^{t h}$ Ordinary Moment of the NMF Distribution