Preprint

Article

Practical Entropy Accumulation for Random Number Generators with Image Sensor-Based Quantum Noise Sources

Altmetrics

Downloads

231

Views

279

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 June 2023

Posted:

16 June 2023

You are already at the latest version

Alerts

Abstract

The efficient generation of high-quality random numbers is essential in the operation of cryptographic modules. The quality of a random number generator is evaluated by the min-entropy of its entropy source. Typical method used to achieve high min-entropy of the output sequence is an entropy accumulation based on a hash function. This is grounded in the famous Leftover Hash Lemma which guarantees a lower bound on the min-entropy of the output sequence. However, the hash function based entropy accumulation has slow speed in general. For a practical perspective we need a new efficient entropy accumulation with the theoretical background for the min-entropy of the output sequence. In this work, we obtain the theoretical bound for the min-entropy of the output random sequence through the very efficient entropy accumulation using only bitwise XOR operations, where the input sequences from the entropy source are independent. Moreover we examine our theoretical results by applying to the quantum random number generator that uses dark noise arising from image sensor pixels as its entropy source.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

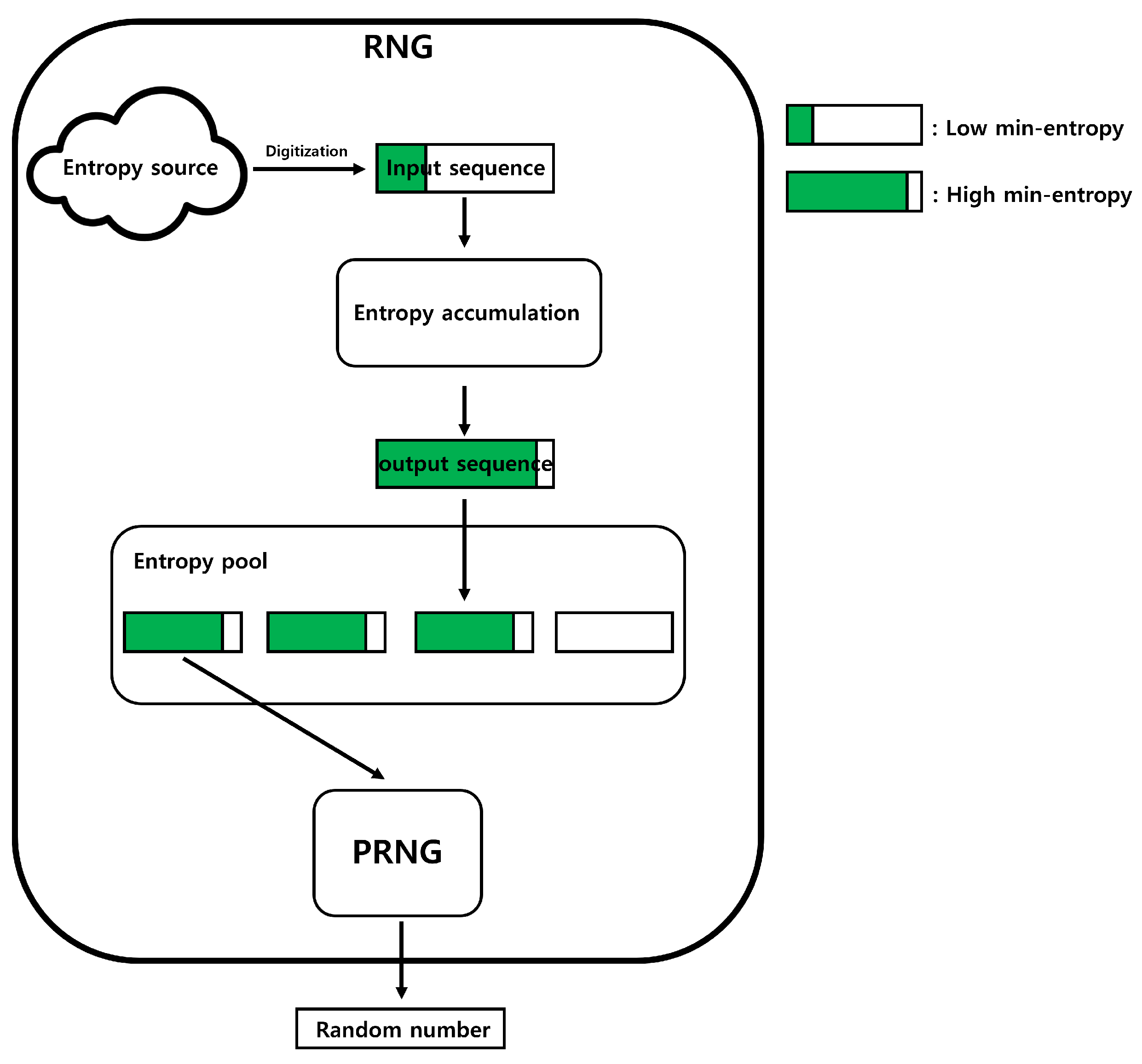
A random-number generator (RNG) is an important component of cryptographic systems used by cryptographic modules to generate random values, such as cryptographic keys. An RNG can be divided into three main processes: digitization, entropy accumulation, and Pseudorandom number generation (PRNG). Digitization is the process of converting entropy sources into binary data. We call the converted binary data as the "input sequence.” Typically, the input sequence has a low min-entropy. Entropy accumulation is the process of transforming input sequences into data with high min-entropy. We denote the input sequence that has undergone the entropy accumulation process as the "output sequence.” PRNG is composed of deterministic algorithms, such as block ciphers or hash functions, and it assumes the output sequence as input, and then outputs the final "Random number.” The operation of the RNG is illustrated in Figure 1.

Although unpredictable random numbers can be generated using a digitized entropy source, this is impractical in cryptographic systems because of the significant amount of time required. The PRNG was used to address this limitation. A PRNG produces the same output with the same input. This implies that the generated random numbers are not unpredictable. However, the PRNG can generate multiple random numbers in a short time because the length of the output is longer than the length of the input. Therefore, if the length of the input of PRNG is small but random, the output of the PRNG provides good random numbers. Consequently, the high min-entropy of the input sequence can be observed as an important factor in constructing an RNG.

Entropy accumulation aims to enhance the low-min entropy of the input sequence. Hash functions are used to accumulate the entropy. If X represents the input sequence, H represents the hash function and

X^{'}

represents the output sequence, then the entropy accumulation can be expressed as

X^{'} = H (X)

. Hash functions are used in entropy accumulation because of the leftover hash lemma, which guarantees a lower bound of the min-entropy of the output sequence [1]. However, hash functions are computationally slow, which makes it challenging to perform entropy accumulation at high speeds in practical scenarios. Therefore, determining an efficient entropy accumulation without using hash functions is a significant and realistic challenge.

1.1. Related works

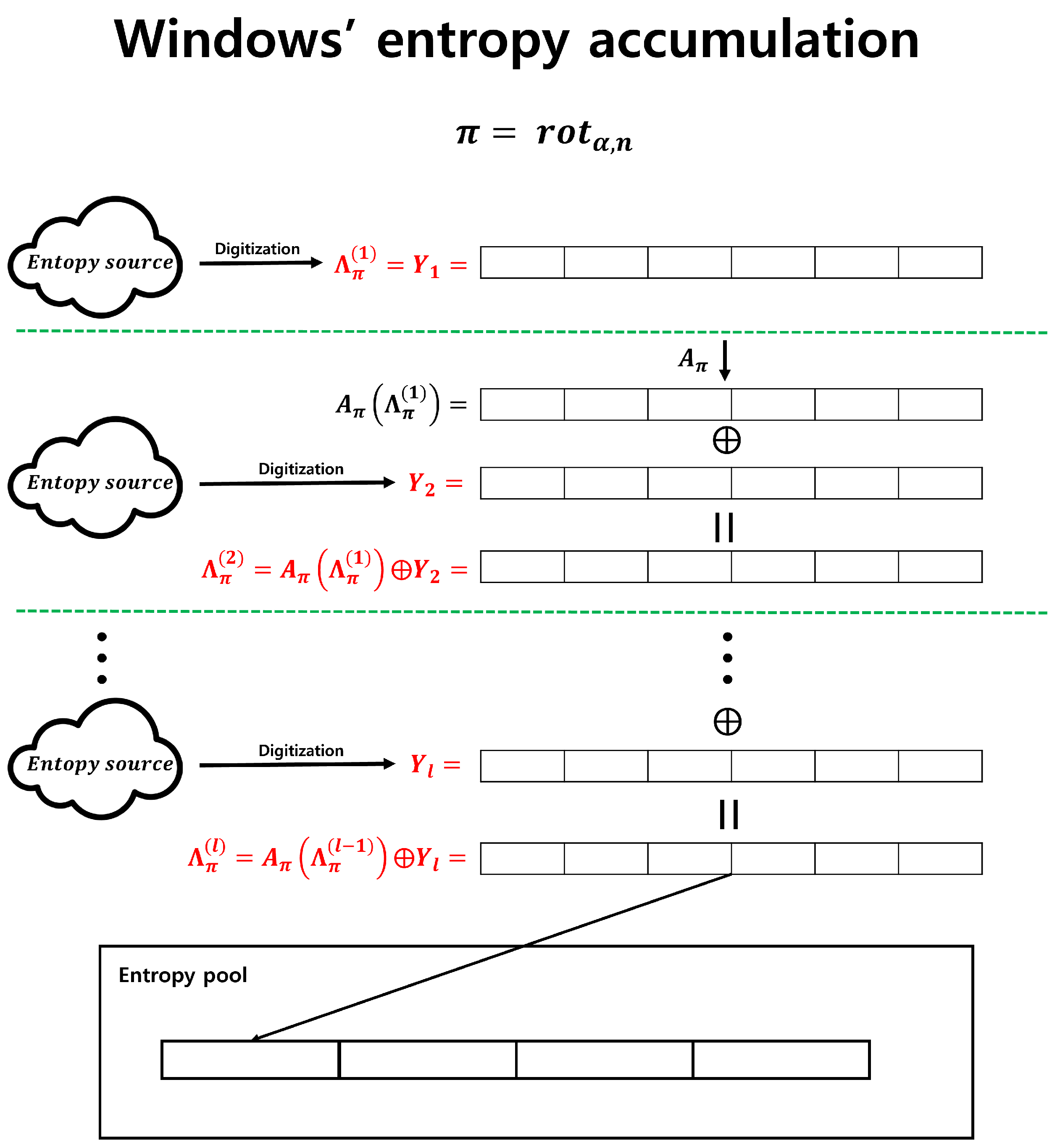
One of the example of entropy accumulation not using hash function is Microsoft Windows’ RNG [2]. Windows RNG uses only the bitwise XOR operation and bit permutation

r o t_{(α, n)}

for the entropy accumulation. In particular, if we employ the following notation, the entropy accumulation operation of Windows can be depicted as shown in Figure 3.

$Y_{1}, Y_{2}, \dots, Y_{l}$ : $n - b i t$ input sequences.
$π : {0, 1, \dots, n - 1} \to {0, 1, \dots, n - 1}$ , $π$ is one to one.
$A_{π} : {0, 1}^{n} \to {0, 1}^{n}$ , $A_{π} (b_{0}, b_{1}, \dots, b_{n - 1}) : = A_{π} (b_{π (0)}, b_{π (1)}, \dots, b_{π (n - 1)})$ .
$r o t_{(α, n)} : {0, 1, \dots, n - 1} \to {0, 1, \dots, n - 1}$ , $r o t_{(α, n)} (i) : = i - α (mod n$ ).

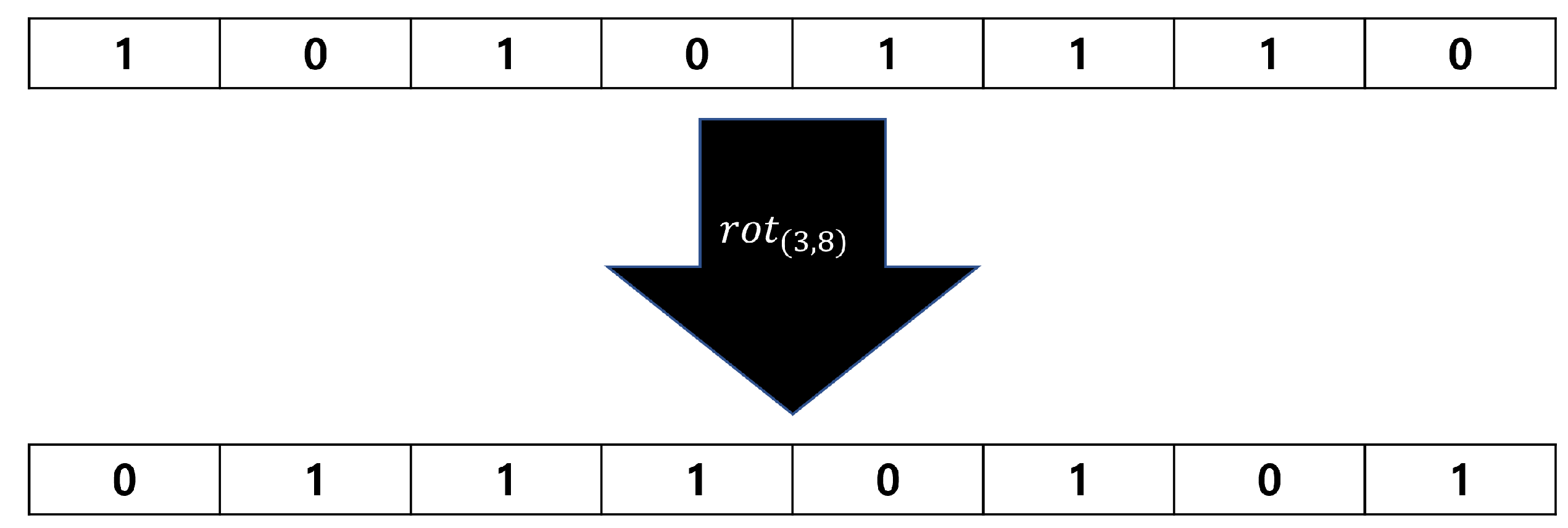
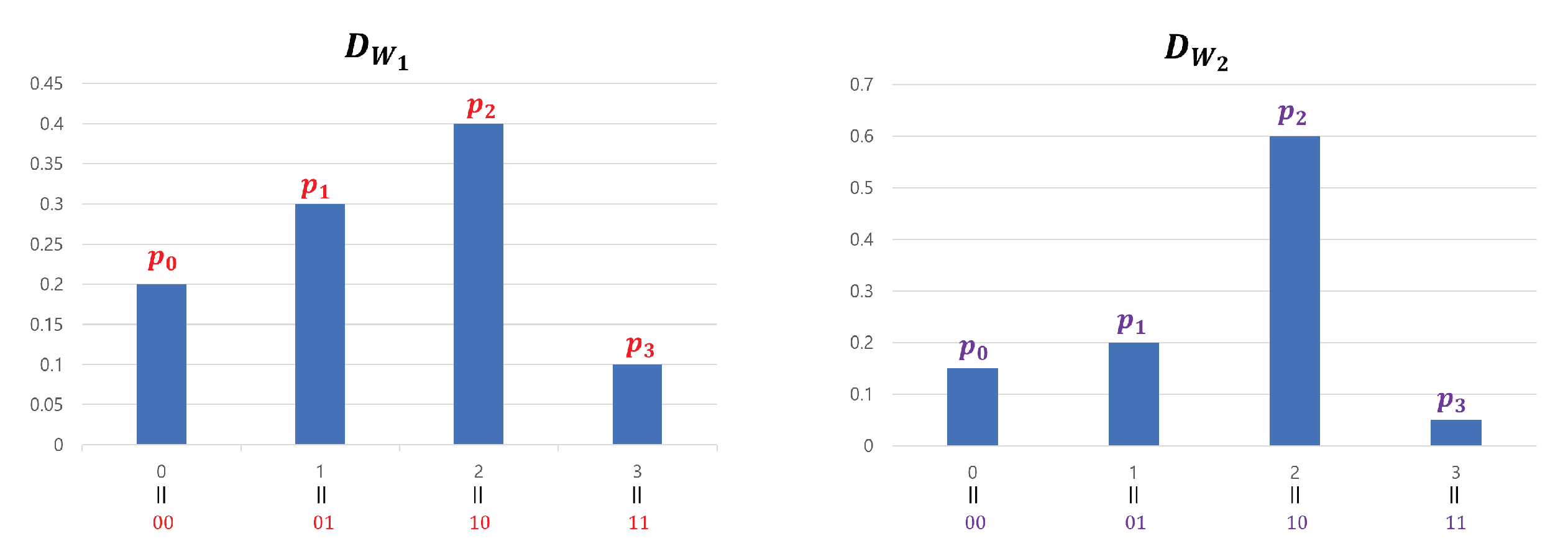
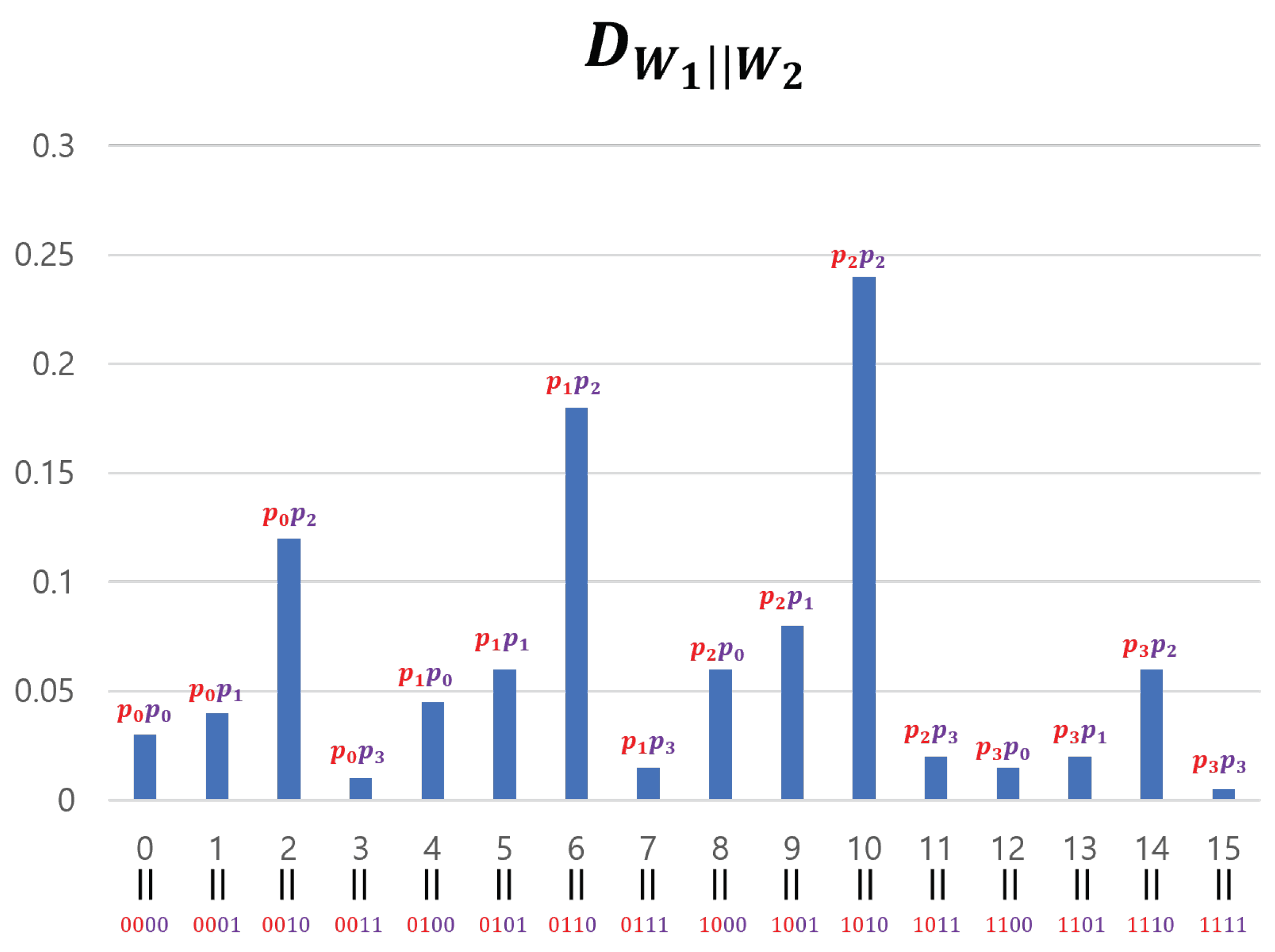
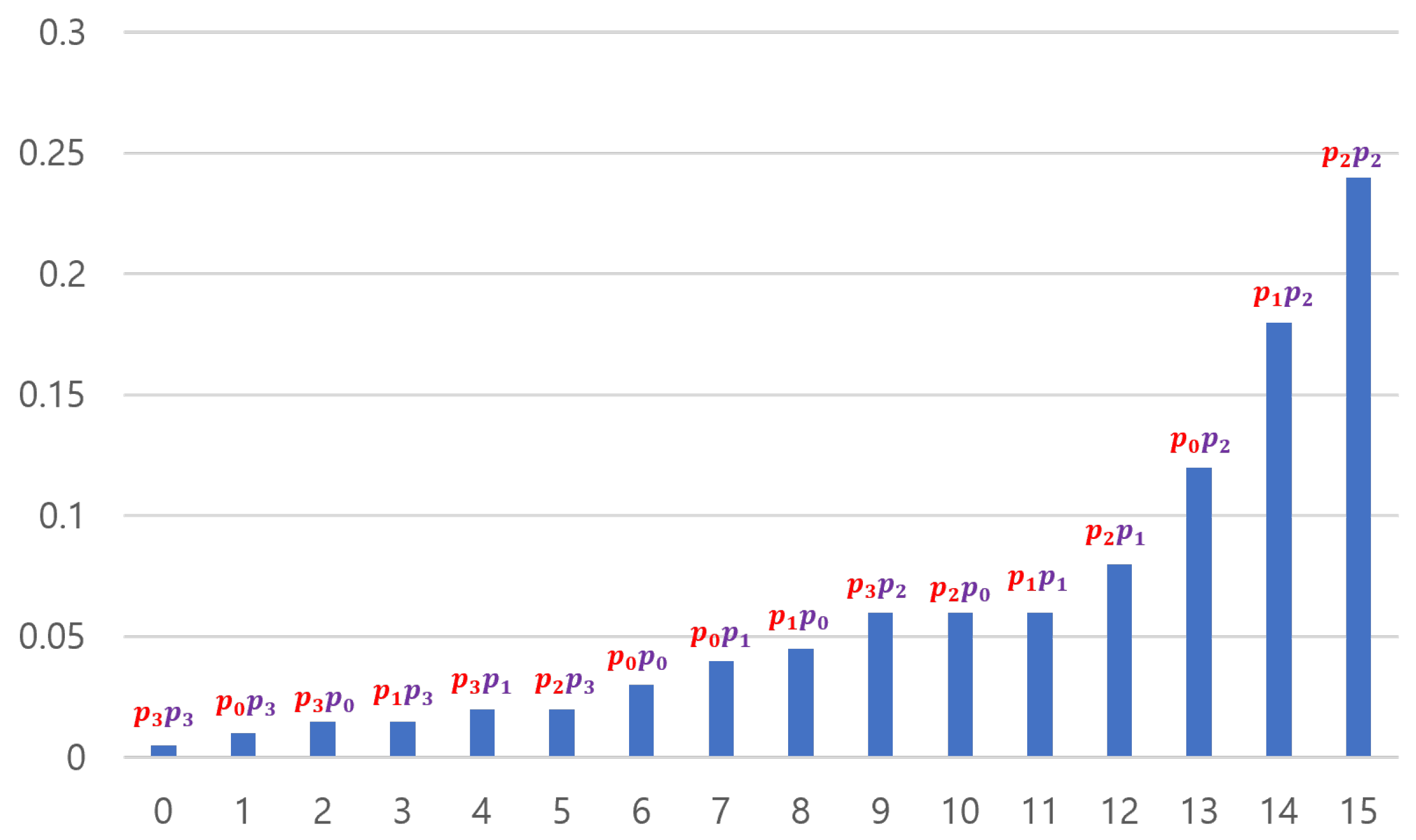
Figure 2 is an example of the $r o t_{(3, 8)}$ operation on an 8-bit input sequence.
$Λ_{π}^{(l)} : {0, 1}^{n} \to {0, 1}^{n}$ , $Λ_{π}^{(l)} : = \{\begin{matrix} Y_{1} & if l = 1 \\ A_{π} (Λ_{π}^{(l - 1)}) \oplus Y_{l} & if l \geq 2 \end{matrix}$

The Windows RNG accumulates output sequences relatively quickly in an entropy pool because it uses bit permutations and bitwise XOR operations without employing hash functions. Despite these advantages, it has not been proven whether the entropy accumulation of Windows RNG guarantees a lower bound for the min-entropy of the output sequence, as does the leftover hash lemma when using a hash function. Therefore, it has been challenging to consider this method of secure entropy accumulation. However, recent research presented at Crypto 2021 analyzed Microsoft Windows RNG. In [3], the security of Windows RNG was analyzed by providing the number of iterations of bit permutation and bitwise XOR to surpass an arbitrary min-entropy under three conditions. First, the input sequences must be independent. Second, the probability distribution of input sequences must follow the "2-monotone distribution.” Third, the "covering number" of the bit permutation must be finite. [3] claimed that the three conditions just mentioned are easy to satisfy. However, satisfying these conditions may be challenging for hardware entropy sources rather than software entropy sources, particularly when managing multiple entropy sources. The first and third conditions are easily satisfied, as in the case of Windows. The second condition may seem easy to achieve, but it is challenging. Therefore, to handle entropy sources other than Windows, a more relaxed condition is required than that presented in [3].

1.2. Our contributions

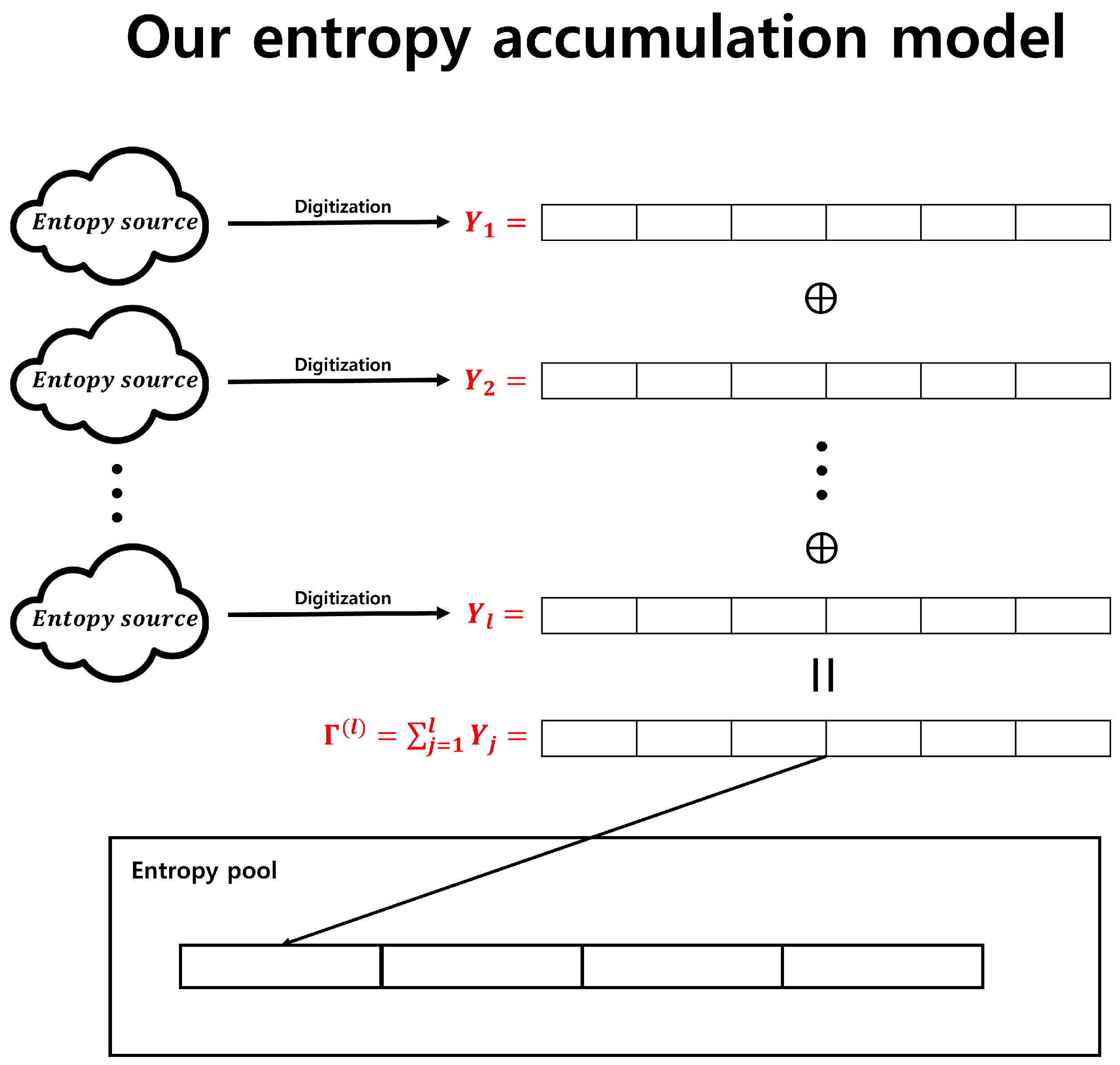
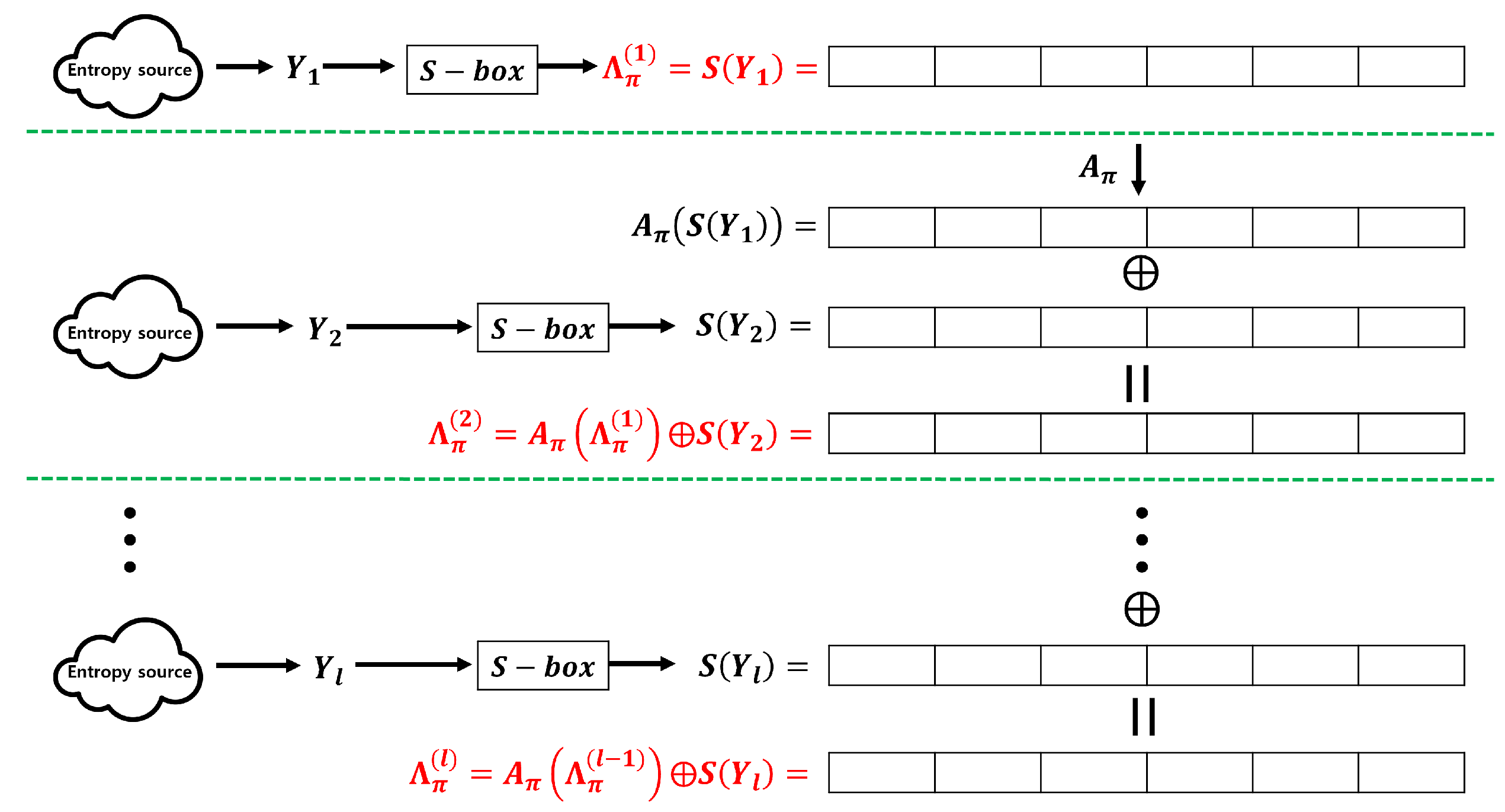
The contributions of this study are twofold. First, we provide entropy accumulation that does not require hash functions and uses only bitwise XOR operations to generate output sequences. In particular, if we employ the following notation, the proposed entropy accumulation can be depicted as shown in Figure 4.

$Y_{1}, Y_{2}, \dots, Y_{l}$ : $n - b i t$ input sequences.
$Γ^{(l)} = \sum_{j = 1}^{l} Y_{j}$ .

This method requires only two conditions for the input sequences, making it relatively easier to satisfy than the Windows entropy accumulation.

Second, we establish a min-entropy lower bound for a secure random number generator and demonstrate that our entropy accumulation successfully surpasses this lower bound when applied to our RNG. We used image-sensor-based quantum random number generators as the entropy sources. Quantum random-number generators utilize quantum phenomena to generate high-quality entropy sources. Although conventional quantum random number generators can generate high-quality entropy sources using single-photon detectors, their practicality is limited for economic reasons. To address this issue, a research conducted in 2014 replaced the role of single-photon detectors with that of the shot noise of optical black pixels (OBP) in an image sensor [4]. Furthermore, because each pixel outputs shot noise independently, all the entropy sources can be considered independent of each other.

The remainder of this paper is organized as follows. In Chapter 2, we remind the theoretical background and propose our main theorem which guarantees the lower bound of min-entropy for the output sequence of image sensor-based RNG. In Section 3, we describe the process of applying the theory outlined in Section 2 to an image-sensor-based quantum random number generator. We establish a min-entropy lower bound based on three standards and provide experimental results demonstrating that the output sequences generated by applying our theory to the input sequences have a min-entropy higher than the established lower bound. Furthermore, we estimate the entropy accumulation speed based on the frames per second (FPS) of the image sensor used and compared the speed of entropy accumulation with that of the commercially available ID Quantique’s QRNG Chip. In Section 4, we compare our theory to the result in [3]. Note that the theory in [3] cannot be directly applied to our input sequences without some additional components. Section 5 is the conclusion.

2. Theoretical background and Main theorem

In this section, we describe the theoretical background of entropy accumulation using only the XOR operation. In particular, we use the following notation:

$Z_{m}^{n}$ : Direct product of n copies of the group $Z_{m}$ . Note that the bitwise XOR operation corresponds to the + operation over $Z_{2}^{n}$ .
$F (Z_{m}^{n})$ : The space of all complex valued functions on $Z_{m}^{n}$ .
$Γ^{(l)} = \sum_{j = 1}^{l} Y_{j}$ , where, $Y_{j} \in Z_{2}^{n}$ is $n - b i t$ random variable that represents the input sequence.
${∥ f ∥}_{m i n} = min {| f (x) | : x \in Z_{m}^{n}}$ , $f \in F (Z_{m}^{n})$ .
${∥ f ∥}_{\infty} = max {| f (x) | : x \in Z_{m}^{n}}$ , $f \in F (Z_{m}^{n})$ .
$D_{X}$ : Probability distribution of the random variable X.
$H_{m i n} (D_{X}) = - {log}_{2} {∥ D_{X} ∥}_{\infty}$ . $H_{m i n} (D_{X})$ implies the min-entropy of $D_{X}$ .

We show that, as the number of input sequences required to generate one output sequence, represented by l, approaches infinity,

H_{m i n} (D_{Γ^{(l)}})

converges to n. Furthermore, we provide the optimal value of l necessary to surpass the specified min-entropy

α (< n)

. First, we provide a solution for the case

n = 1

and explain why this solution is inappropriate for the general

n - b i t

case. Thereafter, we provide a general solution using a Discrete Fourier Transform and Convolution.

First, we show why the problem we’re trying to solve is challenging. The difficult point of our problem is that in order to determine the value of

D_{Γ^{(l)}}

, complex linear operations must be performed on the function values of

D_{Y_{j}}

. For example, Suppose

n = 2

Y_{1}, Y_{2}, Y_{3}

are independent, and

D_{Y_{1}}, D_{Y_{2}}, D_{Y_{3}}

are identical to the distribution D. The distribution D is determined as

D (0, 0) = \frac{1}{8}, D (0, 1) = \frac{1}{4}, D (1, 0) = \frac{3}{8}, D (1, 1) = \frac{1}{4}

. Let us calculate

D_{Γ^{(3)}}

which suffices to show the complexity of computation.

\begin{matrix} D_{Γ^{(3)}} (0, 0) = \sum_{x \oplus y \oplus z = (0, 0)} D_{Y_{1}} (x) D_{Y_{2}} (y) D_{Y_{3}} (z) = D (0, 0) D (0, 0) D (0, 0) + \\ D (0, 0) D (0, 1) D (0, 1) + \dots + D (1, 1) D (1, 1) D (0, 0) = \frac{124}{512} \approx 0.242 . \\ D_{Γ^{(3)}} (0, 1) = \sum_{x \oplus y \oplus z = (0, 1)} D_{Y_{1}} (x) D_{Y_{2}} (y) D_{Y_{3}} (z) = D (0, 0) D (0, 0) D (0, 1) + \\ D (0, 0) D (0, 1) D (0, 0) + \dots + D (1, 1) D (1, 1) D (0, 1) = \frac{128}{512} = 0.25 . \end{matrix}

\begin{matrix} D_{Γ^{(3)}} (1, 0) = \sum_{x \oplus y \oplus z = (1, 0)} D_{Y_{1}} (x) D_{Y_{2}} (y) D_{Y_{3}} (z) = D (0, 0) D (0, 0) D (1, 0) + \\ D (0, 0) D (0, 1) D (1, 1) + \dots + D (1, 1) D (1, 1) D (1, 0) = \frac{132}{512} \approx 0.258 . \\ D_{Γ^{(3)}} (1, 1) = \sum_{x \oplus y \oplus z = (1, 1)} D_{Y_{1}} (x) D_{Y_{2}} (y) D_{Y_{3}} (z) = D (0, 0) D (0, 0) D (1, 1) + \\ D (0, 0) D (0, 1) D (1, 0) + \dots + D (1, 1) D (1, 1) D (1, 1) = \frac{128}{512} = 0.25 . \end{matrix}

From the above calculations, we derive two features. First, to calculate one function value of

D_{Γ^{(l)}}

, we must sum

2^{(l - 1) n}

terms. That is, to calculate

D_{Γ^{(l)}} (x) = \sum_{x_{1} \oplus x_{2} \oplus \dots \oplus x_{l} = x} D_{Y_{1}} (x_{1}) D_{Y_{2}} (x_{2}) \dots D_{Y_{l}} (x_{l}),

(1)

the first

l - 1

terms

x_{1}, x_{2}, \dots x_{l - 1}

could be any value and the last term

x_{l}

is automatically determined by equation

x_{1} \oplus x_{2} \oplus \dots \oplus x_{l} = x

. Because there is

2^{n}

choices respectively, the total terms would be

2^{(l - 1) n}

; however, it is difficult to calculate. Second, as l grows,

D_{Γ^{(l)}}

tends to uniform distribution. The distance between original distribution D and the uniform distribution I with respective to infinite norm

{∥ D - I ∥}_{\infty}

of above example is

\frac{1}{8}

. However, we can observe that

{∥ D_{Γ^{(3)}} - I ∥}_{\infty}

\frac{1}{128}

. As l grows, the terms that should be computed to calculate the function value grow rapidly; consequently, the impact of one function value will decrease. Although this phenomenon seems natural, still the following questions are remain: Under what conditions does this convergence happen? How about the convergence rate? How can we prove the related results?

2.1. Entropy accumulation with $n = 1$

Let us consider the relatively simple case of

n = 1

and

Y_{j}

following an independent and identical distribution(IID). In this case, all

Y_{j}

follow the same distribution

D (= D_{Y_{j}})

and a recursive relationship

Γ^{(j + 1)} = Γ^{(j)} \oplus Y_{j + 1}

is established. Thus, we can express

D_{Γ^{(j + 1)}} (1)

based on the following relationship:

D_{Γ^{(j + 1)}} (1) = D_{Γ^{(j)}} (1) [1 - D_{Y_{j + 1}} (1)] + [1 - D_{Γ^{(j)}} (1)] D_{Y_{j + 1}} (1) .

(2)

(2) is derived based on the property that the sum of two bits resulting in 1 can be obtained by adding 1 and 0, or 0 and 1. Moreover,

D_{Γ^{(j + 1)}} (1)

in (2) can be interpreted as a point where

D_{Γ^{(j)}} (1)

and

1 - D_{Γ^{(j)}} (1)

are internalized into

1 - D_{Y_{j + 1}} (1) : D_{Y_{j + 1}} (1)

. Because

D_{Γ^{(j)}} (1)

and

1 - D_{Γ^{(j)}} (1)

are symmetric about

x = \frac{1}{2}

, the condition

0 < D (1) < 1

causes the convergence of

D_{Γ^{(j)}} (1)

\frac{1}{2}

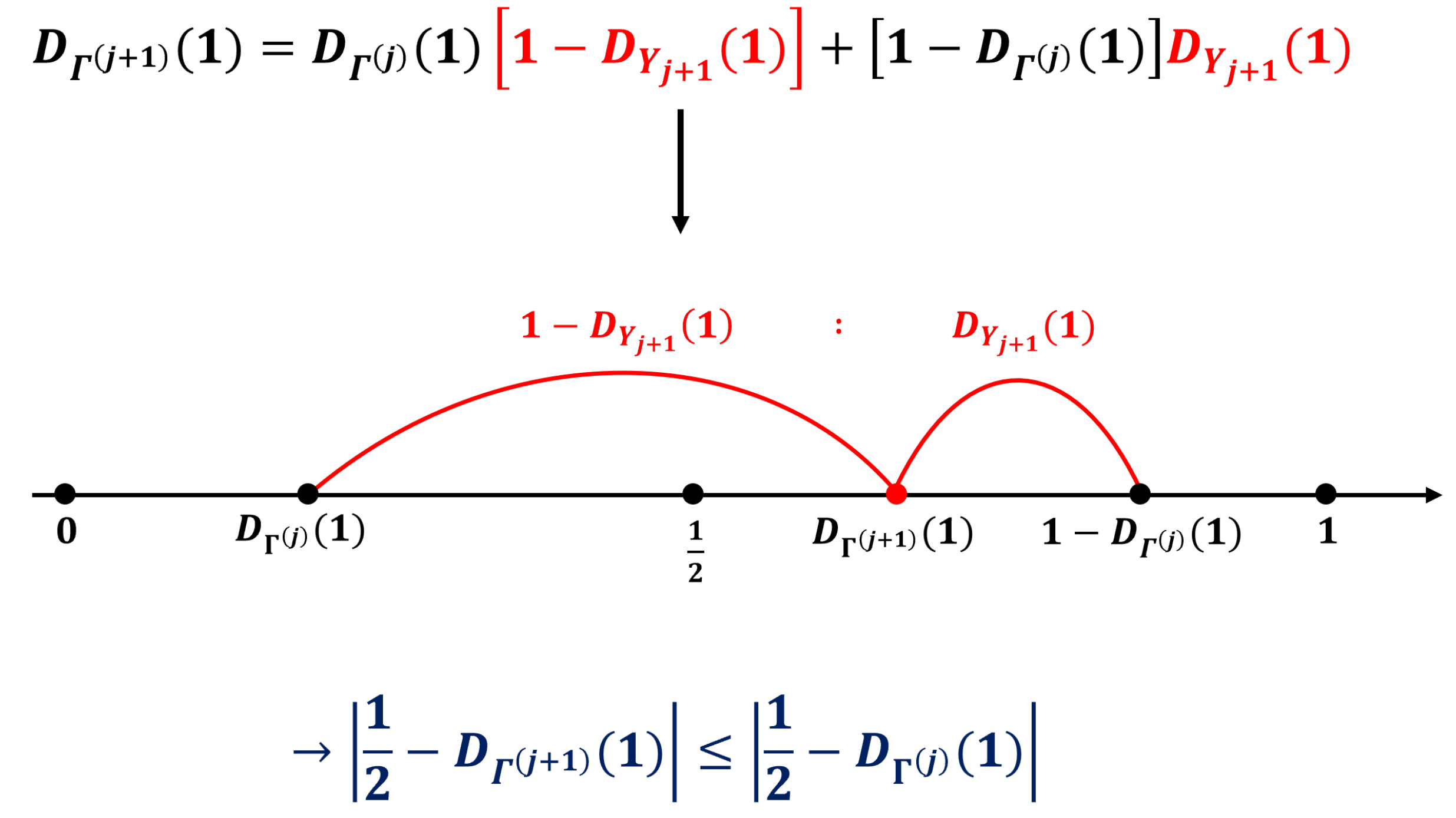
(i.e., the maximum possible entropy) as j increases. Figure 5 illustrates the scenario.

A more specific formula exists to accurately illustrate this situation. The following lemma, often referred to as the "Piling Up Lemma," further details this [5].

Fact 1

(Piling Up Lemma [5]). Let

Y_{1}, Y_{2}, \dots, Y_{l}

be independent one-bit random variables, and let

Γ^{(l)} : = \sum_{j = 1}^{l} Y_{j}

. Then, the following equation holds:

D_{Γ^{(l)}} (0) = \frac{1}{2} + 2^{l - 1} \prod_{j = 1}^{l} [D_{Y_{j}} (0) - \frac{1}{2}] .

Because

0 < | D_{Y_{j}} (0) - \frac{1}{2} | < \frac{1}{2}

for each j,

2^{l - 1} \prod_{j = 1}^{l} [D_{Y_{j}} (0) - \frac{1}{2}]

converges to 0 and

D_{Γ^{(l)}} (0)

converges to 1/2 as l approaches infinity.

This equation cannot be applied when n is greater than 2. When

n = 2

or more, the probability that each bit produces 0 or 1 converges to 1/2; however, we cannot sum up the min-entropies of each position to calculate the total min-entropy because it is allowed only when all bits are independent of each other. Therefore, a new method is required for addressing these problems.

2.2. Convolution and Discrete Fourier Transform

In this subsection, we describe techniques applicable in the special case where n equals 1 as well as in more general cases. First, we reformulated the problem using the concept of convolution.

Definition 1

(Convolution). The Convolution of

f, g \in F (Z_{m}^{n})

is defined as follows:

f * g (x) : = \sum_{y \in Z_{m}^{n}} f (x - y) g (y) .

For the entropy accumulation problem of interest,

m = 2

. Using the language of convolution, (1) becomes

D_{Γ^{(l)}} = D_{Y_{1}} * D_{Y_{2}} * \dots * D_{Y_{l}}

. The entropy accumulation problem is reduced to a problem of handling this convolution. Fortunately, there exists a mathematical concept, the "Fourier Transform," that harmonizes well with convolution.

Definition 2

(Discrete Fourier Transform). The Discrete Fourier Transform of

f \in F (Z_{m}^{n})

is defined as:

\hat{f} (t) : = \sum_{x \in Z_{m}^{n}} f (x) e^{- \frac{2 π i}{m} x \cdot t} .

A Discrete Fourier Transform is the mapping from

F (Z_{m}^{n})

F (Z_{m}^{n})

. In fact, this transform is one-to-one mapping. Proposition 1 supports this.

Lemma 1.

t \neq 0

\sum_{x \in Z_{m}^{n}} e^{- \frac{2 π i}{m} x \cdot t} = 0

Proof.

First, note that

\begin{matrix} \sum_{x \in Z_{m}^{n}} e^{- \frac{2 π i}{m} x \cdot t} = \sum_{x \in Z_{m}^{n}} e^{- \frac{2 π i}{m} x \cdot t (\mod m)} . \end{matrix}

We define

ϕ_{t} : Z_{m}^{n} \to Z_{m}

as:

\begin{matrix} ϕ_{t} (x) : = x \cdot t (\mod m) . \end{matrix}

Then,

ϕ_{t}

is a homomorphism :

\begin{matrix} ϕ_{t} (x + y) = (x + y) \cdot t (\mod m) = x \cdot t (\mod m) + y \cdot t (\mod m) = ϕ_{t} (x) + ϕ_{t} (y) . \end{matrix}

t \neq 0

ϕ_{t}^{- 1} (0) \neq Z_{m}^{n}

. Therefore, for every

s \in Z_{m}

ϕ_{t}^{- 1} (s)

contain the same number of elements. Let the number of element be N, then

\begin{matrix} \sum_{x \in Z_{m}^{n}} e^{- \frac{2 π i}{m} x \cdot t} = \sum_{x \in Z_{m}^{n}} e^{- \frac{2 π i}{m} ϕ_{t} (x)} = N \sum_{s \in Z_{m}} e^{- \frac{2 π i}{m} s} = 0 . \end{matrix}

The last equality holds because each

e^{- \frac{2 π i}{m} s}

is the root of complex equation

z^{m} - 1 = 0

. □

Lemma 2.

Let f be the element in

F (Z_{m}^{n})

and

\hat{f}

be the Fourier transform function. Thus, the following holds.

\frac{1}{m^{n}} \sum_{t \in Z_{m}^{n}} \hat{f} (t) e^{\frac{2 π i}{m} x \cdot t} = f (x) .

Proof.

By Lemma 1,

\sum_{t \in Z_{m}^{n}} f (s) e^{- \frac{2 π i}{m} (x - s) \cdot t} = 0

s \neq x

. Therefore,

\begin{matrix} \frac{1}{m^{n}} \sum_{s \in Z_{m}^{n}} \sum_{t \in Z_{m}^{n}} f (s) e^{- \frac{2 π i}{m} (x - s) \cdot t} = \frac{1}{m^{n}} \sum_{t \in Z_{m}^{n}} f (x) e^{- \frac{2 π i}{m} (x - x) \cdot t} = \frac{1}{m^{n}} \sum_{t \in Z_{m}^{n}} f (x) = f (x) . \end{matrix}

□

Proposition 1.

Let f and g be the elements of

F (Z_{m}^{n})

. If

\hat{f} = \hat{g}

f = g

Proof.

We assume that

\hat{f} = \hat{g}

. Then,

\begin{matrix} f (x) = \frac{1}{m^{n}} \sum_{t \in Z_{m}^{n}} \hat{f} (t) e^{\frac{2 π i}{m} x \cdot t} = \frac{1}{m^{n}} \sum_{t \in Z_{m}^{n}} \hat{g} (t) e^{\frac{2 π i}{m} x \cdot t} = g (x) \end{matrix}

holds for every

x \in Z_{m}^{n}

from Lemma 2.

□

The following theorem asserts that the convolution product of functions is represented as a multiplication in the transformed space. This plays a significant role in proving our main theorem.

Proposition 2.

Let f and g be the elements of

F (Z_{m}^{n})

. Then,

\hat{f * g} = \hat{f} \hat{g}

Proof.

By the definitions of convolution and Discrete Fourier Transform,

\begin{matrix} \hat{f * g} (t) = \sum_{x \in Z_{m}^{n}} \sum_{y \in Z_{m}^{n}} f (x - y) g (y) e^{- \frac{2 π i}{m} x \cdot t} = \sum_{x \in Z_{m}^{n}} \sum_{y \in Z_{m}^{n}} f (x - y) e^{- \frac{2 π i}{m} (x - y) \cdot t} g (y) e^{- \frac{2 π i}{m} y \cdot t} \\ = \sum_{x \in Z_{m}^{n}} f (x - y) e^{- \frac{2 π i}{m} (x - y) \cdot t} \sum_{y \in Z_{m}^{n}} g (y) e^{- \frac{2 π i}{m} y \cdot t} = \sum_{x \in Z_{m}^{n}} f (x) e^{- \frac{2 π i}{m} x \cdot t} \sum_{y \in Z_{m}^{n}} g (y) e^{- \frac{2 π i}{m} y \cdot t} \\ = \hat{f} (t) \hat{g} (t) . \end{matrix}

□

To intuitively determine why

Γ^{(l)}

converges to a uniform distribution, we must understand both the properties of the Discrete Fourier Transform applied to the distribution and the Discrete Fourier Transform of a uniform distribution.

Proposition 3.

Let D be an arbitrary probability distribution and I be a uniform distribution of

Z_{m}^{n}

. Then,

(i): For all $t \in Z_{m}^{n}, | \hat{D} (t) | \leq 1$ .
(ii): $\hat{D} (0) = 1$ .
(iii): For all $t \in Z_{m}^{n}, \hat{I} (t) = δ_{t, 0}$ .

The symbols

δ_{t, 0}

denote the Kronecker delta. The Kronecker delta is defined as 1 when t is zero vector and 0 for all other t.

Proof.

proof of (a) :

\begin{matrix} | \hat{D} (t) | = | \sum_{x \in Z_{m}^{n}} D (x) e^{- \frac{2 π i}{m} x \cdot t} | \leq \sum_{x \in Z_{m}^{n}} | D (x) e^{- \frac{2 π i}{m} x \cdot t} | = \sum_{x \in Z_{m}^{n}} D (x) = 1 . \end{matrix}

proof of (b) :

\begin{matrix} \hat{D} (0) = \sum_{x \in Z_{m}^{n}} D (x) e^{- \frac{2 π i}{m} x \cdot 0} = \sum_{x \in Z_{m}^{n}} D (x) = 1 . \end{matrix}

Proof of (c): We know from part (a) that

\hat{I} (0) = 1

. For the remaining

t \neq 0

\begin{matrix} \hat{I} (t) = \sum_{x \in Z_{m}^{n}} I (x) e^{- \frac{2 π i}{m} x \cdot t} = \frac{1}{m^{n}} \sum_{x \in Z_{m}^{n}} e^{- \frac{2 π i}{m} x \cdot t} = 0 . \end{matrix}

The last equality is based on Lemma 1. □

From Proposition 2, we have

\hat{D_{Γ^{(l)}}} = \hat{D_{Y_{1}}} \hat{D_{Y_{2}}} \dots \hat{D_{Y_{l}}}

. By Proposition 3,

\hat{D_{Γ^{(l)}}} (0) = 1

, whereas for

t \neq 0

, the value of

\hat{D_{Γ^{(l)}}} (t)

approaches 0 as l increases. Specifically,

\hat{D_{Γ^{(l)}}}

converges to

δ_{, t, 0}

as l increases. Since the Discrete Fourier Transform is an one-to-one function by Proposition 1, we can infer that

D_{Γ^{(l)}}

converges to I as l increases.

2.3. Main Theorem

In the previous subsection, we confirmed that

D_{Γ^{(l)}}

converges to a uniform distribution I as l increases. In this subsection, we present a solution to the entropy accumulation problem based on this approach. Specifically, we aim to find a condition for the random variable

Y_{j}

and a value for l such that

D_{Γ^{(l)}}

achieves a specific min-entropy. The following theorem is one of the main results of our study:

Theorem 1.

Let

Y_{1}, Y_{2}, \dots Y_{l}

be independent

n - b i t

random variables, and

Γ^{(l)} : = Y_{1} \oplus Y_{2} \oplus \dots \oplus Y_{l}

. We define

ω : = min {{∥ D_{Y_{1}} ∥}_{m i n}, {∥ D_{Y_{2}} ∥}_{m i n}, \dots, {∥ D_{Y_{l}} ∥}_{m i n}}

. Then,

H_{m i n} (D_{Γ^{(l)}}) \geq n - {log}_{2} [1 + (2^{n} - 1) {(1 - 2^{n} ω)}^{l}] \approx n - \frac{1}{ln 2} (2^{n} - 1) {(1 - 2^{n} ω)}^{l} .

Note that the condition for

n - b i t

random variables

Y_{1}, Y_{2}, \dots Y_{l}

is not an IID. Because the above theorem only requires the independence of random variables without the condition of identical distribution, it can be effectively applied when using parallel entropy sources. We provide the proof of Theorem 1.

Proof.

For any function

f \in L (Z_{2}^{n})

, we have

\hat{f} (t) = \sum_{x \in Z_{2}^{n}} f (x) e^{π i (x \cdot t)} = \sum_{x \in Z_{2}^{n}} f (x) {(- 1)}^{x \cdot t},

(3)

\frac{1}{2^{n}} \sum_{t \in Z_{m}^{n}} \hat{f} (t) e^{π i (x \cdot t)} = \frac{1}{2^{n}} \sum_{t \in Z_{m}^{n}} \hat{f} (t) {(- 1)}^{x \cdot t} = f (x) .

(4)

This is obtained from Lemma 2 with

m = 2

. Using the function

ϕ_{t}

of Lemma 2, (3) and (4) can be written as

\hat{f} (t) = \sum_{x \in Z_{2}^{n}} f (x) e^{π i (x \cdot t)} = \sum_{x \in Z_{2}^{n}} f (x) {(- 1)}^{x \cdot t} = \sum_{x \in ϕ_{t}^{- 1} (0)} f (x) - \sum_{x \in ϕ_{t}^{- 1} (1)} f (x),

(5)

\frac{1}{2^{n}} \sum_{t \in Z_{2}^{n}} \hat{f} (t) e^{π i (x \cdot t)} = \frac{1}{2^{n}} \sum_{t \in Z_{2}^{n}} \hat{f} (t) {(- 1)}^{x \cdot t} = \frac{1}{2^{n}} [\sum_{t \in ϕ_{x}^{- 1} (0)} \hat{f} (t) - \sum_{t \in ϕ_{x}^{- 1} (1)} \hat{f} (t)] = f (x) .

(6)

We apply (5) to each

D_{Y_{j}}

with

t \neq 0

. Because

\sum_{x \in Z_{2}^{n}} D_{Y_{j}} (x) = 1

and

D_{Y_{j}} (x) > ω > 0

\begin{matrix} |\hat{D_{Y_{j}}} (t)| & = |\sum_{x \in ϕ_{t}^{- 1} (0)} D_{Y_{j}} (x) - \sum_{x \in ϕ_{t}^{- 1} (1)} D_{Y_{j}} (x)| \\ = |\sum_{x \in ϕ_{t}^{- 1} (0)} [D_{Y_{j}} (x) - ω] - \sum_{x \in ϕ_{t}^{- 1} (1)} [D_{Y_{j}} (x) - ω]| \\ \leq |\sum_{x \in Z_{2}^{n}} [D_{Y_{j}} (x) - ω]| = 1 - 2^{n} ω . \end{matrix}

(7)

From Theorems 2 and (7),

\begin{matrix} |D_{Γ^{(l)}} (t)| = \frac{1}{2^{n}} |\sum_{t \in ϕ_{x}^{- 1} (0)} \hat{D_{Γ^{(l)}}} (t) - \sum_{t \in ϕ_{x}^{- 1} (1)} \hat{D_{Γ^{(l)}}} (t)| \leq \frac{1}{2^{n}} \sum_{t \in Z_{2}^{n}} |\hat{D_{Γ^{(l)}}} (t)| = \\ \frac{1}{2^{n}} \sum_{t \in Z_{2}^{n}} \prod_{j = 1}^{l} |\hat{D_{Y_{j}}} (t)| = \frac{1}{2^{n}} [\prod_{j = 1}^{l} |\hat{D_{Y_{j}}} (0)| + \sum_{t \in Z_{2}^{n} / {0}} \prod_{j = 1}^{l} |\hat{D_{Y_{j}}} (t)|] \leq \frac{1}{2^{n}} [1 + (2^{n} - 1) {(1 - 2^{n} ω)}^{l}] . \end{matrix}

Therefore,

\begin{matrix} H_{m i n} (D_{Γ^{(l)}}) = max {- {log}_{2} |D_{Γ^{(l)}} (t)| : t \in Z_{2}^{n}} \geq n - {log}_{2} [1 + (2^{n} - 1) {(1 - 2^{n} ω)}^{l}] \\ \approx n - \frac{1}{ln 2} (2^{n} - 1) {(1 - 2^{n} ω)}^{l} . \end{matrix}

The final approximation is based on the Taylor theorem. □

3. Applying Theorem 1 to Image Sensor-based RNG

In this section, we describe the process of applying Theorem 1 to an image-sensor-based random number generator. First, we describe the process of generating the input sequences from the entropy sources of the image sensor. Subsequently, we verify whether the generated input sequences satisfy the assumptions of Theorem 1. Next, we establish the lower bound for the min-entropy, which is considered secure based on three standards. terter, we provide the theoretical number of iterations required to achieve a min-entropy higher than the established lower bound. Furthermore, we validate our theory using experimental results. Finally, we estimated the entropy accumulation speed based on frames per second (FPS) of the image sensors used. Thereafter, we compared and analyzed the random-number generation speed of our system with that of the ID Quantique’s QRNG chip.

3.1. Image Sensor-based RNG

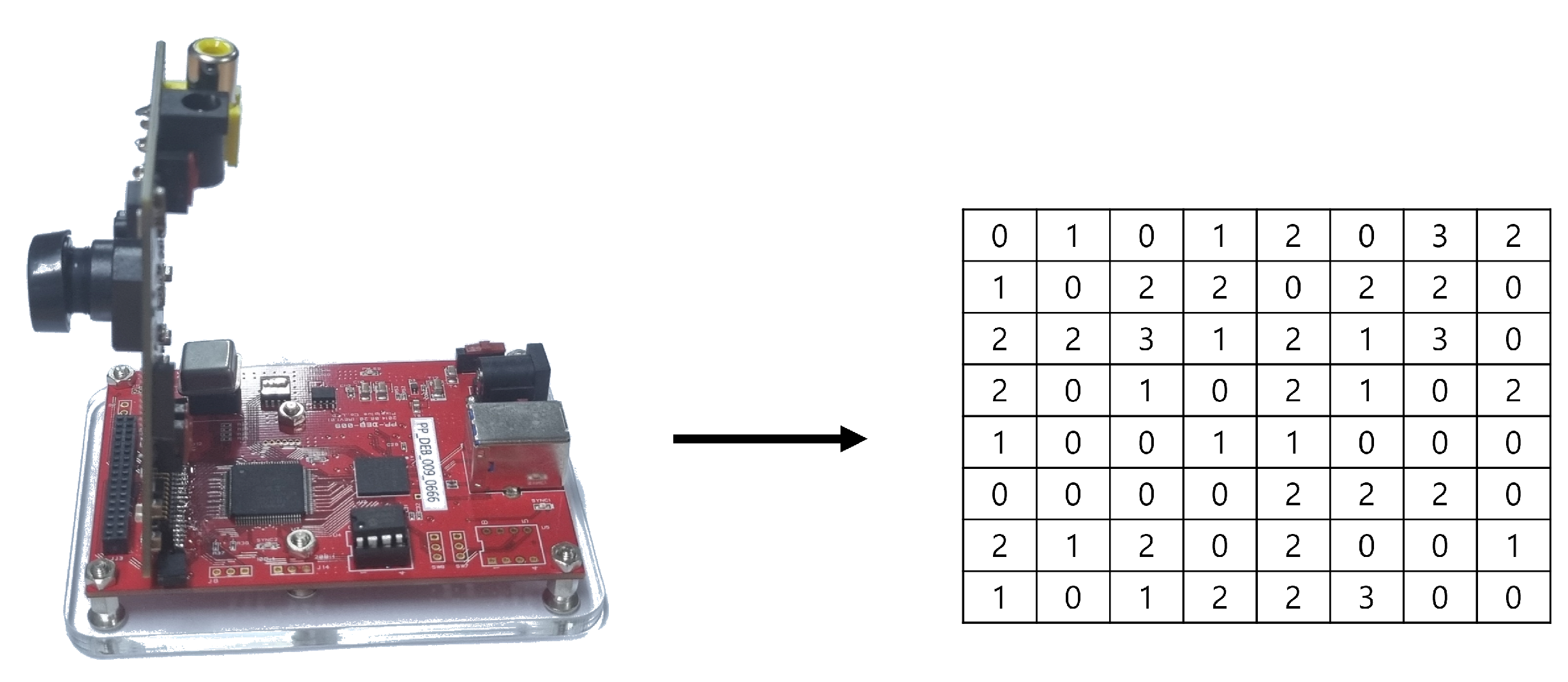
We use ’PV 4209K’ image sensor, which utilizes 11,520 optical black pixels (OBP) as physical entropy sources. Each OBP of the image sensor transmits 2-bit data to a PC. The PC sequentially stores the 2-bit data transmitted by the multiple OBPs. See Figure 6.

3.2. Experimentation process for entropy accumulation

Before describing the entropy accumulation experiments, we use the following notation:

$W_{i}$ : A random variable corresponding to the 2-bit data of the i-th optical black pixel (OBP). "If the value of i reaches the last pixel (11,520), the next value of i refers to the first pixel."
$Y_{j} : = W_{4 j - 3} ∥ W_{4 j - 2} ∥ W_{4 j - 1} ∥ W_{4 j} .$ For example, if $W_{1} = (0, 1)$ , $W_{2} = (1, 1)$ , $W_{3} = (0, 0)$ , $W_{4} = (1, 0)$ , $Y_{1}$ becomes $Y_{1} = (0, 1, 1, 1, 0, 0, 1, 0)$ .
$Γ_{k}^{(l)} : = \sum_{j = (k l - l + 1)}^{k l} Y_{j}$ . This refers to the k-th output sequence, which is generated by adding (XOR) l input sequences.

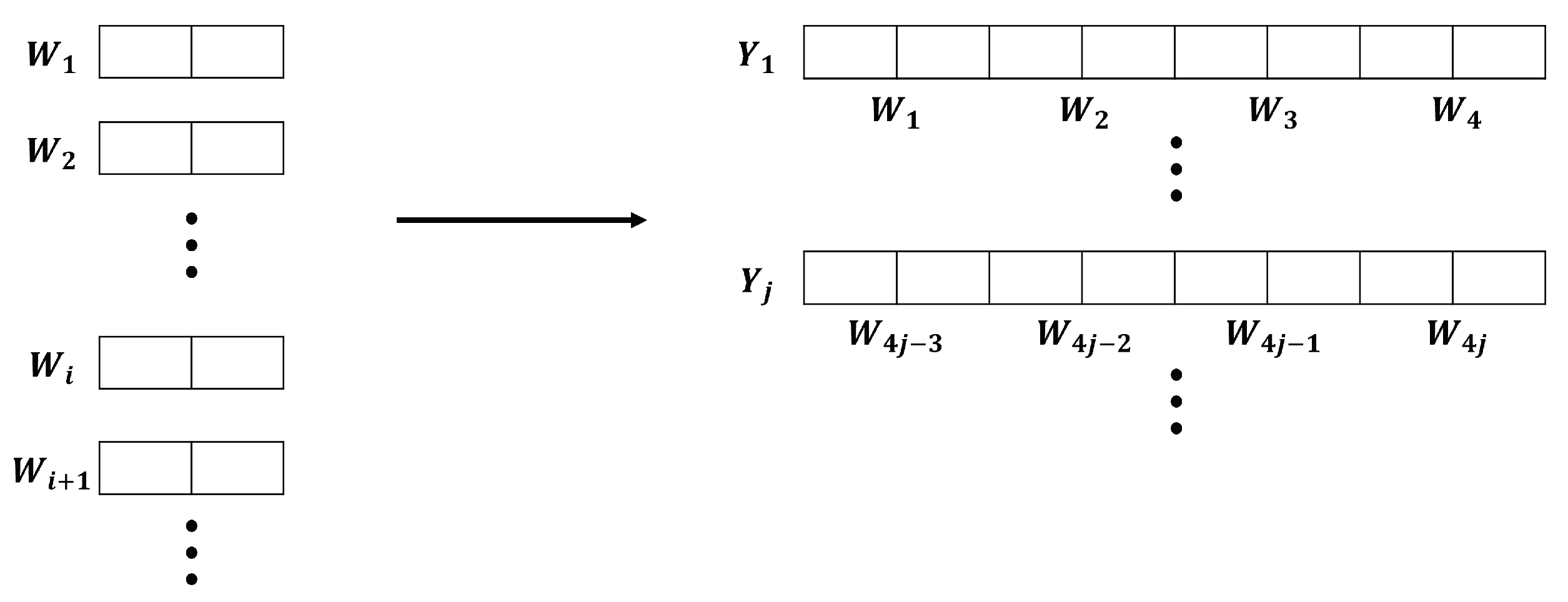
To experimentally validate entropy accumulation, we utilized the verification method outlined in [6]. [6] is a min-entropy estimation tool, which estimates the min-entropy of output sequences by collecting 1,000,000 n-bit output sequences. However, there is a requirement that the value of n must be at least 8. Therefore, to satisfy this condition, we created new 8-bit data

Y_{j}

by concatenating four 2-bit datasets

W_{4 j - 3}

W_{4 j - 2}

W_{4 j - 1}

W_{4 j}

, and

Y_{j}

becomes an input sequence. This process is shown in Figure 7.

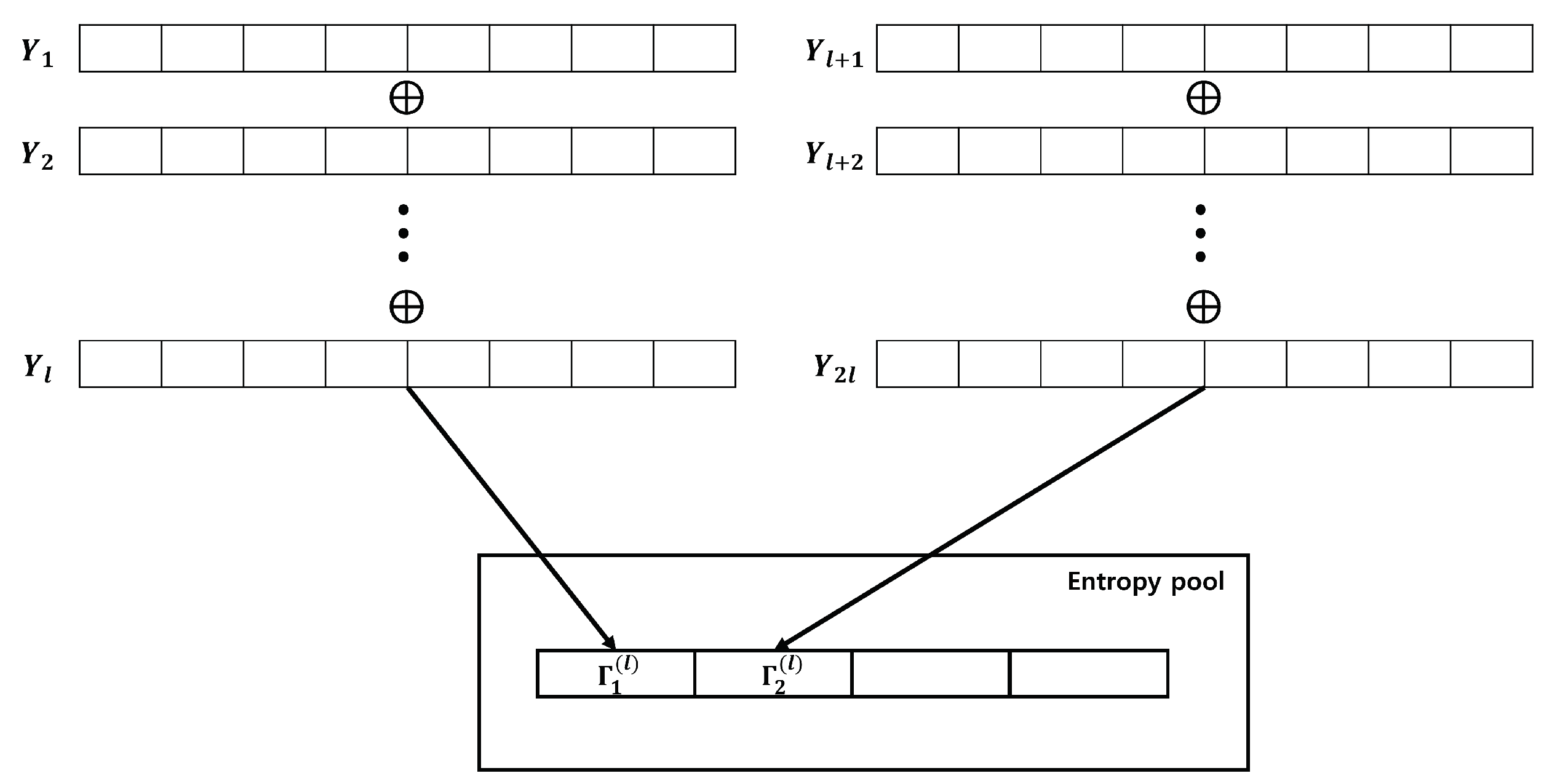
After setting

Y_{j}

, we select the XOR operation iteration number(

l - 1

) and accumulate

Γ_{k}^{(l)}

in the entropy pool. This process is illustrated in Figure 8.

The number l is determined using Theorem 1. After collecting

Γ_{k}^{(l)}

(1 \leq k \leq 1, 000, 000)

in the entropy pool, we used [6] to verify the min-entropy.

3.3. Setting lower bound of min-entropy

We provide three evaluation criteria that can be used to determine the lower bound of the min-entropy, which a true random number generator must exceed, acquired through the entropy accumulation process.

3.3.1. Maximum value of Most Common Value Estimate

In [6], when the output sequences are determined to follow the IID, the Most Common Value Estimate is assumed to be the min-entropy of the output sequences [6]. However, there is an upper bound on the min-entropy value in the Most Common Value Estimate. Regardless of the output sequences used for the test, this upper bound cannot be exceeded. The Most Common Value Estimate estimates the min-entropy as described in Algorithm 1.

Algorithm 1:Most Common Value Estimate

Input:

S = (s_{1}, \dots, s_{L})

, L : Length of S,

S_{i} \in {0, 1}^{n}

(1 \leq i \leq L)

Output: Min-entropy of dataset

S : H_{m i n}

1:: Calculate the mode of S. We denote this value by $M O D E$
2:: $\hat{p} = \frac{M O D E}{L}$
3:: $p_{u} = min (1, \hat{p} + 2.576 \sqrt{\frac{\hat{p} (1 - \hat{p})}{L - 1}})$
4:: $H_{m i n} = - {log}_{2} p_{u}$

To compute the upper bound of the Most Common Value Estimate for an 8-bit dataset S, where the length of S is 1,000,000, the mode of S should be one. That is

\hat{p} = 1 / 256

. Using

\hat{p}

, we obtained

H_{m i n} = 7.94

. Therefore, it is reasonable for the lower bound of the min-entropy to not exceed 7.94.

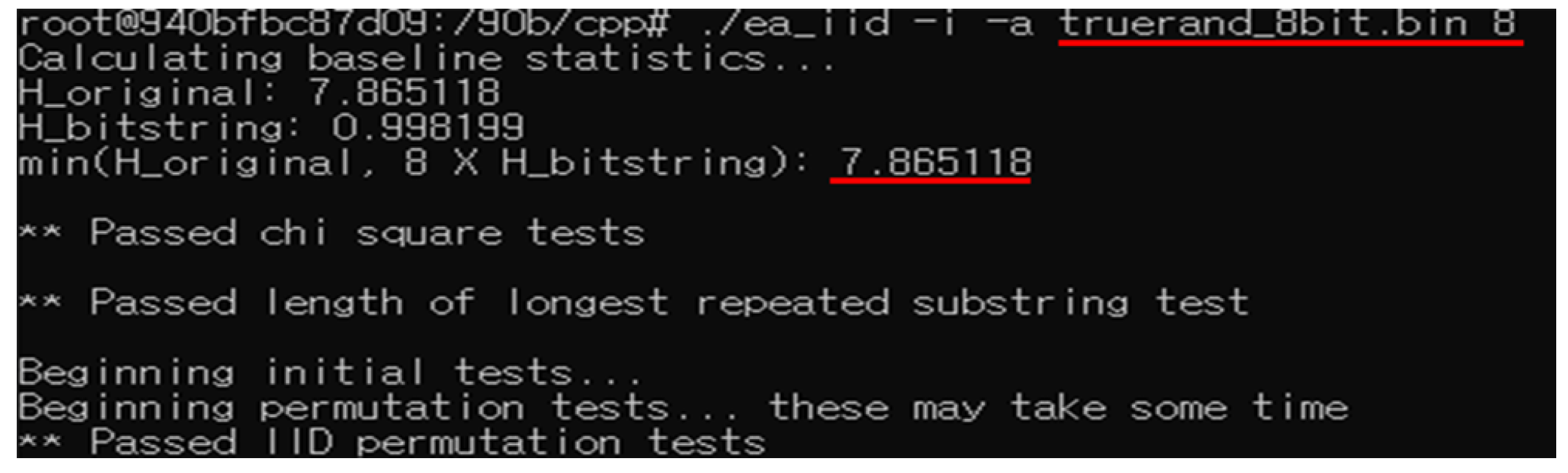
3.3.2. True Random 8-bit in [6]

[6] provides True Random Data in 1-bit, 4-bit, and 8-bit units as samples for evaluating min-entropy. From Figure 9, it can be confirmed that the min-entropy of true random 8-bit data in [6] is approximately 7.86.

3.3.3. Criterion of Min-entropy by BSI AIS 20/31 [7]

The Federal Office for Information Security in Germany (Bundesamt für Sicherheit in der Informationstechni, BSI) asserts in the AIS 20/31 document that the output sequences of a cryptographic random number generator should have a min-entropy of 0.98 per bit. In the case of 8-bit data, 7.84 becomes the lower bound of entropy.

From the three criteria mentioned above, we have chosen 7.86 as the min-entropy lower bound. This value, which is smaller than 7.94 and more stringent than 7.84, appears to be a valid choice for the lower bound.

3.4. Applying Theorem 1 to input sequences

In this subsection, we use Theorem 1 and obtain l. Instead of directly applying Theorem 1 to

Y_{j}

, we employ a "divide and conquer" approach to compute the total min-entropy. Before explaining this strategy, note that each

W_{i}

can be regarded as an independent random variable. This assumption is reasonable because all pixels can be considered independent entropy sources.

Because we conducted the experiment with eight bits, n must be eight when applying Theorem . However, this results in the following problem: the required number l is exceedingly large. To address this issue, we exploit the fact that

Y_{j}

is constructed by concatenating four independent entropy sources.

Γ_{k}^{(l)}

is generated by considering the XOR of l instances in

Y_{j}

. Therefore, if we break down

Γ_{k}^{(l)}

into two bits, then

Γ_{k}^{(l)}

can be considered as four concatenations of the XOR of l instances of

W_{i}

. This can be expressed by the following formula:

\begin{matrix} Γ_{k}^{(l)} = \sum_{j = (k l - l + 1)}^{k l} W_{4 j - 3} ∥ W_{4 j - 2} ∥ W_{4 j - 1} ∥ W_{4 j} = \\ (\sum_{j = (k l - l + 1)}^{k l} W_{4 j - 3}) ∥ (\sum_{j = (k l - l + 1)}^{k l} W_{4 j - 2}) ∥ (\sum_{j = (k l - l + 1)}^{k l} W_{4 j - 1}) ∥ (\sum_{j = (k l - l + 1)}^{k l} W_{4 j}) . \end{matrix}

The four parts of

Γ_{k}^{(l)}

are independent of each other. Therefore, we calculated the total min-entropy by individually determining the min-entropy for each of the four parts, and then summing them up. If the min-entropy of each 2-bit segment of

Γ_{k}^{(l)}

is greater than 1.965,

H_{m i n} (Γ_{k}^{(l)})

will be greater than 7.86. Theorem 1 is applied to the four 2-bit segments of

Γ_{k}^{(l)}

. To apply Theorem 1, the following two conditions must be satisfied: The first pertains to the independence of

W_{i}

. The second condition states that the value of

ω

should exceed zero. For the first condition, we established that each

W_{i}

could be regarded as an independent random variable. For the second condition, we can estimate the value of

ω

by analyzing the probability distribution of the data transmitted by each OBP. We constructed the probability distribution of each

W_{i}

using 2-bit data transmitted by each of the 11,520 OBPs over 2000 transmissions. From the obtained distribution, we can confirm that the value of

{∥ D_{W_{i}} ∥}_{m i n}

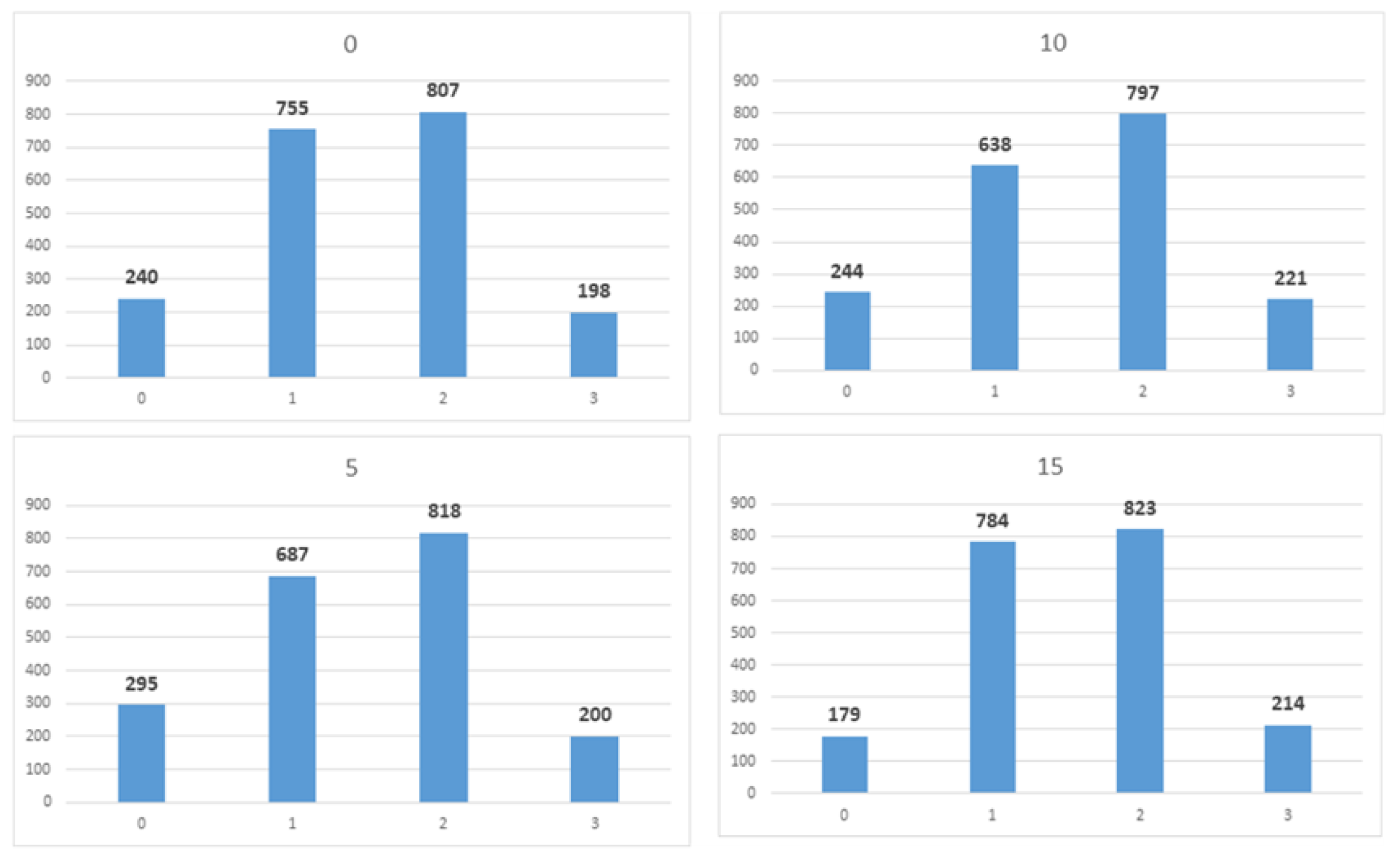
is greater than 0.075 for all i. Figure 10 illustrates the probability distribution of four randomly selected OBPs. It can be observed that each number has appeared at least 150 times.

Therefore, we estimate that

ω

is at least

0.075

. From Theorem 1, the inequality

\begin{matrix} 2 - \frac{1}{ln 2} (2^{2} - 1) {(1 - 2^{2} ω)}^{l} \geq 1.965 \end{matrix}

provides the number l necessary for the min-entropy of each 2-bit segment of

Γ_{k}^{(l)}

to exceed 1.965.

\begin{matrix} 2 - \frac{1}{ln 2} (2^{2} - 1) {(1 - 2^{2} ω)}^{l} \geq 1.965 \\ \Rightarrow \frac{0.035 \cdot ln 2}{3} \geq {(0.7)}^{l} \\ \Rightarrow \frac{ln (\frac{0.035 \cdot ln 2}{3})}{ln (0.7)} \leq l \\ \Rightarrow 15.845 \leq l \end{matrix}

From the last inequality, we can conclude that if we use 15 XOR operations to create

Γ_{k}^{(l)}

H_{m i n} (Γ_{k}^{(l)})

exceeds 7.86.

3.5. Experimental Result

We describe the experimental validation of the results in Section 3.4. We predicted that through 15 XOR operations for entropy accumulation, more than 7.86 bits of entropy per eight bits would be guaranteed. Upon conducting actual experiments, it was confirmed that even with only four XOR operations, more than 7.86 of min-entropy per 8 bits was accomplished. Table 1 presents the experimental results.

The experimental results are analyzed as follows. When

l = 1

, it refers to the case where the XOR operation is not used, and the min-entropy per 8-bit is 3.305, which is lower than the min-entropy calculated based on the probability distribution of the two bits from the pixels.

Min-entropy depends on the maximum value of the probability distribution function. By observing the 2-bit probability distribution, we confirmed that the maximum value of the probability distribution function was 0.425. This can also be confirmed from Figure 10, where all the numbers (0, 1, 2, 3) in the four randomly selected distributions do not exceed 850. Therefore, when calculating the min-entropy of two bits, the lower bound of

H_{m i n} (D_{W_{i}})

is 1.2344, and the lower bound of

H_{m i n} (D_{Y_{j}})

created by concatenating the four

D_{W_{i}}

is 4.9378.

The min-entropy estimated through the probability distribution is lower than that estimated by [6] because of the conservative measurement method of [6]. In [6], the output sequence is determined whether follows the IID track or the Non-IID track before measuring min-entropy. If the output sequence follow the IID track, the min-entropy measured by the most common value estimation method becomes the final min-entropy of the output sequence. However, if the output sequence follow the non-IID track, the smallest value among the min-entropies measured by the other 10 methods, including the Most Common Value Estimate, becomes the final min-entropy of the output sequence. For

l = 1

, it was confirmed that the original output sequence followed a non-IID track. Therefore, the min-entropy value estimated by [6] was smaller than that calculated based on the probability distribution.

As the value of l increases, it can be observed that the increment of min-entropy decreases. This is because the maximum possible min-entropy value is 7.94, and as it approaches this number, the amount of min-entropy that can be increased by increasing the number of XOR operations becomes small. The greatest change in the min-entropy value occurs when l changes from

l = 1

l = 2

. This is because the output sequence follows the IID track if

l \geq 2

3.6. Estimation of entropy accumulation speed

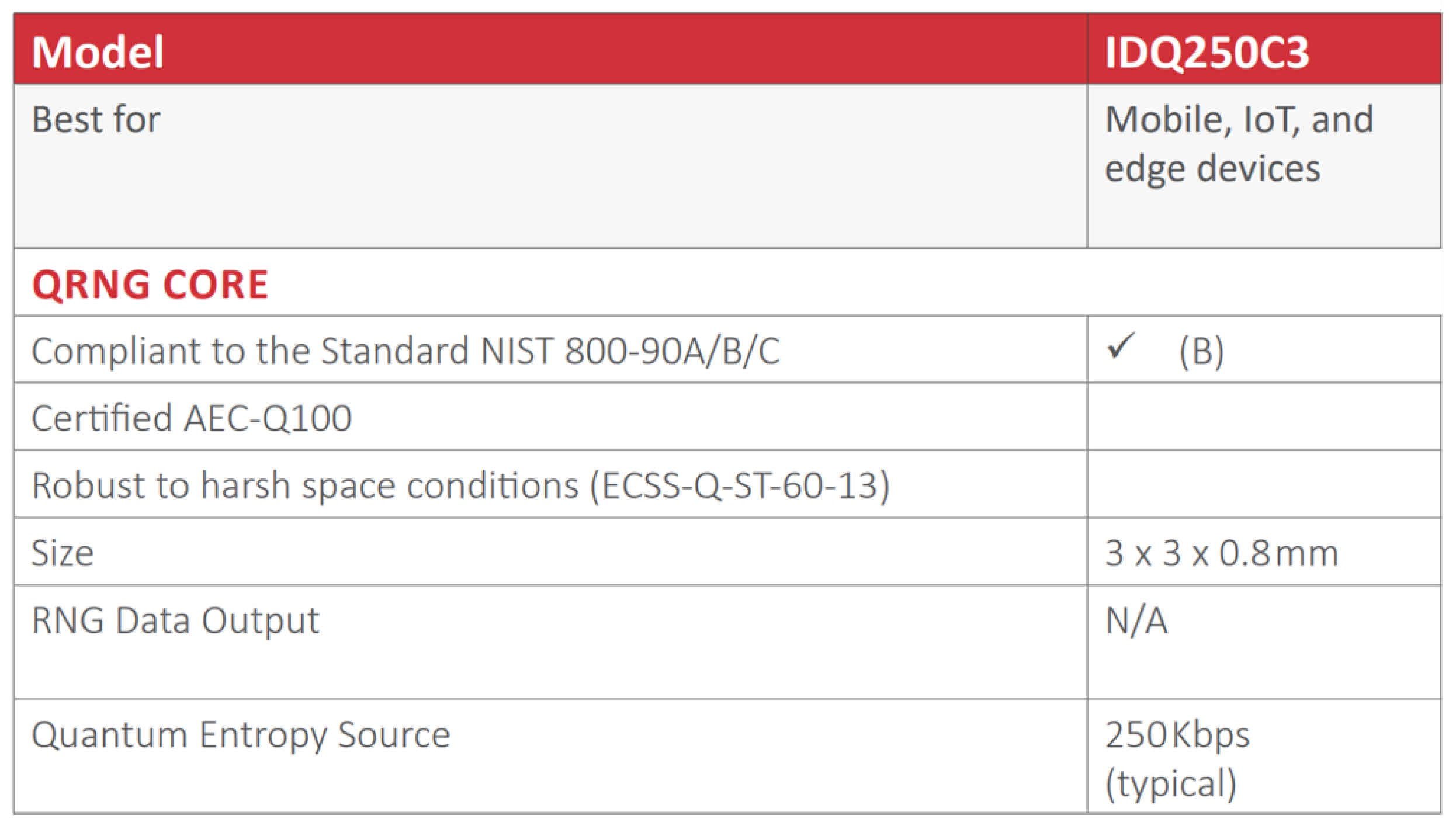
Finally, we estimate the speed of entropy accumulation of the image sensor-based RNG, and compare its performance with the similar RNG product ’IDQ250C3’ by ID Quantique.

The frames per second (FPS) of the image sensor were set to 6. Therefore, the image sensor transmitted 2-bit data six times per second from 11,520 OBP, implying that a total of

11, 520 \times 12 = 138, 240

bits were transferred per second. Consequently, 17,280 pieces of 8-bit data

Y_{j}

are used per second. According to the results in Section 3.4, to obtain a min-entropy of 7.86 per 8 bits,

Γ_{k}^{(l)}

should be created using four

Y_{j}

. Therefore, 4,320 pieces of

Γ_{k}^{(l)}

could be created per second, yielding an entropy accumulation speed of approximately 33.9 Kbps.

As shown in Figure 11, the entropy accumulation speed of the ’IDQ250C3’ QRNG Chip by ID Quantique is 250 Kbps [8]. The entropy accumulation speed of the image-sensor-based RNG experimentally confirmed in this study was 33.9 Kbps. While there is a difference in entropy accumulation speed compared to ’IDQ250C3’,’ there are differences, such as the implementation of hardware chips, the FPS of the image sensor, and the number of pixels used. If the image-sensor-based RNG proposed in this study selects the optimized FPS and number of pixels and undergoes hardware implementation, it would have sufficient performance for use in real cryptographic systems.

4. Applying Windows’ entropy accumulation to our input sequences

In this section, we describe the entropy accumulation theory in [3] and calculate the number of operations that must be iterated when applying it to the input sequence

Y_{j}

. First, we describe what the 2-monotone distribution and the covering number, which are essential concepts in [3]. Thereafter, we present Theorem 5.2 of [3](which is the main result of [3]) with our notation.

Next, we explain why [3] cannot be directly applied to our entropy accumulation model, and suggest an additional S-box operation as a solution. With this additional operation, we can apply Theorem 5.2 of [3] and overcome the limitations of the original theory. Finally, we provide the theoretical number of operations necessary to guarantee a min-entropy of 7.86 per 8 bits when Theorem 5.2 of [3] is applied to the RNG.

4.1. Windows’ Entropy Accumulation

The covering number is used to measure the efficiency of the permutations used in entropy accumulation. The efficiency of entropy accumulation increased as the covering number of permutations decreased.

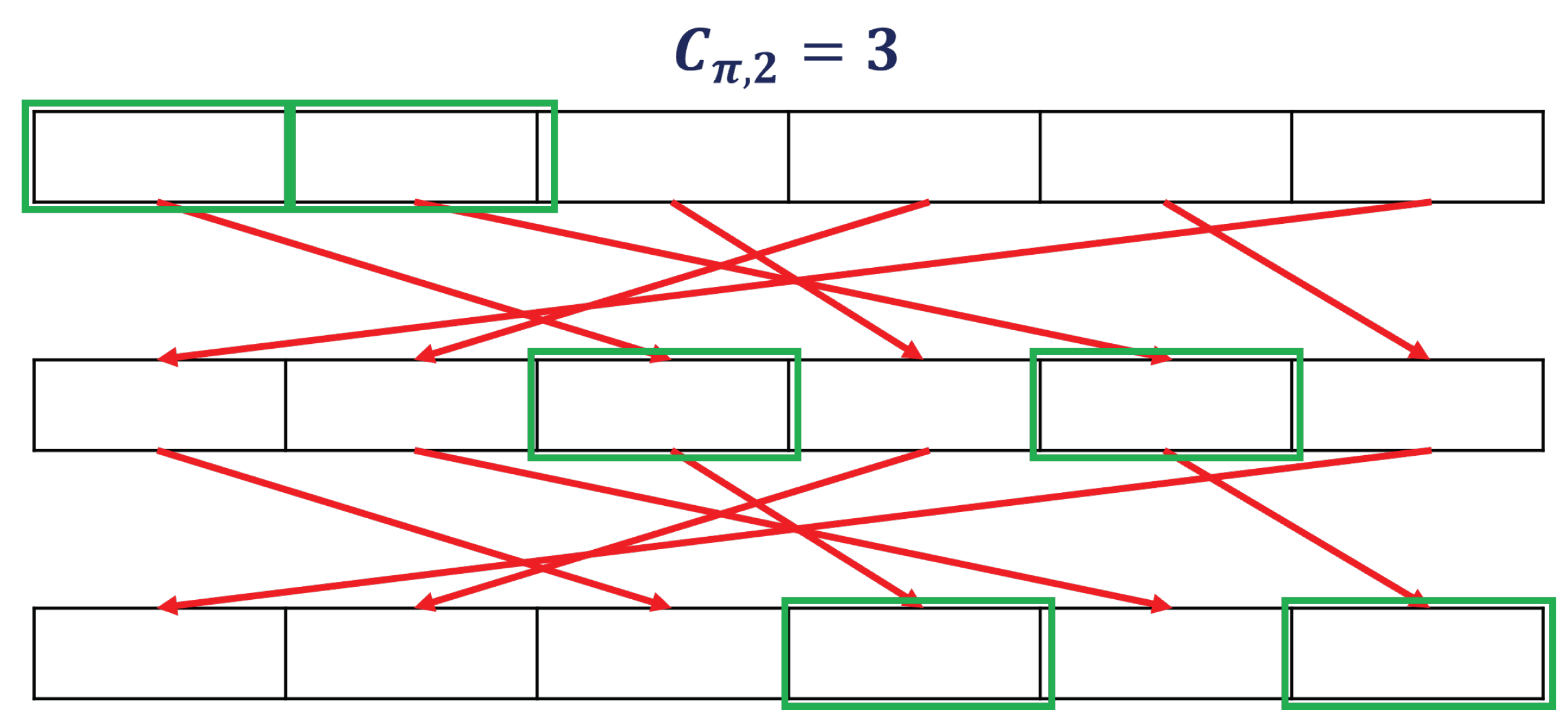
Definition 3

(covering number). For a permutation

π : \{0, 1, . . ., n - 1\} \to \{0, 1, . . ., n - 1\}

, and an integer

1 \leq k \leq n

, the

c o v e r i n g n u m b e r

C_{π, k}

is the smallest natural number m such that

{π^{l} (j) : 0 \leq j < k, 0 \leq l < m} = {0, 1, . . ., n - 1} .

(8)

If no such m exists, then

C_{π, k} = \infty

;

Figure 12 shows the calculation of the number of coverings.

One special property of an entropy source in [3] is 2-monotone distribution. The definition is as follows:

Definition 4

(2-monotone distribution). The probability distribution

D_{X}

of an n-bit random variable X follows a 2-monotone distribution if its domain can be divided into two disjoint intervals, where

D_{X}

is a monotone function.

A 2-monotone distribution has at least one inflection point (peak), because it is divided into two monotonic intervals.

Based on these definitions, we can state Theorem 5.2 of [3].

Theorem 2

(Theorem 5.2 of [3]). Suppose that for independent n-bit random variables

Y_{1}, Y_{2}, . . ., Y_{l}

, the probability distributions

D_{Y_{1}}, D_{Y_{2}}, . . ., D_{Y_{l}}

have a min-entropy of at least

k (\geq 2)

and follow a 2-monotone distribution. Let

π : \{0, 1, . . ., n - 1\} \to \{0, 1, . . ., n - 1\}

be a permutation and

m = C_{π, k^{'}}

be a covering number where

k^{'} = ⌊\frac{k}{2}⌋

. Let

Λ_{π}^{(l)} = A_{π}^{l - 1} (Y_{1}) \oplus A_{π}^{l - 2} (Y_{2}) \oplus \dots \oplus Y_{l}

. Then, for any

l \geq m

, the following holds.

H_{m i n} (D_{Λ_{π}^{(l)}}) \geq n - (⌊\frac{n}{k^{'}}⌋ + 1) \cdot l o g_{2} (1 + 2^{k^{'} - (\frac{k}{2}) ⌊\frac{l}{m}⌋}) \approx n (1 - 2^{\frac{k}{2} - \frac{k l}{2 m}}) .

One can easily observe that As n increased,

H_{m i n} (D_{Λ_{π}^{(l)}})

converged to n.

4.2. Windows’ Entropy Accumulation without 2-monotone condition

Theorem 2 provides a min-entropy lower bound for

Λ_{π}^{(l)}

with only three restrictions. The conditions under which the input sequences are independent, and the covering number of permutations is finite, are relatively easy to satisfy. However, it is challenging to satisfy the condition that all input sequences follow a 2-monotone distribution is quite challenging to satisfy. In particular, for the image sensor entropy sources used, input sequences follow a 2-monotone distribution are unattainable.

We generated

Y_{j}

by concatenating four 2-bit entropy sources:

W_{4 j - 3}, W_{4 j - 2}, W_{4 j - 1}, W_{4 j}

. We used this method only for experimental verification(SP-800-90b requires at least 8-bit data), and

H_{m i n} (Γ^{(l)})

was theoretically calculated by adding the four min-entropy values of the 2-bit segment of

Γ^{(l)}

(see Section 3.4). However, if we apply Theorem 2 to our input sequences, we cannot use the divide-and-conquer approach. This is because while

D_{W_{i}}

definitely satisfies a 2-monotone (as can be observed in Figure 10), Theorem 2 requires input sequences with a min-entropy of two or more. Note that the 2-bit entropy sources

W_{i}

cannot achieve this condition. For this reason, when applying Theorem 2 to our input sequences, we must use the concatenation method for theoretical, rather than experimental, reasons. However, if the input sequences are processed in a concatenated manner, it is impossible to satisfy the 2-monotone assumption. We explain this using a four-bit example. Figure 13 represents the probability distribution of 2-bit entropy sources

W_{1}

and

W_{2}

that follow a 2-monotone distribution. The probability distribution of

W_{1} ∥ W_{2}

, created by concatenating the two entropy sources, is shown in Figure 14.

If we consider

{4 i - 3, 4 i - 2, 4 i - 1, 4 i}

as one group, there are four groups and the overall shape of

D_{W_{1} ∥ W_{2}}

is similar to that of

D_{W_{1}}

. However, the shape of each group’s graph is similar to

D_{W_{2}}

. The shape of such a concatenated distribution tends to become more complex as the entropy sources become more concatenated. Therefore, inevitably, the distribution of the input sequences assumes a shape that is far from a 2-monotone. However, if

Y_{j}

passes through a "good" S-box, the data can be transformed to follow a 2-monotone distribution (in particular, a monotone distribution). For example, if

W_{1} ∥ W_{2}

passes through an S-box S in Table 2,

D_{S (W_{1} ∥ W_{2})}

follows a monotone distribution. This is illustrated in Figure 15. The method for creating such S is simple. After obtaining the distribution of concatenated data, arrange the distribution values in ascending order and input the elements of the domain that provide the distribution values into the S-box in order. For example, as shown in Figure 14,

D_{W_{1} ∥ W_{2}}

has a minimum value at

x = 15

and the second-smallest value at

x = 3

. If x values are arranged in this manner, they become 15, 3, 12, 7,⋯, 2, 6, and 10. Inputting these in sequence into the S-box creates S results in Table 2.

Although we provide an example of transforming 4-bit data created by concatenating two 2-bit entropy sources, this method can be applied to arbitrary n-bit data. With this method, even if the input sequences do not follow the 2-monotone distribution, Theorem 2 can be applied even if the input sequences do not follow a two-monotone distribution. However, memory is required to store the S-box, and the accumulation speed can be reduced owing to additional operations. Additionally, significant amounts of meaningful data may be required to estimate the distribution. Figure 16 illustrates the Windows’ entropy accumulation process using an additional S-box.

4.3. Applying Theorem 2

In this subsection, we determine the number l required for

Λ_{π}^{(l)}

to exceed an entropy of 7.86 bits per eight bits by applying Theorem 2 to

S (Y_{j})

. We did not conduct actual experiments because of the numerous S-boxes that needed to be implemented, and the vast amount of data required to estimate

D_{Y_{j}}

To apply Theorem 2, the first step is obtaining

H_{m i n} (D_{S (Y_{j})})

: As the S-box does not change the min entropy,

H_{m i n} (D_{Y_{j}})

is used instead. Using [6] to estimate

H_{m i n} (D_{Y_{j}})

requires 1,000,000 pieces of

Y_{j}

, which is practically impossible. Therefore, we set

k = 4.9378

, which is the lower bound of

H_{m i n} (D_{Y_{j}})

, estimated using 2,000 pieces of

W_{i}

data, as mentioned in Section 3.5. Note that the estimated min-entropy at

l = 1

in Table 1 of Section 3.5 and the previously estimated min-entropy have explicitly different estimation targets. With

k = 4.9378

k^{'} = ⌊\frac{k}{2}⌋ = 2

. If we set

π = r o t_{(2, 8)}

, the covering number

m = C_{π, k ’}

becomes four, which is the minimum value of every possible

π

. Thus, we opted to use

r o t_{(2, 8)}

as a bit permutation for the entropy accumulation. Considering these considerations, l can be calculated as follows:

\begin{matrix} n (1 - 2^{\frac{k}{2} - \frac{k l}{2 m}}) \geq 7.86 \\ \Rightarrow \frac{n - 7.86}{n} \geq 2^{\frac{k}{2} (1 - \frac{l}{m})} \\ \Rightarrow \frac{ln (n - 7.86) - ln n}{ln 2} \geq \frac{k}{2} (1 - \frac{l}{m}) \\ \Rightarrow l \geq m [1 - \frac{2}{k} (\frac{ln (n - 7.86) - ln n}{ln 2})] \\ \Rightarrow l \geq 4 [1 - \frac{2}{4.9378} (\frac{ln (8 - 7.86) - ln 8}{ln 2})] = 13.4559 . \end{matrix}

That is, if we assume

l = 14

to create

Λ_{π}^{(l)}

H_{m i n} (D_{Λ_{π}^{(l)}})

will exceed the value 7.86.

In Section 3.4, we observed that our theory yields

l = 16

. Although Theorem 2 may yield slightly superior results, the difference is insignificant. Considering the time consumed for additional S-box and bit permutations, and the storage space for S-boxes, we can conclude that our entropy accumulation provides more practical results.

5. Conclusions

The contributions of this study can be summarized as follows: First, we propose entropy accumulation using bitwise XOR alone, without the use of hash functions. Furthermore, we provide a theory that proposes the number of XOR operations that must be repeated to obtain a specific min-entropy.

Second, we established 7.86 as the lower bound for the min-entropy per 8-bits, which was considered secure based on the three benchmarks. To surpass this lower bound, our proposed theory yielded

l = 16

, which implies that 15 XOR operations are needed. We then implemented an actual RNG to verify the theory. Our experimental results indicated that if we use XOR operations just 4 times, the generated output sequences exceeded the lower bound. The entropy source used in this experiment is an image-sensor-based RNG, PV 4209 K.

Finally, we compare our entropy accumulation to the Windows entropy accumulation. In order to ensure the lower bound of min-entropy of the output sequences generated by entropy accumulation method in Windows, it is necessary for the input sequences to follow a 2-monotone distribution. To overcome this problem, we show that if we added additional S-boxes, it is possible to ensure the lower bound of min-entropy of the output sequences. We then calculated the theoretical number l. We obtained that

l = 14

, whereas our entropy accumulation yielded

l = 16

. Considering the requirements for additional S-box operations and bit permutation, as well as the storage space of the S-box, we confirmed that our entropy accumulation gives more practical results.

Funding

This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (No. 2021M1A2A2043893) and Ministry of Science and ICT, South Korea(1711174177).

References

Shoup, V. A computational introduction to number theory and algebra; Cambridge university press, 2009.
Ferguson, N. The windows 10 random number generation infrastructure, 2019.
Dodis, Y.; Guo, S.; Stephens-Davidowitz, N.; Xie, Z. No time to hash: On super-efficient entropy accumulation. Advances in Cryptology–CRYPTO 2021: 41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, –20, 2021, Proceedings, Part IV 41. Springer, 2021, pp. 548–576. 16 August.
Park, B.K.; Park, H.; Kim, Y.S.; Kang, J.S.; Yeom, Y.; Ye, C.; Moon, S.; Han, S.W. Practical true random number generator using CMOS image sensor dark noise. IEEE Access 2019, 7, 91407–91413. [Google Scholar] [CrossRef]
Matsui, M. Linear cryptanalysis method for DES cipher. Advances in Cryptology—EUROCRYPT’93: Workshop on the Theory and Application of Cryptographic Techniques Lofthus, Norway, –27, 1993 Proceedings 12. Springer, 1994, pp. 386–397. 23 May.
Turan, M.S.; Barker, E.; Kelsey, J.; McKay, K.A.; Baish, M.L.; Boyle, M.e. Recommendation for the entropy sources used for random bit generation. NIST Special Publication 2018, 800, 102. [Google Scholar]
Peter, M.; Schindler, W. A Proposal for Functionally Classes for Random Number Generators. Ais.20/31 2022.
https://idquantique.co.kr/quantis-qrng-chip/.

Figure 1. Operation of an RNG.

Figure 2. Example of the

r o t

permutation when

n = 8

and

α = 3

Figure 2. Example of the

r o t

permutation when

n = 8

and

α = 3

Figure 3. Windows’ entropy accumulation.

Figure 4. Entropy accumulation using only bitwise XOR operation.

Figure 5. Our entropy accumulation with

n = 1

Figure 5. Our entropy accumulation with

n = 1

Figure 6. Data transmission process of image sensor.

Figure 7. Concatenation of 2-Bit Data to Form 8-Bit input sequence.

Figure 8. Accumulating entropy source using XOR operation.

Figure 9. Min-Entropy of True Random 8-bit.

Figure 10. Probability distribution of each OBP.

Figure 11. Entropy accumulation speed of IDQ250C3.

Figure 12. Illustration of Covering number when

C_{π, 2} = 3

. The covering number is 3 because all bits are covered using the permutation operation twice.

Figure 12. Illustration of Covering number when

C_{π, 2} = 3

. The covering number is 3 because all bits are covered using the permutation operation twice.

Figure 13. Example of two distributions which follow a 2-monotone distribution.

Figure 14. Distribution of concatenated entropy sources.

Figure 15. Distribution of S-boxed concatenated entropy sources.

Figure 16. Windows’ entropy accumulation with additional S-box.

Table 1. Min-entropy Values Corresponding to Number of XOR Operation Repetitions.

l	i	j	k	Min-entropy per 8-bit
1	4,000,000	1,000,000	1,000,000	3.305
2	8,000,000	2,000,000	1,000,000	7.115
3	12,000,000	3,000,000	1,000,000	7.700
4	16,000,000	4,000,000	1,000,000	7.852
5	20,000,000	5,000,000	1,000,000	7.864

Table 2. 4-bit S-box which is used to

W_{1} ∥ W_{2}

to create monotone distribution.

Table 2. 4-bit S-box which is used to

W_{1} ∥ W_{2}

to create monotone distribution.

x	15	3	12	7	13	11	0	1	4	14	8	5	9	2	6	10
$S (x)$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Practical Entropy Accumulation for Random Number Generators with Image Sensor-Based Quantum Noise Sources

Abstract

1. Introduction

1.1. Related works

1.2. Our contributions

2. Theoretical background and Main theorem

2.1. Entropy accumulation with n = 1

2.2. Convolution and Discrete Fourier Transform

2.3. Main Theorem

3. Applying Theorem 1 to Image Sensor-based RNG

3.1. Image Sensor-based RNG

3.2. Experimentation process for entropy accumulation

3.3. Setting lower bound of min-entropy

3.3.1. Maximum value of Most Common Value Estimate

3.3.2. True Random 8-bit in [6]

3.3.3. Criterion of Min-entropy by BSI AIS 20/31 [7]

3.4. Applying Theorem 1 to input sequences

3.5. Experimental Result

3.6. Estimation of entropy accumulation speed

4. Applying Windows’ entropy accumulation to our input sequences

4.1. Windows’ Entropy Accumulation

4.2. Windows’ Entropy Accumulation without 2-monotone condition

4.3. Applying Theorem 2

5. Conclusions

Funding

References

MDPI Initiatives

Important Links

Subscribe

2.1. Entropy accumulation with $n = 1$