Prerpints.org logo
Preprint
Article

A Tightly Coupled Indoor Positioning Method Using Widespread 5G and Low-Cost Magnetometer Based on Multi-Input CNN

Altmetrics

Downloads

239

Views

71

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 June 2023

Posted:

13 June 2023

Read the latest preprint version here

Alerts
Abstract
With the urgent need of precise positioning faced by internet of things (IoT) applications, the universality and cost of indoor positioning devices become key factors. Since the 5G network has been widely deployed, new opportunity is brought by tightly fusing the traditional low-cost sensors, i.e., the magnetometer. In this study, using 5G channel state information (CSI) and geomagnetic data, a multi-input convolutional neural network (CNN) localization system was proposed. First, to generate a data tensor that is easy for CNN processing, the raw data was reconstructed individually. Then, to comprehensively incorporate the features of 5G CSI and geomagnetic strength data, the ReLU function was chosen as the activation function of the convolutional layer. After that, a multi-input CNN was trained using the incorporated geomagnetic strength and CSI amplitude in the off-line side, and the trained CNN was recorded as a location fingerprint, which can be used for the user position prediction. Finally, in the online side and using a multi-input CNN, the 2-D coordinates are estimated and tested indoors in a typical conference room scenario. The results showed that longer sampling time of fingerprint data result in better uniqueness of the reference point, while the data collection time of locating points does not need to be long. Taking the positioning efficiency and accuracy into consideration, a sampling time of 3s at the reference point and 0.2s at the locating point are recommended. The positioning accuracy using the proposed method was 1.41 m, with an improvement of 22.9% compared with the 5G positioning, and an improvement of 18.0% compared with the 5G and geomagnetic fusing positioning using single CNN.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

The internet of things (IoT) is a vision for the development of the internet world. With the advancement of internet technology, the fields of smart homes, smart transportation, and smart cities are making progress in automation and intelligence. Location-based services are one of the basic services of the mobile internet [1], and high-precision indoor intelligent positioning services have gradually become a necessary requirement for people's daily lives. Currently, the most widely used location service technology is the global navigation satellite system (GNSS), which can provide a broad and universal technical guarantee for navigation and positioning in open environments and meet the location requirements in most scenarios. However, in indoor environments, due to complex and changing electromagnetic environments and obstructions, GNSS cannot be directly and effectively applied. On the one hand, the ultrasonic and laser positioning technologies have the disadvantages of poor universality and high deployment costs, and cannot meet the high-precision and wide-coverage positioning needs of the IoT. On the other hand, in the fields represented by railway tunnels, mine detection, and disaster relief, it is necessary to determine the location of relevant workers. In addition, people spend 80% of their time indoors [2], and providing high-precision and reliable location information is the foundation of various indoor applications. This is also one of the key challenges that the current national comprehensive PNT system urgently needs to solve [3]. Therefore, indoor positioning technology has received widespread attention from scholars [4].
In recent years, with the development of communication technology and various sensor technologies, indoor positioning technology is also booming. Currently, the most widely used methods are based on distance measurement, angle measurement, and fingerprint information sampling. Among them, the observation quantities based on distance measurement include time of arrival (TOA) and time difference of arrival (TDOA) measurements. Using TOA, the propagation time of the signal is used to calculate the distance between the base station and the target point, and the target point position is obtained through the intersection method [5,6]. Due to the fast speed of radio signal propagation [7], TOA requires a high-precision time synchronization system between base stations, which greatly increases the positioning cost and makes it difficult to deploy effectively on a large scale. TDOA is an improvement on TOA [8], which does not require direct acquisition of signal arrival time to calculate the distance between the terminal and the base station, it calculates the distance between the terminal and the base station by subtracting the signal arrival times, reducing the requirement for device consistency [9]. Since an accurate measurement of the time difference of signal propagation is required, the same situation is face by the TDOA [10]. In addition, under complex scenes, the non-line-of-sight (NLOS) signal will lead to large ranging and positioning errors.
The angle of arrival (AOA) measurement belongs to the second measurement. By obtaining the phase difference of the signal through the coherent solution of the base station array antenna, AOA estimates the terminal coordinates using the converted angle [11]. Since a time synchronization system is not required, the positioning cost can be reduced with fewer base stations [12]. However, to achieve better positioning effects, this method requires the addition of a large-scale antenna array and the signals must propagate through direct paths between signals [13]. In an indoor environment, the multipath effect is serious, leading to poor signal quality, and the complex decoherence algorithm also increases the computational complexity.
The last fingerprint-based method does not require related calculations or time synchronization modules, and also not affected by NLOS. The positioning system is divided into an offline stage and an online stage, wherein the offline stage collects the environment fingerprint information of the test area in advance and establishes an offline fingerprint database, and to obtain the position of the test point, the online stage matches the real-time environment fingerprint information of the test point with the data in the offline fingerprint database [14]. The characteristic including receive signal strength information (RSSI), channel state information (CSI), and geomagnetic information can be selected as fingerprints [15]. Without signal calculation, this method can set different densities of fingerprint information collection points according to different scenes. But since the time and manpower cost required for offline fingerprint collection is relatively high, if the surrounding environment changes, it will cause certain interference to signal collection and offline matching. However, with the development of deep learning algorithms, dynamic updating of the fingerprint database can be achieved, and the anti-interference performance of the fingerprint database can be improved by adding additional sensors. Compared with TOA, TDOA, and AOA, the fingerprint method has stronger performance in terms of deployment cost and applicability.
In this contribution, the existing research on indoor positioning methods is reviewed first, followed by the introduction of the research status of fingerprint positioning. Next, the acquisition and pre-processing of 5G CSI and geomagnetic data, as well as the fusion positioning algorithm of 5G CSI and geomagnetic are elaborated. Then, experimental verification is carried out. Finally, the main conclusions are drawn.

2. Related Works

Affected by the indoor complex environment on radio signal propagation, most of the research has been carried out using multi-sensor integration methods and deep learning algorithms. Li et al. used the RSSI of Wi-Fi signal as fingerprinting feature data and neural network model algorithm, a higher accuracy than traditional machine learning algorithms was obtained [16]. To enrich fingerprint database information, Liu et al. used the amplitude of CSI of Wi-Fi signal instead of RSS as fingerprint data, and the convolutional neural networks (CNN) was utilized as a classification algorithm, as a result the positioning accuracy at sub-meter level in small indoor and outdoor scenes was achieved [17]. Since the geomagnetic-based positioning technique does not require the installation of signal transmitting equipment, Ding et al. proposed a CNN-based geomagnetic indoor positioning method with low cost and large coverage area. And compared with the traditional k-nearest neighbor (KNN) positioning method, this method showed higher accuracy and robustness [18]. However, the above single sensor-based positioning method has certain disadvantages in terms of technical cost, positioning accuracy, and stability [19,20], i.e., the vulnerability of Wi-Fi signal to interference and the low spatial resolution of geomagnetic matching [21].
To overcome the shortcomings of a single sensor, an alternative scheme is the multi-sensor information fusion. Pan et al. proposed a Wi-Fi-assisted magnetic field matching positioning method, in which the Wi-Fi was applied for coarse localization and constructing a standard circle, and geomagnetic data was then used for precise localization within the standard circle. As result, the positioning accuracy was improved through reducing the mis-matching rate caused by the multipath effect of Wi-Fi signals [22]. Using the Wi-Fi signals to determine the initial position by random sampling consistency algorithm, Ruan et al. used geomagnetic matching based on adaptive filtering to correct the positioning results for pedestrian dead reckoning (PDR), which effectively overcome the PDR accumulation error [23]. With the application of the fifth-generation mobile communication network (5G), a new 5G air interfaces-based positioning has received widespread attention [24]. Since 5G uses orthogonal frequency-division multiplexing technology to obtain the system's CSI, which is more stable and abundant in the aspect of CSI feature information than that of Wi-Fi technology [25,26]. By combining the CNN with bi-directional long short-term memory network (BiLSTM), Ruan et al. designed a feature- and sample-based deep network with dual attention mechanism to extract implicit spatial and temporal information of 5G CSI respectively, and meter-level positioning accuracy in indoor office scenarios was achieved [27]. Using the simulated 5G CSI, Gao et al. used ray-tracing channel model for indoor and outdoor localization. However, the effectiveness of this method should be verified with the measured data under real scenarios [28]. Ruan et al. used unsupervised deep self-encoder network to reconstruct CSI features and weighted the reference point coordinates by supervised learning, an average indoor positioning error of 2.14 m was obtained [29]. Fusing 5G, geomagnetic data and visual inertial odometry, Yang et al. used error back propagation neural network (BPNN) to improve the positioning accuracy [30]. In this context, by tightly fusing the widespread 5G and low-cost geomagnetic sensor, this paper proposes a positioning method based on multi-input CNN, in which a short-time collected CSI and three-dimensional (3D) geomagnetic information is utilized as location fingerprints, the high-dimensional CSI information and low-dimensional geomagnetic data are convolved respectively, then fusion positioning is performed, and finally the experiments are carried out to validate the proposed algorithm.
Currently, the 5G base stations have been widely deployed. And hence, signals emitted by the base station can be received by any 5G terminal user, which will not limit the number of users. In addition, a low-cost geomagnetic sensor with the accuracy of is 1 utilized. Since the geomagnetic sensors with similar performance have already equipped by current smartphones, the geomagnetic data can be obtained conveniently and quickly, thus significantly reducing the positioning cost. Therefore, the proposed method has high applicability and practicality.

3. Methodology

Multi-input CNN is a machine learning algorithm developed on the basis of single CNN. It by exploiting the correlation between multiple inputs and learning multiple different types of features, the model performance and generalization are enhanced, and the accuracy is improved by combining different types of data. Besides, to reduce the risk of overfitting and improve the robustness of the system, the amount of data is increased. To fully extract features from different data, the multi-input CNN, instead of single-input CNN, can construct different network branches according to the input data type and dimensionality. Considering the different dimensions of CSI and geomagnetic data, a multi-input CNN model for 5G CSI and geomagnetic fusion is utilized here.
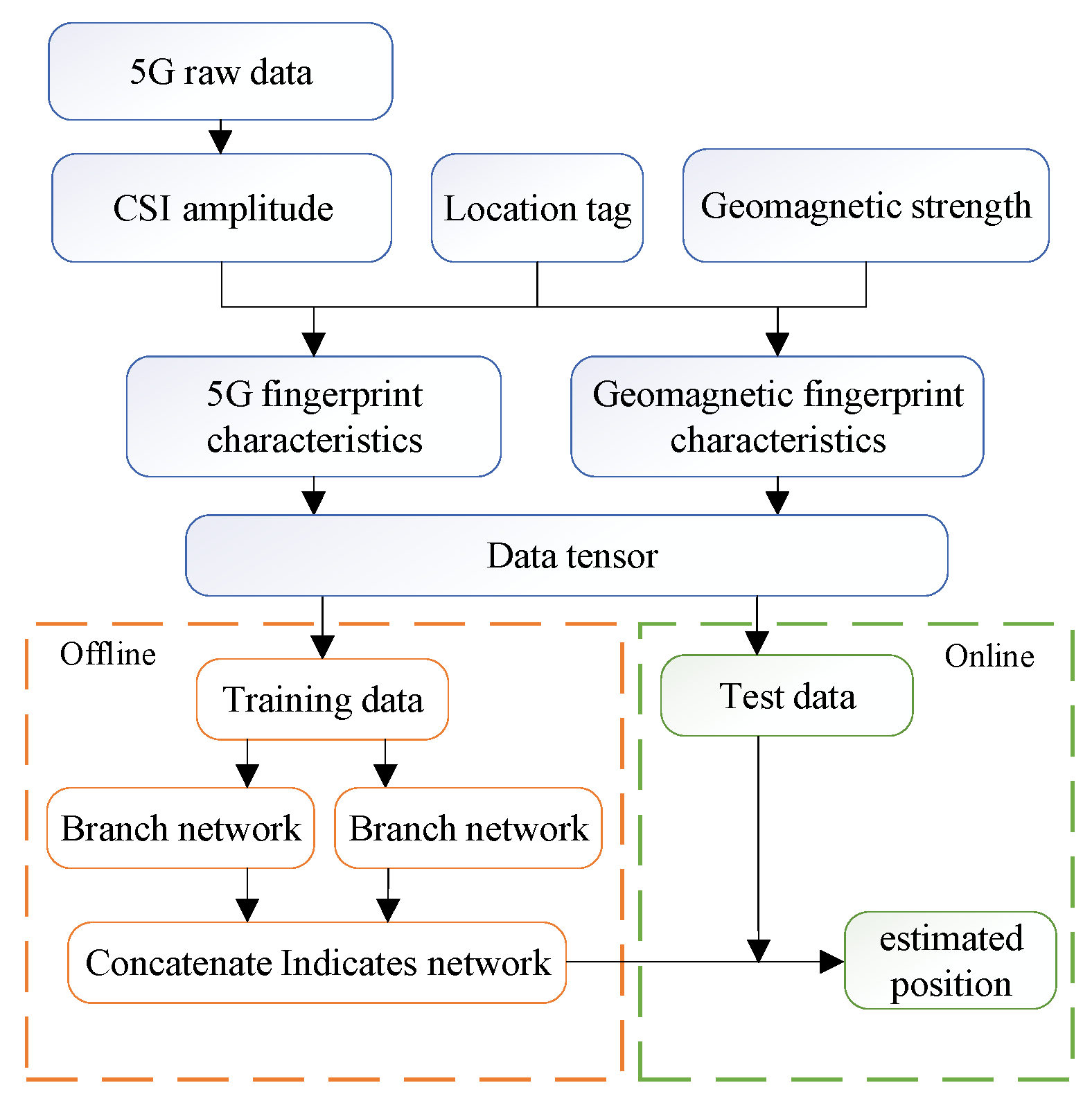
Figure 1 gives the flowchart of the proposed algorithm, wherein preprocessing, training and online localization are involved. Firstly, raw 5G data and geomagnetic strength data are collected. and the 5G CSI amplitude information and the three-axis geomagnetic strength data are extracted to create a composite location fingerprint. After that, to facilitate the subsequent CNN processing, the above data is constructed into tensor-type data. During the training phase of the neural network, using 5G CSI amplitude and geomagnetic tensor data used as input layers, and corresponding coordinates as output layers, they are input into different network branches. Besides, the training results are continuously optimized by adjusting the number of training iterations and network structures. A comprehensive multi-input CNN network is created by combining the established two branches. In the online real-time positioning stage, the measured data is input into the trained multi-input network to obtain the coordinates.

3.1. Data Collection and Preprocessing

The principle of fingerprint localization is to describe the different locations according to the different data collected at each location. The uniqueness of location is represented according to the uniqueness of data features, so the construction of fingerprint data has a great impact on the overall positioning effect. In applications, the characteristics of fingerprint data can be enhanced by extending the data sampling time and increasing the types of sensors to improve the accuracy of fingerprint positioning. However, extending the time of data a sampling will reduce the practical applicability of fingerprint positioning. Therefore, it is necessary to comprehensively consider the positioning timeliness and positioning accuracy.
This section describes the sampling and pre-processing of 5G CSI and geomagnetic data.

3.1.1. 5G CSI Data Pre-Processing

In a 5G wireless network, the received signal ψ on the ν th subcarrier between the transmitting antenna ρ and the receiving antenna τ can be represented as:
ψ τ ρ ( ν ) = H τ ρ ( ν ) × ξ ρ τ ( ν ) + ε τ ρ ( ν )
where, ξ ρ τ ( ν ) is the transmitted signal, ψ τ ρ ( ν ) is the Gaussian white noise, H τ ρ ( ν ) is the channel frequency response (CFR) in the frequency domain, which contains both amplitude and phase information. It can be described by the following equation:
H τ ρ ( ν ) = H τ ρ ( ν ) e j × sin ∠ H
where, H τ ρ ( ν ) and ∠ H represent their amplitude response and phase response, respectively.
The CSI data collected in this paper consists of 60 discrete samples of the 5G new radio NR channel impulse response, which represents the amplitude information of 60 subcarriers. The amplitude information of each subcarrier is used as fingerprint information for the fingerprint database. The sampling frequency is 50 Hz, and the collected data can be represented by matrix H (Equation 3). Each element of the matrix is represented as a a + b × i complex numbers, and hence the amplitude information of each carrier wave S = a 2 + b 2 In the creation of fingerprint database, the initial 5G CSI is a discrete numerical matrix that cannot be directly input into the CNN, thus it needs to be pre-processed, which means that 1s data needs to be processed by expanding to a tensor format grayscale image data, and the location labels should be added, so as to construct a complete position fingerprint data.
H = H 11 , ⋯ , H 1 N ⋮ ⋮ H M 1 , ⋯ , H MN
where, M = 50 ⋅ t , t is sampling time, N is subcarrier number.
In the positioning based on 5G NR, CSI generally refers to the channel state information obtained by the 5G signal receiver through demodulation. It includes information on signal transmission, signal scattering, environmental attenuation, distance attenuation, etc. [30]. Due to the complex and changeable propagation environment, the CSI amplitudes at different locations vary with different propagation paths, but CSI at the same location remains relatively stable. There is a certain mapping relationship between the location and CSI. 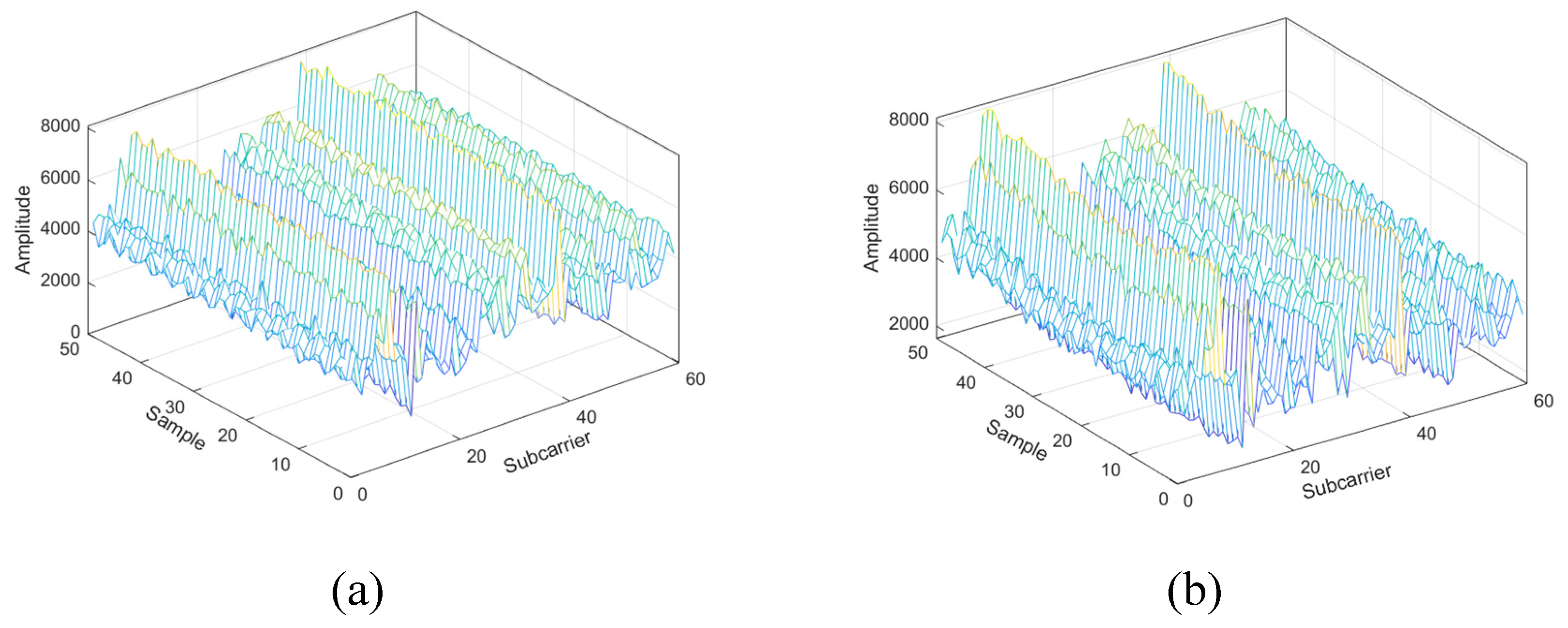Figure 2 describes the 5G CSI amplitudes at two different locations. The amplitudes of 60 subcarriers at the same location all remain stable within 1 s, and the CSI amplitude have different variation rules of different locations, which can be used to represent the change of location and establish the mapping relationship between the CSI and location. Obviously, the longer the sampling time of CSI, the richer the location features described and the stronger the unique features of the fingerprint. Undoubtedly, the long sampling time will reduce the practicality of the algorithm, therefore a balance needs to be found between the richness of the fingerprint information and the positioning efficiency.

3.1.2. Geomagnetic Data Pre-Processing

The geomagnetic intensity reflects the spatial distribution characteristics of the Earth's magnetic field. It should be noted that in indoor environments, geomagnetic information may be affected by steel frame structures [30], i.e., reinforced concrete, leading to geomagnetic anomalies. However, such anomalies make the surrounding buildings more unique in the aspect of feature textures, which can be used for indoor fingerprint positioning. In addition, unlike wireless signal propagation paths that are affected by the layout of indoor objects, geomagnetic data is not affected by complex indoor environments. Once the location of magnetic objects is fixed, the positioning becomes relatively stable.
In the paper, the collected geomagnetic data are the intensity values of the X, Y, and Z-axis geomagnetic components and the geomagnetic model value, and the coordinate system is determined by the device itself. To fully utilize the data, the three-axis components of the geomagnetic field are selected as fingerprint data, and due to the relatively low accuracy of the geomagnetic sensor, the influence of different directions of the geomagnetic vector is ignored. Since CNN has been proven to have excellent abilities in the image feature extraction, the above three-axis component data is reconfigured into image-type data, and the initial geomagnetic data format was 3 × n ⋅ t .
N = X 1 ⋯ X n ⋅ t Y 1 ⋯ Y n ⋅ t Z 1 ⋯ Z n ⋅ t
where, N is a set of geomagnetic data, n is the frequency, t is the sampling time.
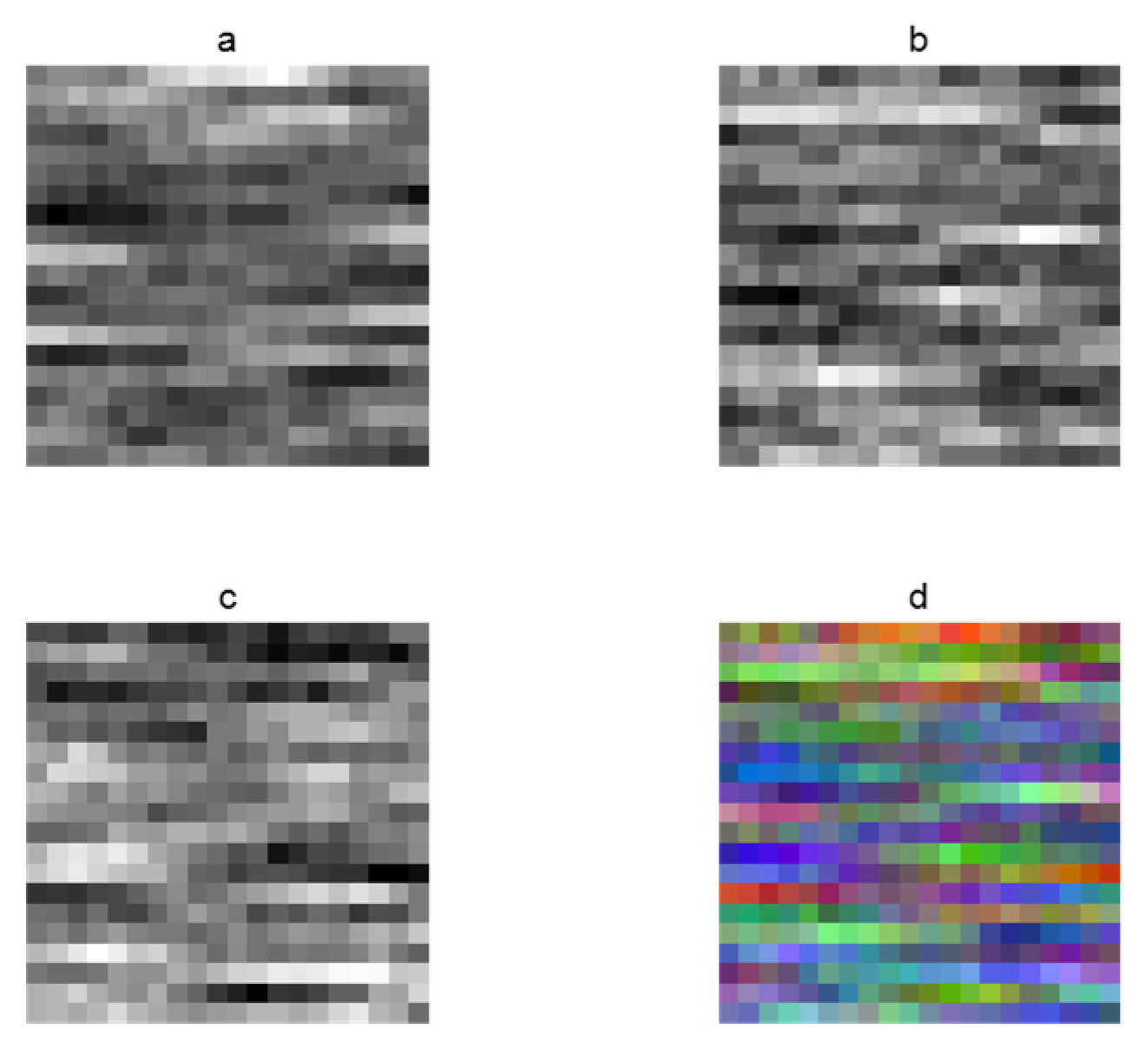
To fully utilize geomagnetic data for network processing, Figure 3 shows the reconstruction of data structure using the "reshape" function. First, to form a grayscale image, the data on each axis component is extracted and filled in order into a m × m matrix, and m × m = n ⋅ t , as shown in (a), (b), and (c). After filling the three-axis components into the matrix, they are stacked and constructed into a format similar to "RGB" using the "Vstack" function, as shown in (d). Then, the data of the three-axis components are expanded to 3 × m × m according to the architecture of neural network, and the channel order is adjusted. Finally, location labels are added to construct complete fingerprint database data for training.

3.2. Multi-Input Convolutional Neural Network Model

The performance of matching algorithm directly affects the positioning effectiveness. Since the used low-cost geomagnetic sensor has low accuracy, the algorithm optimization is required to improve the positioning accuracy. This section describes the network architecture and network-related parameter settings.

3.2.1. Network Architecture

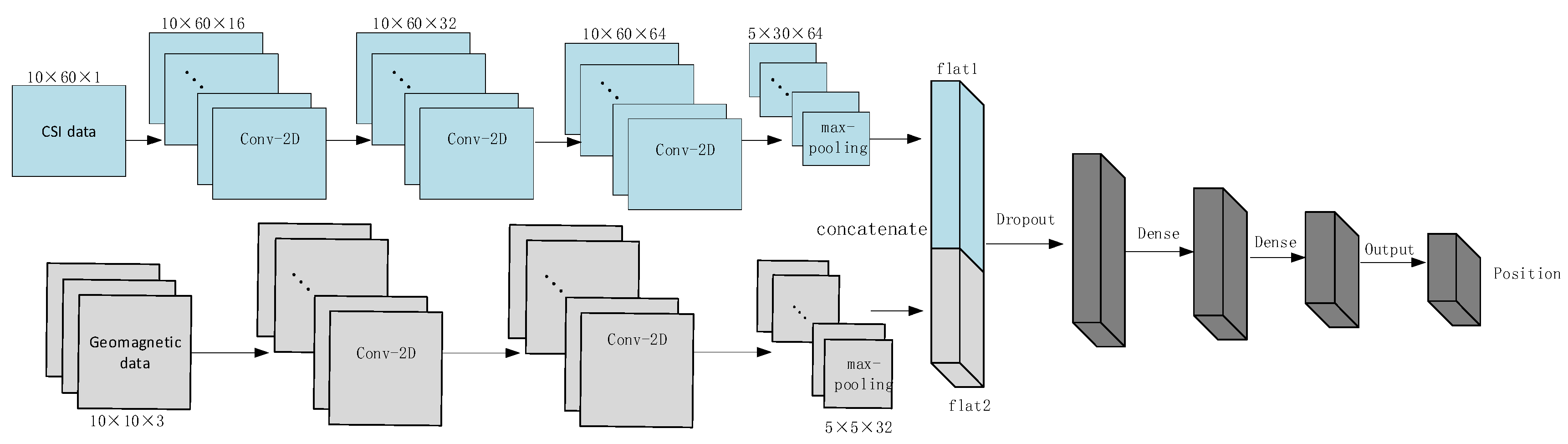
Figure 4 shows the schematic diagram of multi-input convolutional neural network framework. The multi-input CNN model is constructed using the functional API from Keras, in which two input branches consisting of 5G CSI amplitude and reconstructed geomagnetic three-axis component data.
Firstly, to fully extract the features of the input data, the two branches are designed as different network structures according to different data types. And to speed up network convergence, the batch-normalization (BN) is performed after each convolutional layer in the aforementioned two branches.
And then, due to the relatively small dimensionalities of the two datasets, and to ensure that the same dimension of the input and output of the convolutional layers, the "padding" parameter of the convolutional layer is set to "same". To further reduce the number of neurons, a 2 × 2 max-pooling layer is added before the fully expanded layer, and N sets of matrices with a format of m , n can be obtained. And the "Flat" function is used to fully expand and concatenate them into a one-dimensional array of N × m × n .
Finally, after the feature extraction of the two types of data using their respective networks, the two sets of data are concatenated and fused by using the "concatenate" function. Due to the large number of inner elements which may cause overfitting, "Dropout" is added to randomly drop some neurons. After adding multiple Dense layers, the number of elements in the array can be significantly reduced.
By setting different output dimensions in the Dense layer, the neural network can automatically adjust the number of elements in hidden layer K. After the full connection layer, the Linear activation function establishes the mapping relationship between the output array and the corresponding position coordinates. By setting the output neuron number of the last Dense layer as 2, wherein the x and y components are output

3.2.2. Network Parameter Setting

The multi-input CNN is composed of several single CNN branches, and different network structures of different network branches can set according to the input data. The single CNN model is generally divided into three parts: the convolutional layer, the pooling layer, and the fully connected layer. To solve different problems, it is usually necessary to construct specific forms of these three layers and modify the corresponding parameters to construct a CNN model that adapts to different applications.
  • Convolutional layer
The main function of the convolutional layer is to extract features from the input data through the convolution kernel. One convolutional kernel is responsible for one channel, extracting features from different channels to improve the forward calculation rate of the network. The input data can be either raw data or the output from the previous layer. The convolution kernel continuously slides on the corresponding input matrix, and after multiplying the convolutional kernel elements with the original elements of the local matrix at the sliding position, the sum is obtained as:
x j n = f ∑ i ∈ M j x i n − 1 ⋅ k i j n + b i n
where, x j n is the n layer of the j feature map, f is the activation function, M is the set of input feature maps; k is the convolution kernel, b is the bias. In the actual first convolution calculation, x i is CSI data H and geomagnetic data N reconstructed into picture format. And at the beginning of the operation, a convolution kernel k will be randomly generated, which will be adjusted according to the calculation deviation during the back propagation.
2.
Activation function
In a neural network, a functional relationship needs to be established between the output of the node of the upper layer and the input of the node of the lower layer, which is called the activation function. The selection of activation function is very important for the network. ReLU function is the most commonly used activation function, which is a piecewise linear function and belongs to unilateral inhibition function. the ReLU function which can speed up the training of the network. In addition, the derivative of the positive part is always equal to 1, which can effectively avoid the problem of gradient disappearance and explosion in the backward propagation of deep networks. Therefore, this paper selects the ReLU function as the activation function for the convolutional layer and fully connected layers shown as:
y = x , x > 0 0 , x ≤ 0
The last layer is the output layer, because it is used for regression prediction, so the activation function of the output layer is set as linear activation function. Specifically, assuming that the data processed by the fully connected layer is X = x 1 , x 2 , ⋯ , x n , and the target value of the data to be predicted is y , then the expression for predicting the value is shown as:
y ^ = ∑ i = 1 n w i x i + b
where, w i is the weight parameter corresponding to the i feature; b is the bias, y ^ is the predicted value used to distinguish the true value y . Mean squared error (MSE) is used during training to fit the training set data by optimizing w i .
3.
Optimizer
To get the best network parameters, we need to set up an optimizer for the network. In this paper, the adaptive moment estimation (Adam) parameter optimization method is utilized, which combines the advantages of the AdaGrade algorithm and the RMSProp optimization algorithm. This optimizer allows the gradient descent to be performed quickly in the backpropagation calculation. It also integrates the first-order moment estimation and second-order moment estimation of the gradient, calculates the update step, preserves the historical gradient information, and avoids falling into the global optimum. The function is shown as:
m t = δ 1 m t − 1 + 1 − δ 1 g t v t = δ 2 v t − 2 + 1 − δ 2 g t 2
where, m t and v t are the estimates of the first and second moments of the gradient, δ 1 and δ 2 are the exponential decay rates of the current estimate, g t is the gradient calculated in this iteration.
Before the iteration, the estimates of the first and second moments can deviate significantly, so a correction is needed. The corrected function is shown as:
m ^ t = m t 1 − δ 1 t v ^ t = v 1 − δ 2 t
where, m ^ t and v ^ t are the revised estimate of the first and second moments, t is the number of current iterations.
After correction, the gradient can be updated to:
w t = w t − 1 − α ⋅ m ^ t v ^ t + ε
where, w is the gradient, α is the learning rate, ε is avoid small constants with a denominator of zero.
4.
Loss function
In order to measure the gap between the output value of the network model and the real value, and to adjust the corresponding parameters according to this gap, a loss function is required. The mean square error (MSE) loss function is the most commonly used loss function in regression calculation. The loss function index is MSE shown as:
M S E = 1 n ∑ i = 1 n L ^ x ^ , y ^ − L x , y 2
where, L ^ and L are the predicted values and true values of the coordinates, respectively.
5.
Batch_size and epoch
Batch_size should be set according to the size of the data volume. If batch_size is too small, network convergence will fail. If batch_size is too large, each iteration takes longer. When a complete data set passes through the neural network once and returned once, this process is called an epoch. If the epoch is too small, the weight update time in the neural network will reduce, and the fitted curve will be underfitted and cannot be used effectively for regression prediction. If the epoch is too large, the weight update time in the neural network will increase and the fitting curve will overfit, resulting in a good fit for the training dataset and a poor fit for the test dataset. Therefore, it is necessary to choose a better batch_size and epoch to minimize the loss function. After multiple trainings, the epoch and batch_size are set to 60 and 6, respectively.

4. Experiment and Discussion

To verify the positioning performance of the proposed method, a better fingerprint data construction method based on 5G sensor is first selected, and then the geomagnetic sensor data is further coupled. Field tests are conducted in indoor scenarios.
The equipment used in the experiment is shown in Table 1. The device used for geomagnetic acquisition is Wit-motion, and the sampling frequency is set to 100 Hz and the magnetic field accuracy is 1mg, 5G The sampling frequency and accuracy of existing geomagnetic collection apps based on smartphones can achieve the accuracy of this device, such as Physics Tools
To verify the feasibility of the proposed method, we chose to conduct the relevant experiment in a typical meeting room scenario, the conference room is 12 m long and 9 m wide. The experimental scene is shown in Figure 5, in which Figure 5a is the simplified diagram and Figure 5b is the actual diagram.

4.1. Determination of Data Sampling Time and Positioning Time Using 5G Base Station

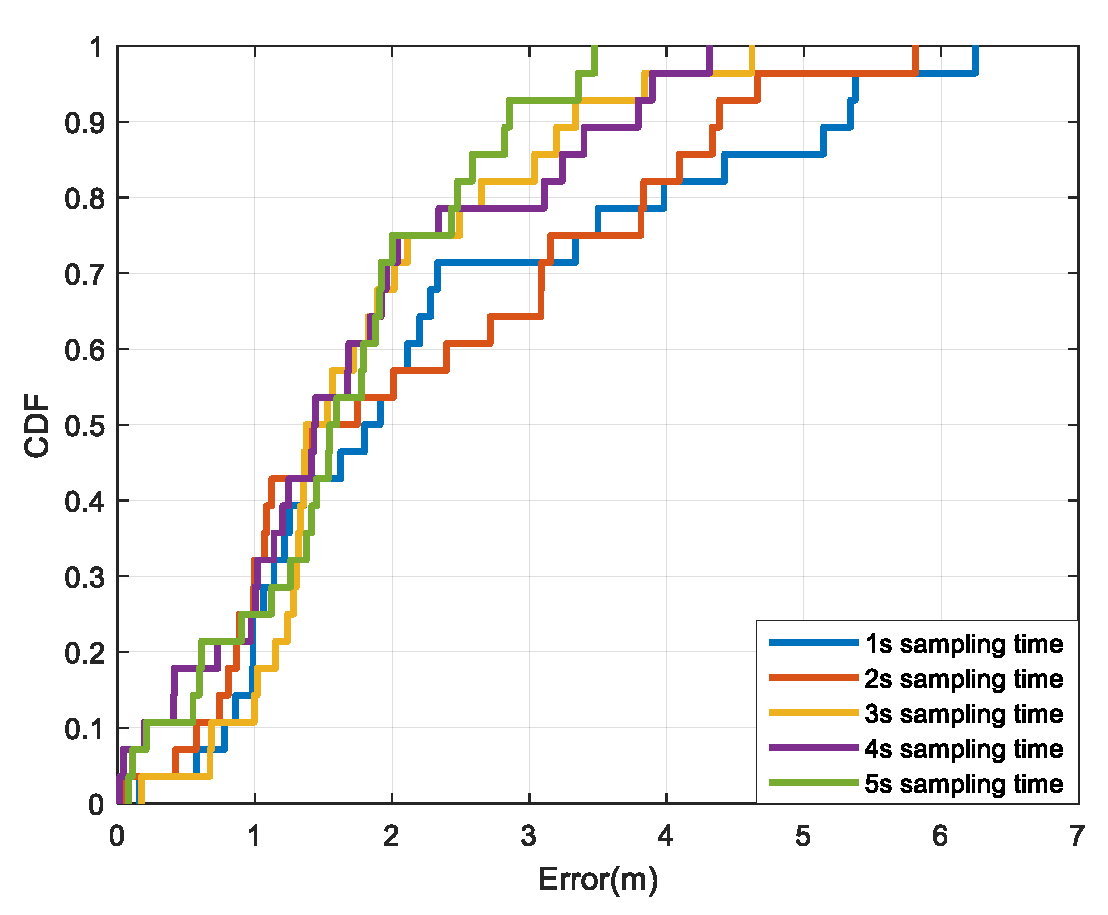
The uniqueness of location fingerprint and the effectiveness of real-time positioning are the important indicators for evaluating the fingerprint positioning algorithms. To obtain abundant and unique location fingerprint information, more signal features are usually measured by spending observation time. However, it is often difficult to observe continuously for a long time in the actual practice. Therefore, how to effectively balance positioning accuracy and timeliness is of critically importance. To provide a reliable way to construct fingerprint data, this study designed a data collection frequency experiment. Firstly, fingerprint data collection points are evenly set in the meeting room. Five groups of data are collected at each point, and the collection time is 1s, 2s, 3s, 4s, and 5s, respectively. Then, test points are set outside the fingerprint collection points, and the test points are evenly distributed in the meeting room. Considering that pedestrians pass a certain point in a short time during dynamic positioning, the positioning time is set to 0.2 s, and there are a total of 5 positioning schemes when combined.
Figure 6 shows the cumulative distribution function (CDF) of the positioning errors using different approaches. It can be seen that as the sampling time of fingerprint data increases, the overall positioning accuracy gradually improves. With the sampling time as 3 s or longer, the percentage of positioning error within 2 m increases, and the maximum error decreases, hence the positioning result is more stable. On the condition of 5 s sampling time, the maximum positioning error is the smallest, and the average positioning error is the best. Since the positioning time is 0.2s, the train dataset with longer sampling time can be divided into more training sub datasets, and hence the model with stronger robustness and fitting ability can be obtained.
Table 2 further lists the statistical results using the five schemes. When the sampling time is increased from 1s to 3 s, the probability of error distribution within 2 m increases from 0.53 to 0.714, and the average positioning error decreases from 2.31 m to 1.83 m, with an improvement of approximately 20.7%. When the sampling time increases from 3 s to 5 s, the probability of error distribution within 2 m increases from 0.714 to 0.75, and the average positioning error decreases from 1.83 meters to 1.63 m. Although the positioning results have been improved by 10.9%, the time of fingerprint sampling is nearly doubled, which greatly improves the workload when updating the fingerprint database in the later stage, and increases the subsequent maintenance cost of fingerprint database.
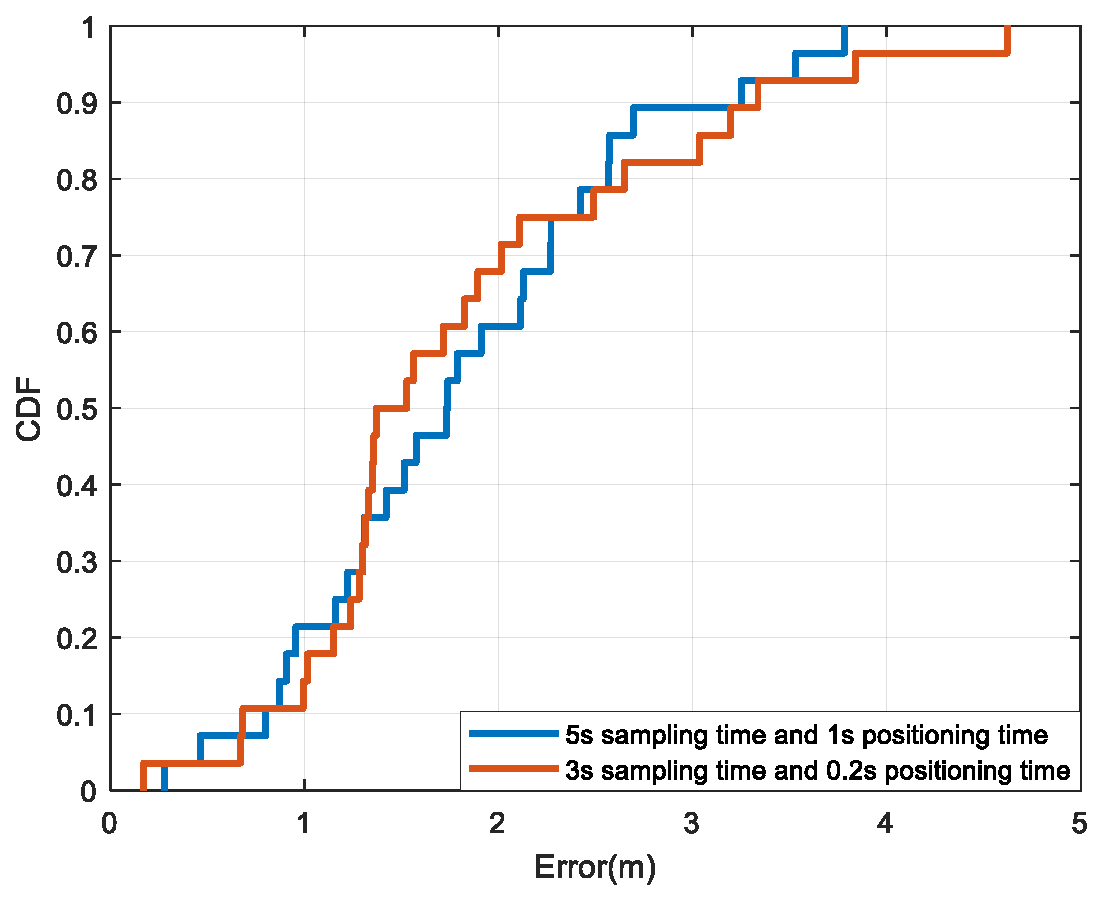
Additionally, the experiment with 5s sampling time and 1s positioning time was further carried. Figure 7 shows the CDFs of the experiment with 5s sampling time and 1s positioning time and the experiment with 3s sampling time and 0.2s positioning time. It can be seen that the positioning results of the two schemes are very close. The maximum positioning error caused by misalignment with 5s sampling time and 1s positioning time is slightly larger, and the possible reason is that the 0.2 s positioning time contains fewer feature values, and the similarity between some points is relatively higher, making it difficult to effectively distinguish and match. However, the probability of error distribution within 2 m is higher than that of using 5s sampling time and 1s positioning time.
Table 3 further shows the average, maximum, and minimum positioning errors under different conditions. It can be concluded that the positioning performance of the two scheme is basically the same. Therefore, taking the positioning accuracy and time consumption into consideration, a sampling time of 3 s and a positioning time of 0.2s are utilized to construct fingerprint data.

4.2. Evaluation of Positioning Performance Using 5G, Magnetometer, and Tightly Coupled Method

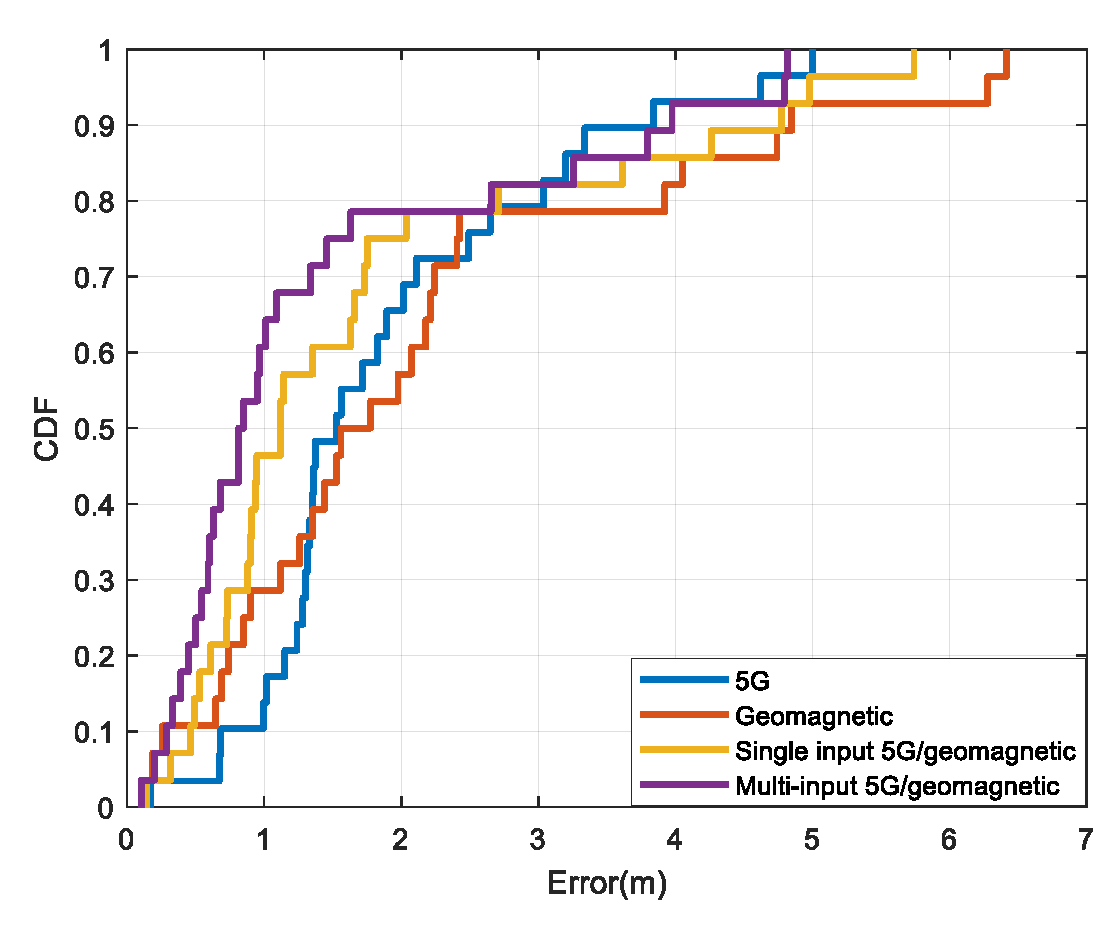
Using the determined data sampling time and positioning time, the positioning performances of 5G positioning, geomagnetic positioning, and tightly coupled positioning of 5G and geomagnetic were evaluated. Additionally, the multi-input CNN algorithm and the single-input CNN algorithm were also compared. Figure 8 shows the CDFs using different mode. It can be seen that
(1) Using the 5G positioning mode, the positioning errors are mostly within 3 m, but there are individual points with larger errors. The possible reasons can be attributed to the long distance from the receiving end to the transmitting end, since the surrounding environment is relatively complex, the signal propagation is affected.
(2) Using the geomagnetic positioning mode, the positioning errors are distributed within 3m, and the maximum positioning error exceeds 6m, which has a great impact on the overall positioning result. This is because the spatial resolution of the geomagnetic field is not high. When the positioning area becomes larger, the geomagnetic data of some points are very similar, which cannot effectively distinguish the mismatching situation.
(3) For the 5G fusion geomagnetic positioning mode, the overall error is reduced compared to 5G single base station, and the positioning errors are mostly within 2 m, which is about 6% higher than the precision of 5G single base station positioning and has been improved to some extent, the maximum positioning error is also optimized due to the influence of geomagnetic data. In the fusion of 5G and geomagnetic data, if a traditional single-input CNN algorithm is used, the maximum positioning error is slightly reduced, but the overall improvement is not significant. This is because after combining the two types of data and then using the same convolutional network to extract data features, it is impossible to extract the features of these two data with different dimensions and different nature. However, the multi-input CNN algorithm performs is a fusion at the final positioning level, and the characteristics of the data itself have been fully considered in the pre-convolutional operation, the overall positioning error of multi-input CNN is 1.41 m, and the overall positioning accuracy has been improved by about 22.9%. In addition, by adding geomagnetic data, it has a certain correcting effect on the positioning results, which can make up for the shortcomings of a single sensor. This is because the geomagnetic data is not affected by the propagation path and can still give a stable position output even in complex environments, but the overall positioning accuracy is not high due to the magnitude of geomagnetic changes and the accuracy of sensor measurements.
Table 4 further shows the statistical results of different positioning modes. The average positioning errors of 5G positioning, geomagnetic positioning, multi-input 5G and geomagnetic positioning, single-input 5G and geomagnetic positioning are 1.83 m, 2.15 m, 1.72 m and 1.41m, respectively. Among which, the multi-input 5G and geomagnetic positioning shows the best performance.

5. Conclusions

We propose a multi-sensor data fusion positioning method based on multi-input CNN model by utilizing the respective benefits of 5G CSI and geomagnetic strength localization methods in response to the issue that traditional location fingerprint algorithms cannot effectively solve the problem of data fusion failure due to inconsistent data formats of different sensors and the large positioning errors of a single sensor. The experimental findings demonstrate that the multi-input CNN algorithm performs better than the single-input CNN strategy. The fused method's total location accuracy in indoor conference rooms has increased by roughly 22.9% when compared to a 5G single base station. The approach we used can increase indoor localization accuracy.
Therefore, the conclusions of this article are as follows:
1. The balance experiment of positioning accuracy and positioning timeliness shows that the sampling time of offline fingerprint data can be appropriately extended to improve positioning accuracy when indoor positioning is performed.
2. Increasing sensors can improve the richness of fingerprint data and thus improve positioning accuracy in indoor positioning.
3. For multi-sensor fusion positioning, different networks can be set according to different data types using multi-input CNN to improve the model's feature extraction capabilities.
4. In the application process, low-cost geomagnetic sensors are fused with 5G for indoor positioning and the positioning accuracy can meet the needs of most indoor scenarios without increasing the positioning cost.
The localization strategy based on the fusion of 5G CSI and geomagnetic field intensity described in this article enhances the localization results to a certain extent, and the cost of the used geomagnetic sensor is low, which has good promotion ability for indoor localization. However, there are still deficiencies when choosing parameters for the network training process, such as training batches, etc. To speed up the parameter selection process, optimization functions will be added to the network as a whole in next work. Additionally, the localization method used in this article makes single-point capture more labor-intensive. As a result, continuous sampling will be taken into consideration in the future, and the raw data generated from continuous observation will be processed for noise reduction. Unmanned vehicles will thus be employed in future work as platforms to accomplish continual positioning.

Author Contributions

Conceptualization, Zhenhao Cheng and Dongqing Zhao; methodology, Zhenhao Cheng and Dongqing Zhao; data, Wenzhuo Guo and Luguang Lai; writing-original draft preparation, Zhenhao Cheng; writing-review, Dongqing Zhao and Linyang Li. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Nature Science Foundation of China (Grant No. 42104033, 41774037), Postdoctoral Science Foundation of China (Grant Nos. 2022M712442).

Data Availability Statement

If necessary, please direct further enquiries to the corresponding author.

Acknowledgments

We would like to thank the editors and the anonymous reviewers for their constructive suggestions and comments, which helped to improve this paper's quality.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kim, S.; Ha, S.; Saad, A.; Kim, J. Indoor positioning system techniques and security, 2015 Forth International Conference one Technologies and Networks for Development (ICeND), Lodz, Poland, 2015; pp. 1-4. [CrossRef]
  2. Yuan, J.; He, Y.; Research on intelligent indoor location method based on Wi-Fi fingerprint. International Journal of Communication Networks and Distributed Systems. 2021, 26, 319–333. [CrossRef]
  3. Wang, H. Q.; Gao, K. X.; Lv, H. W. Survey of high-precision localization and the prospect of future evolution. Journal on Communications. 2021, 42, 198-21. [CrossRef]
  4. Wan, X. Y.; Sun Y H; Wang Z Y. Principle and future trends of indoor positioning in 6G. Telecommunications Science, 2021, 37, 91-104.
  5. Xu, Y.; Jiang, W.; Sha, X. TOA estimate algorithm based UWB location. 2009 International Forum on Information Technology and Applications, Chengdu, China, 2009, pp. 249-252. [CrossRef]
  6. Zhu, X.; Zhu, W.; Chen, Z. Direct localization based on motion analysis of single station using TOA. 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi'an, China, 2018, pp. 1823-1827.
  7. Namdar, M.; Basgumus, A.; Guney, A. Performance analysis of the TOA cooperative localization estimation algorithm for 5G cellular networks[C], 2018 26th Signal Processing and Communications Applications Conference (SIU), Izmir, Turkey, 2018, pp. 1-4. [CrossRef]
  8. Mo, Y.; Cai, Y.; Bang, W. A novel indoor localization method based on virtual AP estimation. 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 2012, pp. 5508-5512. [CrossRef]
  9. Zang, L.; Shen, C.; Zhang, K.; Xu, L.; Chen, Y. Research on hybrid algorithm based on TDOA, 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 2020, 539-542. [CrossRef]
  10. Song, W. W.; Lin, W.; Lou, Y. D. Research on TDOA positioning with BDS+5G space time datum. Geomatics and Information Science of Wuhan University, 2023, 1-10.
  11. Tao, C.; Zhou, B. Indoor localization with smart antenna system: multipath mitigation with MIMO beamforming scheme. 2017 IEEE 14th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Orlando, FL, USA, 2017, pp 303-307. [CrossRef]
  12. Subramanian, A. P.; Deshpande, P.; Jie, G. Drive-By Localization of Roadside Wi-Fi Networks, IEEE INFOCOM 2008 The 27th Conference on Computer Communications, Phoenix, AZ, USA, 2008, pp. 718-725. [CrossRef]
  13. Kim, S.; Park, S.; Ji, H.; Shim, B. AOA-TOA based localization for 5G cell-less communications, 2017 23rd Asia-Pacific Conference on Communications (APCC), Perth, WA, Australia, 2017, pp. 1-6. [CrossRef]
  14. Zhang, L.; Wu, L.; Zhang, Z.; Dang, J.; Zhu, B.; Wang, L. AoA and amplitude fingerprint based indoor intelligent localization scheme for 5G wireless communications. 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 2021, pp. 1-5. [CrossRef]
  15. Khalajmehrabadi, A.; Gatsis, N.; Akopian, D. Modern WLAN fingerprinting indoor positioning methods and deployment challenges, in IEEE Communications Surveys & Tutorials, 2017, 19, 1974-2002. [CrossRef]
  16. Li, R. F. Research on Wi-Fi location fingerprint indoor localization algorithm based on neural network. Industrial Instrumentation & Automation, 2022, 285, 109-113.
  17. Liu, S. H.; Wang, X. D.; Wu, N. A CNN-based CSI fingerprint indoor localization method. Chinese Journal of Engineering, 2021, 43, 1512-1521.
  18. Ding, R.; Sun, Y. C.; Sun, P.; Li, Y. Geomagnetic indoor localization based on convolutional neural network. Practical Electronics,2020, 36-37+30.
  19. Wang, L.; Luo, H.; Wang, Q.; Shao, W.; Zhao F.A hierarchical LSTM-based indoor geomagnetic localization algorithm, in IEEE Sensors Journal, 2022, 22, 1227-1237. [CrossRef]
  20. Zhang, C.; Qin, N.; Xue, Y.; Yang, L. Received signal strength-based indoor localization using hierarchical classification, Sensors, 2020, 20, 1067. [CrossRef]
  21. Ma, X. Y.; Zhang, J. S.; Li, T. A geomagnetic reference map construction method based on convolutional neural network. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47, 1918-1926. [CrossRef]
  22. Pan, H.; Xiang, Y.; Xiong, J.; Zhao, Y. F.; Huang, Z. W.; Xiao, X. H. Application of a wi-fi/geomagnetic combined positioning method in a single access point environment. Wireless Communications and Mobile Computing, 2021; Volume 8. [CrossRef]
  23. Ruan, K.; Wang, M.; Luo, L.; Xiong, L. Q.; Song, X. Y. Indoor localization algorithm based on geomagnetic field /Wi-Fi /PDR of smartphone. Journal of Computer Applications, 2018, 38, 2598-2602.
  24. Han, S.; Li, Y.; Meng, W. X.; Li, C.; Liu, T. Q.; Zhang, Y. B. Indoor localization with a single wi-fi access point based on OFDM-MIMO. IEEE Systems Journal, 2019, 13, 964-972. [CrossRef]
  25. Zimaglia, E.; Riviello, D. G.; Garello, R. A novel deep learning approach to CSI feedback reporting for NR 5G cellular systems," 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 2020, pp. 47-52. [CrossRef]
  26. Barneto, C. B.; Riihonen, T.; Turunen, M.; Koivisto, M.; Talvitie, T.; Valkama, M. Radio-based Sensing and Indoor Mapping with Millimeter-Wave 5G NR Signals, 2020 International Conference on Localization and GNSS (ICL-GNSS), Tampere, Finland, 2020, pp. 1-5.
  27. Ruan, Y.; Chen, L.; Zhou, X.; Guo, G.; Chen, R. Hi-Loc: hybrid indoor localization via enhanced 5G NR CSI. In IEEE Transactions on Instrumentation and Measurement, 2022, 71, 1-15. [CrossRef]
  28. Gao, K.; Wang, H.; Lv, H.; Liu, W. Towards 5G NR high-precision indoor positioning via channel frequency response: A new paradigm and dataset generation method, IEEE J. Sel. Areas Communication, 2022, 40, 2233-2247. [CrossRef]
  29. Ruan, Y.; Chen, L.; Zhou, X.; Guo, G.; Chen, R. iPos-5G: Indoor positioning via commercial 5G NR CSI, in IEEE Internet of Things Journal, 2023, 10, 8718-8733. [CrossRef]
  30. Yang, C.; Cheng, Z.; Jia, X; Zhang, L; Li, L; Zhao, D. A novel deep learning approach to 5G CSI/Geomagnetism/VIO Fused Indoor Localization. Sensors, 2023, 23, 1311. [CrossRef]
  31. Li, Q.; Liao, X. W.; Liu, M. M. Indoor localization based on CSI fingerprint by siamese convolution neural network. IEEE Transactions on Vehicular Technology, 2021, 70, 12168-12173. [CrossRef]
  32. Chen, J.; Shan, Z.; Deng, J. H.; Zeng, Y. Multi-source fusion indoor positioning algorithm based on neural network. Computer Systems & Applications, 2022, 31. 224-230.
Preprints 76463 g001
Figure 1. Flowchart of a tightly coupled indoor positioning method using widespread 5G and low-cost magnetometer based on multi-input CNN.
Figure 1. Flowchart of a tightly coupled indoor positioning method using widespread 5G and low-cost magnetometer based on multi-input CNN.
Preprints 76463 g001
Preprints 76463 g002
Figure 2. 3-D images of CSI data collected at different locations. The left and right panels represent two different locations, respectively.
Figure 2. 3-D images of CSI data collected at different locations. The left and right panels represent two different locations, respectively.
Preprints 76463 g002
Preprints 76463 g003
Figure 3. The reconstruction of data structure using the "reshape" function (a), (b) and (c) are the gray image of geomagnetic triaxial data, respectively, and (d) is color image after superposition.
Figure 3. The reconstruction of data structure using the "reshape" function (a), (b) and (c) are the gray image of geomagnetic triaxial data, respectively, and (d) is color image after superposition.
Preprints 76463 g003
Preprints 76463 g004
Figure 4. Schematic diagram of multi-input convolutional neural network framework (blue is 5G fingerprint feature input network; gray is geomagnetic fingerprint feature input network; black is fused data after concatenation; Conv-2D indicates that the convolution type adopted is 2-dimensional convolution).
Figure 4. Schematic diagram of multi-input convolutional neural network framework (blue is 5G fingerprint feature input network; gray is geomagnetic fingerprint feature input network; black is fused data after concatenation; Conv-2D indicates that the convolution type adopted is 2-dimensional convolution).
Preprints 76463 g004
Preprints 76463 g005
Figure 5. Conference room. (a) Experimental approaches. (b) Scenario photograph. The circular points are the sampling points, the triangular points are the points to be located, and a total of 56 training points and 28 test points are selected. The middle is the AP at the transmitter end. A conference table is placed in the center of the room, and tables and chairs are placed around the room (grey shaded parts).
Figure 5. Conference room. (a) Experimental approaches. (b) Scenario photograph. The circular points are the sampling points, the triangular points are the points to be located, and a total of 56 training points and 28 test points are selected. The middle is the AP at the transmitter end. A conference table is placed in the center of the room, and tables and chairs are placed around the room (grey shaded parts).
Preprints 76463 g005
Preprints 76463 g006
Figure 6. The CDFs of the cumulative distribution of errors in indoor offices (The vertical is the cumulative distribution of errors, and the horizontal is the error).
Figure 6. The CDFs of the cumulative distribution of errors in indoor offices (The vertical is the cumulative distribution of errors, and the horizontal is the error).
Preprints 76463 g006
Preprints 76463 g007
Figure 7. The CDFs of the experiment with 5s sampling time and 1s positioning time and the experiment with 3s sampling time and 0.2s positioning time.
Figure 7. The CDFs of the experiment with 5s sampling time and 1s positioning time and the experiment with 3s sampling time and 0.2s positioning time.
Preprints 76463 g007
Preprints 76463 g008
Figure 8. The CDFs of the 5G positioning, geomagnetic positioning, multi-input 5G and geomagnetic positioning, single-input 5G and geomagnetic positioning.
Figure 8. The CDFs of the 5G positioning, geomagnetic positioning, multi-input 5G and geomagnetic positioning, single-input 5G and geomagnetic positioning.
Preprints 76463 g008
Table 1. The experimental equipment used in the experiment.
Table 1. The experimental equipment used in the experiment.
Name Type Parameter
Magnetometer Wit-motion HWT901B-232 Output frequency: 100 Hz
Accuracy: 1 mg
5G Receiver LWB210XT Output frequency: 50 Hz
Sub-carriers: 60
Antenna number: 1
Table 2. Statistical errors of different combinations.
Table 2. Statistical errors of different combinations.
Sampling time
(s)		 Positioning time
(s)		 Mean error
(m)		 Maximum error
(m)		 Minimum error
(m)		 Error <2m
(%)
1 0.2 2.31 6.25 0.16 53.6
2 0.2 2.20 5.81 0.04 57.1
3 0.2 1.83 4.62 0.17 71.4
4 0.2 1.71 4.31 0.02 71.4
5 0.2 1.63 3.48 0.08 75.0
Table 3. Positioning errors of the experiment with 5s sampling time and 1s positioning time and the experiment with 3s sampling time and 0.2s positioning time.
Table 3. Positioning errors of the experiment with 5s sampling time and 1s positioning time and the experiment with 3s sampling time and 0.2s positioning time.
Sampling time
(s)		 Positioning time
(s)		 Mean error
(m)		 Maximum error
(m)		 Minimum error
(m)		 Error <2m
(%)
3 0.2 1.83 4.62 0.17 71.4
5 1 1.80 3.78 0.28 60.7
Table 4. Positioning errors of different positioning methods.
Table 4. Positioning errors of different positioning methods.
Positioning Mode Mean error
(m)		 Maximum error
(m)		 Minimum error
(m)		 Error <2m
(%)
5G positioning 1.83 4.62 0.17 71.4
Geomagnetic positioning 2.15 6.41 0.13 57.1
Single input 5G and geomagnetic positioning 1.72 5.74 0.14 75.0
Multi-input 5G and geomagnetic positioning 1.41 4.81 0.19 78.6
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated