One New Property of a Class of Linear Time-Optimal Control Problems

Preprint

Article

One New Property of a Class of Linear Time-Optimal Control Problems

Altmetrics

Downloads

Views

235

Comments

A peer-reviewed article of this preprint also exists.

Borislav Penev^*

This version is not peer-reviewed

Submitted:

12 June 2023

Posted:

12 June 2023

You are already at the latest version

Alerts

Abstract

The paper deals with one new property of the linear time-optimal control problems with real eigenvalues of the system, no matter of the number of eigenvalue multiplicity. This property unveils a prospective of synthesizing the time-optimal control without the need of describing the switching hyper-surfaces. The already chrestomathy example of the time-optimal control of a double integrator is resolved by the new technique and compared with the classical synthesis.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Since the first studies of Feldbaum [1,2], the Pontryagin’s Principle of Maximum [3], etc. [4,5,6,7,8,9] the theory of the linear time-optimal control problem has been achieved maturity – the main theoretical issues have been thoroughly studied and answered. This historical evolution and facts are a solid foundation for the progress in this field [10,11,12]. At the same time the applied aspects of this problem are always very interesting and attractive due to the fact it is great in many cases to achieve a transition from one to another system state in minimum time within the maximum utilization of the available system resources – control input's constraints as well as constraints on some state space variables, and all this being organized in a form of synthesis. As it is mentioned even in recent papers on the topic [12] “there are plenty of researches trying to solve the problem analytically, while there is still no complete time optimal analytical solution for systems higher than second order.” The authors say also in [12] „this paper has proposed a global time optimal control law for triple integrator with input saturation and full state constraints" while with regard to the obtained result it is said that “An analytical state feedback form control law has been synthesized based on the switching surfaces and curves”. In [13], the dissertation [14], as well as in next papers [15,16,17,18], some new properties of a class of linear time-optimal control problems are presented which are the basis of the author’s method for synthesis of the time-optimal control for a class of problems of any order without the need of describing the switching hyper-surfaces. The study [19] shows the possibility for a practical application of the method. The so developed method covers a class of linear systems with real non-positive simple eigenvalues. One new property of the linear time-optimal control problem is discovered and proven here, which reveals the possibility for an expansion of the author’s method to the general case of real non-positive eigenvalues of the systems with no limitations with regard to the number of their eigenvalue multiplicity.

The paper is organized in the following way. In Section 2 the new property of the linear time-optimal control problem is theoretically represented. In Section 3 the solution of the chrestomathy example of the time-optimal control problem of a double integrator is obtained, first – in the classical way, and next – by application of the new property of the class of problems and the method [14]. The conclusions are provided in Section 3.

2. Formulation of the Problem and Solution

Let us consider the following linear time-optimal control problem of order

n

n \geq 2

. The system is described by the equations (1) and let us suppose it is normal and with real non-positive eigenvalues. It should be mentioned that every one normal system with real eigenvalues could be transformed to such type of representation. The initial state at the moment

t_{0} = 0

of the system (1) is (2) and the target state at the moment

t_{f}

represents the origin (5) of the system’s state space where

t_{f}

is unspecified. The admissible control

u (t)

is a piecewise continuous function that takes its values from the range (3), which is continuous on the boundaries of the set of allowed values (3) and in the points of discontinuity

τ

we have (4).

The problem is to find an admissible control

u (x)

which transfers the system (1) from its initial state (2) to the final state (5) in minimum time, i.e. minimizing the performance index (6). Let us refer to this problem as “Problem P(n)”.

\begin{array}{l} \begin{matrix} {\dot{x}}_{i} = \sum_{j = 1}^{n - 1} a_{i j} x_{j} + b_{i} u, & i = 1,2, \dots, n - 1, \end{matrix} \\ {\dot{x}}_{n} = \sum_{j = 1}^{n - 1} a_{n j} x_{j} + λ_{n} x_{n} + b_{n} u . \end{array}

(1)

x_{0} = {(\begin{matrix} x_{10} \dots & x_{(n - 1) 0} & x_{n 0} \end{matrix})}^{T}

(2)

{- u}_{0} \leq u (t) \leq u_{0}, u_{0} = c o n s t > 0

(3)

u (τ) = u (τ + 0) .

(4)

{x (t_{f}) = x}_{f} = {(\underset{n}{\underset{⏟}{\begin{matrix} 0 \dots & 0 & 0 \end{matrix}}})}^{T}

(5)

J = t_{f} \to m i n .

(6)

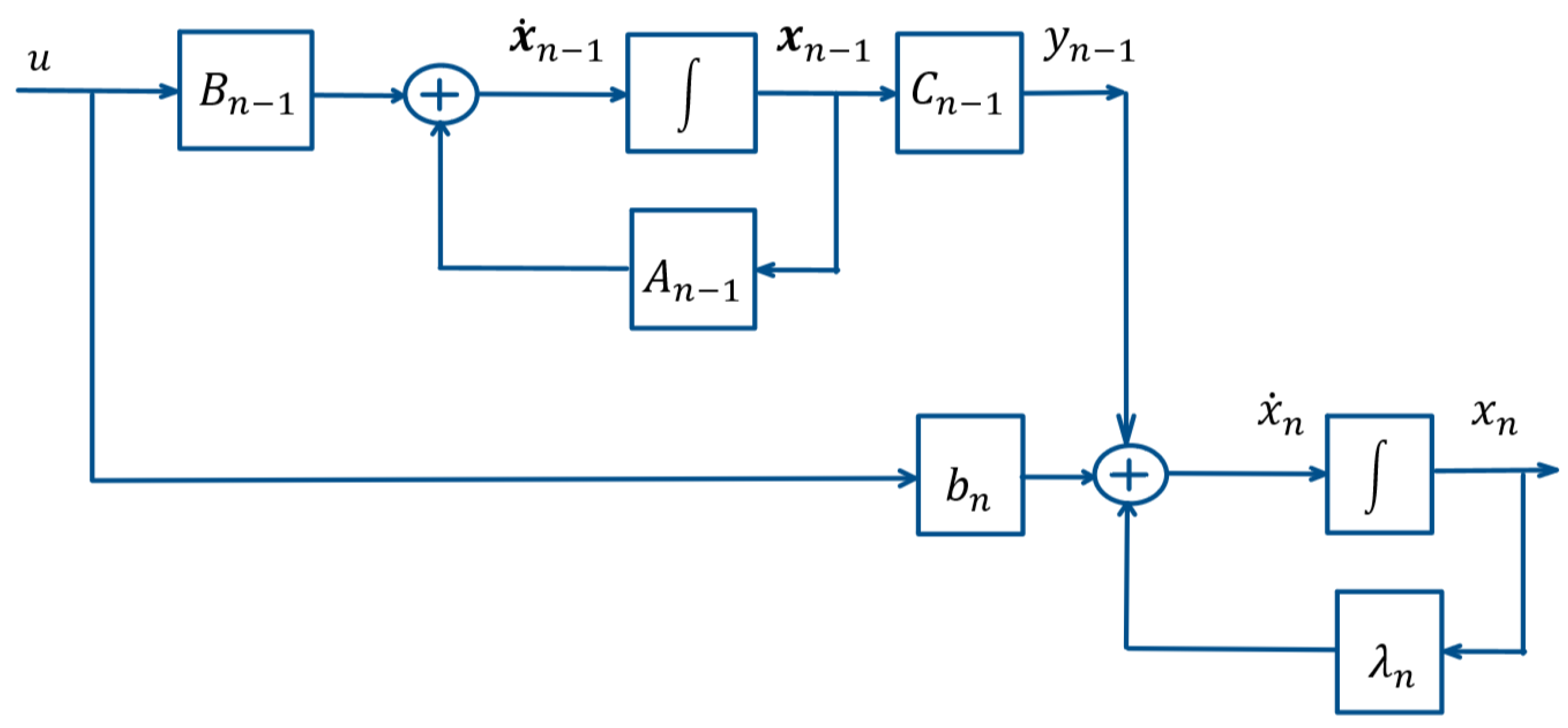
The form of the equations of the system (1) allows introducing the linear sub-system (9) of order

(n - 1)

with the state-space vector

x_{n - 1}

(8) and scalar output

y_{n - 1}

by the matrixes

A_{n - 1}, B_{n - 1}, C_{n - 1}

in the way (7). Thus the system (1) could be represented by (9) in the form (10) which is depicted also in Figure 1. With regard to the sub-system (9) its initial state represents

x_{(n - 1) 0}

(11) and the relation between the initial state (2) of the system (1) and the initial state (11) of the sub-system (9) represents (12).

\begin{array}{l} A_{n - 1} = (\begin{matrix} \begin{array}{l} \begin{matrix} a_{11} \\ \begin{matrix} a_{21} \\ ⋮ \\ a_{n - 1,1} \end{matrix} \end{matrix} & \begin{matrix} a_{12} \\ \begin{matrix} a_{22} \\ ⋮ \\ a_{n - 1,2} \end{matrix} \end{matrix} \end{array} & \begin{matrix} \begin{matrix} \dots \\ \dots \end{matrix} \\ \begin{matrix} \dots \end{matrix} \end{matrix} & \begin{matrix} a_{1, n - 1} \\ \begin{matrix} a_{2, n - 1} \\ ⋮ \\ a_{n - 1, n - 1} \end{matrix} \end{matrix} \end{matrix}), \\ \begin{matrix} B_{n - 1} = (\begin{matrix} b_{1} \\ \begin{matrix} b_{2} \\ ⋮ \\ b_{n - 1} \end{matrix} \end{matrix}), & C_{n - 1} = (\begin{matrix} \begin{matrix} a_{n 1} & a_{n 2} \end{matrix} & \begin{matrix} \dots & a_{n, n - 1} \end{matrix} \end{matrix}) . \end{matrix} \end{array}

(7)

x_{n - 1} = {(\begin{matrix} x_{1} & \dots & x_{n - 1} \end{matrix})}^{T} .

(8)

\begin{array}{l} {\dot{x}}_{n - 1} = A_{n - 1} x_{n - 1} + B_{n - 1} u, \\ y_{n - 1} = C_{n - 1} x_{n - 1} . \end{array}

(9)

\begin{array}{l} {\dot{x}}_{n - 1} = A_{n - 1} x_{n - 1} + B_{n - 1} u, \\ \begin{matrix} y_{n - 1} = C_{n - 1} x_{n - 1} \end{matrix}, \\ {\dot{x}}_{n} = λ_{n} x_{n} + y_{n - 1} + b_{n} u . \end{array}

(10)

x_{(n - 1) 0} = {(\underset{n - 1}{\underset{⏟}{\begin{matrix} x_{10} & \dots & x_{(n - 1) 0} \end{matrix}}})}^{T} .

(11)

x_{0} = (\begin{matrix} x_{(n - 1) 0} \\ x_{n 0} \end{matrix}) .

(12)

Let as formulate now the following linear time-optimal control problem of order

(n - 1)

which we shall call “Problem P(n-1)”. The system represents the equations (9).The initial state of the system (9) at the moment

t_{0} = 0

is (11) and the target state at the moment

t_{(n - 1) f}

which is preliminary unspecified is the origin (13) of the (n-1)-dimensional state-space of the system (9). The admissible control

u (t)

represents a piecewise continuous function that takes its values from the range (3), which is continuous on the boundaries of the set of allowed values (3) and in the points of discontinuity

τ

we have (4). The Problem P(n-1) consists of synthesizing an admissible control

u (x_{n - 1})

which transfers the system (9) from its initial state (11) to the final state (13) and minimizes the performance index (14).

{x_{n - 1} (t_{(n - 1) f}) = x}_{(n - 1) f} = {(\underset{n - 1}{\underset{⏟}{\begin{matrix} 0 & \dots & 0 \end{matrix}}})}^{T} .

(13)

J_{n - 1} = t_{(n - 1) f} \to m i n .

(14)

Let us assume we have found the solution of Problem P(n-1) and denote by

t_{(n - 1) f}^{o}

the optimal time – the minimum time (15) of (14), by

u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

the optimal control, and by

x_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

the optimal trajectory in the (n-1)-dimensional state-space of the system (9), which is described by (16) and (17).

{m i n (J}_{n - 1}) = t_{(n - 1) f}^{o} .

(15)

x_{n - 1}^{o} (t) = e^{A_{n - 1} t} x_{(n - 1) 0} + \int_{0}^{t} e^{A_{n - 1} τ} B_{n - 1} u_{n - 1}^{o} (t - τ) d τ for t \in [0, t_{(n - 1) f}^{o}] .

(16)

x_{n - 1}^{o} (t_{(n - 1) f}^{o}) = {(\underset{n - 1}{\underset{⏟}{\begin{matrix} 0 & \dots & 0 \end{matrix}}})}^{T} .

(17)

Let us denote the scalar output of the system (9) in case it is the result of the optimal vector-function

x_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

y_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}]

. In that case

y_{n - 1}^{o} (t)

represents (18) and (19).

y_{n - 1}^{o} (t) = C_{n - 1} x_{n - 1}^{o} (t) for t \in [0, t_{(n - 1) f}^{o}] .

(18)

y_{n - 1}^{o} (t_{(n - 1) f}^{o}) = C_{n - 1} x_{n - 1}^{o} (t_{(n - 1) f}^{o}) = 0 .

(19)

Let us define

x_{n 0}^{1}

(21) as an initial state of the n-th coordinate of the state-space vector

x

of the system (1) or (10) and consider the trajectory

x^{1} (t)

in the n-dimensional state-space of Problem P(n) with initial state in the point

x_{0}^{1}

with coordinates (20) – (21)under the optimal control

u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

of Problem P(n-1).

x_{0}^{1} = (\begin{matrix} x_{(n - 1) 0} \\ x_{n 0}^{1} \end{matrix}) .

(20)

x_{n 0}^{1} = - \frac{\int_{0}^{t_{(n - 1) f}^{o}} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ}{e^{λ_{n} t_{(n - 1) f}^{o}}} .

(21)

The vector-function

x^{1} (t)

based on the representation of the system (1) in form (10) represents (22). The first (n-1) variables of the vector-function in (22) represent according to (16) the optimal vector-function

x_{n - 1}^{o} (t)

of Problem P(n-1), while in (22) with regard to the last n-th variable of

x^{1} (t)

the function

y_{n - 1} (τ)

represents the scalar output of the system (9) which is the result in this case of the optimal vector-function

x_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}]

. According to (18)

y_{n - 1} (τ)

y_{n - 1}^{o} (τ)

in this case. Thus we obtain (23) for

x^{1} (t)

(22).

x^{1} (t) = (\begin{matrix} e^{A_{n - 1} t} x_{(n - 1) 0} + \int_{0}^{t} e^{A_{n - 1} τ} B_{n - 1} u_{n - 1}^{o} (t - τ) d τ \\ e^{λ_{n} t} x_{n 0}^{1} + \int_{0}^{t} e^{λ_{n} (t - τ)} (y_{n - 1} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) for t \in [0, t_{(n - 1) f}^{o}] .

(22)

x^{1} (t) = (\begin{matrix} x_{n - 1}^{o} (t) \\ e^{λ_{n} t} x_{n 0}^{1} + \int_{0}^{t} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) for t \in [0, t_{(n - 1) f}^{o}] .

(23)

With regard to

x^{1} (t)

(23) at the moment

t = t_{(n - 1) f}^{o}

we obtain (24). Then by substitution of

x_{n - 1}^{o} (t_{(n - 1) f}^{o})

by (17) and

x_{n 0}^{1}

by (21) we obtain successively (25), (26), and (27).

x^{1} (t_{(n - 1) f}^{o}) = (\begin{matrix} x_{n - 1}^{o} (t_{(n - 1) f}^{o}) \\ (\begin{matrix} e^{λ_{n} t_{(n - 1) f}^{o}} x_{n 0}^{1} + \\ + \int_{0}^{t_{(n - 1) f}^{o}} e^{λ_{n} (t - τ)} (y_{n - 1} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) \end{matrix}) .

(24)

\begin{array}{l} x^{1} (t_{(n - 1) f}^{o}) = \\ = (\begin{matrix} {(\underset{n - 1}{\underset{⏟}{\begin{matrix} 0 & \dots & 0 \end{matrix}}})}^{T} \\ (\begin{matrix} e^{λ_{n} t_{(n - 1) f}^{o}} (- \frac{\int_{0}^{t_{(n - 1) f}^{o}} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ}{e^{λ_{n} t_{(n - 1) f}^{o}}}) + \\ + \int_{0}^{t_{(n - 1) f}^{o}} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) \end{matrix}) \end{array} .

(25)

\begin{array}{l} x^{1} (t_{(n - 1) f}^{o}) = \\ = (\begin{matrix} {(\underset{n - 1}{\underset{⏟}{\begin{matrix} 0 & \dots & 0 \end{matrix}}})}^{T} \\ (\begin{matrix} - \int_{0}^{t_{(n - 1) f}^{o}} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \\ + \int_{0}^{t_{(n - 1) f}^{o}} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) \end{matrix}) \end{array} .

(26)

x^{1} (t_{(n - 1) f}^{o}) = (\begin{matrix} {(\underset{n - 1}{\underset{⏟}{\begin{matrix} 0 & \dots & 0 \end{matrix}}})}^{T} \\ 0 \end{matrix}) = {(\underset{n}{\underset{⏟}{\begin{matrix} 0 \dots & 0 & 0 \end{matrix}}})}^{T} .

(27)

Thus we obtain that the trajectory

x^{1} (t)

in the n-dimensional state-space of the system (1) or (10) with initial point

x_{0}^{1}

(20) – (21) under the optimal control

u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

of Problem P(n-1) ends at the moment

t = t_{(n - 1) f}^{o}

in the origin of the n-dimensional state-space of Problem P(n). Taking into account that the function

u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

is the optimal control of Problem P(n-1) and thereby it represents a piecewise constant function with amplitude

u_{0}

and number of switchings maximum (n-2), i.e. with number of intervals of constancy maximum (n-1) [7] (Chapter 2, §6, Theorem 2.11, p. 116), the trajectory

x^{1} (t)

lies wholly on the switching hyper-surface of Problem P(n).

Let us now consider the trajectory

x (t)

(28) in the n-dimensional state-space of Problem P(n) with initial point representing the initial state

x_{0}

(2) or (12) of Problem P(n) under the optimal control

u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

of Problem P(n-1). The first (n-1) variables of the vector-function in (28) represent according to (16) the optimal vector-function

x_{n - 1}^{o} (t)

of Problem P(n-1). With regard to the last variable of

x (t)

in (28) the function

y_{n - 1} (τ)

is the scalar output of the system (9) which is the result of the optimal vector-function

x_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}]

. According to (18) the function

y_{n - 1} (τ)

represents

y_{n - 1}^{o} (τ)

in this case. Thus we obtain (29) for

x (t)

(28).

x (t) = (\begin{matrix} e^{A_{n - 1} t} x_{(n - 1) 0} + \int_{0}^{t} e^{A_{n - 1} τ} B_{n - 1} u_{n - 1}^{o} (t - τ) d τ \\ e^{λ_{n} t} x_{n 0} + \int_{0}^{t} e^{λ_{n} (t - τ)} (y_{n - 1} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) for t \in [0, t_{(n - 1) f}^{o}] .

(28)

x (t) = (\begin{matrix} x_{n - 1}^{o} (t) \\ e^{λ_{n} t} x_{n 0} + \int_{0}^{t} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) for t \in [0, t_{(n - 1) f}^{o}] .

(29)

Let us consider now the difference between the two vector-functions

x (t)

(29) and

x^{1} (t)

(23). We obtain successively (30) and (31).

\begin{array}{l} x (t) - x^{1} (t) = \\ = (\begin{matrix} x_{n - 1}^{o} (t) \\ e^{λ_{n} t} x_{n 0} + \int_{0}^{t} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) - \\ - (\begin{matrix} x_{n - 1}^{o} (t) \\ e^{λ_{n} t} x_{n 0}^{1} + \int_{0}^{t} e^{λ_{n} (t - τ)} (y_{n - 1}^{o} (τ) + b_{n} u_{n - 1}^{o} (τ)) d τ \end{matrix}) \end{array} for t \in [0, t_{(n - 1) f}^{o}] .

(30)

x (t) - x^{1} (t) = (\begin{matrix} {(\underset{n - 1}{\underset{⏟}{\begin{matrix} 0 & \dots & 0 \end{matrix}}})}^{T} \\ e^{λ_{n} t} (x_{n 0} {- x}_{n 0}^{1}) \end{matrix}) for t \in [0, t_{(n - 1) f}^{o}] .

(31)

We could state with regard to the last n-th coordinate of (31)

e^{λ_{n} t} (x_{n 0} {- x}_{n 0}^{1})

for

t \in [0, t_{(n - 1) f}^{o}]

If $x_{n 0} {= x}_{n 0}^{1}$ , then the initial state $x_{0}$ (2) or (12) of Problem P(n) coincides with the point $x_{0}^{1}$ with coordinates (20) – (21). We have already shown that $x_{0}^{1}$ is a point of the switching hyper-surface of Problem P(n) and the trajectory with initial point $x_{0}^{1}$ under the optimal control $u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],$ of Problem P(n-1) lies wholly on the switching hyper-surface of Problem P(n) and ends at the moment $t = t_{(n - 1) f}^{o}$ in the origin of the n-dimensional state-space of the system (1) or (10) of Problem P(n);
If $x_{n 0} {\neq x}_{n 0}^{1}$ , then the initial state $x_{0}$ (2) or (12) of Problem P(n) does not coincide with the point $x_{0}^{1}$ with coordinates (20) – (21). The expression $e^{λ_{n} t} (x_{n 0} {- x}_{n 0}^{1})$ for $t \in [0, t_{(n - 1) f}^{o}]$ does not change it sign and is not equal to zero because of the fact $t_{(n - 1) f}^{o}$ is a finite time. Thus the trajectory with initial state $x_{0}$ (2) or (12) of Problem P(n) under the optimal control $u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],$ of Problem P(n-1) lies entirely above or below the switching hyper-surface of Problem P(n) nowhere intersecting it and ends at the moment $t = t_{(n - 1) f}^{o}$ in a point of the coordinate axis $x_{n}$ different from zero.

Thus, the following theorem has been proven.

Theorem 1.

The trajectory of the system (1) or (10) with initial point in

x_{0}

(2) under the optimal control

u_{n - 1}^{o} (t), t \in [0, t_{(n - 1) f}^{o}],

of Problem P(n-1) lies wholly on the switching hyper-surface of Problem P(n) and ends at the moment

t = t_{(n - 1) f}^{o}

in the origin of the n-dimensional state-space of the system (1) or (10) of Problem P(n) or lies entirely above or below the switching hyper-surface of Problem P(n) nowhere intersecting it and ends at the moment

t = t_{(n - 1) f}^{o}

in a point of the coordinate axis

x_{n}

different from zero.

3. Example

Let us consider the following example of synthesizing the time-optimal control of a double integrator [7] (§ 3. Example. The problem of synthesis, p. 38), [10] (Chapter 7, Problem 7.1, p. 150), [11], which has already become a chrestomathy example and as such even found a place in online optimal control courses on world platforms with video content [20,21,22,23] (it should be noted that these online resources are often volatile and unavailable after some time). First, we will show namely this classical synthesis, and after that – the synthesis based on the expansion of the author’s method [14] by the new property, which allows synthesizing without the need of describing the switching hyper-surfaces and applicable now in case of multiple number of system’s eigenvalues (the example here is with regard to double zero).

The system is described by the variables

y

(position) and

v

(velocity) and represents (32). Let the constraints of the admissible control

u

(3), (4), be (33).

\begin{matrix} \frac{d y}{d t} = v, \\ \frac{d v}{d t} = u . \end{matrix}

(32)

{- u}_{0} \leq u (t) \leq u_{0}, u_{0} = 1 .

(33)

3.1. Classical Synthesis

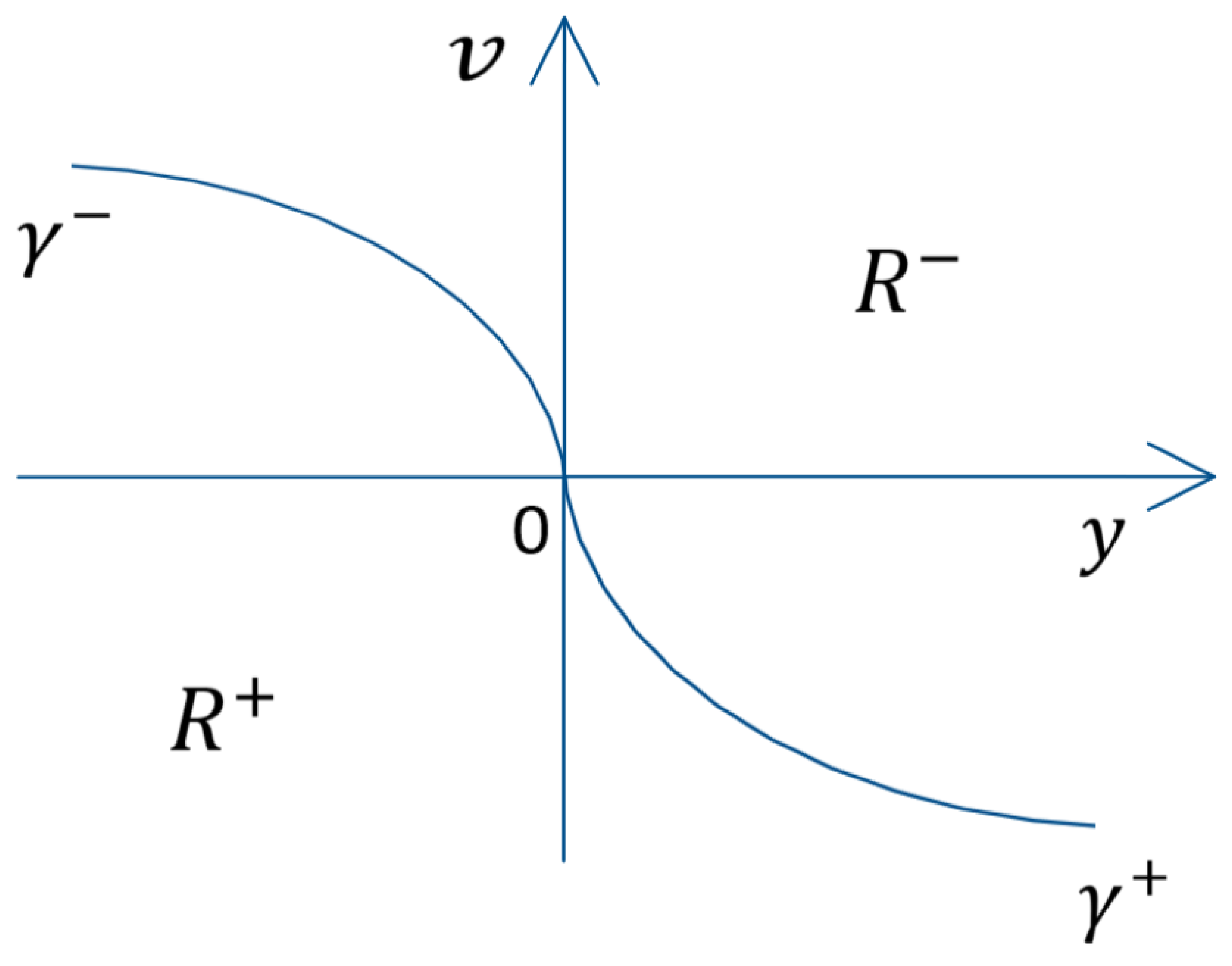
The switching curve

S_{2}

in the phase plane

y v

is described by (34). The two pieces

γ^{+}

and

γ^{-}

of the switching curve

S_{2}

are the parts of the parabolas representing the phase trajectories going through the origin of the phase plane in case of constant control

u = u_{0}

u = {- u}_{0}

respectively. The two areas

R^{+}

and

R^{-}

(35) in the phase plane, below and above the switching curve

S_{2}

(34) respectively, represent the areas where the optimal control takes a value

u_{0}

with regard to the points of

R^{+}

and

{(- u}_{0})

with regard to the points of

R^{-}

. The areas

R^{+}

and

R^{-}

as well as the parts

γ^{+}

and

γ^{-}

S_{2}

are shown in Figure 2. The time-optimal control is synthesized in form (36). After substitution of

R^{+}

and

R^{-}

by (35) as well as

γ^{+}

and

γ^{-}

by (34) in (36) the synthesized optimal control becomes (37).

\begin{matrix} S_{2} = γ^{+} \cup γ^{-} \cup (0,0), \\ γ^{+} = \{(y, v) : y = \frac{v^{2}}{2 u_{0}}, v < 0\}, \\ γ^{-} = \{(y, v) : y = \frac{{- v}^{2}}{2 u_{0}}, v > 0\} . \end{matrix}

(34)

\begin{matrix} R^{+} = \{(y, v) : y + s i g n (v) \frac{v^{2}}{2 u_{0}} < 0\}, \\ R^{-} = \{(y, v) : y + s i g n (v) \frac{v^{2}}{2 u_{0}} > 0\} . \end{matrix}

(35)

u (y, v) = \{\begin{matrix} 0 & w h e n & (y, v) \equiv (0,0), \\ + u_{0} & w h e n & (y, v) \in R^{+} \cup γ^{+}, \\ {- u}_{0} & w h e n & (y, v) \in R^{-} \cup γ^{-} . \end{matrix}

(36)

u (y, v) = \{\begin{array}{l} \begin{matrix} 0 & \begin{array}{l} w h e n & (y, v) \equiv (0,0), \end{array} \end{matrix} \\ \begin{array}{l} + u_{0} & (\begin{matrix} \begin{matrix} w h e n & (y + s i g n (v) \frac{v^{2}}{2 u_{0}} < 0) \end{matrix} \\ \begin{matrix} o r w h e n & (y - \frac{v^{2}}{2 u_{0}} = 0, v < 0) \end{matrix} \end{matrix}), \end{array} \\ \begin{matrix} {- u}_{0} & (\begin{matrix} \begin{matrix} w h e n & (y + s i g n (v) \frac{v^{2}}{2 u_{0}} > 0) \end{matrix} \\ \begin{matrix} o r w h e n & (y + \frac{v^{2}}{2 u_{0}} = 0, v > 0) \end{matrix} \end{matrix}) . \end{matrix} \end{array}

(37)

3.2. Synthesis Based on the New Property and the Method [14]

Let us now turn to the synthesis based on the method developed in [14] and widen by the new property. One of the main properties which form the foundations of this method is with regard to the trajectory in the state-space of one time-optimal control problem of higher order generated by the control representing the solution of the problem of the lower order where all the time-optimal control problems of descending order are generated by the problem of the utmost order and form a class of problems. As we have shown here the new property represents an expansion covering the general case of systems with real eigenvalues, no matter of the number of eigenvalue multiplicity. The example here considers a system of order two, so the synthesis is directly based on the solution of the problem of order one, which allows expressing also analytically the solution of the initial problem.

Step 1. First we make a suitable change of variables in the way (38) and obtain a representation by

(x_{1}, x_{2})

which could be done also by the matrix

T

(39) – (40) in the way (41). Thus we obtain (43) and (44) from the initial system (32) through its matrix representation (42). The system (44) is now in the form (1). Then (44) in form (10) is represented as (45) – (46) (as (1) in form (10)). The sub-system of (45) – (46) is (47) or (48).

\begin{matrix} y = x_{2}, & v = x_{1} . \end{matrix}

(38)

T = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) .

(39)

\begin{array}{l} T^{- 1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}), \\ T^{- 1} T = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) = E . \end{array}

(40)

(\begin{matrix} y \\ v \end{matrix}) = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) .

(41)

(\dot{\begin{matrix} y \\ \dot{v} \end{matrix}}) = (\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}) (\begin{matrix} y \\ v \end{matrix}) + (\begin{matrix} 0 \\ 1 \end{matrix}) u .

(42)

(\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{matrix}) = T^{- 1} (\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}) T (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + T^{- 1} (\begin{matrix} 0 \\ 1 \end{matrix}) u .

(43)

(\begin{matrix} {\dot{x}}_{1} \\ {\dot{x}}_{2} \end{matrix}) = (\begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) + (\begin{matrix} 1 \\ 0 \end{matrix}) u .

(44)

\begin{array}{l} {\dot{x}}_{1} = A_{1} x_{1} + B_{1} u, \\ \begin{matrix} y_{1} = C_{1} x_{1}, \end{matrix} \\ {\dot{x}}_{2} = λ_{2} x_{2} + y_{1} + b_{2} u, \end{array}

(45)

\begin{array}{l} x_{1} = (x_{1}), \\ A_{1} = (0), B_{1} = (b_{1}) = (1), C_{1} = (1), \\ λ_{2} = 0_{1}, b_{2} = 0 . \end{array}

(46)

\begin{matrix} {\dot{x}}_{1} = A_{1} x_{1} + B_{1} u, \\ \begin{matrix} y_{1} = C_{1} x_{1} . \end{matrix} \end{matrix}

(47)

\begin{matrix} {\dot{x}}_{1} = 0 x_{1} + 1 u, \\ \begin{matrix} y_{1} = 1 x_{1} . \end{matrix} \end{matrix}

(48)

Step 2. Solving Problem P(1). The eigenvalue of

A_{1}

is 0. The optimal control of Problem P(1),

u_{1}^{o} (t)

for

t \in [0, t_{1 f}^{o}],

is (49) – (50) [14] (pp. 50-52).

u_{1}^{o} (t) = \{\begin{matrix} 0 & w h e n & x_{10} = 0, \\ \begin{matrix} s_{11}^{o} u_{0} & f o r & t \in [0, t_{11}^{o}] \end{matrix} & w h e n & x_{10} \neq 0 . \end{matrix}

(49)

\begin{array}{l} s_{11}^{o} = - s i g n (b_{1} x_{10}), \\ t_{11}^{o} = \frac{| x_{10} |}{| b_{1} | u_{0}} . \end{array}

(50)

m i n J_{1} = t_{1 f}^{o} = \{\begin{matrix} 0 & w h e n & x_{10} = 0, \\ t_{11}^{o} & w h e n & x_{10} \neq 0 . \end{matrix}

(51)

Step 3. Calculating the value of the variable

x_{2 w}

. The variable

x_{k w}

is defined in [14] (pp. 39-40), [16] (p. 320), [17] (p. 41) and in case of expanding the class of time-optimal control problems it represents here at

k = n

the n-th coordinate of the vector

x (t)

(29) at the moment

t = t_{(n - 1) f}^{o} .

In case

n = 2

the variable

x_{2 w}

represents (52). With regard to the system (47) or (48) of Problem P(1) the variable

x_{2 w}

(52) becomes (53) and after simplifying – (55).

x_{2 w} = e^{λ_{2} t} x_{20} + \int_{0}^{t_{1 f}^{o}} e^{λ_{2} (t - τ)} (y_{1}^{o} (τ) + b_{2} u_{1}^{o} (τ)) d τ .

(52)

x_{2 w} = x_{20} + x_{10} t_{11}^{o} + \frac{b_{1} s_{11}^{o} u_{0}}{2} {t_{11}^{o}}^{2} .

(53)

x_{2 w} = x_{20} + \frac{x_{10} | x_{10} |}{| b_{1} | u_{0}} + \frac{(- s i g n (b_{1} x_{10})) {x_{10}}^{2}}{2 b_{1} u_{0}} .

(54)

x_{2 w} = x_{20} + \frac{s i g n (x_{10}) {x_{10}}^{2}}{2 {| b}_{1} | u_{0}} .

(55)

Step 4. Applying the theorem for synthesizing the optimal function in the initial state [14] (Theorem 3.2, pp. 40-43), [16] (Theorem 3, p. 320), [17] (Theorem 3, p. 41). According to this theorem and its corollaries the time-optimal control in the initial state of Problem P(2) represents (56).

The variable

x_{k +}

, respectively

x_{2 +}

in (56), is a term introduced in [14] (p. 38), [16] (pp. 319-320) which defines the relation of the points of the axis

x_{k}

of the state-space of the system of Problem P(k) from the considered class of problems to the switching hyper-surface of the same Problem P(k). The value of the variable

x_{k +}

is determined by a procedure called “axes initialization” [14] (Chapter 3, Section 3.3, pp. 60-88), [17] (pp. 41-45).

With regard to the example

x_{2 +} = - 1

(57). This means that all the points of the negative semi-axis

O x_{2}

are above the switching curve of Problem P(2) and the optimal control value for them is

+ u_{0}

while all the points of the positive semi-axis

O x_{2}

are below the switching curve of Problem P(2) and the optimal control value for them is

- u_{0}

Thus with regard to the initial state

(x_{10}, x_{20})

based on (56) after substitution of

x_{2 w}

by (55) and

x_{2 +}

(57) we obtain (58). So, the synthesized optimal function with regard to a state

(x_{1}, x_{2})

is (59). Taking into account

b_{1} = 1

according to (46), (59) becomes (60).

u^{o} (0) = u^{o} (x_{10}, x_{20}) = \{\begin{matrix} u_{0} & w h e n & x_{2 +} x_{2 w} > 0, \\ u_{1}^{o} (0) & w h e n & x_{2 +} x_{2 w} = 0 \\ - u_{0} & w h e n & x_{2 +} x_{2 w} < 0 . \end{matrix},

(56)

x_{2 +} = - 1 .

(57)

u^{o} (0) = u^{o} (x_{10}, x_{20}) = \{\begin{matrix} u_{0} & w h e n & - (x_{20} + \frac{s i g n (x_{10}) {x_{10}}^{2}}{2 {| b}_{1} | u_{0}}) > 0, \\ u_{1}^{o} (0) & w h e n & (x_{20} + \frac{s i g n (x_{10}) {x_{10}}^{2}}{2 {| b}_{1} | u_{0}}) = 0 \\ - u_{0} & w h e n & - (x_{20} + \frac{s i g n (x_{10}) {x_{10}}^{2}}{2 {| b}_{1} | u_{0}}) < 0 . \end{matrix},

(58)

u^{o} (x_{1}, x_{2}) = \{\begin{matrix} u_{0} & w h e n & - (x_{2} + \frac{s i g n (x_{1}) {x_{1}}^{2}}{2 {| b}_{1} | u_{0}}) > 0, \\ - s i g n (b_{1} x_{1}) u_{0} & w h e n & (x_{2} + \frac{s i g n (x_{1}) {x_{1}}^{2}}{2 {| b}_{1} | u_{0}}) = 0, \\ - u_{0} & w h e n & - (x_{2} + \frac{s i g n (x_{1}) {x_{1}}^{2}}{2 {| b}_{1} | u_{0}}) < 0 . \end{matrix}

(59)

u^{o} (x_{1}, x_{2}) = \{\begin{matrix} u_{0} & w h e n & (x_{2} + \frac{s i g n (x_{1}) {x_{1}}^{2}}{2 u_{0}}) < 0, \\ - s i g n (x_{1}) u_{0} & w h e n & (x_{2} + \frac{s i g n (x_{1}) {x_{1}}^{2}}{2 u_{0}}) = 0, \\ - u_{0} & w h e n & (x_{2} + \frac{s i g n (x_{1}) {x_{1}}^{2}}{2 u_{0}}) > 0 . \end{matrix}

(60)

It is easy seen, taking into account the relation (38) or (41) between

(y, v)

and

(x_{1}, x_{2}),

the analytical expression of the synthesized here optimal control (60) is identical with the expression obtained by the classical synthesis (37).

3.3. Simulation Results

Let us employ for illustration two initial states (61) и (62). The corresponding initial states in the state-space

(x_{1}, x_{2})

of the system (44) are (63) and (64). At Step 2 with regard to (63) we obtain according to (49) – (50) the result (65).At Step 3 according to (53) with regard to

x_{2 w}

we obtain (66). Thus, at Step 4 according to (56) and (57) the result for the time-optimal control in the initial state (63)

u^{o} (0) = u^{o} (0,10)

is (67). Analogically, with regard to the initial state (64) at Step 2 we obtain again (65), but with regard to

x_{2 w}

the result is (68), which leads to

u^{o} (0, - 10)

(69).

(y_{0}, v_{0}) = (10,0) .

(61)

(y_{0}, v_{0}) = (- 10,0) .

(62)

(x_{10}, x_{20}) = (0,10) .

(63)

(x_{10}, x_{20}) = (0, - 10) .

(64)

\begin{matrix} s_{11}^{o} = 0, t_{11}^{o} = 0, \\ t_{1 f}^{o} = 0, \\ u_{1}^{o} (t) = 0 . \end{matrix}

(65)

x_{2 w} = x_{20} = 10 .

(66)

u^{o} (0) = u^{o} (0,10) = - u_{0} = - 1 .

(67)

x_{2 w} = x_{20} = - 10 .

(68)

u^{o} (0) = u^{o} (0, - 10) = u_{0} = 1 .

(69)

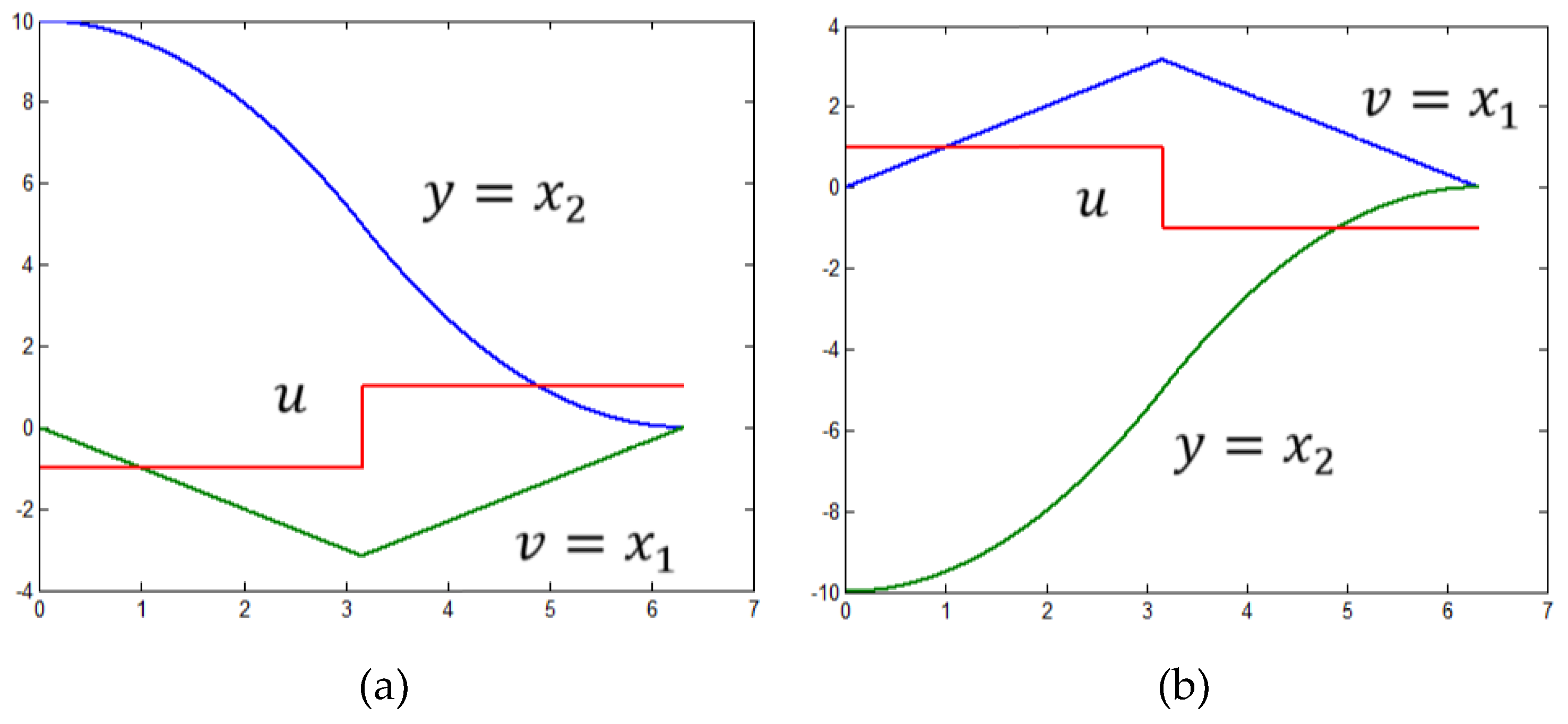
Figure 3 shows the near time-optimal processes with an accuracy

ε_{r} = 1.0 e - 03

with regard to the considered initial states while the trajectories in the phase plane

y v

of the system (32) are shown in Figure 4a. The blue phase trajectory is with regard to the initial state

(y_{0}, v_{0}) = (10,0)

. The red one is with regard to the initial state

(y_{0}, v_{0}) = (- 10,0) .

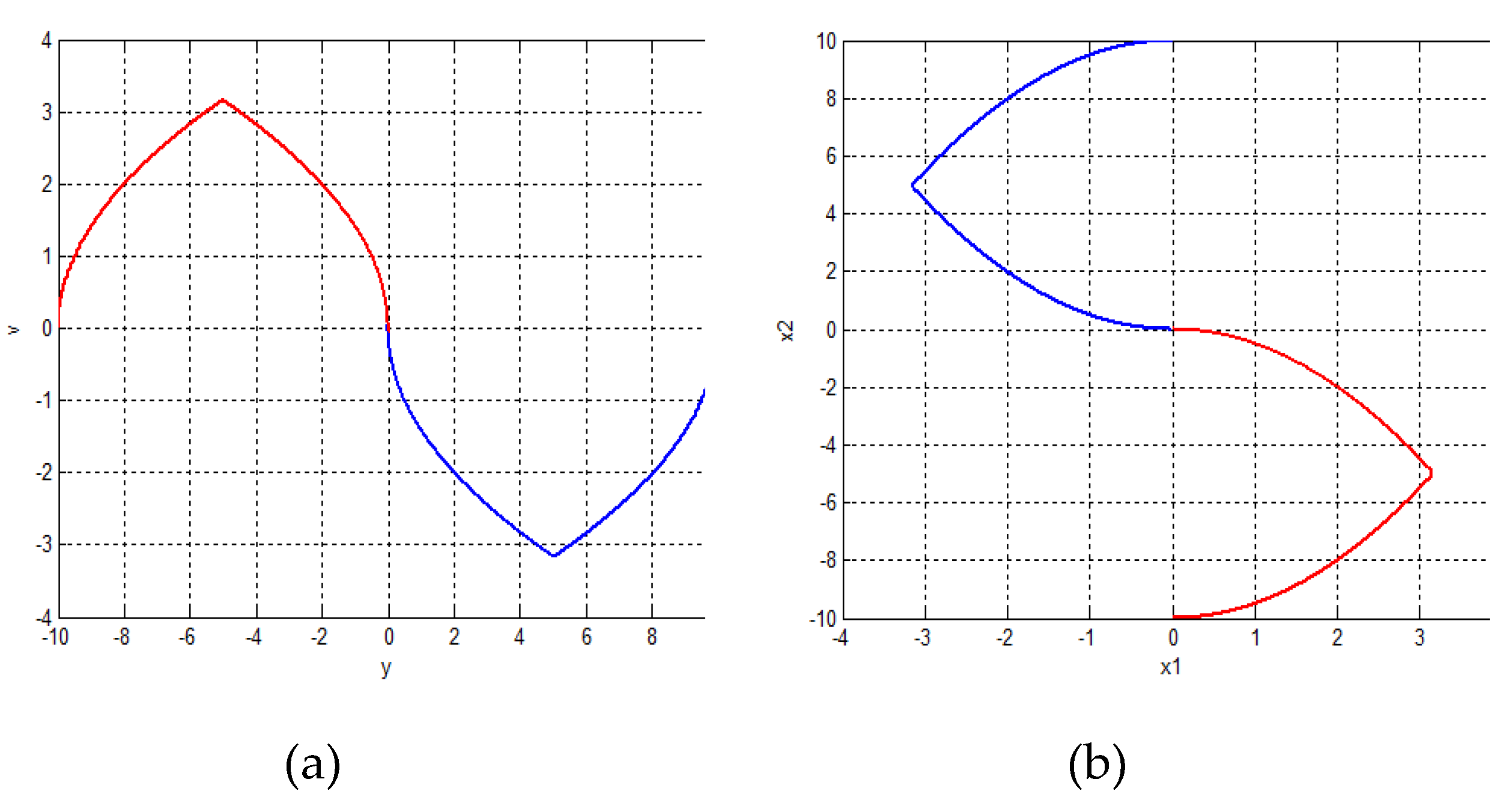
The near time-optimal trajectories with regard to the corresponding initial states in the state-space

(x_{1}, x_{2})

of (44)

(x_{10}, x_{20}) = (0,10)

and

(x_{10}, x_{20}) = (0, - 10)

are represented in the phase plane

x_{1} x_{2}

of (44) in Figure 4b. The blue trajectory in with regard to the state

(x_{10}, x_{20}) = (0,10)

, but the red one is with regard to

(x_{10}, x_{20}) = (0, - 10) .

The conversion of the trajectories shown in Figure 4b by the relation (41) returns the identical result shown in Figure 4a.

4. Conclusions

A new property of the linear time-optimal control problem in case the system eigenvalues are real is discovered and proven. This property unveils the prospective of an expansion of the author’s method of synthesizing the time-optimal control without the need of describing the switching hyper-surfaces for systems of any order, which has been developed for the systems with simple real non-positive eigenvalues, to the general case of systems with real non-positive eigenvalues no matter of the number of eigenvalue multiplicity. The synthesis of time-optimal control of a double integrator is represented first by the classical technique and then by the new method. It is shown the identity of the final analytical and numerical results.

Funding

The research is partially funded by the project BG05M2OP001-1.002-0023-С01 - Competence center "Intelligent mechatronic, eco- and energy-saving systems and technologies".

Conflicts of Interest

The author declares no conflict of interest.

References

Feldbaum, A. A. The simplest relay automatic control systems, Automation and Remote Control 1949, Vol. X, № 5, (in Russian).
Feldbaum, A. A. Optimal processes in automatic control systems, Automation and Remote Control 1953, Vol. XIV, № 6, (in Russian).
Pontryagin, L. S.; Boltyanskii, V. G.; Gamkrelidze, R. V. and Mischenko, E. F. The Mathematical Theory of Optimal Processes, Pergamon Press, Oxford, 1964.
Athans, M.; Falb, P. L. Optimal control. An introduction to the theory and its applications, McGraw-Hill, 1966.
Lee, E. B.; Markus, L. Foundations of optimal control theory, Wiley & Sons Inc., 1967.
Bryson, A. E.; Ho, Y. C. Applied optimal control, Blaisdell Publishing Company, 1969.
Бoлтянский, В. Г. Математические метoды oптимальнoгo управления, Мoсква, Наука, 1969. / Boltyanskii V. G. Mathematical Methods of Optimal Control, Holt, Rinehart and Winston, New York, 1971.
Leitmann, G. The calculus of variations and optimal control, Plenum Press, 1981.
Pinch, E. R. Optimal Control and the Calculus of Variations, Oxford University Press, Oxford, 1993.
Locatelli, A. Optimal control of a double integrator, Cham, Switzerland: Springer, 2017, Studies in Systems, Decision and Control, Volume 68, Online ISBN 978-3-319-42126-1. [CrossRef]
Romano, M.; Curti, F. Time-optimal control of linear time invariant systems between two arbitrary states, Automatica 2020, Volume 120, 109151, ISSN 0005-1098. [CrossRef]
2020; 12. Suqin He; Chuxiong Hu; Yu Zhu; Masayoshi Tomizuka, Time optimal control of triple integrator with input saturation and full state constraints, Automatica 2020, Volume 122, 109240, ISSN 0005-1098. [CrossRef]
Penev, B. A proof of one property of one class of time optimal control problems (in Russian), Journal of the Technical University at Plovdiv (BULGARIA) "Fundamental Sciences and Applications" 1997, Vol. 5, Series A - Pure and Applied Mathematics, ISSN 1310-8271, pp. 139-147, Available on URL: https://www.researchgate.net/publication/266360795_A_proof_of_a_property_of_a_class_of_problems_for_optimal_fast-action.
Penev, B. G. A Method for Synthesis of Time-Optimal Control of Any Order for a Class of Linear Problems for Time-Optimal Control, Ph.D. Dissertation, Technical University of Sofia, 1999 (in Bulgarian). Available on URL: https://www.researchgate.net/publication/337290119_A_Method_for_Synthesis_of_Time-Optimal_Control_of_Any_Order_for_a_Class_of_Linear_Problems_for_Time-Optimal_Control_in_Bulgarian_Metod_za_sintez_na_optimalno_po_brzodejstvie_upravlenie_ot_proizvolen_r.
Penev, B. A Proof of One Property of a Class of Linear Time Optimal Control Problems, Journal of the Technical University at Plovdiv “Fundamental Sciences and Applications” 2006, VOL. 13 (4), pp. 181-186, ISBN 1310 – 8271. Available on URL: http://www.tu-plovdiv.bg/content/files/VOL.13(4).B_709.pdf.
Penev, B. G.; Christov, N. D. On the Synthesis of Time Optimal Control for a Class of Linear Systems, in Proc. 2002 American Control Conference, Anchorage, May 8-10, 2002, Vol. 1, pp. 316-321. [CrossRef]
Penev, B. G.; Christov, N. D. On the State-Space Analysis in the Synthesis of Time-Optimal Control for a Class of Linear Systems, in Proc. 2004 American Control Conference, Boston, June 30 - July 2, 2004, Session “Optimal control I”, Schedule code WeA02.4, Vol.1, pp. 40- 45. [CrossRef]
Penev, B. G.; Christov, N. D. A fast time-optimal control synthesis algorithm for a class of linear systems, in Proc. 2005 American Control Conference, Portland, 8-10 June 2005, Session “Optimal Control Theory”, Schedule code WeB10.6, Vol. 2, pp. 883- 888. [CrossRef]
Penev, B. G., Analysis of the possibility for time-optimal control of the scanning system of the GREEN-WAKE's project lidar, monograph, 2012, A study within the research project "Demonstration of Light Detection and Ranging based wake vortex detection system incorporating an atmospheric hazard map" or GREEN-WAKE, Grant agreement ID: 213254, EU 7th Framework Program for Research and Technological Development, arXiv:1807.08300.
L7.3 Time-optimal control for linear systems using Pontryagin's principle of maximum, Graduate course on "Optimal and Robust Control" (B3M35ORR, BE3M35ORR, BEM35ORC) given at Faculty of Electrical Engineering, Czech Technical University in Prague: https://www.youtube.com/watch?v=YiIksQcg8EU.
Solution of Minimum - Time Control Problem with an Example. https://www.youtube.com/watch?v=Oi90M3cS8wg.
Alexandre Girard, Commande optimale: exemple pour le temps minimum d'une masse avec une limite de force, Modélisation, analyse et commande des robots, Exemple d'un calcul de loi de commande optimale, https://www.youtube.com/watch?v=wKjEAXFvXlQ.
Рютин, К.C. Вариациoннoе исчисление и oптимальнoе управление - 12. Задача быстрoдействия, https://www.youtube.com/watch?v=u7FtLP5BWeg.

Figure 1. Schematic representation of the initial system (1) in form (10).

Figure 2. Representation of the areas

R^{+}

and

R^{-}

as well as the two parts

γ^{+}

and

γ^{-}

of the switching curve

S_{2}

in the phase plane

y v

Figure 2. Representation of the areas

R^{+}

and

R^{-}

as well as the two parts

γ^{+}

and

γ^{-}

of the switching curve

S_{2}

in the phase plane

y v

Figure 3. Near time-optimal process with an accuracy

ε_{r} = 1.0 e - 03

with regard to the initial state: (а)

(y_{0}, v_{0}) = (10,0)

with corresponding

(x_{10}, x_{20}) = (0,10)

; (b)

(y_{0}, v_{0}) = (- 10,0)

with corresponding

(x_{10}, x_{20}) = (0, - 10)

Figure 3. Near time-optimal process with an accuracy

ε_{r} = 1.0 e - 03

with regard to the initial state: (а)

(y_{0}, v_{0}) = (10,0)

with corresponding

(x_{10}, x_{20}) = (0,10)

; (b)

(y_{0}, v_{0}) = (- 10,0)

with corresponding

(x_{10}, x_{20}) = (0, - 10)

Figure 4. Phase trajectories of the near time-optimal processes with an accuracy

ε_{r} = 1.0 e - 03

in the phase plane: (a)

y v

of the system (32); (b)

x_{1} x_{2}

of the system (44).

Figure 4. Phase trajectories of the near time-optimal processes with an accuracy

ε_{r} = 1.0 e - 03

in the phase plane: (a)

y v

of the system (32); (b)

x_{1} x_{2}

of the system (44).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

One New Property of a Class of Linear Time-Optimal Control Problems

Abstract

1. Introduction

2. Formulation of the Problem and Solution

3. Example

3.1. Classical Synthesis

3.2. Synthesis Based on the New Property and the Method [14]

3.3. Simulation Results

4. Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe