Prerpints.org logo
Preprint
Article

Hydraulic Planning in Insular Urban Territories: The Case of Madeira Island—Ribeira Brava, Tabua

Altmetrics

Downloads

93

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 June 2023

Posted:

09 June 2023

You are already at the latest version

Alerts
Abstract
This study’s primary goal was to conduct an analysis on the flood propensity of the Tabua (Ribeira Brava) drainage basin’s main watercourse. In addition to that, this study also recommends two different methodologies in order to mitigate flood’s impacts, namely by dimensioning a detention basin and adjusting the riverbed roughness coefficient. Regarding the study on the flood propensity, it was necessary to resort to geomorphological data, which was obtained when characterizing the watershed; that data was crucial to determine the expected peak flow rate, according to the Gumbel Distribution methodology and considering a 100 years return period, and to perform necessary tasks in the SIG ArcGIS software. Lastly, it was also analyzed the drainage capacity of this drainage basin’s river mouth, in order to conclude whether it would have the capacity to drain the total volume of rainwater if an extreme flood event was to happen. Indeed, the main results point out that this watershed’s river mouth doesn’t have the necessary drainage capacity to cope with an extreme event, for the return period that was considered. As a consequence of that, the two mitigation measures aforementioned were developed considering Tabua (Ribeira Brava) drainage basin’s specific features: the sizing of the detention basin was estimated through the Dutch Method and the Simplified Triangular Hydrograph Method, while the adjustment of the roughness coefficient was considered a valid solution to enhance the drainage capacity of this river mouth.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Nowadays, a society’s sustainable development is significantly influenced by aspects such as weather and climate [1]. For instance, extreme weather conditions are perceived as a risk to the integrity of both the social and economic spheres [1]. As a consequence of the higher level of climate instability, the incidence and intensity of hazardous hydrometeorological phenomena have been increasing [2]. Indeed, the changes in land use, the increase in terms of population density, the geological characteristics, and the region where a certain region is located are all aspects that can be seen as major contributing factors to most disasters that occur due to climate change [3,4].
In the definition of climate change, one can encompass the variations that occur in terms of the average climatic conditions, either globally or from a regional perspective. It results from the synergy that arises between the variability that is naturally associated with the climate and all the major modifications in terms of the atmosphere’s composition mainly caused by human actions [5]. Moreover, climate change is currently considered one of the biggest threats to the world [6]. As the temperature rapidly increases, due to anthropogenic disturbances, both the patterns of rainfall and the hydrological cycle might end up being altered [7,8]. These alterations in terms of the climate have the capacity to interfere with elements such as the temperature and the rainfall – especially, the extreme temperature and rainfall events – as previous studies with observed data [6,7,9] and projected future data [6,8,10] have demonstrated. Those rapid changes in climate extremes are believed to originate severe disasters – namely, floods and droughts. Hence, studies on this particular field have gathered massive attention globally as the aforementioned aspects enhance the importance that a correct planning and management of water resources has. Nonetheless, despite being a global phenomenon, extremes’ changes can’t be seen as homogenous across the world; in fact, there are large differences in terms of frequency, temporal and spatial extent across different regions of the globe [6,11,12]. Hence, to provide different perspectives that account for those differences, it’s encouraged for scientists to investigate multiple regions of the world, offering unique perspectives [6].
In recent times, climate experts have been focusing on mitigating the negative impacts of climate-extremes, especially in urban areas, since those are areas where studies point out to substantial increases in regard to high air temperature extremes [1,13]. However, only approximately 10% of the urban areas were affected with an increase in terms of the frequency of precipitation extremes [1,13]. The positive relationship that exists between the intensity of daily extreme precipitation and global warming is an evidence-based fact. Indeed, it has been determined that the rate of increase is approximately 7% per degree of global warming [1,14]. One other major concern has to do with a scenario where hot and wet extremes meet. For instance, precipitation extremes, when preceded by a heatwave, can have their effects amplified, which ultimately leads to a greater flash-flood risk [1,15]. As aforementioned, these significant climate changes are able to affect temperature and rainfall extremes – that has been proven by resorting both to observed data and to simulated future data [6,7,8]. Considering that such abrupt changes end up leading to severe events, namely floods and droughts, studies whose focus has been directed to these extremes received global attention, as the importance of accurately planning and managing water resources increased [1,6]. Consequently, decision-makers and policy officials that operate in the field of disaster management, especially, have been encouraged to develop and implement mitigating and preventive strategies regarding the occurrence of floods. This occurred mainly due to the changes that took place in the meteorological and socio-economic fields, which ultimately contributed to an increase in this type of phenomenon’s frequency [4].
Cities are frequently facing serious and recurring natural disasters, and flooding is an event that can be highlighted. Due to the acceleration of the urbanization process, population and economic activities ended up becoming highly concentrated, which can be translated into more significant social and economic damages from flooding when compared to the pre-urbanization period [16,17,18]. Flooding can be classified as the rising or even the overflowing of a water flow. Just like droughts and hurricanes, for example, floods are classified as a natural and severe phenomenon; nevertheless, they can be influenced by a region’s characteristics, such as the soil type, the vegetation, and the weather [18,19]. Because of the huge amount of impacts that this phenomenon causes – in terms of natural devastation, economic and social losses, and, ultimately, human lives – since it occurs in areas of large human presence, floods are considered a “natural disaster” [19,20,21]. Flooding events often result from heavy rainfall and their effects are mostly felt in urban locations that are disorderly occupied and located in hazardous areas. Indeed, the human need for water resources “forced” cities to be built near rivers [20,21,22,23]. Past civilizations looked to establish their cities in the surrounding areas of rivers because of their need for water; this need arose due to multiple purposes, since irrigation, animal necessity, and to assure a more fertile land [19]. Therefore, one can conclude that urban areas are more prone to be affected by floods not only due to climate change but also as a consequence of an inadequately conducted urbanization process [19,24]. Nevertheless, recent observations point out to an increase in terms of the frequency of flooding disasters mostly because of climate change. In fact, climate change has led to higher levels of annual precipitation and increased runoffs from a hydrological perspective – these two factors, when combined, contribute to a higher risk of flooding [4]. As floodings tend to become more recurrent, there has been a growing effort to create accurate flood risk maps, in order to sustainably prevent these risks and, therefore, protect both the population and the infrastructure [4,25].
Floods are seen as a harmful and recurrent natural disaster that generate obstacles to the socioeconomic development of a significant amount of regions worldwide [26,27,28,29,30]. From 1990 to 2016, it is believed that floods all over the globe originated losses of approximately USD 723 billion [17]. Urban areas are the ones that are more prone to be affected by floods, in part, due to population growth and climate change, but also because of the increasing intensity and recurrence of these events [31,32,33,34]. By 2030, around 40% of all the cities around the globe will be located in regions where the risk of flooding is high, with such a scenario affecting approximately 54 million people [35]. Regarding Southeastern Asia, by 2030, 82% of urban areas will be inserted in high-frequency flood zones [36]. In order to be able to develop accurate risk management plans regarding sustainable land use planning, it is necessary a deep understanding of the relationship that exists between floods and urban growth [37,38]. This type of extreme event brings risk mostly to people living either in the watercourses vicinity or in areas with fewer slopes [19,20,21,22]. Additionally, the hydrological dynamics of floodplains, rivers, and coastal regions can be influenced by processes of both natural and human-induced nature, and that ends up altering aspects such as the surface runoff and the water infiltration process [19]. Thus, one can find in floods one of the biggest challenges that humanity will have to face in the near future, especially because of their huge capacity to provoke destruction [39,40]. In fact, as recent years have already been affected by the climate change, extreme flood events’ frequency has increased, which can be interpreted as a clear and significant threat to humanity [39,41,42].
The flood system has spatial-temporal dynamics, which makes it highly complex, involves uncertainties, and integrates multiple challenges within a system that is responsible for giving rise to complex phenomena [43]. In regard to flood risk management, research assumes a key role in estimating flood hazards and enhancing people’s understanding of the complex flood risk components, both from an environmental and socioeconomic perspective [44].
The risk that is associated with floods results from a combination of hazard, exposure, and vulnerability; thus, flood risk management will consist in reducing the damage and/or intensity of the flood [17,22,45,46,47]. In recent decades, scientific advancements have led to significant alterations regarding the approach utilized to mitigate the negative impacts of floods. Structural measures to control the impacts of floods (e.g. dikes, embankments, etc.) are being substituted by new and more comprehensive models of flood risk management [20,48]. These new approaches consider risk assessment studies – studies that consider flood hazard and exposure/vulnerability factors – to estimate the probabilities and the consequences associated with flood events [17,21]. Multiple methodologies have been adopted in order to allow the computation of these indicators. On the one hand, the hazard approaches consider: measurement-based, field surveys [49,50], hydrodynamic models [51,52], and GIS and Remote Sensing [17,20,21,22] in linear modeling of flood risk through overlaying component layers with associated analytical hierarchical process (AHP)-based computed weights. On the other hand, the indicators related to land cover might be divided into two different categories: (i) traditional terrestrial mapping [38,53]; and (ii) land cover classification, which is mostly built around observations via satellite [38,54]. The arise of satellite sensors – for example, Landsat, Satellite Pour Observation de la Terre (SPOT), and Sentinel 2 – has been extremely important to enable a quicker and easier land cover classification, as well as to facilitate the study of land cover evolution. Moreover, remote sensing allows a quicker acquisition of data, when compared to field survey methods, which also end up being more expensive [55].
The assessment of the risks associated with flooding is a crucial step when defining suitable management strategies [56]. Over the past few decades, studies have concentrated efforts on developing methodologies for assessing flood risk at multiple scales and considering various goals. Mishra et al. [57] developed an index to analyze the flood propensity of an Indian river – the Kosi River – which is mostly based on hazard – considering aspects of geomorphologic nature, the distance to the active channel, the slope, and also the levels of rainfall – and on the socioeconomic vulnerability (population and its characteristics, household, and female densities; levels of literacy; alterations in the cover and use of land; existing intersections between roads and the river; road density). In addition to that, Chinh Luu et al. [58] studied the flood risk’s temporal variations; in order to obtain a deeper knowledge in regard to this phenomenon’s dynamics and, as a consequence of that, to be capable of formulating appropriate strategies of mitigation, this study integrated multiple aspects – the hazard and the level of exposure and vulnerability of a certain region. Dang et al. [59] delineated the key roles required to enhance flood risk assessment methodologies that aim to support the decision-making process. Flood risk indices were divided by the authors into three components: social–economic, physical, and environmental. Kron [60] elaborated flood risk indices that considered flooding probability and its hypothetical consequences, the social-economic vulnerabilities of the region, and its environment. Begun et al. [17] combined the probability of occurring a flood with the losses that the event would eventually bring. Multiple methodologies aiming to study flood propensity were developed in several areas. But they end up being limited in a comprehensive framework that supports decision-makers to get a better perception of the aggravating risk causes. Additionally, the focus of most of these studies lies on assessing the flood propensity at a specific time; however, Penning-Rowell et al. [61] claims that mitigation measures are more effective when they’re evaluated continuously. Jhong et al. [17] reinforces the idea that, to diminish the risk of flooding, understanding the level of vulnerability and hazard at different times is of extreme importance; this also is crucial from a land management perspective since it allows a more accurate analysis of the temporal and spatial trends that are more likely to exist in the future [62].
To assure that a flood study in an urban region will assist in the process of implementing appropriate forecasting and mitigation strategies, it must consider multiple aspects. Indeed, these aspects encompass obtaining topographical data, describing the phenomenological processes that are usually associated with flood currents and their interaction with both structures and infrastructure, in addition to choosing adequate algorithms to solve model equations, which allows obtaining the results [63]. Analysis of this nature must generate the so-called hazard and risk maps, i.e., maps that show the final representation of results through graphic products [64].
A major priority regarding the management of urban disasters is to mitigate the negative effects of urban floods [18,65,66]. Since urban floods risk assessment is capable to identify the probabilities and the main causes associated with the flooding phenomenon, it can be perceived as a key element to prevent and reduce the occurrence of urban floods [18,67,68,69]. Thus, aiming to prevent significant losses, it becomes fundamental to implement methods that diminish the risk of floods. Multiple factors might be pointed out when discussing the level of vulnerability of a certain region to floods – relief characteristics, the compactness coefficient of the watershed, the intensity and distribution of the rainfall, the occupation and use of the soil as well as its types. An approach based on Geographic Information Systems (GIS) enables the determination of the regions that are more susceptible to floods, which can be seen as a great assistance to the decision-making process in this particular field [19,70,71].
Storm sewers, gutters, culverts, tunnels, pipes, detention basins, and other mechanical devices are among the most commonly used measures to control floods [72]. Moreover, advanced gray infrastructure is utilized in some runoff control methods aiming to guide excess surface flow into disposal and storage sites [73]. However, considering a climate system that in recent times has been severely affected by extreme weather events, these strategies ended up not being nimble enough to effectively handle large levels of runoff [74,75]. To improve urban areas’ capacity to “resist” to floods, different alternative methodologies and concepts have been introduced in different parts of the globe. For instance, the low impact development (LID) in the US [76], the sustainable urban drainage systems (SUDS) in the UK [77], the water-sensitive urban design (WSUD) in Australia [78], or even the “sponge city” in China [79] are examples of alternative approaches.
A recent report from the European Environment Agency [80] highlighted that a significant number of European nations and organizations have already worked on policies and laws, both at regional and national levels, to enhance cities’ adoption of mitigation measures to address the effects of climate change, a strategy that is in line the input by the European Strategy on Adaptation to Climate Change. In addition to the fact that extreme events have become more frequent, the increasing apprehension among all stakeholders has originated a significant focus on this matter. Nonetheless, the changes that occur in terms of land use don’t gather that much attention, which may be concerning because, if a soil is sealed, the effects of climatic extremes might end up being amplified [81,82].
So, finding new land management strategies assumes a high level of importance, in line with what was outlined by the European Strategy, where it’s indicated the necessity for the member states to define adaptation plans to fight the effects of climate change, on a national, regional, and local scope. It is also important to engage municipalities on climate change and to provide all the support needed to implement adaptation measures locally. In fact, the municipal scale has the highest levels of effectiveness, in part due to the fact that municipalities are responsible for managing land use, through urban planning [81].
Regarding land planning, two important lines of study arise: (i) the analysis and adoption of mitigation strategies after the events occurred; (ii) the increment in terms of the territory’s resilience, in order to allow it to more easily adapt to the new scenarios that might end up arising as a result of the aforementioned changes and, therefore, mitigate risks that may derive from them, considering that more permeable soils can be translated into soils that are more prepared for absorbing heavy rains [38,81].
Consequently, prevention assumes a crucial role in both scenarios and that can be achieved by appropriately planning and designing the territory. The fact is management and solutions end up having multiple approaches and there’s a need to integrate them. Here, planning is particularly relevant as this step focuses precisely on the root causes of the problems as well as on preventive measures [38,81].
Based on that, the current study aims to conduct a hydrological analysis focused on this particular region, aiming to estimate the expected peak flow rate, considering a time of recurrence of 100 years; a posteriori, establish a comparison between this value and the drainage capacity that this watershed’s stream mouth possesses. After demonstrating that the mouth’s hydraulic characteristics are not enough to drain the estimated peak flow rate, it became necessary to size a detention basin as a mitigation measure aiming to normalize the flow downstream. The ultimate goal was to allow the mouth to operate normally, considering the dimensions that it currently has. Moreover, this study also focuses on the need for structural actions on the region of the mouth, a measure that, it’s worth saying, wouldn’t implicate significant urban impacts. This structural intervention would be associated with an alteration of the physical features of the stream’s riverbed and walls, namely, the coefficient of roughness. Thus, to increase the drainage capacity, the minimum characteristics of the stream end up being verified, without the necessity for dimensional changes.

2. Materials and Methods

2.1. Area of Study

This study analyses the Tabua (Ribeira Brava) watershed, which is located on Madeira Island’s southern slope, latitude 32°40′ N and longitude 17°50′ W [23,83]. It belongs to the Ribeira Brava municipality and acts as the precipitation catchment area, supplying one of the municipality’s main streams, as it can be seen in Figure 1.
Similar to Funchal, which is Madeira’s main municipality, this watershed is significantly exposed to flooding events, as observed both in 2010 and 2013, when flooding provoked serious losses, from material and human perspectives. As the Tabua (Ribeira Brava) watershed is located in an area with significantly high levels of urbanization, this region’s soil has a relatively high rate of sealing, mostly due to the presence of buildings and pavements [20,23]. Additionally, as it is demonstrated in Figure 2, the presence of vegetation and sedimentation in this watershed’s river mouth needs to be considered since it reduces the channel’s drainage capacity.
The level of conservation of the stream is significantly homogeneous throughout the part of its length that is located in the urban area – and might be confirmed in situ. Its reduced slope can be seen as the main cause for the excess of sedimentation and vegetation, which ultimately results in a slower drainage process and contributes to drag sediments with a larger grain size.

2.2. Schematic of the Methodology

The methodology that was adopted in this study is divided into 6 stages, as Figure 3 shows.
This study’s approach started with an intensive review of literature, aiming to collect the largest possible amount of important information to assure a precise characterization of this basin, both from a morphometric and hydrological perspective. Hence, after conducting the literature review mentioned above, the methodologies suggested by different authors were considered in order to a flood propensity analysis with a satisfactory level of reliability. Finally, the steps mentioned in Figure 3 are depicted below.

2.3. Morphometric Characterization of the Watershed

Regarding a watershed’s morphometric characterization, the key parameters to be use are the following [84,85,86,87]:
  • Gravelius Index—KC: The relationship between the perimeters of the basin under study and a perfectly circular one—both with identical areas—was utilized to estimate the level of similarity of the watershed’s geometric shape to a perfect circle [86]. This parameter can be obtained through Equation (1). Considering that this is a dimensionless parameter, a value close to “1” can be translated into a watershed whose shape will be similar to a perfect circle, regardless of its dimensions; as watersheds with rounded shapes tend to present higher levels of flood propensity, values closer to “1” will be associated with a greater risk regarding this type of phenomenon [86]. Therefore, we will have the following classifications for Kc: 1.00 - 1.25 Basin with high propensity for large floods; 1.25 - 1.50 Basin with medium tendency to large floods; > 1.50 Basin not subject to large floods.
K C = P / 2 × π × A
where:
  • P = Watershed’s perimeter, in “km”;
  • A = Area of the watershed, in “km2”.
  • Elongation Factor—KL: The relationship between the watershed being analyzed and a rectangle—both with identical areas—was used to estimate the elongation of the watershed, regardless of its dimensions. It can be obtained resorting to Equation (2). If a certain watershed has an elongation factor higher than “2”, then it can be classified as an elongated one [86].
K L = L E l E = K C × A 1.128 × 1 + 1 − 1.128 K C 2 K C × A 1.128 × 1 − 1 − 1.128 K C 2
where:
  • LE = Equivalent length, in “km”;
  • lE = Equivalent width, in “km”;
  • KC = Gravelius Index, a dimensionless parameter, in “/“;
  • A = Area of the watershed, in “km2”.
  • Shape Factor—KF: Relates the watershed’s average length and width. This parameter can be obtained through Equation (3). Lower values are associated with more elongated watersheds – and, therefore, with watersheds where the risk of flooding is lower – regardless of their size. Additionally, if the value is close to “1”, then the basin’s format will be similar to a square. Therefore, we will have the following classifications for KF: 1.00 - 0.75 Basin with high propensity for large floods; 0.75 - 0.50 Basin with medium tendency to large floods; < 0.50 Basin not subject to large floods.
K F = A / L B 2
where:
  • A = Area of the watershed, in “km2”;
  • LB = Watershed’s length, in “km”.
The length of a given watershed might be estimated using the distance between the stream’s mouth and its furthest point. Nonetheless, it’s worth mentioning that a watershed’s length doesn’t necessarily have to be equal to its main watercourse’s length. Some variations between these two values might arise as a result of the larger size that the main watercourse tends to have, mostly because of its sinuosity. Resorting to the MDE file, which was provided by LREC-RAM (the Regional Civil Engineering Laboratory of the Autonomous Region of Madeira), it was now possible to conduct a morphological characterization of both the Tabua (Ribeira Brava) watershed and its main watercourse. In order to avert restrictions associated with using a single method, the data that was gathered during this study were utilized in the equations of various authors.
First, to conduct a morphometric analysis, it was necessary to establish a hierarchy based on the order and magnitude of the watercourses; for that reason, both the Strahler and the Shreve classifications were utilized [87]. Indeed, these two classifications that were mentioned can be estimated by conducting a hydrological analysis of the DEM file, a process that involves obtaining the “flow direction” and “flow accumulation” rasters through the “flow order” tool [20]. Additionally, studies point out that the Strahler classification is highly connected with a watershed’s ratio of branching/bifurcation. Equation (4) allows the estimation of each degree of branching or bifurcation [20,21,84,86].
R B = N i N i + 1
where:
  • Ni = Number of watercourses classified as “i”, a dimensionless parameter, in “/”;
  • Ni+1 = Number of watercourses classified as “i + 1”, a dimensionless parameter, in “/”;
This can be obtained by dividing the number of watercourses of a certain order and the number of watercourses encompassed in the order immediately above, regardless of their dimensions. Moreover, the average level of bifurcation is obtained based on Equation (5).
R B ¯ = ∏ i = 1 i − 1 N i N i + 1 i − 1 = N 1 i − 1
where:
  • Ni = Number of watercourses classified as “i”, a dimensionless parameter, in “/”;
  • Ni+1 = Number of watercourses classified as “i + 1”, a dimensionless parameter, in “/”;
  • N1 = Number of first-order watercourses.
As this parameter only denotes the arithmetic mean of bifurcation ratios, it is also dimensionless. Additionally, a key aspect for an accurate morphometric characterization of any watershed is its concentration time. This parameter indicates the time that the watershed’s total area needs to contribute for the drainage process that will culminate in the stream’s mouth [20,21,84,86,87].
Considering that the equations utilized to calculate the time of concentration are empirical, different methodologies might end up originating varying results for the same parameter. Therefore, in order to avert extreme results, it is advisable to calculate the arithmetic mean. In this case, the arithmetic mean was calculated using the results that derived from the methodologies of Kirpich, Témez, and Giandotti (Equations (6), (7), and (8), respectively) [86].
t C = 57 × L 3 / ( H M A X − H M I N ) 0.385
where:
  • tC = Concentration time, in “minutes”;
  • L = Main watercourse’s length, in km;
  • HMAX = Main watercourse’s maximum height, in “m”;
  • HMIN = Main watercourse’s minimum height, in “m”.
t C = L i 0.25 0.76
where:
  • tC = Concentration time, in “hours”;
  • L = Main watercourse’s length, in “km”;
  • i = Main watercourse’s slope, in “m/m”.
t C = 4 + A + 1.5 × L 0.8 × H M
where:
  • tC = Concentration time, in “hours”;
  • A = Area of the watershed, in “km2”;
  • L = Main watercourse’s length, in “km”;
  • HM = Watershed’s average height, in “m”.

2.4. Precipitation Analysis

The precipitation analysis that was conducted in this research was based on a probabilistic analysis regarding short-term extreme events. As such, in order to enable this analysis, data was gathered from public sources, namely precipitation-related information automatically recorded by the National Water Resources Information System (SNIRH) – (period of sixteen years). The Gumbel Distribution was selected here because it was the probabilistic methodology that would better fit the already acquired data and the anticipated forecasts for the watersheds located in Madeira [20,21]. Hence, Equation (9) can be utilized to estimate the annual maximum daily precipitation.
P E S T = P M + S ' × K T
where:
  • PEST = Estimated maximum annual daily precipitation, in “mm”;
  • PM = Average annual daily precipitation, in “mm”;
  • S′ = Standard deviation of the sample, in “mm;”
  • KT = Frequency Factor, a dimensionless parameter, in “/”;
where:
S ' = ∑ X i − X M 2 n ' 0.5
where:
  • Xi = Sample value, in “mm”;
  • XM = Sample mean, in “mm”;
  • n′ = Number of samples.
K T = − 6 0.5 π × 0.577216 + ln ⁡ ln ⁡ T R T R − 1
where:
  • TR = Return period, in “years”.
A posteriori, given a certain duration, the intensity of the precipitation might be determined utilizing Equation (12).
I = P E S T × k t C
where:
  • I = Intensity of the precipitation, in “mm/h”;
  • PEST = Estimated maximum annual daily precipitation, in “mm”;
  • tC = Concentration time, in “hours”;
  • k = Coefficient of time distribution, a dimensionless parameter, in “/”;
where:
k = 0.181 × ln ⁡ t C + 0.4368
where:
  • tC = Concentration time, in “hours”.
Given that the annual maximum daily precipitation is applicable only to events that last an entire day, the coefficient of time distribution assumes a key importance. Thus, since a watershed’s concentration time is equal to the duration of the precipitation event, if one was to utilize the total level of daily precipitation, it would ultimately result in oversized hydraulic structures [86,88].

2.5. Drainage Capacity of the River Mouth and Peak Flow Rate

The Manning-Strickler equation presented in Equation (14) was utilized to calculate the stream mouth’s capacity of drainage; then, it was established a comparison between the value obtained and the projected flow considering an extreme event, for a period of recurrence of 100 years. Moreover, to estimate the projected flow, multiple methodologies that had a significant level of support among researchers were utilized, namely: Forti, Rational, Giandotti, and Mockus (Equations (16), (17), (18), and (19), respectively).
Q M = 1 n × A M × R 2 3 × i
where:
  • QM = Stream mouth’s capacity of drainage, in “m3/s”.
  • AM = Area of the river mouth cross-section, in “m2”;
  • R = Hydraulic radius, in “m”;
  • i = River mouth’s average slope, in “m/m”;
  • n = Coefficient of roughness of the riverbed and walls, in “m−1/3 s”, Table A1.
where:
R = B + 2 × h A M
where:
  • B = River mouth runoff section’s width, in “m”;
  • h = River mouth runoff section’s height, in “m”;
  • AM = Area of the river mouth cross-section, in “m2”.
It’s worth mentioning that previous studies that focused in this area were used as the main base to gather information regarding aspects such as the stream’s height and width in the mouth area [86]. In fact, the confirmation of this first parameter was possible due to the utilization of the georeferencing process.
Q F o r t i = A × b × 500 125 + A + c
where:
  • QForti = Peak flow rate by Forti, in “m3/s”;
  • A = Area of the watershed, in “km2”;
  • b = For this parameter, it was considered the value “2.35” for maximum daily precipitation below 200 “mm” and the value “3.25” for levels above 200 “mm”;
  • c = For this parameter, it was considered the value “0.5” for maximum daily precipitation below 200 “mm” and the value “1” for levels above 200 “mm”.
Q R a t i o n a l = C × I × A 3.6
where:
  • QRational = Peak flow rate by the rational methodology, in “m3/s”;
  • C = Coefficient of surface runoff, Table A2;
  • I = Intensity of the precipitation, in “mm/h”;
  • A = Area of the watershed, in “km2”.
Q G i a n d o t t i = λ × A × P M A X t C
where:
  • QGiandotti = Peak flow rate by Giandotti, in “m3/s”;
  • λ = Reduction coefficient, Table A3;
  • A = Area of the watershed, in “km2”;
  • PMAX = Height of precipitation considering a duration identical to the time of concentration, in “mm”;
  • tC = Concentration time, in “hours”.
Q M o c k u s = 2.08 × A × P E S T × C t C + 0.6 × t C
where:
  • QMockus = Peak flow rate by Mockus, in “m3/s”;
  • A = Area of the watershed, in “km2”;
  • PEST = Level of precipitation estimated, in “cm”;
  • C = Coefficient of surface runoff, Table A2;
  • tC = Concentration time, in “hours”.
In order to guarantee that the population is secure, the dimensions of hydraulic structures have to consider a value of Fill Rate below 85% [86,88]. Hence, the implementation of mechanisms that enable the regulation of the runoff – for instance, spillways – assumes a significant level of importance.
As aforementioned, Equation (20) is used to calculate the Fill Rate. If the mouth has not enough capacity of drainage to deal with the level of rain flow that exists in the watershed and can’t assure that the safety margin is accomplished, it becomes necessary to estimate the dimensions of accurate structures of mitigation, like detention basins.
F R = Q P Q M × 100
where:
  • FR = Fill Rate, in “%”;
  • QP = Each methodology’s peak flow rate, in “m3/s”;
  • QM = Stream mouth’s capacity of drainage, in “m3/s”.
The Fill Rate is related with a given section’s capacity of drainage regarding a certain flow. Therefore, in a scenario where this parameter is superior than 100%, the section isn’t capable to deal with such a high level of water, which ultimately leads to an overflowing [86].

2.6. Detention Basin Sizing

As previously mentioned, in scenarios where the mouth isn’t capable of handling the volume of rainwater, it becomes necessary to dimension a spillway, in order to guarantee the flow’s normalization that will ultimately reach the stream’s mouth. In this case, a spillway of the Cipolleti type was picked due to its capacity of facilitating the runoff and reducing turbulence in the areas where there is contact with water [85,89]. Its dimensions were calculated utilizing Equation (21).
Once the flow to be drained to the mouth has been established and regulated, it becomes possible to calculate the level of water that the detention basin will retain. To determine this level of water, two approaches were considered: the Dutch Method and the Simplified Triangular Hydrograph – STH (Equations (22) and (23), respectively).
Q S = 1.86 × L S D × H D 1.5
where:
  • QS = Flow drained by spillway, in “m3/s”;
  • LSD = Sill’s width, in “m3/s”;
  • HD = Height of the waterline above the sill, in “m”.
V A = ( Q P − Q S ) × t C × 3600
V A = Q P − Q S × ( 2 × t C − 2 × [ Q S / { Q P / t C } ] ) 2
where:
  • VA = Volume of storage, in “m3”;
  • QP = Each methodology’s peak flow rate, in “m3/s”;
  • QS = Flow drained by the spillway, in “m3/s”;
  • tC = Concentration time, in “hours”.
It should be noted that the base for Equation (23) can be found in the STH’s geometric examination (Figure A1). Indeed, this equation was established by taking into account an event that lasts, at least, twice as much as a watershed’s time of concentration. Considering that the last particle of rainwater to get to the stream’s mouth would come from the farthest point, and would be generated in the last moment of the precipitation event, it becomes clear that it would be necessary to consider the value of the concentration time for the volume drained by the river mouth [86].
Given that the Dutch Method fails to account for the damping and delay of the precipitation hydrograph, the hydraulic structures whose dimensions are estimated considering this methodology might end up being oversized [90], as Figure 4 demonstrates, where qs: spillway’s runoff capacity; tc: time of concentration; tMAX: maximum duration of precipitation (base); td: time delay until the process of accumulation of water starts in the detention basin; Ha,MAX: maximum capacity of storage; i(tMAX): intensity of precipitation associated with the maximum duration.
Thus, it was demonstrated that, when resorting to the Dutch Method, the storage process and precipitation initiate at the same time, which is an unrealistic scenario, given that storage will not begin until the moment when the flow drained downstream exceeds the spillway’s capacity of runoff.

2.7. Modification of the Roughness Coefficient

Additionally, from a structural perspective, as a mitigation strategy, the alteration of the coefficient of roughness of the watercourse’s riverbed and walls was considered. One of most significant advantages associated with this measure is the fact that it enhances the capacity of drainage by diminishing the friction level. This measure consists of modifying the value associated with the “n” parameter in the Manning-Strickler equation aiming to enhance a certain watercourse’s flow; that might be accomplished by changing the material that covers both the stream’s riverbed and walls [86].

3. Results

The values that are presented in this section correspond to the results generated as a result of the application of the aforementioned formulas. Thus, in order to assess the morphometric traits of this watershed’s principal watercourse, it became necessary to conduct an individual analysis, which focused on the parameters presented in Table 1, establishing correlations with reference values recommended by various authors.
The first parameter analyzed, which is related with the watershed’s area, has a significant level of relevance when studying the water volume drained to the mouth. Moreover, considering its area, a watershed can be classified as: Very Large > 20 km2; Large > 10 km2; Medium > 1 km2 and Small < 1 km2 [91]. In line with what the table above illustrates, this watershed can be classified as “Small”, which can be translated into a lower propensity to flooding when compared to larger watersheds. Nonetheless, it’s worth mentioning that reference values tend to be arbitrary; therefore, they may end up differing in accordance with the type of analysis that is being done [91].
This watershed’s borders have higher altitudes when compared to its central region, as Figure 5 demonstrates, which indicates a steep slope that will enhance a rapid supply to the main course, originating higher volumes of water in the stream and, ultimately, in the river mouth.
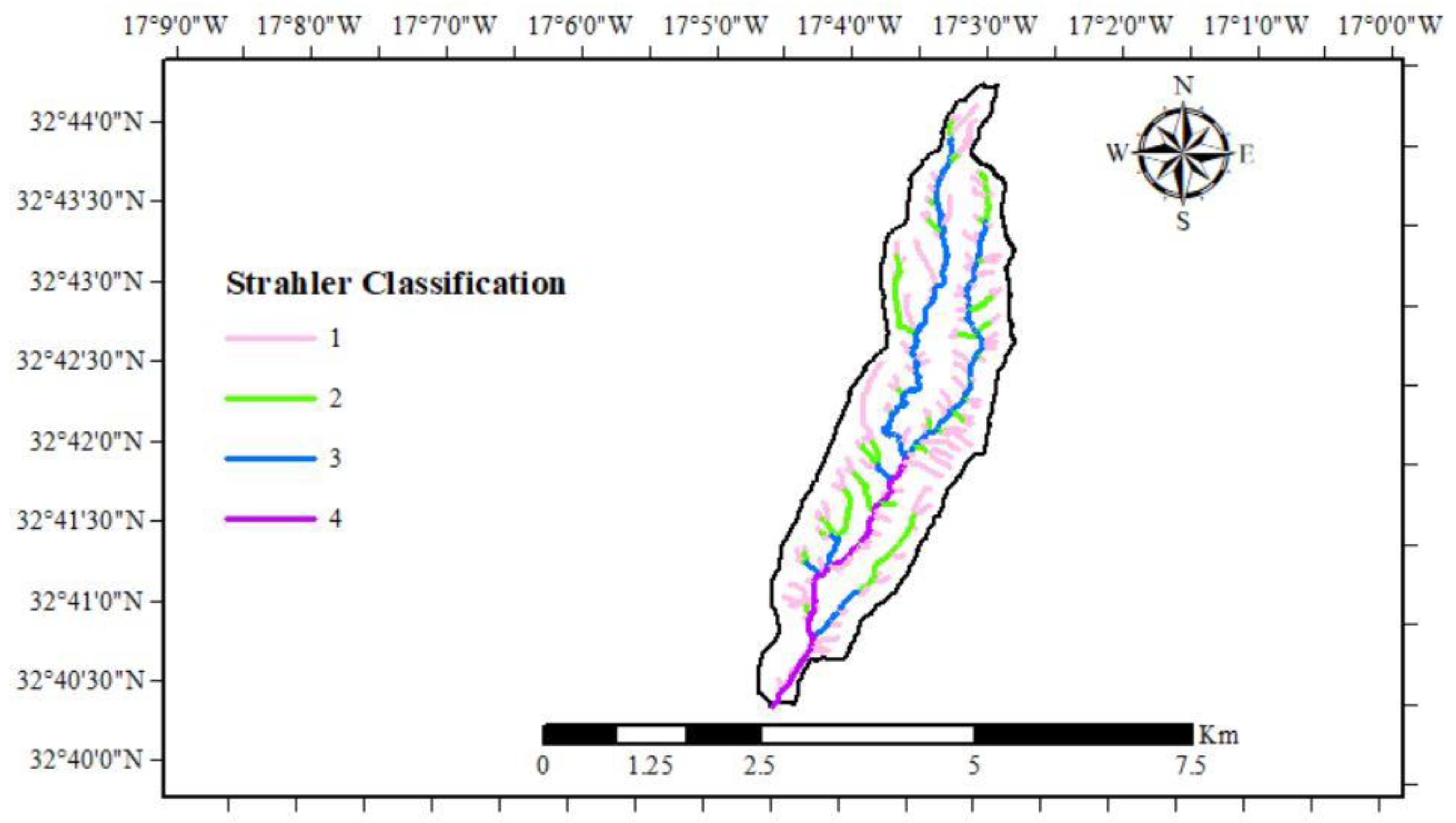
In regard to this watershed’s system of drainage, illustrated in Figure 6, the presence of numerous watercourses – mostly, medium- or even low-order watercourses that end up supplying the principal watercourse – is associated with a larger drainage capacity. In fact, this indicator can be interpreted as the behavior of a certain area, hydrographically speaking, which has as its key aspect the probability of generating new watercourses. In basins with larger hydric densities, there’s a bigger tendency to generate new watercourses – and, as a consequence of that, these basins usually have a larger number of ephemeral channels [86,87].
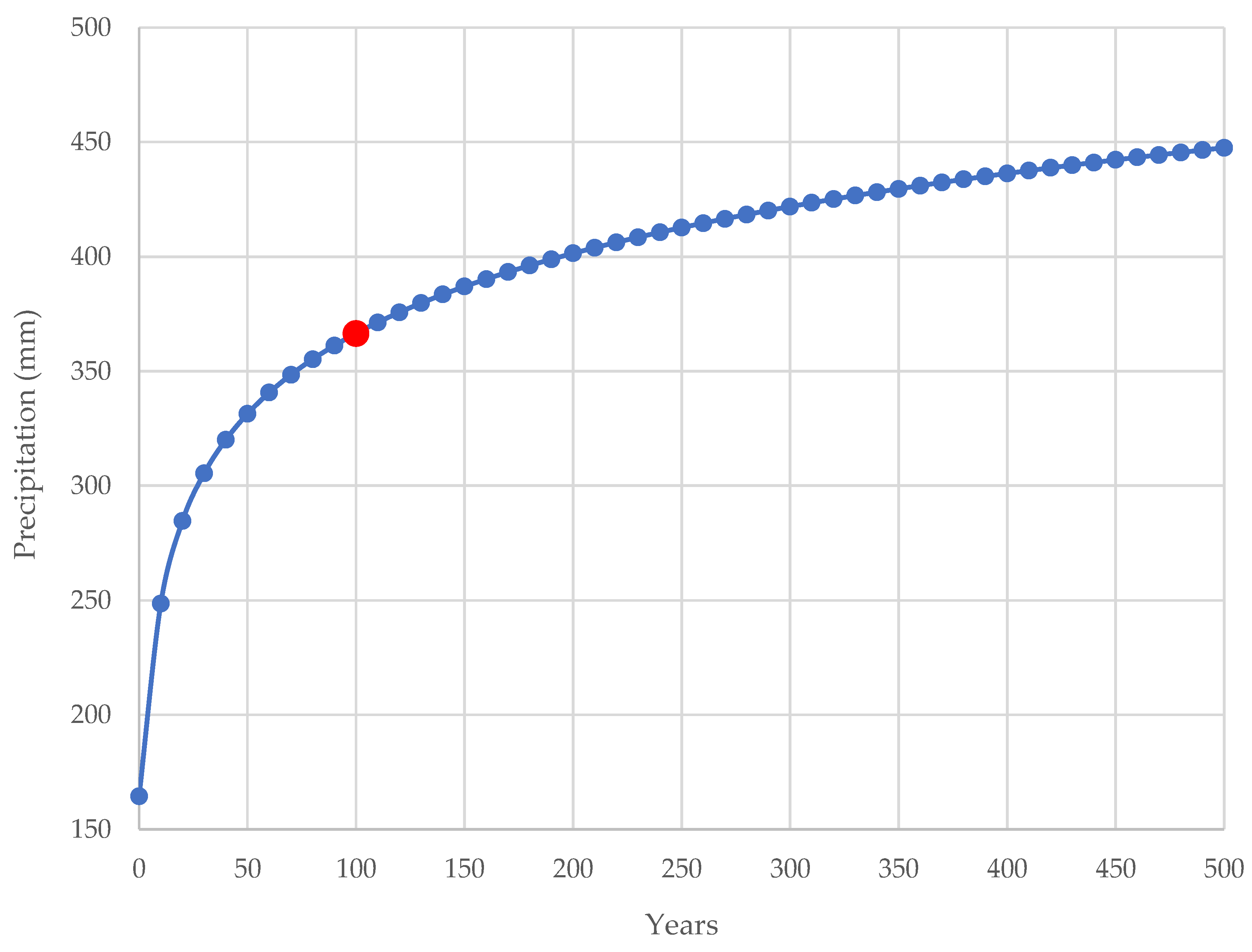
To conduct the precipitation analysis, it was necessary to resort to the data from the National Information System on Water Resources (SNIRH) [92], as it gathers data from a period of sixteen years. This data might be observed in Table A4 and Figure A2 (daily maximums). Thus, the Gumbel Distribution’s probabilistic processing allowed to obtain the values that are present on Table 2.
Subsequently, the peak flow rates were calculated using the formulas that were mentioned in the previous section (Equations (16), (17), (18), and (19)), as shown in Table 3; that was possible because the precipitation intensity for a recurrence time of 100 years had already been determined. Regarding the surface drainage coefficient, the value of 0.500 was utilized in the rational methodology (Table 4) since the region in which the study is focused can be classified as a peripheral area with commercial buildings. In other words, this value is associated with the parcel of water that usually is drained superficially, that is, half of the total precipitation.
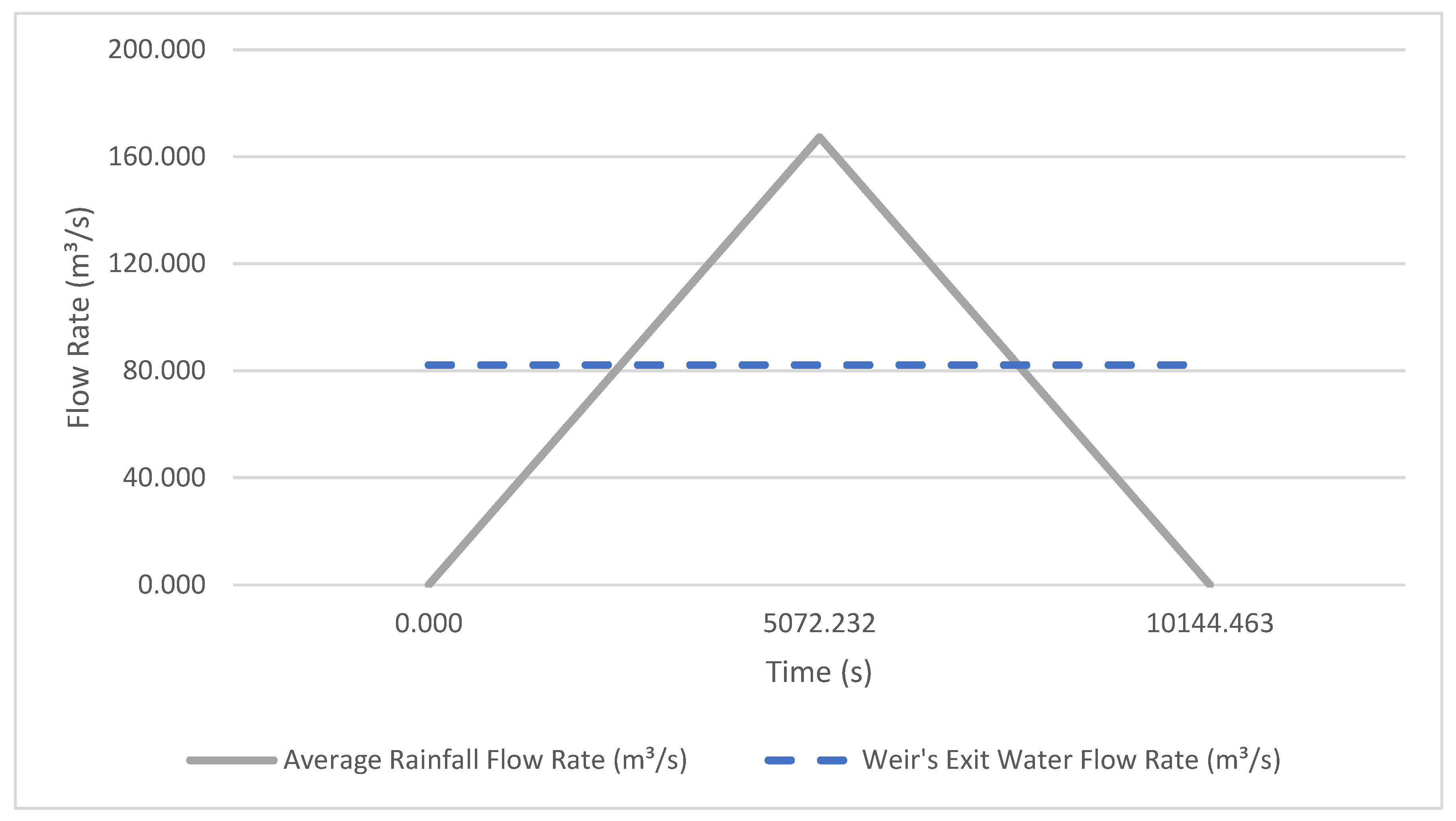
In terms of the river mouth’s capacity of drainage, it became necessary to resort to the Manning–Stickler equation to analyze whether a detention basin would be necessary in this case or not; the results gathered in this process can be found in Table 6. Nonetheless, it is relevant to point out that the bed and walls of the stream don’t have the same coefficients of roughness. Hence, the river mouth’s capacity of drainage was calculated through a weighted mean, considering the respective coefficients. Regarding the stream walls, since they present a satisfactory condition, n = 0.020; on the contrary, the stream bed is in a poorer condition, with a surface partly covered by vegetation and stones, which implicates n = 0.040 (Table A1). One other crucial aspect lies on the fact that the river mouth region has a remarkably low scope, which is usually associated with a deceleration of the water flow and a decrease in terms of the capacity of drainage. In order to simulate a critical scenario, it was considered a 0.01 m/m slope in the reference section.
Table 6 shows that both the Giandotti and the Mockus methodologies have exceeded the limit of 85% for the Fill Rate. So, it becomes necessary to define and implement flow control and mitigation measures in the river mouth area. Based on that assumption, the sizing of a detention basin was carried out, taking into account the methodologies referred above, while also considering the spatial and urban limitations associated with the existing infrastructures located in the stream surroundings.
Since the detention basin’s dimensions depend on the exceeding flow, a Cipolletti trapezoid spillway’s size was estimated, aiming to regularize and control the flow that will end up draining downstream. The characteristics of the spillway are listed in Table 7.
After that, both the Dutch Method and the STH were utilized to estimate the dimensions of the detention basins. These methodologies have as one of their most significant drawbacks the fact that they’re considered simplified approaches, as they don’t consider multiple factors; consequently, the use of these methodologies might end up resulting in an overestimation of this structure. Moreover, aiming to diminish the implementation works’ environmental and urban impacts, the detention basin’s height and width were fixed, as they were set considering the existing cross-section values. Thus, the structure’s length was the only geometric variable; nevertheless, this variable is limited by the main watercourse’s length.
After resorting to the previously mentioned methodologies, it became possible to obtain the results presented by Table 8.
Lastly, the alteration of the roughness coefficient was also considered since this measure would mitigate the flooding effects while simultaneously keeping the riverbed vegetation intact. So, Table 9 displays values that are related to the improvement of the conservation level of the riverbed, with the objective of enhancing its drainage capacity by reducing the friction that exists between the covering material and the fluid.
To sum up, the altered walls’ coefficients of roughness are related to the surface with concrete finishing in good condition, notwithstanding the fact that the riverbed maintains its stony and vegetated feature, although in good condition. Table 10 shows the values associated with these coefficients.

4. Discussion

Since this study’s main objective was to analyze the necessity to implement simplified mitigation measures in the watershed under study, the detention basin revealed to be an efficient measure to control the flow in the river mouth area; this strategy can be classified as a structural measure [86]. Indeed, the Fill Rate dropped to 59% as a result of this mitigation measure, while, initially, the Fill Rate was superior for any of these methodologies: Forte (82%), Rational (68%), Giandotti (144%), and Mockus (118%). Hence, it has been demonstrated that the detention basin enables the river mouth to operate significantly below the 85% limit that was previously mentioned. In addition to that, this study is in line with the analysis that was undertaken by the Regional Directorate for Territorial Ordering and Environment (DROTA), as Table 11 demonstrates, which is a positive indicator regarding this study’s level of accuracy.
One of the objectives of this study was to find mitigation measures that didn’t cause significant impacts, either in the waterway or in its surroundings. This occurs due to the fact that natural elements and values located in cities are key for the environmental recovery of an urban region [96]. Moreover, urban and natural systems are coexistent, which means that their type of management needs to be an integrated one – as it is a regional space requirement and has significant importance for a region’s sustainability [97,98]. If not, a disorganized urbanization process might lead to urban voids [99].
Therefore, the streams’ cross-section dimensions weren’t altered, resulting in length as the only dimensional variable. Considering that fact, the utilization of the Dutch Method originated in oversized results, as the total length of the detention basin surpassed the length that the main waterway possesses. As a result, it would be necessary to modify one of the other dimensions – height, and width. So, in this scenario, the Dutch Method can’t provide a satisfactory level of accuracy for the urban conditions that were imposed.
Regarding the STH method, it could be applied in this case because the detention basin’s total length is shorter in comparison with the main watercourse’s length.
In terms of the roughness coefficient alteration, the final decision was to preserve the riverbed’s stony and vegetated characteristics since the main focus would be enhancing its level of conservation. In addition to that, this decision was also based on the fact that removing the entirety of the sediments, vegetation, and stones located in the riverbed is a strategy that would involve multiple costs (monetary costs, time spent, etc.). As for the walls, frequent maintenance won’t be needed, due to the fact that wear by abrasion would take place in an alluvial channel that has a bigger tendency for draining high volumes of water, in addition to large granular sediments.
The alteration of the roughness coefficient, despite being considered a simple mitigation measure, had satisfactory effects (with the exception of Giandotti’s methodology), which enables the river mouth to avoid working above the filling limit. In fact, the STH method and the alteration of the coefficient of roughness can be adopted simultaneously, and that would lead to a detention basin with a reduced length and, therefore, with an optimized dimension.
Nonetheless, these methodologies are simplified in nature, that is, don’t take into account local specificities. This originates results with an excessive safety margin that will ultimately cause oversized structures.

5. Conclusions

This study’s main results point out the flood susceptibility of the Tabua (Ribeira Brava) watershed if an extreme precipitation event was to take place, as reported by DROTA in their Flood Risk Report. One of the most significant contributing factors for that is the presence of vegetation and stones on the stream bed’s surface, diminishing its runoff capacity. This also contributes to the deceleration of the water flow, which, ultimately, reduces the capacity of drainage; this can be verified especially in the areas with lower slopes – for instance, the river mouth. Indeed, the fact that the mouth’s capacity of drainage here analyzed was insufficient ended up being sustained by 2/4 of the utilized methodologies: Mockus and Giandotti.
In terms of the simplified mitigation measures that were proposed, the Dutch Method suggested a length for the detention basin that was superior to the main watercourse’s length; this led to the conclusion that this methodology couldn’t be applied in a scenario like this. In contrast, the Simplified Triangular Hydrograph Method enabled the implementation of this structure without modifying the stream’s width and/or height.
Lastly, the promotion of alterations regarding the roughness coefficient also generated positive effects regarding flood mitigation. This can be seen as even more satisfactory in the sense that this measure is relatively simple to implement.
As it is unfeasible to consider all the aspects that constitute a more accurate and complete study in this case, further analyses can be undertaken to complement or reinforce the results obtained. For instance, studies that focus on the capacity of drainage of the implemented urban hydraulic system, aiming to decrease the volume stored on the detention basins; analyses that consider the deposition of sediments, considering the main watercourse’s entrainment velocity [100]; monitoring of the level of deterioration presented by the walls of the artificial canal as a result of abrasion, and the estimation of the recommended time for maintenance (processes of desilting and silting); the impacts of the quality of the water discharged on the artificial water channel’s degradation process [101,102]; study of projections related with the growth of urban areas in the region here analyzed and whether that process will end up influencing the increase of the flow; analyses aiming to estimate the costs associated with the establishment of the mitigation strategies suggested by this analysis; studies on the impacts of the tide level in an artificial channel’s process of drainage and whether there’s a connection with the probability of occurring downstream floods or not; and studying the effects that this type of channels has regarding territorial planning – i.e., adaptation considering rural watersheds.
The results obtained in this study reinforce the conclusions that similar analyses – that also resorted to simulations and case study analysis as main drivers for scientific development – present [103,104].

Author Contributions

For research articles with several authors, the following statements should be used “Conceptualization, S.L., R.A., M.F. and L.G.; methodology, S.L.; software, S.L. and L.G.; validation, S.L. and L.G.; formal analysis, S.L. and L.G.; investigation, S.L.; resources, L.G.; data curation, S.L. and L.G.; writing—original draft preparation, S.L., R.A., M.F. and L.G.; writing—review and editing, S.L.; visualization, R.A., M.F. and L.G.; supervision, R.A., M.F. and L.G.; project administration, S.L.. All authors have read and agreed to the published version of the manuscript.”.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are openly available. Also, it is possible to contact one of the study authors.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Manning-Strickler roughness coefficients (Source: [94]).
Table A1. Manning-Strickler roughness coefficients (Source: [94]).
Channel Type and Description Very Good Good Regular Bad
Mortared stone masonry 0.017 0.020 0.025 0.030
Rigged stone masonry 0.013 0.014 0.015 0.017
Dry stone masonry 0.025 0.033 0.033 0.035
Brick masonry 0.012 0.013 0.015 0.017
Smooth metal gutters (semicircular) 0.011 0.012 0.013 0.016
Open channels in rock (irregular) 0.035 0.040 0.045 -
Channels with bottom on land and slope with stones 0.028 0.030 0.033 0.035
Channels with stony bed and vegetated slope 0.025 0.030 0.035 0.040
Channels with concrete coating 0.012 0.014 0.016 0.018
Earth channels (rectilinear and uniform) 0.017 0.020 0.023 0.025
Dredged canals 0.025 0.028 0.030 0.033
Clay conduits (drainage) 0.011 0.012 0.014 0.017
Vitrified clay conduits (sewage) 0.011 0.013 0.015 0.017
Flattened wooden plank conduits 0.010 0.012 0.013 0.014
Gabion 0.022 0.030 0.035 -
Cement mortar surfaces 0.011 0.012 0.013 0.015
Smoothed cement surfaces 0.010 0.011 0.012 0.013
Cast iron coated tube with tar 0.011 0.012 0.013 -
Uncoated cast iron pipe 0.012 0.013 0.014 0.015
Brass or glass tubes 0.009 0.010 0.012 0.013
Concrete pipes 0.012 0.013 0.015 0.016
Galvanized iron pipes 0.013 0.014 0.015 0.017
Rectilinear and uniform clean streams and rivers 0.025 0.028 0.030 0.033
Streams and rivers cleared rectilinear and uniform with stones and vegetation 0.030 0.033 0.035 0.040
Streams and rivers cleared rectilinear and uniform with intricacies and wells 0.035 0.040 0.045 0.050
Spread margins with little vegetation 0.050 0.060 0.070 0.080
Spread margins with lots of vegetation 0.075 0.100 0.125 0.150
Table A2. Surface runoff coefficients (Source: [93]).
Table A2. Surface runoff coefficients (Source: [93]).
Urban Areas
Occupation of the Land Coefficient of Surface Runoff
Green Areas Lawns in sandy soils 0.050–0.200
Lawns on heavy soils 0.150–0.350
Parks and cemeteries 0.100–0.350
Sports fields 0.200–0.350
Commercial Areas City district 0.700–0.950
Periphery 0.500–0.700
Residential Areas Town-center villas 0.300–0.500
Villas on the outskirts 0.250–0.400
Apartment buildings 0.500–0.700
Industrial Areas Dispersed industry 0.500–0.800
Concentrated industry 0.600–0.900
Railways 0.200–0.400
Streets and Roads Paved 0.700–0.900
Concrete 0.800–0.950
In brick 0.700–0.850
Table A3. Giandotti reduction coefficients (Source: [94]).
Table A3. Giandotti reduction coefficients (Source: [94]).
A (km2) λ “C” Equivalent
<300 0.346 1.250
300–500 0.277 1.000
500–1000 0.197 0.710
1000–8000 0.100 0.360
8000–20,000 0.076 0.270
20,000–70,000 0.055 0.200
Table A4. Precipitation historical data (Source: [92]).
Table A4. Precipitation historical data (Source: [92]).
n Year (mm)
1 1998/1999 170.000
2 1999/2000 180.700
3 2000/2001 135.000
4 2001/2002 190.000
5 2002/2003 195.400
6 2003/2004 141.000
7 2004/2005 103.200
8 2005/2006 91.400
9 2006/2007 141.400
10 2007/2008 104.600
11 2008/2009 155.000
12 2009/2010 257.800
13 2010/2011 148.400
14 2011/2012 288.600
15 2012/2013 267.400
16 2013/2014 61.200
Preprints 76174 g0a1
Figure A1. Ternary phase diagram.
Figure A1. Ternary phase diagram.
Preprints 76174 g0a1
Preprints 76174 g0a2
Figure A2. Expected rainfall for Tabua (Ribeira Brava) watershed.
Figure A2. Expected rainfall for Tabua (Ribeira Brava) watershed.
Preprints 76174 g0a2

References

  1. Evstigneev, V.P.; Naumova, V.A.; Voronin, D.Y.; Kuznetsov, P.N.; Korsakova, S.P. Severe Precipitation Phenomena in Crimea in Relation to Atmospheric Circulation. Atmosphere 2022, 13, 1712. [Google Scholar] [CrossRef]
  2. Coumou, D.; Robinson, A. Historic and Future Increase in the Global Land Area Affected by Monthly Heat Extremes. Environ. Res. Lett. 2013, 8, 034018. [Google Scholar] [CrossRef]
  3. Diaz, J.H. Global Climate Changes, Natural Disasters, and Travel Health Risks. J. Travel Med. 2006, 13, 361–372. [Google Scholar] [CrossRef] [PubMed]
  4. Ighile, E.H.; Shirakawa, H.; Tanikawa, H. Application of GIS and Machine Learning to Predict Flood Areas in Nigeria. Sustainability 2022, 14, 5039. [Google Scholar] [CrossRef]
  5. Pinna, M.S.; Loi, M.C.; Calderisi, G.; Fenu, G. Extremes Rainfall Events on Riparian Flora and Vegetation in the Mediterranean Basin: A Challenging but Completely Unexplored Theme. Water 2022, 14, 817. [Google Scholar] [CrossRef]
  6. Das, S.; Kamruzzaman, M.; Islam, A.R.M.T.; Zhu, D.; Kumar, A. Comparison of Future Changes in Frequency of Climate Extremes between Coastal and Inland Locations of Bengal Delta Based on CMIP6 Climate Models. Atmosphere 2022, 13, 1747. [Google Scholar] [CrossRef]
  7. Fowler, H.J.; Ali, H.; Allan, R.P.; Ban, N.; Barbero, R.; Berg, P.; Blenkinsop, S.; Cabi, N.S.; Chan, S.; Dale, M.; et al. Towards Advancing Scientific Knowledge of Climate Change Impacts on Short-Duration Rainfall Extremes. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2021, 379, 20190542. [Google Scholar] [CrossRef]
  8. Tang, B.; Hu, W.; Duan, A. Future Projection of Extreme Precipitation Indices over the Indochina Peninsula and South China in CMIP6 Models. J. Clim. 2021, 34, 8793–8811. [Google Scholar] [CrossRef]
  9. Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes Under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
  10. Frías, M.D.; Mínguez, R.; Gutiérrez, J.M.; Méndez, F.J. Future Regional Projections of Extreme Temperatures in Europe: A Nonstationary Seasonal Approach. Clim. Change 2012, 113, 371–392. [Google Scholar] [CrossRef]
  11. Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Wehner, M. Changes in Temperature and Precipitation Extremes in the CMIP5 Ensemble. Clim. Change 2013, 119, 345–357. [Google Scholar] [CrossRef]
  12. Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the Extremes. Clim. Change 2006, 79, 185–211. [Google Scholar] [CrossRef]
  13. Mishra, V.; Ganguly, A.R.; Nijssen, B.; Lettenmaier, D.P. Changes in Observed Climate Extremes in Global Urban Areas. Environ. Res. Lett. 2015, 10, 024005. [Google Scholar] [CrossRef]
  14. Hodnebrog, Ø.; Marelle, L.; Alterskjær, K.; Wood, R.R.; Ludwig, R.; Fischer, E.M.; Richardson, T.B.; Forster, P.M.; Sillmann, J.; Myhre, G. Intensification of Summer Precipitation with Shorter Time-Scales in Europe. Environ. Res. Lett. 2019, 14, 124050. [Google Scholar] [CrossRef]
  15. Chen, Y.; Liao, Z.; Shi, Y.; Li, P.; Zhai, P. Greater Flash Flood Risks From Hourly Precipitation Extremes Preconditioned by Heatwaves in the Yangtze River Valley. Geophys. Res. Lett. 2022, 49, e2022GL099485. [Google Scholar] [CrossRef]
  16. Hemmati, M.; Ellingwood, B.R.; Mahmoud, H.N. The Role of Urban Growth in Resilience of Communities Under Flood Risk. Earths Future 2020, 8, e2019EF001382. [Google Scholar] [CrossRef] [PubMed]
  17. Nguyen, H.D.; Fox, D.; Dang, D.K.; Pham, L.T.; Viet Du, Q.V.; Nguyen, T.H.T.; Dang, T.N.; Tran, V.T.; Vu, P.L.; Nguyen, Q.-H.; et al. Predicting Future Urban Flood Risk Using Land Change and Hydraulic Modeling in a River Watershed in the Central Province of Vietnam. Remote Sens. 2021, 13, 262. [Google Scholar] [CrossRef]
  18. Wu, Z.; Xue, W.; Xu, H.; Yan, D.; Wang, H.; Qi, W. Urban Flood Risk Assessment in Zhengzhou, China, Based on a D-Number-Improved Analytic Hierarchy Process and a Self-Organizing Map Algorithm. Remote Sens. 2022, 14, 4777. [Google Scholar] [CrossRef]
  19. de Carvalho, R.C.F.; Moreira, T.R.; de Souza, K.B.; Costa, G.A.; Zanetti, S.S.; Barbosa, K.V.; Filho, C.B.C.; Miranda, M.R.; Guerra Filho, P.A.; dos Santos, A.R.; et al. GIS-Based Approach Applied to Study of Seasonal Rainfall Influence over Flood Vulnerability. Water 2022, 14, 3731. [Google Scholar] [CrossRef]
  20. Lousada, S.; Cabezas, J.; Castanho, R.A.; Gómez, J.M.N. Hydraulic Planning in Insular Urban Territories: The Case of Madeira Island—Ribeira Brava. Water 2021, 13, 2951. [Google Scholar] [CrossRef]
  21. Lousada, S.; Gonçalves, L.; Atmaca, A. Hydraulic Planning in Insular Urban Territories: The Case of Madeira Island—São Vicente. Water 2022, 14, 112. [Google Scholar] [CrossRef]
  22. Lousada, S.; Castanho, R.A. GIS-Based Assessment of Morphological and Hydrological Parameters of Ribeira Dos Socorridos and Ribeira Do Vigario Basins, Madeira Island, Portugal. Curr. World Environ. 2021, 16, 408–426. [Google Scholar] [CrossRef]
  23. Lousada, S.A.N.; Moura, A.D.S.; Gonçalves, L.B. Numerical modelling of the flow rate in artificial water channels: application to Ribeira Brava´s stream. Rev. Bras. Planej. E Desenvolv. 2020, 9, 39–59. [Google Scholar] [CrossRef]
  24. Berndtsson, R.; Becker, P.; Persson, A.; Aspegren, H.; Haghighatafshar, S.; Jönsson, K.; Larsson, R.; Mobini, S.; Mottaghi, M.; Nilsson, J.; et al. Drivers of Changing Urban Flood Risk: A Framework for Action. J. Environ. Manage. 2019, 240, 47–56. [Google Scholar] [CrossRef]
  25. Danso-Amoako, E.; Scholz, M.; Kalimeris, N.; Yang, Q.; Shao, J. Predicting Dam Failure Risk for Sustainable Flood Retention Basins: A Generic Case Study for the Wider Greater Manchester Area. Comput. Environ. Urban Syst. 2012, 36, 423–433. [Google Scholar] [CrossRef]
  26. Damage and Casualties Modelling as Part of a Vulnerability Assessment for Tsunami Hazards: A Case Study from Aceh, Indonesia - Marchand - 2009 - Journal of Flood Risk Management - Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/10.1111/j.1753-318X.2009.01027.x (accessed on 1 March 2023).
  27. Pradhan, B.; Youssef, A.m. A 100-Year Maximum Flood Susceptibility Mapping Using Integrated Hydrological and Hydrodynamic Models: Kelantan River Corridor, Malaysia. J. Flood Risk Manag. 2011, 4, 189–202. [Google Scholar] [CrossRef]
  28. Dawod, G.M.; Mirza, M.N.; Al-Ghamdi, K.A. GIS-Based Estimation of Flood Hazard Impacts on Road Network in Makkah City, Saudi Arabia. Environ. Earth Sci. 2012, 67, 2205–2215. [Google Scholar] [CrossRef]
  29. Robi, M.A.; Abebe, A.; Pingale, S.M. Flood Hazard Mapping under a Climate Change Scenario in a Ribb Catchment of Blue Nile River Basin, Ethiopia. Appl. Geomat. 2019, 11, 147–160. [Google Scholar] [CrossRef]
  30. Francesch-Huidobro, M.; Dabrowski, M.; Tai, Y.; Chan, F.; Stead, D. Governance Challenges of Flood-Prone Delta Cities: Integrating Flood Risk Management and Climate Change in Spatial Planning. Prog. Plan. 2017, 114, 1–27. [Google Scholar] [CrossRef]
  31. Carter, J.G. Urban Climate Change Adaptation: Exploring the Implications of Future Land Cover Scenarios. Cities 2018, 77, 73–80. [Google Scholar] [CrossRef]
  32. Stoleriu, C.C.; Urzica, A.; Mihu-Pintilie, A. Improving Flood Risk Map Accuracy Using High-Density LiDAR Data and the HEC-RAS River Analysis System: A Case Study from North-Eastern Romania. J. Flood Risk Manag. 2020, 13, e12572. [Google Scholar] [CrossRef]
  33. Assessment of Flash Flood Susceptibility Potential in Moldavian Plain (Romania) - Iosub - 2020 - Journal of Flood Risk Management - Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/10.1111/jfr3.12588 (accessed on 1 March 2023).
  34. Huţanu, E.; Mihu-Pintilie, A.; Urzica, A.; Paveluc, L.E.; Stoleriu, C.C.; Grozavu, A. Using 1D HEC-RAS Modeling and LiDAR Data to Improve Flood Hazard Maps Accuracy: A Case Study from Jijia Floodplain (NE Romania). Water 2020, 12, 1624. [Google Scholar] [CrossRef]
  35. Güneralp, B.; Seto, K.C. Futures of Global Urban Expansion: Uncertainties and Implications for Biodiversity Conservation. Environ. Res. Lett. 2013, 8, 014025. [Google Scholar] [CrossRef]
  36. Güneralp, B.; Güneralp, İ.; Liu, Y. Changing Global Patterns of Urban Exposure to Flood and Drought Hazards. Glob. Environ. Change 2015, 31, 217–225. [Google Scholar] [CrossRef]
  37. Ran, J.; Nedovic-Budic, Z. Integrating Spatial Planning and Flood Risk Management: A New Conceptual Framework for the Spatially Integrated Policy Infrastructure. Comput. Environ. Urban Syst. 2016, 57, 68–79. [Google Scholar] [CrossRef]
  38. Lousada, S.; Cabezas, J.; Castanho, R.A.; Gómez, J.M.N. Land-Use Changes in Insular Urban Territories: A Retrospective Analysis from 1990 to 2018. The Case of Madeira Island—Ribeira Brava. Sustainability 2022, 14, 16839. [Google Scholar] [CrossRef]
  39. Xu, C.; Yang, J.; Wang, L. Application of Remote-Sensing-Based Hydraulic Model and Hydrological Model in Flood Simulation. Sustainability 2022, 14, 8576. [Google Scholar] [CrossRef]
  40. Dottori, F.; Szewczyk, W.; Ciscar, J.-C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Author Correction: Increased Human and Economic Losses from River Flooding with Anthropogenic Warming. Nat. Clim. Change 2018, 8, 1021–1021. [Google Scholar] [CrossRef]
  41. Rehman, S.; Sahana, M.; Hong, H.; Sajjad, H.; Ahmed, B.B. A Systematic Review on Approaches and Methods Used for Flood Vulnerability Assessment: Framework for Future Research. Nat. Hazards 2019, 96, 975–998. [Google Scholar] [CrossRef]
  42. Mateo-Garcia, G.; Veitch-Michaelis, J.; Smith, L.; Oprea, S.V.; Schumann, G.; Gal, Y.; Baydin, A.G.; Backes, D. Towards Global Flood Mapping Onboard Low Cost Satellites with Machine Learning. Sci. Rep. 2021, 11, 7249. [Google Scholar] [CrossRef] [PubMed]
  43. Lin, K.; Chen, H.; Xu, C.-Y.; Yan, P.; Lan, T.; Liu, Z.; Dong, C. Assessment of Flash Flood Risk Based on Improved Analytic Hierarchy Process Method and Integrated Maximum Likelihood Clustering Algorithm. J. Hydrol. 2020, 584, 124696. [Google Scholar] [CrossRef]
  44. Yang, W.; Xu, K.; Lian, J.; Bin, L.; Ma, C. Multiple Flood Vulnerability Assessment Approach Based on Fuzzy Comprehensive Evaluation Method and Coordinated Development Degree Model. J. Environ. Manage. 2018, 213, 440–450. [Google Scholar] [CrossRef] [PubMed]
  45. Koks, E.E.; Jongman, B.; Husby, T.G.; Botzen, W.J.W. Combining Hazard, Exposure and Social Vulnerability to Provide Lessons for Flood Risk Management. Environ. Sci. Policy 2015, 47, 42–52. [Google Scholar] [CrossRef]
  46. Flood Maps and Their Potential Role in Local Spatial Planning: A Case Study from Slovakia | Water Policy | IWA Publishing. Available online: https://iwaponline.com/wp/article/20/5/1042/41469/Flood-maps-and-their-potential-role-in-local (accessed on 2 March 2023).
  47. Meyer, V.; Scheuer, S.; Haase, D. A Multicriteria Approach for Flood Risk Mapping Exemplified at the Mulde River, Germany. Nat. Hazards 2009, 48, 17–39. [Google Scholar] [CrossRef]
  48. Meyer, V.; Haase, D.; Scheuer, S. Flood Risk Assessment in European River Basins—Concept, Methods, and Challenges Exemplified at the Mulde River. Integr. Environ. Assess. Manag. 2009, 5, 17–26. [Google Scholar] [CrossRef]
  49. Luu, C.; Von Meding, J.; Kanjanabootra, S. Assessing Flood Hazard Using Flood Marks and Analytic Hierarchy Process Approach: A Case Study for the 2013 Flood Event in Quang Nam, Vietnam. Nat. Hazards 2018, 90, 1031–1050. [Google Scholar] [CrossRef]
  50. Chau, V.N.; Holland, J.; Cassells, S.; Tuohy, M. Using GIS to Map Impacts upon Agriculture from Extreme Floods in Vietnam. Appl. Geogr. 2013, 41, 65–74. [Google Scholar] [CrossRef]
  51. Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood Inundation Modelling: A Review of Methods, Recent Advances and Uncertainty Analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
  52. Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking Urban Flood Models of Varying Complexity and Scale Using High Resolution Terrestrial LiDAR Data. Phys. Chem. Earth Parts ABC 2011, 36, 281–291. [Google Scholar] [CrossRef]
  53. Talukdar, S.; Singha, P.; Mahato, S.; Shahfahad Pal, S.; Liou, Y.-A.; Rahman, A. Land-Use Land-Cover Classification by Machine Learning Classifiers for Satellite Observations—A Review. Remote Sens. 2020, 12, 1135. [Google Scholar] [CrossRef]
  54. Akodéwou, A.; Oszwald, J.; Saïdi, S.; Gazull, L.; Akpavi, S.; Akpagana, K.; Gond, V. Land Use and Land Cover Dynamics Analysis of the Togodo Protected Area and Its Surroundings in Southeastern Togo, West Africa. Sustainability 2020, 12, 5439. [Google Scholar] [CrossRef]
  55. Wittke, S.; Yu, X.; Karjalainen, M.; Hyyppä, J.; Puttonen, E. Comparison of Two-Dimensional Multitemporal Sentinel-2 Data with Three-Dimensional Remote Sensing Data Sources for Forest Inventory Parameter Estimation over a Boreal Forest. Int. J. Appl. Earth Obs. Geoinformation 2019, 76, 167–178. [Google Scholar] [CrossRef]
  56. de Moel, H.; Jongman, B.; Kreibich, H.; Merz, B.; Penning-Rowsell, E.; Ward, P.J. Flood Risk Assessments at Different Spatial Scales. Mitig. Adapt. Strateg. Glob. Change 2015, 20, 865–890. [Google Scholar] [CrossRef]
  57. Mishra, K.; Sinha, R. Flood Risk Assessment in the Kosi Megafan Using Multi-Criteria Decision Analysis: A Hydro-Geomorphic Approach. Geomorphology 2020, 350, 106861. [Google Scholar] [CrossRef]
  58. Luu, C.; Tran, H.X.; Pham, B.T.; Al-Ansari, N.; Tran, T.Q.; Duong, N.Q.; Dao, N.H.; Nguyen, L.P.; Nguyen, H.D.; Thu Ta, H.; et al. Framework of Spatial Flood Risk Assessment for a Case Study in Quang Binh Province, Vietnam. Sustainability 2020, 12, 3058. [Google Scholar] [CrossRef]
  59. Dang, N.M.; Babel, M.S.; Luong, H.T. Evaluation of Food Risk Parameters in the Day River Flood Diversion Area, Red River Delta, Vietnam. Nat. Hazards 2011, 56, 169–194. [Google Scholar] [CrossRef]
  60. Kron, W. Flood Risk = Hazard • Values • Vulnerability. Water Int. 2005, 30, 58–68. [Google Scholar] [CrossRef]
  61. Socioeconomic Scenarios and Flood Damage Assessment Methodologies for the Taihu Basin, China.
  62. Mechler, R.; Bouwer, L.M. Understanding Trends and Projections of Disaster Losses and Climate Change: Is Vulnerability the Missing Link? Clim. Change 2015, 133, 23–35. [Google Scholar] [CrossRef]
  63. Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global Flood Risk under Climate Change. Nat. Clim. Change 2013, 3, 816–821. [Google Scholar] [CrossRef]
  64. Gambardella, C.; Parente, R.; Scotto di Santolo, A.; Ciaburro, G. New Digital Field of Drawing and Survey for the Automatic Identification of Debris Accumulation in Flooded Areas. Sustainability 2023, 15, 479. [Google Scholar] [CrossRef]
  65. Wang, P.; Li, Y.; Yu, P.; Zhang, Y. The Analysis of Urban Flood Risk Propagation Based on the Modified Susceptible Infected Recovered Model. J. Hydrol. 2021, 603, 127121. [Google Scholar] [CrossRef]
  66. Huang, H.; Chen, X.; Zhu, Z.; Xie, Y.; Liu, L.; Wang, X.; Wang, X.; Liu, K. The Changing Pattern of Urban Flooding in Guangzhou, China. Sci. Total Environ. 2018, 622–623, 394–401. [Google Scholar] [CrossRef]
  67. Dhiman, R.; VishnuRadhan, R.; Eldho, T.I.; Inamdar, A. Flood Risk and Adaptation in Indian Coastal Cities: Recent Scenarios. Appl. Water Sci. 2018, 9, 5. [Google Scholar] [CrossRef]
  68. Zhao, L.; Zhang, T.; Fu, J.; Li, J.; Cao, Z.; Feng, P. Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data. Remote Sens. 2021, 13, 4381. [Google Scholar] [CrossRef]
  69. Zhou, Y.; Shen, D.; Huang, N.; Guo, Y.; Zhang, T.; Zhang, Y. Urban Flood Risk Assessment Using Storm Characteristic Parameters Sensitive to Catchment-Specific Drainage System. Sci. Total Environ. 2019, 659, 1362–1369. [Google Scholar] [CrossRef] [PubMed]
  70. Cai, T.; Li, X.; Ding, X.; Wang, J.; Zhan, J. Flood Risk Assessment Based on Hydrodynamic Model and Fuzzy Comprehensive Evaluation with GIS Technique. Int. J. Disaster Risk Reduct. 2019, 35, 101077. [Google Scholar] [CrossRef]
  71. Costache, R.; Trung Tin, T.; Arabameri, A.; Crăciun, A.; Ajin, R.S.; Costache, I.; Reza Md. Towfiqul Islam, A.; Abba, S.I.; Sahana, M.; Avand, M.; et al. Flash-Flood Hazard Using Deep Learning Based on H2O R Package and Fuzzy-Multicriteria Decision-Making Analysis. J. Hydrol. 2022, 609, 127747. [Google Scholar] [CrossRef]
  72. Dhakal, K.P.; Chevalier, L.R. Urban Stormwater Governance: The Need for a Paradigm Shift. Environ. Manage. 2016, 57, 1112–1124. [Google Scholar] [CrossRef] [PubMed]
  73. Omitaomu, O.A.; Kotikot, S.M.; Parish, E.S. Planning Green Infrastructure Placement Based on Projected Precipitation Data. J. Environ. Manage. 2021, 279, 111718. [Google Scholar] [CrossRef]
  74. Livin’ Large with Levees: Lessons Learned and Lost | Natural Hazards Review | Vol 9, No 3. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%291527-6988%282008%299%3A3%28150%29 (accessed on 1 March 2023).
  75. Ahern, J. From Fail-Safe to Safe-to-Fail: Sustainability and Resilience in the New Urban World. Landsc. Urban Plan. 2011, 100, 341–343. [Google Scholar] [CrossRef]
  76. Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and Implementation of Low Impact Development – A Review. Sci. Total Environ. 2017, 607–608, 413–432. [Google Scholar] [CrossRef]
  77. Li, L.; Collins, A.M.; Cheshmehzangi, A.; Chan, F.K.S. Identifying Enablers and Barriers to the Implementation of the Green Infrastructure for Urban Flood Management: A Comparative Analysis of the UK and China. Urban For. Urban Green. 2020, 54, 126770. [Google Scholar] [CrossRef]
  78. Duan, Y.; Gao, Y.G.; Zhang, Y.; Li, H.; Li, Z.; Zhou, Z.; Tian, G.; Lei, Y. “The 20 July 2021 Major Flood Event” in Greater Zhengzhou, China: A Case Study of Flooding Severity and Landscape Characteristics. Land 2022, 11, 1921. [Google Scholar] [CrossRef]
  79. Nguyen, T.T.; Ngo, H.H.; Guo, W.; Wang, X.C.; Ren, N.; Li, G.; Ding, J.; Liang, H. Implementation of a Specific Urban Water Management - Sponge City. Sci. Total Environ. 2019, 652, 147–162. [Google Scholar] [CrossRef]
  80. Urban Adaptation in Europe — European Environment Agency. Available online: https://www.eea.europa.eu/publications/urban-adaptation-in-europe (accessed on 1 March 2023).
  81. Leone, A.; Grassini, L.; Balena, P. Urban Planning and Sustainable Storm Water Management: Gaps and Potential for Integration for Climate Adaptation Strategies. Sustainability 2022, 14, 16870. [Google Scholar] [CrossRef]
  82. Pelorosso, R.; Leone, A.; Boccia, L. Land Cover and Land Use Change in the Italian Central Apennines: A Comparison of Assessment Methods. Appl. Geogr. 2009, 29, 35–48. [Google Scholar] [CrossRef]
  83. Tabua. Wikipédia Enciclopédia Livre 2021.
  84. Tucci, C.E.M. Gestão de Águas Pluviais Urbanas. 1993, 270.
  85. Gonçalves, L.B.; Lousada, S.A.N. ANÁLISE PROBABILÍSTICA DE CHEIAS E O USO DE BACIAS DE DETENÇÃO COMO MEDIDA MITIGADORA: APLICAÇÃO À BACIA DE SANTA LUZIA. 2020, 16.
  86. Lousada, S.A.N.; Camacho, R.F. Hidrologia, recursos hídricos e ambiente: aulas teóricas; Universidade da Madeira, 2018; Vol. 1; ISBN 978-989-8805-33-1.
  87. Geomorfologia - Antonio Christofoletti.Pdf. Available online: https://www.academia.edu/42262596/Geomorfologia_Antonio_Christofoletti (accessed on 28 March 2022).
  88. Tucci, C.E.M.; Porto, R.L.L.; Barros, M.T.L. de Drenagem urbana. 1995.
  89. Vieira, I.; Barreto, V.; Figueira, C.; Lousada, S.; Prada, S. The Use of Detention Basins to Reduce Flash Flood Hazard in Small and Steep Volcanic Watersheds – a Simulation from Madeira Island. J. Flood Risk Manag. 2018, 11, S930–S942. [Google Scholar] [CrossRef]
  90. David, L.M.; de Carvalho, R.F. BACIAS DE RETENÇÃO PARA CONTROLO DE CHEIAS: Reflexão sobre métodos de dimensionamento. 2008, 19.
  91. Beck, H.E.; Bruijnzeel, L.A.; van Dijk, A.I.J.M.; McVicar, T.R.; Scatena, F.N.; Schellekens, J. The Impact of Forest Regeneration on Streamflow in 12 Mesoscale Humid Tropical Catchments. Hydrol. Earth Syst. Sci. 2013, 17, 2613–2635. [Google Scholar] [CrossRef]
  92. SNIRH > Dados de Base. Available online: https://snirh.apambiente.pt/index.php?idMain=2&idItem=1&objCover=920123704&objSite=920685506 (accessed on 6 March 2023).
  93. Ven-Te Chow Handbook of Applied Hydrology; McGraw-Hill, 1964;
  94. Gonçalves, J.A.V. Caracterização do coeficiente de rugosidade e seu efeito no escoamento em canais naturais: simulação e modelação (à escala) no laboratório de hidráulica: aplicação às ribeiras do Funchal. masterThesis, 2017.
  95. Plano de Gestão de Riscos de Inundação Da RAM - PGRI-RAM – Google Drive. Available online: https://drive.google.com/drive/folders/0BxPHHom7Ioe6bUQybkdoY2RvSVE?resourcekey=0-YYBZnl-ByzCMyDd6INwQUg (accessed on 6 March 2023).
  96. Castanho, R.A. EVOLUCIÓN DEL PROCEDIMIENTO DE PLANEAMIENTO URBANO EN LA PENÍNSULA IBÉRICA Y SUS HUELLAS EN EL PAISAJE URBANO. RETOS DE FUTURO. Rev. Monfrague Desarro. Resiliente 2017.
  97. Urbanismo e Território – As Políticas Públicas | Edições Sílabo.
  98. Loures, L. Planning and Design in Postindustrial Land Transformation: East Bank Arade River, Lagoa - Case Study. 2011.
  99. Alexandre Castanho, R.; Lousada, S.; Manuel Naranjo Gómez, J.; Escórcio, P.; Cabezas, J.; Fernández-Pozo, L.; Loures, L. Dynamics of the Land Use Changes and the Associated Barriers and Opportunities for Sustainable Development on Peripheral and Insular Territories: The Madeira Island (Portugal). In Land Use - Assessing the Past, Envisioning the Future; Carlos Loures, L., Ed.; IntechOpen, 2019 ISBN 978-1-78985-703-0.
  100. Yu, B.Y.; Wu, P.; Sui, J.; Ni, J.; Whitcombe, T. Variation of Runoff and Sediment Transport in the Huai River €“ A Case Study. J. Environ. Inform. 2020, 35, 138–147. [Google Scholar] [CrossRef]
  101. Shrestha, N.K.; Wang, J. Water Quality Management of a Cold Climate Region Watershed in Changing Climate. J. Environ. Inform. 2019, 35, 56–80. [Google Scholar] [CrossRef]
  102. Li, Z.; Li, J.J.; Shi, X.P. A Two-Stage Multisite and Multivariate Weather Generator. J. Environ. Inform. 2019, 35, 148–159. [Google Scholar] [CrossRef]
  103. Vargues, P.; Loures, L. Using Geographic Information Systems in Visual and Aesthetic Analysis: The Case Study of a Golf Course in Algarve. WSEAS Trans. Environ. Dev. 2008, 4. [Google Scholar]
  104. Nunes, J.R.; Ramos-Miras, J.; Lopez-Piñeiro, A.; Loures, L.; Gil, C.; Coelho, J.; Loures, A. Concentrations of Available Heavy Metals in Mediterranean Agricultural Soils and Their Relation with Some Soil Selected Properties: A Case Study in Typical Mediterranean Soils. Sustainability 2014, 6, 9124–9138. [Google Scholar] [CrossRef]
Preprints 76174 g001
Figure 1. The Tabua (Ribeira Brava) watershed. (Source: Authors by ESRI ArcGIS, 2020).
Figure 1. The Tabua (Ribeira Brava) watershed. (Source: Authors by ESRI ArcGIS, 2020).
Preprints 76174 g001
Preprints 76174 g002aPreprints 76174 g002b
Figure 2. Observation of the study area - state of conservation of Tabua (Ribeira Brava) main watercourse river mouth (from east to river mouth) (source: authors).
Figure 2. Observation of the study area - state of conservation of Tabua (Ribeira Brava) main watercourse river mouth (from east to river mouth) (source: authors).
Preprints 76174 g002aPreprints 76174 g002b
Preprints 76174 g003
Figure 3. Organogram of the adopted methodology.
Figure 3. Organogram of the adopted methodology.
Preprints 76174 g003
Preprints 76174 g004
Figure 4. (A) Dutch method; (B) STH method (Source: [27]).
Figure 4. (A) Dutch method; (B) STH method (Source: [27]).
Preprints 76174 g004
Preprints 76174 g005
Figure 5. Hypsometric map—DEM file (Source: Authors by ESRI ArcGIS, 2020).
Figure 5. Hypsometric map—DEM file (Source: Authors by ESRI ArcGIS, 2020).
Preprints 76174 g005
Preprints 76174 g006
Figure 6. Strahler classification (Source: Authors by ESRI ArcGIS, 2020).
Figure 6. Strahler classification (Source: Authors by ESRI ArcGIS, 2020).
Preprints 76174 g006
Table 1. Parameters calculated or extracted from ArcGIS.
Table 1. Parameters calculated or extracted from ArcGIS.
Parameter Measurement Unit Result
Area km2 8.809
Perimeter km 22.530
Main Watercourse’s Length km 9.272
Main Watercourse’s Maximum Height m 1547.650
Main Watercourse’s Minimum Height m 0.000
Average Time of Concentration hours 1.409
Gravelius Coefficient of Compactness dimensionless 2.141
Elongation Factor dimensionless 12.334
Shape Factor dimensionless 0.151
Number of Watercourses units 335.000
Average Bifurcation Ratio dimensionless 4.172
Strahler Classification dimensionless 4.000
Table 2. Precipitation parameters.
Table 2. Precipitation parameters.
Parameter Symbol Measurement Unit Result
Average Annual Precipitation PM mm 164.443
Standard Deviation S′ mm 64.424
Frequency Factor KT dimensionless 3.136
Coefficient of Time Distribution k dimensionless 0.592
Maximum Annual Daily Precipitation PEST mm 366.521
Precipitation Intensity I mm/h 91.920
Table 3. Peak flow rate.
Table 3. Peak flow rate.
Methodology Flow (m3/s)
Forti 115.787
Rational 95.355
Giandotti 201.727
Mockus 165.218
Table 4. Surface drainage coefficient adopted (Source: [93]).
Table 4. Surface drainage coefficient adopted (Source: [93]).
Urban Areas
Occupation of the Land Coefficient of Surface Drainage
Commercial Area City Center 0.700–0.950
Peripheral Areas 0.500–0.700
Table 5. Adopted Giandotti’s reduction coefficient (Source: [94]).
Table 5. Adopted Giandotti’s reduction coefficient (Source: [94]).
Area (km2) λ Equivalent “C”
<300 0.346 1.250
Table 6. Assessment of the need for detention basin implementation.
Table 6. Assessment of the need for detention basin implementation.
Parameter Measurement Unit Result
River Mouth’s Width m 10.000
River Mouth’s Height m 3.000
River Mouth’s Capacity of Drainage m3/s 140.359
Fill Rate—Forti (pre-regularization) % 82
Fill Rate—Rational (pre-regularization) % 68
Fill Rate—Giandotti (pre-regularization) % 144
Fill Rate—Mockus (pre-regularization) % 118
Table 7. Application of the Cipolletti spillway.
Table 7. Application of the Cipolletti spillway.
Parameter Measurement Unit Result
Spillway’s Width m 8.500
Height of the Spillway Sill m 3.00
Outflow of the Spillway m3/s 82.151
Fill Rate—Giandotti (post-regularization) % 59
Fill Rate—Mockus (post-regularization) % 59
Table 8. Detention basin sizing.
Table 8. Detention basin sizing.
Parameter Measurement Unit Result
Width m 10.000
Height m 3.000
Length—Dutch Method (Giandotti) m 20,217.169
Length—STH Method (Giandotti) m 11,983.932
Length—Dutch Method (Mockus) m 14,044.453
Length—STH Method (Mockus) m 7,061.140
Table 9. Modification of the roughness coefficient.
Table 9. Modification of the roughness coefficient.
Parameter Measurement Unit Result
Wall Roughness Coefficient—Modified m−1/3 0.012
Riverbed Roughness Coefficient—Modified m−1/3 0.030
Drainage Capacity of the River Mouth—Modified m3/s 196.200
Fill Rate—Rational (post-modification) % 49
Fill Rate—Giandotti (post-modification) % 103
Fill Rate—Mockus (post-modification) % 84
Table 10. Adopted roughness coefficient (Source: [94]).
Table 10. Adopted roughness coefficient (Source: [94]).
Channel Typology of the Channel Very Good Good Regular Bad
Channel with a vegetated and stony slope 0.025 0.030 0.035 0.040
Concrete finishing surface 0.011 0.012 0.013 0.015
Table 11. Watersheds with high flood risk. (Source: [95]).
Table 11. Watersheds with high flood risk. (Source: [95]).
Municipality Watershed
Ribeira Brava Ribeira Brava
Tabua
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated