Submitted:
09 June 2023
Posted:
09 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
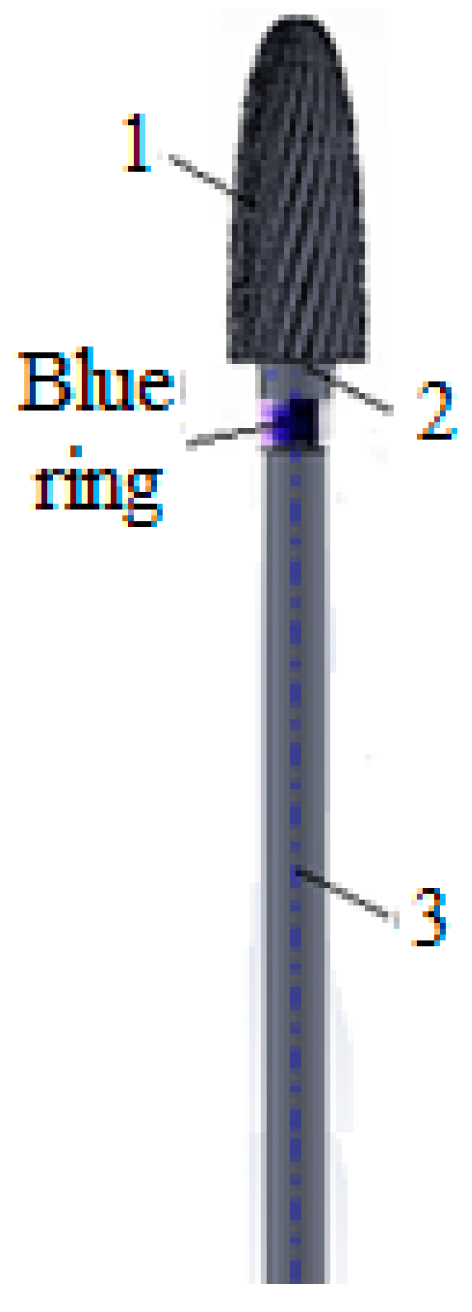

3. Results
3.1. Estimation of wear and durability of dental burs

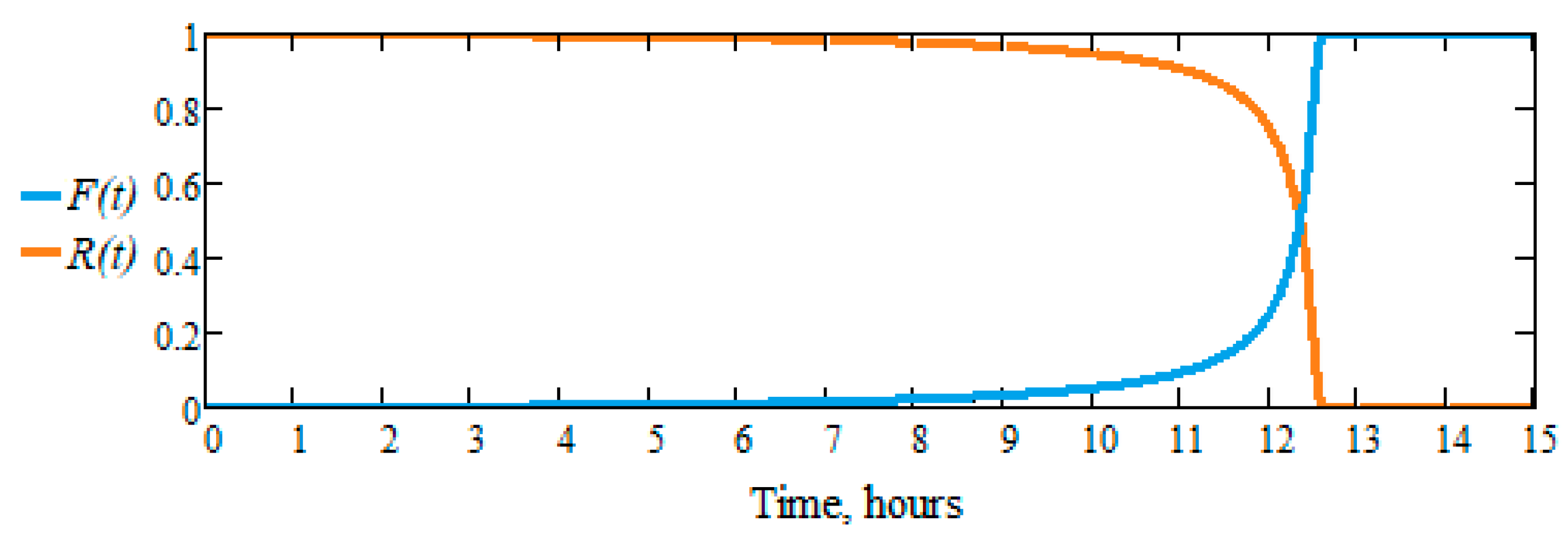
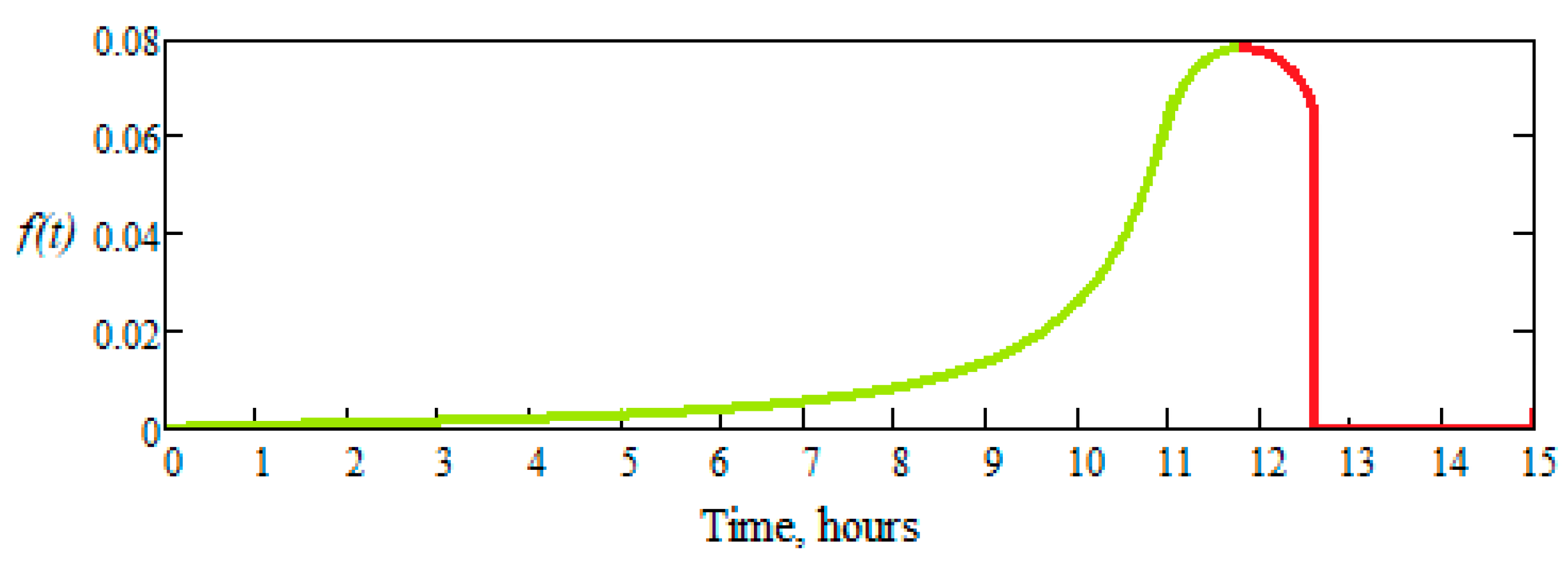
3.2. Reliability of dental burs. The reliability-durability correlation
- -
- the active part of dental burs operates with a very low probability of failure until a time, tmin, after which it increases rapidly until a time, tmax, when practically no bur is usable anymore, in general;
- -
- the time interval for removing from use the active part of a dental bur, tmax − tmin, is due to the small differences between the manufacturing characteristics of the same type of active part of dental burs (slightly different masses, angles, etc.).
- -
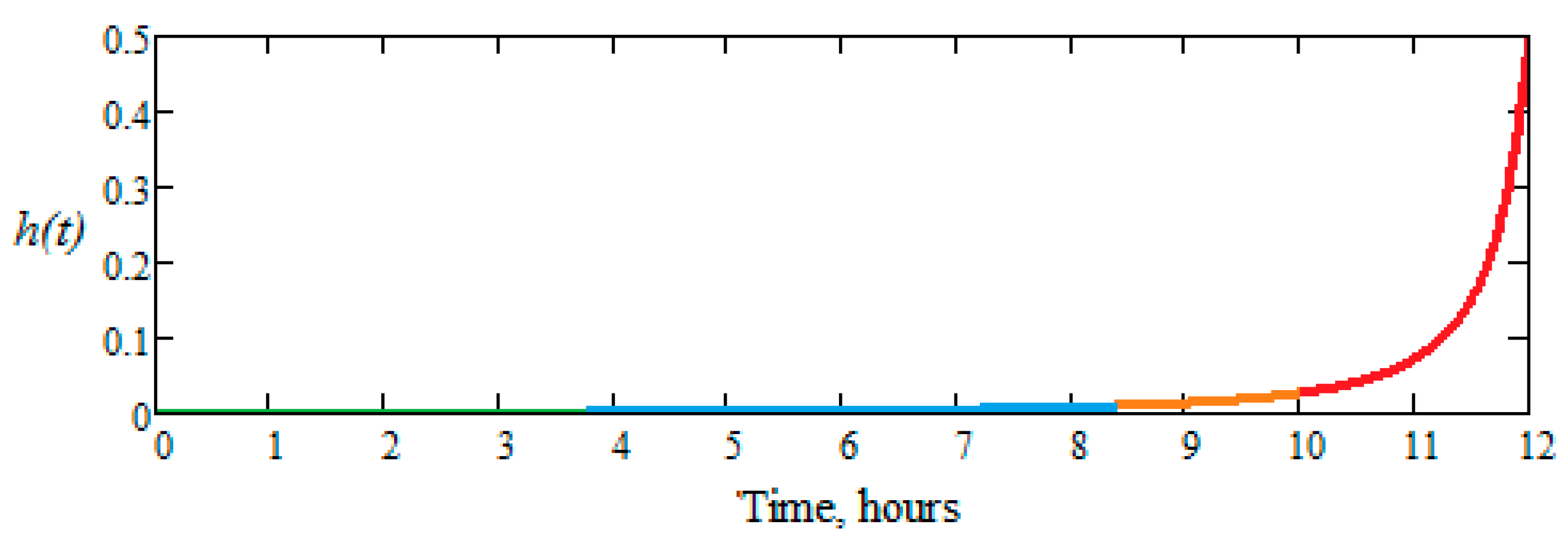
- the first zone, when t Є (0, 4) hours, there is no risk of failure, and h(t) has a linear variation, close to zero;
- -
- the second zone, when t Є (4, 8) hours, there are minimal (very low) chances of failure, although h(t) has a linear variation with a very small slope;
- -
- the third zone, when t Є (8, 10) hours, h(t) begins to increase, has a curvilinear variation, so the phenomenon of wear becomes visible, and the risk of failure is increasing;
- -
- the fourth zone, when t Є (10, 12) hours, h(t), increases suddenly, following an exponential curve and the risk of failure is very high.
4. Discussions
Conclusions
- The study presented in this paper was limited to the analysis and the consideration of only one parameter, mw, to establish and evaluate the durability and reliability of a type of dental bur, but it can be extended/applied, to other functional parameters of the active part of dental burs (seating angle, clearance angle, sharpening angle, tip circle area, etc.).
- The wear phenomenon of the active part of a dental bur limits the durability and reliability of dental burs and is studied based on the experimental results obtained in the work process and validated by interpolation and led to polynomial functions which approximate very well the dependent parameter, mw, considered in the experimental program.
- Additionally, these functions allowed the determination of the limit (extreme) wear values, where dental bur becomes ineffective, although the material and configuration allow it to be efficient (i.e., a small amount of dental bur material lost, removes an amount more from the milled dental material), in the period of time determined analytical and experimental.
- At the same time the interpolation of the experimental data/results led to practical applications, useful for the extension of the life of the dental bur, even for the optimization of the parameters of operation, execution, and maintenance; establishing some possible criteria for replacing the worn ones; the provision of ideas for constructive solutions, or the extension of the lifetime of the materials from which the dental burs are made.
- The complete solution of the problem without experimental information becomes an approximate one because the experiments were performed on only one type of dental bur. The results closest to reality are those given by the interpolation function of the third degree, and they are in good agreement with the experimental results.
- The results obtained by interpolation showed that the dental bur during the work process has a high efficiency (mw is very low) during the first 11 hours of operation when the life increased by about 10 %. After 11 hours of operation, mw increases relatively exponentially; thus, it is recommended that the dental bur is normally replaced with a new one to ensure dental high material processing standards.
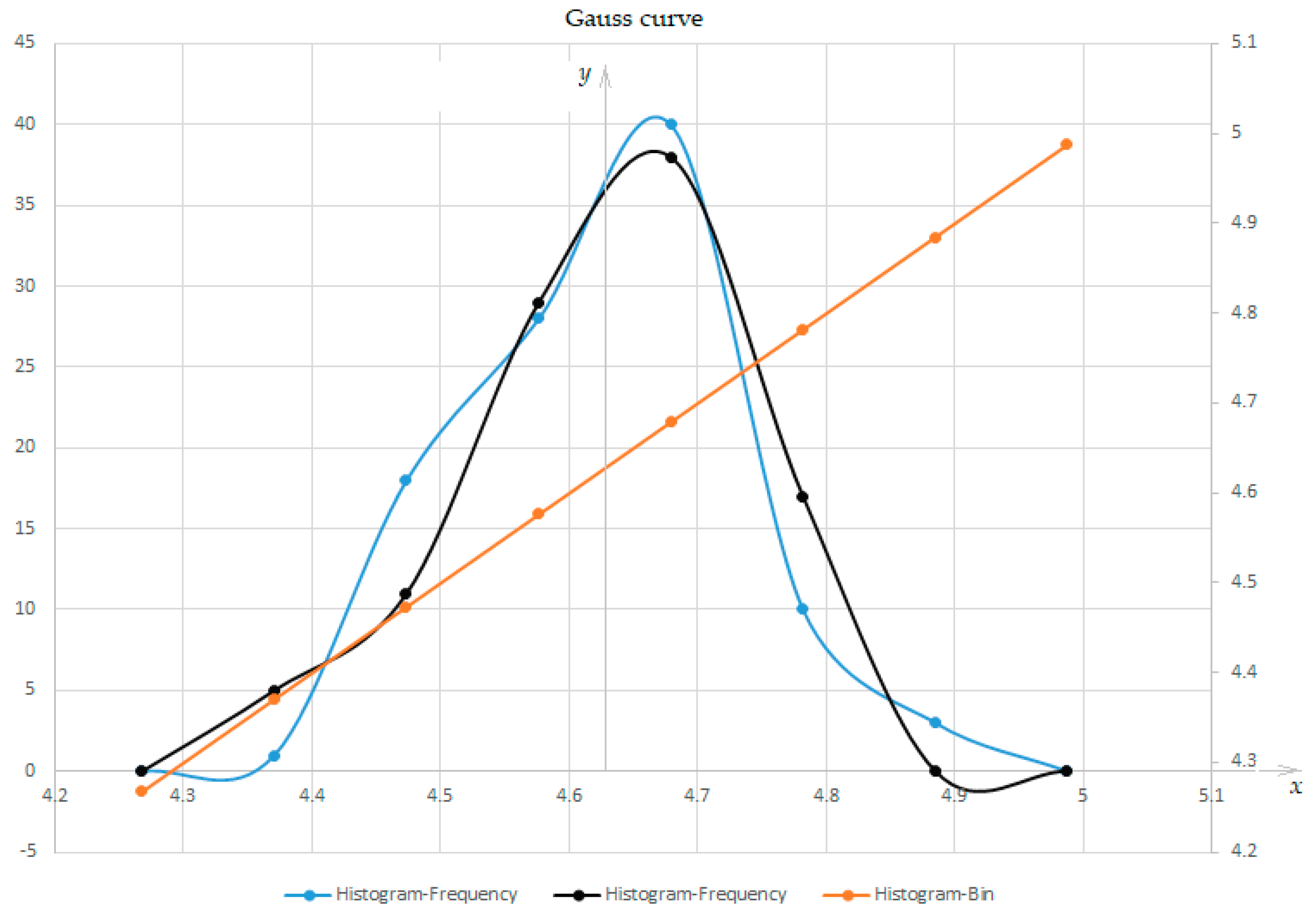
- The researched parameter, mw measured by weighing, was observed to take different values and randoms between two limits, each value has its own frequency (a number of repetitions), and the distribution of these values (with their frequency) can be represented by a normal distribution law, based on Gauss's function.
- A similar study can be justified by other functional parameters of the active part of the researched dental bur, with the goal to check if the method used is validated, regarding the extension of the lifetime (durability) or even optimization of their operation (reliability).
- It is proposed, the continuation of the research method by obtaining several experimental data and supplementary information for a more complete solution to the problem of wear of the active part of dental burs, method extension on other functional parameters that were not monitored, and other types of dental burs in order to record the parameters, using new deterministic or even statistical models of the phenomenon.
- In this way, will be validated the influence (importance) of the parameter, mw, of the work regime together with the other parameters mentioned in the paper. The mathematical model obtained based on the structured and discussed experimental data in this paper will be used to investigate the possibilities of improving or optimizing the working regimes of dental burs and other characteristic/functional parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- http://dexonline.net.
- Burlacu, G.; Danet, N.; Bandrabur, C.; Duminica, T. Reliability, Maintainability and Availability of Technical Systems; MatixRom: Buharest, Romania, 2005. (In Romanian) [Google Scholar]
- Bârsan-Pipu, N.; Isaic-Maniu, A.; Vodă, V.G. Failure. Statistical Models with Applications; Economică: Bucharest, Romania, 1997. (In Romanian) [Google Scholar]
- Tudor, A.; Mirică, R.-F.; Laurian, T. Reliability of mechanical systems; BREN: Bucharest, Romanian, 2003. (In Romanian) [Google Scholar]
- https://ro.wikipedia.org/wiki/Fiabilitate.
- https://doctoruldedinti.info/freze-stomatologice/.
- https://en.wikipedia.org/wiki/Milling_cutter.
- Materials, Equipment, Instruments and Dental Consumables. Available online: https://www.dentotal.ro/ (accessed on 9 February 2022).
- Saracin, I.A.; Ilie, F.; Voicu, G. Structural properties of the friction couple, dental milling cutter-dental material, before the work process. Sci. Bull. Series B 2022, 84, 237–246. [Google Scholar]
- Saracin, A.; Voicu, G.; Saracin, I.; Pandia, O. Detemination of use of dental materials and stemmatological frees on stand. In Proceedings of the Conference “Engineering for Rural Development”, Jelgava, Latvia; 2019. [Google Scholar]
- Bakša, T.; Kroupa, T.; Hanzl, P.; Zetek, M. Durability of Cutting Tools during Machining of Very Hard and Solid Materials. Procedia Engineering 2015, 100, 1414–1423. [Google Scholar] [CrossRef]
- Jozic, S.; Lela, B.; Bajic, D. A New Mathematical Model for Flank Wear Prediction Using Functional Data Analysis Methodology. Adavances in Materials Science and Engineering 2014, 2014, 138168. [Google Scholar] [CrossRef]
- Ilie, F.; Saracin, I.A.; Voicu, G. Study of Wear Phenomenon of a Dental Milling Cutter by Statistical–Mathematical Modeling Based on the Experimental Results. Materials 2022, 15, 1903. [Google Scholar] [CrossRef] [PubMed]
- Fry, R.; McManus, S. Smooth Bump Functions and Geometry of Banach Spaces, A Brief Survey. Expositiones Mathematicae 2002, 20, 143–183. [Google Scholar] [CrossRef]
- Rowland, T. Bump Function. From Math World—A Wolfram Web Resource, created by Eric W. Weisstein. https://mathworld.wolfram.com/BumpFunction.html.
- Tampu, I. The metal cutting process. Tool life, T&T Magazine—Technique and Technology, 2018. (In Romanian). https://www.ttonline.ro/revista/scule/procesul-de-aschiere-a-metalelor-durata de viata a sculei and https://www.mecholic.com/2018/11/taylor-formula-for-tool-life.html.
- Caado-Vara, R.; Canal-Alonso, A.; Martin-del Rey, A.; De la Prieta, F.; Prieto, J. Smart Buildings IoT Networks Accuracy Evolution Prediction to Improve Their Reliability Using a Lotka–Volterra Ecosystem Model. Sensors 2019, 19, 4642. [Google Scholar] [CrossRef] [PubMed]
- Cardei, P.; Saracin, A.; Saracin, I. A classical mathematical model applied for the study of the phenomenon of wear of dental mills. Preprint RG. [CrossRef]
- https://dexonline.ro/definitie/uzur%C4%83.
- Gatabazi, P.; Mba, J.C.; Pindza, E.; Labuschagne, C. Grey Lotka-Volterra models with application to cryptocurrencies adoption. Chaos, Solitons & Fractals 2019, 122, 47–57. [Google Scholar] [CrossRef]


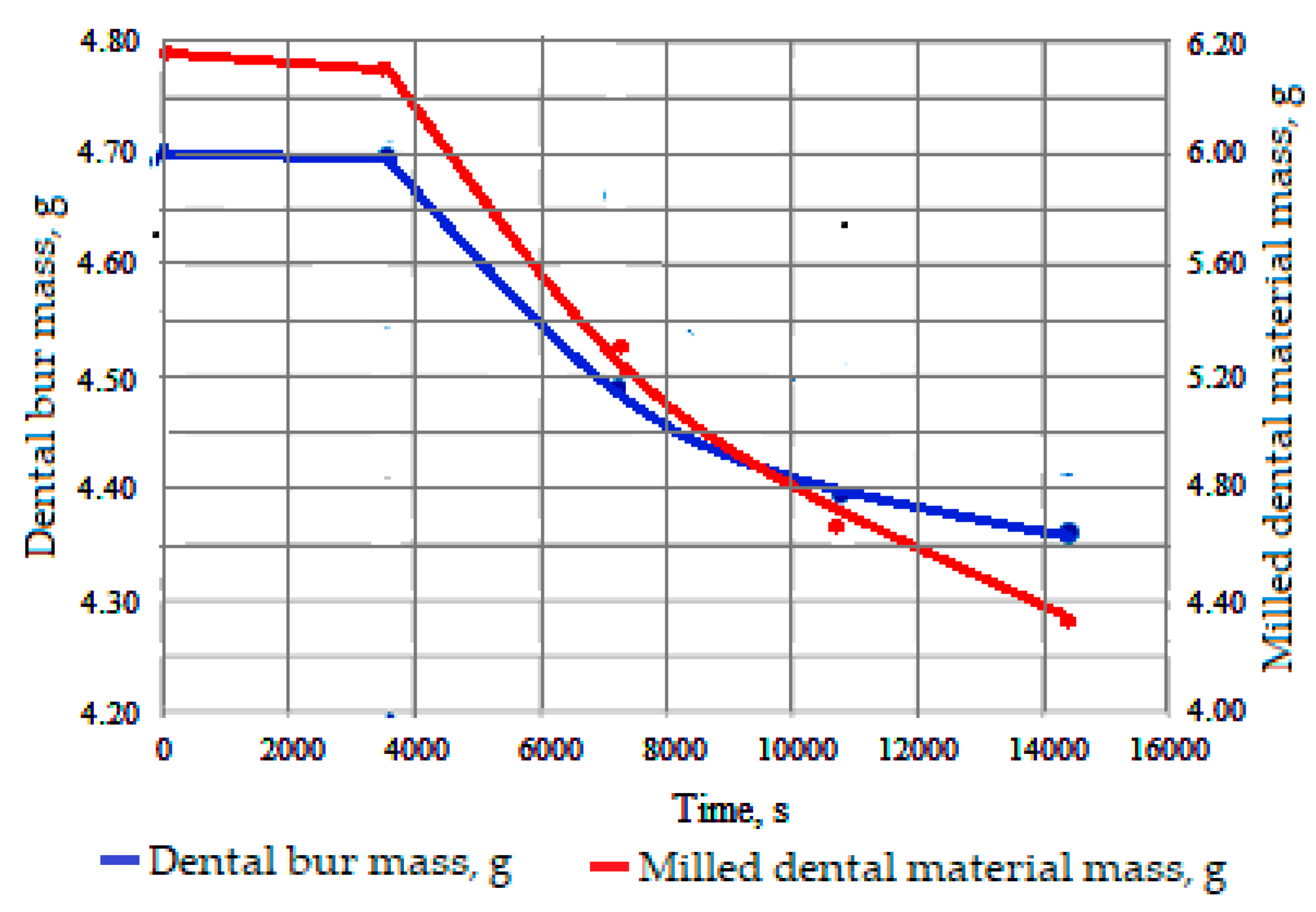
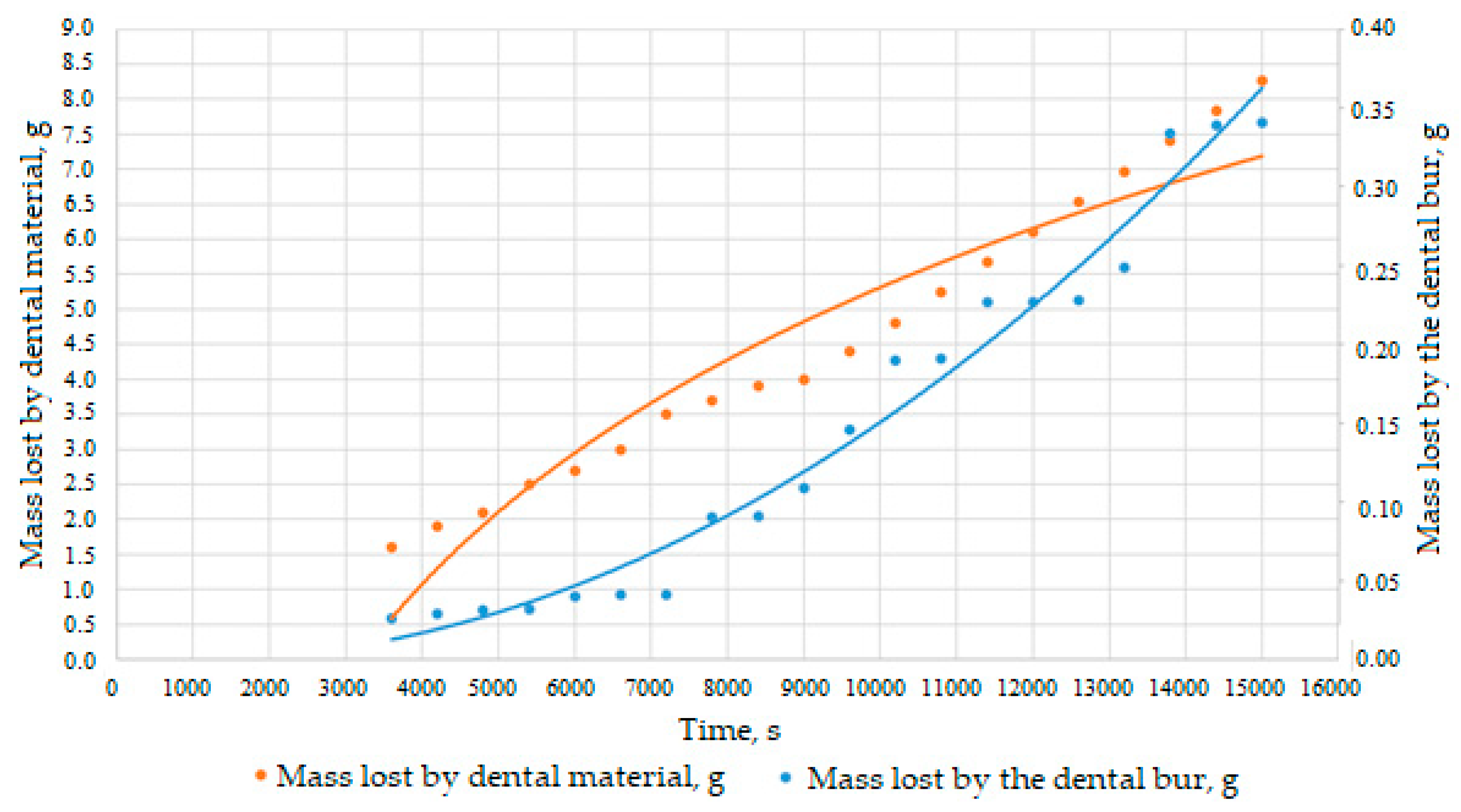
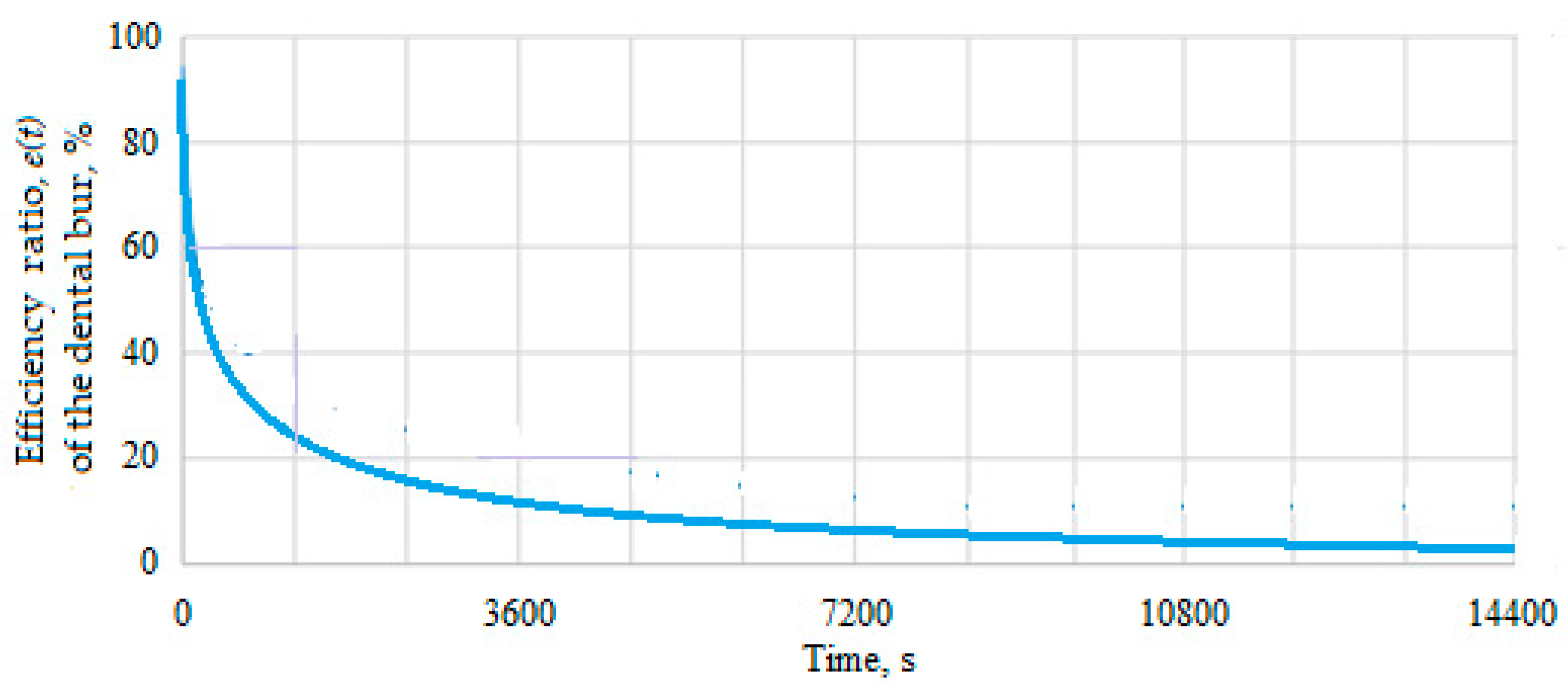
| Parameter | Notation | Unit of measurement | Parameter type |
|---|---|---|---|
| Time | t | sec, min, hours | Command |
| Mass lost by dental bur wear | mw | g | Input/Output |
| Milled mass (of dental material) | mm | g | Qualitative |
| Advance (Feed) | s | mm | Command |
| Rotational speed of dental bur | n/ω | rpm/s−1 | Command |
| Type of bur/Features | Mass, mf [g] | Total length, [mm] | Length of the active part, [mm] | Average diameter, [mm] | Maximum diameter, [mm] |
|---|---|---|---|---|---|
| Specimen dental bur | 4.701 | 52.750 | 14.500 | 5.400 | 6.200 |
| Name | Mass, mm [g] | Total length, [mm] | Diameter, [mm] |
|---|---|---|---|
| Sample dental material | 6.18 | 13.00 | 8.60 |
| mw—values by interpolation of the degree polynomial (function): | |||
|---|---|---|---|
| Polynomial coefficients | Degree I | Degree II | Degree III |
| c00 | −0.315 | −0.003346 | 0 |
| c10 | 1.746·10−5 | −6.150·10−5 | 6.744·10−5 |
| c01 | 3.866·10−4 | 2.275·10−4 | −5.699·10−4 |
| c11 | 0 | 1.333·10−8 | −1.028·10−8 |
| c20 | 0 | 3.792·10−9 | −8.736·10−9 |
| c02 | 0 | 1.518·10−8 | 6.156·10−7 |
| c21 | 0 | 0 | 1.762·10−12 |
| c12 | 0 | 0 | −1.82·10−12 |
| c30 | 0 | 0 | 3.37·10−13 |
| c03 | 0 | 0 | −1.038·10−10 |
| ε % | 7.828 | 1.733 | 0.486 |
| Rotation speed, [rpm] | Lifetime (durability) in hours, for mw, given by the polynomial interpolation function of: | ||
|---|---|---|---|
| Degree I | Degree II | Degree III | |
| 7,000 | 12.753 | 11.720 | 11.517 |
| 12,000 | 8.558 | 7.886 | 7.824 |
| 20,000 | 5.998 | 5.984 | 5.795 |
| 35,000 | 3.623 | 3.597 | 3,464 |
| No. crt. | Rotational speed of dental bur, rpm | Lifetime (duration). calculated for mw, hours |
|---|---|---|
| 1 | 7,000 | 11.373 |
| 2 | 10.265 | |
| 3 | 12.613 | |
| 4 | 11.214 | |
| 5 | 11.620 | |
| 6 | 12,000 | 7.634 |
| 7 | 7.488 | |
| 8 | 8.358 | |
| 9 | 7.354 | |
| 10 | 7.786 | |
| 11 | 20,000 | 5.898 |
| 12 | 5.911 | |
| 13 | 5.098 | |
| 14 | 5.684 | |
| 15 | 5.884 | |
| 16 | 35,000 | 3.275 |
| 17 | 3.153 | |
| 18 | 3.523 | |
| 19 | 3.497 | |
| 20 | 3.372 | |
| Average time valuesof calculated life, hours | 7,000 | 11.417 |
| 12,000 | 7.724 | |
| 20,000 | 5.695 | |
| 35,000 | 3.364 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





