Material Evaluation and Dynamic Powder Deposition Modeling of PEEK/CF Composite for Powder-bed Fusion Process

1. Introduction

Selective laser sintering, as an essential category of multiple additive manufacturing technologies, is able to produce polymeric composite materials economically and with obvious flexibility [1]. Polymeric composites such as Poly-ether-ether-ketone (PEEK)/carbon fiber (CF) have attracted the attention of researchers as well as industrialists due to outstanding performances such as high specific strength and specific modulus. However, the laser-sintered PEEK/CF components are usually brittle because of their poor interfacial affinity, and inner voids. These defects are strongly associated with the powder packing quality upon deposition. Thus, the investigation of the powder deposition process incorporating the detailed material properties is necessary, so that the expected behaviors of the laser-sintered PEEK/CF composites can be achieved.

The particle dynamic model has been widely employed to study the interactions between particles in macro-scale or micro-scale, especially the powder deposition process [2,3]. The powder property, bulk material property, and interfacial features of composite powders are key factors influencing the packing quality of deposited layers in the powder-bed fusion (PBF) process. Thus, the detailed material evaluation for the dynamic model is significant to reveal the deposition mechanism of composite powders. The evaluation of specific materials has been carried out, such as agriculture [4,5,6], soil [7,8], and rock [9,10,11]. However, little research has conducted the raw material evaluation correlating with the polymer and polymer-based composite powders. Opposite to the pure materials, the multi-component composite powders will improve the quantities of to-be-determined constants. It also brings some parameters that cannot be measured directly, such as surface energy.

When exploring these specific properties, the reliable approach is to perform either in-situ measurements or laboratory experiments. Vu-Quoc et al. [12] measured the restitution coefficient in soybeans by conducting drop tests from various heights. They used the data from high-speed video to determine the final parameters. Marczewska et al. [13] utilized the triaxial test to investigate the effects of particle-particle sliding friction and contact stiffness, including Young’s modulus, Poisson’s ratio, and dilatancy. Other experimental measurements such as uniaxial tension, slope test, direct shear test, etc…also play an important role. However, it is difficult to measure the specific contact parameters in CF-reinforced composite powders. Since preparing the pure CF sample is a struggle, causing inconvenience in the corresponding experiments. Thus, it is appropriate to compute the specific coefficient by the finite element simulation in macro-scale. Some parameters can not be measured by experiments such as surface energy, which can be determined by the design of experiments (DOE) method. Yoon et al. [9] employed the response surface method and the Plackett-Burman (PB) design to acquire suitable parameters to simulate the uniaxial compression of bonded rock. Johnstone [14] used the DOE method to calibrate the dynamics model based on experimental measurements. E. X. Zu et al. [15] carried out the simulation of coke accumulation based on the Hertz-Mindlin (no-slip) contact model. The core of their study is to determine the contact parameters. The number of investigated factors has a great influence on the complexity of the DOE. So the number of studied factors should be reduced as much as possible especially for the composite powders. Moreover, the multi-phase characteristics of polymer composite powders significantly increase the number of undetermined parameters, causing difficulties in calibrating the DEM parameters. Thus, this work proposes a parameter design method called "Plackett Burman (PB)-Box Behnken design (BBD)-Genetic Algorithm (GA)" for the DEM model parameter calibration process. This method mainly aims at contact parameters that are difficult to measure experimentally. It can quickly obtain the functional relationship between the significant parameters and the target value, and determine the optimal parameter combination. Importantly, this method possesses universality for multi-phase powder systems.

In this work, to develop a reliable powder dynamics model for powder deposition in PBF, a systematic framework for material evaluation of PEEK/CF powders with different compositions is proposed. Therein, the powder properties, bulk material properties, and interfacial features are calibrated by experimental measurement, numerical simulation, and DOE method. The powder dynamics model for PEEK/CF powders is experimentally verified by the fluidity-reflected angle of repose (AOR). Ultimately, the powder deposition processes of PEEK and PEEK/CF powders are evaluated and analyzed through the experiments and the validated dynamics model.

2. Discrete element method

2.1. Contact model theory

The discrete element method (DEM) is utilized to simulate the dynamic behaviors of PEEK/CF composite powders. In the DEM simulation, the particles are modeled as discrete entities to describe the dynamics of particle flow. The translation, rotation, and location of the particles can be characterized by Newton's laws of motion, which is described as [16,17]:

$$m_i\frac{{dv}_i}{dt}={\displaystyle \sum F_{c,i}{+m}_{i}g}$$

(1)

$$\frac{d\left(I_i\cdot {\omega }_i\right)}{dt}=R_i\cdot {\displaystyle \sum M_{c,i}}$$

(2)

where m_i, ω_i, v_i, I_i are the mass, angular velocity, translational velocity, and moment of inertia, respectively. F_c,i is the contact force, M_c,i is the contact torque, R_i is the rotation matrix.

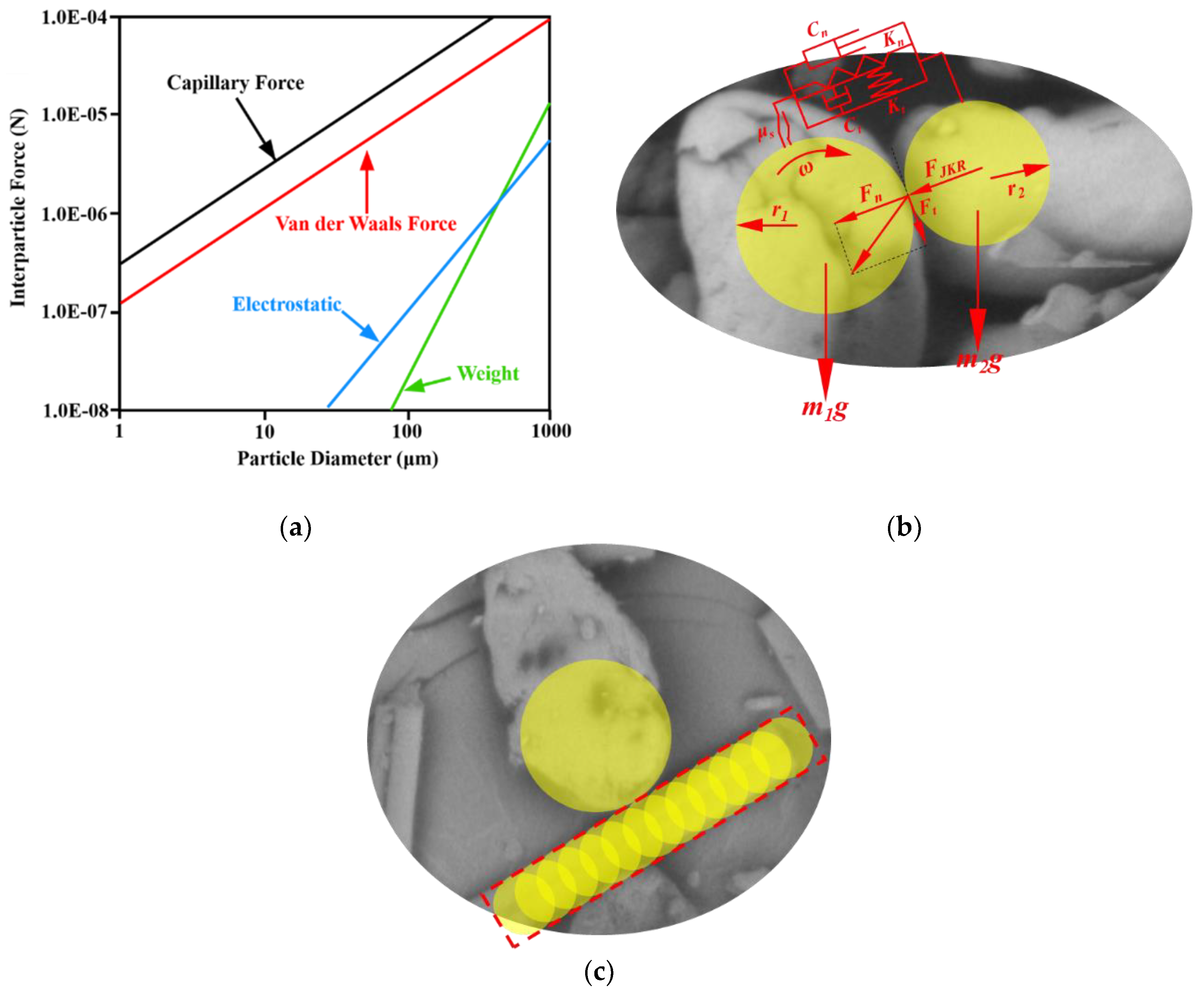
The relationship between cohesive force and particle size is shown in Figure 1(a) [18,19]. It appears that the cohesive forces such as Van der Waals force, electrostatic force, and capillary force are greater than the gravity of particles when the particle size is less than 100 μm, which reduces the powder fluidity and makes inconvenience for the powder-spreading process. In reality, the powder is preheated and dried before the powder-spreading process. Thus, the capillary force can be ignored.

(1)

Hertz-Mindlin contact model

The rationality of the Hertz-Mindlin contact model has been widely recognized in the particle-related research field [20,21]. In order to accurately characterize the stress-strain relationship between particles considering the adhesion, this work adopts Hertz-Mindlin and Johnson Kendall Roberts (JKR) model for polymers and their composite powders, which is implemented using EDEM software. Among them, the Hertz-Mindlin model is the foundation of the DEM method, and the parameter of surface energy in the JKR model can comprehensively characterize the bonding effect between particles caused by the van der Waals force and the electrostatic force [22]. Therefore, the Hertz Mindlin and JKR models possess universality in the DEM simulation of other thermoplastic polymers and their composite powders.

In the Hertz-Mindlin model, the normal and tangential force components between particles are calculated based on the Hertzian contact theory and the Middlein-Deresiewicz method respectively [23,24]. Both normal and tangential force between particles have damping components. The damping coefficient is related to the restitution coefficient [25].The tangential friction force between particles follows the Coulomb's law of friction, and the rolling friction between particles is computed based on the Contact-Directional-Constant-Torque model [17,26].

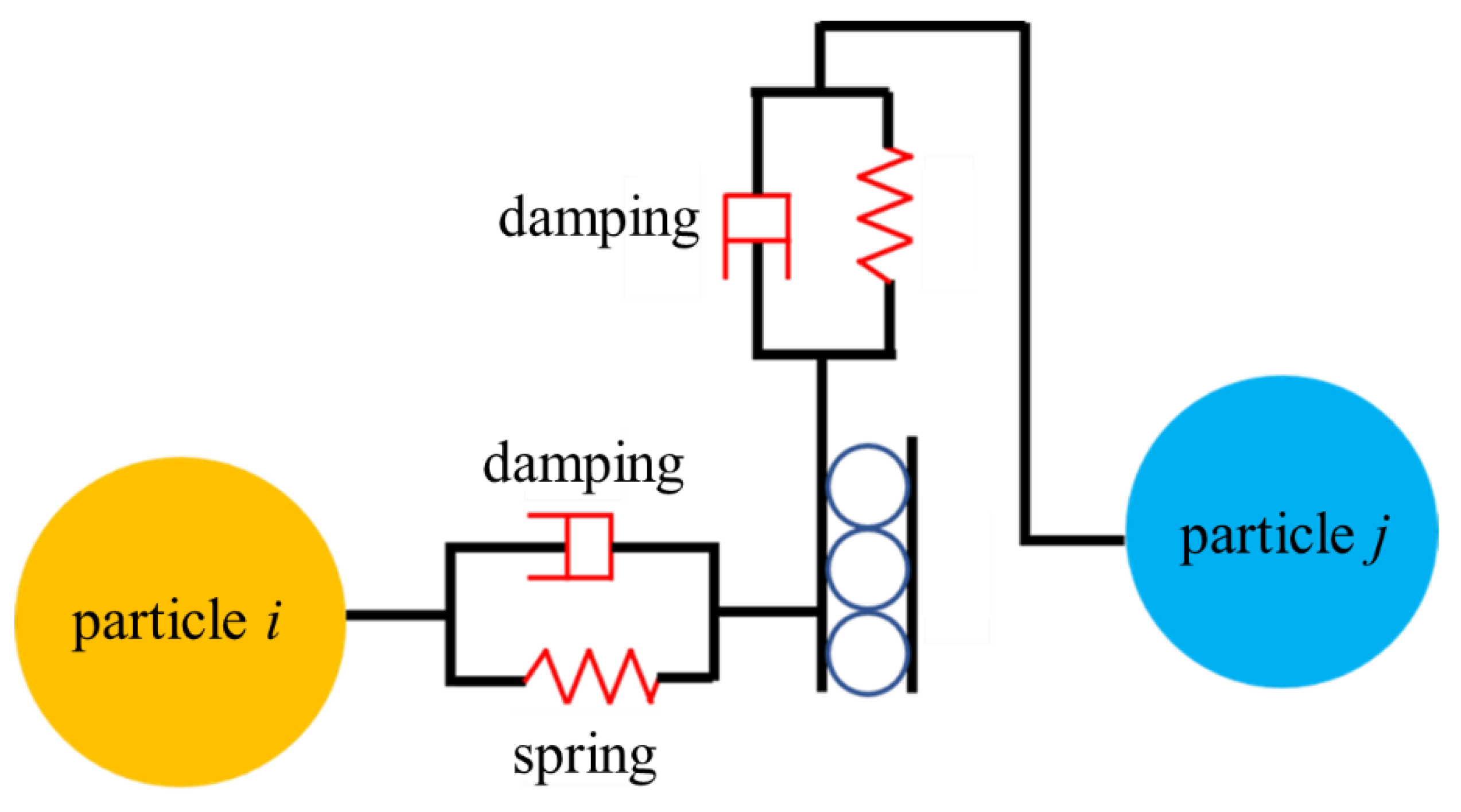
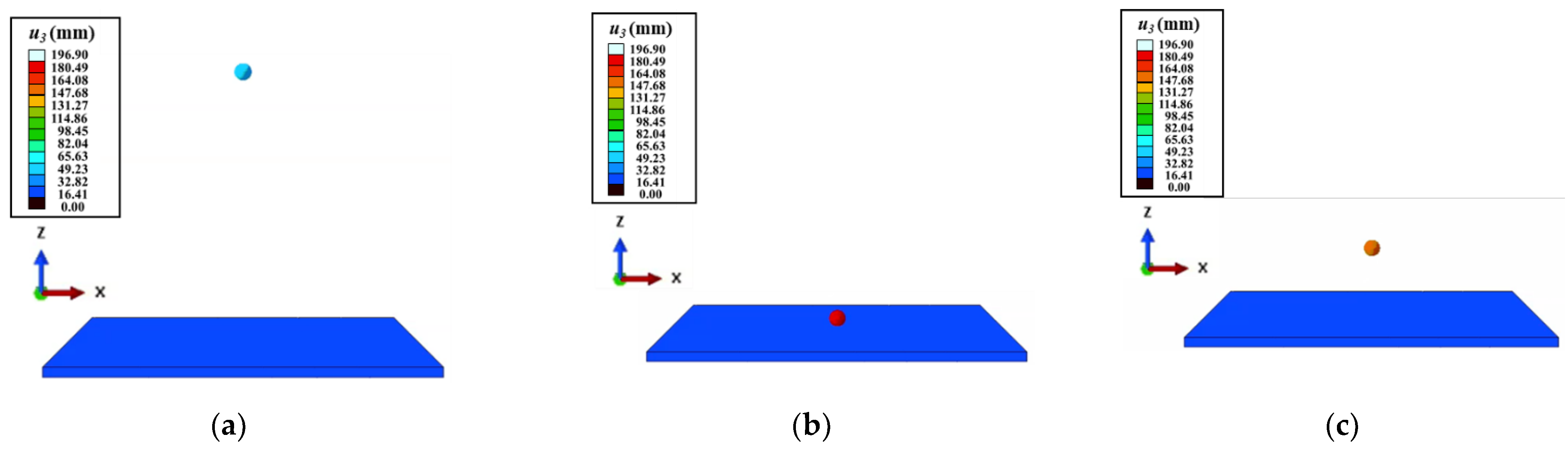
Figure 2 shows the schematic diagram of the Hertz Mindlin model for adjacent particles i and j, where the normal contact force on particle i can be expressed as

$$F_{CN}{=F}_{CN,E}{+F}_{CN,D}$$

(3)

where F_CN,E is the normal elastic force, F_CN,D is the normal damping force. The F_CN,E is computed based on the Hertz contact theory, which is described as

$$F_{CN,E}{=-K}_n\times {\alpha }_n^{1.5}$$

(4)

where α_n is the normal contact displacement (overlap of adjacent particles). The Contact constant K_n is expressed as

$$K_n=\frac{4G\sqrt{r^{*}}}{3\left(1-\upsilon \right)}$$

(5)

where G is the shear modulus of the particle. r^* is the radius of the local curvature. υ is the Poisson's ratio.

The normal damping force F_CN,D between particles is expressed as

$$F_{CN,D}=-2\sqrt{\frac{5}{6}}{\beta }^{*}\sqrt{m^{*}\times k_n}\times v_{re,n}$$

(6)

where v_re,n is the component of the relative velocity of particle i relative to particle j along the normal direction. k_n is the normal contact stiffness, β^* is the damping coefficient, m^* is the equivalent mass. Therein, the damping coefficient and normal contact stiffness can be expressed as

$$\beta *=\frac{lne}{\sqrt{{ln}^2{e+\pi }^2}}$$

(7)

$$k_n=\frac{2G}{1-\upsilon }{\left(\frac{3\left(1-\upsilon \right)\times r^{*}\times F_{CN,E}}{4G}\right)}^{\frac{1}{3}}$$

(8)

where e is the restitution coefficient between particles. The equivalent mass m^* and equivalent curvature radius r^* of particles are respectively described as

$$m^{*}=\frac{m_i\times m_j}{m_i{+m}_j}$$

(9)

$$r^{*}=\frac{r_i\times r_j}{r_i{+r}_j}$$

(10)

where m_i and m_j represent the masses of adjacent particles i and j. r_i and r_j are the radiuses of adjacent particles i and j.

The tangential contact force F_CT between adjacent particles can be expressed as

$$F_{CT}{=F}_{CT,E}{+F}_{CT,D}$$

(11)

where F_CT,E is the elastic force along the tangential direction, F_CT,D is the damping force along the tangential direction. The tangential elastic force F_CT,E, can be expressed in incremental form as

$$F_{CT,E}{=F}_{CT,E,\left(n-1\right)}{+\Delta F}_{CT,E}$$

(12)

where F_CT,E,(n-1) is the tangential elastic force of the previous analysis step; ∆F_CT,E is the increment of the tangential elastic force in the current analysis step, which is described as

$${\Delta F}_{CT,E}{=k}_t\times {\Delta \alpha }_t$$

(13)

where ∆α_t is the tangential displacement increment, k_t is the tangential spring stiffness, and expressed as

$${\Delta \alpha }_t{=v}_{re,t}\times \Delta t$$

(14)

$$k_t=\frac{2}{2-\upsilon }{\left(6\left(1-\upsilon \right)\times G^2\times r^{*}\times F_{CN,E}\right)}^{\frac{1}{3}}$$

(15)

where v_re,t is the relative tangential velocity between particles, ∆t is the step time. Meanwhile, the tangential damping force between adjacent particles can be expressed as

$${\Delta F}_{CT,D}=-2\sqrt{\frac{5}{6}}\times {\beta }^{*}\times \sqrt{m^{*}\times k_t}\times v_{re,t}$$

(16)

It is worth noting that the tangential force between adjacent particles is related to the frictional force between particles (μ_sF_CN, μ_s is the static friction coefficient). In the simulation process, the rolling friction can not be ignored, which is achieved by applying a torque to the contact surface of the particles.

$${\tau }_i{=-\mu }_r{F}_{CN}{R}_i{\omega }_i$$

(17)

where R_i is the distance from the contact point to the mass center, μ_r is the rolling friction coefficient, ω_i is the unit angular velocity vector at the contact point.

(2)

JKR theory

The Hertz Mindlin with JKR contact model can form an adhesive force contact model between particles, mainly considering the influence of van der Waals forces in the contact area. In this model, the normal elastic contact force between particles is computed based on the JKR theory [27], including the overlap of particles δ, interaction parameters, and surface energy γ, which can be described as

$$F_{JKR}=-4\sqrt{{\pi \gamma E}^{*}}{\alpha }^{\frac{3}{2}}+\text{}\frac{{4E}^{*}}{{3r}^{*}}{\alpha }^3$$

(18)

$$\delta =\frac{{\alpha }^2}{r^{*}}-\sqrt{\frac{4\pi \gamma \alpha }{E^{*}}}$$

(19)

$$\frac{1}{E*}=\frac{\left({1-\upsilon }_i^2\right)}{E_i}+\frac{\left({1-\upsilon }_j^2\right)}{E_j}$$

(20)

where E^* is the equivalent Young's modulus, r^* is the equivalent curvature radius, α is the contact radius of particles.

It is discovered that several parameters are involved in the aforementioned model, such as static friction coefficient, rolling friction coefficient, restitution coefficient, and surface energy. Therefore, it is essential to carry out the parameter-calibration work through the material characterization.

2.2. Parameter classification of the Discrete Element Model

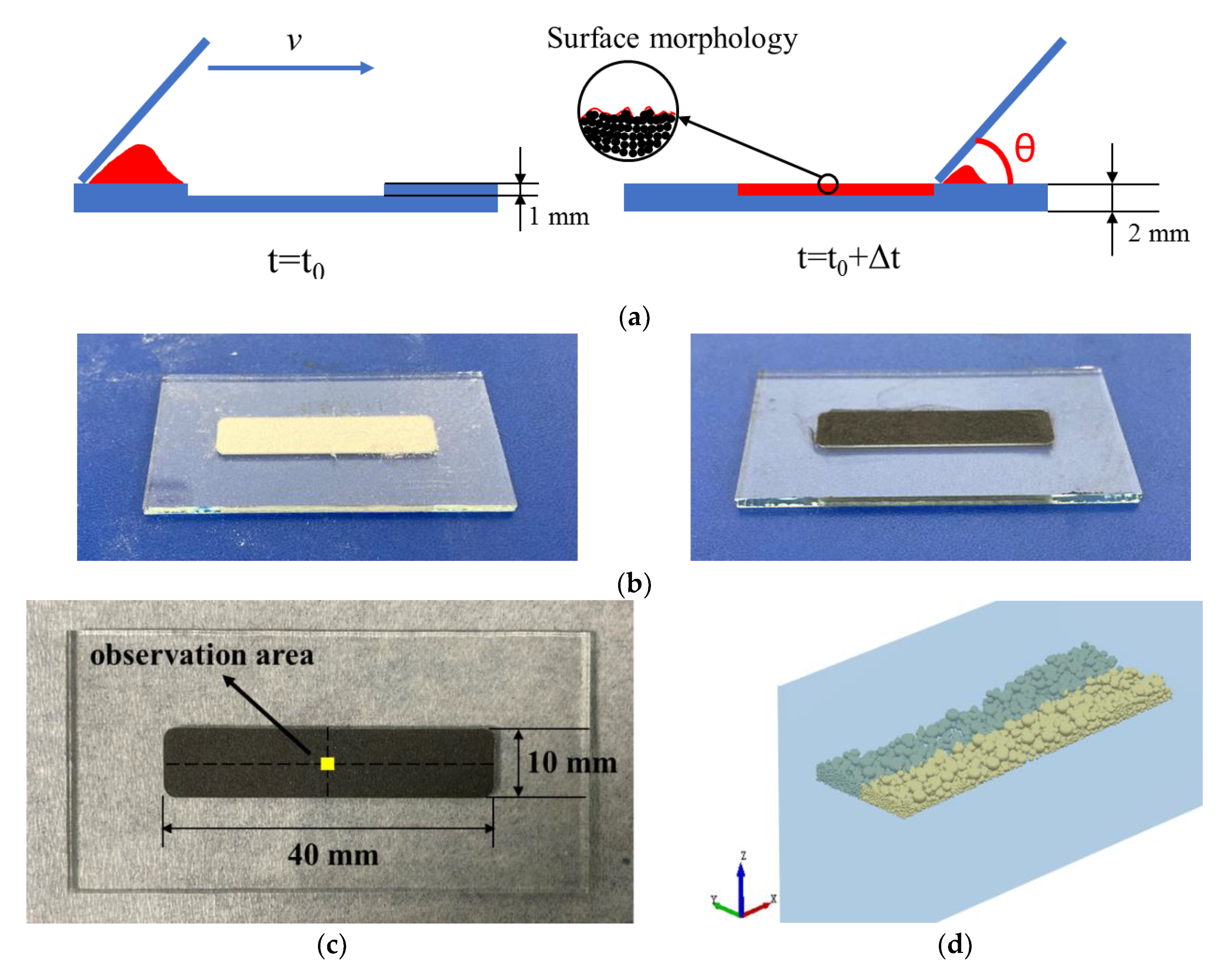
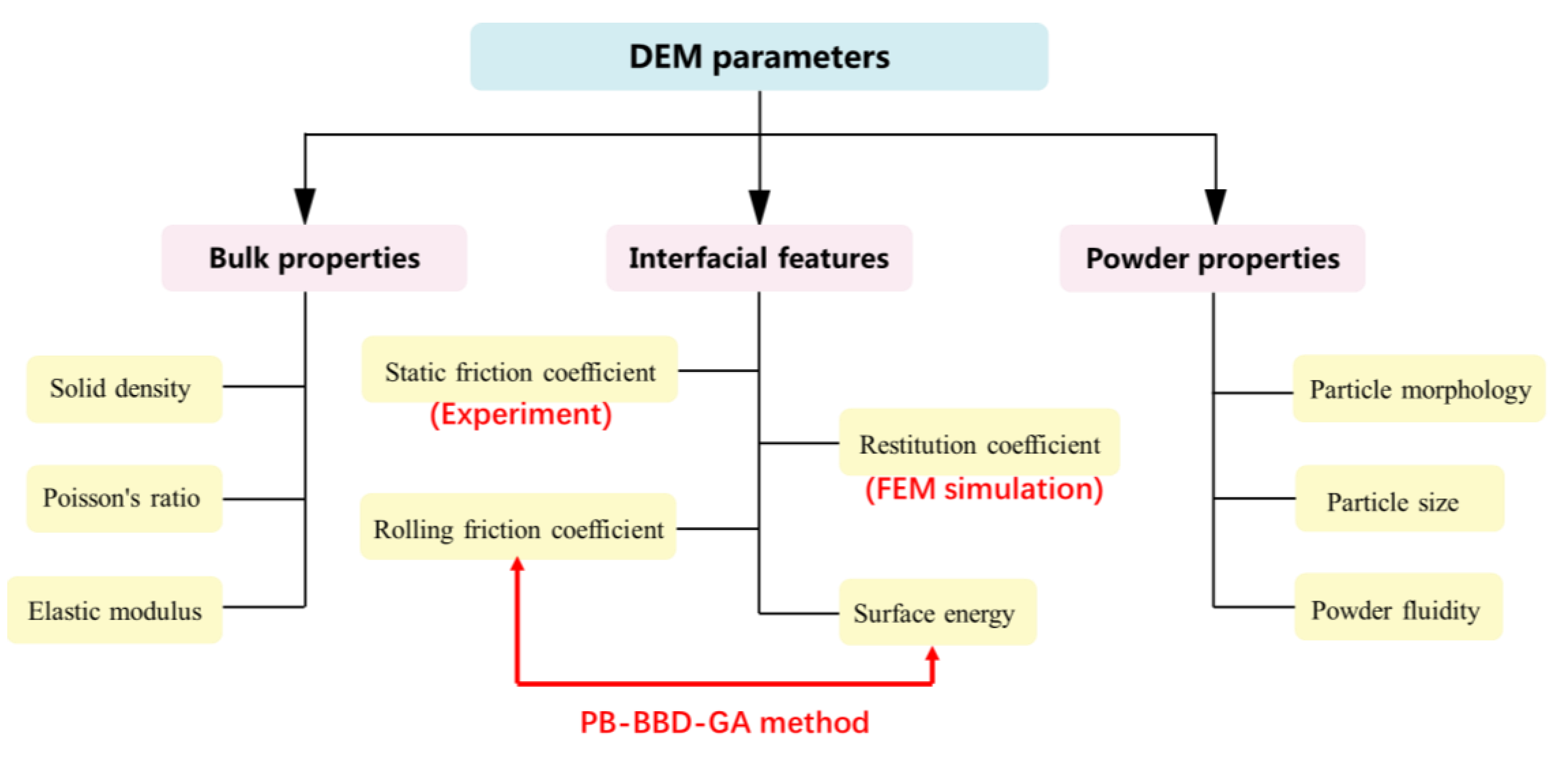
The first step of the DEM simulation is to calibrate numerous parameters through the comprehensive material characterization. Figure 3 shows the parameters involved in the DEM model, which can be divided into three categories.

(1) Solid-phase parameters: solid phase density, elastic modulus, and Poisson's ratio;

(2) Contact parameters between particles: static friction coefficient, rolling friction coefficient, restitution coefficient, and surface energy.

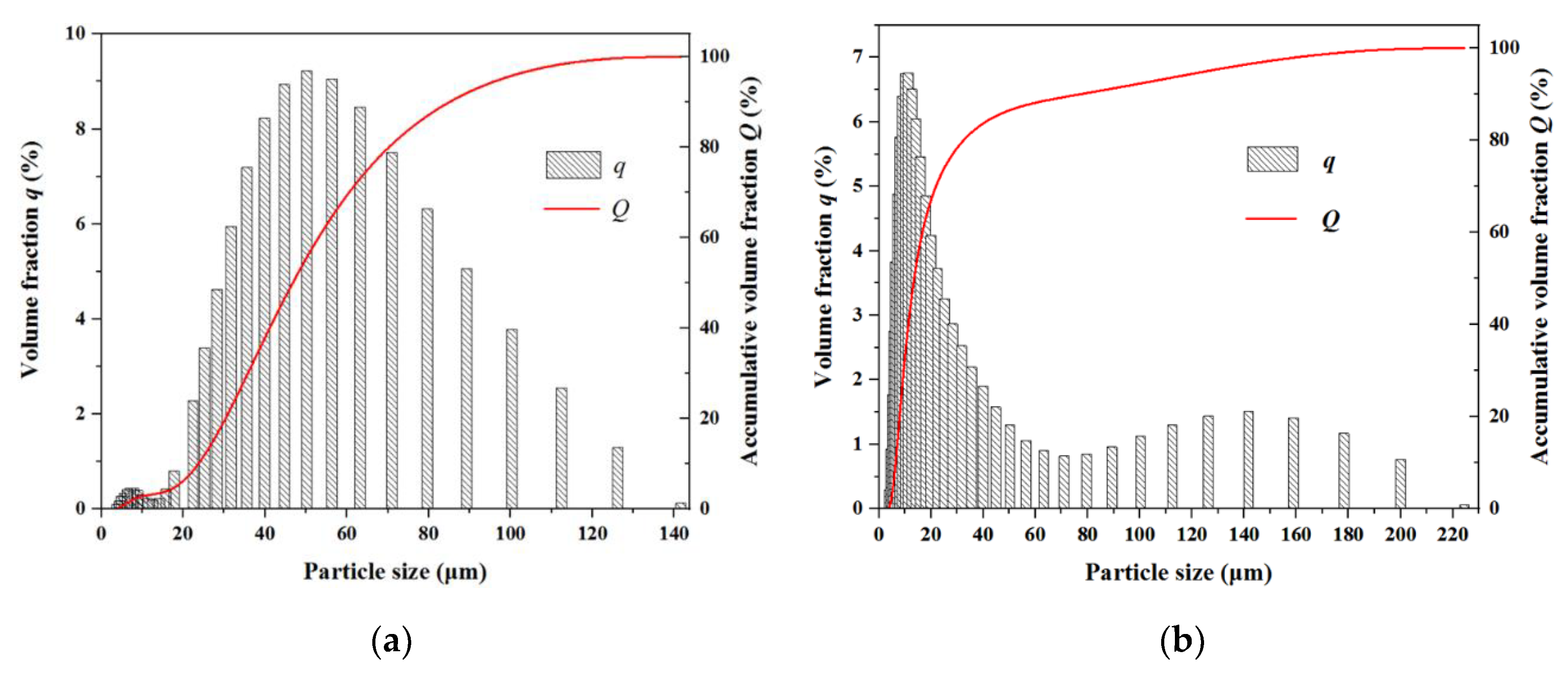
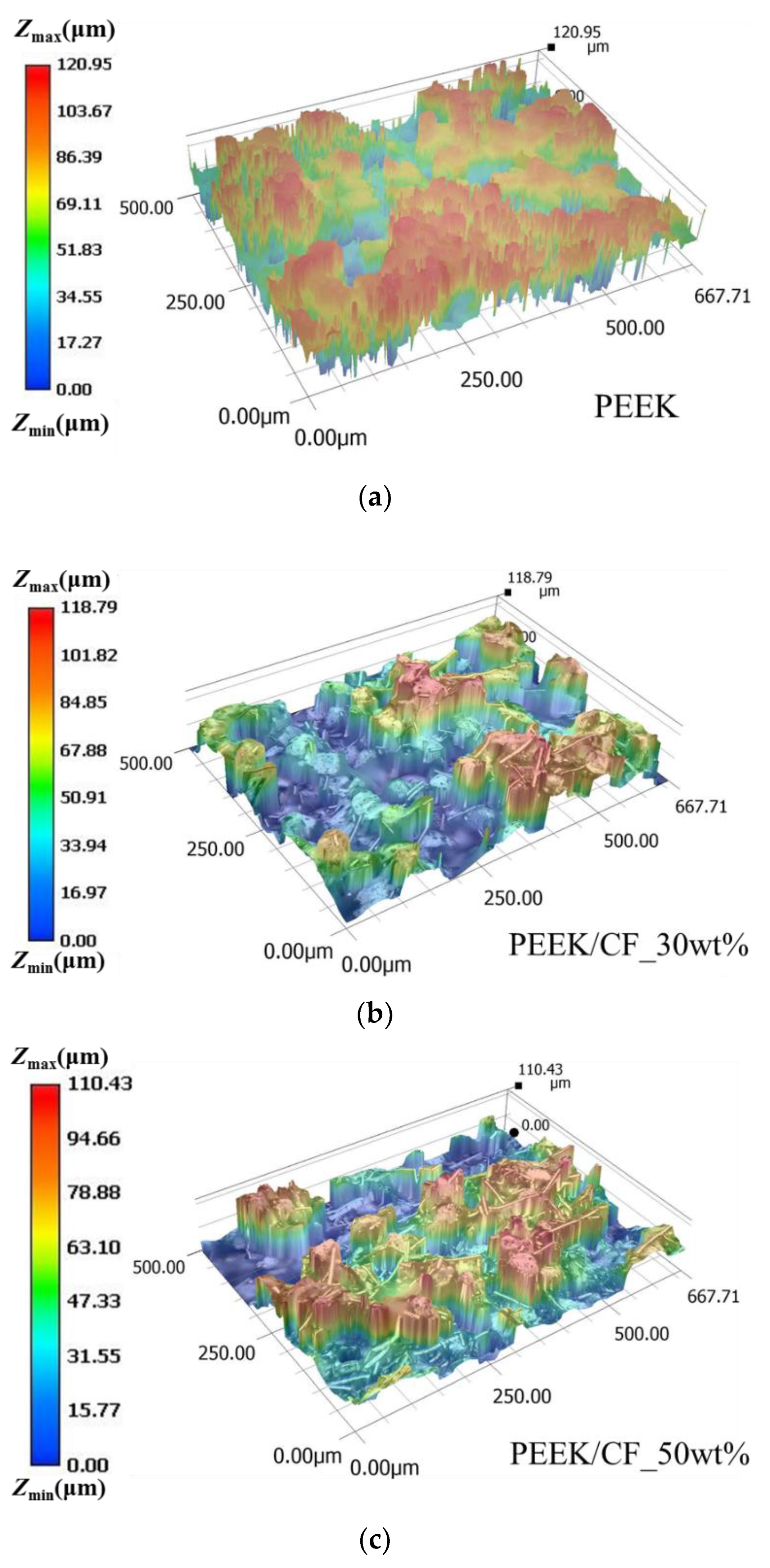
(3) Powder-phase parameters: particle morphology, particle size, and powder fluidity.

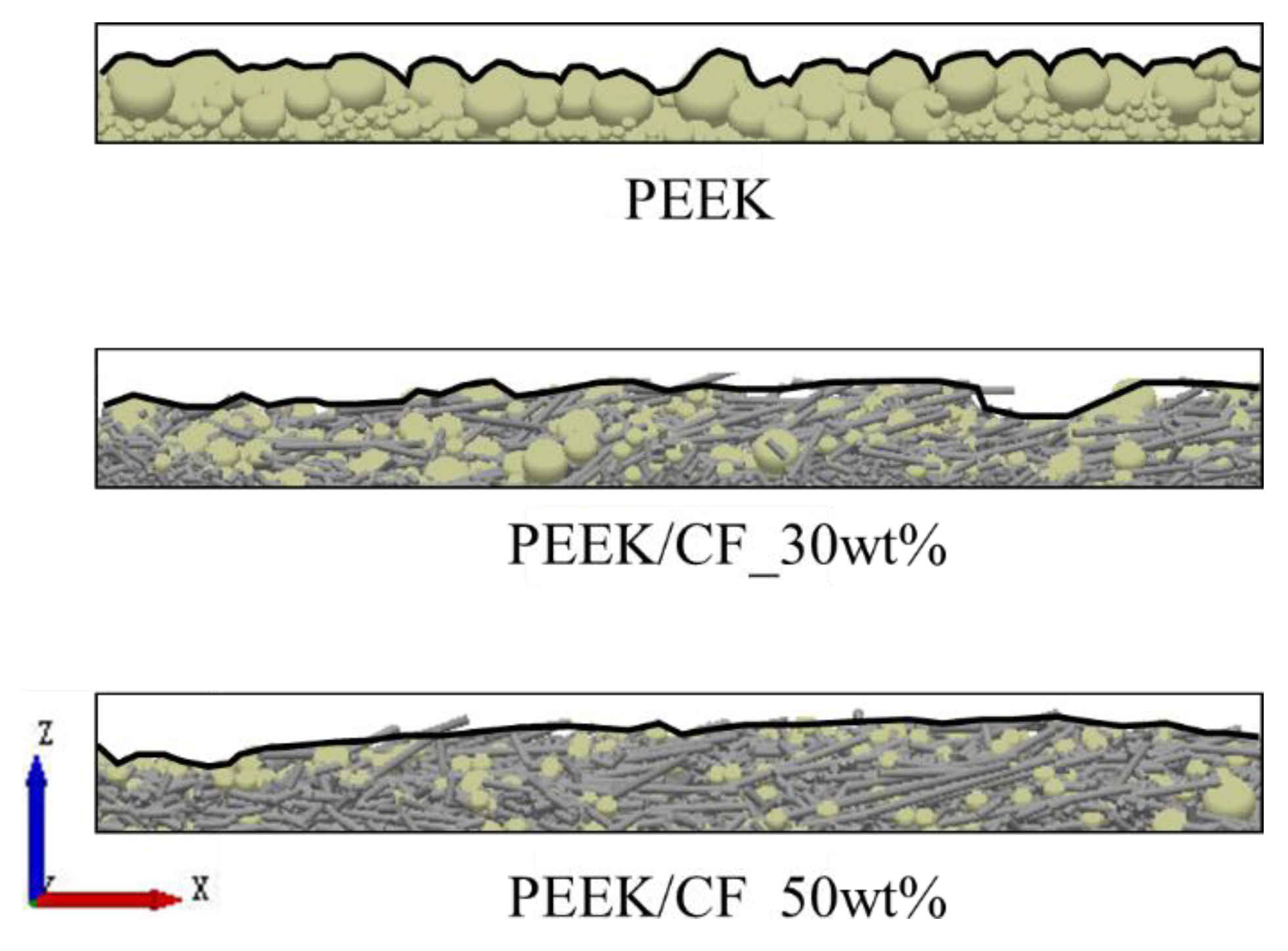
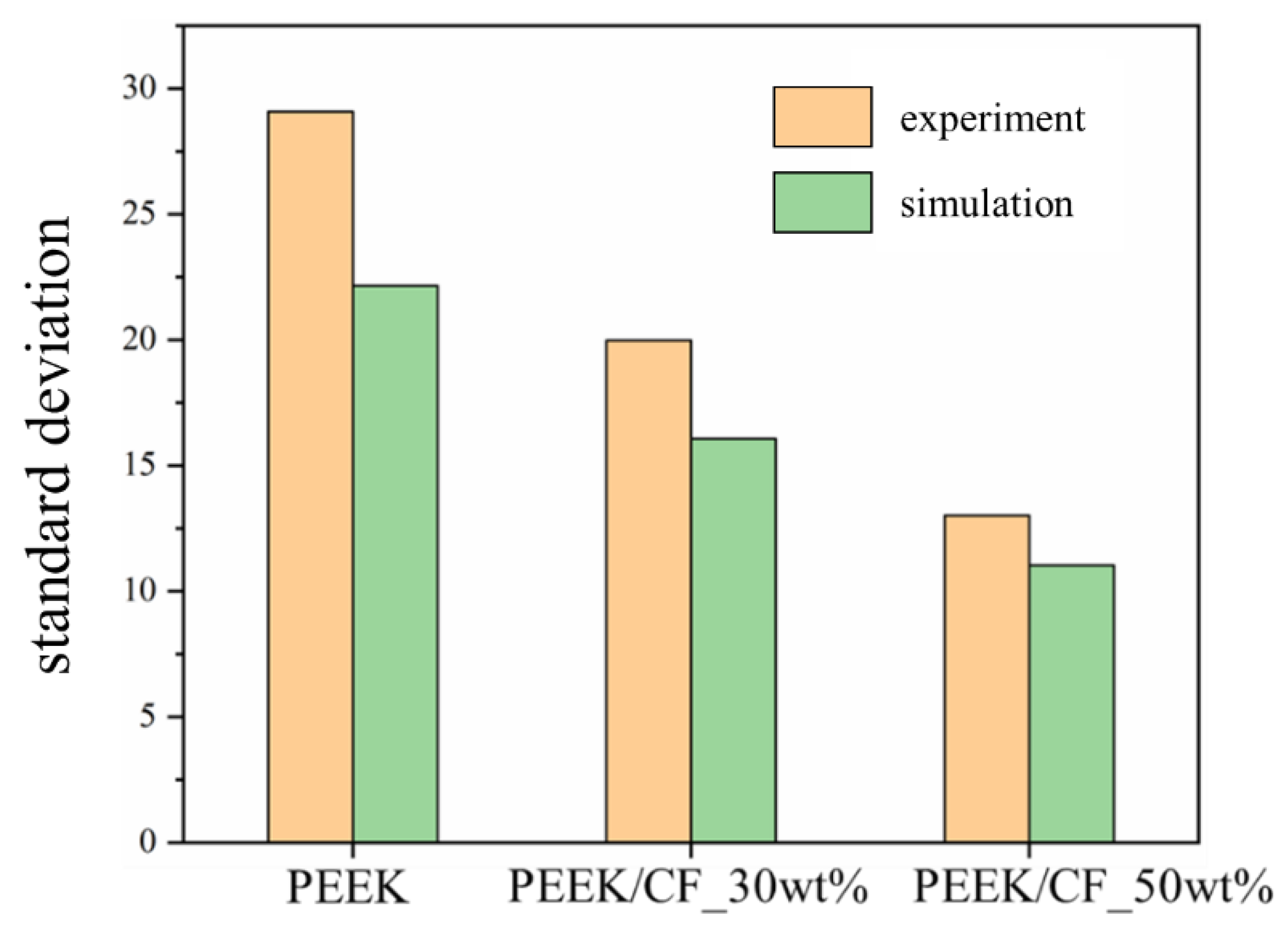
For composite powders, the contact forms between particles can be further divided into three patterns of "particle-particle", "particle-reinforced phase", and "reinforced phase- reinforced phase". Specifically, the particle size and the static friction coefficient between particles are directly measured. The restitution coefficient is obtained by the FEM simulation. The rolling friction coefficient and surface energy are achieved by the "PB-BBD-GA" parameter-design method. This method extends the GA on the basis of traditional PB and BBD methods, avoiding the uncertainty of traditional methods in predicting the optimal parameter combination. The "PB-BBD-GA" method can quickly obtain the functional relationship between significant parameters and target values, and determine the unknown parameter combination more accurately and efficiently.

2.3. Analysis step and particle modeling

The DEM simulation is proceeding based on the time step. In the numerical computation, a differential equation needs to be transformed into a difference equation for the iterative solution. The time step is the time difference between two adjacent iterations. The time step is usually set to 20%-30% of Rayleigh time, which makes the simulation stable and time-saving. Rayleigh time is determined as [28]

$$T_R=1{.625R}_{min}\sqrt{\frac{\rho }{E}}$$

(21)

where R_min is the minimum radius of spherical members and ρ is the density. In this work, the Rayleigh time is 6.4175e-9 s and the DEM results are recorded every 0.001 s.

The particle model is established based on its morphology in the DEM simulation, and the spherical particles are computationally efficient compared with the non-spherical particles. Importantly, the contact model for spherical particles should include rolling resistance to model the rotational motion of actual non-spherical particles. In contrast, the rolling resistance can be omitted when utilizing the non-spherical particles [29]. In this work, the spherical particles are modeled and the rolling resistance represented by the rolling friction coefficient is determined lastly. Meanwhile, a multi-sphere method, by which multiple spheres with the same or different sizes are clumped to approximate the irregularly-shaped particle (such as CF in this work), is employed in the model [30], as shown in Figure 1(c).

3. Material and the experimental method

3.1. Material characterization

This work selects the materials of PEEK and PEEK/CF powders, which possess the features of poor powder fluidity and high difficulty in powder deposition process, as the representative research object. The adopted powders are the PEEK, PEEK/CF_30wt%, and PEEK/CF_50wt%, which are featured by the weight fraction of CF. The inherent properties of the compositions of PEEK and CF are listed in Table 1, which includes important input factors of the subsequent-introduced powder dynamics model.

As shown in Figure 3, a large number of constants need to be determined, which are detailly described as follows.

(1)

Angle of repose

Powder fluidity is a comprehensive characterization and deeply impacts the powder deposition process. The AOR can reflect the powder fluidity in a simple and convenient fashion. In this paper, the AOR is measured according to the GB11986-89. As shown in Figure 4, a funnel is fixed above the horizontal plate, through which the particle sample falls, and the AOR of the cone is measured. Both experiments and the DEM model follow this standard.

(2)

Particle morphology and particle size distribution

Particle morphology and particle size distribution have important impacts on powder fluidity and computational efficiency. The TM4000PLUS scanning electron microscope (SEM) equipment is utilized in the high vacuum circumstance and at a voltage of 5 kV to acquire the SEM images that characterized the morphological features of PEEK powders and PEEK/CF composite powders. The objective area of the SEM image is limited. So the Malvern laser particle sizer (Mastersizer 2000, the United Kingdom) is utilized to measure the accurate particle size distribution of PEEK and CF.

(3)

Bulk density

The measurement method for the bulk density of PEEK and PEEK/CF powders is shown in Figure 5. Prepare a 100 ml graduated cylinder, and place the funnel at a certain height directly above the cylinder. The powder falls freely from the funnel mouth and fills the cylinder. Thereafter, screed the surface of the graduated cylinder, place it on the electronic scale to measure its mass, and obtain the bulk density of the powders ultimately.

(4)

Static friction coefficient

The inclined plane test can be used to measure the static friction coefficient. The friction coefficient between different materials can be achieved by replacing the material of the inclined plane or sample. At first, the inclined plane is placed horizontally, and the sample is placed at the fixed position of the inclined plane. Then lift the slope slowly, and stop the inclined plane when the sample starts to slide. The position of the inclined plane at this moment is recorded through a camera and the tilt angle is read. The static friction coefficient is the tangent value of the inclination angle.

(5)

Restitution coefficient

The restitution coefficient is the ratio of the separation velocity and the approaching velocity of the two objects along the normal direction of the contact before and after the collision, which is only related to the material of the collision objects [33]. Generally, it can be experimentally measured. Fix the plate, and a ball falls freely above the plate. The coefficient of restitution can be calculated by recording the fall height and bounce height of the ball (the restitution coefficient between different materials is achieved by changing the materials of the plate and the free-falling ball). However, measuring the restitution coefficient associated with pure CF is a struggle due to the difficulty in producing the products in pure CF in reality. Thus, it is appropriate to calculate the restitution coefficient by the simulation. The process of free-falling and bouncing for a small ball is achieved by FEM simulation (as shown in Figure 6) [34]. The restitution coefficient is computed as

$$e=\frac{v_{off}}{v_{app}}$$

(22)

where v_app is the speed of the ball approaching the plate, v_off is the speed of the ball away from the plate. e denotes the restitution coefficient.

(6)

Rolling friction coefficient and surface energy

Experimentally measuring the rolling friction coefficient and surface energy is a struggle even impossible to achieve. Thus, the DOE including the PB, BBD, and GA is employed to determine them.

PB design is a two-level (-1 and +1) experimental design method, which attempts to screen and determine the factors that significantly impact the results with the least number of trials. In this work, AOR is used as the response value to screen eight factors corresponding to the powders of PEEK/CF_30wt%. These factors with their initial parameter spaces are listed in Table 2. When determining the parameter space, the ratio of high and low levels of the two parameters is set to be identical in order to prevent significance fluctuation between the investigated factors [35]. The detailed design and results of the PB design are discussed in Section 4.2.

The BBD design is utilized to further investigate the optimal points of the key factors based on the PB results. The computed results are analyzed afterward by the response surface method. The corresponding variables are coded as follows:

$$X_i=\left(x_i{-x}_0\right)/{\Delta x}_i\left(i=1,2,\mathrm{...},k\right)$$

(23)

where X_i is the coded value of the independent factor, x₀ is the real value at the center point, x_i is the real value, and ∆x_i is the value of step-change.

The BBD model can be described by the quadratic equation:

$${Y=\beta }_0+{\displaystyle \sum {\beta }_i{X}_i}+{\displaystyle \sum {\beta }_{\mathrm{ii}}{X}_i^2}+{\displaystyle \sum {\beta }_{\mathrm{ij}}{X}_i}{X}_j\left(i=1,2,\mathrm{...},k\right)$$

(24)

where Y is the predicted response value (AOR in this work). X_i and X_j are the coded independent variables. β₀ is the offset term, β_i is the linear term, β_ii is the squared term, and β_ij is the interaction term.

GA is developed by imitating the mechanism of natural biological evolution. It is an efficient, parallel, global searching method, which can automatically acquire and accumulate knowledge about the searching space, and the searching process is adaptively controlled to obtain the optimal solution. The entire GA is achieved based on the Matlab GA toolbox in this work.

3.2. Powder deposition process

The reliability of the complete model is supposed to be experimentally verified. The comprehensive indicator AOR can be used as the target, which reflects the overall performance of the studied powder. In addition, this work investigates the effect of CF on the surface properties of the deposited powder layer through powder deposition experiments (similar to the scraper form of the actual PBF process) and corresponding simulation.

The surface roughness is the key factor in the powder deposition process. It has a great influence on the sintering process and the subsequent recoating process. Thus, it is necessary to investigate powder deposition through the powder dynamics model. By comparing with the corresponding experiment, the powder dynamics model can be further verified by this practical application.

The powder deposition is experimentally conducted based on a piece of slotted glass, which is shown in Figure 7(a). The preparation steps are proceeded as follows: (1) Prepare a piece of glass with a groove of 0.8-1 mm; (2) load enough powder manually in front of the groove; (3) use another piece of glass to scrape the loaded powders slowly from left to right with a tilt angle of around 45°; (4) the surface of the powders in the groove is smooth with the naked eye as shown in Figure 7(b); (5) The surface morphology of the target zones (Figure 7(c)) is measured by a microscope (J6000, Keyence, Shanghai, China). The observed area is located at the center of the powder layer.

In the DEM model, set the same conditions as the experiment. When the simulation of the powder deposition process is completed, obtain the surface particle contour curve at the center of the powder layer (as shown in Figure 7(d)). The fluctuation of the contour curve reflects the flatness of the powder surface.

4. Results and discussion

This section firstly describes the material properties of PEEK and PEEK/CF in detail, including the particle morphology, particle size, and AOR, determines the contact parameters between particles (such as rolling friction coefficient, restitution coefficient, and surface energy), and experimentally verifies the reliability of the determined parameters. Secondly, the powder deposition process is investigated through the experiment and the DEM simulation. The influence of CF particles on the surface performance of the powder deposition layer is analyzed.

4.1. Material evaluation

The particle size distribution is obtained as input information in DEM, and it significantly influences the computational efficiency. The SEM pictures of pure PEEK and PEEK/CF_30wt % are given in the following Figure 8. It shows that powder particles of PEEK are almost ellipsoidal. The diameter of CF is uniform, but the length distribution is obviously dispersed. To specifically characterize the particle size information, the powders of PEEK and CF are detected through the laser particle sizer and the results are given in Table 3 and Figure 9.

It shows that the average particle size of PEEK is larger than that of CF. The majority of PEEK particles are in the range of 30-60 μm while the lengths of numerous CF particles are scoped by 5-20 μm.

The restitution coefficient and the static friction coefficient are directly acquired according to the finite element simulation and inclined plane test respectively. The corresponding results are summarized in Table 4. It appears that the PEEK-related static friction coefficients reach higher values compared with the CF-CF, which is caused by the irregular shapes and unsmooth surface property of the PEEK particles. The glass-related static friction coefficients are minimum due to the glossy surface. As for the restitution coefficient, the PEEK particles possess good elasticity inducing the PEEK-related restitution coefficients to present larger values than the CF-related restitution coefficients.

The bulk density results of PEEK and PEEK/CF powders are shown in Table 5. It is observed that the bulk density of PEEK/CF is higher than that of the PEEK powder, and the bulk density of PEEK/CF increases with the increase of the CF mass fraction. Because the solid-phase density of CF is slightly higher than that of the PEEK, and most CF particles have smaller sizes, filling the pores between PEEK particles.

4.2. Results of DOE

The rolling friction coefficient and surface energy can not be directly measured through experimental methods, so the "PB-BBD-GA" method is used to acquire the optimal combination of rolling friction coefficient and surface energy. Therein, the PB design aims to determine the significant parameters of related rolling friction coefficient and surface energy. Detailed design and response results of the PB test are listed in Table 6. The significance analysis of the model and corresponding factors is given in Table 7.

As shown in Table 7, both R2 and Adjusted-R2 are close to 1, which means that the model and the chosen response value of AOR are reasonable. The significance can be reflected by the P-value. The p-value less than 0.05 correlates with the significant factor. Therefore, the parameters of PEEK-PEEK rolling friction coefficient (X0), PEEK-CF rolling friction coefficient (X1), and PEEK-PEEK surface energy (X5) have significant effects on the AOR. Among them, the influence of X0, X1, and X5 are in descending order, which can be obtained through the F-value. This indicates that the effect of the rolling friction coefficient is greater than that of surface energy in this work. Since the ellipsoidal particles of PEEK are replaced by round particles, the rolling friction coefficient should be utilized to make up for the shape approximation in the powder dynamics simulation. Analogous treatment is also found in the literature of [36,37]. Regarding the parameter of rolling friction coefficient/surface energy, the general influence order of PEEK-PEEK, PEEK-CF, and CF-CF is in descending trend, which means that the interaction between CF particles is minimally effective in the composite powders PEEK/CF.

Since the significant parameters (X0, X1, X5) are determined by the PB test, the remaining insignificant parameters can be reasonably fixed before the BBD design. The parameters of X2, X3, and X4 are fixed as 0.01, X6 and X7 are set to 0.001. Sequentially, the detailed BBD design (correlated with the parameters of X0, X1, and X5) and response-value of AOR are listed in Table 8. The variance analysis of the whole model and the corresponding factors are given in the following Table 9. Herein, the insignificant quadratic and cross-terms are eliminated for the convenience of analysis and subsequent calculation. The P-value of the model is extremely small, which shows that the entire model is reliable and the AOR can be reasonably predicted. Interestingly, the significance of cross-terms is greater than that of the quadratic term (eliminated here) in this numerical example.

Based on the results of the BBD design, the quadratic regression model for the response value (AOR) and the investigated variables (X0, X1, X5) can be established as:

$$\begin{array}{l}{\mathit{ROE}}_{\mathit{real}}=20.17425+52{.10569X}_0+60{.21470X}_1+228{.37659X}_5\\ -117{.3365X}_0{X}_1-1150{.8167X}_1{X}_5\\ (0.01\le X_0\le 0.2,0.01\le X_1\le 0.2,0.001\le X_5\le 0.02)\end{array}$$

(25)

$$\begin{array}{l}{\mathit{ROE}}_{\mathit{cod}}=35.29+4.92A+4.34B+0.475C-2.47\mathrm{AB}-1.59\mathrm{BC}\\ (A,B,C\in \left[-1,1\right])\end{array}$$

(26)

Therein, Eq. (25) is in terms of the actual factors and can be utilized to predict the AOR. Eq. (26) is in terms of the coded factors, which is necessary for the subsequent GA. In Eq. (26), the term A corresponds to X0, B corresponds to X1, and C corresponds to X5. The upper (-1) and lower limits (1) of the value range of term A correlated with the upper (0.01) and lower limits (0.2) of factor X0, which is also correspondingly applied for the terms B and C.

When the predictive equation of AOR is acquired based on the BBD design, the corresponding optimal parameters of rolling friction coefficient and surface energy can be achieved by making the predicted AOR equal to the experimental value (34.23° for the PEEK/CF_30wt%). Thus, the objective equation for the GA is expressed as

$${\left({\mathit{ROE}}_{\mathit{cod}}-34.23\right)}^2=0$$

(27)

Eq. (27) is input into the MATLAB GA toolbox with the value range of [–1,1] for all corresponding variables. The results are given in Table 10. So far, all the essential factors have been determined for the powder dynamics model.

4.3. Experimental verification

The calibrated DEM model for the PEEK/CF composite powders should be experimentally verified. As a comprehensive index of powder properties, AOR can be utilized to conduct the experimental verification work. The AOR experiment is carried out based on the standard GB11986-89. The Experimental AOR results of PEEK, PEEK/CF_30wt%, and PEEK/CF_50wt% are shown in Figure 10(a), with the detailed data listed in Table 11. The simulation results are shown in Figure 10(b), and the detailed data are given in Table 12. It appears that the experimental and simulation results show a maximal variance of 4.89 %, which can indicate the high reliability and effectiveness of the developed powder dynamics model.

It also reveals that the pure PEEK possesses the largest AOR, which implies the minimum of powder fluidity. With the addition of CF, the AOR of the composite powder decreases and the powder fluidity rises. Importantly, the AOR decreases with the increase of the weight fraction of CF, exhibiting improved powder fluidity. Since the powder fluidity is greatly affected by the cohesive effect between particles of PEEK-PEEK, PEEK-CF, and CF-CF. The influence of PEEK-PEEK, PEEK-CF, and CF-CF interfacial reactions on the composite AOR is in descending order (discussed in Section 4.2). The PEEK-related cohesion plays a dominant role in the PEEK/CF powder packing. Thus, the increased volume fraction of CF leads to the decrease of total cohesive interaction between particles, resulting in improved powder fluidity.

4.4. Evaluation of the powder deposition

The investigation of the powder deposition process is necessary to achieve the expected behaviors of the laser-sintered parts in PEEK/CF composites. The surface properties and recoating difficulty of powder layers can be evaluated in a qualitative fashion by the powder deposition process. Figure 11 shows the micro-pictures of the surface topography and undulation of PEEK, PEEK/CF_30wt%, and PEEK/CF_50wt%. It appears that the image quality of the surface morphology of PEEK is worse than the other two composite powders. This indicates a violent surface fluctuation of the PEEK powders, which is caused by the inhomogeneous particle distribution-induced porosity. With the addition of the CF, the surface quality is improved and also meliorates with the increase of the weight fraction of CF, which is caused by the particle distribution of the adopted CF. As shown in Figure 9(b), numerous CF particles exhibit the size range of 5-20 μm. These small and uneven CF particles exactly fill the inter-particle cavity among PEEK powders, and the surface of its powder bed is observed smoothly.

Figure 12 shows the cross-sections of the simulated powder deposition results. It also shows that drastic undulation occurs on the PEEK surface. The surface fluctuation of PEEK/CF_30wt% is slightly mitigated and improved a lot for the PEEK/CF_50wt%, which is consistent with the experimental results. The standard deviation of the surface contour curve of the powder deposition layer is used to quantitatively characterize the fluctuation of the layer surface. The fluctuation of the layer surface decreases with the decrease of the standard deviation, and the corresponding powder layer becomes smoother.

The experimental and simulation results of the standard deviation of the surface contour curve are shown in Figure 13 and Table 13. According to the experimental results, the surface smoothness of PEEK/CF_30wt% is increased by 31.3% compared to the PEEK powder, while the surface smoothness of PEEK/CF_50wt% powder is improved by 55.2% compared to PEEK powder. According to the simulation results, compared to the PEEK powder, the surface smoothness of the PEEK/CF_30wt% is increased by 27.4%, and 50.2% improved of the PEEK/CF_50wt% powder. The similar results of experimental and simulation further verifies the reliability of the DEM model.

In summary, the method of systematic material evaluation possesses universal applicability for different types of composite powders even multi-component composites. The powder dynamic modeling for composite powders has been developed to well simulate the composite powder deposition. The deposition parameters can be optimized using the DEM approach effectively.

5. Conclusions

This work proposes a systematic framework for material evaluation to incorporate with powder dynamics model for numerical investigation of composite powder deposition. PEEK/CF as typical feedstock materials of laser sintering are investigated, and the interaction of short CF and PEEK powders are quantified upon deposition. It shows that the AOR decreases with the increase of the weight fraction of CF. This indicates the improved powder fluidity with the addition of a proper percentage of CF with the length in 5-20 µm. The surface quality is also improved with the increase of the weight fraction of CF.

Importantly, this method is generally applicable to investigate the dynamic behaviors of different types of composite powders including multi-component particles. The developed deposition model can be helpful to optimize the deposition parameters and material composition so as to improve the packing quality of composite powders, which significantly influences the PBF process of composite materials in additive manufacturing.