Generalized Virtual Displacement Principles of Deformed Objects with Methods of Analytical Mechanics

Preprint

Article

Generalized Virtual Displacement Principles of Deformed Objects with Methods of Analytical Mechanics

Altmetrics

Downloads

116

Views

Comments

Chun Xiang^*,

Chun Xiang^*,

This version is not peer-reviewed

Submitted:

01 June 2023

Posted:

01 June 2023

You are already at the latest version

Alerts

Abstract

Analytical mechanics is the most basic discipline. The basic principles of analytical mechanics should also be applicable to general deformed objects. However, the virtual displacement principle proposed by analytical mechanics is only applicable to particle systems and rigid body systems, but not to general deformed objects. In this paper, the generalized virtual displacement principle of general deformed objects (such as, elastic objects, plastic objects, elasto-platic objects and flexible objects etc ) is derived by the method of analytical mechanics, which is also applicable to particle systems and rigid body systems. First of all, according to the method of analytical mechanics, the external force, internal force, constraint reaction force and elastic recovery force of the deformed object system under the equilibrium state are analyzed, and the concepts of virtual displacement, ideal constraint and virtual work are introduced, and the generalized virtual displacement principle (also called generalized virtual work principle) of deformed objects is proposed; secondly, vector form, coordinate component form and generalized coordinate form of generalized virtual displacement principle of deformed object are given; thirdly, as the application of the principle, the virtual displacement principle of deformed objects in plane polar coordinate system, space cylindrical coordinate system and spherical coordinate system is given; finally, a brief conclusion is drawn. This work unifies the virtual displacement principle of elastic object, plastic, elastoplastic etc deformed object systems and rigid object systems with the basic method of analytical mechanics. It is a basic principle for dealing with the static problems of deformed objects. This work also lays a foundation for the further study of the dynamics of deformed object systems.

Keywords:

Subject: Computer Science and Mathematics - Robotics

1. Introduction

Analytical mechanics is a mechanical system suitable for studying macro object. However, now his research objects are the particle system, and the number of particles can be from one to infinity. Particle system can be regarded as an ideal model of mechanical system composed of macro objects, such as rigid body, elastomeric, elastic-plastic, continuous medium and their complex. These rigid bodies and deformed objects can be studied by the method of analytical mechanics. Analytical mechanics uses generalized coordinates, puts forward ideal constraints, and studies the motion of macro objects from the perspective of finding the energy of the system[1,2]. Analytical mechanics puts forward two basic principles of constraint mechanics system, namely, virtual displacement principle and d'Alembert-Lagrange principle (also known as general dynamic equation). Using the virtual displacement principle, we can solve the static problems of the constrained object system. Using the D’alamber-Lagrange principle, we can further derive various forms of dynamic equations and solve the dynamic problems of the constrained dynamical system. [3] The important concept of virtual displacement of an object is put forward in analytical mechanics. The virtual displacement of an object must meet the constraints of the object. It is a collection of infinitesimal displacements that may occur in the space region at a certain instant or at a certain position. There can be an infinite number of virtual displacements, which are independent of the motion of the object. The two basic principles of analytical mechanics are based on this concept[4,5]. We should point out that the most basic virtual displacement principle given by analytical mechanics should be applicable to rigid bodies and deformed objects, while analytical mechanics only gives the virtual displacement principle of rigid objects and their combinations, which solves the static problems of rigid objects [1,2,3,4]. Obviously, the virtual displacement principle given previously in analytical mechanics is limited in application.

We can divide macroscopic objects into rigid bodies and deformed objects. The static and dynamic problems of rigid bodies and their combinations have been comprehensively and deeply studied in existing theories of analytical mechanics, which has been formed. [5,7,8] Deformable objects can be divided into elastic objects and elastic-plastic objects. The principle of virtual displacement of deformed objects has been given in structural mechanics, which is a basic principle of deformed objects[9,10]. The principle of virtual displacement of deformed objects is that the virtual work done directly by external forces (including volume force and area force) is equal to the strain energy required of deformed objects, or the principle of virtual displacement is obtained by using the second law of thermodynamics. However, in these studies, the important concepts of virtual displacement and ideal constraint are rarely discussed. In fact, the virtual displacement of deformation object must meet the constraint condition, and the constraints are the ideal constraint. Elastic-plastic objects are deformable objects that can be elastic or plastic in different environments. Elastoplasticity is a basic property in material forming. The virtual displacement principle of elastic-plastic objects is of great value in the research of material forming. The establishment of the virtual displacement principle of elastic-plastic deformable body is also based on the fact that the virtual work of the external force on the deformable body is equal to the virtual strain energy of the elastic body. We should point out that the virtual displacement principle of elastic-plastic objects must also be limited by ideal constraints. It can be seen that the virtual displacement principle of deformed objects in structural mechanics and elasticity rarely involves the concept of ideal constraints, nor is it based on the balance of deformed objects under external forces.

In the history of scientific development, people always try to unify the basic theories of mechanics, elastic mechanics, continuum mechanics, thermodynamics, electromagnetics, solids and deformed objects to better reveal the development laws of nature. At the turn of the 20th century, attempts to unify laws of mechanics and laws of reversible thermodynamics were made successfully by Hadamard [11] for thermal expansion of ideal gas. Efforts to unify two laws continued and was extended to irreversible thermodynamic law recently [12,13]. In 1973, Germain [14] extended the principle of virtual work in classical continuum mechanics for continua to multipolar media, called principle of Virtual Power, which was further extended by Maugin to couple the thermo-mechanical field with electro-magnetic field [15]. At the end of 20th century, many research works of the irreversible thermodynamic that included irreversible thermodynamics done by Maugin [16] and others afterwards have been summarized in a major research monograph. A unified procedure for constructing theories of thermomechanics of multipolar media was initiated by Green and Rivlin[17] and then extended to include thermodynamics by Green and Naghdi[18,19]. Attempts were made by Sieniutycz and Berry [20] to define a Lagrangian in an action-type integral for the deformation of continuum with dissipation, and by Maugin [21] to develop the analytical mechanics of dissipative materials. In all these major works except the one by Biot, the constitutive equations of material must still be supplemented from the laws of thermodynamics or other postulates. In 2011, Pao et al unify the principle of virtual power of thermomechanics for fluids and solids with dissipation[22]. In recent years, the principle of virtual displacement has been widely used in science and engineering technology, and many good results have been achieved [23,24,25,26]. For the deformed object system, the key to solve the problem is to consider the physical properties (constitutive relations) of the object materials.

In this paper, the generalized principle of virtual displacement of constrained deformed objects is proposed by using the method of analytical mechanics. For the deformed object in equilibrium, based on the concept of ideal constraint, under the action of volume external force and area external force, the virtual displacement satisfying the constraint conditions of the deformed object is introduced, and the virtual displacement principle of the general deformed object is proposed. The generalized virtual displacement principle proposed by is general, which is not only suitable for elastic objects, plastic objects and flexible material objects, but also suitable for rigid objects.

The research of this paper is divided into the following parts: Section 1, introduction; section 2, in this part, the generalized principle of virtual displacement of deformed objects is proposed using the method of analytical mechanics; section 3, several forms of virtual displacement principle of deformed object are given; section 4, virtual displacement principle of deformed objects is applied in plane polar coordinate, space cylindrical and spherical coordinates; section 5, a simple conclusion is given.

2. Generalized Virtual Displacement Principle of the Deformation Objects

The generalized virtual displacement principle of deformed object is a basic principle of deformed object dynamics. It can solve the static problems of deformed object, including the deformation problem when the system is in equilibrium or uniform motion under the action of external force. In this section, we only study the deformation problem in equilibrium, and the conclusion is also suitable for the deformation problem in uniform motion.

2.1. Establishing of Virtual Displacement Principle

For a deformed volume element ΔV_i in equilibrium state, it is affected by external force including the volume force

f_{i}^{V}

distributed in the region V and the area force

f_{i}^{S}

acting on the area ΔS_i，the other are internal forces

f_{i}^{i}

（namely gravitation between particles），elastic restoring force

f_{i}^{I}

and constraint force

R_{i}

， the resultant force is equal to zero, namely

f_{i}^{V} + f_{i}^{S} + f_{i}^{i} + f_{i}^{I} + R_{i} = 0

(1)

At a certain time t, it is assumed that the deformed volume element has a virtual displacement

δ r_{i}

, then the virtual work of the forces on the deformed object is written in the form

\begin{array}{l} Δ W = \sum_{i = 1}^{N} f_{i}^{V} \cdot δ r_{i} Δ V_{i} + \sum_{i = 1}^{N} f_{i}^{S} \cdot δ r_{i} Δ S_{i} + \sum_{i = 1}^{N} f_{i}^{i} \cdot δ r_{i} Δ V_{i} \\ + \sum_{i = 1}^{N} f_{i}^{I} \cdot δ r_{i} Δ V_{i} + \sum_{i = 1}^{N} R_{i} \cdot δ r_{i} Δ S_{i} = 0 \end{array}

(2)

where ΔS_i is the deformed area element.

Since the gravitation between particles is a pair of forces and reactions, so

\sum_{i = 1}^{N} f_{i}^{i} \cdot δ r_{i} Δ V_{i} = 0.

(3)

Assumption based on the concept of ideal constraints, one has

\sum_{i = 1}^{N} R_{i} \cdot δ r_{i} Δ V_{i} = 0.

(4)

Substitution of Eqs.( 3) , (4) into Eq.(2) ,we have

Δ W = \sum_{i = 1}^{N} f_{i}^{V} \cdot δ r_{i} Δ V_{i} + \sum_{i = 1}^{N} f_{i}^{S} \cdot δ r_{i} Δ S_{i} + \sum_{i = 1}^{N} f_{i}^{I} \cdot δ r_{i} Δ V_{i} = 0,

(5)

then the virtual work of deformable body under the virtual displacement

δ r_{i}

can be written the following form

δ W = \int_{V} f_{}^{V} \cdot δ r d V + \int_{V} f_{}^{S} \cdot δ r d S + \int_{V} f_{}^{I} \cdot δ r d V = 0

(6)

It is well known that the relationship of between the virtual work of elastic resilience and the virtual strain energy of defamation object is the flowing form

δ U = - \int_{V} f^{I} \cdot δ r d V = \int_{V} σ_{i j} δ ε_{i j} d V

(7)

Substitution of the Eq.(7) into the Eq.(6), one has

δ U = \int_{V} f_{}^{V} \cdot δ r d V + \int_{S} f_{}^{S} \cdot δ r d S = δ W,

(8)

δ U = \int_{V} σ_{i j} δ ε_{i j} d V = \int_{V} f^{v} \cdot δ r d V + \int_{S} f^{s} \cdot δ r d S = \int_{V} (f^{V} + \nabla \cdot f^{S}) \cdot δ r d V .

(9)

The Eq. (8) or Eq. (9) are called the generalized virtual displacement principle of deformation object in the equilibrium. Where the volume force

f_{}^{V}

is a force there are proportional to the mass of each particle of a deformed object, such as gravity, magnetic force and

f_{}^{S}

the inertial force, reaction force and friction force etc. We call

f^{V} + \nabla \cdot f^{S} = f

equivalent volume force.

2.2. Formulation of generalized virtual displacement principle

Generalized virtual displacement principle: the sufficient and necessary condition for the balance of an object is the sum of the virtual work on the virtual displacement of the active force acting on the defamation object, under the ideal constraint, including the external force and the elastic restoring force, is equal to zero. That is the sum of virtual works of the external force equal the strain energy of defamation object.

We proposed that the virtual displacement principle of defamation object, which it is a generalized principle on body balance. Using this principle, we can obtain the virtual displacement principles of elastic object, plastic object, elastic-plastic object and flexible object etc. we can also obtain the virtual displacement principles of the particle, the rigid object, the multibody.

3. Several Forms on the Virtual Displacement Principle

In this section, we give the several different expressions of virtual displacement principle of deformed objects.

3.1. Vector Form on the Virtual Displacement Principle

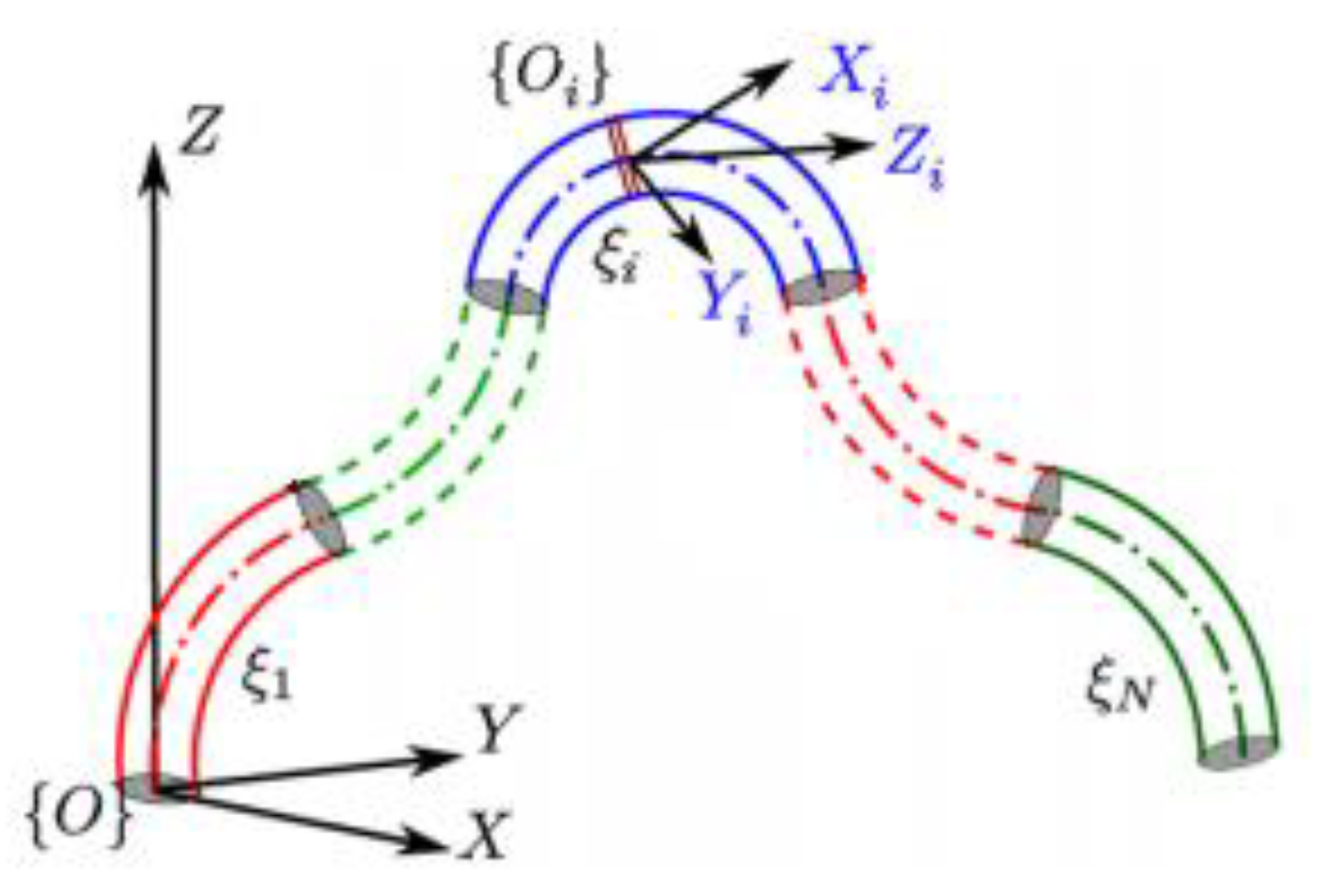
A deformed object as shown in Figure 1: Let an elastic body consist of N flexible volume elements, which deform under the action of external force. The inertial coordinate system is established at the bottom of the elastic body, the unit vectors of the coordinate axis are (e₁, e₂, e₃), and the other end is the free end.

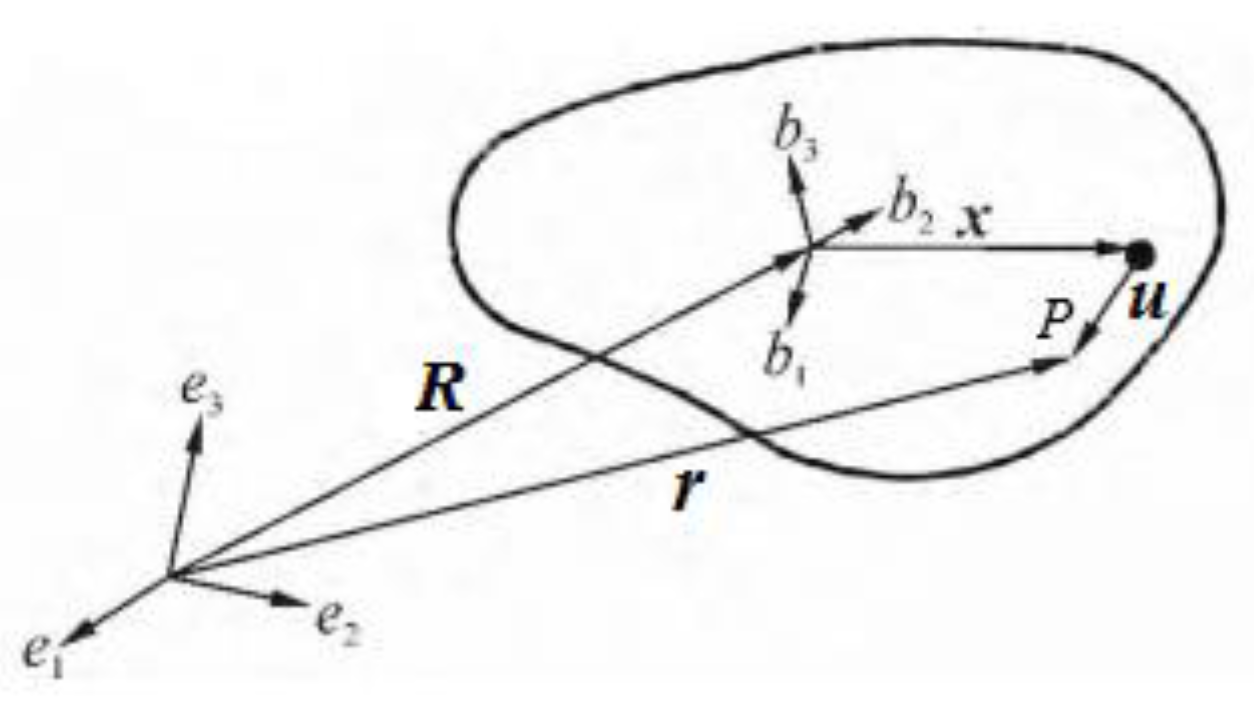
Different from the rigid body system, the deformation of body under the action of external force, and the relative position of each point in the system also changes. In order to accurately describe the motion and deformation of the body, the fixed inertial coordinate system (e₁, e₂ e₃) and the moving coordinate system (b₁, b₂, b₃) are established. For any point in the deformable body, the position vector is expressed in Figure 2.

For a deformed object, the radius vector

δ r

of volume element is written as

δ r = δ (R + A x + A u) = δ X + δ u ， X = R + A x

(10)

where

δ R

is the virtual displacement of centroid of deformed object, A is the coordinate transformation matrix,

δ X

is the virtual displacement of rigid body time, and

δ u

is the virtual displacement of deformation object. The Eq. (6) is expressed in the form

\begin{array}{l} δ W = \int_{V} f^{V} \cdot δ X d V + \int_{S} f^{S} \cdot δ X d S \\ + \int_{V} f^{V} \cdot A δ u d V + \int_{S} f^{S} \cdot A δ u d S + \int_{V} f^{I} \cdot A δ u d V = 0 ， \end{array}

(11)

we should points out that the Eq.(11) is the generalized virtual displacement principle of deformable object in equilibrium state. That is the sum of the virtual work done by the volume force, area force and elastic restoring force of deformable object equal to zero in equilibrium state. At this time, the spatial motion of the deformable object is in states of static or uniform motion, and the virtual displacement principle of rigid object in equilibrium state needs to be satisfied, that is

\int_{V} f_{}^{V} \cdot δ X d V + \int_{S} f^{S} \cdot δ X d S = 0,

(12)

then the deformation motion of the object must also be in the state of static or uniform motion, which satisfies the virtual displacement principle, namely

\int_{V} f^{V} \cdot δ u d V + \int_{S} f_{}^{S} \cdot δ u d S + \int_{V} f_{}^{I} \cdot δ u d V = 0,

(13)

namely

\int_{V} f^{V} \cdot δ u d V + \int_{S} f_{}^{S} \cdot δ u d S = \int_{V} (f^{V} + \nabla \cdot f_{}^{S}) \cdot δ u d V = \int_{V} f \cdot δ u d V = \int_{V} σ δ ε d V .

(14)

The Eq.(11) are called the vector forms of generalized virtual displacement principle for defamation objects. We are also Eq.(14) the vector forms of virtual displacement principle of defamation objects and the Eq.(12) the virtual displacement principle of the particle system and Rigid objects.

Now we give the following conclusions: for the deformed object in equilibrium or static state, its overall motion satisfies the virtual displacement principle (12) of rigid body, and the deformation motion satisfies the virtual displacement principle (14) of deformed object.

δ u = 0

, the Eq.(11) express the vector forms of virtual displacement principle (12) of the rigid objects.

If we focus of the deformation of objects on the equilibrium problem, then the Eq.(14) expresses the vector forms of virtual displacement principle of defamation objects.

3.2. Coordinate component form of virtual displacement principle:

Take the inertial coordinate system, the unit vectors of their coordinate axis are (e₁, e₂, e₃), and we express the external forces

f^{V}

and

f^{S}

, elastic restoring force

f^{I}

and virtual displacement in the form of inertial coordinate system. The external force

f^{V}, f^{^{S}}, f^{I}

and

δ r

are written the component forms respectively

\begin{array}{l} f^{V} = f_{x}^{V} e_{1} + f_{y}^{V} e_{2} + f_{z}^{V} e_{3}, f^{S} = f_{x}^{S} e_{1} + f_{y}^{S} e_{2} + f_{z}^{S} e_{3}, \\ f_{i}^{I} = f_{x}^{I} e_{1} + f_{y}^{I} e_{2} + f_{z}^{I} e_{3} \end{array}

(15)

and

\begin{array}{l} δ r = δ (A x + A u) = \\ + A δ x e_{1} + A δ y e_{2} + A δ z e_{3} + A δ u e_{1} + A δ v e_{2} + A δ w e_{3} . \end{array}

(16)

where A is a transformation matrix between two coordinate systems.

Then the virtual displacement principle is expressed the following coordinate component forms

\begin{array}{l} \int_{V} A [f_{x}^{V} δ x + f_{y}^{V} δ y + f_{z}^{V} δ z] d V \\ + \int_{V} [(f_{x}^{V} + f_{x}^{I}) A δ u + (f_{y}^{V} + f_{y}^{I}) A δ v + (f_{z}^{V} + f_{z}^{I}) A δ w] d V \\ + \int_{S} (f_{x}^{S} δ x + f_{y}^{S} δ y + f_{z}^{S} δ z) d S + \int_{S} (f_{x}^{S} A δ u + f_{y}^{S} A δ v + f_{z}^{S} A δ w) d S = 0 ， \end{array}

(17)

namely

\int_{V} [f_{x}^{V} δ x + f_{y}^{V} δ y + f_{z}^{V} δ z] d V + \int_{S} (f_{x}^{S} δ x + f_{y}^{S} δ y + f_{z}^{S} δ z) d S = 0

(18)

\begin{array}{l} \int_{V} [(f_{x}^{V} + f_{x}^{I}) A δ u + (f_{y}^{V} + f_{y}^{I}) A δ v + (f_{z}^{V} + f_{z}^{I}) A δ w] d V \\ + \int_{S} (f_{x}^{S} A δ u + f_{y}^{S} A δ v + f_{z}^{S} A δ w) d S = 0. \end{array}

(19)

the Eq.(18) is also written as

\begin{array}{l} \int_{V} (f_{x}^{V} A δ u + f_{y}^{V} A δ v + f_{z}^{V} A δ w) d V \\ + \int_{S} (f_{x}^{S} A δ u + f_{y}^{S} A δ v + f_{z}^{S} A δ w) d S = \int_{V} σ_{i j} δ ε_{i j} d V . \end{array}

(20)

We should point out Eq.(18) is the coordinate component form of generalized virtual displacement principle of the deformed object considering the overall motion (rigid body) in the equilibrium state, and Eq.(20) is the coordinate component form of generalized virtual displacement principle of the deformed object in the equilibrium state.

3.3. Generalized coordinate form of the virtual displacement principle.

The virtual displacement principle is the most common principle of statics and it is widely used to solve the statics problems. The virtual displacement principle on generalized coordinates is expressed by: Under the double-sided, ideal, Holonomic and stable constraints, the necessary and sufficient condition for the equilibrium of deformation body is that the sum of the element work in any virtual displacement of the volume force, area force and elastic resilience acting on the system is equal to zero.

In the deformation body composed of N units, we take any unit body dV_i and its area dS_i , which it affected by the external force

f_{i}^{V}

, the area force

f_{i}^{S}

, elastic restoring force

f_{i}^{I}

and constraint force

R_{i}

Supposing the deformation body suffering l holonomic constraints, and the number of independent variables describing the system is n=3N-l, then the system described by n generalized coordinates q_1, q_2,

\dots

_,q_n. The position of a point of deformed object is represented as

r = r (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}), x_{i} = x_{i} (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}), i = 1, 2, 3

(21)

the position of a point of a deformed object is represented. This deformation displacement can be expressed as

u_{i} = u_{i} (x_{1} (q), x_{2} (q), x_{3} (q)) = u_{i} (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}), i = 1, 2, 3

(22)

The stress and strain components can be written, respectively, as

\begin{array}{l} σ_{i j} = σ_{i j} (x_{1} (q), x_{2} (q), x_{3} (q)) = σ_{i j} (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}), \\ ε_{i j} = ε_{i j} (x_{1} (q), x_{2} (q), x_{3} (q)) = ε_{i j} (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}) . \end{array}

(23)

The components of virtual displacement

δ r

δ x

and

δ u

are expressed, respectively, in the following forms

\begin{array}{l} δ r = \frac{\partial r}{\partial q_{s}} δ q_{s}, s = 1, 2, \cdot \cdot \cdot, n \\ δ x_{1} = δ x = \frac{\partial x}{\partial q_{s}} δ q_{s}, δ x_{2} = δ y = \frac{\partial y}{\partial q_{s}} δ q_{s}, δ x_{3} = δ z = \frac{\partial z}{\partial q_{s}} δ q_{s}, \\ δ u = \frac{\partial u}{\partial x_{i}} \frac{\partial x_{i}}{\partial q_{s}} δ q_{s} = \frac{\partial u}{\partial q_{s}} δ q_{s}, δ v = \frac{\partial v}{\partial x_{i}} \frac{\partial x_{i}}{\partial q_{s}} = \frac{\partial v}{\partial q_{s}} δ q_{s}, δ w = \frac{\partial w}{\partial x_{i}} \frac{\partial x_{i}}{\partial q_{s}} = \frac{\partial w}{\partial q_{s}} δ q_{s} . \end{array}

(24)

The virtual strain

δ ε_{i j},

virtual stress

δ σ_{i j}

, which can be expressed as the forms of generalized coordinates respectively

\begin{array}{l} ε_{i j} = ε_{i j} (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}), σ_{i j} = σ_{i j} (q_{1}, q_{2}, \cdot \cdot \cdot, q_{n}) \\ δ ε_{i j} = \frac{\partial ε_{i j}}{\partial x_{i}} \frac{\partial x_{i}}{\partial q_{s}} δ q_{s} = \frac{\partial ε_{i j}}{\partial q_{s}} δ q_{s} ， (s = 1, 2, \cdot \cdot \cdot, n; i, j = 1, 2, 3) \\ δ σ_{i j} = \frac{\partial σ_{i j}}{\partial x_{i}} \frac{\partial x_{i}}{\partial q_{s}} δ q_{s} = \frac{\partial σ_{i j}}{\partial q_{s}} δ q \end{array}

(25)

The generalized virtual displacement principle of deformation objects are written in following general coordinate form

\begin{array}{l} \int_{V} σ_{i j} \frac{\partial ε_{i j}}{\partial q_{s}} δ q_{s} d V = \int_{V} (f_{x}^{V} \frac{\partial x}{\partial q_{s}} + f_{y}^{V} \frac{\partial y}{\partial q_{s}} + f_{z}^{V} \frac{\partial z}{\partial q_{s}}) δ q_{s} d V \\ + \int_{S} (f_{x}^{S} \frac{\partial x}{\partial q_{s}} + f_{y}^{S} \frac{\partial y}{\partial q_{s}} + f_{z}^{S} \frac{\partial z}{\partial q_{s}}) δ q_{s} d S \\ + \int_{V} (f_{x}^{V} \frac{\partial u}{\partial q_{s}} + f_{y}^{V} \frac{\partial v}{\partial q_{s}} + f_{z}^{V} \frac{\partial w}{\partial q_{s}}) δ q_{s} d V \\ + \int_{S} (f_{x}^{S} \frac{\partial u}{\partial q_{s}} + f_{y}^{S} \frac{\partial v}{\partial q_{s}} + f_{z}^{S} \frac{\partial w}{\partial q_{s}}) δ q_{s} d S \\ = \int_{V} Q_{s}^{V} δ q_{s} d V + \int_{S} Q_{s}^{S} δ q_{s} d S + \int_{V} Φ_{s}^{V} δ q_{s} d V + \int_{S} Φ_{s}^{S} δ q_{s} d S . \end{array}

(26)

When the deformed body being in equilibrium, we have the virtual displacement principles of rigidity objects as

\int_{V} Q_{s}^{V} δ q_{s} d V + \int_{S} Q_{s}^{S} δ q_{s} d S = 0,

(27)

and the virtual displacement principles of deformation objects

\int_{V} σ_{i j} \frac{\partial ε_{i j}}{\partial q_{s}} δ q_{s} d V = \int_{V} Φ_{s}^{V} δ q_{s} d V + \int_{S} Φ_{s}^{S} δ q_{s} d S,

(28)

where the

Φ_{s}^{V}

Φ_{s}^{S}

are generalized volume and area forces, and the strain energy is the following form

\begin{array}{l} \int_{V} σ_{i j} δ ε_{i j} d V = \int_{V} σ_{i j} \frac{\partial ε_{i j}}{\partial q_{s}} δ q_{s} d V = \int_{V} σ_{i j} \frac{\partial ε_{i j}}{\partial x_{i}} \frac{\partial x_{i}}{\partial q_{s}} δ q_{s} d V ， \\ i, j = 1, 2, 3; s = 1, 2, \cdot \cdot \cdot, n \end{array}

(29)

We should show that the q_s are lengths,

Φ_{s}^{V}

Φ_{s}^{S}

are the generalized forces, and the q_s is angles,

Φ_{s}^{V}

Φ_{s}^{S}

the generalized moments.

The Eqs.(27) and (28) are called the virtual displacement principle of deformed objects and rigid objects under the generalized coordinate respectively， and the Eq.(26) the generalized virtual displacement principle of deformed objects in the generalized coordinate .

4. Application of the Generalized Virtual Displacement Principle of Deformation Object

In this section, we give the virtual displacement principles and constitutive relations of deformation objects under polar coordinate, cylindrical coordinate and spherical coordinate systems using the generalized virtual displacement principle of systems.

4.1. Polar Coordinate Form of the Virtual Displacement Principle of Elastic Plane Problems

In the study of plane problems, the section geometry (boundary) of some objects is circular and annular shaped, we taking generalized coordinates q₁=r, q₂=

θ

. That is described by polar coordinate

(r ， θ)

and subject to volume forces

f_{r}, f_{θ}

and area forces

F_{r}, F_{θ}

. In this section, we give the polar coordinate form of the virtual displacement principle of plane deformation problems.

The relationships between rectangular coordinates and polar coordinates are written as

x = r \cos θ, y = r \sin θ,

(30)

and

\begin{array}{l} \frac{\partial}{\partial x} = \frac{\partial}{\partial r} \frac{\partial r}{\partial x} + \frac{\partial}{\partial θ} \frac{\partial θ}{\partial x} = \cos θ \frac{\partial}{\partial r} - \frac{\sin θ}{r} \frac{\partial}{\partial θ}, \\ \frac{\partial}{\partial y} = \frac{\partial}{\partial r} \frac{\partial r}{\partial y} + \frac{\partial}{\partial θ} \frac{\partial θ}{\partial y} = \sin θ \frac{\partial}{\partial r} - \frac{\cos θ}{r} \frac{\partial}{\partial θ} . \end{array}

(31)

We can obtain

\nabla^{2} = \frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} = \frac{\partial^{2}}{\partial r^{2}} + \frac{1}{r} \frac{\partial}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}} .

(32)

Strain components

ε_{r}, ε_{θ}

and

γ_{r θ}

are written as []

ε_{r} = \frac{\partial u_{r}}{\partial r}, ε_{θ} = \frac{u_{r}}{r} + \frac{1}{r} \frac{\partial u_{θ}}{\partial θ}, γ_{r θ} = \frac{1}{r} \frac{\partial u_{r}}{\partial θ} + \frac{\partial u_{θ}}{\partial r} - \frac{u_{θ}}{r} .

(33)

where

u_{r}, u_{θ}

are the displacements along

r, θ

direction.

In the polar coordinate system, the stresses in the plane are written as

σ_{r}, σ_{θ}, τ_{r θ}

. For plane stress problem, the constitutive relation:

ε_{r} = \frac{1}{E} (σ_{r} - v σ_{θ}), ε_{θ} = \frac{1}{E} (σ_{θ} - v σ_{r}), γ_{r θ} = \frac{2 (1 + ν)}{E} τ_{r θ},

(34)

for plane strain problem, the constitutive relation:

σ_{r} = \frac{1 - v^{2}}{E} (ε_{r} - \frac{v}{1 - v} ε_{θ}), σ_{θ} = \frac{1 - v^{2}}{E} (ε_{θ} - \frac{v}{1 - v} ε_{r}), τ_{r θ} = \frac{2 (1 + v)}{E} γ_{r θ} .

(35)

Using the virtual displacement principle of plane elastic body we can obtain the equilibrium equations in the following polar coordinate form [31]

\begin{array}{l} \frac{\partial σ_{r}}{\partial r} + \frac{1}{r} \frac{\partial τ_{r θ}}{\partial θ} + \frac{1}{r} (σ_{r} - σ_{θ}) + f_{r} = 0, \\ \frac{\partial τ_{r θ}}{\partial r} + \frac{1}{r} \frac{\partial σ_{θ}}{\partial θ} + \frac{2 τ_{r θ}}{r} + f_{θ} = 0, \end{array}

(36)

and strain compatibility equation as

\frac{1}{r^{2}} \frac{\partial^{2} ε_{r}}{\partial θ^{2}} + \frac{1}{r} \frac{\partial^{2}}{\partial r^{2}} (r ε_{θ}) - \frac{1}{r^{2}} \frac{\partial^{2}}{\partial r \partial θ} (r γ_{r θ}) - \frac{1}{r} \frac{\partial ε_{r}}{\partial r} = 0.

(37)

The stress in plane strain problem are expressed by

\begin{array}{l} σ_{r} = \frac{E}{1 - v^{2}} (ε_{r} + v ε_{θ}) = \frac{E}{1 - v^{2}} [\frac{\partial u_{r}}{\partial r} + v (\frac{1}{r} \frac{\partial u_{θ}}{\partial θ} + \frac{u_{r}}{r})], \\ σ_{θ} = \frac{E}{1 - v^{2}} (ε_{θ} + v ε_{r}) = \frac{E}{1 - v^{2}} (\frac{1}{r} \frac{\partial u_{θ}}{\partial θ} + \frac{u_{r}}{r} + v \frac{\partial u_{r}}{\partial r}), \\ τ_{r θ} = \frac{E}{2 (1 + v)} γ_{r θ} = \frac{E}{2 (1 + v)} (\frac{1}{r} \frac{\partial u_{θ}}{\partial θ} + \frac{\partial u_{θ}}{\partial r} - \frac{u_{θ}}{r}) . \end{array}

(38)

When the volume force

f_{r} = f_{θ} = 0

, the stress component in the basic equation of the stress method can be expressed as an unknown function

φ (r, θ) = 0

to be solved, and the equation satisfied by the stress function

φ (r, θ)

[31]

\nabla^{4} φ (r, θ) = {(\frac{\partial^{2}}{\partial r^{2}} + \frac{1}{r} \frac{\partial}{\partial r} + \frac{1}{r^{2}} \frac{\partial^{2}}{\partial θ^{2}})}^{2} φ (r, θ) = 0,

(39)

the stress component

σ_{r}, σ_{θ}, τ_{r θ}

of the polar coordinate system is obtained by the differential of

φ (r, θ)

, that is,

\begin{array}{l} σ_{r} = \frac{1}{r^{2}} \frac{\partial^{2} φ}{\partial θ^{2}} + \frac{1}{r} \frac{\partial φ}{\partial r}, σ_{θ} = \frac{\partial^{2} φ}{\partial r^{2}}, \\ τ_{r θ} = τ_{θ r} = - \frac{\partial}{\partial r} (\frac{1}{r} \frac{\partial φ}{\partial θ}) = \frac{1}{r^{2}} \frac{\partial φ}{\partial θ} - \frac{1}{r} \frac{\partial^{2}}{\partial r \partial θ} \end{array}

(40)

4.2. Cylindrical coordinate form of the virtual displacement principle of elastic object

For dynamic problems, the choice of coordinate system itself has nothing to do with the solution of the problem, but the choice of coordinate system is closely related to the description of dynamic equations and boundary conditions of the problem. In other words, the choice of coordinate system directly affects the difficulty of solving the problem.

In this section, we taking the generalized coordinates

q_{1} = r, q_{2} = θ, q_{3} = z

, then the virtual displacement principle of deformation objects in the cylindrical coordinate system is obtained with the generalized virtual displacement principle Eq.(27) of deformation objects.

In the cylindrical coordinate system, the position coordinates of a point m in space are represented by

(r, θ, z)

. The relationships between rectangular coordinates and generalized coordinates are

x = r \cos θ, y = r \sin θ, z = z .

(41)

The displacement components in generalized coordinates (cylindrical coordinates) are

u_{r} = u_{r} (r, θ, z), u_{θ} = u_{θ} (r, θ, z), w = w (r, θ, z),

(42)

the stress components as

\begin{array}{l} σ_{r} = σ_{r} (r, θ, z), σ_{θ} = σ_{θ} (r, θ, z), σ_{z} = σ_{z} (r, θ, z), \\ τ_{r θ} = τ_{r θ} (r, θ, z), τ_{θ z} = τ_{θ z} (r, θ, z), τ_{z r} = τ_{z r} (r, θ, z), \end{array}

(43)

and the strain components as

\begin{array}{l} ε_{r} = ε_{r} (r, θ, z), ε_{θ} = ε_{θ} (r, θ, z), ε_{z} = ε_{z} (r, θ, z), \\ γ_{r θ} = τ_{r θ} (r, θ, z), γ_{θ z} = γ_{θ z} (r, θ, z), γ_{z r} = γ_{z r} (r, θ, z) . \end{array}

(44)

The relationship between strain components and displacement components in generalized coordinates are the following form

\begin{array}{l} ε_{r} = \frac{\partial u_{r}}{\partial r}, ε_{θ} = \frac{u_{r}}{r} + \frac{1}{r} \frac{\partial u_{θ}}{\partial θ}, ε_{z} = \frac{\partial w}{\partial z}, \\ γ_{r θ} = \frac{1}{r} \frac{\partial u_{r}}{\partial θ} + \frac{\partial u_{θ}}{\partial r} - \frac{u_{θ}}{r}, γ_{z θ} = \frac{1}{r} \frac{\partial w}{\partial θ} + \frac{\partial u_{θ}}{\partial z}, γ_{r z} = \frac{\partial u_{r}}{\partial z} + \frac{\partial w}{\partial r} . \end{array}

(45)

The Eqs. (45) are also called the strain tensor of an elastic body in cylindrical coordinate.

The constitutive relations of deformation object in cylindrical coordinates are written as [31]

\begin{array}{l} σ_{r} = λ φ + 2 μ ε_{r}, σ_{θ} = λ φ + 2 μ ε_{θ}, σ_{z} = λ φ + 2 μ ε_{z}, \\ τ_{z r} = μ γ_{z r}, τ_{r θ} = μ γ_{r θ}, τ_{z θ} = μ γ_{z θ}, \end{array}

(46)

where

λ = \frac{E v}{(1 + v) (1 - v)}, μ = \frac{E}{2 (1 + v)} .

(47)

We call Eqs. (46) the constitutive relations of an elastic deformation object in cylindrical coordinate.

In cylindrical coordinates, the equilibrium equation of elastic object are obtained using the virtual displacement principle Eq.(27) [31]

\begin{array}{l} \frac{\partial σ_{r}}{\partial r} + \frac{1}{r} \frac{\partial τ_{r θ}}{\partial θ} + \frac{\partial τ_{z r}}{\partial z} + \frac{σ_{r} - σ_{θ}}{r} + F_{r} = 0, \\ \frac{\partial τ_{r θ}}{\partial r} + \frac{1}{r} \frac{\partial σ_{θ}}{\partial θ} + \frac{\partial τ_{z θ}}{\partial z} + \frac{2 τ_{r θ}}{r} + F_{θ} = 0, \\ \frac{\partial τ_{z r}}{\partial r} + \frac{1}{r} \frac{\partial τ_{z θ}}{\partial θ} + \frac{\partial τ_{z}}{\partial z} + \frac{2 τ_{z r}}{r} + F_{z} = 0. \end{array}

(48)

For the problem of axi-symmetry, that is, when the geometry, boundary conditions and constraints of the elastic body are symmetrical to a certain axis of symmetry, such as the z-axis, according to the symmetry of deformation, we have

u_{r} = u_{r} (r, z), u_{θ} = 0, w = w (r, z),

the strain tensor of an elastic body as

\begin{array}{l} ε_{r} = \frac{\partial u_{r}}{\partial r}, ε_{z} = \frac{\partial w}{\partial z}, \\ γ_{r θ} = 0, γ_{z θ} = 0, γ_{r z} = \frac{\partial u_{r}}{\partial z} + \frac{\partial w}{\partial r}, \end{array}

(49)

and the shear stress as

τ_{r θ} = τ_{z θ} = 0.

(50)

The equilibrium equation in axi-symmetry coordinates of elastic object, the Eqs.(48) can be written in the following form

\begin{array}{l} \frac{\partial σ_{r}}{\partial r} + \frac{\partial τ_{z r}}{\partial z} + \frac{σ_{r} - σ_{θ}}{r} + F_{r} = 0, \\ \frac{\partial τ_{z r}}{\partial r} + \frac{\partial σ_{z}}{\partial z} + \frac{2 τ_{z r}}{r} + F_{z} = 0. \end{array}

(51)

4.3. Virtual Displacement Principle of Elastic Objects in Spherical Coordinate Systems

When we taking the generalized coordination

q_{1} = r, q_{2} = θ, q_{3} = φ

, the virtual displacement principle of elastic object in the spherical coordinate system is given with the virtual displacement principle Eq.(27) of deformation objects.

In the spherical coordinate system, the position coordinates of a point m in space are represented by

(r, θ, ϕ)

. The relationships between rectangular coordinates and spherical coordinates are

x = r \sin θ \cos ϕ, y = r \sin θ \sin ϕ, z = r \cos θ .

We use

u_{r} (r, θ, φ), u_{θ} (r, θ, φ), u_{ϕ} (r, θ, φ)

to represent the displacement components of the spherical coordinate system respectively, and the relationship between strain components and displacement components in spherical coordinates are the following form

\begin{array}{l} ε_{r} = \frac{\partial u_{r}}{\partial r}, ε_{θ} = \frac{u_{r}}{r} + \frac{1}{r} \frac{\partial u_{θ}}{\partial θ}, ε_{φ} = \frac{1}{r \sin θ} \frac{\partial u_{φ}}{\partial φ} + \frac{u_{θ}}{r} \cot θ + \frac{u_{r}}{r}, \\ γ_{r θ} = \frac{1}{r} \frac{\partial u_{r}}{\partial θ} + \frac{\partial u_{θ}}{\partial r} - \frac{u_{θ}}{r}, γ_{r φ} = \frac{1}{r \sin θ} \frac{\partial u_{r}}{\partial φ} + \frac{\partial u_{φ}}{\partial r} - \frac{u_{φ}}{r}, \\ γ_{θ φ} = \frac{1}{r} (\frac{\partial u_{φ}}{\partial θ} - u_{φ} \cot θ) + \frac{1}{r \sin θ} \frac{\partial u_{θ}}{\partial φ}, \end{array}

(52)

equations (52) are also called the strain tensor of an elastic body in spherical coordinates.

Constitutive relations of elastic object in spherical coordinate system are [31]

\begin{array}{l} σ_{r} = \frac{E}{1 + v} (\frac{v}{1 - 2 v} φ + ε_{r}), σ_{θ} = \frac{E}{1 + v} (\frac{v}{1 - 2 v} θ + ε_{θ}), σ_{φ} = \frac{E}{1 + v} (\frac{v}{1 - 2 v} θ + ε_{φ}), \\ τ_{r φ} = \frac{E}{2 (1 - 2 v)} γ_{r φ}, τ_{r θ} = \frac{E}{2 (1 - 2 v)} γ_{r θ}, τ_{θ φ} = \frac{E}{2 (1 - 2 v)} γ_{θ φ} . \end{array}

(53)

In spherical coordinates, the equilibrium equations of elastic object are obtained, using the virtual displacement principle Eq.(27) in the following form

\begin{array}{l} \frac{\partial σ_{r}}{\partial r} + \frac{1}{r} \frac{\partial τ_{θ r}}{\partial θ} + \frac{1}{r \sin θ} \frac{\partial τ_{φ r}}{\partial φ} + \frac{1}{r} (2 σ_{r} - σ_{θ} - σ_{φ} + τ_{r θ} \cot θ) + F_{r} = 0, \\ \frac{\partial τ_{r θ}}{\partial r} + \frac{1}{r} \frac{\partial σ_{θ}}{\partial θ} + \frac{1}{r \sin θ} \frac{\partial τ_{φ θ}}{\partial φ} + \frac{1}{r} ((σ_{θ} - σ_{φ}) \cot θ + 3 τ_{r θ}) + F_{θ} = 0, \\ \frac{\partial τ_{r φ}}{\partial r} + \frac{1}{r} \frac{\partial τ_{θ φ}}{\partial θ} + \frac{1}{r \sin θ} \frac{\partial σ_{φ}}{\partial φ} + \frac{1}{r} (3 τ_{r φ} + 2 τ_{θ φ} \cot θ) + F_{φ} = 0. \end{array}

(54)

For the problem of spherical symmetry, that is, the geometry of the object, constraints, external forces and other external factors are symmetrical to a certain point (such as the origin of the coordinate system).

According to the symmetry of the deformation of the object, the displacement of a point of the deformed object are written by

u_{r} = u_{r} (r), u_{θ} = 0, u_{ϕ} = 0

, and some shear strains and shear stresses are equal to zero, i.e

γ_{r θ} = γ_{r ϕ} = γ_{θ ϕ} = 0,

and

τ_{r θ} = τ_{r ϕ} = τ_{θ ϕ} = 0

, The rest of the strain and stress components are only a function of coordinate r, independent of

θ and ϕ

The strain components and stress components are written by

ε_{r} = \frac{d u_{r}}{d r}, ε_{θ} = ε_{φ} = \frac{u_{r}}{r} .

(55)

σ_{θ} = σ_{φ} = σ_{T} .

(56)

Constitutive relations are the following form

σ_{r} = \frac{E}{1 + v} (\frac{v}{1 - 2 v} φ + ε_{r}), σ_{T} = \frac{E}{1 + v} (\frac{v}{1 - 2 v} φ + ε_{T}), φ = ε_{r} + 2 ε_{T}

(57)

The virtual displacement principle of elastic objects in spherical symmetrical coordinates can be written as [31]

\frac{d σ_{r}}{d r} + \frac{2 (σ_{r} - σ_{T})}{r} + F_{r} = 0,

(58)

that is written in the form

\frac{E}{1 + v} \frac{1 - v}{1 - 2 v} (\frac{d^{2} u_{r}}{d r^{2}} + \frac{2}{r} \frac{d u_{r}}{d r} - \frac{2 u_{r}}{r^{2}}) + F_{r} = 0.

(59)

5. Conclusions

Based on the current situation that the virtual displacement principle of rigid objects and deformed objects is studied separately, this paper adopts the method of analytical mechanics, the concept of ideal constraint and virtual displacement are introduced, the generalized virtual displacement principle of deformed objects is proposed; the generalized virtual displacement principle of deformable objects is general, which is applicable to both deformable objects of various materials and rigid objects. This research lays a foundation for solving the dynamic problems of flexible, intelligent and bionic material object systems in equilibrium.

Funding

This work was supported by the Natural Science Foundation of China (11872335), the Major science and technology projects of the Ministry of Water Resources of China (SKS-2022053), and Key R&D Plan Projects in Zhejiang Province of China (2022C02035).

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Disclosures: The authors declare no conflicts of interest.

References

J H Wang Analytical Dynamics (Beijing: Higher Education Press) (1958) (in Chinese).
B Chen Analytical Dynamics (Beijing: Peking University Press) (2017) (in Chinese).
F X Mei, D Liu and Y Luo Advanced Analytical Mechanics (Beijing: Beijing College of Science and Technology Press) (1993) (in Chinese).
J L Synge, and B A Griffith Principles of Mechanics (New York McGraw-Hill Inc.) (1970).
D T Greenwood Classical Dynamics (New York Prentice Hall) (1977).
H Goldstein Classical Mechanics (Massachusetts Addison-Wesley Publishing Co., Reading) p8 (1980).
L N Hand and J D Finch Analytical Mechanics (Cambridge: Cambridge University Press) (1998).
V I Arnold Mathematical Methods of Classical Mechanics (New York Springer Verlag) (1989).
Z D Xu and L W Ma Structural mechanics (Beijing: Science and Technology Press) (2007) (in Chinese).
L L Yu and Z G Yang Structural Mechanics (Second Edition) (Beijing: China Electric Power Press) (2014) (in Chinese).
J Hadamard Nature A71 196 (1904).
M A Biot Phys. Rev. A97 1463 (1955).
M A Biot Advances in applied mechanics (New York: Academic Press) Vol 24 p1-90 (1984).
P Germain SIAM Journal of Applied Mathematics A25 p556 (1973).
G A Maugin Acta Mechanica A35 p1 (1980).
G A Maugin Thermomechanics of nonlinear irreversible behaviors (Singapore: World Scientific Publishong Co.) (1999).
A E Green and R S Rivlin Proceedings of Royal Society of London Series A A284 p303 (1965).
A E Green and P M Naghdi Proceedings of Royal Society of London Series A A432 p171 (1991.
A E Green and P M Naghdi Proceedings of Royal Society of London Series A A448 p335 (1995).
S Sieniutycz and R S Berry Phys. Rev. E A 47 p1765(1993).
G A Maugin Rendiconti del Seminario Matematico Universitá e Politecnico di Torino A 58 p171 (2000).
Y H Pao , L S Wang and K C Chen International Journal of Engineering Science A49 p1502 (2011).
P J Blanco, A Clausse and R A Feijoo Comput. Methods. Appl. Mech. Engrg. A315 p760 (2017.
T Zhang, P Shi and X K Yue Mechanical Systems and Signal Processing A179 p109351 (2022).
M Groß, J Dietzsch and C Röbiger Comput. Methods Appl. Mech. Engrg A350 p595 (2019).
E Benvenutia , A Chiozzia , G Manzinib and N Sukuma Comput. Methods. Appl. Mech. Engrg. A390 p114352 (2022).
C Kim and M G Lee International Journal of Solids and Structures A233 p111204 (2021).
Y Mei and S Avril International Journal of Solids and Structures A178 p136 (2019).
X Wang , W Wu , H Zhu and H. Zhang Computers and Geotechnics A146 p104710 (2022).
D Huyssteena , F L Rivarolab and G Etseb , P Steinmann Appl. Mech. Engrg. A393 p114549 (2022).
Z L Xu Elasticity (Beijing: People’s Education Press) (1982) (in Chinese).
G T Yang Introduction of Elastoplastic Mechanics (Beijing: Tsinghua University Press) (2004) (in Chinese).

Figure 1. Elastic body consist of N flexible volume elements.

Figure 2. Position vector representation.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Generalized Virtual Displacement Principles of Deformed Objects with Methods of Analytical Mechanics

Abstract

1. Introduction

2. Generalized Virtual Displacement Principle of the Deformation Objects

2.1. Establishing of Virtual Displacement Principle

2.2. Formulation of generalized virtual displacement principle

3. Several Forms on the Virtual Displacement Principle

3.1. Vector Form on the Virtual Displacement Principle

3.2. Coordinate component form of virtual displacement principle:

3.3. Generalized coordinate form of the virtual displacement principle.

4. Application of the Generalized Virtual Displacement Principle of Deformation Object

4.1. Polar Coordinate Form of the Virtual Displacement Principle of Elastic Plane Problems

4.2. Cylindrical coordinate form of the virtual displacement principle of elastic object

4.3. Virtual Displacement Principle of Elastic Objects in Spherical Coordinate Systems

5. Conclusions

Funding

Data Availability Statement

References

MDPI Initiatives

Important Links

Subscribe