Principles of Artificial Neural Networks and Machine Learning for Bioinformatics Applications

1. Introduction

Symmetry and invariance is a central concept in physics, mathematical and biological systems, and has been established since the early 20th century that fundamental principles of nature are based on symmetry [1]. In the last decade, technologies such as genomic sequencing have enabled an exponential increase [2] of the data that describe the molecular elements, structure and function of biological systems. Furthermore, data generation in fields as diverse as physics, software development and social media [3], have resulted in datasets of scale not previously available to scientists. This data abundance, has been fundamental for the ever accelerating advancements in the field of machine learning, deep learning and artificial intelligence, where we now have algorithms that can be trained to make discoveries from the data, at a level that closely matches human intuition.

The field of deep learning and artificial intelligence, has developed rapidly within the span of a few years, and while researchers have developed hundreds of successful algorithms, there currently few unifying principles to organize systematically the machine learning algorithms. In a seminal proto-book by Bronstein et al. [4], a range of systematization principles for the different Artificial Neural Network (ANN) architectures and deep learning algorithms were presented, based on the concepts of symmetry and mathematical group theory. The authors also introduced the concept of geometric deep learning, and demonstrated how the group theory, function invariance and equivariance principles, can be used as basis towards composing and describing the various deep learning algorithms. Along these lines, in the present manuscript we explain the structure of ANNs and the principles of machine learning algorithms, while providing a review of mathematical and statistical foundations related to the development of artificial intelligence applications with bioinformatics data.

2. The Structure of Artificial Intelligence and Neural Networks

We will first describe the structures and function of deep learning and Artificial Neural Networks (ANNs) that are the basis of artificial intelligence [5]. Assume a dataset consisting of n pairs of ${\left(x_i,y_i\right)}_n$, with the $x_i$ being n data points and $y_i$ their labels. Each $x_i$ data point can be for example be a number, a vector (array of numbers), or a matrix (grid of numbers) storing diffent types of bioinformatics data. The data and labels can be of various formats, such as binary (two-option) as for example $y_i=1$ "inhibits cancer growth", or $y_i=0$ "does not inhibit cancer". The labels can also be continuous numbers such as for example $y_i=0.3$ meaning 30% inhibition, or a composite label such as $y_i=\left(\mathrm{0,1},0\right)$ representing respectively drug attributes such as '0 - no inhibition', '1 - yes for toxicity', '0 - not metabolized'. Similarly, the input data points can also be composite such as for example $x_i=\left(\mathrm{50,100}\right)$ representing two measuments for a single biological entity. Independently of the label structure, the deep learning algorithms and the overall goal of artificial intelligence applications for bioinformatics, is to first train the ANN with data for which the labels are known, and then perform classification of newly generated data, by predicting their labels.

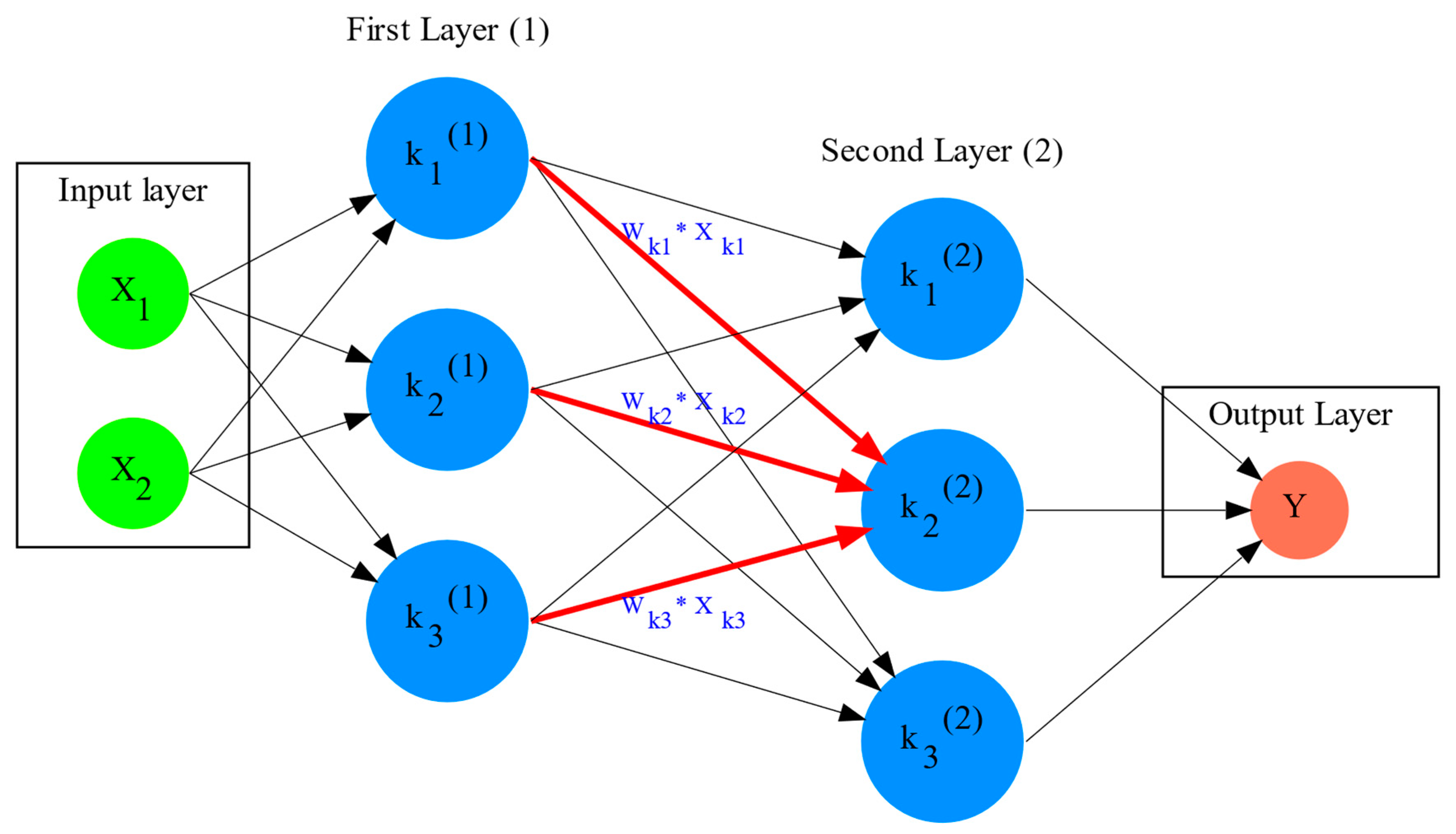
The simplest structure of an artificial neural network as shown on Figure 1 is "fully connected", with each neuron k in the ANN having a number of incoming and outgoing connections corresponding to the number of neurons in previous and next layer in the neural network. For example the neuron $k_0^1$ of the First Layer (1) on Figure 1, has $n=2$ incoming and $n=3$ outgoing connections, corresponding respectively to the "input layer" with two neurons, and three connections with the neurons of the internal ("hidden layer") labeled Second Layer (2) on the figure. The internal layers are called "hidden" since they do not receive input data directly, similarly to the neurons performing cognition in animal brains, as opposed to sensory neurons. While the hidden layers can have an arbitrary number of neurons based on the complexity of the label classification problem we need the ANN to resolve [6], the input layer has the exact number of neurons corresponding to the input data structure. On Figure 1 for example we have two input neurons, and the data can be of the form $x_i=\left(\mathrm{50,100}\right)$. Finally, the output layer has a number of neurons corresponding to the number of labels $y_i$ per input data point in the data, and on Figure 1 there is a single label.

of the second hidden layer, can be expressed with the formula ${\sigma }_{k_1^{\left(\begin{array}{c}2\end{array}\right)}}=\sum _{k_{\mathrm{0,1},2}}^{\left(\begin{array}{c}1\end{array}\right)}{w}_{k0}*x_{k0}+w_{k1}*x_{k1}+w_{k2}*x_{k2}-b$, which is the aggregation of neuron signals from the first layer, shown as red arrows on the figure. The b is the threshold that needs to be overcome by the aggregation sum in order for the neuron to fire, and then the neuron will transmit a signal along the line shown towards the output on the final layer on the figure. The reader should refer to the text for more details.

Similar to neural networks in animal brains, the computational abstractions used in machine learning and artificial intelligence, model neurons as computational units performing signal summation and threshold activation. Specifically, each artificial neuron performs a summation of incoming signals from its connected neighbooring neurons in the preceeding layer on the network, shown for example as red arrows on Figure 1 for ${\sigma }_{k_1^{\left(\begin{array}{c}2\end{array}\right)}}$. The signal processing across the ANN transitions from input data $x_i$ on the leftmost layer (Figure 1), to output of data labels $y_i$ on the right end. Within each neuron, when the aggregated input reaches a certain threshold, the neuron "fires" and transmits a signal to the next layer. The signals coming into the neuron can be either the data directly from the input layer, or signals generated by activation of the neurons in the intermediate - "hidden" layers. The summation and thresholding computation within each neuron is represented with the function ${\sigma }_k=\sum _1^k{w}_k*x_k-b$, where the $w_k$ is the connection weights of the preceding neurons. Each connection arrow on Figure 1 has a different weight, such as for example $x_{k0}$ which is the incoming signal from the neuron ${\sigma }_{k_0^{\left(\begin{array}{c}1\end{array}\right)}}$ to neuron ${\sigma }_{k_1^{\left(\begin{array}{c}2\end{array}\right)}}$, multiplied by the weight $w_{k0}$, which represents the strength of the connection between these two artificial neurons.

For the majority of applications, the weight values $w_k$ are the only elements in the ANN structure that are variable, and are adjusted by the algorithms during training with the input data. This is similar to the biological brain, where learning takes place by strengthening connections among neurons [7]. However, unlike the biological brain the ANNs used in practice for data analysis have fixed connections between the neurons and the structure of the neural network does not change during training and learning to recognize and classify new data. The last term b in the summation, represents a threshold that needs to be surpassed such as $\sum _1^k{w}_k*x_k>b$, in order for the neuron to activate. One final step before the output value of the neuron is tranmitted, is the application of a "logit" function to the summation value, that is represented as $\phi \left({\sigma }_k\right)$. The $\phi$ can be selected from a range of non-linear functions depending on the the type of input data, and the specific analysis and data classification domain for which the ANN will be used [5]. The value of the logit function is the output of the neuron, which is transmitted to its connected neurons in the next layer through the outgoing connections, shown as an arrows on Figure 1 and corresponding to the brain cell axons in the biological analogy. Multiple layers of neurons connected together in layers (Figure 1), along with multiple connections per layer each having each own weight $w_k$, forms the Artificial Neural Network (ANN).

From a mathematical formalism perspective, a trained ANN is a function $f$ that predicts labels $y_{pre{d}_i}$ such as for example 'no inhibition', 'yes for toxicity' etc., for different types of input data $x_i$ ranging from histology images to drug molecules represented as graph data structures. Therefore, the ANN performs data classification as a mapping function $f\left(x_i\right)=y_{pre{d}_i}$, from the input data to the labels. Furthermore, the $f\left(x_i\right)$ is a non-linear function, since it is an aggregate composition of the non-linear functions $\phi \left({\sigma }_k\right)$ of the individual interconnected neurons in the network [5]. As a result, the $f\left(x_i\right)$ can classify labels for data inputs that originate from complex data distributions, and this fact enables ANNs to achieve higher analytical power compared to typical statistical learning algorithms [8]. The $f\left(x_i\right.$ is estimated by fitting a training dataset, which correlates labels $y_i$ to data points $x_i$. With hundreds of papers and monographs that have been written on the technical details of training ANNs, we will next attempt to briefly summarize the process and refer the reader to the citations for further details.

As mentioned previously, the only variable element in the ANN structure are the weights $w_k$ of the neuron connections, and therefore training an ANN to classify data is the estimation of the weights. Furtheromre, the training process involves minimizing the error $E$, which is the difference between the labels $y_{pre{d}_i}$ predicted by the function $f$ and the true labels $y_i$. This error metric is akin to true/false positive and negatives (precision and recall) used in statistics, however diffent formulas are used for its estimation for multi-label or complex input data to the ANN (for more details, [9]). The neuron connection weight $w_k$ estimation by the algorithm takes place by fitting the network function $f$ on a large training dataset of ${\left\{x_i,y_i\right\}}_i^n$ pairs of input data and labels, while the error $E$ is calculated by using a subset of the data for testing and validation. The training algorithm starts with an initial value of the weights, and then performs multiple cycles (called "epochs") towards estimating the function $f$ by fitting the data $x_i$ to the network and calculating the error $E$ by comparing predicted $y_{pre{d}_i}$ and the true labels $y_i$. At the end of each cycle "backpropagation" is performed [8], which involves a gradient descent optimization algorithm, in order to fine tune the weights of the individual neurons and minimize $E$. The gradient descent [10] searches the possible combinations of weight values, and since it is a heuristic algorithm it minimizes $E$, but cannot reach zero error. At the completion of multiple training cycles the training algorithm identifies a set of weights which best fit the data, and the ANN settles on the optimal values that estimate the $\phi \left({\sigma }_k\right)$ function for ${\sigma }_k=\sum _1^k{w}_k*x_k-b$, where $w_k$ is the weight in each interconnected neuron. Consequently, the overall $f$ represented by the network is also estimated,since as it was mentioned previously is the composition of the individual $\phi \left({\sigma }_k\right)$ neuron functions. Once the artificial neural network training has been completed by finding the most optimal set of weights, it is now ready to be used for label prediction with new, unknown $x_i$ data.

3. Artificial Intelligence, Group Theory, Symmetry and Invariance

We conclude, by reviewing how the principles of group theory, symmetry and invariance, provide a foundational framework to understand the function of machine learning algorithms, and the classifying power of ANNs in relation to statistical variance, transformations, and non-homogeneity in the input data. In broad terms, symmetry is the analysis of geometric and algebraic mathematical structures, and can have applications with data found in the fields of physics, molecular biology and machine learning. A core concept in symmetry is invariance, which in our context is changing data coordinates, such as shifting a drug molecule in space or a cancer histology tissue sample, while leaving the shape of the object unchanged [4]. Following such a change which as will be formally defined later in the text as invariant transformation, the machine learning algorithms and ANNs must be able to recognize a drug molecule following rotation, or a tissue to be recognized as cancerous from a shifted histology image.

In order to link the abstract symmetry concepts with data classification in machine learning, following the terminology of Bronstein et al., we consider the input data $x_i$ to originate from a symmetry domain $\Omega$. 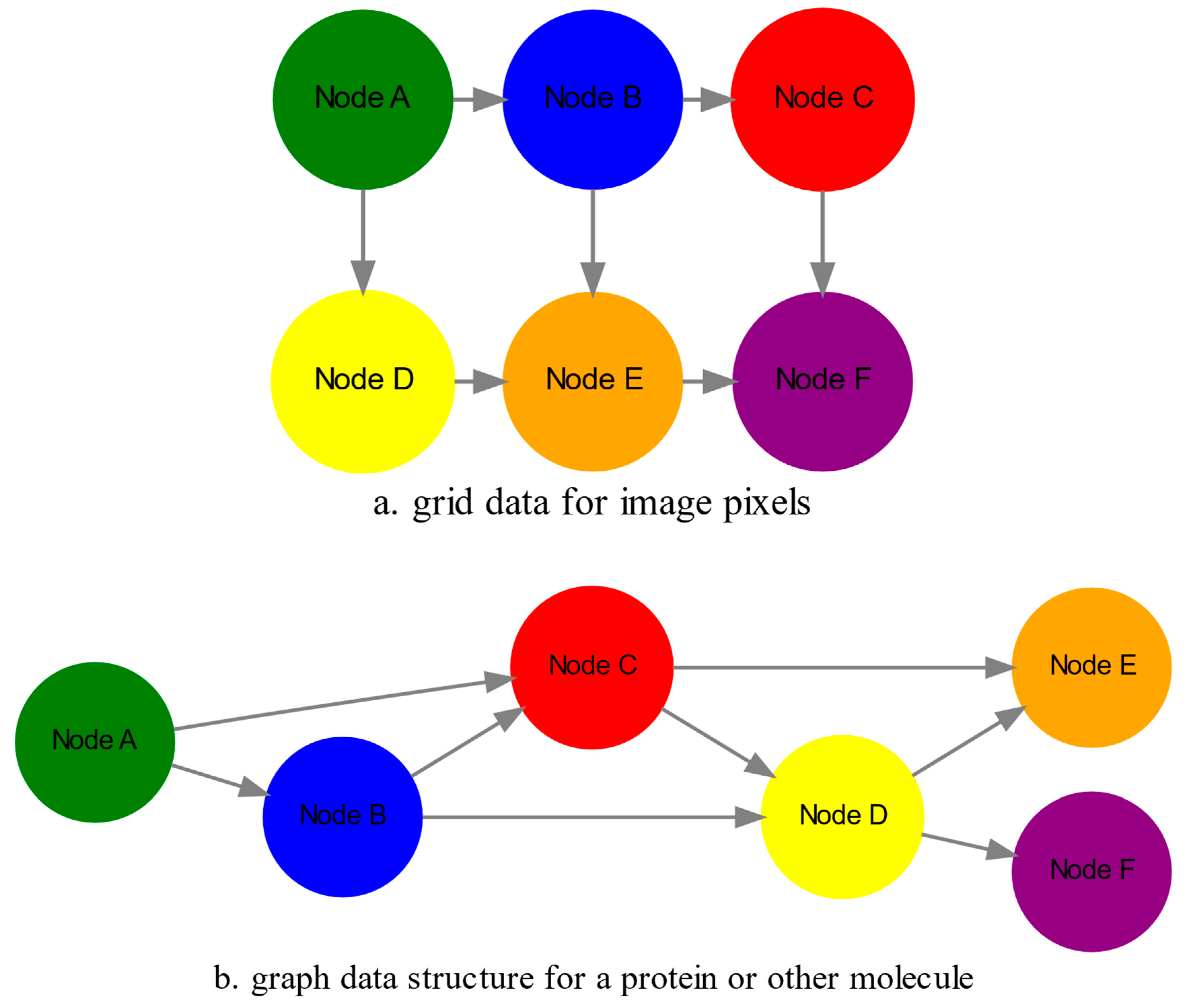The $\Omega$ is the structure upon which the data are based, and upon the domain structure we train the artificial neural networks to perform classification, through the label prediction function $f$ as mentioned in the earlier section. For example, microscopy images are essentially 2-dimensional numerical grids of n x n pixels (Figure 2a), with each pixel having a value for the light intensity captured when the image was taken. In this case the data domain is a grid of integers ($\mathbb{Z}$), represented as $\Omega :{\mathbb{Z}}_n\times {\mathbb{Z}}_n$. Similarly, for color images the data domain is $x_i:\Omega \to {\mathbb{Z}}_n^3\times {\mathbb{Z}}_n^3$, with three overlayed integer grids each representing the green, blue and red layers composing the color image. In either case, the $\Omega$ contains all possible combinations of pixel intensities, while the specific pixel value combinations of the images in the input data $x_i$ are a "signal" $\mathrm{X}\left(\Omega \right)$ from the domain. The ANN data classification and label prediction function $y_{pre{d}_i}=f\left(x_i\right)$ is applied on the signal $\mathrm{X}\left(\Omega \right)$ which is essentially a subset of the domain $\Omega$.

A symmetry group $G$ contains all possible transformations of the input signal $\mathrm{X}\left(\Omega \right)$ called symmetries $g$ or otherwise group actions. A symmetry transformation $g$ preserves the properties of the data, such as for example not distorting the objects in the image during rotation. The members of the symmetry group $g\in G$ are the associations of two or more coordinate points $u,v\in \Omega$ on the data domain (grid in our image example). Between these coordinates, the image can be rotated, shifted or otherwise transformed without any distortion. Therefore, the key aspect of the formal mathematical definition of the group, is that the data attributes are preserved during object distortions that are common during the experimental acquisition of bioinformatics data. The concept of symmetry groups is important towards modeling the performance of machine learning algorithms, for classifying the data patterns correctly, despite the variability found in the input data.

, is composed of nodes $V$ shown as circles, and edges connecting the nodes and shown as arrows. It can represent a protein, where the amino acids are the nodes and the peptide bonds between amino acids are the edges.

Another important data structure for bioinformatics is a graph $G=(V,E)$, composed of nodes $V$ representing biological entities, and edges which are the connections between pairs of nodes (Figure 2b). In a specific instance of a graph for a real-world object, the edges are a subset of all possible links between nodes. An example graph data structure for a biological molecule such a protein or a drug, would represent the amino acids or atoms as node entities, and the chemical bonds between each of these entities as edges. The edges can correspond to either the carbonyl-amino (C-N) peptide bonds between amino acids and molecular interactions across the peptide chain on the protein structure, or the chemical bonds between atoms in a drug molecule. Furthermore, attributes in the molecular data such as for example polarity and amino acid weight, or drug binding properties can be represented as $s$ - dimensional node attributes, where s are the attributes assigned to each node. Similarly, the edges or even entire graphs can have attributes, for experimental data measured on the molecular interactions represented by the edges, and measurements of the properties of the complete protein or drug. Finally, from an algorithmic perspective , images are a special case of graphs where the nodes are the pixels, and connect with edges in a structured pattern that form of a grid (Figure 2a) representing the adjacent position of the pixels.

Having established the mathematical and algorithmic parallels between graphs and images, we will now utilize the principles of the symmetry group $G$ to examine the analytical and classification power of machine learning ANNs, in relation to variability and transformations in the data. For both data types such as input images or molecules represented as graphs that are shifted or rotated, we establish the concept of invariance through the principles of group theory and symmetry. These are the foundational mathematical and algorithmic formalisms, that can be used to model the performance and output of machine learning algorithms ANNs in relation to the variability in the dataset. Consecutively, these principles can then be extrapolated and generalized for other types of data beyond graphs and images, for which ANNs are trained for prediction and classification. While we present the group and symmetry definitions following a data-centric approach, we will nonetheless still follow the mathematical formalism, when describing how the group operations can transform the input data. Furtermore, different types of data can have the same symmetry group, and different transformations can be performed by the same group operation. For example, an image with a triangle which essentially is a graph with three nodes, can have the same rotational symmetry group as a graph of three nodes or a numerical sequence of three elements.

When chemical and biological molecules are represented as graphs as described earlier, the nodes $V$ can be in any order depending on how the data were measured during the experiment. This does not change the meaning of the data, and as long as the edges E representing the connections between the molecules are not modified, we have a proper representation of the molecular entity independently of the ordering of V. In this case, where two graphs for the same molecule have the same edges but different ordering of nodes, they are called isomorphic. Any machine learning algorithm performing pattern recognition on graphs, should not depend on the ordering of nodes so that classification with ANNs and artificial intelligence is not affected by experiment measurement variations in real-world data. This is something that is taken for granted with human intelligence, where for example we can recognize an object even when a photograph is rotated at an angle. Returning to our formal definitions, in order for ANNs algorithms to equivalently recognize isomorphic graphs, the functions $\phi \left({\sigma }_k\right)$ and overall $f\left(x_i\right)$ of the ANN acting on graph data should be permutation invariant.This means that for any permutation of the input dataset, the output value of these functions are identical independently of the ordering of the nodes V for example in the case of graphs. This concept can be similarly applied to images, which as mentioned previously are special cases of fully connected graphs, and furthermore these principles can also be generalized to other data types beyond images or graphs.

In order to formalize further the concept of invariance, and since both examples of the image and graphs are similarly points on a grids on a two dimemensional plane, we can use linear algebra. Specifically, by using a matrix we can represent the data transformations as group actions $g$, within the symmetry group $G$. The use of matrices enables us to connect the group symmetries with the actual data, through matrix multiplications that modify the coordinates of the object and consecutively represent the data transformations through the multiplication. The dimensions of the matrix $n\times n$ are usually similar to these of the signal space $\mathrm{X}\left(\Omega \right)$ for the data (for example, ${\mathbb{Z}}_n\times {\mathbb{Z}}_n$ images). The the matrix dimensions not depend on the size of the group i.e. the number of possible symmetries, or the dimensionality of underlying data domain $\Omega$. With this definition in place, we can formalize symmetries and group actions for modifying data objects, and the use of matrix and linear transformations as basis for connecting invariance in relation to variability in the data.

We will now conclude by establishing the mathematical and linear algebra formalisms, for resilience of the ANNs and machine learning algorithm pattern recognition, in relation to transformations in the data. While our framework is on a two-dimensional, grid data domain $\Omega$, the formalisms developed here can also be extrapolated without loss of generality to any number of dimensions or data formats. We will first connect matrices to group actions $g$ (rotations, shifts etc.) in the symmetry group $g\in G$, by defining a function $\theta$ that maps the group to a matrix as $\theta :G\to \mathbf{M}$. As mentioned previously, a matrix $\mathbf{M}\in R^{n\times n}$ of numerical values (integers, fractions, positive and negative), when multiplied to the coordinate values of an object on the plane $\Omega$, it rotates or shifts the object coordinates for the exact amount correponsing to the group action within the symmetry group.

With these definitions in place, we will now connect the matrix formalisms with the neural network estimator function $y_{pre{d}_i}=f\left(x_i\right)$, that is identified by adjusting neuron connection weights during multiple training cycles with the input data. Our goal is to leverage the mathematical formalisms of group symmetry and invariance, in order to establish the ANN resilience for classifying and assigning labels to new data points. The data points originate from real-world data that might contain tranformations and distortions. We first define that the estimator function of the ANN to be invariant, if the condition for the input data holds such as $f(\mathbf{M}\times x_i)=f\left(x_i\right)$ for all matrices $\mathbf{M}$ representing the actions $g\in G$ within the symmetry group. This formula presents the condition required for the neural network function to be invariant: its output value is the same whether the input data $x_i$ are transformed or not (i.e an image or graph is not rotated on the plane), as this is represented by the matrix multiplication $\mathbf{M}\times x_i$ . Therefore, the output values $y_{pre{d}_i}=f\left(x_i\right)$ by the ANN which are essentially predicted output labels (i.e $y_{pre{d}_i}$ = potent drug / not potent etc.) based on the input data, are resilient to noisy and deformed real-world data, when the network estimator function is invariant. In a different case, the estimator function approximated by the ANN can be equivariant and defined as $f(\mathbf{M}\times x_i)=\mathbf{M}\times f\left(x_i\right)$. This means that the output of the ANN will be modified, but the label prediction result will be equally shifted along with the shift in the input data.

Up to this point, we have discussed only discrete tranformations in linear algebra terms, with matrix multiplications that result in a shift of coordinates and rigid transformations of the data, such as a rotation of the image or the graph by a specific angle on the grid $\Omega$. However, we can have also also have continuous, more fine grained shifts which is common with real-world data. In this case, the ANNs algorithms should be able to recognize patterns, classify and label the data without any loss of performance. Mathematically, the continuous transformations follow equally with the invariant and equivariant functions described earlier. If for example the domain $\Omega$ contains data that have smooth transformations and shifts, such as moving images (video) or shifts of molecules and graphs that preserve continuity in a topological definition [11], in this case we have a homeomorphism instead of invariance.

Finally, if the rate of continuous transformation of the data is quantifiable, meaning that the function $\theta$ that maps the group to a matrix is differentiable, then the members of the symmetry groups will be part of a diffeomorphism. As it follows from the principles of calculus, in this case infinitely multiple matrices $f\left(\right(M)$ will be needed to be produced by $\theta$ for the continuous change of the data coordinates at every point. These differentiable data structures are common with manifolds, which for example could be used to represent proteins in fine detail. In this case the molecule would be represented as cloud with all atomic forces around the structure, instead of the discrete data structure of nodes and edges of a graph. Finally, if the manifold structure includes also a metric of distance between its points to further quantify the data transformations, in this case we will have an isometry during the transformation due to a group action from the symmetry group.

4. Conclusion

The accelerated developments in the fields of Machine Learning and Artificial Intelligence in recent years, have also had significant impact in the field of Bioinformatics. Due to the rapid developements, there has been diminished opportunity to categorize the algorithms and their applications, along with their perfomance with different types of bioinformatics data. By leveraging the symmetry and group theory mathematical formalisms, we can establish the priciples of operation of Artificial Intelligence algorithms with bioinformatics data and the directions for future development in the field.