Submitted:
31 May 2023
Posted:
01 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Results and Discussion
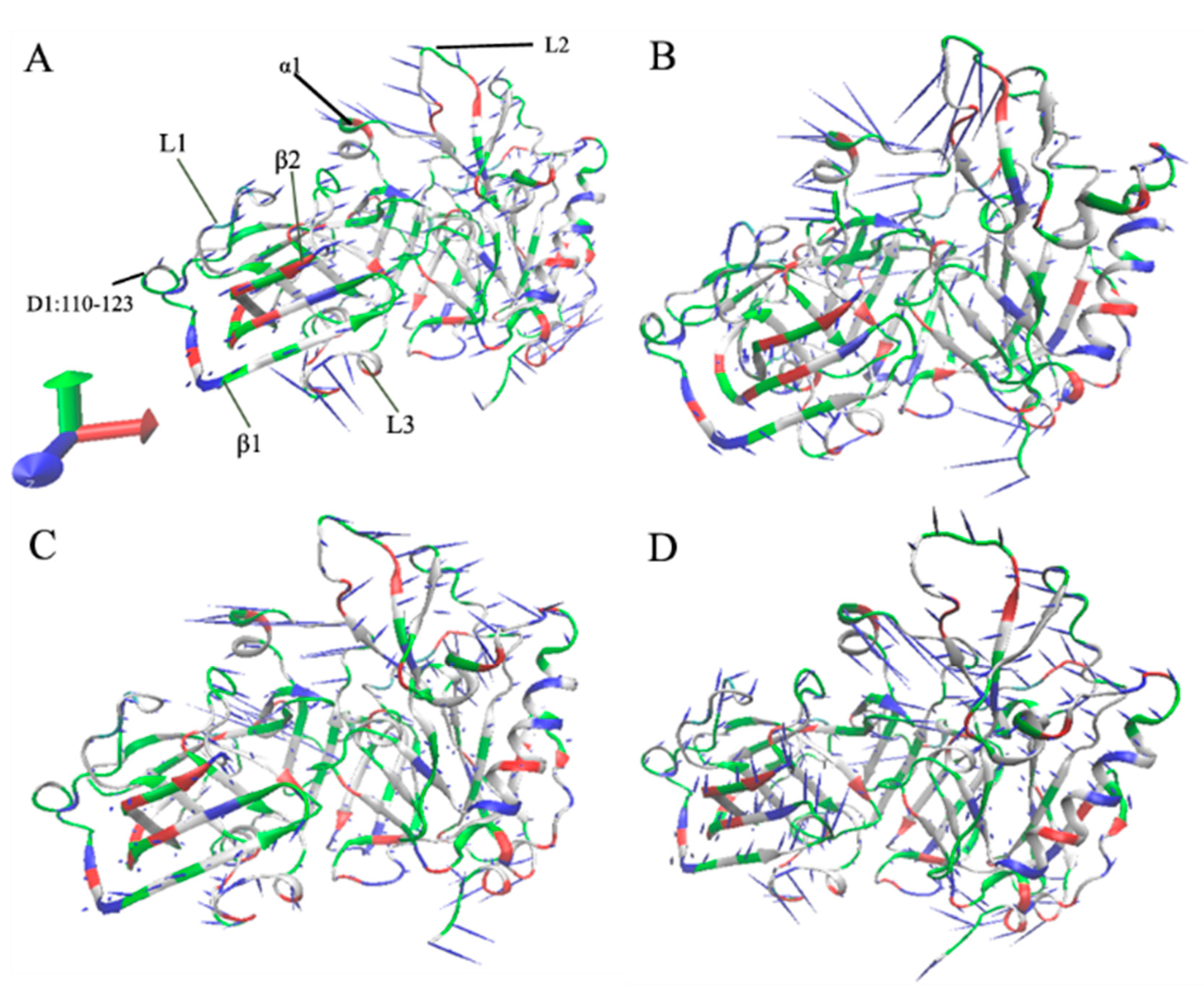
2.1. Dynamics Equilibrium and Structural Fluctuation
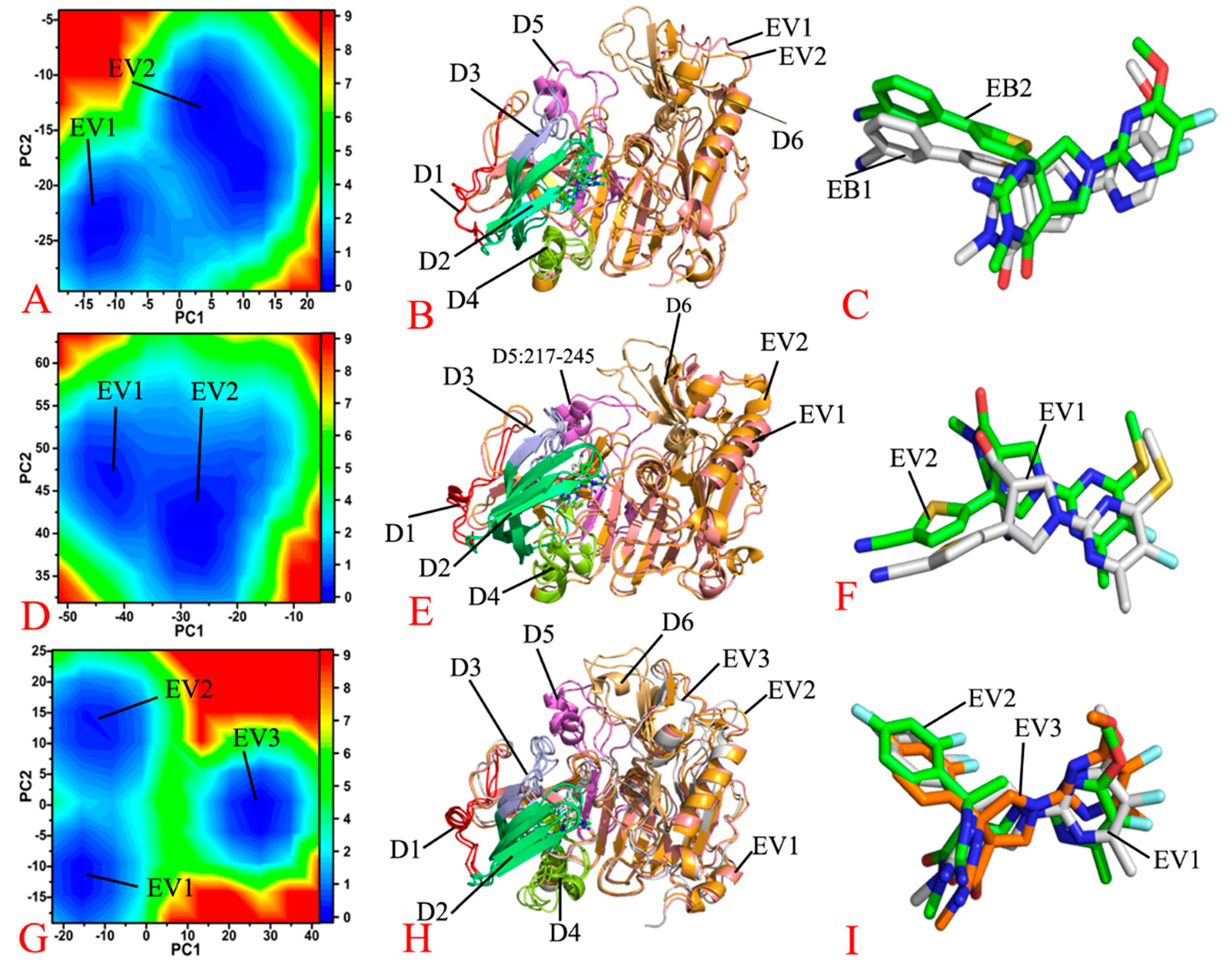
2.2. Conformational Changes of BACE1 and Free Energy Profiles
3.3. Comparative Calculations of Binding Free Energies
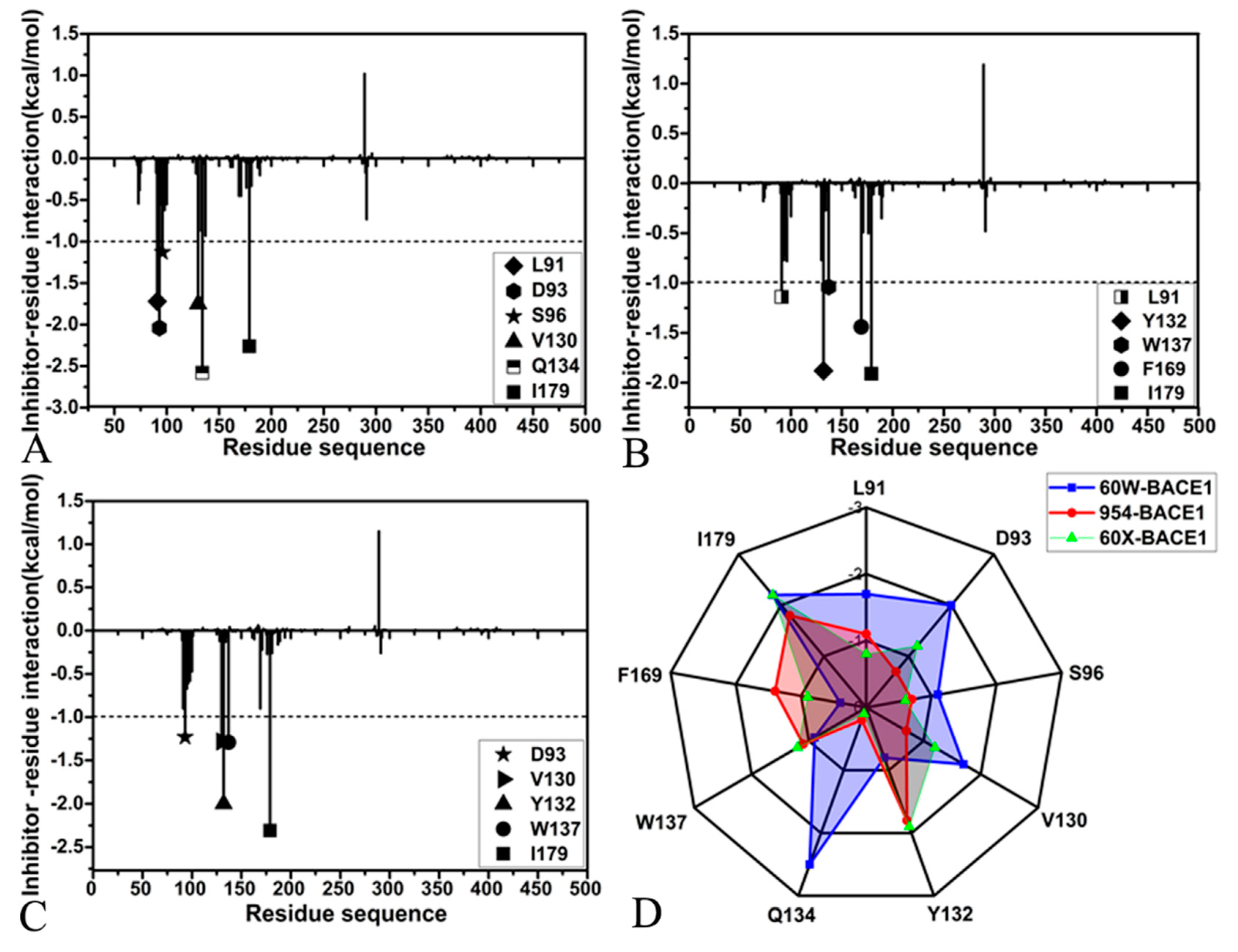
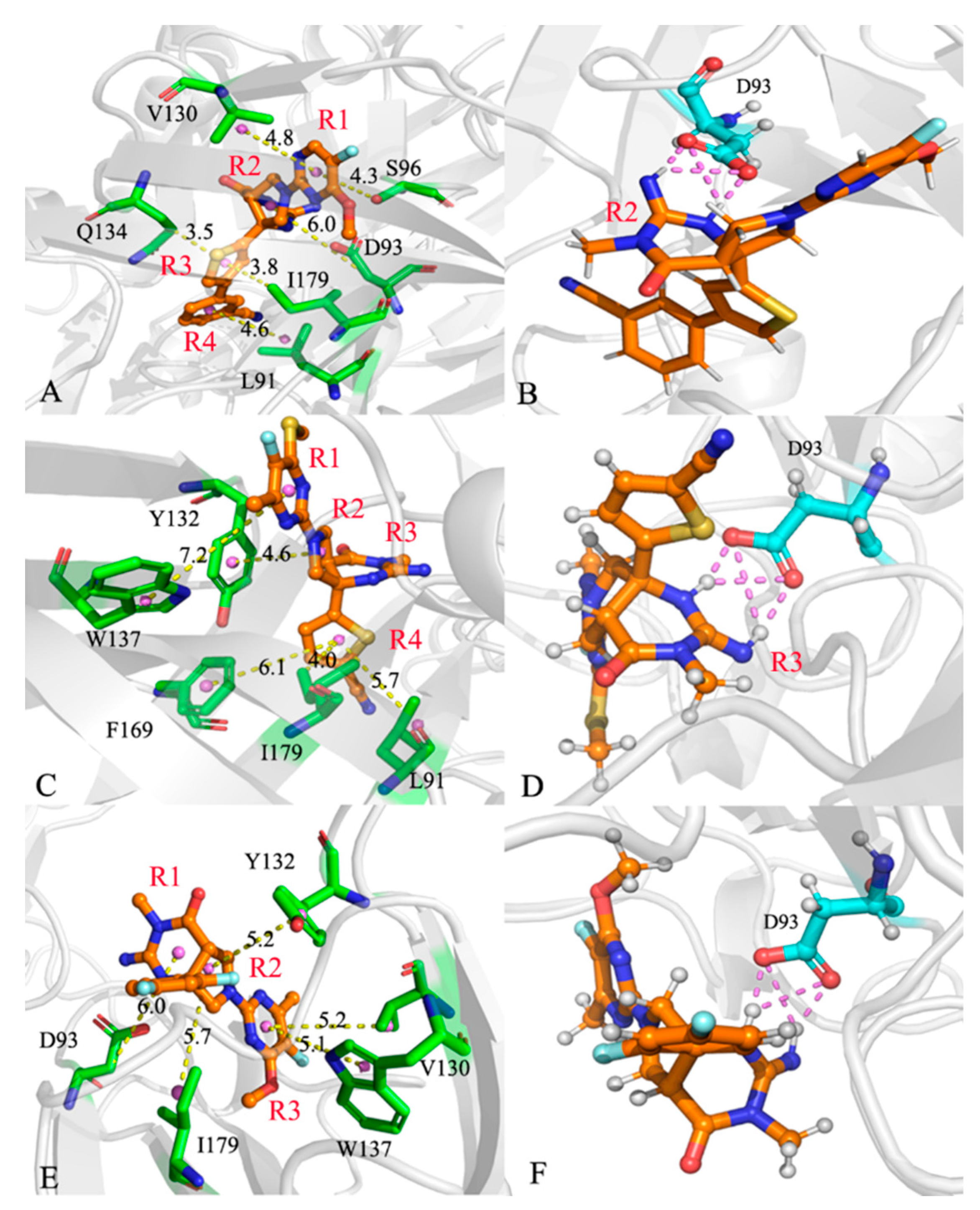
2.4. Analyses of Inhibitor-BACE1 Interaction Networks
3. Materials and Methods
3.1. Construction of Initial Systems
3.2. MD Simulations
3.3. Calculations of Solvated Interaction Energy
3.4. MM-GBSA Calculations
3.5. Principal Component Analysis
3.6. Dynamics Cross-correlation Map
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Goedert, M.; Spillantini, M.G. A Century of Alzheimer's Disease. Science 2006, 314, 777–781. [Google Scholar] [CrossRef]
- 2017 Alzheimer's disease facts and figures. Alzheimer's & Dementia 2017, 13, 325–373.
- Mendiola-Precoma, J.; Berumen, L. C.; Padilla, K.; Garcia-Alcocer, G. Therapies for Prevention and Treatment of Alzheimer’s Disease. BioMed Research International 2016, 2016, 2589276. [Google Scholar] [CrossRef]
- Armstrong, R.A. The molecular biology of senile plaques and neurofibrillary tangles in Alzheimer’s disease. Folia Neu ropathol. 2009, 47, 289–299. [Google Scholar]
- Vassar, R. BACE1 inhibitor drugs in clinical trials for Alzheimer’s disease. Alzheimer's Res. Ther. 2014, 6, 89. [Google Scholar] [CrossRef]
- Sadleir, K. R.; Kandalepas, P. C.; Buggia-Prévot, V.; Nicholson, D. A.; Thinakaran, G.; Vassar, R. Presynaptic dystrophic neurites surrounding amyloid plaques are sites of microtubule disruption, BACE1 elevation, and increased Aβ generation in Alzheimer’s disease. Acta Neuropathol. 2016, 132, 235–256. [Google Scholar] [CrossRef] [PubMed]
- Fobare, W. F.; Solvibile, W. R.; Robichaud, A. J.; Malamas, M. S.; Manas, E.; Turner, J.; Hu, Y.; Wagner, E.; Chopra, R.; Cowling, R. Thiophene substituted acylguanidines as BACE1 inhibitors. Bioorg. Med. Chem. Lett. 2007, 17, 5353–5356. [Google Scholar] [CrossRef]
- Malamas, M. S.; Barnes, K.; Johnson, M.; Hui, Y.; Zhou, P.; Turner, J.; Hu, Y.; Wagner, E.; Fan, K.; Chopra, R. Di-substituted pyridinyl aminohydantoins as potent and highly selective human β-secretase (BACE1) inhibitors. Bioorg. Med. Chem. 2010, 18, 630–639. [Google Scholar] [CrossRef] [PubMed]
- Jordan, J. B.; Whittington, D. A.; Bartberger, M. D.; Sickmier, E. A.; Chen, K.; Cheng, Y.; Judd, T. Fragment-Linking Approach Using 19F NMR Spectroscopy To Obtain Highly Potent and Selective Inhibitors of β-Secretase. J. Med. Chem. 2016, 59, 3732–3749. [Google Scholar] [CrossRef]
- Vassar, R.; Kovacs, D. M.; Yan, R.; Wong, P. C. The β-Secretase Enzyme BACE in Health and Alzheimer's Disease: Regulation, Cell Biology, Function, and Therapeutic Potential. J. Neurosci. 2009, 29, 12787–12794. [Google Scholar] [CrossRef]
- Zou, Y.; Li, L.; Chen, W.; Chen, T.; Ma, L.; Wang, X.; Xiong, B.; Xu, Y.; Shen, J. Virtual Screening and Structure-Based Discovery of Indole Acylguanidines as Potent β-secretase (BACE1) Inhibitors. Molecules 2013, 18, 5706–5722. [Google Scholar] [CrossRef]
- Malamas, M. S.; Erdei, J.; Gunawan, I.; Turner, J.; Hu, Y.; Wagner, E.; Fan, K.; Chopra, R.; Olland, A.; Bard, J. Design and Synthesis of 5,5′-Disubstituted Aminohydantoins as Potent and Selective Human β-Secretase (BACE1) Inhibitors. J. Med. Chem. 2010, 53, 1146–1158. [Google Scholar] [CrossRef]
- Xu, Y.; Li, M.-j.; Greenblatt, H.; Chen, W.; Paz, A.; Dym, O.; Peleg, Y.; Chen, T.; Shen, X.; He, J. Flexibility of the flap in the active site of BACE1 as revealed by crystal structures and molecular dynamics simulations. Acta Crystallogr. D 2012, 68, 13–25. [Google Scholar] [CrossRef]
- Ruderisch, N.; Schlatter, D.; Kuglstatter, A.; Guba, W.; Huber, S.; Cusulin, C.; Benz, J.; Rufer, A. C.; Hoernschemeyer, J.; Schweit zer, C. Potent and Selective BACE-1 Peptide Inhibitors Lower Brain Aβ Levels Mediated by Brain Shuttle Transport. eBioMedicine 2017, 24, 76–92. [Google Scholar] [CrossRef]
- Fujimoto, K.; Matsuoka, E.; Asada, N.; Tadano, G.; Yamamoto, T.; Nakahara, K.; Fuchino, K.; Ito, H.; Kanegawa, N.; Moechars, D. Structure-Based Design of Selective β-Site Amyloid Precursor Protein Cleaving Enzyme 1 (BACE1) Inhibitors: Targeting the Flap to Gain Selectivity over BACE2. J. Med. Chem. 2019, 62, 5080–5095. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, J.; Yin, B.; Pang, L.; Wang, W.; Zhu, W. Molecular Mechanism of Binding Selectivity of Inhibitors toward BACE1 and BACE2 Revealed by Multiple Short Molecular Dynamics Simulations and Free-Energy Predictions. ACS Chem. Neurosci. 2019, 10, 4303–4318. [Google Scholar] [CrossRef] [PubMed]
- Johansson, P.; Kaspersson, K.; Gurrell, I. K.; Bäck, E.; Eketjäll, S.; Scott, C. W.; Cebers, G.; Thorne, P.; McKenzie, M. J.; Beaton, H. Toward β-Secretase-1 Inhibitors with Improved Isoform Selectivity. J. Med. Chem. 2018, 61, 3491–3502. [Google Scholar] [CrossRef] [PubMed]
- Oehlrich, D.; Prokopcova, H.; Gijsen, H. J. M. The evolution of amidine-based brain penetrant BACE1 inhibitors. Bioorg. Med. Chem. Lett. 2014, 24, 2033–2045. [Google Scholar] [CrossRef]
- Cebers, G.; Alexander, R. C.; Haeberlein, S. B.; Han, D.; Goldwater, R.; Ereshefsky, L.; Olsson, T.; Ye, N.; Rosen, L.; Russell, M. AZD3293: Pharmacokinetic and Pharmacodynamic Effects in Healthy Subjects and Patients with Alzheimer’s Disease. J. Alzheimer's Dis. 2017, 55, 1039–1053. [Google Scholar]
- Chen, J.; Yin, B.; Wang, W.; Sun, H. Effects of Disulfide Bonds on Binding of Inhibitors to β-Amyloid Cleaving Enzyme 1 De coded by Multiple Replica Accelerated Molecular Dynamics Simulations. ACS Chem. Neurosci. 2020, 11, 1811–1826. [Google Scholar] [CrossRef]
- Cheng, Y.; Judd, T. C.; Bartberger, M. D.; Brown, J.; Chen, K.; Fremeau, R. T., Jr.; Hickman, D.; Hitchcock, S. A.; Jordan, B.; Li, V. From Fragment Screening to In Vivo Efficacy: Optimization of a Series of 2-Aminoquinolines as Potent Inhibitors of Beta-Site Amyloid Precursor Protein Cleaving Enzyme 1 (BACE1). J. Med. Chem. 2011, 54, 5836–5857. [Google Scholar] [CrossRef] [PubMed]
- Butler, C. R.; Ogilvie, K.; Martinez-Alsina, L.; Barreiro, G.; Beck, E. M.; Nolan, C. E.; Atchison, K.; Benvenuti, E.; Buzon, L.; Doran, S. Aminomethyl-Derived Beta Secretase (BACE1) Inhibitors: Engaging Gly230 without an Anilide Functionality. J. Med. Chem. 2017, 60, 386–402. [Google Scholar] [CrossRef] [PubMed]
- Koriyama, Y.; Hori, A.; Ito, H.; Yonezawa, S.; Baba, Y.; Tanimoto, N.; Ueno, T.; Yamamoto, S.; Yamamoto, T.; Asada, N. Discovery of Atabecestat (JNJ-54861911): A Thiazine-Based β-Amyloid Precursor Protein Cleaving Enzyme 1 Inhibitor Advanced to the Phase 2b/3 EARLY Clinical Trial. J. Med. Chem. 2021, 64, 1873–1888. [Google Scholar] [CrossRef]
- Rueeger, H.; Lueoend, R.; Machauer, R.; Veenstra, S. J.; Holzer, P.; Hurth, K.; Voegtle, M.; Frederiksen, M.; Rondeau, J.-M.; Tintelnot-Blomley, M. Synthesis of the Potent, Selective, and Efficacious β-Secretase (BACE1) Inhibitor NB-360. J. Med. Chem. 2021, 64, 4677–4696. [Google Scholar] [CrossRef]
- Bao, H. Y.; Wang, W.; Sun, H. B.; Chen, J. Z. Binding modes of GDP, GTP and GNP to NRAS deciphered by using Gaussian accelerated molecular dynamics simulations. SAR QSAR in Environ. Res. 2023, 34, 65–89. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Wang, P.; Tu, G.; Yang, F.; Zheng, G.; Li, X.; Li, X.; Chen, Y.; Yao, X.; Zhu, F. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys. Chem. Chem. Phys. 2018, 20, 6606–6616. [Google Scholar] [CrossRef]
- Wang, J.; Arantes, P. R.; Bhattarai, A.; Hsu, R. V.; Pawnikar, S.; Huang, Y.-m. M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. WIREs Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef]
- Sun, Z.; Gong, Z.; Xia, F.; He, X. Ion dynamics and selectivity of Nav channels from molecular dynamics simulation. Chem. Phys. 2021, 548, 111245. [Google Scholar] [CrossRef]
- Shao, Q.; Xiong, M.; Li, J.; Hu, H.; Su, H.; Xu, Y. Unraveling the catalytic mechanism of SARS-CoV-2 papain-like protease with allosteric modulation of C270 mutation using multiscale computational approaches. Chem. Sci. 2023. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, X.; Peng, C.; Wang, J.; Xu, Z.; Chen, K.; Shi, J.; Zhu, W. D3Pockets: A Method and Web Server for Systematic Analysis of Protein Pocket Dynamics. J. Chem. Inf. Model. 2019, 59, 3353–3358. [Google Scholar] [CrossRef]
- Xue, W.; Yang, F.; Wang, P.; Zheng, G.; Chen, Y.; Yao, X.; Zhu, F. What Contributes to Serotonin–Norepinephrine Reuptake Inhibitors’ Dual-Targeting Mechanism? The Key Role of Transmembrane Domain 6 in Human Serotonin and Norepinephrine Transporters Revealed by Molecular Dynamics Simulation. ACS Chem. Neurosci. 2018, 9, 1128–1140. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; He, Q.; Gong, Z.; Kalhor, P.; Huai, Z.; Liu, Z. A General Picture of Cucurbit[8]uril Host–Guest Binding: Recali brating Bonded Interactions. Molecules 2023, 28, 3124. [Google Scholar] [PubMed]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Yu, R. Molecular Dynamics and Free Energy Studies on the Wild-type and Double Mutant HIV-1 Protease Complexed with Amprenavir and Two Amprenavir-Related Inhibitors: Mechanism for Binding and Drug Resistance. J. Med. Chem. 2007, 50, 1177–1188. [Google Scholar] [CrossRef] [PubMed]
- Amadei, A.; Linssen, A. B. M.; Berendsen, H.J.C. Essential dynamics of proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef]
- Levy, R. M.; Srinivasan, A. R.; Olson, W. K.; McCammon, J.A. Quasi-harmonic method for studying very low frequency modes in proteins. Biopolymers 1984, 23, 1099–1112. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. Probing mutation-induced conformational transformation of the GTP/M-RAS complex through Gaussian accelerated molecular dynamics simulations. J. Enzym. Inhib. Med. Ch. 2023, 38, 2195995. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. The switch states of the GDP-bound HRAS affected by point mutations: a study from Gaussian accelerated molecular dynamics simulations and free energy landscapes. J. Biomol. Struct. Dyn. 2023. [CrossRef]
- Auffinger, P.; Westhof, E. RNA hydration: three nanoseconds of multiple molecular dynamics simulations of the solvated tRNAAsp anticodon hairpin. J. Mol. Biol. 1997, 269, 326–341. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Yu, Y.; Liu, D.; Zhao, J.; Zhang, L. Deciphering Selectivity Mechanism of BRD9 and TAF1(2) toward Inhib itors Based on Multiple Short Molecular Dynamics Simulations and MM-GBSA Calculations. Molecules 2023, 28, 2583. [Google Scholar] [CrossRef]
- Chen, J.; Liu, X.; Zhang, S.; Chen, J.; Sun, H.; Zhang, L.; Zhang, Q. Molecular mechanism with regard to the binding selectivity of inhibitors toward FABP5 and FABP7 explored by multiple short molecular dynamics simulations and free energy analyses. Phys. Chem. Chem. Phys. 2020, 22, 2262–2275. [Google Scholar] [CrossRef] [PubMed]
- Suruzhon, M.; Bodnarchuk, M. S.; Ciancetta, A.; Viner, R.; Wall, I. D.; Essex, J.W. Sensitivity of Binding Free Energy Calculations to Initial Protein Crystal Structure. J. Chem. Theory Comput. 2021, 17, 1806–1821. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Zheng, Q. Multiple Molecular Dynamics Simulations and Free-Energy Predictions Uncover the Susceptibility of Var iants of HIV-1 Protease against Inhibitors Darunavir and KNI-1657. Langmuir 2021, 37, 14407–14418. [Google Scholar] [CrossRef] [PubMed]
- Caves, L. S. D.; Evanseck, J. D.; Karplus, M. Locally accessible conformations of proteins: Multiple molecular dynamics simula tions of crambin. Protein Sci. 1998, 7, 649–666. [Google Scholar] [CrossRef] [PubMed]
- Knapp, B.; Ospina, L.; Deane, C. M. Avoiding False Positive Conclusions in Molecular Simulation: The Importance of Replicas. J. Chem. Theory Comput. 2018, 14, 6127–6138. [Google Scholar] [CrossRef]
- Wang, W.; Kollman, P. A. Free energy calculations on dimer stability of the HIV protease using molecular dynamics and a continuum solvent model11Edited by B. Honig. J. Mol. Biol. 2000, 303, 567–582. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Kollman, P. A. Computational study of protein specificity: The molecular basis of HIV-1 protease drug resistance. Proc. Natl. Acad. Sci. U. S. A. 2001, 98, 14937–14942. [Google Scholar] [CrossRef]
- Wang, J.; Morin, P.; Wang, W.; Kollman, P. A. Use of MM-PBSA in Reproducing the Binding Free Energies to HIV-1 RT of TIBO Derivatives and Predicting the Binding Mode to HIV-1 RT of Efavirenz by Docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. [Google Scholar] [CrossRef]
- Naïm, M.; Bhat, S.; Rankin, K. N.; Dennis, S.; Chowdhury, S. F.; Siddiqi, I.; Drabik, P.; Sulea, T.; Bayly, C. I.; Jakalian, A. Solvated Interaction Energy (SIE) for Scoring Protein−Ligand Binding Affinities. 1. Exploring the Parameter Space. J. Chem. Inf. Model. 2007, 47, 122–133. [Google Scholar] [CrossRef]
- Tzoupis, H.; Leonis, G.; Mavromoustakos, T.; Papadopoulos, M. G. A Comparative Molecular Dynamics, MM–PBSA and Ther modynamic Integration Study of Saquinavir Complexes with Wild-Type HIV-1 PR and L10I, G48V, L63P, A71V, G73S, V82A and I84V Single Mutants. J. Chem. Theory Comput. 2013, 9, 1754–1764. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Zhu, T.; Zhang, Q.; Zhang, J. Z. H. A Comparative Insight into Amprenavir Resistance of Mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 Protease Based on Thermodynamic Integration and MM-PBSA Methods. J. Chem. Inf. Model. 2015, 55, 1903–1913. [Google Scholar] [CrossRef] [PubMed]
- Leonis, G.; Steinbrecher, T.; Papadopoulos, M. G. A Contribution to the Drug Resistance Mechanism of Darunavir, Amprenavir, Indinavir, and Saquinavir Complexes with HIV-1 Protease Due to Flap Mutation I50V: A Systematic MM–PBSA and Thermodynamic Integration Study. J. Chem. Inf. Model. 2013, 53, 2141–2153. [Google Scholar] [CrossRef] [PubMed]
- Aldeghi, M.; Heifetz, A.; Bodkin, M. J.; Knapp, S.; Biggin, P. C. Predictions of Ligand Selectivity from Absolute Binding Free Energy Calculations. J. Am. Chem. Soc. 2017, 139, 946–957. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M. R.; Pitera, J. W.; Swope, W. C.; Pande, V. S. Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 2003, 119, 5740–5761. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Pang, L.; Zhang, J. Z. H.; Zhu, T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. [Google Scholar] [CrossRef] [PubMed]
- Aldeghi, M.; Heifetz, A.; Bodkin, M. J.; Knapp, S.; Biggin, P. C. Accurate calculation of the absolute free energy of binding for drug molecules. Chem. Sci. 2016, 7, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Saravanan, K.; Sugarthi, S.; Suganya, S.; Kumaradhas, P. Probing the intermolecular interactions, binding affinity, charge den sity distribution and dynamics of silibinin in dual targets AChE and BACE1: QTAIM and molecular dynamics perspective. J. Biomol. Struct. Dyn. 2022, 40, 12880–12894. [Google Scholar] [CrossRef] [PubMed]
- Ellis, C. R.; Tsai, C.-C.; Hou, X.; Shen, J. Constant pH Molecular Dynamics Reveals pH-Modulated Binding of Two Small-Mol ecule BACE1 Inhibitors. J. Phys. Chem. Lett. 2016, 7, 944–949. [Google Scholar] [CrossRef]
- Bao, L.-Q.; Baecker, D.; Mai Dung, D. T.; Phuong Nhung, N.; Thi Thuan, N.; Nguyen, P. L.; Phuong Dung, P. T.; Huong, T. T. L.; Rasulev, B.; Casanola-Martin, G. M. Development of Activity Rules and Chemical Fragment Design for In Silico Discovery of AChE and BACE1 Dual Inhibitors against Alzheimer's Disease. Molecules 2023, 28, 3588. [Google Scholar] [CrossRef]
- Hernández-Rodríguez, M.; Correa-Basurto, J.; Gutiérrez, A.; Vitorica, J.; Rosales-Hernández, M. C. Asp32 and Asp228 determine the selective inhibition of BACE1 as shown by docking and molecular dynamics simulations. Eur. J. Med. Chem. 2016, 124, 1142–1154. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Wang, W.; Sun, H.; Zhang, Q.; Liu, X. Binding of Inhibitors to BACE1 Affected by pH-Dependent Protonation: An Exploration from Multiple Replica Gaussian Accelerated Molecular Dynamics and MM-GBSA Calculations. ACS Chem. Neurosci. 2021, 12, 2591–2607. [Google Scholar] [CrossRef]
- Hatmal, M. m. M.; Jaber, S.; Taha, M. O. Combining molecular dynamics simulation and ligand-receptor contacts analysis as a new approach for pharmacophore modeling: beta-secretase 1 and check point kinase 1 as case studies. J. Comput. Aid. Mol. Des. 2016, 30, 1149–1163. [Google Scholar] [CrossRef] [PubMed]
- Mandal, M.; Wu, Y.; Misiaszek, J.; Li, G.; Buevich, A.; Caldwell, J. P.; Liu, X.; Mazzola, R. D.; Orth, P.; Strickland, C. Struc ture-Based Design of an Iminoheterocyclic β-Site Amyloid Precursor Protein Cleaving Enzyme (BACE) Inhibitor that Lowers Central Aβ in Nonhuman Primates. J. Med. Chem. 2016, 59, 3231–3248. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-T.; Su, Z.-Y.; Hsieh, C.-H.; Chen, C.-L. Predictions of Binding for Dopamine D2 Receptor Antagonists by the SIE Method. J. Chem. Inf. Model. 2009, 49, 2369–2375. [Google Scholar] [CrossRef] [PubMed]
- Cui, Q.; Sulea, T.; Schrag, J. D.; Munger, C.; Hung, M.-N.; Naïm, M.; Cygler, M.; Purisima, E. O. Molecular Dynamics—Solvated Interaction Energy Studies of Protein–Protein Interactions: The MP1–p14 Scaffolding Complex. J. Mol. Biol. 2008, 379, 787–802. [Google Scholar] [CrossRef] [PubMed]
- Webb, B.; Sali, A. Comparative Protein Structure Modeling Using MODELLER. Current Protocols in Bioinformatics 2014, John Wiley & Sons, Inc., 2014; pp 2015.2016.2011-2015.2016.2032.
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A. V. H++ 3.0: automating pK prediction and the preparation of biomolecular struc tures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, W537–W541. [Google Scholar] [CrossRef] [PubMed]
- Salomon-Ferrer, R.; Case, D. A.; Walker, R. C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Case, D. A.; Cheatham III, T. E.; Darden, T.; Gohlke, H.; Luo, R.; Merz Jr., K. M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Tian, C.; Kasavajhala, K.; Belfon, K. A. A.; Raguette, L.; Huang, H.; Migues, A. N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef] [PubMed]
- Joung, I. S.; Cheatham, T. E., III. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
- Joung, I. S.; Cheatham, T. E., III. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [PubMed]
- Jakalian, A.; Jack, D. B.; Bayly, C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameteriza tion and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef] [PubMed]
- Jakalian, A.; Bush, B. L.; Jack, D. B.; Bayly, C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P. A.; Case, D. A. Automatic atom type and bond type perception in molecular mechanical cal culations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R. M.; Caldwell, J. W.; Kollman, P. A.; Case, D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- He, X.; Man, V. H.; Yang, W.; Lee, T.-S.; Wang, J. A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys. 2020, 153. [Google Scholar] [CrossRef]
- Izaguirre, J. A.; Catarello, D. P.; Wozniak, J. M.; Skeel, R. D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M. L.; Darden, T.; Lee, H.; Pedersen, L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A. W.; Poole, D.; Le Grand, S.; Walker, R. C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef] [PubMed]
- Götz, A. W.; Williamson, M. J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R. C. Routine Microsecond Molecular Dynamics Simu lations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef] [PubMed]
- Purisima, E. O. Fast summation boundary element method for calculating solvation free energies of macromolecules. J. Comput. Chem. 1998, 19, 1494–1504. [Google Scholar] [CrossRef]
- Purisima, E. O.; Nilar, S. H. A simple yet accurate boundary element method for continuum dielectric calculations. J. Comput. Chem. 1995, 16, 681–689. [Google Scholar] [CrossRef]
- Bhat, S.; Purisima, E. O. Molecular surface generation using a variable-radius solvent probe. Proteins 2006, 62, 244–261. [Google Scholar] [CrossRef]
- Perdih, A.; Bren, U.; Solmajer, T. Binding free energy calculations of N-sulphonyl-glutamic acid inhibitors of MurD ligase. J. Mol. Model. 2009, 15, 983–996. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef]
- Sun, H.; Duan, L.; Chen, F.; Liu, H.; Wang, Z.; Pan, P.; Zhu, F.; Zhang, J. Z. H.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 7. Entropy effects on the performance of end-point binding free energy calculation approaches. Phys. Chem. Chem. Phys. 2018, 20, 14450–14460. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D. A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Tsui, V.; Case, D. A. Theory and applications of the generalized born solvation model in macromolecular simulations. Biopoly mers 2000, 56, 275–291. [Google Scholar] [CrossRef]
- Miller, B. R., III; McGee, T. D., Jr.; Swails, J. M.; Homeyer, N.; Gohlke, H.; Roitberg, A. E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, A. D. Gene duplications in the structural evolution of chymotrypsin. J. Mol. Biol. 1979, 128, 49–79. [Google Scholar] [CrossRef]
- Roe, D. R.; Cheatham, T. E., III. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Wang, W.; Pang, L.; Zhang, Q.; Liu, X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J. Chem. Inf. Model. 2021, 61, 1954–1969. [Google Scholar] [CrossRef]
- Yu, Z.; Su, H.; Chen, J.; Hu, G. Deciphering Conformational Changes of the GDP-Bound NRAS Induced by Mutations G13D, Q61R, and C118S through Gaussian Accelerated Molecular Dynamic Simulations. Molecules 2022, 27, 5596. [Google Scholar] [CrossRef]
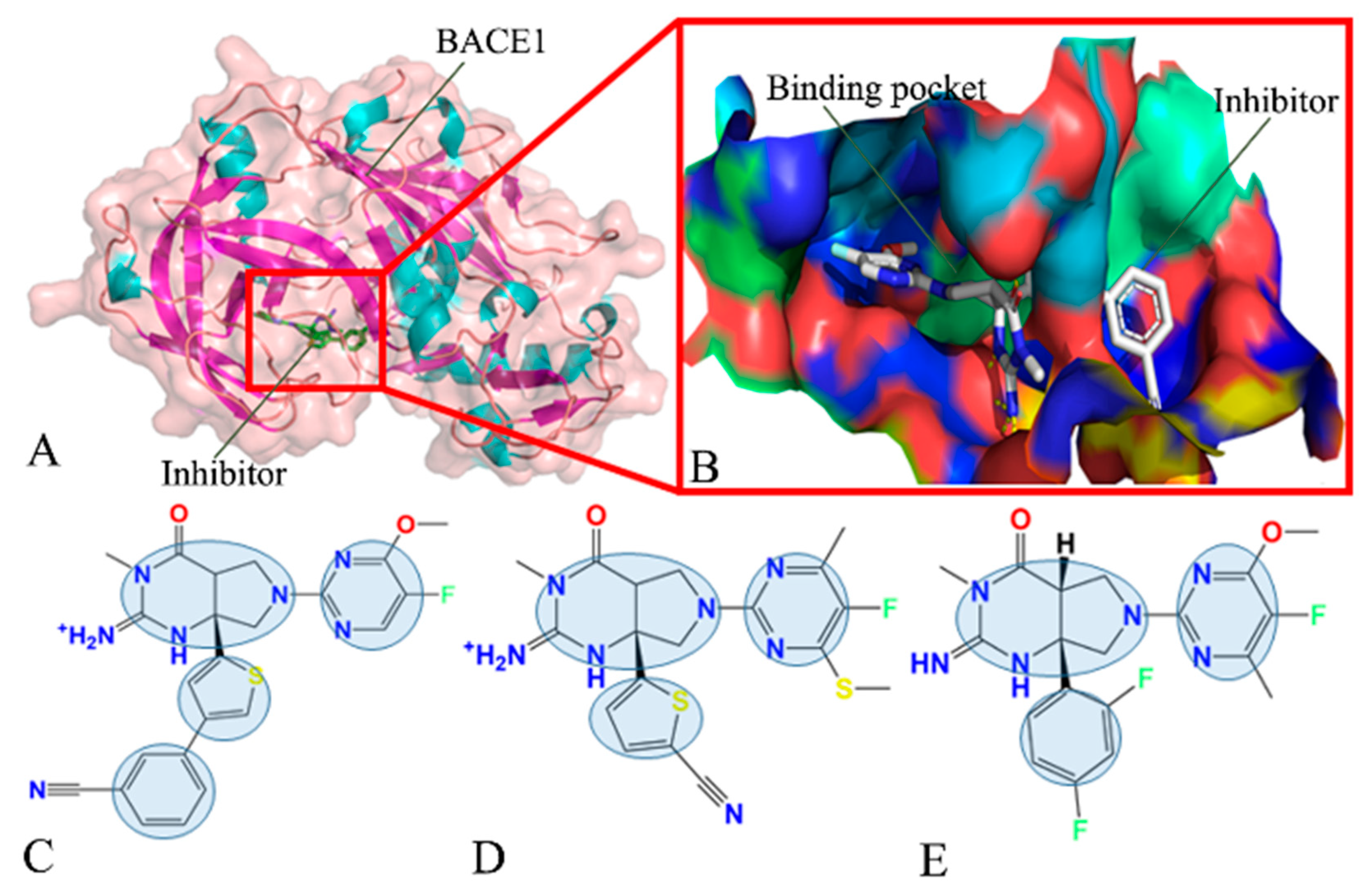
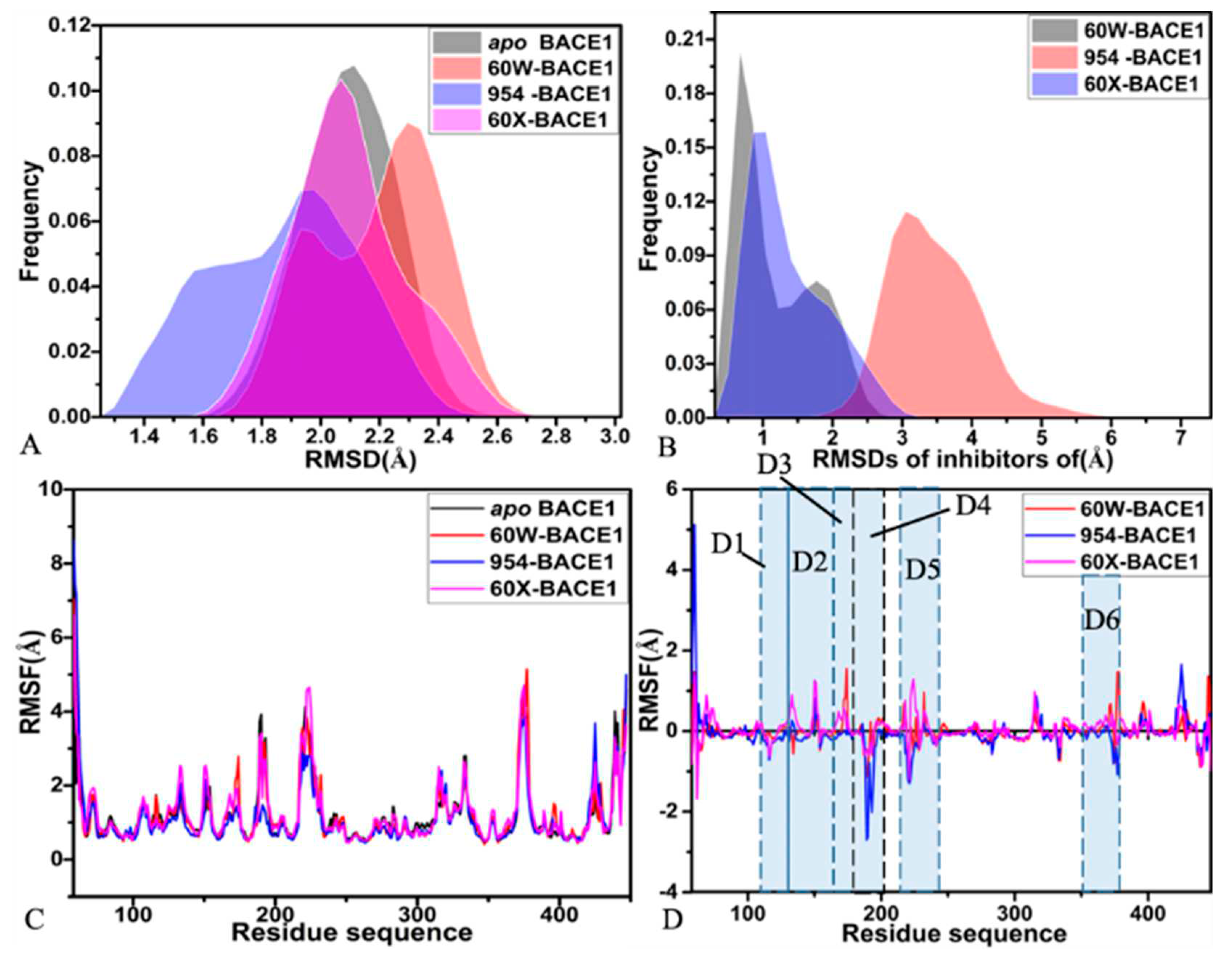
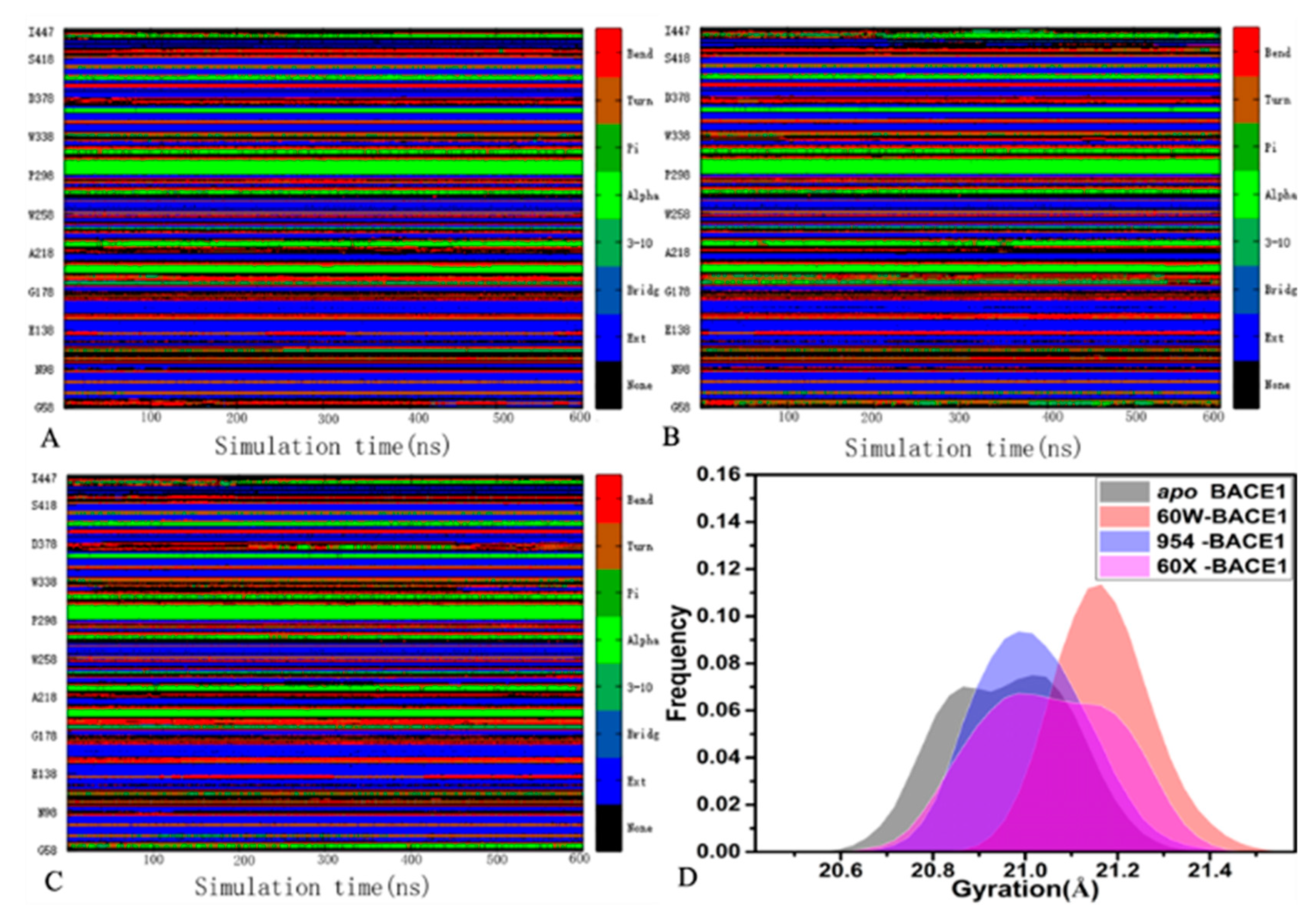
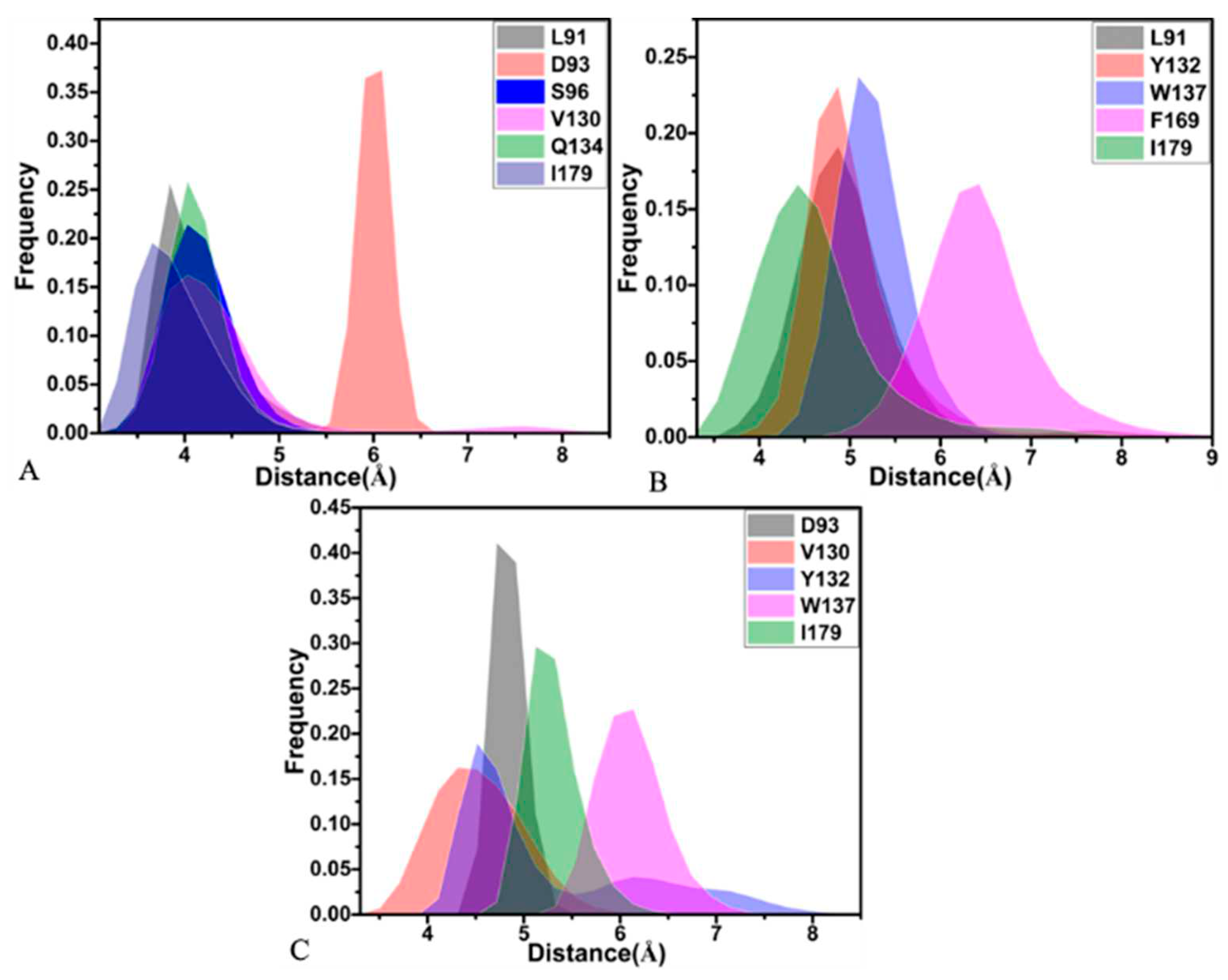
| Components | 60W-BACE1 | 954-BACE1 | 60X-BACE1 | |||
| average | StdErr | average | StdErr | average | StdErr | |
| -54.53 | 0.50 | -42.68 | 0.97 | -42.50 | 0.43 | |
| -16.18 | 0.35 | -12.55 | 0.42 | -15.22 | 0.29 | |
| 24.77 | 0.37 | 21.27 | 0.57 | 22.80 | 0.37 | |
| -10.63 | 0.09 | -8.14 | 0.18 | -8.05 | 0.06 | |
| -2.89 | 0.00 | -2.89 | 0.00 | -2.89 | 0.00 | |
| b | -8.82 | 0.07 | -7.30 | 0.11 | -7.39 | 0.05 |
| c | -12.3 | -10.0 | -11.4 | |||
| Parameters | IGB=1 | IGB=2 | IGB=5 | IGB=66 |
| a | 0.0072 | 0.005 | 0.005 | 0.005 |
| a | 0.00 | 0.00 | 0.00 | 0.00 |
| b | mbondi | mbondi2 | mbondi2 | bondi |
| Energy | 60W | 954 | 60X | ||||||||||||||||
| IGB=1 | IGB=2 | IGB=5 | IGB=66 | IGB=1 | IGB=2 | IGB=5 | IGB=66 | IGB=1 | IGB=2 | IGB=5 | IGB=66 | ||||||||
| -36.23 | -36.23 | -36.23 | -36.23 | -28.25 | -28.25 | -28.25 | -28.25 | -33.88 | -33.88 | -33.88 | -33.88 | ||||||||
| -54.58 | -54.58 | -54.58 | -54.58 | -42.36 | -42.36 | -42.36 | -42.36 | -42.31 | -42031 | -42.31 | -42.31 | ||||||||
| 46.47 | 54.13 | 11.96 | 69.01 | 35.94 | 42.71 | 5.57 | 55.77 | 40.06 | 46.70 | 6.31 | 56.78 | ||||||||
| -7.21 | -5.00 | -5.00 | -5.00 | -5.64 | -3.92 | -3.92 | -3.92 | -5.71 | -3.96 | -3.96 | -3.96 | ||||||||
| b | 10.24 | 17.9 | -24.27 | 32.78 | 7.69 | 14.46 | -22.98 | 27.52 | 6.18 | 12.82 | -27.57 | 22.9 | |||||||
| c | -61.79 | -59.58 | -59.58 | -59.58 | -48 | -46.28 | -46.28 | -46.28 | -48.02 | -46.27 | -46.27 | -46.27 | |||||||
| d | -51.55 | -41.68 | -83.85 | -26.8 | -40.31 | -31.82 | -69.26 | -18.76 | -41.84 | -33.45 | -73.84 | -23.37 | |||||||
| 22.52 | 18.60 | 18.94 | |||||||||||||||||
| -29.03 | -19.16 | -61.33 | -4.28 | -21.71 | -13.22 | -50.66 | -0.16 | -22.9 | -14.51 | -54.9 | -4.43 | ||||||||
| e | -12.3 | -10.0 | -11.4 | ||||||||||||||||
| Inhibitor | Residue | ||||||||||
| 60W | L91 | -1.35 | -0.07 | -1.42 | 0.06 | -0.18 | -0.12 | -0.05 | -0.00 | -0.05 | -1.72 |
| D93 | -0.59 | -0.19 | -0.78 | -16.62 | -0.45 | -17.08 | 15.42 | 0.51 | 15.93 | -2.04 | |
| S96 | -1.69 | -0.36 | -2.05 | 1.39 | -0.24 | 1.15 | -0.47 | 0.37 | -0.10 | -1.13 | |
| V130 | -1.43 | -0.11 | -1.54 | -0.03 | -0.09 | -0.12 | 0.03 | 0.07 | 0.10 | -1.75 | |
| Y132 | -0.04 | -0.07 | -0.11 | -0.02 | 0.15 | 0.13 | 0.03 | -0.02 | 0.01 | 0.03 | |
| Q134 | -2.96 | -0.74 | -3.70 | -0.26 | -0.76 | -1.02 | 0.99 | 1.52 | 2.51 | -2.58 | |
| W137 | -1.34 | -0.04 | -1.38 | -0.06 | 0.03 | -0.03 | 0.59 | -0.03 | 0.56 | -0.93 | |
| F169 | -0.69 | -0.14 | -0.83 | 0.11 | -0.14 | -0.03 | 0.20 | 0.25 | 0.45 | -0.45 | |
| I179 | -1.81 | -0.21 | -2.02 | 0.17 | -0.05 | 0.12 | -0.11 | -0.12 | -0.23 | -2.26 | |
| 954 | L91 | -0.95 | -0.05 | -1.00 | 0.07 | -0.23 | -0.16 | -0.04 | 0.15 | 0.11 | -1.14 |
| D93 | -0.37 | -0.10 | -0.47 | -12.67 | -0.32 | -12.99 | 12.51 | 0.28 | 12.79 | -0.77 | |
| S96 | -1.47 | -0.34 | -1.81 | 1.09 | 0.22 | 1.31 | -0.13 | 0.00 | -0.13 | -0.78 | |
| V130 | -0.72 | -0.09 | -0.81 | -0.02 | -0.03 | -0.05 | 0.04 | 0.13 | 0.17 | -0.77 | |
| Y132 | -2.32 | -0.11 | -2.43 | -0.99 | 0.08 | -0.91 | 1.70 | 0.01 | 1.71 | -1.88 | |
| Q134 | -0.23 | -0.06 | -0.29 | -0.36 | -0.04 | -0.40 | 0.39 | 0.06 | 0.45 | 0.27 | |
| W137 | -1.66 | -0.04 | -1.70 | -0.38 | 0.03 | -0.35 | 1.14 | -0.02 | 1.12 | -1.04 | |
| F169 | -1.44 | -0.32 | -1.76 | -0.46 | -0.63 | -1.09 | 0.57 | 0.96 | 1.52 | -1.44 | |
| I179 | -1.64 | -0.13 | -1.77 | 0.13 | -0.02 | 0.11 | -0.12 | -0.04 | -0.16 | -1.91 | |
| 60X | L91 | -0.75 | -0.05 | -0.79 | 0.10 | -0.19 | -0.09 | -0.06 | 0.11 | 0.05 | -0.90 |
| D93 | -0.30 | -0.11 | -0.41 | -15.06 | -0.44 | -15.5 | 14.33 | 0.44 | 14.77 | -1.23 | |
| S96 | -1.71 | -0.35 | -2.06 | 1.34 | -0.04 | 1.30 | 0.07 | 0.24 | 0.31 | -0.61 | |
| V130 | -1.14 | -0.11 | -1.25 | -0.06 | 0.06 | 0.00 | 0.07 | 0.03 | 0.10 | -1.28 | |
| Y132 | -2.52 | -0.13 | -2.65 | -0.61 | -0.12 | -0.73 | 1.47 | 0.18 | 1.65 | -2.00 | |
| Q134 | -0.12 | -0.05. | -0.17 | -0.20 | -0.04 | -0.24 | 0.24 | 0.07 | 0.31 | -0.13 | |
| W137 | -1.55 | -0.04 | -1.59 | -0.86 | 0.06 | -0.80 | 1.25 | -0.05 | 1.20 | -1.29 | |
| F169 | -1.04 | -0.21 | -1.25 | -0.10 | -0.30 | -0.40 | 0.35 | 0.47 | 0.82 | -0.90 | |
| I179 | -1.91 | -0.24 | -2.15 | 0.19 | -0.11 | 0.08 | -0.11 | -0.01 | -0.12 | -2.31 |
| compound | aHydrogen bonds | Distance(Å) | Angle (°) | bOccupancy (%) |
| 60W-BACE1 | A93-OD1…60W-H3-N1 | 3.0 | 157.1 | 91.1 |
| A93-OD2…60W-H1-N | 2.8 | 163.3 | 82.4 | |
| A93-OD2…60W-H3-N1 | 3.2 | 147.8 | 54.1 | |
| A93-OD1…60W-H1-N | 3.1 | 143.8 | 46.7 | |
| 954-BACE1 | A93-OD2…954-H4-N2 | 3.1 | 150.1 | 76.7 |
| A93-OD1…954-H4-N2 | 3.1 | 149.5 | 75.6 | |
| A93-OD1…954-H2-N1 | 2.8 | 159.6 | 49.2 | |
| A93-OD2…954-H2-N1 | 2.9 | 158.5 | 46.9 | |
| 60X-BACE1 | A93-OD2…60X-H5-N4 | 3.1 | 150.4 | 89.1 |
| A93-OD1…60X-H5-N4 | 3.1 | 149.3 | 84.4 | |
| A93-OD1…60X-H1-N3 | 2.8 | 161.6 | 62.7 | |
| A93-OD2…60X-H1-N3 | 2.9 | 157.7 | 48.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





