Prerpints.org logo
Preprint
Article

A Simplified Silty Sand Model

Altmetrics

Downloads

99

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 May 2023

Posted:

31 May 2023

You are already at the latest version

Alerts
Abstract
A unified critical state model has been developed for both clean sand and silty sand using the modified Cam-clay model (MCC). The main feature of the proposed model is a new critical state line equation in the e-ln(p) plane that is capable of handling both straight and curved test results. With this feature, the error in calculating plastic volumetric strain is eliminated in theory. Another crucial feature of the model is the transformed stress tensor based on the SMP (spatially mobilized plane) criterion, which takes into account the proper shear yield and failure of soil under three-dimensional stresses. Additionally, the proposed model applies the intergranular void ratio with the fines influence factor for silty sand. Only eight soil parameters are required for clean sand, and a total number of twelve soil parameters are needed for silty sand.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The modified Cam-clay (MCC) model was originally developed to describe the stress-strain-strength characteristics of normally-consolidated clay based on Roscoe and Burland’s critical state theory [1]. A number of modifications have been made to the MCC to improve its ability to model geomaterials, such as [2,3,4,5,6,7,8,9,10,11,12,13]. Within the MCC and its family, the critical state void ratio ( e c s ) defined by the critical state line (CSL) is assumed to be a straight line lower than the normally consolidated line (NCL) with the same slope λ, as shown in Figure 1(a). The distance between the NCL and CSL is assumed to be λ − κ ln ⁡ 2 . Eq. (1) contains two fitting parameters: Γ, the limiting critical state void ratio, usually defined as e c s at p =1.0, and λ, which represents the constant slope of the CSL. However, unlike clay, the literature shows that the CSL of granular soil is not a straight line, e.g., [14,15,16,17,18,19,20]. A power function curve shown in eq. (2) provides a better representation for granular soil. In eq. (2), Γ acts as the upper bound of e c s , while λ,   p a   a n d   ξ are the fitting parameters. Although p a is recommended, it is not necessary to be the atmospheric pressure (approximately 101 kPa). Thus, eq. (2) requires three fitting parameters. It should be noted that the slope of CSL in eq. (2) is not a constant but a varied value λ ¯ . A comparison between eq. (1) and eq. (2) is demonstrated in Figure 1(b). Using eq. (1) for granular soil would result in a significant error in the volumetric plastic strain ( ∆ ε v p = ∆ e p / ( 1 + e 0 ) ) . Therefore, a power function curve is popularly used for sand or silty sand. However, this form of the power function can be problematic in sand models when dealing with high pressure because it cannot provide a straight portion after the curved portion. Figure 2(a) shows the concavity on the extension of eq. (2) after fitting the laboratory data [2], where the dashed line deviated from the trend of a straight line. To achieve a proper function of e c s in the e-ln(p) for granular soil, including clean sand and silty sand, without any error in the volumetric plastic strain calculation, a curve illustrated in Figure 2(b) is required.
e c s = Γ − λ ln ⁡ p
e c s = Γ − λ p / p r e f ξ
Matsuoka et al. [4] were the first to revise the shear yield and shear failure in the MCC model from the extended Mises criterion to the SMP criterion by introducing the transformed stress. Yao et al. [5] successfully applied the transformed stress of [4] to model loose and dense sand, depending on two key factors, i.e., the initial density ( e 0 ) and mean effective stress ( p 0 ). Furthermore, Yao et al. [6] proposed another transformed stress, in conjunction with a new hardening parameter, to the MCC model to model both clay and sand. Finally, in this study, a new curve of the CSL in the e-ln(p) is derived, which has the ability to fit a straight line, curved line, and a curved line connected with a straight line. Therefore, the sand model developed by Yao et al. [5] can be extended for both clean sand and silty sand. Additionally, we have made some revisions to the work of Yao et al. [5] to take into account the effect of the participation of fines in sand by applying the concept of the equivalent intergranular void ratio ( e * ) proposed by Thevanayagam and Martin [21] and the fines influence factor (β) proposed by Lashkali [22]. The roundness of both sand and fines can settle the arguments in the load bearing mechanism of many silty sands in the literature, according to the work of Lashkali [22]. With these ideas, it is possible to oversimplify the soil characteristics in the critical state model for silty sand.

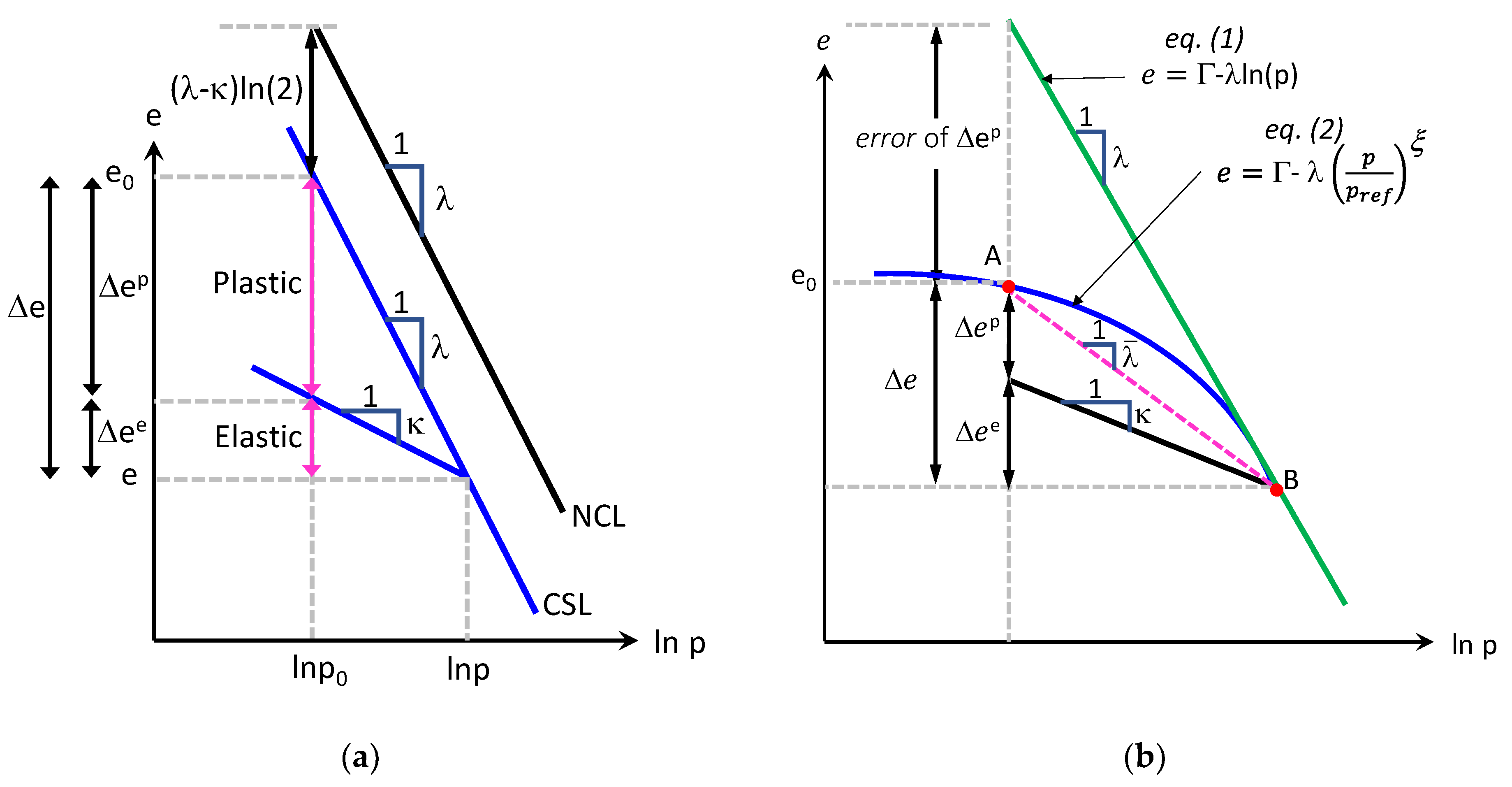
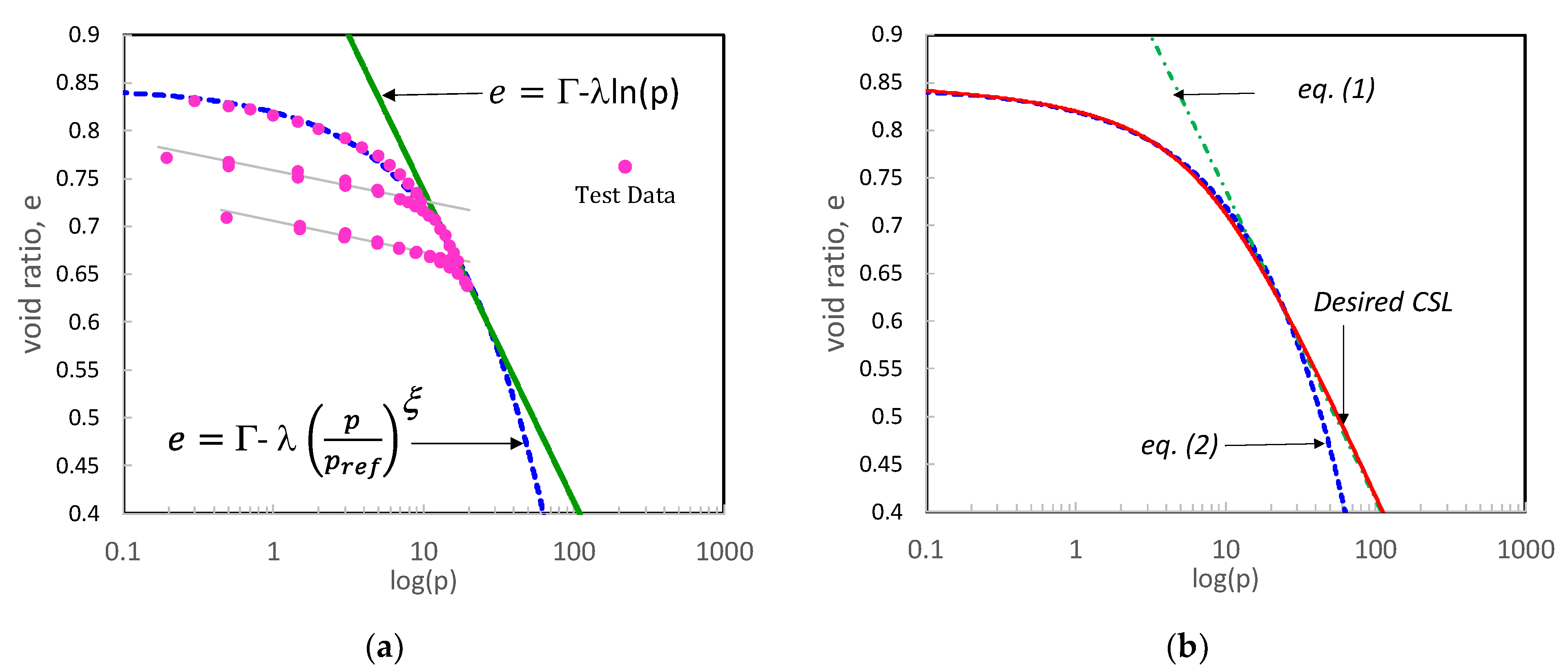
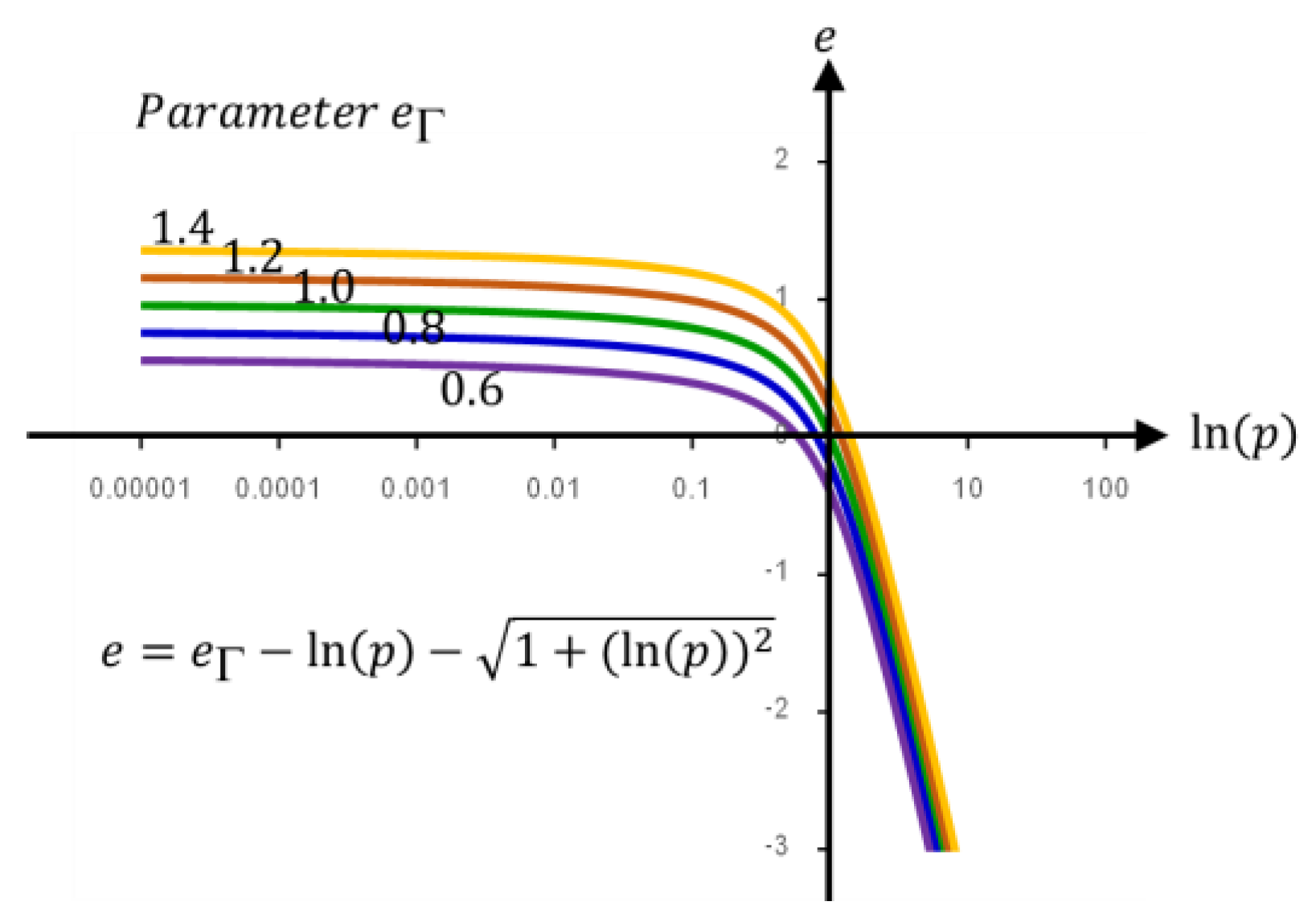
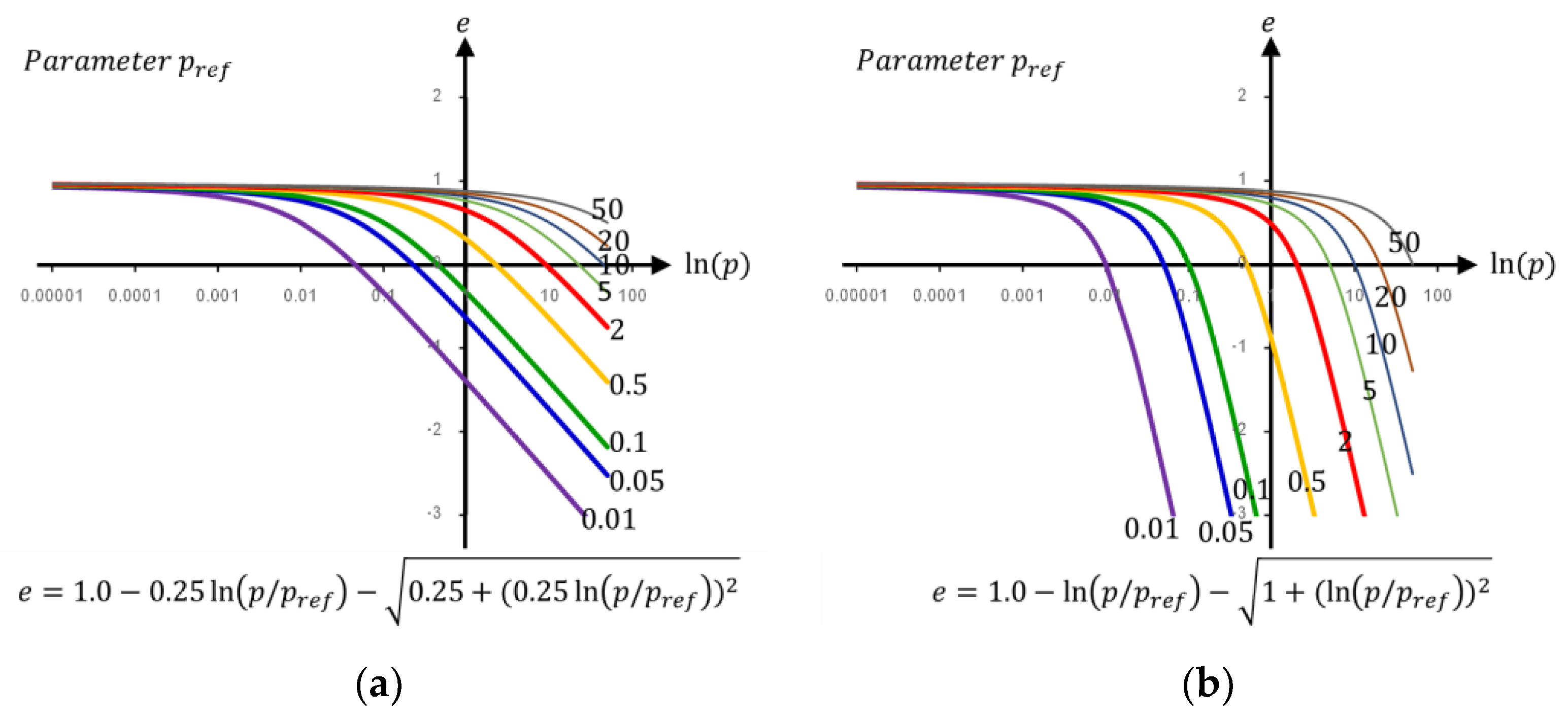
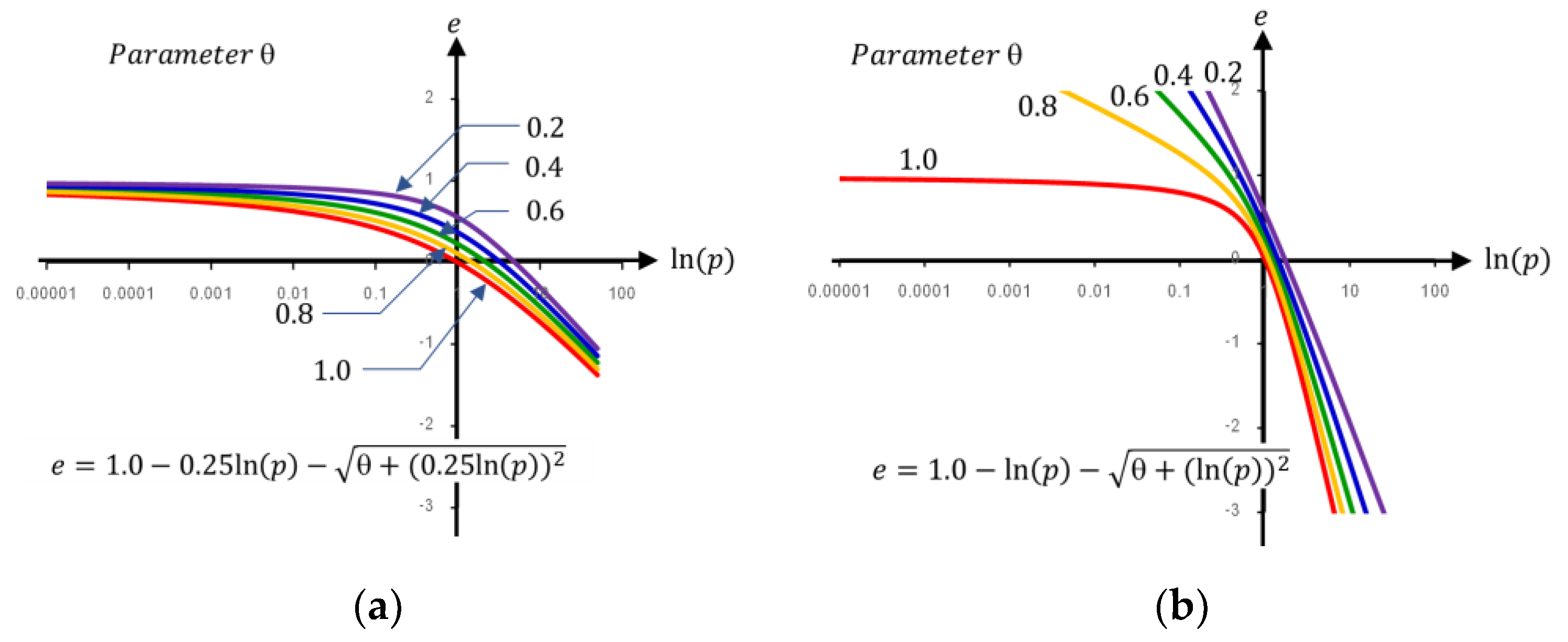
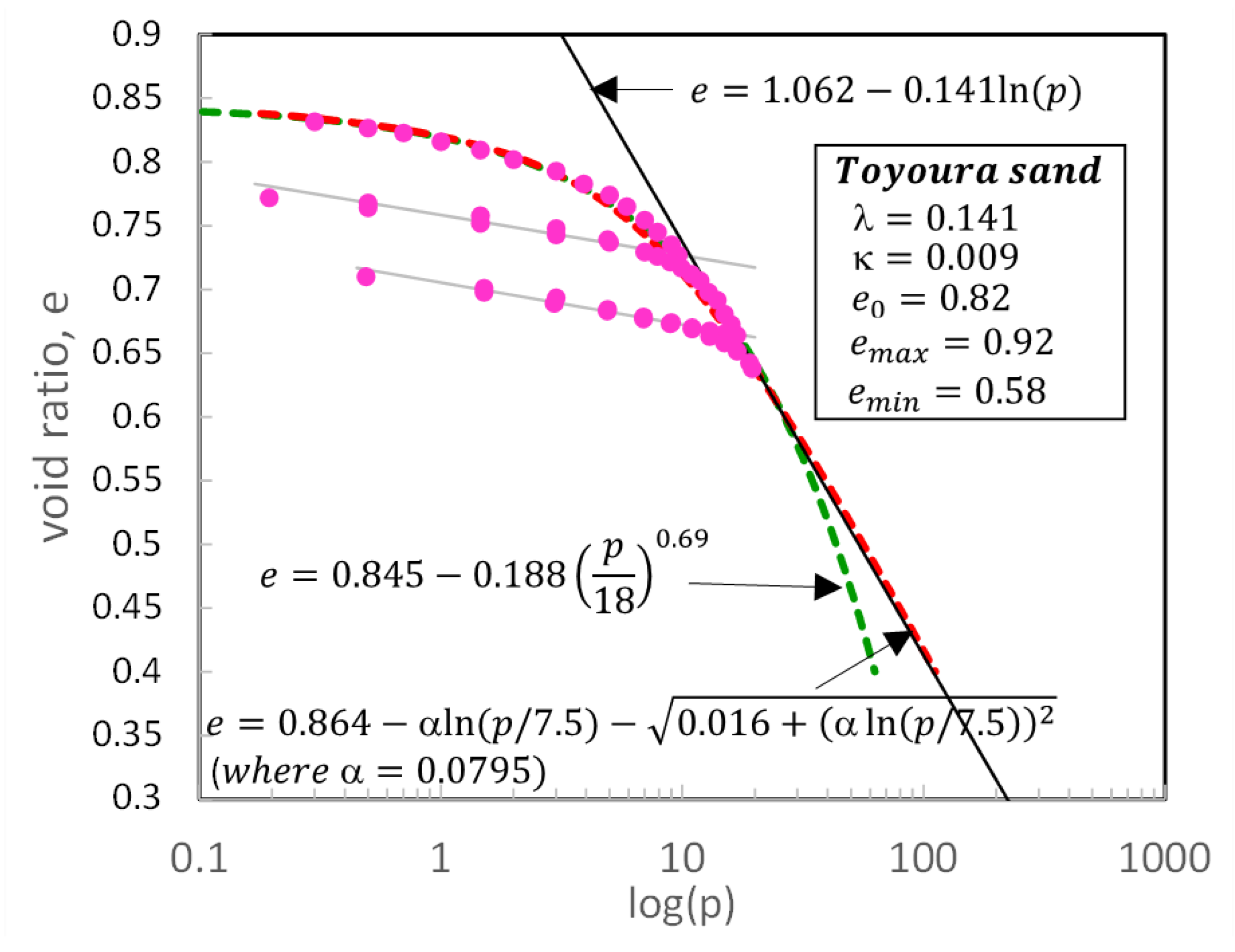
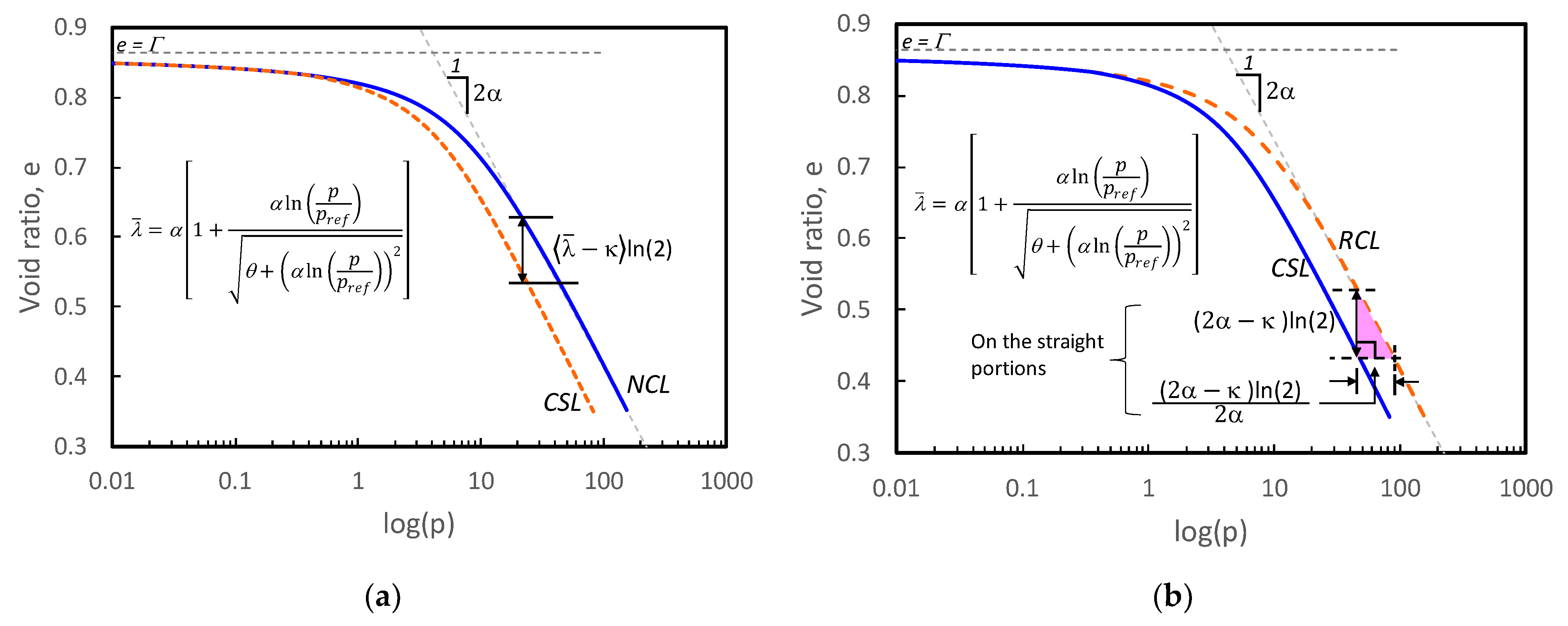
2. The Critical State Line in e-ln(p) plane

As mentioned earlier, the MCC model adopted a straight line of the CSL, but a curved line is valid for sand and silty sand. To address this, the proposed CSL should have the following features:
1)
The equation should provide both the curved portion and the connecting straight line
2)
One of the fitting parameters should be the desired slope of the straight portion
3)
The equation should consist of the parameters that can adjust to fit various curvatures and locations
4)
All parameters should be determined from a conventional test
By incorporating these features, the proposed CSL can better capture the behavior of sand and silty sand, and provide more accurate predictions for engineering analyses.
Eq. (3) presents the new CSL with four fitting parameters: Γ, which controls the vertical translation of the curve;   p r e f , which is a positive reference pressure controlling the horizontal translation; θ, which controls the curvature of the upper portion; and α, which controls the slope of the lower portion. It is recommended that the value of α = λ / 2 or a value close to λ / 2 , where λ is the slope of CSL in eq. (1). To investigate eq. (3), variations of all fitting parameters were demonstrated in Figure 3, Figure 4, Figure 5 and Figure 6. Notably, when θ = 0, the curvature of the CSL vanishes and eq. (3) becomes a straight line with a slope of 2α, as shown in eq. (4). Furthermore, when θ = 0 and p r e f = 1 , eq. (3) reduces to eq. (1) with α = λ / 2 . Figure 7, the test results of Toyoura sand [2] were plotted against eq. (1), eq. (2) and eq. (3) to evaluate their performance. Eq. (5) and eq. (6) present the slope  λ ¯   of eq. (3) in terms of tangential and secant, respectively.
e = Γ − α ln ⁡ p p r e f − θ + α ln ⁡ p p r e f 2
e = Γ − 2 α ln ⁡ p p r e f
While eq. (3) requires more parameters than eq. (1-2), all four parameters can be determined by fitting the same test data used for eq. (1-2), without requiring additional testing. Therefore, eq. (3) satisfies all the aforementioned features.
λ ¯ t = ∂ e ∂ ( l n p ) = α 1 + α ln ⁡ p p r e f θ + α ln ⁡ p p r e f 2
λ ¯ s = − ∆ e ∆ ln ⁡ p = = α + θ + α ln ⁡ p 1 p r e f 2 − θ + α ln ⁡ p 2 p r e f 2 / l n p 2 p 1
In the MCC model and its family, the CSL and NCL are both assumed to be a straight line with a constant slope λ (see Figure 1) and the vertical distance of λ − κ ln ⁡ 2 [5]. In the proposed model, once the curve of NCL is obtained using eq. (3), the CSL is assumed to locate below the NCL with a distance of λ ¯ − κ ln ⁡ 2 , where < > represents the Macualey brackets (i.e., λ ¯ − κ = λ ¯ − κ when λ ¯ − κ ≥ 0   and zero otherwise). The shape and location of NCL compared to the CSL for this case are shown in Figure 8 (a). It is evident that both the CSL and NCL contain both curved and straight portions. Within the curve portion, the NCL and CSL have different slopes, and these lines are close together when the mean effective stress converges to a very small value ( p → 0 ). On the other hand, the CSL is parallel to the NCL with the same slope within the straight portion. This implies that the new CSL is not only applicable for granular soil but also for clay in the MCC model.
In addition, a curved of RCL can also be derived from the CSL by assuming that the shape of the CSL and the RCL are identical. Therefore, both CSL and RCL have the same parameters i.e., Γ, α and θ. The remaining parameter of the RCL is p r e f which can be determined by the horizontal translation of the CSL to the right until the vertical distance between the two straight portions of the CSL and RCL is equal to λ ¯ − κ ln ⁡ 2 ≈ 2 α − κ ln ⁡ 2 . Since the straight portions are parallel with the slope of 2 α , then the horizontal distance between two straight lines is 2 α − κ ln ⁡ 2 / ( 2 α ) . Hence, the parameter p r e f R C L = p r e f C S L * 2 ^ ( ( 2 α − κ ) / ( 2 α ) ) .

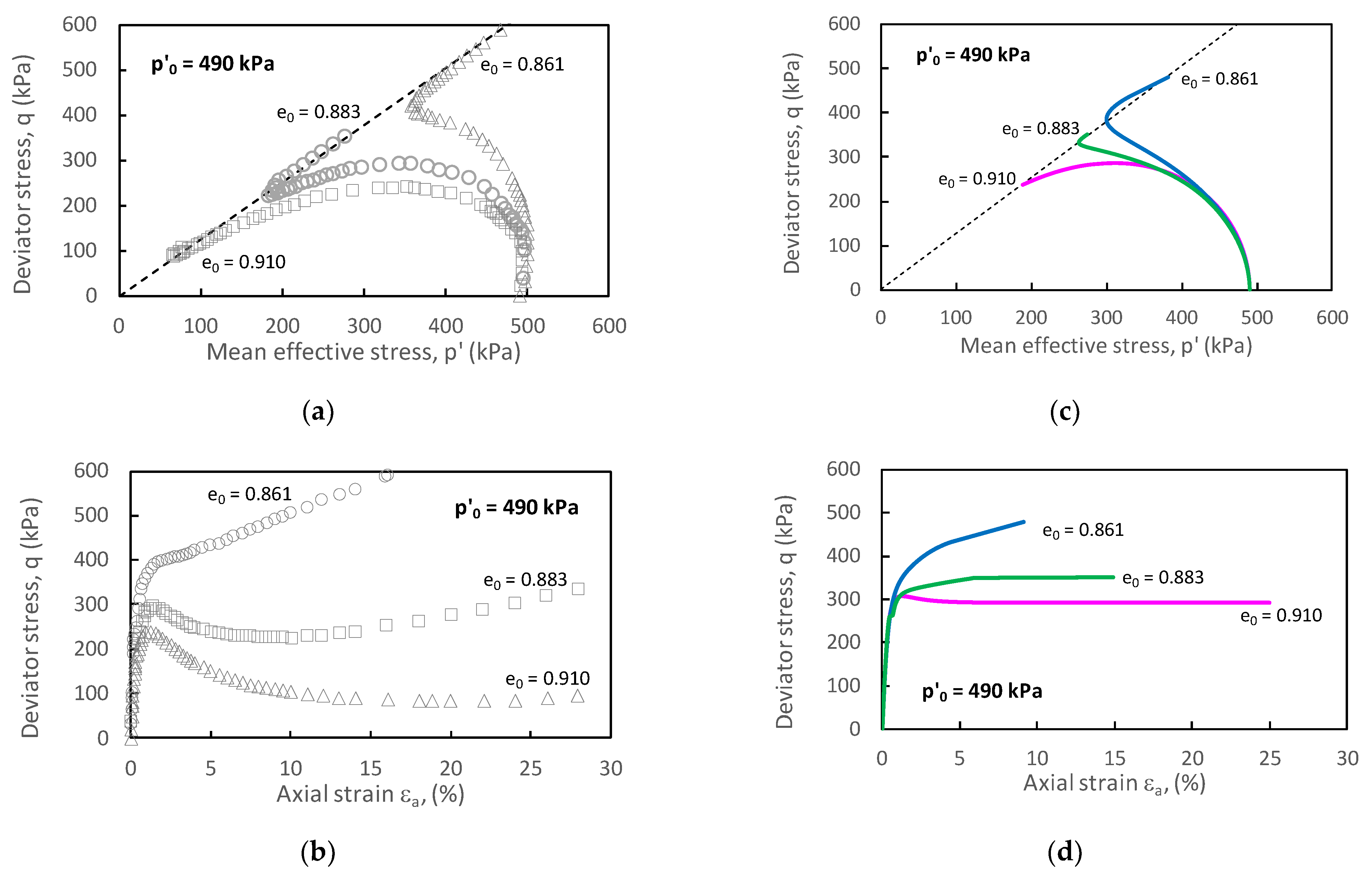
3. Critical State Model for Clean Sand

In the work of Yao et al. [5], the NCL was used as a key tool to distinguish between loose and dense sand, using as a reference control line (RCL). Therefore, in this case, the terms loose and dense refer to sands that are looser or denser than the RCL. Due to changes in the RCL and CSL, some revisions were required to the model presented in [5]. Before describing the revisions in detail, a clearly summary of sand behavior for both loose and dense conditions is stated as follows:
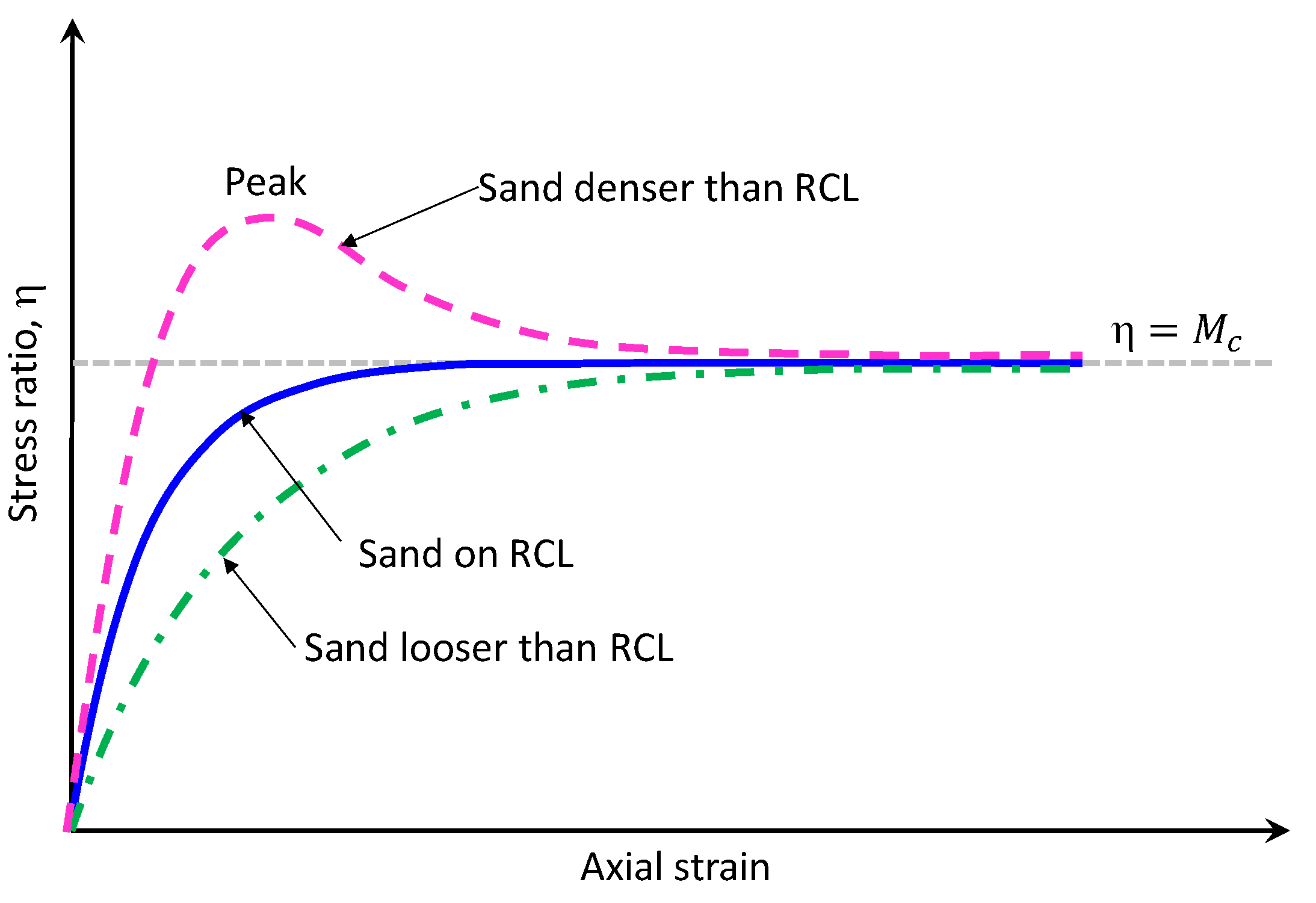
1)
Sand on RCL exhibits only volume contraction during shearing, and the stress ratio η = q / p reaches its maximum value at the critical state, where η = M c and M c is the slope of the critical state line on p-q plane.
2)
Sand that is looser than the RCL (sheared from a point above the RCL) exhibits only volume contraction, but with the larger amount than sand on the RCL and finally reaches the same maximum stress ratio as sand on the RCL at η = M c .
3)
Sand that is denser than the RCL (sheared from a point below the RCL) exhibits volume contraction in early stage, followed by dilation (the stress ratio is greater than the maximum stress ratio of sand on the RCL, i.e., ( η = M f ) > M c , and finally converges to the stress ratio η = M c .
It is evident that both sand on RCL and sand looser than RCL have no peak, but reach the same maximum stress ratio at the critical state, while a peak exists in dense sand during shearing before reaching the critical state. Figure 9 depicts the concept mentioned above.

3.1. Hardening parameter H

The equation for the hardening parameter H in the MCC model and in Yao et al. [5] are shown in eq. (7) and eq. (8), respectively. In eq. (7), λ is a constant representing the slope of the straight NCL and a variable c p is defined as cp=(λ-κ) (l-k)/(1+e0). In eq. (8), despite using the straight NCL in [5], the varied slope of the NCL λ ¯ is assumed in such a way that c ¯ p = ( λ ¯ - κ ) / ( 1 + e 0 ) = [(λ-κ)/(1+e0)](Mc/Mf), where Mc and Mf are the stress ratio at the critical state and stress ratio during shearing. As mentioned in the early section, loose sand has no peak, so Mf = Mc, resulting in eq. (8) becomes eq. (7) of the MCC model. On the other hand, for dense sand, Mf ≥ Mc during shearing. In this paper, a new value of λ ¯ can be calculated directly from the RCS without any assumption using the secant slope of the RCL in eq. (6). Therefore, the final version of H in the proposed model is shown in eq. (9).
H = ∫ d H = ∫ 1 c p d ε v p   ; ( c p = λ − κ 1 + e 0 )
H = ∫ d H = ∫ 1 c p ¯ M c 4 M f 4 M f − 4 η * 4 M c 4 − η * 4 d ε v p   ; ( c ¯ p = λ ¯ − κ 1 + e 0 = λ − κ 1 + e 0 M c 4 M f 4 )
where η * is the maximum stress ratio during shearing.
H = ∫ d H = ∫ 1 c p ¯ M f − 4 η * 4 M c 4 − η * 4 d ε v p   ; ( c ¯ p = λ ¯ − κ 1 + e 0   ;   λ ¯   c a l c u l a t e d   b y   e q .   ( 6 ) )

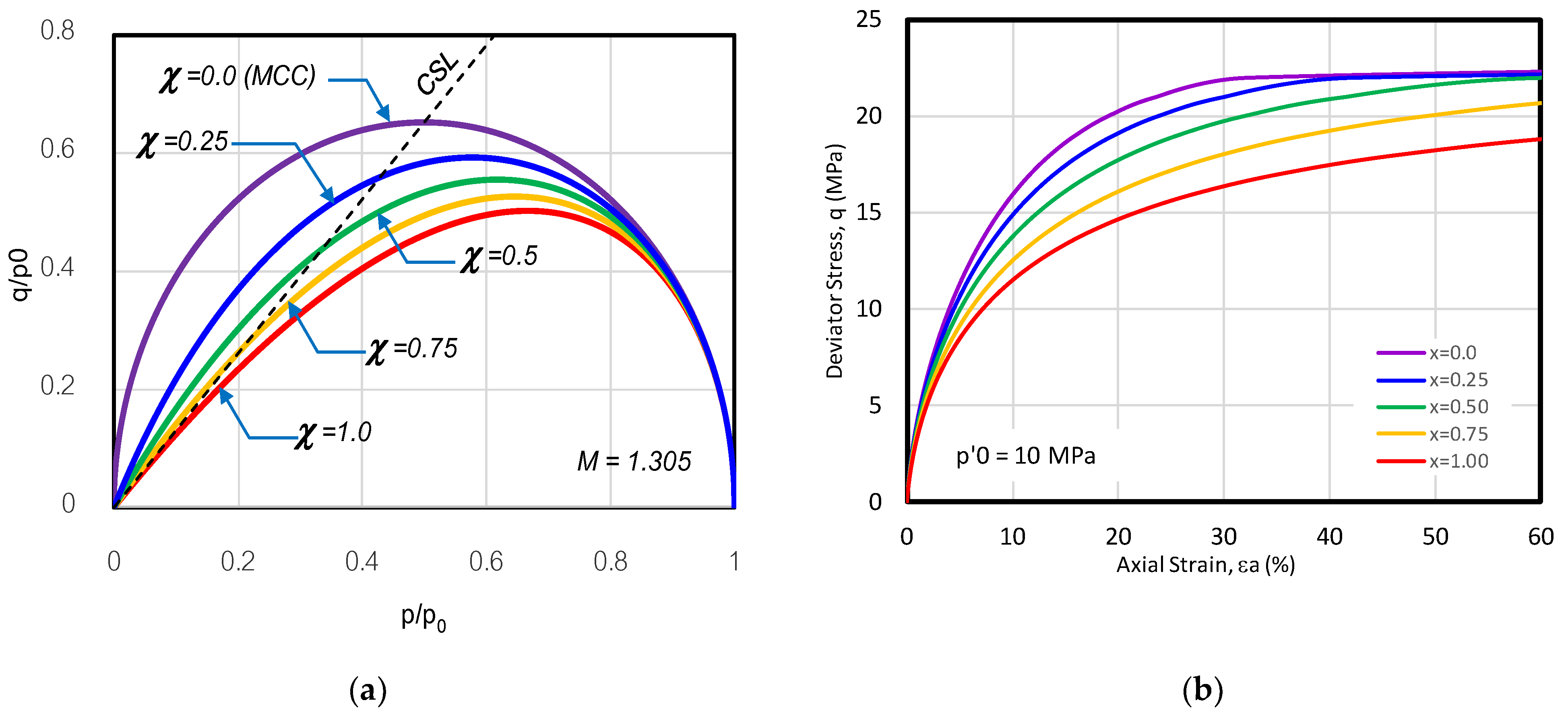
3.2. Yield function

The yield function of the MCC model is represented by an ellipse in p-q plane, as shown in eq. (10). To account for the behavior of loose sand, Yao et al. [5] introduced the initial state parameter χ ( 0 ≤   χ   ≤   1 ) into the MCC model, resulting in a Lemniscate-shaped yield function [23] as shown in eq. (11). The value of χ is zero when sand is on the RCL, and χ increases with distance above the RCL i.e., χ links to both the shape of the yield function and the distance above the RCL. Hence, χ can describe the degree of looseness of sand. Figure 10 (a) shows the yield functions of eq. (10) and eq. (11).
f = ln ⁡ p p 0 + ln ⁡ 1 + η 2 / M 2 = ∫ d H
f = ln ⁡ p p 0 + ln ⁡ 1 + η 2 / M 2 1 − χ η 2 / M 2 = ∫ d H
According to [5], the original value of χ is derived by the stress path of a constant mean effective stress (p’ = p’0) as expressed in eq. (12). The modified χ by incorporating the yield function in eq. (11) and the new hardening in eq. (9) by the same method of [5] is shown in eq. (13).
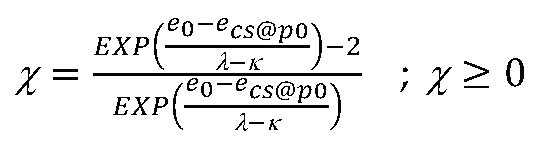
Preprints 75155 i001
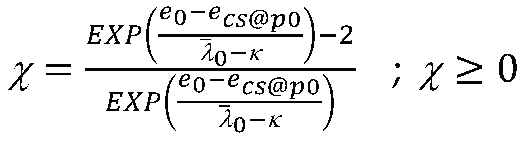
Preprints 75155 i002
where e c s @ p 0 is the critical void ratio calculated by eq. (3) at the initial mean stress p 0 . In eq. (13) λ ¯ 0 is calculated using the tangential slope of the RCL in eq. (5) at the initial mean effective stress p0.
The state parameter χ in eq. (13) is constant during shearing and depends on both the initial mean effective stress p0 and the initial void ratio e0. For sand on the RCL, the λ ¯ t and λ ¯ s in eq. (5-6), respectively, are applicable. For loose sand, the e0 is located above the RCL, the λ ¯ t can be assumed by the interpolation function as shown in eq. (14). Figure 10 illustrates the effect of the initial parameter χ to the yield function and stress-strain curves from the drained triaxial compression simulation. Figure 11 shows the comparison between the test results and the predictions from the MCC, Sand model by Yao et al. [5] and the proposed model. In the analyses, seven soil parameters for loose sand are listed in Table 1 [2].
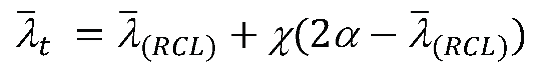
Preprints 75155 i003
In Figure 11, the predictions from both the MCC model and sand model by Yao at al. [5] overestimate the shear strength of sand. However, the results from [5] provides a better result than the MCC’s because of the improvement of the plastic strain calculation through the parameter χ. For the proposed model with both the initial parameters χ and λ ¯ , the prediction agrees well with test results.

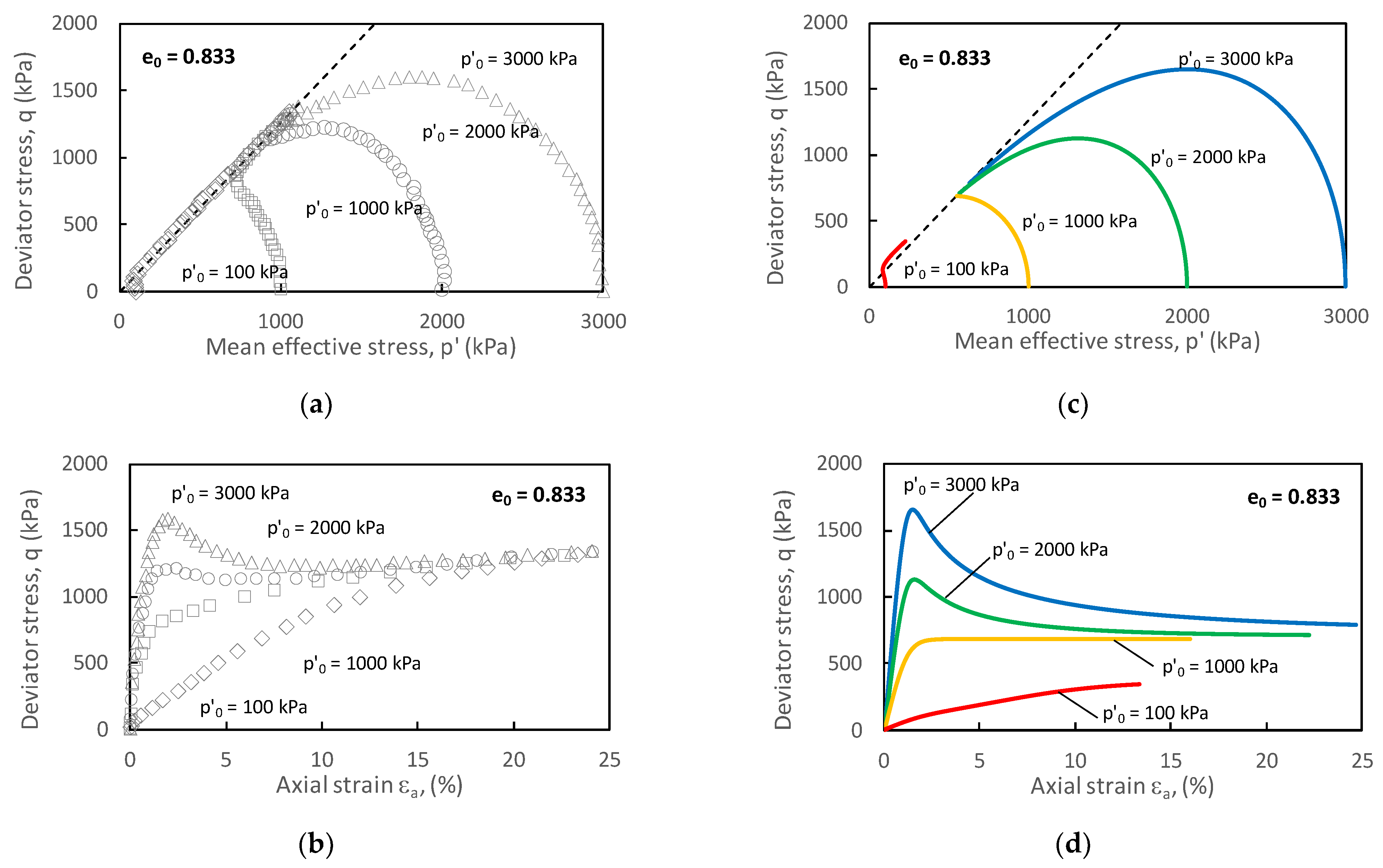
3.3. Peak strength of dense sand

In [5], the yield function of the MCC model can be used for dense sand without the modifications i.e., χ = 0 in eq. (11-12). The goal then becomes identifying the peak in the stress-strain relationship of dense sand. A beautiful derivation for another state parameter χ 2 controlling M f during shearing is introduced to the MCC model in Yao et al. [5] as shown in eq. (15). The additional soil parameter M f m a x and Nd are required to work with its state parameter. Although this formulation works, it required the densest condition for sand in the calculation. Furthermore, Yao et al. [5] assumed the slope of the densest condition to be the same value of the slope of the unloading-reloading curve with a constant slope κ. The computation for M f is required to be changed in order to simplify the model for sand and silty sand.
Been and Jeffries [24] introduced the effective state parameter for sand ψ = e − e c s where e and e c s are the void ratio and the critical state void ratio at the same mean effective stress, respectively. In [25,26], the relationships of M f are proposed relating to ψ = e − e c s . Some researchers have hypothesized that the ratio e / e c s could function as a state parameter e.g., [27]. However, other researchers such as [28,29] favor using the mean effective stresses ratio p / p c s where p and p c s are the current and critical state mean effective stress. According to a comprehensive review by Lashkari [30], two of the most effective state variables which can provide a reasonable peak strength M f of granular soil are Ω = I D l n ⁡ ( p c s / p ) and ψ = e − e c s , where I D = ( e m a x − e ) / ( e m a x − e m i n ) is the relative density, e m a x the maximum void ratio and e m i n the minimum void ratio. The expression for M f from Ω and ψ are shown in eq. (16) and eq. (17), respectively. In this research, we utilized the equation of Manzari and Dafalias [26] in eq. (17) in order to achieve the basic model without requiring many extra parameters.
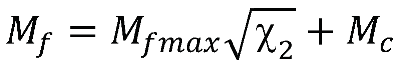
Preprints 75155 i004
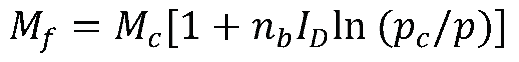
Preprints 75155 i005
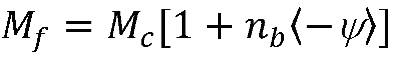
Preprints 75155 i006
Before moving forward to the next section of modeling silty sand, the predictive capability of clean sand for both loose and dense conditions are demonstrated by the comparison between the model prediction and two sets of the test results from Verdugo [31] and Verdugo and Ishihara [32]. Adding n b to the model, eight soil parameters listed in Table 2 from [30,31,32] are used in the analyses for dense sand.
Figure 12 and Figure 13 show the comparison of the test results and the calculation from the proposed model. In Figure 12, the results of the undrained triaxial tests at the initial mean effective stress of 490 kPa and three different initial void ratios of 0.861, 0.883, and 0.910 are demonstrated. Figure 12 (a) through (b) depict the test results, while Figure 12 (c) through (d) illustrate the results of calculation by the proposed model. The peak can be observed in the stress-strain curves of e0 = 0.883 and 0.910 on both the test results and the calculation. Figure 13 shows the results of the undrained triaxial tests for a fixed value of the initial void ratio e0= 0.833 and four different values of the initial mean effective stresses of 3,000, 2,000, 1,000 and 100 kPa. The peak occurred on the stress-strain curves of p0 = 3,000, 2,000, 1,000 kPa. The result demonstrates agreement between the peak from the calculation and the test. It is important to notice that when shearing reached the critical state, all stress-strain curves in Figure 13b,d tended to the same shear strength.

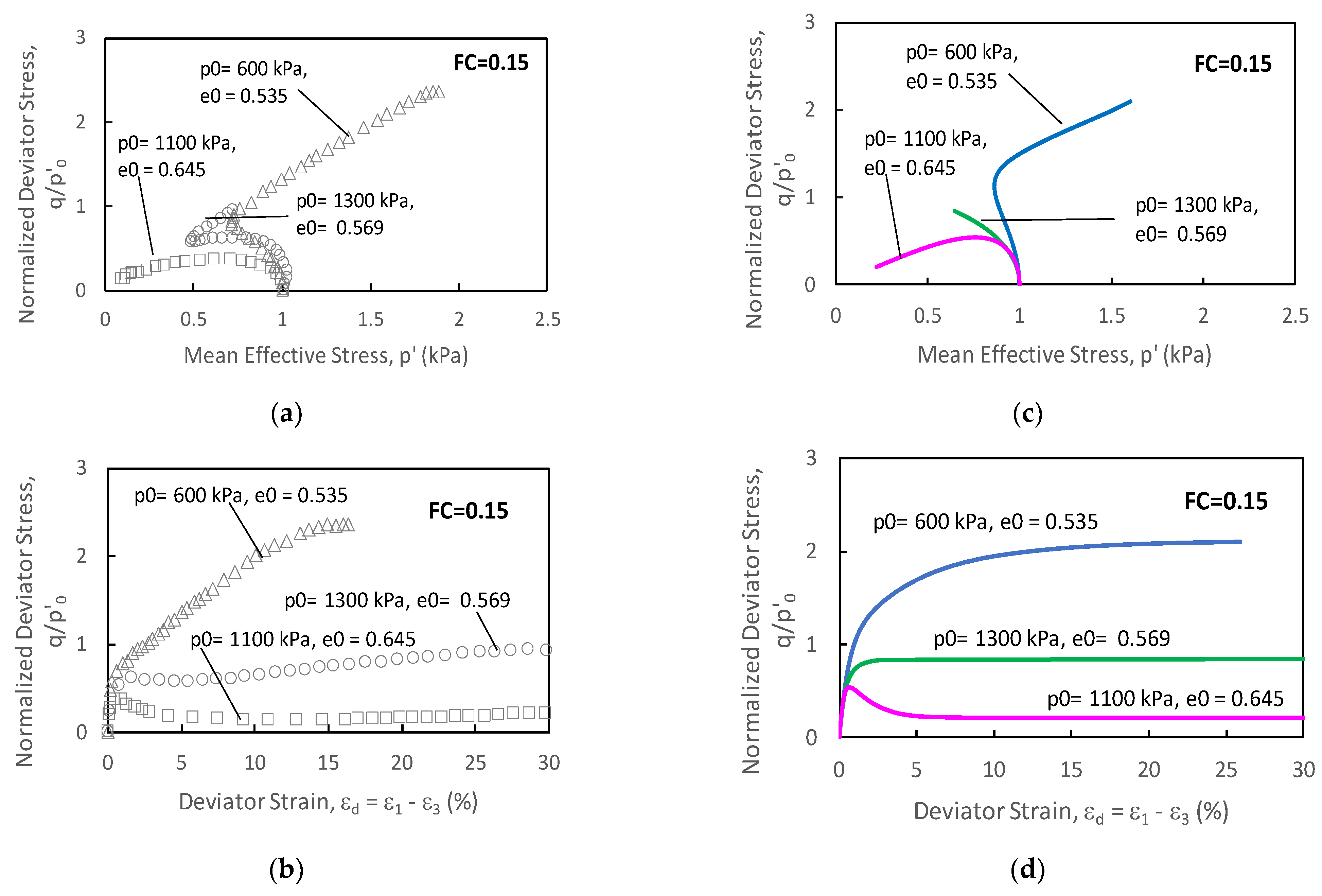
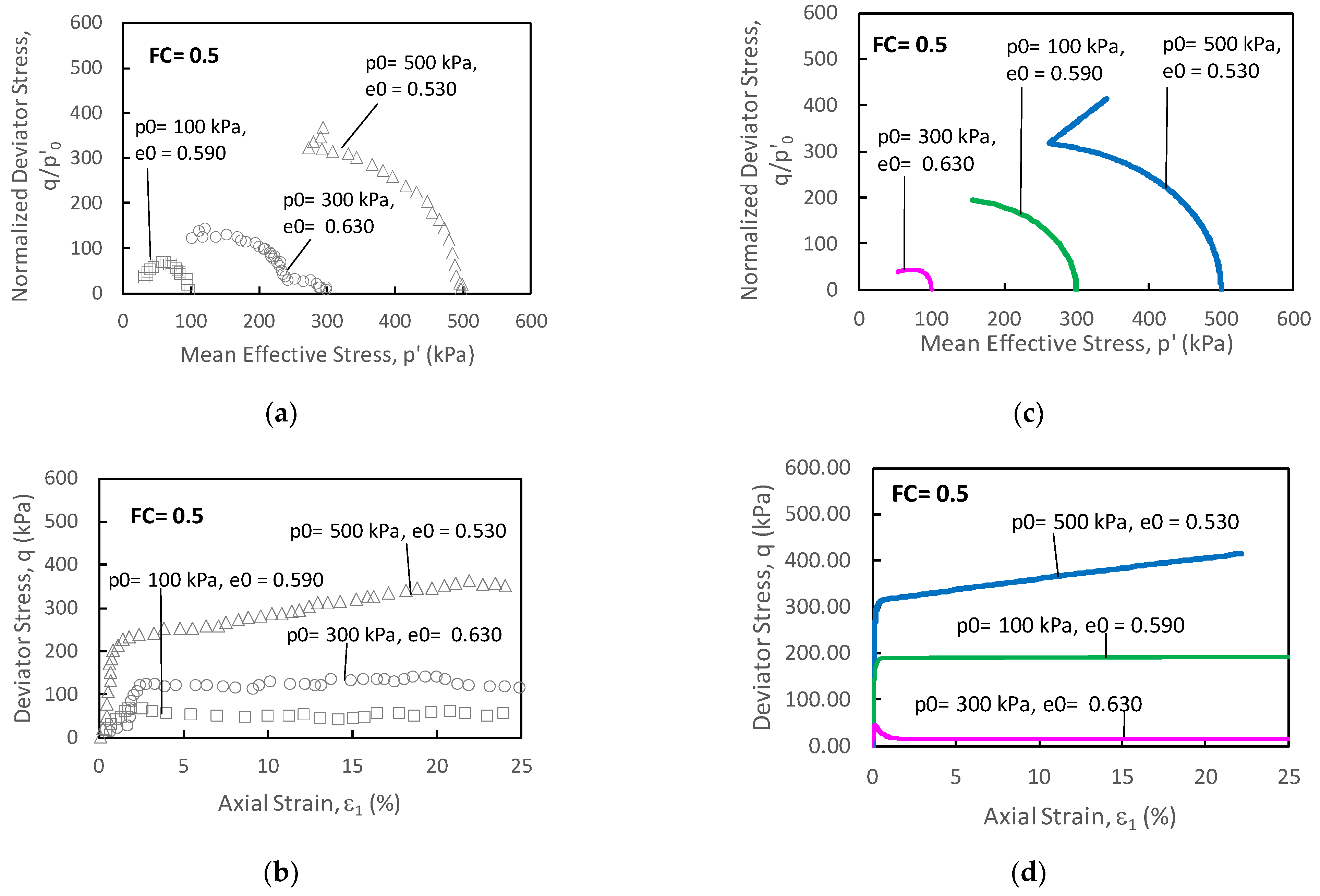
4. Critical State Model for silty sand

Due to the partial participation of fines in the void between sand grains. The equivalent intergranular void ratio (e*) suggested by Thevanayagam and Martin [21] was employed in place of the global void ratio to account for the effect of fines in sand. The equation of e* is expressed as follow
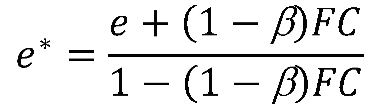
Preprints 75155 i007
where β represents the fines influence factor and FC represents the amount of fines content. The reasonable value of β is 0 ≪ β ≪ 1 . When β = 0 , β = 1 and 0 < β < 1 fines take no action, fully action and partial action in the load bearing mechanism, respectively. The dependence of β on the particle size ratio SR = (d10 of host sand)/(d50 of silt) was discovered using experimental data from Ni et al. [33]. The empirical equation for β, presented by Lashkari [22], takes into account the impacts of the particle size ratio SR as well as the roundness of the soil grains as stated as follows
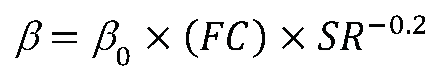
Preprints 75155 i008
where
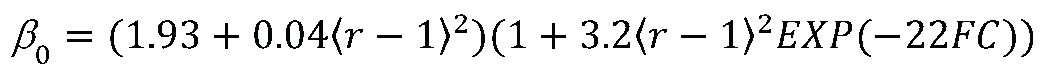
Preprints 75155 i009
and r is the ratio of the average roundness of sand (rc) and fines (rf), respectively.
It is generally accepted that the CSL in the e-p space gradually moves downward when FC increases e.g., [18,34,35,36,37,38,39]. However, when drawing in terms of the equivalent intergranular void ratio e*, the CSL are close together in a narrow range. As a result, for different FC, a specific curve of the e*-p can be established. In this paper, the e* in eq. (18) is used to model the silty sand. Therefore, the state parameter for silty sand becomes ψ * = e * − e c s and the M f for silty sand expressed as follow
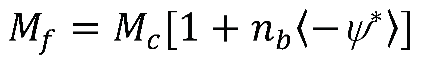
Preprints 75155 i010
The amount of FC also affects the stress ratio at the critical state M c . In the work of Lashkari [22], the value of M c for the specific FC can be determined by the concept of threshold fines content ( F C t h ) expressed in eq. (22). The stress ratio at the critical state for FC ( M c ( F C ) ) can be calculated by Lashkari [22] in eq. (23) with two more parameters i.e., M c ( 0 ) where the M c at zero fines content and ∆ M c = M c F C t h − M c 0 . The equations for the F C t h by Rahman [18], M c ( F C ) and by Lashkari [22] are presented in eq. (22-23).
F C t h = 0.4 1 1 + E X P ( 0.50 − 0.13 × S R ) + 1 S R
M c F C = M c 0 + 3 2 ∆ M c F C F C t h 2 − 1 2 ∆ M c F C F C t h 3
As described above, five additional parameters are required in the analysis of silty sand i.e., rc, rf, SR, M c ( 0 ) and ∆ M c . Two sets of silty sand test results [18,39] are compared to the calculation of the proposed model as shown in Figure 14 and Figure 15.

5. Conclusions

Adding fines into voids of sand leads to a complex behavior of a whole silty sand. The degree of participation of fines in the load-bearing mechanism can be modeled using the intergranular void ratio e* and the fines influence factor β. Two key factors affecting the value of β are the particle size ratio SR and the roundness of soil grain (both sand and silt). To model the behavior of silty sand precisely, the critical state model has a rise in the complexity leading to twenty or more soil parameters. Therefore, most critical state for silty sand is not practical in general analysis especially for the limited budget project. Therefore, the simple silty sand model is needed. The modified Cam clay model (MCC) including the model in the MCC’s family is considered as the simple critical state model in terms of the number of soil parameters. Much modification has been introduced to the MCC to improve its capability e.g., the SMP yield and failure criterion, effective hardening for both clay and sand, yield function for contractive soil. However, the MCC model and its family lack the link to the curve of the CSL which fits to behavior of granular soil. This paper introduces a new equation for the CSL which can be applied for the CSL in the straight-type, the curved type and the curve connecting by the straight portion. Four fitting parameters are used to control the shape and location of the CSL without extra testing. This feature not only improves the prediction for sand but also extends the capability of the model for silty sand in both drained and undrained analyses. Only eight parameters are required for clean sand (i.e., Γ, α, θ, p r e f , κ, ν, M c and n b ). Five extra parameters are needed for silty sand i.e., rc, rf, SR, M c ( 0 ) and ∆ M c ). It is worth to note that the M c is no longer required for silty sand because M c can be calculated from M c ( 0 ) and ∆ M c . Therefore, a total number of soil parameters for silty sand are twelve. The agreement between the prediction of the proposed model and the existing testing results from distinct researchers confirm that the proposed model is suitable for further analyses of both clean sand and silty sand.

References

  1. Roscoe, K. H.; Burland, J. B. On the generalized stress strain behavior of “wet” clay. In Engineering Plasticity; Cambridge Univ. Press, 1968; pp. 535–609. [Google Scholar]
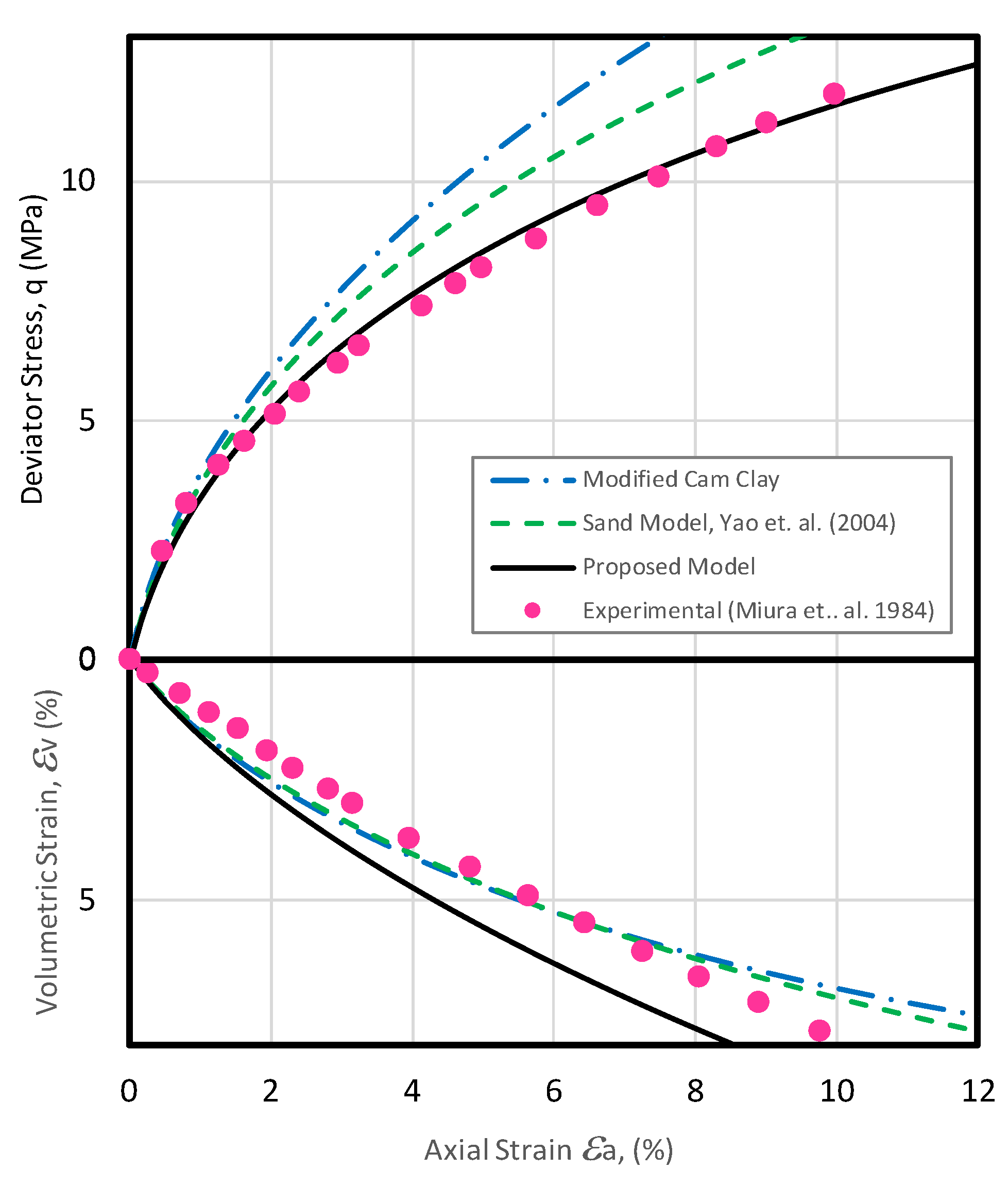
  2. Miura, N.; Murata, H.; Yasufuku, N. Stress-Strain Characteristics of Sand in a Particle-Crushing Region. Soils Found. 1984, 24, 77–89. [Google Scholar] [CrossRef]
  3. Miura, N.; Murata, H.; Yasufuku, N. Stress-strain characteristics of sand in a particle-crushing region. Soils and Foundations 1990, 17, 241–252. [Google Scholar] [CrossRef]
  4. Matsuoka, H.; Yao, Y.-P.; Sun, D. The Cam-Clay Models Revised by the SMP Criterion. Soils Found. 1999, 39, 81–95. [Google Scholar] [CrossRef]
  5. Yao, Y.P.; Sun, D.A.; Luo, T.A. Critical state model for sands dependent on stress and density. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28, 323–337. [Google Scholar] [CrossRef]
  6. Yao, Y.; Sun, D.; Matsuoka, H. A unified constitutive model for both clay and sand with hardening parameter independent on stress path. Comput. Geotech. 2007, 35, 210–222. [Google Scholar] [CrossRef]
  7. Suebsuk, J.; Horpibulsuk, S.; Liu, M.D. A critical state model for overconsolidated structured clays. Comput. Geotech. 2011, 38, 648–658. [Google Scholar] [CrossRef]
  8. Cao, L. F.; Teh, C. I.; Chang, M. F. Undrained cavity expansion in modified Cam clay I: Theoretical analysis. Geotechnique 2001, 51, 323–334. [Google Scholar] [CrossRef]
  9. Grimstad, G.; Degago, S.A.; Nordal, S.; Karstunen, M. Modeling creep and rate effects in structured anisotropic soft clays. Acta Geotech. 2010, 5, 69–81. [Google Scholar] [CrossRef]
  10. Yin, Z.-Y.; Xu, Q.; Hicher, P.-Y. A simple critical-state-based double-yield-surface model for clay behavior under complex loading. Acta Geotech. 2013, 8, 509–523. [Google Scholar] [CrossRef]
  11. Miranda, P.; Vargas, E.; Moraes, A. Evaluation of the Modified Cam Clay model in basin and petroleum system modeling (BPSM) loading conditions. Mar. Pet. Geol. 2019, 112, 104112. [Google Scholar] [CrossRef]
  12. Miranda, P.; Vargas, E.; Moraes, A. Evaluation of the Modified Cam Clay model in basin and petroleum system modeling (BPSM) loading conditions. Mar. Pet. Geol. 2019, 112, 104112. [Google Scholar] [CrossRef]
  13. Ou, C. Y.; Liu, C. C.; Chin, C. K. Anisotropic viscoplastic modeling of rate-dependent behavior of clay. International Journal for Numerical and Analytical Methods in Geomechanics 2011, 35, 1189–1206. [Google Scholar] [CrossRef]
  14. Li, X.S.; Wang, Y. Linear Representation of Steady-State Line for Sand. J. Geotech. Geoenvironmental Eng. 1998, 124, 1215–1217. [Google Scholar] [CrossRef]
  15. Yang, Z.X.; Li, X.S.; Yang, J. Quantifying and modelling fabric anisotropy of granular soils. Géotechnique 2008, 58, 237–248. [Google Scholar] [CrossRef]
  16. Yang, J.; Wei, L.; Dai, B. State variables for silty sands: Global void ratio or skeleton void ratio? Soils Found. 2015, 55, 99–111. [Google Scholar] [CrossRef]
  17. Murthy, T. G.; Loukidis, D.; Carraro, J. A. H.; Prezzi, M.; Salgado, R. Undrained monotonic response of clean and silty sands. Géotechnique 2007, 57, 273–288. [Google Scholar] [CrossRef]
  18. Rahman, M.; Lo, S.R.; Baki, A.L. Equivalent granular state parameter and undrained behaviour of sand–fines mixtures. Acta Geotech. 2011, 6, 183–194. [Google Scholar] [CrossRef]
  19. Rahman, M. M.; Lo, S. C.; Dafalias, Y. F. Modelling the static liquefaction of sand with low-plasticity fines. Géotechnique 2014, 64, 881–894. [Google Scholar] [CrossRef]
  20. Duriez, J.; Vincens, É. Constitutive modelling of cohesionless soils and interfaces with various internal states: An elasto-plastic approach. Comput. Geotech. 2015, 63, 33–45. [Google Scholar] [CrossRef]
  21. Thevanayagam, S.; Martin, G. Liquefaction in silty soils—screening and remediation issues. Soil Dyn. Earthq. Eng. 2002, 22, 1035–1042. [Google Scholar] [CrossRef]
  22. Lashkari, A. Recommendations for extension and re-calibration of an existing sand constitutive model taking into account varying non-plastic fines content. Soil Dynamics and Earthquake Engineering 2014, 61–62, 212–238. [Google Scholar] [CrossRef]
  23. Taiebat, M.; Dafalias, Y.F. Simple Yield Surface Expressions Appropriate for Soil Plasticity. Int. J. Géoméch. 2010, 10, 161–169. [Google Scholar] [CrossRef]
  24. Been, K.; Jefferies, M.G. A state parameter for sands. Géotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
  25. Manzari, M.T.; Dafalias, Y.F. A critical state two-surface plasticity model for sands. Géotechnique 1997, 47, 255–272. [Google Scholar] [CrossRef]
  26. Manzari, M.T.; Dafalias, Y.F. Simple plasticity sand model accounting for fabric change effects. ASCE J Eng Mech 2004, 130, 622–634. [Google Scholar] [CrossRef]
  27. Wan, R.; Guo, P. A simple constitutive model for granular soils: Modified stress-dilatancy approach. Comput. Geotech. 1998, 22, 109–133. [Google Scholar] [CrossRef]
  28. Wang, Z.L.; Dafalias, Y.F.; Li, X.S.; Makdisi, F.I. State pressure index for modeling sand behavior. ASCE J Geotech Geoenviron Engng 2002, 128, 511–519. [Google Scholar] [CrossRef]
  29. Vesić, A.S.; Clough, G.W. Behavior of Granular Materials Under High Stresses. J. Soil Mech. Found. Div. 1968, 94, 661–688. [Google Scholar] [CrossRef]
  30. Lashkari, A. On the modeling of the state dependency of granular soils. Comput. Geotech. 2009, 36, 1237–1245. [Google Scholar] [CrossRef]
  31. Verdugo, R. PhD dissertation, University of Tokyo, 1992; p. 1992.
  32. Verdugo, R.; Ishihara, K. The Steady State of Sandy Soils. Soils Found. 1996, 36, 81–91. [Google Scholar] [CrossRef]
  33. Ni, Q.; Tan, T.S.; Dasari, G.R.; Hight, D.W. Contribution of fines to the compressive strength of mixed soils. Géotechnique 2004, 54, 561–569. [Google Scholar] [CrossRef]
  34. Stamatopoulos, C.A. An experimental study of the liquefaction strength of silty sands in terms of the state parameter. Soil Dyn. Earthq. Eng. 2010, 30, 662–678. [Google Scholar] [CrossRef]
  35. Ventouras, K.; Coop, M.R. On the behavior of Thanet sand: an example of an uncemented natural sand. Géotechnique 2009, 59, 727–738. [Google Scholar] [CrossRef]
  36. Cubrinovski, M.; Rees, S. Effects of fines on undrained behavior of sands. ASCE geotechnical publication 2008, 1–11. [Google Scholar]
  37. Rahman, M.M.; Lo, S.R.; Gnanendran, C.T. On equivalent granular void ratio and steady state behavior of loose sand with fines. Can Geotech J 2008, 45, 1439–1456. [Google Scholar] [CrossRef]
  38. Papadopoulou, A.; Tika, T. The Effect of Fines on Critical State and Liquefaction Resistance Characteristics of Non-Plastic Silty Sands. Soils Found. 2008, 48, 713–725. [Google Scholar] [CrossRef]
  39. Huang, Y.-T.; Huang, A.-B.; Kuo, Y.-C.; Tsai, M.-D. A laboratory study on the undrained strength of a silty sand from Central Western Taiwan. Soil Dyn. Earthq. Eng. 2004, 24, 733–743. [Google Scholar] [CrossRef]
Preprints 75155 g001
Figure 1. Critical state line (CSL): (a) Normally consolidation line (NCL) and critical state line in MCC and MCC’s family; (b) Comparison between CSL in eq. (1) and eq. (2).
Figure 1. Critical state line (CSL): (a) Normally consolidation line (NCL) and critical state line in MCC and MCC’s family; (b) Comparison between CSL in eq. (1) and eq. (2).
Preprints 75155 g001
Preprints 75155 g002
Figure 2. Comparison of critical state lines: (a) Test data [2] vs eq. (1) and eq. (2); (b) required CSL vs eq. (1) & eq. (2).
Figure 2. Comparison of critical state lines: (a) Test data [2] vs eq. (1) and eq. (2); (b) required CSL vs eq. (1) & eq. (2).
Preprints 75155 g002
Preprints 75155 g003
Figure 3. Effects of parameter Γ in eq. (3) for 0.6 ≤ Γ ≤ 1.2.
Figure 3. Effects of parameter Γ in eq. (3) for 0.6 ≤ Γ ≤ 1.2.
Preprints 75155 g003
Preprints 75155 g004
Figure 4. Effect of parameter p r e f of eq. (3) when e Γ =1.0: (a) α=θ= 0.25; (b) α=θ= 1.0.
Figure 4. Effect of parameter p r e f of eq. (3) when e Γ =1.0: (a) α=θ= 0.25; (b) α=θ= 1.0.
Preprints 75155 g004
Preprints 75155 g005
Figure 5. Effect of parameter θ of eq. (3) when e Γ =1.0: (a) at low value α= 0.25; (b) at high value α= 1.0.
Figure 5. Effect of parameter θ of eq. (3) when e Γ =1.0: (a) at low value α= 0.25; (b) at high value α= 1.0.
Preprints 75155 g005
Preprints 75155 g006
Figure 6. Effect of parameter α for e-p in equation (3) for θ=1.0: (a) e Γ = 0.6; (b) e Γ = 1.0; (c) e Γ = 1.4.
Figure 6. Effect of parameter α for e-p in equation (3) for θ=1.0: (a) e Γ = 0.6; (b) e Γ = 1.0; (c) e Γ = 1.4.
Preprints 75155 g006
Preprints 75155 g007
Figure 7. Evaluation of eq. (1), eq. (2) and (3) for Toyoura sand (experimental data from [2]).
Figure 7. Evaluation of eq. (1), eq. (2) and (3) for Toyoura sand (experimental data from [2]).
Preprints 75155 g007
Preprints 75155 g008
Figure 8. Shape and location of the CSL compared to the RCL in the proposed model using the tangential slope λ ¯ in eq. (5): (a) CSL is derived from the NCL; (b) RCL is derived from the CSL.
Figure 8. Shape and location of the CSL compared to the RCL in the proposed model using the tangential slope λ ¯ in eq. (5): (a) CSL is derived from the NCL; (b) RCL is derived from the CSL.
Preprints 75155 g008
Preprints 75155 g009
Figure 9. Schematic drained stress-strain curves of sand at different initial state.
Figure 9. Schematic drained stress-strain curves of sand at different initial state.
Preprints 75155 g009
Preprints 75155 g010
Figure 10. Effect of parameter χ to the MCC model: (a) yield function of the MCC (eq. (7) vs yield function of loosed sands eq. (8) (χ = 0 to 1); (b) stress-strain curves for loose sands from drained triaxial compression simulation using both parameter χ and λ ¯ .
Figure 10. Effect of parameter χ to the MCC model: (a) yield function of the MCC (eq. (7) vs yield function of loosed sands eq. (8) (χ = 0 to 1); (b) stress-strain curves for loose sands from drained triaxial compression simulation using both parameter χ and λ ¯ .
Preprints 75155 g010
Preprints 75155 g011
Figure 11. Comparison of the predictions from the MCC model, sand model [5] and the proposed model to the test data [2].
Figure 11. Comparison of the predictions from the MCC model, sand model [5] and the proposed model to the test data [2].
Preprints 75155 g011
Preprints 75155 g012
Figure 12. Undrained triaxial compression test results of clean sand at p0=490 kPa: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Figure 12. Undrained triaxial compression test results of clean sand at p0=490 kPa: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Preprints 75155 g012
Preprints 75155 g013
Figure 13. Undrained triaxial compression test results of clean sand at e0 = 0.833: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Figure 13. Undrained triaxial compression test results of clean sand at e0 = 0.833: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Preprints 75155 g013
Preprints 75155 g014
Figure 14. Undrained triaxial compression test results of silty sand for FC=0.15 (Rahman et al. [18]: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Figure 14. Undrained triaxial compression test results of silty sand for FC=0.15 (Rahman et al. [18]: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Preprints 75155 g014
Preprints 75155 g015
Figure 15. Undrained triaxial compression test results of silty sand for FC=0.50 (Huang et al. [39]: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Figure 15. Undrained triaxial compression test results of silty sand for FC=0.50 (Huang et al. [39]: (a) stress path (test results); (b) stress-strain curves (test results); (c) stress path (proposed model) (d) stress-strain curves (proposed model).
Preprints 75155 g015
Table 1. Soil parameters for drained analyses.
Table 1. Soil parameters for drained analyses.
Soil Model Γ α θ p r e f λ κ M c ν
MCC and Sand Model [5] 1.97 - - - 0.141 0.009 1.305 0.3
Proposed Model 0.864 * 0.0795 * 0.016 * 7.5 * - 0.009 1.305 0.3
* Fitting parameters from existing data of the NCL (see Figure 7).
Table 2. Soil Parameters for undrained analyses.
Table 2. Soil Parameters for undrained analyses.
Soil Parameter Γ α θ p r e f κ M c ν n b
Proposed Model 0.864 * 0.0795 * 0.004 * 3.06 * 0.02 1.265 0.25 1.34
* Fitting parameters from existing data of the CSL.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated