Prerpints.org logo
Preprint
Article

Groundwater Level Trend Analysis and Prediction in the Upper Crocodile (West) Basin, South Africa

Altmetrics

Downloads

169

Views

59

Comments

0

Submitted:

25 May 2023

Posted:

29 May 2023

You are already at the latest version

Alerts
Abstract
Disasters related to climate change on our water resources are on the rise in terms of scale and severity. Therefore, predicting groundwater levels (GWL) is a crucial means to aid adaptive capacity towards disasters related to climate change in our water resources. In this study Gradient Boosting (GB) regression modelling approach for GWL prediction as a function of rainfall and antecedent GWL is used. Firstly, we sought to demonstrate the effects of rainfall changes on our groundwater resources through a Mann-Kendall trend analysis. Secondly, we evaluated the relationship between the input and response variables and determined the optimal lag times between the variables using autocorrelations and cross-correlations. Lastly a predictive model was developed for eight groundwater stations in the Upper Crocodile. 50 % of the groundwater stations revealed declining trends, while 25% had no trends and the other 25% showed an increasing trend. Generally low cross-correlation maximum (CCmax) were obtained, with the highest CCmax being 0.299 at an optimal lag of 2-month. While the highest autocorrelation was 0.969 at a 1-month lag. The best groundwater predictive model had R2 and MSE of 0.66 and 0.06, respectively. The stations that generally performed better had both high autocorrelation and cross-correlation coefficients. GB model performed satisfactorily in predicting GWL for most of the stations in the study area. Therefore, GB can be used for GWL prediction in the Upper Crocodile.
Keywords: 
Subject: Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

Climate change has led to a recurrence of hydrological extremes such as droughts and floods and future projections reveal an increase of such events (IPCC:2014, 2014; Ziervogel et al., 2014). Mishra & Singh, (2010) reported a number of droughts in Africa, Europe, Asia, Australia and North America dating as far back as 1890. Wanders et al.,(2015) projected an increase in drought duration and severity over 27% of the world, this includes; most parts of South America, Southern Africa and the Mediterranean. Most parts of Southern Asia, have been experiencing accelerated droughts due to rising temperatures in past few decades (Dilawar et al., 2021; Prodhan et al., 2022). In Uganda, 2 465 human lives were lost due to drought, this was globally the highest mortality due to drought in 2022. Climate change has also led to a number of floods at a global scale which resulted to 7 954 human lives lost in 2022 (Centre for Research on the Epidemiology of Disasters, 2023) this number exceeds the global average from 2002 to 2021. Countries with the highest mortality due to floods in 2022 include; India at 2035, Pakistan at 1739, Nigeria at 608 and South Africa at 544.
The impacts of these hydrological extremes in an arid to a semi-arid country like South Africa are significant. For example, the droughts experienced in most parts of the country in the hydrological year 2015 to 2016 led to negative socio-economic impacts. The agricultural industry contracted by 6.5 % while the electricity, gas and water industry contracted by 2.8 % in the first quarter of 2016 (Schreiner et al., 2018). Various parts of the country experienced water restrictions due to the droughts. This drought in the Western Karoo region of the Eastern Cape were incurred until early 2020 (Archer et al., 2022). The multi-year drought in the Eastern Cape resulted into low groundwater levels and subsequently dried up some boreholes (Holmes et al., 2022). On the contrary, the neighbouring province, Kwa Zulu Natal (KZN) has been experiencing frequent floods, like in April 2019 (Bopape et al., 2021; Olanrewaju & Reddy, 2022). Recently, in April 2022, KZN experienced one of the major floods in the country resulting in over 400 lives lost over the disastrous floods (Madzivhandila, Thanyani S, Maserumule, 2022). What is evident in literature is that disasters related to climate change are on a steep rise but the adaptive capacity towards these extreme seems to be lacking (Chandrasekara et al., 2021; Hussain et al., 2020; Quesada-Román et al., 2020). This gap, coupled with freshwater scarcity thus exacerbates the importance of understanding the interplay between climate and water resources, such knowledge is essential for the sustenance of water resources.
Freshwater is the most widely used form of water resources. Approximately 97% of the Earth’s total water is available as seawater which is saline and freshwater makes up about 3% (Gude & Nirmalakhandan, 2009; Liu, 2011). Approximately 69% of the freshwater is available in glaciers, polar caps and in the atmosphere. Groundwater proportion amounts to approximately 30% of the freshwater. While 0.3% is available as surface water in rivers, lakes and dams. The growing number of extreme climate events and population growth have further strained surface water resources, making it an unreliable source. Groundwater thus, plays a vital role in an arid to semi-arid region like South Africa. A study by the Department of Water Affairs (DWA), (2010) revealed that an additional 5 500 million m3 per annum of groundwater storage was available for use by small towns, mines, villages and individuals. Moreover, this groundwater potential could be increased by recharging aquifers during wet periods and preserving groundwater supplies for use during dry/drought periods (Pietersen et al., 2011). Pietersen et al. (2011) further showed that over 80% of rural communities in North West and Kwa-Zulu Natal provinces of South Africa get their water from groundwater sources and the same applies to over 50% communities in the Eastern Cape. In terms of urban areas, City of Tshwane combines water from boreholes with surface water in its bulk distribution system. Some towns such as De Aar rely solely on groundwater sources for its water supply.
Groundwater availability is affected by a wide range of factors which include; land use land cover (LULC), baseflow index, which refers to the proportion of baseflow to the total streamflow (Bloomfield et al., 2009), soil type, catchment area, catchment slope, precipitation, evapotranspiration and catchment geology (Bloomfield et al., 2009; Zomlot et al., 2015). Precipitation is by far the climatic parameter that closely relates to groundwater availability and water resources in general, serving as a major input into the hydrological cycle. In South Africa, the most available form of precipitation is rainfall. Rainfall, according to a study conducted by Mohan et al., (2018) was found to be one of the major factors affecting groundwater recharge. A similar study in USA also found that 80% of recharge variation is explained by Mean Annual Precipitation (Keese et al., 2005). Similarly findings by Sun & Cornish (2005) reveal that variations in recharge can primarily be explained by the climatic factor compared to land-use changes. The studies outlined above illustrate the importance of rainfall events in groundwater recharge. However, a study conducted in South Africa indicated that the lag time between rainfall events and groundwater level responses is less understood (Xu & Beekman, 2019). Similarly Qi et al., (2018) and Condon et al., (2021) highlight a knowledge gap on the direct response of groundwater levels to precipitation. The lag time is important for groundwater level prediction purposes and in developing the early warning systems.
One of the major challenges incurred in understanding the lag between rainfall events and groundwater level responses is that groundwater levels are often not available in real-time (Van Loon et al., 2017). There is a lack of data on the actual use of groundwater resources, and the state of aquifers is unknown in many parts of the world. Modellers are faced with dispersed data or data scarcity, especially in arid to semi-arid areas. Data such as aquifer geometry or hydraulic parameters are often unknown (Alfaro et al., 2017; Oke & Fourie, 2017). Monitoring networks and consistent in situ groundwater measurements are unavailable in some places (Sahoo et al., 2018). There are inaccuracies in recharge and pumping estimates (Castellazzi et al., 2018).
Nowadays, models are used to provide a cost-effective means of representing a system and aid in understanding the interplay between processes involved in a system. Various groundwater quantity models have been used in the past to enhance management of groundwater resources. The models include; physically-based numerical models such as MODFLOW (Lyazidi et al., 2020; Ostad-Ali-Askari et al., 2019), data-driven models employing artificial intelligence (Ibrahem Ahmed Osman et al., 2021; Sahoo et al., 2018) and a hybrid of the two (Malekzadeh et al., 2019; Rezaei et al., 2021; Zeydalinejad, 2022). In the past, physically-based numerical models were extensively employed in modelling and predicting groundwater levels (Ahmadi et al., 2022; Hussein et al., 2020). The physically-based numerical models however, are often time-consuming, require extensive amount of input data that are often not available and require some level of expertise in measuring the parameters used in the models(Sharafati et al., 2020a). The growing availability of big data, through remote sensing and Internet of Things (IoT) have made data-driven modelling such as machine learning (ML) a favourable modelling tool. Machine learning is a field of artificial intelligence that employs algorithms to learn complex patterns from data and able to predict unobserved data (Aderemi et al., 2022; Murdoch et al., 2019). According to Osman et al.,( 2022) ML models are estimated to be adequately efficient in modelling groundwater levels. Artificial Neural Networks (ANNs) and Support Vector Machines (SVM) rank amongst the widely used ML models in groundwater level modelling (Ahmadi et al., 2022; Sharafati et al., 2020b). Recently a growth in the use of ensemble machine learning techniques has been observed and one of the advantages that the ensemble techniques offer is lower computational cost (Wei et al., 2022). One of the commonly used ML ensemble techniques is Gradient Boosting (GB) algorithm. GB algorithm was successfully used in Iran for predicting monthly GWL (Sharafati et al., 2020a), In Slovenia, GB outperformed linear regression, random forest, decision tree algorithms for predicting GWL. Again in a Moroccan study where ten ML where compared in predicting groundwater withdrawals , GB outperformed all the algorithms (Ouali et al., 2023). In a South African study, GB also outperformed five ML algorithms among which ANNs and Support Vector Regresion (SVR), the dominantly used ML were included. Despite the accuracy and computational efficiency of GB , literature on the use ensemble ML techniques such as GB in predicting GWL is still lacking (Osman et al., 2022; Sharafati et al., 2020a).
Considering the growing rate of disasters related to climate change, freshwater scarcity and the gap that exist in adaptive capacity to climate change related disasters. This study leverages on the under exploited GB ML technique in predicting groundwater levels for the Upper Crocodile basin in South Africa. The aim of this study is to predict GWLs in an effort to contribute towards building adaptive and mitigation capacity to climate-related disasters. The objectives in achieving this main goal are as follows; 1) To demonstrate the effects of climate events on our groundwater resources through trend analysis. 2) To evaluate the relationships and determine lag times between input variables and the response variable using autocorrelations and cross-correlations. 3) To predict GWLs in quaternary A21D of the Upper Crocodile. A study of this nature is vital in aiding on-time decision making for groundwater resource management.

2. Materials and Methods

2.1. Study Area Description

The study area is the Upper Crocodile (West) located in North-West and Gauteng province of South Africa. Its geographic location is between the coordinates -25.678 latitude; 27.341 longitude and -25.678 latitude; 28.472 longitude. The towns covered in the Upper Crocodile (West) area are; Krugersdorp, Magaliesburg, Centurion, Midrand and Kempton Park. This basin is the second most populated basin in the country.
The Upper Crocodile is a semi-arid region. It is characterised by warm summers with average daily minimum temperatures of 10ºC to maximum temperatures of 30ºC and cold winters with minimum temperatures of 1ºC to maximum temperatures of 15ºC (DWAF, 2004) . The rainy season is in Summer which commences in October and ends in March the following year. Rainfall usually peaks in December and January. The mean annual rainfall ranges between 600 mm and 800 mm per annum (Schulze, 2012). The mean annual evaporation (MAE), exceeds the MAP, with the MAE at an average of approximately 1 600 mm per annum (DWAF, 2004).
Hydrologically, the Upper Crocodile (West) falls under the Limpopo water management area, primary drainage region A. The primary drainage regions are further broken down into secondary, tertiary and subsequently quaternary drainage regions. To be more exact, the Upper Crocodile (West) is in the secondary drainage region A2 and tertiary drainage A21. For this study, the quaternary drainage regions lying upstream of the Hartbeespoort dam were considered which makes up approximately 4 100 km2 (i.e. quaternary drainage A21A to A21H). The main rivers in the Upper Crocodile are the Crocodile, Magalies, Jukskei and Hennops. The main dams are the Hartbeespoort dam in quaternary A21H and the Rietvleidam in A21A. Figure 1 below displays the study area.
The main source of water supply in the study area is the Vaal dam, which is transferred through the Rand Water bulk distribution system from the Upper Vaal Water Management Area. The other important source of water supply in the study area is groundwater from dolomitic aquifers which are mainly found in the quaternaries; A21A (North East of Johannesburg), quaternary A21B (near Centurion) and quaternary A21D (near Krugersdorp). Dolomite-based aquifers (karst aquifers) are among the most prolific water-bearing formations due to their soluble nature (Abiye et al., 2015). Groundwater from these karst aquifers is used in the City of Tshwane, North East of Johannesburg and Krugersdorp area for agricultural, domestic and industrial use (DWAF, 2004). Projections reveal more potential for usage of this groundwater resource (Meyer, 2014), which may be beneficial for this rapidly developing area.
The Upper Crocodile is characterised by karst aquifers which are generally deep and high-yielding as well as fractured aquifers which are shallow and have lower yield (Abiye et al., 2015). The specific yield of the fractured aquifers in the study area ranges between 0.01 L/s and 0.98 L/s while the karst aquifers’ is in the range of 15 L/s to 124 L/s. This makes karst aquifers a vital source of water in the study area. Approximately 10 % of the City of Tshwane’s water supply is from these Karst aquifers. Recharge to the karst aquifers in Gauteng ranges between 7% to 15% of the Mean Annual Precipitation (MAP) (Meyer, 2014) and this could be attributed to the Mean Annual Evaporation (MAE) which far exceeds the MAP. Borehole depths in the karst aquifers reach 250 m depth and water table level can go below 10 m to 50 m (DWAF, 2004). The economic activities taking place in the Upper Crocodile (West) are mainly industrial, mining and residential which contribute a significant amount of the country’s Gross Domestic Product (GDP) (DWAF, 2004). This study area was chosen because of groundwater data availability and the economic importance of this area in South Africa. Due to data availability and the high spatial-temporal variability of the parameters under study, this study focused on quaternary A21D of the Upper Crocodile. The total area of A21D is 371.54 km2.

2.2. Data sources and acquisition

Daily rainfall data were obtained from the South African Weather Service (SAWS). The station that was selected for data analysis was 0512746 7. The choice of this stations was informed by historical data availability and the proximity of the rainfall stations to shallow groundwater monitoring stations. The station is located at latitude; -25.9436 and longitude; 27.9188, as shown in Figure 1.
Groundwater data were obtained from the Department of Water and Sanitation (DWS) through the National Ground Water Archive, available online. The stations that were selected for analysis in this study are shown in Table 1. Most of these stations are shallow and were selected based on data availability. Also, the stations unlike most stations had daily groundwater levels in some instances.
Raw hydrometeorological data very rarely come complete and ready to use. Especially in situ data, as a result cleaning and processing is required. One of the major challenges incurred with raw time series data is inconsistent frequency of data collection, handling blanks and the data are often big to detect the errors using human eye. This particular groundwater data set came with inconsistent frequencies, the frequencies were first fixed to a monthly frequency using the resample function in Pandas. Pandas is a data analysis tool built in the Python Programming language. After fixing the time frequency, the missing groundwater levels were filled in using interpolation.

2.3. Trend analysis

The Mann-Kendall test was applied in studying trends for data obtained from eight groundwater stations. Figure 1 shows the location of the groundwater stations in relation to one another and the rainfall station. The Mann-Kendall test is a non-parametric test used to identify trends in time series data (Mann, 1945). The test has successfully been used in analysing hydro-meteorological datasets such as climate, environmental parameters, streamflow and groundwater levels in the past (Alhaji et al., 2018; Gyamfi et al., 2016; Mathivha et al., 2021). One of the advantages of this test is that it does not require data to be normally distributed (Alhaji et al., 2018), and hydrometeorological data are usually not normally distributed. The Mann-Kendall test is founded on the correlations between sequences and ranks. In this test, a test statistic S is obtained by computing the difference between subsequent data values. Equation (1) to equation (5) describe the test, xi and xj in the equations represent the values of a sequence where, j is greater i and n represent the length of the time series. The Mann-Kendall statistic (S) is given as (Mann, 1945) ;
S = ∑ i = 1 n − 1 ∑ j = i + 1 n s g n ( x j − x i ) ≈ ∑ i = 1 n − 1 ∑ j = i + 1 n s g n ( θ )
where s g n ( θ ) satisfies any of the following conditions;
s g n ( θ ) = { 1   i f   θ > 0 0   i f   θ = 0 − 1   i f   θ < 0
When n ≥ 8, the statistic S is approximately normally distributed with the mean and variance as follows:
E ( S ) = 0
V ( S ) = n ( n − 1 ) ( 2 n + 5 ) − ∑ i = 1 m t i   i ( i − 1 ) ( 2 i + 5 ) 18
where m   is the number of groups of tied ranks and t i   is the number of ties of extent i. The standardized Z M K is computed as follows;
Z M K = { S − 1 V a r ( S )   S > 0 0   S = 0 S + 1 V a r ( S )   S < 0
ZMK measures the significance of the test. In this study the null hypothesis (H0) assumed that there is no trend while the alternative hypothesis (H1) assumed that there is a trend. The null H0 was rejected if | Z M K | > Z 1 − α at a significance interval of α = 0.05. The Mann Kendall analysis was conducted using Python.

2.4. Cross Correlation analysis

A cross-correlation function measures the strength of a linear relationship between two time series data depending on a time lag between them (Denić-Jukić et al., 2020). It assesses the similarity between a time series and a lagged version of another time series as a function of the lag (Rahmani & Fattahi, 2021). Theoretically, the cross-correlation functions are explained in equation (6) to equation (7) (Denić-Jukić et al., 2020), where x represents the input time series while y represents the output time series from a hydrological system. Equation (6) defines the covariance function between x and y , both with length n .
c x y ( k ) = 1 n ∑ t = 1 n − k ( x t − μ x ) ( y t + k − μ y ) ; k = 0 , ± 1 , ± , … , m
( 6 )
where μ x is the mean of x and   μ y is the mean of y . m is the time interval in which the analysis is carried out or rather the total number of correlation coefficients obtained from the analysis and k is the number of time lags. Equation (7) defines the cross-correlation function between time series x and y .
r x y ( k ) = { c x y ( k ) σ x σ y ; k ≥ 0 c y x ( − k ) σ x σ y ; k < 0 }
where σ x is the standard deviation of x and   σ y is the standard deviation of y .
The application of cross-correlations play a vital role in hydrology and this is evident in, Rahmani & Fattahi (2021); Seo et al., (2019); Valois et al., (2020). What is common in the three studies is that the studies cross-correlated climatic parameters with the availability of water resources, with Valois et al., (2020) focusing on precipitation and groundwater recharge which is closely related to this study. While Seo et al., (2019) demonstrated the importance of pre-proccessing climate data through using cross-correlations. In the study it was deduced that precipitation and temperature cross-correlations aid in improving hydrologic simulations. One of the vital features of cross-correlation analysis is its ability to express the interdepence of parameters, a feature that is helpful in selecting input parameters for models that are data-driven. In this study we cross-correlated rainfall with groundwater levels, for the study period 2011 to 2020 and the data were analysed at a monthly time step ( k ) . Cross-correlations between rainfall from rainfall station 0512746 7 and the eight groundwater stations selected for this study were computed, the highest possible lags for this analysis was 117 lags ( k ) .

2.5. Autocorrelation Analysis

Groundwater level fluctuations are greatly influenced by historical groundwater level (Wei et al., 2022), thus knowledge on how the previous month’s groundwater levels affect the succeeding month’s groundwater levels is essential. Autocorrelation analysis were thus conducted in this study to determine the interdependence of succeeding groundwater levels and to determine the optimal lag between succeeding records. An autocorrelation function is referred to the measure of strength of linear relationship among succeeding values in a time series depending on the lag time between the values (Denić-Jukić et al., 2020). The function is represented as follows:
r x x ( k ) = c x x ( k ) σ x 2   ; k ≥ 0
In this study an autocorrelation analysis was done on historical groundwater levels for the study period 2011 to 2020.

2.6. Gradient Boosting Regression

Gradient boosting (GB) regression is a machine learning technique that uses ensemble trees by stacking them additively to provide final predictions (Sharafati et al., 2020b). It sequentially adds predictors to an ensemble with each predictor correcting its predecessor (Géron, 2019). A GB model consists of; the predictor and response variables, a base learner, a differential loss function and a number of iteration trees. In each iteration; a negative gradient is calculated, the base learner function is fitted to the negative gradient, then the base learner function is trained and the best gradient is found.
GradientBoostingRegressor from Scikit-learn was used and employed on Python. The input variables for the predictive model were, antecedent groundwater levels and rainfall. Rainfall and antecedent groundwater level are the most used input variables for predicting GWLs using ML models (Ahmadi et al., 2022). Lag times for the input variables were generated using cross-correlations for rainfall and autocorrelations for antecedent groundwater levels. The predictive model was then generated for the period 2011 to 2020. Training data for the model were from January 2011 to April 2018 and validation data were from May 2018 to September 2020.

2.7. Performance Criteria

The performance of the model was evaluated using the coefficient of determination (R2) and the Mean Squared Error (MSE). The expressions for R2 and MSE are given in (9) and (10) respectively.
R 2 = [ ∑ i = 1 n ( O i − S i ) ( S i − S ¯ ) ( ∑ i = 1 n ( O i − O ¯ ) 2 ) 0.5 ( ∑ i = 1 n ( S i − S ¯ ) 2 ) 0.5 ] 2
( 9 ) M S E = 1 n ∑ i = 1 n ( O i − S i ) 2
where;
Oi = measured data, Si = predicted data, O ¯ = mean of measured data, S ¯ = mean of predicted data, n = number of observations.
R2 describes the proportion of the variance in measured data explained by the model, its values range between 0 and 1 with values close to 1 indicating a variance with less error and values close to 0 indicating a high error variance. While MSE measures the average of the squares of the errors. The MSE is always positive and it is 0 for predictions that are completely accurate. It captures the bias (i.e. the difference of estimated values from the actual values) variance (i.e. how far are the estimates spread out).

3. Results and Discussions

3.1. Trend Analysis

The non-parametric Mann Kendall test results on groundwater are shown in Table 2 . Trends are detected in a dataset when the p-value in Table 2 is smaller than alpha (which was 0.05 in this study). Two increasing trends were detected for groundwater station A2N0800 and A2N0799, making up 25% of the groundwater stations under study (refer to Table 2). The two stations lie furthest from the Bloubankspruit river, they are located close to each other and are at higher elevations compared to the other stations. A2N0800 is located at an altitude of around 1655 and A2N0799 at an altitude of around 1 636 m. As mentioned in the introduction, rainfall is a major input into the hydrogeological system and the increasing trends are attributed to rainfall. The rainfall that occurred in early 2017, which according to Figure 2 is the maximum rainfall and served as a major contribution to this increasing trend. Also, precipitation is generally higher at higher elevations due to cooler weather that has deficiencies in holding moisture and as result it rains more frequently in higher elevation than at lower elevations. At lower elevations it is generally humid, thus the moisture gets trapped and consequently this leads to lesser rainfall in those areas(Sokol & Bližňák, 2009).
Secondly, the increase may be attributed to lower surface water-groundwater interchange when compared to the stations that lie closest to the Bloubankspruit river which may be losing water to the river during dry periods.
There were four stations that showed a decreasing trend which are; A2N0795, A2N0794, A2N0802 and A2N0805 amounting to 50% of the total groundwater stations under the study. The decreasing trends can be attributed to the low rainfall in 2015, according to Figure 3, 2015 recorded the lowest rainfall of around 423 mm. We also generally observe lower rainfall between 2012 and 2015, which were below the mean annual rainfall for the study area of around 600 mm to 800 mm (Schulze, 2012) . We also note another dry hydrological year 2018 to 2019 which could also be a contributing factor to the declining trend.
Groundwater can be a vital source of streamflow, particularly during droughts/dry seasons (Valois et al., 2020). The shallow boreholes lying along the Bloubankspruit river may have lost the water towards the river during the drier hydrological years. What is also worth noting is that all the stations with decreasing trends lie on the malmani dolomine. Aquifers that lie on dolomine, named karst aquifers are known to be highly permeable, this property coupled with the fact that the boreholes are shallow, facilitated the movement of water from the boreholes into the nearby Bloubankspruit river. Furthermore, the stations with decreasing trends are located in farms and may be losing the water due to abstractions for agricultural purposes.
The remaining 25% of stations did not indicate a trend, which are stations; A2N0801 and A2N0806, shown in Figure 4. What is common with these two stations is that they are located somewhere between the stations with increasing trends and those with decreasing trends. The cause of this could also be attributed to the abrupt climate change that was incurred in the country during the past decade as well as the increase in population.

3.2. Cross correlations

The main parameters of interest when studying cross-correlations were the maximum cross-correlation (CCmax) and the lag in months associated with the CCmax (Caren & Pavlić, 2021). Table 3 shows the results of the CCmax and the optimal lag time for each groundwater station. The lag time shown in this table informed the rainfall-groundwater time lag to be used in the predictive model.
Generally, stations with deeper groundwater levels, had longer lag times and weaker cross-correlations and the shallower groundwater stations had stronger correlations and shorter lags. This can be associated with the underlying hydrogeological parameters. Station A2N0802 had the highest CCmax at a lag of one month. The stations A2N0806, A2N0805 and A2N0795 had negligible CCmax and thus the lag time associated with them were ignored. According to Wei et al., (2022), correlations coefficients that are less than 0.15 imply that the variables (i.e. groundwater level and rainfall in this case) are uncorrelated. The cause of this poor correlations may be attributed to the frequency at which the groundwater levels are monitored. The average lag between rainfall and groundwater level for the stations under this study was a two-months lag and that was informed by the results in Table 3. A similar study in the South African context (Kanyama, 2021) used a lag of two months. Thus, for the prediction model of groundwater levels, rainfall of the previous two months was used as an independent variable.

3.3. Autocorrelations

Autocorrelations give us the lag at which a variable can be correlated with itself. Antecedent groundwater levels are the second independent variable that was used in the predictive model, thus it is also imperative to gain knowledge on the optimal lag at which the variable groundwater level can be correlated with itself, and Table 4 reveals such information.
All the maximum autocorrelations for the stations considered in this study were all at an optimal lag of one month and the correlations are higher than the rain-groundwater correlations (cross-correlation). This then suggests that groundwater levels of the previous month will serve as independent variables of the succeeding month. Therefore, the lag times for the two independent variables in the predictive model are; (1) 2 months for Rainfall and (2) 1 month for historical groundwater levels.

3.4. Gradient Boosting Regression Results

The results obtained using GB regression model are presented in Figure 5 and Table 5. The station with the best predictive model was station A2N0800 at R2 of 0.66 and MSE of 0.06 since it has the highest R2 and the lowest MSE. The value of the R2 is not too high but satisfactory, it can be improved by increasing the frequency at which groundwater measurements are taken. Kanyama et al., (2020) obtained the best R2 of 0.75, thus the R2 obtained in this study is relatively good considering that the model had two independent variables while in Kanyama et al., (2020) three, independent variables were used which were; temperature, precipitation and discharge. Sharafati et al., (2020b) also obtained R2 in the range of 0.66 to 0.94. Also, what we noted about the station is that it was among the stations with an increasing trend according to MK analysis. The station is also among the shallow stations and therefore faster fluctuations on the GWL due to rainfall are expected. However, station A2N0802 is also shallow and had among the highest CCmax, but had the worst predictive model at R2 and MSE of 0.01 and 0.51 respectively. The autocorrelation of station A2N0802 according to Table 4 was among the lowest and from the MK trend analysis we observed that the GWL in the station follow a decreasing trend which was in the previous section attributed to the high streamflow and groundwater exchange as the station lies near a stream.
What was also worth noting with the predictive model for A2N0802 was that the original model performed better than the model after hyperparameter tuning which was not the case with other models, their performance improved with hyperparameter tuning.
The second station that performed relatively low was A2N0806. What is worth noting about station A2N0806 is that in Table 3 it was among the stations with the lowest CCmax and in Table 4 it had the lowest autocorrelations and there was no trend detected from the station. The last station with poor performance was A2N0795, which had the lowest CCmax among all the stations.

4. Conclusions and Recommendations

The aim of this study was to predict GWLs in an effort to contribute towards building adaptive and mitigation capacity to climate-related disasters. The effects of climate on our groundwater resources were demonstrated through MK trend analysis wherein the trends were justified by changes in rainfall; 50 % of the groundwater stations revealed a negative trend, 25% a positive trend and the remaining 25% showed no trend. The negative trend was mainly attributed to low rainfalls between 2012 and 2015 and the high surface water-groundwater exchange that occurs in the stations that lie along the rivers, particularly when rainfall amounts are low. While the positive trends were associated with higher rainfalls that took place around 2017 and the altitude of the stations that experienced positive trends.
Rainfall-GWL cross-correlations analysis indicated that the optimal lag for the two variables was 2 months with the highest CCmax of 0.299. Autocorrelations were generally higher than cross-correlation at the high of 0.979. The optimal lag for the autocorrelations was 1-month. Thus, the predictive model had two independent variables; rainfall at a 2-months lag and antecedent GWL at 1-month lag. The best performing predictive model, which employed gradient boosting regression machine learning technique had R2 and MSE of 0.66 and 0.06 respectively. Generally, stations which had a weak autocorrelation or a weak cross-correlation coefficient or both correlations were weak performed low. The study deduced the significance of autocorrelations and cross-correlations in demonstrating the relationship between input and response variables for predictive modelling. The study thus recommends an increase in the frequency at which GWLs are monitored, this will aid in improving rainfall-GWL cross-correlation and enhance the robustness of the predictive model. Consequently, this will aid in mitigating the negative impacts of climate change in our groundwater resources.

References

  1. Abiye, T. A. , Mengistu, H., Masindi, K., & Demlie, M. (2015). Surface Water and Groundwater Interaction in the Upper Crocodile River Basin, Johannesburg, South Africa: Environmental Isotope Approach. South African Journal of Geology 118, 109–118. [CrossRef]
  2. Aderemi, B. A. , Olwal, T. O., Ndambuki, J. M. M., & Rwanga, S. S. (2022). Groundwater Levels Forecasting Using Machine Learning Models: A Case Study of the Groundwater Region 10 at Karst Belt, South Africa. SSRN Electronic Journal 200049. [CrossRef]
  3. Ahmadi, A. , Olyaei, M., Heydari, Z., Emami, M., Zeynolabedin, A., Ghomlaghi, A., Daccache, A., Fogg, G. E., & Sadegh, M. (2022). Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water (Switzerland) 14, 1–22. [CrossRef]
  4. Alfaro, P. , Liesch, T., & Goldscheider, N. (2017). Modélisation de la surexploitation des eaux souterraines dans le Sud de la Vallée du Jourdain avec peu de données. Hydrogeology Journal 25, 13419–1340. [CrossRef]
  5. Alhaji, U. U. , Yusuf, A. S., Edet, C. O., Oche, C. O., & Agbo, E. P. (2018). Trend Analysis of Temperature in Gombe State Using Mann Kendall Trend Test. Journal of Scientific Research and Reports 20(3), 1–9. [CrossRef]
  6. Archer, E. , du Toit, J., Engelbrecht, C., Hoffman, M. T., Landman, W., Malherbe, J., & Stern, M. (2022). The 2015-19 multi year drought in the Eastern Cape, South Africa: it’s evolution and impacts on agriculture. Journal of Arid Environments 196, 104630. [CrossRef]
  7. Bloomfield, J. P. , Allen, D. J., & Griffiths, K. J. (2009). Examining geological controls on baseflow index (BFI) using regression analysis: An illustration from the Thames Basin, UK. Journal of Hydrology 373, 164–176. [CrossRef]
  8. Bopape, M. J. M. , Sebego, E., Ndarana, T., Maseko, B., Netshilema, M., Gijben, M., Landman, S., Phaduli, E., Rambuwani, G., van Hemert, L., & Mkhwanazi, M. (2021). Evaluating south african weather service information on idai tropical cyclone and kwazulu-natal flood events. South African Journal of Science 117, 1–13. [CrossRef]
  9. Caren, M. , & Pavlić, K. (2021). Autocorrelation and cross-correlation flow analysis along the confluence of the kupa and sava rivers. Rudarsko Geolosko Naftni Zbornik 36, 67–77. [CrossRef]
  10. Castellazzi, P. , Longuevergne, L., Martel, R., Rivera, A., Brouard, C., & Chaussard, E. (2018). Quantitative mapping of groundwater depletion at the water management scale using a combined GRACE/InSAR approach. Remote Sensing of Environment 205, 408–418. [CrossRef]
  11. Centre for Research on the Epidemiology of Disasters. (2023). Disasters in numbers 2022.
  12. Chandrasekara, S. S. K. , Kwon, H. H., Vithanage, M., Obeysekera, J., & Kim, T. W. (2021). Drought in south asia: A review of drought assessment and prediction in south asian countries. Atmosphere 12. [CrossRef]
  13. Condon, L. E. , Kollet, S., Bierkens, M. F. P., Fogg, G. E., Maxwell, R. M., Hill, M. C., Fransen, H. J. H., Verhoef, A., Van Loon, A. F., Sulis, M., & Abesser, C. (2021). Global Groundwater Modeling and Monitoring: Opportunities and Challenges. Water Resources Research 57, 1–27. [CrossRef]
  14. Denić-Jukić, V. , Lozić, A., & Jukić, D. (2020). An application of correlation and spectral analysis in hydrological study of neighboring karst springs. Water (Switzerland) 12. [CrossRef]
  15. Dilawar, A. , Chen, B., Arshad, A., Guo, L., Ehsan, M. I., Hussain, Y., Kayiranga, A., Measho, S., Zhang, H., Wang, F., Sun, X., & Ge, M. (2021). Towards understanding variability in droughts in response to extreme climate conditions over the different agro-ecological zones of Pakistan. Sustainability (Switzerland) 13. [CrossRef]
  16. DWAF. (2004). Crocodile River (West) and Marico Water Management Area: Internal Strategic Perspective of the Crocodile River (West) Catchment. Department of Water Affairs and Forestry, South Africa 03/000/00/, 160.
  17. Géron, A. (2019). Hands-on Machine Learning whith Scikit-Learing, Keras and Tensorfow. In O’Reilly Media, Inc.
  18. Gude, V. G. , & Nirmalakhandan, N. (2009). Desalination at low temperatures and low pressures. Desalination 244, 239–247. [CrossRef]
  19. Gyamfi, C. , Ndambuki, J. M., & Salim, R. W. (2016). A Historical Analysis of Rainfall Trend in the Olifants Basin in South Africa. Earth Science Research 5(1), 129. [CrossRef]
  20. Holmes, M. , Campbell, E. E., Wit, M. De, & Taylor, J. C. (2022). South African Journal of Botany The impact of drought in the Karoo - revisiting diatoms as water quality indicators in the upper reaches of the Great Fish River, Eastern Cape, South Africa. South African Journal of Botany 149, 502–510. [CrossRef]
  21. Hussain, M. , Butt, A. R., Uzma, F., Ahmed, R., Irshad, S., Rehman, A., & Yousaf, B. (2020). A comprehensive review of climate change impacts, adaptation, and mitigation on environmental and natural calamities in Pakistan. Environmental Monitoring and Assessment 192. [CrossRef]
  22. Hussein, E. A. , Thron, C., Ghaziasgar, M., Bagula, A., & Vaccari, M. (2020). Groundwater prediction using machine-learning tools. Algorithms 13, 1–16. [CrossRef]
  23. Ibrahem Ahmed Osman, A. , Najah Ahmed, A., Chow, M. F., Feng Huang, Y., & El-Shafie, A. (2021). Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Engineering Journal 12(2), 1545–1556. [CrossRef]
  24. IPCC:2014. (2014). Climate Change 2014: Impacts, Adaptation, and Vulnerability. BMJ (Online) 349. [CrossRef]
  25. Kanyama, Y. (2021). Application of machine learning techniques in predicting groundwater levels and discharge rates in the North West aquifers.
  26. Kanyama, Y. , Ajoodha, R., Seyler, H., Makondo, N., & Tutu, H. (2020). Application of Machine Learning Techniques in Forecasting Groundwater Levels in the Grootfontein Aquifer. 2020 2nd International Multidisciplinary Information Technology and Engineering Conference, IMITEC 2020. [CrossRef]
  27. Liu, J. (2011). Water Ethics and Water Resource Management - UNESCO Bangkok Regional Unit for Social and Human Sciences in Asia and the Pacific. Available online: http://unesdoc.unesco.org/images/0019/001922/192256E.pdf.
  28. Lyazidi, R. , Hessane, M. A., Moutei, J. F., & Bahir, M. (2020). Developing a methodology for estimating the groundwater levels of coastal aquifers in the Gareb-Bourag plains, Morocco embedding the visual MODFLOW techniques in groundwater modeling system. Groundwater for Sustainable Development 11, 100471. [CrossRef]
  29. Madzivhandila, Thanyani S, Maserumule, M. H. (2022). The Irony of A “Fire Fighting” Approach Towards Natural Hazards in South Africa: Lessons From Flooding Disaster in KwaZulu-Natal. Journal of Public Administration 57, 191–194.
  30. Malekzadeh, M. , Kardar, S., & Shabanlou, S. (2019). Simulation of groundwater level using MODFLOW, extreme learning machine and Wavelet-Extreme Learning Machine models. Groundwater for Sustainable Development 9, 100279. [CrossRef]
  31. Mann, H. B. (1945). Non-Parametric Test Against Trend. Econometrica 13, 245–259. [CrossRef]
  32. Mathivha, F. I. , Nkosi, M., & Mutoti, M. I. (2021). Evaluating the relationship between hydrological extremes and groundwater in Luvuvhu River Catchment, South Africa. Journal of Hydrology: Regional Studies 37, 100897. [CrossRef]
  33. Meyer, M. (2014). Hydrogeology of Groundwater Region 10: The Karst Belt (WRC Project No. K5/1916).
  34. Mishra, A. K. , & Singh, V. P. (2010). A review of drought concepts. Journal of Hydrology 391, 202–216. [CrossRef]
  35. Mohan, C. , Western, A. W., Wei, Y., & Saft, M. (2018). Predicting groundwater recharge for varying land cover and climate conditions-a global meta-study. Hydrology and Earth System Sciences 22, 2689–2703. [CrossRef]
  36. Murdoch, W. J. , Singh, C., Kumbier, K., Abbasi-Asl, R., & Yu, B. (2019). Definitions, methods, and applications in interpretable machine learning. Proceedings of the National Academy of Sciences of the United States of America 116(44), 22071–22080. [CrossRef]
  37. Oke, S. A. , & Fourie, F. (2017). Guidelines to groundwater vulnerability mapping for Sub-Saharan Africa. Groundwater for Sustainable Development 5, 168–177. [CrossRef]
  38. Olanrewaju, C. C. , & Reddy, M. (2022). Assessment and prediction of flood hazards using standardized precipitation index—A case study of eThekwini metropolitan area. Journal of Flood Risk Management 15, 1–12. [CrossRef]
  39. Osman, A. I. A. , Ahmed, A. N., Huang, Y. F., Kumar, P., Birima, A. H., Sherif, M., Sefelnasr, A., Ebraheemand, A. A., & El-Shafie, A. (2022). Past, Present and Perspective Methodology for Groundwater Modeling-Based Machine Learning Approaches. Archives of Computational Methods in Engineering 29, 3843–3859. [CrossRef]
  40. Ostad-Ali-Askari, K. , Ghorbanizadeh Kharazi, H., Shayannejad, M., & Zareian, M. J. (2019). Effect of management strategies on reducing negative impacts of climate change on water resources of the Isfahan–Borkhar aquifer using MODFLOW. River Research and Applications 35, 611–631. [CrossRef]
  41. Ouali, L. , Kabiri, L., Namous, M., Hssaisoune, M., Abdelrahman, K., Fnais, M. S., Kabiri, H., El Hafyani, M., Oubaassine, H., Arioua, A., & Bouchaou, L. (2023). Spatial Prediction of Groundwater Withdrawal Potential Using Shallow, Hybrid, and Deep Learning Algorithms in the Toudgha Oasis, Southeast Morocco. Sustainability (Switzerland) 15. [CrossRef]
  42. Prodhan, F. A. , Zhang, J., Pangali Sharma, T. P., Nanzad, L., Zhang, D., Seka, A. M., Ahmed, N., Hasan, S. S., Hoque, M. Z., & Mohana, H. P. (2022). Projection of future drought and its impact on simulated crop yield over South Asia using ensemble machine learning approach. Science of the Total Environment 807, 151029. [CrossRef]
  43. Qi, P. , Zhang, G., Xu, Y. J., Wang, L., Ding, C., & Cheng, C. (2018). Assessing the influence of precipitation on shallow groundwater table response using a combination of singular value decomposition and cross-wavelet approaches. Water (Switzerland) 10. [CrossRef]
  44. Quesada-Román, A. , Villalobos-Portilla, E., & Campos-Durán, D. (2020). Hydrometeorological disasters in urban areas of Costa Rica, Central America. Environmental Hazards 1–15. [CrossRef]
  45. Rahmani, F. , & Fattahi, M. H. (2021). A multifractal cross-correlation investigation into sensitivity and dependence of meteorological and hydrological droughts on precipitation and temperature. Natural Hazards 109, 2197–2219. [CrossRef]
  46. Rezaei, M. , Mousavi, S. F., Moridi, A., Eshaghi Gordji, M., & Karami, H. (2021). A new hybrid framework based on integration of optimization algorithms and numerical method for estimating monthly groundwater level. Arabian Journal of Geosciences 14. [CrossRef]
  47. Sahoo, M. , Kasot, A., Dhar, A., & Kar, A. (2018). On Predictability of Groundwater Level in Shallow Wells Using Satellite Observations. Water Resources Management 32(4), 1225–1244. [CrossRef]
  48. Schreiner, B. G. , Mungatana, E. D., & Baleta, H. (2018). Impacts of Drought Induced Water Shortages in South Africa: Economic Analysis Report to the Water Research Commission. 2604, pp. 1–85. Available online: www.wrc.org.za.
  49. Schulze, R. E. (2012). A 2011 Perspective On Climate Change And The South African Water Sector. In WRC Report No. TT 518/12. Available online: http://www.wrc.org.za/wp-content/uploads/mdocs/TT 518-12.pdf.
  50. Seo, S. B. , Das Bhowmik, R., Sankarasubramanian, A., Mahinthakumar, G., & Kumar, M. (2019). The role of cross-correlation between precipitation and temperature in basin-scale simulations of hydrologic variables. Journal of Hydrology 570, 304–314. [CrossRef]
  51. Sharafati, A. , Asadollah, S. B. H. S., & Neshat, A. (2020a). A new artificial intelligence strategy for predicting the groundwater level over the Rafsanjan aquifer in Iran. Journal of Hydrology 591, 125468. [CrossRef]
  52. Sharafati, A. , Asadollah, S. B. H. S., & Neshat, A. (2020b). A new artificial intelligence strategy for predicting the groundwater level over the Rafsanjan aquifer in Iran. Journal of Hydrology 591, 125468. [CrossRef]
  53. Sokol, Z. , & Bližňák, V. (2009). Areal distribution and precipitation-altitude relationship of heavy short-term precipitation in the Czech Republic in the warm part of the year. Atmospheric Research 94, 652–662. [CrossRef]
  54. Sun, H. , & Cornish, P. S. (2005). Estimating shallow groundwater recharge in the headwaters of the Liverpool Plains using SWAT. Hydrological Processes 19(3), 795–807. [CrossRef]
  55. Valois, R. , MacDonell, S., Núñez Cobo, J. H., & Maureira-Cortés, H. (2020). Groundwater level trends and recharge event characterization using historical observed data in semi-arid Chile. Hydrological Sciences Journal 65, 597–609. [CrossRef]
  56. Van Loon, A. F. , Kumar, R., & Mishra, V. (2017). Testing the use of standardised indices and GRACE satellite data to estimate the European 2015 groundwater drought in near-real time. Hydrology and Earth System Sciences 21, 1947–1971. [CrossRef]
  57. Wanders, N. , Wada, Y., & Van Lanen, H. A. J. (2015). Global hydrological droughts in the 21st century under a changing hydrological regime. Earth System Dynamics 6(1), 1–15. [CrossRef]
  58. Wei, A. , Chen, Y., Li, D., Zhang, X., Wu, T., & Li, H. (2022). Prediction of groundwater level using the hybrid model combining wavelet transform and machine learning algorithms. Earth Science Informatics 15(3), 1951–1962. [CrossRef]
  59. Xu, Y. , & Beekman, H. E. (2019). Review: Groundwater recharge estimation in arid and semi-arid southern Africa. Hydrogeology Journal 27, 929–943. [CrossRef]
  60. Zeydalinejad, N. (2022). Artificial neural networks vis-à-vis MODFLOW in the simulation of groundwater: a review. Modeling Earth Systems and Environment 8, 2911–2932. [CrossRef]
  61. Ziervogel, G. , New, M., Archer van Garderen, E., Midgley, G., Taylor, A., Hamann, R., Stuart-Hill, S., Myers, J., & Warburton, M. (2014). Climate change impacts and adaptation in South Africa. Wiley Interdisciplinary Reviews: Climate Change 5, 605–620. [CrossRef]
  62. Zomlot, Z. , Verbeiren, B., Huysmans, M., & Batelaan, O. (2015). Spatial distribution of groundwater recharge and base flow: Assessment of controlling factors. Journal of Hydrology: Regional Studies 4, 349–368. [CrossRef]
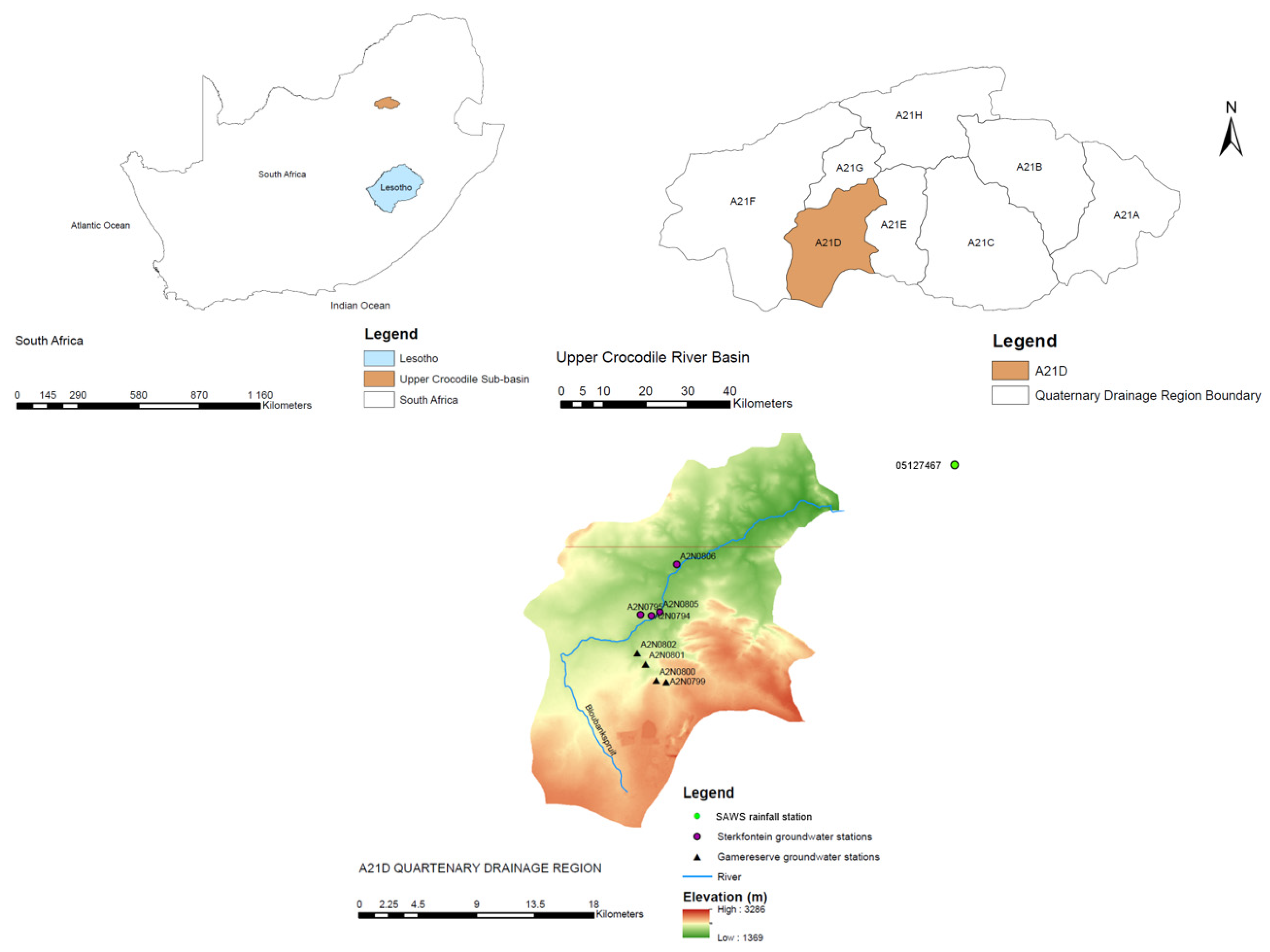
Preprints 74745 g001
Figure 1. Study Area.
Figure 1. Study Area.
Preprints 74745 g001
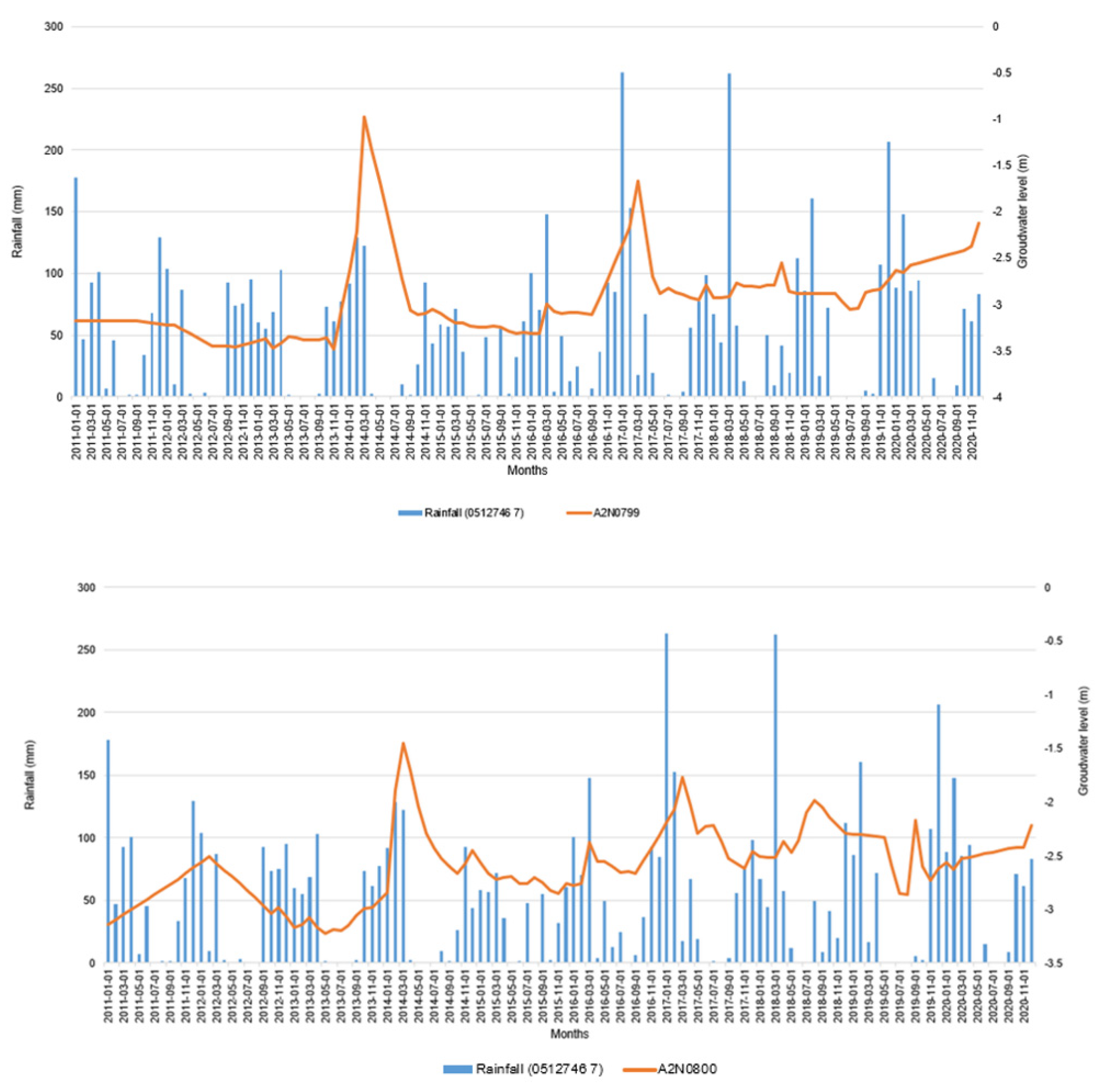
Preprints 74745 g002
Figure 2. Groundwater stations with increasing MK trend.
Figure 2. Groundwater stations with increasing MK trend.
Preprints 74745 g002
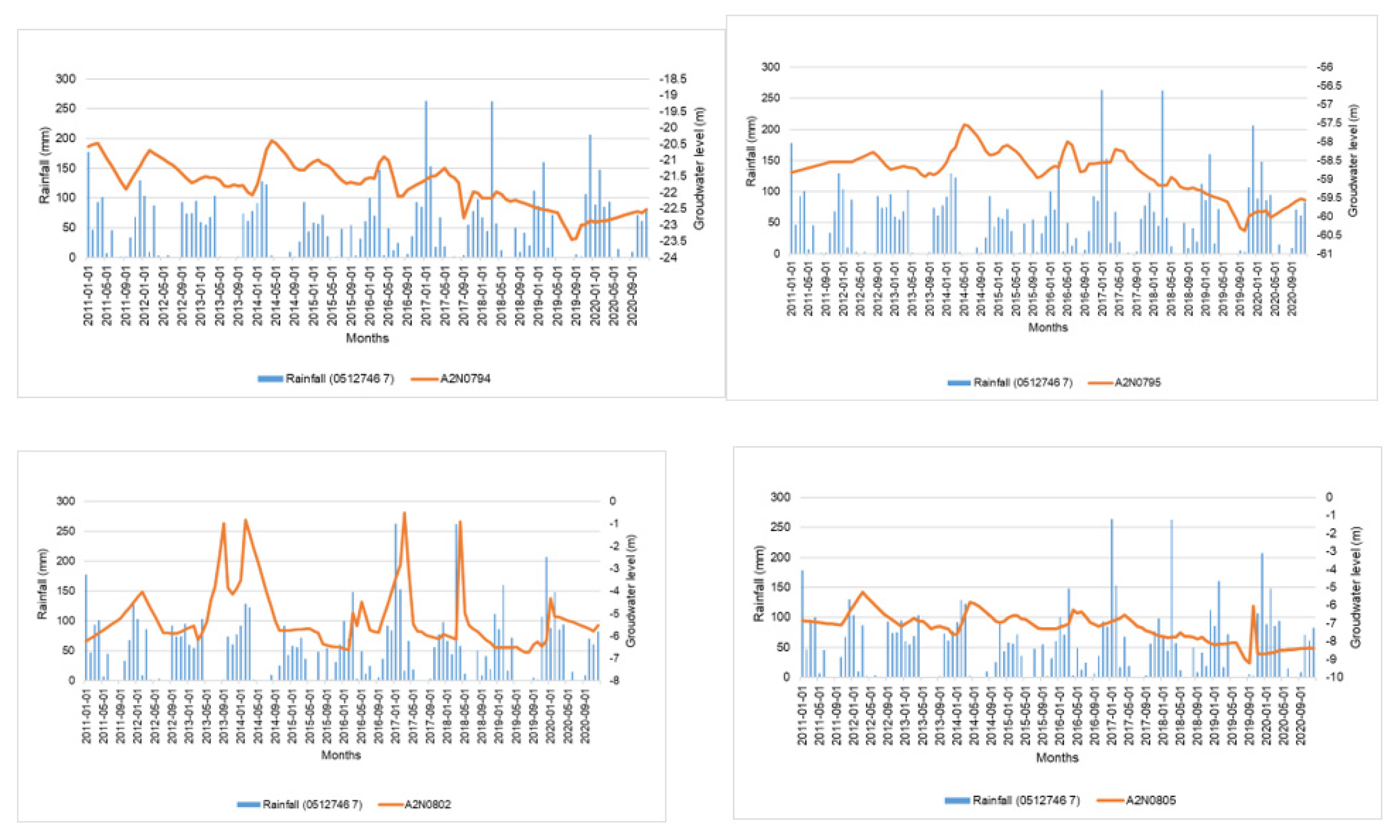
Preprints 74745 g003
Figure 3. Groundwater stations with decreasing MK trend.
Figure 3. Groundwater stations with decreasing MK trend.
Preprints 74745 g003
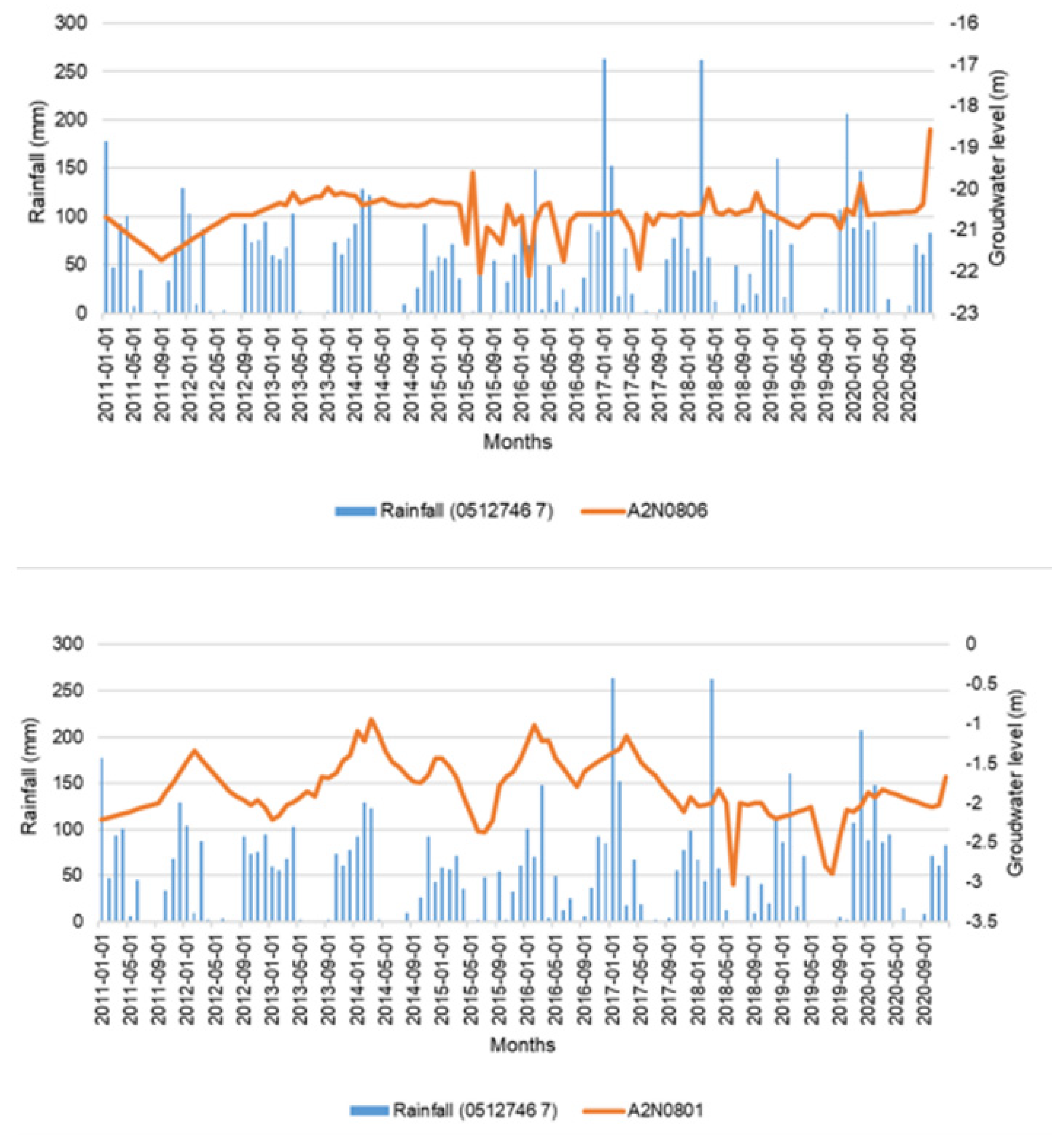
Preprints 74745 g004
Figure 4. Groundwater stations with no trend.
Figure 4. Groundwater stations with no trend.
Preprints 74745 g004
Preprints 74745 g005
Figure 5. Hydrograph of the original versus predicted GWL for best stations.
Figure 5. Hydrograph of the original versus predicted GWL for best stations.
Preprints 74745 g005
Table 1. Groundwater stations selected for the analysis.
Table 1. Groundwater stations selected for the analysis.
STATION NUMBER LATITUDE LONGITUDE START DATE QUATERNARY
A2N0794 -26.048 27.709 01/09/2008 A21D
A2N0795 -26.047 27.702 01/09/2008 A21D
A2N0799 -26.093 27.719 01/09/2008 A21D
A2N0800 -26.092 27.712 01/09/2008 A21D
A2N0801 -26.081 27.705 01/09/2008 A21D
A2N0802 -26.073 27.699 01/09/2008 A21D
A2N0803 -26.036 27.715 01/09/2008 A21D
A2N0805 -26.045 27.715 01/09/2008 A21D
A2N0806 -26.012 27.727 01/09/2008 A21D
Table 2. Groundwater Mann Kendall results from 2011 to 2020.
Table 2. Groundwater Mann Kendall results from 2011 to 2020.
Groundwater stations
Parameter A2N0794 A2N0795 A2N0799 A2N0800 A2N0801 A2N0802 A2N0805 A2N0806
Trend Decreasing Decreasing Increasing Increasing No trend Decreasing Decreasing No trend
P-value 0.000 0.000 0.000 0.000 0.055 0.001 0.000 0.133
Z -9.606 -7.277 7.460 6.496 -1.917 -3.176 -8.896 1.502
Tau -0.593 -0.448 0.461 0.401 -0.118 -0.196 -0.547 0.093
S -4236.000 -3249.000 3289.000 2865.000 -846.000 -1401.000 -3972.000 663.000
Var(S) 194360.000 199213.667 194262.333 194357.000 194314.000 194361.667 199240.000 194333.000
Slope -0.017 -0.011 0.006 0.005 -0.002 -0.007 -0.018 0.001
Table 3. Rainfall-Groundwater level cross-correlations.
Table 3. Rainfall-Groundwater level cross-correlations.
STATION LAG(MONTHS) CCmax
A2N0794 3 0.145
A2N0799 2 0.288
A2N0800 2 0.2
A2N0801 1 0.239
A2N0802 1 0.299
A2N0806 0 0.094
A2N0795 3 0.065
A2N0805 3 0.097
Table 4. Groundwater level autocorrelations.
Table 4. Groundwater level autocorrelations.
STATION LAG (MONTHS) AUTOCORRELATION
A2N0794 1 0.94
A2N0799 1 0.892
A2N0800 1 0.865
A2N0801 1 0.851
A2N0802 1 0.755
A2N0806 1 0.417
A2N0795 1 0.969
A2N0805 1 0.848
Table 5. Model performance evaluation.
Table 5. Model performance evaluation.
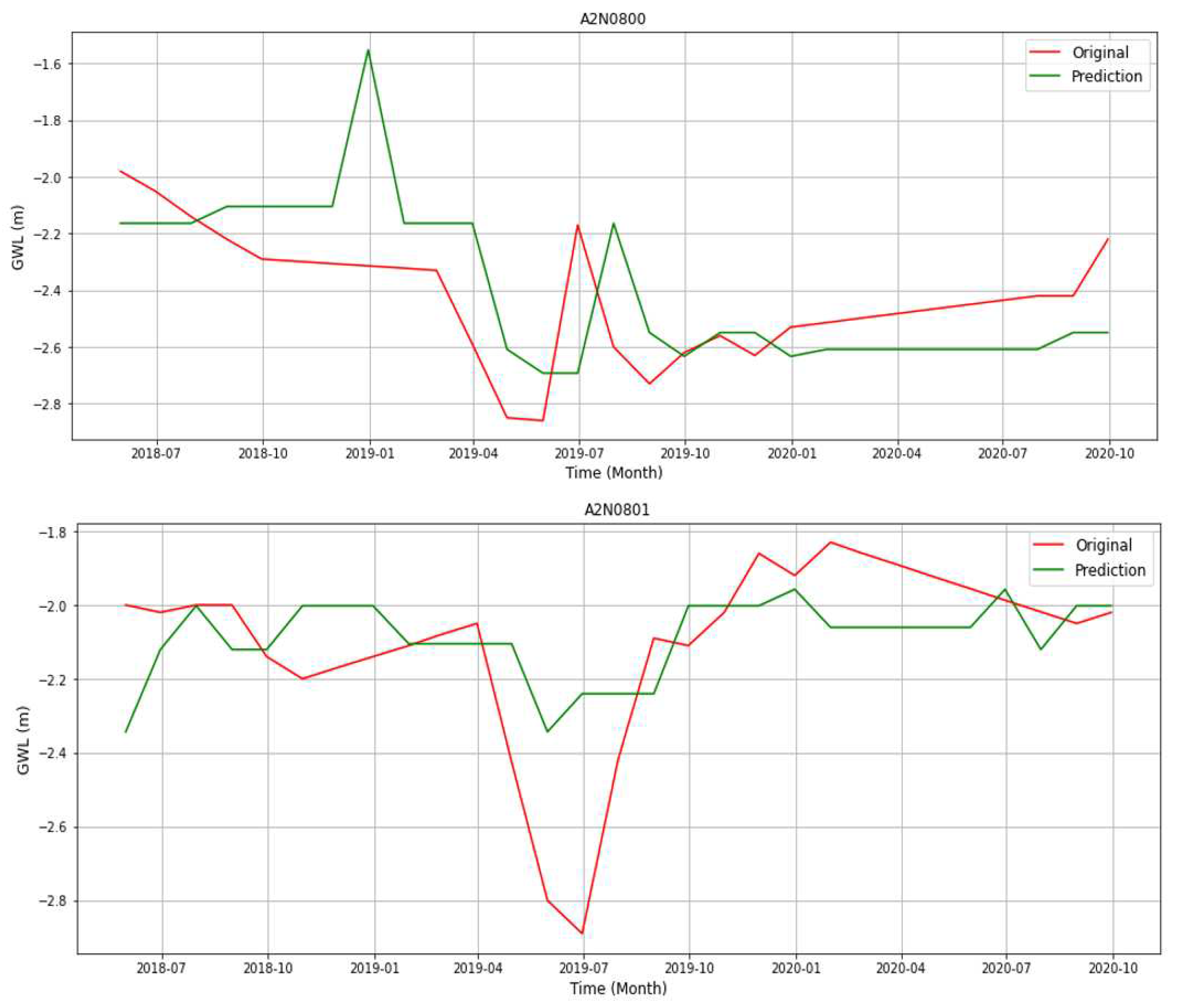
STATION MSE R2
A2N0794 0.41 0.51
A2N0799 0.12 0.5
A2N0800 0.06 0.66
A2N0801 0.04 0.62
A2N0802 0.51 0.01
A2N0806 0.13 0.05
A2N0795 0.53 0.33
A2N0805 0.83 0.53
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated