Intriguing Self-optimization: Gradient Sign and Fractional Order Gradient

Preprint

Article

Intriguing Self-optimization: Gradient Sign and Fractional Order Gradient

Altmetrics

Downloads

132

Views

Comments

This version is not peer-reviewed

Submitted:

19 May 2023

Posted:

23 May 2023

You are already at the latest version

Alerts

Abstract

The gradient descent algorithm has become the standard algorithm for computing the extreme values of functions, but for multivariate functions this algorithm is mostly ineffective. This is because the convergence rate of each element is inconsistent in most cases. However, in this paper, we found that the gradient sign is a self-optimizing operator, ensuring that the convergence rate is consistent across all elements. This also explains, from an optimization perspective, the success of the Fast Gradient Sign Method (FGSM) in generating adversarial samples that are indistinguishable from the normal input, but can easily fool neural networks. We also found that the fractional order gradient is also self-optimizing, and that the convergence speed of this algorithm can be controlled by adjusting the order of the gradient. Experiments suggest that this algorithm not only generates adversarial samples faster than other algorithms, but that a single source image can generate many such samples. This algorithm is also more effective than others at generating adversarial samples from simple images.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

In the past decade or so, deep neural networks (DNNs) have made significant breakthroughs in fields as diverse as image processing, speech recognition, autonomous vehicles and machine translation. However, DNNs are vulnerable to adversarial samples, which are indistinguishable from normal input, but are prone to be misjudged by DNNs. This problem was first introduced in 2013 by Szegedy et al.[1]. They pointed out two counterintuitive aspects of DNNs. The first is that it is the whole space of activations, not individual units, that contains the semantic information. The second is that local generalization is not valid for neural networks, which means that a simple optimization procedure can be used to find adversarial samples, which are imperceptible small perturbations of the input image, but are misclassified by DNNs. Formally, this problem can be described as a box-constrained optimization problem as follows:

minimize {‖r‖}_{2}

subject

t o :

1 . f (x + r) = l 2 . x + r \in {[0,1]}^{m}

where f is the function mapping the input image to the correct output label,

r

is the minimum perturbation measured by the 2-norm, and

x + r

is the image closest to

x

but misclassified as the label

l

. This problem is not easy to solve, but it can be transformed into the following nonlinear optimization scheme, which Szegedy et al. solved using the complicated L-BFGS algorithm.

m i n i m i z e c ∙ |r| + {l o s s}_{f} (x + r, l) s u b j e c t t o : x + r \in {[0,1]}^{m}

(1)

However, on large datasets, the L-BFGS algorithm seems to be less commonly used than improved algorithms such as the Adelta[2] and Adam[3] algorithms. It is time-consuming and does not scale to large datasets[4].

Goodfellow et al. are of the opinion that the main cause of the vulnerability of DNNs is their linearity[5]. The output of the adversarial sample is represented by the formula below:

w^{T} x^{'} = w^{T} x + w^{T} η

The small perturbation input

η

can cause the output to grow by

w^{T} η

. Maximizing this increase subject to the max norm constraint on

η

gives

η = s i g n (w)

. This is then an optimal max norm constraint perturbation:

η = ε s i g n (\nabla_{x} J (θ, x, y)

where

θ

refers to the parameters of the model, and

x

is the input, y is the true label,

J (θ, x, y)

is the loss function for training. They called this algorithm as “fast gradient sign method” (FGSM). So the adversarial sample is:

x^{'} = x + η = x + ε s i g n (\nabla_{x} J (θ, x, y)

This algorithm is fast, but due to the one-shot attack it results in a low success rate if

ε

is small. Whilst a large

ε

can have a positive effect on attack performance, the interference can be noticeable. In this paper, we will prove that the gradient sign descent algorithm is a special gradient descent optimization algorithm, where the learning rate of each element is different and varies at each step, so that the convergence rate of each element of a multivariate function is consistent.

Madry et al. proposed an iterative version of FGSM called projected gradient descent (PGD) with perturbations constrained within the given small domain to guarantee that the adversarial example designed in this way converges to a point in the neighborhood of the source input[6]. It is clear that PGD uses the convergence associated with the sign of gradient. But it is not optimal because these constraints are given artificially, not obtained through optimization methods.

Nicholas Carlini and David Wagner have introduced 7 improved objective functions and used existing optimization algorithms such as Adam to obtain adversarial examples, abbreviated as CW algorithms[7]. The best of these algorithms can be represented as the following optimization function:

m i n i m i z e D (x, x + δ) + c ∙ f (x + δ)

Where

f (x^{'}) = m a x (\max \{{Z (x^{'})}_{i} : i \neq t\} - Z {(x^{'})}_{t}, - κ)

s u b j e c t t o : x + δ \in {[0,1]}^{n}

The effect of the CW attack is very significant, but the speed of generating adversarial samples is indeed too slow. In this paper, we propose a self-optimizing fractional order gradient descent (FOGD) algorithm that runs more than 10 times faster than the CW algorithm and ensures that each element converges uniformly to a certain extreme value. Experiments show that it outperforms over the state-of-the-art optimization algorithm for generating large adversarial samples. It also has obvious advantages for small and simple images which are difficult to use for the creation of adversarial samples.

The rest of this paper is structured as follows. In Section 2, we introduce the related work on the adversarial attacks and defense methods of DNNs. In Section 3, we introduce the previous work concerning with the fractional calculus and the fractional order gradient descent method. We prove that the first order gradient sign can be used to optimize for multivariate functions, and show that the fractional order gradient descent method is a self-optimizing method for obtaining the extreme values of multivariate functions. In Section 4, we perform experiments to confirm the success rate of the attack, the visual quality of the adversarial samples and the speed of generating examples using our method. In Section 5, we discuss the promising directions and present the concluding considerations.

2. Related Work

Since DNNs play a very important role in modern science, and at the same time they face underlying threats that are difficult to overcome, adversary and defense related to DNNs has attracted much interest. In addition to the related work presented in Section 1, there is a large amount of work on this aspect. Here we focus on the most relevant.

Papernot et al. illustrated that not all regions of the input domain are conducive to finding adversarial samples. They compute the forward derivative and construct an adversarial saliency map to find pairs of pixels to architect the set of input features relevant to the adversary’s goal, and then modify the selected input features by increasing or decreasing pixel intensities[8].This algorithm is often abbreviated as JSMA. However, due to its huge memory overhead, it will always fail on large images[7], such as a 299 x 299 x 3 image from the ImageNet datasets[9].

The DeepFool method attempts to find the smallest distance from the data point to the decision boundary so as to obtain the smallest perturbation, alternatively it can be thought of as a gradient descent algorithm with an adaptive step size that is automatically chosen at each iteration step[4]. In each attack step, it linearizes the decision boundary hyperlane using the Taylor extension as below[10].

F = {x : f (x) \approx f (x_{0}) + < \nabla_{x} f (x_{0}) ∙ (x - x_{0}) > = 0}

The key algorithms in the iterative process are described as following.

l = \arg \min_{k \neq k'} \frac{|{f'}_{k}|}{{‖{w'}_{k}‖}_{2}} r_{i} = \frac{|{f'}_{l}|}{{‖{w'}_{l}‖}_{2}^{2}} {w'}_{l}

where i is the i-th iteration step,

{f'}_{k}

is the difference between the loss of the label k and the loss of label with the highest confidence,

{w'}_{l}

is the corresponding difference of the gradients,

r

is the perturbation. For more details please refer to[4].

Papernot et al. found that adversarial patterns have the property of transferability, meaning that as long as both models are trained for the same task, adversarial samples crafted on one model will successfully attack the other, despite the two models having different architectures and being trained on different datasets[11]. Y. Liu et al. conduct an extensive study of the transferability across large models and large scale datasets and find that non-target adversarial samples are more likely to transfer[12]. They generate transferable adversarial examples using an ensemble of multiple models.

Black box attacks were first introduced by Papernot et al. in [11,13]. In the case where the adversary has no knowledge of the target model’s internals or its training data, the adversary also can construct local substitutes to successfully create adversarial examples. This strategy suggests that the study of white box attacks is not outdated. On the contrary, in-depth study on adversarial samples can improve the robustness of the networks and reasonably withstand various attacks.

3. Self-optimizing Gradient Descent

The steepest gradient descent algorithm is a classic optimization method used in machine learning to find local minima. In practice, however, it is difficult to find extremes using gradient alone, because the descent speed of each element is in most cases inconsistent. Some elements cross the low lying area, while others are still far from it. This results in repeated oscillations without reaching extremes. 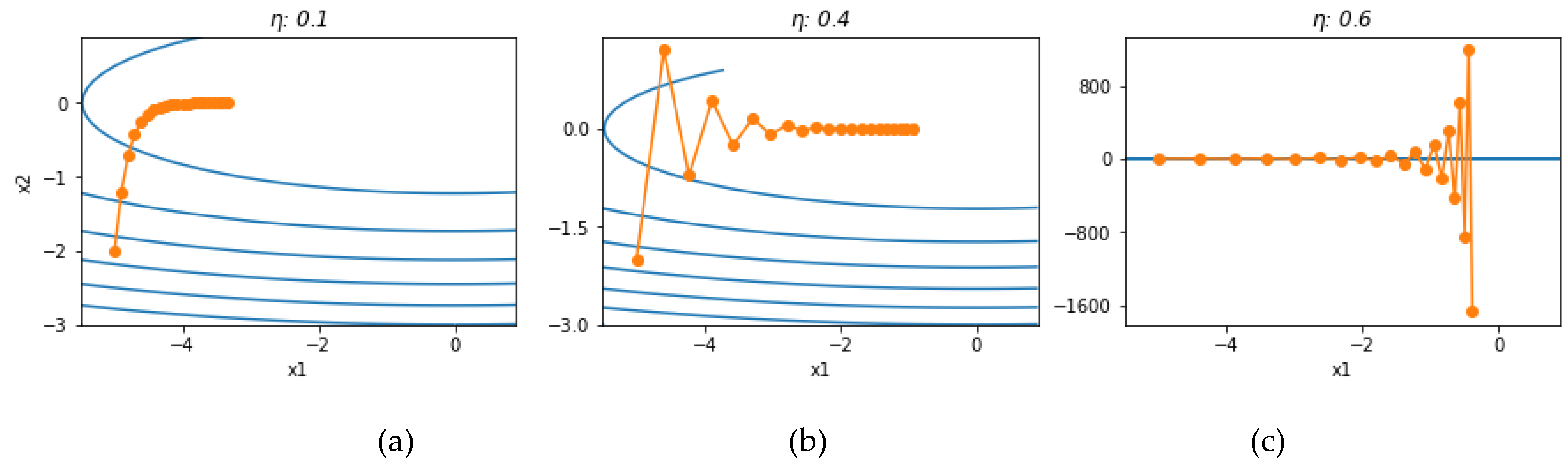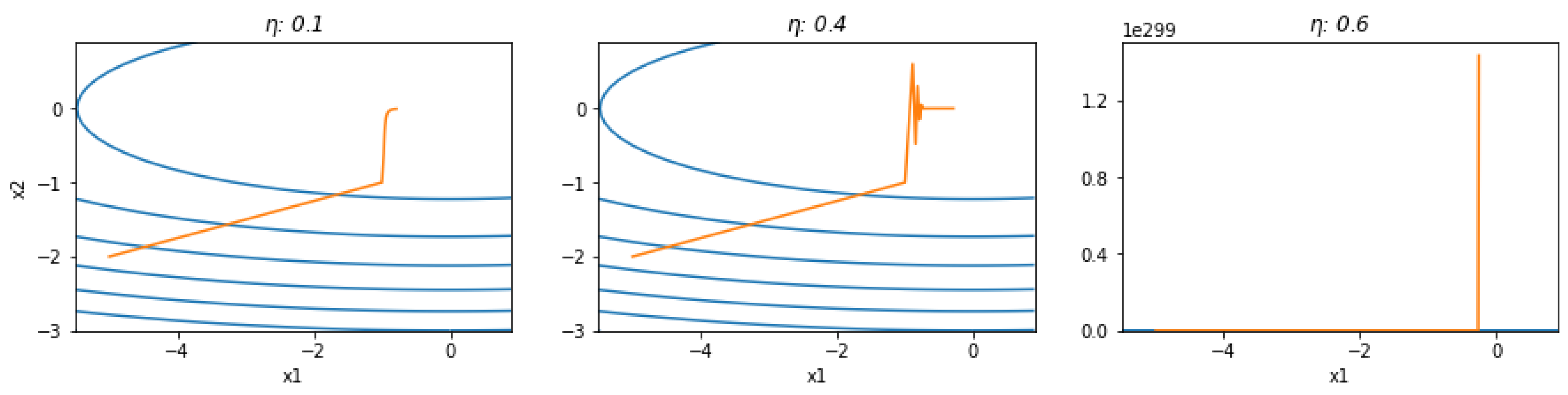Figure 1 intuitively illustrates this problem, assuming the objective function

f (x) = 0.1 x_{1}^{2} + 2 x_{2}^{2}

which maps a two-dimensional vector

{[x_{1}, x_{2}]}^{T}

into a scalar. Setting the initial values to [-5, -2] and iterating 20 times, we obtain the trajectories of the independent variables for different learning rates. See the case source for more details[14].

To address this problem, several methods have been developed to avoid oscillations in the iterative process. Such as Momentum [15], Adelta[2], Adam[3]. In this paper we found that the gradient sign and the fractional order gradient are both self-optimizing operators, without the need for additional optimization methods, the convergence speed of the latter can be controlled because the order of the fractional gradient is freely selectable.

3.1. Gradient Sign for Extreme Values of Multivariate Functions

Let

f (x)

be a smooth convex function with a unique extreme point

x *

. To reach

x *

, the step of each iteration is

x_{k + 1} = x_{k} - η \nabla_{x} f (x_{k})

(2)

where

x

is univariate and

η > 0

According to the traditional theory, the search algorithm in (2) guarantees the convergence to the extreme point

x *

. We modify the above algorithm slightly to obtain a gradient sign descent method(GSDM), as shown below

x_{k + 1} = x_{k} - η s i g n (\nabla_{x} f (x_{k}))

(3)

Theorem 1. The search algorithm in (3) may converge to the extreme value

x *

Proof.

x_{K + 1} = x_{k} - η \nabla_{x} f (x_{k}) = x_{k} - \frac{\nabla_{x} f (x_{k})}{|\nabla_{x} f (x_{k})|} η ∙ |\nabla_{x} f (x_{k})| = x_{k} - ρ ∙ s i g n (\nabla_{x} f (x_{k}))

w h e r e ρ = η ∙ |\nabla_{x} f (x_{k})|

(4)

Because (2) converge to the extreme value

x^{*}

, when

k \to \infty

x_{k + 1} = x_{k} = x^{*}

\nabla_{x} f (x_{k}) = 0

s i g n (\nabla_{x} f (x_{k})) = 0

. This completes the proof.

Remark 1.

GSDM as (3), applied to the multivariate function, makes each unit step size keep in coordinate.

It is clear that for every unit the step size is the same

η

as shown in (3).

Remark 2.

The convergence speed of GSDM is slower than that of the traditional gradient steepest descent algorithm.

As can be seen from the above proof of GSDM, the learning rate

η = \frac{ρ}{|\nabla_{x} f (x_{k})|}

(assuming

ρ

is a constant greater than 0) becomes smaller as the function changes more, as the function changes less the learning rate becomes larger, and as it approaches an extreme value the learning rate becomes infinitely large. To avoid dividing the denominator by 0, the learning rate can be calculated using the following formula

η = \frac{ρ}{|\nabla_{x} f (x_{k})| + ε}

where

ε

is sufficiently small.

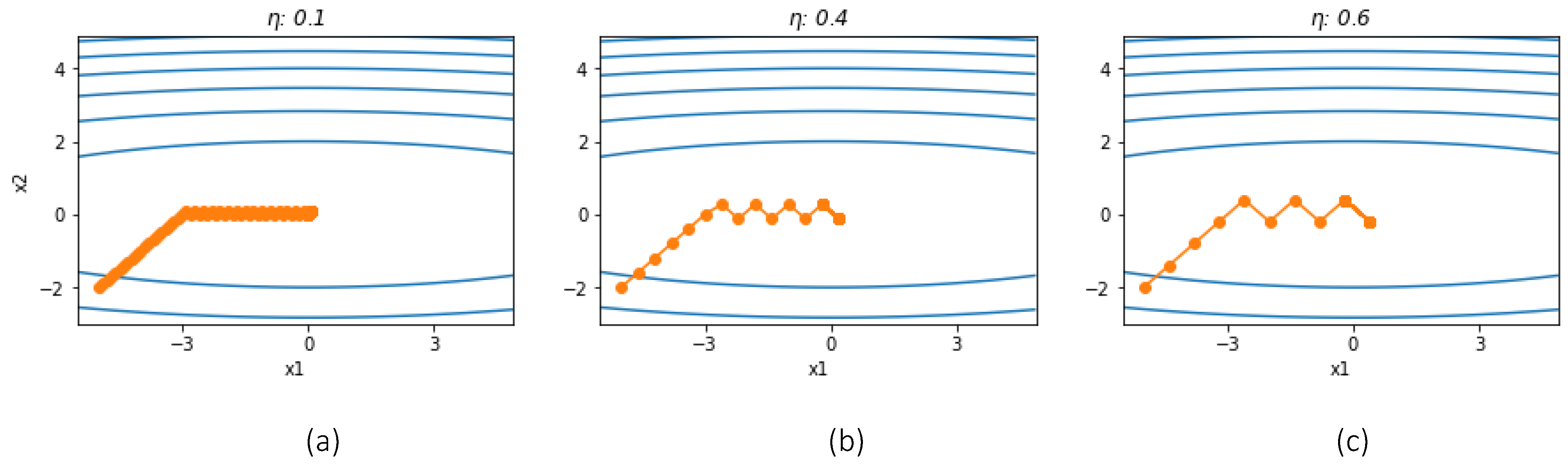
Let’s still take the function

f (x) = 0.1 x_{1}^{2} + 2 x_{2}^{2}

as an example. Following (3) to iterate 40 steps, the other conditions remain unchanged, and the change process of the two variables is shown in Figure 2.

3.2. Fractional Order Gradient for Extreme Values of Multivariate Functions

Fractional calculus, in which the order of integrals or derivatives is arbitrary, not just integrity, has been widely used in a variety of research areas in recent decades[16]. Grünwald, Letnikov, Riemann, Liouville and Caputo et al. have made outstanding contributions to fractional calculus[17].It provides us with useful tools for solving problems involving special functions of mathematical physics as well as their extensions and generalizations in one or more variables[18].

The Caputo’s derivative with order

α

of the smooth function f(t) is as defined as[17]

{}_{t_{0}}^{c}{D_{t}^{α} f (t) = \frac{1}{Γ (n - α)} \int_{t_{0}}^{t} {(t - τ)}^{n - α - 1} f^{(n)} (τ) d τ}

where

n - 1 < α < n

Γ (∙)

is the gamma function.

The Caputo’s derivative can also be rewritten in the form of the classical Taylor series[19]:

{}_{t_{0}}^{c}{D_{t}^{α} f (t) = \sum_{i = n}^{\infty} \frac{f^{(i)} (t_{0})}{Γ (i + 1 - α)} {(t - t_{0})}^{i - α}}

(5)

Theorem 2. Assuming that f(t) is a smooth convex function with a unique extreme value

t^{*}

, the following iterative method guarantees that the argument t approximates the extreme value t*.

t_{k + 2} = t_{k + 1} - η ∙ {}_{t_{k}}^{c}{D_{t_{k + 1}}^{α} f (t)}

(6)

where

0 < α < 1

and

η > 0

Please refer to [19] for a detailed description of the proofing process.

Taking only the first item in (5), (6) can be modified as the following formula, which is more intuitive.

t_{k + 2} = t_{k + 1} - η ∙ f^{(1)} (t_{k + 1}) {|t_{k + 1} - t_{k}|}^{1 - α}

(7)

where

0 < α < 2

and

η > 0

. See [19] for the derivation process. If

α = 1

, (7) becomes the traditional gradient descent method.

From (7) we conclude that this iteration contains not only the information of the current step

t_{k + 1}

, but also the information of the previous step

t_{k}

, so that each iteration in (7) contains more information compared to the traditional gradient descent method. This constant updating of information makes this algorithm similar to the Momentum method. We still use the previous binary function to show that the fractional order gradient descent method (FOGDM) described above has self-optimizing properties and that the co-ordination effect of each element is better than GSDM. 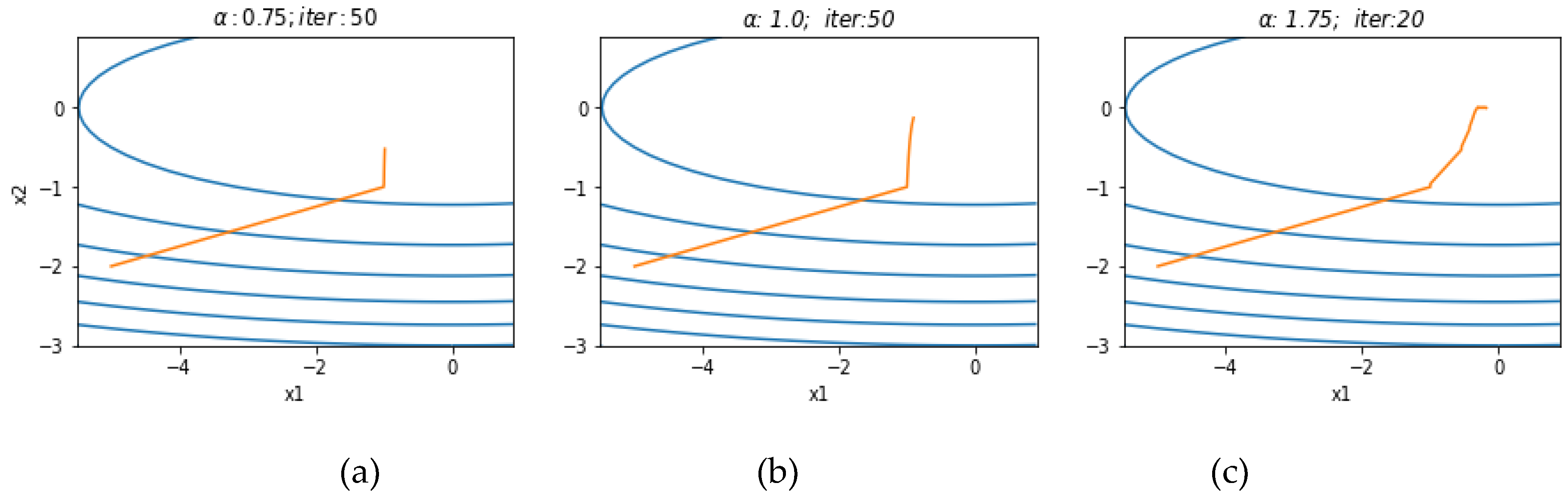Figure 3 shows the trajectory of each element of the FOGD method at different orders of fractional derivative.

The three plots in Figure 3 are set to the same learning rate

η = 0.01

. (a) After 50 iterations, the two directions are far from the extreme point. (b) is the traditional gradient descent method, with the x1 direction further from the extreme value. (C) Two directions are almost always consistently close to the extreme point with the highest velocity, and the number of iterations required is reduced to 20.

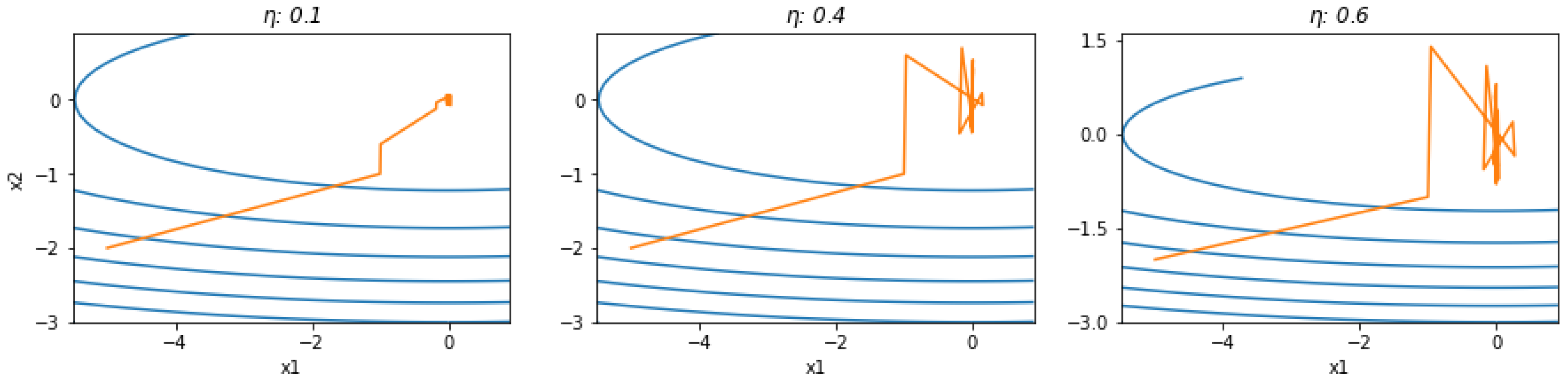
Figure 4 and Figure 5 illustrate the effect of different learning rates on convergence.

From the above analysis, we conclude that:

1) When the order of the derivative is in the interval (1, 2), FOGDM converges faster and more stable than GSDM and the traditional steepest gradient descent method.

2) FOGDM and GSDM have the property of self-optimization, whereas the traditional steepest gradient descent method does not.

3.3. Optimization For Minimal Perturbations

To find the adversarial instance

x'

that is closest to the given image

x

, the most intuitive and reasonable assumptions are the following formulations:

m i n i m i z e D (x^{'}, x) s u c h t h a t C (x^{'}) \neq C (x) x' \in {[0,1]}^{n}

where

C (∙)

is the label into which the classifier maps the input, and

D (x^{'}, x)

is used to measure the difference between the original image

x

and the adversarial sample

x^{'}

. Currently, p-norm,

L_{\infty}

distance and

L_{0}

distance are widely used. There is no doubt that the difference between the two images, which is imperceptible to the human eye but allows the machine to make different judgments, is a problem that is still unclear. What we do know is that the smaller the Euclidean distance between the two images, the harder it is for the human eye to distinguish. Therefore, in this paper we use the

L_{2}

distance to measure the difference between two images. The objective function can be expressed by the following formula:

m i n i m i z e {‖x^{'} - x‖}_{2}^{2} + c ∙ f (x^{'}) s u b j e c t t o : x' \in {[0,1]}^{n}

(8)

where

f (∙)

is the loss function, such as the cross-entropy function, corresponding to the target or non-target labels, and c is a constant used to determine the relative contribution of the distance function to the loss function.

The expressions in (8) are the same as those in (1) introduced in Section 1, they are the simplest formulae and we will prove by experiments in the next section that they are also practicable for large images. We use the tanh function to constrain

x^{'}

in (8), which is reasonable and useful[7].

In (8), the second term

f (x^{'})

can also be calculated using different variations of the loss function as in [7]. The following equation is an effective method.

f (x^{'}) = m a x (\max (\{Z {(x^{'})}_{i : i \neq t}\}) - Z {(x^{'})}_{t}, - κ)

(9)

where Z function is the output layer of the classifier without using the softmax function and

κ

is a given constant called the confidence, and t is the index of the target label.

As introduced in Section 1, (1) is complemented in the L-BFGS method, which is complex and computationally expensive. In this paper, we exploit the fact that the FOGDM has self-optimizing properties to compute adversarial samples as in Algorithm 1.

Algorithm 1. FOGDM:

1. Input: Image

x

, classifier

f

m a x_i t e r

, the order

α

2. Output: the adversarial example

x'

3.Initialize:

w_{0} = x, w_{1} = w_{0} + 0.01

4.for _ in range(

m a x_i t e r

5. loss =

M S E L o s s (w_{1} - x) + c ∙ f (w_{1})

w_{2} = w_{1} - η ∙ \nabla_{w_{1}} J (w_{1}) ∙ {|w_{1} - w_{0}|}^{1 - α}

w_{0} = w_{1}, w_{1} = w_{2}

return

x ’ = (T a n h (w_{1}) + 1) / 2

where

\nabla_{w_{1}} J (w_{1})

is the gradient of loss function against

w_{1}

We can also use GSDM to implement (8) or its variants, as in algorithm 2.

Algorithm 2. GSDM:

1. Input: Image

x

, classifier

f

m a x_i t e r

2. Output: the adversarial example

w

3.Initialize:

w = x

4.for _ in range(

m a x_i t e r

5. loss =

M S E L o s s (w - x) + c ∙ f (w)

w = w - η ∙ s i g n (\nabla_{w} f (w))

w = t a n h (w)

return

w

4. Experimental Results

Using the above self-optimizing GSDM and FOGDM, we crafted adversarial samples with two neural network models, Lenet and resnet50, on the MNIST and Oxford-III Pet datasets respectively. A comparative study was also carried out with the three most popular algorithms, CW, PGD and DeepFool. We also show the visual performance of these adversarial samples and the average relative rate (arr) of change of the different algorithms. The arr is defined as below:

a r r = E_{x} \frac{{‖x^{'} - x‖}_{2}}{{‖x‖}_{2}} = \frac{1}{|D|} \sum_{x \in D} \frac{{‖x^{'} - x‖}_{2}}{{‖x‖}_{2}}

where D is the test dataset, x’ is the adversarial example and x is the original image in the test dataset. The arr metric is used to measure the size of the change in the adversarial sample based on the source image. Intuitively, it is reasonable and realistic. Accordingly, the relative rate of change of a single adversarial sample can be defined as follows.

r e l a t i v e r a t e o f c h a n g e = \frac{{‖x^{'} - x‖}_{2}}{{‖x‖}_{2}}

4.1. On the Oxford-IIIT Pet Dataset

The Oxford-IIIT Pet Dataset is a dataset of 37 categories with 200 color images for each class2. But in this paper, we got the dataset from the website of kaggle3, which has 35 classes with 7390 color images. The images are of different scales, so we resize them all to the same size

299 \times 299

. This dataset can be seen as a small ImageNet dataset[20].

We use the resnet50 model, which can be downloaded from the official PyTorch website, as our target. The output layer of the original model is modified from 1000 classes to 35 classes. We trained the model using a fine tuning technique to transfer the knowledge learned from the ImageNet dataset, with a learning rate of 0.01 for the output layer and 0.001 for the other layers, achieving a training accuracy of 99.9%. From these images, we randomly selected 1000 images to form a test set as the source samples to generate adversarial examples. The experiment was run on the kaggle platform using the Tesla GPU 100. In Table 1, we report the accuracy, the time spent and the average relative rate of change (arr) on the test set after attack.

The value of c in (8) affects the ease of misclassification and the arr; the higher the c, the easier it is for the classifier to misclassify, but also the higher the arr. In our experiments, we found that when c is greater than 4, FOGDM needs only 5 iterations to obtain an adversarial sample that is undetectable to the human eye and sufficient for the classifier to misclassify. For the experiments in Table 1, we set c=1 and the number of iterations was set to 10. Table 1 shows that FOGDM is 10 times faster than CW and faster than others without any loss of accuracy.

Figure 6 illustrates some of the adversarial examples in different algorithms. No matter how carefully one observes, it is difficult to visually detect the differences between the adversarial samples produced by these algorithms and the source images.

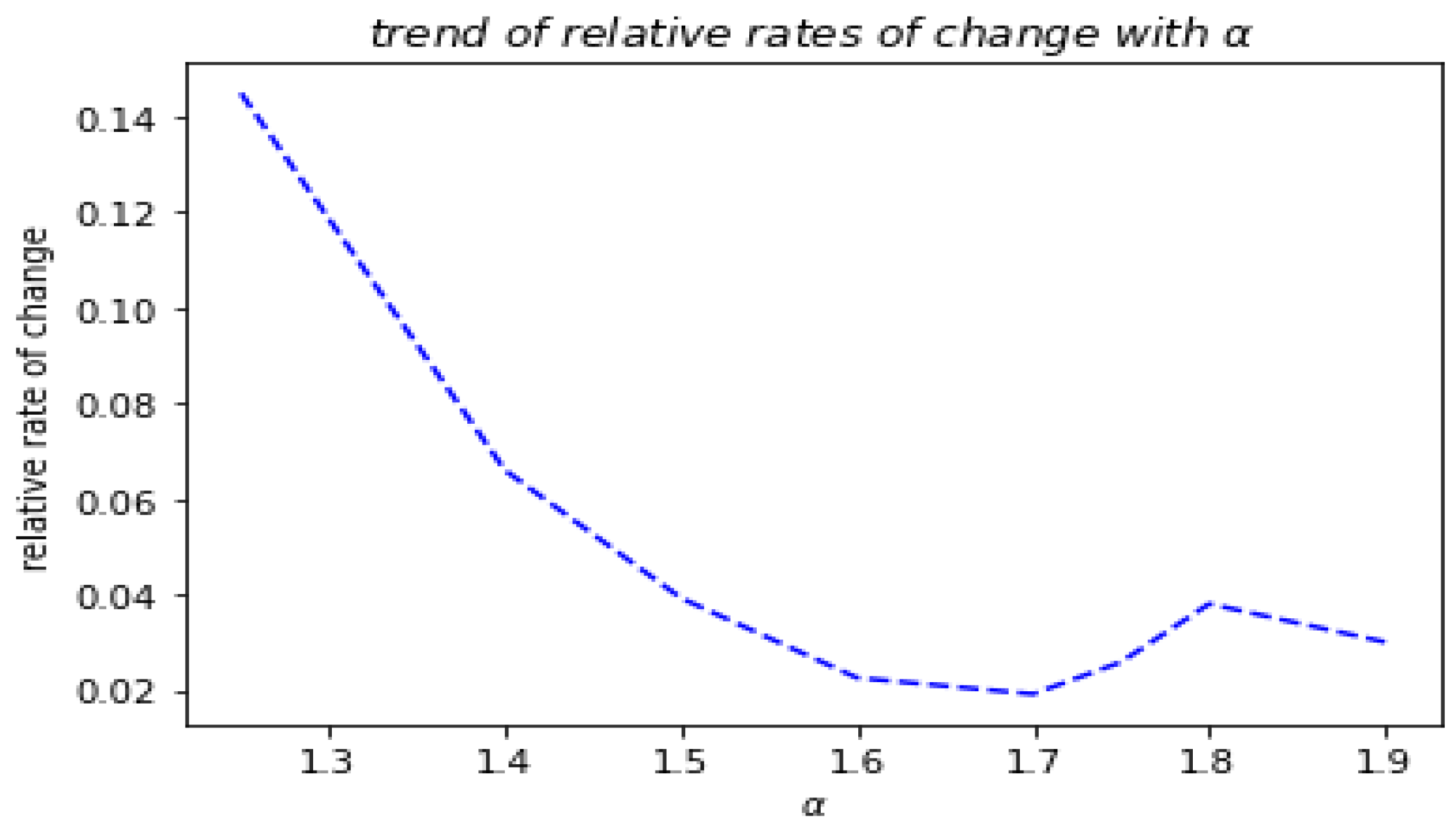
Figure 7 shows the adversarial samples generated with c=1, after 50 iterations and taking different orders of the fractional derivative. Although we cannot distinguish them by eye, they are different according to the relative rate of change from the original image, as shown in Figure 8, which correspond to the orders of the fractional derivative. The rates suggest that the images shown in Figure 7 are different from each other, although they come from the same image of the last and are taken with the same algorithm. This phenomenon perhaps shows that these images reach different extreme points so that the difference with the original image cannot be perceived.

As shown in Figure 8, when α is 1.7, the adversarial samples are the least modified relative to the original image. However, they are all imperceptible to the human eye.

4.2. On the MNIST Dataset

The MNIST dataset consists of 70000 handwritten digital images, each of which is a

28 \times 28

0-9 handwritten digital image. The black background is represented by 0, and grey pixels are represented by a floating point between 0-1. The closer to 1, the whiter the color. Of these, 60,000 are from the training set and 10,000 from the test set. We choose a slightly modified Lenet neural network to generate adversarial samples, with two convolutional layers plus two fully connected layers and a log-softmax activation function for the output layer[21]. The network parameters are pre-trained and the network had a classification accuracy of 98.1% on the test set. The experiment was run on the Kaggle platform using the Tesla GPU 100.

The results of this experiment are shown in Table 2. In this experiment, we find that it is difficult for FOGDM to simply use (8) to make the classifier to misclassify. Therefore, we modified the second term of the objective function similar to (9), with the only difference being that the activation function of the output layer is

l o g_s o f t m a x (∙)

. And, the number of iterations was changed from 10 in the previous experiment to 100 in this experiment. The order of fractional gradient is set as 1.9. For PGD, the constraint of the perturbations are modified from 2/255 to 48/255, and for CW, the confidence

κ

has been adjusted to 10 this time, while the last experiment was only 0.For GSDM, we select non-target attack as FGSM. Without these adjustments, it is essentially impossible for the classifier to make incorrect judgments. Table 2 shows that for simple networks, GSDM has no advantage in terms of successful attack probability. Although the objective function is the same, FOGDM increases the probability of a successful attack by a factor of one over CW.

DeepFool appears to have significant advantages in terms of time, attack accuracy, and the average relative rate of change from Table 2, but it is visually noticeable and appears to perform worse than other algorithms shown in Figure 9. This also suggests that the simpler the image, the harder it is to fool neural networks by modifying the original image in a way that is indistinguishable to the naked eyes. It also shows that the average relative rate of change is not a very effective measurement tool, as a lower rate of change does not necessarily mean a better visual result. A small relative rate of change may be a necessary condition, but it is not a sufficient condition. Figure 9 also shows that CW, FOGDM, GSDM only modify important pixels and their neighbors, while PGD, DeepFool tend to adjust the whole image. This is more evident in the digits 0, 1 and 7. Interestingly, for digit 1, the classifier misclassified it as 9 using FOGDM and GSDM, so the adversarial examples are closer to 9. This also suggests that the adversary is modifying the image to mislead the classifier, rather than attacking the classifier itself.

5. Conclusion & Outlook

In this paper, we proposed self-optimizing gradient descent algorithms, FOGDM and GSDM. We illustrate the consistency of each element of the bivariate function converging to the extreme point and find that when the order of fractional gradient is between 1 and 2, FOGDM converges stably and quickly. Based on the two of the algorithms we find that FOGDM has advantages over CW and the other state of the art algorithms in terms of time for large images. And, for small or simple images, using the same objective function, FOGDM is in a more successful attack than CW.

We also show that the different orders of the fractional gradient can lead to different effective adversarial samples after the same iterations. This phenomenon may provide us with a new direction to explore the unknown world of DNNs. In addition, the formation process of adversarial samples generated by FOGDM and GSDM is worth studying in depth. It may lead us to find the laws between pixel changes and the corresponding classification results, allowing us to find more effective methods for DNNs to defend against adversarial attacks. Perhaps, in addition to the robustness of the machine model itself, the success of the attack depends on several factors, such as the simplicity of the image and the optimization strategy. Fractional order gradients open up new avenues of investigation for us.

Acknowledgments

The work was supported in part by the National Natural Science Foundation of China(Grant No.~62171303), in part by China South Industries Group Corporation (Chengdu) Fire Control Technology Center Project (non-secret) (Grant No.~HK20-03), in part by the National Key Research and Development Program Foundation of China (Grant No.~2018YFC0830300).

1	The code for experiments is made available at: https://github.com/mulertan/self_optimizing/tree/main
2	https://www.robots.ox.ac.uk/~vgg/data/pets/
3	https://www.kaggle.com/datasets/tanlikesmath/the-oxfordiiit-pet-dataset

References

W.Z. Christian Szegedy, Ilya Sutskever,Joan Bruna,Dumitru Erhan,Ian Goodfellow,Rob Fergus, Intriguing properties of neural networks, ICLR(2013), (2013).
M.D. Zeiler, ADADELTA: AN ADAPTIVE LEARNING RATE METHOD, https://arxiv.org/abs/1212.5701, 2012.
B.J.A. Kingmma D, A method for stochastic optimization, Proceeding of the 3rd International Conference on Learning Representation, Workshop Track, San Diego,USA, 2015.
S.M. Moosavi-Dezfooli, A. S.M. Moosavi-Dezfooli, A. Fawzi, P. Frossard, Ieee, DeepFool: a simple and accurate method to fool deep neural networks, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Ieee, Seattle, WA, 2016, pp. 2574-2582.
J.S.C.S. Ian J. Goodfellow, EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES, ICLR(2015), (2015).
Madry, A. Makelov, L. Schmidt, D. Tsipras, A. Vladu, Towards Deep Learning Models Resistant to Adversarial Attacks, (2017).
Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. 2017 IEEE Symposium on Security and Privacy (SP). LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 39–57.
Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The Limitations of Deep Learning in Adversarial Settings. 2016 IEEE European Symposium on Security and Privacy (EuroS&P). LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; pp. 372–387.
Russakovsky, ImageNet Large Scale Visual Recognition Challenge, International Journal of Computer Vision (IJCV), 115(3) (2015) 211–252. [CrossRef]
X. Han, M. X. Han, M. Yao, L. Haochen, D. Deb, L. Hui, T. Jiliang, A.K. Jain, Adversarial Attacks and Defenses in Images, Graphs and Text: A Review arXiv, arXiv (USA), (2019) 31 pp.-31 pp.
N. Papernot, P. N. Papernot, P. Mcdaniel, I. Goodfellow, Transferability in Machine Learning: from Phenomena to Black-Box Attacks using Adversarial Samples, (2016).
Y. Liu, X. Y. Liu, X. Chen, C. Liu, D. Song, Delving into Transferable Adversarial Examples and Black-box Attacks, (2016).
Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical Black-Box Attacks against Machine Learning. ASIA CCS ‘17: ACM Asia Conference on Computer and Communications Security. LOCATION OF CONFERENCE, United Arab EmiratesDATE OF CONFERENCE; pp. 506–519.
Z.C.L. Aston Zhang, Mu Li, and Alexander J. Smola, Dive into Deep Learning, http://www.d2l.ai/, 2021.
Q. Ning, On the momentum term in gradient descent learning algorithms, Neural Networks, (1999).
Pu, Y.-F.; Zhou, J.-L.; Zhang, Y.; Zhang, N.; Huang, G.; Siarry, P. Fractional Extreme Value Adaptive Training Method: Fractional Steepest Descent Approach. IEEE Trans. Neural Networks Learn. Syst. 2013, 26, 653–662. [Google Scholar] [CrossRef]
Podlubney, Fractional Differential Equations, Lightning Source Inc1998.
H.M.S. Anatoly A. Kilbas, Juan J. Trujillo, Theory and Applications of Fractional Diffeential Equations, ELSEVIER2006.
Chen, Y.; Gao, Q.; Wei, Y.; Wang, Y. Study on fractional order gradient methods. Appl. Math. Comput. 2017, 314, 310–321. [Google Scholar] [CrossRef]
J.D. O. Russakovsky, H. J.D. O. Russakovsky, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein,, a.L.F.-F. A. C. Berg, ImageNet large scale visual recognition challenge, IJCV, (2015).
LeCun, Y.; Haffner, P.; Bottou, L.; Bengio, Y. Object recognition with gradient-based learning. In Shape, Contour and Grouping in Computer Vision, Springer: Berlin/Heidelberg, Germany, 1999; pp. 319–345.

Figure 1. (a) The learning rate is too low for both variables to reach the extreme point; (b) reaching the convergence point faster in the x2 direction; (c) has a large learning rate, with x1 converging but diverging in the x2 direction.

Figure 2. (a), (b) and (c) show that each unit moves towards the extreme point in a consistent manner, but when it reaches the vicinity of the extreme point there are oscillations that make it difficult to converge. The magnitude of the oscillations is closely related to the learning rate.

Figure 3. Variable change trajectory with same learning rate, different derivative orders.

Figure 4. The effect of different learning rates on convergence with the same derivative order α=1.75 after 80 iterations. When the learning rate is high, there is no divergence, although there are small oscillations.

Figure 5. The effect of different learning rates on convergence with the same derivative order α=0.75 after 40 iterations. When

η = 0.6

, there is divergence.

Figure 5. The effect of different learning rates on convergence with the same derivative order α=0.75 after 40 iterations. When

η = 0.6

, there is divergence.

Figure 6. From left to right are the source graphs and the adversarial samples generated by the CW, DeepFool, PGD, FOGDM and GSDM algorithms. In the first row, the ground true label is ‘russian’, but misclassified as ‘american’ or ‘boxer’. In the second row, the true label is ‘Sphynx’, but misclassified as ‘german’ or ‘american’.

Figure 7. The true label is ‘Yorkshire’, but the first 8 images are classified as Abyssinian with different values of α.

Figure 8. Different relative rates of change corresponding to the order of fractional derivative.

Figure 9. From left to right, the first column shows the source image from the test set, while the second and the subsequent columns show the adversarial samples generated by the CW, PGD, DeepFool, FOGD, and GSD algorithms, respectively. Visually, CW and FOGD have advantages.

Table 1.

algorithm	CW	DeepFool	PGD	FOGDM	GSDM
accuracy	2.0%	2.0%	1.0%	2.0%	1.0%
time(seconds)	2461.96	552.45	1113.74	249.91	531.43
arr	0.133	0.001	0.016	0.049	0.077

Table 2.

algorithm	CW	PGD	DeepFool	FOGDM	GSDM
accuracy	41.0%	36.6%	1.3%	19.2%	59.3%
time(seconds)	234.87	157.19	30.21	222.82	202.13
arr	0.579	0.442	0.187	0.431	0.154

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Intriguing Self-optimization: Gradient Sign and Fractional Order Gradient

Abstract

1. Introduction

2. Related Work

3. Self-optimizing Gradient Descent

3.1. Gradient Sign for Extreme Values of Multivariate Functions

3.2. Fractional Order Gradient for Extreme Values of Multivariate Functions

3.3. Optimization For Minimal Perturbations

4. Experimental Results

4.1. On the Oxford-IIIT Pet Dataset

4.2. On the MNIST Dataset

5. Conclusion & Outlook

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe