Submitted:
18 May 2023
Posted:
19 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
Modification of the Drude - Sommerfeld Equation. Variant N. Mott
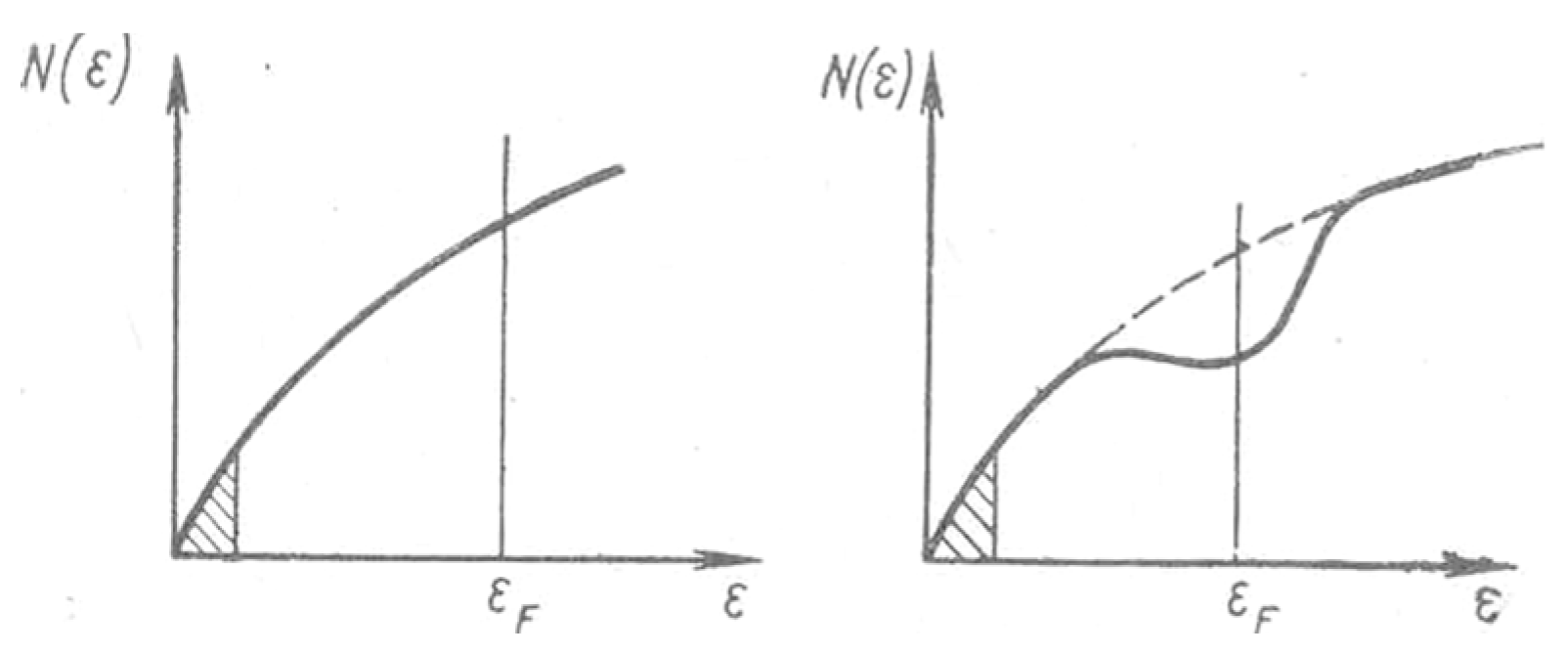
Modification of the Drude-Sommerfeld Equation. Author's Variant
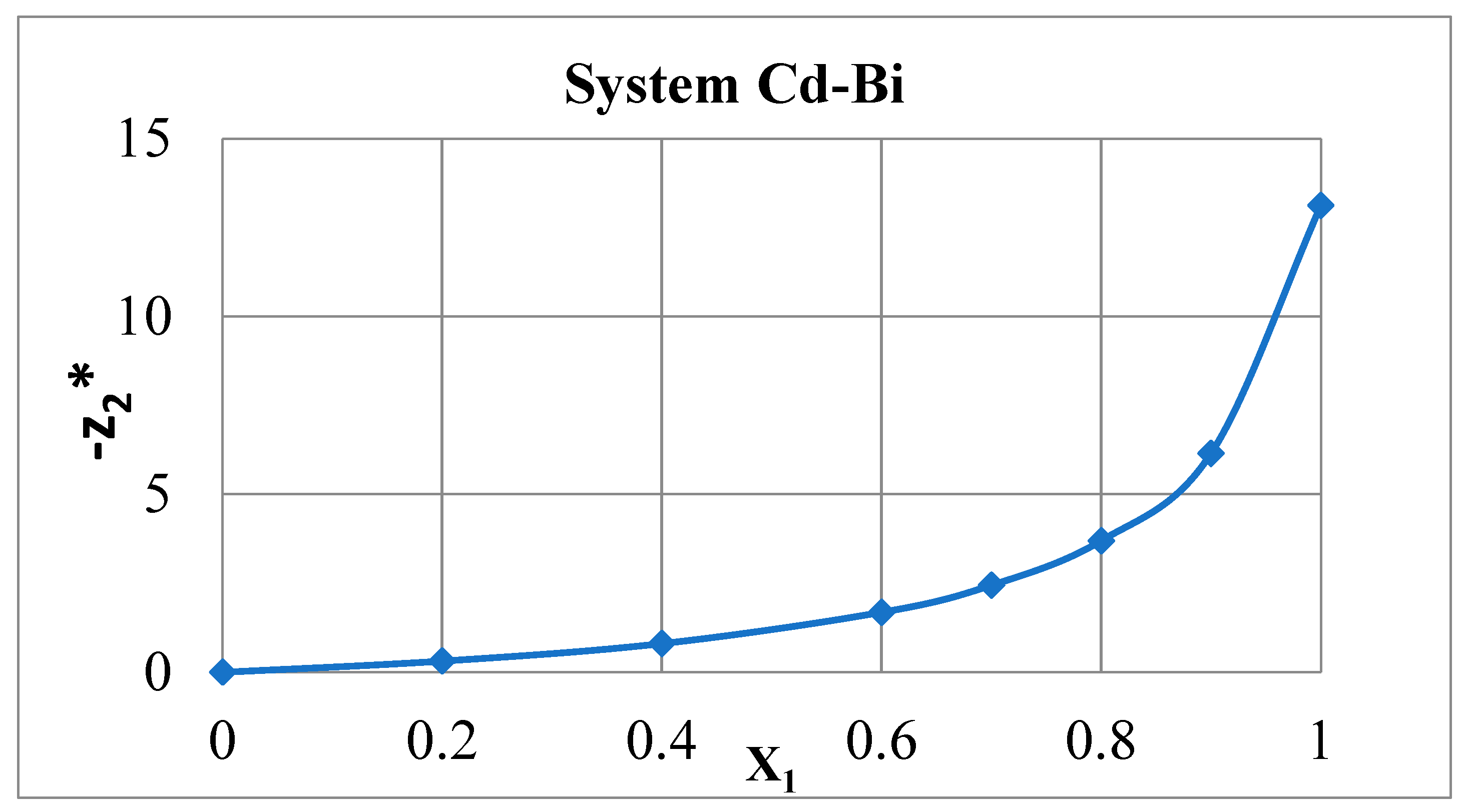
3. Results
Electromigration Equations
4. Discussing
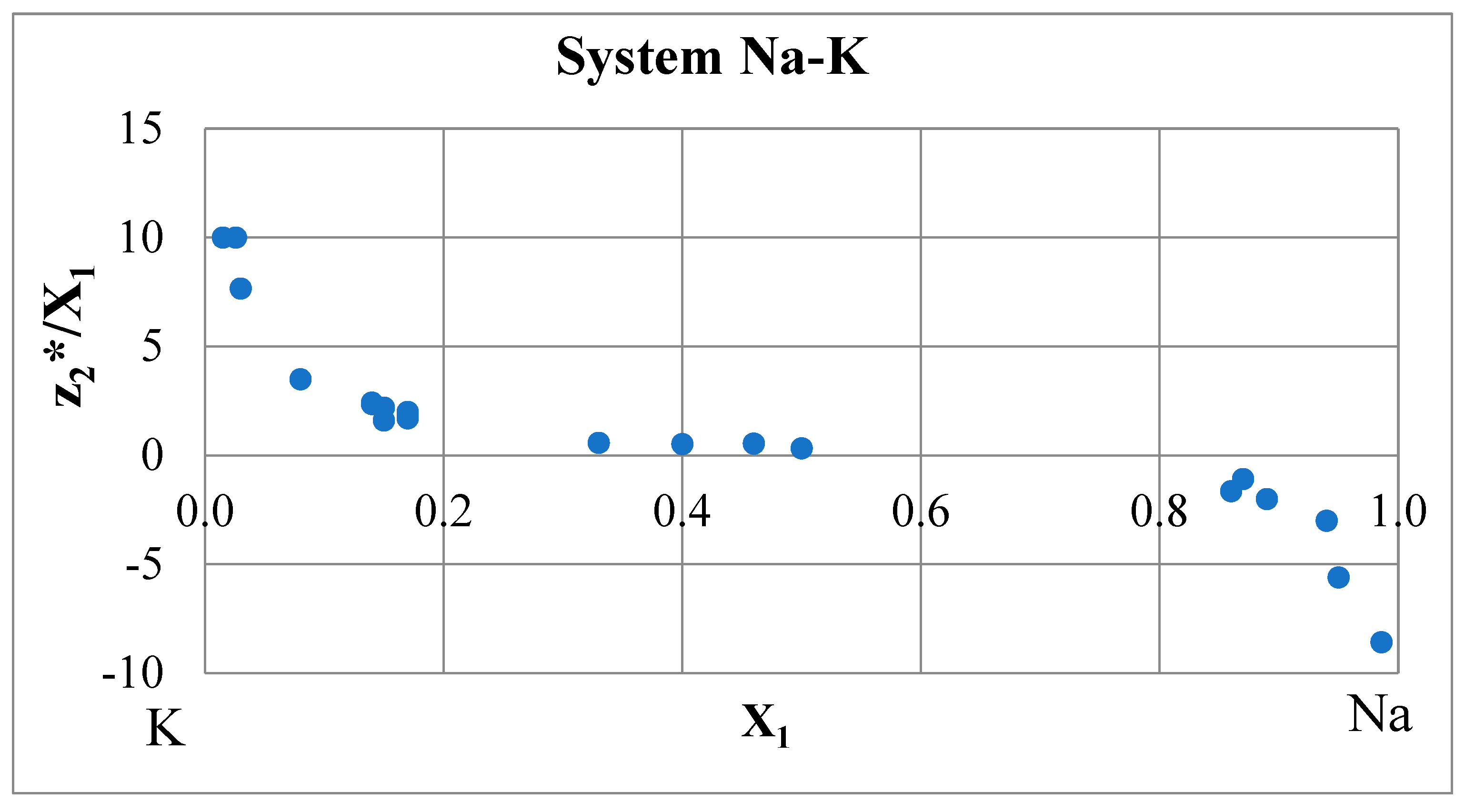
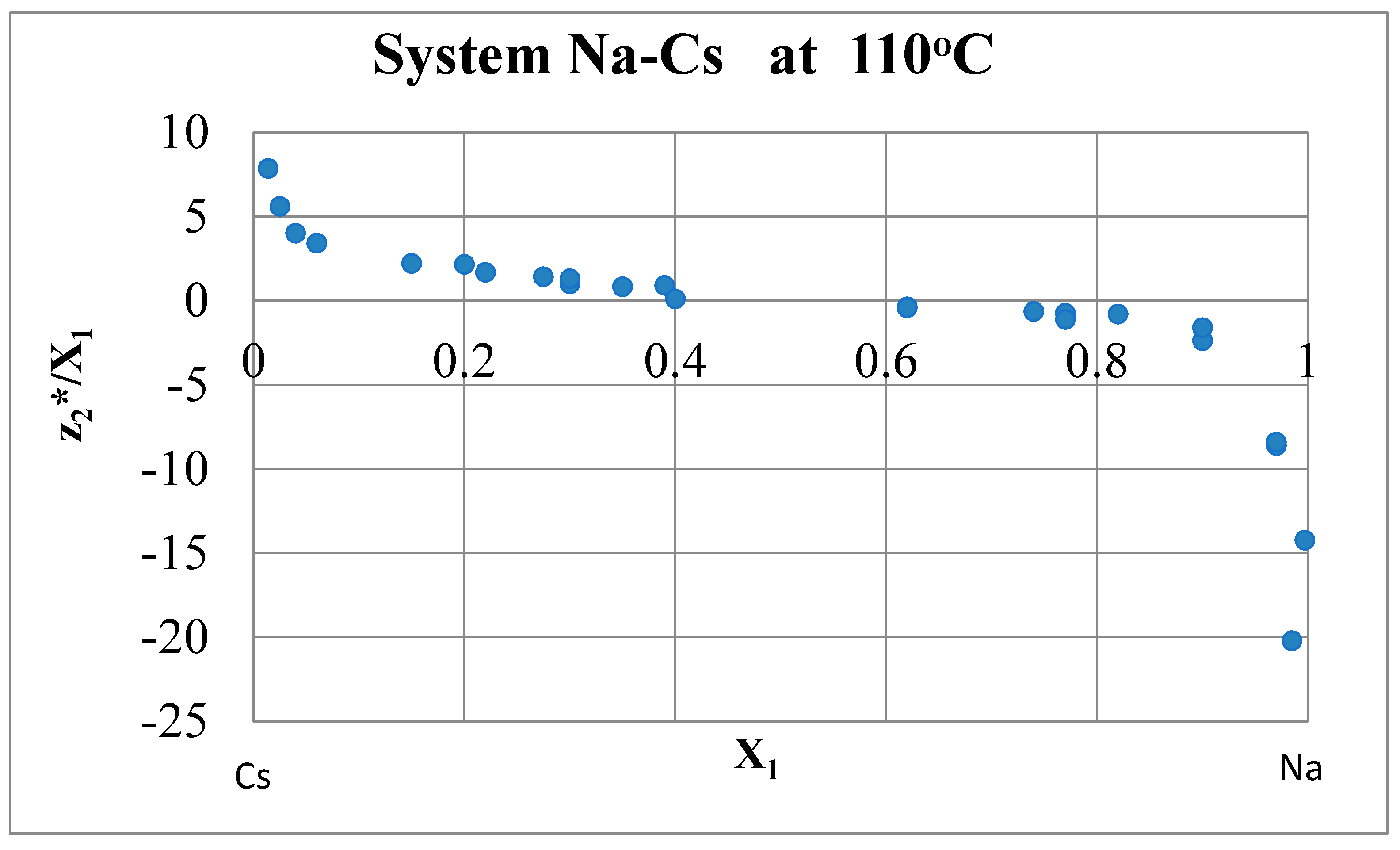
Relationship between Effective Charge and Electrical Resistance. Drude-Sommerfeld Variant
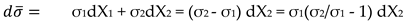
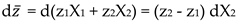
N. Mott Variant. Integral Relations
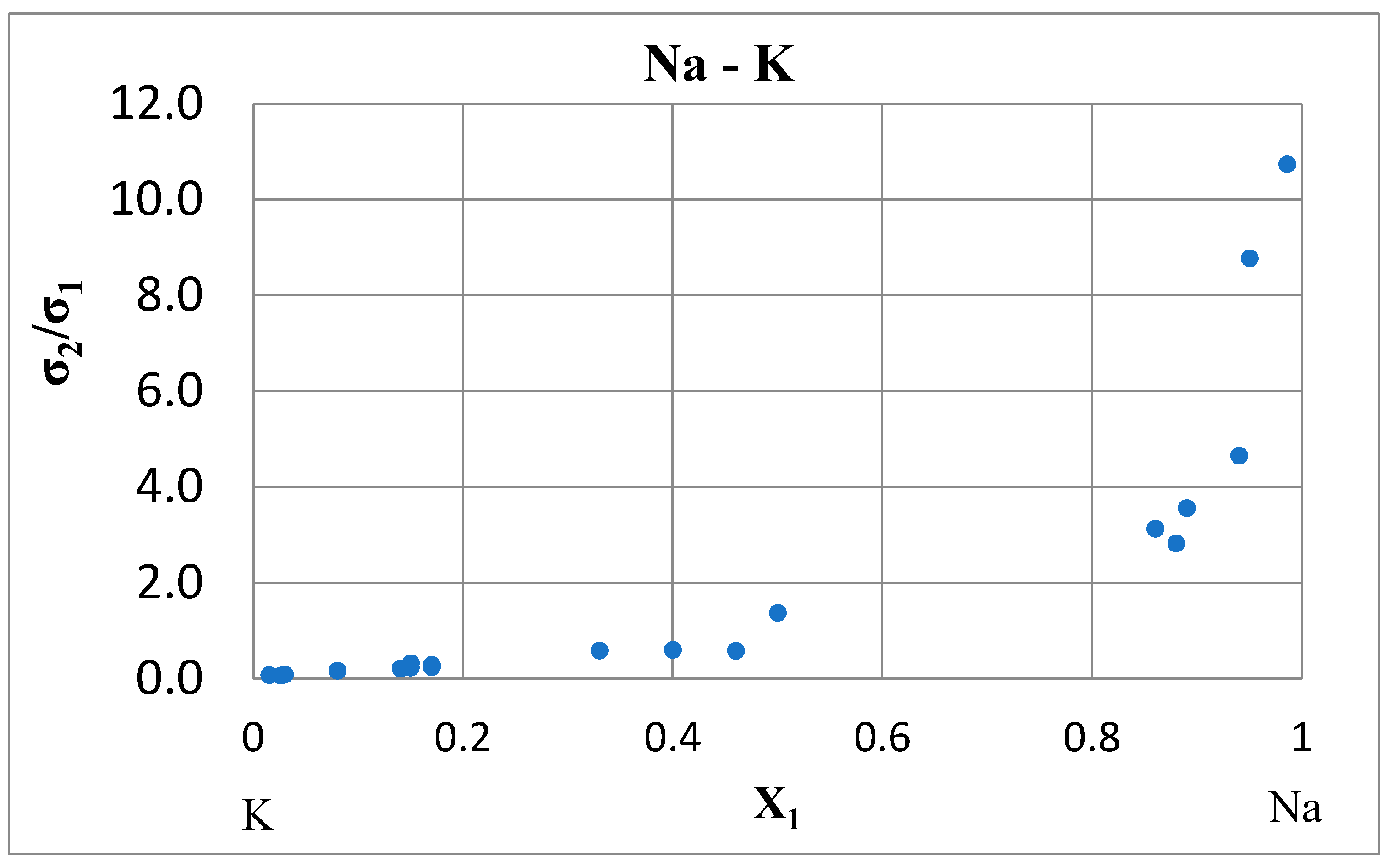
Consistency Rule
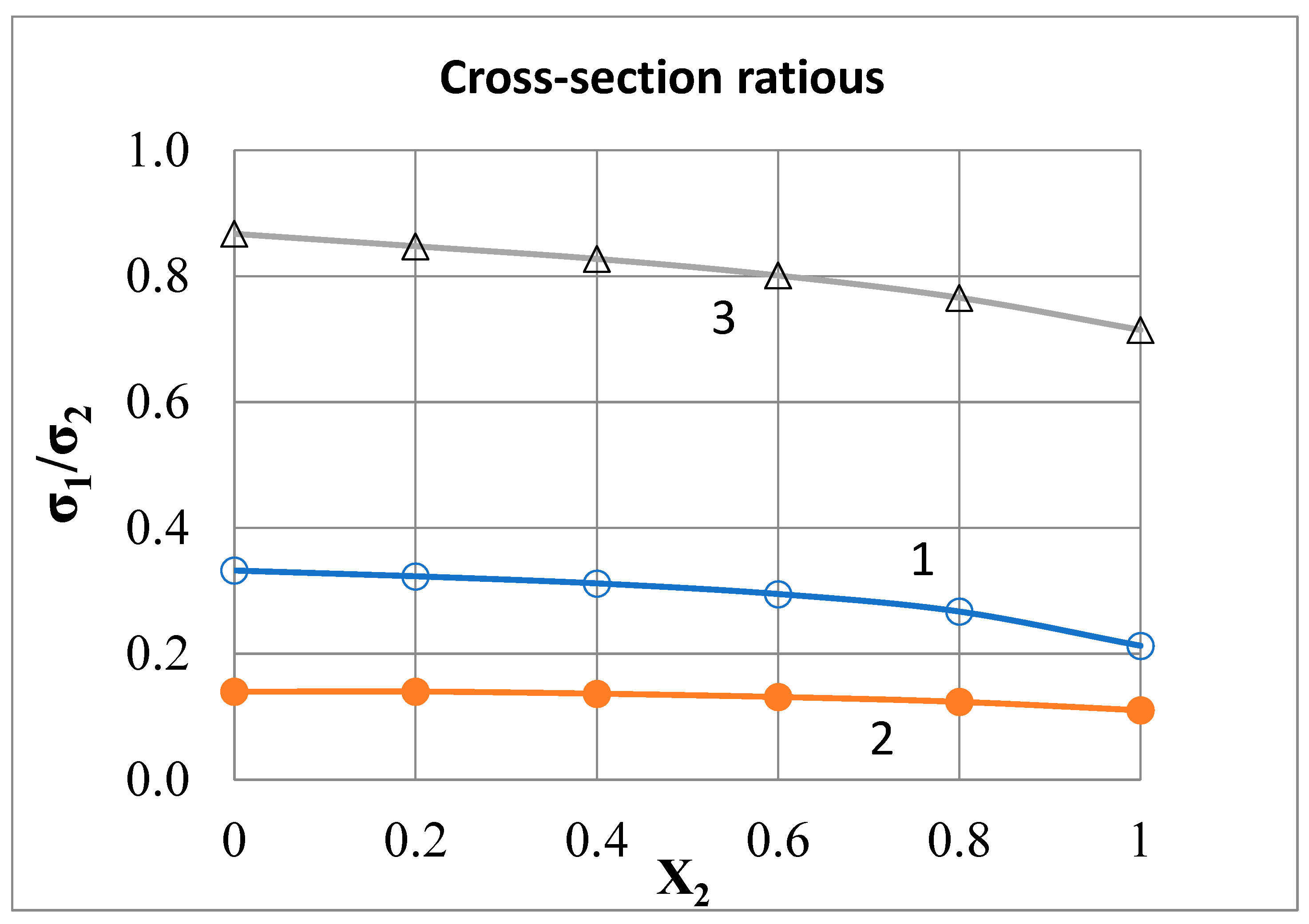
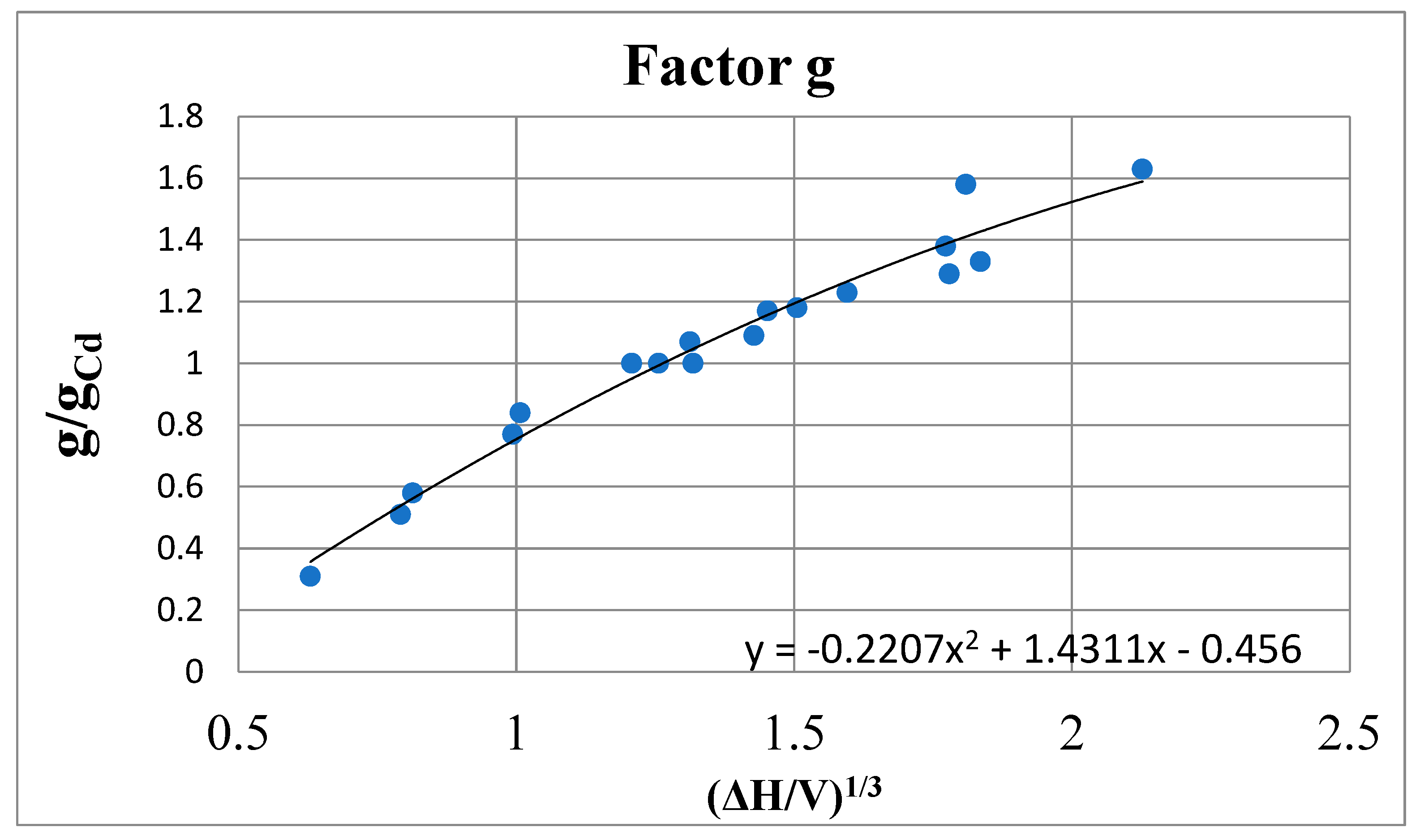
Calculation of the Factor g
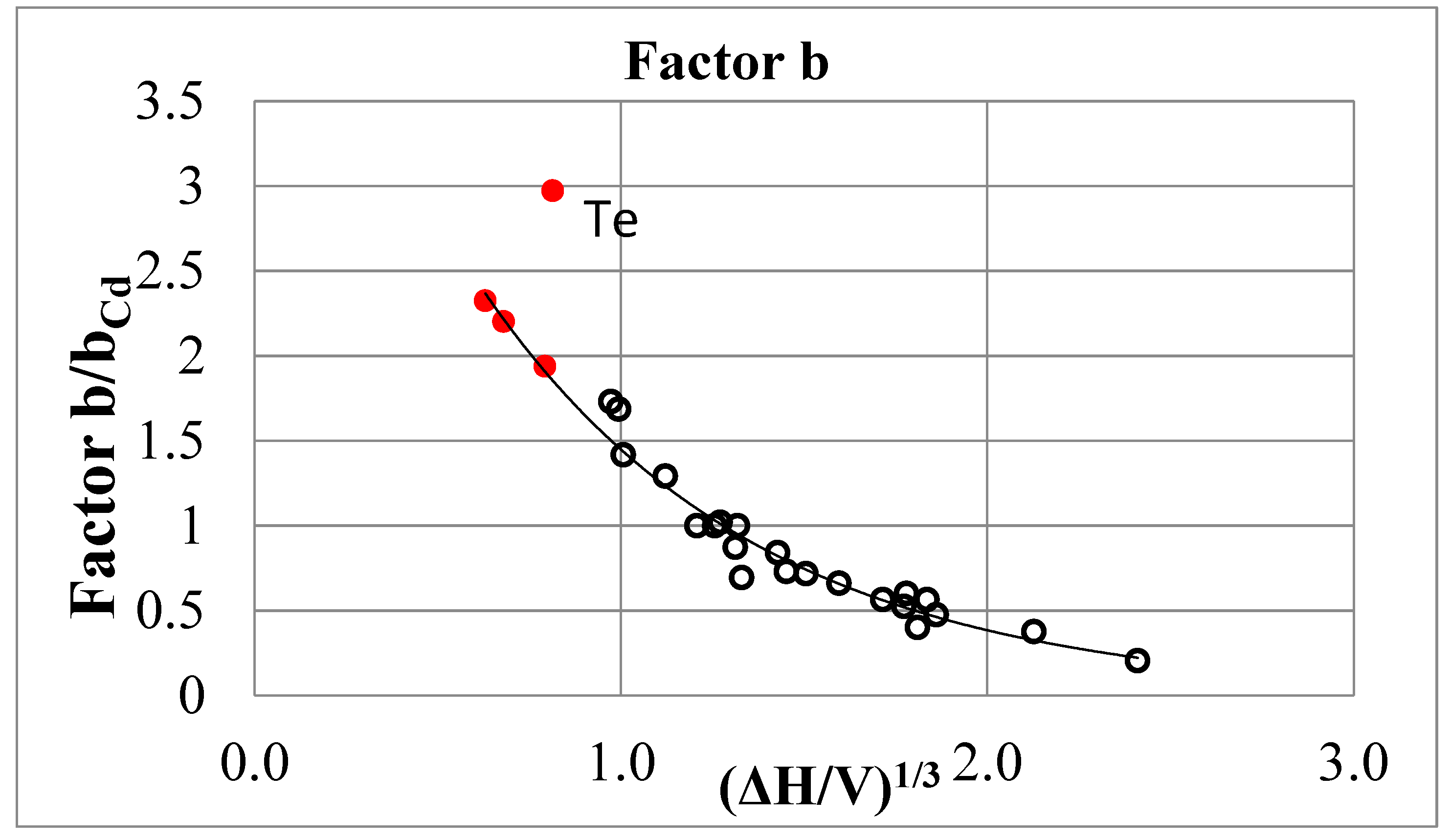
Alternative Variant of the Author
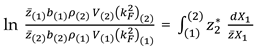
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwarz, K.E. Elektrolytische Wanderung in flüssigen und festen Metallen, Barth, J.A. 1940.
- Seith, W. and Heumann, T. Diffusion in Metallen, Springer: Berlin, 1955.
- Fiks V.B. Ionic Conductivity in Metals and Semiconductors [in Russian], Nauka: Moscow, USSR, 1969.
- Belashchenko, D.K. Transport phenomena in liquid metals and semiconductors [in Russian]. Atomizdat: M., 1970.
- Kuzmenko, P.P. Electrotransfer, thermal transfer and diffusion in metals [in Russian]. Vishcha shkola: Kyiv, 1983.
- Belashchenko, D.K. The Study of liquid metals by the electromigration method [in Russian]. Metallurgy: M., 1974.
- Mikhailov, V.A.; Bogdanova, D.D. Electrotransfer in liquid metals [in Russian]. Nauka: Novosibirsk, 1978.
- Ho P.S.; Kwok T. Electromigration in metals. Rep. Prog. Phys. 1989 52 301-348. [CrossRef]
- Sorbello, R. Theory of Electromigration. J. Physics C: Solid State Physics 1998 51 159-231.
- Kremann, R.; Müller, R. Elektromotorische Krafte, Elektrolyse and Polarisation, 2 Teil. Leipzig, 1931; Handb.der allgemeine Chemie, Bd. 8, S. 616.
- Huntington, H.B.; Grone, A.R. Current-Induced Marker Motion in Gold Wires. J. Physics and Chemistry of Solids 1961 20(1-2) 76-87.
- Verhoeven, J. Electrotransport in Metals // Metallurgical Reviews 1963 8(31) 311-368.
- Belashchenko, D.K. Electrotransfer in liquid metals [in Russian]. Advances in Chemistry (Moscow) 1965 34 530-564.
- Black, J.R. Electromigration—a brief survey and some recent results. IEEE Trans. Electron Devices ED-16 1969 4 338–347. [CrossRef]
- Huntington, H.B. Diffusion in solids: recent developments, Ed. Nowick A.S. and Burton J.J., Academic, New York, 1975 pp.303-352.
- 16 Cher Ming Tan; Arijit Roy. Electromigration in ULSI interconnects. Materials Science and Engineering 2007 58 1–75.
- Yu-chen Liu; Shih-kang Lin. A Critical Review on the Electromigration Effect, the Electroplastic Effect, and Perspectives on Effect of Electric Current upon Alloy Phase Stability. arXiv:1908.01170 [cond-mat.mtrl-sci] (2019).
- Fiks, V.B. On the mechanism of ion mobility in metals [in Russian]. Soviet Phys. - Solid State 1959 1(1) 16-30.
- Fiks, V.B.; Kaganov, M.I.; Lifshits, I.M. On the scattering of an electron by an impurity center [in Russian]. Soviet Phys. - Solid State 1964 6(12) 2723-2731.
- Huntington, H.B. Effect of driving forces on atom motion. Thin Solid Films 1975 25 265–280. [CrossRef]
- Sorbello, R. A pseudopotential based theory of the driving forces for electromigration in metals. J. Physics and Chemistry of Solids 1973 34 937-950. [CrossRef]
- Sorbello, R.S. Electromigration in liquid metal alloys. physica status solidi (b) 1978 86(2) 671 - 678. [CrossRef]
- Drakin, S.I. Transfer and distribution of metal alloy components in an electric field [in Russian]. Russ. J. Phys. Chem. 1953 27 1586-1593.
- Ziman, J.M. A theory of the electrical properties of liquid metals. Philos. Mag. 1961 6 1013-1034. [CrossRef]
- Ziman, J.M. Electrons and Phonons. The Theory of Transport Phenomena in Solids, Oxford University Press, Oxford, 1960.
- Mott, N.F. Electrons in Disordered Structures. Advances in Physics 1967 16 (61) 49-144. [CrossRef]
- Mott, N.F. The electrical properties of liquid mercury. Phil. Mag. 1966 13 989-1014. [CrossRef]
- Kubo, R.A General expression for the conductivity tensor. Canada. J Phys. 1956 34 1274-1277.
- Greenwood, D.A. The Boltzmann Equation in the Theory of Electrical Conduction in Metals. Proc. Phys. Soc. London 1958 71 585-596. [CrossRef]
- Faber, T.E. In: Proc. Int. Coll. on Optical Props and Electronic Structure of Metals and Alloys. 13-16 Sept. 1965. North - Holland Publ., Amsterdam, 1966.
- Fiks, V.B. Dynamic (effective) charge of metal ions [in Russian]. Soviet Phys. - Solid State 1964 6(8) 2307.
- Kharkov, E.I. Relation between the parameters of electrotransfer and electrical resistance of liquid binary alloys [in Russian]. Ukr. Phys. Journal 1966 11 677-678.
- Shaw, R.E. Convection effects during electrotransport of liquid Metals. Doctoral thesis. Iowa State Univ. 1972. [CrossRef]
- Belashchenko, D.K. Electromigration in liquid binary alloys and its connection with electrical resistance [in Russian]. Izv. vuzov. Ferrous Metallurgy 1962 No. 5 120-125.
- Belashchenko, D.K. On the relationship between electrotransport and electrical conductivity of liquid metallic solutions in the Mott model [in Russian]. Russ. J. Phys. Chem. 1970 44 2907-2910. [CrossRef]
- Belashchenko, D.K.; Gushchina, E.I. Application of the electrotransport method for the analysis of electronic states in liquid metallic solutions based on the one-parameter Mott model [in Russian]. Metal Phys. Metallography 1970 30 295-302.
- Drakin, S.I.; Maltsev, A.K. Electrodiffusion in K-Na alloy [in Russian]. Russ. J. Phys. Chem. 1957 31 2036-2041.
- Kremann, R.; Bauer, F.; V o g r i n, A.; Sch e i b e1, H. Uber den Wechsel im Wanderungssinn der Alkali- und anderer Metalle bei der Elektrolyse der betreffenden Amalgame in Abh ä ngigkeit von der Konzentration. Monatsh. für Chemie. 1930 56 35-65. [CrossRef]
- Rudenko, A.G.; Golovinsky, N.P.; Kharkov, E.I. Electrotransfer in the Cd-Zn system [in Russian]. Metal Phys. Metallography 1968 25(3) 560-562.
- Zhmudsky, A.3.; Kharkov, E.I.; Rudenko, A.G. Double inversion of electrotransport in the Al-Zn system in the liquid state [in Russian]. Metal Phys. Metallography 1967 23 559-562.
- Aksenova, L.I.; Belashchenko, D.K. Electrotransport, electrical resistance and density of electronic states in melts of the Na-K system [in Russian]. High Temperature 1971 9 722-730.
- Larson S. et al. Atomic transport in solids and liquids; Proc. Europhysics Conference. Marstrand, Sweden, June 15-19, 1970. Ed. A. Lodding and T. Lagerwall. Tu-12. ISBN 3921015006, 9783921015001.
- Aksenova, L.I.; Belashchenko, D.K.; Pertsin, A.I. Electrotransfer, electrical resistance and density of electronic states in Cs - K and Na - Cs melts [in Russian]. High Temperature 1971 9(6) 1159-1167.
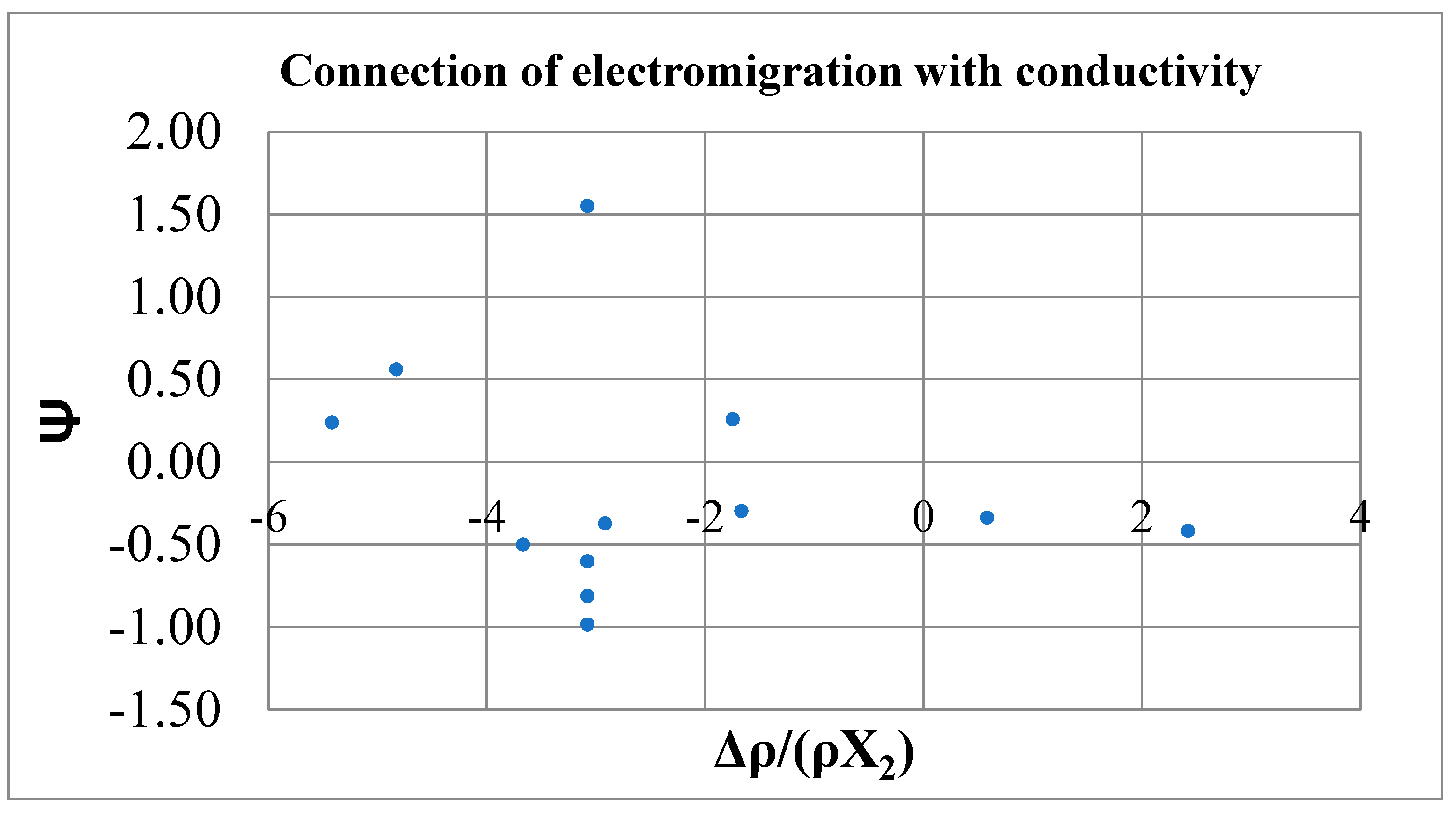
| Impurity | Δρ/c, μΩ. cm/at.% | Δρ/X2ρ1 | V2, cm3/mol | |
| Li | -2.0 | -1.67 | 13.48 | 0.16 |
| Na | 0.7 | 0.58 | 24.8 | -0.22 |
| К | 2.9 | 2.42 | 47.9 | -0.66 |
| Cs | - | - | 11.7 | -2.43 |
| Ag | -3.7 | -3.08 | 29.08 | 0.72 |
| Au | - | - | 9.52 | 0.73 |
| Mg | - | - | 14 | 0.5 |
| Ca | -3.51 | 2.92 | 14 | <0.05 |
| Zn | -4.4 | -3.67 | 18.1 | 0.62 |
| Cd | -3.7 | -3.08 | 19.44 | 0.62 |
| Cd | - | - | 20.9 | 0.83 [33] |
| Tl | -2.1 | -1.75 | 17.3 | 0.0 |
| Pb | -5.8 | -4.83 | 11.8 | 0.0 |
| Bi | -3.7 | -3.08 | 13.48 | -0.69 |
| Sn | -6.5 | -5.42 | 24.8 | 0.33 |
| Triangle | A |
| Cd-Bi-Pb | 1.057 ± 0.04 |
| Sn-Bi-Pb | 1.077 |
| Cd-Sn-Bi | 0.99 |
| Ag-Cu-Sn | 0.98 ± 0.03 |
| Ag-Cu-Ge | 1.03 ± 0.03 |
| K-Na-Cs | 0.97 ± 0.12 |
| Cd-In-Tl, everywhere | 0.995 |
| Cd-In-Tl, in Tl, 5 in Cd and In, linearly depends on the concentration | 1.043 |
| Cd-In-Tl, in Tl, 3 in Cd and In, linearly depends on the concentration | 1.053 |
| Cd-In-Tl, everywhere | 1.092 |
| Cd-In-Tl, in Tl, 1 in Cd and In, linearly depends on the concentration | 0.927 |
| Cd-In-Tl, everywhere | 0.930 |
| Hg-In-Tl, everywhere | 0.991 0.03 |
| Metal | T, oC | g/gCd [6] | b/bCd | ΔHsubl, kcal/mol | Vmol, cm3/mol | ΔHsubl/V |
| Cs | 110 | 0.31 | (10.41) | 17.97 | 72.2 | 0.249 |
| K | 110 | 0.51 | (3.84) | 20.95 | 42.35 | 0.496 |
| Te | 500 | 0.58 | (2.97) | 11.9 | 22.15 | 0.538 |
| Hg | 300 | 0.77 | 1.69 | 14.54 | 14.67 | 0.981 |
| Na | 250 | 0.84 | 1.42 | 25.0 | 24.50 | 1.02 |
| Cd | 300-500 | 1.00 | 1.00 | 24.54 | 14.07 | 1.76 |
| Bi | 300-500 | 1.00 | 1.00 | 41.05 | 20.8 | 1.98 |
| Pb | 300-500 | 1.00 | 1.00 | 45.44 | 19.08 | 2.29 |
| Tl | 350 | 1.07 | 0.87 | 40.8 | 18.08 | 2.26 |
| Zn | 500 | 1.09 | 0.84 | 28.56 | 9.82 | 2.91 |
| Sb | (500) | 1.17 | 0.73 | 57.5 | 18.8 | 3.06 |
| In | 350 | 1.18 | 0.72 | 55.56 | 16.32 | 3.41 |
| Sn | 300-500 | 1.23 | 0.66 | 68.77 | 16.96 | 4.06 |
| Ga | 300 | 1.29 | 0.60 | 64.4 | 11.44 | 5.63 |
| Al | 580 | 1.33 | 0.57 | 67.8 | 10.96 | 6.18 |
| Ag | 1100 | 1.38 | 0.53 | 63.3 | 11.36 | 5.57 |
| Ge | 1100 | 1.58 | 0.40 | 78.2 | 13.2 | 5.92 |
| Cu | 1100 | 1.63 | 0.38 | 72.8 | 7.57 | 9.62 |
| Li | - | 1.20 | 0.69 | 32.2 | 13.72 | 2.35 |
| Rb | - | 0.42 | 5.67 | 18.11 | 57.9 | 0.313 |
| Au | - | 1.33 | 0.57 | 84.6 | 16.8 | 5.04 |
| Be | - | 2.21 | 0.20 | 74.1 | 5.3 | 14.0 |
| Mg | - | 0.99 | 1.02 | 31.5 | 15.33 | 2.05 |
| Ca | - | 0.88 | 1.29 | 38.6 | 27.4 | 1.41 |
| Ba | - | 0.76 | 1.73 | 35.7 | 38.7 | 0.92 |
| Si | - | 1.45 | 0.48 | 71 | 11.2 | 6.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).