1. Introduction
Linear quadratic Gaussian (LQG) control problem stems from the optimal stochastic control theory of the systems with additive Gaussian white noises and state/control-dependent, which combines the concept of linear quadratic regulators for full state feedback and Kalman filters for state estimation [
1,
2,
3]. Recently, the optimal LQG control has been applied in various fields, such as the robots of power substation, all-electric vehicles, electrical safety engineering networked control systems (NCSs) [
5,
6,
7,
9]. Specificly, for mobile monitoring robot in a ultrahigh-voltage power substation, the LQG conotrol is proposed to minimize the difference between the actual SNIR and its expectation and the change in transmitting power[
4]. These motivate us to study the more complicated LQG control systems with multiple input delays and multiplicative noises.
It is generally known that random time delay and packet dropout always occur in the data transmission of NCSs. Many literatures have been investigated on LQG control problems with input delays and packet loss [
8,
10,
11,
12,
13,
14]. Basin [
8] presented an optimal linear regulator (LQR) with input delay by using the duality principle. Cacace[
10] studied the LQG problems for linear system with single input delay. Matni[
11] presented an explicit solution to a two-player distributed LQG problem in which communication between controllers occurs across a communication link with varying delay. Basin[
12] further established a necessary and sufficient condition of the optimal LQR control for the linear system with multiple input delays. Zhang[
14] studied the classical LQR problem with multiple input delays for both continuous-time and discrete-time cases.
On the other hand, packet dropout is generally described as the multiplicative noises. Many references have focused on the LQG system with multiplicative noises [
15,
16,
17]. Gupta[
15] solved the optimal LQG problem with packet-dropping links by decomposing the problem into a standard LQR state-feedback controller designing. Liang[
16] studied the optimal control and stabilization problems for NCSs with remote controller and local controller subject to packet dropout. For systems with both input delay and packet dropout, Liang[
18] presented the optimal LQR controller, and derived the necessary and sufficient condition for the mean-square stabilization. Liang[
19] considered the discrete-time LQG system with input delay and multiplicative noises, and obtained both optimal state feedback controller and suboptimal output feedback controller.
The aforementioned literatures are mainly focused on single delay and packet dropout. To our best knowledge, little progress has been made on the optimal LQG control for time-varying systems with multiple input delays and multiplicative noises.
Motivated by the work of [
18,
19,
20], this paper studies the optimal LQG control for discrete time-varying system involving with multiple delays and multiplicative noises. The main contributions of this paper are summarized as follows: 1) When the state variables can be observed exactly, by introducing the stochastic maximum principle for system with multiple delays and multiplicative noises, a solution to the forward backward differential equations (FBSDEs) is obtained based on the coupled Riccati equations. 2) In terms of the solution to the FBSDEs, a necessary and sufficient condition is given for the optimal LQG control. 3) When the state variables are partially observed, we derive a suboptimal linear output feedback controller by linearizing the optimal estimator and neglecting higher order terms.
The rest of the paper is organized as follows. In
Section 2, we give the results of optimal state feedback control problem. In
Section 3, we derive a suboptimal linear output feedback controller for the LQG systems involving multiple input delays and multiplicative noises. Numerical examples are provided in
Section 4. Conclusions are given in
Section 5.
Notation: denotes the n-dimensional real Euclidean space. I presents the unit matrix of appropriate dimension. The superscript denotes the transpose of the matrix. denotes a complete probability space on which random variable are defined such that is the natural filtration generated by and , i.e., , augmented by all the null sets in . A symmetric means that it is a positive definite (positive semi-definite) matrix. represents the trace of matrix A.
2. State Feedback Controller
When the state variable
can be observed exactly, we consider the following discrete time-varying LQG system with multiple input delays and multiplicative noises
where
is the state,
is the input control with the delay
,
is the scalar white noise with zero mean and variance
,
is the random variables satisfying
and
.
and
with
are coefficient matrices with compatible dimensions.
and
are correlated with
,
,
. The initial state
,
for
are known.
The associated cost function for system (
1) is given by
where
and
are positive semi-definite constant matrices with appropriate dimensions, control cost matrix
should be positive definite matrix, and
N is the horizon length.
Problem 1. Find the unique -measurable state feedback controller , for , to minimize (2) subject to (1).
For simplicity, we make the following definitions
for
. Then the system (
1) becomes
Following the similar discussion of [
19], in virtue of the Pontryagin’s maximum principle for (
3) and (
2), we have
for
, where
is the costate with
for
.
For further study, the following coupled Riccati difference equations are given:
where
with
The terminal values are given by
Remark 1. As can be seen that the costate equations (4)-(6) are quite different from those of Liang [19] and Zhang [20]. What’s more, the coupled Riccati equations (7)-(13) are more complicated than those in Liang [19] and Zhang [20].
It is stressed that the key to solve the optimal LQG control problem is to obtain the solution to the FBSDEs (
3) and (
4)-(6). We now show the solution to the FBSDEs in the following lemma.
Lemma 1.
Supposing that are positive definite for , the following equation
is the solution to FBSDEs (3) and (4)-(6), with
where and for . Besides, , satisfy the coupled equations (7), (12), (13).
Now we are ready to present the solution to Problem 1.
Theorem 1.
There exists the unique -measurable for Problem 1 if and only if , for , are positive definite. In this case, the optimal controller is given by
The associated optimal performance index is as
where , , , , , , satisfy the coupled equations (7)-(13),(16),(17) and , for .
Remark 2.
We make the coefficients of the system (3) and the cost function (2) to be time-invariant. When there is no time delay in system (3), i.e., , we have that . Considering the noise-uncorrelated case with , it is obviously obtained that the coupled equations (10) and (12) can be rewritten as
Substituting and into (11) and (13), it can be derived that for . Then the difference equations (8) and (9) yield to
The optimal controller reduces to
which is exactly the result of Moore[2].
Remark 3.
When the system (3) is a time-invariant system, (3) can be rewritten as
with , , . The performance index becomes
By using the results of Theorem 1, the optimal time-invariant LQG controller yields that
and the minimal cost function is as (19) where the coefficient matrices in , , , , are time-invariant.
In view of obtaining the special case of optimal LQG control for system (
3), now we shall show the results for the general system with multiple delays and multiplicative noises.
Consider the following general discrete time-varying system
and the cost function is as (
2).
Problem 2. Find the unique -measurable state feedback controller , for , to minimize the cost function (2) subject to the system (20).
Combining the system (
20) and the cost function (
2), we apply the Pontryagin’s maximum principle to yield the following costate equations:
with
for
, and
for
.
We introduce the following coupled Riccati equations subject to the system with multiple deleys:
for
, where the terminal value is as (
14).
Now we give the main results for Problem 2 in the following theorem.
Theorem 2.
There exists the unique -measurable for Problem 2 if and only if , for , are positive definite. In this case, the optimal controller is calculated by
where
and the optimal cost is as
where for .
In addition, the relationship of the optimal costate and state is as (16) in Lemma 1.
Proof. The proof is similar to that of Theorem 1, and to save the space of the paper, we omit it here. □
3. Output Feedback Controller
When the state variable
are partially observed, we study the following discrete-time stochastic system:
where
is the measurement,
is the scalar white noise with zero mean and variance
,
and
are Gaussian zero-mean white noises with covariance
and
.
and
are deterministic matrices with compatible dimensions. In this case, the initial value
is known,
,
,
and
are independent of each other.
Obviously, there exist multiplicative noises
and
in system (
29). As we can not obtain the exact information of the state by (
29), we introduce the state estimation to design the controller instead. We first obtain the linear optimal state estimator for by applying standard filtering results in [
3]. Then, we will derive the suboptimal linear state estimate feedback controller through the following linearizations.
The aim of this section is to find the suboptimal linear state estimate feedback controller for system (
29) in order to minimize the cost function (
2).
First, we introduce the linear optimal state estimator in Lemma 2.
Lemma 2.
Based on the system (29) with input delays and multiplicative noises, the linear optimal estimator is given by
where
Besides, the estimator error covariance matrix is
The initial values and .
Now, the state estimation is obtained, and we can consider (
30) as the state instead of the unavailable exact state information. Observing (
3) and (
30), we know that the filter gain
on
should be affine, so that we can apply the results of Theorem 1 in this section. Then, we will linearize the filter gain
.
Applying first order of Taylor expansion on
through the fixed point
, the linearization of
yields
Ignoring the quadratic and higher order terms in (
31), and plug (
30) into it, the approximation of
becomes
With (
30)-(
32), the cost function (
2) can be reorganized as
In this case, the coupled Riccati equations can be derived as
where
with
, with the terminal values
and
where
with the initial value
.
Now, we can find the suboptimal controller to minimize the cost function (
33) subject to (
29), by the results of Theorem 1.
Theorem 3.
The suboptimal linear state estimate feedback controller for system (29) that minimizes the cost function (33) is given by
The minimized cost function is given by
4. Numerical examples
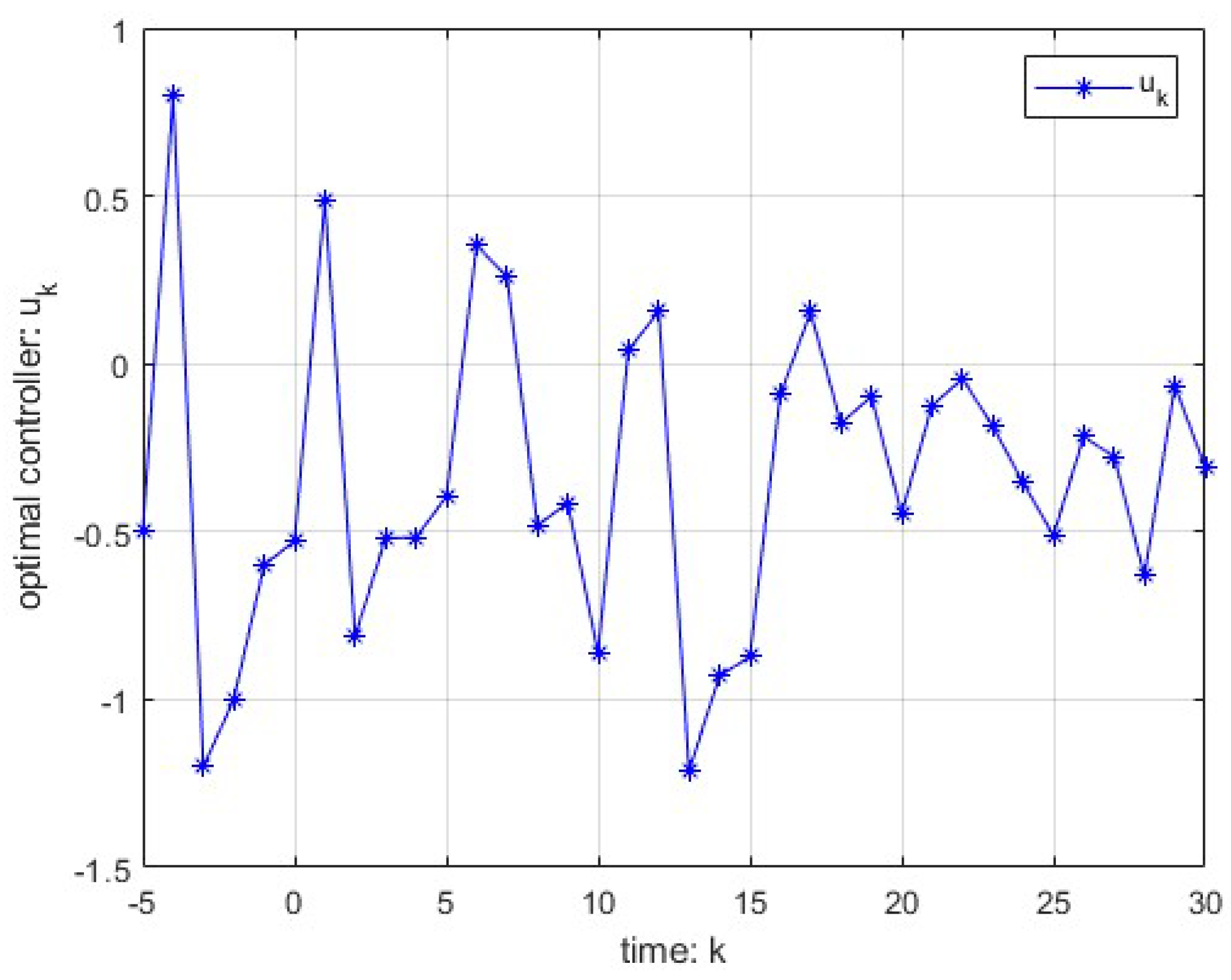
Example 1 Consider the scalar case of time-invariant LQG control system (
3) in Remark 3. We consider the case that the additive noise
is the zero-mean white noise. The associate parameters are as
with the initial values
and the cost function (
2) with
. When the delay
, and
, by applying Theorem 1 and the equations (
7)-(13), direct calculations yield that
for
. It can be obviously known that
is positive definite for
. Thus, there exists a unique
from Theorem 1, and the optimal controller can be calculated with (
18), which is shown in
Figure 1.
Accordingly, the associated optimal value of (17) is =107.5150.
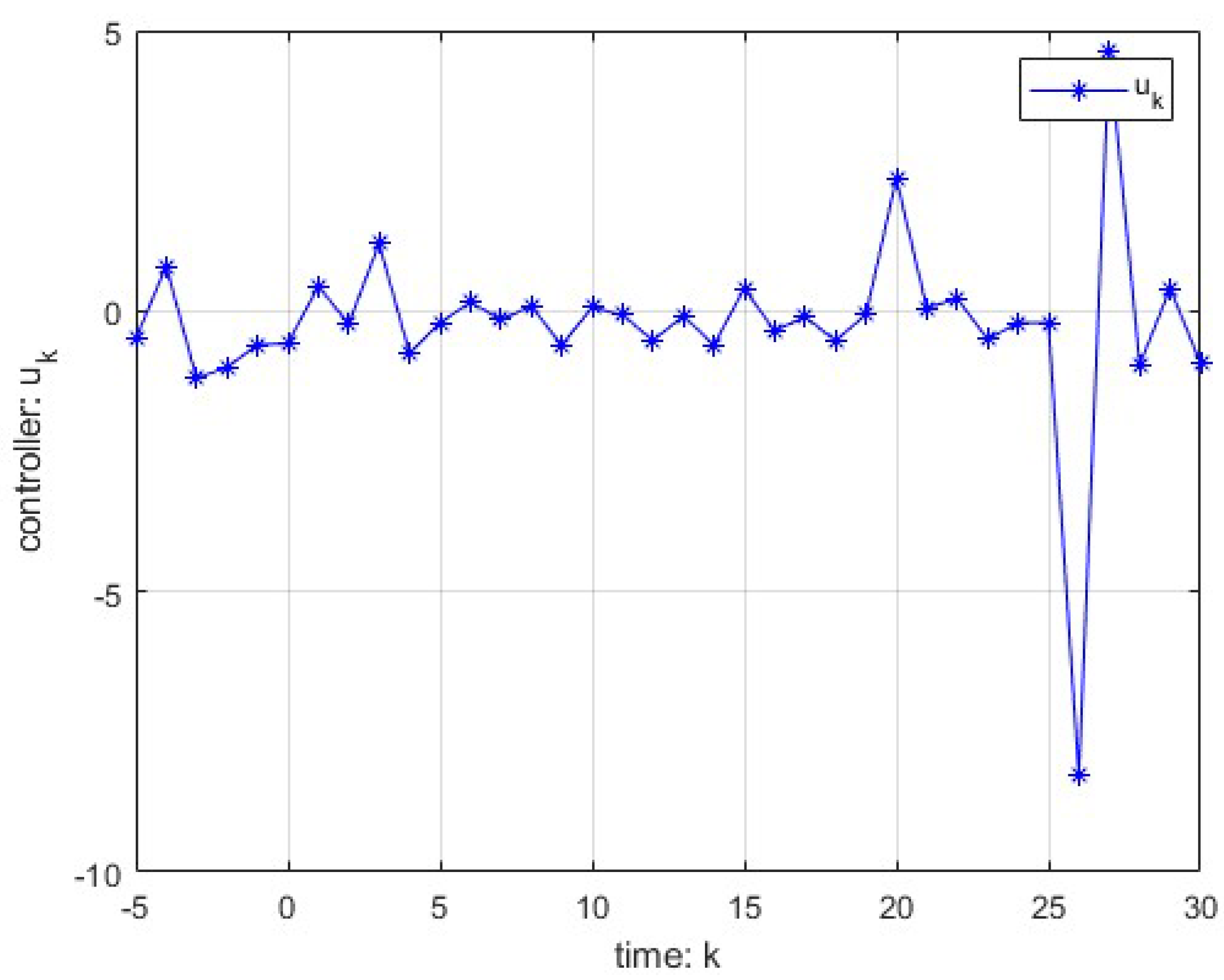
In order to illustrate that the proposed LQG controller can minimize performance index, let us consider the time-invariant standard state feedback controller
. Based on the above parameters and by substituting into cost function, the controller
are shown in
Figure 2, and the associated value is
=255.0603, which confirmed the effectiveness of the algorithm.
Example 2 Consider the discrete time-varying LQG control system with multiple delays and multiplicative noises with
,
, and the cost function (
2). The associate coefficients are:
When the delay time is
and the final time is
, given the initial value
by applying Theorem 1 and (
8)-(13), it yields that
For
,
, thus, there is an optimal solution to the LQG system with multiple delays and state/control noises from Theorem 1. Based on the above data, the optimal controller can be calculated as
According to (17), the optimal performance index of system (
3) is
.
5. Conclusions
In this paper, the discrete time-varying optimal linear quadratic Gaussian (LQG) control problem involving multiple delays and state/control- dependent noises has been studied. A necessary and sufficient condition for the existence of unique optimal controller to the problem is given, which is based on the obtained maximum principle and the relationship between the state and costate. Under this context, the optimal controller and the minimized performance index are represented. What’s more, as the state variables observed partially, the suboptimal linear state estimate feedback controllers for the LQG models with input delays and multiplicative noises are derived.
Author Contributions
Conceptualization, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; methodology, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; validation, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; formal analysis,Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; investigation, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; resources, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; data curation, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; writing—original draft preparation, Qiyan Zhang and Chunyang Sheng; writing—review and editing, Qiyan Zhang, Chunyang Sheng, Xiao Lu and Haixia Wang; funding acquisition, Chunyang Sheng, Xiao Lu and Haixia Wang. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (62273213, 62073199, 62103245, 62203280), Natural Science Foundation of Shandong Province for Innovation and Development Joint Funds (ZR2022LZH001), Natural Science Foundation of Shandong Province (ZR2020MF095, ZR2022MF341), Taishan Scholarship Construction Engineering.
Data Availability Statement
The data of this study is included within the article.
Conflicts of Interest
The authors declare no conflict of interest with respect to the research, authorship, and/or publication of this article.
Appendix A The proof of Lemma 1
Utilizing the maximum principle (
4)-(6) to system (
3) with cost function (
2). We can obtain for
,
With (9)-(11), the optimal controller
is as
From (
4)-(6), we also have
Substituting (
7), (12) and (13),
yields
We have verified (
15) for
. Assuming that
are as (
15) for all
with
, then we will show that (
15) also holds for
. Set
to be optimal for all
, with equations (
3) and (
15),
can be calculated as
Insert
to (5), (5) will become
Thus, the optimal controller is given by
for
. Using the equations (
3),(5) and (
A1),
yields that
which implies that (
15) holds for
.
Analogy with the method, assuming that
are as (
15) for all
, and we will verify that (
15) also holds for
. As
is calculated as (
A1), then for
, (6) will be obtained
where
After inserting (
3) and (
A2), and combing like terms, we can summarize that
Now, the optimal controller for
is obtained as
In the same way, substituting
into (5), we can also prove that
This completes the proof of the lemma.
Appendix B The proof of Theorem 1
"Necessity": Suppose there exists the unique
-measurable
to make the cost function (
2) minimized. We will show by induction that
are positive definite and the optimal controller can be designed as (
15). Define
for
, and when
the above equation becomes
Using (
3), we can obviously know that the uniqueness of the optimal controller only depends on whether
. Then setting
, and
,
can be presented as
We know that
is expressed as a quadratic function of
, and as there is a unique solution for system (
3), then
, it follows that
, i.e.
is positive definite for
. In order to accomplish the proof, we assume
for all
. Then we will prove that
. With (
3), (5) and (6), for
, we construct that
Adding from
to
on both sides of the above equation in order to get the form of
, we have
Using (
2), it yields that
Setting
,
as same as the condition
. And plugging (
16) into (
A4), we obtain
Similarly to the case above, we obviously get for all . This ends the proof of necessity.
"Sufficiency": Suppose
for
is true, we will show the uniqueness of the
-measurable
to minimize (
2). Denoted by
First, for
, using the equivalent substitution
,
, and
, we calculate as follows
Construct the equation
, then we have
Denote
and by virtue of (
A6) and (
7)-(13), and adding from
to
on both sides of (
A5), then we get
Then the cost function (
2) becomes
As
, the unique optimal controller must match the condition
. In this case, the cost function (
2) will be the minimum, i.e., the optimal controller is
and the optimal cost is as (
19).
Above all, the proof of sufficiency is completed.
Appendix C The proof of Lemma 2
By applying standard filtering results in [? ], we can obtain the linear optimal estimator for system (
29) as follows.
In view of the jointly gaussian nature of
and
, we know
Using (
29) and the orthogonality of
and
, the covariance matrixes yield
where
is independent of
with zero mean,and the error covariance matrix
Substituting above equations into (
A8), it becomes
with
The proof of Lemma 2 is completed.
References
- H. Kwakernaak, Optimal filtering in linear systems with time delays, IEEE Transactions on Automatic Control, vol. 12, no. 2, pp. 169-173, 1967. [CrossRef]
- J. B. Moore, X. Y. Zhou, A. E. B. Lim, Discrete time LQG controls with control dependent noise, Systems and Control Letters, vol. 36, no. 3, pp. 199-206, 1999. [CrossRef]
- B. D. O. Anderson, J. B. Moore, Optimal filtering, Courier Corporation, 2012.
- W. Sun, K. Wei, Z. Liu, et al, Linear quadratic gaussian control for wireless communication reliability for a mobile monitoring robot in a UHV power substation, IEEE Systems Journal, 2022.
- A. Kalbat, Linear quadratic gaussian (lqg) control of wind turbines, 2013 3rd International Conference on Electric Power and Energy Conversion Systems, pp. 1-5, 2013.
- X. Yu, X. Liu, X. Wang, et al, Vibration control of improved LQG for wheel drive electric vehicle based on uncertain parameters, Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, vol. 235, no. 8, pp. 2253-2264, 2021. [CrossRef]
- A. Florescu, A. Bratcu, I. Munteanu, et al, LQG optimal control applied to on-board energy management system of all-electric vehicles, IEEE Transactions on Control Systems Technology, vol. 23, no. 4, pp. 1427-1439, 2014. [CrossRef]
- M. Basin, J. Rodriguez-Gonzalez, R. Martinez-Zuniga, Optimal control for linear systems with time delay in control input, Journal of The Franklin Institute, vol. 341, no. 3, pp. 267-278, 2004.
- E. G. Strangas, G. Clerc and H. Razik,and A. Soualhi, Electrical safety-engineering of renewable energy systems, Wiley Press, 2021.
- F. Cacace, F. Conte, A. Germani, Memoryless approach to the LQ and LQG problems with variable input delay, IEEE Transactions on Automatic Control, vol. 61, no. 1, pp. 216-221, 2015. [CrossRef]
- N. Matni, J. C. Doyle, Optimal distributed LQG state feedback with varying communication delay, 52nd IEEE Conference on Decision and Control, pp. 5890-5896, 2013.
- M. Basin M, J. Rodriguez-Gonzalez, Optimal control for linear systems with multiple time delays in control input, IEEE Transactions on Automatic Control, vol. 51, no. 1, pp. 91-97, 2006.
- X. Lu, N. Wang, Q. Qi, et al, Further Study on Networked Control Systems with Unreliable Communication Channels, International Journal of Control Automation and Systems, vol. 19, no. 2, pp. 1-10, 2020.
- H. Zhang, G. Duan, L. Xie, Linear quadratic regulation for linear time-varying systems with multiple input delays, Automatica, vol. 42, no. 9, pp. 1465-1476, 2006. [CrossRef]
- V. Gupta, B. Hassibi, R. M. Murray, Optimal LQG control across packet-dropping links, Systems and Control Letters, vol. 56, no. 6, pp. 439-446, 2007. [CrossRef]
- X. Liang, J. Xu, Control for networked control systems with remote and local controllers over unreliable communication channel, Automatica, vol. 98, pp. 86-94, 2018. [CrossRef]
- X. Chen, Y. Zhu, Uncertain random linear quadratic control with multiplicative and additive noises, Asian Journal of Control, vol. 23, no. 6, pp. 2849-2864, 2021. [CrossRef]
- H. Zhang, L. Li, J. Xu, et al, Linear quadratic regulation and stabilization of discrete-time systems with delay and multiplicative noise, IEEE Transactions on Automatic Control, vol. 60, no. 10, pp. 2599-2613, 2015.
- X. Liang, J. Xu, H. Zhang, Discrete-time LQG control with input delay and multiplicative noise, IEEE Transactions on Aerospace and Electronic Systems, vol. 53, no. 6, pp. 3079-3090, 2017. [CrossRef]
- X. Liang, J. Xu, H. Zhang, Optimal control and stabilization for networked control systems with packet dropout and input delay, IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 64, no. 9, pp. 1087-1091, 2016. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).