Hybrid Source Multi-Port Quasi-Z-Source Converter with Fuzzy Logic-Based Energy Management

Preprint

Article

Hybrid Source Multi-Port Quasi-Z-Source Converter with Fuzzy Logic-Based Energy Management

Altmetrics

Downloads

179

Views

Comments

A peer-reviewed article of this preprint also exists.

Gorkem Say^*

Seyed Hossein Hosseini,Parvaneh Esmaili

Gorkem Say^*

Seyed Hossein Hosseini,Parvaneh Esmaili

This version is not peer-reviewed

Submitted:

16 May 2023

Posted:

16 May 2023

You are already at the latest version

Alerts

Abstract

In this paper, a fuzzy logic-based energy management system and multi-port quasi-z-source converter are proposed that utilizes hybrid renewable energy sources. The system ensures that each energy source module can be used individually by employing fuzzy logic to define power modes. This approach also helps prevent switching losses resulting from extra switching of the source modules. Also, the proposed energy management does not have a mathematical model, so applicability is simple and it is suitable for different multiple input topologies. The Mamdani fuzzy inference system can be designed to capture the nonlinear behavior of the system because of the linguistic rules. Moreover, by adopting the quasi-z-source network to the end of the multi-port converter, the switching losses of the multi-port modules have been significantly reduced. The simulation results are obtained using MATLAB Simulink, and the experimental results are obtained by connecting the circuit to MATLAB Simulink via an Arduino Due.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Over the past two decades, renewable energy sources have gained significant importance due to the energy crisis, wars, and environmental factors. As a result, sustainable systems are required in every industry. Although renewable sources have low output power, different sources can be connected to boost the output power. Multiple input converters have the ability to connect more than one power source to each other. In some specific applications, it is not enough to connect multiple sources together, and it requires a direct power flow of each source to manage energy circulation under certain conditions. For instance, photovoltaic (PV) array output power is decreased under dark conditions, and it is mandatory to add another power source to meet the load demand.

Another parameter to consider is the source type. In the literature, there are numerous types of multiple-input converters. In [1], the authors explained the combinations and rules of multiple input converters. Different connection methods of several types of sources have been shown in this paper. Some basic rules, such as parallel voltage sources, cannot be connected to each other if voltage levels are different. Furthermore, in some specific converters, more than one source cannot supply power simultaneously. Nejabathkhah proposed a hybrid input source connected via a novel three-input DC-DC converter [2]. The sources have the ability to supply power simultaneously, and a battery can be connected as a source to give a bidirectional power flow. Moreover, a small-signal model was obtained for controlling the sources. In [3], multiple inputs are connected via switches to the load using coupled inductors, and the circuit configuration is simple compared to other converters. However, only one source can transfer energy at the same time. In [4], the authors proposed a multiple-input topology with parallel connection type via switches. In this paper, all of the inputs share an inductor, and active switches have the ability to achieve Zero Current Switching (ZCS) by using the switching strategy presented in the paper. On the other hand, the power flow is only in one direction. In [5], the authors proposed a converter with a galvanically isolated system. It has two bridges at the primary and secondary sides of the transformer, and the power flow is controlled. The current capacity of the sources should be equal because of the series connection of the sources [5].

Three sources multiple input converter is proposed in [6]. The converter’s application area is electric vehicles with fuel cells, PV arrays, and battery units. The limitation of the converter is that it has three inputs [6]. A three-Port DC-DC converter is proposed in [7]. It has a high step-up ratio with reduced voltage stresses. Moreover, the power is bidirectional and has the ability to charge the battery with the load and other sources. Besides, the maximum input source number is three [7]. The presented converter in [8] proposes DC-DC multiport converter with Dual active bridges. The modules are connected as a ring type. One of the advantages is that the structure is bidirectional. The authors in [9] proposed a dual-input dual-output bidirectional multiport dc–dc converter. One of the sources is the battery storage system, which has a low voltage stress on semiconductor switches. However, it has only two inputs and it is not clear if MPPT can be achieved from other sources. In [10], the authors proposed a multi-port converter with multiple outputs where sources can deliver the power simultaneously. In the next paper, a non-isolated multiple source converter is proposed, and the step-up ratio is higher compared with other non-isolated topologies [11]. In this paper, the authors have considered the normalized voltage stress on switches and diodes. Moreover, the number of sources can be increased, and voltage gain will be increased depending on the source count. The same author proposed a new version of [11] in reference [12]. The voltage gain in this paper is higher, where the component number and voltage stress are decreased compared to [11]. Power flow can be simultaneous or individual in both references.

The Z-Source topology can exceed the limitations of traditional V-I source power converters and consists of x-shaped two capacitors and two inductors. Because of the structure, shoot-through mode is not forbidden and this brings one more control axis to increase the output voltage without damaging the components [13]. In [14], an improved z-source converters is proposed to decrease z-source converters disadvantages but it still has discontinuous input current. Besides, capacitor voltage and inductor current surge has been reduced and inrush current is limited. To make a common ground for the z-source topology, a common grounded z-source converter is proposed in [15]. It brings low stress on semiconductors and decreases the component sizes but impedance network capacitors are still large to obtain high voltage. The authors in [16], proposed a quasi-z-source converter that obtains lower voltage stress on components and continuous input current but it has lower voltage gain compared with a common grounded z-source. The proposed converter in [17], offers a new quasi-z-source converter with increased component numbers. The converter has a high-boost performance with different combinations. In addition, the converter has problems such as large voltage spikes. In [18], the authors proposed a multi-input quasi-Z-source converter that combines different power sources by implementing an auxiliary circuit. However, the operation range is not wide and the design is not simple. Moreover, switches are faced with high current stress.

The paper [19] provides a comprehensive review of different energy management system strategies, including the key factors, methods, and functions involved. However, experimental tests haven’t been done to show system performance under real-world conditions. The authors of several papers, including [20,21,22,23,24], have used fuzzy logic as an energy management system, which has the advantage of not requiring a mathematical model of the system, making it easier to control. The paper [25] focuses on optimizing hydrogen consumption while considering battery degradation. But the system complexity and application area can limit the feasibility of the proposed energy management system. [26] proposes a maximum efficiency range recognition-based energy management control system that controls fuel cell consumption and power flow between two sources using methods such as sequential quadratic programming algorithm (SQP) and equivalent consumption minimum strategy (ECMS). But the estimation of equivalent factors in ECMS can be influenced by the specific characteristics of the driving cycle being analyzed. The paper [27] uses instantaneous optimization and mathematical equations to explain the structure assumptions. Besides, the proposed approach may not be easily applicable to situations with stochastic demands, and the authors acknowledge that while the locally optimal solution it provides can be effective, it may not be the globally optimal control policy. In [28], a multi-agent-based energy management system is proposed, with three different levels, each with unique duties. However, As dealing with complex decision problems, MAS-based energy management strategy may exhibit inadequate real-time performance in decision-making The paper [29] introduces adaptive neuro-fuzzy inference systems for power management, using a three-phase inverter as a converter type. However, this approach requires data sets from the learning part of the system history. [30] proposes an adaptive droop control method for power management using battery, supercapacitor, and fuel cell hybrid sources, although large-scale operations can pose challenges to the control strategy. [31] uses a hybrid power storage system and a model predictive method for control strategy, predicting future output power based on historical data and applying a dynamic algorithm to the management strategy. Attaining high performance through this method requires accurate system models, as well as information about future driving conditions. The authors in [32] published a case study for energy management systems that included PV, batteries, and grids as hybrid sources. A traditional DC-DC bidirectional converter was used for the battery pack. However, this system has some disadvantages, such as limited application areas. The sliding-mode energy management strategy was proposed in [33] with the nonlinearity of the double integral. In addition, several technical challenges may arise as a result of connecting renewable sources to the power grid.

This study discusses the fuzzy logic-based energy management system of a hybrid source multi-port quasi-z-source converter, which includes PV, wind turbine, and battery sources. In addition, the mathematical model of the quasi-z-source multi-port converter, simulations of the entire system, and experimental results are presented. The proposed system can manage energy flow from the sources without complex control algorithms because of the Fuzzy logic. One of the biggest features is the modularity of the power management, in other words not only source number can be increased but also the source types can be changed. Moreover, by setting up the quasi-z-source network to a multi-port converter, the voltage gain is increased and the voltage stress of the input module switches is decreased.

This study is divided into several sections. Section 2 discusses the multi-port quasi-z-source converter. Section 3 explains the proposed fuzzy-logic-based energy management system. Section 4 and Section 5 present simulation and experimental results, respectively. In Section 6, a discussion of the results is presented. Finally, conclusions are included in section 7.

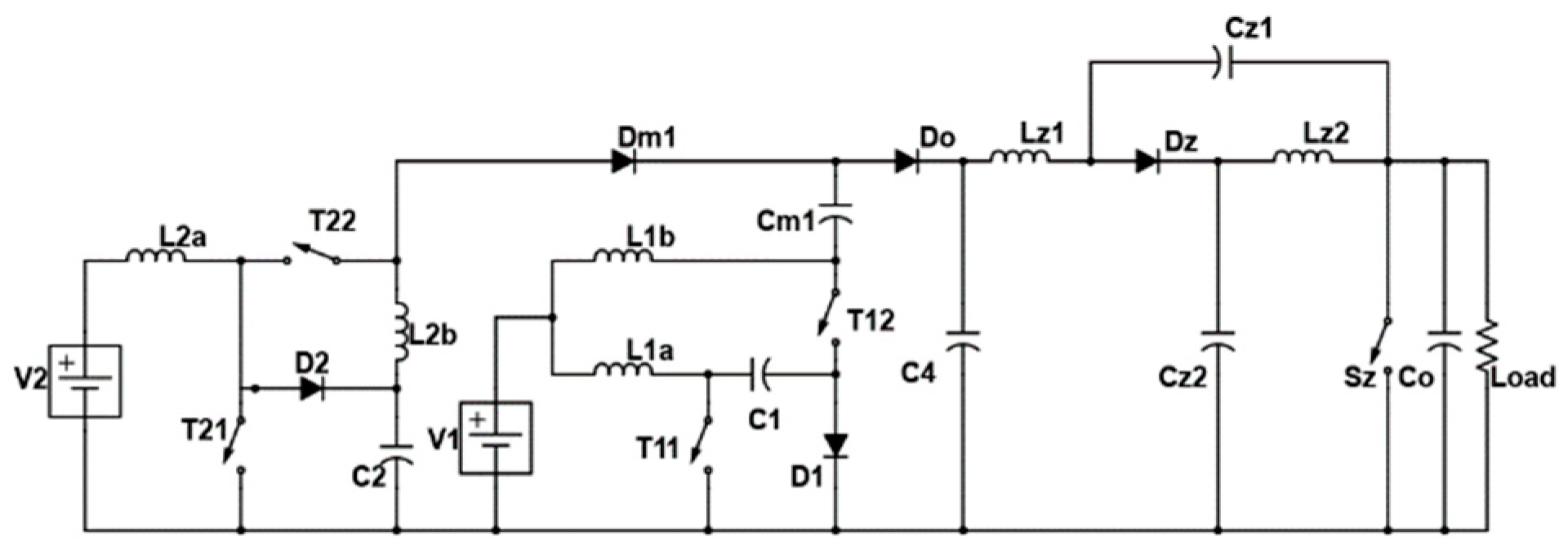
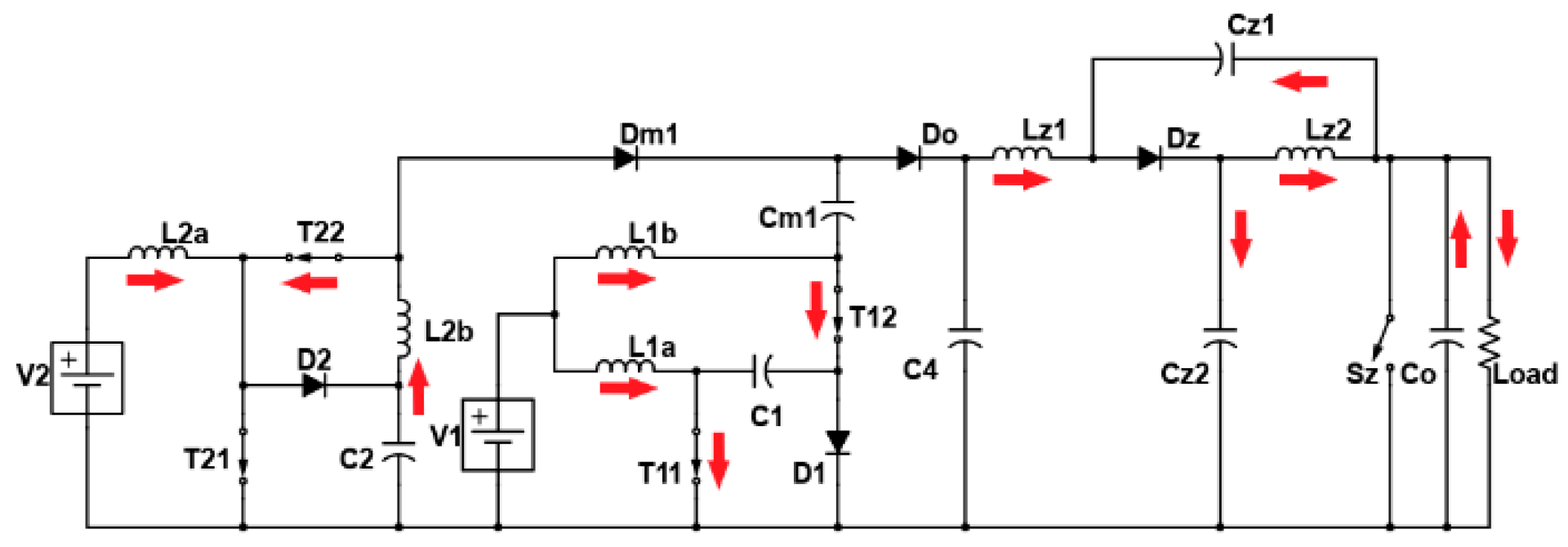
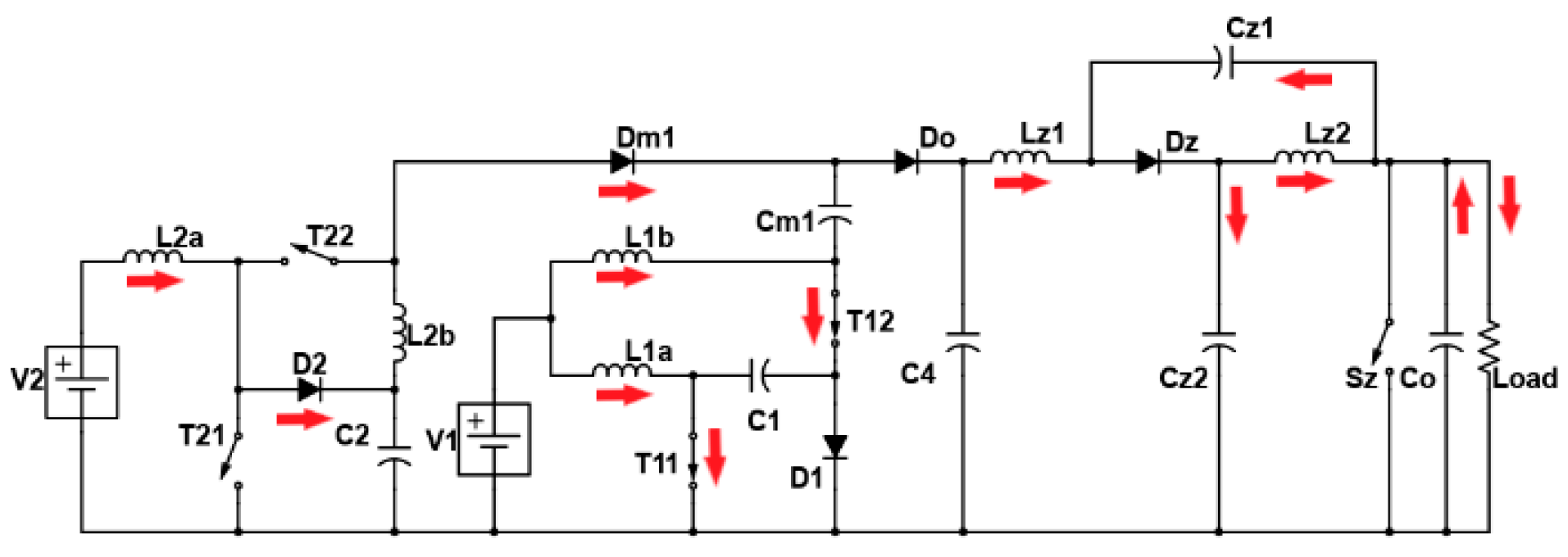
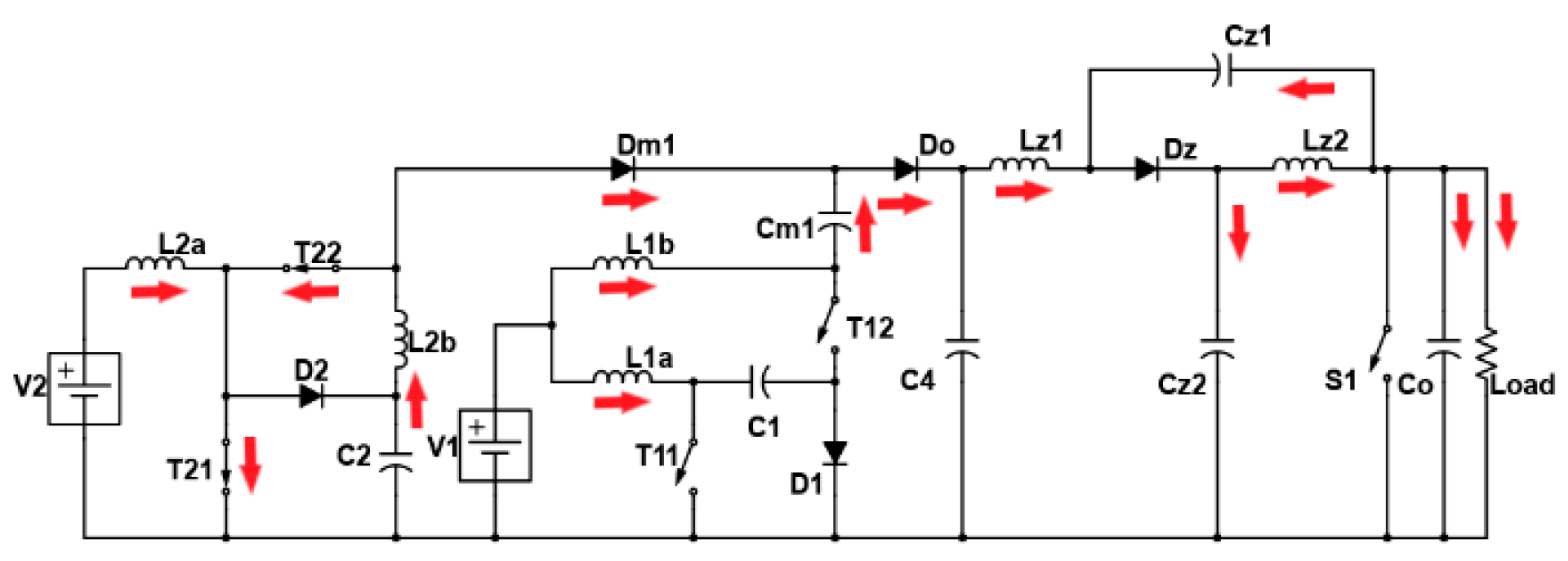
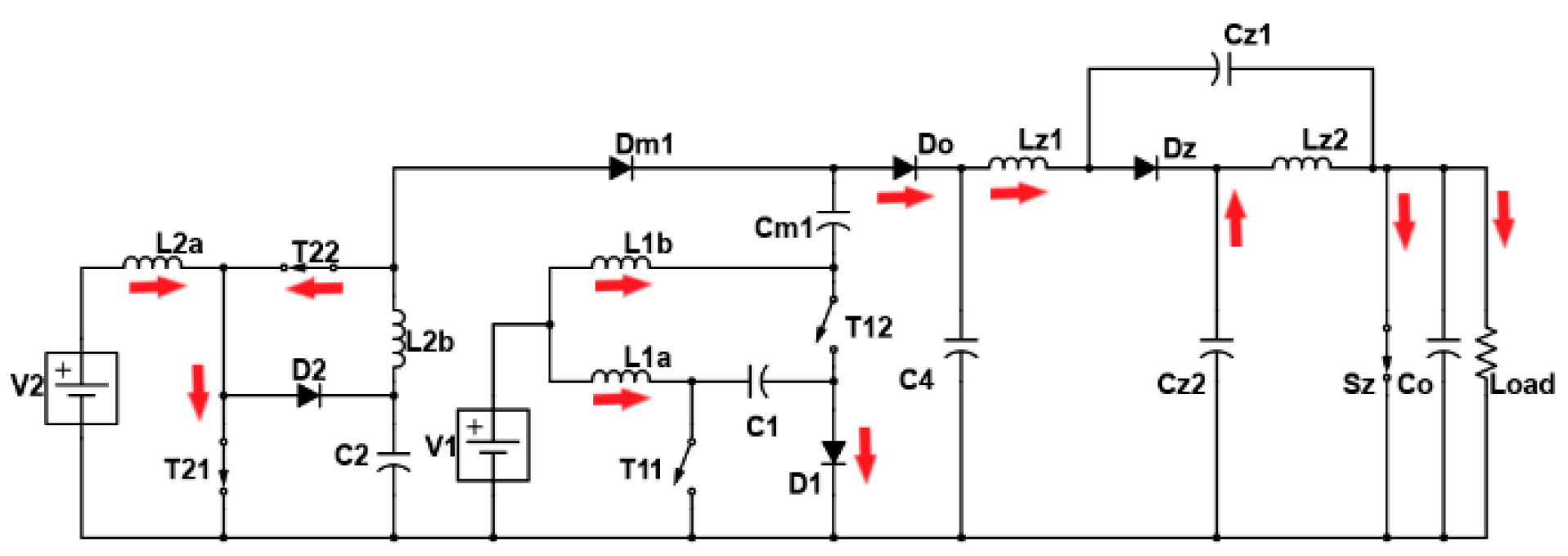
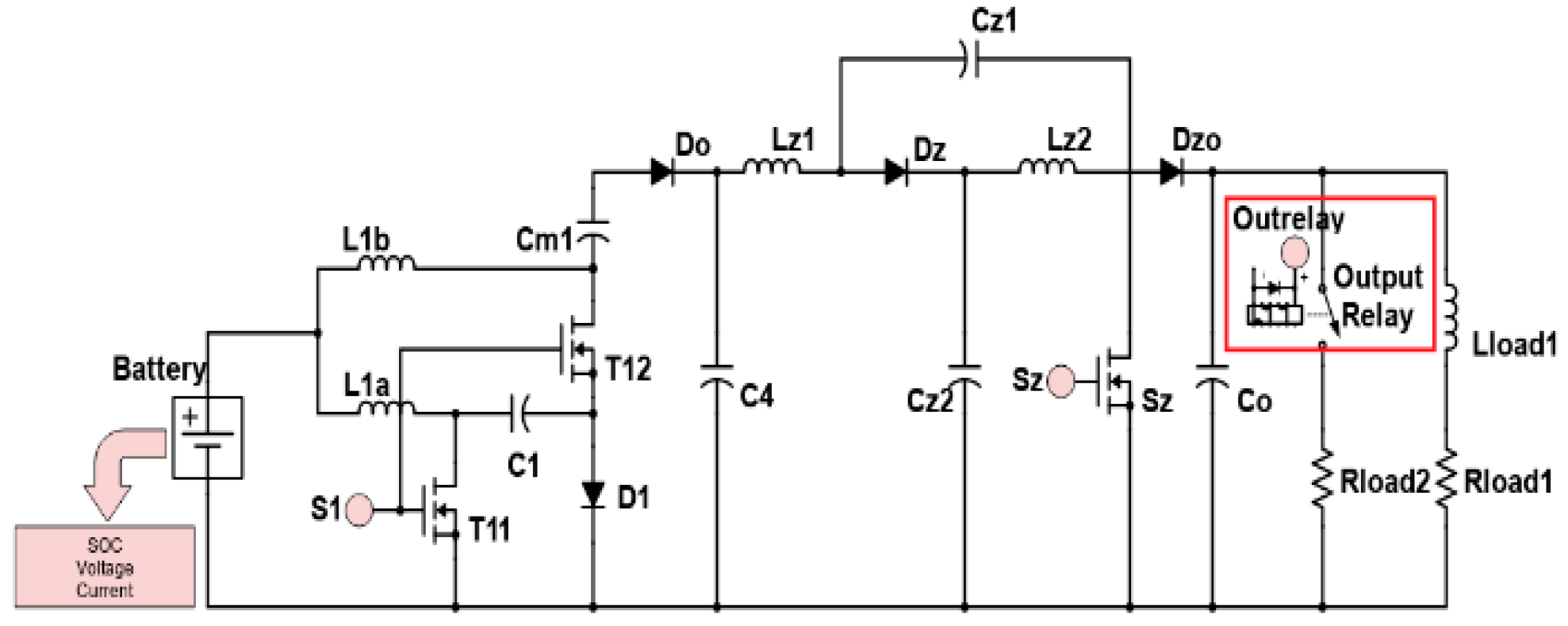
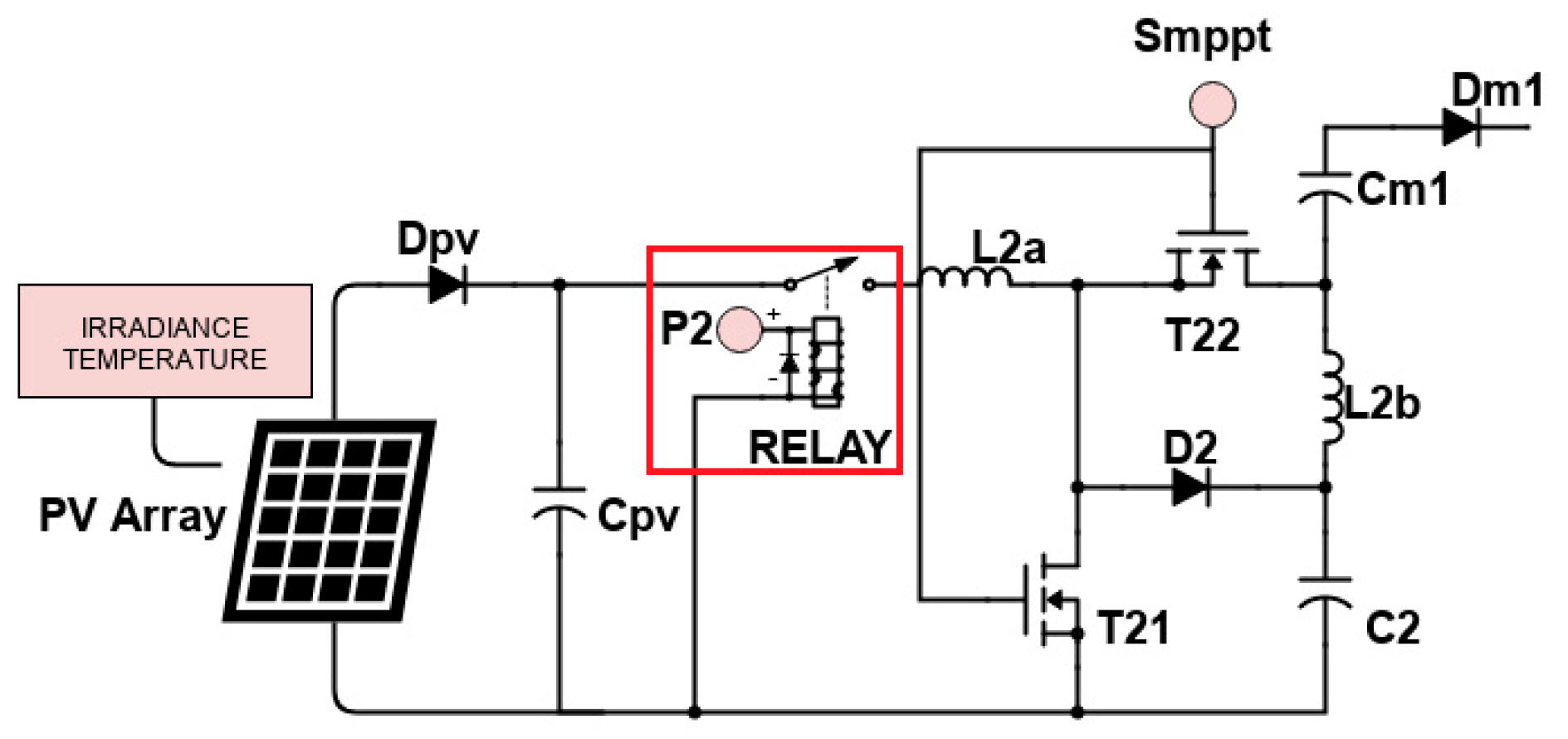
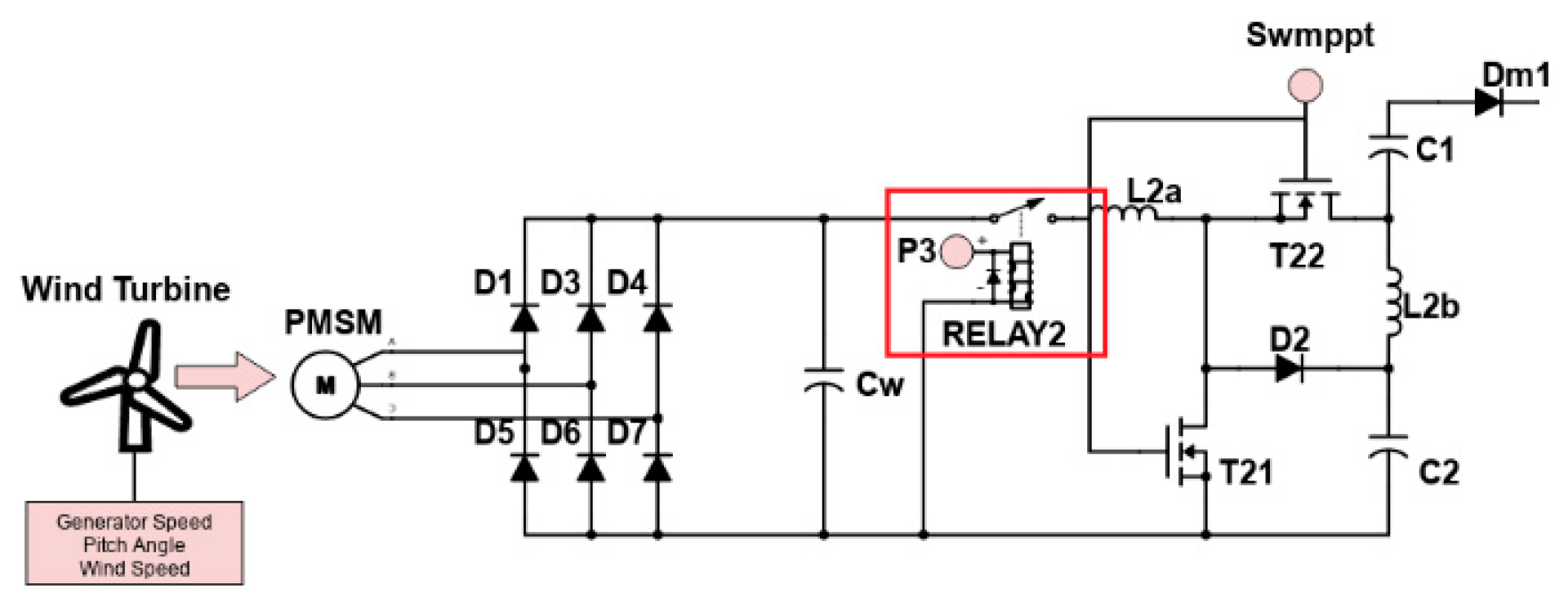
2. Proposed Multi-Port Converter with Quasi-Z-Source Network

A quasi-Z-source network was added to the multiport converter [8], as shown in Figure 1. By adding the quasi-z-source network, the voltage gain of all systems is increased using the quasi-z-source’s unique feature, which is the shoot-through mode. Moreover, as a result of the multiport converters, the DC bus voltage is decreased, leading to a decrease in the voltage stresses of the multiport converter switches. The number of input sources can be variable and is denoted b by n. For simplicity, a two-input scenario was considered. Each module consists of two inductors: a capacitor, a diode, and two switches. The modules are connected to each other via a diode and capacitor. A quasi-Z-source network was adopted on the output side. The switches of each module should be turned ON and OFF at their respective times and the quasi-z-source switch SZ can be switched independently

2.1. Working Modes and Mathematical Expressions

Mode 1a (t₀-t₁): In this mode, except S_z, all of the switches (T_1,2, T_1,1, T_2,2, T_2,1) are turned ON, this makes D₁, D₂, D_m1 reverse biased, besides, Quasi-z-source network’s diode is forward biased. Additionally, L_1a, L_1b, L_2a, and L_2b are charged by the input sources and capacitor, besides, Quasi-z-source network inductors L_Z1 and L_Z2 discharge their energy to the load, at the same time, V_C4 charges the network capacitors C_Z1 and C_Z2. Waveforms of mode 1a can be seen in the below Figure 2.

V_L1a = V₁

(1)

V_L1b = V₁ + V_C1

(2)

V_L2a = V₂

(3)

V_L2b = V_C2

(4)

V_LZ1 = V_C4 – V_CZ1

(5)

V_LZ2 = -V_CZ2

(6)

V_SZ = V_CZ1 + V_CZ2

(7)

Mode 1b (t₁-t₂): Switches (T_1,2, T_1,1, T_2,2, T_2,1) remain in the same position, but, Quasi-z-source network switch S_Z is turned on and this makes diode D_Z reverse biased. In this state inductors L_Z1 and L_Z2 start to get charged and store energy while capacitors C_Z1 and C_Z2 discharge energy. As the S_Z is turned ON, the Quasi-z-source side of the converter enters the shoot-through mode which is not forbidden in the z-source topology.

Figure 3. Mode1b.

V_LZ1 = V_CZ2 + V_C4

(8)

V_SZ = 0

(9)

V_LZ2 = V_CZ1

(10)

V_dZ = V_CZ1 + V_CZ2

(11)

Mode 2a (t₂-t₃): Mode 2a can be seen in Figure 4, the switches of the second module (T_2,2, T_2,1) are turned OFF, and diodes D₂ and D_m1 become forward biased. The capacitor of the second module, C₂, begins to charge from its input source V₂ and inductor L2a. Moreover, capacitor C_m1 begins to charge from the second source V₂, L_2a, and L_2b. Switch S_Z is not active and diode D_Z is forward-biased. The load is get energized by inductors L_Z1 and L_Z2. Equations from 5, 6, 7, and 8 are also valid for this mode. This mode is shown in Figure 4.

V_L1a = V₁

(12)

V_L1b = V₁ + V_C1

(13)

V_L2a = V₂ – V_C2

(14)

V_L2b = V_C1 + V_C2 - V_CM1

(15)

Mode 2b (t₃-t₄): Quasi-z-source switch S_Z is turned ON while the rest of the switches stay in the same position and this mode is shown in Figure 5. Quasi-z-source network enters a shoot-through state and network inductors L_Z1, L_Z2 get charged by the input source, and capacitors C_Z1 and C_Z2 discharge their energy. Equations from 8 to 11 are valid for this condition too.

Mode 3a (t₄-t₅): In this mode, the switches of the first module (T_1,2, T_1,1) are turned OFF while the switches of the second module (T_2,2, T_2,1) are turned ON. The capacitor C₄ is powered by the first input source V₁, L_1b, and C_m1. The Switch S_Z is turned off and it is in the non-shoot-through mode again. And the quasi-z-source part is the same with modes 1a and 2a, so equations 5, 6, and 7 are the same in this mode. The mode 3a can be seen in Figure 6.

V_L2b = V_C2

(16)

V_L2b = V₁ - V_C1

(17)

V_L2a = V₂

(18)

V_L1b = V₁ + V_CM1 - V_C4

(19)

Mode 3b (t₅-t₆): the last mode is 3b and shown Figure 7. In this mode, input module switches remain the same while the quasi-z-source network switch is switched ON. Quasi-z-source network enters shoot-through mode and equations 8, 9, 10, and 11 remain the same in this mode.

Calculations can be done in two parts to make the system understandable; the first part of calculations includes the multi-port side and the second part of calculations includes the quasi-z-source network side. The first part’s gain can be multiplied by the second part’s gain. Using the volt-second balance rule, the voltage of the inductor over one switching period is 0. Therefore, the inductor voltages of the two input modules can be written as follows:

V_L1a(t) = 0 = V₁d₁ + (V₁ - V_C1) * (1 - d₁)

(20)

V_C1 = 1 / (1 - d₁) * V₁

(21)

V_L1b(t) = 0 = (V₁ + V_C1) * d₁ + (V₁ + V_CM1 - V_C4) * (1 – d₁)

(22)

0 = V₁d₁ + V_C1d₁ + V₁ - V_C4 * (1-d₁) + V_CM1 * (1-d₁)

(23)

V_C4 = (1/(1-d₁)) * V₁ + (d1/(1-d₁)) + V_CM1

(24)

V_L2a(t) = 0 = V_C2d₂ + (V₂ – V_C2) * (1-d₂)

(25)

= V₂ d₂ + V₂ - V₂d₂ – V_C2 * (1-d₂)

(26)

V_C2 = 1/(1-d₂) * V₂

(27)

V_L2b(t) = 0 = V_C2d₂ + (V_C1 + V_C2 - V_CM1) * (1 – d₂)

(28)

= V_C2d₂ + V_C1 * (1 – d₂) + V_C2 - V_C2d₂ - V_CM1 * (1 – d₂)

(29)

V_CM1 = V_C1 + 1/(1-d₂) * V_C2

(30)

d₁ and d₂ are the duty cycle of the switches of module 1 and module 2, respectively.

By substituting

V_{c_{1}}

V_{c_{2}}

V_{C_{m 1}}

into

V_{C 4}

, the capacitor C₄ voltage of the system can be calculated.

V_C4 = (1/(1-d₁)) * V₁ + (d1/(1-d₁)) + V_CM1

(31)

V_C4 = ((2-2d₁+d₁)/(1-d₁)²) * V₁ + (1/(1-d₂)²) * V₂

(32)

V_C4 = ((2-d₁)/(1-d₁)²) * V₁ + (1/(1-d₂)²) * V₂

(33)

Rest of the calculations are related to the output voltage and quasi-z-source network elements. The shoot-through duty cycle can be found in the following expression;

d_Z = 1 / T_Z, T_z=T-T_o

(34)

d_z= duty cycle of the quasi-z-source switch shoot-through mode

T_z= shoot-through period

T_o= non-shoot-through period

By using the volt-second balance rule, the voltage of the quasi-z-source inductors can be calculated for the steady state.

{\bar{V}}_{LZ 1} = 0 = (T_{0} * V_{C 4} - V_{CZ 1} + T_{Z} * (V_{CZ 2} - V_{C 4})) / T

(35)

0 = (1 - d_z) * (V_C4 – V_CZ1) + d_Z * (V_CZ2 – V_C4)

(36)

From V_CZ2 = V_CZ1 – V_C4

0 = V_C4 – V_CZ1 + d_zV_CZ1 + d_zV_CZ1 – d_ZV_C4

(37)

V_CZ1 = ((1 - d_Z) / (1 – 2d_Z)) * V_C4

(38)

{\bar{V}}_{LZ 2} = 0 = (T_{0} (- V_{CZ 2}) + T_{Z} (V_{CZ 1})) / T

(39)

By subtracting V_CZ1 = V_CZ2 + V_C4

0 = -V_CZ2 + d_ZV_CZ2 + d_Z * (V_CZ2 + V_C4)

(40)

d_ZV_C4 = V_CZ2 * (1-2d_Z)

(41)

V_CZ2 = (d_Z / (1 – 2d_Z)) * V_C4

(42)

V_{C_{z 1}}

and

V_{C_{z 2}}

are the voltages of the quasi-z-source network capacitors, and by summing capacitor voltages, the output voltage can be calculated.

So, by using

V_{0} = V_{C_{z 1}} + V_{C_{z 2}}

V₀ = ((1 – d_Z)/(1 – 2d_Z)) * V_C4 + ((d_Z)/(1 – 2d_Z)) * V_C4

(43)

V₀ = (1 / (1 – 2d_Z)) * V_C4

(44)

Figure 8. Waveforms for different working modes.

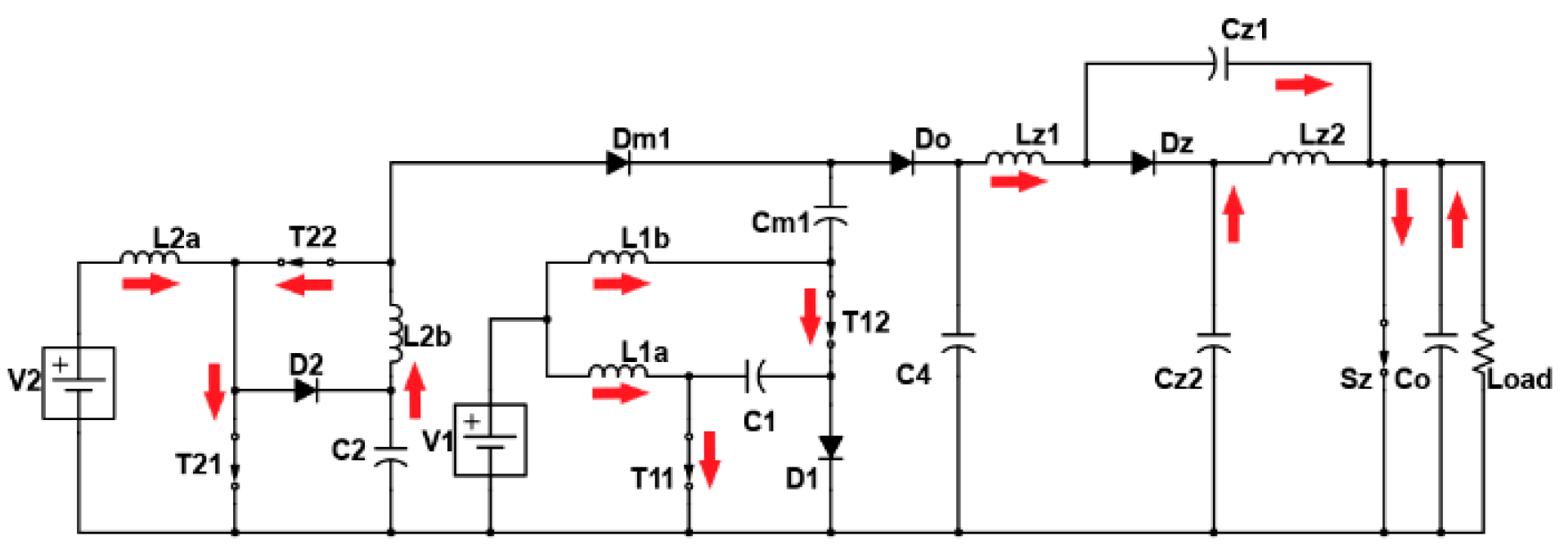
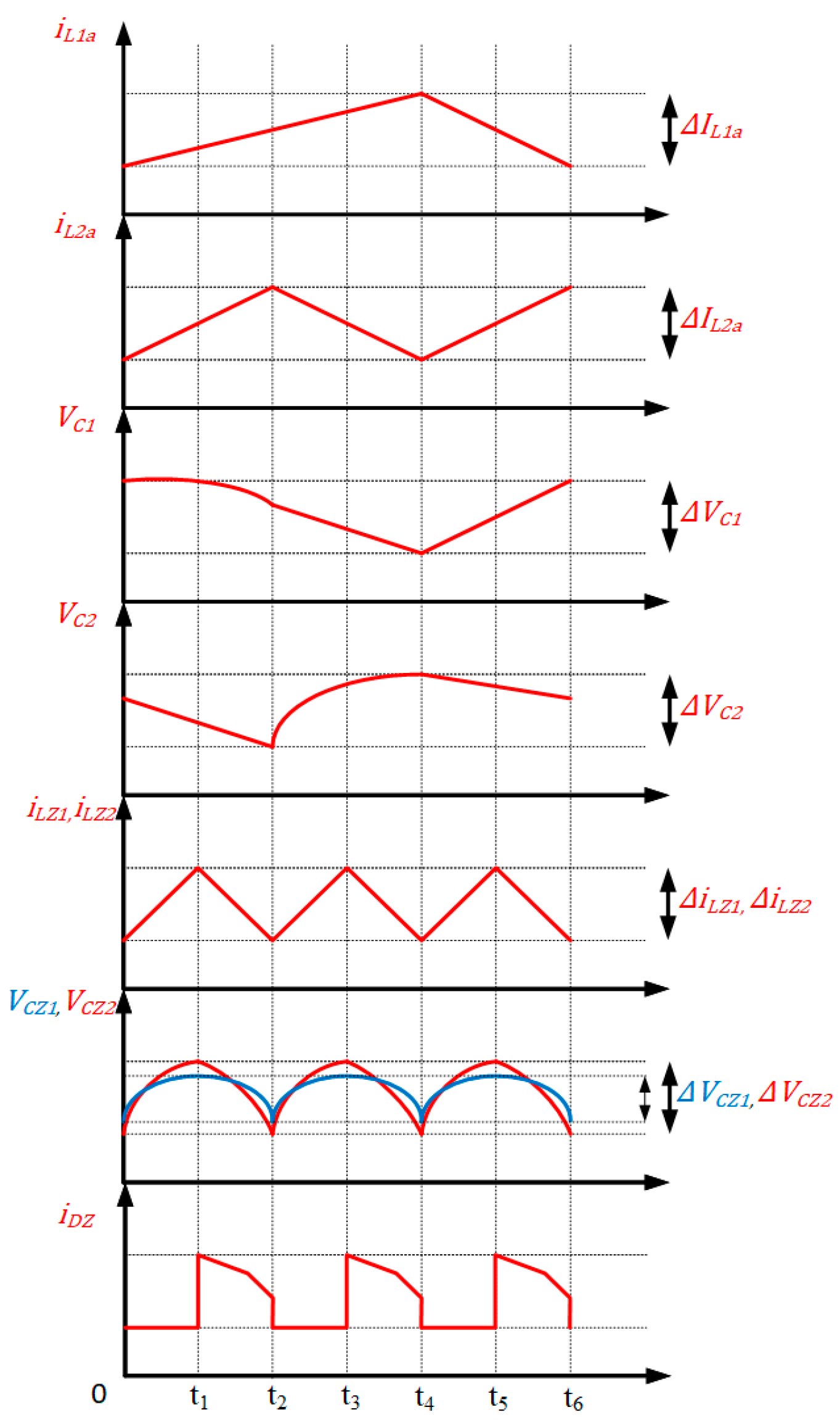
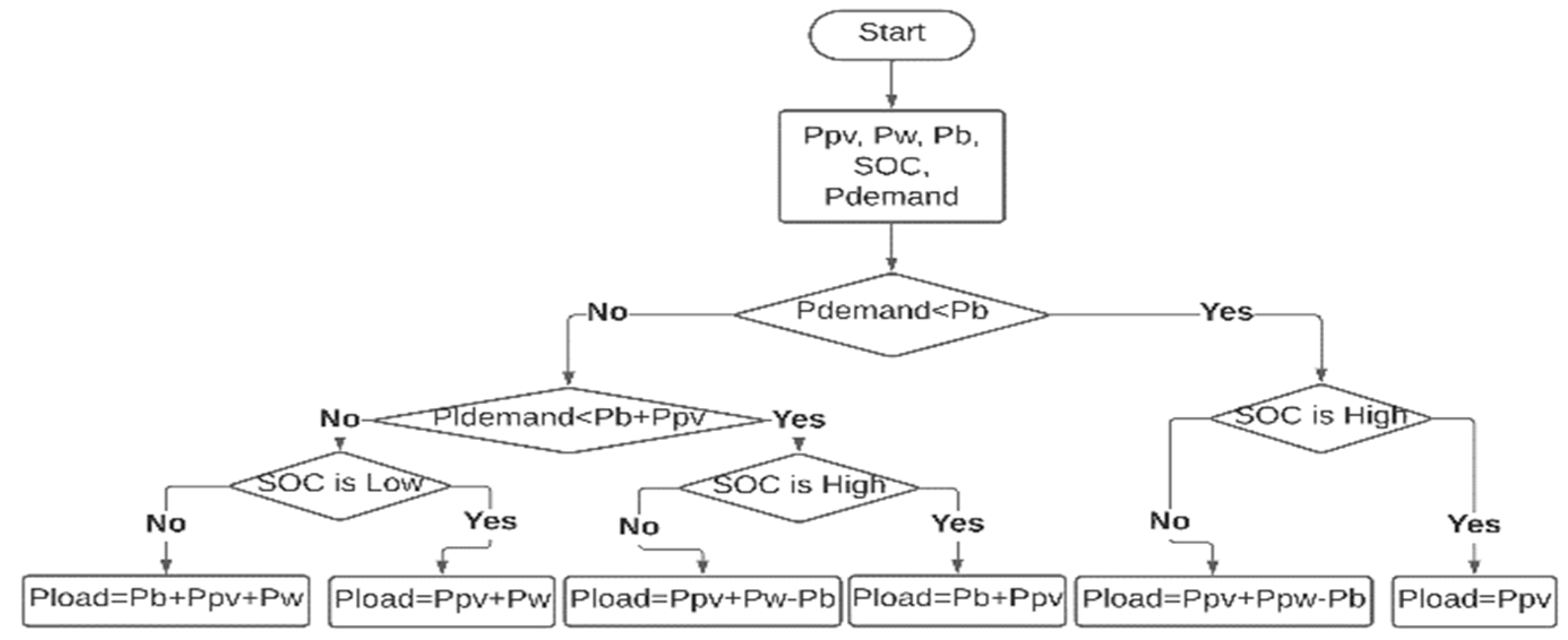
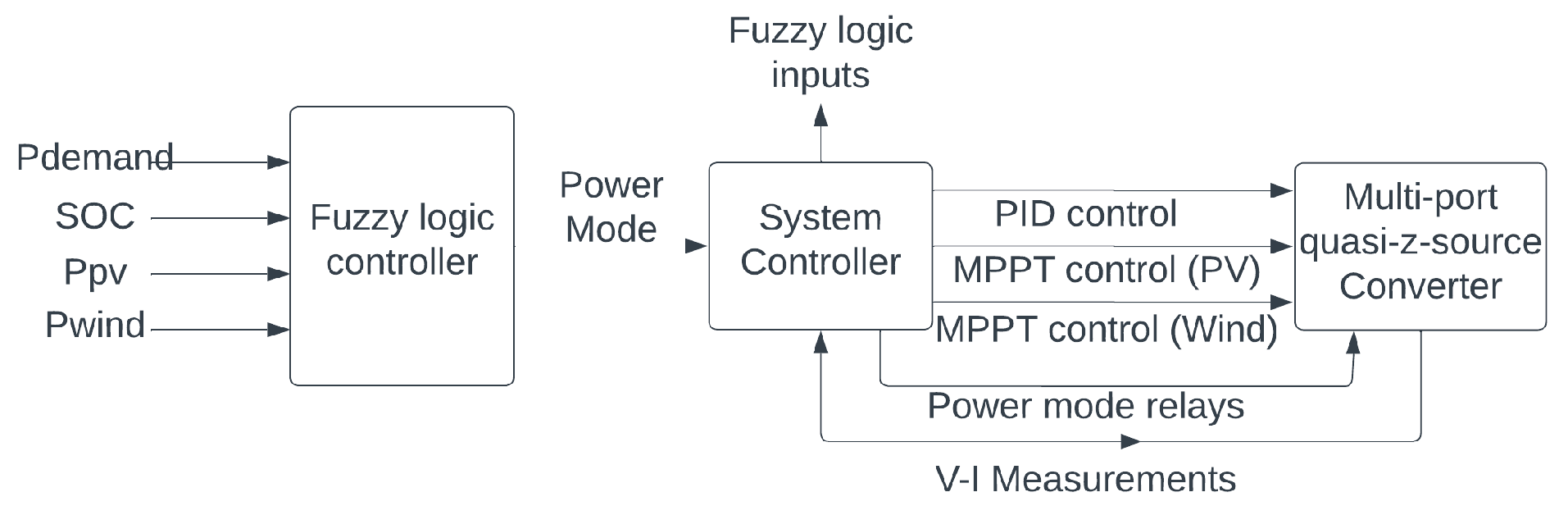
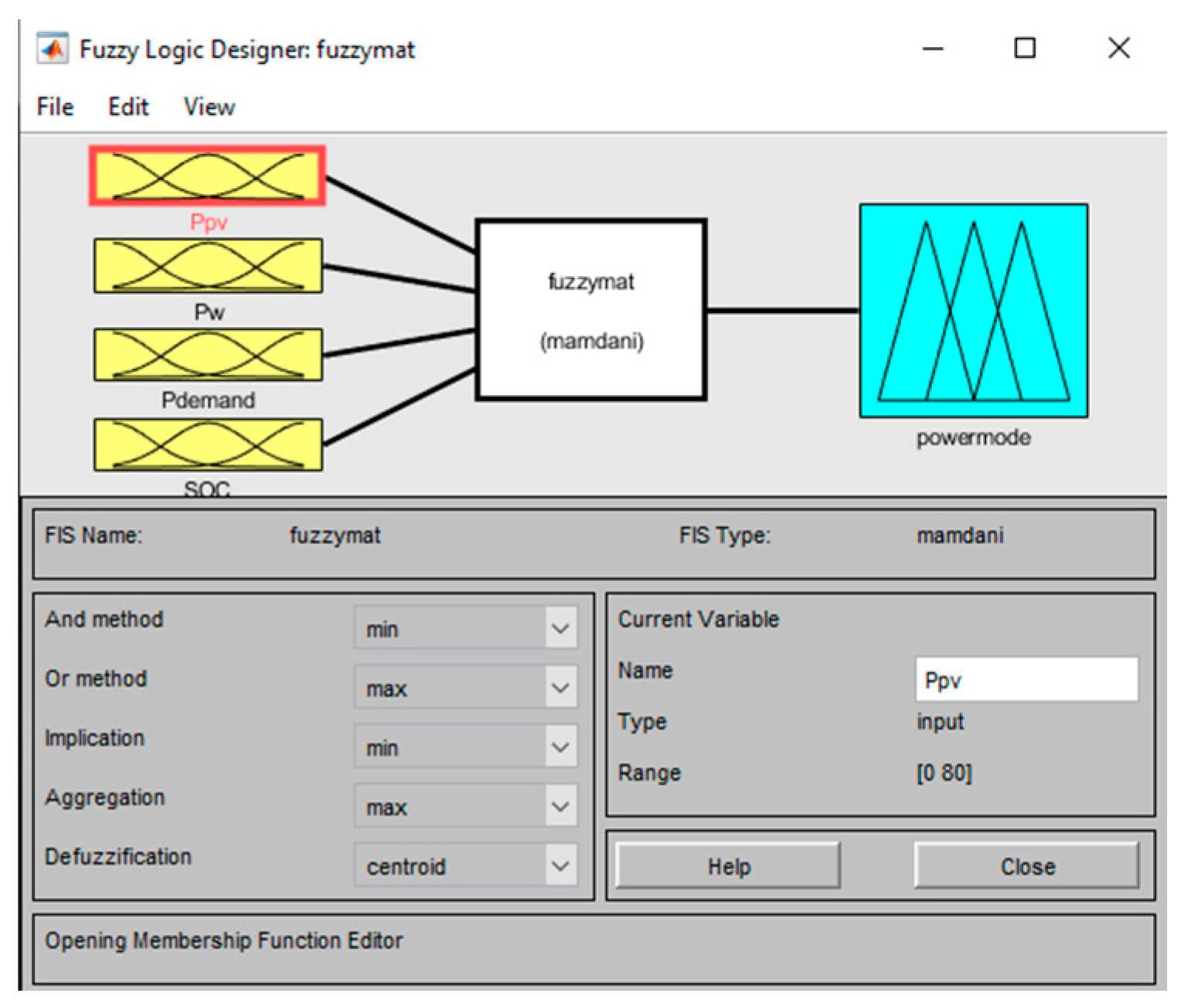
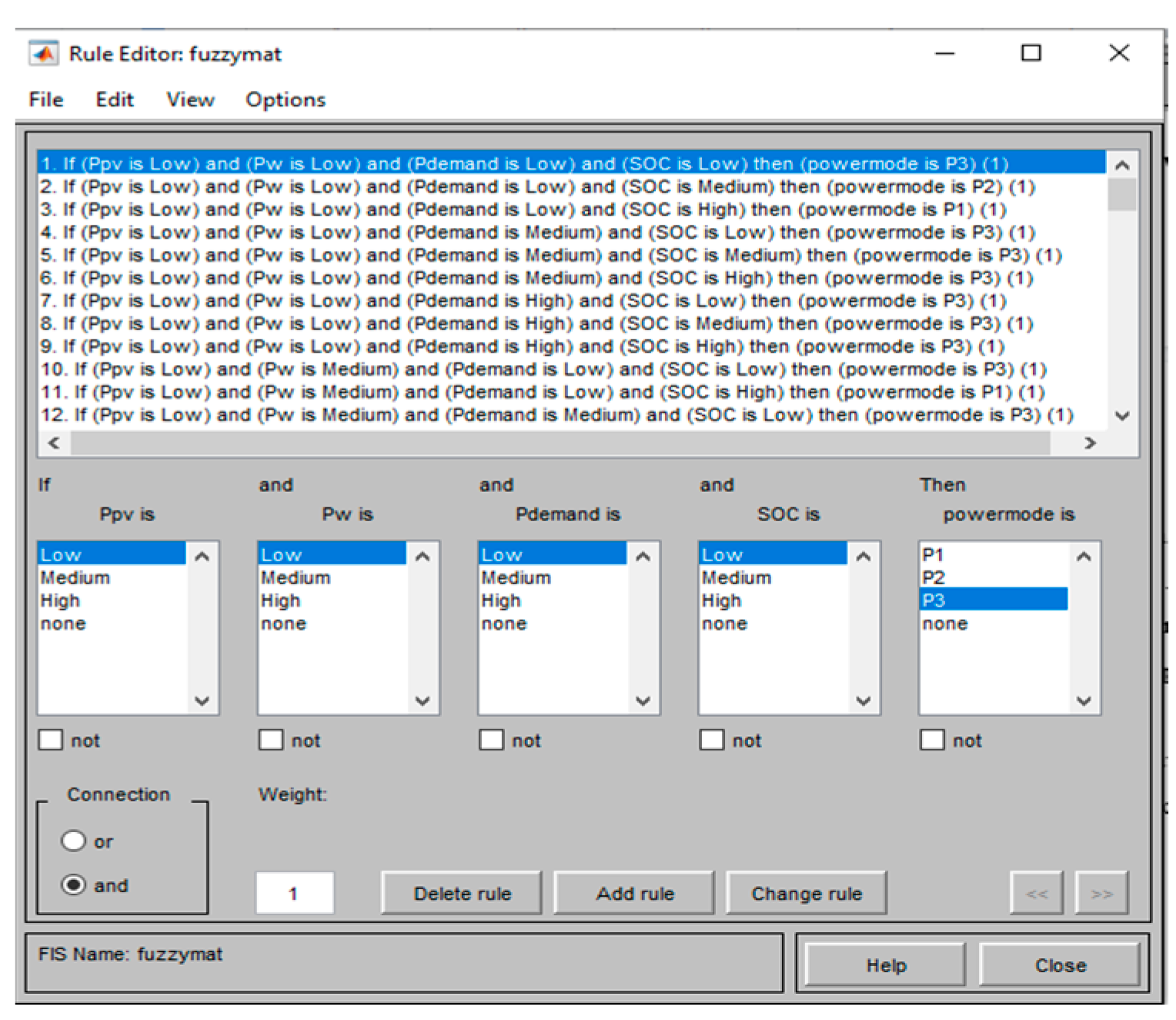
3. Proposed Energy Management Strategy

Hybrid renewable sources with multiple inputs offer distinct advantages over regular power sources. To capitalize on these benefits, wise system planning and power management are required. Fuzzy logic is widely used in various smart applications to achieve higher efficiency owing to its lack of requirements for mathematical modelling, applicability to nonlinear systems, and need for only expert guidance [9,10,11,12,13]. The classical fuzzy-logic strategy consists of three levels: fuzzification, fuzzy inference, and defuzzification. During the fuzzification process, the knowledge database enters the system and converts the data into fuzzy linguistic variables. The next step is fuzzy inference, where the rules are defined. The final step is defuzzification, where the fuzzy linguistic variables are converted into understandable values. Figure 9 shows a flowchart that defines the process priority and logic of the energy management systems. According to the flowchart, the powers of the parameters are defined in the first step, and the parameters are then processed. The battery is compared with the simultaneous output power (Pdemand) in the first process, and depending on the outcome, the path is selected. If the battery cannot supply sufficient power to the output, PV power is added to the battery power, and the sum of the two sources is compared with the simultaneous output power. Depending on the answer to the comparison, the Battery SOC level is checked, and wind power is enabled at both SOC levels. If the sum of the two sources is greater than the simultaneous output power, then the State of the Charge (SOC) level is checked and wind power is enabled depending on the SOC level. If the battery can satisfy the simultaneous output power, then the battery SOC level is checked, and other sources are enabled depending on the SOC level.

The Mamdani method is used as the inference method in the proposed system because it is easier to apply and depends on expert definitions [35]. A non-complex system is important for expanding the applicability; therefore, this method has been selected instead of the Sugeno method. The fuzzy logic controller in the proposed system has four inputs (the power of the PV array and wind turbine, instantaneous load power or demanded power, battery SOC, and an output (power mode). The membership functions were configured according to the power ratings of the inputs, and were divided into three membership functions: low, medium, and high.

The rules of the system were established based on power levels, with 81 rules requiring specification one by one using if-then rules. Fuzzy logic generates numbers between 1 and 3, including 1 and 3, as the output power mode. Based on the power mode output, the system controller regulates each module by attaching or detaching the sources from the rest of the circuit through the power mode relays. A block diagram of the controller system is shown in Figure 10.

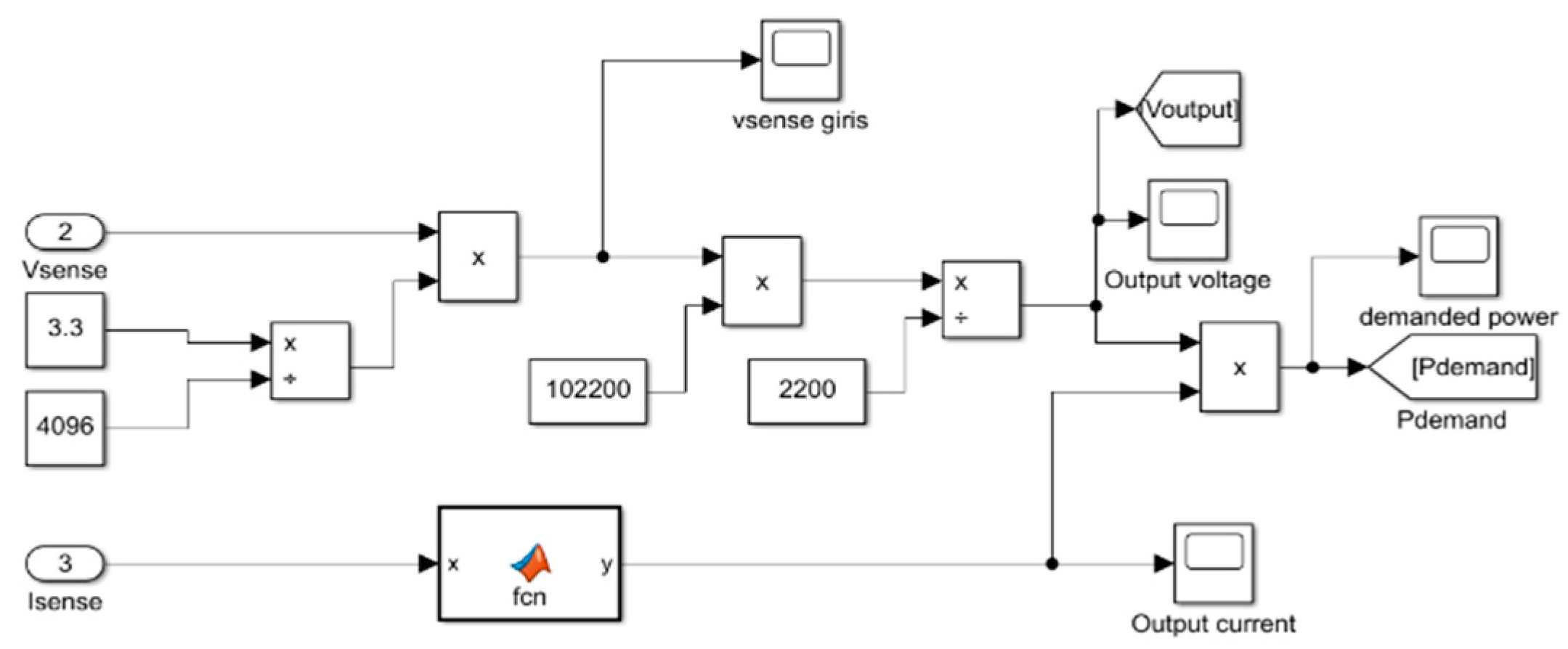
4. Simulation of the Proposed Control System

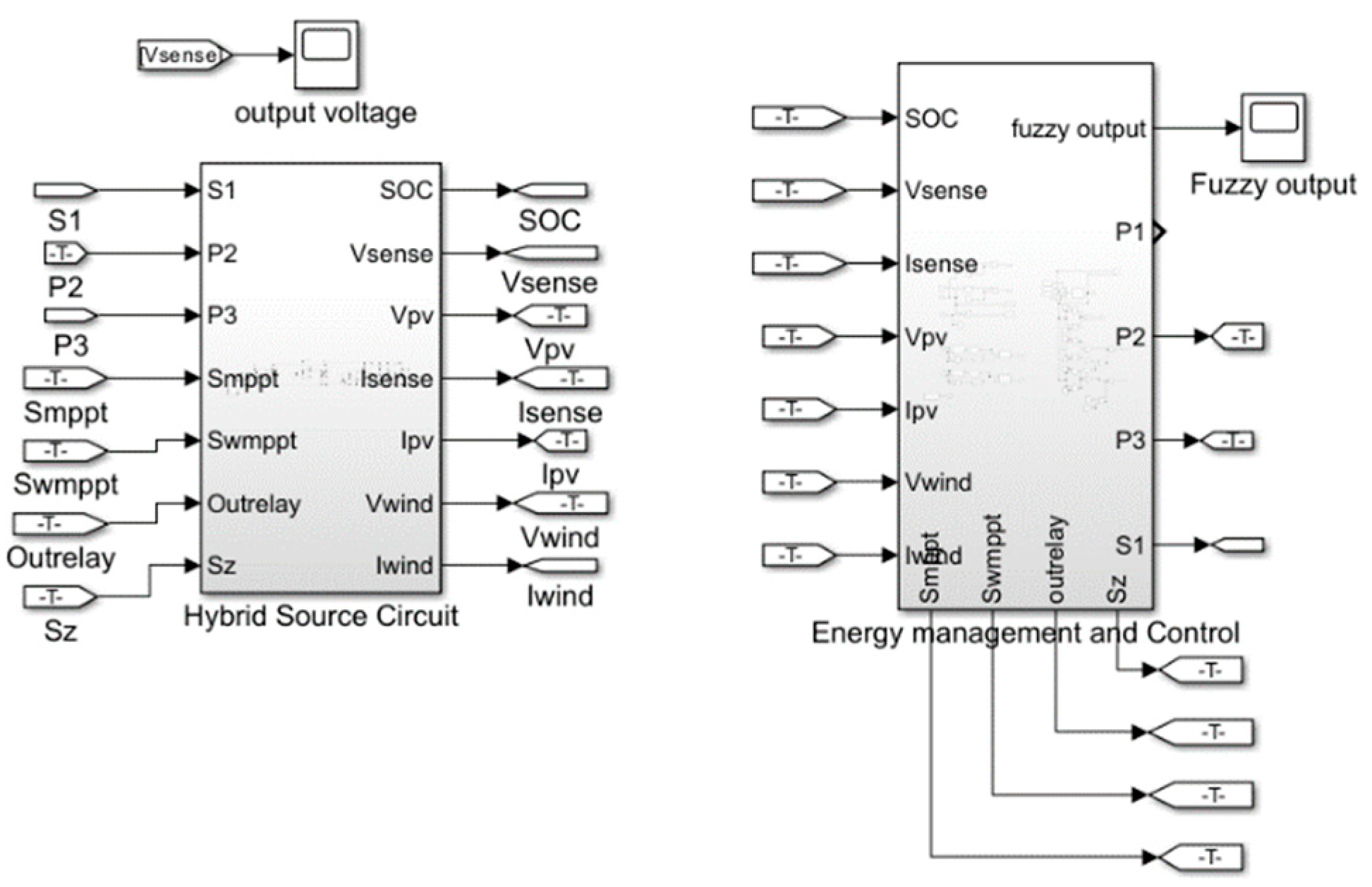
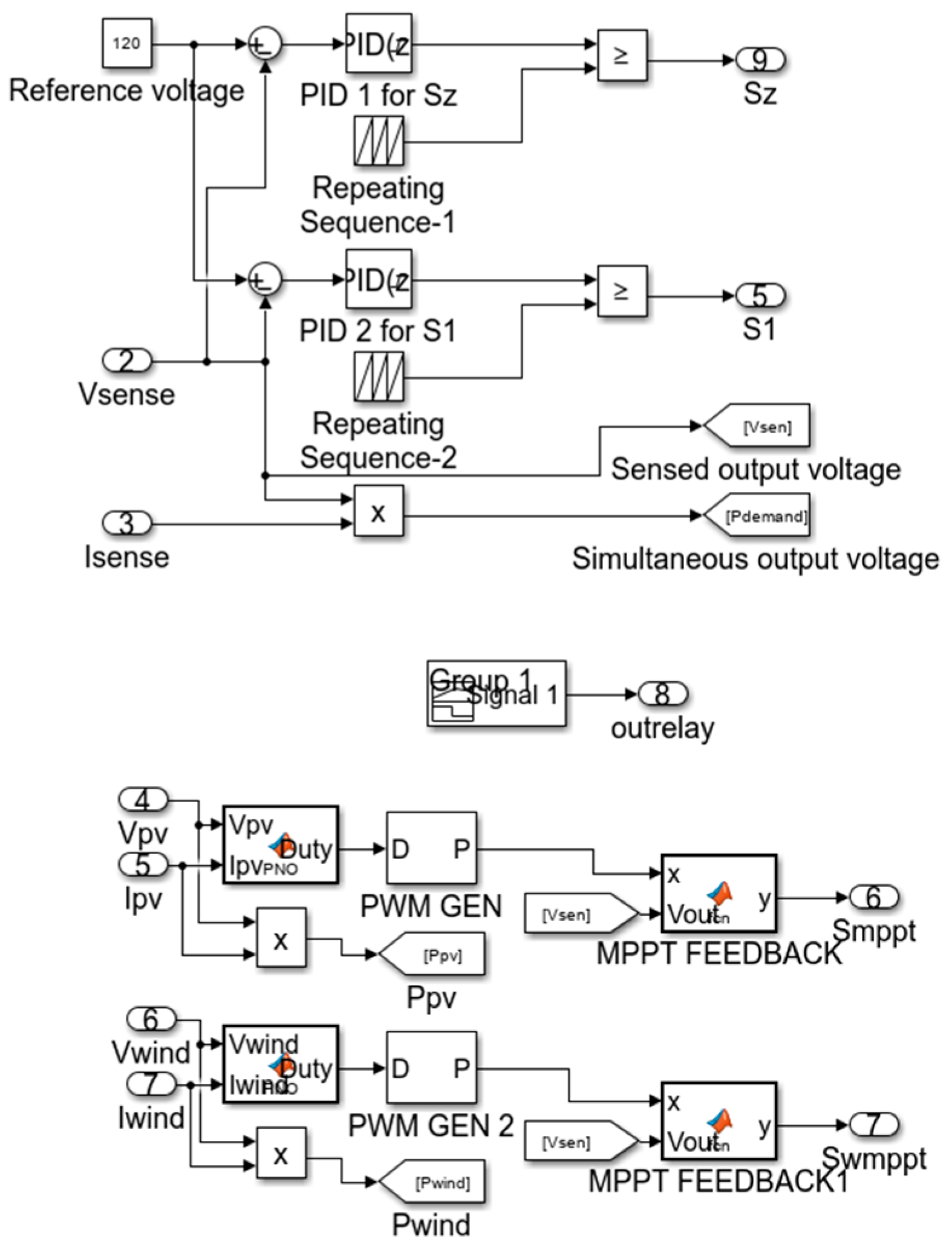
4.1. Simulink Model

The simulation was performed in MATLAB Simulink and was divided into two main sections. The first section is the multi-port converter block, where all circuit elements and measurements have been performed. The second section is the energy management and control block, where the entire control strategy is located. The two main blocks are illustrated in Figure 11. Separating the simulation into two main blocks served two purposes: modularity for the experimental tests and making it more understandable. There are 3 hybrid sources–battery, PV panel, and wind turbine–were used to perform the simulations and experimental tests. The S1, Smppt, Swmppt, and Sz are switching signals of module 1, module 2, module 3, and quasi-z-source switch respectively. S1 is the battery module switching signal which is the output of the PID controller. Smppt and Swmppt are the PV module and Wind module switching signals, respectively, which are the outputs of the MPPT control algorithms. P2 and P3 are the power mode control signals for the PV module relay and Wind module relay respectively, modules can be attached and detached by controlling relays and Outrelay is the control signal of the second load relay for activation of the extra load. SOC, Vsense, VPV, Isense, IPV, Vwind, and Iwind are the measurements from the circuit which are the battery state of the charge, output voltage, PV voltage, output current, PV current, wind voltage, and wind current respectively. The measured parameters were used for the control algorithms and energy management system.

Figure 12 shows the output section and first module of the circuit. The first module is always connected to the quasi-z-source network; however, during fault conditions, it does not supply power to the circuit. The battery should supply power to the system at all times because the rest of the sources are discontinuous. This means that the power supplied by the PV and wind turbine can be interrupted owing to weather conditions. The load was an RL load of 440 Ω and 33 µH. Additionally, according to the scenario, an extra resistive load is connected in parallel to the main load after 0.3 seconds of the simulation starting by switching the output relay, which can be seen in the red rectangle in Figure 12. The output power is monitored as the demanded power for the control strategy.

The second module is the PV module, which is attached to the circuit, as shown in Figure 13. The relay attaches or detaches the PV array based on the fuzzy-logic output, and the relay is shown in red rectangles in Figure 13. The PV array has two inputs that can be adjusted according to irradiance and temperature scenarios.

The irradiance level was set using the signal builder in Simulink and the level ranges from 0 W/m2 to 915 W/m2 and then decreases to 530 W/m2 after a certain period. The temperature is fixed at 25 Celsius. The specifications of the PV array have been taken from the experimental kit “Deneysan YE-1050” datasheet and are shown in Table 1.

The third module is the Wind Turbine module, which provides mechanical input to the permanent magnet synchronous machine (PMSM) to obtain a Simulink model of the wind turbine. The PMSM has a 3-phase output, which is converted to DC form with 3-phase bridge rectifiers. Module 3 is shown in Figure 14, and the module specifications are taken from the experimental kit “Deneysan YE-1050” datasheet. The second relay is controlled according to the fuzzy output and is shown in red rectangular in Figure 14.

Energy management was performed using the Mamdani fuzzy logic method. The MATLAB fuzzy logic designer toolbox was used to configure the system. The fuzzy logic system has four inputs: the power of the PV array, wind turbine, instantaneous load power (demanded), and battery SOC. The power mode is the output of the fuzzy logic controller. The fuzzy-logic designer toolbox is illustrated in Figure 15. All membership functions were defined according to power ratings.

The rules of the system are set after specifying the membership functions. There are 81 rules in the system and the rule editor can be seen in Figure 16, moreover, a detailed rule list can be seen in the Appendix A. All of these possibilities are considered to provide precise results. Based on the membership functions and rules, the dynamic response of the fuzzy logic system can be viewed in the surface viewer of the fuzzy logic toolbox, as shown in Figure 17.

The membership functions for descriptors can be defined with a straight-line formula which is;

(y₂ – y₁) / (x₂ – x₁) = (y – y₁) / (x – x₁)

(45)

Where y=µ, x=x_T

y is the membership function and x is the input variable so the membership function can be expressed as;

µ = (((y₂ – y₁) * (x – x₁)) / (x₂ – x₁)) + y₁

(46)

By using the membership function formula, each membership function of the inputs can be expressed one by one,For PV;

µ_L = (4 - x_PV) / 4 [0,4]

(47)

µ_M = (x_PV - 4) / 8 [4,12]

(48)

µ_M = ((12 - x_PV) / 53) – 53 [12,65]

(49)

µ_H = (x_PV - 65) / 25 [65,80]

(50)

For Wind;

µ_L = (1 – x_W) / 130 [0,130]

(51)

µ_M = (x_W - 110) / 90 [110,200]

(52)

µ_M = ((200 – x_W) / 80) – 1 [200,280]

(53)

µ_H = (x_W - 260) / 140 [260,400]

(54)

For demanded power;

µ_L = (1 – x_d) / 35 [0,25]

(55)

µ_M = (x_d - 35) / 25 [35,60]

(56)

µ_M = ((60 – x_d) / 50) + 1 [60,110]

(57)

µ_H = (x_d - 110) / 290 [110,300]

(58)

And finally, for the SOC;

µ_L = (1 – x_SOC) / 290 [0,25]

(59)

µ_M = (x_SOC - 25) / 25 [25,50]

(60)

µ_M = ((50 – x_SOC) / 25) + 1 [50,75]

(61)

µ_H = (x_SOC - 75) / 25 [75,100]

(62)

By using membership formulas and rules, the exact result of the output can be obtained using the weighted average method. The weighted average method is a widely utilized defuzzification method that is considered relatively simple and is expressed as follows:

x* = (∑µ_n * x̅) / ∑ x̅_n

(63)

x* = ((µ_x1 * x̅₁) + (µ_x2 * x̅₂) + (µ_x3 * x̅₃) + (µ_x4 * x̅₄)) / (x̅₁ + x̅₂ + x̅₃ + x̅₄)

(64)

x^{*}

is the defuzzied value and

{\bar{x}}_{1}

and

{\bar{x}}_{2}

are the centroid of the trapeziums which are reflections of inputs to output. As a result, by using the above formulas, any conditions of the rules can be calculated.

4.2. Other Control Parameters

The controlling of the switches has been done using different methods depending on the type of the source, and the control methods can be seen in Figure 18. For the battery module (T₁₁, T₁₂) and quasi-z-source part (S), closed-loop proportional-integral-derivative (PID) controllers were used. The reference output voltage is compared with the measured output voltage, and the resulting error is inputted into a proportional integral derivative (PID) block. The output of the PID block is the duty cycle of the switch, and the relational operator compares the duty cycle and repeating sequence at a fixed frequency to convert the number of duty cycles into a square-wave waveform.

Due to their characteristics, the PV array and the wind turbine need to be examined separately to obtain their Maximum Power Point (MPP). The Perturb and Observe method has been applied to track the MPP, as shown in Figure 18. The Perturb and Observe method has an initial duty cycle, which increases or decreases by an amount of delta value according to the dV and dP values. The dV and dP values represent the differences between the instantaneous voltage/power and the old voltage/power, respectively.

Moreover, there are maximum and minimum limits for the desired duty cycle. The Perturb and Observe method outputs the duty cycle number, which is then input into the pulse width modulation (PWM) generator to obtain the waveform for the switches of the modules. To achieve closed-loop control, one more control parameter had to be added to the end of the PWM generator, which takes the output voltage and compares it with the reference output voltage.

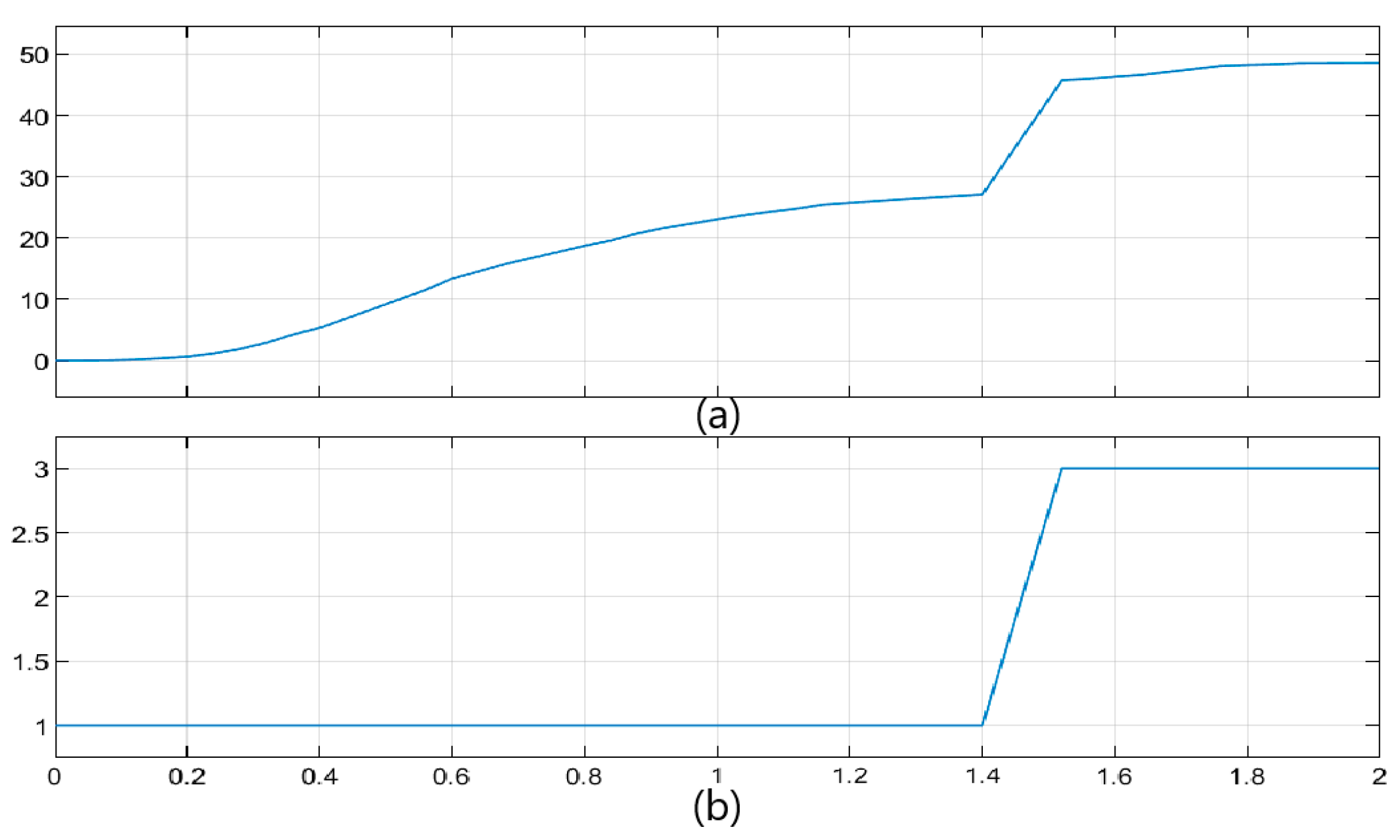
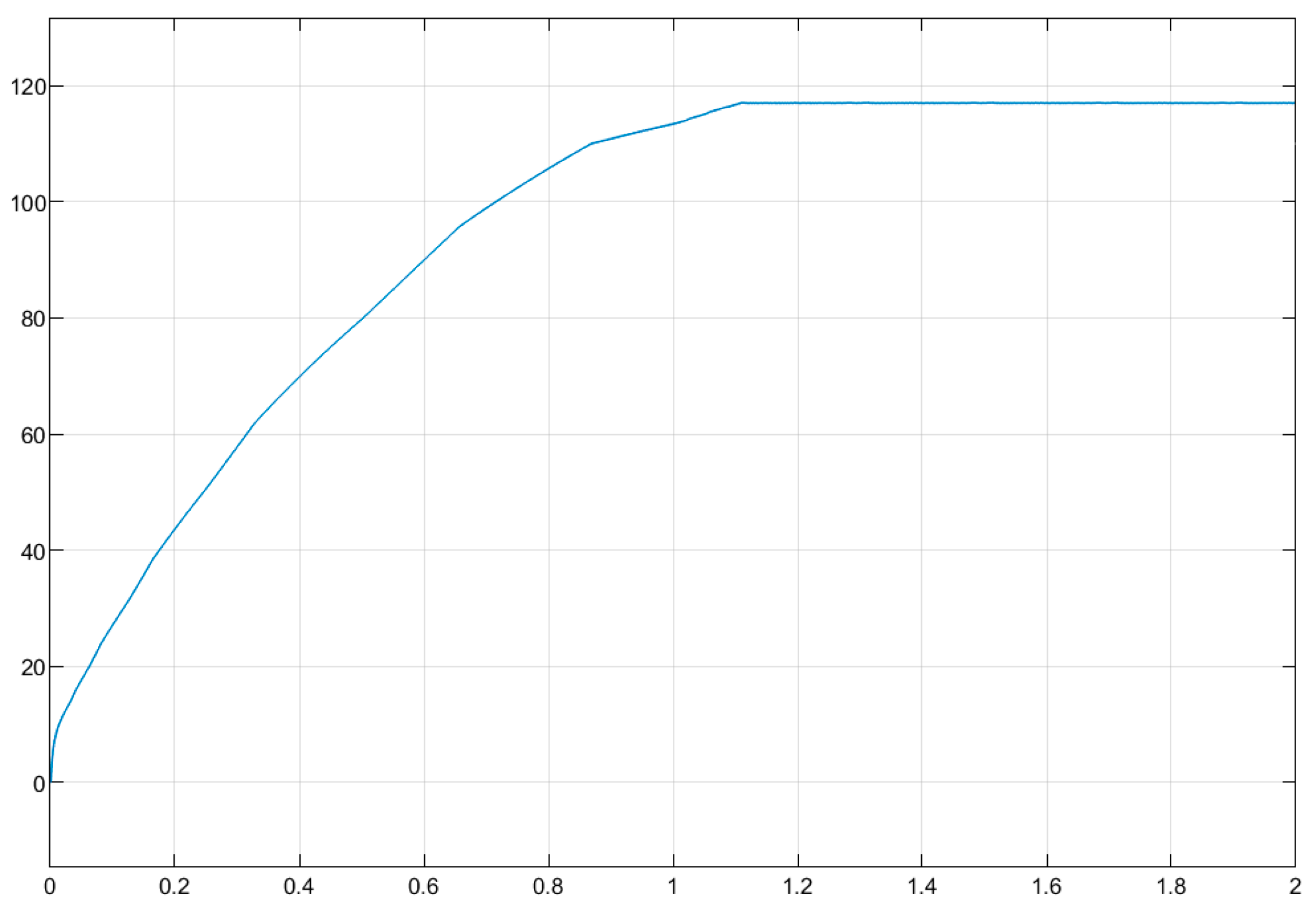
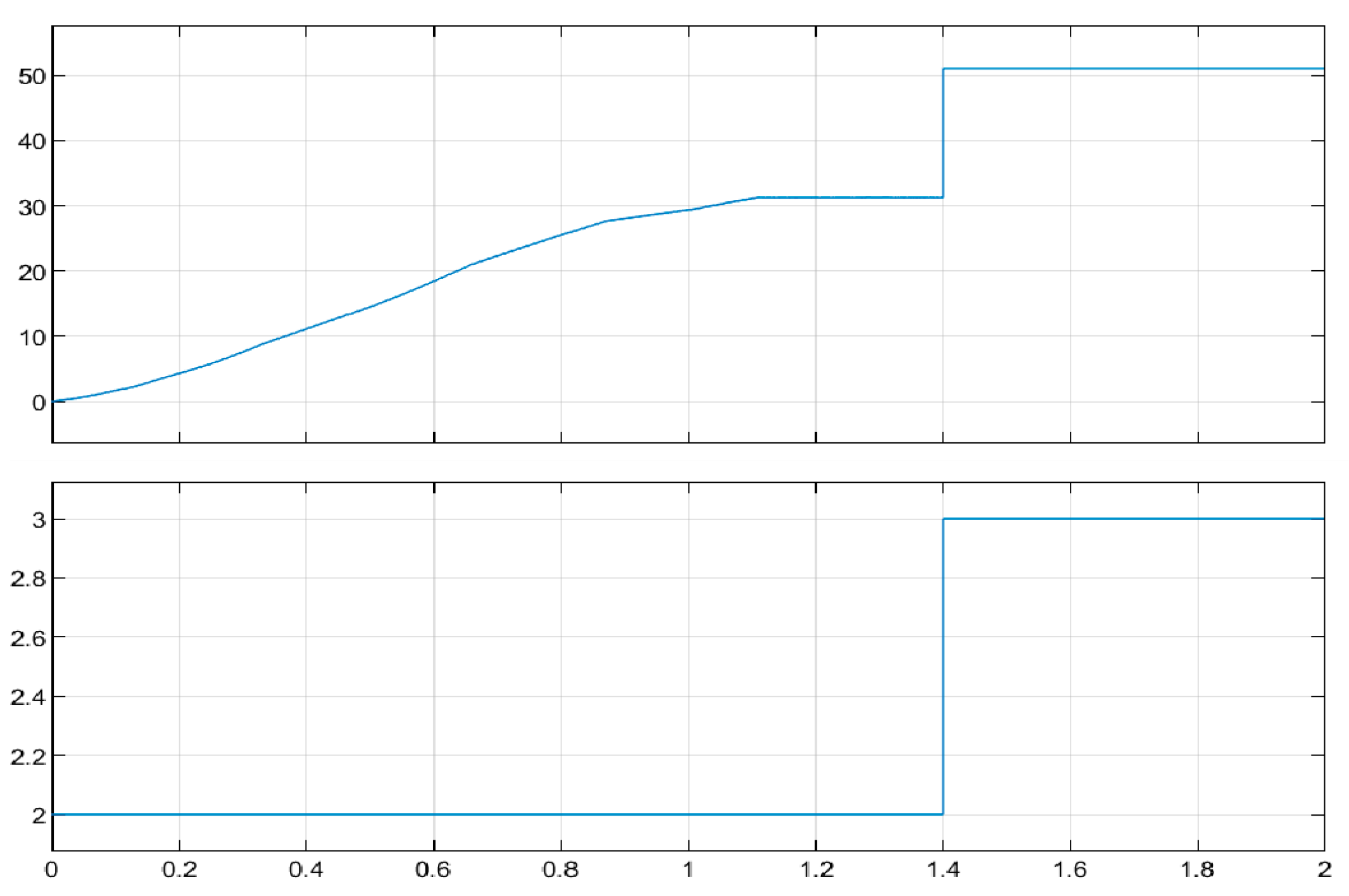
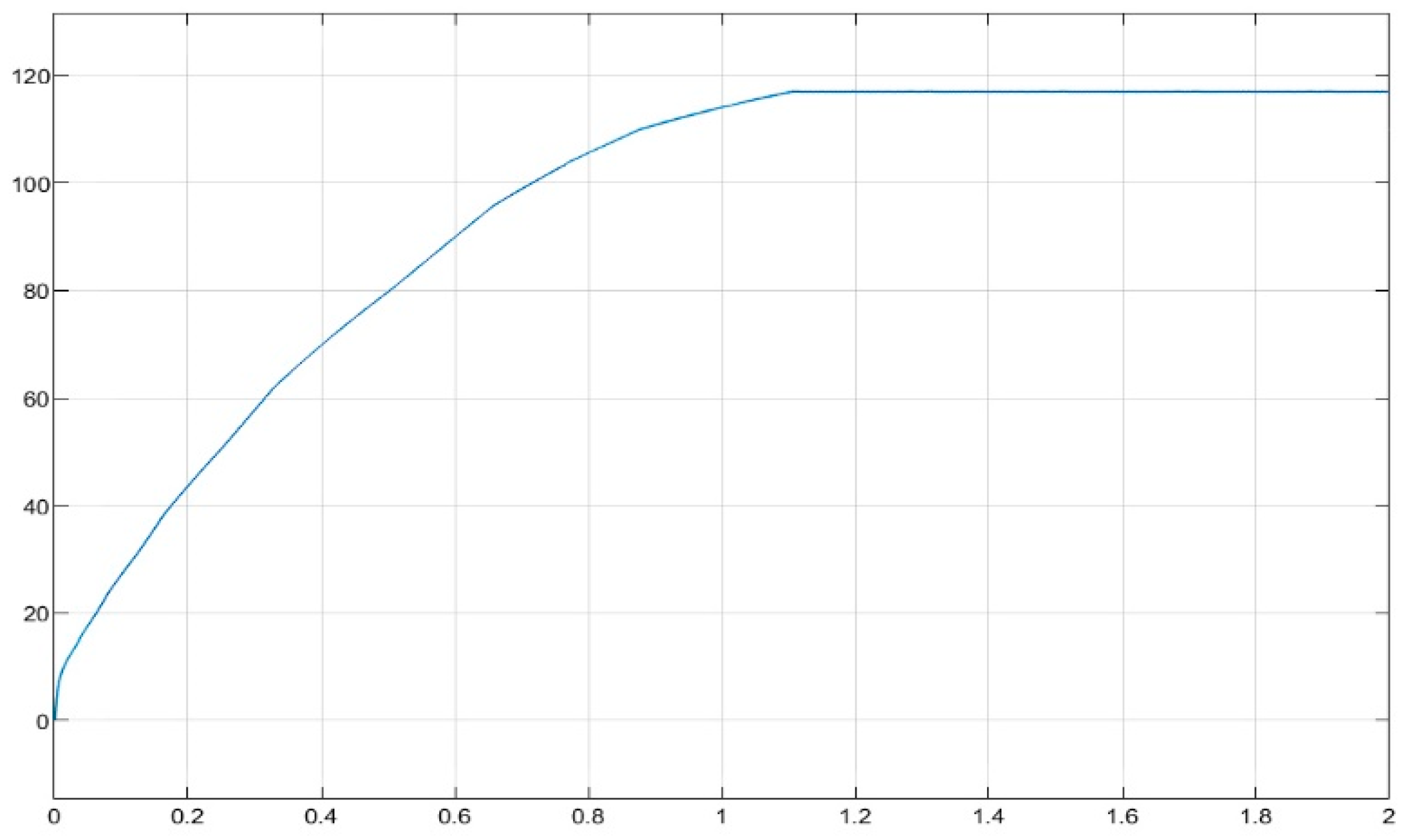
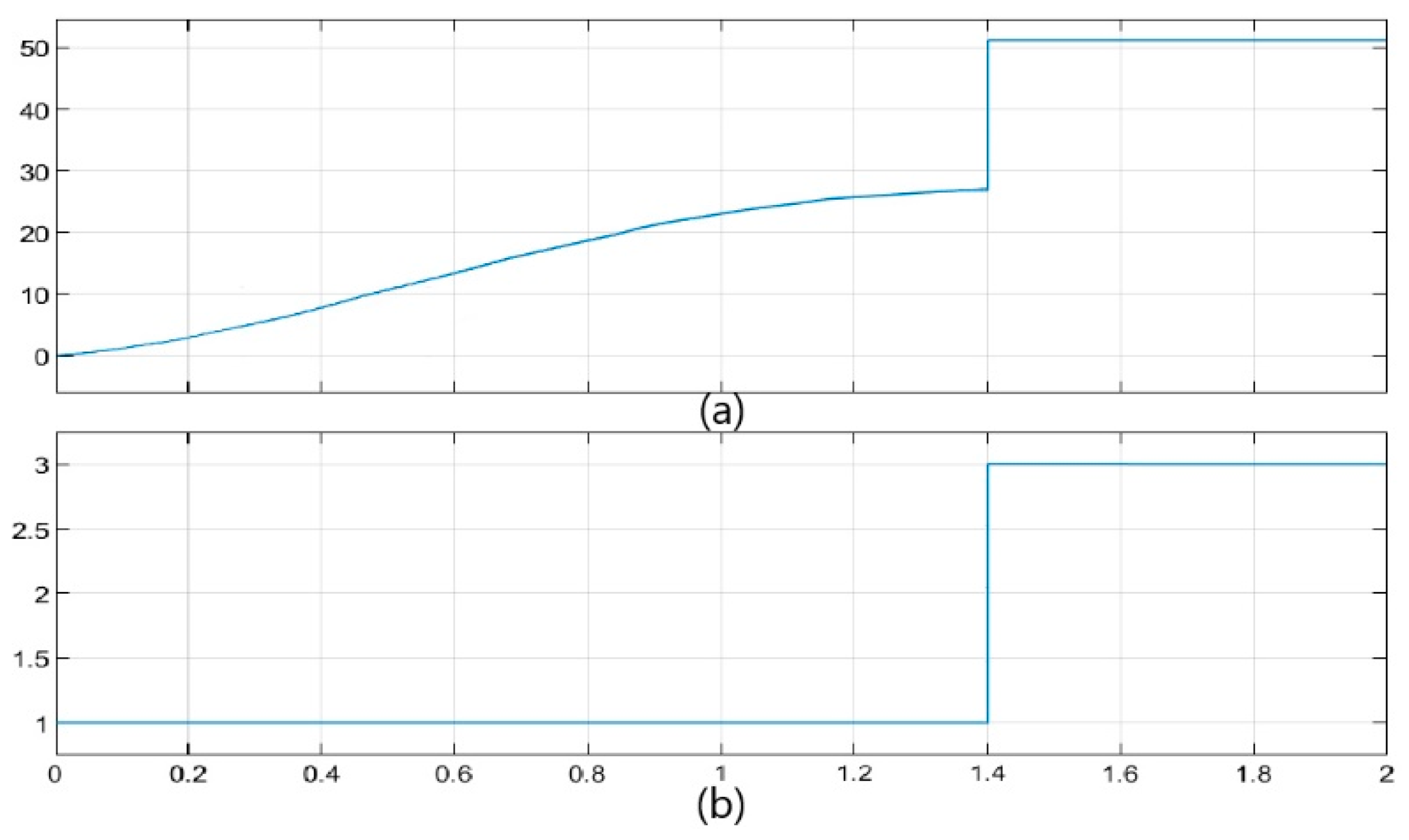
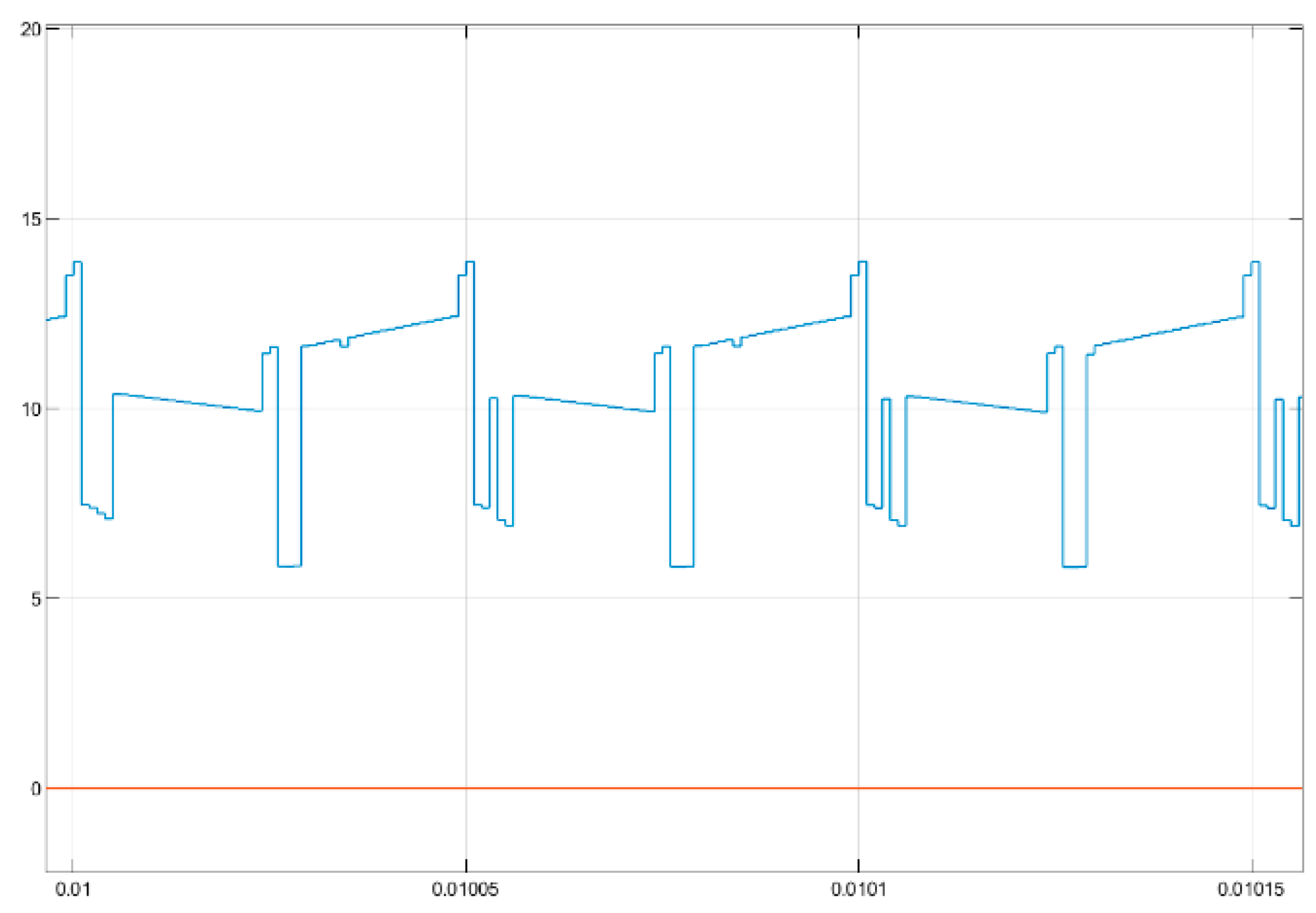
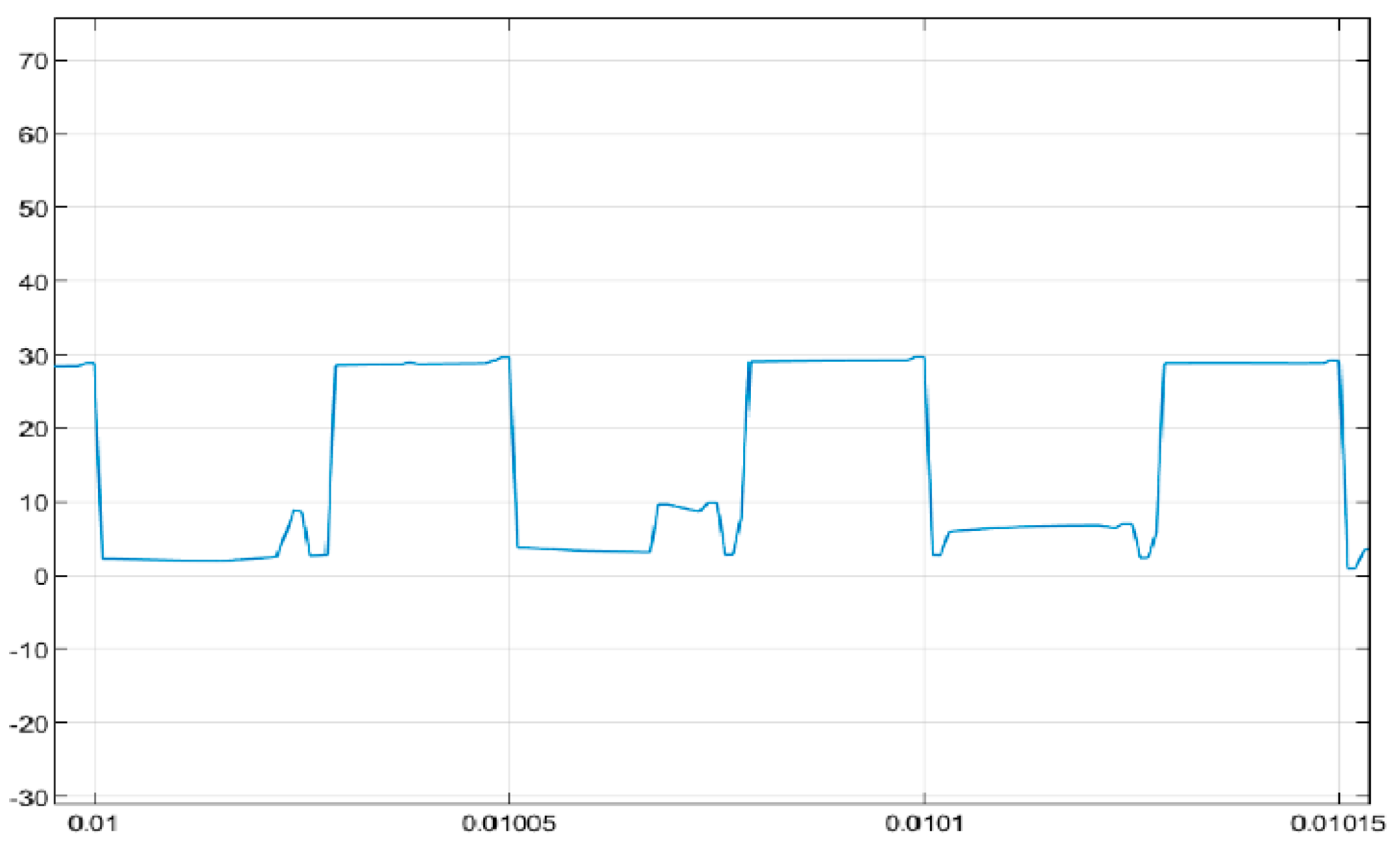
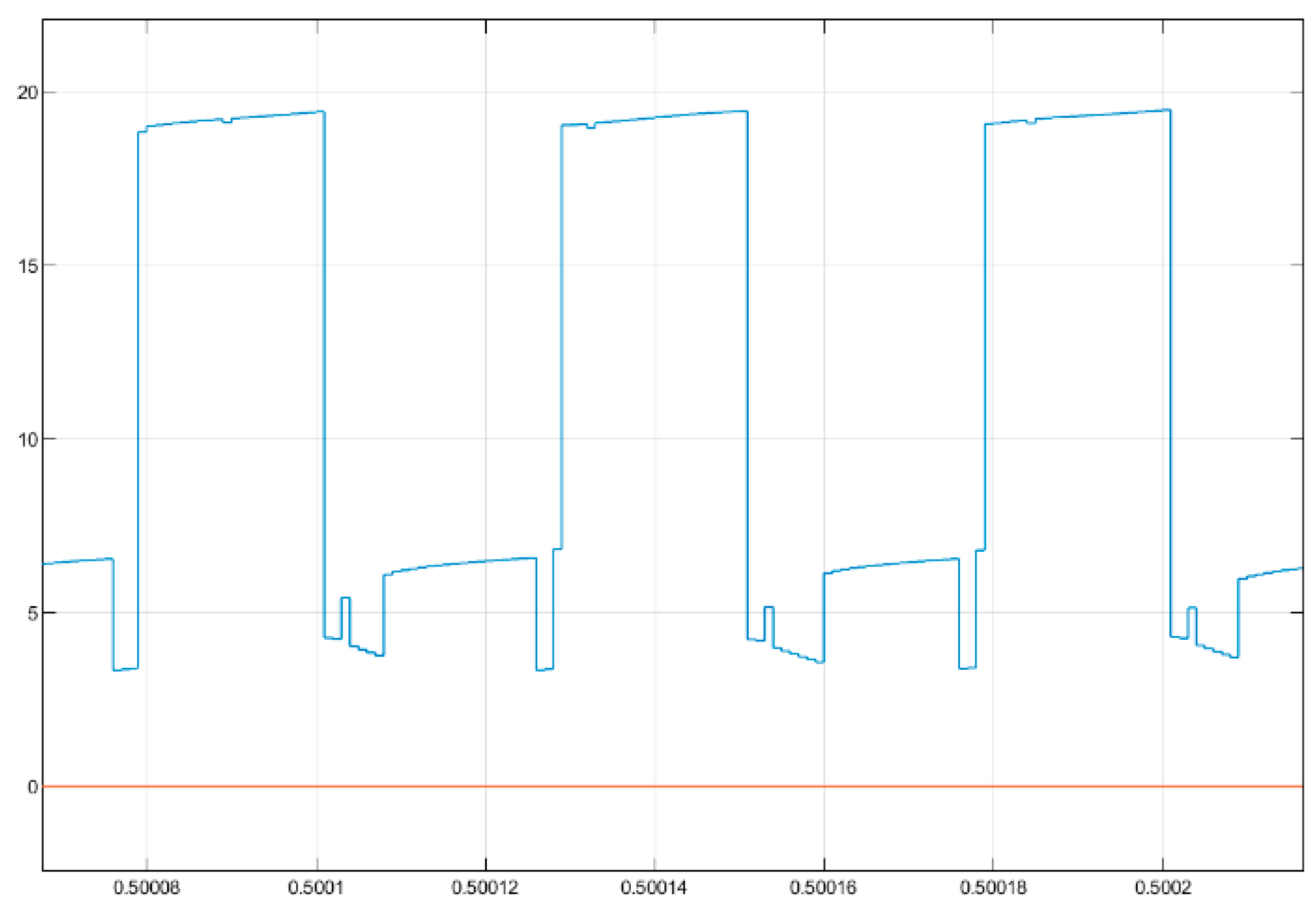
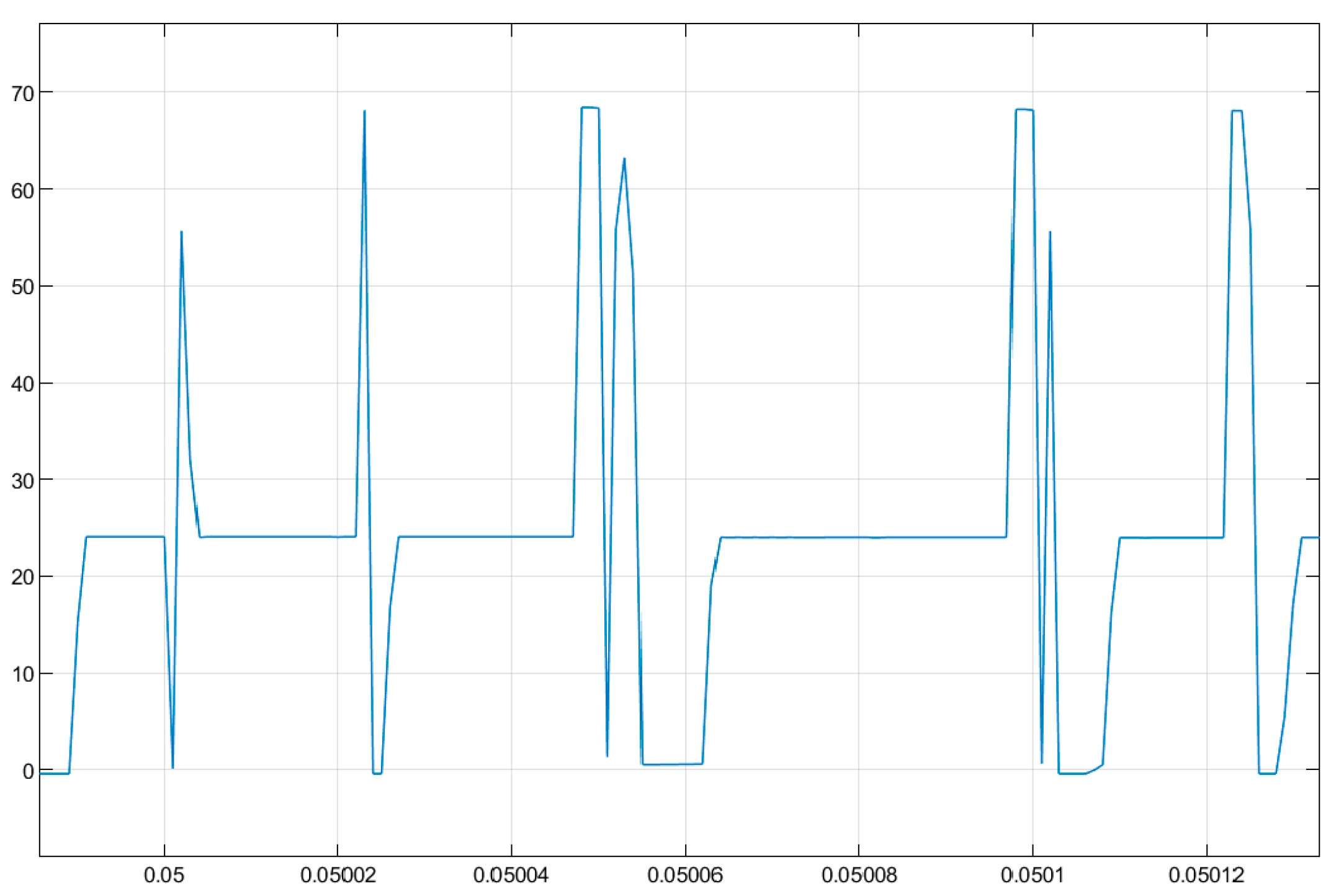
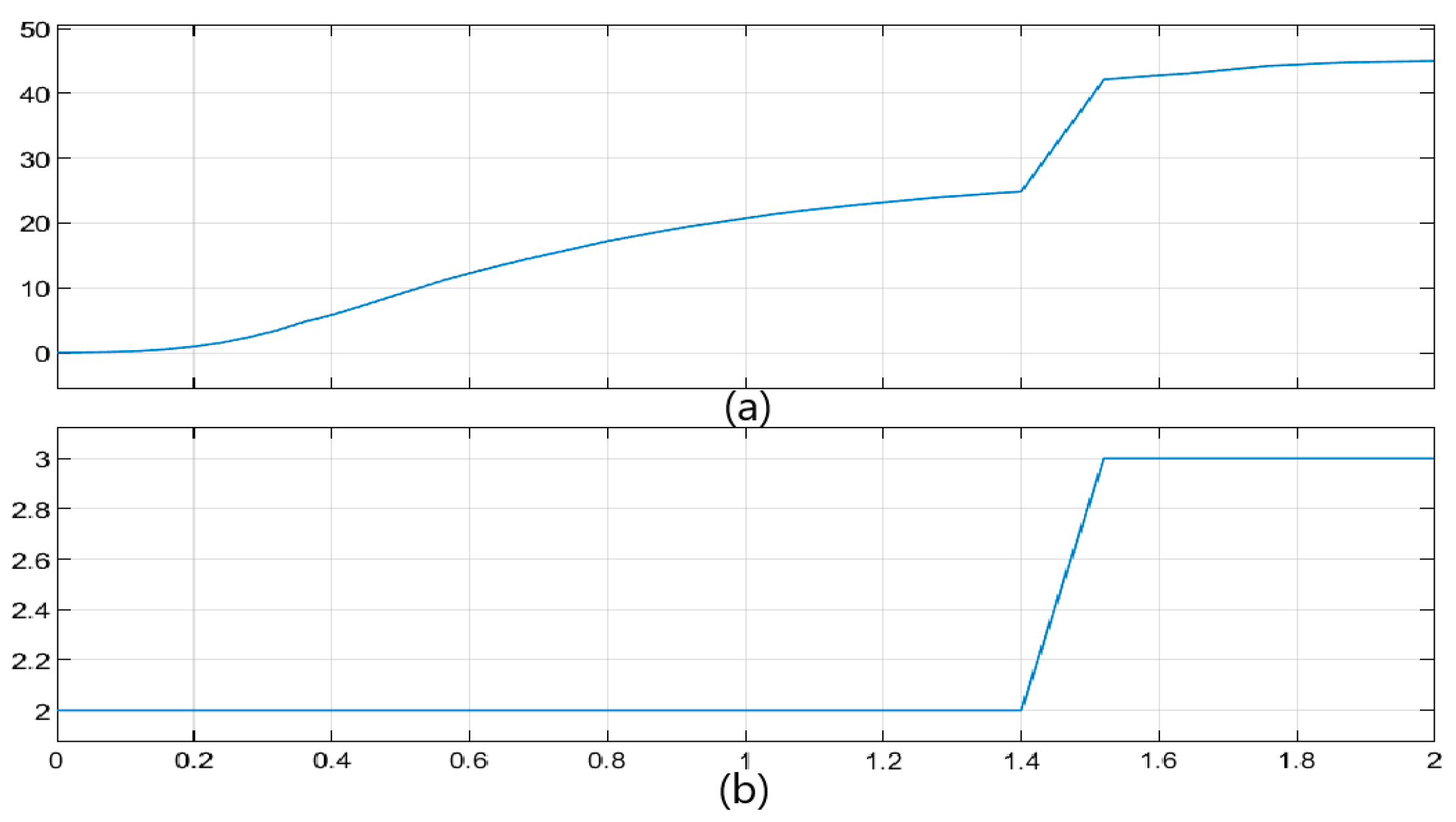
4.3. Simulation Results

The simulation duration is 2 seconds, and the step change of the load is 1.4 seconds. According to the first scenario, the battery SOC is 40%, and the converter reaches the target output voltage at 1.08 seconds. At the step change, there are no changes in the output voltage, as shown in Figure 19. While the battery SOC is at 40%, the fuzzy output starts at mode 2, and at the step change, the instantaneous power increases up to 52 watts. At the same moment, the fuzzy output changes mode from 2 to 3, as shown in Figure 20. An important point to note is that at the beginning, all of the sources are activated by the control system until the voltage reaches up to 115V. This logic is intended to help the output voltage reach the desired level as soon as possible.

In the second scenario, the battery SOC is 95%, and the output voltage reaches the target almost at the same time as in the previous case, thanks to the starting strategy of the control system, as shown in Figure 21. In Figure 22, depending on the power levels of the sources, the fuzzy output starts with power mode 1, and at the load changes, the power mode switches to mode 2. After several microseconds, even though the power is increased, there are no changes in the power mode depending on the SOC level of the battery and the PV power.

The voltage stress comparison of the switches has been made in the following Figure 23 and Figure 24. The first module’s switch T₁₂ is compared with a quasi-z-source network and without a quasi-z-source network, the voltage stress with the quasi-z-source network is around 15 V. Besides the voltage stress of the switch T₁₂ without the quasi-z-source network is around 30 V peak under the same conditions. The quasi-z-source network delays the output voltage to reach the target value of 120 V, which is around 1.1 seconds but there is a big difference in voltage stress. This is because the voltage gain of the multi-port side does not need to be high, the quasi-z-source network has a higher gain, and this lowers the voltage stresses of the switches on the multi-port side.

The voltage stress difference between the two configurations increased at higher voltages. For the multi-port quasi-z-source network, the voltage stress of switch T12 remains at 19 V when the output voltage reaches its desired value, as shown in Figure 25. In addition, for the multi-port without a quasi-z-source case, the voltage stress of switch T12 at the desired output has a 68 V peak, as can be seen in Figure 26. Both waveforms have different timing because the output voltages reach 120 V at different times.

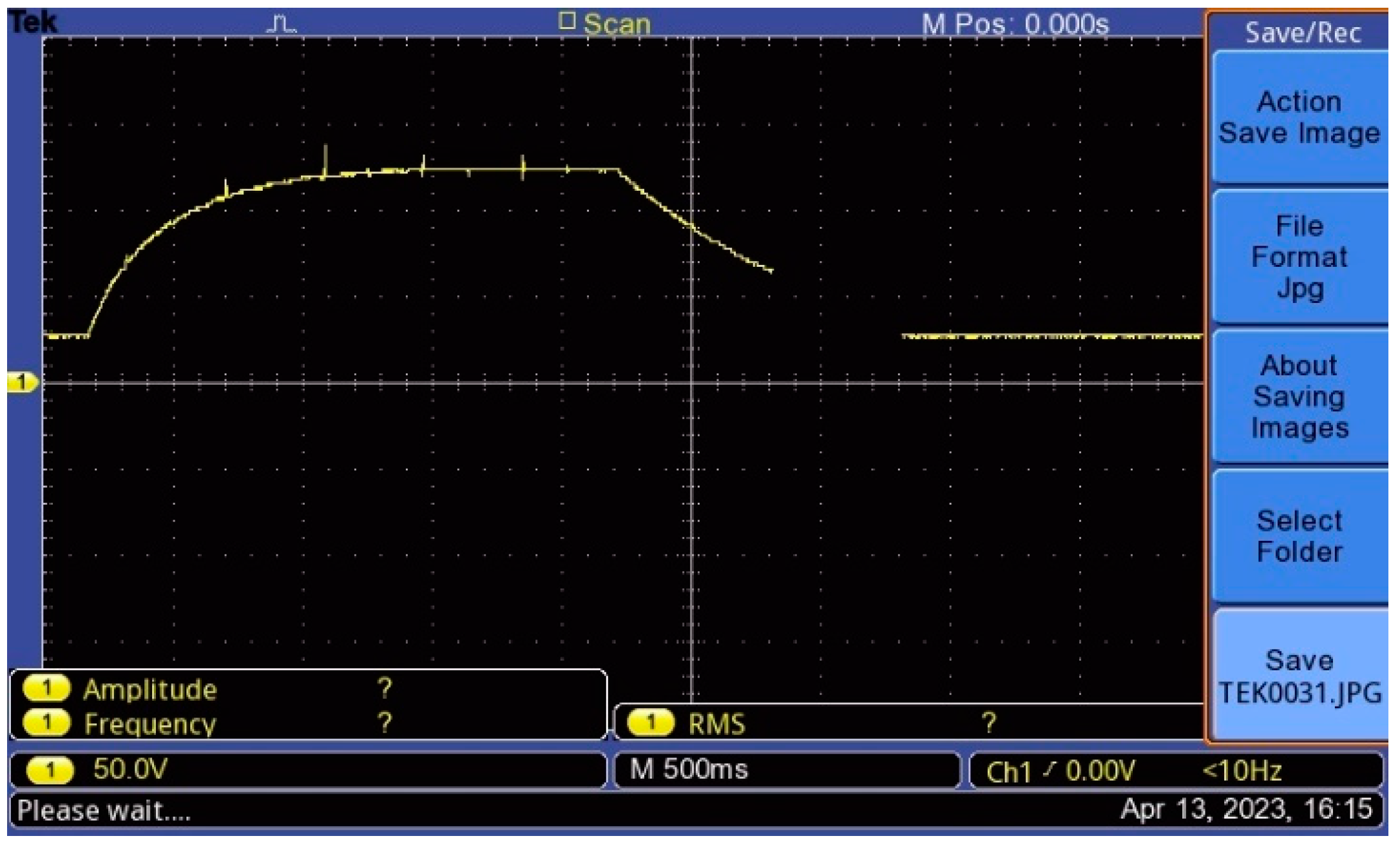
5. Experimental Test

Experimental tests consist of several sections, such as component selection, printed circuit board (PCB) layout design, PCB component assembly, and measurements. Arduino is an embedded platform that can be programmed to generate signals, read analog values, or connect different devices. The Arduino DUE is selected as the main controller for the experiments because it can be connected to MATLAB Simulink and is suitable for the process. Additionally, several configurations are required to enable the use of the Arduino platform in MATLAB Simulink. For example, the MATLAB Support package for the Arduino hardware has to be installed from the add-on explorer. The experimental setup shown in Figure 33. In Figure 33, the multiport quasi-Z-source can be seen in a blue rectangle on the PCB, the load side can be seen in a green rectangle and finally, the Arduino Uno, Arduino DUE, and the digital-to-analog converter can be seen in red rectangles.

During the experimental tests, the DENEYSAN YE-1050 experiment kit’s PV array, wind turbine, and battery were used to obtain power. The ACS712 current sensor was used for current measurements, but it could not be connected directly to an Arduino DUE because the ACS712 current sensor has a 5V analog output signal, while the Arduino DUE has a maximum 3.3V analog input. Therefore, the ACS712 current sensor was connected to the Arduino UNO, which communicated with a Digital-to-Analog converter to send the read current value to the Arduino DUE. Voltage divider resistors were used to measure the voltages and calculate the power (voltage multiplied by the current). This process can be seen in Figure 27. Before multiplying the voltage and the current, the voltage resistor formula was applied to calculate the actual measured voltage.

Table 2. Component Values.

Components	Values
L_1a, L_2a, L_1b, L_2b, L_3a, L_3b	100 µH
C₁, C₃	47 µF
C₂	470 µF
C_m1, C_m2	470 µF
C_o	680 µF
C_PV, C_Wind	470 µF
C_Z1, C_Z2	33 µF
L_Z1, L_Z2	100 µH
Load 1	440 ohm, 33 µH
Load 2	680 ohm

During the designing of the PCB layout, the traces had to be wide enough to handle the current and voltage. According to IPC-2221 regulations, the amount of current can be calculated by the following formula:

A = (T * W * 1.378[(mils/oz) / (ft)²]

(65)

A= Area of the trace.

T= Trace thickness.

W= Trace width.

I_MAX = ((k * T_RISE^b) * A^c)

(66)

T_RISE= Maximum desired temperature in Celsius

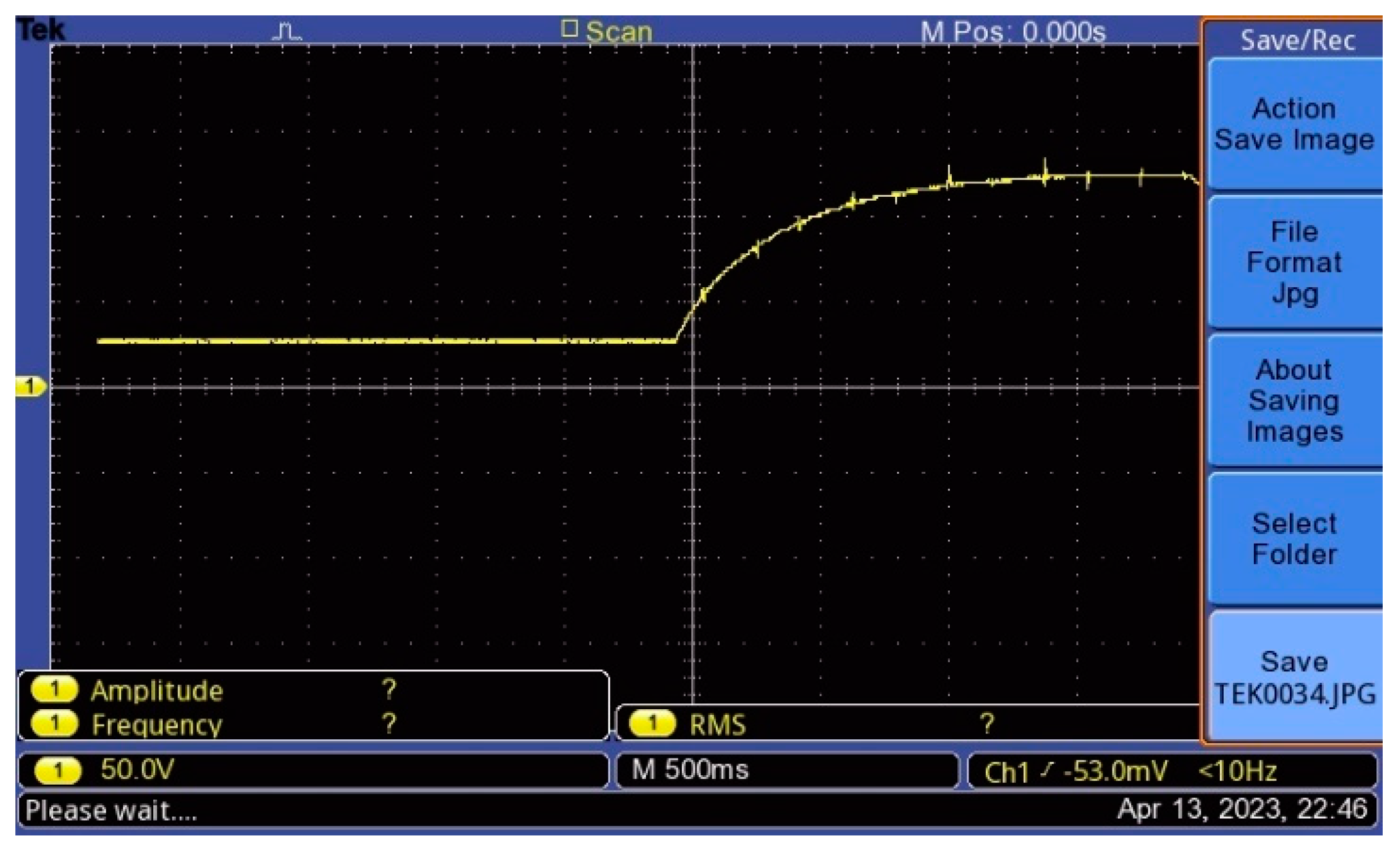
5.1. Experimental Results

The experimental configurations were the same as the simulation configurations, and the results are shown in the following. Experimental result waveforms were obtained using an oscilloscope with 50 V/div and 500 ms/div. Moreover, the current measurements are directly taken from the ACS712 current sensor via the Arduino UNO, sent to the Arduino DUE via the DAC, and reflected in MATLAB Simulink. Therefore, MATLAB Simulink scopes show the live data obtained from the current sensor. As explained before, these measured values are multiplied by the voltage to obtain the power values, and the results are shown in Figure 28 and Figure 29.

In the first scenario, the battery SOC was 40%, and the desired output voltage was reached at the desired output voltage in 1 second. After reaching the target, the PID corrected and stabilized the output voltage. The second load is activated at 1.4 s and there are no changes in the output voltage, finally, the test is completed at 2 then the voltage started to drop and it can be seen in Figure 28.

In the second scenario, the battery SOC level was 90%, and the target output voltage reached the desired level in 1 seconds. The PID made corrections and stabilized the output voltage to the desired level, the output voltage shown in Figure 30.

The SOC level of the battery plays a significant role in the starting point of the power mode. The system has the capability to meet the load demand at the starting point and depending on the power ratings, it changes after 1.4 seconds. Depending on the measurements of all of the sources, the energy management system decided to activate all of the sources when the load demand increased. Figure 32 shows the C_z2 voltage of the quasi-z-source network, the voltage is only around 75 V which is carrying less voltage stress.

Figure 31. (a) Output power (b) fuzzy system output of the scenario 2 experimental tests.

6. Discussion and Comparison

Both simulation and experimental results are the same each other. The only difference between the simulation and experimental tests that is fuzzy slope. But this difference is so small and it is not affecting the result so it can be neglected. In this section, differences and comparison will be discussed.

The difference is the slope of the fuzzy logic output. The slew rate of the fuzzy output is 0 at the simulations. On the other hand, in the real world, there are delay and tolerances, therefore the slope can be predictable but also can be neglected because it is not affecting the result. In addition, MATLAB Simulink configuration can be another reason. Other than this, the reactions of the fuzzy logic output of both simulation and experimental tests are similar.

Figure 33. Proposed system experimental setup.

Table 3 shows the comparison of the proposed energy management and other research can be made in the literature [25,27,28], which have more complex systems, making them less attractive. In addition, the proposed energy management strategy has no mathematical algorithm, and it is rule-based; therefore, experts can easily adapt the energy management system to a larger number of sources. Moreover, the referenced [29,31] needs data sets from the history. Besides proposed system requires only the fuzzy rules which are defined by the user. The study in [33] can face technical problems as renewable sources are connected. However, the proposed system can accept any type of source by implementing control algorithms based on the source type. The PID control algorithm is applied to the first module, which is battery connected, and different MPPT algorithms are applied to the second and third modules, which are the PV and Wind sources, respectively.

7. Conclusion

The proposed energy management system and multi-port quasi-z-source converter have been presented, simulated, and tested under various conditions, including load changes. The results show that the simulation and experimental tests match each other, indicating the effectiveness of the proposed system. The system can be adapted to different systems by simply changing the parameters, making it suitable for both simulation and real-world applications. Furthermore, simultaneous power flow from multiple sources can feed the load side, and more power sources can be added to the system if required. In addition, the voltage stresses on the switches of the multi-port side are significantly reduced with the quasi-z-source network. In future work, attention can be given to battery charging and the overall system efficiency to improve the sustainability of the management system.

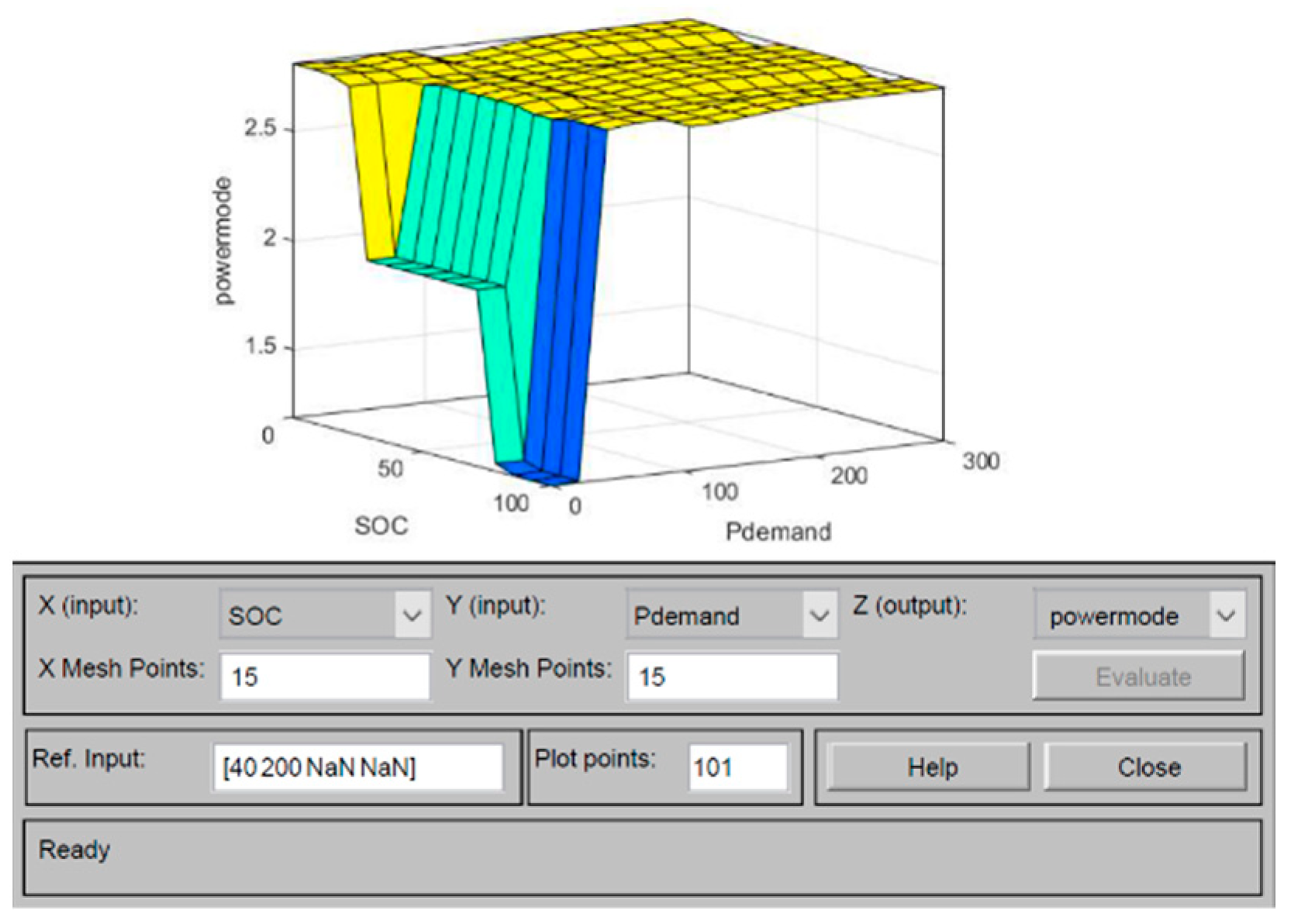
Appendix A

The fuzzy logic entire rule list can be seen below.

If P_pv is low and P_wind is low and P_demand is low and SOC is low then power mode is P3
If P_pv is low and P_wind is low and P_demand is low and SOC is medium the power mode is P2
If P_pv is low and P_wind is low and P_demand is low and SOC is high then the power mode is P1
If P_pv is low and P_wind is low and P_demand is medium and SOC is low then power mode is P3
If P_pv is low and P_wind is low and P_demand is medium and SOC is medium then power mode is P3
If P_pv is low and P_wind is low and P_demand is medium and SOC is high then power mode is P3
If P_pv is low and P_wind is low and P_demand is high and SOC is low then power mode is P3
If P_pv is low and P_wind is low and P_demand is high and SOC is medium then power mode is P3
If P_pv is low and P_wind is low and P_demand is high and SOC is high then power mode is P3
If P_pv is low and P_wind is medium P_demand is low and SOC is low then power mode is P3
If P_pv is low and P_wind is medium P_demand is low and SOC is medium then power mode is P2
If P_pv is low and P_wind is medium P_demand is low and SOC is high then power mode is P1
If P_pv is low and P_wind is medium P_demand is medium and SOC is low then power mode is P3
If P_pv is low and P_wind is medium P_demand is medium and SOC is medium then power mode is P3
If P_pv is low and P_wind is medium P_demand is medium and SOC is high then power mode is P3
If P_pv is low and P_wind is medium P_demand is high and SOC is low then power mode is P3
If P_pv is low and P_wind is medium P_demand is high and SOC is medium then power mode is P3
If P_pv is low and P_wind is medium P_demand is high and SOC is high then power mode is P3
If P_pv is low and P_wind is high P_demand is low and SOC is low then power mode is P3
If P_pv is low and P_wind is high P_demand is low and SOC is medium then power mode is P2
If P_pv is low and P_wind is high P_demand is low and SOC is high then power mode is P1
If P_pv is low and P_wind is high P_demand is medium and SOC is low then power mode is P3
If P_pv is low and P_wind is high P_demand is medium and SOC is medium then power mode is P3
If P_pv is low and P_wind is high P_demand is medium and SOC is high then power mode is P3
If P_pv is low and P_wind is high P_demand is high and SOC is low then power mode is P3
If P_pv is low and P_wind is high P_demand is high and SOC is medium then power mode is P3
If P_pv is low and P_wind is high P_demand is high and SOC is high then power mode is P3
If P_pv is medium and P_wind is low and P_demand is low and SOC is low then power mode is P3
If P_pv is medium and P_wind is low and P_demand is low and SOC is medium the power mode is P2
If P_pv is medium and P_wind is low and P_demand is low and SOC is high then the power mode is P1
If P_pv is medium and P_wind is low and P_demand is medium and SOC is low then power mode is P3
If P_pv is medium and P_wind is low and P_demand is medium and SOC is medium then power mode is P3
If P_pv is medium and P_wind is low and P_demand is medium and SOC is high then power mode is P3
If P_pv is medium and P_wind is low and P_demand is high and SOC is low then power mode is P3
If P_pv is medium and P_wind is low and P_demand is high and SOC is medium then power mode is P3
If P_pv is medium and P_wind is low and P_demand is high and SOC is high then power mode is P3
If P_pv is medium and P_wind is medium P_demand is low and SOC is low then power mode is P3
If P_pv is medium and P_wind is medium P_demand is low and SOC is medium then power mode is P2
If P_pv is medium and P_wind is medium P_demand is low and SOC is high then power mode is P1
If P_pv is medium and P_wind is medium P_demand is medium and SOC is low then power mode is P3
If P_pv is medium and P_wind is medium P_demand is medium and SOC is medium then the power mode is P3
If P_pv is medium and P_wind is medium P_demand is medium and SOC is high then power mode is P3
If P_pv is medium and P_wind is medium P_demand is high and SOC is low then power mode is P3
If P_pv is medium and P_wind is medium P_demand is high and SOC is medium then power mode is P3
If P_pv is medium and P_wind is medium P_demand is high and SOC is high then power mode is P3
If P_pv is medium and P_wind is high P_demand is low and SOC is low then power mode is P3
If P_pv is medium and P_wind is high P_demand is low and SOC is medium then power mode is P3
If P_pv is medium and P_wind is high P_demand is low and SOC is high then power mode is P1
If P_pv is medium and P_wind is high P_demand is medium and SOC is low then power mode is P3
If P_pv is medium and P_wind is high P_demand is medium and SOC is medium then power mode is P3
If P_pv is medium and P_wind is high P_demand is medium and SOC is high then power mode is P3
If P_pv is medium and P_wind is high P_demand is high and SOC is low then power mode is P3
If P_pv is medium and P_wind is high P_demand is high and SOC is medium then power mode is P3
If P_pv is medium and P_wind is high P_demand is high and SOC is high then power mode is P3
If P_pv is high and P_wind is low and P_demand is low and SOC is low then power mode is P2
If P_pv is high and P_wind is low and P_demand is low and SOC is medium the power mode is P2
If P_pv is high and P_wind is low and P_demand is low and SOC is high then the power mode is P1
If P_pv is high and P_wind is low and P_demand is medium and SOC is low then power mode is P3
If P_pv is high and P_wind is low and P_demand is medium and SOC is medium then power mode is P3
If P_pv is high and P_wind is low and P_demand is medium and SOC is high then power mode is P2
If P_pv is high and P_wind is low and P_demand is high and SOC is low then power mode is P3
If P_pv is high and P_wind is low and P_demand is high and SOC is medium then power mode is P3
If P_pv is high and P_wind is low and P_demand is high and SOC is high then power mode is P3
If P_pv is high and P_wind is medium P_demand is low and SOC is low then power mode is P2
If P_pv is high and P_wind is medium P_demand is low and SOC is medium then power mode is P2
If P_pv is high and P_wind is medium P_demand is low and SOC is high then power mode is P1
If P_pv is high and P_wind is medium P_demand is medium and SOC is low then power mode is P3
If P_pv is high and P_wind is medium P_demand is medium and SOC is medium then power mode is P3
If P_pv is high and P_wind is medium P_demand is medium and SOC is high then power mode is P2
If P_pv is high and P_wind is medium P_demand is high and SOC is low then power mode is P3
If P_pv is high and P_wind is medium P_demand is high and SOC is medium then power mode is P3
If P_pv is high and P_wind is medium P_demand is high and SOC is high then power mode is P3
If P_pv is high and P_wind is high P_demand is low and SOC is low then power mode is P2
If P_pv is high and P_wind is high P_demand is low and SOC is medium then power mode is P2
If P_pv is high and P_wind is high P_demand is low and SOC is high then power mode is P1
If P_pv is high and P_wind is high P_demand is medium and SOC is low then power mode is P3
If P_pv is high and P_wind is high P_demand is medium and SOC is medium then power mode is P3
If P_pv is high and P_wind is high P_demand is medium and SOC is high then power mode is P2
If P_pv is high and P_wind is high P_demand is high and SOC is low then power mode is P3
If P_pv is high and P_wind is high P_demand is high and SOC is medium then power mode is P3
If P_pv is high and P_wind is high P_demand is high and SOC is high then power mode is P3

References

Yan Li; Dongsheng Yang; Xinbo Ruan A Systematic Method for Generating Multiple-Input DC/DC Converters. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference; IEEE, September 2008; pp. 1–6.
Nejabatkhah, F.; Danyali, S.; Hosseini, S.H.; Sabahi, M.; Niapour, S.M. Modeling and Control of a New Three-Input Dc-Dc Boost Converter for Hybrid PV/FC/Battery Power System. IEEE Trans Power Electron 2012, 27, 2309–2324. [CrossRef]
Argentini, S.; Pietroni, I.; Mastrantonio, G.; Viola, A.; Zilitinchevich, S. Characteristics of The. 2006, 51, 1–14.
Dobbs, B.G.; Chapman, P.L. A Multiple-Input DC-DC Converter Topology. IEEE Power Electronics Letters 2003, 1, 6–9. [CrossRef]
Karthikeyan, V.; Gupta, R. Multiple-Input Configuration of Isolated Bidirectional DC–DC Converter for Power Flow Control in Combinational Battery Storage. IEEE Trans Industr Inform 2018, 14, 2–11. [CrossRef]
Ahrabi, R.R.; Ardi, H.; Elmi, M.; Ajami, A. A Novel Step-Up Multiinput DC–DC Converter for Hybrid Electric Vehicles Application. IEEE Trans Power Electron 2017, 32, 3549–3561. [CrossRef]
Dezhbord, M.; Mohseni, P.; Hosseini, S.H.; Mirabbasi, D.; Islam, Md.R. A High Step-Up Three-Port DC–DC Converter With Reduced Voltage Stress for Hybrid Energy Systems. IEEE Journal of Emerging and Selected Topics in Industrial Electronics 2022, 3, 998–1009. [CrossRef]
Nazih, Y.; Abdel-Moneim, M.G.; Aboushady, A.A.; Abdel-Khalik, A.S.; Hamad, M.S. A Ring-Connected Dual Active Bridge Based DC-DC Multiport Converter for EV Fast-Charging Stations. IEEE Access 2022, 10, 52052–52066. [CrossRef]
Jalilzadeh, T.; Rostami, N.; Babaei, E.; Hosseini, S.H. Bidirectional Multi-port Dc–Dc Converter with Low Voltage Stress on Switches and Diodes. IET Power Electronics 2020, 13, 1593–1604. [CrossRef]
Ninma Jiya, I.; Van Khang, H.; Kishor, N.; Ciric, R.M. Novel Family of High-Gain Nonisolated Multiport Converters With Bipolar Symmetric Outputs for DC Microgrids. IEEE Trans Power Electron 2022, 37, 12151–12166. [CrossRef]
Varesi, K.; Hosseini, S.H.; Sabahi, M.; Babaei, E. Modular Non-Isolated Multi-Input High Step-up Dc-Dc Converter with Reduced Normalised Voltage Stress and Component Count. IET Power Electronics 2018, 11, 1092–1100. [CrossRef]
Varesi, K.; Hosseini, S.H.; Sabahi, M.; Babaei, E. A Multi-Port High Step-Up DC-DC Converter with Reduced Normalized Voltage Stress on Switches/Diodes. 9th Annual International Power Electronics, Drive Systems, and Technologies Conference, PEDSTC 2018 2018, 2018-Janua, 1–6. [CrossRef]
Fang Zheng Peng Z-Source Inverter. IEEE Trans Ind Appl 2003, 39, 504–510. [CrossRef]
Tang, Y.; Xie, S.; Zhang, C. An Improved $Z$-Source Inverter. IEEE Trans Power Electron 2011, 26, 3865–3868. [CrossRef]
Shen, H.; Zhang, B.; Qiu, D.; Zhou, L. A Common Grounded Z-Source DC–DC Converter With High Voltage Gain. IEEE Transactions on Industrial Electronics 2016, 63, 2925–2935. [CrossRef]
Anderson, J.; Peng, F.Z. Four Quasi-Z-Source Inverters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference; IEEE, June 2008; pp. 2743–2749.
Hosseini, S.M.; Ghazi, R.; Nikbahar, A.; Eydi, M. A New Enhanced-boost Switched-capacitor Quasi Z-source Network. IET Power Electronics 2021, 14, 412–421. [CrossRef]
Torki Harchegani, A.; Asghari, A.; Jazaeri, M. A New Soft-switching Multi-input Quasi-Z-source Converter for Hybrid Sources Systems. IET Renewable Power Generation 2021, 15, 1451–1468. [CrossRef]
Biasini, R.; Onori, S.; Rizzoni, G. A Near-Optimal Rule-Based Energy Management Strategy for Medium Duty Hybrid Truck. International Journal of Powertrains 2013, 2, 232. [CrossRef]
Petrović, D.J.; Lazić, M.M.; Lazić, B.V.J.; Blanuša, B.D.; Aleksić, S.O. Hybrid Power Supply System with Fuzzy Logic Controller: Power Control Algorithm, Main Properties, and Applications. Journal of Modern Power Systems and Clean Energy 2021, 1–9.
Ganguly, P.; Kalam, A.; Zayegh, A. Fuzzy Logic-Based Energy Management System of Stand-Alone Renewable Energy System for a Remote Area Power System. Australian Journal of Electrical and Electronics Engineering 2019, 16, 21–32. [CrossRef]
Koulali, M.; Mankour, M.; Negadi, K.; Mezouar, A. Energy Management of Hybrid Power System PV Wind and Battery Based Three Level Converter. TECNICA ITALIANA-Italian Journal of Engineering Science 2019, 63, 297–304. [CrossRef]
Baset, D.A.-E.; Rezk, H.; Hamada, M. Fuzzy Logic Control Based Energy Management Strategy for Renewable Energy System. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE); IEEE, March 2020; pp. 1–5.
Teo, T.T.; Logenthiran, T.; Woo, W.L.; Abidi, K.; John, T.; Wade, N.S.; Greenwood, D.M.; Patsios, C.; Taylor, P.C. Optimization of Fuzzy Energy-Management System for Grid-Connected Microgrid Using NSGA-II. IEEE Trans Cybern 2021, 51, 5375–5386. [CrossRef]
Zhang, Z.; Guan, C.; Liu, Z. Real-Time Optimization Energy Management Strategy for Fuel Cell Hybrid Ships Considering Power Sources Degradation. IEEE Access 2020, 8, 87046–87059. [CrossRef]
Wang, T.; Li, Q.; Wang, X.; Qiu, Y.; Liu, M.; Meng, X.; Li, J.; Chen, W. An Optimized Energy Management Strategy for Fuel Cell Hybrid Power System Based on Maximum Efficiency Range Identification. J Power Sources 2020, 445, 227333. [CrossRef]
Namwook Kim; Sukwon Cha; Huei Peng Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. IEEE Transactions on Control Systems Technology 2011, 19, 1279–1287. [CrossRef]
Yu, J.; Dou, C.; Li, X. MAS-Based Energy Management Strategies for a Hybrid Energy Generation System. IEEE Transactions on Industrial Electronics 2016, 63, 3756–3764. [CrossRef]
Garcia, P.; Garcia, C.A.; Fernandez, L.M.; Llorens, F.; Jurado, F. ANFIS-Based Control of a Grid-Connected Hybrid System Integrating Renewable Energies, Hydrogen and Batteries. IEEE Trans Industr Inform 2014, 10, 1107–1117. [CrossRef]
Li, Q.; Wang, T.; Dai, C.; Chen, W.; Ma, L. Power Management Strategy Based on Adaptive Droop Control for a Fuel Cell-Battery-Supercapacitor Hybrid Tramway. IEEE Trans Veh Technol 2018, 67, 5658–5670. [CrossRef]
Zhang, S.; Xiong, R.; Sun, F. Model Predictive Control for Power Management in a Plug-in Hybrid Electric Vehicle with a Hybrid Energy Storage System. Appl Energy 2017, 185, 1654–1662. [CrossRef]
Suthar, S.; Pindoriya, N.M. Energy Management Platform for Integrated Battery-Based Energy Storage – Solar PV System: A Case Study. IET Energy Systems Integration 2020, 2, 373–381. [CrossRef]
Ghosh, S.K.; Roy, T.K.; Pramanik, M.A.H.; Mahmud, M.A. A Nonlinear Double-integral Sliding Mode Controller Design for Hybrid Energy Storage Systems and Solar Photovoltaic Units to Enhance the Power Management in DC Microgrids. IET Generation, Transmission & Distribution 2022, 16, 2228–2241. [CrossRef]

Figure 1. Multi-port quasi-z-source converter with 2 inputs.

Figure 2. Mode 1a.

Figure 4. Mode 2a.

Figure 5. Mode 2b.

Figure 6. Mode 3a.

Figure 7. Mode 3b.

Figure 9. Flow chart of the management strategy.

Figure 10. Block diagram of the overall system.

Figure 11. Main blocks of the simulation.

Figure 12. First module and output side of the circuit.

Figure 13. Second module.

Figure 14. Third module.

Figure 15. Fuzzy logic designer toolbox.

Figure 16. Rules of the fuzzy logic.

Figure 17. Surface viewer.

Figure 18. Control of the switches.

Figure 19. Output voltage of scenario 1.

Figure 20. (a) Output power, (b) fuzzy system output of scenario 1.

Figure 21. Output voltage of scenario 2.

Figure 22. (a) Output power, (b) fuzzy system output of scenario 2.

Figure 23. Voltage stress on the switch T₁₂ with the quasi-z-source network.

Figure 24. Voltage stress on the switch T₁₂ without quasi-z-source network.

Figure 25. Voltage stress on the switch T₁₂ with the quasi-z-source network at 120 V output.

Figure 26. Voltage stress on the switch T₁₂ without a quasi-z-source network at 120 V output.

Figure 27. Power calculation.

Figure 28. Output voltage of the scenario 1 experimental tests.

Figure 29. (a) Output power (b) fuzzy system output of the scenario 1 experimental tests.

Figure 30. Output voltage of the scenario 2 experimental tests.

Figure 32. C_z2 Voltage of the quasi-z-source network.

Table 1. PV Array specifications.

Open-circuit voltage V_OC (V)	22.77
Short-circuit current I_SC (A)	5.86
Voltage at Maximum Power Point V_mp (V)	18.3
Current at Maximum Power Point I_mp (A)	5.5

Table 3. Comparison of the different energy management references and proposed energy management.

Reference	Adv. / Disadv.	Response Time	Complexity	No. of Inputs
[25]	Fuel economy is good, system durability is high, Complex system, limited application area	-	High	3 inputs (Fuel cell, battery, Super Capacitor)
[27]	Reasonable assumptions, Complex system	+	High
[28]	High decision-making time, Complex system	-	High	3 inputs (PV, Wind turbine, Battery)
[29]	Hybrid sources, Needs datasets	+	Medium	5 inputs (Grid, PV, Wind turbine, Fuel Cell, Battery)
[31]	Can predict future, large-scale operations are difficult, Needs datasets	+	Medium	2 inputs (LTO; Li-Ti-O battery, NCM; Ni-Co-Mn battery)
Proposed System	No mathematical algorithm, fuzzy rules, can adapt high number of sources	+	Low	N numbered (any type of source including renewable sources)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Hybrid Source Multi-Port Quasi-Z-Source Converter with Fuzzy Logic-Based Energy Management

Abstract

1. Introduction

2. Proposed Multi-Port Converter with Quasi-Z-Source Network

2.1. Working Modes and Mathematical Expressions

3. Proposed Energy Management Strategy

4. Simulation of the Proposed Control System

4.1. Simulink Model

4.2. Other Control Parameters

4.3. Simulation Results

5. Experimental Test

5.1. Experimental Results

6. Discussion and Comparison

7. Conclusion

Appendix A

References

MDPI Initiatives

Important Links

Subscribe