Inference on a Multi-Patched Epidemic Model with Partial Mobility, Residency and Demography: The Case of 2020 COVID-19 Outbreak in Hermosillo, Mexico

1. Introduction

The mathematical modeling of infectious diseases has been a continuously growing research area over the past few decades. This is due to the significant impact that infectious diseases can have on a wide range of important areas, including social, health, and economic development, whose main driving factor is human populationThe mathematical modeling of infectious diseases has witnessed continuous growth as a research area in recent decades. This growth has been primarily motivated by the substantial impact that contagious diseases have on various crucial domains, including social, health, and economic development. [1,2,3,4,5].These domains are intricately linked to human population interaction, which serves as a key driving factor.

Indeed, works such as [6] and [7], raised awareness on the fact that the emergence and re-emergence of infectious diseases had historically been neglected as a significant threat to public health. Understanding the propagation dynamics of infectious diseases has thus become a central issue for epidemiologists and theoreticians [8,9,10,11,12]. Such knowledge would in turn lead to the formulation of robust infection mitigation policies, yielding, in the end, a healthy human population, that significantly contributes to the economic development of their respective nations.Such knowledge would subsequently enable the formulation of effective infection mitigation policies. These policies, in turn, would contribute to maintaining a healthy human population, thereby significantly bolstering the economic development of their respective nations.

Since its advent and declaration as a pandemic in March 2020 by the WHO, COVID-19 has undeniably wrecked havoc and drastically impacted the lives and livelihoods of the global human population. In terms of significance, COVID-19 has been compared to the influenza pandemic of 1948-20, [8] but these are not yet equated in terms of severity. The 1918 influenza pandemic had an estimated death toll of 40 Million lives and infected 1/3 of the world population as compared to COVID-19 which so far has a death toll of 6.6 Million and confirmed cases of 633 Million (less than 10% of total human population) [13]. However, the urgency in the need for more research on COVID-19, and other infectious diseases, is qualified by the warnings from scientists in the recent past about the likelihood of another pandemic striking at any momentHowever, the urgency for conducting further research on COVID-19 and other infectious diseases is underscored by the warnings issued by scientists in recent times regarding the imminent threat of another pandemic. These cautionary alerts emphasize the pressing need to proactively study and understand these diseases to be better prepared for any potential future outbreaks. [14]. These studies seek understanding the dynamics of the infection propagation, control and mitigation strategies. and include but are notThey encompass various aspects, including but not limited to model selection, statistical inference, uncertainty quantification and prediction using empirical epidemiological data. Such studies furnish epidemiologists and policymakers with useful information on the impact of control and eradication measures and formulation of effective response strategies in anticipation of a new pandemic crisis.valuable information in relation to the effectiveness of control and eradication measures. This knowledge facilitates the formulation of proactive response strategies in anticipation of a potential new pandemic crisis.

At the core of the transmission dynamics of infectious and communicable diseases like COVID-19 is human behaviour and interaction. Consequently, it behooves researchers and epidemiologists involved in the study of infectious diseases to accurately incorporate human behaviour as a critical component of the models used in modelling infectious diseases [15]. One such human behaviour that has, over the years, fundamentally shaped person to person transmission of infectious diseases in the face of an outbreak is formulation of human networks, population mobility and travel,One significant human behavior that has consistently influenced person-to-person transmission of infectious diseases during outbreaks is mobility. [10,16,17,18,19,20,21]. The mobility and its travel patterns promote the creation of temporal social connections and networks that both local and global, play a crucial role in the spread of diseases. Human mobility, an undeniably crucial component of human existence and survival, not only plays a critical role in the spread and propagation of an epidemic [18,22,23,24], but it also crucially determines the spreading speed of infectious diseases, [23,25,26]. There is therefore no gainsaying that deep understanding of the role of human mobility in the spread of infectious diseases is central in the quest to have a clear view, for instance, of the impact of control strategies such as mobility restrictions [27,28,29,30,31].

Developments in epidemiological research have confirmed that traditional compartmental epidemic models are deficient in modeling strong heterogeneous disease spread, as they were formulated with the assumption of interaction of a well-mixed homogeneous population [15,32,33]. It is widely recognized that humans do not exhibit homogeneous mobility patterns, [15], which highlights the importance of incorporating heterogeneous population behavioral responses in epidemiological models as emphasized by [34]. The literature is replete with a plethora of proposed models for capturing human heterogeneous mobility and dispersal and most of them are mostly geo-meta-population-multi-patched based, as can be seen inThe scientific literature offers a wide array of proposed models that aim to capture the heterogeneous mobility and dispersal patterns observed among humans. Many of these models consists of human groups of spatially separated populations which interact at some level (geo-meta-population-multi-patched framework), as evidenced by numerous references in the literature [e.g., [26,27,34,35,36,37,38,39,40,41,42]. Although modelling geo-spatial-temporal spread of infectious diseases is a complex task [43], models such as the ones in the mentioned references have crucially attempted to accurately capture human mobility in different settings. Nevertheless, there is still need to incorporate more realistic mobility patterns that reflect more complex mobility scenarios [17], which is an inevitable reality of human behaviour. In some situations, an appropriate approach could be to describe the connection between the spread of infectious diseases and the fraction of time that residents spend in different patches (homogeneous in terms of some characteristic, e.g. risk of infection) in the course of their traveling In certain scenarios, it may be highly desirable to explore the relationship between the spread of infectious diseases and the proportion of time individuals spend in different locations during their travels [44]. This approach considers the impact of human movement on disease transmission and how it relates to the amount of time spent in locations, each having specific characteristics, such as the risk of infection level. These locations, that are homogeneous within them and possibly different between them, are usually referred in the literature as patches. Then, a single-patch model reduces to a model with a well-mixed homogeneous population where every susceptible individual can become infected with the same probability. The concept of multi-patches not only allows to consider locations with different characteristics but helps in capturing the spatial dynamics and interactions, produced by the human mobility, that influence the spread of infectious diseases.

Once an appropriate epidemic model has been formulated, a myriad of analysis relevant to epidemiologists, policy makers and public health officials can be conducted. These include but are not limited to theoretical analysis and numerical simulations [see e.g., [39,40,45,46,47], inference, uncertainty quantification and predictions [see e.g., [14,48,49,50,51,52,53]. Most studies modelling population mobility and the spread of infectious diseases, particularly using meta-population-multi-patched models, have tended to focus on theoretical and global properties and numerical simulations of such models. There is relatively scanty literature published on inference and uncertainty quantification on epidemic models with population mobility. To our knowledge, to this date, the only research work that has come close to performing inference, uncertainty quantification and predictions on a multi-patch epidemic model is [51] who developed and used a projected Stein Variational Gradient Descent (pSVGD) algorithm to model COVID-19 in the states of New Jersey and Texas in the US. However, their model did not incorporate population mobility as they modeled the dynamics and severity of COVID-19 inside and outside long-term care (LTC) facilities where the interaction was introduced through some contact matrix. Other works that have addressed the problem of statistical inference for epidemics on networks are [54] and [55]. These models consider families of networks of contact that remains constant through time. Filling the gap left by the conspicuous lack of literature on uncertainty quantification and Bayesian inverse problems on meta-population-multi-patched epidemic models, forms the central motivation of the present study. To this end, we perform inference and uncertainty quantification, using COVID-19 confirmed cases in Hermosillo, Mexico, on a multi-patched epidemic model with mobility, residency and demography. This model was proposed and theoretical analyzed inTo achieve this objective, we conduct inference and uncertainty quantification using COVID-19 confirmed cases in Hermosillo, Mexico. We employ a multi-patched epidemic model that incorporates mobility, residency, and demography. This model was proposed and theoretically analyzed in [42].

Solving an inverse problem involves the combination of actual observed data and the model to deduce the values of the parameters that characterizes the said modelSolving an inverse problem entails the utilization of both observed data and a model to deduce the parameter values that characterize the dynamics producing the observations [56,57,58]. However, using models that are sufficient and are well posed in capturing heterogeneity and complexity of human behaviour, such as mobility, when modelling the spread of infectious diseases, leads to the introduction of innumerable parametersHowever, employing models that adequately capture the heterogeneity and complexity of human behavior, such as mobility, in modeling the spread of infectious diseases, introduces numerous parameters [51,59] that poses a plethora of challenges when solving . This, in turn, presents a multitude of challenges when addressing inverse problems (fit) and conducting inference (uncertainty quantification). To faceconfront the problems originated by the complex system and its high dimensional parameter space, we divide the problem into two parts. The first one is related to the mobility parameters that describe the proportion of individuals who move, and the time spent in each of the sub regions/patches. The second one, is associated to the numerical fit or statistical inference of the initial conditions and the parameters for the infectious agent and individual evolution of infected individuals.

The rest of this article is organized as follows: In Section 2, we present and describe the epidemic model on which the present analysis is centered. Section 3 discusses how the COVID-19 data used in this work was obtained. In Section 4, a discussion on the estimation of the mobility parameters and residence times of the epidemic model using mobile phone sensing data and the Brownian bridge model, is presented. We elucidate the formulation of the deterministic inversion model and the corresponding results in Section 5. Section 6 entails Bayesian model formulation, inference and the obtaining results. Finally, we give concluding remarks and possible extensions of the present work in Section 7.

2. The multi-patch model with mobility, residency and demography

The emergence and re-emergence of infectious diseases over the past several decades has led to the formulation, by researchers and epidemiologists, of numerous mathematical models that incorporate varied and distinct disease propagation dynamics. The central purpose of such models is to provide fundamental quantitative information and utilitarian guidelines in disease outbreak management and mitigation policy formulations. Provision of such useful information by such models is anchored on their ability to incorporate and capture realistic situations and disease transmission parameters. One such parameter, that has played a crucial role in the spread of infectious diseases, is human population mobility [16,17,18,21,39,40,60].

Several aspects of human history, such as social and economic, have been significantly impacted by the effects of the spread of infectious disease viruses among mobile sectors of human civilization [21]. Undoubtedly, the effects of the current COVID-19 pandemic is a demonstration of the devastating consequences of the interchange between human population mobility and transmission of infectious diseases. For instance, in December 2019, Wuhan, China was the only understood geographical boundary of COVID-19 [61,62,63,64,65]. However, it can be postulated that human mobility within and between cities in China and around the world aided the spread of the pathogen to a significant portion of the planet earth. In a span of three months, the pathogen had posed monumental health, social and economic stress to the point of being declared a pandemic by the WHO on March 11, 2020. Even though the exact nature of the contagion remained unclear, there was recognition of the undeniable interplay between the swift spread of the virus and human mobility through the universally known modes of travel [16,66,67,68,69]. Indeed, besides aiding the spread of COVID-19, such close relationship between population mobility and the spread of infectious diseases has the potential of shaping the emergence of future epidemics. Consequently, in order to formulate robust guidelines to manage both the current ongoing COVID-19 and possible future pandemics, there is dire need to construct appropriate epidemic models that accurately capture population mobility behaviour.

Human mobility, being a geo-spatio-temporal phenomena [17,43,70,71], can be modelled by meta-population-multi-patched models [4,34,39,40,42,44], as traditional homogeneous compartmental models are incapable of capturing such a strong heterogeneous human behaviour [15,17,34,51]. Once such models have been constructed, a wide spectrum of quantitative analysis that leads to deep understanding of the reciprocity of mobility and the spread of infectious diseases can be conducted. For instance, researchers and epidemiologists may focus on theoretical properties and numerical simulations of the model or parameter estimation, uncertainty quantification and predictions. In this research, we focus on the latter, using COVID-19 confirmed cases in Hermosillo, Mexico and a multi-patched SEIRS compartmental epidemic model with residency and demography. The model was proposed, and its theoretical properties analyzed byin [42]. For this model, human mobility is viewed as including not just travel between two locations, but the multiple temporal interactions that people have while traveling to various destinations. It is crucial to emphasize that in for this model human mobility encompasses more than just travel between two locations. It encompasses the multiple temporal interactions that individuals experience while traveling to different destinations.

The following ordinary differential equations (1) constitute the full form of the said patchymulti-patch non-linear model.This model extends the traditional compartmental SEIR model but in also divides the population into different compartments based on their disease status: Susceptible (S), Exposed (E), Infected (I), and Recovered (R). Most individuals start in the susceptible compartment (S) but when one of them comes into contact with an infectious individual, he moves from the susceptible compartment into the exposed compartment (E), meaning that he has been infected but is not yet infectious. This individual leaves the E compartment to enter the I compartment where he can transmit the disease to susceptible individuals. Over time, infected individuals either recover from the disease or may succumb to it. Once individuals recover, they move to the recovered compartment (R), gaining immunity to the disease. In the proposed model, the population dynamic also considers births (into the S compartment) and deaths (not produced by the disease).

Its parameters The parameters of model (1) are described in Table 1. We refer the reader to [42] for a full description of the arguments leading up to this model formulation.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\dot{S}}_i\hfill & ={\Lambda }_i-{\beta }_i(1-{\alpha }_i)S_i\frac{(1-{\alpha }_i)I_i+{\sum }_{k=1}^n{\tilde{p}}_{ki}{I}_k}{(1-{\alpha }_i)N_i+{\sum }_{k=1}^n{\tilde{p}}_{ki}{N}_k}-\sum _{j=1}^n\left({\beta }_j{\tilde{p}}_{ij}{S}_i\frac{(1-{\alpha }_j)I_j+{\sum }_{k=1}^n{\tilde{p}}_{kj}{I}_k}{(1-{\alpha }_j)N_j+{\sum }_{k=1}^n{\tilde{p}}_{kj}{N}_k}\right)\hfill \\ & -{\mu }_i{S}_i+{\tau }_i{R}_i\hfill \\ {\dot{E}}_i\hfill & ={\beta }_i(1-{\alpha }_i)S_i\frac{(1-{\alpha }_i)I_i+{\sum }_{k=1}^n{\tilde{p}}_{ki}{I}_k}{(1-{\alpha }_i)N_i+{\sum }_{k=1}^n{\tilde{p}}_{ki}{N}_k}+\sum _{j=1}^n\left({\beta }_j{\tilde{p}}_{ij}{S}_i\frac{(1-{\alpha }_j)I_j+{\sum }_{k=1}^n{\tilde{p}}_{kj}{I}_k}{(1-{\alpha }_j)N_j+{\sum }_{k=1}^n{\tilde{p}}_{kj}{N}_k}\right)\hfill \end{array}\begin{array}{c}\hfill -({\kappa }_i+{\mu }_i)E_i\\ \hfill {\dot{I}}_i& ={\kappa }_i{E}_i-({\gamma }_i+{\psi }_i+{\mu }_i)I_i\hfill \\ \hfill {\dot{R}}_i& ={\gamma }_i{I}_i-({\tau }_i+{\mu }_i)R_i\hfill \end{array}\right.\end{array}$$

(1)

where ${\tilde{p}}_{kj}={\alpha }_k{p}_{kj}$, $i=1,2,\cdots ,n$ and n is the number of patches.

Model (1) is limited to infectious diseases with single strain mutation. That is, in the formulation of the model, [42] assume that the recovered individuals in each patch are conferred with partial immunity, which they lose at a rate ${\tau }_i$. These individuals then reenter the susceptible compartment but it is only in relation to the same strain of the pathogen. However, many infectious diseases, including COVID-19, which is the center of this research, have several pathogenic strains whose dynamic properties should be studied for complete sensible management of emerging and re-emerging outbreaks with multiple variants. To this end, model (1) can be improved to include multiple COVID-19 disease strains.

Works such as [72,73,74,75,76] have considered models that incorporate several disease strains and mutations, with some of them focusing on this property for COVID-19 disease. Even though these works are mostly single-patch based, they provide valuable insights and useful starting point to extend model (1) to this important direction.

3. The data

In 2020, the University of Sonora signed an agreement with the government of the State of Sonora that provided the geo-referenced COVID-19 cases in Hermosillo, Mexico, from 2020-01-01 to 2020-09-06. On the other hand, using mobile phone GPS data from 2020-09-21 to 2020-11-15, [4] estimated mobility parameters and residence times in Hermosillo’s 582 urban AGEBs (Basic Census Geographical Units). As we are interested in modelling the number of cases in four important zones in Hermosillo (each aggregating AGEBs as shown in Figure 1), we use the geo-referenced and GPS information to obtain the number of COVID cases and estimate the mobility and residence within and between zones.Based on an institutional agreement between the University of Sonora (UNISON) and the Secretaría de Salud del Estado de Sonora (SSA), a collaborative effort was undertaken to provide accurate and reliable information to the population of Sonora during the sanitary emergency. As part of this initiative, researchers from the Mathematics Department at UNISON were granted access to georeferenced data pertaining to COVID-19 cases in Hermosillo, Mexico. The dataset encompassed the period from January 1, 2020, to September 6, 2020. It is important to emphasize that the usage of this data is strictly limited to academic activities in accordance with UNISON’s agreements with public institutions, and utmost care has been taken to safeguard sensitive and private information.

Furthermore, on September 14th, 2020, UNISON entered into a specific agreement, referenced as 12615-5700000-000412, to provide statistical consulting services to LUMEX CONSULTORES, S.C. Esteemed research professors from the Mathematics Department, including co-author J.F.E., provided these consulting services. The dataset provided by LUMEX CONSULTORES, S.C. comprised a comprehensive collection of approximately 80 million records, each containing the GPS position and timestamp of nearly 300,000 devices. These devices were geographically located within Hermosillo city between September 21st, 2020, and November 15th, 2020. The usage of this data was explicitly authorized for non-profit and academic activities, with appropriate credits duly acknowledged. Notably, user privacy was carefully protected through the meticulous anonymization of the data, employing distinct alphanumeric IDs for each individual device.

In a separate study, Ramirez et al. (2022) utilized mobile phone GPS data from September 21st, 2020, to November 15th, 2020, to estimate mobility parameters and residence times in Hermosillo’s 582 urban AGEBs (Basic Census Geographical Units) [4]. In alignment with our research objectives of modeling the number of COVID-19 cases in four key zones within Hermosillo, which aggregate AGEBs as illustrated in Figure 1, we employed the geo-referenced and GPS information to obtain the number of COVID-19 cases and estimate mobility and residence patterns within and between these zones.

The two geo-referenced databases only have a small time overlap and using this small period, we would not have sufficient data to learn the quite complex model (1), which has numerous epidemiological parameters to be estimatedThe two geo-referenced databases utilized in this study do not exhibit a temporal overlap, thereby limiting the feasibility of employing the complex model (1), which relies on the estimation of numerous epidemiological parameters. To address this problem, we have elected to use the weighted global COVID-19 data by zonal proportions.

The global confirmed positive COVID-19 cases in Hermosillo (Figure 3) are available in [77], a website managed by Consejo Nacional de Ciencias y Technología (CONACYT), since 2020-02-26. We use the weighted global cases by considering the zonal proportions of the global COVID-19 data, and we justify this selectiona selection we justify as in Figure 2, from which we can observe that the proportions of the available zonal COVID-19 data are approximately stable from June 2020. We therefore project that the data will have the same behaviour within the period for which the mobility parameters and mobility residence times were estimated. The global (Figure 3) and derived zonal COVID-19 cases, however, exhibits high variability. We therefore smoothen it using 7-days moving averages and use the smoothed version for the rest of the analysis.

Most models that have been proposed to analyze and predict COVID-19 incidence, since the emergence of SARS-CoV-2, assume that all infected individuals are observed, which is inexact due to under-reporting of disease incidence. This assumption undermines the accuracy of the models and their predictions. Emerging diseases, such as COVID-19, Typhoid fever, Hepatitis B, Epstein-Barr virus and Zika, that present a large fraction of asymptomatic pathogen carriers, are often characterized by incidence under-reporting during disease surveillance [78,79,80,81]. Coupled with asymptomatic and subclinical carriers, a phase that is prevalent with COVID-19 disease [82,83,84,85], another source of under-counting of disease incidence is lack of systematic testing. It is therefore necessary to account for under-reporting when modeling and fitting COVID-19 disease incidence, as failure to do so will lead to underestimation of epidemiological characteristics of the disease, especially the transmission parameter [86].

In modelling COVID-19 observed incidence for eight American countries, [86] reported an under-reporting of Mexico COVID-19 cases by a factor of 15. This acute under-reportingcases identification problem corroborated the observation in [87], that Mexico has one of the lowest numbers of COVID-19 tests performed per reported cases. We believe that this under-reporting cascaded down to the local Mexico states and cities like Hermosillo. In order to account for this under-reporting, we inflated the smoothed observed COVID-19 incidence, which was obtained from the weighting procedure previously explained, by a factor of 15 to obtain the daily incidence data. We subsequently consider the inflated data (see Figure 4) as the true observed daily COVID-19 incidence in Hermosillo, Mexico, and use it for inference in this research.

In addition to using real count data for model fitting and uncertainty quantification, we also utilized simulated incidence data generated from the model. Our goal was to assess the parameter and initial conditions identifiability of the inverse problem and statistical inference under the model. To this end, we used epidemiological parameters of COVID-19 gathered from various literature as presented in Table 2, and simulated from model (1), daily observed incidences for each zone in Hermosillo. For this simulation, we used epidemiological parameter values close to the ones used by [88], who modelled lockdown relaxation period of COVID-19 in Hermosillo. The parameters and initial condition values used in the simulation can be seen in Table 3. The latter were based on the total population of each zone. After the simulation of the zonal incidence from the model, we added a normal noise $e_t\sim \mathcal{N}(I_i\left(t\right),\sigma =100)$, to incorporate variability in the model data. The final simulated incidence for each zone in Hermosillo is presented in Figure 5.

4. Estimation of the mobility and Residence time parameters

The present study involves solving an inverse problem and performing uncertainty quantification on system (1), using 2020 COVID-19 confirmed cases in Hermosillo, Mexico. Such data may not be sufficient in estimating all the mobility and infection parameters, as well the initial conditions present in the system. Moreover, simultaneous estimation of several parameters oftentimes leads to parameter non-identifiability problems [109,110,111,112,113,114,115]. As such, we use the mobile phone sensing data used in [4] for purposes of estimating the mobility vector ${\alpha }_i$, $i=1,2,\cdots ,n$ and the mobility residence time matrices $\mathbb{P}=\left(p_{ij}\right)$, $i=1,2,\cdots ,n$, $j=1,2,\cdots ,n$ which we will incorporate into system (1). Using mobile consecutive pings,4] estimated the mobility parameters vectors and mobility residence time matrices of 582 urban AGEBs in Hermosillo, Mexico, for three periods, each divided into two parts. In this research, we use the same GPS pings during the Third Period – First Part (2020-09-21 to 2020-10-11). Using this information, we estimate the mobility and residence time matrix of four zones in Hermosillo. Since we are interested in evaluating the forecasting (after November 2020) under the model, this period was selected as its start date was closer to the last period of considered COVID-19 cases. We note that we can also use mobility data from other periods and parts, and employ a similar procedure that we describe next, to estimate mobility and residence times for the four zones, within the period and part of interest.

Solving the inverse problem and performing uncertainty quantification on system (1) for a total number of AGEBs (patches) poses a logical set-up challenge. Thus, using well-defined geographical demarcations of Hermosillo, we group the 582 AGEBs into four main zones. These zones, together with their corresponding total population, are shown in Figure 1. The mobility parameter vector ${\alpha }_i$,and residence times $p_{ij}$, $i=1,2,3,4$, $j=1,2,3,4$ were estimated by searching for individuals who activated at least 11 pings and left their AGEBs within and between the zones. For the individual AGEBs, [4] estimates the probability density functions at position z for any individual originating from AGEB/patch r as

$${\widehat{h}}_r\left(z\right)=\frac{1}{n_r}\sum _{j=1}^{n_r}{h}_{rj}\left(z;{\widehat{\sigma }}_{rj},\delta \right),$$

(2)

where $n_r$ is the patch population size, $h_{rj}$ is the density of the expected time of the j-th individual originating from the r-th patch, ${\widehat{\sigma }}_{rj}$ is the maximum likelihood estimate of the individual standard deviation of the mobility of the j-th resident from the r-th patch, and ${\delta }^2$ is the variance of the geolocation error. After grouping and renaming the composing AGEBs of each of the four zones, we have

$$n_{{}_1}^{[\ell ]}{\widehat{h}}_{{}_1}^{[\ell ]}\left(z\right)=\sum _{j=1}^{n_{{}_1}}{h}_{1j}^{[\ell ]}\left(z;{\widehat{\sigma }}_{1j}^{[\ell ]},\delta \right),\cdots ,n_{{}_{n_{\ell }}}^{[\ell ]}{\widehat{h}}_{{}_{n_{{}_{\ell }}}}^{[\ell ]}\left(z\right)=\sum _{j=1}^{n_{{}_1}}{h}_{n_{{}_{\ell }}j}^{[\ell ]}\left(z;{\widehat{\sigma }}_{n_{{}_{\ell }}j}^{[\ell ]},\delta \right),$$

(3)

where the subscript index $[\ell ]$ indicates that the said quantity is in zone ℓ and $n_{\ell }$ represents the total number of AGEBs in the ℓ-th zone.

From (3), we can obtain the estimated probability density function at location z for any individual originating from patch r in zone ℓ as

$${\widehat{h}}_{{}_{\ell }}^{*}\left(z\right)=\frac{1}{N^{[\ell ]}}\sum _{r=1}^{n_{{}_{\ell }}}\sum _{j=1}^{n_r}{h}_{rj}^{[\ell ]}\left(z;{\widehat{\sigma }}_{rj}^{[\ell ]},\delta \right).$$

(4)

where $N^{[\ell ]}={\sum }_{j=1}^{n_r}{n}_j^{[\ell ]}$. Then the expected occupation time in A of a resident of zone ℓ can thus be obtained, from (4), as

$${\widehat{P}}_{{}_{\ell }}\left(A\right)={\int }_A{\widehat{h}}_{{}_{\ell }}^{*}\left(z\right)dz=\frac{1}{N^{[\ell ]}}{\int }_A\sum _{r=1}^{n_{{}_{\ell }}}\sum _{j=1}^{n_r}{h}_{rj}^{[\ell ]}\left(z;{\widehat{\sigma }}_{rj}^{[\ell ]},\delta \right)dz.$$

(5)

As has been mentioned, for this research, we consider the mobility parameter and the mobility residence matrix for the Third Period – First Part (2020-09-21 to 2020-10-11), which we compute, using the above procedure, and obtain

$$\alpha ={\left(\begin{array}{cccc}0.9668,& 0.9265,& 0.9692,& 0.9680\end{array}\right)}^{\top }\mathrm{and}\mathbb{P}=\left(\begin{array}{cccc}0.8164& 0.1289& 0.0372& 0.0175\\ 0.1222& 0.8119& 0.0215& 0.0444\\ 0.0722& 0.0504& 0.7293& 0.1481\\ 0.0313& 0.1166& 0.1278& 0.7243\end{array}\right).$$

5. Deterministic inversion

Due to their exponential growth in time, the state variables of the dynamical system (1) are extremely sensitive to the input parameters. This sensitivity cascades uncertainty into the pre-inferred parameter values, which, in turn, may result into blow-up or significant uncertainty in the model outputs. To have a robust and desirable model analysis, it is imperative to avoid such model blow-ups by first determining the optimal model parameters that fits the measured data. Moreover, prior knowledge of point parameter estimates is necessary for meaningful uncertainty quantification. To this end, we begin by deterministically inverting system (1) in this section, and then subsequently perform uncertainty quantification on the inferred point parameters in the next section. Following is an outline of the formulation of the inversion problem and the results.

5.1. Formulation of the model to minimize

Let $\mathbf{x}=(\mathbf{S},\mathbf{E},\mathbf{I},\mathbf{R})\in {\left(L^2(0,T)\right)}^{4n}$ where $T>0$, $\mathbf{S}={(S_1,\cdots ,S_n)}^{\top }$, $\mathbf{E}={(E_1,\cdots ,E_n)}^{\top }$, $\mathbf{I}={(I_1,\cdots ,I_n)}^{\top }$ and $\mathbf{R}={(R_1,\cdots ,R_n)}^{\top }$, denote the state variables in system (1) for n patches. Let $m_i$ be the dimension of patch i parameters to be estimated. Then, we have the total number of patch i parameters to be estimated, denoted as ${\theta }_i=\{{\theta }_{i1},\cdots ,{\theta }_{i{m}_i}\}$. Consequently, the total number of parameters, $m={\sum }_{i=1}^n{m}_i$, for the global system is ${\theta }_{}={\bigcup }_{i=1}^n{\theta }_i\in {\mathbb{R}}_{+}^m$. System (1) can be viewed as a mapping $\Psi \left(\theta \right)=\mathbf{x}$ where $\Psi :{\mathbb{R}}_{+}^m⟶{\left(L^2(0,T)\right)}^{4n}$, (i.e., $\Psi$ maps the parameters to be estimated to the state variables) and it defines an initial value problem of the form;

$$\dot{\mathbf{x}}=f(\mathbf{x},\theta ),\mathbf{x}\left(t_0\right)={\mathbf{x}}_{\mathbf{0}}\in {\mathbb{R}}^n,t_0\in \mathbb{R}.$$

(6)

The function f in the forward problem (6) is continuous and satisfies Lipschitz condition with respect to $\mathbf{x}$[116]. Thus, given $\theta$, problem (6) has a unique solution $\mathbf{x}$.

Besides the numerically simulated states $\mathbf{x}$, the inverse problem requires, as an input, directly measured state variables at a discrete set of points $t_1,t_2,\cdots ,t_k$. In most circumstances, not all of the state variables of the system can be directly observed. For instance, in epidemiology, data on new confirmed cases of infected individuals is readily available compared to data on other epidemiological statuses of the population. For this reason, we use the new cases reported in periods of time (days, weeks, for example) from the model to formulate the inverse problem.

Let ${\mathbf{y}}_{\mathrm{obs}}={\{y_{1,t},\cdots ,y_{n,t}\}}_{t=1}^M$, $M\in \mathbb{N}$, denote the observed new infected cases in each unit/period of time $t\in 1,2,\cdots ,M$, for the n patches. Let $Z_i(t,\theta )$ be the incidence in Patch i, during $(t-1,t]$ , derived from the numerical solution of the forward problem (6) with parameter vector $\theta$. The objective function of the inverse problem is thus defined as

$$F\left(\theta \right)=\sum _{i=1}^n\sum _{t=1}^M\frac{{\left\{Z_i(t,\theta )-y_{i,t}\right\}}^2}{Z_i(t,\theta )}.$$

(7)

Consequently, the inverse problem becomes: compute $\widehat{\theta }\in \Theta$ such that

$$\widehat{\theta }=\underset{\theta \in \Theta }{argmin}F\left(\theta \right)\mathrm{s}.\mathrm{t}\Psi \left(\theta \right)=\mathbf{x},$$

(8)

where $\Theta$ is the feasible region of the parameter $\theta$.

Problem (8) can be optimized using methods such as Landweber in [116,117,118,119], faster methods such as Levenberg-Marquardt or gradient based numerical non-linear least squares minimization algorithms such as Sequential Least SQuares programming algorithm (SLSQP) in [e.g, [51,120]. Due to the complexity of the forward problem (6), the inverse problem (8) is complex, high dimensional and computationally intensive. As a consequence, problem (8) creates a complex landscape, making it difficult for gradient-based algorithms and other optimization techniques to find the global minima, thereby easily failing to reach the optimal solution. As an alternative, we solve problem (8) using Genetic Algorithm (GA), a type of the diverse machine learning Evolutionary Algorithms (EAs), that uses heuristic search and optimization methods. Besides their efficacy in the optimization of problems involving numerous parameters with large feasible regions (i.e, problems with increased dimensionality) and multiple local optima, GAs do not require gradient computations which may sometimes be computationally challenging or unavailable altogether [121,122].

5.2. Results

Since we are dealing with four zones, we minimize Equation (7) as in (8), for $n=4$. Besides estimating the epidemiological parameters ${\bigcup }_{i=1}^4\{{\beta }_i,{\kappa }_i,{\gamma }_i\}$, we also estimate the initial conditions ${\bigcup }_{i=1}^4\{E_{i,0},I_{i,0}\}$. Thus, from the deterministic inversion, we estimate a total of 20 parameters; $\theta ={\bigcup }_{i=1}^4\{{\beta }_i,{\kappa }_i,{\gamma }_i,E_{i,0},I_{i,0}\}$.

Table 4 and Table 5 shows the estimated parameters, while Figure 6 and Figure 7 presents the fitted incidence for the simulated and observed data, respectively. For the simulated incidence, the fit is visibly good, even though there is variation in the estimated parameters from the real ones (see Table 3) and a more important difference on the initial conditions. These disparities can be as a result of the noise that was added to the simulated data, andwhich represent an important modification to the original simulated incidence, especially in the early stages of the outbreak. As in complex models, we can also face the situation where there exists different sets of parameters that would give an equally good fit to the zonal model incidences.

As the estimated parameters from the GA give a good fit for the model incidence, we used them as a guide in specifying the initial sampling points for Stan and t-walk when performing Bayesian inference and uncertainty quantification in the next section. The values were particularly important for t-walk to begin sampling as without them, the algorithm does not converge and completely fails. In addition, as there are no literature that provides the spaces (upper and lower bounds) for the initial conditions of the incubation and prevalence states parameters for Hermosillo, we used the estimates of the said parameters from GA as a guide to set their boundaries in the Bayesian procedure.

6. Bayesian inference

Deterministic inversion of epidemic models have gained prominence in learning the trajectories of the epidemic using measured epidemiological data. However, deterministic inversion ignores inherent uncertainties due to imperfect data, stochasticity, model structural discrepancies and even parameter uncertainties that usually plagues the epidemic model. In order to make robust, valid and reliable decisions regarding management, prediction and forecasts of current and future epidemics, good treatment and quantification of such uncertainties is imperative. In this section, we use Bayesian techniques to quantify uncertainties that characterize the epidemic model (1), its parameters and the observed Hermosillo COVID-19 infection data and provide credible intervals for the model output.

Over the last few decades, Bayesian inference has become an important mechanism by providing an optimal probability platform for learning unknown parameters of a system given observed data. A Bayesian framework learns the trajectories of the unknown parameters by updating their prior distributions to the posterior distribution. Such prior updates and exploitation of the parameter space of the posterior distribution can be achieved using the standard Monte Carlo Markov Chain (MCMC) methods. Moreover, MCMC has somewhat led to approximate estimation of intractable posterior distributions, which often characterizes the modelling of real world phenomena. Estimation of such intractable posterior distribution has been a long-standing challenge in the realm of Bayesian inference, [123]. We use t-walk and Stan, which are MCMC based algorithms, to simulate the posterior distribution. Following is a detailed account on how the Bayesian framework is treated in this section.

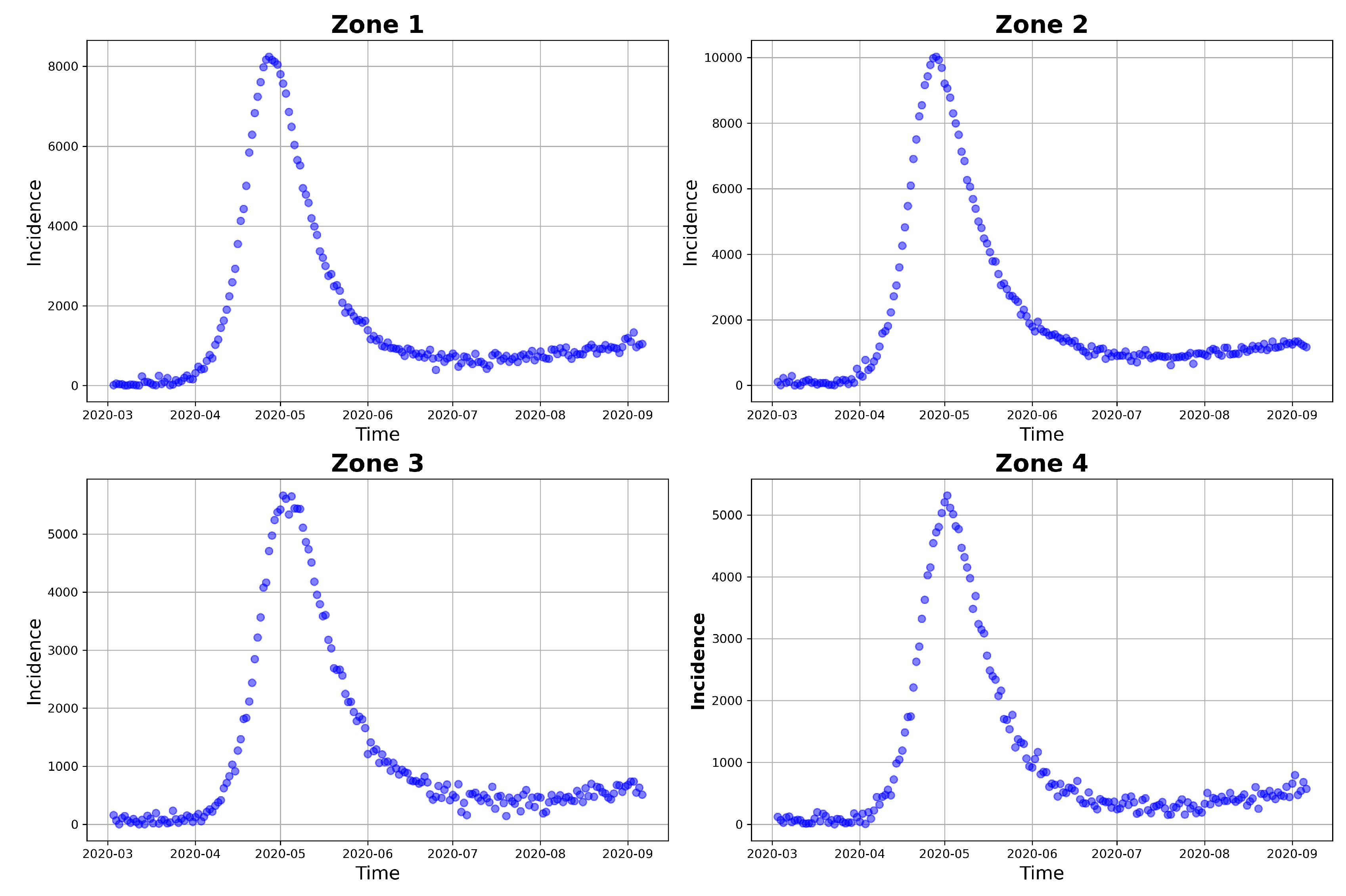
6.1. Building the Posterior Distribution

In Bayesian realm, the observed data, ${\mathbf{y}}_{\mathrm{obs}}$ is fixed while the state variable $\mathbf{x}$ and the parameter $\theta$ are considered as random variables. In this setting, the Bayes’ theorem defines the posterior distribution as

$$\pi \left(\theta |{\mathbf{y}}_{\mathrm{obs}}\right)\propto p\left({\mathbf{y}}_{\mathrm{obs}}|\theta \right)\pi \left(\theta \right),$$

(9)

where $\pi \left(\theta \right)$, called the prior distribution, codifies our belief about the unknown parameter $\theta$ before the data is observed and $p\left({\mathbf{y}}_{\mathrm{obs}}|\theta \right)$, called the likelihood distribution, codifies all the information available regarding how the observed data ${\mathbf{y}}_{\mathrm{obs}}$ was obtained. From the Bayesian perspective, (9) constitutes thean inverse problem which may be solved by using the Maximum a posteriori (MAP), that is thean argument that maximizes the posterior ($\arg {\max }_{\theta \in \Theta }\pi \left(\theta |{\mathbf{y}}_{\mathrm{obs}}\right)$), or the posterior mean ($\mathbb{E}\left[\pi \left(\theta |{\mathbf{y}}_{\mathrm{obs}}\right)\right]$) or posterior median, as the optimal value $\widehat{\theta }$ of $\theta$.

Since we are dealing with count data, which by their very nature are events that occur between a given period of time, a Poisson process would be a natural and meaningful starting point for modeling and performing inference on the observed cases. However, count data, especially epidemiological observations, usually exhibit more variations than is implied by the Poisson distribution, pointing to inherent over-dispersion in the data. Such variations may be due to sampling, aggregation and environmental variability or a combination of both factors making count data to have inherent over-dispersion. It is therefore not possible that count epidemiological data portrays equal mean-variance relationship, as is contemplated by the Poisson distribution. In fact, [124] posits that most commonly used approaches contemplates a quadratic mean-variance relationship. The mean-variance relationship in modeling count data, like epidemiological data, can adequately be described by the negative-binomial distribution as it has an additional parameter that permits the variance to be larger than the mean [125,126,127]. Moreover, the negative binomial distribution is a mixture of the Poisson and Gamma distribution [127,128], a pointer to the fact that the Poisson distribution is still involved in the modelling even when the negative binomial distribution is used.

We assume that the observed data follows the negative binomial distribution with one dispersion parameter $\nu$ and we write $y\sim NB(\nu ,p)$ where p is the probability of success. The distribution has the form

$$p\left(y|\mu ,\theta \right)=\left(\begin{array}{c}y+\nu -1\\ \nu \end{array}\right){\left(\frac{\mu }{\mu +\nu }\right)}^{\nu }{\left(\frac{\nu }{\mu +\nu }\right)}^y,$$

(10)

where

$$\mu =\mathbb{E}\left(Y\right)=\frac{\nu p}{1-p}\mathrm{and}\mathrm{Var}\left(Y\right)+\frac{{\mu }^2}{\nu }=\mu +\rho {\mu }^2\mathrm{with}\rho =\frac{1}{\nu }.$$

It is noteworthy that $\rho {\mu }^2>0$ is the additional variance allowed by the Negative Binomial distribution with respect to the Poison distribution, and that the parameter $\rho$ can be viewed as controlling the dispersion of the observed data.

We acknowledge that there are other forms of the Negative binomial distribution. For instance, [49] achieved success in modelling COVID-19 and hospital demand in Mexico using a Negative binomial distribution with two over-dispersion parameters. This distribution was proposed by [124]. However, in a model with numerous parameters to estimate as ours, it is our view that additional parameters would further increase the dimensionality of the already complex optimization problem.

We now construct the posterior distribution for the present multi-patched study. Using the already defined observed data and the variable $\theta$ in the previous section, we assume that the observed cases of each patch follow a negative-binomial distribution with over-dispersion parameter (the number of failures before first success) ${\nu }_i$ and success probabilities

$$p_i=\frac{{\mu }_i}{{\mu }_i+{\nu }_i},$$

where ${\mu }_i$ is the theoretical mean of the negative binomial distribution which can be taken as patch i incidence

$${\mu }_i(j,\theta )=Z_i(j,\theta ),i=1,2,\dots ,nj=1,2,\cdots ,M.$$

(11)

With this setting in mind, we have that if $y_{i,j}$, represents the incidence in Patch i observed in day j with theoretical mean ${\mu }_i(j,\theta )$, as in (11), then we have that

$$y_{i,j}|\theta \sim NB\left({\nu }_i,\frac{{\mu }_i(j,\theta )}{{\mu }_i(j,\theta )+{\nu }_i}\right).$$

Then the likelihood from Patch i, $i=1,2,\cdots ,n$, corresponds to

$$\begin{array}{cc}\hfill p_i({\mathbf{y}}_i=(y_{i,1},\cdots ,y_{i,M})|\theta )& =\prod _{j=1}^M\frac{\Gamma (y_{i,j}+{\nu }_i)}{y_{ij}!\Gamma \left({\nu }_i\right)}{\left(\frac{{\mu }_i(j,\theta )}{{\mu }_i(j,\theta )+{\nu }_i}\right)}^{{\nu }_i}{\left(\frac{{\nu }_i}{{\mu }_i(j,\theta )+{\nu }_i}\right)}^{y_{i,j}}\hfill \\ \hfill & \propto \left(\prod _{j=1}^M\frac{\Gamma (y_{i,j}+{\nu }_i)}{\Gamma \left({\nu }_i\right)}\right){\left(\frac{{\mu }_i(j,\theta )}{{\mu }_i(j,\theta )+{\nu }_i}\right)}^{M{\nu }_i}{\left(\frac{{\nu }_i}{{\mu }_i(j,\theta )+{\nu }_i}\right)}^{{\sum }_{j=1}^M{y}_{i,j}}.\hfill \end{array}$$

Hence, the likelihood of the combined data from the n patches is given as $p\left({\mathbf{y}}_{\mathrm{obs}}|\theta \right)={\prod }_{i=1}^n{p}_i\left({\mathbf{y}}_i|\theta \right)$.

To establish the prior distribution, we opt to define the joint prior distribution as the product of the marginal. That is, if we denote $\theta ={\cup }_{i=1,\dots ,n,\ell =1,\dots ,m_i}{\theta }_{i\ell }$, where ${\theta }_{i\ell }$ is the ℓ-parameter associated to Patch i, then

$$\pi \left(\theta \right)=\prod _{\ell =1}^{m_1}g\left({\theta }_{1l}\right)\prod _{\ell =1}^{m_2}g\left({\theta }_{2l}\right)\cdots \prod _{\ell =1}^{m_n}g\left({\theta }_{nl}\right)=\prod _{i=1}^n\left[\prod _{\ell =1}^{m_i}g\left({\theta }_{il}\right)\right].$$

(12)

where $m_i$ is the number of parameters for Patch i.

The posterior distribution of the parameters from all the n patches can thus be obtained as the product of (9) and (12) as (9).

6.2. Results

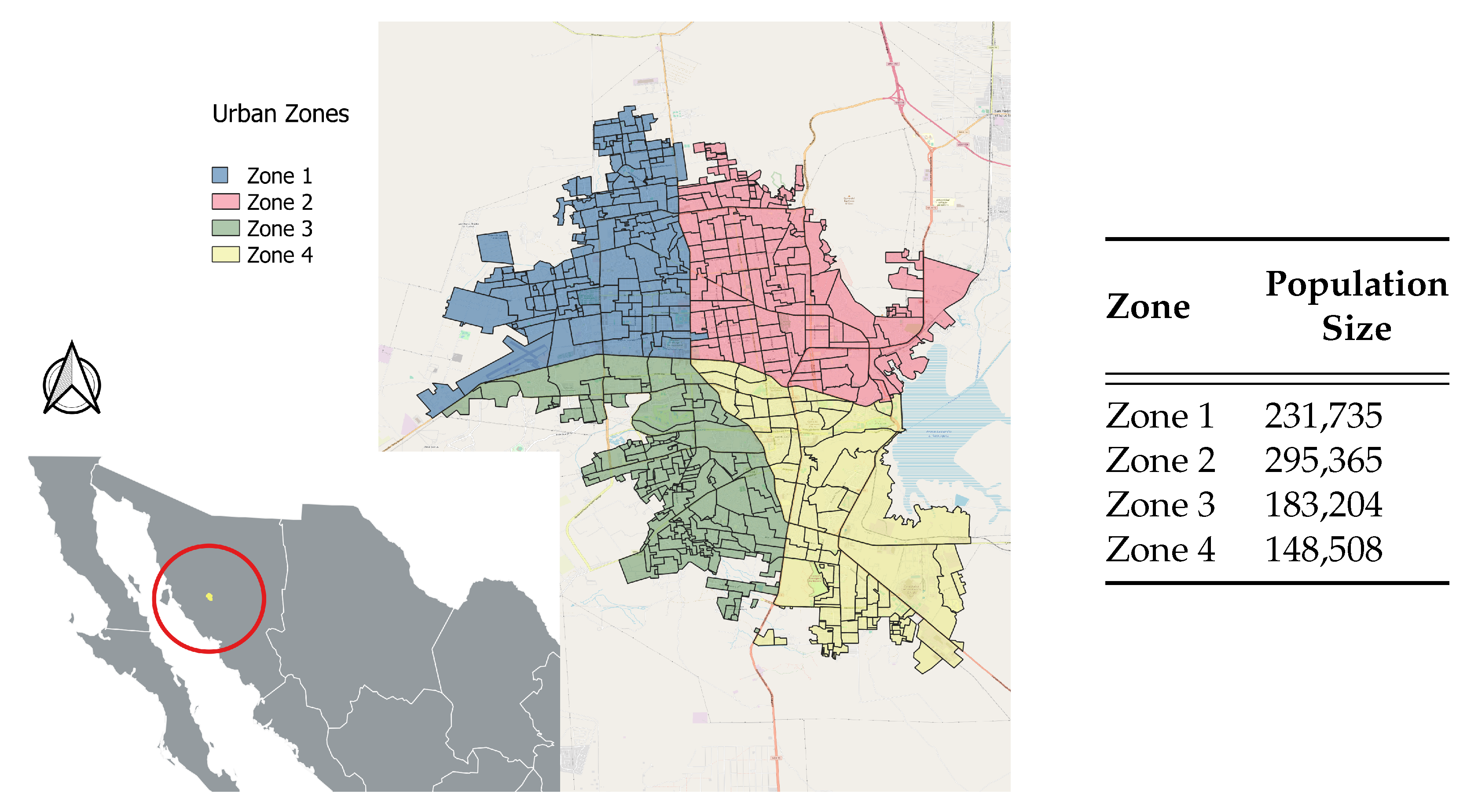
We note, from the deterministic inversion section, that we are interested in estimating for each zone i, $i=1,2,3,4$, the transmission, incubation and recovery rates ${\beta }_i$, ${\kappa }_i$ and ${\gamma }_i$ as well as the exposed, infected and incidence initial conditions $E_{i,0}$ and $I_{i,0}$. For the Bayesian inference, also called probabilistic inversion, there is an addition of four over-dispersion parameters ${\nu }_i$, for each zone’s observed incidence data. The dispersion parameters can be loosely defined as the number of trials before we encounter the first successful infection in each zone. These parameters come with the negative binomial distribution, which we use as the distribution of the observed zonal incidences. We thus have, for the Bayesian inference in this section, a total of 24 parameters,

$$\theta =\bigcup _{i=1}^4\{{\beta }_i,{\kappa }_i,{\gamma }_i,E_{i,0},I_{i,0},{\nu }_i\},$$

(13)

that we estimate.

An important problem that has been the topic of recent research, is the selection of adequate prior distributions, their corresponding hyperparameters and the delimitations of the parametric spaces of the parameters to be estimated [129,130,131]. In this research, for the epidemiological parameters, we choose prior distributions with 95% of their body falling within the parametric spaces (upper and lower bounds) provided from COVID-19 literature as in Table 2.

In this way, we use the following prior distributions for each of the parameters;

$$\begin{array}{cc}\hfill {\beta }_i& \sim \mathrm{LogNorm}({\mu }_i,{\sigma }_i)=g\left({\beta }_i\right),\hfill \\ \hfill {\kappa }_i& \sim \mathrm{Gamma}(4.5264,19.1006)=g\left({\kappa }_i\right),\hfill \\ \hfill {\gamma }_i& \sim \mathrm{Gamma}(1.9826,3.6943)=g\left({\gamma }_i\right),\hfill \\ \hfill E_{i,0}& \sim \mathrm{Unif}(a_i,b_i)=g\left(E_{i,0}\right),\hfill \\ \hfill I_{i,0}& \sim \mathrm{Unif}(0,10)=g\left(I_{i,0}\right),\hfill \\ \hfill {\nu }_i& \sim \mathrm{Gamma}(0.7561,0.2714)=g\left({\nu }_i\right).\hfill \end{array}$$

where the hyperparameters for the log Normal prior distributions of the contact parameters are ${\mu }_1=-0.0529$, ${\mu }_2=-0.0975$, ${\mu }_3=-0.8562$, ${\mu }_4=-0.2583$ and ${\sigma }_1={\sigma }_2={\sigma }_3={\sigma }_4=0.2803$, while those for the exposed states’ initial conditions are $a_1=50$, $b_1=100$, $a_2=70$, $b_2=100$, $a_3=15$, $b_3=50$, and $a_4=0$, $b_4=20$. These prior probability distributions, which we have selected using the mentioned criteria, are versatile and allows for the assumption that some parameter values could occur with lower, equal or higher probability densities.

However, to avoid generalizations, it is imperative to perform a diagnostic analysis of the adequacy and correctness of the selected prior distributions before we begin sampling. These prior distributions should be in coherence with our expectations and correspond to the domain knowledge of each parameter as obtained from the deterministic inversion in the previous section. We desire priors that, in accordance with our deterministic inversion domain experience, permits every conceivable configuration of the data while excluding blatantly ludicrous scenarios. 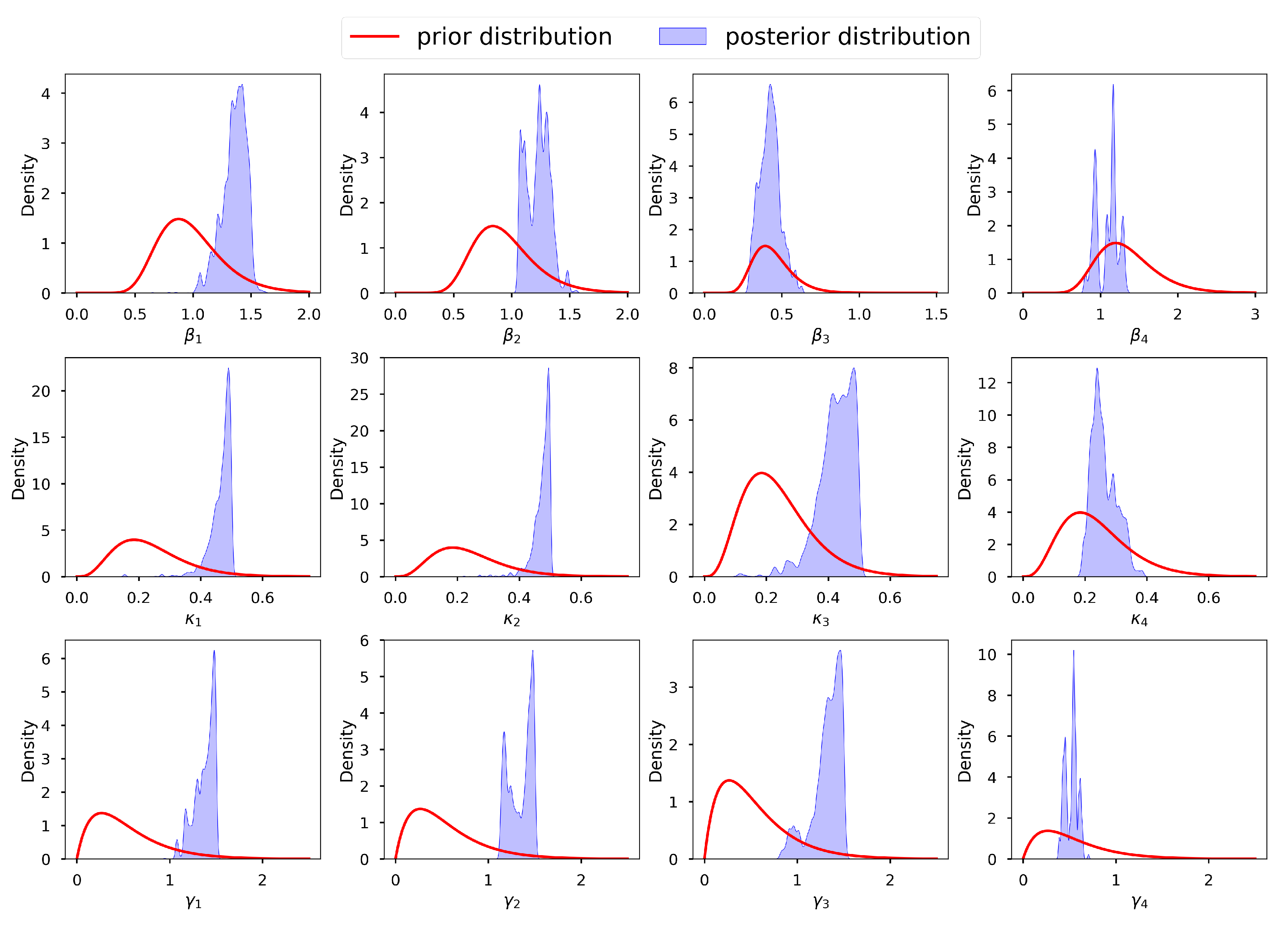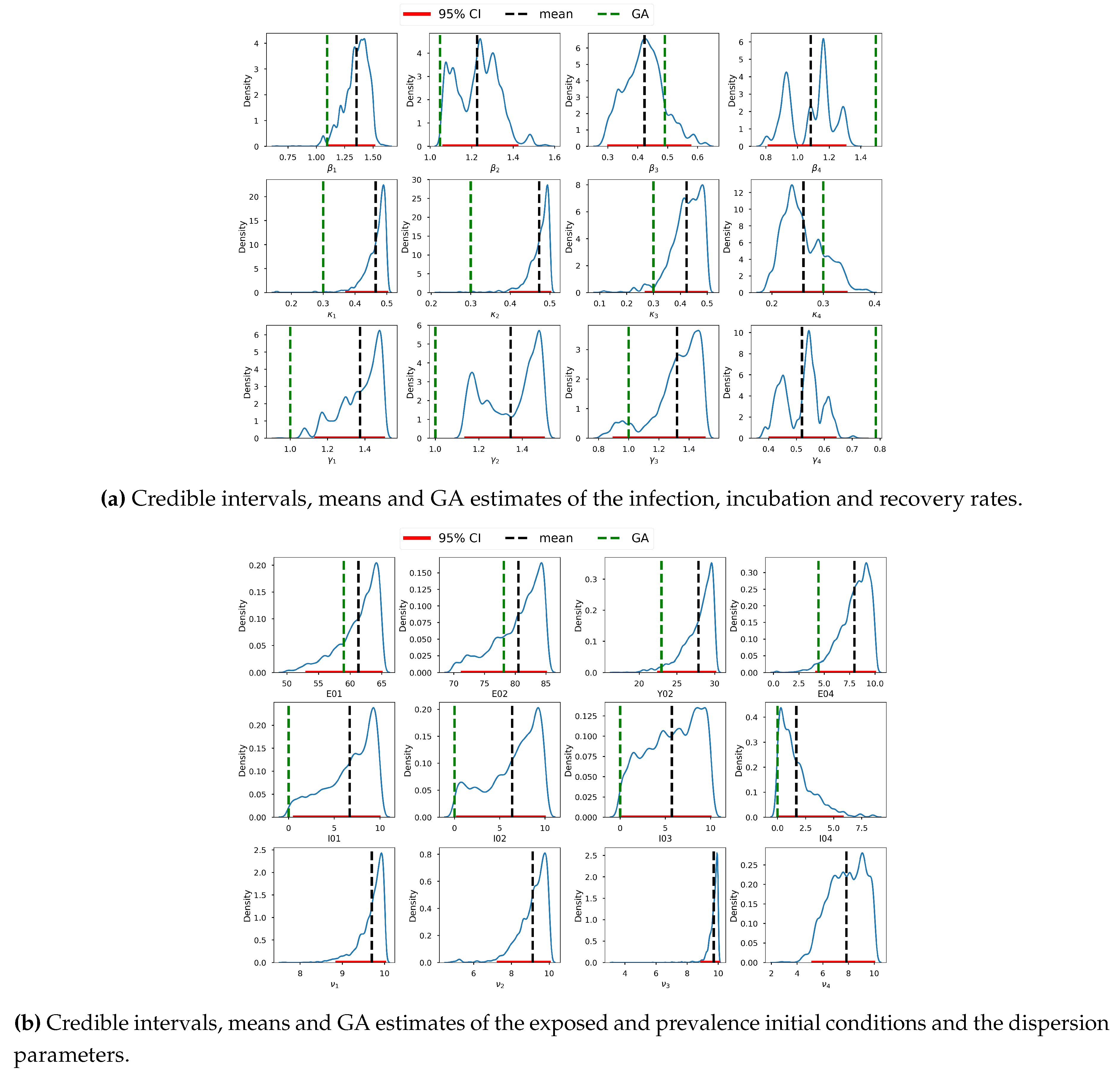Figure 8 shows a graph of the selected prior distributions of the infection, incubation and recovery parameters, vis-à-vis the corresponding posterior distributions. Here we can observe that for most parameters we have allowed for low informative priors and the posterior distributions are within their respective prior probability support. This conforms with the suggestion by [132], that the model should not be overly confined by the priors, which should instead be too wide to encompass a wide variety of situations and data that are incredibly improbable. We thus conclude that our selected prior distributions are adequate and are capable of regularizing our estimates to avoid non-identifiability. We acknowledge that [131] also proposed an interesting criterion for selecting prior distributions together with their corresponding hyperparameters, based on parametric intervals. Applying the assumption of independence of the parameters, the joint prior distribution is $\tilde{\pi }\left(\theta \right)={\prod }_{i=1}^{4}g\left({\beta }_i\right)g\left({\kappa }_i\right)g\left({\gamma }_i\right)g\left(E_{i,0}\right)g\left(I_{i,0}\right)g\left({\nu }_i\right)$.

The likelihood for the four zonal incidence is

$$p\left({\mathbf{y}}_{\mathrm{obs}}|\theta \right)\propto \prod _{i=1}^4\left[\left(\prod _{j=1}^{M_i}\frac{\Gamma (y_{i,j}+{\nu }_i)}{\Gamma \left({\nu }_i\right)}\right){\left(\frac{{\mu }_i(j,\theta )}{{\nu }_i+{\mu }_i(j,\theta )}\right)}^{M_i{\nu }_i}{\left(\frac{{\nu }_i}{{\nu }_i+{\mu }_i(j,\theta )}\right)}^{{\sum }_{j=1}^{M_i}{y}_{i,j}}\right],$$

where, $M_i$ is the total number of days for which we observe the incidence for each zone $i=1,2,3,4$; $y_{i,j}$ is the j-th observed incidence for zone i, and ${\mu }_i(j,\theta )$ is the incidence of model (1). The posterior distribution is thus given as $p\left(\theta \right|{\mathbf{y}}_{\mathrm{obs}})=p\left({\mathbf{y}}_{\mathrm{obs}}\right|\theta )\tilde{\pi }\left(\theta \right)$.

The incidences output from the epidemic model (1) are very sensitive and exhibits a lot of uncertainty to slight changes, especially of the contact, incubation and recovery parameters. As a consequence, it was challenging to provide a wide range of values as support of the posterior distribution in Stan and t-walk. We addressed this challenge by beginning with the deterministic inversion of the epidemic model using GA, as is discussed in the previous section. The output of this inversion are given in Table 5. Consequently, we use the point parameter estimates obtained from the GA as the initial sampling points for t-walk and Stan. Moreover, as there is no literature for the parametric spaces of the incubation and prevalence states initial conditions, we delimit their support in the posterior distribution in the neighbourhood of their point parameter estimates obtained from the GA.

After performing the prior predictive checks, using the t-walk package [133], we obtain posterior samples for each of the 24 parameters (13). MCMC methods, from its definition, produces samples that can have high correlation, harboring some level of redundant information. One way of measuring the level of information redundancy in the posterior sample, is by using the effective sample size (ESS). Theoretically, ESS is the sample size we would obtain if we independently sampled the posterior distribution. 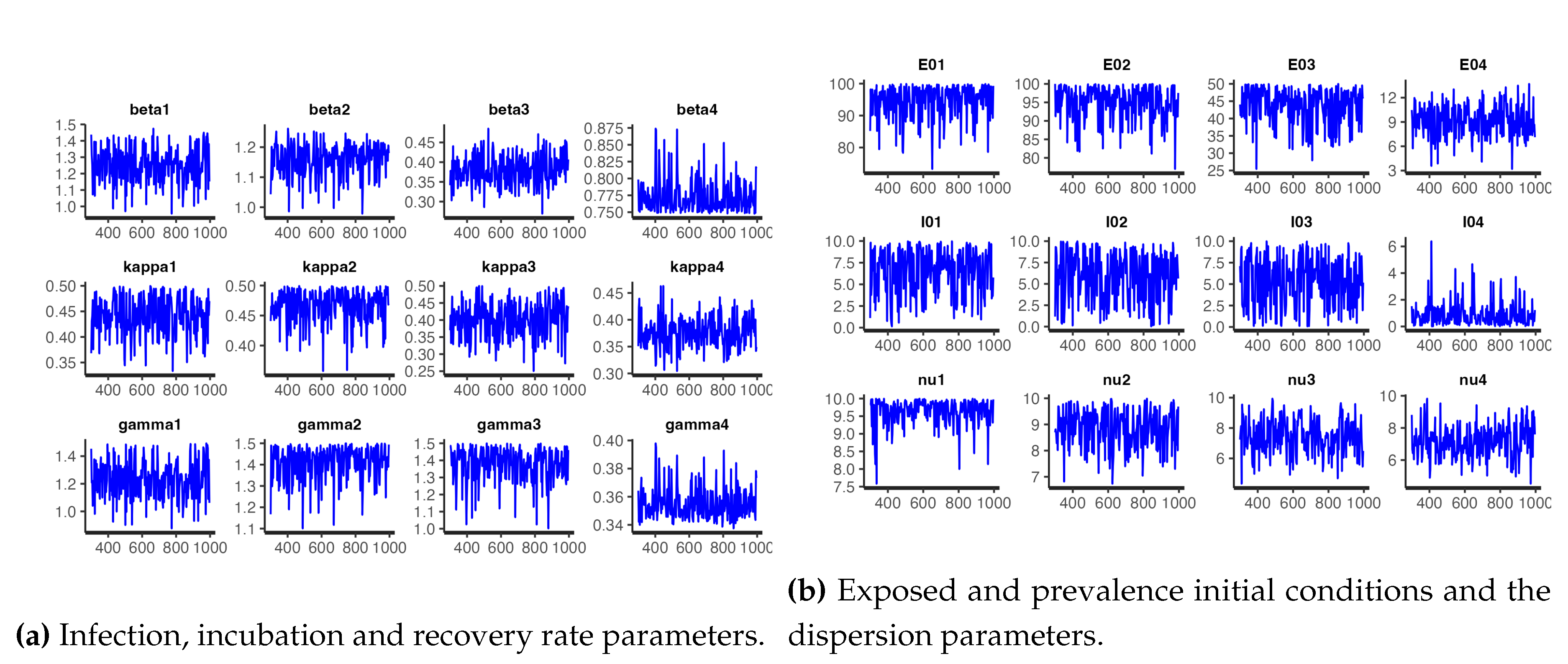The ESS and the proportion of ESS (pESS) of the simulated samples are given in the last two columns of Table A1. Going by how low (high) the values of ESS (pESS) are, we can tell that the simulated chains are highly correlated and thus, this MCMC method requires very high number of iterations. In other words, to obtain samples with insignificant auto correlations can require thinning at large lags, which can remarkably reduces the chains sizes. To obtain chains with reasonable sample sizes for analysis, after running this MCMC method for 1,000,000 iterations, we discarded 360,000 burnin samples and thinned the chains at lag 20.

The summary statistics of the generated samples are given in Table A1 (in the Appendix). As can be observed, the presented summary statistics are; the mean, variance, 95% credible interval (CI), median, ESS and pESS. From this table, we can conclude that in general, all the samples exhibited low variability and that their means are close to the estimates obtained from the GA in the previous section. Further, we can conclude that the means (and medians) are all within the 95% CI. 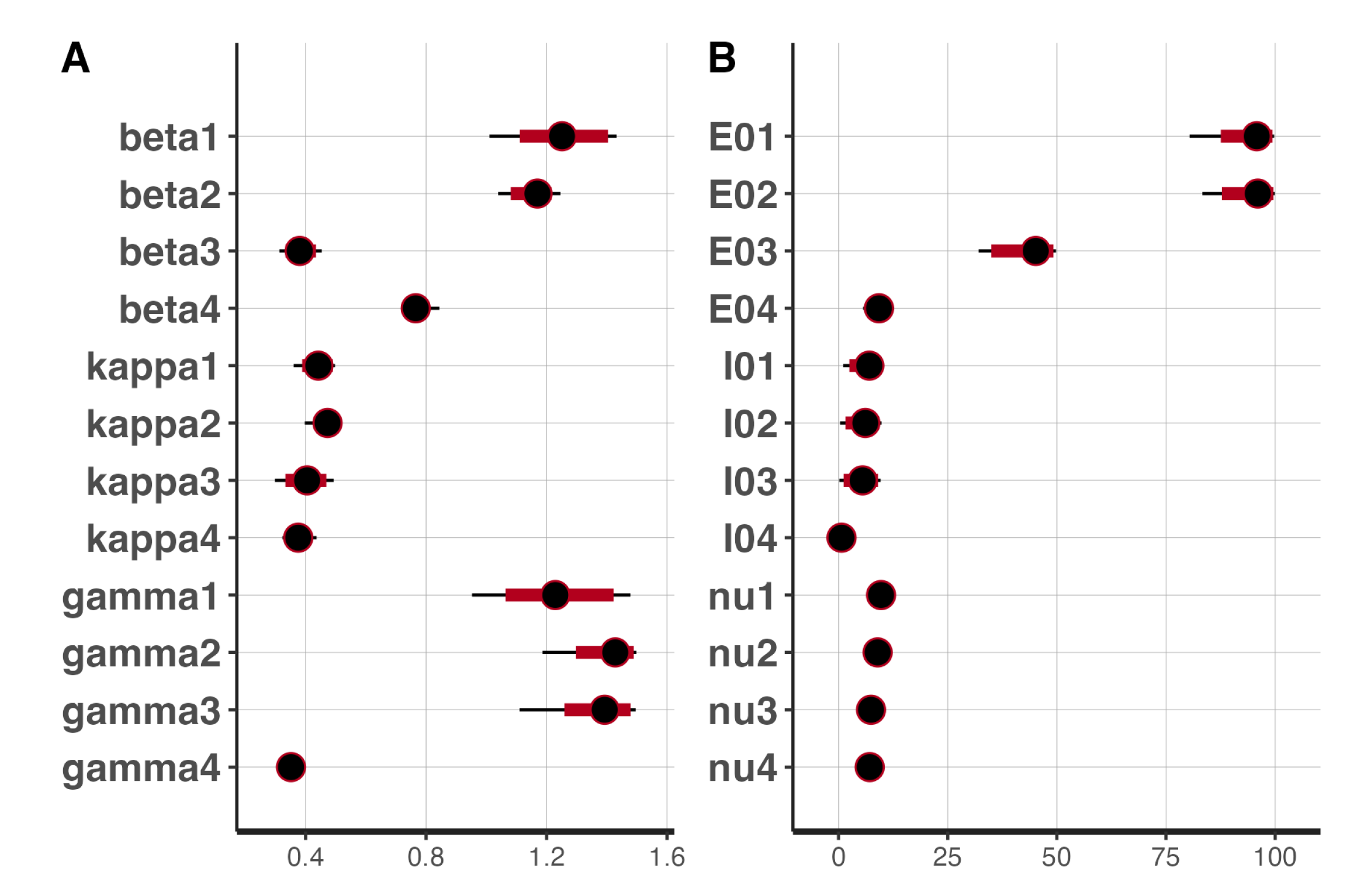The former and the latter observations can be confirmed from Figure 9, which shows the 95% CI of the samples, the mean and the estimates from the GA. Based on the scales of the values in the intervals, we can conclude that the credible intervals (CIs) are generally short, an indication of good estimates.

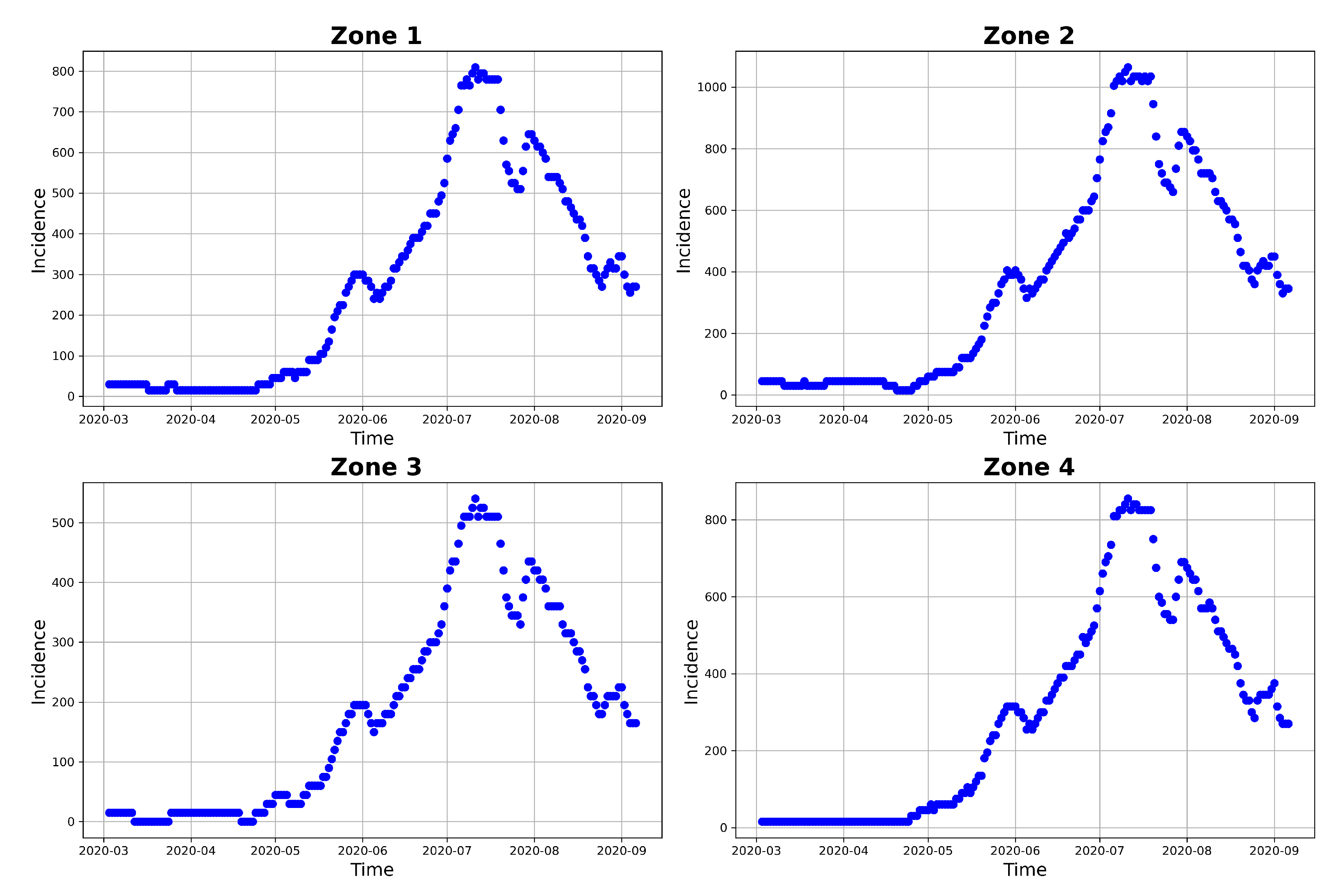
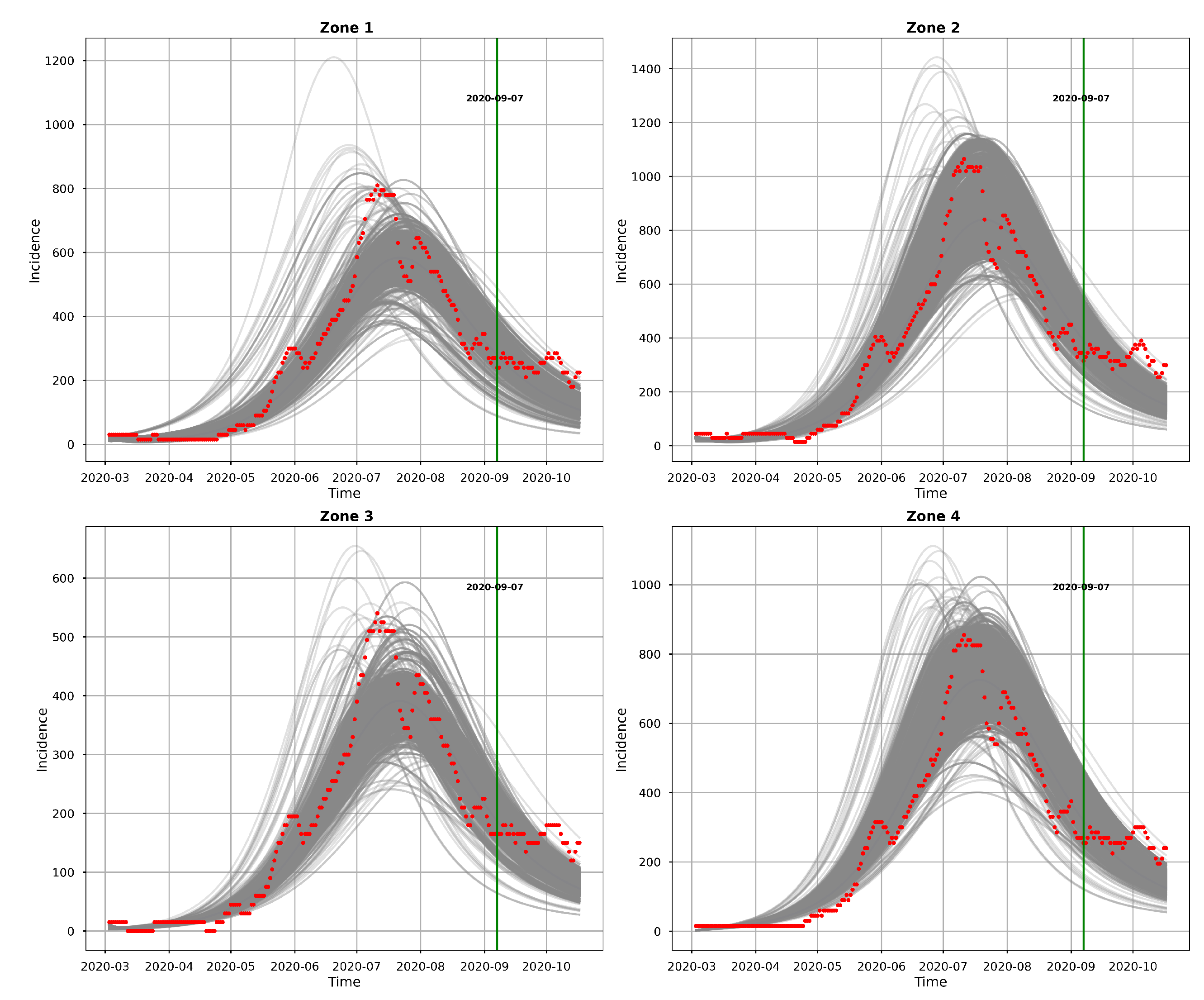
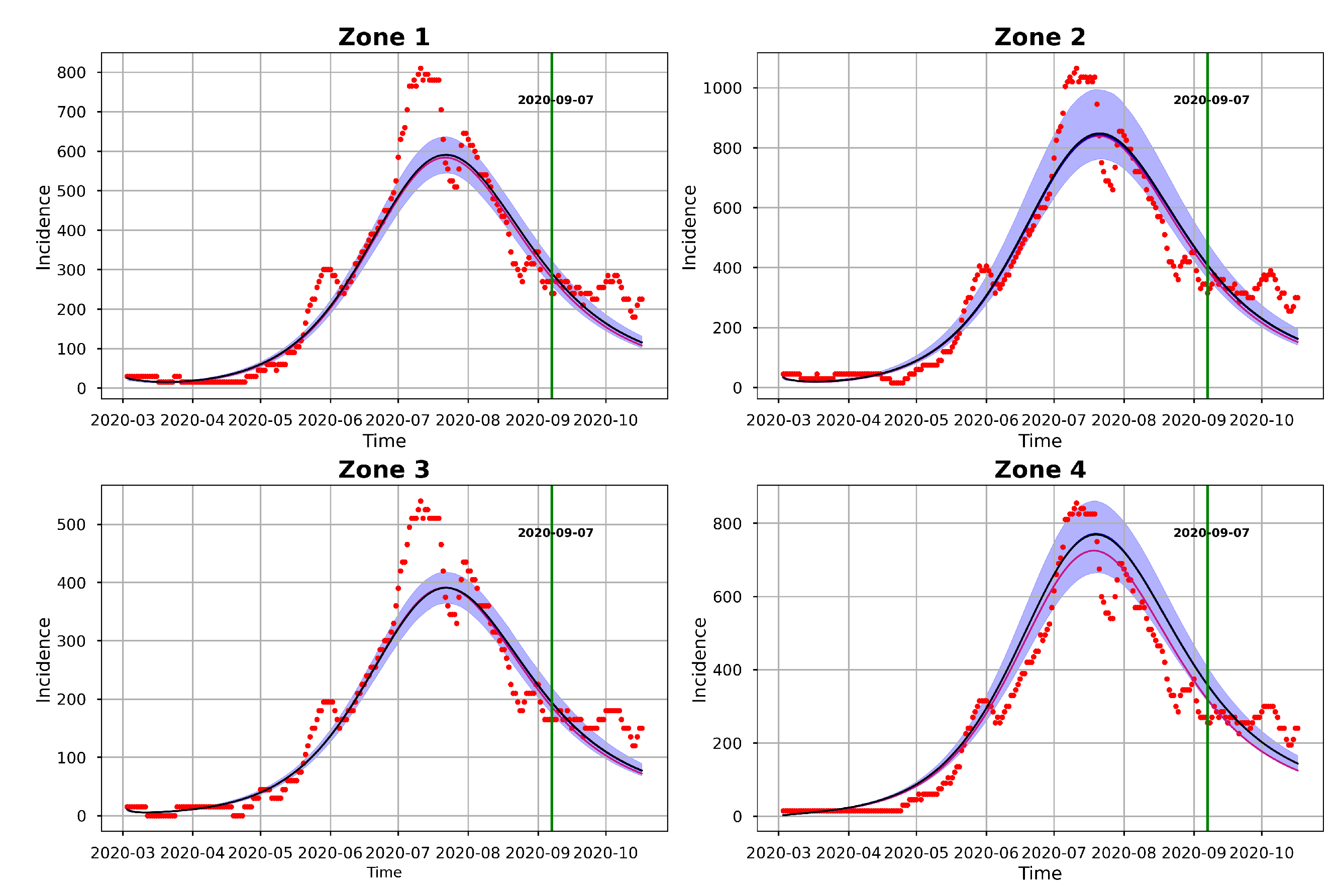
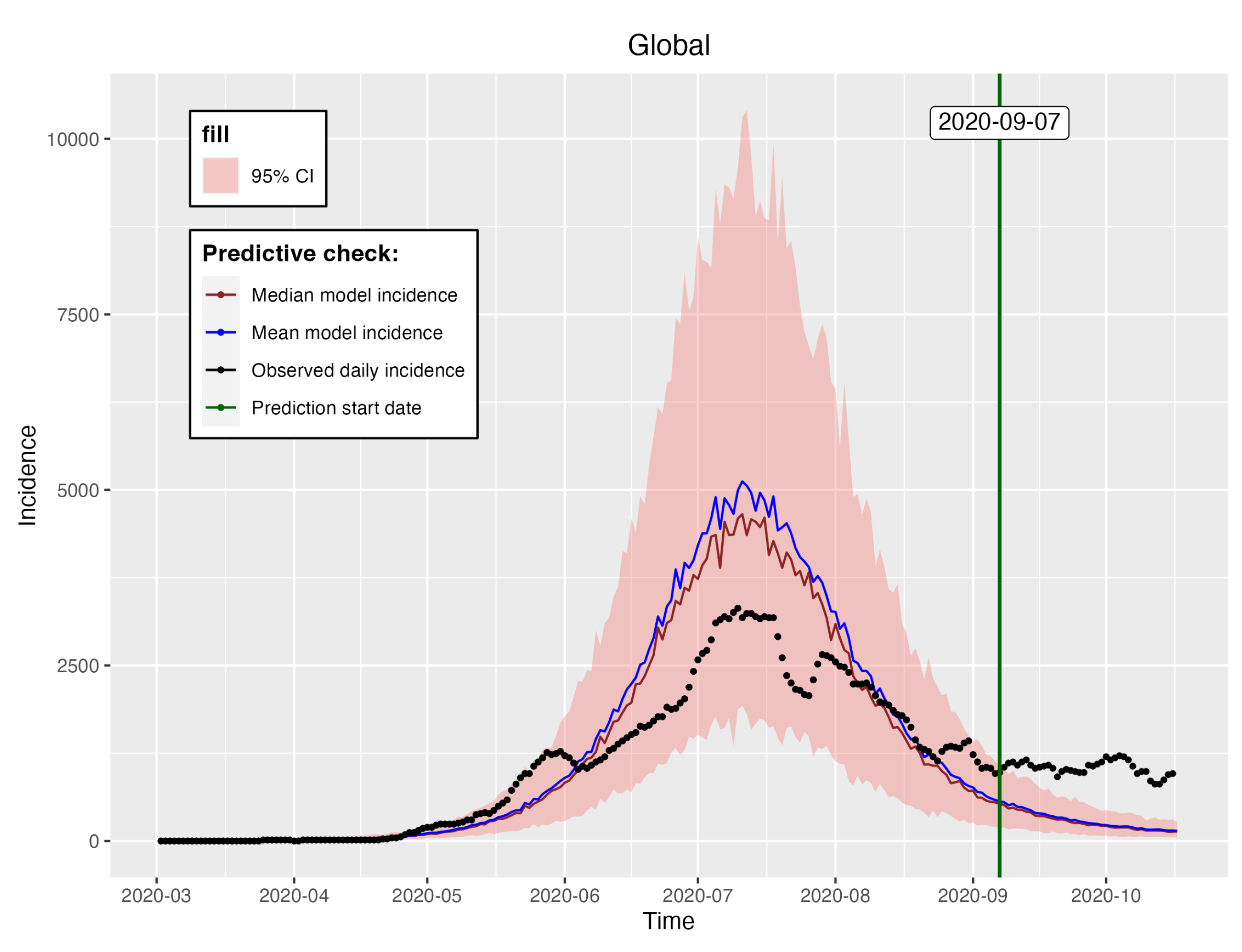
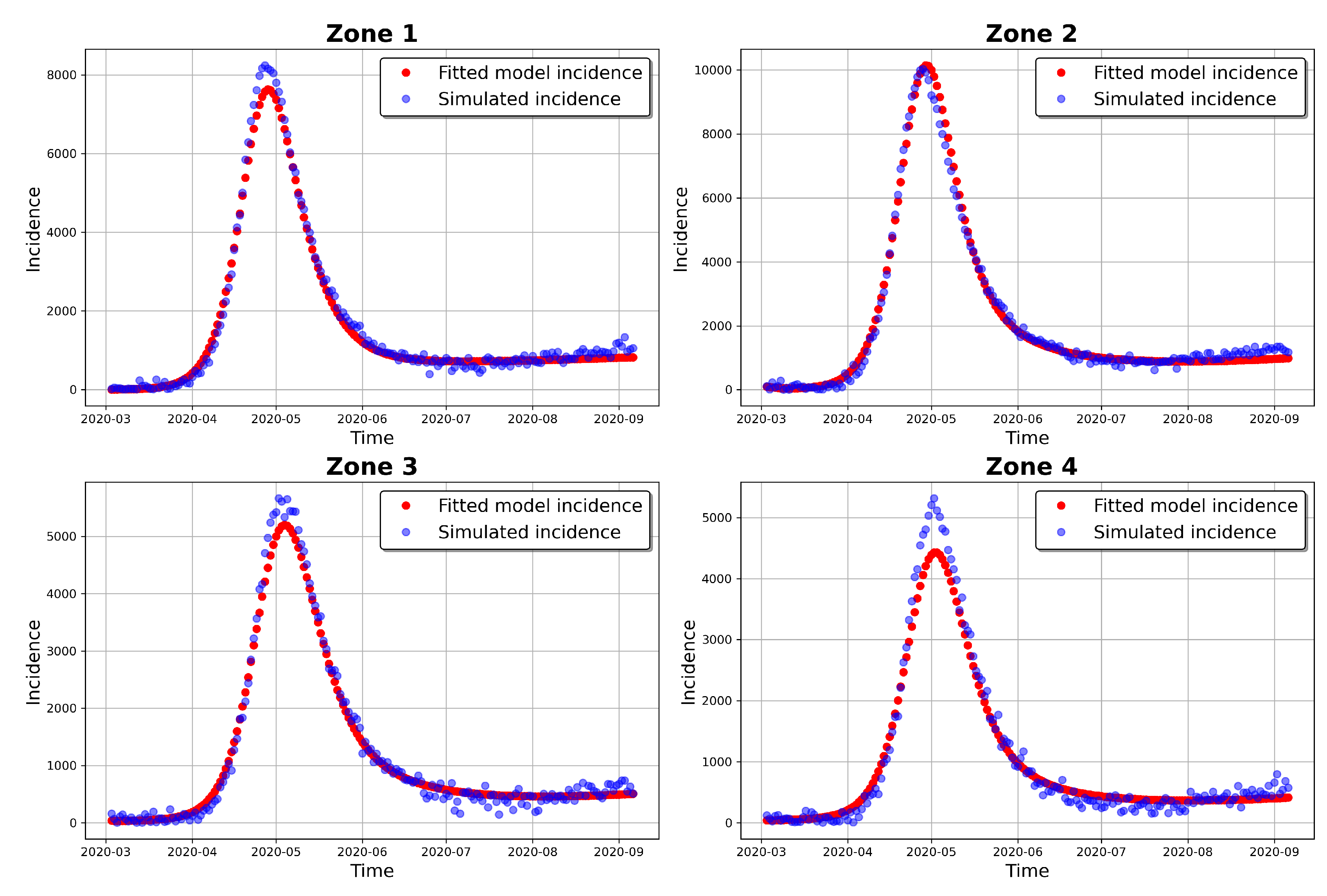
Figure 10 and Figure 11 represents the posterior predictive checks. The figures graph the incidence simulations of model (1) from 2020-02-26 to 2020-10-17. This period includes the dates within which the incidence data was observed (2020-02-26 to 2020-09-06) and 41 days prediction dates (2020-09-07 to 2020-10-17). Figure 10 shows 30,000 model incidences (grey curves), from the first 30,000 MCMC iterations, the observed incidence and the maximum a posteriori (MAP) model incidence. Here, the MAP model incidence, which is apparently covered by the grey curves, is the model incidence output obtained from the parameter values that maximizes the posterior distribution. We can observe from this figure, that 1) our fitted model produces simulations that are consistent with the observed incidence data and 2) the simulated trajectories do not portray diverse or variable changes. Indeed, the latter observation is consistent with our previous observation that there is low variability in the simulated samples.

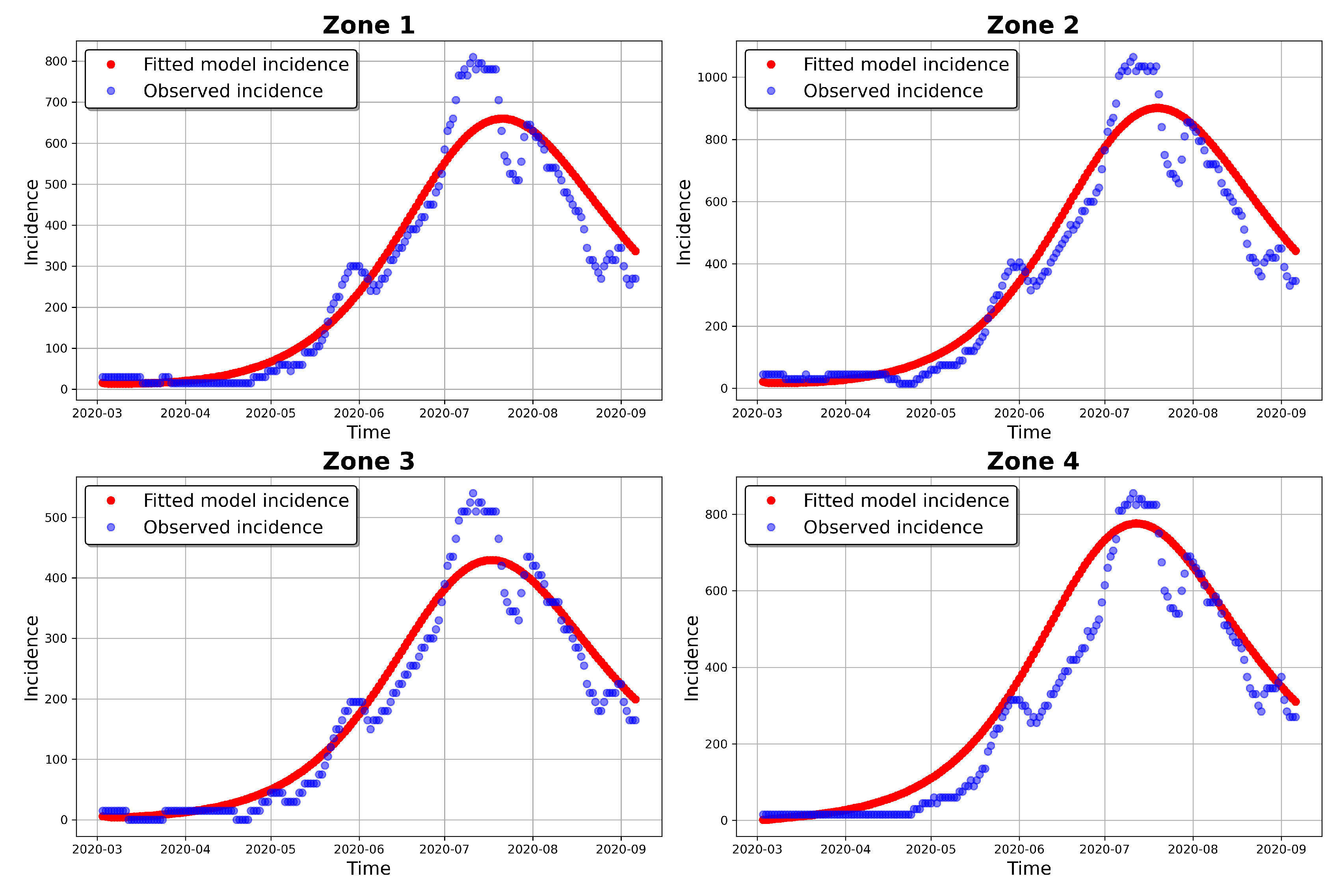
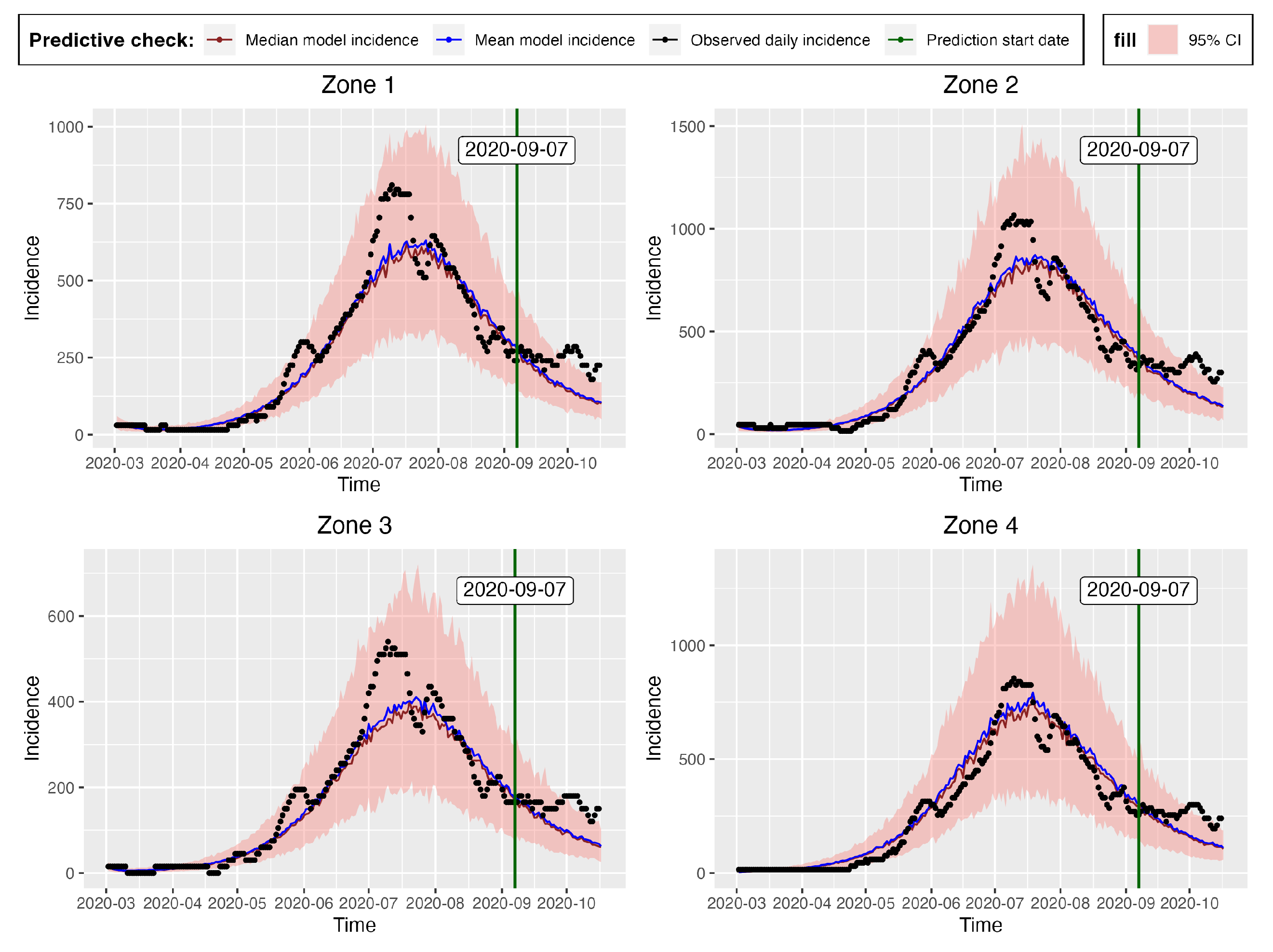
Figure 11 shows the 95% posterior confidence intervals (CIs), the mean, median and the MAP of the simulated model incidences. From this figure we observe that most of the observed training incidences for the four zones, fall outside the 95% CI of the simulated model incidence with zone 1 and zone 3 simulated model incidences providing the narrowest 95% CI. In contrast, zones 2 and 4 have larger 95% prediction CI, and they cover more of the observed incidence. Zone 1 model prediction interval provides the worst coverage of the observed prediction incidences in this zone. The proportions of the observed prediction incidence covered by the 95% CI of simulated model incidence from t-walk are presented in Table 8. As the CIs for the four zones are generally not too wide and covers a small proportion of the training observed incidence, and the prediction observed incidences for zones 3 and 4, we can conclude that the point estimates from t-walk seems adequate, but we tend to underestimate the uncertainty associated with the estimated parameters.

We can observe from both Figure 10 and Figure 11 that the model predicts that there will still be some infection levels beyond 2020-09-06, the date when we observed the last incidence. In fact, the figures reveal that in the four zones, some individuals will still be infected up until 2020-10-17, with the median and map incidences being within the 95% CI.

After checking the adequacy of the prior distributions with respect to the posterior distribution and sampling, using the t-walk package, we also performed sampling of the posterior distribution using the Stan package. Stan is a Hamiltonian Monte Carlo (HMC) based package designed for Bayesian statistical analysis. We refer the reader to [134] for more details about the software and [132,135] for an insight on how the package can be used to perform inference and uncertainty quantification of compartmental epidemic models.

For Stan, we used the same support for the prior distribution as used in t-walk, except for the incubation initial conditions. Using the same support for the incubation initial conditions in t-walk led to very low overall proposal acceptance rate. As such, we had to use a different and shorter support range for all the incubation initial conditions prior distributions in t-walk in order to have reasonable proposals acceptance rate for the algorithm. However, in Stan, the support range for the same parameters were larger as Stan is more robust. For the over-dispersion parameters, we used the transformed versions and sampled their inverses in Stan.

For the model at hand, we ran one chain with 1,000 iterations for each of the 24 parameters and took the first 300 iterations as burn-in samples. The number of iterations is not the same as those obtained from t-walk as Stan requires longer periods of time, than t-walk, to complete each iteration. However, from the analysis, we observe that the chains are importantly less correlated, and we can obtain bigger effective sample sizes. 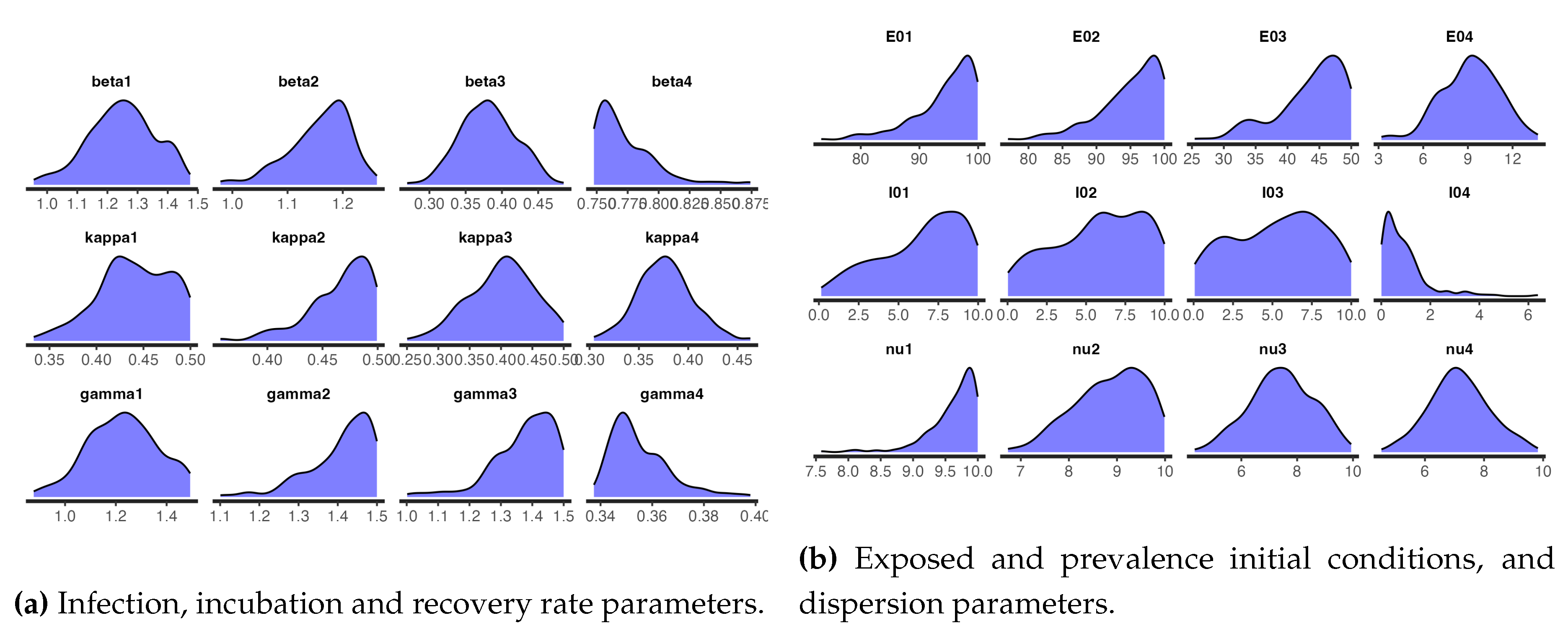Figure 12 and Figure 13 respectively shows the trace plots and the posterior densities of the samples of the estimated parameters. We obtained unit Rhat values from the Stan summary statistics output, an indication that all, except two, of the transitions converged. Additional Stan statistics, particularly, the diagnosis of the pairs plot of a subset of the estimated parameters, (Figure 14), confirms convergence of all, except two of the transitions of the chain during sampling.

Figure 15 shows the 95% CIs of the posterior distributions obtained from Stan. All the parameters, except ${\beta }_1$, ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$, had short CIs. It is noteworthy that just as in t-walk, the samples of the inverse of the over-dispersion parameters, ${\nu }_i$ from Stan had very narrow intervals.

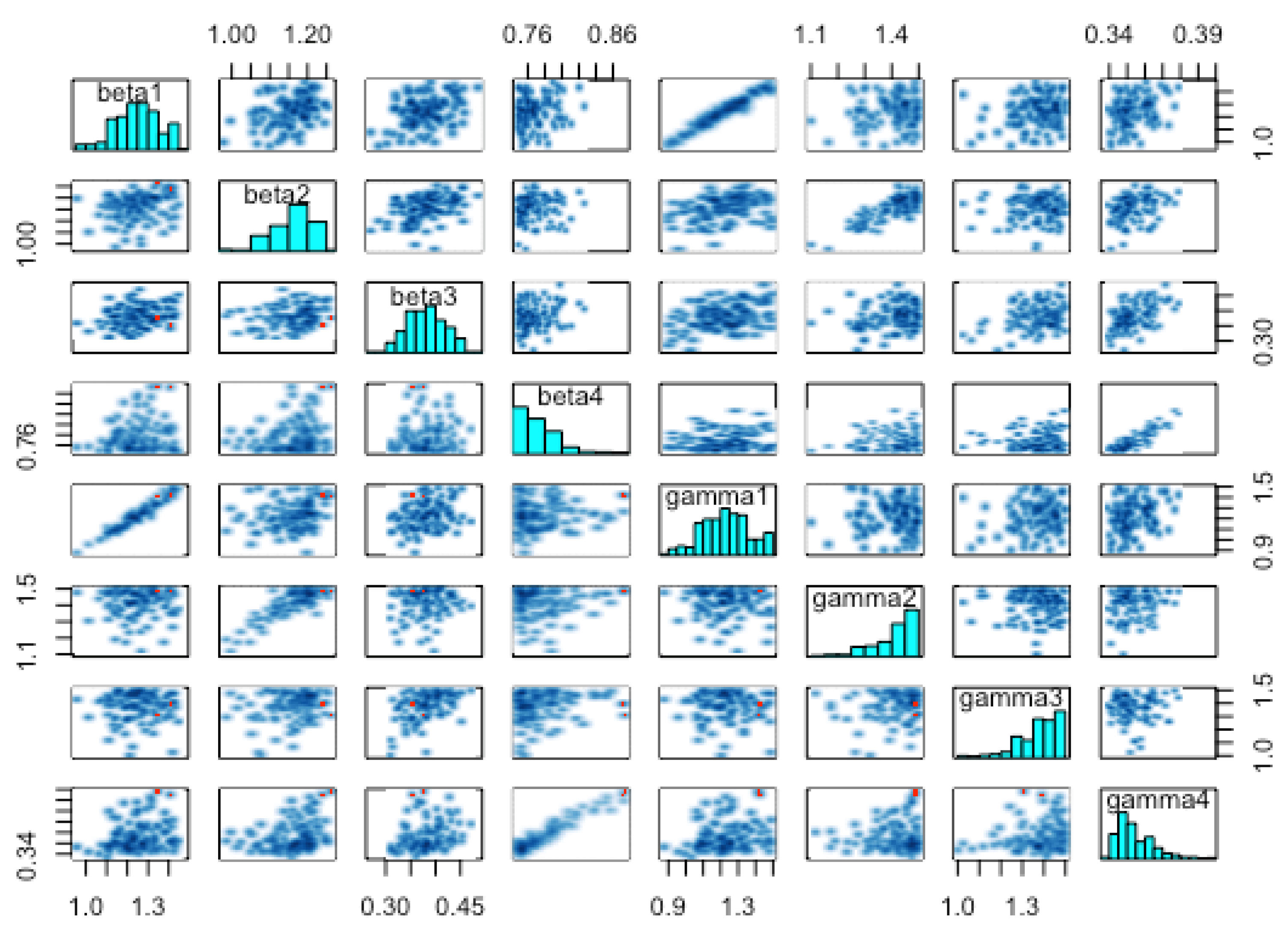
The pairs plot in Figure 14 shows the posterior distributions of the infection and recovery parameters (diagonal figures) and scatter plots (off-diagonal figures) showing the relationship between each of the samples. Since there were many (24) parameters to estimate, it was not appealing to have a joint pairs plot for all of them. In as much as this is the ideal procedure, doing this would lead to a figure with very tiny non-visualizable figure entries. We thus chose to pair the infection and recover rates (see Figure 14), as the scatter plots of these parameters exhibited interesting relationships. For instance, we observe from this figure, that there was a strong linear positive posterior correlation between ${\beta }_1$ and ${\gamma }_1$, ${\beta }_2$ and ${\gamma }_2$ and ${\beta }_4$ and ${\gamma }_4$. In contrast, the infection parameters for the four zones did not exhibit any important relationship among themselves. This was also the case with the recovery parameters.

The summary statistics of the samples as obtained from Stan are shown in Table A2. These statistics are slightly different from the summary statistics from t-walk as displayed in Table A1. The differences in the statistics of the prevalence initial conditions and the over-dispersion parameters are obvious, as we have already mentioned that besides using different support ranges for thesethe distributions of prevalence initial conditions, we transformed and sampled the inverses of the over-dispersion parameters ${\nu }_i$, $i=1,2,3,4$. Otherwise, the slight differences in the statistics of the other parameters could have been occasioned by the difference in how the t-walk and Stan packages performs sampling. Notably, these differences would not lead to a different conclusion regarding the potency of COVID-19 infections in Hermosillo in 2020. The statistics in Table A2 reveals that the point estimates of the parameters are within the 95% CIs as is the case with the estimated parameters from t-walk, as can be seen in Table A1.

The differences in the summary statistics of the samples obtained from both packages is further reflected in Figure 11 and Figure 16, which are the posterior predictive check figures from t-walk and Stan respectively. We can observe that the mean, median and the observed incidences for each zone are all covered by the respective 95% CIs. In comparison, we observe from the t-walk output in Figure 11, that whereas the 95% CI of the epidemic model incidences did not cover some observed daily incidences, the same interval from Stan covered all the training observed zonal incidences. We thus conclude that the estimated parameters from Stan can capture a more realistic uncertainty level, compared to those estimated by t-walk. Both Figure 11 and Figure 16 reveals that COVID-19 infections in the four zones, and consequently, the whole of Hermosillo, was at its peak in mid-July 2020, with a prediction of continued infections beyond 2020-09-06, which was the last date of observed training daily incidences.

Table 2 shows the ranges of the parameters of the model as obtained from various COVID-19 literature. Our results, both from the GA, t-walk and Stan packages (see Table 5, Table A1 and Table A2), indicate that the point estimates of the infection and incubation parameters; ${\beta }_i$ and ${\kappa }_i$, $i=1,2,3,4$, that best fit the incidences for the four zones, were within the ranges from literature. This is however not the case for the recovery parameters, ${\gamma }_i$, whose estimates were obtained as generally averaging close to one day recovery period for the four zones. This result is not surprising, as our incidence data for the four zones were inflated by a large under-reporting factor. This inflation, besides accounting for a possible lack of systematic testing of COVID-19 in Hermosillo, also accounted for the existence of subclinical and asymptomatic COVID-19 patients in the four zones under study. Going by how well the model fits the data, (see Figure 7, Figure 10, Figure 11 and Figure 16), we believe that accounting for incidence under-reporting by a factor of 15, as reported by [86] is realistic.

We further evaluate the prediction capability of the multi-patch model by checking the proportion of the observed zonal prediction incidences that are within the 95% CIs of the zone model incidences. Table 8 shows these proportions obtained from Stan (see Figure 16) and t-walk (see Figure 11). From this table, we can see that Stan produces 95% prediction bands that cover more than 50% of the observed prediction incidences for all the zones. On the other hand, t-walk provides 95% CIs large enough to cover less than 50% of observed prediction incidences for all the four zones, with zone 1 providing the narrowest simulated model incidence CIs that covers only 22.22% of the observed prediction incidence. In effect, we conclude that Stan outperforms t-walk as regards to the percentages of covered observed daily prediction incidence for all the zones.

6.3. Comparison to a single Patch model

To assess the improvement of using a more complex model against the usual single population model, in this section we fit the single-patch model (global SEIRS model) and compare its predictive performance against the multi-patch model with mobility. The systems of differential equations forming the single-patch model are presented in equation (14).

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{S}=\Lambda -\beta SI/N-\mu S+\tau R\hfill \\ \dot{E}=\beta SI/N-(\kappa +\mu )E\hfill \\ \dot{I}=\kappa E-(\gamma +\varphi +\mu )I\hfill \\ \dot{R}=\gamma I-(\mu +\tau )R.\hfill \end{array}\right.\end{array}$$

(14)

We run the single-patch model using similar values of birth, natural death and disease induced mortality rates used in the multi-patched model. We estimated the infection ($\beta$), incubation($\kappa$) and recovery($\gamma$) rates and the initial conditions $E_0$ and $I_0$ for the single patch model. The prior distributions of these parameters and the likelihood of the global observed incidence remains the same as the ones used in the multi-patched model. The initial population was taken as the sum of the zones population sizes, shown in Figure 1. That is, $N_0={\sum }_{i=1}^4{N}_i\left(0\right)=858,812$.

We use the observed global incidence in the period 2020-02-26 to 2020-09-06 to train the global single-patch model and then use the incidence in the period 2020-10-17 to assess the prediction efficiency of the model. Table 6 shows the summary statistics of the estimated parameters. For comparison purposes with the multi-patch model, we sum all the zones’ predicted mean and median incidences and compute the efficiency measures. The efficiency measures used in this case are the Root Mean Squared Error (RMSE) and Mean Absolute Percentage Error (MAPE) defined as

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\sum }_{t=1}^n{\left(Y_t-{\widehat{Y}}_t\right)}^2}\mathrm{and}\mathrm{MAPE}=\frac{100}{n}\sum _{t=1}^n\left|\frac{Y_t-{\widehat{Y}}_t}{Y_t}\right|,$$

where n is the total number of the predicted incidences, $Y_t$ is the actual observed incidence and ${\widehat{Y}}_t$ is the predicted incidence, which in this case is the mean and median incidences for both the multi-patch and global single-patched models.

Figure 17 shows the global single-patch predicted incidences together with the 95% credible incidence intervals, and Table 7 shows the efficiency measures of the predictions both from the multi and single-patched models. From this table, and indeed, comparing Figure 16 and Figure 17, we see that the multi-patched model outperforms the global single patch model, as it gives predicted incidences with lower RMSE and MAPE values. Moreover, Figure 16 reveals that a bigger percentage of the observed prediction and model predicted incidences from the multi-patched model are all within the 95% credible incidence interval. We thus conclude that in modelling COVID-19 in Hermosillo, using the multi-patched model with mobility represents an important improvement compared to the single-patch model.

7. Conclusions

In this work, we have utilized three techniques to estimate the parameters and perform inference and uncertainty quantification on a multi-patched epidemic model with mobility, residency and demography. The analysis has been conducted using mobile phone GPS data and confirmed COVID-19 cases in the four zones of Hermosillo, Mexico. The model incorporates two sets of parameters; 20 mobility and residence times parameters and 20 epidemiological parameters (including the incubation and prevalence initial conditions) which have all been estimated.

The complexity of the epidemic model makes it susceptible to the problem of parameter non-identifiability, a problemcomplication we have addressed by using the two distinctive data sets and different estimation techniques to estimate the two sets of parameters separately. In the first step, we have used Brownian Bridge model and mobile phone GPS data to estimate the first set of 20 mobility and residence times for the four zones in Hermosillo. The next set of the model epidemiological parameters have been estimated using confirmed positive COVID-19 cases and two estimation techniques; deterministic inversion using GA and probabilistic inversion, using two different MCMC methods implemented in the t-walk and Stan statistical packages.

The incidence outputs of the epidemic model are very sensitive to slight changes of its parameters, especially the infection, incubation and recovery rates. This necessitated the use of the deterministic inversion technique as the first step of estimation, as it provided us with an idea of the possible parametric values, and model incidences that best fit the observed incidences. This first step of estimation thus presented us with the scope of the parametric space within which to delimit the support of the posterior distribution and the initial sampling values used in the probabilistic inversion stage, using t-walk and Stan.

In this article, we are not concerned with a detailed comparison of t-walk and Stan, as there could be many factors that affect their performance, that undoubtedly vary among different models. Some of these factors may include the chosen parametrization of the model, the prior distribution and initial values from where the sampling starts. We however mention that some literature have established that it may be difficult to use MCMC-based inference tools to model systems of ODEs, since the relevant likelihood function may contain several local minima that causes them to fail the standard regulatory conditions. In these cases, Stan offers high statistical efficiency and, in complex scenarios, may produce more accurate results compared to t-walk. For the presented epidemic model, Stan performs better than t-walk as the posterior distributions are characterized by highly correlated parameter spaces. We have observed this fact in the present study based on the large ESS proportions obtained from Stan compared to those obtained from t-walk.

The results from the estimation in this study shows that the infection and incubation rates for the four zones in Hermosillo were within the ranges postulated in various COVID-19 literature. However, the recovery parameters fell outside the known COVID-19estimated ranges reported in other COVID-19 studies. This deviation has however been justified as possibly emanating from the inflation of the incidences in the four zones by a factor of 15 to account for under-reporting. . Further, from the estimated parameters, the model presents a good fit to COVID-19 infections in the four zones, and consequently, the whole city of Hermosillo, and under the model it also has its peak in mid-July 2020.

The epidemic model and the results in this research can be useful to public health officials as it not only provides better predictions, but alsoit italso explicitly introduces mobility parameters that can be modified to assess the effectiveness of different levels of mobility restrictions. These restrictions can be global or applied to only some patches. We believe the model and methods then can turn into a user-friendly tool to guide public health policies for management and mitigation of emerging and re-emerging infectious diseases.

The epidemic model in this article is confined within the limits of modelling a single strain of the COVID-19 virus. However, like many infectious diseases, multiple strains of COVID-19, resulting from its gene mutation, have emerged. For instance, four mutants of the pathogen were detected within the first one and a half years of the pandemic. It would therefore be relevant to extend the present epidemic model to include the dynamics of several COVID-19 pathogenic strains. This extension would lead to better understanding and management of future infectious outbreaks.

In addition, besides urban mobility, Tthe epidemic model used in this research did not account for government intervention measures like, such as vaccination and regional or national mobility. As the vaccination campaign in Mexico started in December 2020, this factor is absent, but it would be desirable to introduce these, and other mitigation strategies in future models, for modelling futuresubsequent outbreaks of COVID-19 and other infectious diseases.

It is worth noting that the assumptions for the proposed model include those for the ODEs to describe the dynamics within each patch. While ODEs can be effective in approximating dynamics in many scenarios, there are cases where, even with homogeneous mixing, the mathematical system may fail to accurately represent the behavior of a small population.

One reason for this is the assumption of continuous variables and smooth transitions inherent in ODEs. In small populations, discrete effects and stochastic events can have a significant impact on the dynamics. These discrete effects, such as random fluctuations or individual interactions, introduce variability that is not captured by ODEs, leading to the model inaccurately reflecting the true behavior of the system.

To address this, one option for small spatial scales and patch sizes, is to leverage computational techniques such as agent-based modeling. This approach captures the important variability that arises from individual interactions [136,137,138,139,140,141]. Additionally, to reduce the variability of simulations, relevant contact patterns produced by street or building layouts can be incorporated. At a more detailed level, modeling individual interactions as a network of contacts still allows for fitting or performing statistical inference using computer-intensive methods [55,142,143,144]. Because of this, scaling up these methods on slightly larger patches can pose serious challenges that requiere careful considerations.

Appendix A.1. Posterior statistics from t-walk

Table A1. Statistics of model parameters estimated using probabilistic (twalk) inversion

	Probabilistic inversion (t-walk) statistics
Parameters	Mean	SD	$q_{0.025}$	$q_{0.250}$	$q_{0.5}$	$q_{0.750}$	$q_{0.975}$	ESS	pESS
${\beta }_1$	1.3552	0.1039	1.1166	1.2951	1.3724	1.4307	1.5033	25	0.0008
${\beta }_2$	1.2258	0.1014	1.0668	1.1321	1.2366	1.3036	1.4168	22	0.0007
${\beta }_3$	0.4223	0.0663	0.3046	0.3734	0.4225	0.4629	0.5734	28	0.0009
${\beta }_4$	1.0839	0.1404	0.8218	0.9383	1.1300	1.1700	1.2970	18	0.0006
${\kappa }_1$	0.4649	0.0368	0.3754	0.4510	0.4757	0.4888	0.4989	233	0.0073
${\kappa }_2$	0.4730	0.0294	0.4013	0.4627	0.4811	0.4925	0.4994	112	0.0035
${\kappa }_3$	0.4236	0.0575	0.2735	0.3940	0.4320	0.4683	0.4964	122	0.0038
${\kappa }_4$	0.2614	0.0401	0.1991	0.2318	0.2526	0.2897	0.3436	21	0.0006
${\gamma }_1$	1.3740	0.1082	1.1382	1.3000	1.4047	1.4649	1.4977	22	0.0007
${\gamma }_2$	1.3461	0.1243	1.1416	1.2259	1.3920	1.4620	1.4945	20	0.0006
${\gamma }_3$	1.3196	0.1551	0.9050	1.2604	1.3547	1.4367	1.4959	32	0.0010
${\gamma }_4$	0.5198	0.0673	0.4061	0.4546	0.5358	0.5669	0.6372	18	0.0006
$E_{1,0}$	61.3153	3.1875	53.1884	59.6405	62.2854	63.8354	64.8765	92	0.0029
$I_{1,0}$	6.6851	2.6790	0.6896	4.9450	7.3324	8.9846	9.8718	175	0.0055
$E_{2,0}$	80.5102	3.8104	71.4076	78.1892	81.6369	83.5947	84.8731	88	0.0027
$I_{2,0}$	6.3754	2.8778	0.3521	4.4653	7.1644	8.8401	9.9016	75	0.0023
$E_{3,0}$	27.8516	1.9766	22.5930	26.8572	28.4460	29.3748	29.9438	160	0.0050
$I_{3,0}$	5.7194	2.8518	0.3452	3.4194	6.0118	8.2424	9.8920	288	0.0090
$E_{4,0}$	7.9665	1.5100	4.2772	7.1346	8.2710	9.1433	9.9091	87	0.0027
$I_{4,0}$	1.6821	1.5480	0.0551	0.4926	1.2054	2.3330	5.7315	70	0.0022
${\nu }_1$	9.6957	0.2948	8.8788	9.5804	9.7863	9.9084	9.9933	226	0.0071
${\nu }_2$	9.1320	0.7812	7.3177	8.7525	9.3166	9.7064	9.9798	141	0.0044
${\nu }_3$	9.7135	0.3543	8.9596	9.6075	9.8080	9.9251	9.9939	147	0.0046
${\nu }_4$	7.8458	1.3651	5.2517	6.8248	7.9591	9.0183	9.9349	35	0.0010

Table A1. Statistics of model parameters estimated using probabilistic (twalk) inversion

	Probabilistic inversion (t-walk) statistics
Parameters	Mean	SD	$q_{0.025}$	$q_{0.250}$	$q_{0.5}$	$q_{0.750}$	$q_{0.975}$	ESS	pESS
${\beta }_1$	1.3552	0.1039	1.1166	1.2951	1.3724	1.4307	1.5033	25	0.0008
${\beta }_2$	1.2258	0.1014	1.0668	1.1321	1.2366	1.3036	1.4168	22	0.0007
${\beta }_3$	0.4223	0.0663	0.3046	0.3734	0.4225	0.4629	0.5734	28	0.0009
${\beta }_4$	1.0839	0.1404	0.8218	0.9383	1.1300	1.1700	1.2970	18	0.0006
${\kappa }_1$	0.4649	0.0368	0.3754	0.4510	0.4757	0.4888	0.4989	233	0.0073
${\kappa }_2$	0.4730	0.0294	0.4013	0.4627	0.4811	0.4925	0.4994	112	0.0035
${\kappa }_3$	0.4236	0.0575	0.2735	0.3940	0.4320	0.4683	0.4964	122	0.0038
${\kappa }_4$	0.2614	0.0401	0.1991	0.2318	0.2526	0.2897	0.3436	21	0.0006
${\gamma }_1$	1.3740	0.1082	1.1382	1.3000	1.4047	1.4649	1.4977	22	0.0007
${\gamma }_2$	1.3461	0.1243	1.1416	1.2259	1.3920	1.4620	1.4945	20	0.0006
${\gamma }_3$	1.3196	0.1551	0.9050	1.2604	1.3547	1.4367	1.4959	32	0.0010
${\gamma }_4$	0.5198	0.0673	0.4061	0.4546	0.5358	0.5669	0.6372	18	0.0006
$E_{1,0}$	61.3153	3.1875	53.1884	59.6405	62.2854	63.8354	64.8765	92	0.0029
$I_{1,0}$	6.6851	2.6790	0.6896	4.9450	7.3324	8.9846	9.8718	175	0.0055
$E_{2,0}$	80.5102	3.8104	71.4076	78.1892	81.6369	83.5947	84.8731	88	0.0027
$I_{2,0}$	6.3754	2.8778	0.3521	4.4653	7.1644	8.8401	9.9016	75	0.0023
$E_{3,0}$	27.8516	1.9766	22.5930	26.8572	28.4460	29.3748	29.9438	160	0.0050
$I_{3,0}$	5.7194	2.8518	0.3452	3.4194	6.0118	8.2424	9.8920	288	0.0090
$E_{4,0}$	7.9665	1.5100	4.2772	7.1346	8.2710	9.1433	9.9091	87	0.0027
$I_{4,0}$	1.6821	1.5480	0.0551	0.4926	1.2054	2.3330	5.7315	70	0.0022
${\nu }_1$	9.6957	0.2948	8.8788	9.5804	9.7863	9.9084	9.9933	226	0.0071
${\nu }_2$	9.1320	0.7812	7.3177	8.7525	9.3166	9.7064	9.9798	141	0.0044
${\nu }_3$	9.7135	0.3543	8.9596	9.6075	9.8080	9.9251	9.9939	147	0.0046
${\nu }_4$	7.8458	1.3651	5.2517	6.8248	7.9591	9.0183	9.9349	35	0.0010

Appendix A.2. Posterior statistics from Stan

Table A2. Statistics of model parameters estimated using probabilistic (Stan) inversion

	Probabilistic inversion (Stan) statistics
Parameters	Mean	SD	$q_{0.025}$	$q_{0.250}$	$q_{0.5}$	$q_{0.750}$	$q_{0.975}$	ESS	pESS
${\beta }_1$	1.2476	0.1080	1.0107	1.1807	1.2498	1.3193	1.4317	255	0.3643
${\beta }_2$	1.1591	0.0546	1.0432	1.1294	1.1698	1.2000	1.2460	213	0.3043
${\beta }_3$	0.3811	0.0380	0.3129	0.3543	0.3805	0.4057	0.4536	244	0.3486
${\beta }_4$	0.7728	0.0245	0.7489	0.7548	0.7656	0.7855	0.8440	173	0.2471
${\kappa }_1$	0.4409	0.0377	0.3606	0.4166	0.4427	0.4729	0.4976	188	0.2686
${\kappa }_2$	0.4660	0.0282	0.3973	0.4501	0.4728	0.4881	0.4985	248	0.3543
${\kappa }_3$	0.4019	0.0517	0.2978	0.3641	0.4053	0.4385	0.4930	244	0.3486
${\kappa }_4$	0.3766	0.0280	0.3228	0.3578	0.3758	0.3933	0.4365	196	0.2800
${\gamma }_1$	1.2275	0.1359	0.9530	1.1274	1.2277	1.3274	1.4783	241	0.3443
${\gamma }_2$	1.4091	0.0795	1.2259	1.3692	1.4280	1.4729	1.4980	209	0.2986
${\gamma }_3$	1.3743	0.0983	1.1104	1.3161	1.3922	1.4521	1.4958	204	0.2914
${\gamma }_4$	0.3550	0.0113	0.3408	0.3472	0.3514	0.3612	0.3846	188	0.2686
$E_{1,0}$	94.4414	5.1047	80.4055	92.2135	95.8150	98.3510	99.7569	234	0.3343
$I_{1,0}$	6.5046	2.5618	1.0641	4.6339	7.0732	8.6031	9.8693	202	0.2886
$E_{2,0}$	94.8808	4.5037	83.3513	92.6637	95.9344	98.4198	99.8949	143	0.2043
$I_{2,0}$	5.8008	2.8349	0.3588	3.6777	6.1113	8.2312	9.8222	217	0.3100
$E_{3,0}$	43.6993	5.1480	32.0696	40.9228	45.1198	47.7972	49.8012	224	0.3200
$I_{3,0}$	5.2505	2.8159	0.1604	2.5964	5.4800	7.5498	9.6372	217	0.3100
$E_{4,0}$	9.1961	1.9174	5.6108	7.9395	9.2555	10.4385	12.6814	262	0.3743
$I_{4,0}$	0.8923	0.9075	0.0397	0.2712	0.6660	1.1865	3.4709	202	0.2886
${\nu }_1$	9.6200	0.3765	8.6530	9.4789	9.7231	9.8887	9.9887	167	0.2386
${\nu }_2$	8.8543	0.7276	7.3756	8.3520	8.9653	9.4043	9.8811	222	0.3171
${\nu }_3$	7.4251	1.1378	5.1812	6.6442	7.4181	8.2871	9.4924	146	0.2086
${\nu }_4$	7.1626	1.0035	5.2185	6.4972	7.1173	7.7591	9.2361	151	0.2158

Table A2. Statistics of model parameters estimated using probabilistic (Stan) inversion

	Probabilistic inversion (Stan) statistics
Parameters	Mean	SD	$q_{0.025}$	$q_{0.250}$	$q_{0.5}$	$q_{0.750}$	$q_{0.975}$	ESS	pESS
${\beta }_1$	1.2476	0.1080	1.0107	1.1807	1.2498	1.3193	1.4317	255	0.3643
${\beta }_2$	1.1591	0.0546	1.0432	1.1294	1.1698	1.2000	1.2460	213	0.3043
${\beta }_3$	0.3811	0.0380	0.3129	0.3543	0.3805	0.4057	0.4536	244	0.3486
${\beta }_4$	0.7728	0.0245	0.7489	0.7548	0.7656	0.7855	0.8440	173	0.2471
${\kappa }_1$	0.4409	0.0377	0.3606	0.4166	0.4427	0.4729	0.4976	188	0.2686
${\kappa }_2$	0.4660	0.0282	0.3973	0.4501	0.4728	0.4881	0.4985	248	0.3543
${\kappa }_3$	0.4019	0.0517	0.2978	0.3641	0.4053	0.4385	0.4930	244	0.3486
${\kappa }_4$	0.3766	0.0280	0.3228	0.3578	0.3758	0.3933	0.4365	196	0.2800
${\gamma }_1$	1.2275	0.1359	0.9530	1.1274	1.2277	1.3274	1.4783	241	0.3443
${\gamma }_2$	1.4091	0.0795	1.2259	1.3692	1.4280	1.4729	1.4980	209	0.2986
${\gamma }_3$	1.3743	0.0983	1.1104	1.3161	1.3922	1.4521	1.4958	204	0.2914
${\gamma }_4$	0.3550	0.0113	0.3408	0.3472	0.3514	0.3612	0.3846	188	0.2686
$E_{1,0}$	94.4414	5.1047	80.4055	92.2135	95.8150	98.3510	99.7569	234	0.3343
$I_{1,0}$	6.5046	2.5618	1.0641	4.6339	7.0732	8.6031	9.8693	202	0.2886
$E_{2,0}$	94.8808	4.5037	83.3513	92.6637	95.9344	98.4198	99.8949	143	0.2043
$I_{2,0}$	5.8008	2.8349	0.3588	3.6777	6.1113	8.2312	9.8222	217	0.3100
$E_{3,0}$	43.6993	5.1480	32.0696	40.9228	45.1198	47.7972	49.8012	224	0.3200
$I_{3,0}$	5.2505	2.8159	0.1604	2.5964	5.4800	7.5498	9.6372	217	0.3100
$E_{4,0}$	9.1961	1.9174	5.6108	7.9395	9.2555	10.4385	12.6814	262	0.3743
$I_{4,0}$	0.8923	0.9075	0.0397	0.2712	0.6660	1.1865	3.4709	202	0.2886
${\nu }_1$	9.6200	0.3765	8.6530	9.4789	9.7231	9.8887	9.9887	167	0.2386
${\nu }_2$	8.8543	0.7276	7.3756	8.3520	8.9653	9.4043	9.8811	222	0.3171
${\nu }_3$	7.4251	1.1378	5.1812	6.6442	7.4181	8.2871	9.4924	146	0.2086
${\nu }_4$	7.1626	1.0035	5.2185	6.4972	7.1173	7.7591	9.2361	151	0.2158