Prerpints.org logo
Preprint
Article

Hopf Bifurcation Analysis and Optimal Control of an Infectious Disease with Awareness Campaign and Treatment

Altmetrics

Downloads

202

Views

76

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

04 May 2023

Posted:

05 May 2023

You are already at the latest version

Alerts
Abstract
Infectious diseases continue to be a significant threat to human health and civilization, and finding effective methods to combat them is crucial. In this research, we investigate the impact of awareness campaigns and optimal control techniques on infectious diseases without proper vaccines. Specifically, we develop an SIRS type mathematical model that incorporates awareness campaigns through media and treatment for disease transmission dynamics and control. The model displays two equilibria, a disease-free equilibrium and an endemic equilibrium, and exhibits Hopf bifurcation when the bifurcation parameter exceeds its critical value, causing a switch in the stability of the system. We also propose an optimal control problem that minimizes the cost of control measures while achieving a desired level of disease control. By applying the minimum principle to the optimal control problem, we obtain analytical and numerical results that show how the infection rate of the disease affects the stability of the system and how awareness campaigns and treatment can maintain system stability. This study highlights the importance of awareness campaigns in controlling infectious diseases and demonstrates the effectiveness of optimal control theory in achieving disease control with minimal cost.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

Infectious diseases remain a significant public health threat in the modern era despite remarkable advances in science and technology. Microbes such as bacteria, viruses, parasites, and fungi can easily spread from person to person or between humans and animals through various means, including food, water, air, and soil. Deadly infectious diseases include Human Immunodeficiency Virus (HIV), Tuberculosis (TB), and Hepatitis B Virus (HBV). Additionally, diarrhea is a common problem caused by contaminated food or water that can lead to dehydration and death, particularly in low-income countries. According to the World Health Organization, around 17% of deaths worldwide are due to contagious diseases, and HIV/AIDS and TB accounted for 1.5 million deaths in 2019, respectively. In the same year, diarrhea was responsible for nearly 300,000 deaths. The recent pandemic caused by SARS COV-2 has caused around 6.4 million deaths in 2022, making it another deadly infectious disease. Effective prevention and control strategies for infectious diseases are urgently needed to reduce their impact on public health [1,8,9].
Infectious diseases can have devastating consequences for individuals and communities. To stop the spread of such diseases, basic awareness knowledge is crucial among the population. Health education on different measures can bring the desired change in human behavior, playing a key role in such awareness campaigns [3]. An awareness method requires proper technicality and devices to teach the message to the population. The essential elements of such an awareness campaign are prevention by using specific measures, early detection of the problem, and correct treatment under medical supervision. Reaching out to people through different media channels like social media, mass media, seminars, workshops, and health camps, can disseminate the message of disease prevention and control, tailored to the rural or urban setting of the population [5].
Media campaigns can have a significant impact on controlling the spread of infectious diseases. By educating the public about the signs and symptoms of an infection, how it spreads, and what measures can be taken to reduce the risk of transmission, media campaigns can help to reduce the number of new cases and prevent outbreaks from becoming widespread [7]. For instance, social media platforms can provide accurate and up-to-date information to the public to dispel myths and avoid the spread of misinformation. Public service announcements (PSAs) on television and radio that educate people about infectious diseases and how to protect themselves and others can also be effective. By educating the public about the importance of handwashing, wearing masks, and maintaining social distancing to prevent the spread of infection, media campaigns can encourage people to take preventive measures [10].
In addition, an awareness campaign can promote the importance of vaccination and encourage people to vaccinate in order to reduce their risk of getting sick [4]. Designing and distributing posters and flyers with information about infectious diseases and how to prevent their spread in public places, such as hospitals, schools, shopping malls, and other high-traffic areas, can also be useful. By educating the public about the signs and symptoms of infectious diseases, an awareness campaign can encourage people to seek medical attention if they suspect they may have been exposed. This leads to early detection and treatment, reducing the severity of the illness and preventing its spread to others [12].
It is essential to note that all awareness campaigns should align with the latest guidance from public health authorities and medical professionals to ensure the accuracy and effectiveness of the information being shared. Therefore, media campaigns can be a powerful tool to increase awareness, provide accurate information, and encourage individuals to take preventive measures to stop the spread of infectious diseases.
The impact of media awareness on epidemic outbreaks has been analyzed through model-based mathematical studies [11,13,20,23]. These studies examine the disease dynamics of a well-mixed population, where a portion of the susceptible and infected populations are aware of the disease. In these models, aware susceptible individuals are also vulnerable to disease infection, but at a lower rate than unaware susceptible individuals.
Another area of study focuses on the impact of information transmission on the dynamics of sexually transmitted infections, assuming that the entire population is aware of the risk, but only a certain proportion is able to respond by limiting their contact with infected individuals [27]. Additionally, epidemic models have been developed that consider the cumulative density of the awareness program as a separate variable [19,22].
This research also takes into account the assumption that infected individuals can recover through awareness-induced treatment and join the aware human population. The model incorporates both local awareness, through information from local people and relatives, and global awareness, through radio and TV campaigns. The level of awareness, M ( t ) , decreases over time as aware individuals become unaware. Aware individuals are assumed to become infected at a lower rate than unaware individuals.
Finally, optimal control theory has been applied to maximize awareness and minimize disease control costs. These studies highlight the important role of media awareness in controlling epidemic outbreaks and provide insights into how awareness campaigns can be optimized to be more effective.
Optimization techniques are a key tool for developing effective control strategies for infectious diseases. One important aspect of this is cost-effectiveness, where a cost function is used to capture the economic and social costs of implementing control measures and the health-related costs of the disease. These costs can include things like the cost of treatment, lost productivity, and the cost of implementing control measures such as media campaigns.
To address this, an optimal control problem is proposed in this research, which aims to minimize costs by controlling both media campaign costs and treatment costs. The proposed optimization problem is solved using techniques such as Pontryagin’s maximum principle, which helps to identify optimal control strategies that balance the costs and benefits of different control measures, while taking into account the level of public awareness.
Numerical methods are then used to solve the optimization problem and identify the optimal control strategies. This can help to develop effective and cost-efficient control measures that can be implemented to reduce the spread of infectious diseases. By combining mathematical modeling with optimization techniques, we can develop evidence-based strategies that take into account the complex interactions between the disease, the population, and the various control measures that can be implemented.
The organization of this paper is as follows: Section 2 presents the model and its underlying hypotheses. Section 3 offers analytical findings such as equilibria, stability analysis, and bifurcation analysis. In Section 4, the optimal control problem is formulated. Section 5 presents numerical simulations and discussions. Finally, in Section 6, the paper concludes by highlighting the benefits and usefulness of the results.
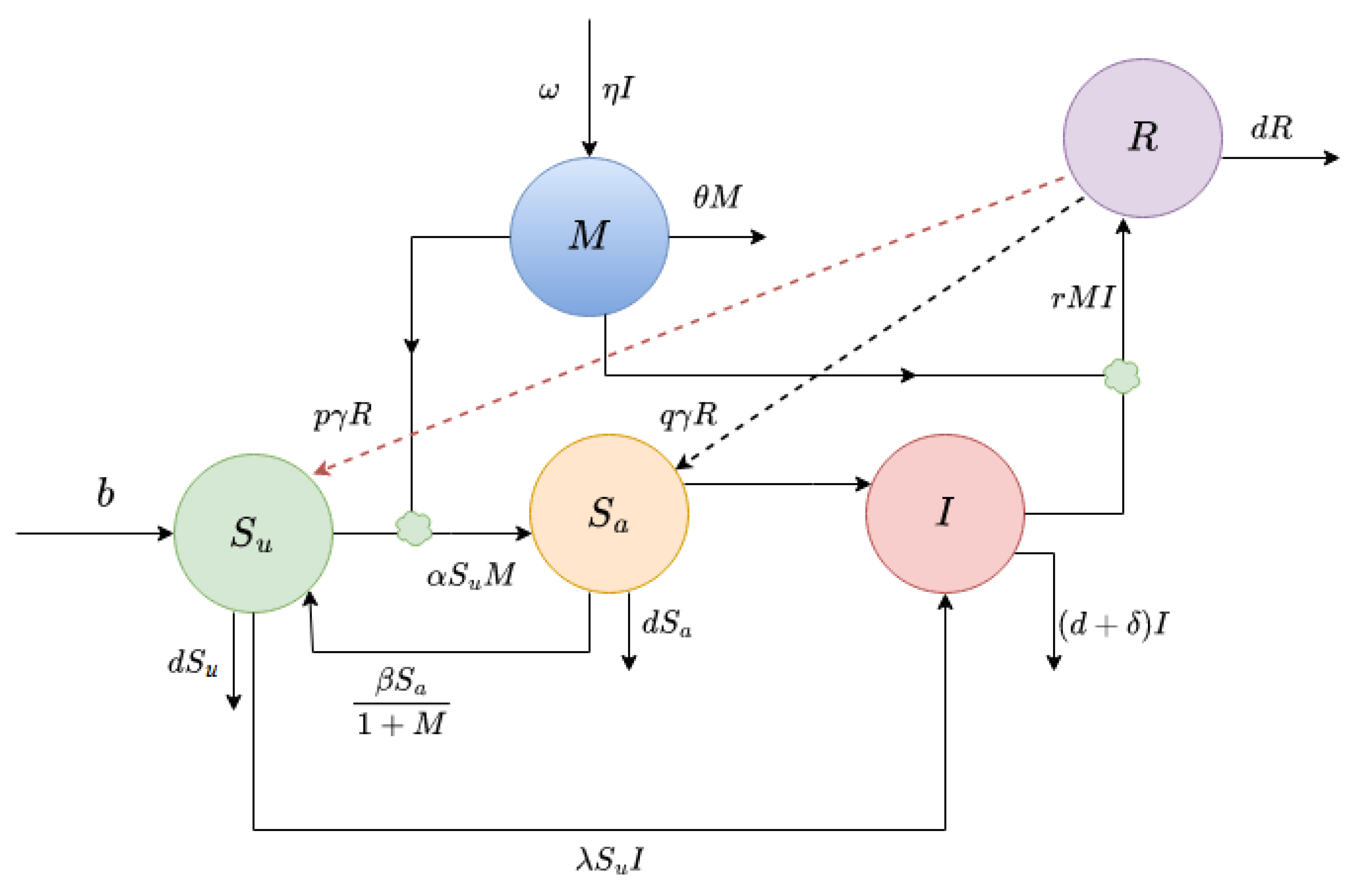
Preprints 72709 g001
Figure 1. Interactions between populations is shown.
Figure 1. Interactions between populations is shown.
Preprints 72709 g001

2. The Mathematical Model

The mathematical model proposed in this study is based on several assumptions. The model has five variables, where S ( t ) and I ( t ) represent the density of susceptible and infected populations at time t, respectively. The disease is transmitted from infected to susceptible individuals following a mass action functional form. A media campaign, denoted as M ( t ) , can be carried out to increase awareness in the susceptible population. This campaign divides the total susceptible population into two subclasses: the unaware susceptible population S u and the aware susceptible population S a . As awareness disseminates, people change their behavior to alter their susceptibility. It is also assumed that infected individuals recover through treatment at a rate γ and after recovery, a fraction p of recovered people join the unaware susceptible class, while the remaining fraction q = ( 1 − p ) join the aware susceptible class.
Several parameters are used to describe the model. These include b, which is the constant recruitment rate in the susceptible population; λ , the disease transmission rate; d, the natural mortality rate of the population; δ , the disease-induced mortality rate of the infected population; and r, the recovery rate. The disease spreads due to direct contact between susceptible and infective individuals at a rate λ , and the transfer rate from aware class to unaware class is denoted as β .
All newly recruited individuals are assumed to be unaware, and the rate of being aware is proportional to the number of infected individuals reported by the media and/or health organization. The depletion of the aware state is inversely proportional to the number of cases. Unaware susceptible individuals become aware susceptible at the rate of α M , where α is the maximum rate at which an unaware susceptible individual becomes aware susceptible. On the other hand, aware susceptible individuals become unaware susceptible at a rate of β / ( 1 + M ) due to memory fading and/or carelessness. Level of awareness increases when an awareness programs are implemented proportionally with the change of unaware infective individuals at a rate of η and cut down at a rate of θ due to their ineffectiveness. Level of awareness also increase from global sources like radio, TV etc. [22] at a rate ω .
The above assumptions lead to the following model:
d S u d t = b − α M S u − λ S u I + β S a 1 + M − d S u + p γ R , d S a d t = α M S u − β S a 1 + M − d S a + q γ R , d I d t = λ S u I − ( d + δ ) I − r M I , d R d t = r M I − d R − γ R , d M d t = ω + η I − θ M ,
with the initial conditions:
S u ( 0 ) > 0 , S a ( 0 ) > 0 , I ( 0 ) ≥ 0 , R ( 0 ) ≥ 0 , M ( 0 ) > 0 .
For the analysis of model (1), the region of attraction is given by the set:
B = ( S u , S a , I , R , M ) ∈ R + 5 : 0 ≤ S u + S a + I + R ≤ b d , 0 ≤ M ≤ ω d + η b d θ .
Thus, all solutions of the model (1) are bounded in B for all t > 0 .
Table 1. List of parameters used for numerical simulations.
Table 1. List of parameters used for numerical simulations.
Parameter Definition Reference Value
( d a y − 1 )
b Constant recruitment rate [21] 12
λ Disease transmission rate [16,19] 0.0005
α Contact rate between unaware [21] 0.0002
susceptible with media
λ Transfer rate of people from [19,21] 0.0052
aware individuals to unaware
d susceptible class Natural death rate [17,21] 0.005
e Additional death rate due to infection [17] 0.007
β Contact rate between - 0.1
unaware infected with media
η Rate of implementation of awareness programs [21] 0.005
θ Depletion rate of awareness program [19,21] 0.06
due to ineffectiveness

3. Dynamics of the system

The system (1) is a set of nonlinear ordinary differential equations. In order to understand the dynamics of the system, we can analyze its steady states, which are the values of the variables at which they do not change with time.

3.1. Existence of Equilibria

The system has two equilibria namely the disease-free steady state E 0 is always existing and is given by E 0 ( S u ¯ , S a ¯ , 0 , 0 , M ¯ ) , where,
M ¯ = ω θ , S u ¯ = b θ ( d ω + β θ + d θ ) d ( α ω 2 + α ω θ + d ω θ + β θ 2 + d θ 2 ) , S a = α b ω ( ω + θ ) d ( α ω 2 + α ω θ + d ω θ + β θ 2 + d θ 2 ) ,
and the endemic equilibrium point E * ( S u * , S a * , I * , R * , M * ) where
I * = ( θ M − ω ) / η , R * = r M * I * μ + γ , S u * = r M * + ( d + δ ) λ , S a * = ( α S u * M * + q γ R * ) ( 1 + M * ) β + d ( 1 + M * ) ,
and M * satisfies the following equation:
c 0 M 3 + c 1 M 2 + c 2 M + c 3 = 0 ,
where,
c 0 = − α d 2 η r − d 2 λ r θ − α d η γ r − d γ λ q r θ , c 1 = − α d 3 η − d 3 η r − d 3 λ θ − α d 2 δ η − α d 2 η γ − α d 2 η r − d 2 η γ r − d 2 δ λ θ − d 2 γ λ θ + d 2 λ ω r − d 2 λ r θ − α d δ η γ − α d η γ r − d δ γ λ θ − b η d λ r θ + d γ λ ω q r − d γ λ q r θ , c 2 = − d 4 η − α d 3 η + d 2 γ λ ω − d 3 δ η − d 3 η γ − d 3 η r + d 3 λ ω − d 3 λ θ − α d 2 δ η − α d 2 η γ − d 2 δ η γ + b d 2 η λ − b η d 2 η r − d 2 η γ r + d 2 δ λ ω − b η d 2 λ θ + d 2 γ λ ω − d 2 δ λ θ − d 2 γ λ θ + d 2 λ ω r − α d δ η γ + b d η γ λ − b η d η γ r − b η d δ λ θ + d δ γ λ ω − b η d γ λ θ − b η δ γ λ θ − d δ γ λ θ + b η d λ ω r + d γ λ ω q r , c 3 = − d 4 η − b η d 3 η − d 3 δ η − d 3 η γ + d 3 λ ω − b η d 2 δ η − b η d 2 η γ − d 2 δ η γ + b d 2 η λ + b η d 2 λ ω + d 2 δ λ ω − b η d δ η γ + b b η d η λ + b b η η γ λ + b d η γ λ + b η d δ λ ω + b η d γ λ ω + b η δ γ λ ω + d δ γ λ ω .
It should be noted that since c 0 < 0 , the following cases can be distinguished: (i) if c 2 > 0 and c 3 > 0 , there exists a unique endemic equilibrium; (ii) if c 1 < 0 , c 2 > 0 , and c 3 < 0 , then (4) has two positive roots, resulting in the possibility of two feasible endemic equilibria; and (iii) if c 1 > 0 , c 2 < 0 , and c 3 > 0 , then (4) has three roots, leading to the possibility of three feasible endemic equilibria.

3.2. Stability analysis of E 0

The Jacobian matrix at the disease-free equilibrium E 0 is
A ( E 0 ) = − α M ¯ − d β 1 + M ¯ − λ S u ¯ p γ − β 1 + M ¯ α M ¯ − β 1 + M ¯ − d 0 q γ β 1 + M ¯ 0 0 λ S u ¯ − r M ¯ − ( d + δ ) 0 0 0 0 r M ¯ − d 0 0 0 η 0 − θ ,
At the disease-free steady state E 0 , the eigenvalues are ρ 1 = − θ , ρ 2 = − d which are both negative. Additionally, ρ 3 = λ S u ¯ − r M ¯ − ( d + δ ) is also negative when the basic reproduction number R 0 < 1 . The remaining eigenvalues can be found by solving the given equation:
ρ 2 + α M ¯ + 2 d + β 1 + M ¯ ρ + ( M ¯ + d ) d + β 1 + M ¯ + d = 0 .
The expression for M ¯ is provided in (3). We can apply the Routh-Rurwitz criteria to determine that the roots of (5), represented by ρ 4 and ρ 5 , have negative values or negative real parts. Therefore, the stability of E 0 is guaranteed if ρ 3 < 0 .
Remark 1.
The detailed numerical calculations indicate that the interior equilibrium E * is feasible when R 0 > 1 , i.e., when the disease-free equilibrium E 0 is unstable. The system (1) has a parameter known as the basic reproduction number, denoted by R 0 , which is given by the following equation:
R 0 = λ S u ¯ r M ¯ + d + δ .
Therefore, based on the definition of R 0 and the stability analysis of E 0 , we can state the following theorem.
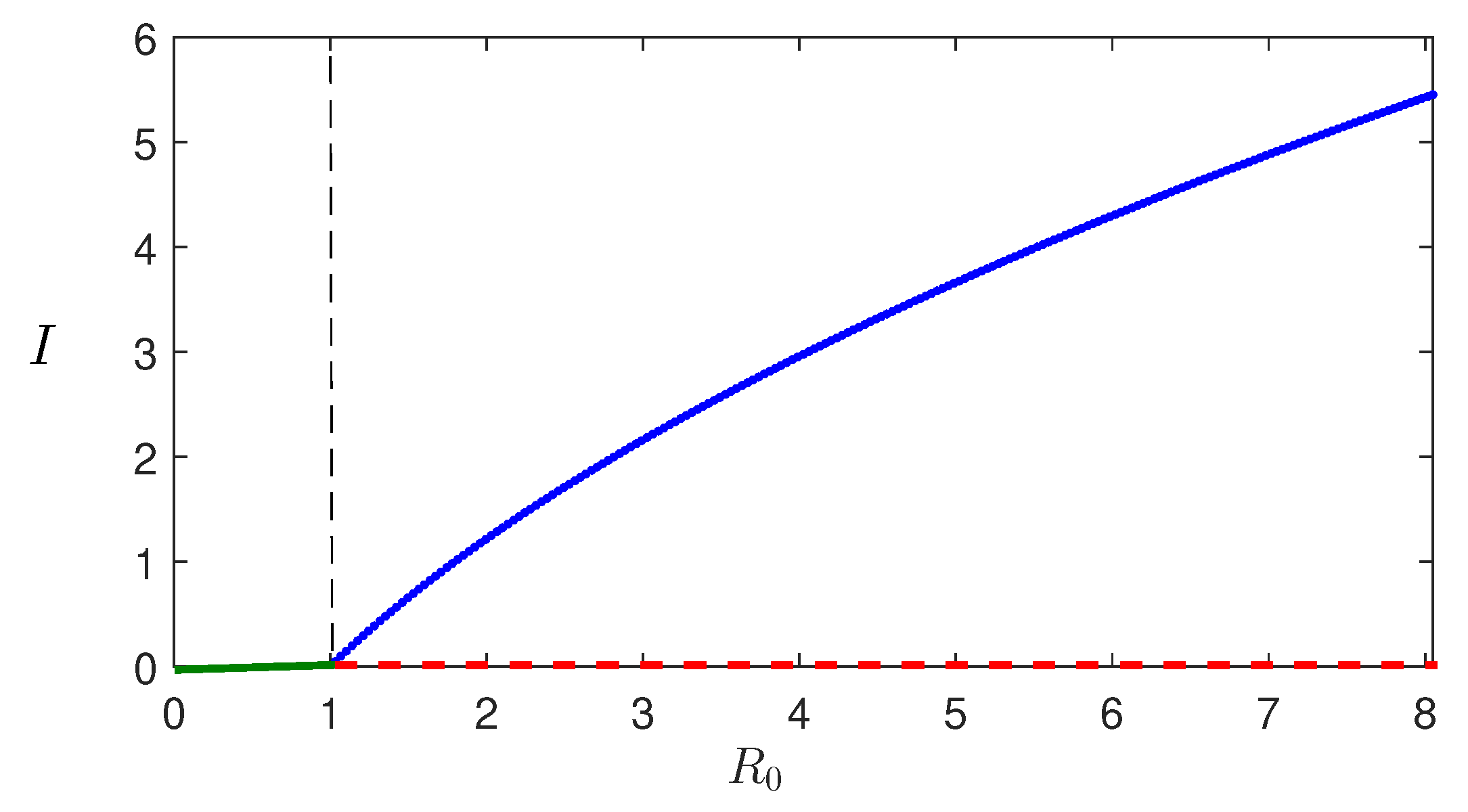
Theorem 1.
For the system (1), the disease-free steady state E 0 is stable if R 0 < 1 , and unstable if R 0 > 1 . At R 0 = 1 , the system undergoes a forward transcritical bifurcation.

3.3. Stability of E * and Hopf bifurcation

The Jacobian matrix J 5 × 5 at any equilibrium point E ( S u , S a , I , R , M ) is determined and its elements J i j are given below by,
J 11 = − α M − λ I − d , J 12 = β 1 + M , J 13 = − λ S u , J 14 = − p γ , J 15 = − β S a ( 1 + M ) 2 , J 21 = α M , J 22 = − β ( 1 + M ) − d , J 23 = 0 , J 24 = q γ , J 25 = β S a ( 1 + M ) 2 , J 31 = λ I , J 32 = 0 , J 33 = λ S u − r M − ( d + δ ) , J 34 = 0 , J 35 = − r I , J 41 = 0 , J 42 = 0 , J 43 = r M , J 44 = − d − γ , J 45 = r I , J 51 = 0 , J 52 = 0 , J 53 = η , J 54 = 0 , J 55 = − θ .
The characteristic equation is given by
x 5 + a 1 x 4 + a 2 x 3 + a 3 x 2 + a 4 x + a 5 = 0 ,
where
a 1 = − J 11 − J 22 − J 33 − J 44 − J 55 , a 2 = − J 12 J 21 + J 11 J 22 − J 13 J 31 + J 11 J 33 + J 22 J 33 + J 11 J 44 + J 22 J 44 + J 33 J 44 − J 35 J 53 + J 11 J 55 + J 22 J 55 + J 33 J 55 + J 44 J 55 , a 3 = J 13 J 22 J 31 − J 12 J 23 J 31 + J 12 J 21 J 33 − J 11 J 22 J 33 − J 14 J 31 J 43 + J 12 J 21 J 44 − J 11 J 22 J 44 + J 13 J 31 J 44 − J 11 J 33 J 44 − J 22 J 33 J 44 − J 15 J 31 J 53 + J 11 J 35 J 53 + J 22 J 35 J 53 + J 35 J 44 J 53 + J 12 J 21 J 55 − J 11 J 22 J 55 + J 13 J 31 J 55 − J 11 J 33 J 55 − J 22 J 33 J 55 − J 11 J 44 J 55 − J 22 J 44 J 55 − J 33 J 44 J 55 , a 4 = J 14 J 22 J 31 J 43 − J 12 J 24 J 31 J 43 − J 13 J 22 J 31 J 44 + J 12 J 23 J 31 J 44 − J 12 J 21 J 33 J 44 + J 11 J 22 J 33 J 44 + J 15 J 22 J 31 J 53 − J 12 J 25 J 31 J 53 + J 12 J 21 J 35 J 53 − J 11 J 22 J 35 J 53 + J 15 J 31 J 44 J 53 − J 11 J 35 J 44 J 53 − J 22 J 35 J 44 J 53 − J 14 J 31 J 45 J 53 − J 13 J 22 J 31 J 55 + J 12 J 23 J 31 J 55 − J 12 J 21 J 33 J 55 + J 11 J 22 J 33 J 55 + J 14 J 31 J 43 J 55 − J 12 J 21 J 44 J 55 + J 11 J 22 J 44 J 55 − J 13 J 31 J 44 J 55 + J 11 J 33 J 44 J 55 + J 22 J 33 J 44 J 55 , a 5 = J 15 J 22 J 31 J 44 J 53 + J 12 J 25 J 31 J 44 J 53 − J 12 J 21 J 35 J 44 J 53 + J 11 J 22 J 35 J 44 J 53 + J 14 J 22 J 31 J 45 J 53 − J 12 J 24 J 31 J 45 J 53 − J 14 J 22 J 31 J 43 J 55 + J 12 J 24 J 31 J 43 J 55 + J 13 J 22 J 31 J 44 J 55 − J 12 J 23 J 31 J 44 J 55 + J 12 J 21 J 33 J 44 J 55 − J 11 J 22 J 33 J 44 J 55 .
If the following conditions hold, all roots of the characteristic equation have a negative real part according to the Routh-Hurwitz criterion:
a 5 > 0 , a 1 a 2 − a 3 > 0 , a 3 ( a 1 a 2 − a 3 ) − a 1 ( a 1 a 4 − a 5 ) > 0 a n d ( a 1 a 2 − a 3 ) ( a 3 a 4 − a 2 a 5 ) + ( a 1 a 4 − a 5 ) ( a 5 − a 1 a 4 ) > 0 .
Thus endemic equilibrium E * is stable if the conditions in (8) hold. The following theorem ensures the occurrence of Hopf bifurcation at the endemic equilibrium.
Theorem 2.
The stability of the interior equilibrium E * depends on whether the conditions in (8) are satisfied. If the conditions are met, then E * is stable, otherwise, it becomes unstable. Moreover, E * undergoes a Hopf-bifurcation at the critical value θ * of the generic parameter θ if either of the following conditions is satisfied
i. 
ϕ ( θ * ) = 0 and d ϕ d θ | θ = θ * ≠ 0 ,where
ϕ ( θ ) = ( a 3 − a 1 a 2 ) ( a 5 a 2 − a 3 a 4 ) − ( a 5 − a 1 a 4 ) 2 ,
with
φ = a 5 − a 1 a 4 a 3 − a 1 a 2 > 0 , a 3 − a 1 φ ≠ 0 ,
ii. 
a 5 = a 1 a 4 , a 3 = a 1 a 2 , a 4 < 0 , a 1 a 3 ≠ 0 ,
a 1 ′ φ 2 + ( a 1 a 2 ′ − a 3 ′ ) φ − ( a 1 a 4 ′ − a 5 ′ ) | θ = θ * ≠ 0 .
where a i ′ ( i = 1 , 2 , . . 5 ) represent the derivatives of a i ( i = 1 , 2 , . . 5 ) with respect to the the genic bifurcation parameter θ and
φ = 1 2 a 2 + a 2 2 − 4 a 4 > 0 .
A formal proof of the Theorem 2 can be found in [28].

4. The optimal control problem

In this section, the aim is to study the impact of optimal treatment and awareness campaign. For this two control parameters u 1 ( t ) (for treatment cost) and u 2 ( t ) (for the cost of awareness campaign). Based on the above assumptions, the above system (equation ) would be:
d S u d t = b − α M S u − λ S u I + β S a 1 + M − d S u + p γ R , d S a d t = α M S u − β S a 1 + M − d S a + q γ R d I d t = λ S u I − ( d + δ ) I − u 1 ( t ) r M I d R d t = u 1 ( t ) r M I − d R − γ R , d M d t = ( 1 − u 2 ( t ) ) ω + η I − θ M ,
For the later use, we rewritten the system (9) in the following form:
d x i d t = f i ( t , x ) ,
where f i (i=1,...,5) are the right sides of system (9) and x i (i=1,...,5) are the state variables corresponding to S u , S a , I , R , M respectively. Our objective is to minimize the cost of the media campaign, treatment, and the number of infected cases. Therefore, we formulate the cost function as follows:
J [ u ( t ) ] = ∫ 0 t f [ A u 1 2 ( t ) + B u 2 2 ( t ) − P M 2 + Q I 2 ( t ) ] d t .
t f is the final time. The parameter P > 0 ) , Q > 0 are the weight constants on the benefit of the cost production and A > 0 is the penalty multiplier. Now, the objective is to find the optimal control pair u * ( t ) = ( u 1 ( t ) , u 2 ( t ) ) such that
J ( u 1 * , u 2 * ) = m i n ( J ( u 1 , u 2 ) : ( u 1 , u 2 ) ∈ U ) where U = U 1 × U 2 , where , U 1 = ( u 1 ( t ) : u 1 is measurable and 0 ≤ u 1 ≤ 1 , t ∈ [ 0 , t f ] ) and U 2 = ( u 2 ( t ) : u 2 is s measurable and 0 ≤ u 2 ≤ 1 , t ∈ [ 0 , t f ] ) .
Here Pontryagin Minimum Principle [29] has been used to find the optimal control pair ( u 1 * ( t ) , u 1 * ( t ) ) .

4.1. Characterization of the Optimal system

The necessary conditions for the optimal control problem can be obtained using Pontryagin’s Minimum Principle, as presented in [29]. Applying this principle to the system, we get the following theorem.
Theorem 3.
Suppose the given optimal control u * ( t ) and the solution ( S u ( t ) , S a ( t ) , I ( t ) , R ( t ) , M ( t ) ) of the corresponding system ( ) minimize J ( u ) over U. Then, by applying Pontryagin’s minimum principle in state, the following theorem holds: there exist adjoint variables ξ 1 , ξ 2 , ξ 3 , ξ 4 , and ξ 5 that satisfy the following equations:
d ξ 1 d t = − ( ξ 1 J 11 + ξ 2 J 21 + ξ 3 J 31 ) , d ξ 2 d t = − ( ξ 1 J 12 + ξ 2 J 22 ) , d ξ 3 d t = − 2 P I − ( ξ 1 J 13 + ξ 2 J 23 + ξ 3 J 33 + ξ 4 J 43 + ξ 5 J 53 ) , d ξ 4 d t = − ( ξ 1 J 14 + ξ 2 J 24 + ξ 3 J 34 + ξ 4 J 44 + ξ 5 J 54 ) , d ξ 5 d t = 2 Q M − ( ξ 1 J 15 + ξ 2 J 25 + ξ 3 J 35 + ξ 4 J 45 + ξ 5 J 55 ) .
along with the boundary conditions, ξ i ( t f ) = 0 , i=1,..,5.
Proof. 
The Hamiltonian can be taken as:
H = A u 1 2 ( t ) + B ( 1 − u 2 ( t ) ) 2 − P M 2 ( t ) + Q I 2 + ∑ i = 1 6 ξ i f i , i = 1 , 2 , . . . , 6 .
According to the maximum principle [22], the unconstrained optimal control variables u * ( t ) satisfies
∂ H ∂ u * = 0 , u * = ( u 1 * , u 2 * ) .
Thus from (14), we have
u 1 * ( t ) = ( ξ i 3 − ξ 4 ) r M I 2 A ,
u 2 * ( t ) = 2 B + ξ 5 ω 2 B .
Due to the boundedness of the optimal control,
u 1 * ( t ) = m a x ( 0 , m i n ( 1 , ( ξ i 3 − ξ 4 ) r M I 2 A ) ) ,
u 2 * ( t ) = m a x ( 0 , m i n ( 1 , 2 B + ξ 5 ω 2 B ) ) .
According to minimum principle [29], we have
d ξ i d t = − ∂ H ∂ x i , i = 1 , 2 , 3 , 4 , 5 ,
where x i ≡ ( S u , S a , I , R , M ) and the necessary condition satisfying the optimal control pair u * ( t ) are
H ( x i ( t ) , u * ( t ) , ξ i ( t ) , t ) = min u ∈ U ( H ( x i ( t ) , u ( t ) , ξ i ( t ) , t ) ) , i = 1 , 2 , 3 , 4 , 5 , 6 .
So, the adjoint system (12) corresponding to the system (9) can be obtained by equation (19). Boundary conditions for adjoint system (12) are ξ i ( t f ) = 0 , ( i = 1 , . . . , 6 ) as the salvage function in objective functional (11) is assumed to be zero. □
Preprints 72709 g002
Figure 2. Forward.
Figure 2. Forward.
Preprints 72709 g002
Preprints 72709 g003
Figure 3. Stability of E 0 in: (a) α − ω , (b) λ − ω parameters planes.
Figure 3. Stability of E 0 in: (a) α − ω , (b) λ − ω parameters planes.
Preprints 72709 g003
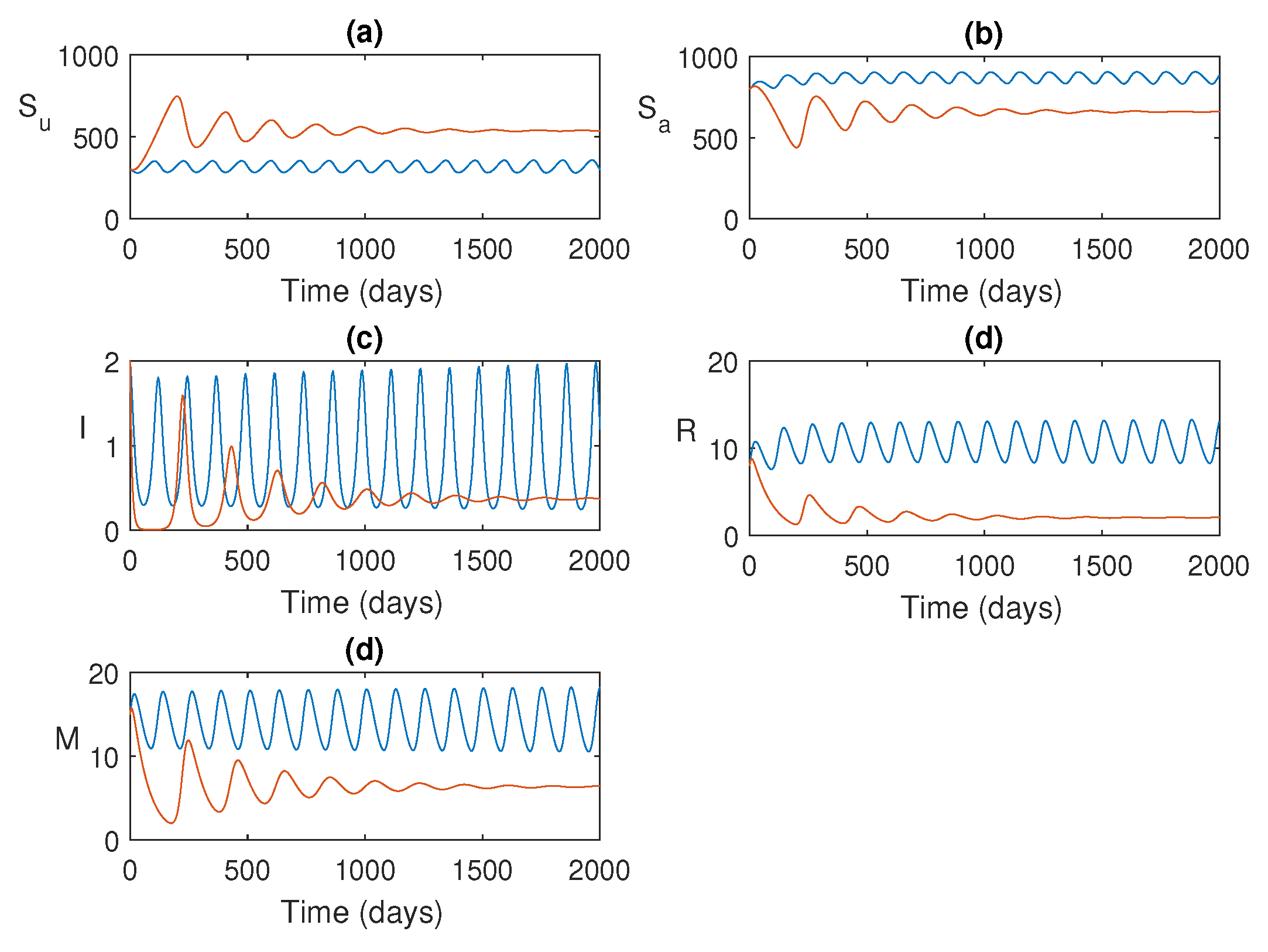
Preprints 72709 g004
Figure 4. Time series solution of the system 1 is plotted. Parameters values are as given in Table 1.
Figure 4. Time series solution of the system 1 is plotted. Parameters values are as given in Table 1.
Preprints 72709 g004
Preprints 72709 g005
Figure 5. Hopf bifurcation taking λ as main parameter. Values of the parameters are same as Figure 4.
Figure 5. Hopf bifurcation taking λ as main parameter. Values of the parameters are same as Figure 4.
Preprints 72709 g005
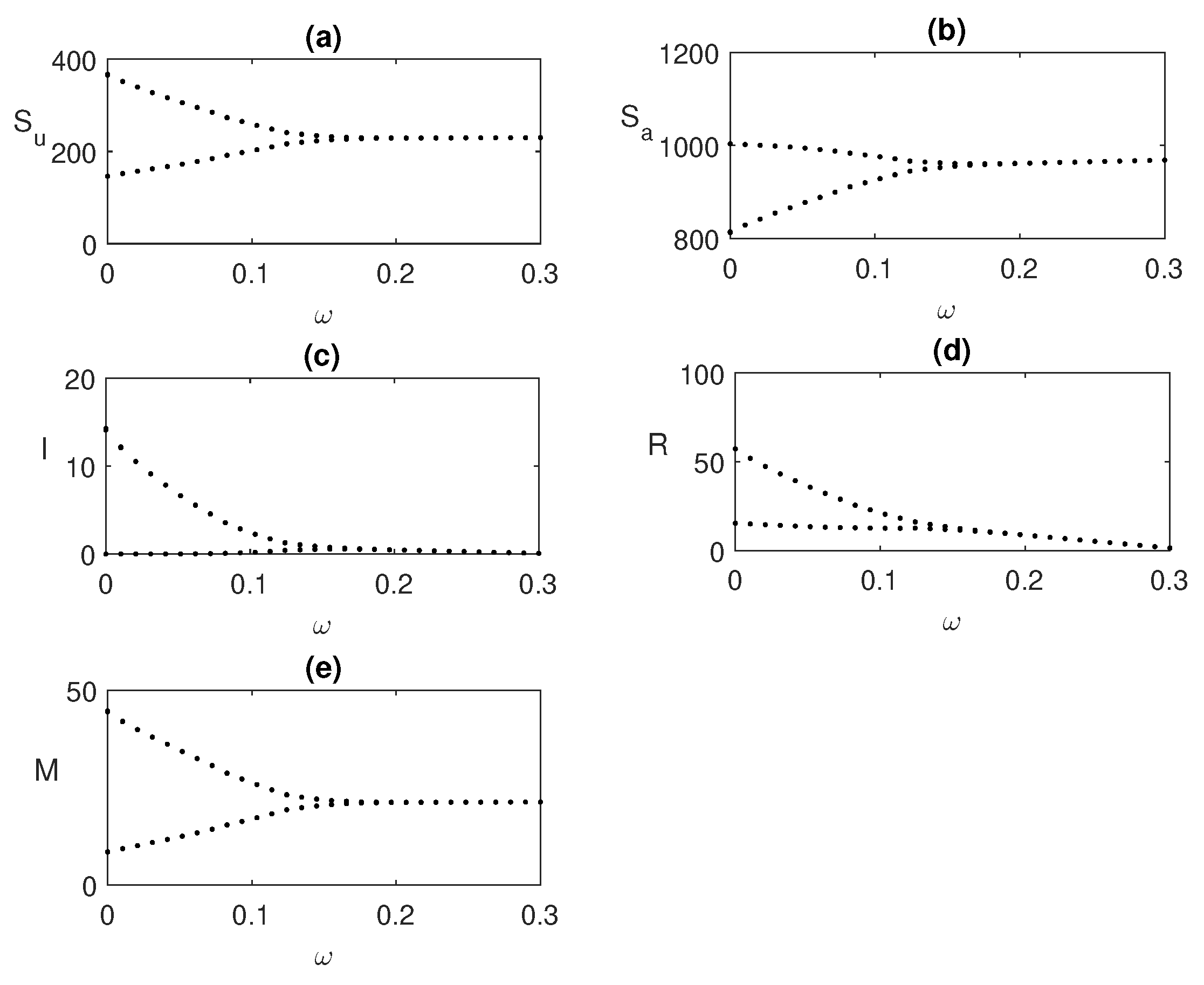
Preprints 72709 g006
Figure 6. Hopf bifurcation taking global awareness rate ω as the bifurcating parameter. Here, λ = 0.001 and rest of the parameters’ values are same as Figure 5.
Figure 6. Hopf bifurcation taking global awareness rate ω as the bifurcating parameter. Here, λ = 0.001 and rest of the parameters’ values are same as Figure 5.
Preprints 72709 g006
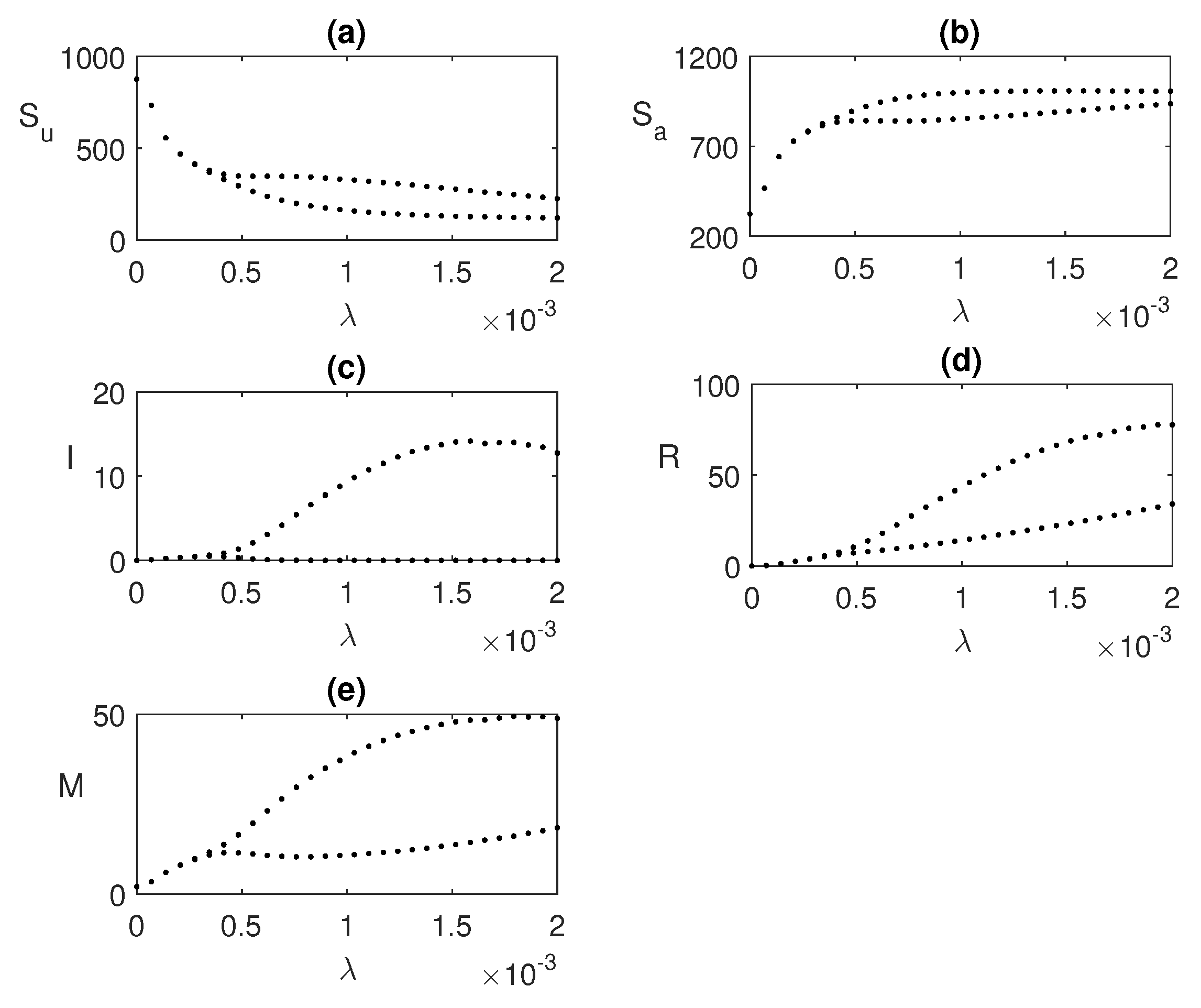
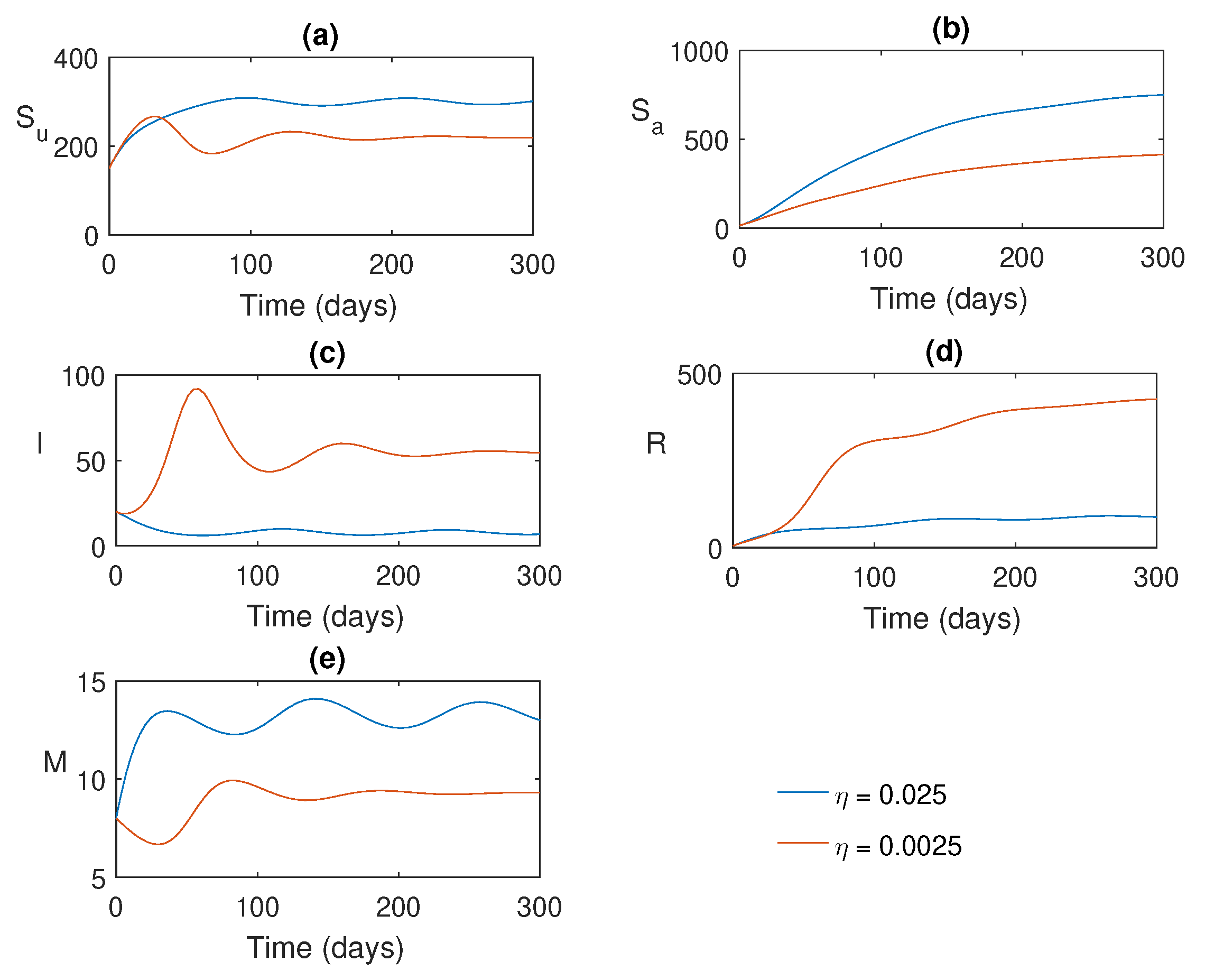
Preprints 72709 g007
Figure 7. Solution trajectories for two different values of the local awareness rate η .
Figure 7. Solution trajectories for two different values of the local awareness rate η .
Preprints 72709 g007

5. Numerical Simulation

This section presents the numerical simulations conducted to investigate the system dynamics. The goal is to examine the impact of increasing infection rate on the system’s behavior using simulations with and without control, in order to verify the theoretical findings.
Figure 4 shows the solution trajectories for two different values of λ . For lower values of λ , the model populations oscillate initially and then converge to the endemic equilibrium (since R 0 > 1 ). However, when λ exceeds a certain threshold value λ * , all populations exhibit periodic oscillations, indicating that they bifurcate into periodic solutions. The bifurcation diagram for the maximum and minimum values of the periodic solutions is shown in Figure 5, where we observe that the stability switch occurs at λ = λ * .
We also explore the bifurcation of ω in Figure 6 for a fixed value of λ = 0.001 , where periodic oscillations exist. As we increase the value of ω , the unstable endemic state becomes stable when ω exceeds a threshold value ω * .

5.1. Numerical solution of the Optimal control problem

We used MATLAB to perform numerical simulations of the optimality system (9).
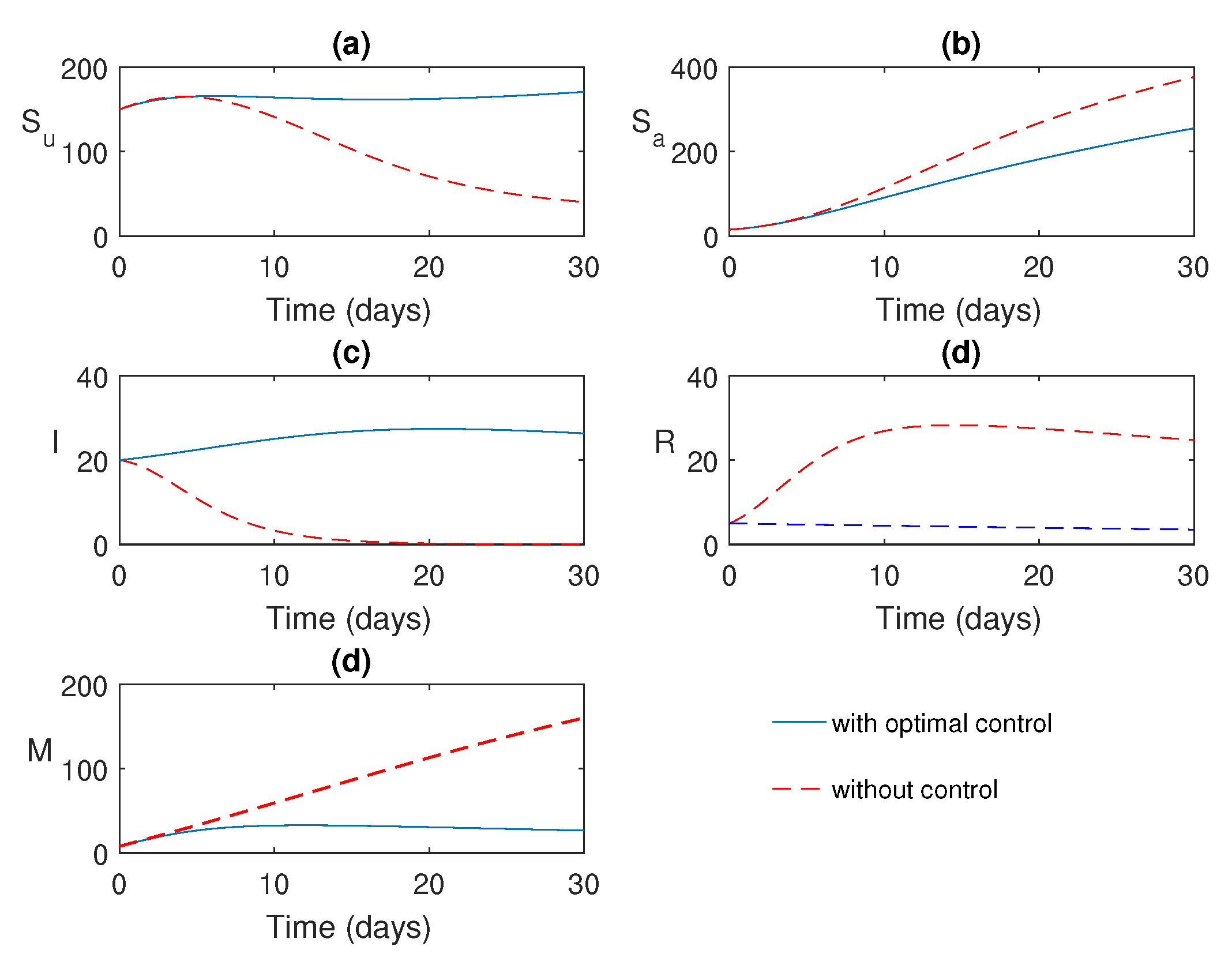
Preprints 72709 g008
Figure 8. Numerical solution of the system (9) with and without control.
Figure 8. Numerical solution of the system (9) with and without control.
Preprints 72709 g008
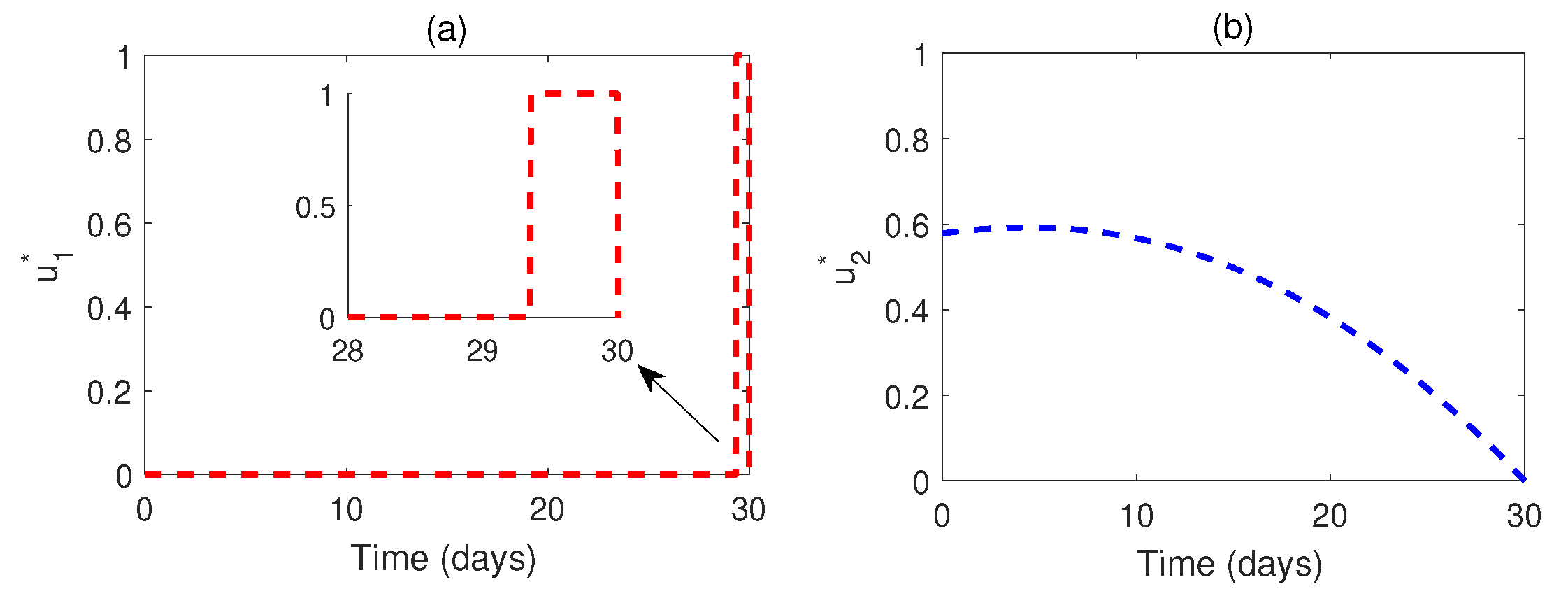
Preprints 72709 g009
Figure 9. Optimal profiles of the optimal control u 1 * and u 2 * .
Figure 9. Optimal profiles of the optimal control u 1 * and u 2 * .
Preprints 72709 g009
The state equations are solved iteratively using an initial guess for the control functions over a desired time interval, employing the fourth-order Runge-Kutta scheme. The adjoint equations are then solved backward in time using the current iteration solutions of the state equations. The control functions are updated using a convex combination of the preceding control functions and the values from the characterization until the change between the values of unknowns at the earlier iteration and the current iteration is negligible [31].
The numerical simulations of the optimal control problem are shown in Figure 8 and Figure 9. Figure 8 illustrates a comparison between the system with and without optimal control. It is evident that optimal control plays a vital role in monitoring the system. The corresponding optimal profiles of the control variables are plotted in Figure 9. The optimal profiles indicate that a high density of awareness campaign is required initially, and treatment is necessary from a later time (after three weeks of disease outbreak).

6. Discussion and Conclusion

The global outbreak of infectious diseases has brought about the urgent need for effective control strategies that can reduce their spread while minimizing the economic and social costs associated with control measures. In this study, a mathematical model has been proposed for the prevalence of infectious disease, taking into account the influence of awareness programs, treatments, and optimal control. This model can help policymakers and public health officials develop effective and cost-efficient control strategies for infectious diseases by incorporating public awareness into the model and using optimization techniques to produce cost-effective control strategies.
Specifically, the proposed awareness-based model is functional and can capture the dynamics of Malaria with awareness-based interventions, while the control-induced model can minimize the cost of malaria management. The dynamics of disease propagation have been studied using the proposed mathematical model both analytically and numerically. The next-generation matrix has been used to derive the basic reproduction number R 0 . Equilibria assessment shows two equilibria of the proposed model: the disease-free and endemic. The disease-free equilibrium is stable for R 0 < 1 , and the endemic equilibrium exists for R 0 > 1 when the disease-free equilibrium becomes unstable. The endemic equilibrium, when it exists, is globally asymptotically stable.
To further improve the effectiveness and efficiency of control strategies, optimal control theory has been applied to awareness-induced interventions for the cost-effective administration of Malaria. The proposed optimal system has been analytically solved using the Pontryagin minimum principle and numerically solved using a specific scheme, which is explained in detail in the study. Optimal profiles of the control variables have been plotted, providing insight into the effect of controls on malaria disease development and the cost sustained in their implementation numerically.
The optimality system consists of six Ordinary Differential Equations (ODEs) from the state and adjoint equations. The optimal solution has been established to be essential and effective in infectious disease control, indicating the potential of this approach for reducing the spread of contagious diseases and minimizing the economic and social costs associated with control measures. Overall, the proposed mathematical model and optimal control strategy can be valuable tools for policymakers and public health officials to develop effective and cost-efficient control strategies for infectious diseases.
To conclude, this article emphasizes the importance of awareness campaigns in controlling the spread of infectious diseases. By educating the public, promoting healthy behaviors, and dispelling misinformation, an effective awareness campaign can help reduce the transmission rate of infectious diseases. Furthermore, the article highlights the role of the World Health Organization in providing resources, guidelines, and tools for the prevention, diagnosis, and treatment of infectious diseases.
The optimal control approach to infectious diseases with awareness-based controls is a promising strategy that can help reduce the spread of contagious diseases while minimizing the economic and social costs associated with implementing control measures. By incorporating public awareness into the model and using optimization techniques to develop cost-effective control strategies, policymakers and public health officials can develop effective and cost-efficient control strategies for infectious diseases. The obtained results from the control-induced model using the maximum principle can be helpful for policymakers in proposing suitable control strategies against infectious diseases.
In summary, this study suggests that awareness campaigns are crucial in controlling infectious diseases, and optimal control theory, combined with media consciousness, is a necessary strategy for infectious disease control. By using this approach, policymakers can develop effective and cost-efficient control strategies that can minimize the economic and social costs associated with controlling infectious diseases.

Conflicts of Interest

Authors declare that there is no conflict of interest.

References

  1. World Health Organization (WHO). Global Tuberculosis Report 2021; WHO: Geneva, Switzerland, 2021; [Available online], https://www.who.int/publications/i/item/9789240037021. [Google Scholar]
  2. Dzinamarira, T.; Imran, M.; Muvunyi, C.M. The Management of Infectious Diseases in Comorbidity with Tuberculosis. Medicina 2022, 58, 1406. [Google Scholar] [CrossRef] [PubMed]
  3. Liu, H., Li, M., Jin, M., Jing, F., Wang, H., & Chen, K. (2013). Public awareness of three major infectious diseases in rural Zhejiang province, China: a cross-sectional study. BMC infectious diseases, 13(1), 1-9. [CrossRef]
  4. Ahorsu, D.K.; Lin, C.Y. The Effect of COVID-19 Vaccine Acceptance, Intention, and/or Hesitancy and Its Association with Our Health and/or Important Areas of Functioning. Vaccines 2023, 11, 368. [Google Scholar] [CrossRef] [PubMed]
  5. Wakefield, M.A.; Loken, B.; Hornik, R.C. Use of mass media campaigns to change health behaviour. The lancet 2010, 376(9748), 1261–1271. [Google Scholar] [CrossRef] [PubMed]
  6. World Health Organisation. WHO Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 11 January 2023).
  7. DCPP, Infectious Diseases, Changes in individual behavior could limit the spread of infectious diseases, Disease Control Priorities Project, 2006. http://www.dcp2.org/file/6/.
  8. WHO, World Health Organisation, Media Centre, Pneumonia – Fact Sheet No 331, 2012. http://www.who.int/mediacentre/factsheets/fs331/en/index.html.
  9. WHO, World Health Organisation, Media Centre, Diarrhoeal Disease – Fact Sheet No 330, 2009. http://www.who.int/mediacentre/factsheets/fs330/en/index.html.
  10. Jones, J.H.; Salathe, M. Early assessment of anxiety and behavioral response to novel swine origin influenza A (H1N1). PLoS ONE 2009, 4, e8032. [Google Scholar] [CrossRef] [PubMed]
  11. Cui, J.; Sun, Y.; Zhu, H. The impact of media on the control of infectious diseases. Journal of Dynamics and Differential Equations 2007, 20, 31–53. [Google Scholar] [CrossRef] [PubMed]
  12. Frolich, M.; Vazquez Alvarez, R. HIV/AIDS knowledge and behaviour: Have information campaigns reduced HIV infection? The case of Kenya. African Development Review 2009, 21, 86–146. [Google Scholar] [CrossRef]
  13. Misra, A.K.; Sharma, A.; Singh, V. Effect of awareness programs in controlling the prevalence of an epidemic with time delay. Journal of Biological Systems 2011, 19, 389–402. [Google Scholar] [CrossRef]
  14. Sharma, A.; Misra, A. Modeling the impact of awareness created by media campaigns on vaccination coverage in a variable population. Journal of Biological Systems 2014, 22, 249–270. [Google Scholar] [CrossRef]
  15. Kiss, I.Z.; Cassell, J.; Recker, M.; Simon, P.L. The impact of information transmission on epidemic outbreaks. Mathematical Biosciences 2010, 225, 1–10. [Google Scholar] [CrossRef]
  16. Greenhalgh, D.; Rana, S.; Samanta, S.; Sardar, T.; Bhattacharya, S.; Chattopadhyay, J. Awareness programs control infectious disease-Multiple delay induced mathematical model. Applied Mathematics and Computation 2015, 251, 539–563. [Google Scholar] [CrossRef]
  17. Hove-Musekwaa, S.D.; Nyabadza, F. The dynamics of an HIV/AIDS model with screened disease carriers. Computational and Mathematical Methods in Medicine 2009, 10, 287–305. [Google Scholar] [CrossRef]
  18. Misra, A.K.; Sharma, A.; Singh, V. Effect of awareness programs in controlling the prevalence of an epidemic with time delay. J. Biol. Sys. 2011, 19, 389–402. [Google Scholar] [CrossRef]
  19. Basir, F.A.; Ray, S.; Venturino, E. Role of media coverage and delay in controlling infectious diseases: A mathematical model. Applied Mathematics and Computation 2018, 337, 372–385. [Google Scholar] [CrossRef]
  20. H. Zhao, Y. Lin, Y. Dai, An SIRS Epidemic Model Incorporating Media Coverage with Time Delay, Comput, Math. Methods Med., 2014, Article ID 680743.
  21. Samanta, S.; Rana, S.; Sharma, A.; Misra, A.K.; Chaattopadhyay, J. Effect of awareness programs by media on the epidemic outbreaks: A mathematical model. Appliesd Matyhematics and Computation 2013, 219, 6965–6977. [Google Scholar] [CrossRef]
  22. Agaba, G.O.; Kyrychko, Y.N.; Blyuss, K.B. Dynamics of vaccination in a time-delayed epidemic model with awareness. Math. Biosci. 2017, 294, 92–99. [Google Scholar] [CrossRef]
  23. Maji, C.; Al Basir, F.; Mukherjee, D.; Nisar, K.S.; Ravichandran, C. COVID-19 propagation and the usefulness of awareness-based control measures: A mathematical model with delay. AIMS Mathematics 2022, 7, 12091–12105. [Google Scholar] [CrossRef]
  24. Misra, A.K.; Sharma, A.; Shukla, J.B. Stability analysis and optimal control of an epidemic model with awareness programs by media. Biosystems 2015, 138, 53–62. [Google Scholar] [CrossRef] [PubMed]
  25. Sharma, N.; Singh, R.; Pathak, R. Modeling of media impact with stability analysis and optimal solution of SEIRS epidemic model. Journal of Interdisciplinary Mathematics 2019, 22(7), 1123–1156. [Google Scholar] [CrossRef]
  26. Yuan, Y.; Li, N. Optimal control and cost-effectiveness analysis for a COVID-19 model with individual protection awareness. Physica A: Statistical Mechanics and its Applications 2022, 603, 127804. [Google Scholar] [CrossRef]
  27. Roy, P.K.; Saha, S.; Basir, F.A. Effect of awareness programs in controlling the disease HIV/AIDS: an optimal control theoretic approach. Advances in Difference Equations 2015, 2015, 1–18. [Google Scholar] [CrossRef]
  28. Al Basir, F.; Blyuss, K.B.; Ray, S. Modelling the effects of awareness-based interventions to control the mosaic disease of Jatropha curcas. Ecological Complexity 2018, 36, 92–100. [Google Scholar] [CrossRef]
  29. Fleming, W.H.; Rishel, R.W. Deterministic and stochastic optimal control, Springer-Verlag, Berlin, 1975.
  30. Abraha, T.; Basir, F.A.; Obsu, L.L.; Torres, D.F. Farming awareness based optimum interventions for crop pest control. Mathematical Bioscience and Engineering 2021, 18(5), 5364–5391. [Google Scholar] [CrossRef] [PubMed]
  31. Lenhart, S.; Workman, J.T. Optimal control applied to biological models, Chapman & Hall/CRC, Boca Raton, FL. 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated