Neural Networks and Adapted Optimal Transport

Preprint

Article

Neural Networks and Adapted Optimal Transport

Altmetrics

Downloads

387

Views

165

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 May 2023

Posted:

09 May 2023

Read the latest preprint version here

Alerts

Abstract

Within Data Science scenario both Machine Learning (ML) and Neural Networks (NNs) are widely used for a plethora of applications, spanning from engineering to biology, from finance to medicine. Meanwhile, the pure analytical analysis of related models used often lacks of detailed description. Trying to close this gap, during recent years the theory of Optimal Transport start becoming more a more popular within the Data Science arena, since it allows for efficient and scalable solutions about what can be broadly referred as Artificial Intelligence tasks, particularly by using approximate solvers through linear programming. More precisely, let us recall that both in ML and statistics, minimizing an objective function over the space of probability measures is fundamental problem. Along this line, the training of a Neural Network through Stochastic Gradient Descent has been shown to be equivalent to a gradient flow in Wasserstein space. Moreover, in many applications, it is crucial to consider the causal structure of the data generating process. In view of providing a possibly unifying as well as efficient approach to latter questions, we consider the Adapted Optimal Transport (AOT) method which allows to incorporate causality constraints into the optimization of the Wasserstein distance. AOT is particularly useful when dealing with laws of stochastic processes, being exploitable to encode an adapted (non-anticipative) constraint into the allocation of mass of the classical OT problem. Accordingly, we provide an in depth exploration of the connections between supervised learning and AOT, providing theoretical insights into the benefits of including causality constraints for developing more robust, scalable and accurate algorithms, while maintainig their computational efforts at minimum possible levels.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The present paper aims at presenting a baseline for the problem of including causality constraint into Machine Learning (ML) tasks as to increase algorithms robustness, scalability and accuracy, particularly when dealing with structured time series-based applications. The analysis starts from a preliminary study of a Supervised Learning problem in terms of a Mean Field Optimal Control Problem (MFOCP), hence providing an overview about the most relevant theoretical aspects that can be useful for a generalization of MFOCP to include the temporal structure of the training data. Accordingly, we provide a complete review about Adapted Optimal Transport (AOT), that is a version of Optimal Transport (OT) enforcing an adapted (with respect to a filtration) constraint. Furthermore, we summarizes state-of-the-art works at the crossroad of probability theory, ML and OT methods. We deepen the introduction of probability measures into ML tasks specifically for Neural Networks (NNs) applications in the context for explainable AI. On the other hand, the use of probability measures can also help to analyze the behavior of specific algorithm, while NNs can be used to approximate functions depending on unknown distributions. Trying to clarify the interplay between probability measures and Neural Networks, we recall possible cross-related cases:

Measure approach for NN training: Probability measures can be used to analyze the behavior of neural networks, both during training and inference. For example, the loss function used to train a neural network can be seen as a divergence between the model distribution and the target distribution, which can be expressed in terms of probability measures, [17]. Similarly, the output of a neural network can be interpreted as a probability distribution over the output space, which can be analyzed using probability theory. This can be useful for understanding the uncertainty of the predictions made by the neural network, such as the Stochastic Deep Networks (SDN) introduced in [25]. The design of a SDN involves a deep architecture that can handle probability distribution inputs and outputs and uses the classical Wasserstein distance as the loss function. Moreover, layers correspond to a sequence of elementary blocks that maps random vectors to random vectors to capture multiple interactions between samples from the distributions.
Probability measures as a tool to regularize neural networks: Probability measures can be used as a tool to regularize neural networks, by adding a regularization term to the loss function that encourages the output of the neural network to match a prior distribution by the so called entropic measure, such as in Eq. (26). Within this case, we mention the entropic version of Sinkhorn algorithm where an entropic regularization is added, developed, e.g., in [40]. This algorithm can be useful for scaling OT problem in high dimensional setting or for generative modeling tasks, where the goal is to learn a distribution that can generate new data samples.
Neural networks to approximate empirical measures: Neural networks can be used to approximate probability measures, such as empirical distributions over a state space for mean field function. We specifically consider this feature in Section 3. Analogously, one can consider NN architecture for learning population dynamics. For example, in [33], the authors focus on a recurrent architecture to model the diffusion of a population by means of a NN by injecting random noise.
Neural Network to learn unknown probability measure for unsupervised learning tasks such as density estimation, where the goal is to learn the underlying distribution of the data. For example, in [21], the authors try to build an algorithm to directly learn a probability measure via an optimal transport metric, also providing some convergence results for the learning algorithm.

The paper is organized in the following paragraphs. In Section 2, we review some basic works dealing with the mathematical formalism and definitions needed to precisely address supervised learning problems within the context of NNs. In Section 3, we review some developed methods to learn, i.e. approximate, mean field functions that depend on probability distribution obtained as limit object of empirical measures. In Section 4, we deal with the problem of optimizing over the set of probability measures with finite 2-moment focusing on JKO-net, an efficient and scalable method to optimize gradient flow in Wasserstein space. In Section 5, we conclude studying variants of the classical Optimal Transport problem, specifically focusing on AOT by also considering the class of equivalence of filtered processes and associated adapted empirical measures.

2. A continuous idealization of NN for a Mean Field Optimal Control Problem

In this section, we present the basic workflow to treat a feed-forward NN as a dynamical system in order to derive the associated population risk minimization problem.

Indeed, in [35], a continuous idealization of Deep Learning (DL) is introduced, to study the Supervised Learning (SL) problem as am Optimal Control Problem, see, e.g. [27] and [36] for more details.

Following [26], SL aims at estimating the function

F : X \to Y

, commonly known as the Oracle, where

X

is a subset of

R^{d}

that contains input arrays such as images, texts, and time series, and

Y

is the corresponding target set. To achieve this, training begins with a set of K input-target pairs

{x_{0}^{i}, y_{T}^{i} = F (x_{T}^{i})}_{i = 1}^{K}

where

$x_{0} \in R^{d}$ denotes the input of the NN;
$x_{T} \in R^{d}$ denotes the output of the NN:
$y_{T} \in R^{l}$ the corresponding target.

For a T-layers network, the Feed-Forward propagation is given by

x_{t + 1} = x_{t} + f (x_{t}, θ_{t}) t = 0, . . ., T - 1

(1)

θ_{t}

being the trainable parameters (e.g. bias, weights) in layer t that belong in to a measurable set

U

with values in subset of the euclidean space

R^{m}

We aim at minimizing over the set of measurable parameters

U

a terminal loss function

Φ : X \times Y \to R

plus a regularization term L over a set of measurable parameters

U

to control the size of parameters. In this way, we can state a Supervised Learning problem as an Empirical Risk Minimization problem, namely

min_{θ \in U} [\frac{1}{K} \sum_{i = 1}^{K} Φ (x_{T}^{i}, y^{i}) + \sum_{t = 0}^{T - 1} L (θ_{t})]

(2)

2.1. Mean Field Optimal Control Problem

The next steps involve moving from the discrete setting to the corresponding continuous idealization by:

going from layer index T to continuous parameter t;
passing from discrete set of inputs/output to distribution $μ_{0}$ that represents the joint distribution in $P_{2} (R^{d} \times R^{l})$ modelling the input-label distribution;
identifying targets y as random variables sampled from the projection over $Y$ of the distribution $μ_{0}$ ;
passing from empirical risk minimization to population risk (i.e. minimization over expectation $E$ ).

Specifically, we pass to the limit both in the layer discretization to obtain a dynamic described by an Ordinary Differential Equation (ODE) instead of finite difference equation (1). Also we identify the input-target pairs as samples from a given distribution

μ_{0}

allowing to write a SL problem as a population risk minimization problem.

In summary, the problem aims approximating the Oracle function

F

using a provided set of training data sampled by a (known) distribution

μ_{0}

by optimizing weights

θ_{t}

to achieve maximal proximity between

x_{T}

(output) and

y_{T}

(target).

More specifically, we consider a probability space

(Ω, F, P)

and we assume inputs

x_{0}

R^{d}

being sampled from a distribution

P (R^{d})

and the corresponding target

y_{T}

R^{l}

belongs to

P (R^{l})

. These variables are considered to be random variables that are jointly distributed according to

μ_{0}

, which is a distribution in the Wasserstein space

W_{2} (R^{(d + l)})

. Given a metric space

(X, d)

, the p-Wasserstein space

W_{p} (X)

is defined as the set of all Borel probability measures on X with finite p-moments, i.e., measures

μ

such that

\int_{X} d {(x, y)}^{p} d μ (x) < \infty

(3)

for some

y \in X

. Here,

d (x, y)

is the metric between x and y, and p is a positive real number. The Wasserstein space can be endowed with the Wasserstein distance, also known as the p-th Wasserstein distance, which is a metric that measures the distance between two probability measures

μ

and

ν

W_{p} (X)

as the infimum of the expected cost of transporting the mass from

μ

ν

W_{p} (μ, ν) = {(inf_{γ \in Γ (μ, ν)} \int_{X \times X} d {(x, y)}^{p} d γ (x, y))}^{1 / p}

(4)

where

Γ (μ, ν)

is the set of all probability measures on

X \times X

with marginals

μ

and

ν

In our setting, the joint measure

μ_{0}

that models the distribution of the input-target pairs and is defined by

μ_{0} : = P (x_{0}, y_{T})

is studied as an element of

W_{2}

Moreover, we assume the controls

θ_{t}

depend on the whole distribution of input-target pairs capturing the mean-field aspect. We consider a measurable set of admissible controls (i.e. training weights)

Θ \subseteq R^{m}

and we state the following Mean Field Optimal Control Problem (MFOCP):

inf_{θ \in L^{\infty} ([0, T], Θ)} J (θ) : = E_{μ_{0}} [Φ (x_{T}, y_{T}) + \int_{0}^{T} L (x_{t}, θ_{t}) d t]

(5)

{\dot{x}}_{t} = f (x_{t}, θ_{t}) 0 \leq t \leq T (x_{0}, y_{T}) \sim μ_{0}

We briefly report basic assumptions we need to have a solution for (5):

$f : R^{d} \times Θ \to R^{d}$ , $L : R^{d} \times Θ \to R$ , $Φ : R^{d} \times R^{l} \to R$ are bounded;
f, L, $Φ$ are Lipschitz continuous with respect to x with the Lipschitz constants of f and L being independent from parameters $θ$ ;
$μ_{0}$ has finite support in $W_{2} (R^{(d + l)})$

Problem (5) can be approached through two different methods: the first one is based on the Hamilton-Jacobi-Bellman (HJB) equation in the Wasserstein space, while the second one is based on a Mean Field Pontryagin Principle. We refer to [30] and [32] for a viscosity solutions to the HJB equation in the Wasserstein space of probability measures and to [19] for a Pontryagin Maximum Principle for constrained optimal control problems in the Wasserstein space of probability measures.

About some generalizations of the presented result, we cite the article [16] where the authors introduce a BSDE technique to solve the Stochastic Maximum Principle to examine the uncertainty associated with DL. The authors employ an Stochastic Differential Equation (SDE) in place of the ODE appearing in (5) to continuously approximate a Stochastic Neural Network (SNN).

2.2. Empirical measures over controls

For the sake of completeness, we mention also a completely different perspective to describe the learning process in a NN, that deals with the introduction of the empirical distribution of the parameters of neurons (instead of the input-target pairs). Indeed, as illustrated, e.g., by Sirignano and Spilipupouls in [43], it is possible to associate to each layer the corresponding empirical measure and build a measure to describe the whole network that takes values in the space of the called nested measure (also known as adapted Wasserstein distance), that we deepen in Section 5. Following this perspective, the method of Stochastic Gradient Descent (SGD) can be formalized as minimization over probability distribution. Moreover, the training of NN is based on the correspondence between empirical measure of neurons

μ_{N}

and the approximated function

f_{N}

. Specifically, the training via gradient descent of a limit of an over-parameterized 1-hidden layer Neural Network with infinite width is equivalent to gradient flow in Wasserstein space [23,26,27,29]. Similarly, the convergence to solutions to SDEs have been obtained as universal continuum objects in the small learning rate regime as proved in, e.g., [22].

3. Learning Mean Field Function

In this section, we study some tools in order to learn functions showing a dependency on a mean field term, such as an empirical distribution over a given state space. We start with a brief description of a dynamica of McKean-Vlasov type.

3.1. The McKean-Vlasov SDE

The McKean-Vlasov dynamic involves a SDE that models the behavior of a large population of interacting particles. In this context, the optimal control problem for this system involves finding a control strategy that minimizes a certain cost function while satisfying the dynamics of the system. In particular, the McKean-Vlasov dynamics can be written as:

d X_{t} = b (X_{t}) d t + \sqrt{ϵ} d W_{t} + \frac{1}{N} \sum_{i = 1}^{N} \int K (X_{t} - X_{i} (t)) d μ_{i} (t) d t,

(6)

where

X_{t}

is the state of the system at time t,

b (X_{t})

is the drift term,

ϵ

is the diffusion coefficient,

W_{t}

is a standard Brownian motion, N is the number of particles in the population,

μ_{i} (t)

is the empirical measure of the particles at time t, and K is a kernel function. Accordingly, the optimal control problem for the McKean-Vlasov dynamics can be written as:

J (u) = E [\int_{0}^{T} L (X_{t}, u_{t}) d t + ϕ (X_{T})],

(7)

subject to the dynamics of the system:

d X_{t} = b (X_{t}) d t + \sqrt{ϵ} d W_{t} + \frac{1}{N} \sum_{i = 1}^{N} \int K (X_{t} - X_{i} (t)) d μ_{i} (t) d t + u_{t} d t,

(8)

where

u_{t}

is the control input,

L (X_{t}, u_{t})

is the instantaneous cost, and

ϕ (X_{T})

is the terminal cost.

A possible approach to the optimal control problem consists in using the Pontryagin Maximum Principle, which gives necessary conditions for optimality. The Hamiltonian of the system is defined as:

H (X_{t}, u_{t}, p_{t}) = L (X_{t}, u_{t}) + p_{t} \cdot [b (X_{t}) + \frac{1}{N} \sum_{i = 1}^{N} K (X_{t} - X_{i} (t))] + \frac{ϵ}{2} {| p_{t} |}^{2},

(9)

where

p_{t}

is the adjoint variable. The optimal control is given by:

u_{t}^{*} = arg min_{u} H (X_{t}, u, p_{t}) .

(10)

The adjoint variable satisfies the following (backward) differential equation:

d p_{t} = - \frac{\partial H}{\partial X} (X_{t}, u_{t}^{*}, p_{t}) d t, p_{T} = \frac{\partial ϕ}{\partial X} (X_{T}) .

(11)

3.2. Mean Field Optimal Transport

In the recent work [12], the authors introduce the Mean Field Optimal Transport (MFOT) problem in the field of Mean Field Control, namely optimal control for McKean-Vlasov dynamics. Differently from classical Mean Field Game (MFG) theory, the final distribution is prescribed while all the agents cooperate in order to minimize a total cost without terminal cost. Indeed we follow the numerical scheme introduced in section 3.1 in [12] to approximate feedback controls.

Let

R^{d}

, describe the state space and denote by

P_{2} (R^{d})

the set of square-integrable probability measures on

R^{d}

. Let

f : R^{d} \times P_{2} (R^{d}) \times R^{k} \to R

be the running cost,

g : R^{d} \times P_{2} (R^{d}) \to R

be the terminal cost,

b : R^{d} \times P_{2} (R^{d}) \times R^{k} \to R^{d}

the drift function and

σ \in R

the non-negative diffusion. Given two distributions

ρ_{0}

and

ρ_{T} \in P_{2} (R^{d})

the aim of MFOT is to compute the optimal feedback control along all the trajectories

v^{*} : [0, T] \times R^{d}

minimizing

J^{M F O T} : v \mapsto E [\int_{0}^{T} f (X_{t}^{v}, μ^{v} (t), v (t, X_{t}^{v})) d t]

(12)

being

μ^{v} (t)

the distribution of

X_{t}^{v}

under the constraint

X^{v}

solves the SDE

\{\begin{matrix} X_{0}^{v} \sim ρ_{0} X_{T}^{t} \sim ρ_{T} d X_{t}^{v} = b (X_{t}^{v}, μ^{v} (t), v (t, X_{t}^{v})) d t + σ d W_{t}, t \in [0, T] \end{matrix}

(13)

Always in [12], the authors present different numerical methods to solve MFOT:

Optimal control via direct approximation of controls v;
Deep Galerkin Method for solving a forward-backward systems of PDEs;
Augmented Lagrangian Method with Deep Learning exploiting the variational formulation of MFOT and the primal/dual approach.

In this section, we focus on the direct method (1) to approximate controls of feedback type by an optimal control formulation. The controls are assumed of feedback form and they are approximated by

g (x, μ) = G (W_{2} (μ, ρ_{T})), μ \in P_{2} (R^{d})

(14)

being

G : R_{+} \to R_{+}

is an increasing function.

The idea is to use the function in Eq. (14) as a penalty for being far from the target distribution

ρ_{T}

instead of the classical terminal cost typical of the MFG/MFC literature. Moreover, discretizing the SDE (13) by an Euler-Maruyama scheme as well as restricting the set of controls v to ones approximated via NNS

v_{θ}

with parameters

θ

helps the development of numerical algorithms. See Section 3.1 in [12] for further details.

3.3. Alternative methods

Another proposed data-driven approach, presented in [8], has been considered to solve a stochastic optimal control problem, where the unknown model parameters were estimated in real-time using a direct filter method. This method involves transitioning from the stochastic maximum principle to approximate the conditional probability density functions of the parameters given an observation, which is a set of random samples.

In [37], the authors report a map that by operating over an appropriate classes of neural networks, specifically the Bin density-based approximation and Cylindrical approximation, is able to reconstruct a mapping between the Wasserstein space of probability measures and an infinite dimensional function space on a similar setting to MFG.

4. Learning Gradient Flow

Numerous problems in ML and statistics deal with minimizing some objective function over probability distributions. A powerful tool for optimizing functionals relies on gradient flow in the Wasserstein space.

4.1. Gradient Flow in Wasserstein space

Beyond OT problems, a popular use of Wasserstein distances is to study gradient flows, following the formalism of minimizing movements studied in [3]. This corresponds to discrete implicit stepping (i.e. proximal maps) for the Wasserstein distance (instead of more common Euclidean or Hilbertian metrics) functionals, for instance to model crowd motions.

In the discrete-time setting, gradient flow in Wasserstein space can be used to study the evolution of probability measures over a sequence of discrete time steps. Consider a probability measure

ρ^{t}

over a finite Euclidean space. The gradient flow of the Wasserstein distance can then be used to find a sequence of probability measures

ρ^{t}

, representing, e.g., the evolution of a distribution of a cloud of points over a finite set

X \in R^{n}

. The Wasserstein distance between two consecutive measure

ρ^{t}

and

ρ^{t + 1}

is minimized along this sequence of measures, which can be seen as a discrete-time analogue of the continuous-time gradient flow.

The dynamic formulation of OT can be solved by means of the so-called Jordan-Kinderlehrer-Otto (JKO) scheme, which consists in an implicit Euler discretization of a Wasserstein gradient flow

ρ^{k} = a r g m i n_{ρ \in P_{2} (R^{n})} [F (ρ) + \frac{1}{2 τ} W_{2}^{2} (ρ^{k - 1}, ρ)],

(15)

with

F

being an energy functional and

τ

the time-discretization update. The solution of this consecutive minimization problems result in a sequence of probability measures in

P_{2} (R^{n})

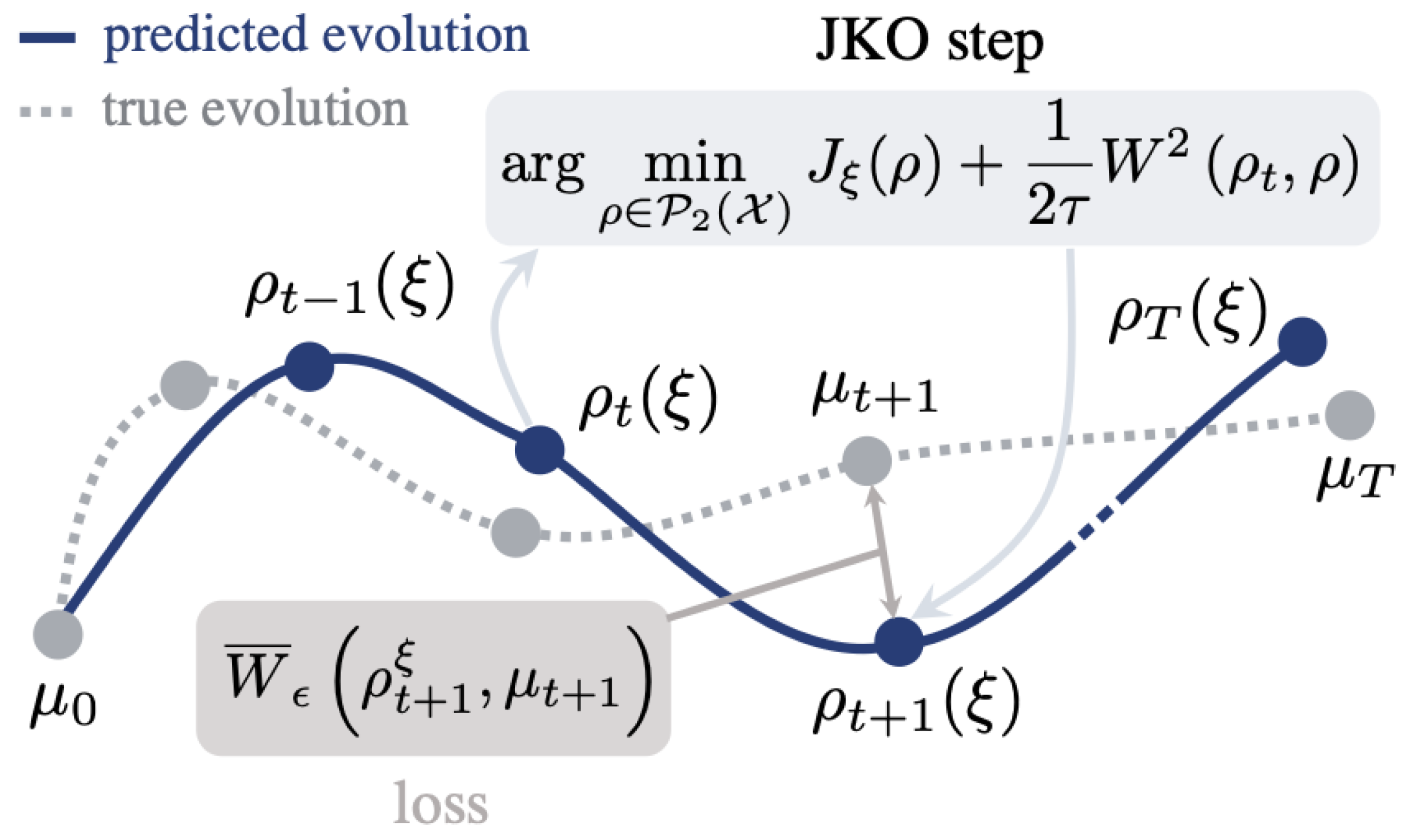
Figure 1. Proximal OT for a population dynamics (from [18]).

The idea is to move from optimization over probability measure of Eq. (15) to an optimization over convex function, which is still challenging, especially in high dimensions. From Brenier’s theorem, for any

ρ \in P_{2, a c}

, there exists a unique

ρ^{k - 1}

-measurable gradient

\nabla ψ : R^{D} \to R^{D}

of a convex function

ψ

s.t.

ρ = \nabla ψ # ρ^{(k - 1)}

4.2. Stochastic Optimization with ICNN and JKOnet

A large variety of dedicated numerical schemes has been proposed for spatial discretization and solving of these time-discrete flows, such as for instance finite differences and Lagrangian schemes. A bottleneck of these schemes is the high computational complexity due to the resolution of an OT-like problem at each time step.

In [7], the authors propose an approach that relies on Input-Convex Neural Networks (ICNN), a class of deep models with a convex output with respect to their inputs introduced in [13], to parameterize the space of convex functions

{ψ_{θ}}

in order to approximate the JKO scheme (15) through

θ^{*} = a r g m i n_{θ} [F (\nabla ψ_{θ} # ρ^{(k - 1)}) + \frac{1}{2 h} \int_{R^{D}} | | x - \nabla ψ_{θ} (x) {| |}_{2}^{2} d ρ^{(k - 1)} (x)]

The authors in [18] investigate the dynamics of a diverse set of points within the framework of Proximal OT using a Jordan-Kinderlehrer-Otto (JKO) flow of measures. These points are observed periodically at different timestamps. The authors propose a 2-level algorithm to capture the trajectories of this population. Specifically, at time

t + 1

, a new configuration is generated that reduces the energy while remaining close to the previous configuration observed at time t, as measured by the Wasserstein distance.

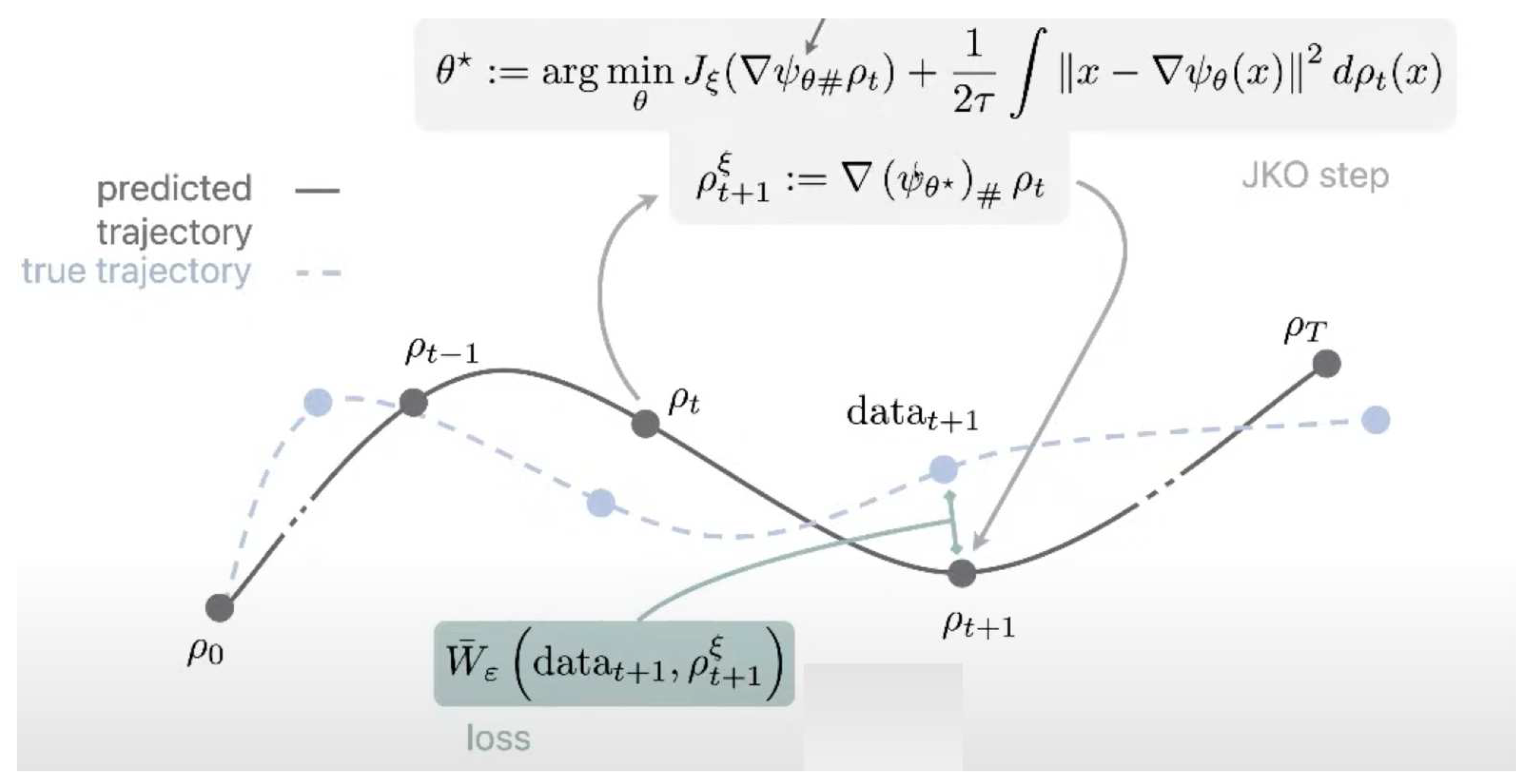
To learn an energy function only through snapshots, the JKOnet algorithm is proposed to compute the JKO flow by a 2-time scale learning algorithm:

- an upper level optimization aiming at minimizing the Wasserstein distance w.r.t. to an energy functional

J_{ψ}

- a lower level optimization of the constrained parameters

θ

of a ICNN, [13].

In Figure 2, we can see an observed trajectory

(μ_{0}, . . ., μ_{T})

of point clouds, we seek parameters

ψ

for the energy

J_{ψ}

such that the predictions

ρ_{1}, . . ., ρ_{T}

following a JKO flow from

ρ_{0} = μ_{0}

are close the observed trajectory, by minimizing (as a function of

ψ

) the sum of Wasserstein distances between

ρ_{t + 1}

, the JKO step from

ρ_{t - 1}

using

J_{ψ}

, and data

μ_{t + 1}

In [31], the authors deal with deep network generative models focusing on the problem of comparing two probability distributions that are degenerate, i.e. distribution in higher-dimensional spaces supported on low-dimensional manifolds, while estimating the parameters of a chosen model that fits observed data.

5. From OT to AOT

After reviewing some variants of the classical OT problem, we present some definitions concerning AOT, i.e. an adapted version of OT.

5.1. OT variants

We start with a brief review of classical OT. Given two marginal distribution

μ \in P (R^{d})

and

ν \in P (R^{d})

, the classical OT problem reads

inf_{π \in Π (μ, ν)} \int c (x . y) π (d x, d y)

(16)

where c is a cost function and

Π (μ, ν)

the set of couplings between

μ

and

ν

We focus on the setting where

μ

and

ν

are distributions computed, e.g., from time series on

R^{d}

, i.e.

μ \sim (X_{1}, . . ., X_{d})

and

ν \sim (Y_{1}, . . ., Y_{d})

The Monge formulation reads

inf_{T : T # μ = ν} \int c (x, T (x)) μ (d x)

(17)

where the infimum is computed over all measurable maps

T : R^{d} \to R^{d}

with the pushforward constraint

T # μ = ν

Some generalizations of the classical 2-marginal OT problem concern:

Martingale Optimal Transport. A first model to encode a temporal adapted structure into OT problems moves within the theory Martingale Optimal Transport (MOT) dealing with transport plans $π$ with martingale couplings. The stability of a sequence of transport plans ${π^{1}, . . ., π^{N}}$ with martingales marginals has been proved to hold in [10], also for the Weak Optimal Transport.
Multi marginal optimal transport problem. Multi-marginal optimal transport problems introduced in [4] are formulated as follows. Consider $M \in N$ probability measures $μ_{1}, . . ., μ_{M}$ on $R^{d}$ and consider the optimization problem

$inf_{π \in Π (μ_{1}, . . ., μ_{M})} \int_{{(R^{d})}^{M}} c (x_{1}, . . ., x_{M}) d π (x_{1}, . . . ., x_{M})$

(18)

with c being a lower semi-continuous cost function defined on ${(R^{d})}^{M}$ with marginal laws $μ_{1}, . . ., μ_{M}$ and $Π (μ_{1}, . . ., μ_{M}) = {π \in R^{d} \times . . . \times R^{d} | \forall 1 \leq i \leq M, \int_{R^{d}} d π = μ_{i}}$

Trying to approximate this problem by discretizing the state space through N points, $x^{1}, . . ., x^{N} \in R^{d}$ chosen and a priori fixed, lead to a linear programming problem of size $N^{M}$ .
From Martingale-constrained to Moment Constrained Optimal Transport . In [5,6], the authors develop algorithms to sample from probability distribution while preserving the convex order enabling to use linear programming solver.

The same authors study the same problem also in [4] following another perspective by relaxing the martingale constraint into a finite number of moment constraints by means of N real-valued bounded (test) function $ϕ_{1}, . . ., ϕ_{N}$ defined on $R^{d}$ .

This method is called Moment Constrained Optimal Transport (MCOT). Differently from multi marginal setting, it is not the state space to be discretized but the marginal laws constrained of Eq. (18) are relaxed into a finite number of moment constraints via some given ${ϕ_{N}}_{1, . . ., N}$ It solves the following:

$inf \int_{R^{d} \times R^{d}} c (x, y) d π (x, y)$

(19)

where the infimum is computed over the set of probability measures $π$ with values in $R^{d} \times R^{d}$ satisfying for all $1 \leq i, j \leq N$

$\int_{R^{d} \times R^{d}} ϕ_{i} (x) d π (x, y) = \int_{R^{d}} ϕ_{i} (x) d μ (x)$

(20)

and

$\int_{R^{d} \times R^{d}} ϕ_{j} (x) d π (x, y) = \int_{R^{d}} ϕ_{j} (y) d ν (y)$

(21)

Always in [4], they prove that MCOT is a generalization of Martingale constrained OT when by means of $L^{1}$ -valued test functions and characteristic functions to enforce the martingale constraint ( see Equation (3.3.11) from [4]).

5.2. Adapted Optimal Transport

Adapted Optimal Transport (AOT) is the natural problem to deal with laws of stochastic processes, as shown in e.g. [1,14,15,34,38]. Intuitively, causality encodes an adapted (nonanticipative) constraint into the allocation of mass of the classical optimal transport problem. The relationship between causal plans and adapted processes is the adapted analogous of the one between transport plans (Kantorovich) and classical transport maps (Monge).

The basic idea of COT relies on the assumption that the transport maps T introduced in (17)have to be adapted.

If, in the classical setting one can split T component-wise by

T (x) = (T_{1}, (x), . . ., T_{d} (x)

, in the COT setting the adapted maps are defined in the form

T (x) = (T_{1}, (x_{1}), T_{2} (x_{1}, x_{2}) . . ., T_{d} (x)

where

T_{t}

depends only on the past component of x, namely

x_{1}, . . ., x_{t}

. Thus, the adapted analogous of (17) is defined as

inf_{T : T # μ = ν,, T adapted} \int c (x, T (x)) μ (d x)

(22)

Concerning coupling, the adaptness of T means that under

π

, the first component of Y until component t should be independent of the component of X after t. This construction allows to include the conditional independence of Y into the set

Π_{c}

of arbitrary causal couplings that is defined by

\begin{matrix} Π_{c} (μ, ν) = {π \in Π (μ, ν) : if (X, Y) \sim π, \\ then (Y_{1}, . . ., Y_{t}) ⊥ ⊥ (X_{t + 1}, . . ., X_{d}) | (X_{1}, . . ., X_{t})} \end{matrix}

Optimizing over the set of causal coupling let us formulate the first

A O T

problem

inf_{π \in Π_{c} (μ, ν)} \int c (x . y) π (d x, d y)

(23)

that is called Causal OT.

In order to provide a symmetrical property that is desirable to give a more robust structure to the problem and also necessary to introduce a proper notion of adapted Wasserstein distance, one may introduce the set of bicausal couplings

Π_{b c}

\begin{matrix} Π_{b c} (μ, ν) = {π \in Π (μ, ν) : if (X, Y) \sim π, \\ then (Y_{1}, . . ., Y_{t}) ⊥ ⊥ (X_{t + 1}, . . ., X_{d}) | (X_{1}, . . ., X_{t})} \\ and (X_{1}, . . ., X_{t}) ⊥ ⊥ (Y_{t + 1}, . . ., Y_{d}) | (Y_{1}, . . ., Y_{t})} \end{matrix}

(24)

and the equivalent Bicausal-OT formulation

inf_{π \in Π_{b c} (μ, ν)} \int c (x . y) π (d x, d y)

(25)

To fix nomenclature, we call Causal OT (23) and Bicausal OT (25), AOT problems. As recently proved in [10], it is possible to write a Linear Program formulation for AOT problems (23) and (25) by discretizing the marginal distributions, see Lemma 3.11 in [10] for further details.

As shown in several works, e.g. [20,24,40], to compute efficiently a solution of OT problems, it is convenient to work with a regularized version of (16) by introducing an entropic regularization in order to apply Sinkhorn’s algorithm [41]. We refer to the landmark book [40] for a complete overview with a detailed treatment of Sinkhorn application in Section 4, [40].

In the same fashion, we provide to Eq. (25) an entropic regularization term to study the following Entropic-AOT

inf_{π \in Π_{b c} (μ, ν)} \int c (x . y) π (d x, d y) + ε D_{K L} (π, μ \otimes ν),

(26)

being

ε

a positive positive constant,

D_{K L}

the Kullback-Leibler divergence and

μ \otimes ν

the product measures between marginals.

In [10] the authors construct an adapted version of Sinkhorn algorithm allowing to handle computations by constructing a sequence of transport plans

π^{k}

that converges (lineraly) to the optimal value of Eq. (26).

In next paragraphs, we review some of the basic tools of the causal framework: the Adapted Wasserstein distance inherited from AOT, the class of equivalence of filtered processes and the Adapted empirical measure.

5.3. Adapted Wasserstein Distance

The starting point is to consider stochastic processes on the canonical space in finite discrete time with values in

R^{d}

. We can represent the law of a stochastic process as a probability measure on

P (R^{d})

. Even at this very early stage, it is clear that the usual weak topology on

P (R^{d})

is not enough for encoding the temporal structure of the process that is crucial for stochastic optimization problem.

Thus, different researchers have introduced topological structure on the set of stochastic processes in order to capture the temporal structure. Among different approaches on defining a distance for multistage stochastic optimization, we focus on nested distance also known as adapted Wasserstein distance.

The notion has been independently defined by Pflug and Pichler [38] in a pure distribution setting, i.e. without reference to probability spaces, by means of particular stochastic processes, called tree processes, and by Lassalle [34] that introduces the so-called causal transport plans in Polish spaces.

Following a dynamical setting, adapted Wasserstein distance can model a distance between laws of stochastic processes integrating also the temporal structure of the data.

Recalling notation and definition from Eq. (25), we define the adapted Wasserstein distance as

{AW}_{p}^{p} (μ, ν) = inf_{π \in Π_{b c} (μ, ν)} E^{π} [| | X - {Y | |}_{p}^{p}], p \in [1, + \infty]

(27)

with

Π_{b c}

being the set of bicausal couplings defined in Eq. (24).

The nested distance represents a compatible metric for the weak adapted topology. More precisely, as proven in [9], the convergence

{AW}_{p}

is equivalent to the convergence in the weak topology plus convergence of the

p^{t h}

moment. On the other hand, a possible limitation is due to the fact that

(P_{p} (R^{d}), {AW}_{p})

is not complete since

P_{p} (R^{d})

. According to [11], a possible method to store the extra information needed for achieving the completion of

(P_{p} (R^{d}), {AW}_{p})

is by introducing the following space of filtered stochastic processes.

5.3.1. The class of filtered processes

We recall Definition 1.1 from [11]: a five-tuple

X (Ω, F, P, {(F_{t})}_{i = 1}^{N}, {(X_{t})}_{i = 1}^{N}),

is called a filtered stochastic processes if

{(F_{t})}_{i = 1}^{N}

is adapted to

{(X_{t})}_{i = 1}^{N}

It is straightforward to extend the notion of adapted Wasserstein distance defined in (27) to filtered processes by the following

{AW}_{p}^{p} (X, Y) = inf_{π \in Π_{b c} (X, Y)} E^{π} [| | X - {Y | |}_{p}^{p}], p \in [1, + \infty];

(28)

We report some properties about the Wasserstein space of stochastic processes:

$({FP}_{p}, {AW}_{p})$ is a geodesic space (assuming $p > 1$ ) and it is the completion of $(P_{p} (R^{d}), {AW}_{p})$ . The first property suggests the possibility an interpolation, in the sense of McCann, also of stochastic processes that is not possible if one considers the usual Wasserstein space $P_{p} (R^{d})$ ;
two filtered processes $X$ and $Y$ are identified if ${AW}_{p} (X, Y) = 0$ . Moreover, this equivalence relation encodes also information about their filtration.
the space of filtered stochastic processes is defined as a set of equivalence classes as in the case of $L^{p}$ spaces. An equivalence class of ${FP}_{p}$ collects all representatives processes that are identical from a probabilistic perspective.

5.3.2. Adapted Empirical Measure

Another key concept in AOT theory concerns constructing empirical measures of stochastic processes also including a dependence on the flow of time.

We report three possible methods to construct adapted empirical measures:

in [38], adapted empirical distribution is constructed via convolution of a smooth kernel with the empirical measure on paths;
in [14,15] the authors project paths on a grid by means of a disjoint union of small cubes projecting the stochastic process into the center of these small cubes;
in [1] the authors show the convergence of adapted empirical measure in $R^{d}$ , removing the assumption of compact support for the underlying distribution. Moreover, the authors introduce the non-uniform adapted empirical measures by defining a non-uniform grid on $R^{d T}$ , dealing with cubes of different sizes, i.e. of lower dimension near the origin, bigger far in the margins.

In all works, they establish convergence of the empirical measure to the true distribution.

6. Conclusions

The present review article provides an all-around and diversified overlook of methods at the overlapping of ML, game theory and probability theory. In doing this, we tried to provide a concrete outlook to possible developments of a challenging research path focused on developing robust algorithms for Adapted optimal transport. Indeed, employing the Sinkhorn algorithm with the addition of the entropic regularization potentially allows to derive a method that can handle the curse of dimensionality. On the other hand, OT problems are sensitive to small perturbations in the input data, which can make the solutions unstable. The application of their convergence results in a causal setting could lead to improved training algorithms and more stable models in the field of causal inference for times series.

Author Contributions

Conceptualization, M.G.; methodology, M.G.; validation, M.G and L.d.P.; formal analysis, M.G.; investigation, M.G.; resources, M.G.; writing—original draft preparation, M.G. and L.d.P; writing—review and editing, M.G. and L.d.P; supervision, L.d.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to kindly thank Beatrice Acciaio for her valuable advice.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds ... are available from the authors.

Abbreviations

The following abbreviations are used in this manuscript:

OT	Optimal Transport
COT	Causal Optimal Transport
AOT	Adapted Optimal Transport
NN	Neural Network
MFOCP	Mean Field Optimal Control Problem
MFG	Mean Field Games
MFC	Mean Field Control
ML	Machine Learning
DL	Deep Learning
MFOT	Mean Field Optimal Transport
SDE	Stochastic Differential Equation
ICNN	Input-Convex Neural Networks
JKO	Jordan-Kinderlehrer-Otto
SNN	Stochastic Neural Network
SGD	Stochastic Gradient Descent
HJB	Hamilton-Jacobi-Bellman
ODE	Ordinary Differential Equation
MCOT	Moment Constrained Optimal Transport
MOT	Martingal Optimal Transport

References

Acciaio, B.; Hou, S. Convergence of Adapted Empirical Measures on $R^{d}$ . 2022 arXiv e-prints. [CrossRef]
Acciaio B.; Kratsios A.; Pammer G. Metric hypertransformers are universal adapted maps. 2022 Preprint, arXiv:2201.13094.
Ambrosio, L.; Gigli, N. Savaré, G- Gradient flows: in metric spaces and in the space of probability measures, Springer Science & Business Media, 2008.
Alfonsi, A.; Coyaud, R.; Ehrlacher, V.; Lombardi, D. Approximation of Optimal Transport problems with marginal moments constraints. Mathematics of Computation, 2020, ⟨10.1090/mcom/3568⟩. ⟨hal-02128374⟩. [CrossRef]
Alfonsi, A.; Corbetta, J.; Jourdain, B. Sampling of one-dimensional probability measures in the convex order and computation of robust option price bounds. International Journal of Theoretical and Applied Finance, 20190(0):1950002, 0. [CrossRef]
Alfonsi, A.; Corbetta, J.; Jourdain, B. Sampling of probability measures in the convex order by Wasserstein projection. arXiv e-prints, page arXiv:1709.05287, Sep 2017.
Alvarez-Melis, D.; Schiff, Y.; Mroueh, Y. Optimizing Functionals on the Space of Probabilities with Input Convex Neural Networks, arXiv e-prints, 2021.
Archibald, R.; Bao, F.; Yong, J. “An Online Method for the Data Driven Stochastic Optimal Control Problem with Unknown Model Parameters”, arXiv e-prints, 2022.
Backhoff-Veraguas, J.; Bartl, D.; Beiglblock, M.; and Eder, M. All adapted topologies are equal. Probab. Theory Related Fields, 178(3-4):1125–1172, 2020. [CrossRef]
Backhoff-Veraguas, J.; Pammer, G. Stability of martingale optimal transport and weak optimal transport. Ann. Appl. Probab. 32 (1) 721 - 752, February 2022. [CrossRef]
Bartl, D.; Beiglböck, M.; Pammer, G. The Wasserstein space of stochastic processes. arXiv e-prints, 2021. [CrossRef]
Baudelet, S.; Frénais, B.; Laurière, M.; Machtalay, A.; Zhu, Y. Deep Learning for Mean Field Optimal Transport. arXiv e-prints 2023. [CrossRef]
Brandon, A.; Xu, L.; Kolter, J.Z. Input Convex Neural Networks Proceedings of the 34th International Conference on Machine Learning, 2017, PMLR 70:146-155.
Backhoff-Veraguas, J.; Beiglboeck, M.; Lin, Y.; Zalashko, A. Causal transport in discrete time and applications. SIAM Journal on Optimization, 2017, 27(4):2528–2562. [CrossRef]
Backhoff-Veraguas, J.; Bartl, D.; Beiglblock, M.; Wiesel, J. Estimating processes in adapted Wasserstein distance. Ann. Appl. Probab. 32 (1) 529 - 550, February 2022. [CrossRef]
Bao, F.; Cao, Y.; Archibald, R.; Zhang, H. Uncertainty quantification for deep learning through stochastic maximum principle. arXiv: 3489122, 2021.
Bonnet, B.; Cipriani, C.; Fornasier, M.; Huang, H. A measure theoretical approach to the mean-field maximum principle for training NeurODEs, Nonlinear Analysis, Volume 227, 2023, 113161, ISSN 0362-546X. [CrossRef]
Bunne, C.; Meng-Papaxanthos, L.; Krause, A.; Cuturi, M. Proximal Optimal Transport Modeling of Population Dynamics, arXiv e-prints, 2021.
Benoît, B. A Pontryagin Maximum Principle in Wasserstein spaces for constrained optimal control problems. ESAIM: COCV, 25 2019 52. [CrossRef]
Carlier, G. On the linear convergence of the multi-marginal Sinkhorn algorithm. SIAM Journal on Optimization, 2022, 32 (2), pp.786-794. [CrossRef]
Canas, G.; Rosasco, L. Learning Probability Measures with respect to Optimal Transport Metrics, Advances in Neural Information Processing Systems 25, 2012.
Chizat, L.; Bach, F. , On the global convergence of gradient descent for overparameterized models using optimal transport. In Advances in neural information processing systems, 2018, pages 3040–305.
Chizat, L.; Colombo, M. , Fernández-Real, X.; and Figalli, A. Infinite-width limit of deep linear neural networks, arXiv e-prints, 2022. [CrossRef]
Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems, 2013 pages 2292–2300.
de Bie, G.; Peyré, G.; Cuturi, M. Stochastic Deep Networks, Proceedings of the 36th International Conference on Machine Learning, 2019. Long Beach, California, PMLR 97.
Di Persio, L. , Garbelli M. Deep Learning and Mean-Field Games: A Stochastic Optimal Control Perspective. Symmetry 2021 13(1):14. [CrossRef]
E, W.; Han, J.; Li, Q. A mean-field optimal control formulation of deep learning. Res Math Sci 6, 10. 2019. [CrossRef]
Feydy, J.; Séjourné, T.; Vialard, F.X.; Amari, S.; Trouve, A.; Peyré, G. Interpolating between Optimal Transport and MMD using Sinkhorn Divergences. Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, 2019, PMLR 89:2681-2690.
Fernández-Real, X. : Figalli, A. The Continuous Formulation of Shallow Neural Networks as Wasserstein-Type Gradient Flows. In: Avila, A., Rassias, M.T., Sinai, Y. (eds) Analysis at Large. Springer, Cham. 2022. [CrossRef]
Gangbo, W.; Mayorga, S.; Swiech, A. Finite Dimensional Approximations of Hamilton-Jacobi Bellman Equations in Spaces of Probability Measures. SIAM Journal on Mathematical Analysis 2021 53:2, 1320-1356. [CrossRef]
Genevay, A.; Peyre, G.; Cuturi, M. Learning Generative Models with Sinkhorn Divergences. Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, 2018, PMLR 84:1608-1617.
Jimenez, C. ; A. Marigonda A.; Quincampoix, M. Dynamical systems and Hamilton-Jacobi-Bellman equations on the Wasserstein space and their L2 representations, 2022. Preprint at https://cvgmt.sns.it/media/doc/ paper/5584/AMCJMQ_HJB_2022-03-30.pdf.
Hashimoto, T.; Gifford, D.; Jaakkola, T. Learning population-level diffusions with generative rnns. International Conference on Machine Learning, 2016, pages 2417–2426.
Lassalle, R. Causal transport plans and their Monge–Kantorovich problems, Stochastic Analysis and Applications 2018, 36:3, 452-484. [CrossRef]
Li, Q.; Lin, T.; Shen, Z. Deep Learning via Dynamical Systems: An Approximation Perspective. 2019 Published in arXiv:1912.10382v1.
Li, Q., Long, C., Cheng, T.; E, W. Maximum principle based algorithms for deep learning. J. Mach. Learn. Res. 2017, 18, 1, 5998–6026.
Pham, H.; Warin, X. Mean-field neural networks: learning mappings on Wasserstein space, 2022 arXiv e-prints.
Pflug, G.; Pichler, A. . A distance for multistage stochastic optimization models. SIAM Journal on Optimization, 2012, 22(1):1-23.
Pichler, A.; Weinhardt, M. The nested Sinkhorn divergence to learn the nested distance. Comput Manag Sci 2022, 19, 269–293. [Google Scholar] [CrossRef]
Peyré, G.; Cuturi, M. Computational Optimal Transport: With Applications to Data Science, Foundations and Trends in Machine Learning, 2019. Vol. 11: No. 5-6, pp 355-607. [CrossRef]
Sinkhorn, R. Diagonal equivalence to matrices with prescribed row and column sums. The American Mathematical Monthly, 1967, 74(4):402–405. [CrossRef]
Seguy, V.; Cuturi, M. , Principal Geodesic Analysis for Probability Measures under the Optimal Transport Metric, 2015 arXiv e-prints.
Sirignano, J.; Spiliopoulos, K. Mean Field Analysis of Deep Neural Networks. Mathematics of Operations Research 2021, 47(1):120-152. [CrossRef]
Xu, T.; Li K., W.; Munn, M.; Acciaio, B. ; COT-GAN: Generating Sequential Data via Causal Optimal Transport. Neural Information Processing Systems (NeurIPS), 2020.
Zalashko, A. ; Causal optimal transport: theory and applications. PhD Thesis, 2017 University of Vienna.

Figure 2. JKOnet 2-level optimization process (from [18]).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Neural Networks and Adapted Optimal Transport

Abstract

1. Introduction

2. A continuous idealization of NN for a Mean Field Optimal Control Problem

2.1. Mean Field Optimal Control Problem

2.2. Empirical measures over controls

3. Learning Mean Field Function

3.1. The McKean-Vlasov SDE

3.2. Mean Field Optimal Transport

3.3. Alternative methods

4. Learning Gradient Flow

4.1. Gradient Flow in Wasserstein space

4.2. Stochastic Optimization with ICNN and JKOnet

5. From OT to AOT

5.1. OT variants

5.2. Adapted Optimal Transport

5.3. Adapted Wasserstein Distance

5.3.1. The class of filtered processes

5.3.2. Adapted Empirical Measure

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Sample Availability

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe