A Software Verification Method for Internet of Things and Cyber-Physical Systems

Preprint

Article

A Software Verification Method for Internet of Things and Cyber-Physical Systems

Altmetrics

Downloads

154

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 May 2023

Posted:

03 May 2023

You are already at the latest version

Alerts

Abstract

With the rise of Internet of Things (IoT) devices and Cyber-Physical Systems, the demand for more functional and high-quality software has increased tremendously. To meet this need, we must reengineer and reuse existing software, as well as develop new software formal verification methods. One such method is based on physical quantities defined by the System International, which have physical dimensions. The homogeneity of physical dimensions in software code enables us to check the software code in the space of base units, making it the first basis of the new software verification method. However, this method cannot check expressions with angles, angle speed, and other similar features. To address this, a transformation for physical value orientation introduced by Siano allows us to check software code for orientational, stabilization, and other related branches. This makes the orientational homogeneity the second basis of the new software verification method. To assess the effectiveness of the proposed method, we developed special software defect models based on the statistical characteristics of software code. We used a special statistical analysis tool to define the statistical characteristics of modern software and analyzed over 2 GB of C++ GITHUB code for drones. Based on the actual distribution of software characteristics, the proposed method can detect over 60% of latent software defects. Implementing this method can significantly reduce testing time, improve reliability, and enhance overall software quality.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

The Internet of Things (IoT) is a contemporary paradigm that comprises a wide range of heterogeneous inter-connected devices capable of transmitting and receiving messages in various formats through different protocols to achieve diverse goals [1]. Presently, the IoT ecosystem encompasses over 20 billion devices, each with a unique identifier that can seamlessly interact via existing Internet infrastructure [2]. These devices have diverse areas of application, ranging from inside the human body to deep within the oceans and underground. IoT refers to a network of physical devices, vehicles, buildings, and other items that are embedded with sensors, software, and other technologies to enable them to collect and exchange data. The main focus of IoT is on enabling communication between these devices to enable automation and control.

CPS (Cyber-Physical Systems), on the other hand, refers to a system of physical, computational, and communication components that are tightly integrated to monitor and control physical processes. CPS typically involves a closed-loop feedback control system that involves sensors, actuators, and computational elements to continuously monitor and adjust physical processes in real-time.

CPS integrates physical components with software components [3]. CPS able to operate on different spatial and temporal scales [4,5]. CPS similar to the IoT.

Control systems coupled to physical systems are a common example of CPS, with applications in various domains such as smart grid, autonomous automobile systems, medical monitoring, industrial control systems, robotics systems, and automatic pilot avionics. CPS are becoming data-rich enabling new and higher degrees of automation and autonomy.

New, smart CPS drive innovation and competition in a range of application domains, including agriculture, aeronautics, building design, civil infrastructure, energy, environmental quality, healthcare, personalized medicine, manufacturing, and transportation. With the ability to collect and process data, CPS are becoming increasingly data-rich, enabling new and higher degrees of automation and autonomy.

Despite some similarities, the primary distinction between IoT and CPS is their focus. CPS is mainly focused on controlling physical processes, while IoT is primarily focused on communication and data exchange between physical devices. CPS is typically used in industrial and manufacturing settings, where it facilitates real-time control of physical processes. On the other hand, IoT has a broader range of applications, including home automation, healthcare, transportation, and other domains, where it enables seamless communication and integration of smart devices.

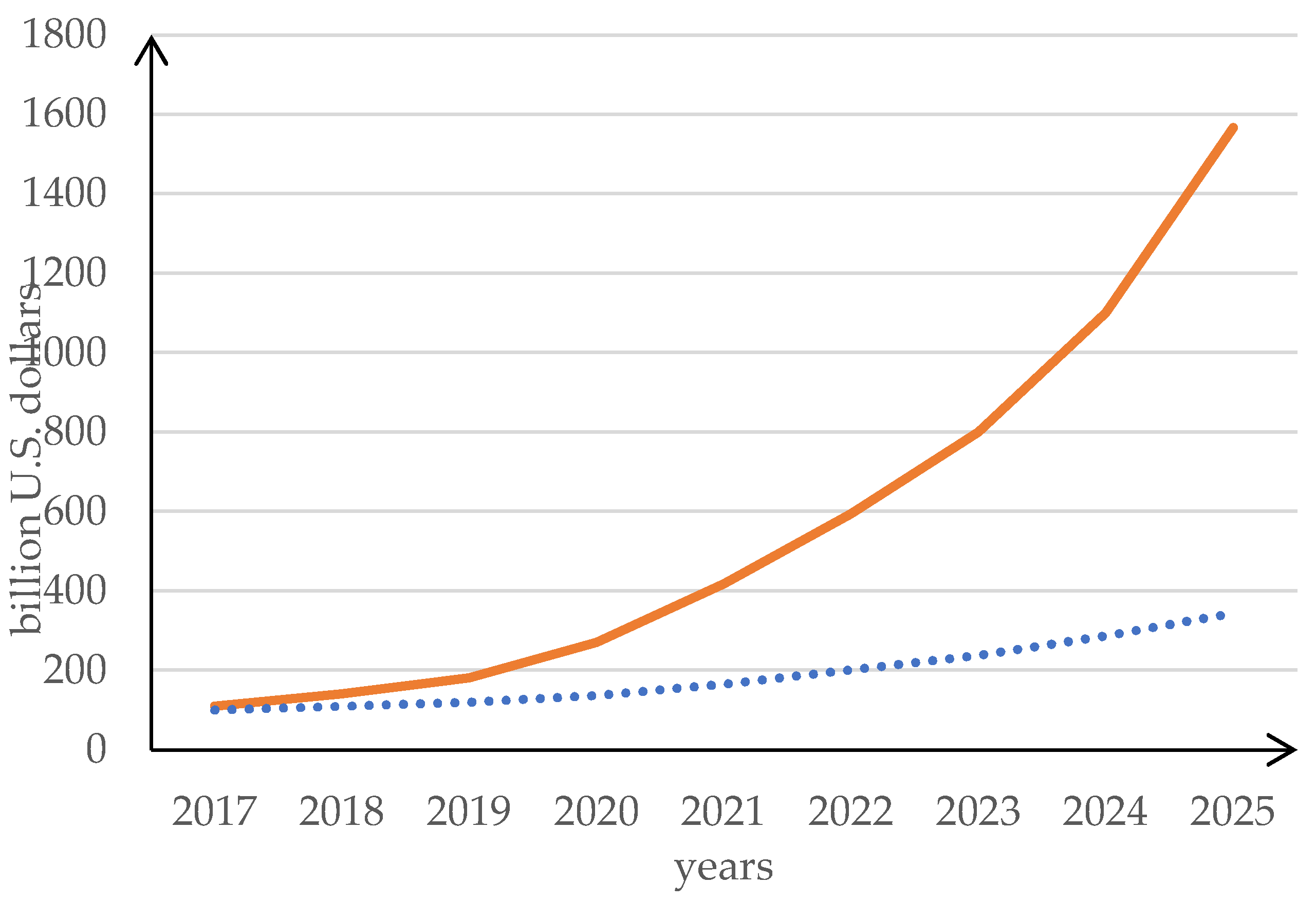
With the ever-increasing number of IoT and CPS devices, the need for more functional and high-quality software has become even more pressing. According to industry estimates, the global IoT market reached $100 billion in 2017, and this figure is projected to soar to $1.6 trillion by 2025 [6]. In 2022, enterprise IoT spending rose by 21.5%, reaching $201 billion. However, IoT Analytics has revised its growth outlook for 2023 to 18.5% (down from 24% previously) [7], as shown in Figure 1.

A model-based approach to CPS development is based on describing both the physical and software parts through models, allowing the whole system to be simulated before it is deployed.

There are several programming languages used in IoT and CPS development, including C/C++, Python, Java, JavaScript, and others. Among these, C/C++ is considered to be the most popular language for IoT development, with a popularity rate of 56.9%, according to recent research [8]. This is due to the fact that IoT devices typically have limited computing resources, and C/C++ is capable of working directly with the RAM while requiring minimal processing power.

CPS languages provide a unified approach to describe both the physical components and control software, making it possible to integrate modeling and simulation. Open standards like FMI [9] and SSP [10] facilitate this integration by defining a model format that uses C language (for behavior) and XML (for interface) to represent pre-compiled models that can be exchanged between tools and combined for co-simulation.

Modelica [11] has been utilized for automatic generation of deployable embedded control software in C code from models, enhancing its utility as a comprehensive solution for modeling, simulation, and deployment of CPS components.

The selection of a programming language for IoT and CPS development is highly dependent on the specific requirements of the project as well as the developer’s proficiency.

Using C++ in embedded systems can be an effective solution despite the limited computing resources of microcontrollers used in small embedded applications compared to standard PCs [12]. The clock frequency of microcontrollers may be much lower, and the amount of available RAM memory may be significantly less than that of a PC. Additionally, the smallest devices may not even have an operating system. To achieve the best performance, it’s essential to choose a programming language that can be cross-compiled on a PC and then transferred as machine code to the device, avoiding any language that requires compilation or interpretation on the device itself, as this can lead to significant resource wastage.

For these reasons, C or C++ is often the preferred language for embedded systems, with critical device drivers requiring assembly language. If you follow the proper guidelines, using C++ can consume only slightly more resources than C, so it can be chosen based on the desired program structure. Overall, choosing the appropriate language for embedded systems can make a significant impact on performance and resource utilization.

The increasing number of IoT and CPS devices has resulted in a growing need for software that is both highly functional and of the utmost quality. As these devices become more ubiquitous and seamlessly integrated into our daily lives, the demand for dependable and efficient software becomes more critical than ever before. As a result, developers are constantly striving to enhance their software development methodologies and technologies to meet the ever-evolving demands of the IoT and CPS landscape.

However, given the increasing importance of IoT and CPS as emerging technologies, it is expected that there will be more literature available on the topic of IoT and CPS software verification and quality assurance.

The typical software development life cycle (SDLC) involves several steps, including requirement analysis, design, implementation, testing and verification, and deployment and maintenance. While testing can increase our confidence in the program’s correctness, it cannot prove it definitively. To establish correctness, we require a precise mathematical specification of the program’s intended behavior, and a mathematical proof that the implementation meets the specification.

IoT verification uses conformance testing [13], randomness testing [14], statistical verification [15] and formal verification [16]. Now there are method named as Model-Based Testing [17]. Closely related to the Model-Based Testing, the Model Checking technique [18] has its representatives in the specific IoT context.

However, such software verification is difficult and time-consuming, and is not usually considered cost-effective. In addition, modern verification methods would not replace testing in SDLC because most programs are not correct initially and need debugging before verification. The primary principle of verification involves adding specifications and invariants to the program, and checking the verification conditions by proving generated lemmas based on the requirement specifications [19]. This makes program verification an alternative or complement to testing.

This article focuses on exploring a formal verification method that utilizes dimensional and orientational homogeneities and natural software invariants, specifically the dimension and orientation of physical quantities stated by the International System of Units (SI) [20,21], Siano [22,23] and authors [24]. By leveraging these invariants, this method can effectively verify the correctness of software and detect errors that may arise due to inconsistent or incorrect use of units and dimensions, as well as incorrect usage of software operations, variables, and procedures, among other things. This approach can provide a reliable and efficient way to verify software correctness, especially for applications that involve physical calculations and measurements.

2. The formal software verification method

Proposed is the utilization of natural software invariants, which are the physical dimensions and spatial orientation of software variables that correspond to real physical quantities. By incorporating these invariants into the program specification, it becomes possible to convert all program expressions into a series of lemmas that must be proven. This enables the verification of the homogeneity and concision of the program.

2.1. Using Dimensional homogeneity in formal software verification

Dimensional Analysis (DA) [25] is a widely used methodology in physics and engineering to find or verify relationships among physical quantities by using their physical dimensions. In the SI a physical quantity’s dimension is the combination of the seven basic physical dimensions: Length (meter, m), Time (second, s), Amount of substance (mole, mol), Electric current (ampere, A), Temperature (kelvin, K), Luminous intensity (candela, cd), and Mass (kilogram, kg). Derived units are products of powers of the base units, and when the numerical factor of this product is one, they are called coherent derived units. The base and coherent derived units of the SI form a coherent set designated as the set of coherent SI units. The word "coherent" in this context means that equations between the numerical values of quantities take the same form as the equations between the quantities themselves, ensuring consistency and accuracy in calculations involving physical quantities.

Some of the coherent derived units in the SI are given specific names, and together with the seven base units, they form the core of the set of SI units. All other SI units are combinations of these 29 units. For instance, plane angle is measured in radians (rad), which is equivalent to the ratio of two lengths; solid angle is measured in steradians (sr), which is equivalent to the ratio of two areas. The frequency is measured in hertz (Hz), which is equivalent to one cycle per second. The force is measured in newtons (N), which is equivalent to kg m/s². The pressure and stress are measured in pascals (Pa), which is equivalent to kg/m s² or N/m². The energy and work are measured in joules (J), which is equivalent to kg m²/s² or N m.

The fundamental principle of DA is based on the fact that a physical law must be independent of the units used to measure the physical variables. According to the principle of dimensional homogeneity, any meaningful equation must have the same dimensions on both sides. This is the fundamental approach to performing DA in physics and engineering.

DA can also be used for formal verification of software code. Existing software analysis tools only check the syntactic and semantic correctness of the code, but not its physical correctness. However, we can consider the program code of systems as a set of expressions consisting of operations and variables (constants).

By using DA, we can verify the physical consistency of the program code and detect errors that may arise due to inconsistent or incorrect use of units and dimensions.

To check the correctness of expressions, we can use the dimensionality of program values. Preservation of the homogeneity of the expressions may indicate the physical usefulness of the expressions. Violation of homogeneity will indicate incorrect use of a program variable or program operation. DA will provide an opportunity to check not only simple expressions, but also calls to procedures and functions. The use of physical dimension will allow to verify the software.

DA is a powerful tool that can be used to ensure the physical correctness of software code. By checking the dimensionality of program values, we can ensure the preservation of the homogeneity of expressions, which may indicate the physical usefulness of the code. In cases where homogeneity is violated, it may indicate an incorrect use of program variables or operations. DA can be applied not only to simple expressions but also to calls to procedures and functions, providing a comprehensive approach to verifying the physical consistency of the software.

We can think of software as a model, and DA can be used to validate this model by ensuring that it satisfies the physical laws and principles governing the system it represents. The use of physical dimensions in this validation process can help to detect and correct errors that may arise due to inconsistent or incorrect use of units and dimensions, ultimately leading to more reliable and accurate software.

Software System:= Sub_System{,Sub_System} – a set of interacting Sub_System

Sub_System := Unit{,Unit} – a set of interacting software units

Unit := operator{,operator} – a ordered set of interacting operators

Operator:=expression{, expression} – a ordered set of expression

Expression := AdditiveOperation|MultiplicativeOperation|FunctionCalling

Let’s introduce a set of "multiplicative" operations {*, / etc }, that generate new physical dimensions, while "additive" operations {+,-, =, <, ≤,>,≥,!= etc} act as checkpoints to ensure dimensional homogeneity. If source code has a set variables and every variable saves some physical dimension than we can use this property (dimensional homogeneity) as a software invariant.

Any software system, subsystem, or unit has a set of input parameters, I={in₁, in₂, in₃, ..., in_k}, and a set of output parameters, O={out₁, out₂, out₃, ..., out_k}. To ensure the dimensional correctness of a software system, we must prove the correctness of each subsystem. To prove the dimensional correctness of each subsystem, we must demonstrate the correctness of each unit. And to demonstrate the dimensional correctness of each unit, we must prove the correctness of each expression, which comprises variables and operations.

Based on the principle of dimensional homogeneity, we can develop a set of lemmas.

By utilizing DA, we can verify the physical dimensions of variables to detect errors caused by inconsistent or incorrect use of units and dimensions, as well as improper use of software operations, variables, and procedures. However, some variables have the same dimensions, such as moments of inertia and angular velocities. To identify software defects caused by incorrect use of variables, we need to inspect expressions involving angles, angular speed, and so on. However, according to the SI, angles are dimensionless values.

2.2. Using Orientational homogeneity in formal software verification

To address this issue, we can utilize features for transformations of angles and oriented values. Siano proposed an orientational analysis (OA) that involves extending physical dimensions to improve DA.

The use of OA can aid in expanding the base unit set while also ensuring dimensional and orientational consistency. Additionally, the OA technique can be applied for the formal verification of software code, allowing for a thorough evaluation of its accuracy and reliability.

Siano’s proposed notation system for representing vector directions involved the use of orientational symbols

l_{x}

l_{y}

l_{z}

. Furthermore, an orientationless symbol represented by

l_{0}

was introduced to represent vectors that do not possess a specific orientation.

For example, a velocity in the x-direction can be represented by

V_{x} ≐ l_{x}

, while a length in the x-direction can be represented by

L_{x} ≐ l_{x}

. Here, the symbol

≐

denotes that the quantity on the left-hand side has the same orientation as the quantity on the right-hand side. In non-relativistic scenarios, mass is considered an orientationless quantity.

In order for equations involving physical variables to be valid, they must exhibit orientational homogeneity, meaning that the same orientation must be utilized on both sides of the equation. Furthermore, it is crucial that the orientations of physical variables are assigned in a consistent manner. For instance, the representation of acceleration in the x-direction as

a_{x} = \frac{Δ V_{x}}{Δ t}

V_{x} ≐ l_{x}

Δ t ≐ l_{0}

and

a_{x} ≐ \frac{l_{x}}{l_{0}}

is only valid if both sides have the same orientation.

But what about orientation of time. From expression

H = \frac{g t^{2}}{2}

we can define the time as follows:

t = \sqrt{\frac{2 H}{g}} ≐ \sqrt{\frac{l_{z}}{l_{z}}} ≐ \sqrt{l_{z} l_{z}} ≐ \sqrt{l_{0}} ≐ l_{0}

The physical quantity of time is considered to be orientationless, meaning it does not possess a specific orientation in space.

In order to maintain orientational homogeneity, it is necessary to introduce a characteristic length scale

l_{0}

, since time is an orientationless quantity. Therefore,

l_{x}

can be expressed as

l_{x} ≐ \frac{l_{x}}{l_{o}} ≐ l_{x}

and

l_{o} l_{x} ≐ l_{x} l_{o} ≐ l_{x}

l_{0}^{- 1} ≐ l_{o}

ensuring that the orientation of

l_{x}

remains consistent. That is why

a_{x} ≐ l_{x}

It is essential to assign orientations to physical variables in a consistent manner. For instance, pressure is defined as force per unit area. If the force is acting in the z-direction, then the area must be normal to it etc.:

P = \frac{F_{z}}{S_{x y}} ≐ \frac{l_{z}}{l_{x} l_{y}} ≐ \frac{l_{z}}{l_{z}} ≐ l_{0}

P = \frac{F_{x}}{S_{y z}} ≐ \frac{l_{x}}{l_{y} l_{z}} ≐ \frac{l_{x}}{l_{x}} ≐ l_{0}

P = \frac{F_{y}}{S_{x z}} ≐ \frac{l_{y}}{l_{x} l_{z}} ≐ \frac{l_{y}}{l_{y}} ≐ l_{0}

In order for pressure to be considered an orientationless quantity, the area S must have the same orientation as the force F. If the force F is in a particular direction, then the area S must be normal to that direction, meaning that both variables have the same orientation. Therefore, pressure can only be orientationless quantity if this consistent orientation is maintained.

We can define as follows:

l_{x} l_{y} ≐ l_{z}

l_{y} l_{z} ≐ l_{x}

l_{x} l_{z} ≐ l_{y}

\frac{l_{x}}{l_{x}} ≐ l_{0}

\frac{l_{y}}{l_{y}} ≐ l_{0}

\frac{l_{z}}{l_{z}} ≐ l_{0}

a ≐ l_{x}

b ≐ l_{y}

c ≐ l_{z}

a volume of space, V, is orientationlless quantity:

V_{a b c} = S_{a b} c ≐ l_{z} l_{z} ≐ l_{0}

V_{a b c} = S_{b c} a ≐ l_{x} l_{x} ≐ l_{0}

V_{a b c} = S_{a c} b ≐ l_{y} l_{y} ≐ l_{0}

Let us take a look at uniformly accelerated motion in the x-direction:

S_{x} = S_{0 X} + v_{x} t + \frac{a_{x} t^{2}}{2}

, where

S_{x}

– total distance,

S_{0 X}

- initial distance,

v_{x}

- velocity,

a_{x}

- acceleration.

According orientational homogeneity

S_{x} ≐ l_{x}

S_{0 X} ≐ l_{x}

v_{x} t ≐ l_{x} l_{0} ≐ l_{x}

\frac{a_{x} t^{2}}{2} ≐ \frac{l_{x}}{l_{0}} {(l_{0})}^{2} ≐ l_{x}

The orientation of derived physical variables, such as kinetic energy, can be determined by properly assigning orientation to primitive variables and applying the corresponding multiplication rules:

K E = \frac{m v_{x}^{2}}{2} + \frac{m v_{y}^{2}}{2} + \frac{m v_{z}^{2}}{2}

K E ≐ l_{0} l_{x} l_{x} + l_{0} l_{y} l_{y} + l_{0} l_{z} l_{z}

K E ≐ l_{0} l_{0} + l_{0} l_{0} + l_{0} l_{0} ≐ l_{0}

Consider the orientation of an angle

α

in the x-y plane. Because,

\tan (α) ≐ \frac{l_{y}}{l_{x}}

and

\lim_{α \to 0} (\tan (α)) = α

we deduce that

α ≐ \frac{l_{y}}{l_{x}} ≐ l_{z}

and an angular velocity

ω_{x y} = \frac{Δ α}{Δ t} ≐ l_{z}

Let us take series:

sine

(α) = α - \frac{α^{3}}{3!} + \frac{α^{5}}{5!} \dots

, cosine

(α) = 1 - \frac{α^{2}}{2!} + \frac{α 4}{4!} \dots

α

has any orientation, then sine(

α

) would also have that orientation, while the cosine(

α

) would be an orientationless quantity. This is because the sine function involves the odd powers of

α

, while the cosine function involves the even powers of

α

Siano demonstrated that orientational symbols have an algebra defined by the multiplication table for the orientation symbols, which is as follows:

\begin{matrix} l_{0} & l_{x} & \begin{matrix} l_{y} & l_{z} \end{matrix} \\ l_{0} & l_{0} & l_{x} & \begin{matrix} l_{y} & l_{z} \end{matrix} \\ l_{x} & l_{x} & l_{0} & \begin{matrix} l_{z} & l_{y} \end{matrix} \\ \begin{matrix} l_{y} \\ l_{z} \end{matrix} & \begin{matrix} l_{y} \\ l_{z} \end{matrix} & \begin{matrix} l_{z} \\ l_{y} \end{matrix} & \begin{matrix} \begin{matrix} l_{0} \\ l_{x} \end{matrix} & \begin{matrix} l_{x} \\ l_{0} \end{matrix} \end{matrix} \end{matrix}

and rules:

\begin{matrix} l_{o} = \frac{1}{l_{o}} & l_{x} = \frac{1}{l_{x}} \\ l_{y} = \frac{1}{l_{y}} & l_{z} = \frac{1}{l_{z}} \end{matrix}

Based on the above, the product of two orientated physical quantities has an orientation as follows:

l_{o} l_{x} = l_{x} l_{o} = l_{x}

l_{o} l_{y} = l_{y} l_{o} = l_{y}

l_{o} l_{z} = l_{z} l_{o} = l_{z}

l_{x} l_{x} = l_{y} l_{y} = l_{z} l_{z} = l_{0}

If a source code contains variables that represent physical quantities with orientations, we can use the property of orientational homogeneity as a software invariant. By applying orientational homogeneity, we can transform the source code into a set of lemmas. Multiplicative operations, such as multiplication and division, introduce new physical orientations. On the other hand, additive operations such as addition, subtraction, and relational operators (e.g., =, <, ≤, >, ≥, !=) serve as checkpoints for verifying orientational homogeneity.

2.3. Examples of software formal verifications

Example 1. Consider the expression

F = m a

, where

F

is a force with physical units of [kg m s^-2],

m

is the mass in [kg], and

a

is the acceleration in [m s^-2]. This expression allows us to derive the orientation and dimension of the product

m a

. If

m

is orientationless (denoted by

m ≐ l_{0}

) and

a

is in the x-direction (denoted by

a ≐ l_{x}

), then

F

has the x-orientation. If

m

has units of [kg] and

a

has units of [m s^-2], then the dimensions of the result are [kg m s^-2]. The assignment operation "=", which is also known as the equality operator, acts as a checkpoint for our software invariants. It ensures that the physical orientation of

F

is equal to the physical orientation of

m a

, and that the physical dimensions of

F

are equal to the physical dimensions of the result.

Example 2. Consider the expression

S = S_{0} + v t + \frac{a t^{2}}{2}

, where

S

represents the total distance,

S_{0}

is the initial distance,

v

is the velocity,

a

is the acceleration, and t is the time. This expression generates two new physical dimensions and orientations:

v t

and

\frac{a t^{2}}{2}

. The second "+" operation checks the dimensions and orientations of

v t

and

\frac{a t^{2}}{2}

. The first "+" operation checks the homogeneity of

S_{0}

and the result of the previous operation. Finally, the assignment operator "=" checks the homogeneity of

S

and the result of the previous operation. By checking the homogeneity of these variables and operations, we can ensure that the physical dimensions and orientations are consistent throughout the expression.

Example 3. When calling procedures and functions, it is not always possible to check the physical dimensions & orientation of the arguments. However, for function signatures such as Type1 someFunction2(Type2 x...), where Type1 and Type2 have information about the physical dimensions and orientations of their arguments, it is possible to check the physical dimensions and orientations of the arguments. Each argument of a function generates a special lemma that can be used to prove dimensional and orientational homogeneities. Only after proving all the lemmas can we prove the correctness of the function call. It is important to note that arguments of exponential and logarithmic functions must be dimensionless and orientationless to preserve dimensional and orientational homogeneities. On the other hand, arguments of trigonometric functions such as sine(x), cosine(x), and tan(x) must be orientated to preserve orientational homogeneity, while also being dimensionless to preserve dimensional homogeneity. The proposed method allows for the checking of physical dimensions and orientations in software units. Repeating this checking helps to ensure the correctness of the software system.

Example 4. Let us take a look at Euler’s rotation equations [26], which have various applications in fields such as cyber-physical systems (CPS) and the Internet of Things (IoT), including unmanned cars, helicopters, and other aerial vehicles.

The general vector form of the equations is

I \dot{ω} + ω \times (I ω) = M

, where M represents the applied torques and

I

is the inertia matrix. The vector

\dot{ω}

represents the angular acceleration.

In orthogonal principal axes of inertia coordinates the equations become

\{\begin{matrix} I_{x} {\dot{ω}}_{x} + (I_{z} - I_{y}) ω_{y} ω_{z} = M_{x} \\ I_{y} {\dot{ω}}_{y} + (I_{x} - I_{z}) ω_{z} ω_{x} = M_{y} \\ I_{z} {\dot{ω}}_{z} + (I_{y} - I_{x}) ω_{x} ω_{y} = M_{z} \end{matrix}

(1)

where

M_{x}

M_{y}

M_{z}

are the components of the applied torques [kg m²s^-2];

I_{x}

I_{y}

I_{z}

are the principal moments of inertia [kg m²];

ω_{x}

ω_{y}

ω_{z}

are the components of the angular velocities [s^-1];

{\dot{ω}}_{x} = \frac{d ω_{x}}{d t}

{\dot{ω}}_{y} = \frac{d ω_{y}}{d t}

{\dot{ω}}_{z} = \frac{d ω_{z}}{d t}

have dimension [s^-2]. However,

M_{k}

I_{k}

ω_{k}

{\dot{ω}}_{k}

have different orientations

l_{k}

, where

k = x, y, z

We can verify the dimensional homogeneity of equation (1), but it is not possible to identify all defects. This is because certain quantities have the same dimensions and cannot be distinguished solely based on their units. For example, the dimensions of the moments of inertia (

I_{x}

I_{y}

I_{z}

) are [kg m²] and angular velocities (

ω_{x}

ω_{y}

ω_{z}

) are [s^-1], and the dimensions of the angular acceleration components (

{\dot{ω}}_{x} = \frac{d ω_{x}}{d t}

{\dot{ω}}_{y} = \frac{d ω_{y}}{d t}

{\dot{ω}}_{z} = \frac{d ω_{z}}{d t}

) are [s^-2], since angles are dimensionless. Therefore, while dimensional analysis can help identify some potential issues with the equation, it may not be able to catch all possible defects.

In the context of equation (1), the parameters (

M_{x}

M_{y}

M_{z}

etc.) may have different orientations or values, which can help in detecting defects.

Furthermore, checking both the dimensional and orientational homogeneities of an equation can improve our ability to detect defects and ensure its correctness. This approach can be useful in formal verification of CPS and IoT software, as it can help identify potential issues before they lead to real-world problems.

Let us assess the probability of detecting a software defect using both DA and OA.

2.4. Software defect detection models

2.4.1. General software defect detection model

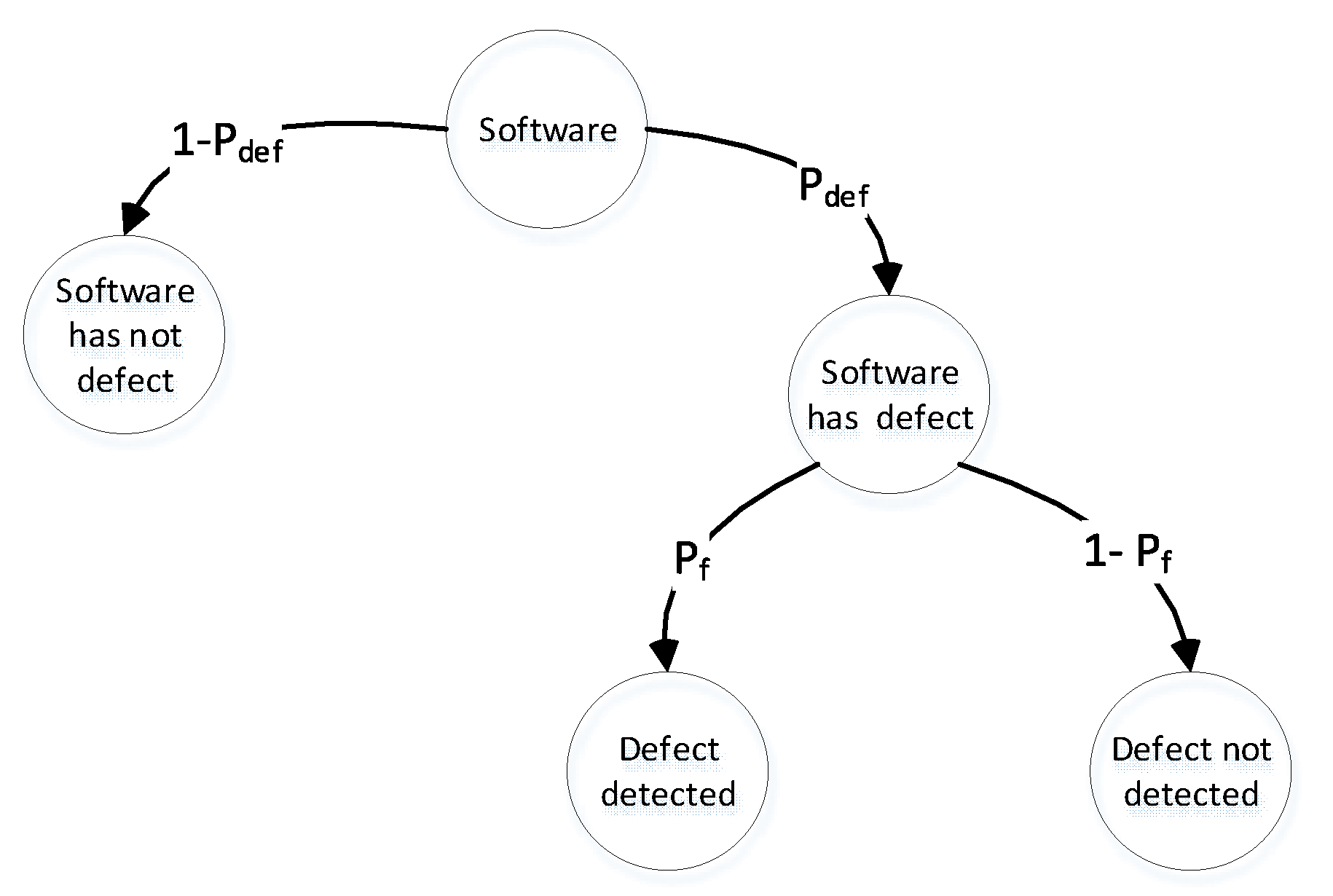
To simplify the analysis, we assume that the software system can only have one defect with a probability of

P_{d e f}

. The model starts with the initial event state of "Software" and branches out into two possible outcomes at the next level: "Software has a defect" and "Software does not have a defect", with probabilities of

P_{d e f}

and

1 - P_{d e f}

, respectively. A tree diagram can be utilized to represent the event space of this defect detection process, as shown in Figure 2.

In the state "Software has defect", our focus shifts to detecting the defect. At the third level, the model branches out into two possible outcomes: "Defect detected" and "Defect not detected", with probabilities of

P_{f}

and

1 - P_{f}

, respectively.

To define the conditional probability of software defect detection, we use the following formula:

η = \frac{P_{d e f} P_{f}}{P_{d e f} P_{f} + P_{d e f} (1 - P_{f})} = \frac{P_{f}}{P_{f} + (1 - P_{f})} = P_{f}

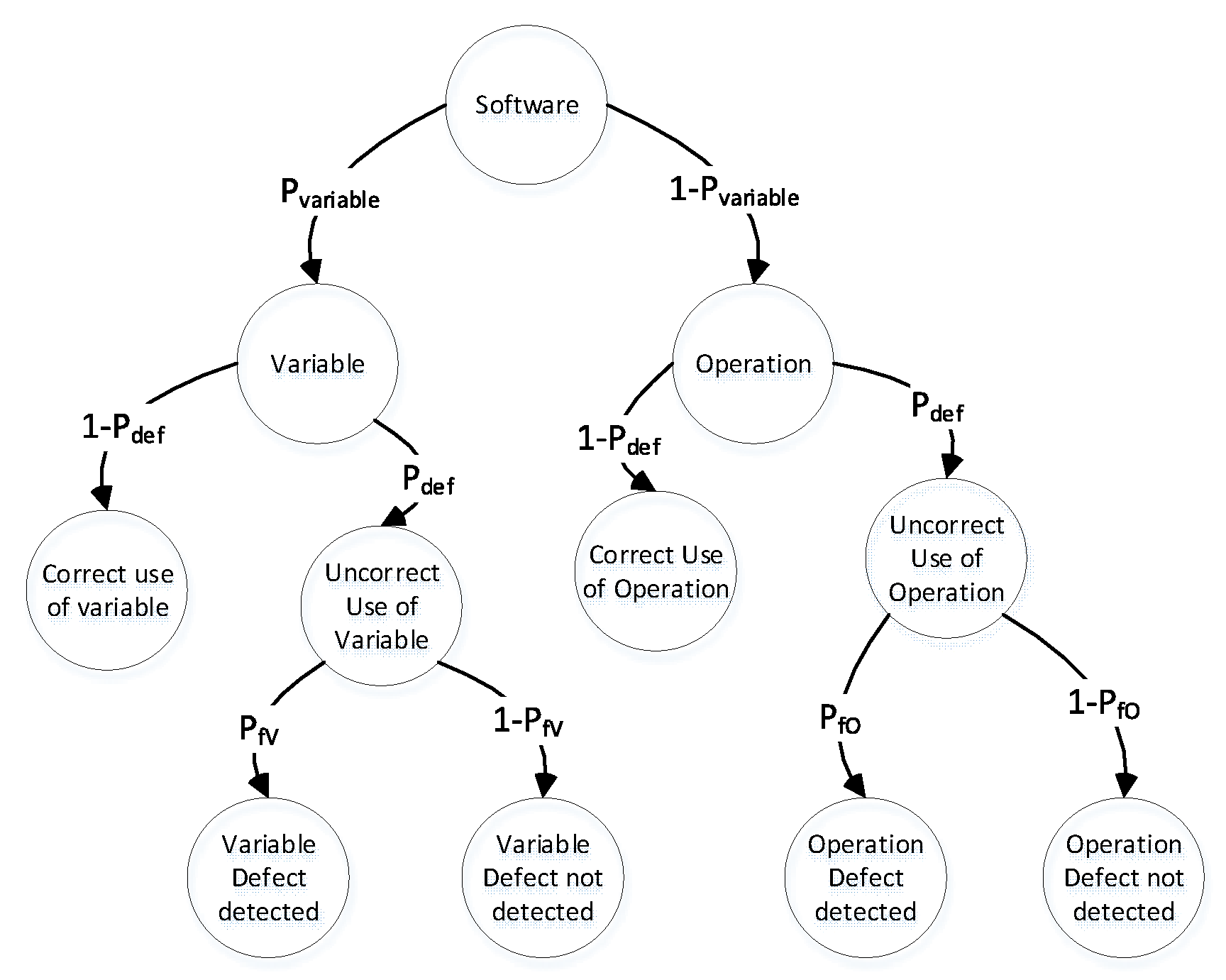
We can also introduce a more complex general software defect detection model (see Figure 3), which accounts for two types of defects: variable defects and operation defects. Despite the presence of multiple types of defects, the model still assumes that there is only one defect present in the system at any given time.

In this more complex model, the software system can have two types of defects: variable defects and operation defects. A "Variable defect" occurs when there is an incorrect usage of a variable in the code, such as using the wrong variable name. An "Operation defect" occurs when there is an incorrect usage of an operation in the code, such as using the wrong operator symbol. Despite the presence of these two types of defects, the model still assumes that only one defect is present in the system at any given time.

In this more complex model, the initial event state is "Software". At the second level, the model branches out into two possible outcomes: "Variable" and "Operation", with probabilities of

P_{var}

and

1 - P_{var}

, respectively.

The "Variable" state has two potential outcomes at the next level: "Correct use of variable" and "Incorrect use of variable", with probabilities of

1 - P_{d e f}

and

P_{d e f}

, respectively.

The "Incorrect use of variable" state then branches out into two possible outcomes at the next level: "Variable defect detected" and "Variable defect not detected", with probabilities of

P_{v f}

and

1 - P_{v f}

, respectively. Here,

P_{v f}

represents the probability of detecting a variable defect in the source code.

In addition to the "Variable" state, the model also has an "Operation" state, which has two possible outcomes at the next level: "Correct use of operation" and "Incorrect use of operation", with probabilities of

1 - P_{d e f}

and

P_{d e f}

, respectively.

The "Incorrect use of operation" state then branches out into two possible outcomes at the next level: "Operation defect detected" and "Operation defect not detected", with probabilities of

P_{o f}

and

1 - P_{o f}

, respectively. Here,

P_{o f}

represents the probability of detecting an operation defect in the source code.

The conditional probability of a software defect can be defined as:

η = \frac{P_{var} P_{d e f} P_{v f} + (1 - P_{var}) P_{d e f} P_{o f}}{P_{var} P_{d e f} P_{v f} + P_{var} P_{d e f} (1 - P_{v f}) + (1 - P_{var}) P_{d e f} P_{o f} + (1 - P_{var}) P_{d e f} (1 - P_{o f})}

η = P_{var} P_{v f} + (1 - P_{var}) P_{o f}

(2)

As per the expression (2), the conditional probability of software defect detection depends on the probability of the software variables used in the source code and the conditional probabilities of detecting defects (defects of operations and defects of variables). We can determine the value of

P_{var i a b l e}

by analyzing the software code statically, i.e., without executing the code. However, to determine the value of

P_{v f}

, we would need to build additional software defect detection models.

2.4.2. Simple model detection of incorrect use of variable based on DA

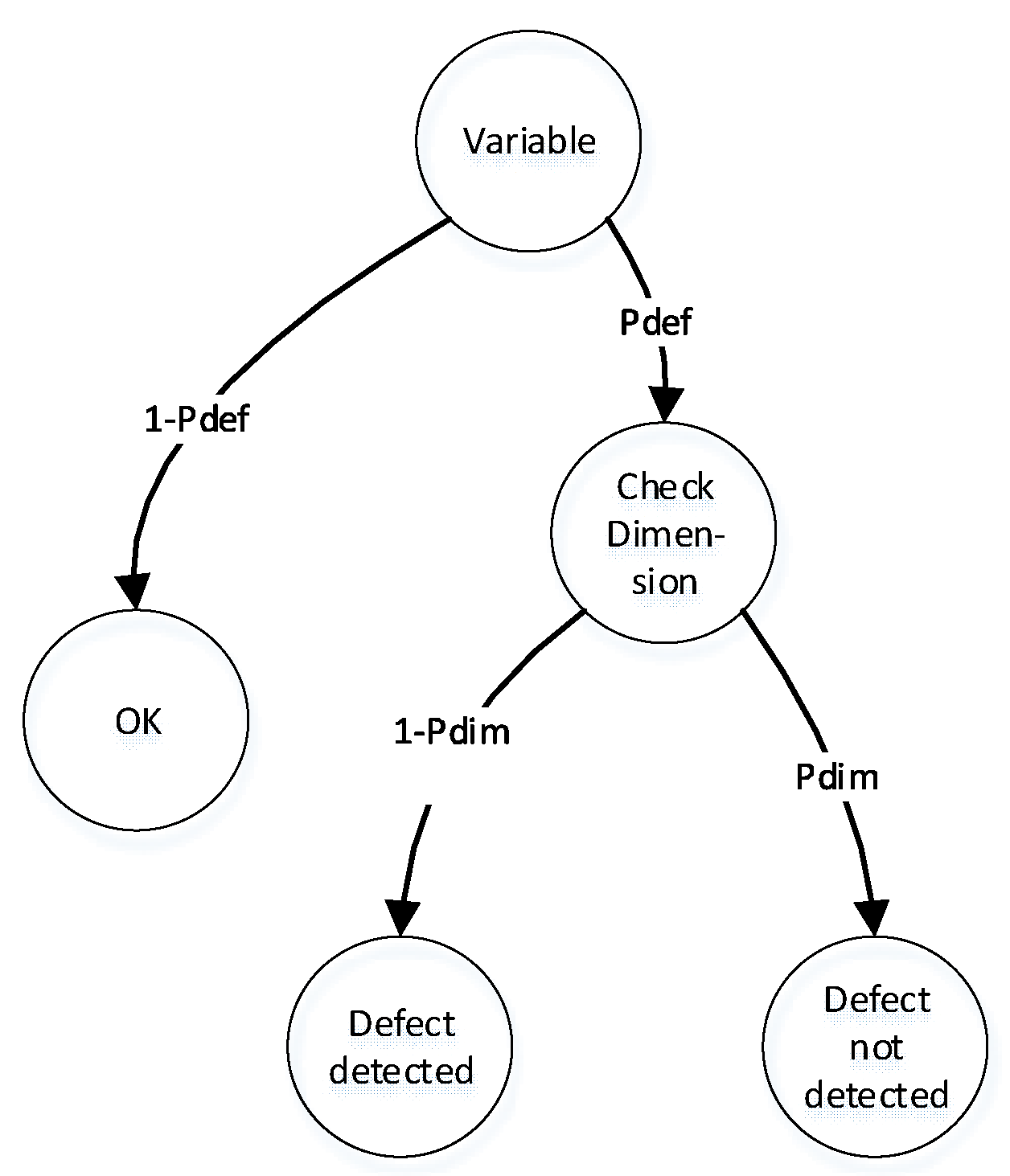
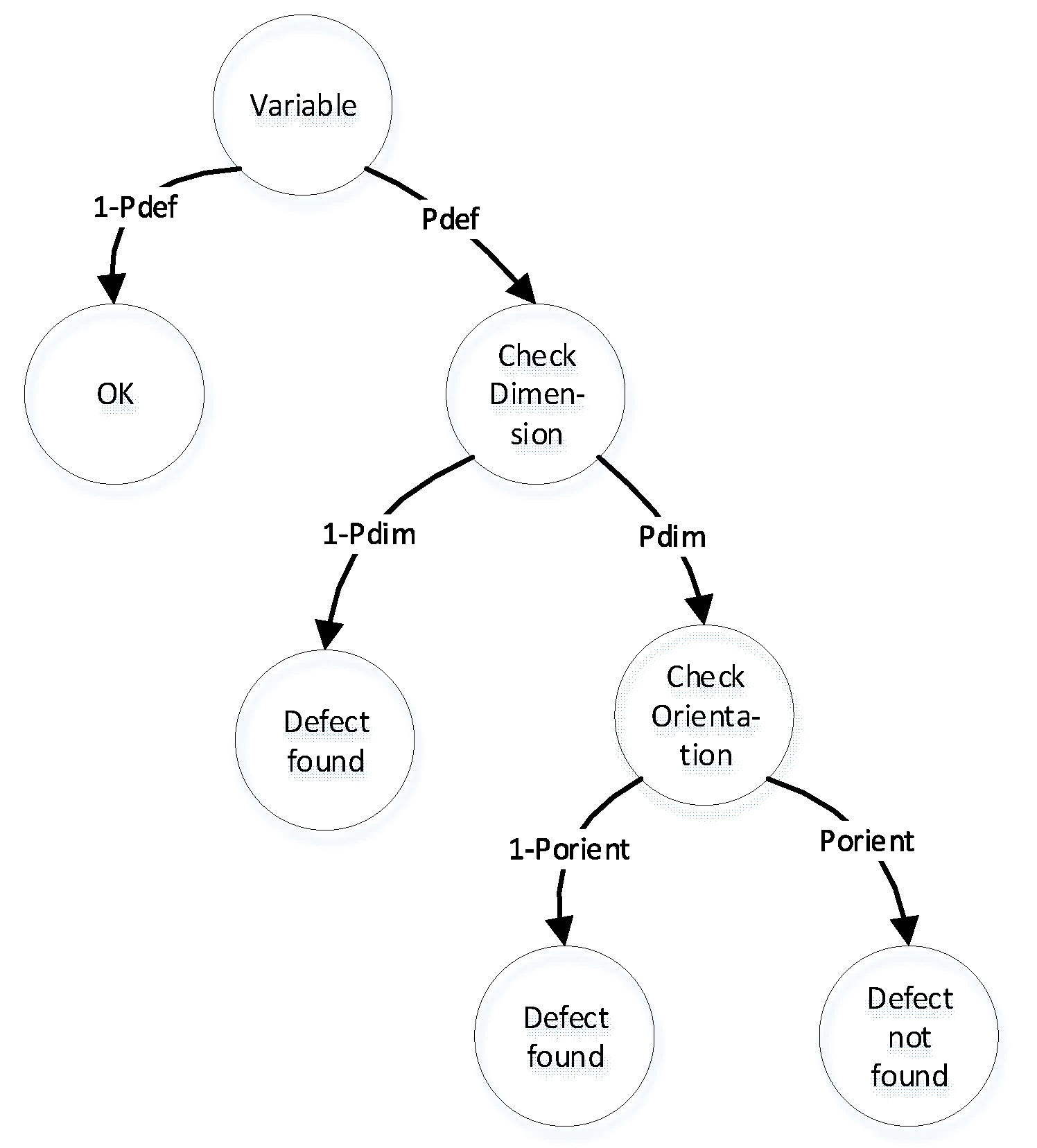
Next, we present the Simple model for detection of incorrect use of variable based on DA, illustrated in Figure 4.

This model has an initial state of ’Variable’. The initial state has two transitions to states ’OK’ and ’Check dimension’ with probabilities

1 - P_{d e f}

and

P_{d e f}

, respectively. In the state ’Check dimension’, we can evaluate the required physical dimension of the variable using dimensional analysis, such as length, mass, time, thermodynamic temperature, etc.

If fact physical dimension equal to needed physical dimension we can‘t detect the software defect. In other case we can detect the software defect. This case has probabilities

P_{\dim}

and

1 - P_{\dim}

, where

P_{\dim}

is a probability of event when two random variables have same physical dimension.

Thus, to determine the conditional probability of defect detection of incorrect use of a program variable, we need to know the probability

P_{\dim}

Let us define the conditional probability of defect detection of incorrect use of a program variable as follows

η = 1 - P_{\dim}

(3)

Let us consider a set of distinct software variables

\{{var}_{1} \dots {var}_{N v}\}

and a set of diverse physical dimensions

\{\dim_{1} \dots \dim_{N d}\}

, where

N_{V}

represents the cardinality of set

\{{var}_{i}\}

and

N_{d}

represents the cardinality of set

\{\dim_{j}\}

To depict the relationship between these variables and dimensions, we can make use of an

N

-matrix (4):

\begin{matrix} \dim_{1} & \dim_{2} & \dim_{3} & \dim_{4} & \dim_{5} & \dim_{6} & \dots & \dim_{N d - 1} & \dim_{N d} \\ {var}_{1} & n_{11} & 0 & 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ {var}_{2} & n_{21} & 0 & 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ {var}_{3} & 0 & n_{31} & 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ {var}_{4} & 0 & 0 & n_{43} & 0 & 0 & 0 & \dots & 0 & 0 \\ {var}_{5} & 0 & 0 & 0 & n_{54} & 0 & 0 & \dots & 0 & 0 \\ {var}_{6} & 0 & 0 & 0 & n_{64} & 0 & 0 & \dots & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ {var}_{N_{V} - 1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & n_{N_{V} - 1, N d} \\ {var}_{N_{V}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & n_{N_{V}, N d} \end{matrix}

(4)

The equation for the total quantity of usages of all software variables which have the same j dimension can be written as:

N_{V A R j} = \sum_{i = 1}^{N_{V}} n_{i j}

(5)

where n_ij represents the total quantity usage of i-variable which has a j-physical dimension, and N_V is the cardinality set of software variables.

Equation (5) shows that the total number of variable usages in the code:

N_{V A R} = \sum_{i = 1}^{N_{V}} \sum_{j = 1}^{N_{D}} n_{i j}

(6)

To define the probability of choosing i-variable and j-variable with the same dimensions, we can use the total number of usages of variables with the j-physical dimension and the total number of usages of all variables in the code:

D_{i j} = \frac{n_{i j}}{N_{V A R}} \frac{(\sum_{i = 1}^{N_{V}} n_{i j}) - n_{i j}}{N_{V A R} - n_{i j}}

(7)

According to (7), the probability of choosing two random variables that have the same physical dimension is given by the following equation:

P_{D i m} = \sum_{i = 1}^{V} \sum_{j = 1}^{K} (\frac{n_{i j}}{N_{V A R}} \frac{(\sum_{k = 1}^{V} n_{k j}) - n_{i j}}{N_{V A R} - n_{i j}})

(8)

Based on (1) and (8), we can define the conditional probability of software defect detection as:

η_{D} = 1 - \sum_{i = 1}^{N_{V}} \sum_{j = 1}^{N_{d}} (\frac{n_{i j}}{N_{V A R}} \frac{(\sum_{k = 1}^{N_{V}} n_{k j}) - n_{i j}}{N_{V A R} - n_{i j}})

(9)

where

n_{i j}

– the item of

N

matrix – the quantity of using of i-variable which has j-physical dimension.

For increasing of conditional probability detection of incorrect use of software variables we need to use other independent property of variables. Using additional independent properties of variables can help increase the conditional probability detection of incorrect use of software variables. This is because using multiple properties helps to reduce the chance of false positives and increase the reliability of the detection model.

2.4.3. Simple model detection of incorrect use of variable based on OA

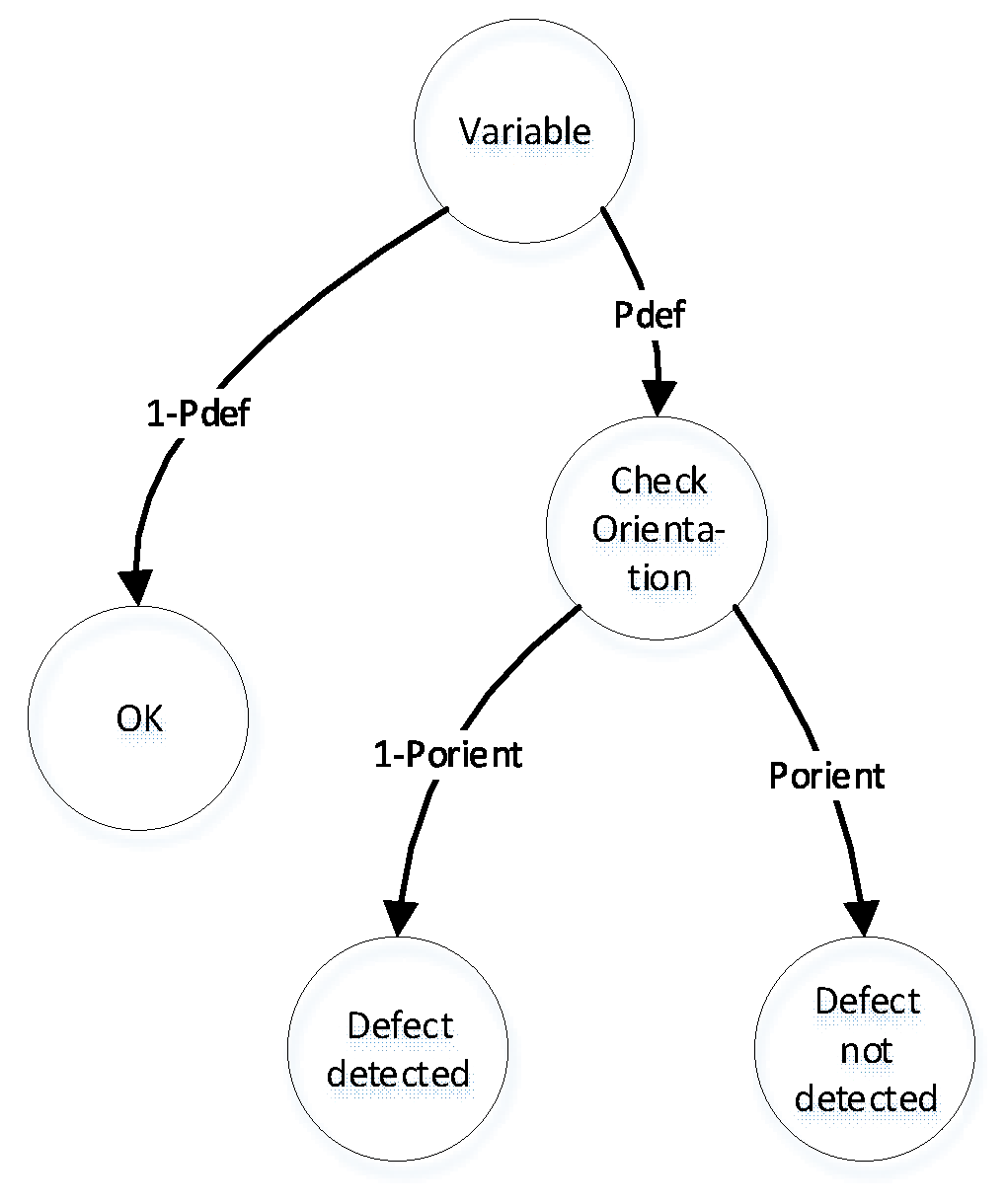
In many cases, variables in CPS or IoT have not only physical dimensions but also orientation information, which can be utilized to enhance the software quality of these systems. Therefore, we introduce a Simple model for the detection of incorrect variable use based on OA (see Figure 5).

According Figure 5 the initial state of model is “Variable”. This state has two transitions to states ’OK’ and ’Check orientation’ with probabilities

1 - P_{d e f}

and

P_{d e f}

, respectively. In the state ’Check orientation’, we can evaluate the required physical orientation of the variable using orientation analysis, such as

l_{0}

l_{x}

l_{y}

and

l_{z}

. If the physical orientation of the variable matches the required orientation, we cannot detect a software defect. However, if the physical orientation is different from the required orientation, we can detect a software defect.

This case has probabilities

P_{o r i e n t a t i o n}

and

1 - P_{o r i e n t a t i o n}

, where

P_{o r i e n t a t i o n}

is the probability that two randomly selected variables have the same physical orientation.

Now we need to define

P_{o r i e n t a t i o n}

This defect model is similar to the dimension defect model of variables. However, in this case, we have four different orientations and

N_{V}

different variables. We can describe the relation between variables and their orientation using an

M

M matrix:

\begin{matrix} l_{0} & l_{x} & \begin{matrix} l_{y} & l_{z} \end{matrix} \\ {var}_{1} & m_{11} & 0 & \begin{matrix} 0 & 0 \end{matrix} \\ {var}_{2} & m_{11} & 0 & \begin{matrix} 0 & 0 \end{matrix} \\ \begin{matrix} {var}_{3} \\ {var}_{4} \\ \begin{matrix} \dots \\ {var}_{N_{V}} \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} \dots \\ 0 \end{matrix} \end{matrix} & \begin{matrix} m_{11} \\ m_{11} \\ \begin{matrix} \dots \\ 0 \end{matrix} \end{matrix} & \begin{matrix} \begin{matrix} 0 \\ 0 \\ \begin{matrix} \dots \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ \begin{matrix} \dots \\ m_{_{N_{V}, 4}} \end{matrix} \end{matrix} \end{matrix} \end{matrix}

(10)

where

l_{k}

is a direction of orientation and k=0, x, y, z.

Because, every software variable (as a host of a physical value) has only one orientation, every i-row of

M

matrix has only one non zero number

m_{i k}

– the item of M matrix – the number of using of i-variable which has k-orientation.

That is why we can use the expression (8) for definition the condition probability of orientation defect detection (11)

η_{L} = 1 - \sum_{i = 1}^{N_{V}} \sum_{k = 0, x, y, z}^{} (\frac{n_{i k}}{N_{V A R}} \frac{(\sum_{n = 1}^{N_{V}} m_{n j}) - m_{i k}}{N_{V A R} - m_{i k}})

(11)

We can increase the conditional probability of software defect detection via concurrent using of DA & OA. Concurrently using DA and OA can increase the conditional probability of software defect detection because it allows for detecting both dimension and orientation defects in software variables. By combining these two methods, we can improve the accuracy of defect detection and reduce the likelihood of undetected defects.

2.4.3. Complex model of detection of incorrect use of variable via OA and DA

The Complex model of detection of incorrect use of variable via OA and DA describe on Figure 6

η_{D L} = \frac{P_{d e f} (1 - P_{\dim}) + P_{d e f} P_{\dim} (1 - P_{o r i e n t a t i o n})}{P_{d e f} (1 - P_{\dim}) + P_{d e f} P_{\dim} (1 - P_{o r i e n t a t i o n}) + P_{d e f} P_{\dim} P_{o r i e n t a t i o n}}

η_{D L} = 1 - P_{\dim} P_{o r i e n t a t i o n} or η_{D L} = 1 - (1 - η_{D}) (1 - η_{L})

(12)

After substitution expressions (9,11) in the (12) we have

η_{D L} = 1 - \sum_{i = 1}^{N_{V}} \sum_{j = 1}^{4} (\frac{m_{i j}}{N_{V A R}} \frac{(\sum_{k = 1}^{N_{V}} m_{k j}) - m_{i j}}{N_{V A R} - m_{i j}}) \sum_{i = 1}^{N_{V}} \sum_{j = 1}^{N_{d}} (\frac{n_{i j}}{N_{V A R}} \frac{(\sum_{k = 1}^{N_{V}} n_{k j}) - n_{i j}}{N_{V A R} - n_{i j}})

(13)

To evaluate the correctness of the conditional probability of software defect detection using DA and OA, we need a model for detecting incorrect use of operations. This model should take into account the types of operations that are commonly used in CPS and IoT software, as well as their potential incorrect use.

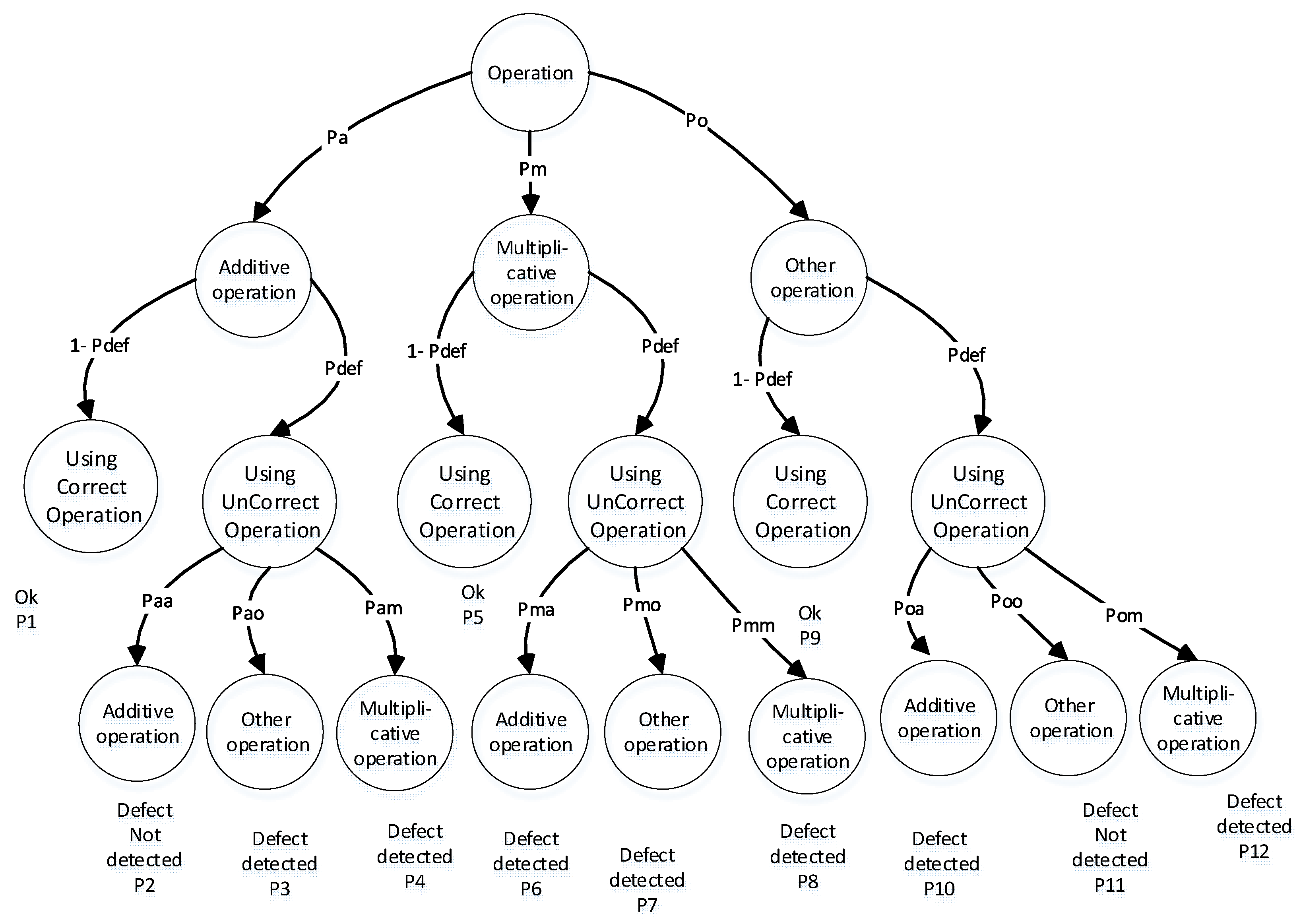
2.4.4. Model of detection of incorrect use of operation via OA and DA

Let us consider three subsets of C++ operations: “additive” (A), “multiplicative” (M), and “other” (O) operations

A={"+", "-", "=", "==", ">=", "<=", "!=", "<", ">", "++", "--", ".*", "->*", ",", ".", "->", "+=", "-=", "**"},

M={"*", "/", "%", "*=", "/=", "%=" },

O={"||", "&&", "&", "|", "^", "~", "<<", ">>", "::", "?", "<<=", ">>=", "&=", "|=", "^=" }

(14)

In addition, we are given three probabilities associated with the utilization of this operation in the source code, namely,

P_{a}

P_{m}

, and

P_{o}

P_{a} + P_{m} + P_{o} = 1

(15)

Let us define

P_{a}

P_{m}

P_{o}

follows as

P_{a} = \frac{N_{a}}{N_{a} + N_{m} + N_{o}}, P_{m} = \frac{N_{m}}{N_{a} + N_{m} + N_{o}}, P_{o} = \frac{N_{o}}{N_{a} + N_{m} + N_{o}},

(16)

where

N_{a}

N_{m}

N_{o}

– total number of operations in file.

In this case, we can build a tree diagram - a model of detection of incorrect use of operation via DA & OA. The model allows us to define the conditional probability of operation defect detection (see Figure 7).

This model also has an initial state of "Operation" and states of "Additive operation", "Multiplicative operation", and "Other operation". After a random mutation of operations, any operation can be replaced by another operation. These events have probabilities

P_{a a}

P_{a o}

P_{a m}

P_{m a}

P_{m o}

P_{m m}

P_{o a}

P_{o o}

P_{o m}

. Additionally, we can conclude that

P_{a a} + P_{a m} + P_{a o} = 1

P_{m a} + P_{m m} + P_{m o} = 1

P_{o a} + P_{o m} + P_{o o} = 1

. We can define the conditional probability of detecting incorrect use of software operations as:

μ = \frac{P_{3} + P_{4} + P_{6} + P_{7} + P_{8} + P_{10} + P_{12}}{P_{2} + P_{3} + P_{4} + P_{6} + P_{7} + P_{8} + P_{10} + P_{11} + P_{12}}

where

P_{2} = P_{a} P_{d e f} P_{a a}

P_{3} = P_{a} P_{d e f} P_{a o}

P_{4} = P_{a} P_{d e f} P_{a m}

P_{6} = P_{m} P_{d e f} P_{m a}

P_{7} = P_{m} P_{d e f} P_{m o}

P_{8} = P_{m} P_{d e f} P_{m m}

P_{10} = P_{o} P_{d e f} P_{o a}

P_{11} = P_{o} P_{d e f} P_{o o}

P_{12} = P_{o} P_{d e f} P_{o m}

Because,

P_{a} + P_{o} + P_{m} = 1

P_{a a} \approx P_{a}

and

P_{o o} \approx P_{o}

μ \approx 1 - P_{a}^{2} - P_{o}^{2}

(17)

3. Results

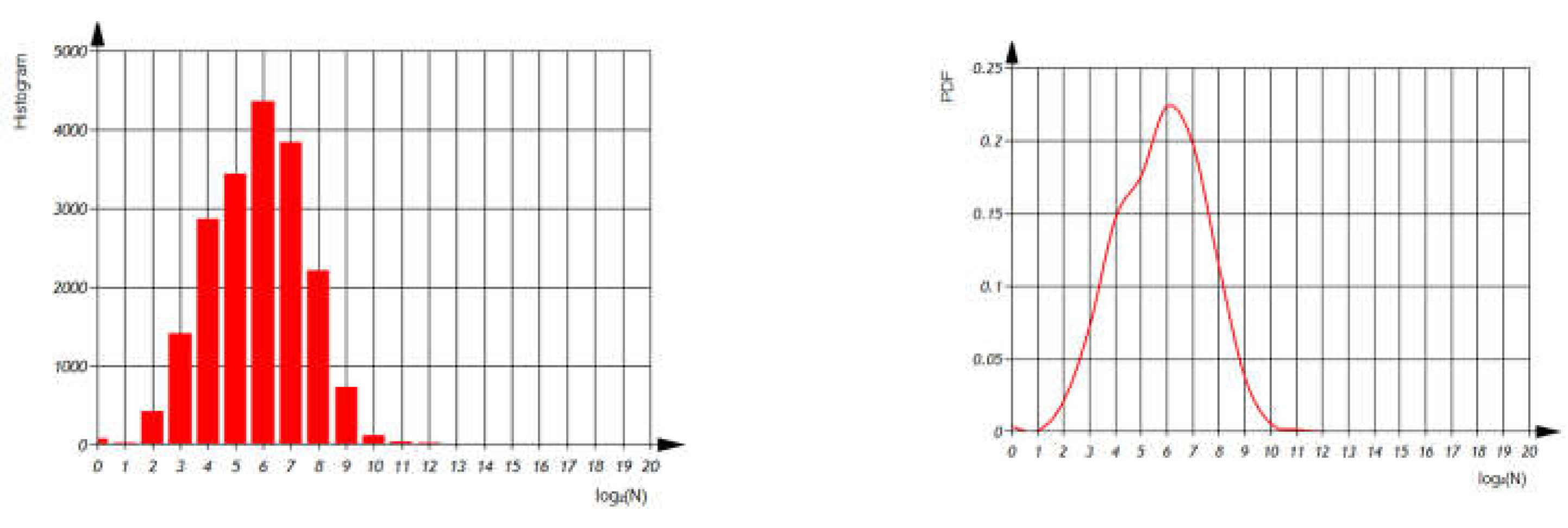
After analyzing the source code of Unmanned Aerial Vehicle Systems (total volume of 2 GBytes and a total number of files of 20,000) saved on GitHub using our own statistical analyzer, the statistical characteristics of the C++ source code were defined:

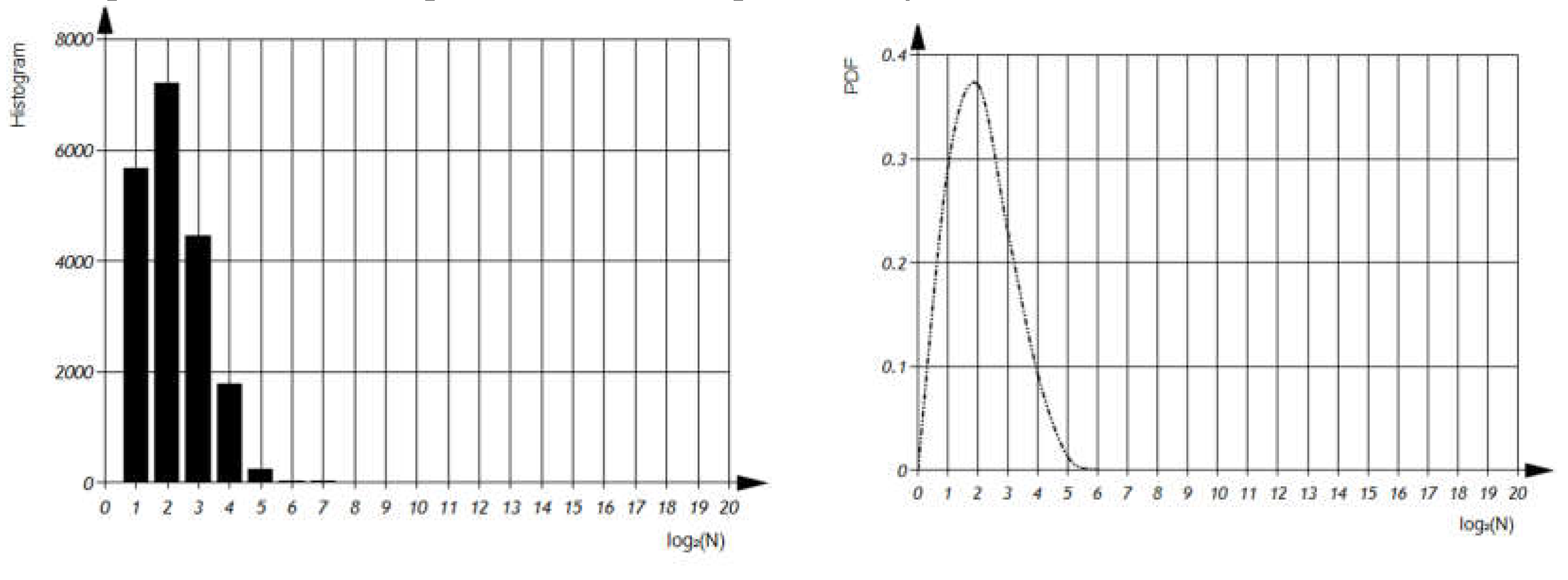
Distribution

N_{var}

– total number of different variables per file (Figure 8).

Distribution

N_{v f i}

- total number of i-variable use per file (Figure 9).

Because,

N_{v f i} = \sum_{j = 0, x, y, z}^{} n_{i j}

N_{v f i} = \sum_{j = 1}^{N d} m_{i j}

Total sum of entries in the columns equals 20000. The integral of the probability density function should be equal to one, as it represents the total probability distribution of the variable.

According to expression (13) and the distributions described in Figure 8 and Figure 9, as well as the uniform distribution for both

n_{i j}

and

m_{i j}

, we can obtain the

η_{D L}

shown in Figure 10.

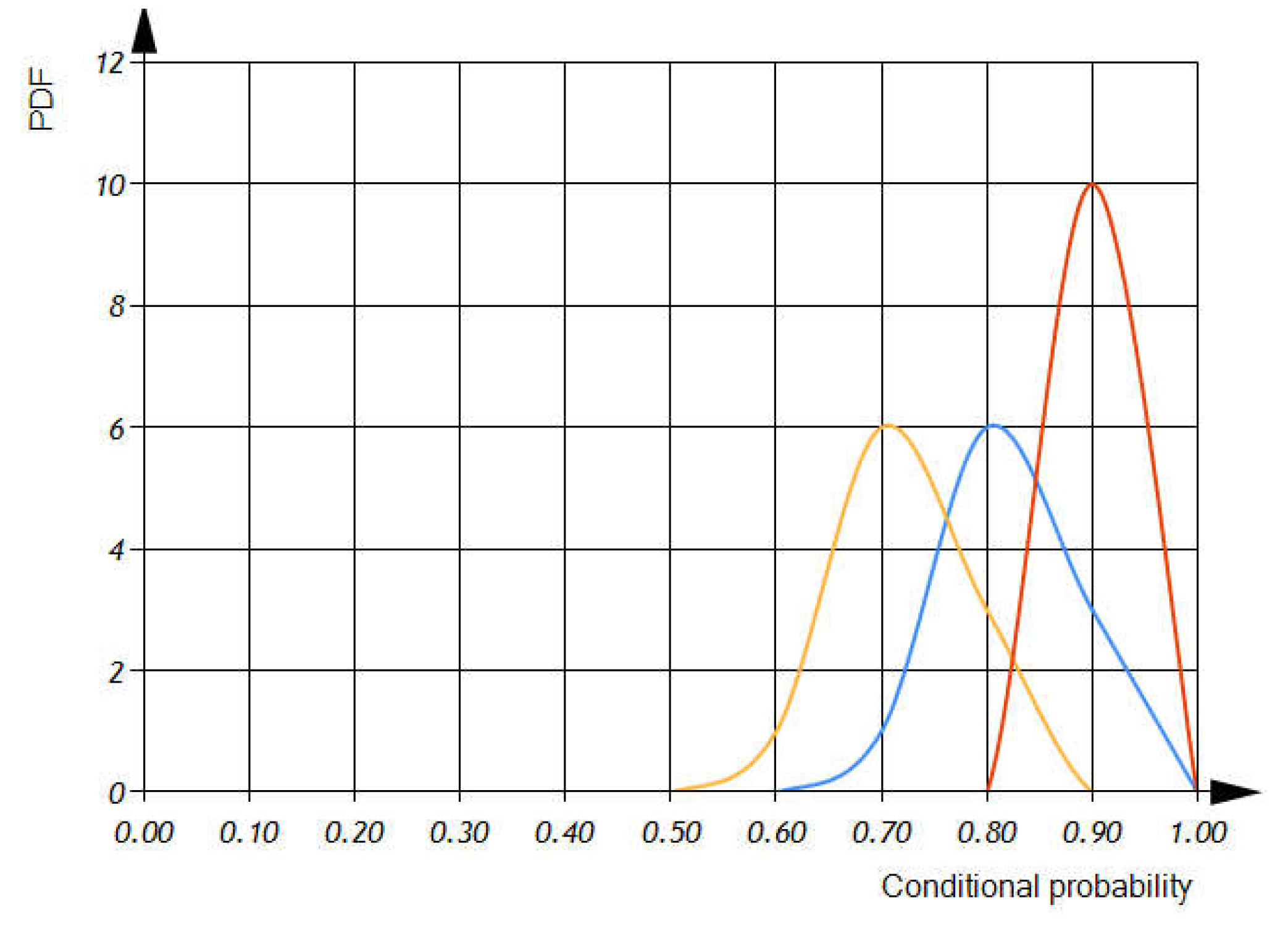
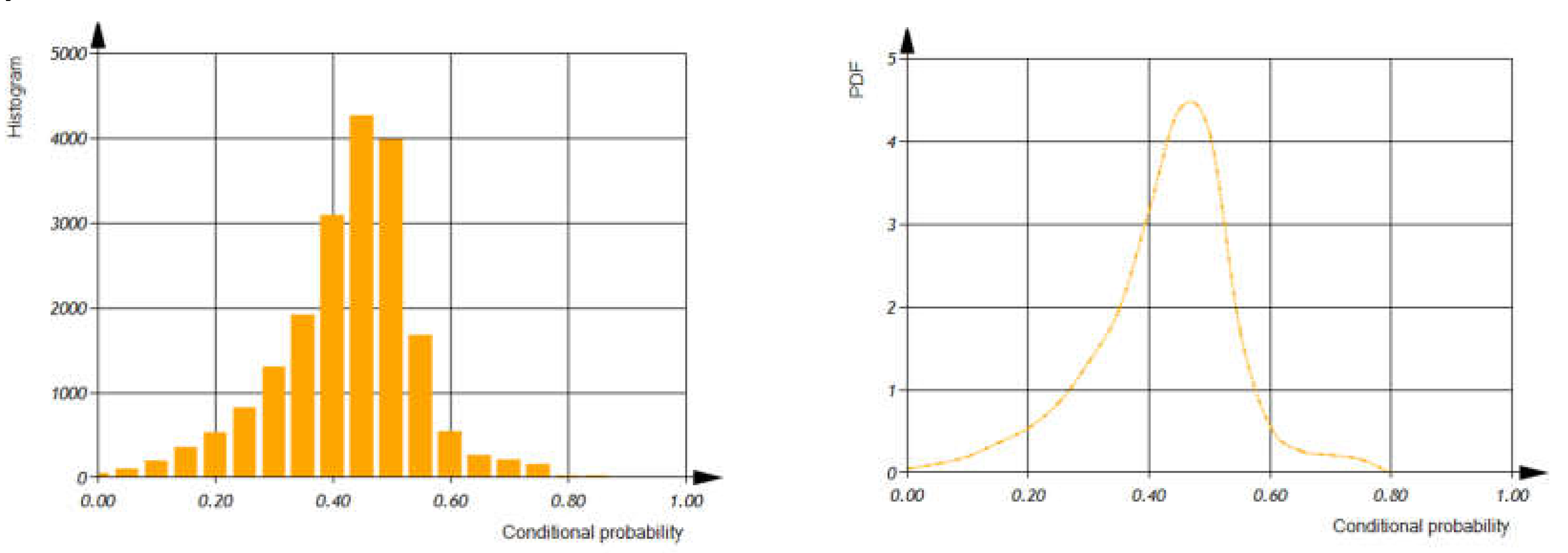
According to Figure 10 we can see that the mean value of the conditional probability of software defect detection through dimension analysis is 0.8, while the mean value of the conditional probability of software defect detection through orientational analysis is 0.7. Since OA and DA are independent, the mean value of the total conditional probability of software defect detection is 0.9.

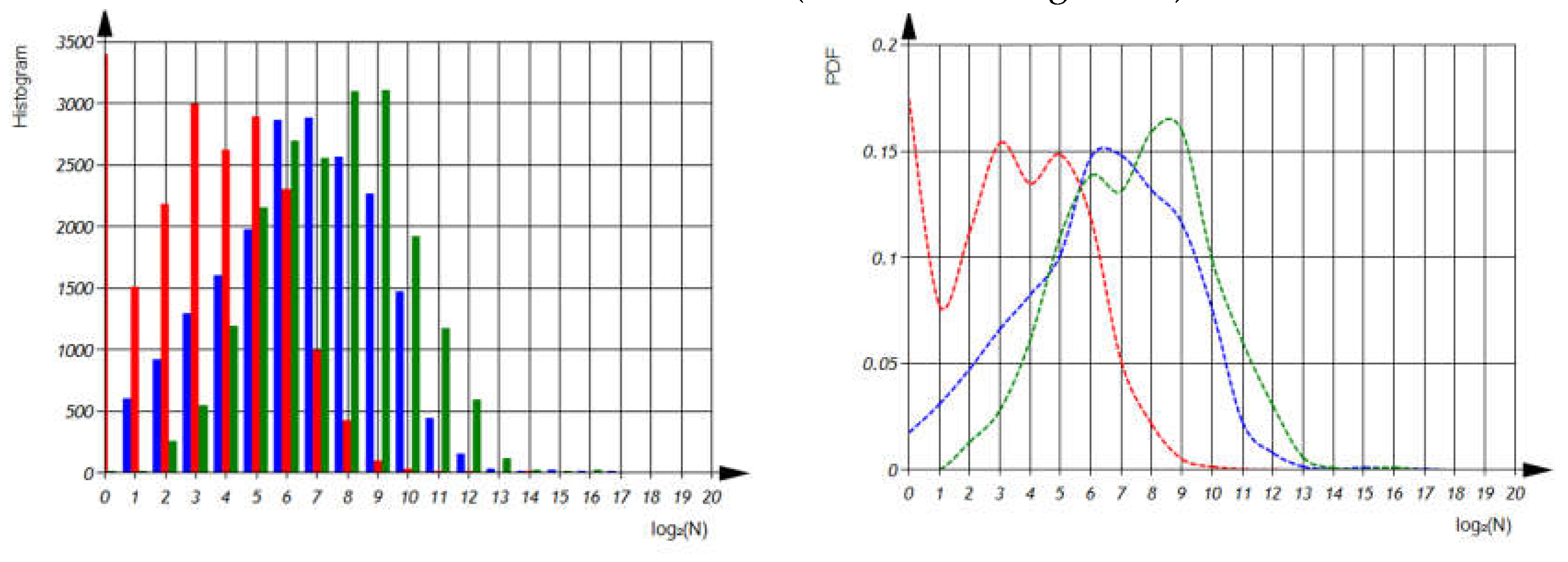
Based on the statistical data of C++ source code:

P_{a}

=0.309±0.161 [0.000... 0.999];

P_{m}

=0.056±0.056 [0.000... 0.636];

P_{o}

=0.635±0.155 [0.000... 0.992] and the conditional probability of detecting incorrect use of software operations as

\bar{μ} = 0.5

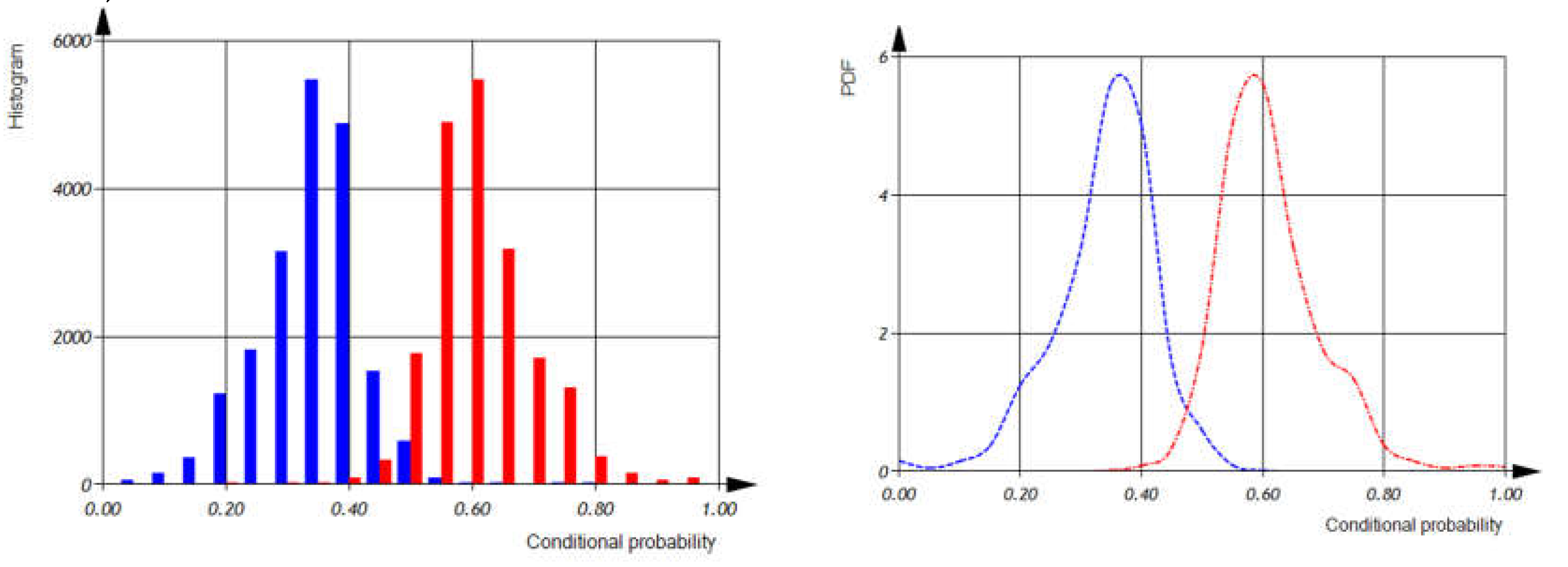
According to expression (16) and the distributions of

N_{a}

N_{m}

N_{o}

(as shown in Figure 11) we can calculate the distributions of

P_{a}

P_{m}

, and

P_{o}

(as shown in Figure 12).

According distributions of

P_{a}

P_{m}

, and

P_{o}

we can calculate the distribution of the conditional probability of operation defect detection (as shown in Figure 13). The mean value of the conditional probability is 0.45.

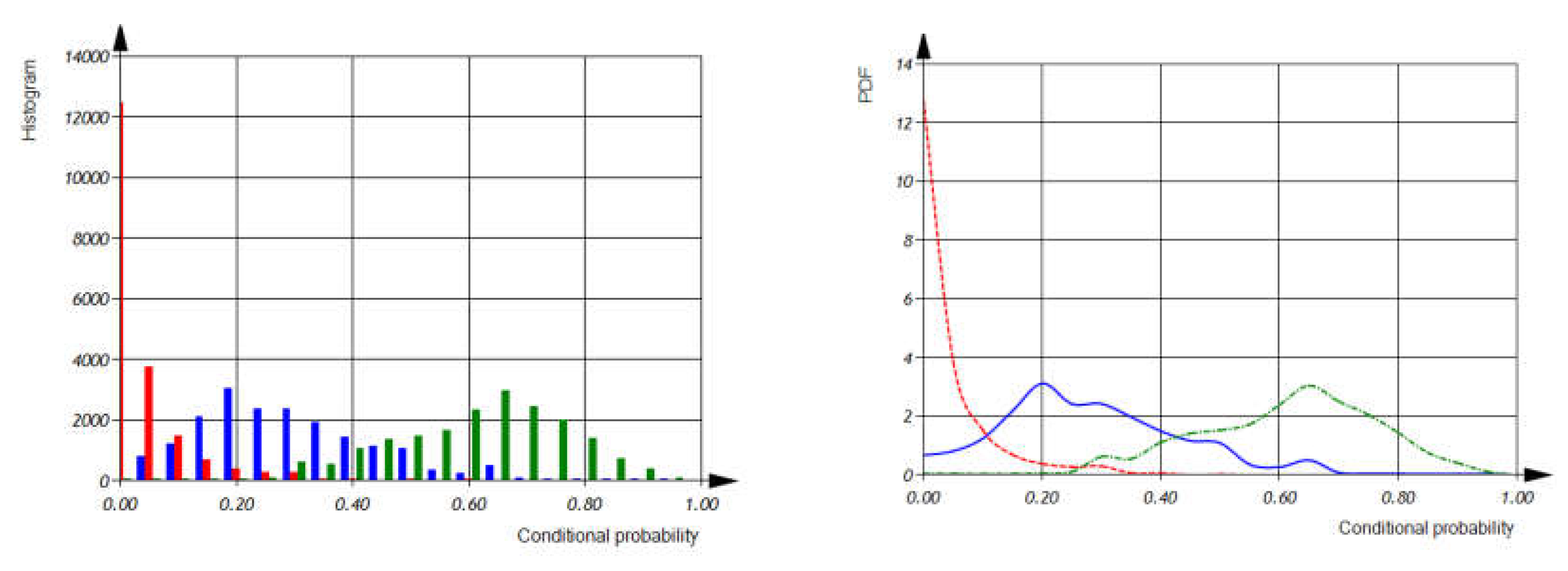
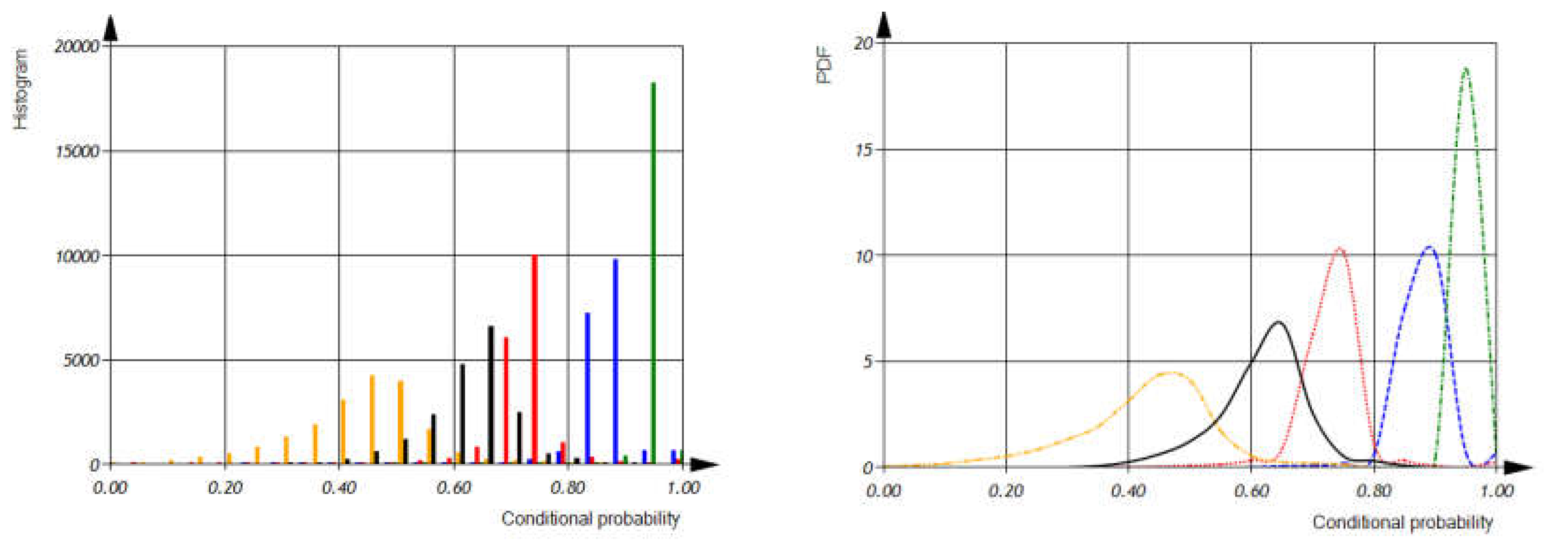
After analyzing real C++ code statistically, we built the distributions of

P_{o}

and

P_{V A R}

(as shown in Figure 14).

Now, we can calculate the conditional probability of software defect detection based on the real source code and the proposed defect models (see expression (2)). Let

η

be the conditional probability, then we have

η = P_{var} P_{v f} + (1 - P_{var}) P_{o f}

, where

P_{var}

- is conditional probability of variables in the source code,

P_{var} + P_{o p e r a t i o n} = 1

P_{v f}

- is conditional probability the defects detection of variable using defect in the source code,

P_{o f}

- is conditional probability the defects detection of operation using defect in the source code

In the next figure, Figure 15, we can see histograms of the conditional probabilities of defect detection.

The proposed method of formal software verification based on dimensional analysis and orientational analysis has demonstrated high effectiveness in detecting over 60% of software defects, including those related to incorrect usage of variables, operations, and functions.

4. Discussion

The proposed method of formal software verification based on dimensional analysis and orientational analysis appears to be an effective approach to detecting software defects. The fact that it can detect over 60% of software defects, including those related to incorrect usage of variables, operations, and functions, is noteworthy and suggests that it could be a valuable tool in software development.

However, it is important to note that no single method can detect all types of software defects, and different methods may be better suited for different types of defects. Thus, while the proposed method shows promise, it should be evaluated and compared to other approaches to determine its overall efficacy and limitations.

To fully assess its overall effectiveness and limitations, it is crucial to develop a concrete tool that can evaluate and compare the proposed method with other existing tools.

One of the imminent tasks is to create a type library for the formal verification of CPS and IoT software during compile time.

5. Conclusions

This article focuses on a formal software verification method based on software invariants derived from both dimensional and orientational analysis. By leveraging the independence of dimensional homogeneity and orientational homogeneity, this method leads to a significant improvement in software quality.

Analyzing real-world GitHub software for unmanned aerial vehicles (drones), the proposed method demonstrates a high level of effectiveness, detecting 90% of incorrect use of software variables and more than 50% of incorrect use of operations. The total conditional probability of defect detection is 60%.

However, the method has certain limitations, such as the need to know the physical dimensions and orientations of source variables at compile-time. Nonetheless, it offers several advantages, including improved programmer productivity, as programmers no longer need to spend time tracking down dimensional and orientational errors during development and run-time. Additionally, the method enables a comprehensive analysis of dimensional and orientational correctness during compile-time and run-time, including the correct use of software variables, operations, functions, and procedures through added argument checking.

Although the proposed method has the potential to enhance software reliability, it requires further research and development of specialized analysis tools to realize its full effectiveness.

Author Contributions

Conceptualization, Y.M.; methodology, Y.M., Y.S.; software, Y.M., Y.S.; validation, Y.M., Y.S.; formal analysis, Y.M., Y.S.; resources, Y.M., Y.S.; data curation, Y.M.; writing—original draft preparation, Y.M., Y.S.; writing—review and editing, Y.M., Y.S.; visualization, Y.M., Y.S.; supervision, Y.M.; project administration, Y.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is contained within this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

Bai, Lan & Dick, Robert & Dinda, Peter. Archetype-based design: Sensor network programming for application experts, not just programming experts. In Proceedings of the 8^th International Conference on Information Processing in Sensor Networks, IPSN 2009, San Francisco, California, USA, 13-16 April 200. [CrossRef]
Internet of Things – number of connected devices worldwide 2015–2025. Available online: https://www.statista.com/statistics/471264/iot-number-of-connected-devices-worldwide/ (accessed on 27 November 2016).
Buffoni, L.; Ochel, L.; Pop, A.; Fritzson, P.; Fors, N.; Hedin, G.; Taha, W.; Sjölund, M. Open Source Languages and Methods for Cyber-Physical System Development: Overview and Case Studies. Electronics 2021, 10, 90. [CrossRef]
Cyber-Physical Systems (CPS). Available online: https://www.nsf.gov/publications/pub_summ.jsp?ods_key=nsf21551&org=NSF (accessed on 11 January 2021).
Cyber-Physical Systems (CPS). Available online: https://ptolemy.berkeley.edu/projects/cps/ (accessed on 11 January 2021).
Forecast end-user spending on IoT solutions worldwide from 2017 to 2025 (in billion U.S. dollars). Available online: https://www.statista.com/statistics/976313/global-iot-market-size/ (accessed on 11 January 2021).
Global IoT market size to grow 19% in 2023—IoT shows resilience despite economic downturn. Available online: https://iot-analytics.com/iot-market-size/ (accessed on 7 February 2023).
Top 3 Programming Languages for IoT Development In 2018. Available online: https://www.iotforall.com/2018-top-3-programming-languages-iot-development (accessed on 9 October 2018).
Functional Mock-Up Interface, Version 2.0. Interface Specification. Available online: https://fmi-standard.org/downloads/ (accessed on 25 July 2014).
System Structure and Parameterization, Version 1.0. Interface Specification. Available online: https://ssp-standard.org (accessed on 01 March 2019).
A Unified Object-Oriented Language for Physical Systems Modeling-Language Specification Version 3.4. Available online: https://www.modelica.org/documents/ModelicaSpec34.pdf (accessed on 10 April 2017).
Technical Report on C++ Performance. Information Technology — Programming languages, their environments and system software interfaces. Available online: https://www.open-std.org/jtc1/sc22/wg21/docs/TR18015.pdf (accessed on 15 February 2006).
Xie, H., Wei, L., Zhou J., Hua, X. Research of Conformance Testing of Low-Rate Wireless Sensor Networks Based on Remote Test Method. In Proceedings of the International Conference on Computational and Information Sciences (ICCIS 2013), Shiyang, China, 21-23 June 2013. [CrossRef]
Parisot, A., Bento, L. M. S., Machado, R. C. S. Testing and selecting lightweight pseudo-random number generators for IoT devices. In Proceedings of the 2021 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0&IoT), Rome, Italy, 07-09 June 2021. [CrossRef]
Bae, H., Sim, S. -H., Choi, Y., Liu, L. Statistical Verification of Process Conformance Based on Log Equality Test. In Proceedings of the 2nd International Conference on Collaboration and Internet Computing (CIC), Pittsburgh, PA, USA, 01-03 November 2016. [CrossRef]
Silva, D.S., Resner, D., de Souza, R.L., Martina, J.E. Formal Verification of a Cross-Layer, Trustful Space-Time Protocol for Wireless Sensor Networks. In: Ray, I., Gaur, M., Conti, M., Sanghi, D., Kamakoti, V. (eds) Information Systems Security. ICISS 2016. Lecture Notes in Computer Science, vol 10063. Springer, 2016; pp. 426-443. [CrossRef]
Ahmad, A. Model-Based Testing for IoT Systems: Methods and tools. PhD Thesis, University Burgundy Franche-Comté, France, 1 June 2018.
Clarke, E. M., Grumberg, O., Kroening D., Peled D., Veith, H. Model Checking, 2nd ed.; MIT Press, 2018; 424 p.
Back, R.-J. Invariant based programming: basic approach and teaching experiences. Formal Aspects Computing 2009, Volume 21(3), pp. 227-244. [CrossRef]
SI Units. Available online: https://www.nist.gov/pml/owm/metric-si/si-units (accessed on 7 March 2023).
The International System of Units (SI) 9th edition 2019 V2.01. Available online: https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf (accessed on 1 December 2022).
Siano, D. B. Orientational analysis—a supplement to dimensional analysis. Journal of the Franklin Institute 1985, Volume 320, Issue 6, pp. 267-283.
Siano, D. B. Orientational analysis, tensor analysis and the group properties of the SI supplementary units. Journal of the Franklin Institute 1985, Volume 320, Issue 6, pp. 285-302.
Santos, L.F. dos; Freitas, A.C. de. Orientational Analysis of the Vesic’s Bearing Capacity of Shallow Foundations. Soils and Rocks, São Paulo, 43(1), 3-9, January-March 2020.
Martínez-Rojas, J.A.; Fernández-Sánchez, J.L. Combining dimensional analysis with model based systems engineering. System Engineering, 26(1), 71-87, January 202. [CrossRef]
Euler’s equations of motion for rigid-body rotation. Available online: https://phys.libretexts.org/Bookshelves/Classical_Mechanics/Variational_Principles_in_Classical_Mechanics_(Cline)/13%3A_Rigid-body_Rotation/13.17%3A_Eulers_equations_of_motion_for_rigid-body_rotation (accessed on 14 March 2021).

Figure 1. The global market of Internet of things (red solid line) and global spending on Enterprise IoT Technologies (blue dot line).

Figure 2. General software defect detection model.

Figure 3. Complex general software defect detection model.

Figure 4. Simple model detection of incorrect use of variable via DA.

Figure 5. Simple model detection of incorrect use of variable via OA.

Figure 6. Complex model of detection of incorrect use of variable via OA and DA.

Figure 7. Complex Model of detection of incorrect use of operation via DA & OA.

Figure 8. The histogram and probability density function of the total number of different variables per file in semi-logarithmic coordinates.

Figure 9. Visualizing variable usage per file using semi-logarithmic histogram and probability density function.

Figure 10. Probability Density Functions of Software Defect Detection based on: 1) DA (blue line); 2) OA (yellow line); 3) Both DA and OA (red line).

Figure 11. Histograms and Probability Density Functions of the Total Number of Additive Operations (Blue Lines), Multiplicative Operations (Red Lines), and Other Operations (Green Lines) per File on Semi-Logarithmic Coordinates.

Figure 12. Histograms and Probability Density Functions of the Conditional Probability of Additive Operations (Blue Lines), Multiplicative Operations (Red Lines), and Other Operations (Green Lines) per File.

Figure 13. Probability Density Function of the Conditional Probability of Software Operation Defect Detection via DA and OA.

Figure 14. Histograms and Probability Density Functions of Conditional Probabilities of Variables (Blue Lines) and Operations (Red Lines) per File.

Figure 15. The histograms and probability density functions of software defect detection conditional probabilities: The histograms and PDF of conditional probabilities of detection via orientational and DA of incorrect use of software operations and variables (Black solid lines). The histograms and PDF of conditional probabilities of detection of incorrect use of software operations (Orange dash dot dot lines). The histograms and PDF of conditional probabilities of detection via OA of incorrect use of software variables (Red dot lines). The histogram and PDF of conditional probabilities of detection via DA of incorrect use of software variables (Blue dash lines). The histogram and PDF of conditional probabilities of detection via DA and OA of incorrect use of software variables (Green dash dot line).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Software Verification Method for Internet of Things and Cyber-Physical Systems

Abstract

1. Introduction

2. The formal software verification method

2.1. Using Dimensional homogeneity in formal software verification

2.2. Using Orientational homogeneity in formal software verification

2.3. Examples of software formal verifications

2.4. Software defect detection models

2.4.1. General software defect detection model

2.4.2. Simple model detection of incorrect use of variable based on DA

2.4.3. Simple model detection of incorrect use of variable based on OA

2.4.3. Complex model of detection of incorrect use of variable via OA and DA

2.4.4. Model of detection of incorrect use of operation via OA and DA

3. Results

4. Discussion

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe