Prerpints.org logo
Preprint
Article

Computational Analysis of Stability of Wave Propagation Against Submerged Permeable Breakwater Using Hybrid Finite Element Method

Altmetrics

Downloads

185

Views

51

Comments

0

Submitted:

01 May 2023

Posted:

02 May 2023

You are already at the latest version

Alerts
Abstract
A wave is an energy that can propagate with a medium, the propagation of a wave moves with respect to time by carrying energy that moves with velocity per unit of time. Sea waves are one of the propagating wave problems that are broken down to produce wave propagation with a relatively inhomogeneous minimum amplitude and speed of sea waves which have their own difficulties in solving them numerically. This study aims to analyze the stability of wave propagation of submerged breakwaters using the Boundary Element Method. This research will approximate the boundary discretization of the breakwater domain and then combine it with the Finite Element Method in determining the moving elements of the velocity of fluid flow through a porous submerged breakwater. This study varies the magnitude of the incoming propagation velocity and the influence of the breakwater distance. The results of this study indicate that the resulting minimal wave assuming v = 1 m/s and the breakwater distance of s = 20 m gives a wave reflection with a minimum wave speed and amplitude of 0.12515 m
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

A wave is a propagating vibration that propagates in a medium or a set of objects that interact with each other. Real examples of waves can be seen in surface wave problems such as ocean waves on the beach. Waves on the surface of the water are a process of interaction between moving air masses and meeting the surface layer of water. This interaction produces a pattern of peaks and valleys which is influenced by the presence of energy and momentum. Basically, surface water waves are not only caused by air masses, but these waves can also be caused by other activities that exist at the bottom of the water depth. [1,2] explains, the propagation speed of surface water waves depends on the water surface tension, hydrostatic pressure, bottom depth, mass density, and gravity. The waves that occur on the surface of the water are caused by several things, such as wind blowing or vibrations at the bottom of the water, for example tsunami waves. [3,4,5].
[6,7] in his research conducted a study on how to reduce the strength of waves at sea level using a breakwater in the form of a porous block. The first thing to do in this research is to form a wave model of the surface of the water through a breakwater in the form of a porous block. The model is formed using the governing equations for surface waves passing through porous beams, namely the continuity equation, momentum equation, potential wave velocity, fluid in porous media, Laplace and Bernoulli equations in fluid and porous media, as well as kinematic and dynamic boundary conditions on the surface. fluid. The resulting model is almost similar to the shallow water equation. In the next procedure, [8,9,10] explains how to find a numerical solution from the model that has been formed. The solution of the numerical solution in the model is carried out by finite difference method implicit scheme corrector predictor. The results of the research conducted explain that the wave amplitude after going through the breakwater has decreased. The attenuation or attenuation of wave strength depends on the number of breakwaters and the height of the breakwaters. In this study the authors will simulate wave breaking using a submerged porous breakwater to find a numerical solution using the Boundary Element Method. Boundary Element Method is one of the approaches that can be used to solve various types of differential equations. Solving the equation is done by discretizing the equation with initial conditions and boundary conditions, then determining the stability of the equation discretization. [11] explains that the boundary element method is a method based on the Taylor series expansion [12]. One approach with the finite difference method is to use an implicit schema. Implicit schemas have the advantage that they are unconditionally stable. The time step Δ t can be taken arbitrarily (large) without causing instability. [13]
Research on breakwaters aims to determine the phenomena that occur with the energy generated from the movement of seawater moving towards coastal areas which are shallow areas [14,15,16,17]. The development of research on breakwaters has been carried out by several mathematicians-physicists who focus on breakwater models [18,19]. In research that has been done, breakwaters with different dimensions will produce different results according to the specified model parameters. In terms of optimizing the breakwater model, it is influenced by several important parameters such as the wave velocity, wave height, depth, pressure, and even Newtonian force which results in momentum in the breakwater [20,21]. In his research, he explained how the analysis of the interaction between models of breakwaters used in three-dimensional problems with porous breakwater models by developing equations from the Navier-Stokes equations resulted in a 3D wave propagation model for surface emerging breakwaters [22,23]. Many simulations of breakwaters have been carried out to find out how much wave reduction is produced from both the speed and wave height values [24,25,26]. Simulation involving different parameters will give complex results in its completion because it is necessary to do a multi-purpose programming model [27,28]. The results of research with a focus on wave propagation stability analysis [29,30] need to consider the magnitude of the reduction of the incident wave so that the amplitude value delivered to the shallow area is at a steady state point. Research on the stability of wave propagation has been carried out [31,32,33,34] to determine the factors that affect stability wave propagation in terms of wave propagation reliability, breakwater reliability and also the probability density function (PDF) value. The resulting impact of large waves is damage to shallow areas and even coastal areas as critical areas [35,36,37]. The optimal wave splitting process aims to reduce the magnitude of wave resonance at the harbor by applying the Helmholtz equation which has complex values as the model state equation with minimizing wave amplitude as the optimization variable [11,38]. The author proposes that a sinking breakwater will provide momentum resistance to subsurface currents so that the amount of momentum that occurs will be reduced from the bottom of the shallow area before the wave propagates to the coastal area [39,40]. The results to be achieved from this study are simulations of wave height ( λ ) from variations in the depth of the breakwater position from the sea surface. This study will also simulate the effect of speed variations on the amplitude of the waves that occur. The formation of a sinking breakwater model will be carried out by testing the reliability of moving against time to reach the stability area against the variations of constraints that are carried out.

2. Materials and Methods

2.1. Breakwater Simulation

Submersible breakwaters are facilities built to break waves under the surface of the water with the aim of dampening and absorbing internal energy from wave propagation underwater. Based on the principle of hydrostatic pressure that the greatest water pressure is at the bottom of the sea water which is expressed by the pressure P of water directly proportional to the depth of sea water h [41,42,43]. Hydrostatic pressure is expressed as:
− δ P = g ρ δ z
where, lim δ z → 0 and the eq (1) can be expressed as:
∂ P ∂ z = − g ρ
write that P , g , ρ , ∂ z respectively represent hydrostatic pressure, gravitational acceleration, fluid density, and changes in water depth [44]. Eq (1) is written with a negative sign with the assumption that the pressure P will decrease with increasing height which is applied to the problem of hydrostatic pressure in the case of an object moving towards the atmosphere. For the sinking breakwater problem, Eq (1) will be an increase in ∂ ‡ which will result in an increase in pressure P so that the pressure will be greater in the bottom area [45]. The submerged breakwater will absorb some of the energy from the bottom area with the aim of reducing the amount of energy that is in the surface area. An illustration of the wave breaking process with a breakwater is shown in Figure 1.
The sinking breakwater will absorb some of the inner energy at the bottom of the wave by releasing the wave propagation that hits the breakwater so that a process of changing momentum occurs in the wave propagation [46,47,48]. The process of breaking waves with a sinking type is often used to control large-scale wave propagation for coastal areas or port areas which maintain the magnitude of wave propagation in coastal areas [49].

2.2. Navier-Stokes Equation on Moving Fluids

The Navier-Stokes equation is a mathematical discipline that formulates fluid problems both for fluids and for the characteristics of fluids [50,51,52,53,54]. The Navier-Stokes equation modeling describes how the value of the velocity vector propagates through the u , v components at the x , y coordinates that move with time. In vector analysis problems it is defined that all fluid quantities are functions of space over time, fluid quantities can be vector values of velocity (v) and acceleration (a) [55,56]. Let a is a vector component of velocity and time vector that can be written as:
a → = d u d t , d v d t
denote that a → = d v → x , y , t d t , consists of components in Eq (3), then by following the chain rule then the value of a → for each component is:
a → x = d u d t = ∂ u ∂ t + ∂ u ∂ x d x d t + ∂ u ∂ y d y d t
a → y = d v d t = ∂ v ∂ t + ∂ v ∂ x d x d t + ∂ v ∂ y d y d t
For each value of d x d t , d y d t is a function of space against time which can be written respectively as u , v which results in the acceleration value in Eq (4)(5) for each components are:
a → x = d u d t = ∂ u ∂ t + v → . ∇ u
a → y = d v d t = ∂ v ∂ t + v → . ∇ v
simply, the vector of a can be written as:
a → = ∂ ∂ t + v → . ∇ v →

2.3. Hybrid Finite Element Method

The application of the Hybrid Finite Element Method is used by determining the initial value of a function that moves with time [57,58]. The equation using Hybrid Finite` elements will provide an efficient solution by separating the wave equation from the momentum equation then linearizing [59].
∫ 0 t F + ∫ 0 r ∂ 2 η ∂ t 2 − c 2 ∂ 2 η ∂ x 2 η * dxdt = ∫ 0 t F + ∫ 0 c B η * dxdt
where r is the region length and t F + = t F + ϵ , where ϵ is a small arbitrary parameter. In the above expression Z * is the fundamental solution of the one-dimensional wave operator, given by:
η * = − 1 2 C H c ( t F − t ) − r
in which H is the Heaviside function and r = ∥ x − s ∥ , s and x indicating the source and field point positions respectively. Integrating the second-order derivatives in (5) twice by parts, the following equation is obtained:
∫ 0 t F + ∫ 0 r ∂ 2 η * ∂ t 2 − c 2 ∂ 2 η * ∂ x 2 η dxdt + ∫ 0 r η * ∂ η ∂ t − η ∂ η * ∂ t 0 t F + d x
− c 2 ∫ 0 t F + η * ∂ η ∂ x − η ∂ η * ∂ x 0 r dt = ∫ 0 t F + ∫ 0 r B η * dxdt
Wave transmission ( H t ) is the height of the wave that is transmitted through the obstacle and is measured by the transmission coefficient ( K t ) calculated by the following equation [6]:
K t = H t H i = E t E i
where K t is the wave transmission, K i is the reflection wave, H t is the value of H t = K t × H i , where H i is the height of inlet wave, E t is the transmission Energy, and E i is the inlet energy. The value of transmission wave E t = 1 8 ρ . g . H t involve ρ is the density of fluids and g is the gravity acceleration.
Theorem 1
Given J, and h as the proposition function f,g for [ u 0 , v 0 ] ∈ H 0 1 ( Ω ) × L 2 ( Ω ) , there exists a unique function J × Ω → R that satisfies the equation
∂ 2 u ∂ t 2 − Δ u + f ( u ) + g ( ∂ u ∂ t ) = h ( t , x ) in C ( J , H − 1 ( Ω ) )
that fulfills the condition v = value ε ∈ C 1 ( J ) and all t ∈ J
d d t ε t = ∫ Ω h t , x − g ∂ u ∂ t t , x ∂ u ∂ t t , x d x .
Proof. 
The result of the existence of unique values is in the general model of the classical method combined with the prior estimation mapping on the maximum interval. Precisely, if formed J δ ∩ [ − δ , δ ] for each δ > 0 for all P > sup { | u 0 | , | v 0 | } , The set X endowed with the topology of C J δ , V ∩ C 1 J δ , H is a complete metric space, for the value v ∈ X , given C ( v ) is the unique solution of z ∈ C ( J δ , V ) ∩ C 1 ( J δ , H ) ∩ C 2 ( J δ , V ′ ) from the problem
∂ 2 z ∂ t 2 − Δ z = h t , x − f v − g ∂ v ∂ t
z ( 0 ) = u 0 , ∂ z ∂ t ( 0 ) = v 0
Preprints 72385 g002
Figure 2. Wave Simulation
Figure 2. Wave Simulation
Preprints 72385 g002

2.4. Wave Attenuation Equation Model

Based on the derivation of the unhindered homogeneous wave equation model in Eq (15), a wave equation model will be formed with the damping of the breakwater which is influenced by external forces that inhibit the propagation of water waves, namely the breakwater [60,61]. The wave damping process is assumed to be a modified form of the equation model by giving a negative value to the wave acceleration ( − u t t ). The magnitude of the negative acceleration illustrates that the external force has a direction opposite to the direction of wave propagation, which will result in a decrease in wave height ( λ ) and a decrease in speed ( u t ) [62,63,64,65]. Then based on the general homogeneous wave equation can be rewritten as:
− u t t − c u x x = P x t → u t t + c u x x = − P x t
Equation (16) is solved by using the separating variable method on the interval x ( 0 , L ) , with the initial conditions u x , 0 = ϕ x , u t x , 0 = ψ x and u 0 , t = u L , t = 0 . Then the solution of the homogeneous wave equation separator method is: u t t = − c 2 u x x , with 0 < x < L , u 0 , t = u L , t = 0 , ∀ t ≥ 0 , u x , 0 = ϕ x , with u t x , 0 = ψ x . Furthermore, for the equation u x , t it can be written that u t t = X x T ′ ′ t and u x x = X ′ ′ x T t , Then the u t t equation, when substituted into the separable equation above, can be written as:
u t t = − c 2 u x x ↔ X x T ′ ′ t = − c 2 X ′ ′ T t ,
so,
T ′ ′ t c 2 T t = − X ′ ′ x X x
The solution to solving Eq (17) is for the problem k = μ 2 = n π L 2 , it can be written that λ n = c n π l . So if the λ n value is substituted into Eq (17) it will produce:
u x , t = ∑ n = 1 ∞ u n x , t = ∑ n = 1 ∞ A n + B n cos t + A n − B n c n π L sin t sin n π L x
It can be concluded that Eq (18) is a homogeneous equation in the interval 0 < x < L . that can be written as:
u x , 0 = ∑ n = 1 ∞ A n + B n sin n π L x = ϕ x

3. Results

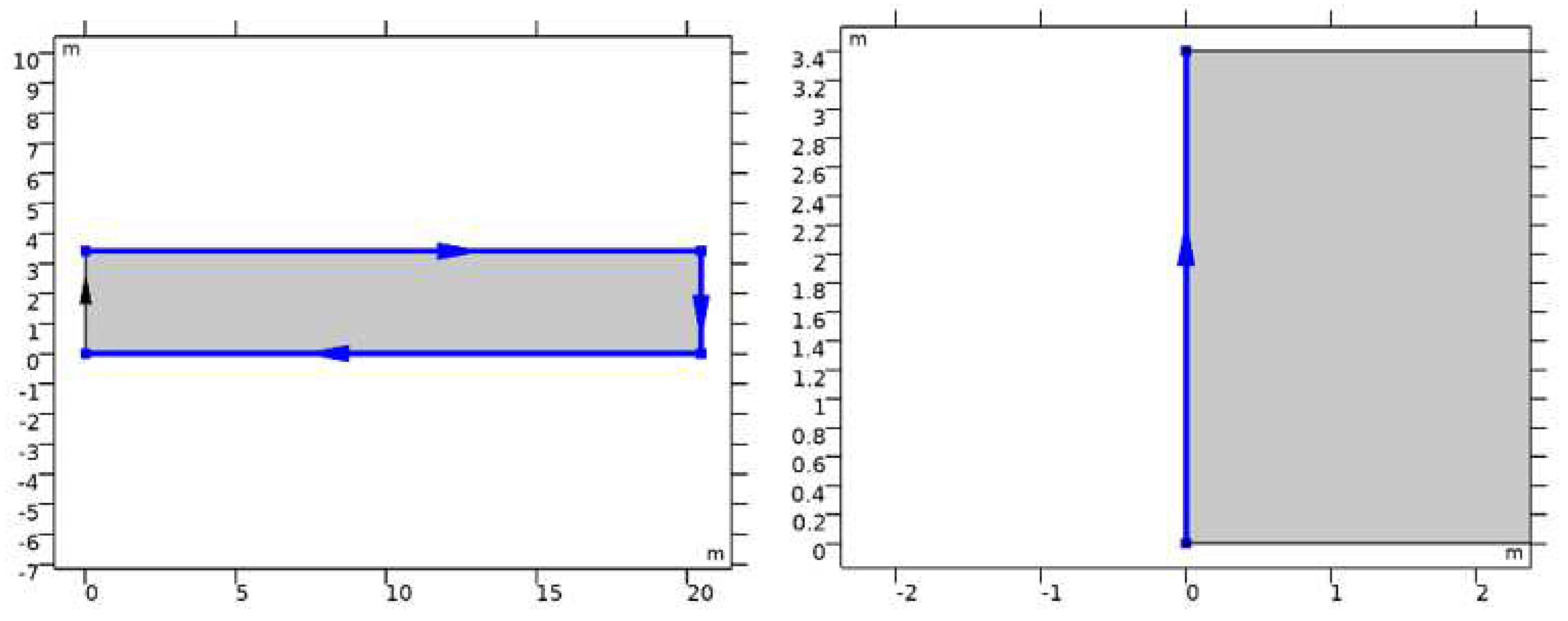
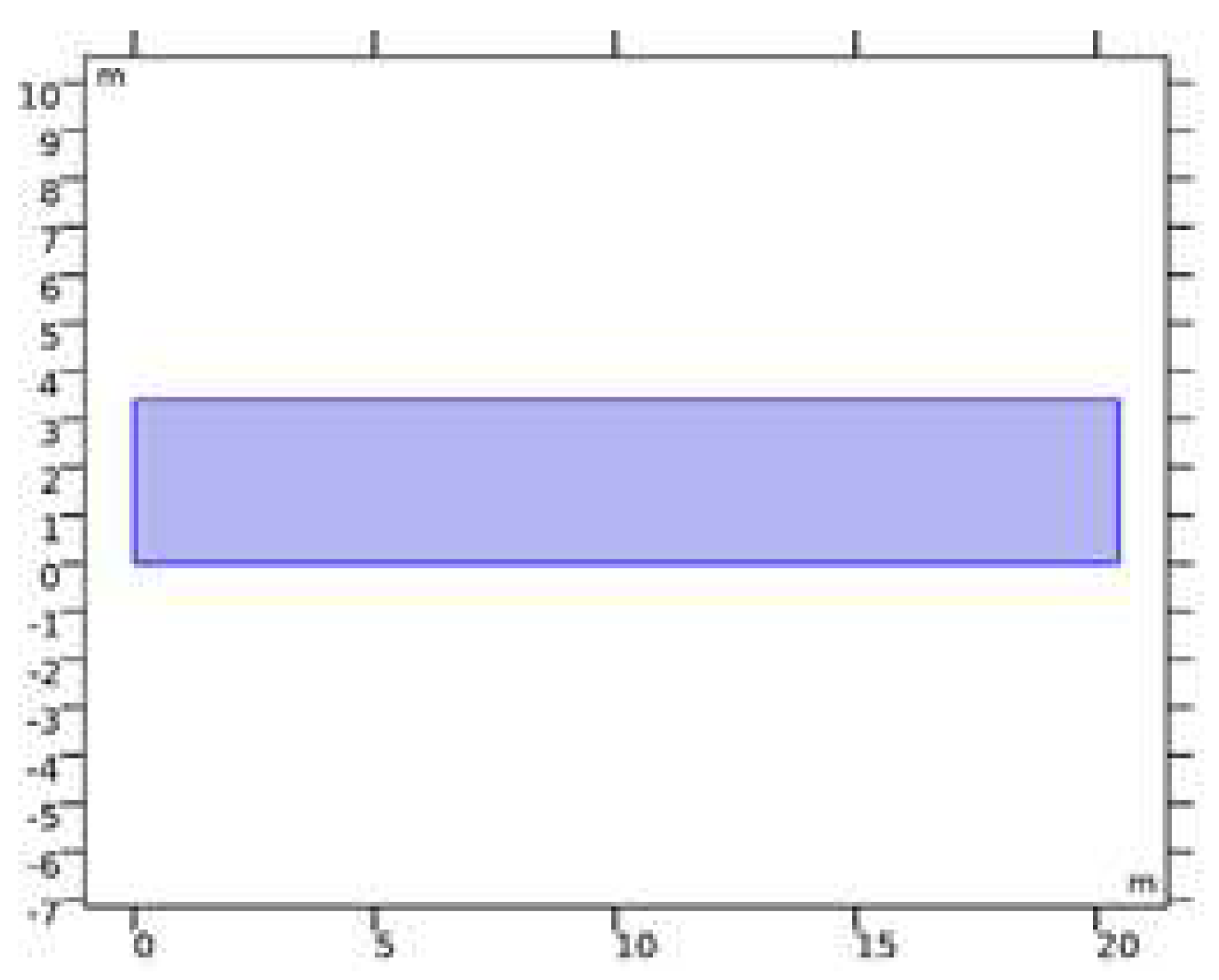
In building a simulation of wave propagation towards a breakwater, it is necessary to initialize the wave model by determining the geometry of the wave model. At this stage a 2D wave model will be formed using COMSOL Multiphysics 5.6 as shown in Figure 3.
In the wave model, the sides that will be the inlet and outlet will be defined with the boundary conditions of each domain.
Preprints 72385 g004
Figure 4. Inlet and Outlet Model
Figure 4. Inlet and Outlet Model
Preprints 72385 g004
The breakwater model walls in Fig (a) and (b) are formed with geometric constraints,
u . n = 0
− Γ h . n = 0
− Γ h . n = g h 2 2
Where the u and n vectors denote the velocity values at the coordinates u x , y , t and the momentum of the flux geometry model, respectively. The Γ h value is the magnitude of the flux conservation of the momentum at each coordinate with the calculation for each coordinate being u x . q x + g . h 2 2 . In the process of meshing the model with finite elements, it was found that the size of the elements formed was 185,845 with 1,772 edges, this resulted in the need for computation in the wave model iteration so as to produce a large change in the value of the wave propagation with respect to time. In the simulation carried out, the research will test how the effect of speed on the distribution of wave velocity values after wave attenuation with each speed of 1 m s , 1.5 m s , and 2 m s . Furthermore, the simulation will be continued with the modification of the breakwater model to the position length of the breakwater with a distance of 10 m, 15 m and 20 m respectively.
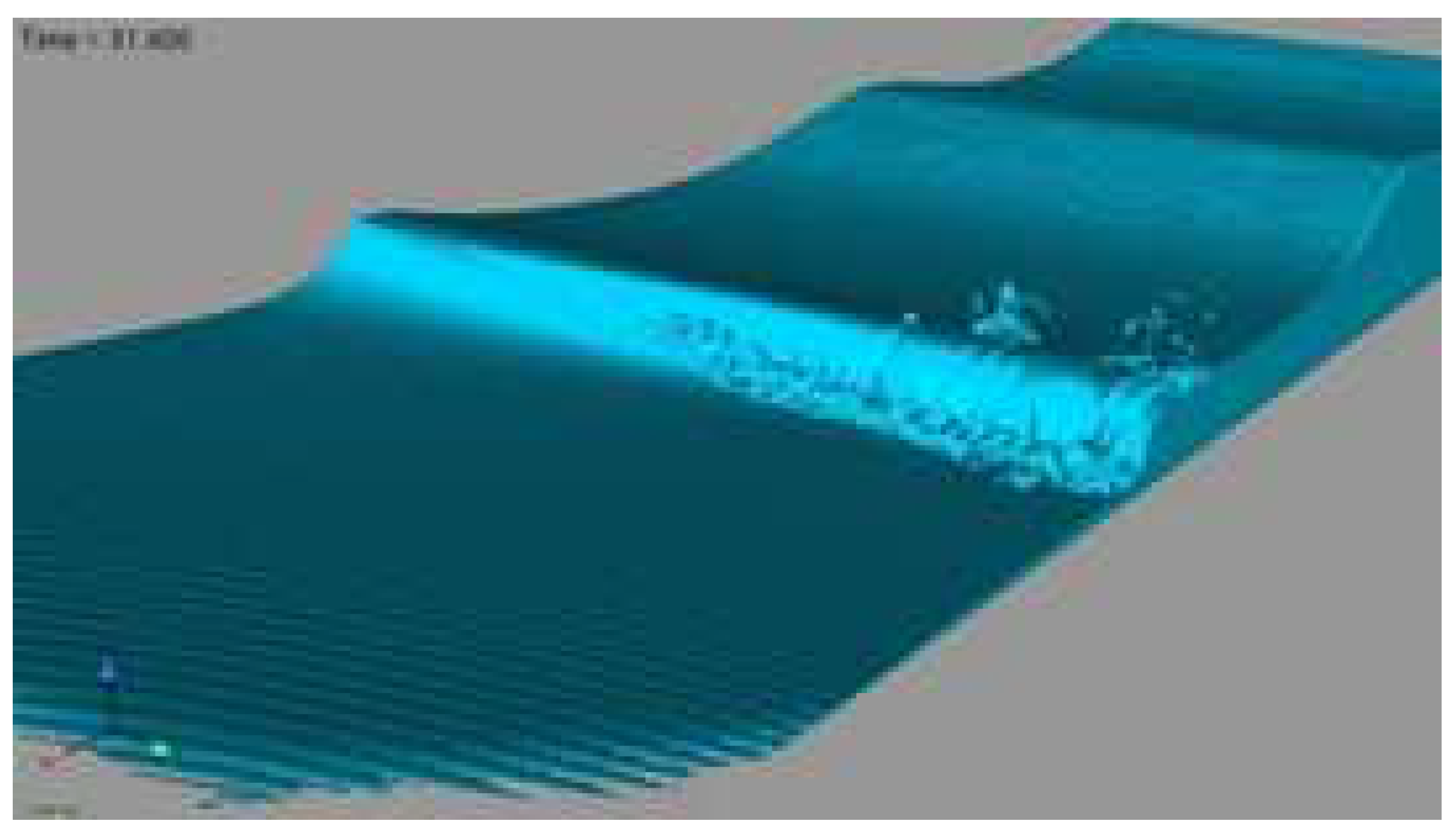
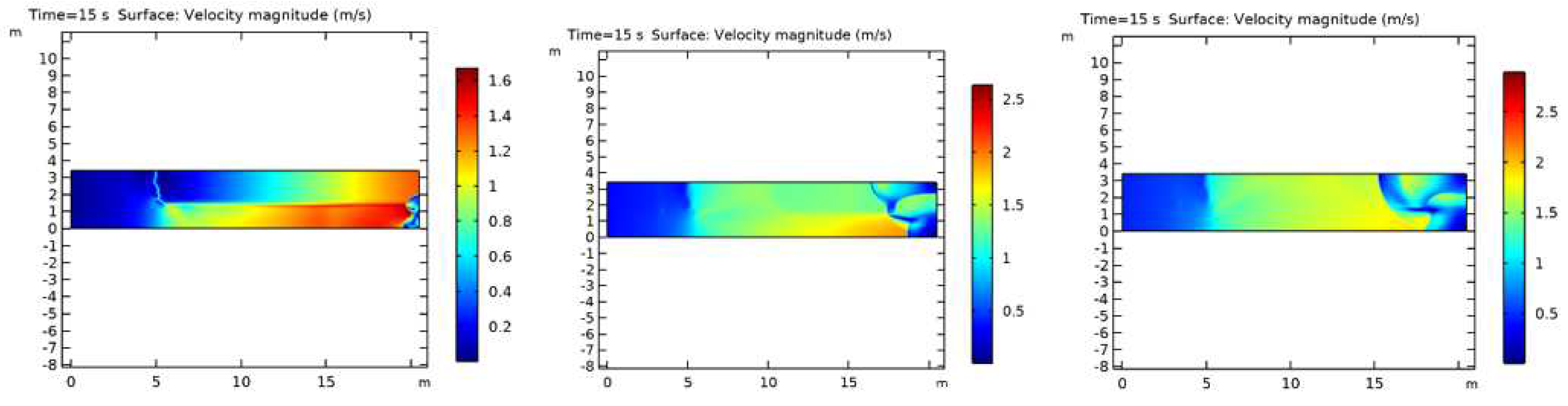
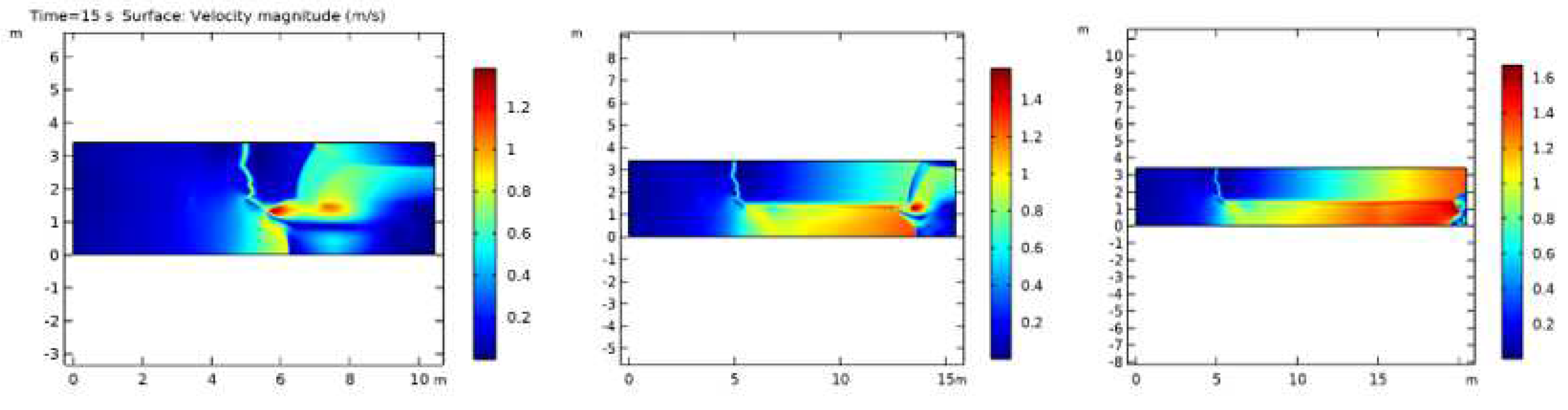
Figure 5. shows the wave breaking process with a sinking breakwater model that has permeable properties and is a propagation in shallow water, the magnitude of the velocity fraction each time is shown in Figure 6. shows the propagation of waves that propagate after a break occurs using a porous submerged breakwater. The amplitude is generated against time and oscillates up to the outlet of the propagation area. The convergence of the wave amplitudes shows that the waves resulting from the wave splitting process show significant results with as many as 4,836 iterations during t = 0 , 10
Preprints 72385 g005
Figure 5. Breakwater Simulation
Figure 5. Breakwater Simulation
Preprints 72385 g005
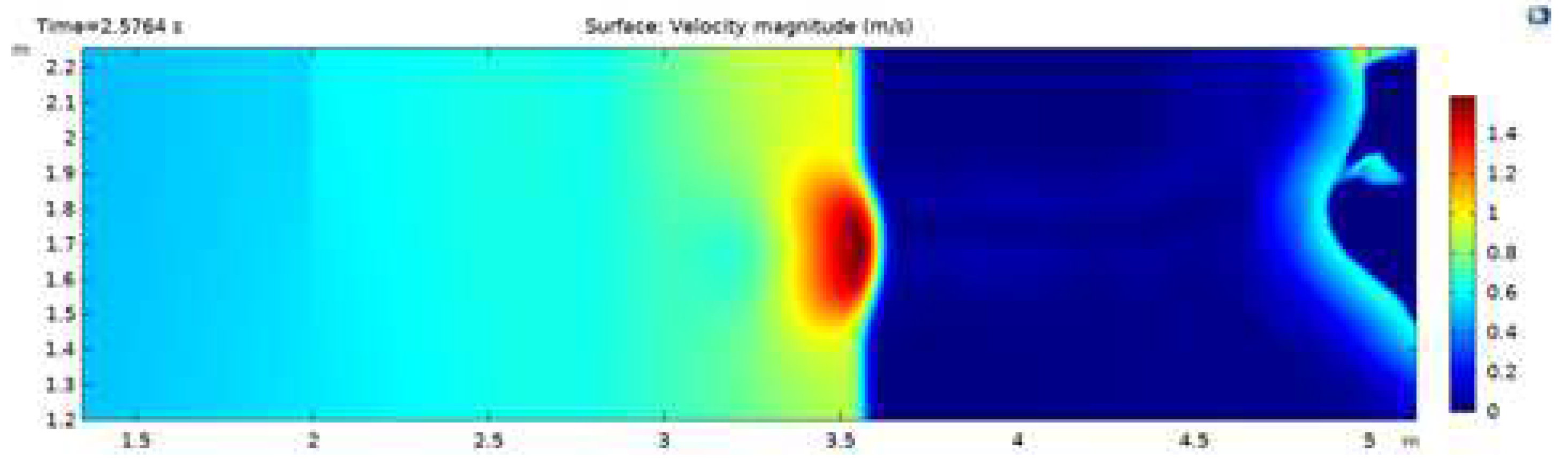
Preprints 72385 g006
Figure 6. Simulation of the velocity of the breakwater breaking process at t = 2.5 s
Figure 6. Simulation of the velocity of the breakwater breaking process at t = 2.5 s
Preprints 72385 g006
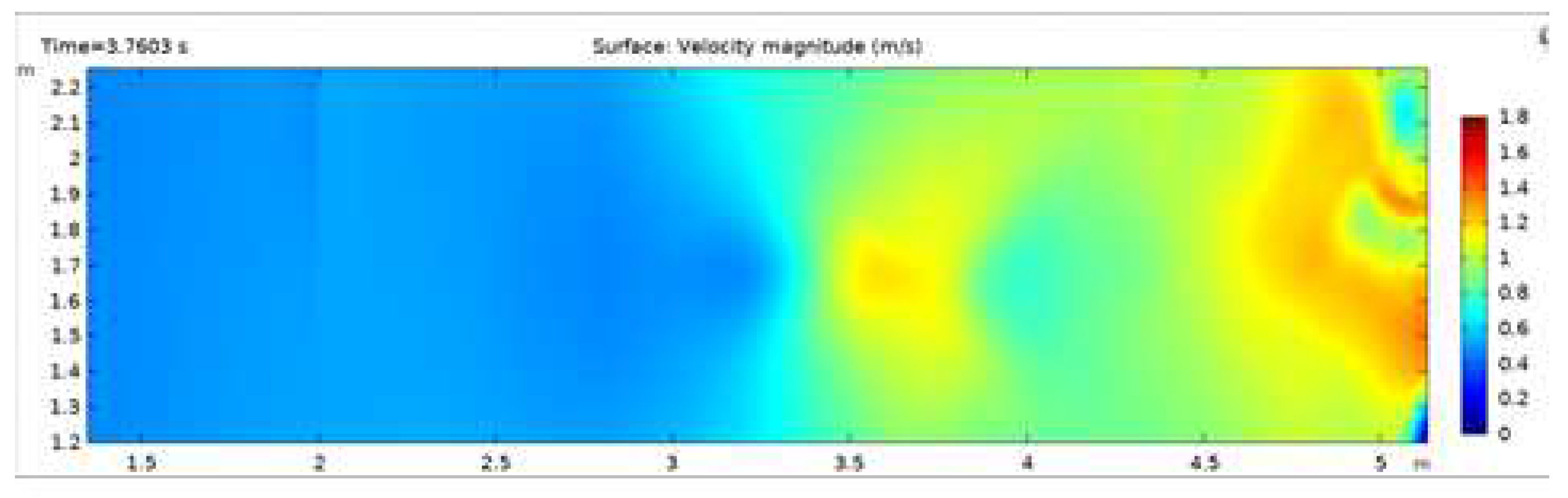
Preprints 72385 g007
Figure 7. Simulation of the speed of the breakwater breaking process at t = 3.7 s
Figure 7. Simulation of the speed of the breakwater breaking process at t = 3.7 s
Preprints 72385 g007
Figure 8 shows the solution of the speed of wave propagation at t = 0 , 10 with the color representation showing the critical area experiencing the greatest velocity. Furthermore, the representation of the stability of wave propagation will be shown in Figure 9.
Figure 9 shows the propagation of waves that propagate after a break occurs using a porous submerged breakwater. The amplitude is generated against time and oscillates up to the outlet of the propagation area. The convergence of the wave amplitudes shows that the waves resulting from the wave splitting process show significant results with as many as 4,836 iterations during t = 0 , 10 . The resolution of the wave amplitude to the elements is shown in Figure 10.
The completion iteration is carried out for 4,386 for t = 0 , 10 . Figure 10 shows that the muted water waves show a very critical amplitude before and after the wave breaking process is carried out, the convergence of the water waves shows that the amplitude on the outlet side becomes lower in the simulation so this shows that the wave breaking process will provide amplitude attenuation and wave propagation speed the minimum. For parameter variations, a simulation is carried out on differences in wave propagation velocity of 1 m/s, 1.5 m/s, 2 m/s to see differences in the distribution of wave speed and amplitude, then the breakwater distance parameter with a constant arrival speed of 1 m/s shown in Figure 11.
The breakwater will dampen the waves and break the wave propagation at each coordinate. Changes in the conservation of momentum will result in a change in the velocity value for each component at the coordinates u x , y , t . The magnitude of the change in velocity that occurs will have an impact on the final velocity of the wave amplitude. The offshore simulation of the breakwater was carried out by modifying the geometry model of the breakwater with constant incoming wave velocity v for distance variations of 10 m, 15 m, and 20 m. The difference in the position of the breakwaters gives a different wave distribution. The model of the breakwater with changing distances is shown in Figure 12.

3.1. Stability Simulation

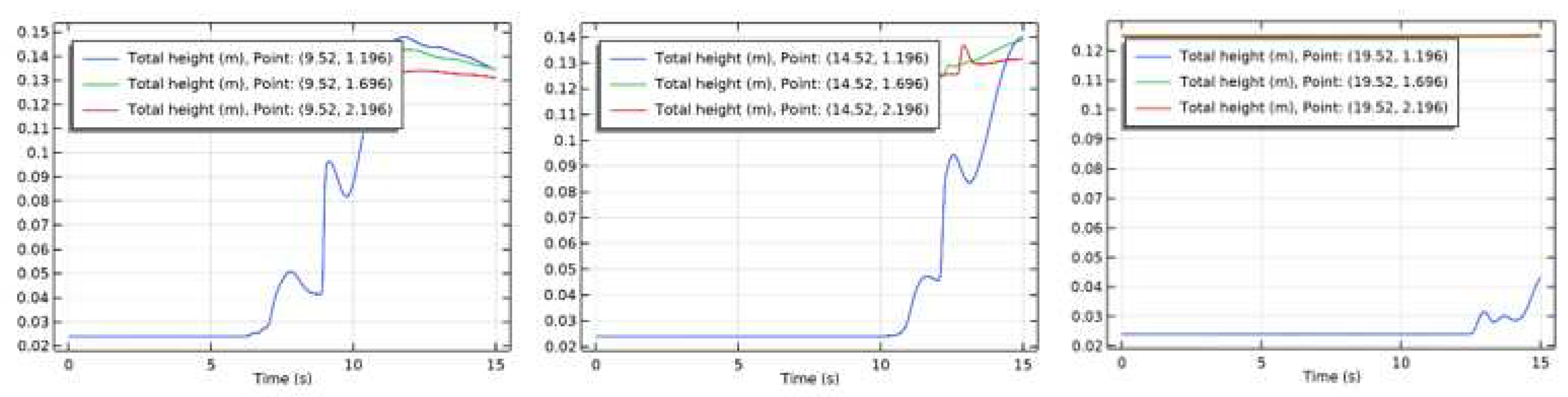
The stability of wave propagation is indicated by the amplitude distribution of sea water waves, given three critical points from the breakwater respectively 1.196 m, 1.696 m, and 2.196 m for variations in the distance of the breakwater, namely 9.52 m, 14.52 m, and 19.52 m. Simulation of wave amplitude distribution for variations in the position of the breakwater is shown in Figure 13.
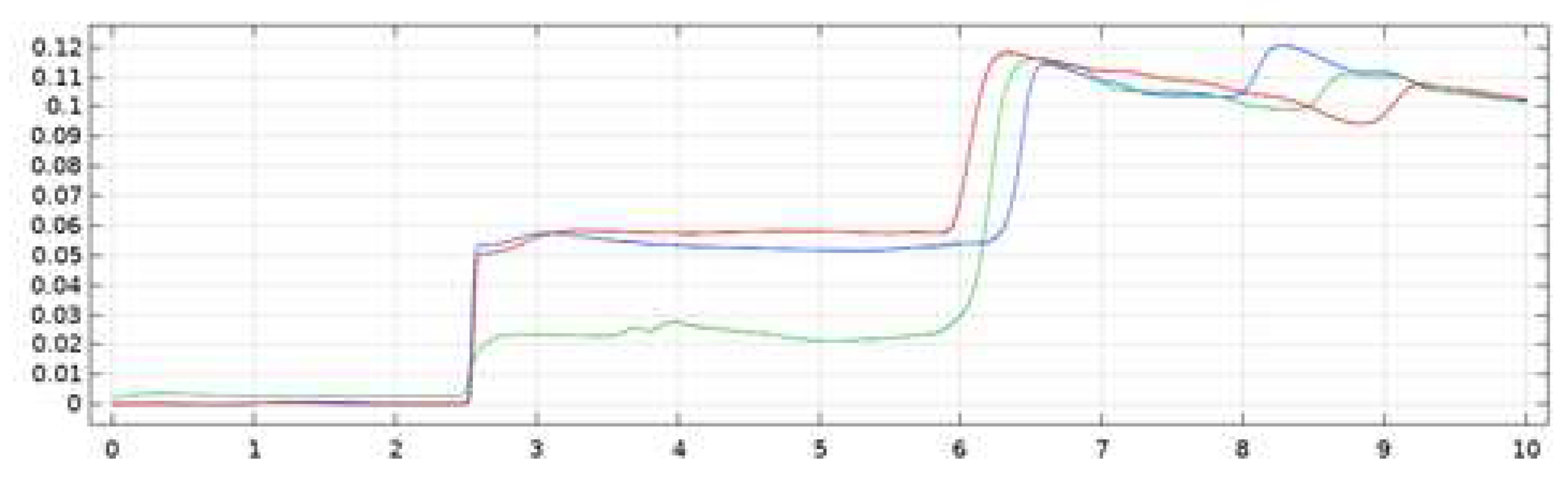
From the simulation results it is shown that the difference in the distance of the breakwater that is carried out will give a difference in the value of the amplitude distribution ( λ ) for each position. The computations are carried out on an interval of 0<t<51 and show that a short distance will give a large amplitude, which means that the wave splitting does not work optimally because it gives such a large wave height value. Placement of the breakwater with a distance of 19.52 m gives a low wave height, it can be seen that the wave amplitude starts to occur at t=10 s the computation is done. The height of each wave is shown in Table 1.
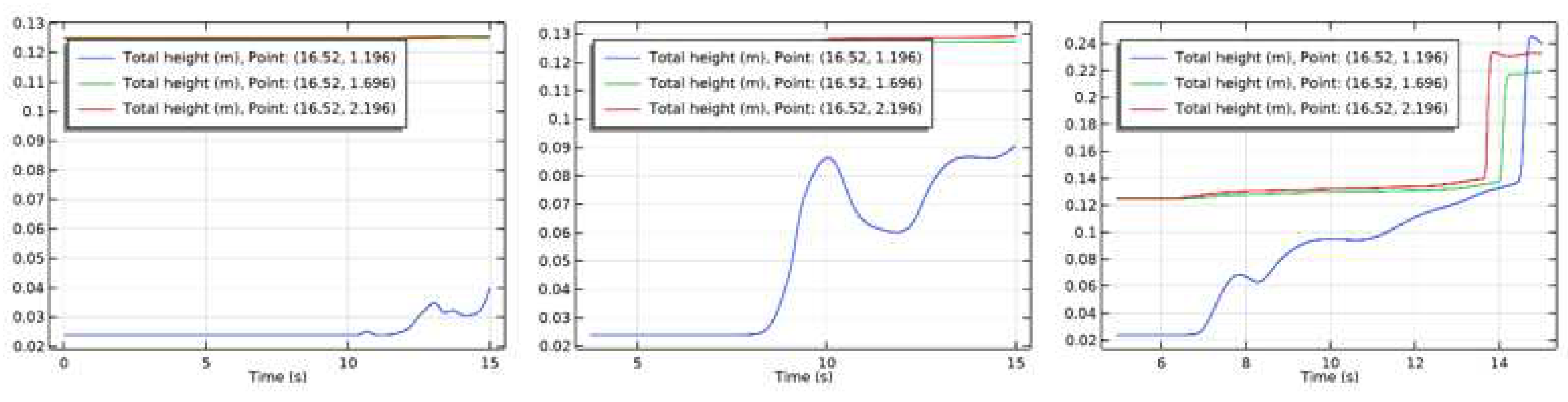
Table 1 shows the magnitude of the wave height that occurs in the t(0.15) interval which gives the result that for a breakwater which is 19.52 m it gives a large wave height on the surface that is equal to 0.12515 m which is the minimum wave height value from a variation of 9 .52 m is 0.13097 m, and a distance of 14.52 m produces a wave height of 0.13161 m. To provide a difference in the computational results that have been obtained, computations will be carried out on variations in the speed of the incoming wave propagation with the assumption that the breakwater is positioned at x= 16.52 m with variations in speed, namely v 1 = 1 m s , v 2 = 1 . 5 m s , v 3 = 2 m s . The simulation is shown in Figure 14.
Figure 14 represents the change in amplitude that occurs due to wave breaking based on variations in propagation speed. Waves that come with v= 2 m/s give the biggest wave height, whereas v= 1 m/s produces the lowest wave height. The simulation results of wave heights for speed variations are shown in Table 2.
Table 2 shows the magnitude of the wave height that occurs in the interval t (0.15] which gives the result that the incoming wave with u t = 1 m/s gives a large wave height on the surface that is equal to 0.12538 m which is the minimum wave height value of the u t variation = 1.5 m/s of 0.12909 m, and u t = 2 m/s produces a wave height of 0.23229 m.

4. Conclusions

Based on the research that has been done, it can be concluded that the simulation of wave attenuation has a significant impact on the value of the wavelength, and the magnitude of the wave propagation velocity generated by the simulation time is 15 seconds with several simulation variations, namely variations in the placement of the breakwater with a distance of 10 m , 15 m, and 20 m. the second variation of the simulation is the variation of wave velocity of 1 m/s, 1.5 m/s, and 2 m/s. The results shown are 0.12515 m respectively.

Funding

This research was funded by TALENTA Research Universitas Sumatera Utara grant number 367/UN5.2.3.1/PPM/KP-TALENTA/2022 and The APC was funded.

Acknowledgments

We thank to Research Institution of Universitas Sumatera Utara for funding this research with the 2022 International collaborative research scheme with research contract 367/UN5.2.3.1/PPM/KP-TALENTA/2022.

Abbreviations

The following abbreviations are used in this manuscript:
MDPI Multidisciplinary Digital Publishing Institute
DOAJ Directory of open access journals
TLA Three letter acronym
LD Linear dichroism

References

  1. W. Bambang, A. A. N Satria Damarnegara, A. Nadjadji, J. Pitojo Tri, Analysis of Waikelo Port Breakwater Failure through 2D Wave Model, Civil and Environmental Science Journal, 1(2) (2018) 088-095. [CrossRef]
  2. G. Fadhlyya Arawaney Abdul, R. Mohd Shahridwan, N. Nor Aida Zuraimi Md, K. Abdul Rahman Mohd, G. Martin, Mathematical Modelling of Wave Impact on Floating Breakwater, Journal of Physics: Conference Series, 890 (2017) 012005. [CrossRef]
  3. M. Keuthen, D. Kraft, Shape Optimization of a Breakwater, Inverse Problems in Science and Engineering, (2015) 936-956. [CrossRef]
  4. S. Kiran A, R. Vijaya, M. Sivakholundu K, Stability Analysis and Design of Offshore Submerged Breakwater Constructed Using Sand Filled Geosynthetic Tubes, Procedia Engineering, 116 (2015) 310-319. [CrossRef]
  5. A. Romano, G. Bellotti, R. Briganti, L. Franco, Uncertainties in the Physical Modelling of the Wave Overtopping Over a Rubble Mound Breakwater: The Role of the Seeding Number and of the Test Duration, Coastal Engineering, 103 (2015) 15–21. [CrossRef]
  6. P. Wei, H. Xiaoyun, F. Yaning, Z. Jisheng, R. Xingyue, Numerical Analysis and Performance Optimization of a Submerged Wave Energy Converting Device Based on the Floating Breakwater, Journal of Renewable and Sustainable Energy, 9 (2017) 044503. [CrossRef]
  7. H. Narayana, M. Sukomal, C. Subba Rao, S. G. Patil, Particle Swarm Optimization Based Support Vector Machine for Damage Level Prediction of Non-Reshaped Berm Breakwater, Applied Soft Computing, 27 (2015) 313-321. [CrossRef]
  8. L. Meng-Yu, L. Chiung-Yu, W. An-Pei, Particle Based Simulation for Solitary Waves Passing over a Submerged Breakwater, Journal of Applied Mathematics and Physics, 2 (2014) 269-276. [CrossRef]
  9. D. Fabio, D. Giovanna, C. Eugenio Pugliese, Simulation of Flow within Armour Blocks in a Breakwater, Journal of Coastal Research, 30(3) 528-536.
  10. Z. Na, G. Ke, Z. Wen Zhong, Two-Dimensional Numerical Wave Simulation for Port with Submerged Breakwater, Applied Mechanics and Materials, 226-228 (2012) 1343-1347. [CrossRef]
  11. T. Kasper, J.S. Steenfelt, L.M. Pedersen, P.G. Jackson, R.W.M.G. Heijmans, NStability of an immersed tunnel in offshore conditions under deep water wave impact, Coastal Engineering 55 (2008) 753–760. [CrossRef]
  12. Z. Kouroush Sadegh, Multi-objective Optimization in Variably Saturated Fluid Flow, Journal of Computational and Applied Mathematics, 223 (2009) 801–819. [CrossRef]
  13. R. Arman, S. Mehrzad, F. Meisam, E. Reza, Numerical Simulation and Optimization of Fluid Flow in Cyclone Vortex Finder, Chemical Engineering and Processing, 47 (2008) 128–137. [CrossRef]
  14. H. Dong-Soo, K. Chang-Hoon, K. Do-Sam, Y. Jong-Sung, Simulation of the Nonlinear Dynamic Interactions between Waves, a Submerged Breakwater and the Seabed, Ocean Engineering, 35 (2008) 511–522. [CrossRef]
  15. F. Koji, Effect of a Submerged Bay-Mouth Breakwater on Tsunami Behavior Analyzed by 2D/3D Hybrid Model Simulation, Springer Science+Business Media, (2006) 39:179–193. [CrossRef]
  16. F. Zhuang, C. Chang, J.J. Lee, Modelling of Wave Overtopping over Breakwater, Coastal Engineering, (1994) 1700-1712. [CrossRef]
  17. D. Yoo, Numerical Modelling of Wave-Induced Currents in a Breakwater Situation, International Journal for Numerical Methods in Engineer, 27 (1989) 21-35 . [CrossRef]
  18. Oleg Igorevich Gusev, Gayaz Salimovich Khakimzyanov, Vasiliy Savelievich Skiba, Leonid Borisovich Chubarov, NShallow water modeling of wave–structure interaction over irregular bottom, Ocean Engineering, 267 (2023) 113284. [CrossRef]
  19. Eliseo Marchesi, Marco Negri, Stefano Malavasi, Development and analysis of a numerical model for a two-oscillating-body wave energy converter in shallow water, Ocean Engineering 214 (2020) 107765. [CrossRef]
  20. I. Karmpadakis, C. Swan, M. Christou, A new wave height distribution for intermediate and shallow water depths, Coastal Engineering 175 (2022) 104130. [CrossRef]
  21. Mostafa M.A. Khater, Thongchai Botmart, NUnidirectional shallow water wave model; Computational simulations, Results in Physics 42 (2022) 106010. [CrossRef]
  22. Jens Wurm, Frank Woittennek , Energy-based Modeling and Simulation of Shallow Water Waves in a Tube with Moving Boundary, IFAC PapersOnLine 55-20 (2022)91–96. [CrossRef]
  23. Shuo Huang, Songwei Sheng, Yage You, Arnaud Gerthoffert, Wensheng Wang, Zhenpeng Wang, Numerical study of a novel flex mooring system of the floating wave energy converter in ultra-shallow water and experimental validation, Ocean Engineering 151 (2018) 342–354. [CrossRef]
  24. Alexander H. Boschitsch, Marcia O. Fenley, Hybrid Boundary Element and Finite Difference Method for Solving the Nonlinear Poisson–Boltzmann Equation,Journal of Computational Chemistry 25 (2003) 936-955. [CrossRef]
  25. Tsang-Jung Chang, Hsiang-Lin Yu, Chia-Ho Wang, Albert S. Chen, Dynamic-wave cellular automata framework for shallow water flow modeling,Journal of Hydrology 613 (2022) 128449. [CrossRef]
  26. R. S. Chen, Edward K. N. Yung, and Ke Wu, Efficient hybrid scheme of finite element method of lines for modelling computational electromagnetic problems, Int. J. Numer. Model. 2005; 18:49–66. [CrossRef]
  27. G. Kounadis, V.A. Dougalis, Galerkin finite element methods for the Shallow Water equations over variable bottom, Journal of Computational and Applied Mathematics 10 (2019) 0377-0427. [CrossRef]
  28. Prashant Kumar, Rupali, Modeling of shallow water waves with variable bathymetry in an irregular domain by using hybrid finite element method, Ocean Engineering 165 (2018) 386–398. [CrossRef]
  29. Zhiqing Zhang, Bohao Zhou, Xibin Li, and Zhe Wang, Second-order Stokes waveinduced dynamic response and instantaneous liquefaction in a transversely isotropic and multilayered poroelastic seabed, Front. Mar. Sci. 9:1082337. [CrossRef]
  30. Prashant Kumar, Rupali, Modeling of shallow water waves with variable bathymetry in an irregular domain by using hybrid finite element method, Ocean Engineering 165 (2018) 386–398. [CrossRef]
  31. Mohammad Hassan Shojaeefard, Seyed Davoud Nourbakhsh, Javad Zare, An investigation of the effects of geometry design on refrigerant flow mal-distribution in parallel flow condenser using a hybrid method of finite element approach and CFD simulation, Applied Thermal Engineering S1359-4311(16)32119-6. [CrossRef]
  32. Saray Busto, Michael Dumbser, and Laura Río-Martín, Staggered Semi-Implicit Hybrid Finite Volume/Finite Element Schemes for Turbulent and Non-Newtonian Flows, Mathematics 2021, 9, 2972. [CrossRef]
  33. Yasuhito Takahashi and Shinji Wakao, Large-Scale Magnetic Field Analysis by the Hybrid Finite Element-Boundary Element Method Combined with the Fast Multipole Method, Electrical Engineering in Japan, Vol. 162, No. 1, 2008. [CrossRef]
  34. Yang Jin, Shuai Li, Lu Ren, A new water wave optimization algorithm for satellite stability, Chaos, Solitons and Fractals 138 (2020) 109793. [CrossRef]
  35. Jiebin Liu, Rubing Ma, Yidan Yuan, Xiaoming Yang, Weimin Ma, Linear stability of a fluid mud-water interface under surface linear long traveling wave based on the Floquet theory,European Journal of Mechanics / B Fluids S0997-7546(20)30630-0. [CrossRef]
  36. M.A. Helal, A.R. Seadawy, M. Zekry, Stability analysis of solutions for the sixth-order nonlinear Boussinesq water wave equations in two-dimensions and its applications, Chinese Journal of Physics S0577-9073(16)30767-5. [CrossRef]
  37. M.A. Helal, Aly R. Seadawy, M. Zekry, Stability analysis solutions of the nonlinear modified Degasperis-Procesi water wave equation, Journal of Ocean Engineering and Science (2017). [CrossRef]
  38. Mitra Jahanbazi, Ilhan Özgen, Rui Aleixo and Reinhard Hinkelmann, Development of a diffusive wave shallow water model with a novel stability condition and other new features, Journal of Hydroinformatics. [CrossRef]
  39. L. Leshshafft, B. Hall, E.Meiburg, and B. Kneller, Deep-water sediment wave formation: linear stability analysis of coupled flow/bed interaction, J. Fluid Mech. (2011), vol. 680, pp. 435–458. [CrossRef]
  40. Steve Levandosky, Stability of solitary waves of a fifth-order water wave model, Physica D 227 (2007) 162–172. [CrossRef]
  41. Ying Wang, Yunxi Guo, Exact traveling wave solutions and L1 stability for the shallow water wave model of moderate amplitude, Anal.Math.Phys. [CrossRef]
  42. A.R. Seadawy, O.H. El-Kalaawy, R.B. Aldenari, Water wave solutions of Zufiria’s higher-order Boussinesq type equations and its stability, Applied Mathematics and Computation 280 (2016) 57–71. [CrossRef]
  43. C.-H. Tseng, Numerical Stability Verification of a Two-Dimensional Time-Dependent Nonlinear Shallow Water System Using Multidimensional Wave Digital Filtering Network, Circuits Syst Signal Process (2013) 32:299–319. [CrossRef]
  44. Omer K Kinaci, Omer F Sukas, and Sakir Bal, Prediction of wave resistance by a Reynolds-averaged Navier–Stokes equation–based computational fluid dynamics approach, J Engineering for the Maritime Environment 1–18. [CrossRef]
  45. Lin-an Liy, and Yo Wang, Stability of Planar Rarefaction Wave to Two-Dimensional Compressible Navier-Stokes Equations, Society for Industrial and Applied Mathematics 50-5 (2018), pp. 4937-4963. [CrossRef]
  46. Imène Hachicha, Global existence for a damped wave equation and convergence towards a solution of the Navier–Stokes problem, Nonlinear Analysis 96 (2014) 68–86. [CrossRef]
  47. K. Mahady, S. Afkhami, J. Diez, and L. Kondic, Comparison of Navier-Stokes simulations with long-wave theory: Study of wetting and dewetting, Physics of Fluids (1994-present) 25, 112103 (2013). [CrossRef]
  48. Bin Li, A 3-D model based on Navier–Stokes equations for regular and irregular water wave propagation, Ocean Engineering 35 (2008) 1842–1853. [CrossRef]
  49. Shuichi Kawashima, Peicheng Zhu, Asymptotic stability of nonlinear wave for the compressible Navier–Stokes equations in the half space,J. Differential Equations 244 (2008) 3151–3179. [CrossRef]
  50. Yeping Li, Vanishing viscosity and Debye-length limit to rarefaction wave with vacuum for the 1D bipolar Navier–Stokes–Poisson equation, Z. Angew. Math. Phys. (2016) 67:37. [CrossRef]
  51. Tai-Ping Liu, Shih-Hsien Yu, Numerical Modelling of Wave-Induced Currents in a Breakwater Situation, International Journal for Numerical Methods in Engineer,Found Comput Math. [CrossRef]
  52. M.M. Rahman, M.M. Noor, K. Kadirgama, M.A. Maleque and Rosli A. Bakar, Modeling, Analysis and Fatigue Life Prediction of Lower Suspension Arm, Advanced Materials Research Vols. 264-265 (2011) pp 1557-1562. [CrossRef]
  53. Tahseen Ahmad Tahseen, M. Ishak and M.M. Rahman, An experimental Study of Heat Transfer and Friction Factor Characteristics of Finned Flat Tube Banks with In-line Tubes Configurations, Applied Mechanics and Materials Vol. 564 (2014) pp 197-203. [CrossRef]
  54. Tulus, Mardiningsih, Sawaluddin, O S Sitompul, A K A M Ihsan, "Shear rate analysis of water dynamic in the continuous stirred tank, IOP Conf. Series: Materials Science and Engineering 308 (2018) 012048. [CrossRef]
  55. Tai-Ping Liu, Wave propagation for the compressible Navier–Stokes equations,ournal of Hyperbolic Differential Equations, Vol. 12, No. 2 (2015) 385–445. [CrossRef]
  56. Haiyan Yin, Jinshun Zhang, Changjiang Zhu, Stability of the superposition of boundary layer and rarefaction wave for outflow problem on the two-fluid Navier–Stokes–Poisson system, Nonlinear Analysis: Real World Applications 31 (2016) 492–512. [CrossRef]
  57. Tulus, T.J. Marpaung,Y.B. Siringoringo, M.R. Syahputra and Suriati, Heat Transfer Simulation on Window Glass Using COMSOL Multiphysic, IOP Conf. Series: Journal of Physics: Conf. Series 1235 (2019) 012065. [CrossRef]
  58. Tulus, C Khairani, T.J. Marpaung and Suriati, Computational Analysis of Fluid Behaviour Around Airfoil With Navier-Stokes Equation, Journal of Physics: Conference Series 1376 (2019) 012003. [CrossRef]
  59. Masna, Tulus and Sawal, "Computational analysis dynamics fluid of flow in dam using COMSOL Multiphysics,Journal of Physics: Conference Series 2421 (2023) 012047. [CrossRef]
  60. Ting Luo, Stability of the composite wave for compressible Navier-Stokes-Allen-Cahn system, Math. Models Methods Appl. Sci. [CrossRef]
  61. Isabel Mercader, Oriol Batiste, and Arantxa Alonso, Continuation of travelling-wave solutions of the Navier–Stokes equations,Int. J. Numer. Meth. Fluids 2006; 52:707–721. [CrossRef]
  62. Xiongfeng Yang, The stability of rarefaction wave for Navier–Stokes equations in the half-line,Math. Meth. Appl. Sci. 2011, 34 1366–1380. [CrossRef]
  63. R. Dewi, Tulus, M. Zarlis and E. B. Nababan, "Integrating Ambulance into GIS in Smart City: Problems and Prospect with P-Median Model," 2022 4th International Conference on Cybernetics and Intelligent System (ICORIS), Prapat, Indonesia, 2022, pp. 1-4. [CrossRef]
  64. Tulus, T J Marpaung, and J L Marpaung, "Computational Analysis for Dam Stability Against Water Flow Pressure, Journal of Physics: Conference Series 2421 (2023) 012013. [CrossRef]
  65. Tulus, J.L. Marpaung, T.J. Marpaung, and Suriati, Computational analysis of heat transfer in three types of motorcycle exhaust materials, Journal of Physics: Conference Series 1542 (2020) 012034. [CrossRef]
Preprints 72385 g001
Figure 1. Submerged Permeable Breakwater Simulation.
Figure 1. Submerged Permeable Breakwater Simulation.
Preprints 72385 g001
Preprints 72385 g003
Figure 3. Breakwater Geometry Model
Figure 3. Breakwater Geometry Model
Preprints 72385 g003
Preprints 72385 g008
Figure 8. Simulation of the velocity of the breakwater breaking process at t = 10 s
Figure 8. Simulation of the velocity of the breakwater breaking process at t = 10 s
Preprints 72385 g008
Preprints 72385 g009
Figure 9. Water wave amplitude breaking
Figure 9. Water wave amplitude breaking
Preprints 72385 g009
Preprints 72385 g010
Figure 10. The results of the wave amplitude simulation in the wave breaking process
Figure 10. The results of the wave amplitude simulation in the wave breaking process
Preprints 72385 g010
Preprints 72385 g011
Figure 11. Resistance of Breakwaters to Changes in Speed
Figure 11. Resistance of Breakwaters to Changes in Speed
Preprints 72385 g011
Preprints 72385 g012
Figure 12. Changes in velocity after wave damping with variations in breakwater distance, namely (a) = 10 m, (b) = 15 m, and (c) = 20 m with conditions v=1 m/s
Figure 12. Changes in velocity after wave damping with variations in breakwater distance, namely (a) = 10 m, (b) = 15 m, and (c) = 20 m with conditions v=1 m/s
Preprints 72385 g012
Preprints 72385 g013
Figure 13. Stability simulation with differences 9.52 m, 14.52 m and 19.52 m wave position
Figure 13. Stability simulation with differences 9.52 m, 14.52 m and 19.52 m wave position
Preprints 72385 g013
Preprints 72385 g014
Figure 14. The difference between the change in the value of λ and the variation in the speed of the incident wave is (a) = 1 m/s, (b) = 1.5 m/s, (c) = 2 m/s
Figure 14. The difference between the change in the value of λ and the variation in the speed of the incident wave is (a) = 1 m/s, (b) = 1.5 m/s, (c) = 2 m/s
Preprints 72385 g014
Table 1. Amplitude Magnitude to variety of position.
Table 1. Amplitude Magnitude to variety of position.
u(x,t) h b =1,196 h b =1,696 h b =2,196
x=9,52 0.13439 0.13438 0.13097
x=14,52 0.13988 0.13859 0.13161
x=19,52 0.043203 0.12468 0.12515
Table 2. Amplitude Magnitude to variety of inlet velocity.
Table 2. Amplitude Magnitude to variety of inlet velocity.
u(x,t) h b =1,196 h b =1,696 h b =2,196
u t =1 0.039990 0.12481 0.12538
u t =1,5 0.090519 0.12726 0.12909
u t =2 0.23979 0.21846 0.23229
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated