Prerpints.org logo
Preprint
Communication

Generation of Ultrashort Pulses in XUV and X-ray FELs via an Excessive Reverse Undulator Taper

Altmetrics

Downloads

92

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 April 2023

Posted:

30 April 2023

You are already at the latest version

Alerts
Abstract
The pulse duration in short-pulse schemes for Self-Amplified Spontaneous Emission Free Electron Lasers (SASE FELs) is limited by the FEL coherence time. A recently proposed concept allows to overcome the coherence time barrier and to get much shorter pulses. When the lasing part of an electron bunch is much shorter than the coherence time, one can suppress the radiation in the long main undulator while preserving microbunching within that short lasing slice. Then a short radiation pulse is produced in a relatively short radiator. A possible suppression method, an excessive reverse undulator taper, is discussed and illustrated numerically in this paper. We also performed first experimental tests of this method at the soft X-ray FEL user facility FLASH. The measured pulse duration approaches 1 fs (FWHM) at the wavelength of 5 nm.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

A possibility to generate few- and sub-femtosecond pulses in Extreme Ultraviolet (XUV) and X-ray FELs was studied theoretically over last twenty years [1,2,3,4,5,6,7], and successful experimental demonstration of production of sub-femtosecond pulses was achieved recently [8,9,10,11]. Typically, the shortest pulse that can be generated in a SASE FEL is limited by FEL coherence time [12] which is given by the slippage of radiation with respect to electrons per FEL gain length.
A method to go beyond the coherence time limit in SASE FELs was proposed in [13]. One can create a short lasing slice within the electron bunch (much shorter than FEL coherence time). In the long main undulator due to the SASE process a microbunching (density modulation at the resonance wavelength) is generated within that short slice but the radiation pulse is much longer (on the order of coherence time) due to the slippage in the undulator. At the second step the modulated electron bunch produces a short radiation pulse in a short radiator, and the long radiation pulse from the main undulator is suppressed or separated from the short pulse. A specific way of selection of a short lasing slice, a laser manipulation of electron bunch with subsequent use of so-called chirp-taper scheme [6] was considered in [13]. However, the general principle can be used for different ways of creation of a short lasing slice, also without a laser. Different methods of suppression (separation) were discussed in [13], one of them is the application of an excessive reverse taper in the main undulator. In this communication we discuss this method in more details and illustrate it with numerical simulations for a short electron bunch, produced in the accelerator without laser manipulation of its properties. We also present first experimental results from XUV and soft X-ray FEL user facility FLASH [14].

2. The concept of excessive reverse taper

To generate short X-ray pulses (much shorter than FEL coherence time) in a SASE FEL, one can make two steps:
  • to generate a short electron bunch (or a short lasing part within longer bunch) and
  • to apply a slippage-suppression mechanism in the undulator.
The latter can be realized in different ways proposed in [13]. In this paper we consider one of them, reverse undulator taper (see Figure 1). The scheme is based on the effect discovered in [15]: in a reverse-tapered undulator the radiation power is strongly suppressed while bunching in the electron beam survives. Reverse taper means an increase of the undulator K value along the undulator length (this can be done by reducing the gaps of undulator segments), in contrast to the standard sign of taper when the K decreases in order to maintain resonance after FEL saturation thus increasing radiation power. A long electron bunch was considered in [15] but the concept also works for short bunches as will be illustrated numerically below in this paper. A short electron bunch propagates in a reverse-tapered main undulator where a strong microbunching is created but the radiation is very weak (and the radiation pulse is much longer than the modulated part of the electron bunch). Then the bunch enters a short radiator, tuned to the resonance with the modulated beam, and produces a short (much shorter than FEL coherence time) and intense radiation pulse. An optimal number of periods in the undulator is approximately equal to the number of cycles in the microbunching. By a proper adjustment of parameters, the radiation background from the main undulator can be made negligible.
Short electron bunches can be generated in accelerator systems by a strong (linear or nonlinear) compression of initially long bunches. In case of nonlinear compression one typically gets a short high-current leading peak (that is lasing) and a low-current long tail [8,14]. One can also use self-fields of the bunch to create high-current spikes in a dedicated chicane [9]. Alternatively, manipulations of long electron bunches with optical lasers, creating a lasing slice that is shorter than the laser wavelength, can be used. There are two most popular laser-based schemes: chirp-taper [6] and eSASE [5]. In the chirp-taper scheme there is a short slice with the strong energy chirp being created by a laser beam in a short undulator. It was shown in [6] that a degrading effect of a linear energy chirp on SASE FEL gain can be compensated for by applying a linear undulator taper as soon as the following condition is satisfied:
d K d z = ( 1 + K 0 2 / 2 ) 2 K 0 1 γ 0 3 d γ d s i n
Here K 0 is the value of undulator parameter at the undulator entrance, ( d γ / d s ) i n is the energy chirp at the undulator entrance, z is the coordinate along the undulator length, and s is the coordinate along the bunch length. The compensation takes place within the slice with the strongest chirp. The rest of the bunch is unchirped (or weakly chirped) and suffers from a strong uncompensated taper, i.e. it practically does not lase.
In the eSASE scheme the laser-induced energy modulation is converted into a density modulation in a chicane, so that a sharp current spike is created that lases most efficiently in the SASE undulator in a similar way as a short bunch generated without a laser. The energy chirp can be created by collective fields of the short bunch itself. The main effect is usually Longitudinal Space Charge (LSC) in the X-ray undulator. It scales there as 1 / γ z 2 = ( 1 + K 2 / 2 ) / γ 2 [16], i.e. it can be much stronger than in a drift (where K = 0 ). When the chirp is mainly accumulated in the undulator and the bunch is sufficiently short, the linear taper in Eq. (1) can be substituted by quadratic taper:
d 2 K d z 2 = ( 1 + K 0 2 / 2 ) 2 K 0 1 γ 0 3 d 2 γ d s d z
with d 2 γ / d s d z being the rate of change of the energy slope d γ / d s along the undulator length. When the energy chirp is accumulated inside and in front of the undulator, the tapering law for compensation can be described as follows:
K ( z ) = K 0 + d K d z z + 1 2 d 2 K d z 2 z 2
with the derivatives from (1) and (2). Thus, for compensation of LSC-induced energy spread one can use both a reverse linear taper and a reverse quadratic taper. Of course, the LSC-induced chirp is nonlinear while the conditions (1) and (2) are valid for a linear chirp. It means that these conditions can provide only a partial compensation which might be sufficient in some practical situations. The LSC-induced chirp has a positive derivative d γ / d s so that K must increase along the undulator length for compensation, i.e. one has to use a reverse taper.
For the purpose of the considered scheme, one should use a stronger reverse taper than that needed for chirp compensation, that is why we call the method “excessive reverse taper”. One can choose excessive linear or quadratic taper in order to suppress the radiation while keeping the strong bunching (more sophisticated taper laws can be considered as well). The proposed scheme works for chirped and unchirped bunches as will be illustrated in the next Section. The concept is easy to realize in practice since the undulator systems of X-ray FELs consist of relatively short segments. Thus, a reverse taper can be applied to a long string of segments while the last one can be used as a radiator. If it is too long, one can install a dedicated short radiator.

3. Numerical example

We illustrate the concept of excessive reverse taper with the parameters of FLASH2 undulator of FEL user facility FLASH, see detailed description in the next Section. The variable-gap undulator consists of twelve segments, each of them has a period of 3.14 cm and is 2.5 m long. We consider an electron beam with the following parameters: energy is 1.2 GeV, rms bunch duration is 1 fs, peak current is 2 kA, rms normalized emittance is 0.8 mm mrad, and rms uncorrelated energy spread is 300 keV. Average beta-function in the undulator is 7 m. FEL wavelength is 5 nm which corresponds to K = 1.24. The FEL simulations are performed with the code SIMPLEX [17].
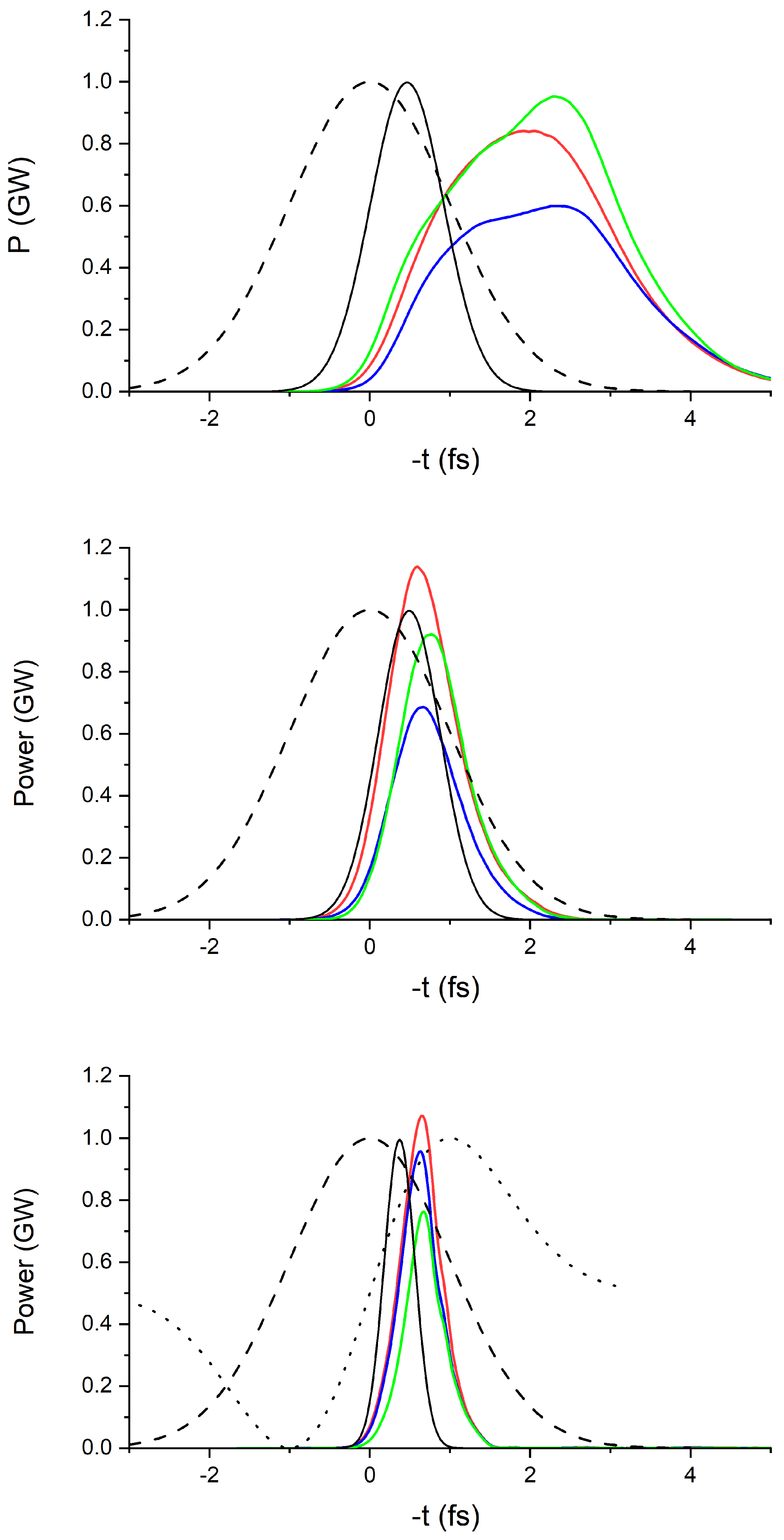
First, we simulate standard SASE regime and ignore LSC effects. The number of undulator segments is 9, and the amplification process is stopped at the onset of saturation. If the undulator is longer, the radiation pulses are getting longer too, but the peak power does not increase. Three typical shots are presented on Figure 2 (upper plot), as three color lines, typical pulse duration is 3 fs (FWHM). The current distribution I ( t ) is shown with dashed line while the solid black line represents the function [ I ( t ) | b ( t ) | ] 2 with b ( t ) being the bunching factor [12] for a typical shot. If the bunching factor is real, the function [ I ( t ) | b ( t ) | ] 2 gives a radiation power profile from a short radiator. One can notice that the radiation pulses on Figure 2 (upper plot) are essentially longer due to the slippage in the last part of the undulator.
Second, we simulate the reverse-tapered configuration, assuming again no energy chirp due to LSC. We use eleven undulator segments and apply the linear reverse taper with the strength d K / d z = 1.5 × 10 − 3 m − 1 to obtain a strong bunching ( ≃ 0.4 − 0.5 ) while suppressing the radiation in this undulator. The radiator has the same period as segments of the main undulator but the number of periods is reduced to 50, the value of K is optimized at 1.243. We also focus the electron beam stronger in the radiator, the beta-function is 2 m. This helps us to increase the radiation power and improve the contrast of short pulses. The results of numerical simulations are shown on Figure 2 (middle plot). Three typical shots are shown as color plots, the pulse duration is now about 1 fs. The function [ I ( t ) | b ( t ) | ] 2 has now smaller width than that for the standard SASE regime shown on the upper plot, thus we can conclude that the excessive reverse taper effectively reduces the width of generated bunching distribution.
Third, we include the LSC-induced energy chirp [16] in the undulator in our simulations. The shape of LSC-wake is shown in Figure 2 (lower plot), it has zero crossing at the location of the maximum current (note that the dotted line is shifted vertically). At the end of the undulator the peak-to-peak energy deviation is about 12 MeV. The main undulator consists of eleven segments, we apply the excessive reverse quadratic taper d 2 K / d z 2 = 5.5 × 10 − 4 m − 2 . The number of periods in the radiator is 50, K equals 1.39, beta-function is 2 m. From Figure 2 (lower plot) one can see that the width of the function [ I ( t ) | b ( t ) | ] 2 is reduced further, this is the consequence of nonlinear energy chirp [18] and excessive reverse taper. Radiation pulses have average duration of 0.6 fs.
We can conclude that our concept (excessive reverse taper in the main undulator plus a short radiator) works well with and without energy chirp, but a strong chirp helps further reduce pulse duration. In principle, the reduction of pulse duration with respect to a standard SASE case can be much stronger than in the considered numerical example provided that one can generate ultrashort electron bunches (or their lasing parts). In other words, there is no conceptual lower limit for FEL pulse duration except the applicability of the standard FEL theory (a pulse must contain many cycles).

4. Experiment at FLASH

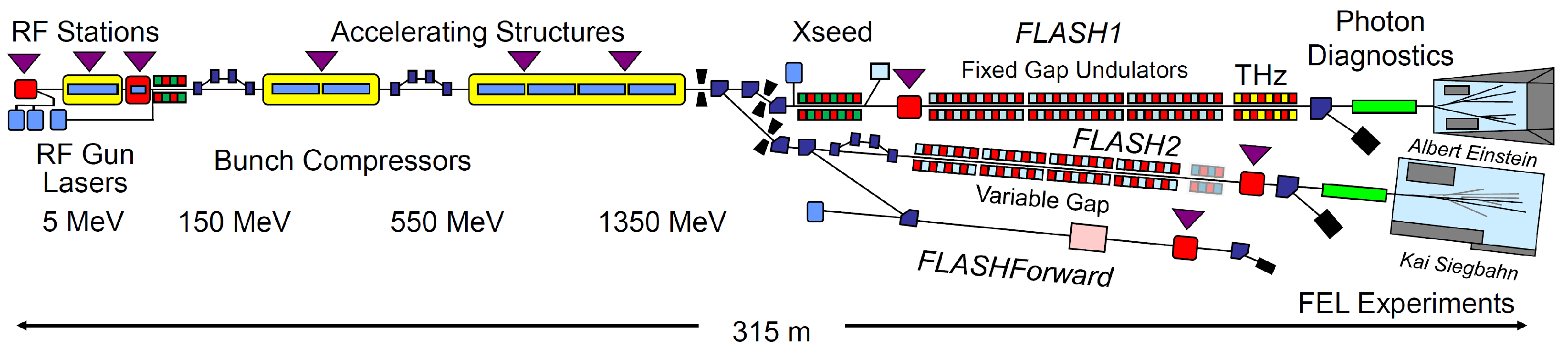
FLASH [14] is the first free-electron laser for XUV and soft X-ray radiation. It covers a wavelength range from 4 nm to about 90 nm with GW peak power and pulse durations between a few fs and 200 fs. The electron bunches with maximum energy of 1.35 GeV are distributed between the two branches, FLASH1 and FLASH2 [19], see Figure 3. The facility is based on the superconducting accelerator which allows to operate in a “burst mode” with long pulse trains (several hundred pulses) at 10 Hz repetition rate. Presently, the facility is being upgraded towards high repetition rate seeding in the FLASH1 branch [20]. The segmented variable-gap undulator of FLASH2 has a period of 3.14 cm and can provide a maximum undulator parameter K about 2.7. FLASH2 hosts twelve 2.5 m long segments with quadrupoles in the intersections.
Electron bunches for FLASH2 are produced in the photoinjector and then longitudinally compressed in three bunch compressors at different electron energies. The last compressor is placed in front of the undulator and the compression takes place at the final beam energy. This simplifies the task of formation of short high-current bunches because the impact of collective effects such as coherent synchrotron radiation and space charge on a quality of short electron bunches are reduced with respect to a final compression at lower energies. Nevertheless, the LSC effect can still be significant as soon as the bunches are strongly compressed.
The experiment was performed in March 2023. The electron energy was 1.2 GeV, the FEL wavelength was 5 nm, undulator K was 1.24. We used a photoinjector laser with 1 ps duration to generate an electron bunch with a charge 80 pC. We performed nonlinear compression [14] in order to generate a short high-current leading peak for production of short radiation pulses. The undulator configuration was as follows: eleven segments were linearly reverse-tapered with the strength d K / d z = 2 × 10 − 3 m − 1 . The 12th undulator segment played the role of the radiator, the value of K was 1.265. In order to effectively reduce the length of this radiator, we used an ambient field correction coil to turn the beam inside that segment, and then we used an iris to cut a part of the photon beam that was horizontally streaked. Average pulse energy in this configuration was 1.5 μ J during the measurement. We used the grating spectrometer [21] to make sure that we generate a single SASE spike [12], or a single longitudinal mode in other words.
To measure pulse duration, we used the autocorrelation method. The split-and-delay unit [22] with the time resolution 120 as was used, the two beams were combined on the screen creating interference fringes. By scaning the delay and measuring the visibility of fringes, we can measure the field autocorrelation: ning the delay and measuring the visibility of fringes, we can measure the field autocorrelation:
A ( τ ) ∝ ∫ − ∞ ∞ E ( t ) E * ( t − τ ) d t
where E ( t ) is the complex amplitude of the electric field. More precisely, we measure the ensemble-averaged modulus of the field autocorrelation.
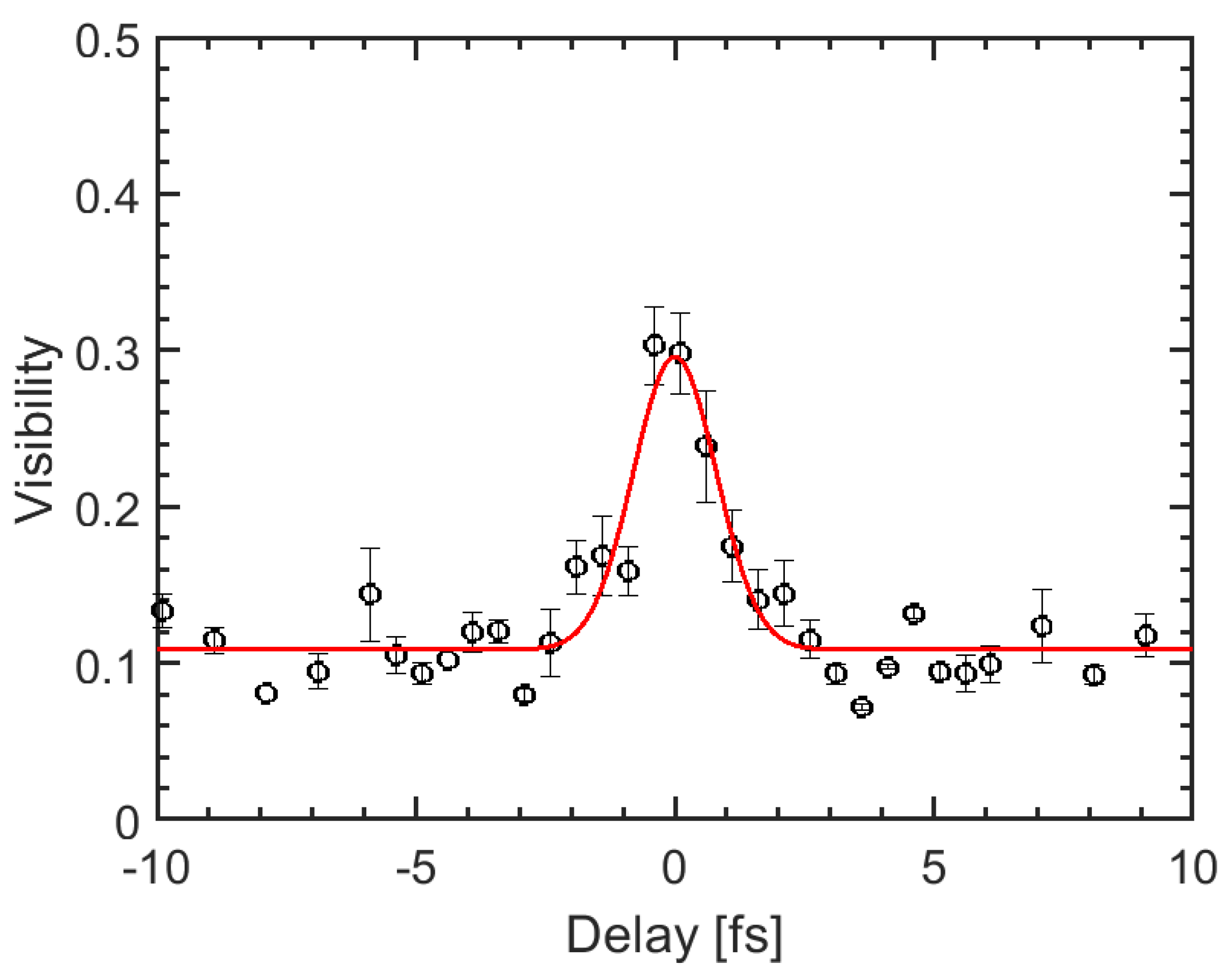
The measured autocorrelation trace is shown in Figure 4. The full width at half maximum (FWHM) of this trace is 1.88 ± 0.21 fs.
The next task is to estimate pulse duration from this measurement. For a Gaussian laser pulse without a frequency chirp, the relation between the FWHM of the intensity distribution τ I F W H M and the FWHM of the field autocorrelation τ A C F W H M is given by a simple relation:
τ I F W H M = 0.5 τ A C F W H M
Our pulses are, in general, non-Gaussian and they can have frequency chirps. To estimate the pulses duration from autocorrelation measurement we can use the coefficient found in numerical simulations. We ran simulations of the considered scheme with different parameters of electron bunch resulted in different energy chirps, and we also considered the case with no chirp. We compared the average pulse duration and the width of the average autocorrelation function in those simulations. We found that instead of factor 0.5 in Eq. (5) we should use the factor 0.67 ± 0.12 , i.e.
τ I F W H M = 0.67 τ A C F W H M
Thus, to our best knowledge, we can estimate pulse duration in this experiment at τ I F W H M = 1.26 ± 0.37 fs.

5. Discussion

In this communication we demonstrated in numerical simulations the validity of previously proposed method [13] of generation of short pulses in SASE FELs, namely excessive reverse taper in the main undulator in combination with a short radiator. Moreover, we performed the experiment at the soft X-ray FEL user facility FLASH and obtained record short pulses for this facility using the proposed undulator configuration. In the future we plan to reduce bunch charge further and to try nonlinear as well as linear compression, and to operate at a higher electron energy and a shorter wavelength (below 4 nm) in order to be able to produce sub-femtosecond pulses at FLASH.

Author Contributions

Conceptualization, E.S.; methodology, E.S.; software, M.D.; validation, E.S. and M.D.; formal analysis, E.S.; investigation, E.S., M.D., M.K., J.R.-S., and H.Z.; resources, M.D., M.K., and H.Z.; data curation, E.S., M.D., H.Z. and M.K.; writing—original draft preparation, E.S.; writing—review and editing, E.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

We would like to thank scientific and technical staff of FLASH for support. We are grateful to L. Schaper for careful reading of the manuscript and useful suggestions, and to W. Leemans for his interest in this work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. E.L. Saldin, E.A. Schneidmiller, M.V. Yurkov, Optics Communications 2002, 212, 377.
  2. E.L. Saldin, E. A. Schneidmiller and M. V. Yurkov, Optics Communications 2004, 237, 153–164.
  3. A.A. Zholents and W.M. Fawley, Phys. Rev. Lett. 2004, 92, 224801.
  4. P. Emma, Z. P. Emma, Z. Huang and M. Borland, Proc. of the FEL2004 Conference, p. 333, http://www.jacow.
  5. A.A. Zholents and G. Penn, Phys. Rev. ST Accel. Beams 2005, 8, 050704.
  6. E.L. Saldin, E.A. Schneidmiller and M.V. Yurkov, Phys. Rev. ST Accel. Beams 2006, 9, 050702.
  7. Y. Ding et al. Phys. Rev. ST Accel. Beams 2009, 12, 060703.
  8. S. Huang et al. Phys. Rev. Lett 2017, 119, 154801.
  9. J. Duris et al. Nature Photonics 2020, 14, 30.
  10. A. Malyzhenkov et al. Physical Review Research 2020, 2, 042018.
  11. A. Trebushinin et al. Photonics 2023, 10, 131.
  12. E.L. Saldin, E.A. E.L. Saldin, E.A. Schneidmiller and M.V. Yurkov, ‘‘The Physics of Free Electron Lasers’’, Springer, Berlin. 1999. [Google Scholar]
  13. E.A. Schneidmiller. Rev. Accel. Beams 2022, 25, 010701.
  14. W. Ackermann et al. Nature Photonics 2007, 1, 336.
  15. E. A. Schneidmiller and M. V. Yurkov. Phys. Rev. ST Accel. Beams 2013, 16, 110702.
  16. G. Geloni et al., Nucl. Instr. and Methods 2007, A583, 228.
  17. T. Tanaka, J. Synchrotron Rad. 2015, 22, 1319.
  18. P. Baxevanis et al. Phys. Rev. Accel. Beams 2018, 21, 110702.
  19. B. Faatz et al. New Journal of Physics 2016, 18, 062002.
  20. L. Schaper et al., Appl. Sci. 2021, 11(20), 9729.
  21. T. Tanikawa et al., Nucl. Instrum. and Meth. 2016, 830, 170–175.
  22. M. Dreimann et al. Journal of Synchrotron Radiation 2023, 30, 479.
Preprints 72271 g001
Figure 1. Conceptual scheme of ultrashort pulse production. A short electron bunch propagates in the reverse-tapered main undulator followed by a short radiator.
Figure 1. Conceptual scheme of ultrashort pulse production. A short electron bunch propagates in the reverse-tapered main undulator followed by a short radiator.
Preprints 72271 g001
Preprints 72271 g002
Figure 2. Typical radiation pulses (color lines) for three different configurations: standard SASE, no LSC (upper plot), reverse linear taper in the main undulator plus short radiator, no LSC (middle plot), and excessive reverse quadratic taper in the main undulator plus short radiator, LSC in the undulator included (lower plot). Black dashed lines represent the current profile I ( t ) (bunch head is on the right), black solid lines show the product [ I ( t ) | b ( t ) | ] 2 for a typical shot, dotted line on the lower plot shows the shape of LSC-wake. All black curves are presented in arbitrary units for a vertical scale, the color curves show radiation power in gigawatts.
Figure 2. Typical radiation pulses (color lines) for three different configurations: standard SASE, no LSC (upper plot), reverse linear taper in the main undulator plus short radiator, no LSC (middle plot), and excessive reverse quadratic taper in the main undulator plus short radiator, LSC in the undulator included (lower plot). Black dashed lines represent the current profile I ( t ) (bunch head is on the right), black solid lines show the product [ I ( t ) | b ( t ) | ] 2 for a typical shot, dotted line on the lower plot shows the shape of LSC-wake. All black curves are presented in arbitrary units for a vertical scale, the color curves show radiation power in gigawatts.
Preprints 72271 g002
Preprints 72271 g003
Figure 3. FLASH layout.
Figure 3. FLASH layout.
Preprints 72271 g003
Preprints 72271 g004
Figure 4. Field autocorrelation trace (measurement).
Figure 4. Field autocorrelation trace (measurement).
Preprints 72271 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated