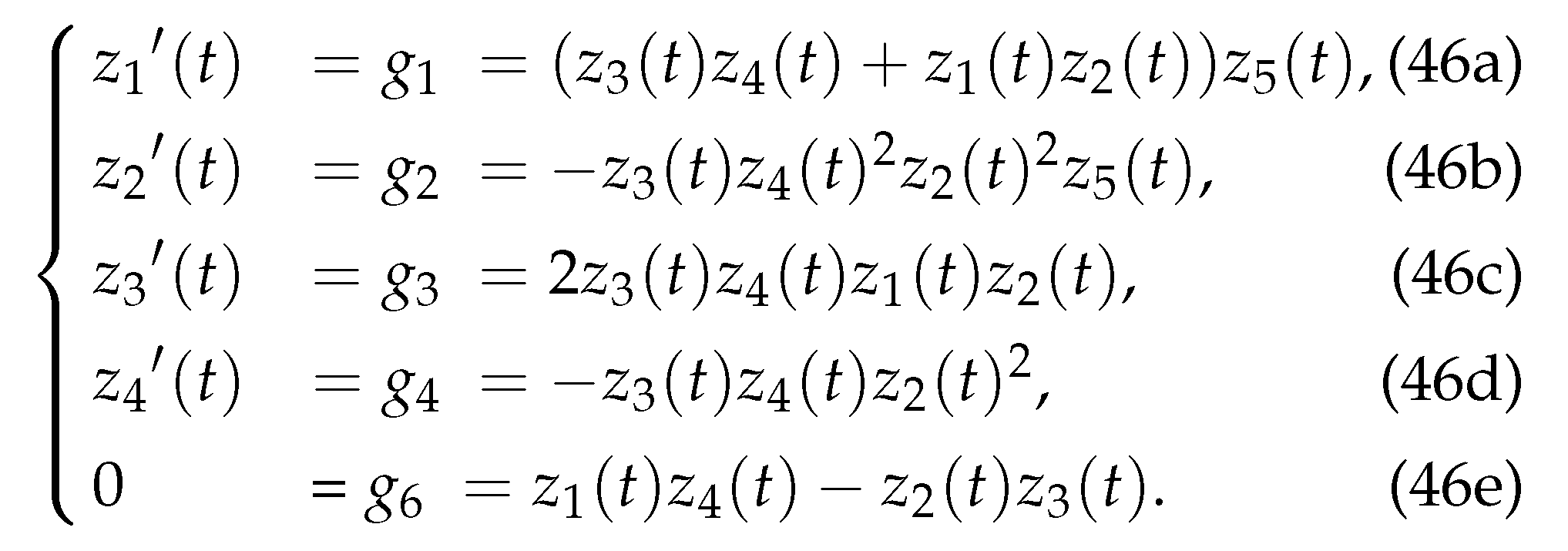1. Introduction
Differential-Algebraic Equations (DAEs) are a class of mathematical models that arise in various fields, such as multibody dynamics [
1], electrical circuits [
2], fluid mechanics [
3], optimal control [
4] and chemical reactions [
5]. DAEs are a natural extension of ordinary differential equations that also involve algebraic equations. As such, they offer a convenient way to model complex systems that involve both dynamic and algebraic components. The study of DAEs has been an active area of research for many years, and numerous numerical methods have been developed to solve these DAEs, particularly for low index systems. These methods include well known Runge-Kutta methods [
6,
7,
8], backward differentiation formulae [
9,
10],and others. However, the efficient solution of DAEs remains a challenging problem due to the presence of algebraic equations that may be nonlinear, implicit, and of high index.
Hessenberg differential algebraic equations (Hessenberg-DAEs) are an important type of differential equation which are also commonly used in the modeling of mechanical systems and electrical circuits.Because of their unique structure, numerical methods for solving Hessenberg-DAEs can differ significantly from those used for other types of differential equations. Over the years, some approaches have been proposed for the numerical solution of Hessenberg-DAEs, including variational iteration method [
11], adomian decomposition method for [
12], exponential integrators [
13]. These methods either lack rigorous theoretical analysis or are only suitable for low-index systems.
One promising approach is the Lie group method whose several variations have been developed specifically for solving (Hessenberg) DAEs with high index in recent years. Lie group methods mostly constitute one-step extensions of classical methods, including Runge-Kutta type formulas [
14]. In mechanical engineering, BDF methods, which have traditionally been used, have been extended to Lie groups as well [
15]. Despite their usefulness, these methods suffer from a numerical disadvantage. Various numerical techniques can be used to compute the matrix exponential, but the properties of these methods, such as stability, accuracy, and efficiency, can impact the results of the Lie-group methods. Based on the structural information of Hessenberg DAEs, C.S.Liu [
16,
17,
18] propose a Lie-group differential algebraic equations (LGDAE) method. By converting the canonical representation of the governing equations for nonholonomic systems, the LGDAE method expresses them in the form of DAE systems, comprising of nonlinear ordinary differential equations and nonlinear algebraic equations. The method is composed of two components: the first component pertains to the Lie-group structure and concerns the numerical solution of nonlinear ordinary differential equations. The second component, the Newton iterative scheme, is used to solve the nonlinear algebraic equations. The LGDAE method has been successfully employed to solve various practical problems such as the heat source recovery problem [
19,
20], sliding mode control problem [
21], and inverse nonlinear vibration problems [
22]. However, it is noteworthy that the LGDAE method is only applicable to systems with index 2.
The main focus of this paper is to investigate Lie group methods for Hessenberg-DAEs with an index of 3 or higher. We present a modified extended Lie group method that incorporates the benefits of Liu’s original method, along with the structural characteristics of Hessenberg-DAEs. Our proposed method enables the accurate solution of high-index Hessenberg-DAEs and effectively captures the behavior of solutions to algebraic constraints. We demonstrate the effectiveness of our method through numerical experiments on some benchmark problems.
The structure of this paper is as follows.
Section 2 presents a brief introduction to Hessenberg-DAEs and Lie group methods. In
Section 3, we present our novel modified extended Lie group DAE method for Hessenberg-DAEs with an index of 3,and provide a theoretical justification for the proposed method.
Section 4 presents the results of numerical experiments on several benchmark problems. Finally, we conclude with a discussion of our results and directions for future research in
Section 5.
2. Preliminaries
In this section, we provide a concise overview of Hessenberg-DAEs and an implicit Lie group methods.
2.1. Hessenberg DAEs
A system of ordinary differential equations (ODEs) with algebraic constraints which can be written in the general form as
is called differential algebraic equation, where
may be singular and the structure and rank of the of this Jacobian matrix may depend on the solution
. An important special case of
1 is the semi-explicit DAE of the form
whose index is 1 if the Jacobian matrix function
is assumed to be nonsingular for all
t. Hessenberg Index-1 is also often referred to as a semi-explicit index-1 system.
Definition 1.
Hessenberg Index-2
where are sufficiently differentiable, the variables of the algebraic part is absent from the constraint and the product of Jacobians is nonsingular. Thus, all algebraic variables play the role of index-2 therefore this is a pure index-2 DAE.
Definition 2.
Hessenberg Index-3
In this case the product of three matrix functions is nonsingular, where , and are , and dimensions respectively. The index of a Hessenberg DAE is found, as in the general case, by differentiation. However, only the algebraic constraints must be differentiated.
Definition 3.
Hessenberg Index-r
In this case the product of three matrix functions is nonsingular.
2.2. Lie group structure of ODEs
A Lie group is a differentiable manifold equipped with a group structure that is consistent with the underlying topology of the manifold. The general linear group is a Lie group, whose manifold is an open subset . Thus, is also an -dimensional manifold. The group composition is given by the matrix multiplication.
The general linear group
gives uniquely a real Lie-algebra
. Consider a one-parameter subgroup
,
, of the general linear group
, which is a curve passing through the group identity at
,
, and which left acts on the n-dimensional Euclidean space
, resulting in a congruence of curves in
,
Owing to the closure property of the Lie group,
also belongs to
. When
is put very close to
t,
is very close to the identity
. Moreover,
defines a string of tangent vectors on the tangent space at the group identity of the group manifold, more precisely, a continuously singly parametrized series of one-dimensional sub-algebra of the real Lie algebra
.
Differentiating Eq. (6), setting
and then using Eq. (7) yields
The flow generated by such a vector field is the congruence of curves resulting from solving the system (8). Essentially, it is very important that when one wants to establish a local coordinate on a smooth manifold on which a finite dimensional Lie-group of transformations is acting, the solution of the differential equations system is necessary.
The Lie-group method possesses a greater advantage than other numerical methods due to its Lie-group structure, and it is a powerful technique to solve ordinary differential equations (ODEs). Here we give a new form of the dynamics in Eq. (4a) or (4b) from the
Lie-group structure. In order to fit the format in Eq. (8), the vector field
on the right-hand side of Eq. (4a) or (4b) can be written as
where
is the coefficient matrix and
denotes the dyadic operation of
and
b, i.e.,
. Here we suppose that
.
2.3. An implicit Lie-group method
The equation (9) provides a new starting point for constructing the Lie-group
approach. In order to develop a numerical scheme, we suppose that the coefficient matrix
is constant with
which can be obtained by taking the values of
and
at a suitable mid-point of
, where
and
h is a small time stepsize.
By introducing new variables
, we obtain an augmented dynamical system
Because the state matrix in Eq. (11) can be decomposed as
the solution of the linear dynamical system can be written analytically as follows
where
,
. We reduce the augmented
system to the
system, obtaining
and
. Note that
is indeed an element in the Lie group
. Therefore, by introducing the auxiliary variable
and the augmented system, we are able to derive an explicit expression for the components of a one-parameter group
.
3. MELGDAE method for index-3 Hessenberg-DAEs
In this section, we present a novel modified extended Lie group DAE (MELGDAE) method for Hessenberg-DAEs with an index of 3,and provide a theoretical justification for the proposed method.
We first calculate the solution by the given variables , , then obtain the solution via given variables , and . Moreover, we compute the solution by the resulting value of and . Hereafter, we denote the loop that solves for the variable as the -loop. The MELGDAE method, which is presented in detail below, utilizes the notation .
-
For the -Loop:
- S1:
Give , , .
- S2:
Estimate
via Euler method as follow,
- S3:
Let .
- S4:
Compute :
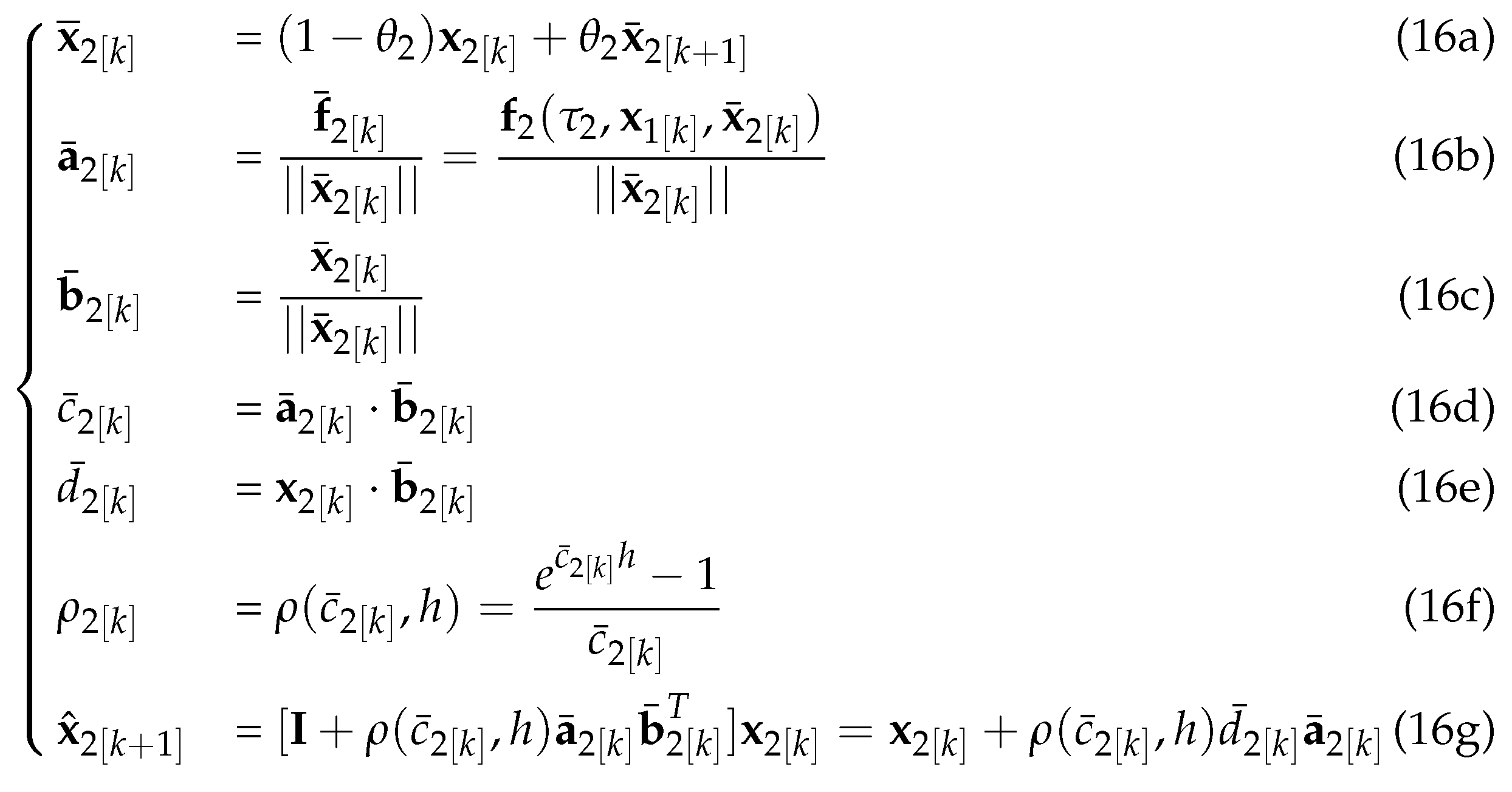
- S5:
If
convergers according to a given stopping criterion
then let
; otherwise, let
and goto S4.
-
For the -Loop:
- S1:
Give , , , resulting from the -Loop.
- S2:
Estimate
via Euler method as follow,
- S3:
Let .
- S4:
Compute :

- S5:
If
convergers according to a given stopping criterion
then let
; otherwise, let
and goto S4.
-
For the -Loop:
- S1:
Let ,.
- S2:
Compute
via Newton iterative method:
where
,
,
. We could obtain
,
from Eq. (14).

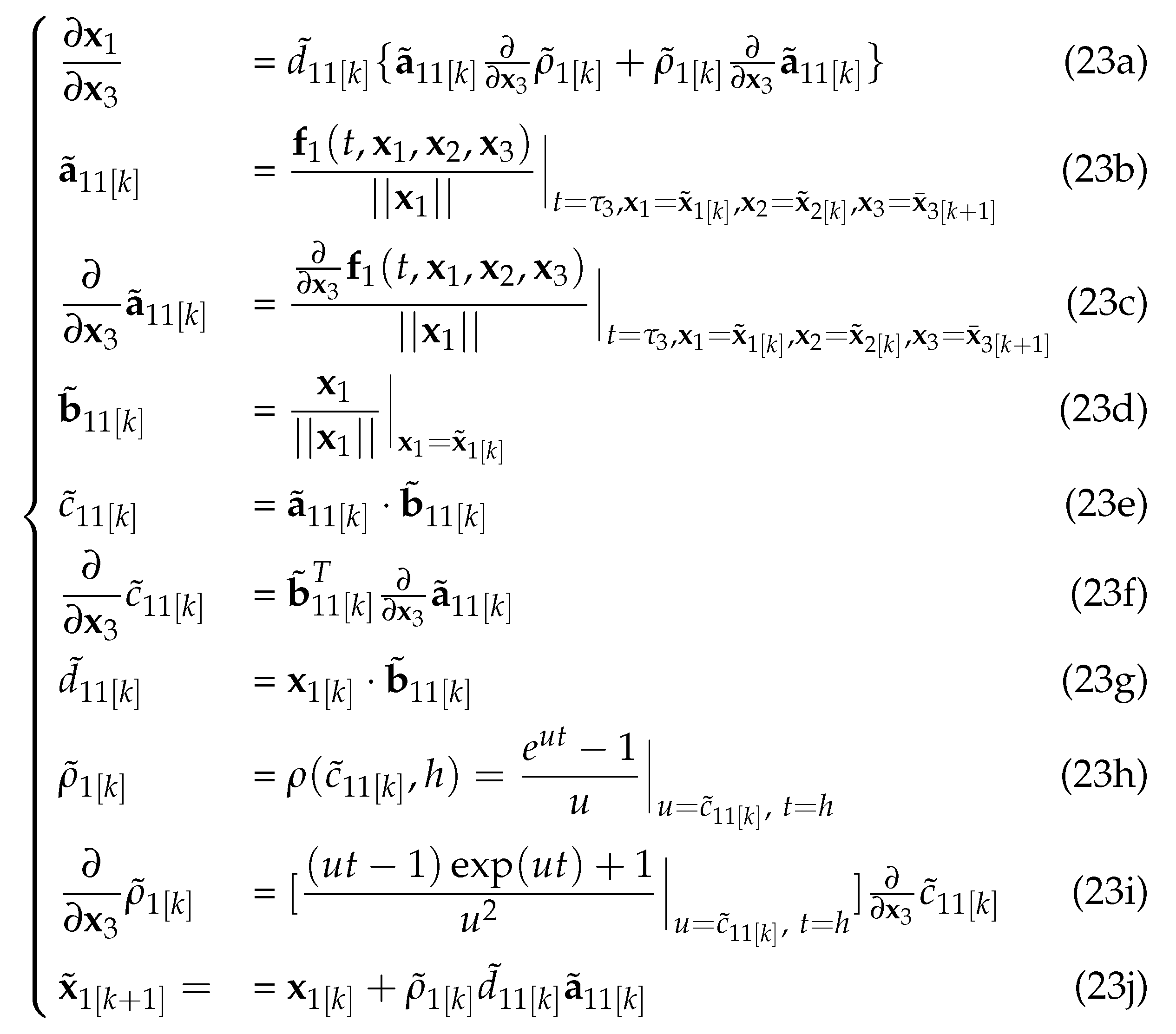
- S3:
If
convergers according to a given stopping criterion
then let
; otherwise, let
and goto S2.
Lemma 1.
([23]) Let be an matrix and be an matrix. Then
where λ is any scalar and denotes the identity matrix.
Lemma 2.
Let be an matrix, be an matrix, and and be non-zero vectors. Define the matrix for . If is nonsingular and , where , then E is nonsingular.
Proof. To prove that is nonsingular, we need to show that its determinant is nonzero.
To begin with, is nonsingluar, that is, . And it is noted that , then .
For case
, we obtain
and using Lemma 1, we have
where
.
Since both and are nonzero, then is also nonzero. Therefore is nonsingular.
For case
, using Lemma 1, we obtain
Moreover, , then , which means that is nonsingular from equation (28). □
Lemma 3.
Let be an matrix, be an matrix, and be an matrix. Let and be nonzero vectors, and let and be nonzero vectors. Define the matrices and , where . Suppose that is nonsingular and that h satisfies
where , , and . Then, the matrix is nonsingular.
Proof. Firstly, is nonsingular, that is and .
Let
that is
is nonsingular. And
and
, where
. By Lemma 2,
is nonsingular, which means
is nonsingular.
Then, let
and
is nonsingular. In addtion,
, if
, where
. By Lemma 2,
is nonsingular, which means
is nonsingular.
It is noted that
where
. Moreover, we are able to obtain
and
.
Then, we obtain
For
, then we obtain the inequality (29). □
Theorem 1. For the -Loop of Hessenberg DAEs with index 3, if h is sufficiently small, then the Jacobian matrix is nonsingular.
Proof. We first compute the
by Eq.(22).
Similarly, we obtain the
from Eq. (23).
Futhermore, we are able to get
where
(
), and
(
) is nonsingular.
From Lemma 1, it is noted that
For small
,
. Moreover, by using Lemma 3, if
where
,
and
, then
is nonsingular. Therefore, satisfying for small
h with
we are able to obtain
is nonsingular. □
4. Numerical Examples
In this section, we do numerical simulation experiments to illustrate the performance of the MELGDAE. All codes are written under Windows 10 system and run on a personal computer with Intel(R) Core(TM) i5-3570 CPU @ GHz, GB RAM and 64-bit operating system.
We consider a Hessenberg DAEs system with index 3 as follows, which can be found in [
24].
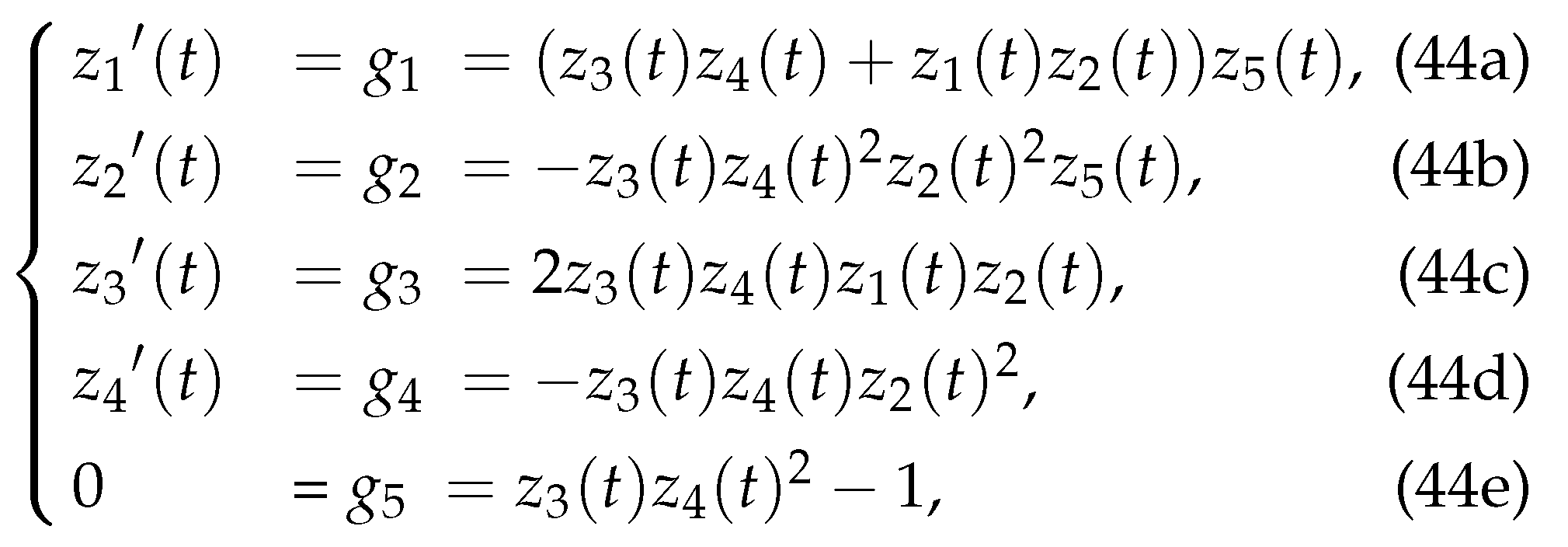
where
,
are the consistent initial values. And the exact solution is given by
Let , and , then .
To obtain DAEs with index 2, we differentiate the constraint
to obtain the following equation.
Then, we are able to obtain index 2 DAEs below.
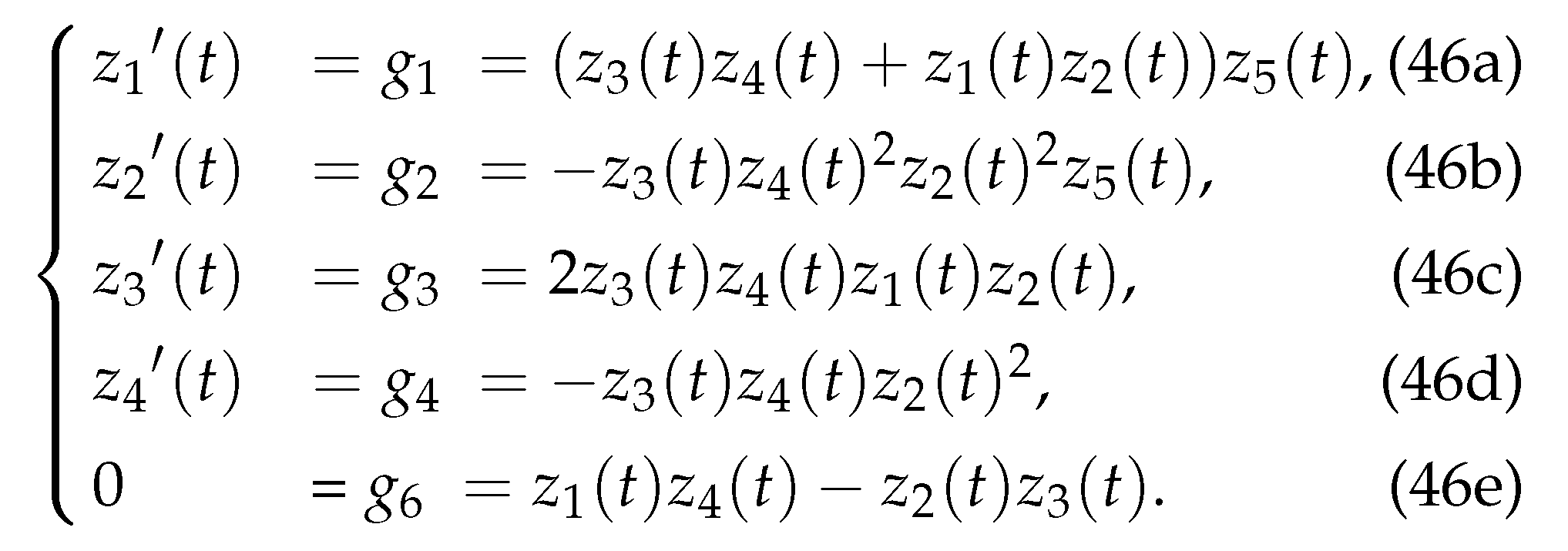
We compared the numerical results of the MELGDAE method with those of RADAU, a code based on implicit Runge-Kutta methods, and MEBDFI, a code based on the MEBDF method that has better theoretical properties than BDF methods, to demonstrate the capability of the MELGDAE method. The comparison was made using the Hessenberg DAEs with index 2 or 3 mentioned above.
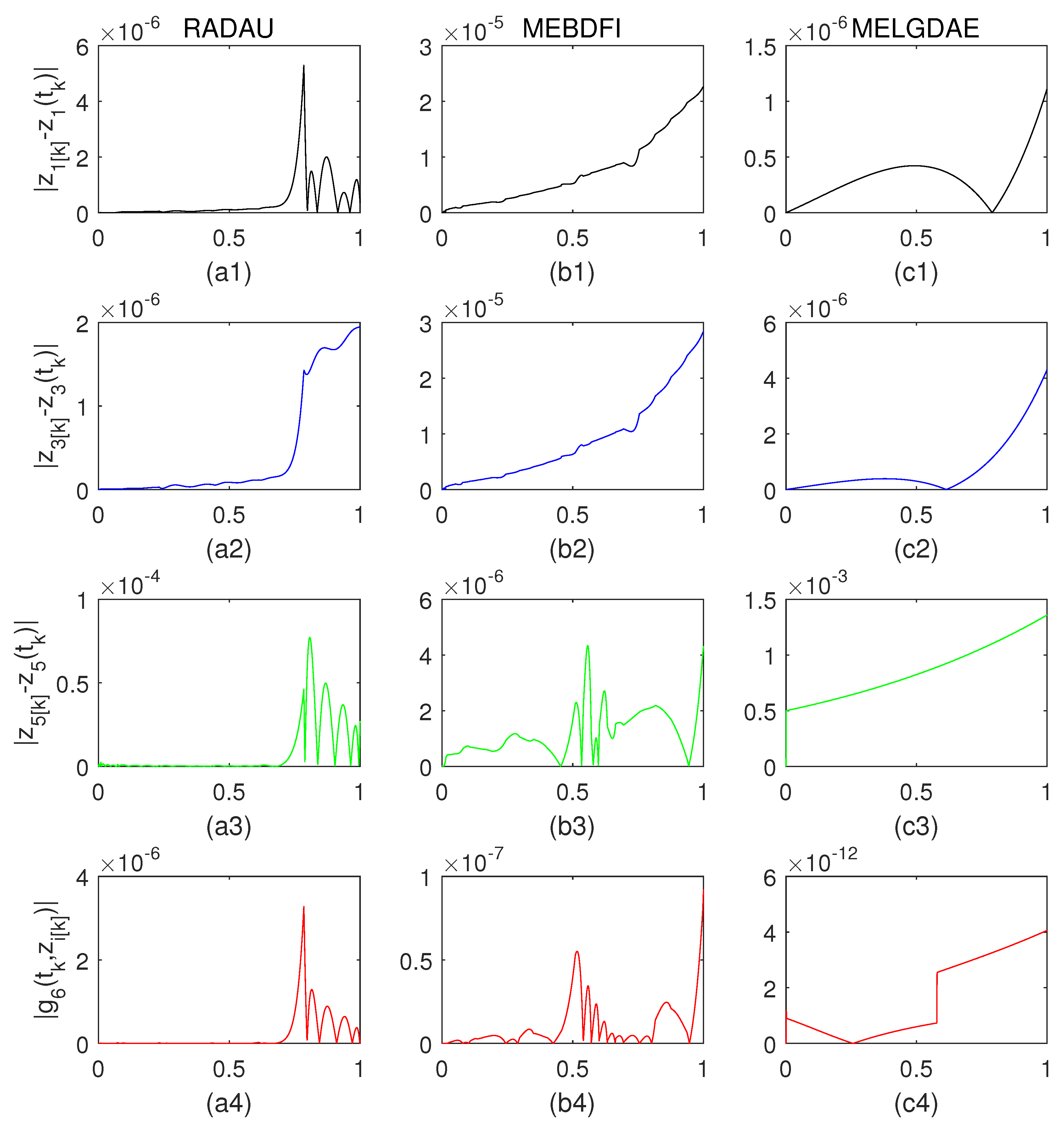
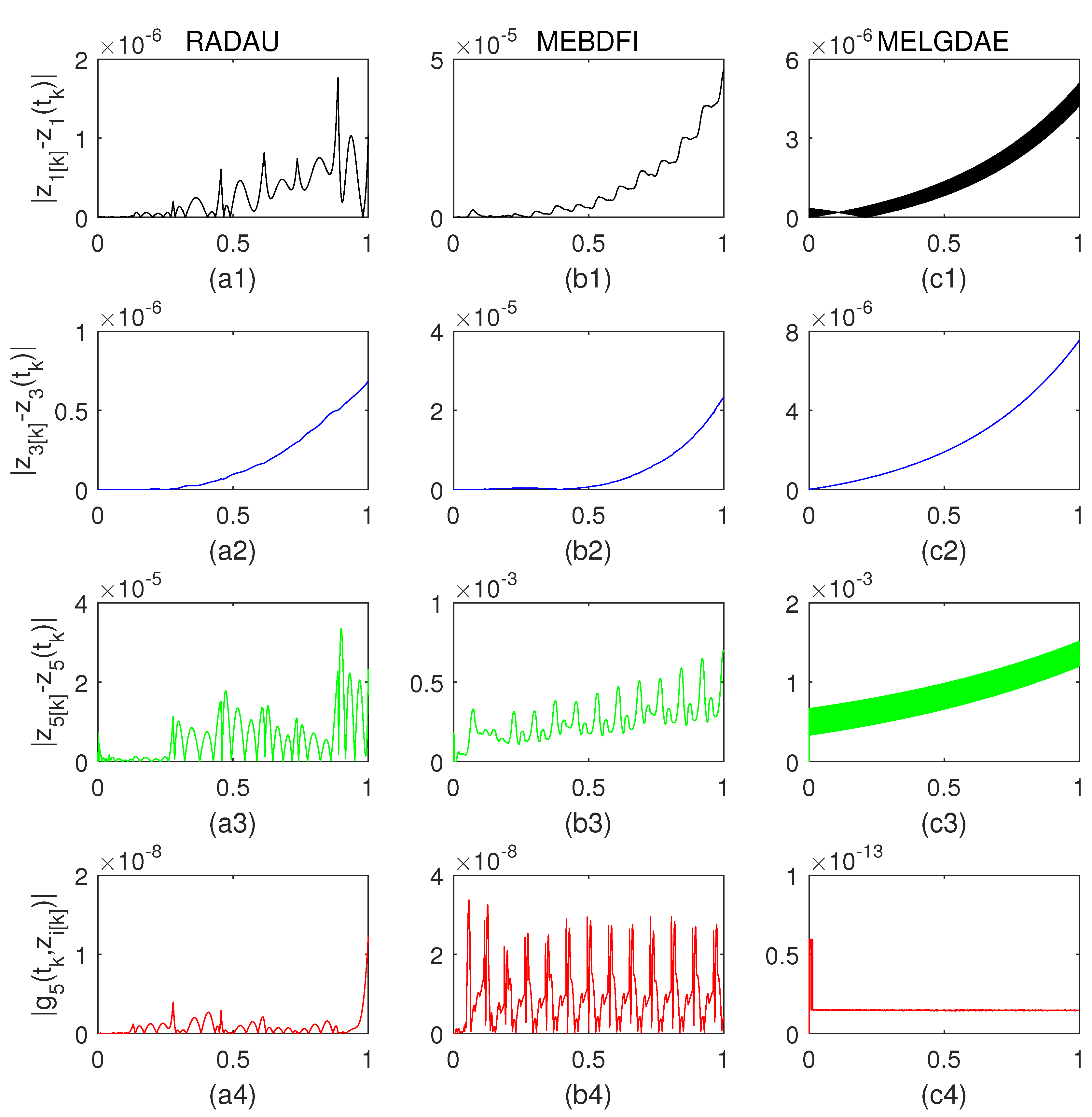
Without loss of generality, we assume the absolute error (
,
,
) is
, the relative error is
, the (initial) step size is
,
. Based on
Figure 1 and
Figure 2, the MELGDAE method showed comparable accuracy with the RADAU method for the differential variables
and
for both index-2 and index-3 Hessenberg DAEs. In contrast, the MEBDFI method was less accurate for these variables. For the algebraic variable
, both RADAU and MEBDFI methods provided more accurate results than the MELGDAE method. However, for the algebraic constraints
and
, the MELGDAE method exhibited significantly higher accuracy compared to the RADAU and MEBDFI methods.
Upon observing
Figure 1 and
Figure 2, it is clear that all three methods exhibit a reduction in the absolute errors of
,
, and
as the index increases from 2 to 3. This reduction is not significant for the MELGDAE and RADAU methods. Therefore, we can conclude that the MELGDAE method has the potential to be extended for computing DAEs systems with an index higher than 3.
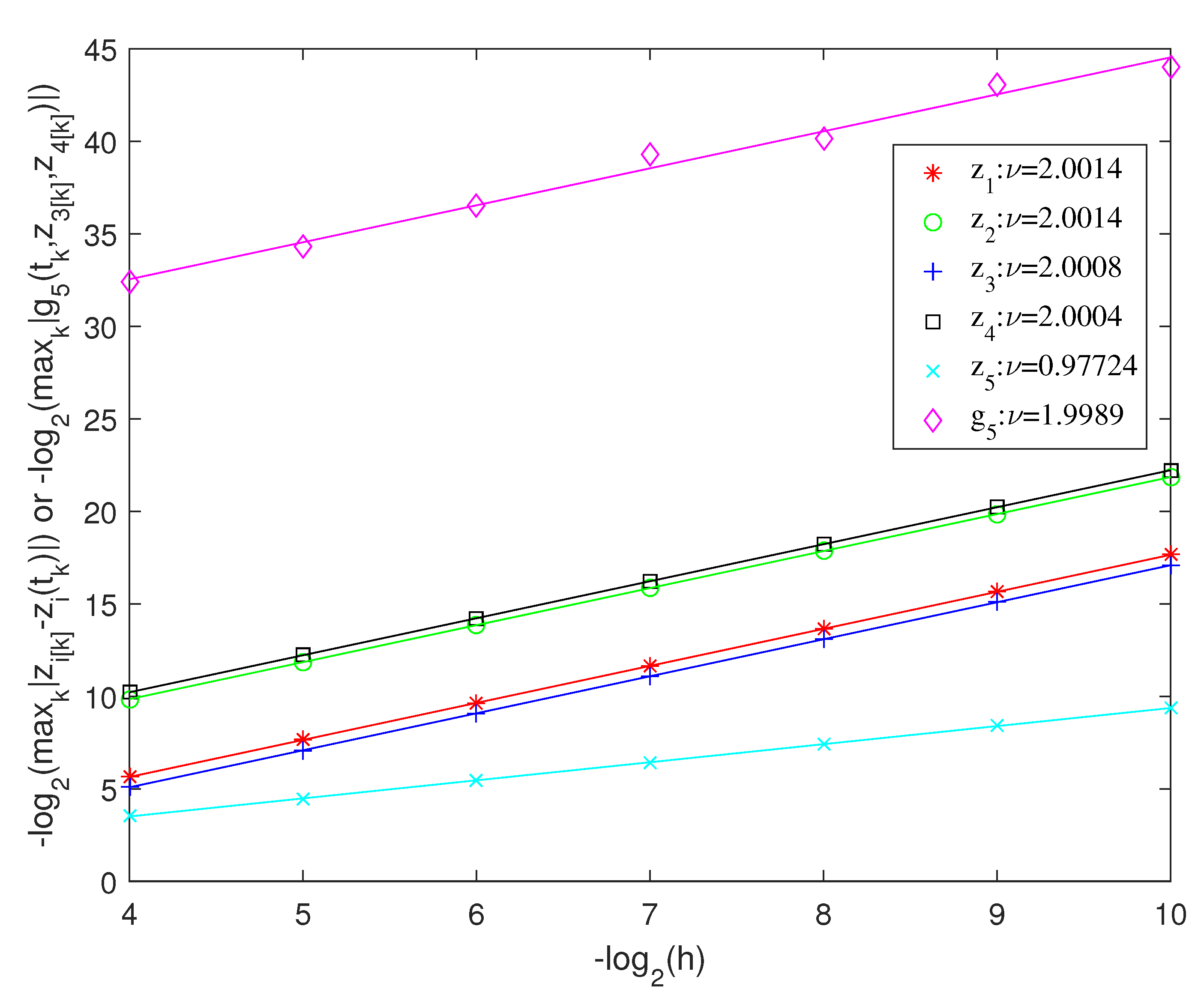
Furthermore, we conducted numerical experiments to verify the convergence accuracy of the MELGDAE method for index 3 DAEs. We assumed
and calculated their constants in
(
) and
, which represents
and
, using the standard least-squares method. The results are presented in
Figure 3, which indicate that the MELGDAE method exhibits second-order convergence for
,
,
, and
(all differential variables) and
(the algebraic constraints), and first-order convergence for
(algebraic variable). Thus, this method may be extended to compute systems with an index of 4 or higher and is suitable for DAE systems that cannot be directly solved using other classical methods.
5. Conclusions
The Modified Extended Lie Group Differential Algebraic Equations (MELGDAE) method was developed in this paper to solve Hessenberg-DAEs with index 3. While the LGDAE method presented in [
18] is only capable of handling index 2 systems, the MELGDAE method can solve higher index systems by taking into account the differential equation components with respect to the index in Hessenberg form. It is worth mentioning that the MELGDAE method demonstrates superior theoretical properties compared to the LGDAEs, as illustrated in Theorem 1.
We conducted a comparison of the MELGDAE method with the standard methods RADAU and MEBDFI on index 2 and 3 DAE systems. The MELGDAE method demonstrated promising results in terms of solution errors when compared to RADAU and MEBDFI, which are known to be powerful on different DAE systems. However, the MELGDAE method excelled in preserving the algebraic constraints. Moreover, all differential variables in index 3 Hessenberg-DAEs exhibited order 2 convergence with the MELGDAE method, whereas MEBDFI in [
24] and RADAU in [
7,
25] demonstrated order reduction. Although the MELGDAE method has high stability and accuracy when solving strong nonlinear Hessenberg DAEs with index 3, there are still some theoretical gaps that need to be addressed in the future. Additionally, the MELGDAE method can be further extended to solve DAEs with an index of 4 or higher, which cannot be directly solved using standard methods.
Author Contributions
J.T. contributed to supervision, methodology, validation,funding acquisition and project administration. J.L. contributed to investigation, computations,funding acquisition and validation.
Funding
This work was partly supported by the NSF of China (No: 12201144), the Science and Technology Program of Guangzhou (No: 202002030138), the GuangDong Basic and Applied Basic Research Foundation (No: 2020A1515110554), the Science and Technology Foundation of Guizhou Province (No: QKHJC-ZK[2021]YB015), and the University-Industry Collaborative Education Program of the Ministry of Education (No: BINTECH-KJZX-20220831-61), China.
Acknowledgments
The authors wish to thank the referee for his or her very helpful comments and useful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schiehlen, W. Multibody system dynamics: roots and perspectives. Multibody System Dynamics 1997, 1, 149–188. [Google Scholar] [CrossRef]
- Winkler, R. Stochastic differential algebraic equations of index 1 and applications in circuit simulation. Journal of computational and applied mathematics 2003, 157(2), 477–505. [Google Scholar] [CrossRef]
- Coffey, T. S.; Kelley, C. T.; Keyes, D. E. Pseudotransient continuation and differential-algebraic equations. SIAM Journal on Scientific Computing 2003, 25(2), 553–569. [Google Scholar] [CrossRef]
- Peng, H. J.; Li, F.; Liu, J. G.; Ju, Z. J. A symplectic instantaneous optimal control for robot trajectory tracking with differential-algebraic equation models. IEEE Transactions on Industrial Electronics 2019, 67(5), 3819–3829. [Google Scholar] [CrossRef]
- Çelik, E.; Karaduman, E.; Bayram, M. Numerical solutions of chemical differential-algebraic equations. Applied Mathematics and Computation 2003, 139(2), 259–264. [Google Scholar] [CrossRef]
- Ascher, U. M.; Petzold, L. R. Projected implicit Runge–Kutta methods for differential-algebraic equations. SIAM Journal on Numerical Analysis 1991, 28(4), 1097–1120. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Stiff differential equations solved by radau methods. Journal of Computational and Applied Mathematics 1999, 111, 93–111. [Google Scholar] [CrossRef]
- Skvortsov, L. M. Diagonally implicit Runge—Kutta methods for differential algebraic equations of indices two and three. Computational Mathematics and Mathematical Physics 2010, 50, 993–1005. [Google Scholar] [CrossRef]
- Cash, J.; Considine, S. An mebdf code for stiff initial value problems. ACM Trans. Math. Softw. 1992, 142–158. [Google Scholar] [CrossRef]
- Cash, J. R. Modified extended backward differentiation formulae for the numerical solution of stiff initial value problems in ODEs and DAEs. Journal of Computational and Applied Mathematics 2000, 125(1), 117–130. [Google Scholar] [CrossRef]
- Karta, M.; Celik, E. On the numerical solution of differential-algebraic equations with Hessenberg Index-3. Discrete Dynamics in Nature and Society 2012, 2012, 12. [Google Scholar] [CrossRef]
- Benhammouda, B. A novel technique to solve nonlinear higher-index Hessenberg differential-algebraic equations by Adomian decomposition method. SpringerPlus 2016, 5(1), 1–14. [Google Scholar] [CrossRef]
- Celledoni, E.; Kometa, B. K. Semi-Lagrangian multistep exponential integrators for index 2 differential–algebraic systems. Journal of Computational Physics 2011, 230(9), 3413–3429. [Google Scholar] [CrossRef]
- Iserles, A.; Zanna, A. Preserving algebraic invariants with Runge–Kutta methods. Journal of Computational and Applied Mathematics 2000, 125(1), 69–81. [Google Scholar] [CrossRef]
- Wieloch, V.; Arnold, M. BDF integrators for constrained mechanical systems on Lie groups. Journal of Computational and Applied Mathematics 2021, 387, 112517. [Google Scholar] [CrossRef]
- Liu, C. S. Preserving constraints of differential equations by numerical methods based on integrating factors. Computer Modeling in Engineering and Sciences 2006, 12(2), 83–107. [Google Scholar]
- Liu, C. S. Finding unknown heat source in a nonlinear Cauchy problem by the Lie-group differential algebraic equations method. Engineering Analysis with Boundary Elements 2015, 50, 148–156. [Google Scholar] [CrossRef]
- Liu, C. S.; Chen, L.; Liu, L. W. Solving mechanical systems with nonholonomic constraints by a Lie-group differential algebraic equations method. Journal of Engineering Mechanics 2017, 143(9), 04017097. [Google Scholar] [CrossRef]
- Liu, C. S. Lie-group differential algebraic equations method to recover heat source in a Cauchy problem with analytic continuation data. International Journal of Heat and Mass Transfer 2014, 78, 538–547. [Google Scholar] [CrossRef]
- Liu, C. S.; Kuo, C. L.; Chang, J. R. Recovering a heat source and initial value by a Lie-group differential algebraic equations method. Numerical Heat Transfer, Part B: Fundamentals 2015, 67(3), 231–254. [Google Scholar] [CrossRef]
- Liu, C. S. A new sliding control strategy for nonlinear system solved by the Lie-group differential algebraic equation method. Communications in Nonlinear Science and Numerical Simulation 2014, 19(6), 2012–2038. [Google Scholar] [CrossRef]
- Liu, C. S.; Chang, C. W. A real-time Lie-group differential algebraic equations method to solve the inverse nonlinear vibration problems. Inverse Problems in Science and Engineering 2016, 24(9), 1569–1586. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: New York, USA, 2012; pp. 66–67. [Google Scholar]
- Jay, L. Convergence of Runge-Kutta methods for differential-algebraic systems of index 3. Applied Numerical Mathematics 1995, 17(2), 97–118. [Google Scholar] [CrossRef]
- Hairer, E.; Lubich, C.; Roche, M. The numerical solution of differential-algebraic systems by Runge-Kutta methods; Springer-Verlag: Berlin, Germany, 1989; pp. 19–20. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
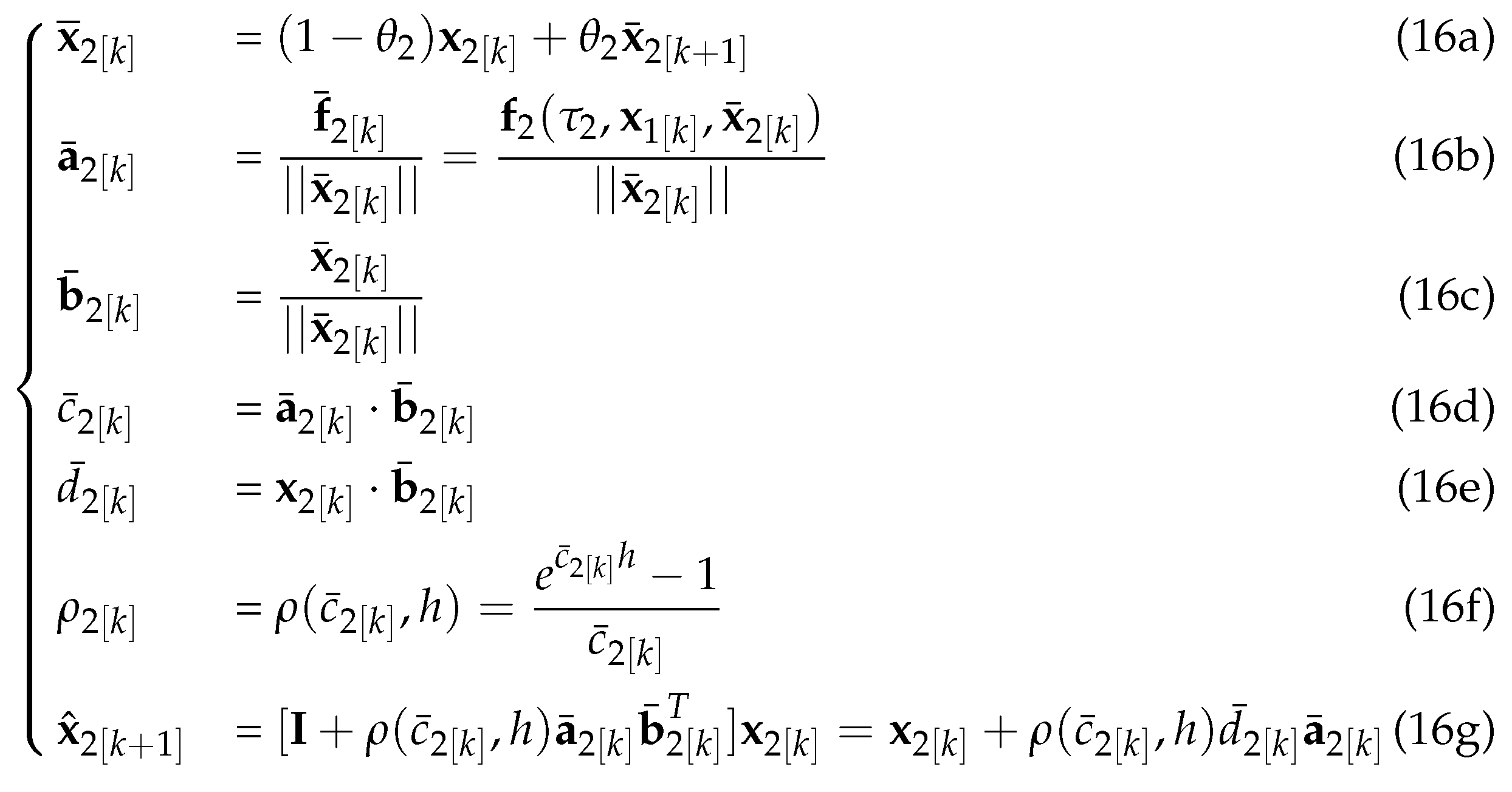


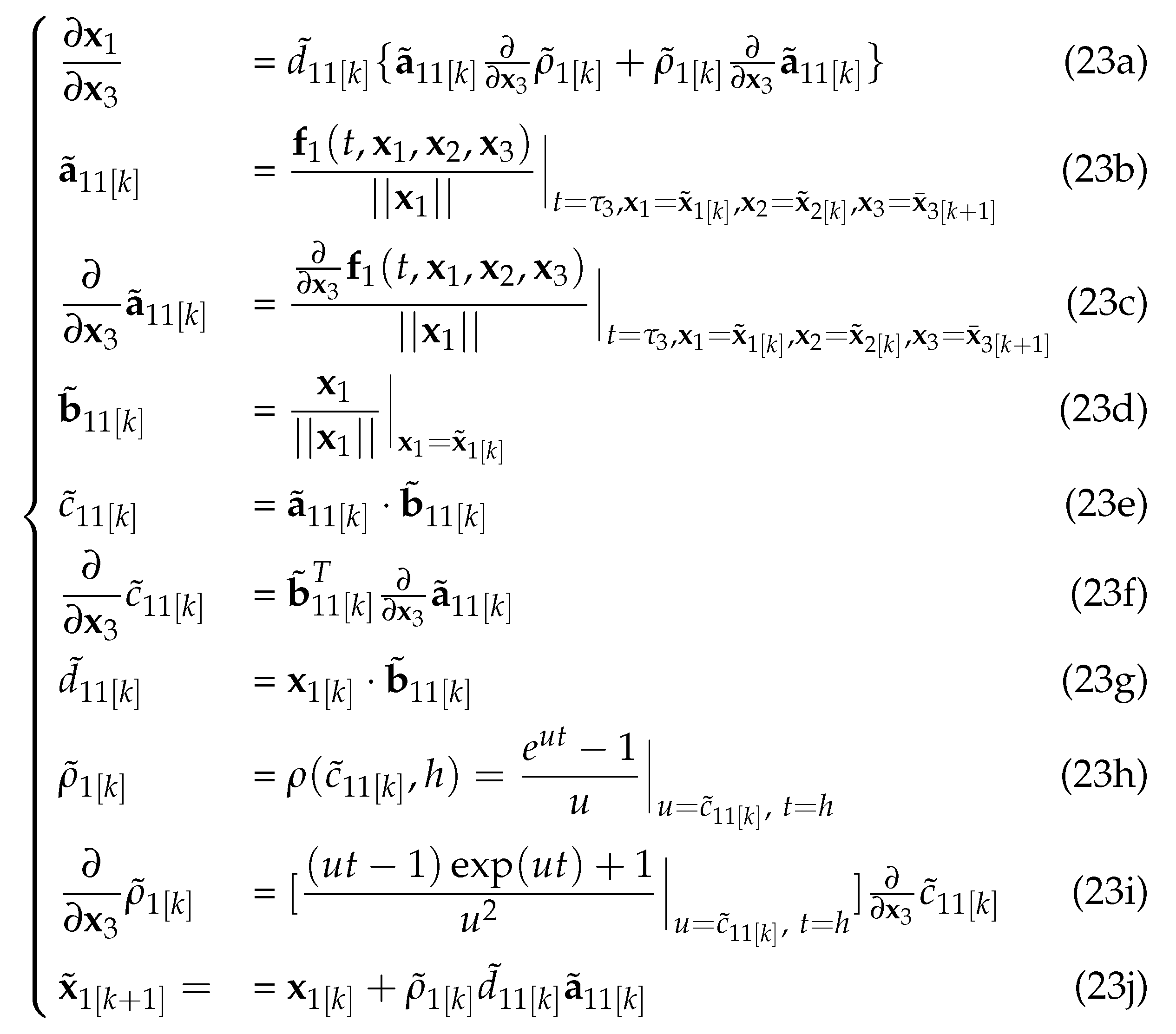
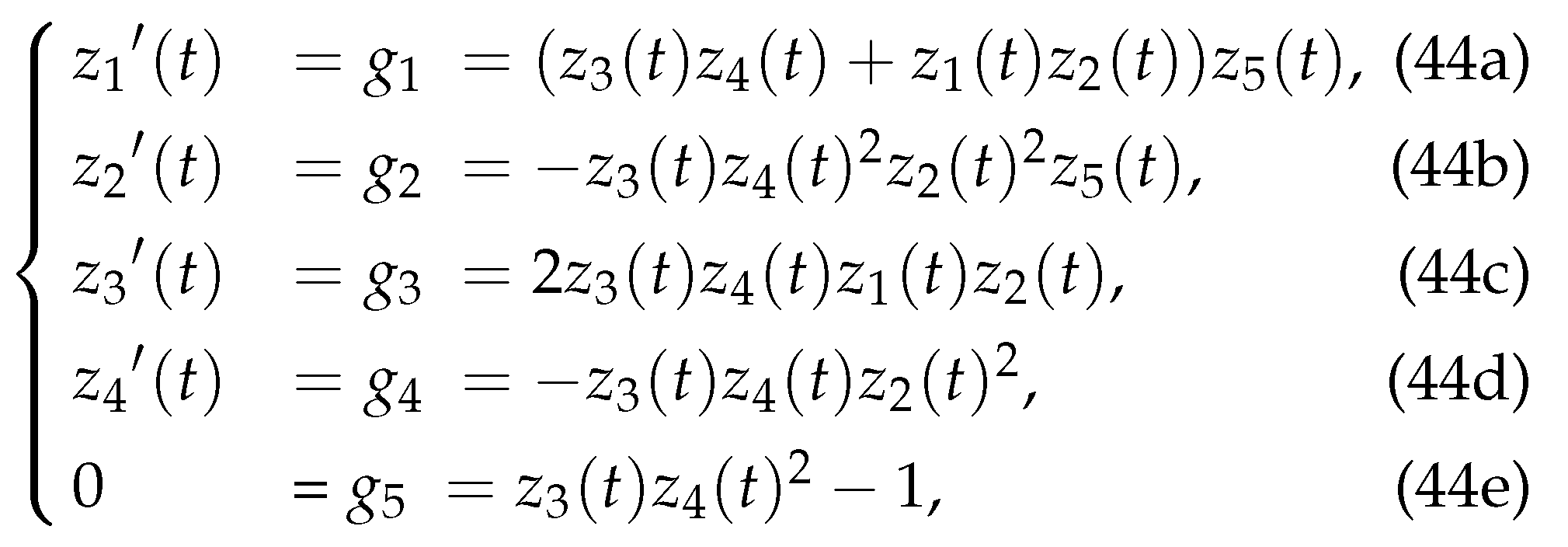 where , are the consistent initial values. And the exact solution is given by
where , are the consistent initial values. And the exact solution is given by