SOC Estimation for Lithium Batteries Based on Fractional Order Model and Robust Unscented Kalman Filter

Lithium batteries are widely used due to their advantages such as high energy density, stable performance, low pollution, and long recyclable life. Accurate SOC estimation is important for the use of lithium batteries. To address the problem of low accuracy of SOC estimation by traditional methods, this paper proposes a joint method of fractional order robust unscented Kalman filter (FORUKF) and robust unscented Kalman filter (RUKF) to estimate SOC. The method is based on a fractional order model (FOM) that combines the unscented transformation (UT) technique, the H∞ observer and the joint estimator. Specifically, an adaptive genetic algorithm (AGA) was first used to identify the parameters of the FOM for lithium batteries and to verify the accuracy of the model. Estimation and updating of the ohmic resistance R0 and the capacity QN in the model in real-time by RUKF and then estimation of the SOC by FORUKF. Finally, the accuracy of FORUKF-RUKF was verified under the Federal Urban Driving Schedule (FUDS), US06 Highway Driving Schedule and Beijing Dynamic Stress Test (BJDST). According to the results, the FORUKF-RUKF estimated SOC was found to have better accuracy and robustness than the RUKF, FOUKF and EKF.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

and the capacity

Q_{N}

in the model in real-time by RUKF and then estimation of the SOC by FORUKF. Finally, the accuracy of FORUKF-RUKF was verified under the Federal Urban Driving Schedule (FUDS), US06 Highway Driving Schedule and Beijing Dynamic Stress Test (BJDST). According to the results, the FORUKF-RUKF estimated SOC was found to have better accuracy and robustness than the RUKF, FOUKF and EKF.

1. Introduction

Due to factors such as energy shortages and the deterioration of the global environment, countries are gradually starting to pay attention to the environmental attributes of their products. And electric cars are gradually replacing petrol cars because of their energy-saving and emission-reducing features. Lithium batteries have high-power density, long service life and mature production technology, therefore being the energy storage device in most electric vehicles [1]. Accurate SOC estimation has always been one of the main focuses of battery research because it helps the user to understand the true condition of the vehicle and to use the battery more scientifically and efficiently.

After years of research, researchers have proposed a variety of SOC estimation methods. For example, the open-circuit voltage (OCV) method [2], which estimates the SOC based on the correspondence between the open-circuit voltage (

U_{O C}

) and the SOC. However, the battery must be left for a long time before accurate OCV measurements can be made. This may cause further problems with the use of the battery. The ampere-hour integration method [3] is a method of integrating the current to estimate the SOC. However, this method tends to gradually accumulate errors in the integration process, eventually leading to large errors in the results. There is also a category of model-based approaches which include: the electrochemical model [4], the “black-box” model [5,6,7,8,9] and the equivalent circuit model [11,12]. The electrochemical model uses mathematical equations to describe the chemical reactions within the battery to estimate the SOC, but the variety and complexity of the chemical reactions that occur within the battery during operation makes it difficult to describe accurately by equations and is computationally intensive. The “black-box” models include the neural network method [5,6,7], fuzzy-logic based method [8] and support vector machine method [9]. The "black-box" approach requires extensive experimentation and then training the model on the experimental data. The accuracy of the final model depends on the accuracy of the data and the algorithm. The equivalent circuit model reflects the internal conditions of the battery by creating a circuit model with components such as resistors and capacitors, combining high accuracy with low complexity. The Kalman filtering algorithm [13,14] provides optimal estimates in the sense of minimum variance with low computational effort and high accuracy.

Capacitors used in integer-order equivalent circuit models are often assumed to be ideal capacitors, which do not correspond to the actual operation of the battery and can cause dispersion phenomena [15]. In recent years, researchers have gradually started to use constant phase element (CPE) to replace the ideal capacitor in the integer order model (IOM) [18] and to build the FOM [16,17] to estimate SOC. Xiong et al. [19] proposed FOUKF to estimate SOC. Verification that SOC estimation with FOM has good reliability. Chen et al. [21] proposed the fractional-order square root unscented Kalman filter (FSR-UKF). Its method inherits the advantages of SR-UKF and provides high accuracy in SOC estimation. Zeng et al. [22] proposed a new fuzzy UKF method to jointly estimate the SOC and SOH, and it was shown that the joint estimation was more reliable than estimating the SOC using UKF alone.

Zhuang et al. [23] proposed the H∞ extended filter (HEF) by adding an H∞ observer [24] to the EKF, and this method improves the estimation accuracy of the traditional EKF method. Ramazan et al. [25] proposed the adaptive RUKF (ARUKF) based on HEF, which is more accurate than both UKF and EKF in estimating SOC. Xiong et al. [26] proposed real-time estimation of battery capacity was achieved using a multi-scale EKF (MIEKF), and finally the SOC was estimated. Ma et al. [27] proposed estimated the SOC using a multi-innovations UKF (MIUKF) and then used the UKF for SOH prediction to update the actual capacity of the SOC estimator, and the experiments showed that the estimated SOC remained highly accurate over multiple tests cycles.

This paper uses FOM and AGA to identify the parameters of the lithium battery model. Combining the H∞ observer with a joint estimator, we propose FORUKF-RUKF to estimate SOC. According to the simulation results, the approach has a higher estimation accuracy. The specific steps of FORUKF-RUKF are: (1) Build FOM and use AGA to identify model parameters. (2) Real-time estimation of ohmic resistance

R_{0}

and capacity

Q_{N}

in lithium battery FOM using RUKF and use

Q_{N}

to calculate the SOH curve (3) Real-time updated

R_{0}

and

Q_{N}

are used in FORUKF to estimate SOC.

2. Battery Modeling

2.1. Fractional Order Calculus

The fractional-order second-order RC model is often used as a model for lithium batteries and the CPE is used to replace the two capacitors in the integer order second order RC model. The state space model of the model can be obtained by applying the definition of fractional order calculus. The G-L definition is the most commonly used method and is calculated as follows.

D^{α} x (t) = \lim_{h \to 0} \frac{1}{h^{a}} \sum_{j = 0}^{[t / h]} {(- 1)}^{j} (\begin{matrix} α \\ j \end{matrix}) x (t - j h)

(1)

(\begin{matrix} a \\ j \end{matrix}) = \{\begin{matrix} 1 & j = 0 \\ \frac{a!}{j! (a - j)!} & j > 0 \end{matrix}

(2)

2.2. Fractional Order Model

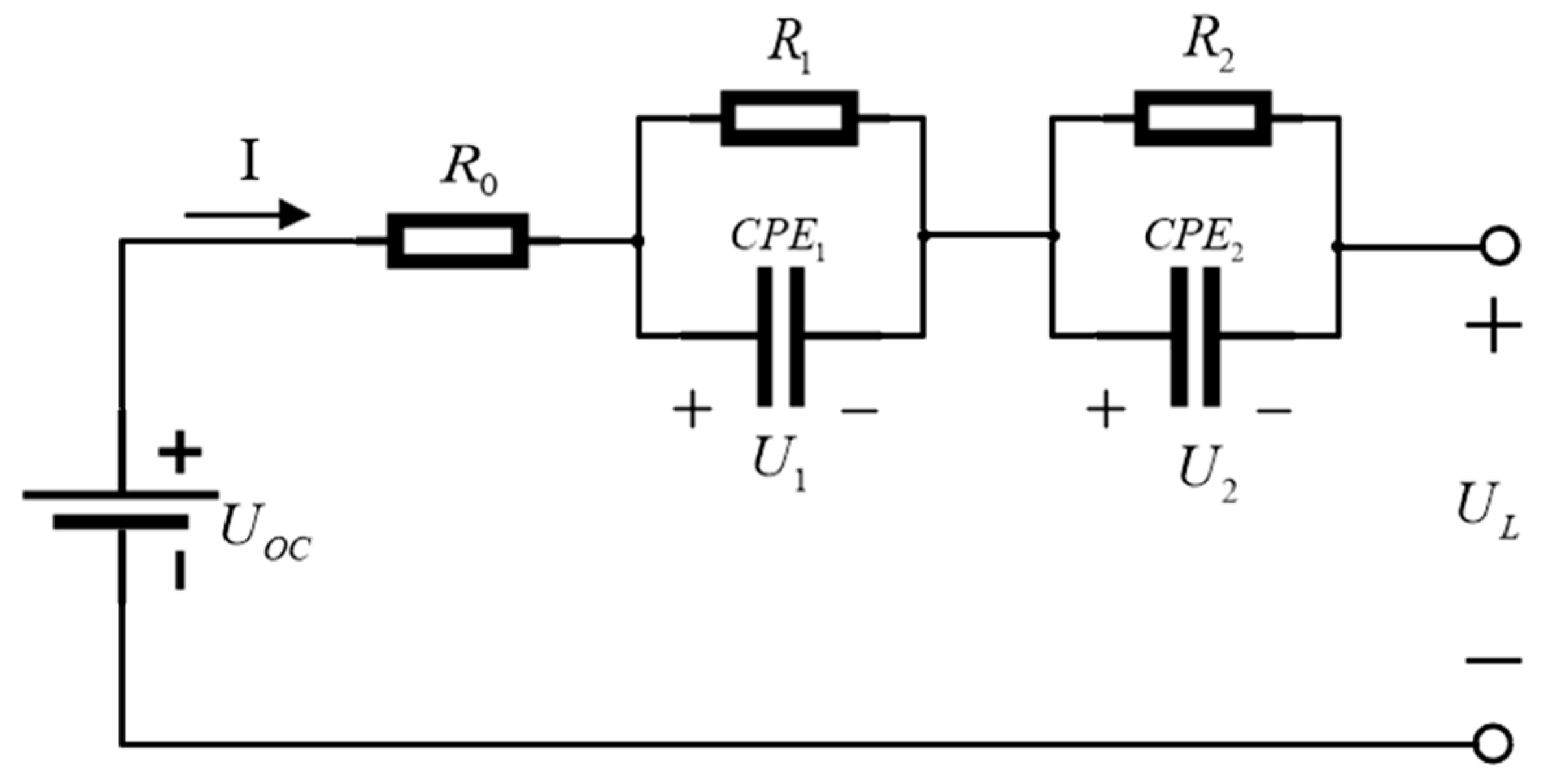
Using a fractional second order RC model [16] as a battery model to describe the dynamic characteristics of the battery is more accurate than using the IOM. The FOM for lithium batteries is shown in Figure 1.

As shown in Figure 1.

U_{O C}

is the open circuit voltage,

U_{L}

is the terminal voltage,

R_{0}

is ohmic resistance, reflecting the instantaneous

U_{L}

of charging and discharging,

R_{1}

and

R_{2}

is resistance，

{C P E}_{1}

and

{C P E}_{2}

represent the constant phase element.

The state space equation of the FOM are as follows:

[\begin{matrix} D^{α} U_{1} \\ D^{β} U_{2} \end{matrix}] = [\begin{matrix} - \frac{1}{R_{1} C_{1}} & 0 \\ 0 & - \frac{1}{R_{2} C_{2}} \end{matrix}] [\begin{matrix} U_{1} \\ U_{2} \end{matrix}] + [\begin{matrix} \frac{1}{C_{1}} \\ \frac{1}{C_{2}} \end{matrix}] I （ t ）

(3)

U_{L} = [\begin{matrix} - 1 & - 1 \end{matrix}] [\begin{matrix} U_{1} \\ U_{2} \end{matrix}] - I (t) R_{0} + U_{o c}

(4)

SOC is defined as:

S O C_{k + 1} = S O C_{k} - \frac{T_{s}}{Q_{new}} I_{k}

(5)

Q_{n e w}

is the rated capacity of the battery.

Converting the integrals of equations (1)-(5) into discrete form gives the discretized state space equations for the FOM:

\{\begin{matrix} x_{k + 1} = A x_{k} + B I_{k} - \sum_{j = 1}^{k + 1} K_{j} x_{k + 1 - j} \\ y_{k} = C x_{k} - R_{0} I_{k} + U_{o c, k} \end{matrix}

(6)

where

A = [\begin{matrix} \frac{- T_{S}^{α}}{R_{1} C_{1}} & 0 & 0 \\ 0 & \frac{- T_{S}^{β}}{R_{2} C_{2}} & 0 \\ 0 & 0 & 1 \end{matrix}]

B = [\begin{matrix} \frac{T_{S}^{α}}{C_{1}} \\ \frac{T_{S}^{β}}{C_{2}} \\ - \frac{T_{S}^{α}}{Q_{N}} \end{matrix}]

C = [\begin{matrix} - 1 \\ - 1 \\ 0 \end{matrix}]

x = [\begin{matrix} U_{1} \\ U_{2} \\ S O C \end{matrix}]

K_{j} = [\begin{matrix} ω_{j}^{α} & 0 & 0 \\ 0 & ω_{j}^{β} & 0 \\ 0 & 0 & 0 \end{matrix}]

ω_{j}^{α} = (- 1) (\begin{matrix} β \\ j \end{matrix})

and

y = U_{L}

3. Parameter Identification

3.1. Description of the Experimental Data

The data used in this article is based on the INR 18650-50R battery with a capacity of 2000mAh. The data is from the CALCE Battery Research Group and uses four operating conditions at 25 °C: DST, FUDS, US06 and BJDST.

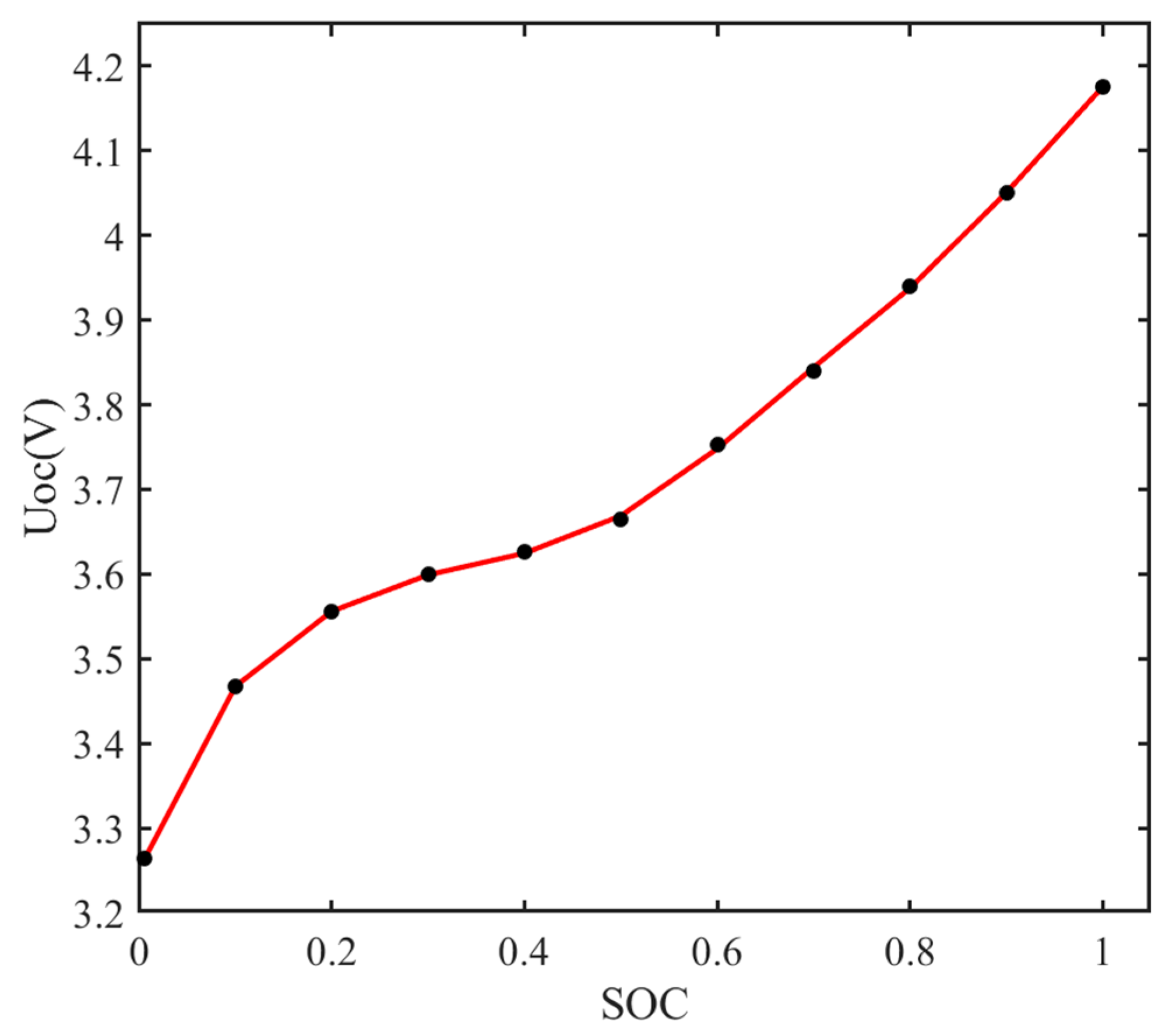
For the subsequent estimation of SOC, the relationship between

U_{O C}

and SOC must first be determined. The fitted curve of

U_{O C}

and SOC is shown in Figure 2 .

-SOC fitting curve.

3.2. Model Parameter Identification

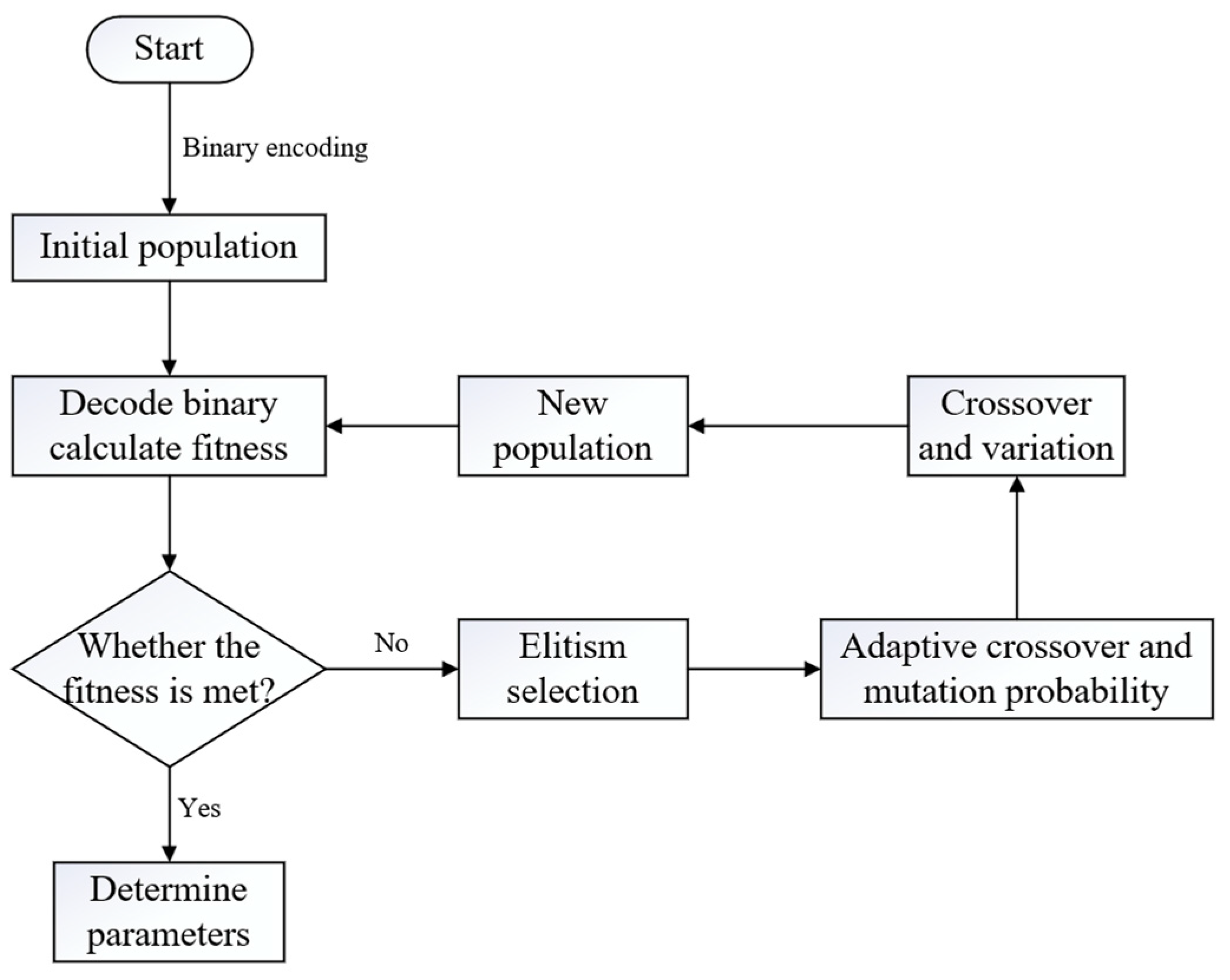
The genetic algorithm can find the global optimal solution for battery parameter identification by following the evolutionary rule of “natural selection, survival of the fittest” in nature. However, the traditional genetic algorithm easily falls into a local optimal solution, leading to inaccurate final results. The adaptive genetic algorithm (AGA) can continuously update the crossover and mutation probability and has a better global search function. In this paper, AGA is used to determine the FOM parameters of batteries under DST conditions.

The initial population is generated randomly by the AGA. Each individual in the population consists of seven genomes (

R_{0}

、

R_{1}

、

R_{2}

、

C_{1}

、

C_{2}

、α、β), and each gene is binary coded. The fitness of each individual is checked, the individuals with high fitness are crossed and mutated to generate a new population, and the cycle continues until the optimal solution with the required fitness is obtained.

Parametric identification of IOM and FOM of a battery under DST conditions with AGA at 25°C

3.3. Model Accuracy Verification

The parameters in Table 1 are used to determine if the parameters are accurate under the DST conditions.

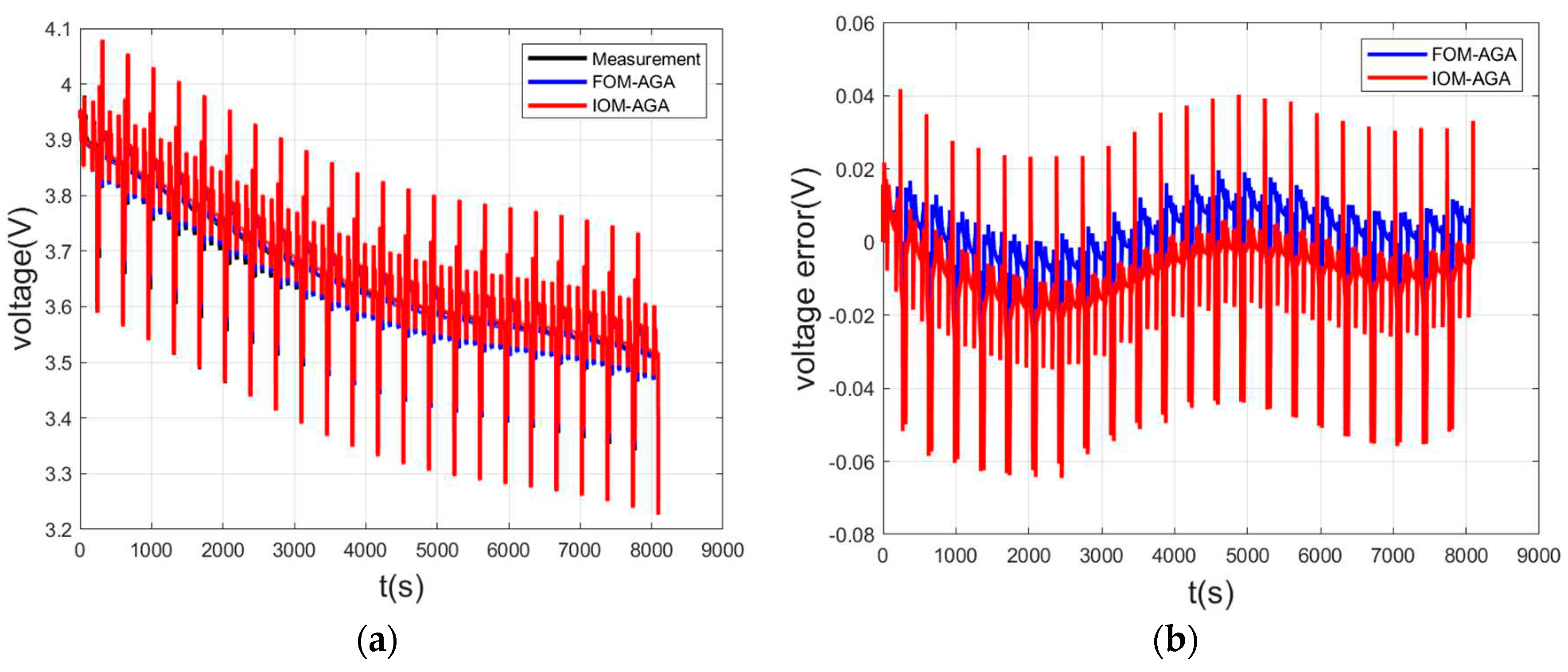
Figure 4. Validation of the model accuracy: (a) voltages; (b) voltage error.

As shown in Table 2, although FOM and IOM can be used as models, the voltage using the FOM is closer to the measured value, so FOM is used as a model for estimating SOC.

4. Battery SOC estimation

4.1. FORUKF

The optimization performance of UKF is determined by the process and noise. The H∞ filter provides the optimal error estimate that minimizes the influence of the worst disturbance on the estimate. The SOC is calculated in this paper using the FORUKF algorithm. FORUKF is implemented using UT technique and H∞ filtering based on the fractional order model. H∞ filtering reduces the effects of worst-case noise and inaccurate initial state. Ramazan et al. [25] gives the H∞ extended filter (HEF):

{\hat{x}}_{k}^{-} = f (x_{k - 1})

(7)

P_{k}^{-} = F_{k} P_{k - 1} F_{k}^{T} + Q_{k}, F_{k} = \frac{\partial f}{\partial x}

(8)

K_{k} = P_{k}^{-} H_{k}^{T} {(H_{k} P_{k}^{-} H_{k}^{T} + R_{k})}^{- 1}, H_{k} = \frac{\partial h}{\partial x}

(9)

R_{r, k} = [\begin{matrix} R_{k} & 0 \\ 0 & - γ I \end{matrix}] + [\begin{matrix} H_{k} \\ I \end{matrix}] P_{k}^{-} [\begin{matrix} H_{k}^{T} & I \end{matrix}]

(10)

{\hat{x}}_{k} = {\hat{x}}_{k}^{-} + K_{k} (y_{k} - h ({\hat{x}}_{k}^{-}))

(11)

P_{k} = P_{k}^{-} - P_{k}^{-} [\begin{matrix} H_{k}^{T} & I \end{matrix}] R_{r, k}^{- 1} [\begin{matrix} H_{k} \\ I \end{matrix}]

(12)

where

{\hat{x}}_{k}^{-}

is the prediction of the state value,

P_{k}^{-}

is the prediction of the error covariance,

K_{k}

is the filter gain, I is the identity matrix, and

F_{k}

and

H_{k}

are Jacobi matrices.

For a non-linear system, the equation of state is:

\{\begin{matrix} x_{k + 1} = f (x_{k}, u_{k}) + ω_{k} \\ y_{k} = g (x_{k}, u_{k}) + v_{k} \end{matrix}

(13)

The procedure of FORUKF is as follows:

(1) Initialization

Initialize covariance

P_{0}

, initial state quantity

{\hat{x}}_{0}

, process noise covariance

Q_{0}

and observation noise covariance

R_{0}

(2) Select Sigma sampling point and weight value

\{\begin{matrix} x_{k - 1}^{0} = {\hat{x}}_{k - 1} \\ x_{k - 1}^{i} = {\hat{x}}_{k - 1} + \sqrt{(n + λ) P_{k - 1}}, i = 1, 2, \dots, n \\ x_{k - 1}^{i} = {\hat{x}}_{k - 1} - \sqrt{(n + λ) P_{k - 1}}, i = n + 1, n + 2, \dots, 2 n \end{matrix}

(14)

The weight value is calculated as follows:

λ = α^{2} (n + k_{i}) - n

(15)

W_{0}^{m} = \frac{λ}{n + λ}

(16)

W_{0}^{c} = \frac{λ}{n + λ} + 1 - α^{2} + β

(17)

W_{i}^{m} = W_{i}^{c} = \frac{1}{2 (n + λ)}, i = 1, 2, \dots, 2 n

(18)

(3) The time is updated to move the sample point from k-1 to k by the state function

{\hat{x}}_{k}^{i} = f ({\hat{x}}_{k - 1}^{i}, u_{k})

(19)

(4) Prior estimation, calculate the result of

{\hat{x}}_{k}^{-}

and

P_{k}^{-}

{\hat{x}}_{k}^{-} = \sum_{i = 0}^{2 n} W_{i}^{m} {\hat{x}}_{k}^{i} - \sum_{j = 1}^{H} K_{j} {\hat{x}}_{k - j}

(20)

P_{k}^{-} = \sum_{i = 0}^{2 n} W_{i}^{c} ({\hat{x}}_{k}^{i} - \sum_{i = 0}^{2 n} W_{i}^{m} {\hat{x}}_{k}^{i}) {({\hat{x}}_{k}^{i} - \sum_{i = 0}^{2 n} W_{i}^{m} {\hat{x}}_{k}^{i})}^{T} +

\sum_{j = 1}^{H} (K_{j} x_{k - j}) \sum_{i = 0}^{2 n} W_{i}^{c} {({\hat{x}}_{k}^{i} - \sum_{i = 0}^{2 n} W_{i}^{m} {\hat{x}}_{k}^{i})}^{T} + \sum_{j = 1}^{H} \sum_{i = 0}^{2 n} W_{i}^{c} ({\hat{x}}_{k}^{i} - \sum_{i = 0}^{2 n} W_{i}^{m} {\hat{x}}_{k}^{i}) {({\hat{x}}_{k - j})}^{T} {(K_{j})}^{T} +

(21)

\sum_{j = 1}^{H} K_{j} {\hat{x}}_{k - j} {({\hat{x}}_{k - j})}^{T} {(K_{j})}^{T} + Q_{k}

(5) Calculate output forecast

{\hat{y}}_{k} = g ({\hat{x}}_{k}^{i}, u_{k})

(22)

(6) Calculation of the measurement estimate

{\hat{y}}_{k}^{-}

and the covariance

P_{k}^{y} P_{k}^{x y}

{\hat{y}}_{k}^{-} = \sum_{i = 0}^{2 n} W_{i}^{m} {\hat{y}}_{k}^{i}

(23)

P_{k}^{y} = {\sum_{i = 0}^{2 n} W_{i}^{c} ({\hat{y}}_{k}^{i} - {\hat{y}}_{k}) ({\hat{y}}_{k}^{i} - {\hat{y}}_{k})}^{T} + R_{k}

(24)

P_{k}^{x y} = \sum_{i = 0}^{2 n} W_{i}^{c} ({\hat{x}}_{k}^{i} - {\hat{x}}_{k}) {({\hat{y}}_{k}^{i} - {\hat{y}}_{k})}^{T}

(25)

(7) Using the extended H∞ filter,

K_{k}

can be obtained:

R_{r, k} = [\begin{matrix} R_{k} & 0 \\ 0 & - γ I \end{matrix}] + [\begin{matrix} H_{k} \\ I \end{matrix}] P_{k}^{-} [\begin{matrix} H_{k}^{T} & I \end{matrix}] = [\begin{matrix} R_{k} + P_{k}^{y} & P_{k}^{x y T} \\ P_{k}^{x y} & - γ^{2} I + P_{k}^{-} \end{matrix}]

(26)

K_{k} = P_{k}^{-} H_{k}^{T} {(H_{k} P_{k}^{-} H_{k}^{T} + R_{k})}^{- 1}

(27)

(8) Update the mean and covariance of the state

P_{k} = P_{k}^{-} - [\begin{matrix} P_{k}^{x y} & P_{k}^{-} \end{matrix}] R_{r, k}^{- 1} {[\begin{matrix} P_{k}^{x y} & P_{k}^{-} \end{matrix}]}^{T}

(28)

{\hat{x}}_{k} = {\hat{x}}_{k}^{-} + K_{k} (z_{k} - {\hat{z}}_{k})

(29)

4.2. SOH estimation strategy

As lithium batteries are used over time, they are constantly being charged and discharged and the rated capacity of the battery gradually decreases. When the capacity drops to the point where the battery can no longer be used properly, it needs to be replaced. And the ohmic resistance also increases. Both of these are slowly changing state variables that correspond to the values of SOH. Updating

Q_{N}

and

R_{0}

in real-time in the calculation can improve the accuracy of the estimate and obtain SOH.

Based on the definition of SOH, the end-of-life criteria for batteries are:

\{\begin{matrix} R_{e o l} = 2 R_{new} \\ Q_{N} = 0.8 Q_{n e w} \end{matrix}

(30)

where

Q_{n e w}

is the rated capacity,

R_{n e w}

represents the ohmic resistance and

R_{e o l}

is the ohmic resistance of the battery when it reaches the end-of-life standard.

This paper uses the rated capacity to estimate the SOH of the battery, expressed as:

S O H = \frac{Q_{N}}{Q_{n e w}}

(31)

Q_{N}

is the current capacity size of the battery.

The equation of estimation

R_{0}

is:

\{\begin{matrix} R_{0, k} = R_{0, k - 1} + ω_{k - 1} \\ U_{L, k} = U_{o c, k} - U_{1, k} - U_{2, k} - R_{0, k} I_{k} + ν_{k} \end{matrix}

(32)

U_{O C, k}

in the observation equation of

R_{0}

is related to the SOC value. The estimation of the internal resistance is completed by the SOC estimation at the k-1 moment and the RUKF algorithm to obtain the

R_{0}

value, which changes in real-time.

The state space model is established with the capacity as the state variable:

\{\begin{matrix} Q_{N, k} = Q_{N, k - 1} + ω_{k - 1} \\ d_{k} = S O C_{k} - S O C_{k - 1} + \frac{η I_{t, k - 1} T}{Q_{N, k - 1}} + υ_{k} \end{matrix}

(33)

The expected value of

d_{k}

in the formula is 0. The relationship between

Q_{N}

and I is established using the ampere-hour integration method and

Q_{N}

at time k is estimated using RUKF based on this state space model.

After obtaining the real-time

R_{0}

and

Q_{N}

, the SOH curve is calculated using

Q_{N}

. Calculate the expression for the SOH curve as:

S O H_{k} = \frac{Q_{N, k}}{Q_{n e w}} \times 100 %

(34)

4.3. FORUKF-RUKF Estimated SOC

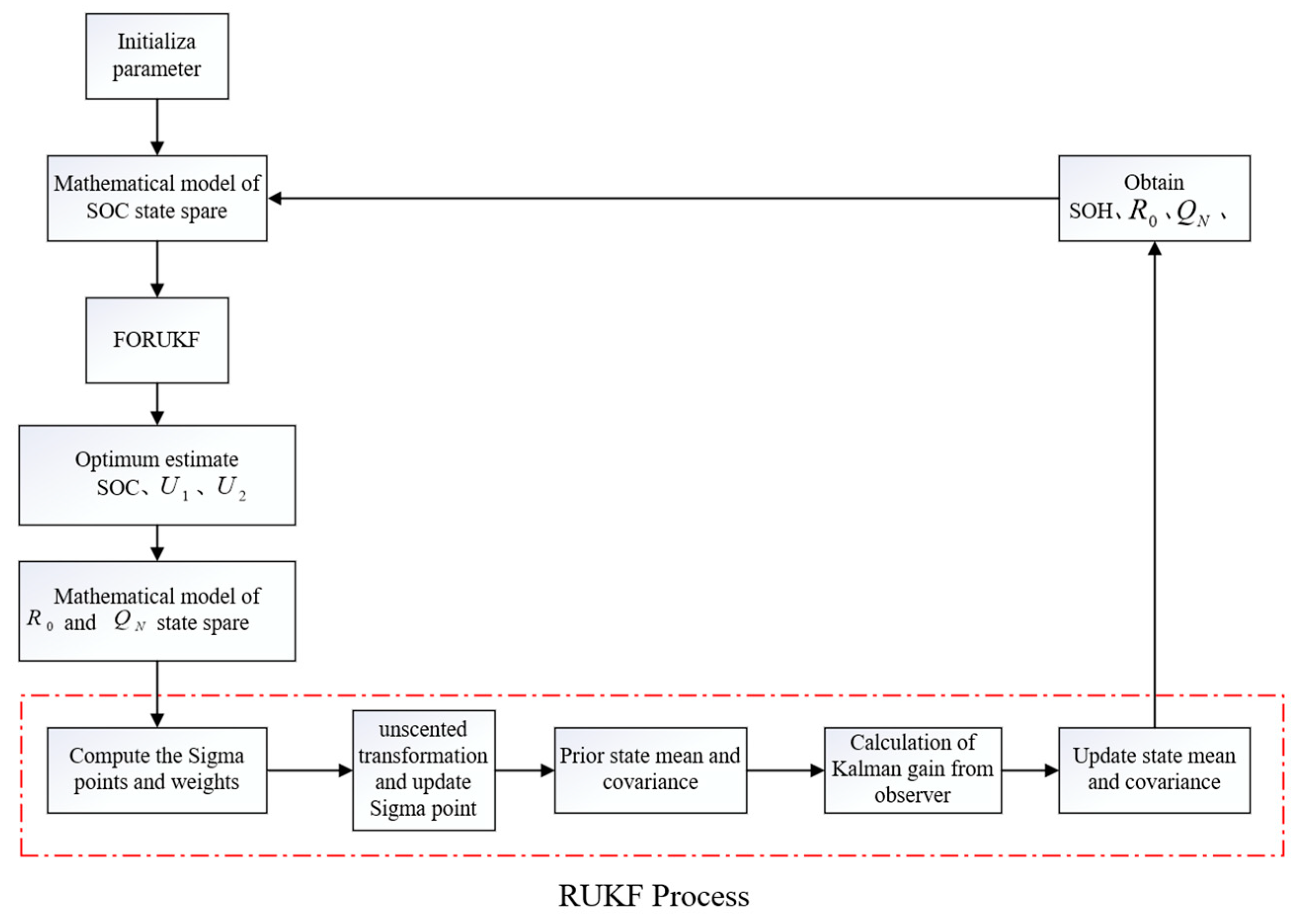
The main process of FORUKF-RUKF is: the SOC value can be calculated by FORUKF under the state space model of equation (3-4), and then the SOH,

R_{0}

Q_{N}

can be estimated by RUKF algorithm under the space model of equations (32)-(34), and the real time changing

R_{0}

Q_{N}

will be fed back to the estimation process of SOC, and the continuous cycle finally achieves estimating the SOC.

Figure 5. Main flow chart of FORUKF-RUKF.

5. Result and Discussion

The results of the algorithm are validated using FUDS, BJDST and US06 conditions. As this open-source data only provides SOC from 0.8 to 0, and as a battery charge below 10% can damage battery life, this paper uses SOC from 0.8 to 0.1.

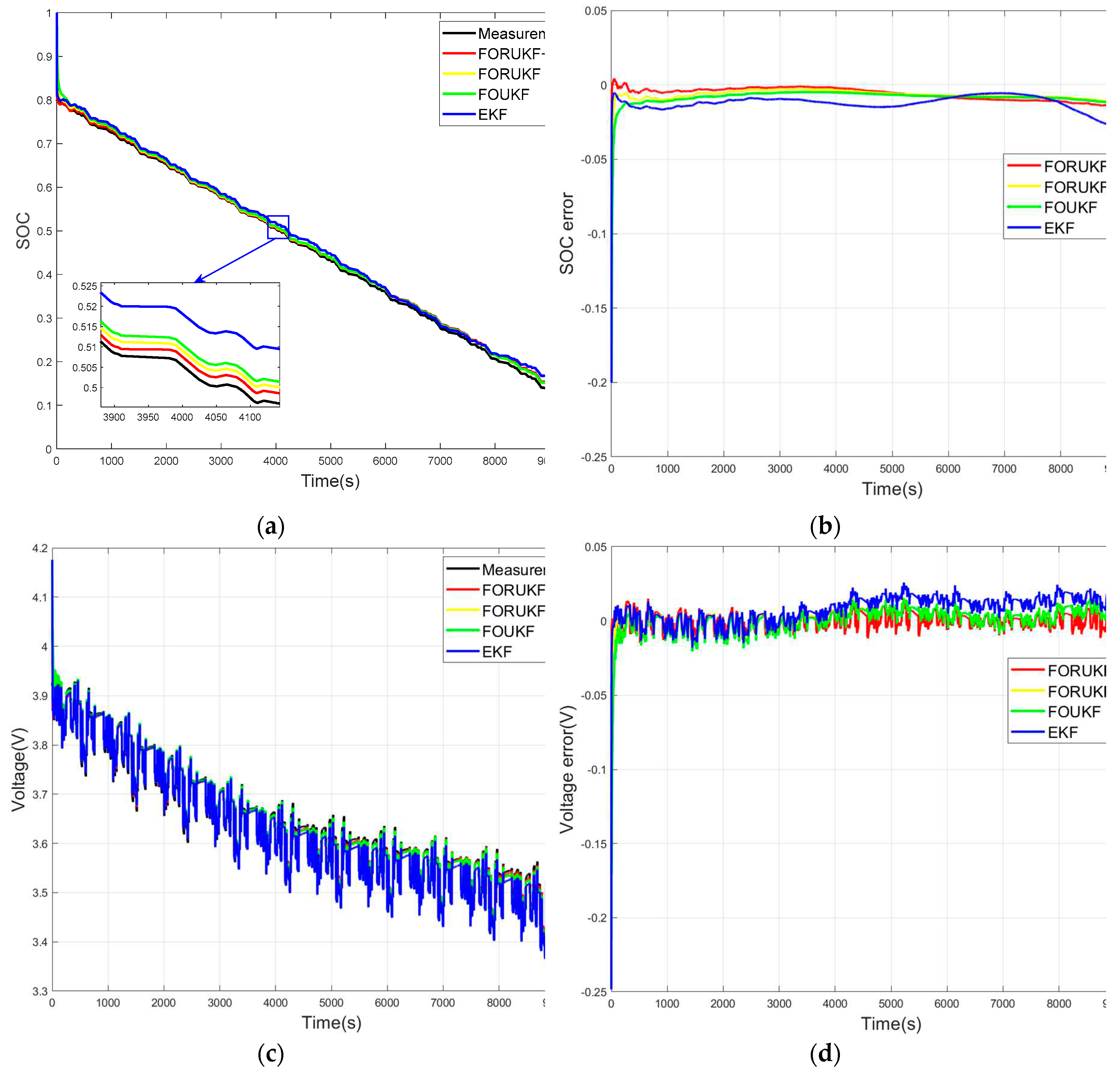
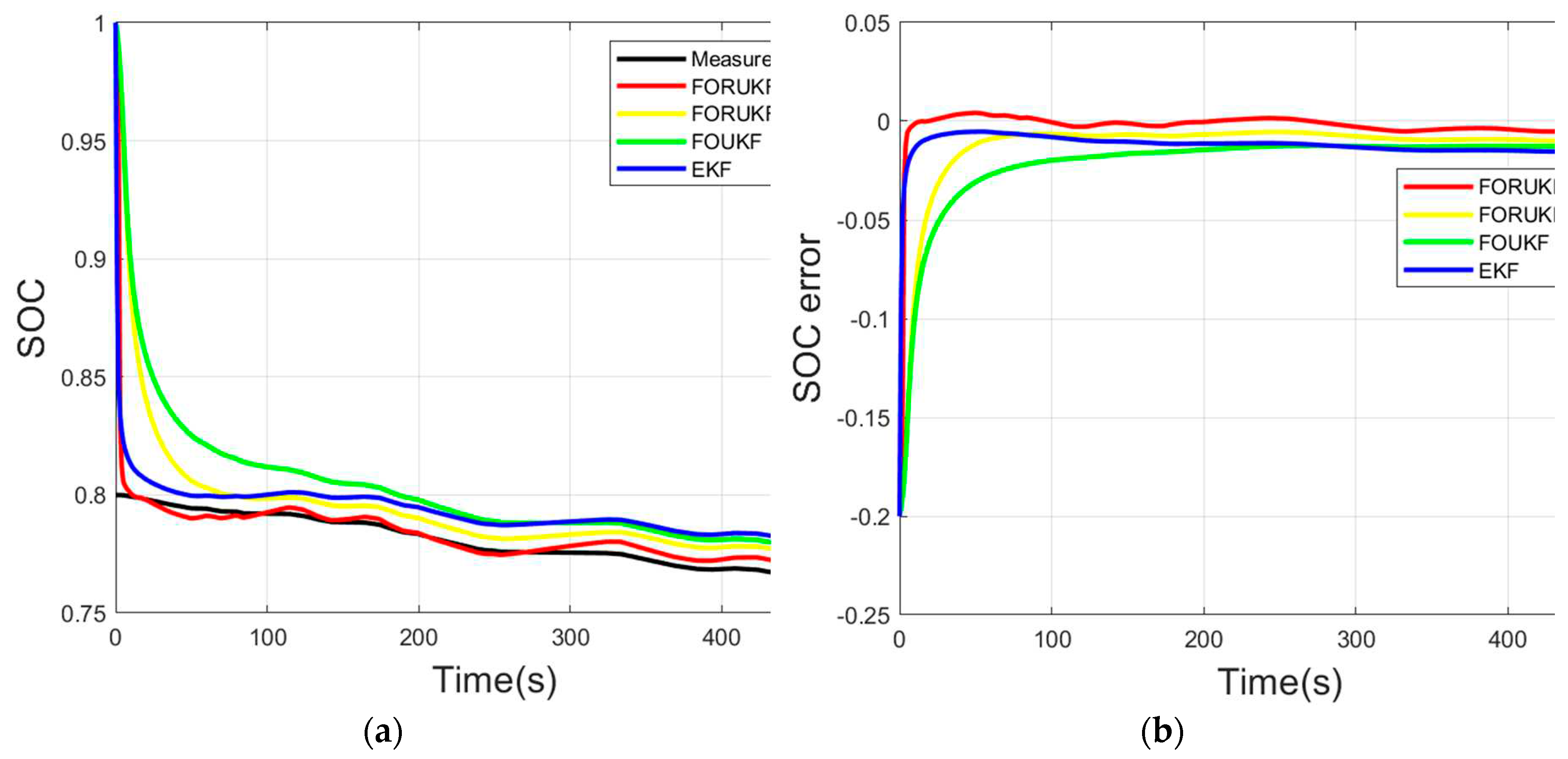
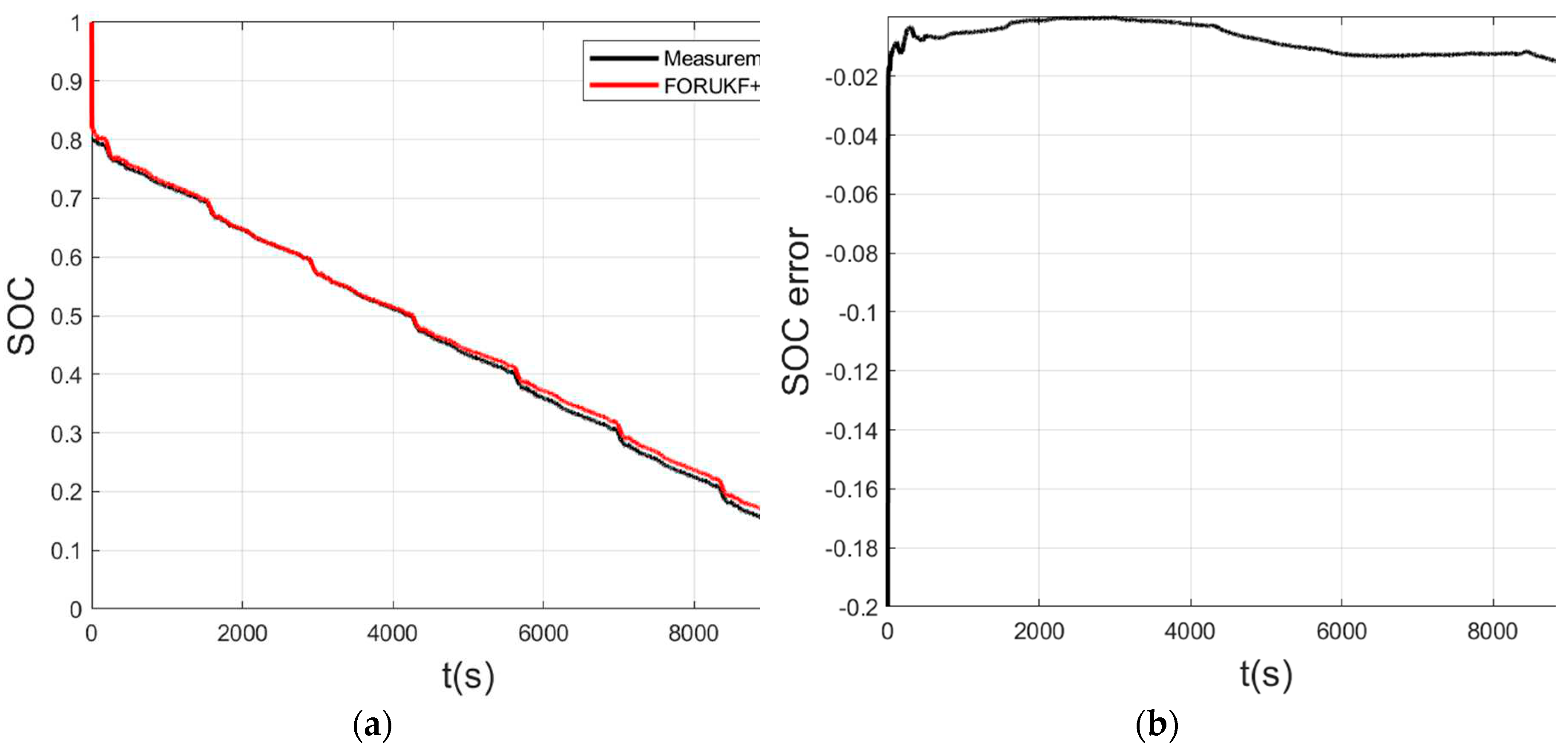
This paper sets the initial value of SOC to 1 and observes whether the algorithm can converge the SOC to 0.8. Comparison of selected EKF, FOUKF and FORUKF algorithms to verify the performance of FORUKF-RUKF. The black line is the measured value, the red line is FORUKF-RUKF, and the blue, green and yellow lines represent EKF, FOUKF and FORUKF respectively, and these four lines are compared to the measured value; the closer to the measured value, the higher the accuracy of the algorithm estimation.

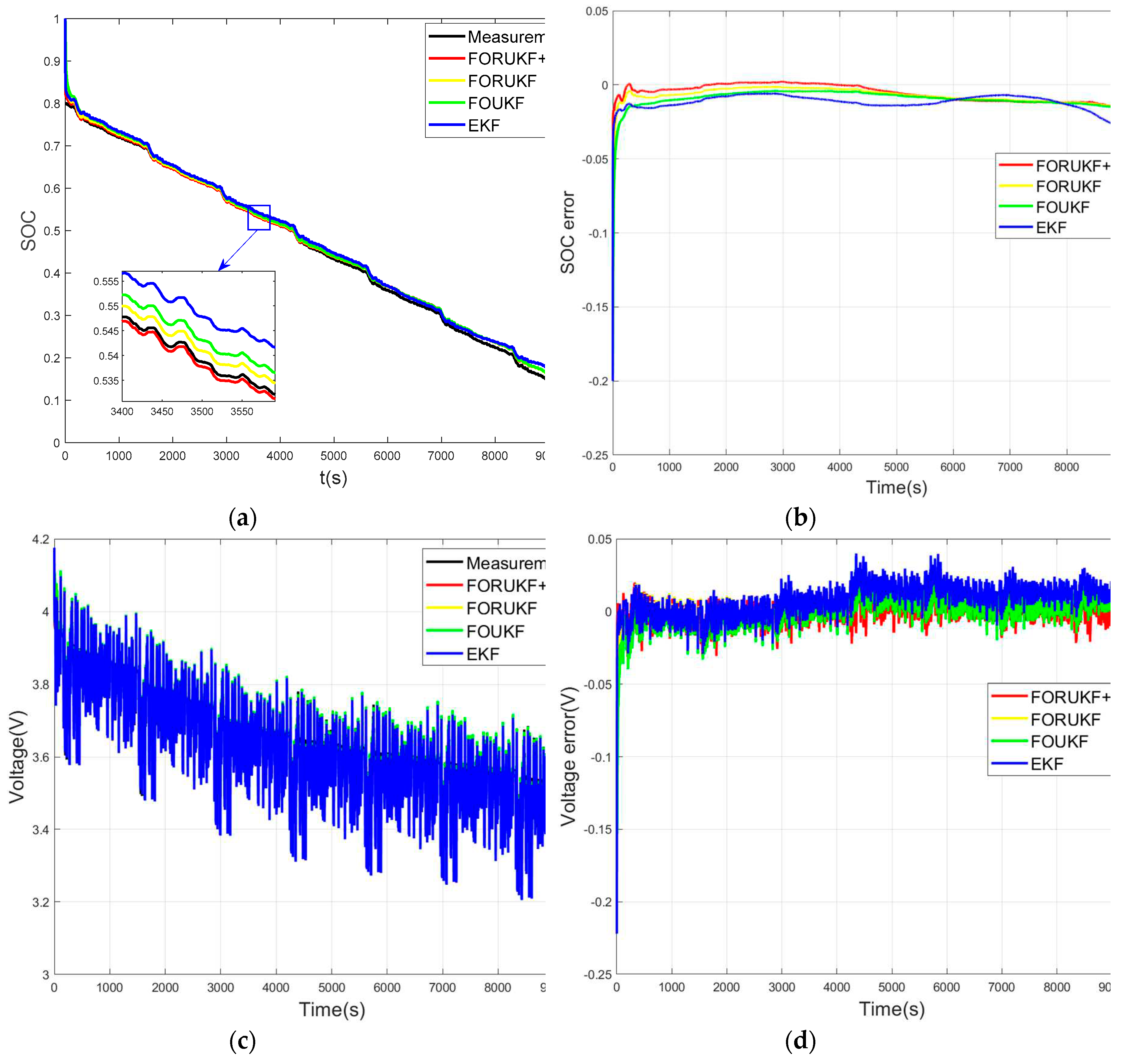
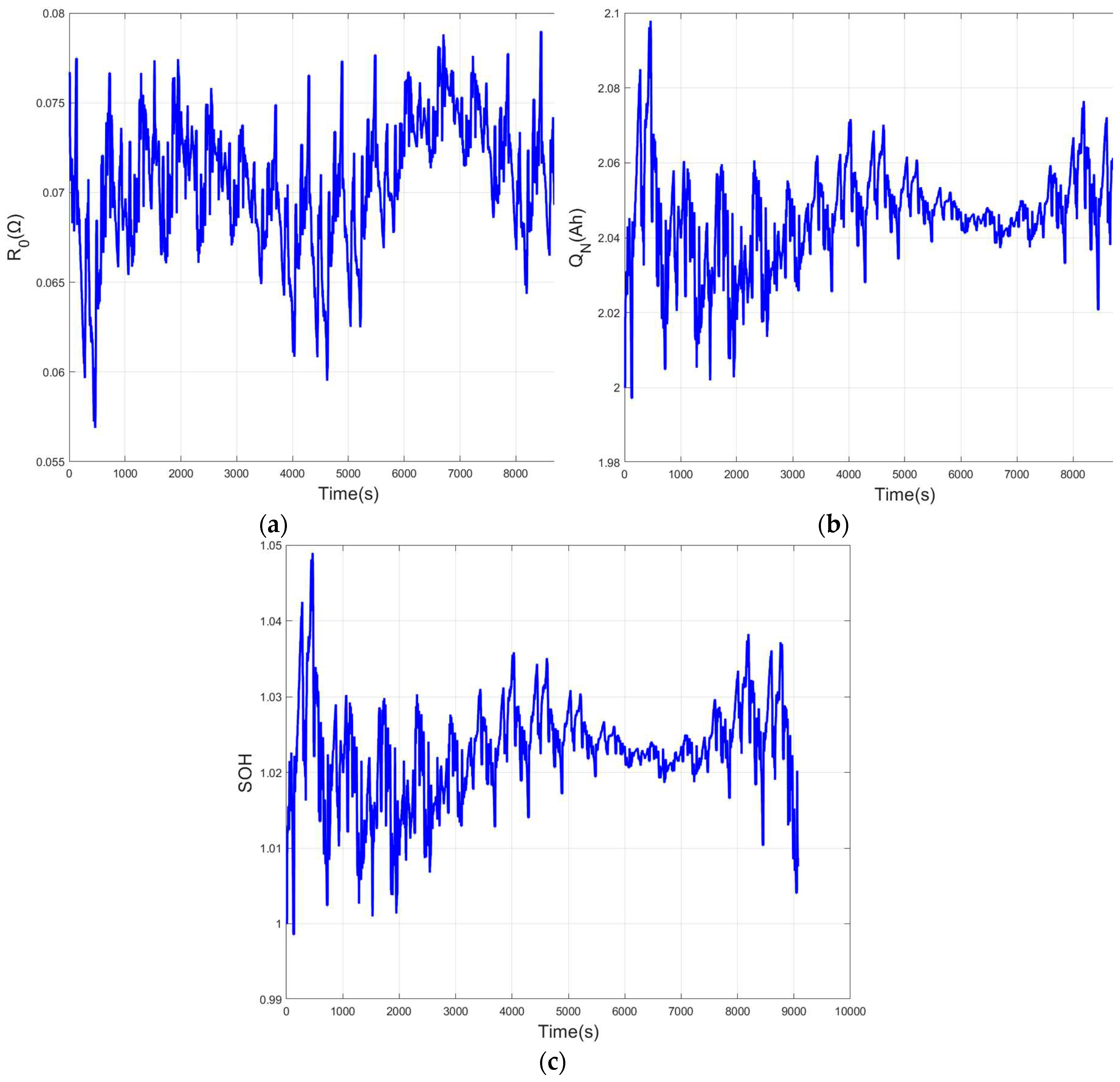
The SOC error and voltage error for the four methods under FUDS conditions are shown in Table 3. The estimated curves and errors of the four methods for estimating SOC and voltage are shown in Figure 6. A comparison of the data shows that FORUKF estimates both SOC and voltage more accurately than EKF and FOUKF, but that the accuracy of FORUKF-RUKF is slightly better than that of FORUKF. The real time varying

R_{0}

and

Q_{N}

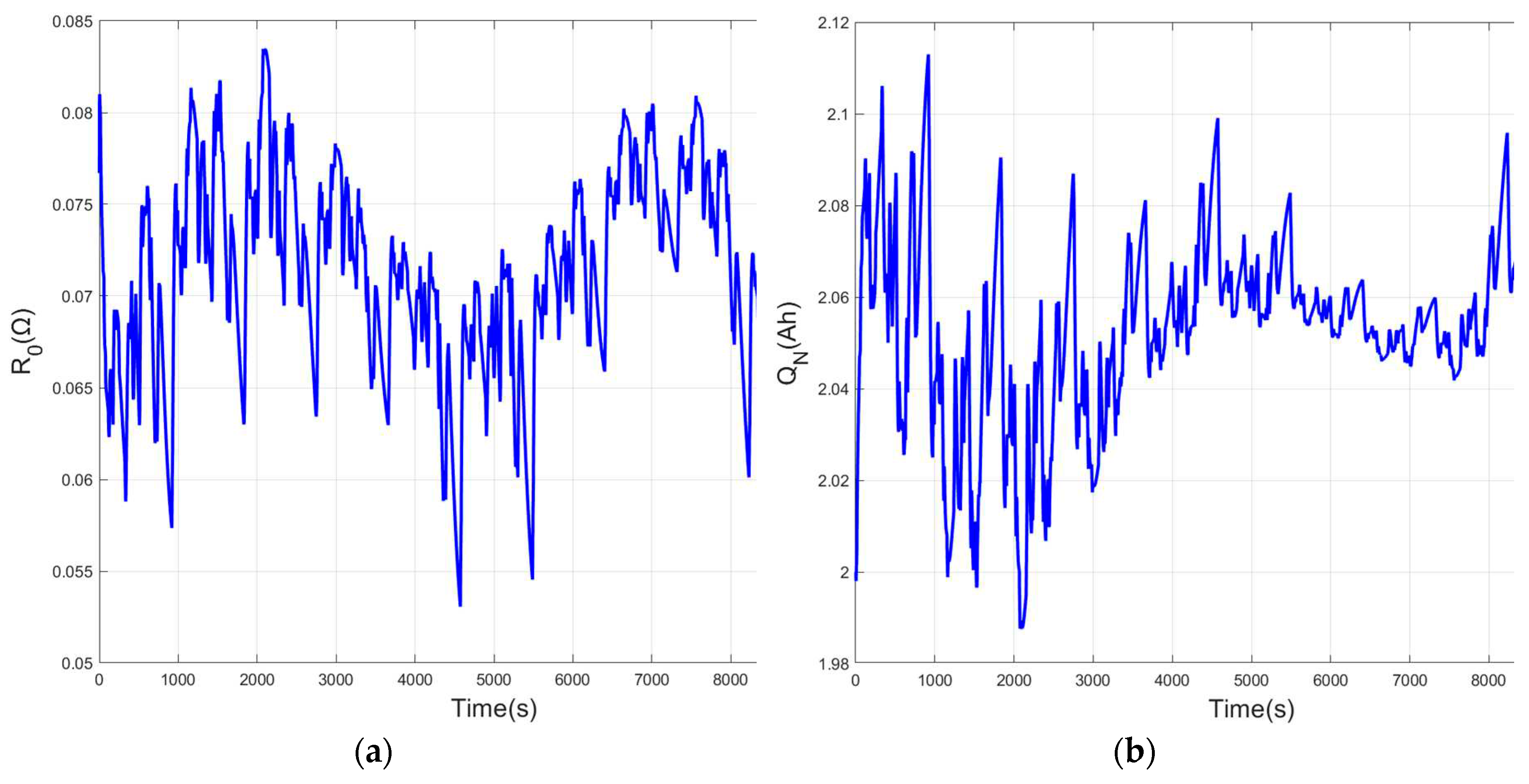
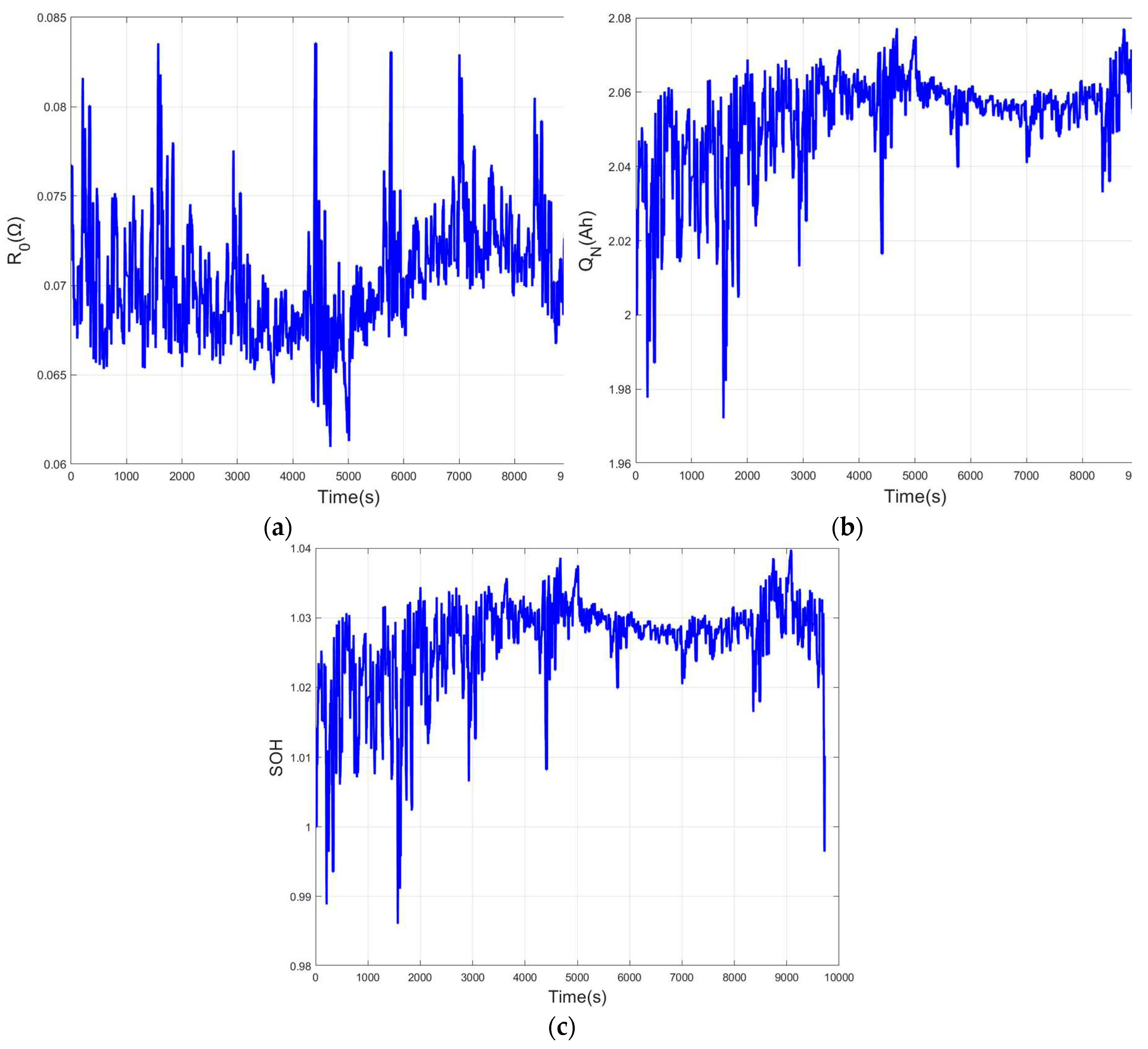
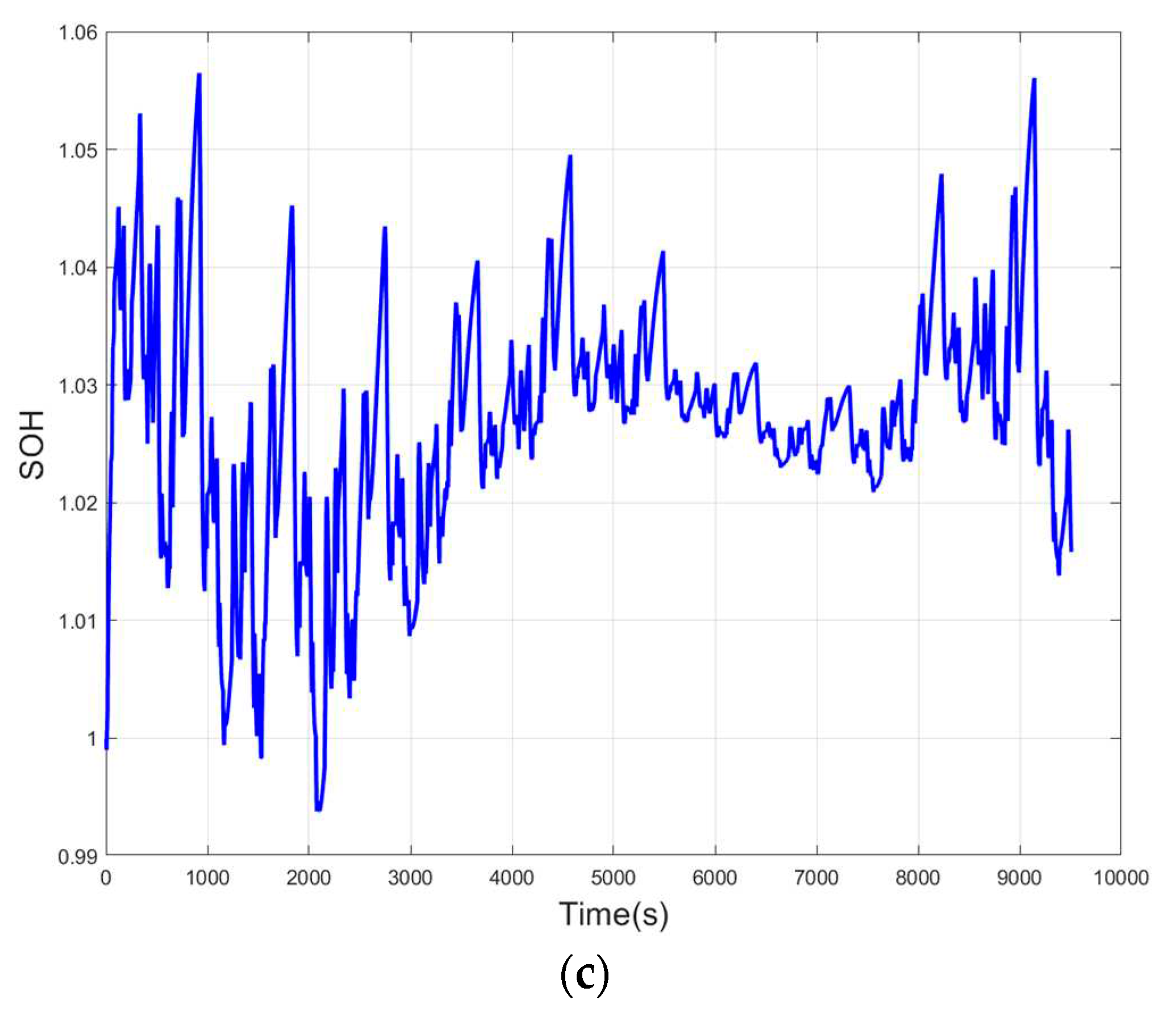
values of the FORUKF-RUKF estimates under the FUDS conditions are shown in Figure 7, and the varying SOH values are obtained by equation (34) and

Q_{N}

values as shown in Figure 7(c).

As can be seen from the comparison of simulations under FUDS conditions is shown in Figure 6, the results estimated by FORUKF-RUKF maintain a high level of accuracy throughout. After setting the wrong initial value, FORUKF-RUKF is the fastest of the four algorithms to approach the measured value. However, when the SOC drops below approximately 30%, the advantages of FORUKF-RUKF are no longer apparent. This is because when the battery drops to a lower SOC, the battery condition also changes significantly and the parameter values obtained using the offline identification of the AGA are no longer suitable for the battery at that point, which is one of the disadvantages of offline parameter identification.

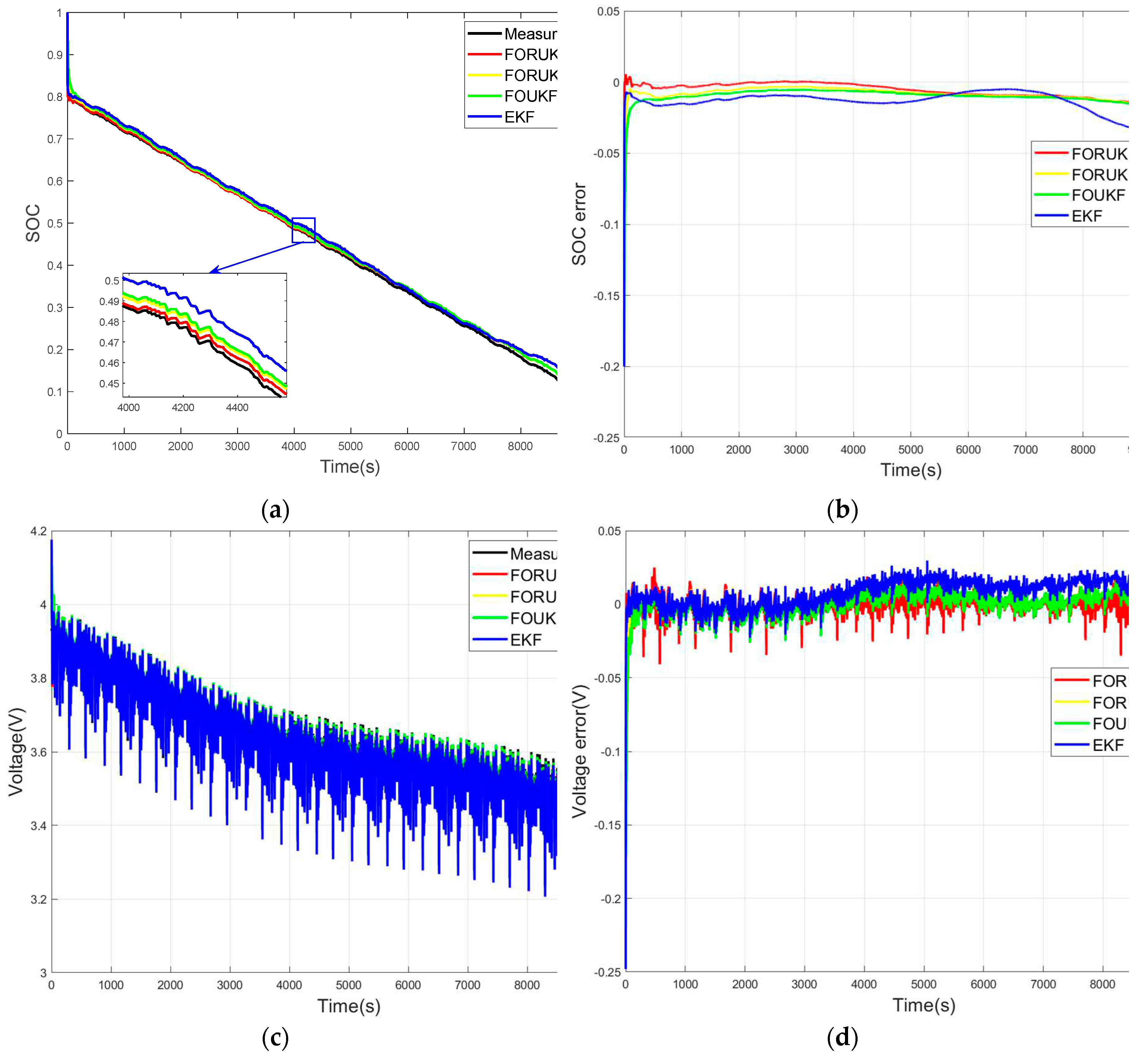
The comparison of the four algorithms for the US06 and BJDST conditions is shown in Figure 8 and 11. It can be seen that after setting the wrong initial value of SOC, all four algorithms can gradually approach the measured value, but FORUKF-RUKF converges to the measured value the fastest. In addition, the FORUKF-RUKF algorithm maintains good accuracy throughout the estimation of the SOC. As shown in Table 3-5, the FORUKF-RUKF algorithm maintains the highest accuracy throughout the estimation of the SOC, and that FORUKF also outperforms the EKF and FOUKF overall. The variation curves of

R_{0}

Q_{N}

, and SOH estimated in real time are shown in Figure 7, which are informative for understanding the current state of the battery. This paper uses equation (34) to calculate SOH, the value of SOH is related to

Q_{N}

, so the curve of SOH is exactly the same as

Q_{N}

is greater than the rated capacity of 2Ah and the SOH is also greater than 1. This is because the battery has not been used much and the battery still has a long service life.

Table 5. Errors of the four algorithms under the BJDST conditions.

Algorithm	SOC Error		Voltage Error
Algorithm	MAE(%)	RMSE(%)	RMSE(mV)
EKF	1.33	1.49	11.8
FOUKF	0.81	1.09	9.4
FORUKF	0.69	0.93	8.7
FORUKF-RUKF	0.67	0.84	6.3

Figure 10. Comparison under the BJDST conditions: (a) SOC; (b) errors of SOC; (c) voltage; (d) errors of voltage.

Figure 11. Curve obtained by the FORUKF-RUKF algorithm under the FUDS conditions: (a)

R_{0}

Figure 11. Curve obtained by the FORUKF-RUKF algorithm under the FUDS conditions: (a)

R_{0}

As can be seen from the SOC estimation results, FORUKF-RUKF, which incorporates the H∞ observer and the joint estimation method, can quickly approximate the observed SOC value with an incorrect initial value of SOC, and the root mean square error of SOC remains minimal in the overall estimation process. The SOH curve, obtained from the estimated

Q_{N}

curve, is also useful in determining the remaining life of the battery.

The stability of the FORUKF-RUKF algorithm is then checked by increasing the variance of the measurement noise. Simulation of large errors in experimental measurements by increasing the variance of the observed noise to verify the robustness of the algorithm. Finally, the data from the FUDS conditions was selected to verify the accuracy of the algorithm. The estimation results of the method under the FUDS conditions are shown in Figure 12.

As shown in Figure 12, the method can still maintain high stability after increasing the variance of the observation noise. This indicates that the method has a strong resistance to interference and is more suitable for practical production.

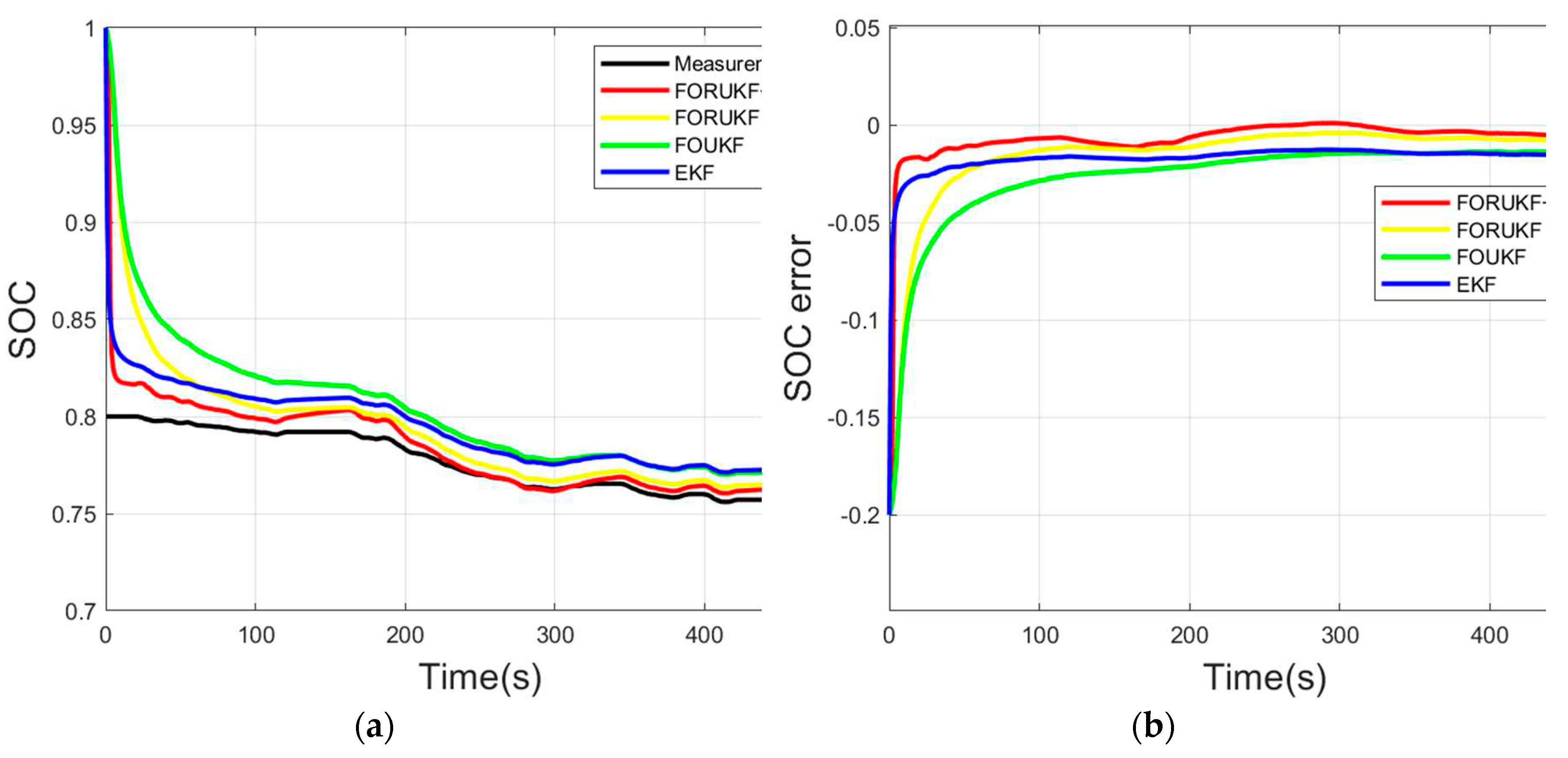
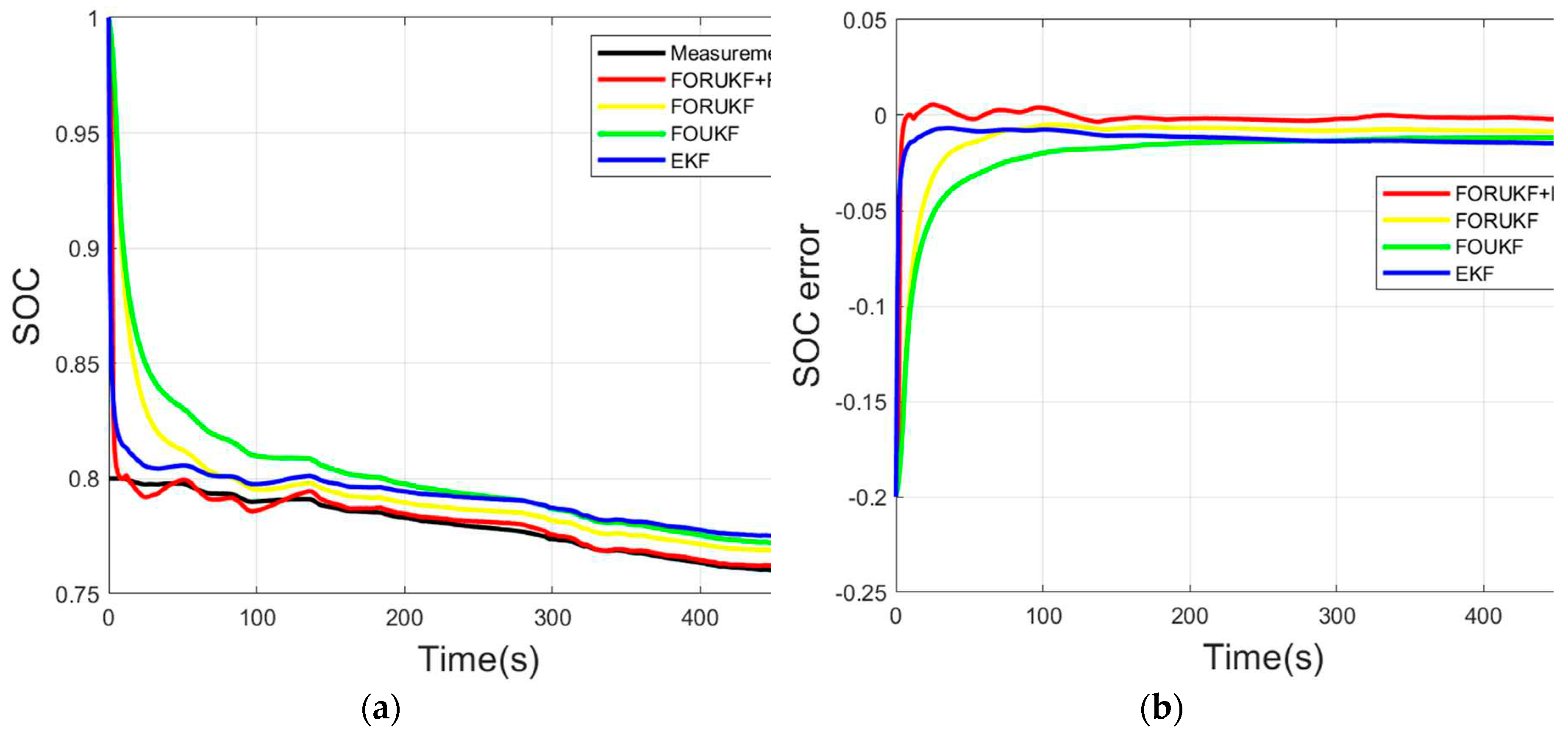
To further verify the robustness of FORUKF-RUKF, the convergence speed of the algorithm is verified in this paper. The SOC in the experimental data starts at 0.8, and we set the initial value of SOC to 1. The MAE and RMSE of the measured SOC in the first 500 seconds versus the measured value. The results are compared with EKF, FOUKF and FORUKF. Smaller errors indicate faster convergence and greater robustness of the algorithm. The comparison of the convergence of the four algorithms under the FUDS, US06 and BJDST conditions are shown in Figure 13-15.

As shown in Figure 13-15, the FORUKF-RUKF algorithm converges to the measured value faster than the EKF, FOUKF, and FORUKF, and then fluctuates up and down around the measured value. An analysis of Table 6-8 shows that the FORUKF-RUKF algorithm has a smaller error in the first 500 seconds than the other three algorithms. The algorithm quickly converges to the measured value, even if the initial SOC value has a large error due to equipment influence. The FORUKF-RUKF algorithm is more stable and robust.

Table 8. Errors of each algorithm in the first 500 seconds of the BJDST conditions.

Algorithm	SOC Error
Algorithm	MAE(%)	RMSE(%)
EKF	1.26	1.49
FOUKF	2.07	1.09
FORUKF	1.30	0.93
FORUKF-RUKF	0.39	0.84

Figure 15. Convergence of each algorithm in the first 500 seconds of the BJDST conditions: (a)SOC; (b)errors of SOC.

6. Conclusions

This paper proposes the FORUKF-RUKF algorithm to estimate the SOC of lithium batteries, which incorporates the H∞ observer and the joint estimation method. Offline parameters of the battery’s FOM were obtained by using the AGA for parameter recognition of the battery’s data under DST conditions. The RUKF in the algorithm estimates the ohmic resistance

R_{0}

and the capacity

Q_{N}

of the battery in real-time, and the battery SOC is estimated together with the FORUKF. The algorithm was validated under the FUDS, US06 and BJDST conditions and it was found that FORUKF-RUKF could converge faster to the measured value and the accuracy of the estimated SOC was better than FORUKF, FOUKF and EKF, with the root mean square error stabilizing within 1%. After setting an incorrect initial value of SOC, the algorithm can still quickly converge to the measured value and its robustness is better than other traditional algorithms. In the future, we will use different batteries and different temperatures to simulate the complex environment of the battery in practical application to further validate the robustness of the algorithm.

Author Contributions

Methodology, W.L.; software, L.X.; validation and data curation, X.L. and B.X.; writing—original draft preparation, W.L.; project administration, L.X. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the project of the Natural Science Foundation of the Higher Education Institute of Anhui Province (grant KJ2019A0106), and by the Huainan City 2021 Key Research and Development Program Projects Province (grant 2021A249).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Diouf, B.; Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy. 2015, 76, 375-380. [CrossRef]
Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [CrossRef]
Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.-I.; Stroe, A.-I.; Teodorescu, R. An overview and comparison of online implementable SOC estimation methods for lithium-ion battery. IEEE Trans. Ind. Appl. 2018, 54, 1583–1591. [CrossRef]
Smith KA, Rahn CD, Wang CY. Model-Based electrochemical estimation and constraint management for pulse operation of lithium ion batteries. IEEE T Control Syst Technol 2010; 18:654–63. [CrossRef]
Shen Y. Adaptive online state-of-charge determination based on neuro-controller and neural network. Energy Conver Manage 2010; 51:1093–8. [CrossRef]
Li X, Wang Z, Zhang L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles. Energy 2019. [CrossRef]
Zahid T, Xu K, Li W, et al. State of charge estimation for electric vehicle power battery using advanced machine learning algorithm under diversified drive cycles. Energy 2018; 162:871e82. [CrossRef]
Malkhandi S. Fuzzy logic-based learning system and estimation of state-of-charge of lead-acid battery. Eng Appl Artif Intell 2006;19(5):479e85. [CrossRef]
Ant on JCA, Nieto PJG, de Cos Juez FJ, et al. Battery state-of-charge estimator using the SVM technique. Appl Math Model 2013;37(9):6244e53. [CrossRef]
Li J, Barillas JK, Guenther C, Danzer MA. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J Power Sources 2013; 230:244–50. [CrossRef]
Hu Y, Yurkovich S. Battery cell state-of-charge estimation using linear parameter varying system techniques. J Power Sources 2012; 198:338–50. [CrossRef]
Lee J, Nam O, Cho BH. Li-ion battery SOC estimation method based on the reduced order extended Kalman filtering. J Power Sources 2007; 174:9–15. [CrossRef]
Yu, Z.; Huai, R.; Xiao, L. State of charge estimation for lithium-ion batteries using a Kalman filter based on local linearization. Energies 2015, 8, 7854–7873. [CrossRef]
Shehab El Din, M.; Hussein, A.A.; Abdel-Hafez, M.F. Improved Battery SOC Estimation Accuracy Using a Modified UKF With an Adaptive Cell Model Under Real EV Operating Conditions. IEEE Trans. Transp. Electrif. 2018, 4, 408–417. [CrossRef]
Huang, J.; Li, Z.; Liaw, B.Y.; Zhang, J. Graphical analysis of electrochemical impedance spectroscopy data in Bode and Nyquist representations. J. Power Sources 2016, 309, 82–98. [CrossRef]
Liu, S.; Dong, X.; Zhang, Y. A New State of Charge Estimation Method for Lithium-Ion Battery Based on the Fractional Order Model. IEEE Access 2019, 7, 122949–122954. [CrossRef]
Yang, Q.; Xu, J.; Cao, B.; Li, X. A simplified fractional order impedance model and parameter identification method for lithium-ion batteries. PLoS ONE 2017, 12, e0172424. [CrossRef]
He, D.; Zhang, W.; Luo, X. Overview of Power Lithium Battery Modeling and Soc Estimation. IOP Conf. Ser. Earth Environ. Sci.2020, 461, 012032. [CrossRef]
Xiong, R.; Tian, J.; Shen, W.; Sun, F. A novel fractional order model for state of charge estimation in lithium ion batteries. IEEE Trans. Veh. Technol. 2019, 68, 4130–4139. [CrossRef]
Ramezani, A.; Safarinejadian, B.; Zarei, J. Novel hybrid robust fractional interpolatory cubature Kalman filters. J. Frankl. Inst.2020, 357, 704–725. [CrossRef]
Liping Chen, Xiaobo Wu, Jose A. Tenreiro Machado,State-of-Charge Estimation of Lithium-Ion Batteries Based on Fractional-Order Square-Root Unscented Kalman Filter. Fractal Fract. 2022, 6, 52. [CrossRef]
M. Zeng, et al., SOC and SOH joint estimation of the power batteries based on fuzzy unscented Kalman filtering algorithm, Energies 12 (16) (2019). [CrossRef]
Zhuang Y, Wang Z, Yu H, Wang W, Lauria S (2013) A robust extended H∞ filtering approach to multi-robot cooperative localization in dynamic indoor environments. Control Eng Pract 21:953–961.
Chandra KPB, Gub DW, Postlethwaite I (2014) A cubature H∞ filter and its square-root version. Int J Control 87(4):764–776.
Ramazan Havangi. Adaptive robust unscented Kalman filter with recursive least square for state of charge estimation of batteries. Electrical Engineering.104,1001-1017(2022). [CrossRef]
R. Xiong, et al., A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion polymer battery in electric vehicles, Appl. Energy 113 (2014) 463–476. [CrossRef]
Lili Ma, Yonghong Xu, Hongguang Zhang.Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order model with multi-innovations unscented Kalman filter method. Journal of Energy Storage 52(2022) 104904. [CrossRef]
Jingjin Wu,Chao Fang, Zhiyang jin, et. A multi-scale fractional-order dual unscented Kalman filter based parameter and state of charge joint estimation method of lithium-ion battery. Journal of Energy Storage 50 (2022) 104666. [CrossRef]
Lin He, Yangyang Wang, Yujiang Wei, et. An adaptive central difference Kalman filter approach for state of charge estimation by fractional order model of lithium-ion battery. Energy 244 (2022) 122627. [CrossRef]
Yue Miao, Zhe Gao. Estimation for state of charge of lithium-ion batteries by adaptive fractional-order unscented Kalman filters. Journal of Energy Storage 51 (2022) 104396. [CrossRef]
Hao Mu,Rui Xiong,Hongfei Zheng,et. A novel fractional order model based state-of-charge estimation method for lithium-ion battery.Applied Energy 207 (2017) 384-393. [CrossRef]

Figure 1. Lithium battery FOM structure.

Figure 2.

U_{O C}

Figure 2.

U_{O C}

Figure 3. AGA algorithm flow.

Figure 6. Comparison under the FUDS conditions: (a) SOC; (b) errors of SOC; (c) voltage; (d) errors of voltage.

Figure 7. Curve obtained by the FORUKF-RUKF algorithm under the FUDS conditions (a)

R_{0}

; (b)

Q_{N}

; (c) SOH.

Figure 7. Curve obtained by the FORUKF-RUKF algorithm under the FUDS conditions (a)

R_{0}

; (b)

Q_{N}

; (c) SOH.

Figure 8. Comparison under the US06 conditions: (a) SOC; (b) errors of SOC; (c) voltage; (d) errors of voltage.

Figure 9. Curve obtained by the FORUKF-RUKF algorithm under the FUDS conditions (a)

R_{0}

; (b)

Q_{N}

; (c) SOH.

Figure 9. Curve obtained by the FORUKF-RUKF algorithm under the FUDS conditions (a)

R_{0}

; (b)

Q_{N}

; (c) SOH.

Figure 12. Estimation results after increasing the variance of the observed noise: (a)SOC; (b)errors of SOC.

Figure 13. Convergence of each algorithm in the first 500 seconds of the FUDS conditions: (a)SOC; (b)errors of SOC.

Figure 14. Convergence of each algorithm in the first 500 seconds of the US06 conditions: (a)SOC; (b)errors of SOC.

Table 1. Parameters of FOM and IOM.

Model	$R_{0}$ /Ω	$R_{1}$ /Ω	$R_{2}$ /Ω	$C_{1}$ /F	$C_{2}$ /F	$α$	$β$
IOM	0.0830	0.1597	0.2550	7,947	41,280	\	\
FOM	0.0767	0.0298	0.0376	5,021	134,639	0.9232	0.9485

Table 2. Voltage errors under FOM and IOM.

Method	MAE/mV	RMAE/mV
FOM-AGA	6.5	7.9
IOM-AGA	11.3	14.8

Table 3. Errors of the four algorithms under the FUDS conditions.

Algorithm	SOC Error		Voltage Error
Algorithm	MAE(%)	RMSE(%)	RMSE(mV)
EKF	1.32	1.53	12.5
FOUKF	0.93	1.28	10.4
FORUKF	0.76	1.08	9.3
FORUKF-RUKF	0.67	0.91	7.9

Table 4. Errors of the four algorithms under the US06 conditions.

Algorithm	SOC Error		Voltage Error
Algorithm	MAE(%)	RMSE(%)	RMSE(mV)
EKF	1.32	1.48	11.9
FOUKF	0.92	1.19	9.5
FORUKF	0.79	1.03	8.7
FORUKF-RUKF	0.57	0.77	7.4

Table 6. Errors of each algorithm in the first 500 seconds of the FUDS conditions.

Algorithm	SOC Error
Algorithm	MAE(%)	RMSE(%)
EKF	1.72	1.53
FOUKF	2.59	1.28
FORUKF	1.53	1.08
FORUKF-RUKF	0.49	0.95

Table 7. Errors of each algorithm in the first 500 seconds of the US06 conditions.

Algorithm	SOC Error
Algorithm	MAE(%)	RMSE(%)
EKF	1.27	1.48
FOUKF	2.09	1.19
FORUKF	1.28	1.03
FORUKF-RUKF	0.28	0.80

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

SOC Estimation for Lithium Batteries Based on Fractional Order Model and Robust Unscented Kalman Filter

Abstract

1. Introduction

2. Battery Modeling

2.1. Fractional Order Calculus

2.2. Fractional Order Model

3. Parameter Identification

3.1. Description of the Experimental Data

3.2. Model Parameter Identification

3.3. Model Accuracy Verification

4. Battery SOC estimation

4.1. FORUKF

4.2. SOH estimation strategy

4.3. FORUKF-RUKF Estimated SOC

5. Result and Discussion

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe