A Common Approach to Three Open Problems in Number Theory

Preprint

Article

A Common Approach to Three Open Problems in Number Theory

Altmetrics

Downloads

547

Views

136

Comments

A peer-reviewed article of this preprint also exists.

Apoloniusz Tyszka^*

This version is not peer-reviewed

Submitted:

17 May 2023

Posted:

18 May 2023

You are already at the latest version

Alerts

Abstract

The following system of equations {x_1 \cdot x_1=x_2, x_2 \cdot x_2=x_3, 2^{2^{x_1}}=x_3, x_4 \cdot x_5=x_2, x_6 \cdot x_7=x_2} has exactly one solution in ({\mathbb N}\{0,1})^7, namely (2,4,16,2,2,2,2). Hypothesis 1 states that if a system of equations S \subseteq {x_i \cdot x_j=x_k: i,j,k \in {1,...,7}} \cup {2^{2^{x_j}}=x_k: j,k \in {1,...,7}} has at most five equations and at most finitely many solutions in ({\mathbb N}\{0,1})^7, then each such solution (x_1,...,x_7) satisfies x_1,...,x_7 \leq 16. Hypothesis 1 implies that there are infinitely many composite numbers of the form 2^{2^{n}}+1. Hypotheses 2 and 3 are of similar kind. Hypothesis 2 implies that if the equation x!+1=y^2 has at most finitely many solutions in positive integers x and y, then each such solution (x,y) belongs to the set {(4,5),(5,11),(7,71)}. Hypothesis 3 implies that if the equation x(x+1)=y! has at most finitely many solutions in positive integers x and y, then each such solution (x,y) belongs to the set {(1,2),(2,3)}. We describe semi-algorithms sem_j (j=1,2,3) that never terminate. For every j \in {1,2,3}, if Hypothesis j is true, then sem_j endlessly prints consecutive positive integers starting from 1. For every j \in {1,2,3}, if Hypothesis j is false, then sem_j prints a finite number (including zero) of consecutive positive integers starting from 1.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: 11D61; 11D85

1. Epistemic Notions Increase the Scope of Mathematics

Nicolas D. Goodman observed that epistemic notions increase the scope of mathematics, see [1]. For many finite sets

X \subseteq N^{m}

, we know an algorithm that decides

X

although no known algorithm computes a positive integer n satisfying

X \subseteq {[0, n]}^{m}

. This holds as for many Diophantine equations the number of rational solutions is finite by applying Faltings’ theorem. Faltings’ theorem tell us that certain curves have at most finitely many rational points, but no known proof gives any bound on the sizes of the numerators and denominators of the coordinates of those points.

In Section 2, Section 3 and Section 4, our knowledge (including conjectures) about the set

X

is different. The considerations in Section 2 imply the existence of the set

X_{2} \subseteq {(N \ {0, 1})}^{7}

whose finiteness/infiniteness is unknown although we conjecture that

card (X_{2}) < ω \Rightarrow X_{2} \subseteq {[2, 16]}^{7}

. The considerations in Section 3 imply the existence of the set

X_{3} \subseteq {(N \ {0})}^{6}

whose finiteness/infiniteness is unknown although we conjecture that

card (X_{3}) < ω \Rightarrow X_{3} \subseteq {[1, (24!)!]}^{6}

. The considerations in Section 4 imply the existence of the set

X_{4} \subseteq {(N \ {0})}^{6}

whose finiteness/infiniteness is unknown although we conjecture that

card (X_{4}) < ω \Rightarrow X_{4} \subseteq {[1, 720!]}^{6}

. For every

j \in {2, 3, 4}

, we know an algorithm that decides the set

X_{j}

2. Composite Numbers of the Form $2^{2^{n}} + 1$

Let

A

denote the following system of equations:

\{x_{i} \cdot x_{j} = x_{k} : i, j, k \in {1, \dots, 7}\} \cup \{2^{2^{x_{j}}} = x_{k} : j, k \in {1, \dots, 7}\}

The following subsystem of

A

has exactly one solution in

{(N \ {0, 1})}^{7}

, namely

(2, 4, 16, 2, 2, 2, 2)

Conjecture 1.

If a system of equations

S \subseteq A

has at most five equations and at most finitely many solutions in

{(N \ {0, 1})}^{7}

, then each such solution

(x_{1}, \dots, x_{7})

satisfies

x_{1}, \dots, x_{7} ⩽ 16

Lemma 1.

[[2] (p. 109)]. For every non-negative integers x and y,

x + 1 = y

if and only if

2^{2^{x}} \cdot 2^{2^{x}} = 2^{2^{y}}

Theorem 2.

Conjecture 1 implies that

2^{2^{x_{1}}} + 1

is composite for infinitely many integers

x_{1}

greater than 1.

Proof.

Assume, on the contrary, that Conjecture 1 holds and

2^{2^{x_{1}}} + 1

is composite for at most finitely many integers

x_{1}

greater than 1. Then, the equation

x_{2} \cdot x_{3} = 2^{2^{x_{1}}} + 1

has at most finitely many solutions in

{(N \ {0, 1})}^{3}

. By Lemma 1, in positive integers greater than 1, the following subsystem of

A

has at most finitely many solutions in

{(N \ {0, 1})}^{7}

and expresses that

\{\begin{matrix} x_{2} \cdot x_{3} & = & 2^{2^{x_{1}}} + 1 \\ x_{4} & = & 2^{2^{x_{1}}} + 1 \\ x_{5} & = & 2^{2^{x_{1}}} \\ x_{6} & = & 2^{2^{2^{2^{x_{1}}}}} \\ x_{7} & = & 2^{2^{2^{2^{x_{1}}} + 1}} \end{matrix}

Since

641 \cdot 6700417 = 2^{2^{5}} + 1 > 16

, we get a contradiction. □

Most mathematicians believe that

2^{2^{n}} + 1

is composite for every integer

n ⩾ 5

, see [3, p. 23].

Open Problem 1

([4] (p. 159)). Are there infinitely many composite numbers of the form

2^{2^{n}} + 1

Primes of the form

2^{2^{n}} + 1

are called Fermat primes, as Fermat conjectured that every integer of the form

2^{2^{n}} + 1

is prime, see [4] (p. 1). Fermat remarked that

2^{2^{0}} + 1 = 3

2^{2^{1}} + 1 = 5

2^{2^{2}} + 1 = 17

2^{2^{3}} + 1 = 257

, and

2^{2^{4}} + 1 = 65537

are all prime, see [4, p. 1].

Open Problem 2

([4] (p. 158)). Are there infinitely many prime numbers of the form

2^{2^{n}} + 1

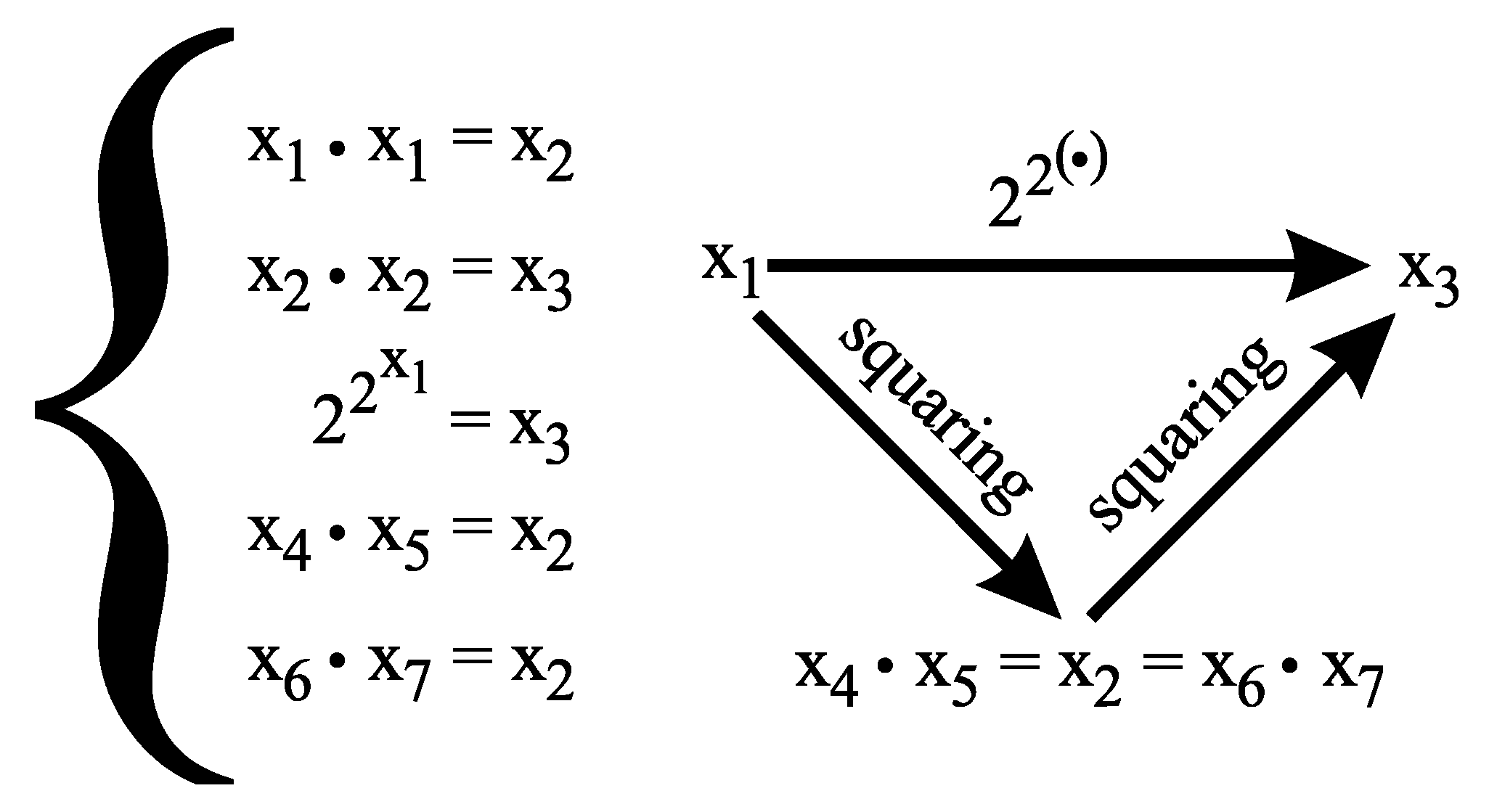
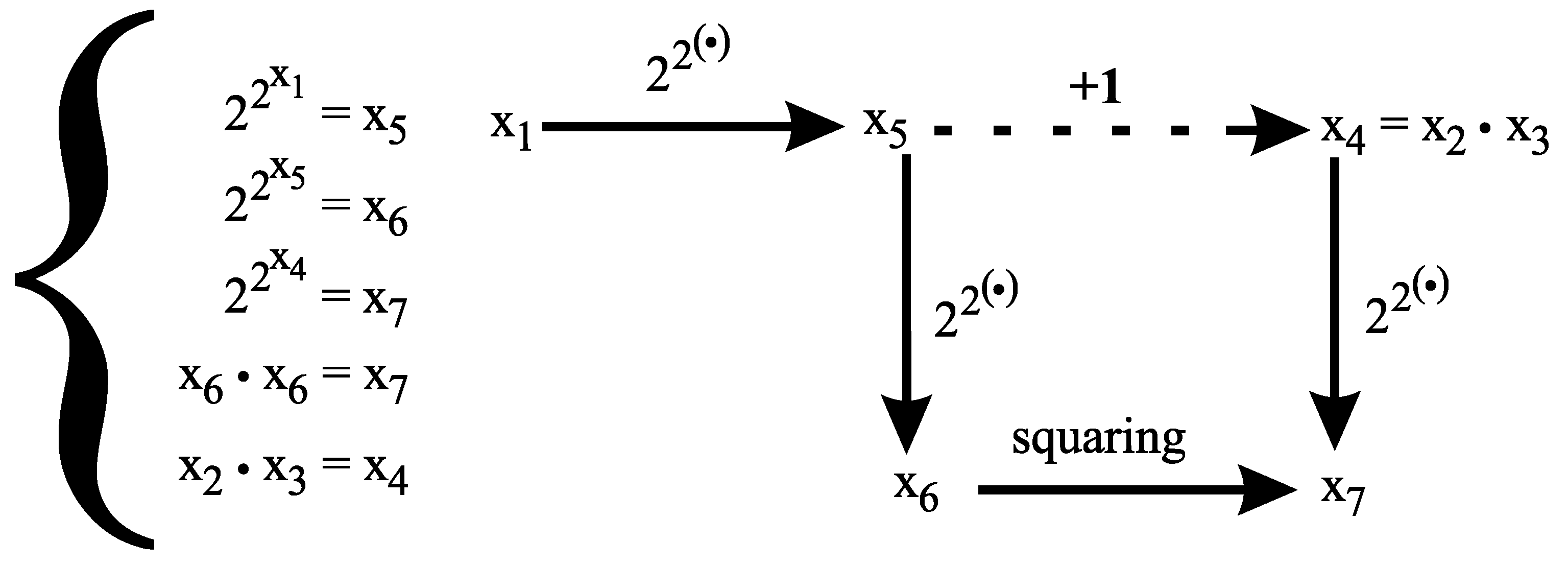
3. The Brocard-Ramanujan equation $x! + 1 = y^{2}$

Let

B

denote the following system of equations:

{x_{i} \cdot x_{j} = x_{k} : i, j, k \in {1, \dots, 6}} \cup {x_{j}! = x_{k} : (j, k \in {1, \dots, 6}) \land (j \neq k)}

The following subsystem of

B

has exactly two solutions in positive integers, namely

(1, \dots, 1)

and

(2, 2, 4, 24, 24!, (24!)!)

Conjecture 3.

If a system of equations

S \subseteq B

has at most finitely many solutions in positive integers

x_{1}, \dots, x_{6}

, then each such solution

(x_{1}, \dots, x_{6})

satisfies

x_{1}, \dots, x_{6} ⩽ (24!)!

Lemma 2.

For every positive integers x and y,

x! \cdot y = y!

if and only if

(x + 1 = y) \lor (x = y = 1)

Theorem 4.

Conjecture 3 implies that if the equation

x_{1}! + 1 = x_{2}^{2}

has at most finitely many solutions in positive integers

x_{1}

and

x_{2}

, then each such solution

(x_{1}, x_{2})

belongs to the set

{(4, 5), (5, 11), (7, 71)}

Proof.

The following system of equations

B_{1}

is a subsystem of

B

. By Lemma 2, in positive integers, the system

B_{1}

expresses that

x_{1} = \dots = x_{6} = 1

\{\begin{matrix} x_{1}! + 1 & = & x_{2}^{2} \\ x_{3} & = & x_{1}! \\ x_{4} & = & (x_{1}!)! \\ x_{5} & = & x_{1}! + 1 \\ x_{6} & = & (x_{1}! + 1)! \end{matrix}

If the equation

x_{1}! + 1 = x_{2}^{2}

has at most finitely many solutions in positive integers

x_{1}

and

x_{2}

, then

B_{1}

has at most finitely many solutions in positive integers

x_{1}, \dots, x_{6}

and Conjecture 3 implies that every tuple

(x_{1}, \dots, x_{6})

of positive integers that solves

B_{1}

satisfies

(x_{1}! + 1)! = x_{6} ⩽ (24!)!

. Hence,

x_{1} \in {1, \dots, 23}

. If

x_{1} \in {1, \dots, 23}

, then

x_{1}! + 1

is a square only for

x_{1} \in {4, 5, 7}

. □

It is conjectured that

x! + 1

is a square only for

x \in {4, 5, 7}

, see [8] (p. 297). A weak form of Szpiro’s conjecture implies that the equation

x! + 1 = y^{2}

has only finitely many solutions in positive integers, see [9].

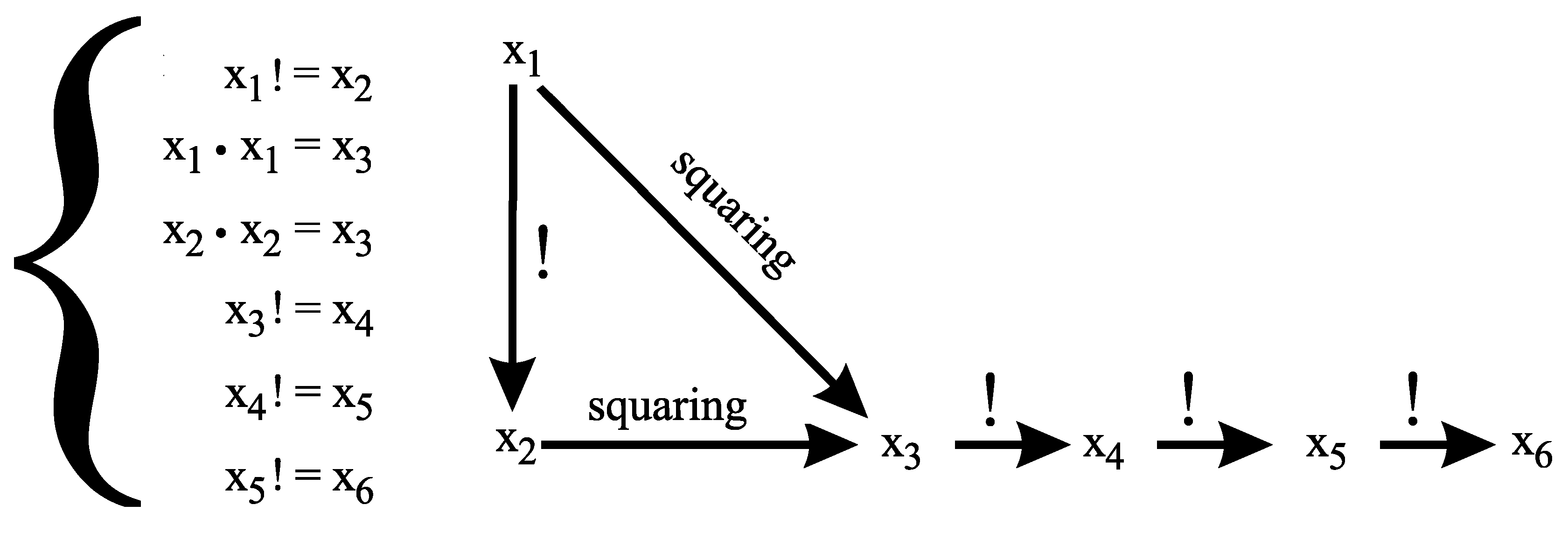
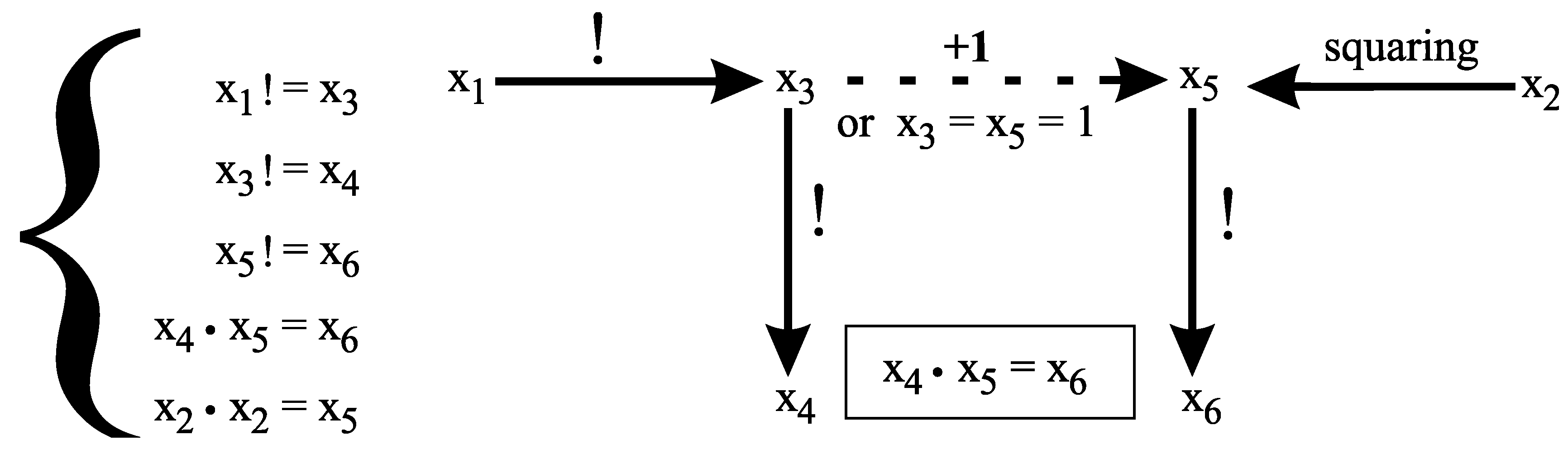
4. Erdös’ Equation $x (x + 1) = y!$

Let

C

denote the following system of equations:

{x_{i} \cdot x_{j} = x_{k} : (i, j, k \in {1, \dots, 6}) \land (i \neq j)} \cup {x_{j}! = x_{k} : (j, k \in {1, \dots, 6}) \land (j \neq k)}

The following subsystem of

C

has exactly three solutions in positive integers, namely

(1, \dots, 1)

(1, 1, 2, 2, 2, 2)

, and

(2, 2, 3, 6, 720, 720!)

Conjecture 5.

If a system of equations

S \subseteq C

has at most finitely many solutions in positive integers

x_{1}, \dots, x_{6}

, then each such solution

(x_{1}, \dots, x_{6}

) satisfies

x_{1}, \dots, x_{6} ⩽ 720!

Theorem 6.

Conjecture 5 implies that if the equation

x_{1} (x_{1} + 1) = x_{2}!

has at most finitely many solutions in positive integers

x_{1}

and

x_{2}

, then each such solution

(x_{1}, x_{2})

belongs to the set

{(1, 2), (2, 3)}

Proof.

The following system of equations

C_{1}

is a subsystem of

C

. By Lemma 2, in positive integers, the system

C_{1}

expresses that

x_{1} = \dots = x_{6} = 1

\{\begin{matrix} x_{1} \cdot (x_{1} + 1) & = & x_{2}! \\ x_{3} & = & x_{1} \cdot (x_{1} + 1) \\ x_{4} & = & x_{1}! \\ x_{5} & = & x_{1} + 1 \\ x_{6} & = & (x_{1} + 1)! \end{matrix}

If the equation

x_{1} (x_{1} + 1) = x_{2}!

has at most finitely many solutions in positive integers

x_{1}

and

x_{2}

, then

C_{1}

has at most finitely many solutions in positive integers

x_{1}, \dots, x_{6}

and Conjecture 5 implies that every tuple

(x_{1}, \dots, x_{6})

of positive integers that solves

C_{1}

satisfies

x_{2}! = x_{3} ⩽ 720!

. Hence,

x_{2} \in {1, \dots, 720}

. If

x_{2} \in {1, \dots, 720}

, then

x_{2}!

is a product of two consecutive positive integers only for

x_{2} \in {2, 3}

because the following MuPAD program

for x2 from 1 to 720 do

x1:=round(sqrt(x2!+(1/4))-(1/2)):

if x1*(x1+1)=x2! then print(x2) end_if:

end_for:

returns 2 and 3. □

The question of solving the equation

x (x + 1) = y!

was posed by P. Erdös, see [5]. F. Luca proved that the

a b c

conjecture implies that the equation

x (x + 1) = y!

has only finitely many solutions in positive integers, see [6].

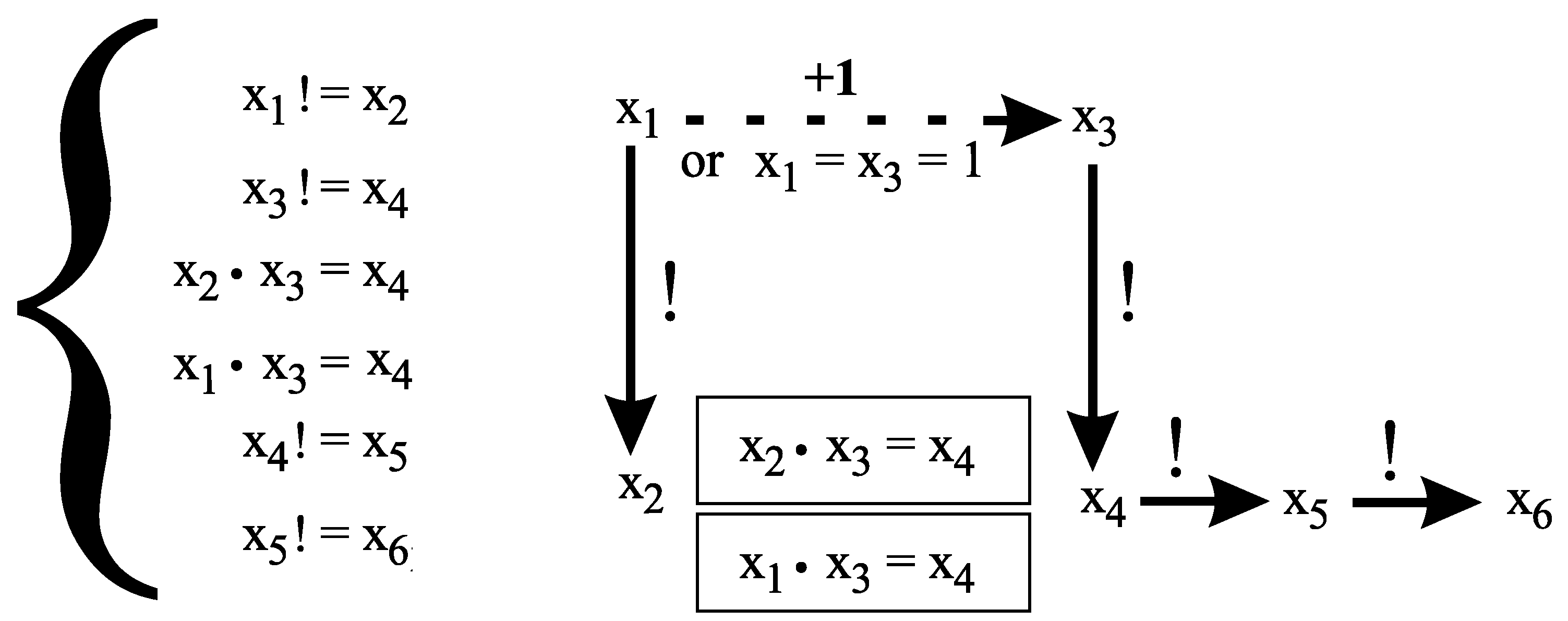
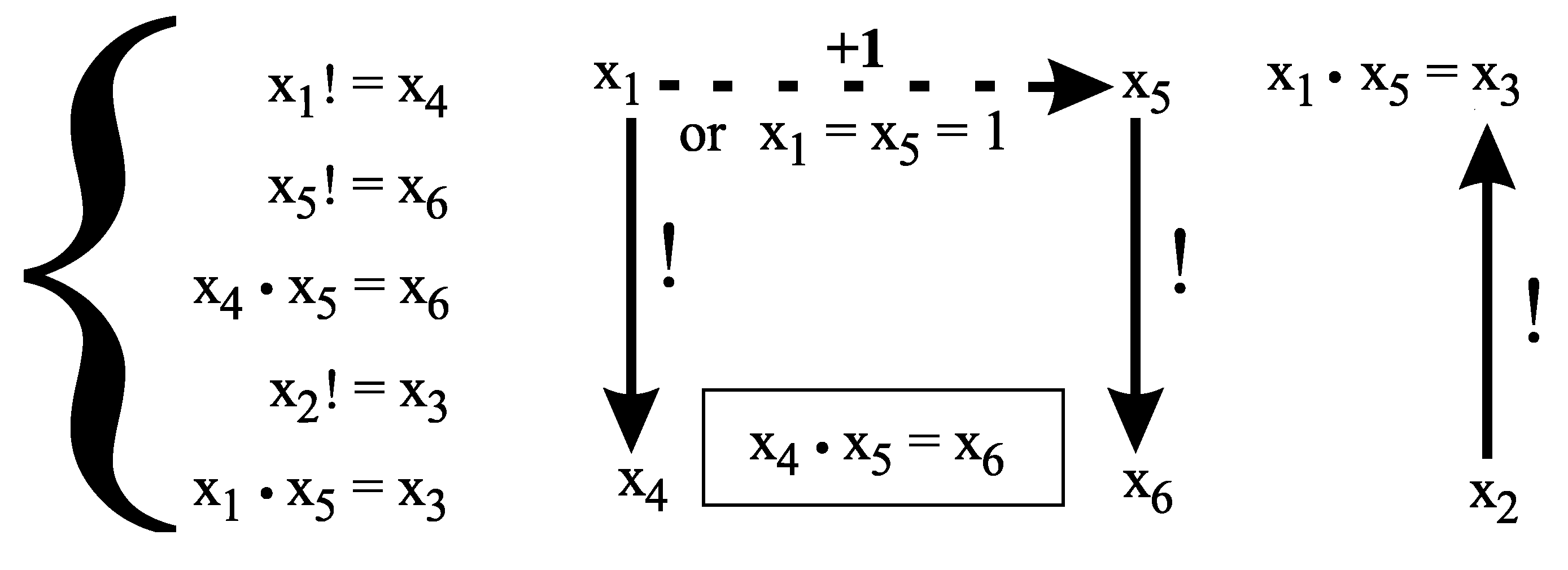
5. Conjectures 3 and 5 Cannot Be Generalized to An Arbitrary Number of Variables

Let

f (1) = 2

f (2) = 4

, and let

f (n + 1) = f (n)!

for every integer

n ⩾ 2

. Let

W_{1}

denote the system of equations

{x_{1}! = x_{1}

. For an integer

n ⩾ 2

, let

W_{n}

denote the following system of equations:

For every positive integer n, the system

W_{n}

has exactly two solutions in positive integers

x_{1}, \dots, x_{n}

, namely

(1, \dots, 1)

and

(f (1), \dots, f (n))

. For a positive integer n, let

Ψ_{n}

denote the following statement: if a system of equations

S \subseteq {x_{i} \cdot x_{j} = x_{k} : i, j, k \in {1, \dots, n}} \cup {x_{j}! = x_{k} : j, k \in {1, \dots, n}}

has at most finitely many solutions in positive integers

x_{1}, \dots, x_{n}

, then each such solution

(x_{1}, \dots, x_{n})

satisfies

x_{1}, \dots, x_{n} ⩽ f (n)

Theorem 7.

Every factorial Diophantine equation can be algorithmically transformed into an equivalent system of equations of the forms

x_{i} \cdot x_{j} = x_{k}

and

x_{j}! = x_{k}

. It means that this system of equations satisfies a modified version of Lemma 4 in [2].

Proof.

It follows from Lemmas 2–4 in [2] and Lemma 2. □

The statement

\forall n \in N \ {0} Ψ_{n}

is dubious. By Theorem 7, this statement implies that there is an algorithm which takes as input a factorial Diophantine equation and returns an integer which is greater than the solutions in positive integers, if these solutions form a finite set. This conclusion is strange because properties of factorial Diophantine equations are similar to properties of exponential Diophantine equations and a computable upper bound on non-negative integer solutions does not exist for exponential Diophantine equations with a finite number of solutions, see [7].

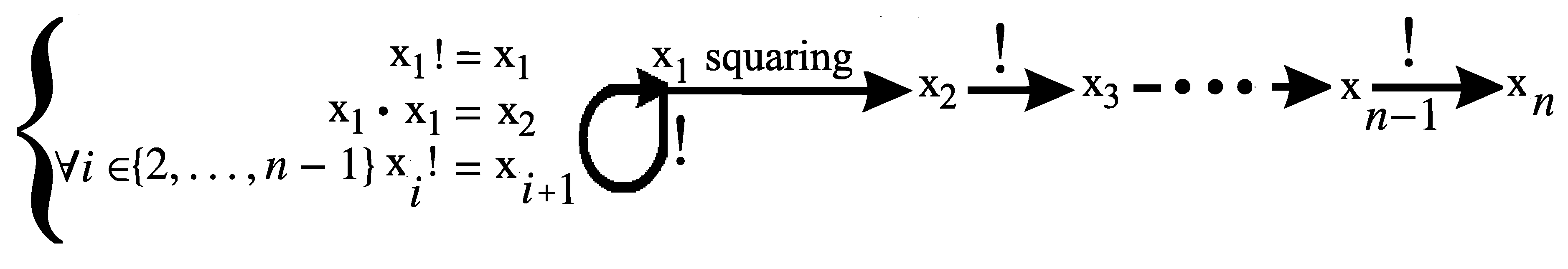
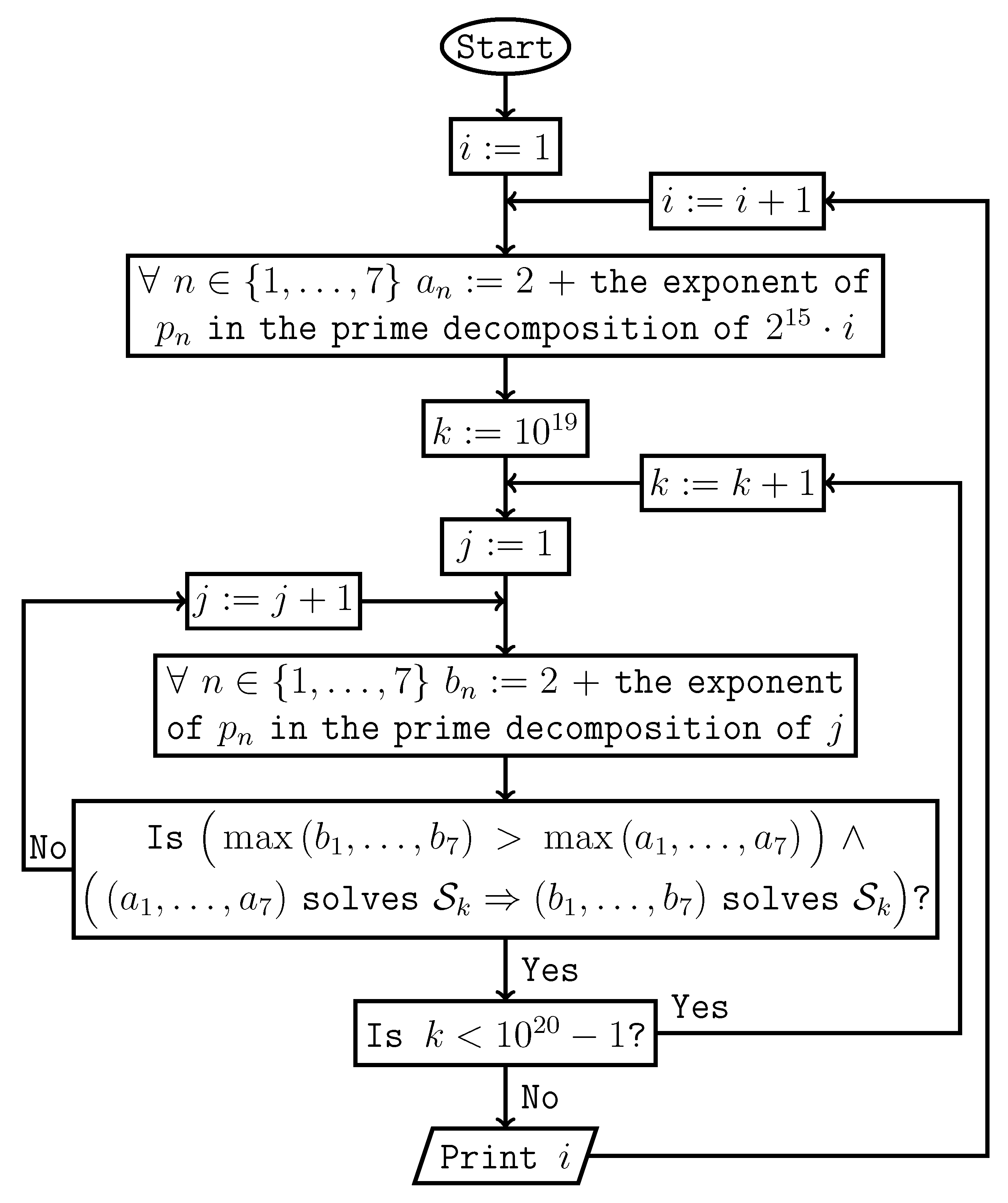
6. Equivalent Forms of Conjectures 1–5

k \in [10^{19}, 10^{20} - 1] \cap N

, then there are uniquely determined non-negative integers

a (0), \dots, a (19) \in {0, \dots, 9}

such that

(a (19) ⩾ 1) \land (k = a (19) \cdot 10^{19} + a (18) \cdot 10^{18} + \dots + a (1) \cdot 10^{1} + a (0) \cdot 10^{0})

Definition 1.

For an integer

k \in [10^{19}, 10^{20} - 1]

S_{k}

stands for the smallest system of equations

S

satisfying conditions(1)and(2).

(1)If

i \in {0, 4, 8, 16}

and

a (i)

is even, then the equation

x_{a (i + 1)} \cdot x_{a (i + 2)} = x_{a (i + 3)}

belongs to

S

when it belongs to

A

(2)If

i \in {0, 4, 8, 16}

and

a (i)

is odd, then the equation

2^{2^{x_{a (i + 1)}}} = x_{a (i + 2)}

belongs to

S

when it belongs to

A

Lemma 3.

{S_{k} : k \in [10^{19}, 10^{20} - 1] \cap N = {S : (S \subseteq A) \land (card (S) ⩽ 5)}

Proof.

It follows from the equality

5 \cdot 4 = 20

. □

For a positive integer n, let

p_{n}

denote the n-th prime number.

Theorem 8.

The following semi-algorithm

{sem}_{1}

never terminates.

If Conjecture 1 is true, then

{sem}_{1}

endlessly prints consecutive positive integers starting from 1. If Conjecture 1 is false, then

{sem}_{1}

prints a finite number (including zero) of consecutive positive integers starting from 1.

Proof.

It follows from Lemma 3. □

Theorem 9.

The following semi-algorithm

{sem}_{2}

never terminates.

If Conjecture 3 is true, then

{sem}_{2}

endlessly prints consecutive positive integers starting from 1. If Conjecture 3 is false, then

{sem}_{2}

prints a finite number (including zero) of consecutive positive integers starting from 1.

Theorem 10.

The following semi-algorithm

{sem}_{3}

never terminates.

If Conjecture 5 is true, then

{sem}_{3}

endlessly prints consecutive positive integers starting from 1. If Conjecture 5 is false, then

{sem}_{3}

prints a finite number (including zero) of consecutive positive integers starting from 1.

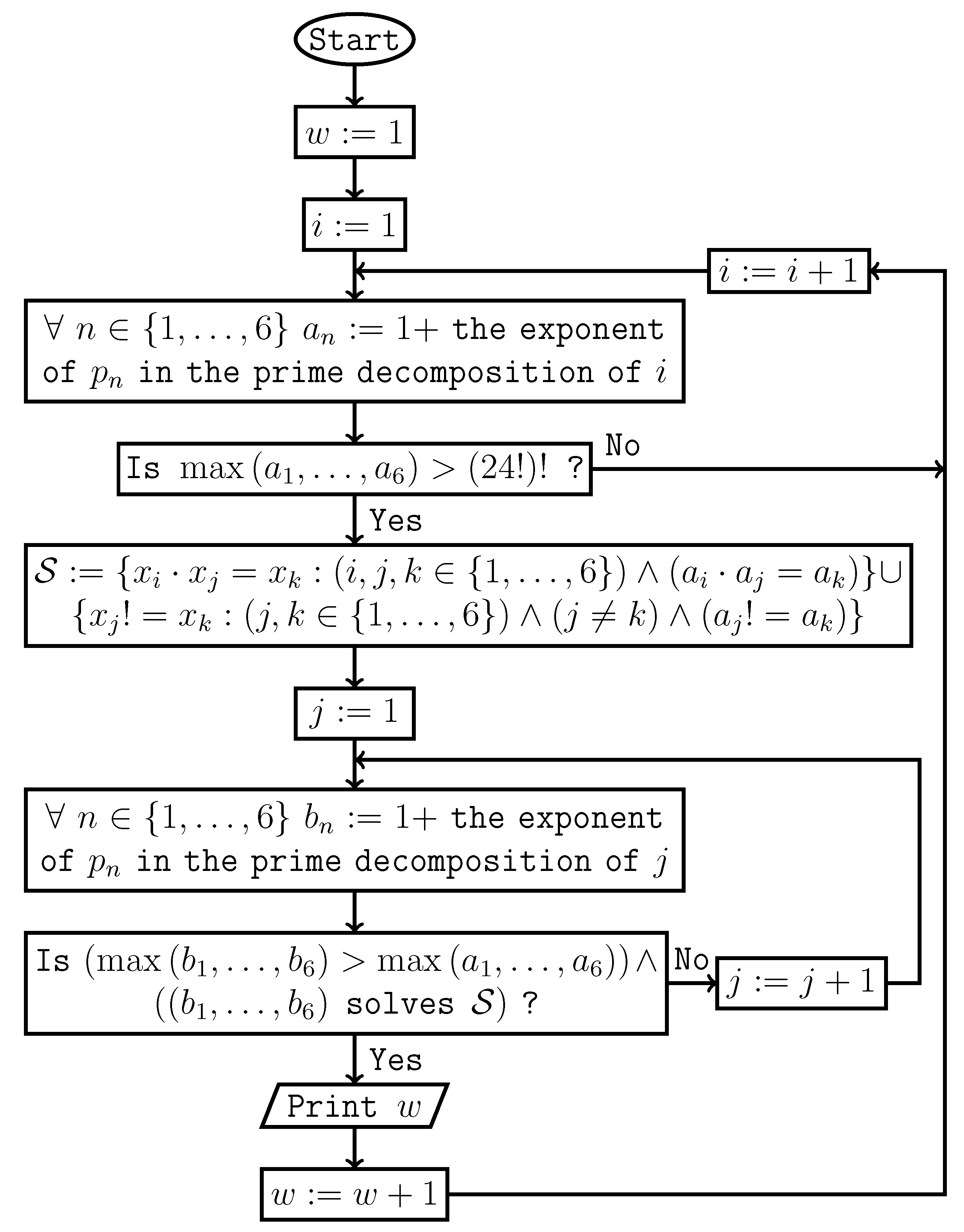
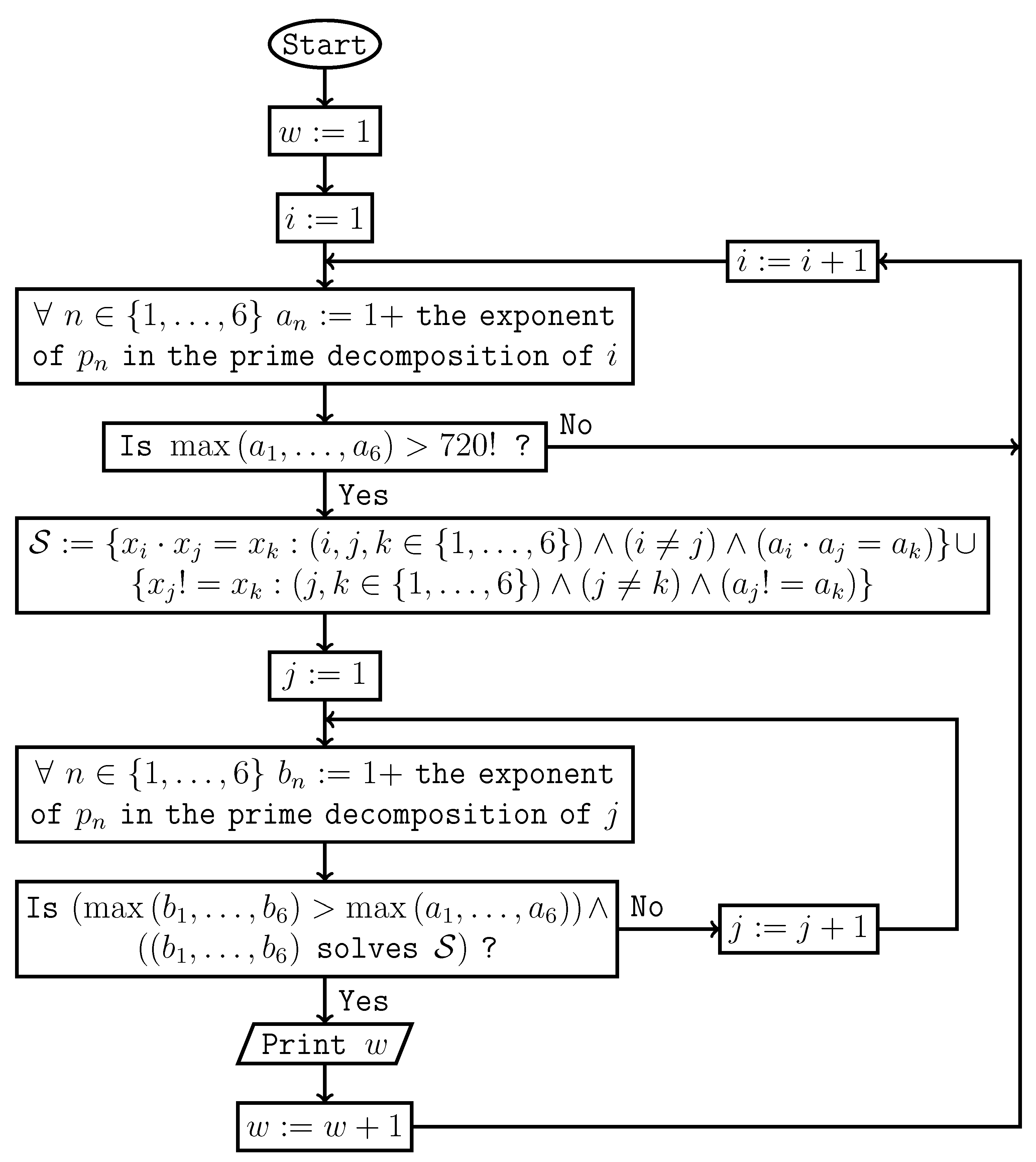
References

N. D. Goodman, The Knowing Mathematician. Synthese 1984, 60, 21–38, Available online: http://link.springer.com/article/10.1007/BF00485616 Reprinted in: H. Leblanc, E. Mendelson, A. Orenstein, Foundations: Logic, Language, and Mathematics, Springer, 1984; pp. 21–38, Available online: http://link.springer.com/book/10.1007/978-94-017-1592-8.
A. Tyszka, A hypothetical upper bound on the heights of the solutions of a Diophantine equation with a finite number of solutions. Open Comput. Sci. 2018,8, 109–114. [CrossRef]
J.-M. De Koninck and F. Luca. Analytic Number Theory: Exploring the Anatomy of Integers; American Mathematical Society: Providence, RI, 2012.
M. Křížek, F. Luca, L. Somer, 17 Lectures on Fermat Numbers: From Number Theory to Geometry, Springer: New York, 2001.
D. Berend and J. E. Harmse, On polynomial-factorial Diophantine equations, Trans. Amer. Math. Soc.2006, 358, 1741–1779.
F. Luca, The Diophantine equation P(x) = n! and a result of M. Overholt, Glas. Mat. Ser. III 2002, 37, 269–273.
Yu. Matiyasevich, Existence of noneffectivizable estimates in the theory of exponential Diophantine equations, J. Sov. Math. 1977, 8, 299–311. [CrossRef]
E. W. Weisstein. CRC Concise Encyclopedia of Mathematics, 2nd ed., Chapman & Hall/CRC: Boca Raton, FL, 2002.
M. Overholt, The Diophantine equation n! + 1 = m², Bull. London Math. Soc.1993, 25, 104.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Common Approach to Three Open Problems in Number Theory

Abstract

1. Epistemic Notions Increase the Scope of Mathematics

2. Composite Numbers of the Form 2 2 n + 1

3. The Brocard-Ramanujan equation x ! + 1 = y 2

4. Erdös’ Equation x ( x + 1 ) = y !

5. Conjectures 3 and 5 Cannot Be Generalized to An Arbitrary Number of Variables

6. Equivalent Forms of Conjectures 1–5

References

MDPI Initiatives

Important Links

Subscribe

2. Composite Numbers of the Form $2^{2^{n}} + 1$

3. The Brocard-Ramanujan equation $x! + 1 = y^{2}$

4. Erdös’ Equation $x (x + 1) = y!$