1. Introduction
Trigonometry is a branch of mathematics that works on the relationship between the side lengths and angles of triangles. It is quite helpful in various contexts, including surveying, navigation, etc. There are six fundamental functions in trigonometry. These functions mainly relate an angle of a right-angled triangle to ratios of two side lengths. The most widely used of these functions are sine, cosine, and tangent. The cosecant, secant, and cotangent are their reciprocals, respectively. This article mainly discusses sine and cosine functions. The sine function means the ratio of the length of the opposite side to that of the hypotenuse in a right-angled triangle. The cosine function means the ratio between the leg adjacent to the angle of the hypotenuse, and the tangent function means the ratio of sine and cosine. As the length of the hypotenuse is always greater than any other side in any right-angled triangle, the value of both sine and cosine is always a real number between 0 and 1, but the value of the tangent function can be any positive or negative real number. Moreover, sine, cosine, and tan are periodic functions. The period of both sine and cosine functions is 2π. Whether the value would be positive or negative depends on the quadrant. If we can calculate the values in one quadrant successfully, then we can quickly get the values in any quadrant. So, this paper shows a different approach to approximate sine and cosine on the interval
. Throughout the history of the development of trigonometry, many ways have been developed to calculate these functions accurately. In computers, the Taylor series is used to calculate sine [
1].
2. Derivation and Accuracy
Figure 2.
Geometrical structure and isosceles triangle.
Figure 2.
Geometrical structure and isosceles triangle.
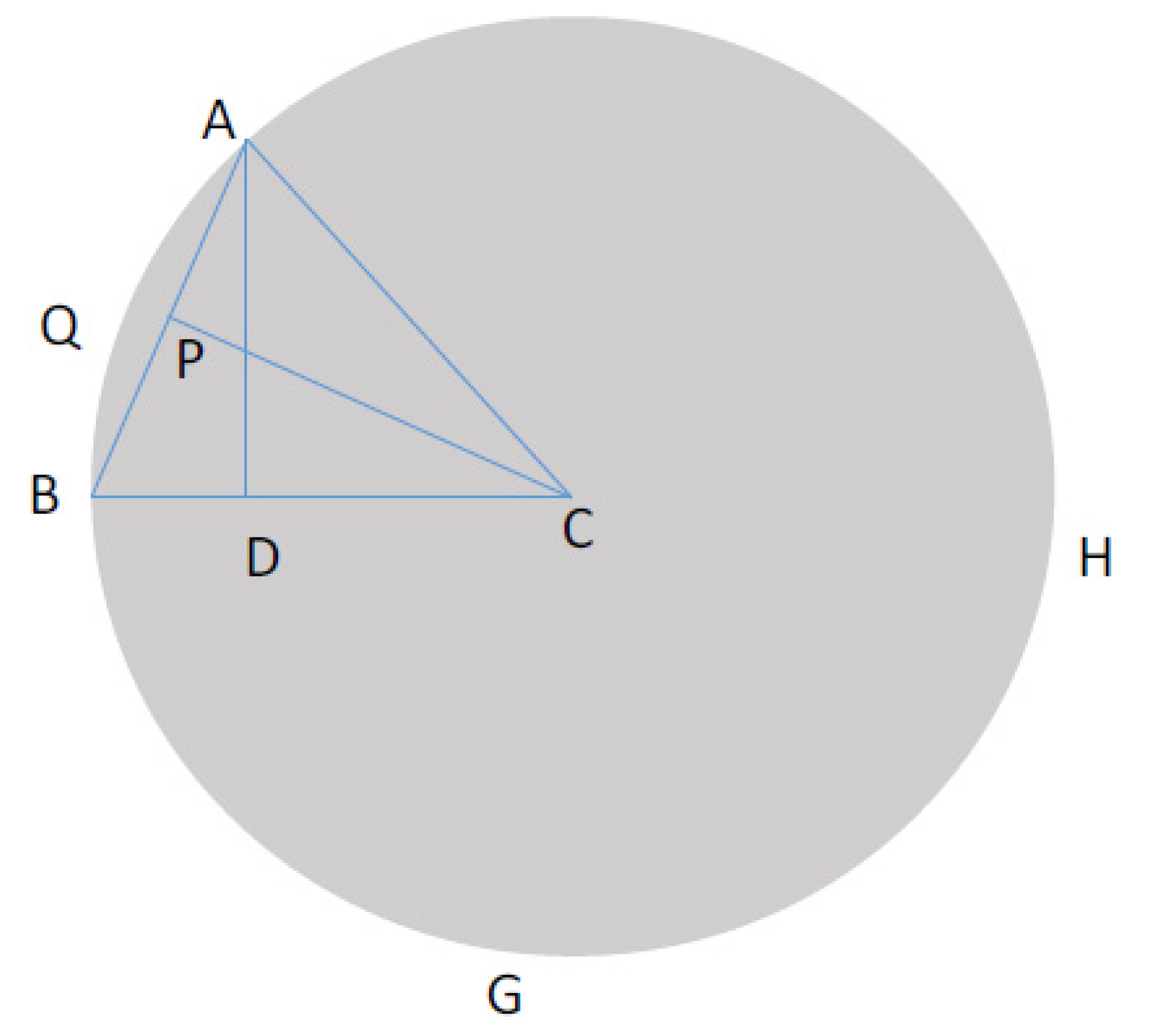
Here, ABC is an isosceles triangle; AQBGH is a circle, and AC and BC are its radii. Let AC=BC=a and AD is perpendicular to BC which means AD is the height of this triangle. Let <ACB=x radian, the chord AB=k, the arc AQB=s, and AD=h. So, the length of the arc AQB= ax [
2]. Now, s= ax.
If we apply the cosine law [
3], AB=
Let
⇨ k =
⇨ k =
. Here, PC is perpendicular to AB, and as it is an isosceles, AP=BP and applying the Pythagorean theorem [
4], BP=
⇨ BP=
.
Now, AB=AP+ BP ⇨AB=BP+ BP ⇨AB=2BP ⇨2BP=AB
Area of the isosceles ABC= = = = .
Also, the area of isosceles ABC is
or
[
5].
So, ⇨ ⇨ ⇨ ⇨⇨Thus, = .
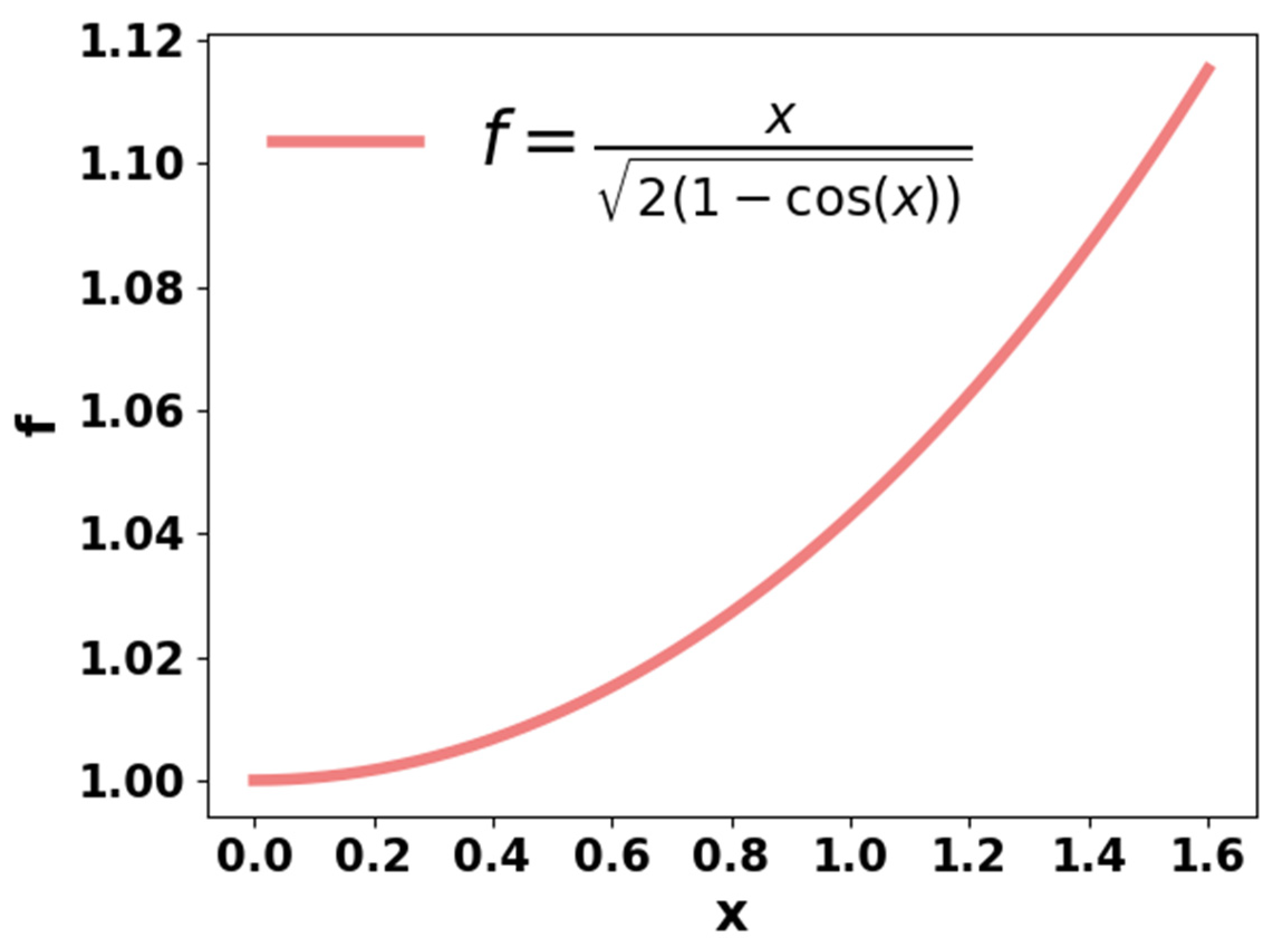
Now, as f = ⇨f = ⇨ f =. ..……………………………….…………….. (1)
.
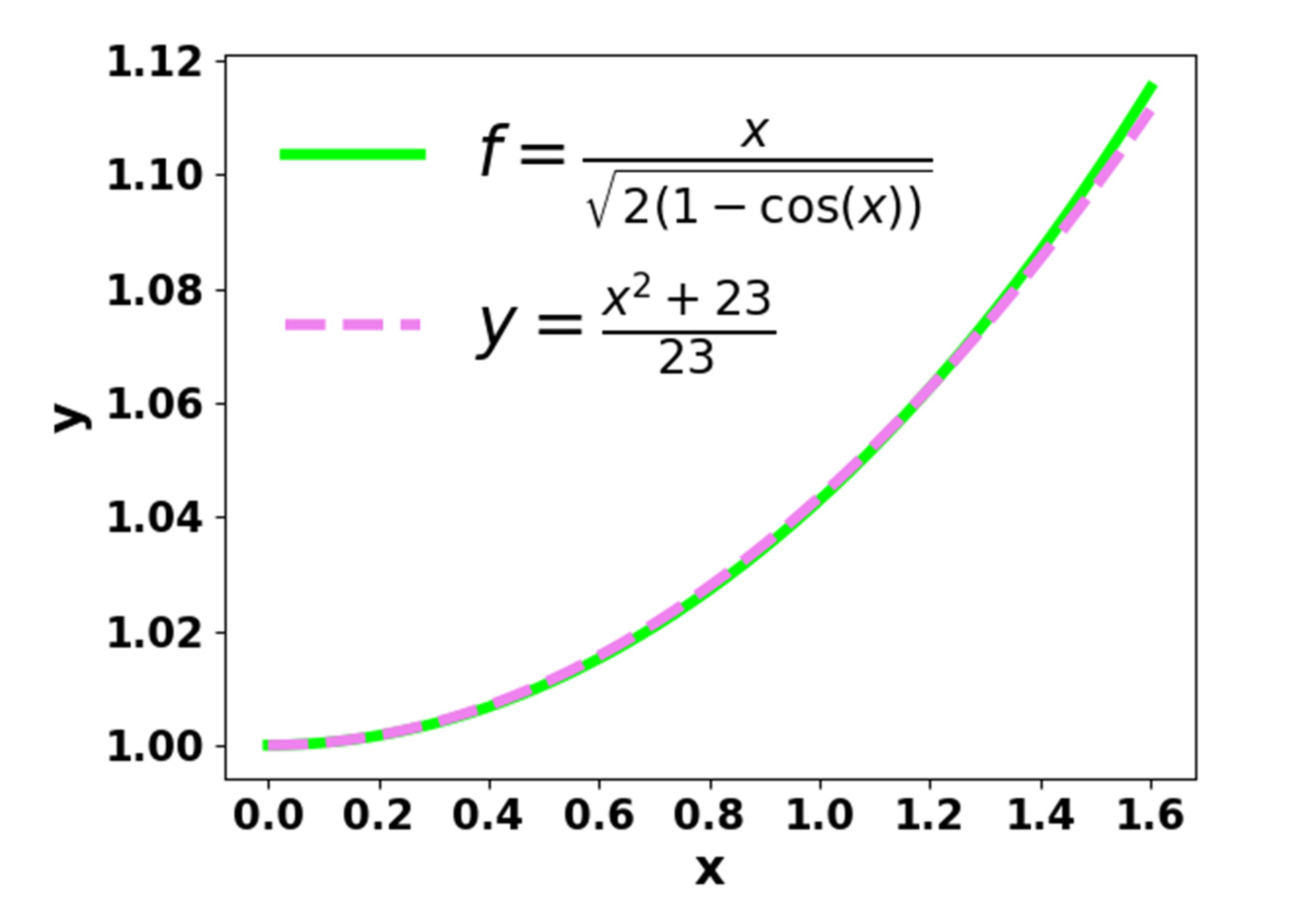
In
Figure 3(a), the part of the graph where x is between 0 and
radian can be considered as a part of a parabola [
6]. The equation of that parabola would be like:
⇨
⇨ y=
...…... (2)
Where, m is a constant. Now, it can assume that when x is between 0 and
radian, f
≈ because this parabola approximates the function of f on the interval [0,
]. Hence,
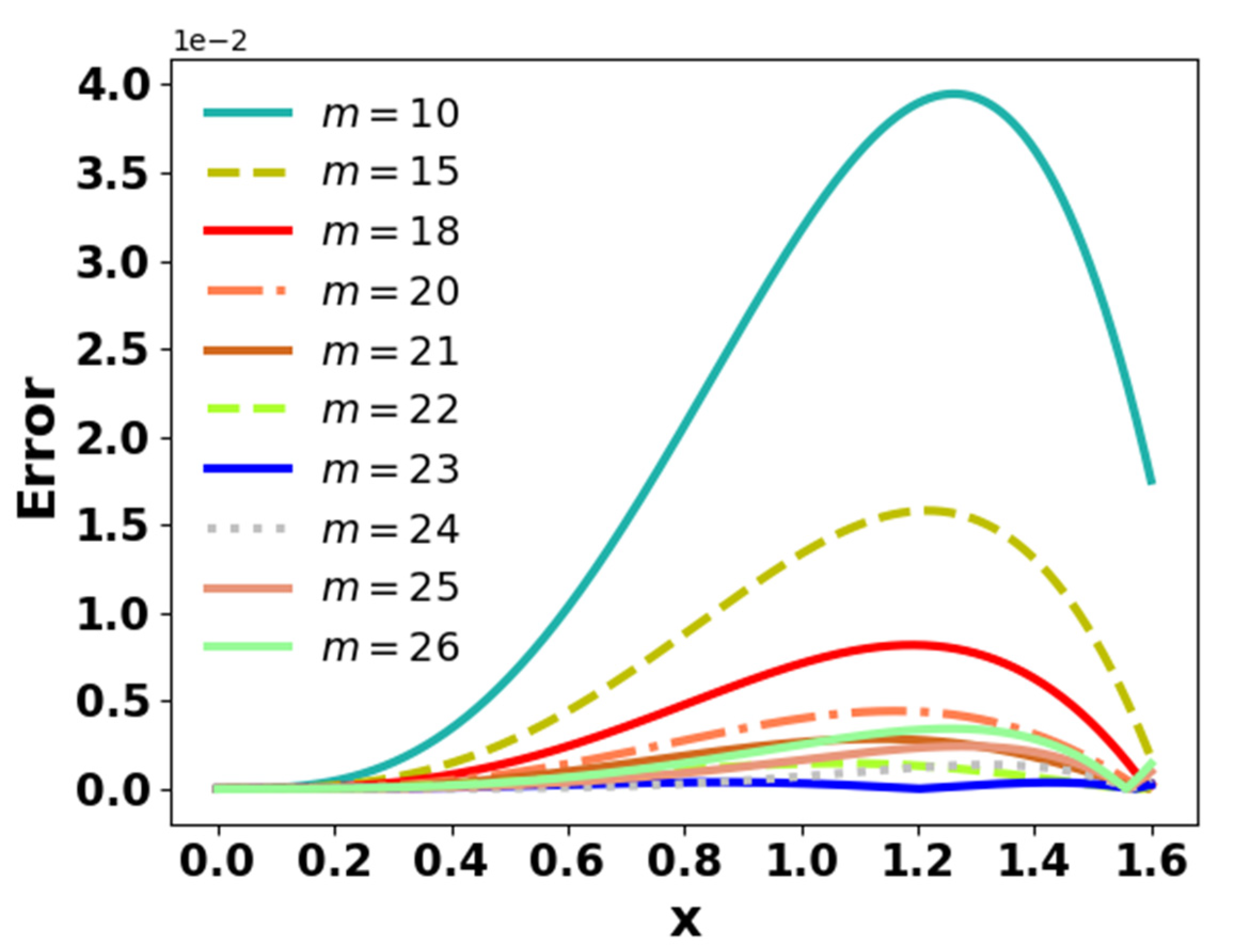
For m=23, it can be noted from
Figure 3(b) that Equation (3) provides a relatively good estimate when the angle is between 0 and
radian.
Figure 3.
(c): Comparison of f = and y = on the interval .
Figure 3.
(c): Comparison of f = and y = on the interval .
From
Figure 3(c), f
≈ . Let
= Replacing x with
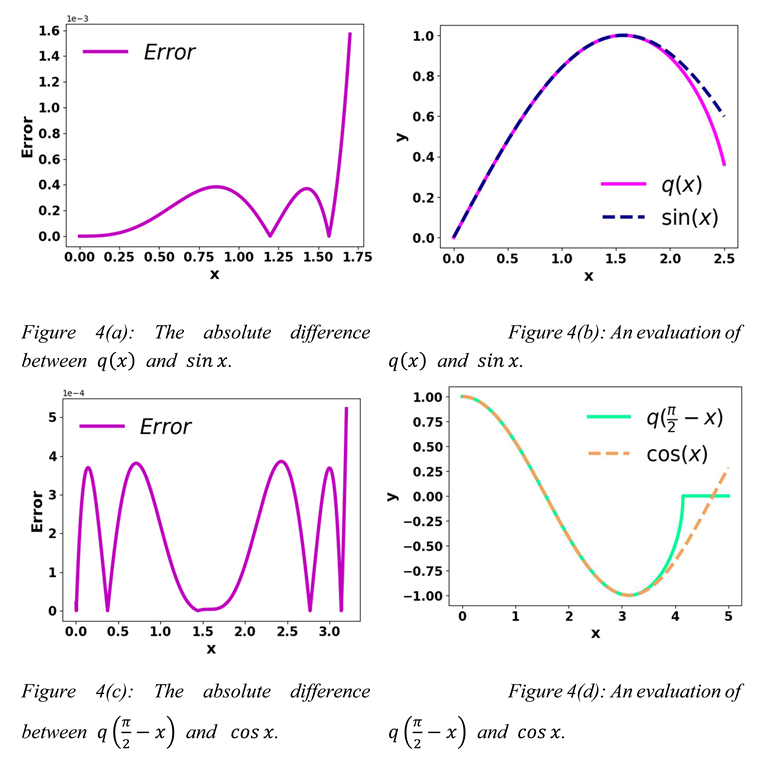
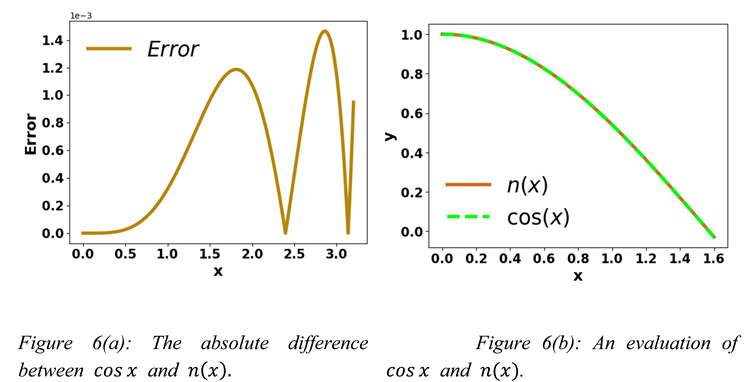
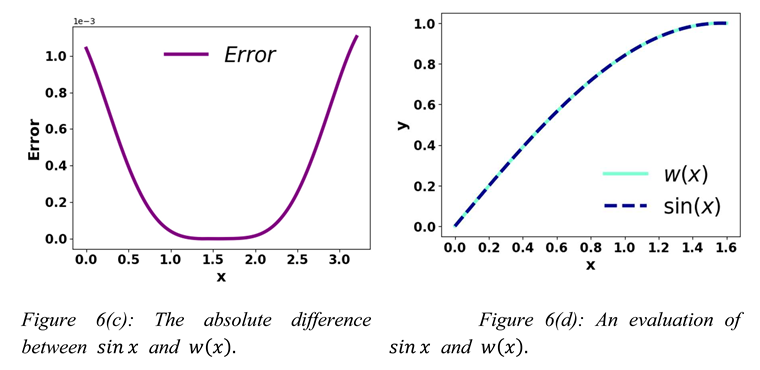
From Figures 4(a), 4(b), 4(c), and 4(d), it is examined that the error is very negligible on the interval [0, ].
So, q(x)
≈ ,
and .
Hence,
Now, f
≈ ≈ ⇨
≈ ⇨
⇨ 1 –
≈ ≈ 1 –
.
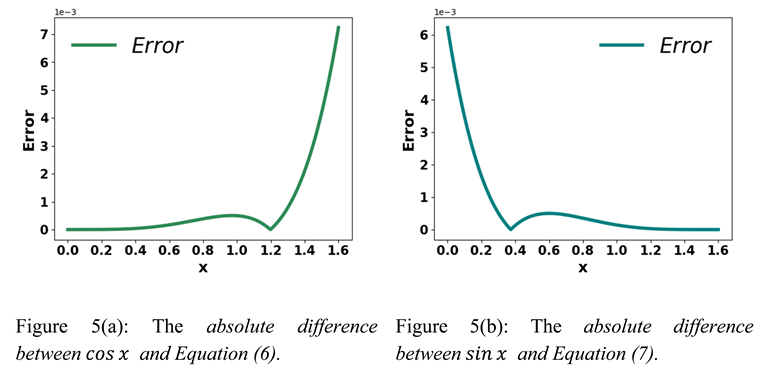
In Figure 5(a), when x is between 0 and
radian, Equation (6) provides better approximation value. So, in order to approximate sine and cosine more accurately, we can use this formula:
. This formula is helpful because
=
.
. So, replacing x with
,
≈ 1- .
Since , we get the following expression
All these formulas approximate well when x is between 0 and radian.
3. Comparing with Bhaskara I’s formula to approximate Sine
There is a formula of 7
th century Indian Mathematician Bhaskara (c.600 – c.680) to approximate sine [
8]. That formula is
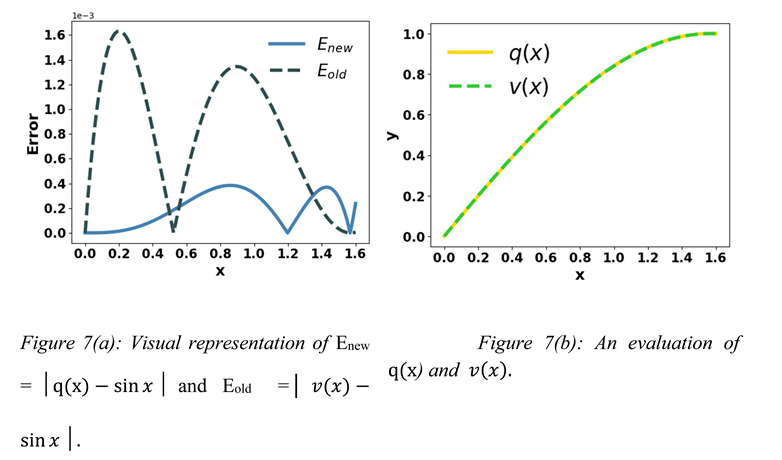
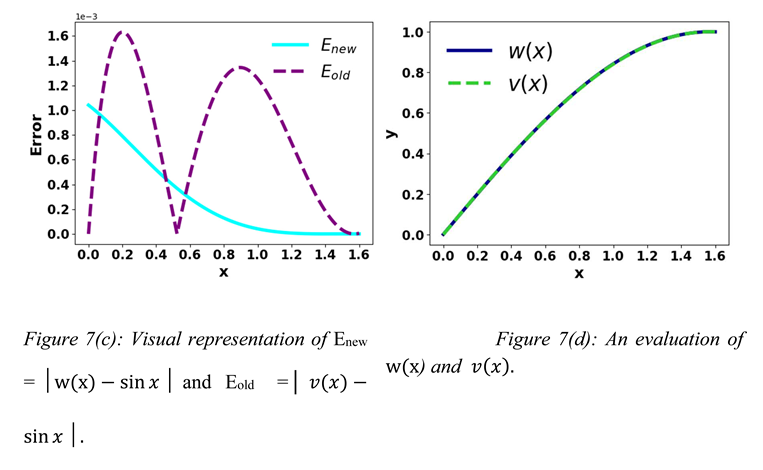
≈ , and Equation (4) is ≈Let v(x) =
Figures 7(a) and 7(c) show that Equations (4) and (9) approximate Sine better than Bhaskara I’s formula in many points, respectively.
4. Comparing with Bhaskara I’s formula to approximate Cosine
The cosine approximation of Mathematician Bhaskara I [
8] is
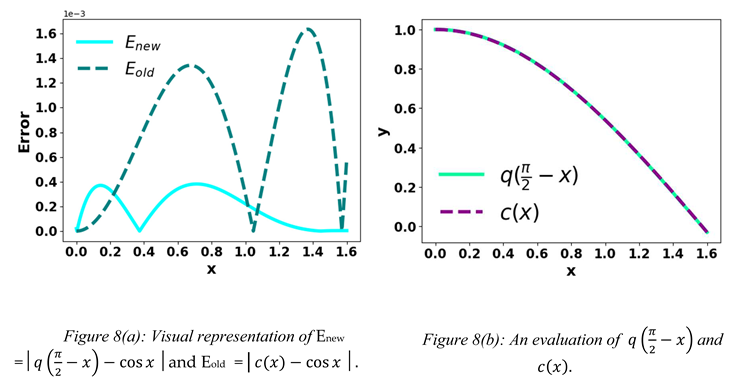
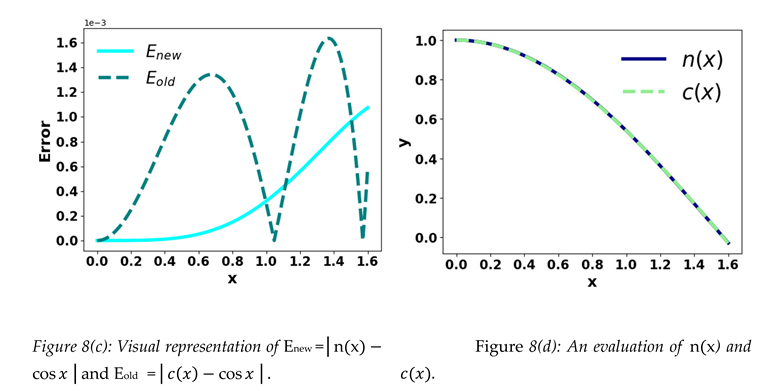
≈ and Equation (5) is
≈ Let c(x) =
.
According to Figures 8(a) and 8(c), the cosine is more closely approximated by Equations (5) and (8) than by Bhaskara I’s formula in many instances.
5. Conclusion
In this paper, we have derived two types of formula to approximate sine and cosine. One type involves square root and another type does not require any use of square root. The formulas are
1. ≈
2. ≈
3. ≈ 1 –
4. ≈ 1 –
5.
6.
All of these formulas approximate well when x is between 0 and radian. As sine and cosine are periodic functions, their value keeps getting the same after a certain angle, which is 2 radian. The value of both sine and cosine is positive when x is between 0 and radian, which means the first quadrant. Moreover, the value of sine and cosine is also positive when x is in the second and fourth quadrants, respectively. So, the value of sine is negative when x is in the third or fourth quadrant. On the other hand, the value of cosine is negative when x is in the second or third quadrant. But as both are positive in the first quadrant, these approximations achieved in this paper can be considered as the approximation of their absolute value. So, if we use these formulas to approximate their absolute value and then consider the quadrant, we can get a proper approximation for any value of x by deciding whether it is negative or positive. Thus, we can use these formulas to approximate sine and cosine in any quadrant. Moreover, these formulas provide a more accurate value than Bhaskara I’s formula in most of the cases on the interval . Thus, these formulas can be used as a better substitution for the Mathematician Bhaskara I’s formula.
Acknowledgments
The author M. Kamrujjaman acknowledged to the University Grant Commission and the University of Dhaka.
Conflicts of Interest
The authors declare no conflict of interest.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).