Submitted:
19 February 2023
Posted:
21 February 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical guidance and analysis
2.1. Fractional differential
2.1.1. Fractional differential definition
2.1.2. Effect of fractional differential on detection signal
2.2. Fractional partial differential
2.2.1. Fractional partial differential equation
2.2.2. Applications of the fractional partial differential equations
3. Online detection data fusion algorithm based on fractional differentiaL
3.1. Fusion algorithm model based on fractional partial differential equations
3.2. Fusion process based on fractional partial differentials
4. Application of algorithm in the information data detection system
4.1. Problem description
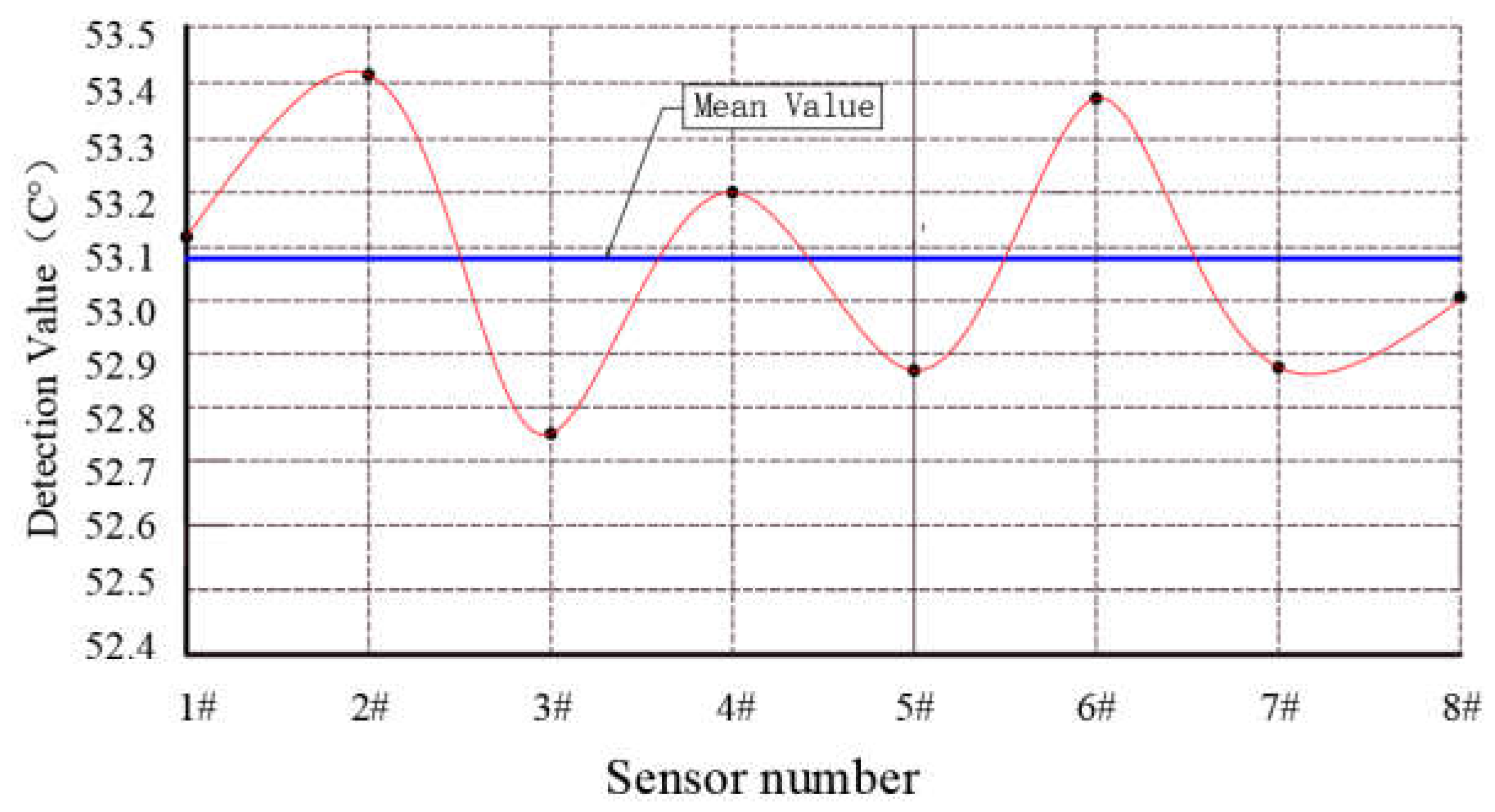
4.2. Analysis and processing of test data
4.3. Fitting of functional relationship between detected value and influence factor
4.3.1. Order of the polynomial
4.3.2. Calculation of polynomial coefficients
4.4. Detection data fusion technology based on fractional differential operator
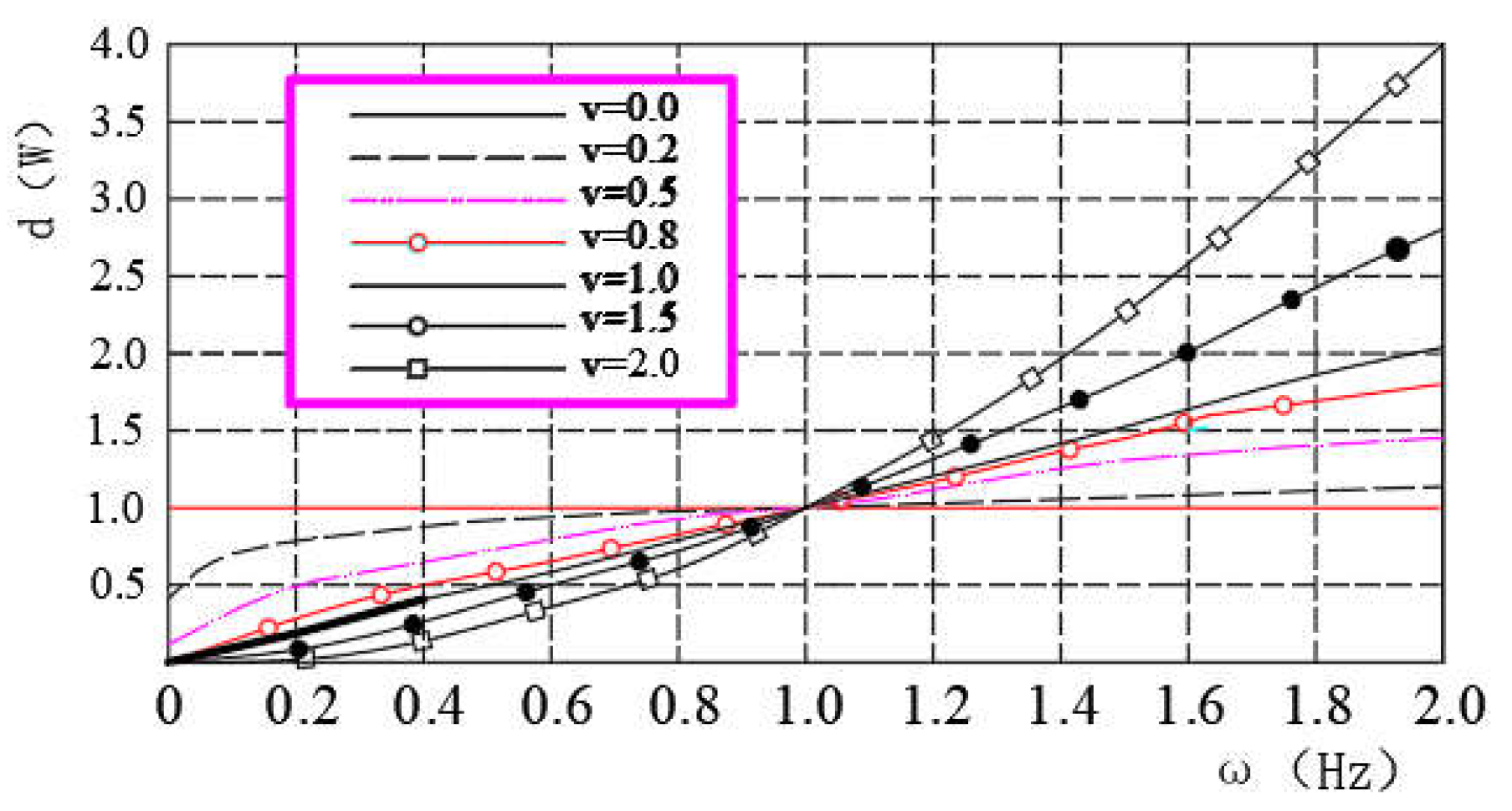
4.4.1. Selection of fractional order v and step h
4.4.2. Data fusion and results analysis
4.4.3. Fusion processing results of detection data by 0.5-order partial differential equation
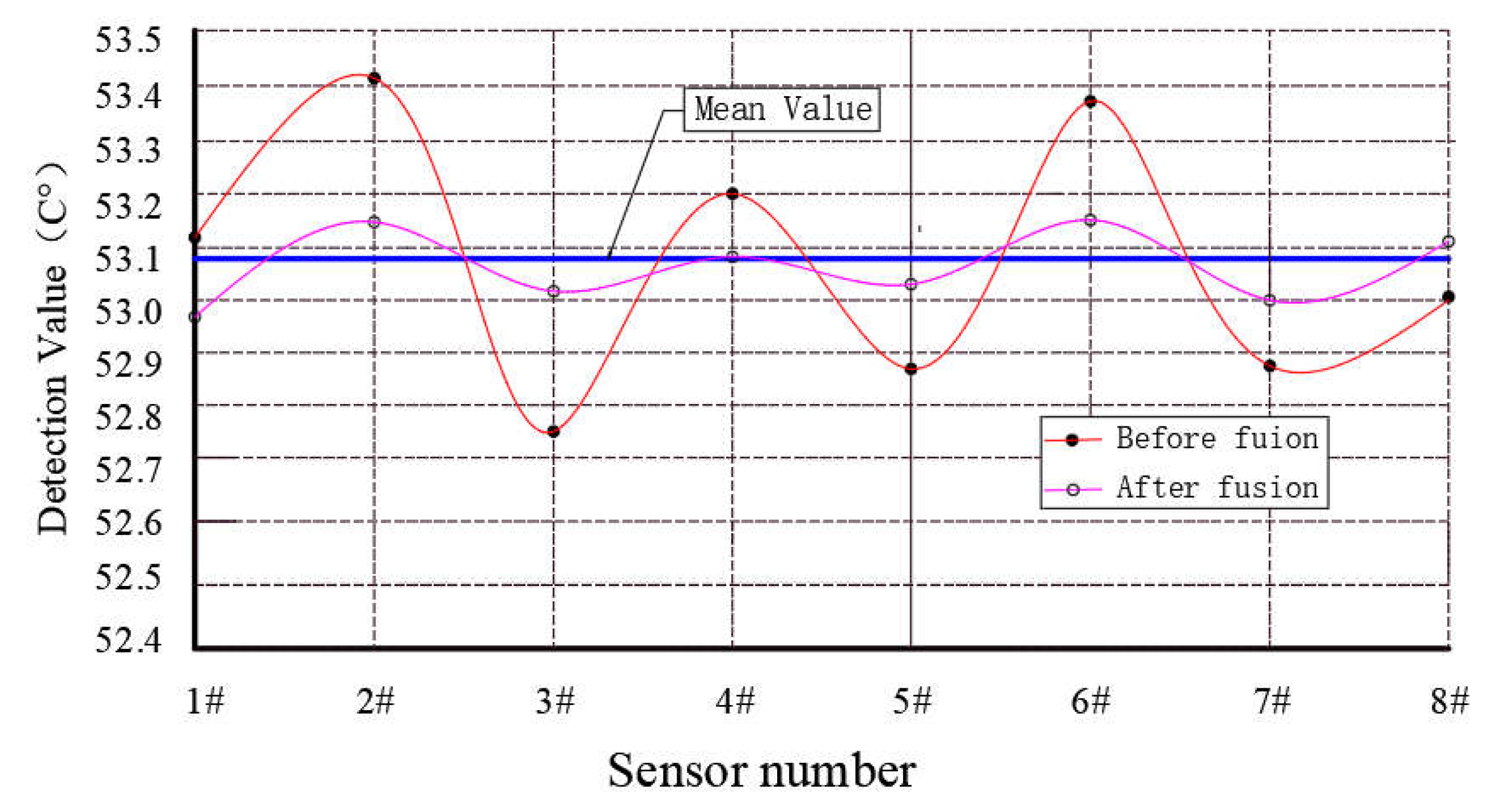
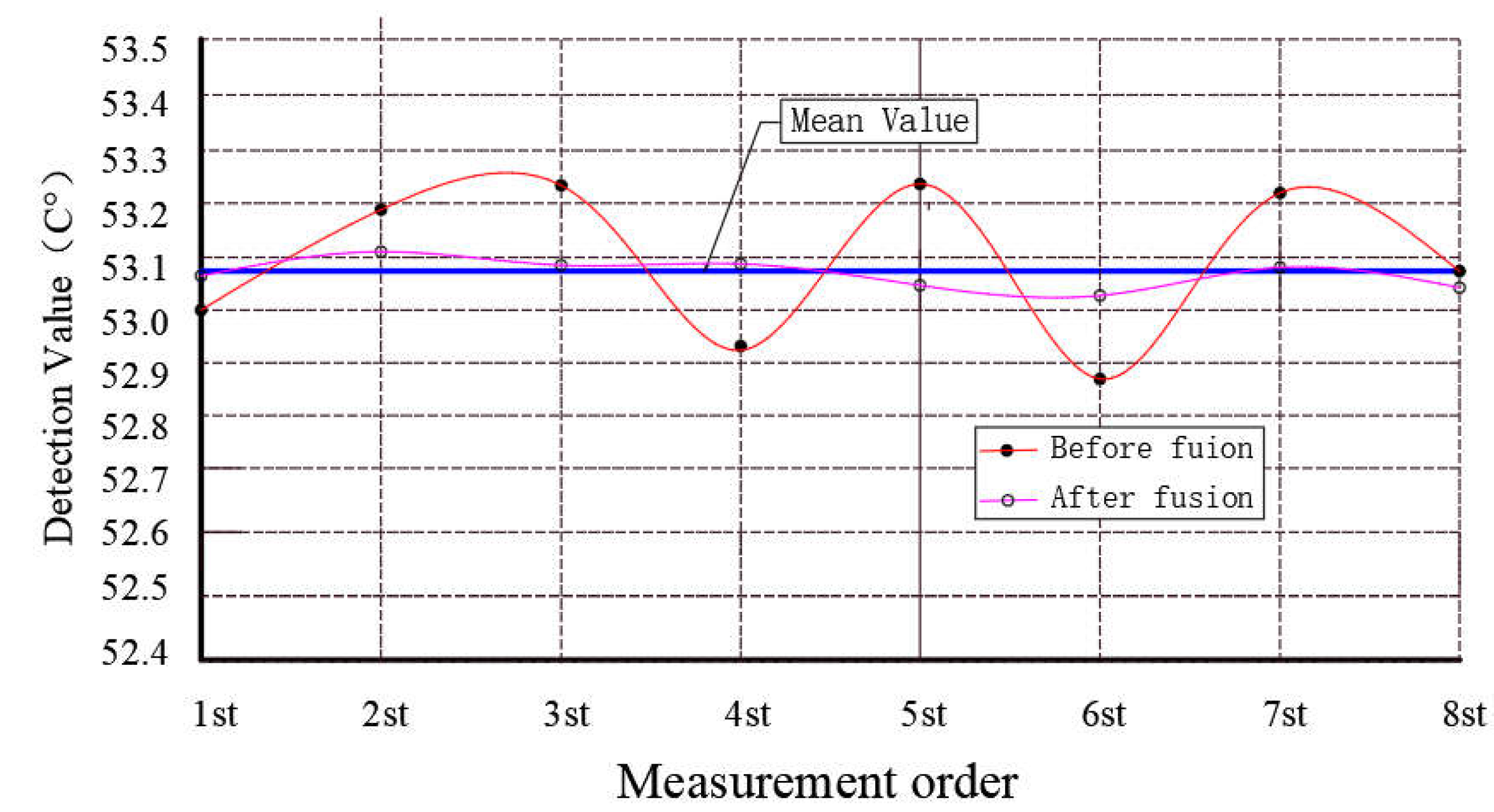
5. Conclusion
Acknowlelgment
References
- Hu, M.-S. Design and development of a high-precision automatic safety valve testing system. Adv. Mech. Eng. 2020, 12. [Google Scholar] [CrossRef]
- Yue, H.; Wu, X.; Shi, Z.; Zhang, Y.; Ye, Y.; Zhang, L.; Fu, Y. A comprehensive cycloid pin-wheel precision reducer test platform integrated with a new dynamic measurement method of lost motion. Metrol. Meas. Syst. 2021, 29, 207–229. [Google Scholar] [CrossRef]
- W. Li, B. Li, C. Shu, et al. New muti-resolotion and muti-scale electromagnetic detection methods for urban underground spaces. Journal of Applied Geophysics 2018, 159, 742–753. [CrossRef]
- W. Li, B. Li, C. Shu, et al. Study on muti-resolotion imaging of urban underground spaces based on high performnce transient electromagnetic source. Chinese Lournal of Applied Geophysics. 2014, 63, 4553–4564.
- Ahmed, N.; Radchenko, A.; Pommerenke, D.; Zheng, Y.R. Design and Evaluation of Low-Cost and Energy-Efficient Magneto-Inductive Sensor Nodes for Wireless Sensor Networks. IEEE Syst. J. 2018, 13, 1135–1144. [Google Scholar] [CrossRef]
- Pal, A.; Kant, K. NFMI: Near Field Magnetic Induction based communication. Comput. Networks 2020, 181. [Google Scholar] [CrossRef]
- Guo, H.; Sun, Z.; Zhou, C. Practical Design and Implementation of Metamaterial-Enhanced Magnetic Induction Communication. IEEE Access 2017, 5, 17213–17229. [Google Scholar] [CrossRef]
- Wang, J.; Gong, Z.; Liu, X.; Guo, H.; Lu, J.; Yu, D.; Lin, Y. Multi-Feature Information Complementary Detector: A High-Precision Object Detection Model for Remote Sensing Images. Remote. Sens. 2022, 14, 4519. [Google Scholar] [CrossRef]
- Muñoz, J.; Molero-Castillo, G.; Benítez-Guerrero, E.; Bárcenas, E. Data fusion as source for the generation of useful knowledge in context-aware systems. J. Intell. Fuzzy Syst. 2018, 34, 3165–3176. [Google Scholar] [CrossRef]
- Hou Xin, Zhang Dongwen, Zhong Ming. Data Aggregation of Wireless Sensor Network Based on Event-Driven and Neural Network. Chinese Journal of Sensors and Actuators 2014, 27, 142–148. [Google Scholar]
- Hedjazi M H, Ghari M. Abolmaesumi P. Distribution of Fiducial Registration Error in Rigid-body Point-based Registration. IEEE Trans. on Medical Imaging 2009, 28, 1791–1801. [Google Scholar] [CrossRef]
- He r, Wang YJ, Wang Q, Zhou Jh, Hu CY. An improved particle swarm optimization based on self-adaptive escape velocity. Journal of Software 2005, 16, 2036–2044, (in Chinese with English abstract). [Google Scholar] [CrossRef]
- Huo, L.; Wu, Z.; Wu, J.; Gao, S.; Chen, Y.; Song, Y.; Wang, S. High-Precision Log-Ratio Spot Position Detection Algorithm with a Quadrant Detector under Different SNR Environments. Sensors 2022, 22, 3092. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q. A High-Precision Spectrum-Detection Algorithm Based on the Normalized Variance of Nonreconstruction Compression Sensing. Math. Probl. Eng. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Liu, J.; Jia, R.; Li, W.; Ma, F.; Abdullah, H.M.; Ma, H.; Mohamed, M.A. High precision detection algorithm based on improved RetinaNet for defect recognition of transmission lines. Energy Rep. 2020, 6, 2430–2440. [Google Scholar] [CrossRef]
- Ru, C.; Zhang, S.; Qu, C.; Zhang, Z. The High-Precision Detection Method for Insulators’ Self-Explosion Defect Based on the Unmanned Aerial Vehicle with Improved Lightweight ECA-YOLOX-Tiny Model. Appl. Sci. 2022, 12, 9314. [Google Scholar] [CrossRef]
- Liu Wenqiang, Liu Zhigang, Li Qiao, et al. High-Precision Detection Method for Structure Parameters of Catenary Cantilever Devices using 3D Point Cloud Data. IEEE TRANSACTIONS ON INSTRUMENTATION AND MEASUREMENT, VOL. 2021, 70.
- LU YIN, SHUANGZHI LI, ZHONGLIANG DENG, et al. A Novel Cycle Slips Detection Model for the High Precision Positioning. ACCESS.2018.2890694.
- Shao, L.; Hu, Y.; Xu, G. A High Precision On-Line Detection Method for IGBT Junction Temperature Based on Stepwise Regression Algorithm. IEEE Access 2020, 8, 186172–186180. [Google Scholar] [CrossRef]
- Duan Xiaomeng, Yin Deshun,.AN Liyuan, et.al. Study on deformation of viscoelastic materials based on Fractional Calculus. SCIENCE CHINA: physics mechanics astronomy 2013, 43, 971–977. [CrossRef]
- B. Gua, X. Pu, F. Haung, Fractional Partial Differential Equations and their Numerical Solutions. World Scientific 2015. [CrossRef]
- Hassan, S.Z.; A E Abdelrahman, M. Solitary wave solutions for some nonlinear time-fractional partial differential equations. Pramana 2018, 91, 67. [Google Scholar] [CrossRef]
- WANG Bao, ZHU Jiaming. Quantitative Analysis of High Temperature Protective Clothing Design Based on Fractional Partial Differential Equation Solution and Optimization Model. Journal of Sichuan University of Science & Engineering(Natural Sicence Edition) 2019, 32, 86–93. [Google Scholar]
- ZHOU Shangbo, WANG Liping, YIN Xuehui. Applications of fractional partial differential equations in image processing. Journal of Computer Applications 2017, 37, 546–552. [Google Scholar]
- SHEN Tianlong. “Dynamics of stochastic Fractional Partial Differential Equations,” Ph.D. dissertation, Dept. Mathematical Theory., National Defense University of science and technology, ChangSha, China, 2017.
- ZUO Yan-hong, CHENG Hua, ZHU Yin-feng. The Algorithm for Multi-sensors Detection Data Fusion Based on Fractional Differential. Science Technology and Engineering 2019, 19, 189–194. [Google Scholar]
- ZUO Yanhong, CHENG Hua, CHENG Tangchun. Application of fractional differential operator in coal mine detection data fusion processing. Journal of China Coal Society 2020, 45, 819–826. [Google Scholar]
- ZUO Yan-hong, ZUO Cheng-ji, FANG Ji-gen. Engine On-line Detection Data Fusion Technology Based on Fractional Integral. Science Technology and Engineering 2021, 21, 644–650. [Google Scholar]
- ZUO Yanhong, CHENG Hua, ZHANG Keren. Fusion algorithm of discrete manufacturing system detection data based on fractional partial differential. Computer Integrated Manufacturing Systems 2015, 21, . 3256–3262. [Google Scholar]
- ZUO Yanhong. “Research on discrete manufacturing inspection data fusion technology based on fractional calculus,” Ph.D. dissertation, Dept. Mechanics Eng., Hefei University of technology, HeFei, China, 2019.
- ZUO Yanhong, CHENG Hua, CHENG Tangchun. On-Line Detection Data Fusion Algorithm of Underground Mobile Equipment Based on Fractional Order Partial Differentia. 2021, 34, 237–243.
- ZUO Yanhong, YAO Yansheng, GENG Guoqing. Application of fractional partial differential in fault diagnosis of industrial robots. Computer Integrated Manufacturing Systems 2022.
- YANG Jia, GONG Fengxun. Improved Dynamic Weighted Multi-sensors Data Fusion Algorithm. Computer Engineering 2011, 37, 97–99. [Google Scholar]
- TU Guoping, YE Suping. Algorithm for the sensors data fusion. JOURNAL OF TRANSDUCER TECHNOLOGY 2003, 22, 30–32. [Google Scholar]
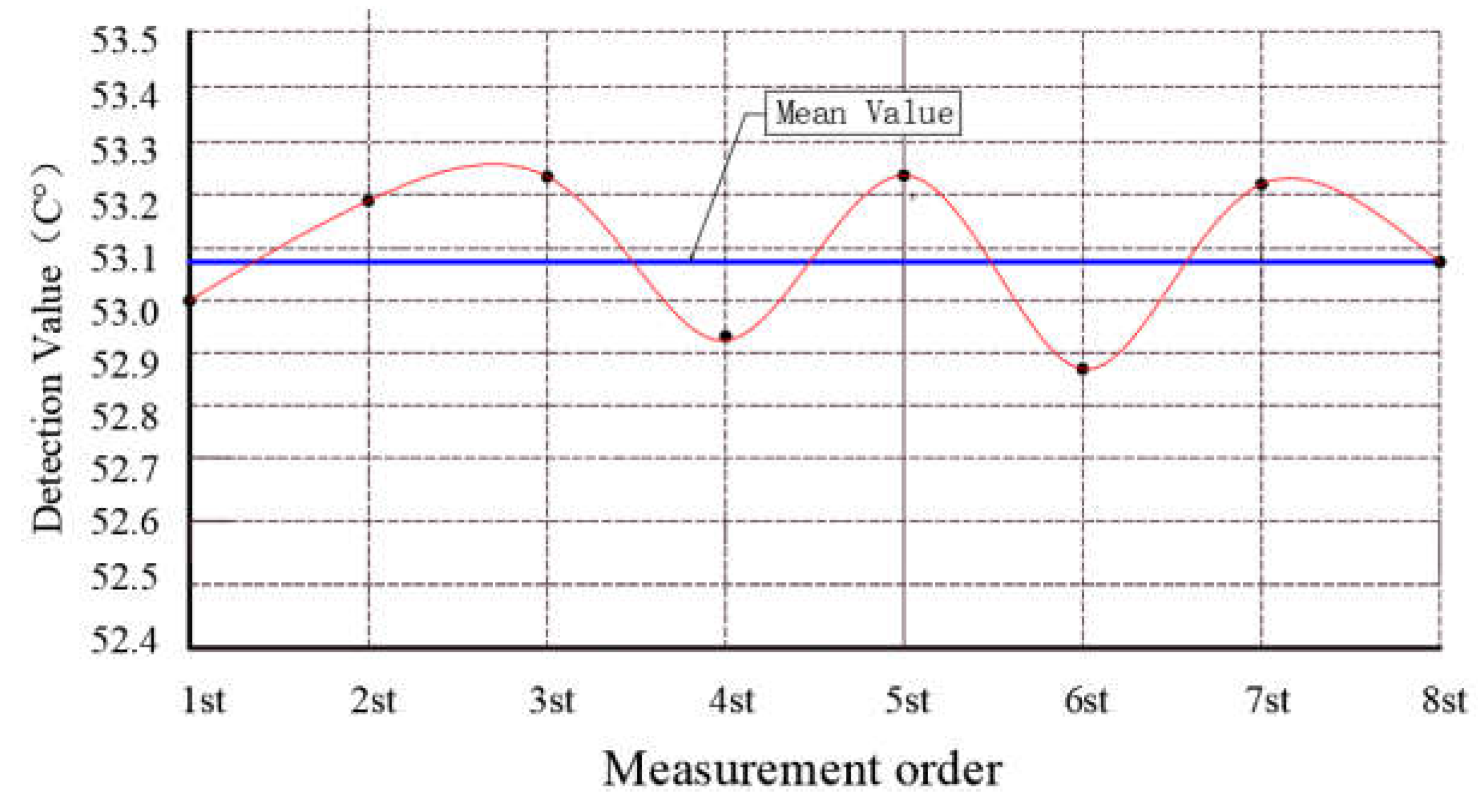
| Number of sampling | Sensor number | Mean value Fj | Standard deviation Sjy |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | |||
| 1st | 53.00 | 53.10 | 52.75 | 53.10 | 52.80 | 53.60 | 57.66 | 52.65 | 53.12 | 0.30 |
| 2st | 53.20 | 54.20 | 52.55 | 53.20 | 52.80 | 53.30 | 58.34 | 53.10 | 53.21 | 0.45 |
| 3st | 53.00 | 53.40 | 48.43 | 52.96 | 53.20 | 53.80 | 52.70 | 53.60 | 53.09 | 0.38 |
| 4st | 56.05 | 53.00 | 52.75 | 53.70 | 52.50 | 53.20 | 52.82 | 52.50 | 52.94 | 0.51 |
| 5st | 47.35 | 53.30 | 52.80 | 53.50 | 46.52 | 53.62 | 53.05 | 53.15 | 53.17 | 0.34 |
| 6st | 52.80 | 53.15 | 52.51 | 53.15 | 53.11 | 52.65 | 52.70 | 52.88 | 53.00 | 0.40 |
| 7st | 53.50 | 53.52 | 52.54 | 53.20 | 52.90 | 53.80 | 53.15 | 53.12 | 53.16 | 0.49 |
| 8st | 53.30 | 53.60 | 53.12 | 52.75 | 52.80 | 53.10 | 52.85 | 53.05 | 53.35 | 0.49 |
| Mean value Fi | 53.13 | 53.41 | 52.72 | 53.20 | 52.87 | 53.38 | 52.88 | 53.01 | 53.07 | |
| Standard deviation Six deviation Six | 0.15 | 0.35 | 0.20 | 0.28 | 0.21 | 0.37 | 0.17 | 0.32 | ||
| Mean value F | 53.07 | |||||||||
| Mean standard deviation Sx 0.251 Mean standard deviation Sy 0.333 Total deviation T 1.580 | ||||||||||
| Number of sampling | Sensor number | |||||||
|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | |
| 1st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 2st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 3st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 4st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 5st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 6st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 7st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| 8st | 63.731 | 64.151 | 63.834 | 63.993 | 63.854 | 64.182 | 63.772 | 64.079 |
| Number of sampling | Sensor number | |||||||
|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | |
| 1st | 59.776 | 59.776 | 59.776 | 59.776 | 59.776 | 59.776 | 59.776 | 59.776 |
| 2st | 59.918 | 59.918 | 59.918 | 59.918 | 59.918 | 59.918 | 59.918 | 59.918 |
| 3st | 59.828 | 59.828 | 59.828 | 59.828 | 59.828 | 59.828 | 59.828 | 59.828 |
| 4st | 59.850 | 59.850 | 59.850 | 59.850 | 59.850 | 59.850 | 59.850 | 59.850 |
| 5st | 59.761 | 59.761 | 59.761 | 59.761 | 59.761 | 59.761 | 59.761 | 59.761 |
| 6st | 59.731 | 59.731 | 59.731 | 59.731 | 59.731 | 59.731 | 59.731 | 59.731 |
| 7st | 59.836 | 59.836 | 59.836 | 59.836 | 59.836 | 59.836 | 59.836 | 59.836 |
| 8st | 59.753 | 59.753 | 59.753 | 59.753 | 59.753 | 59.753 | 59.753 | 59.753 |
| Number of sampling | Sensor number | |||||||
|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | |
| 1st | 61.754 | 61.964 | 61.805 | 61.885 | 61.815 | 61.979 | 61.774 | 61.928 |
| 2st | 61.825 | 62.035 | 61.876 | 61.956 | 61.886 | 62.050 | 61.845 | 61.999 |
| 3st | 61.780 | 61.990 | 61.831 | 61.911 | 61.841 | 62.005 | 61.800 | 61.954 |
| 4st | 61.791 | 62.001 | 61.842 | 61.922 | 61.852 | 62.016 | 61.811 | 61.965 |
| 5st | 61.746 | 61.956 | 61.798 | 61.877 | 61.808 | 61.972 | 61.767 | 61.920 |
| 6st | 61.731 | 61.941 | 61.783 | 61.862 | 61.793 | 61.957 | 61.752 | 61.905 |
| 7st | 61.784 | 61.994 | 61.835 | 61.915 | 61.845 | 62.009 | 61.804 | 61.958 |
| 8st | 61.742 | 61.952 | 61.794 | 61.873 | 61.804 | 61.968 | 61.763 | 61.916 |
| Mean value F0.5 | 61.878 | |||||||
| Amplification factor K | 61.878/53.07=1.166 | |||||||
| Number of sampling | Sensor number | Mean value Fj |
Standard deviation Sjy0.5 |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | |||
| 1st | 52.962 | 53.142 | 53.006 | 53.074 | 53.015 | 53.155 | 52.979 | 53.111 | 53.056 | 0.070 |
| 2st | 53.023 | 53.203 | 53.067 | 53.135 | 53.075 | 53.216 | 53.040 | 53.172 | 53.116 | 0.070 |
| 3st | 52.984 | 53.164 | 53.028 | 53.096 | 53.037 | 53.178 | 53.002 | 53.133 | 53.078 | 0.070 |
| 4st | 52.994 | 53.174 | 53.038 | 53.106 | 53.046 | 53.187 | 53.011 | 53.143 | 53.087 | 0.070 |
| 5st | 52.955 | 53.136 | 53.000 | 53.068 | 53.008 | 53.149 | 52.973 | 53.105 | 53.049 | 0.070 |
| 6st | 52.943 | 53.123 | 52.987 | 53.055 | 52.995 | 53.136 | 52.960 | 53.092 | 53.036 | 0.070 |
| 7st | 52.988 | 53.168 | 53.032 | 53.100 | 53.040 | 53.181 | 53.005 | 53.137 | 53.081 | 0.070 |
| 8st | 52.952 | 53.132 | 52.996 | 53.064 | 53.005 | 53.145 | 52.970 | 53.101 | 53.046 | 0.070 |
| Mean value Fi | 52.975 | 53.155 | 53.019 | 53.087 | 53.028 | 53.168 | 52.993 | 53.124 | 53.069 | 0.070 |
| Standard deviation Six0.5 | 0.026 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | ||
| Mean standard deviation Sx0.5 0.025 Mean standard deviation Sy0.5 0.070 Total deviation T0.5 0.175 | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





