Submitted:
15 February 2023
Posted:
20 February 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- The designed control structure has been validated via simulation for the third-order uncertain Magnetic Levitation System(MLS) to estimate and suppress the combined effect of, the external payload disturbance, the parametric uncertainties.
- The convergence analysis has been carried out for the DESO-FLC based uncertain systems.
- Performance of the proposed design has been compared with the most popular LQR and FLC approaches for diverse operating conditions using the integral error criterion (i.e., ITAE, ISE).
2. Preliminaries
2.1. Extended State Observer (ESO)
2.2. Feedback Linearizing Control (FLC)
3. Problem Statements
- The FLC approach may not provide robust performance in the presence of lumped disturbances. The addition of integral action (i.e., FLC+I) can be seen as one of the solutions to suppress the constant or the slow-varying disturbances [4]. However, the nominal performance of the uncertain system may be degraded using such integral action when there is no disturbance [29].
-
To handle such lumped disturbances for the second order nonlinear systems, the FLC integrated with the Disturbance Observer (i.e, FLC+DO) has been proposed in [21]. Such a method may not suitable for the following type of higher-order nonlinear systems in (13). For brevity, the higher-order system is presented by (14) with in this research.OR
-
The group of uncertain systems presented by (14) has been affected by the multiple nonlinearities (i.e, , , ) and the mismatched lumped disturbance (i.e, ).
- (a)
- Nonlinear terms can be compensated from the output using the FLC methods. Now, the conventional ESO method can be utilized to tackle the matched lumped disturbances for the systems with ICF structure [12]. However, the considered system is affected by the mismatched lumped disturbance and does not follow the ICF structure. Hence, neither the conventional ESO method [27] nor the FLC+DO method [21] may provide robust performance.
- (b)
-
The considered third-order system in (14) can be expressed in the input-output form using the derivatives of output as follows:Hence, based on (15), to compensate for the unwanted effect of the nonlinearities and the disturbances together using the conventional FLC approach, it is recommended to estimate the unknown states, the mismatched lumped disturbance () and it’s first derivative (). For the higher-order systems (i.e, ), estimation of the second and higher order derivatives is required.
- Finally, to get rid of the above-stated problems, it is necessary to investigate and expand the individual functionalities of the FLC and the ESO for the higher-order ( for this research) uncertain systems. In such situations, the usage of ESO methods is more favorable in estimating the unknown states, disturbances, and their higher-order derivatives simultaneously [12,19,21,25,34].
4. Dual Nonlinear Extended State Observer Based FLC (DESO-FLC)
4.1. Dual Extended State Observer (DESO)
4.2. DESO Based Feedback Linearizing Control (DESO-FLC)
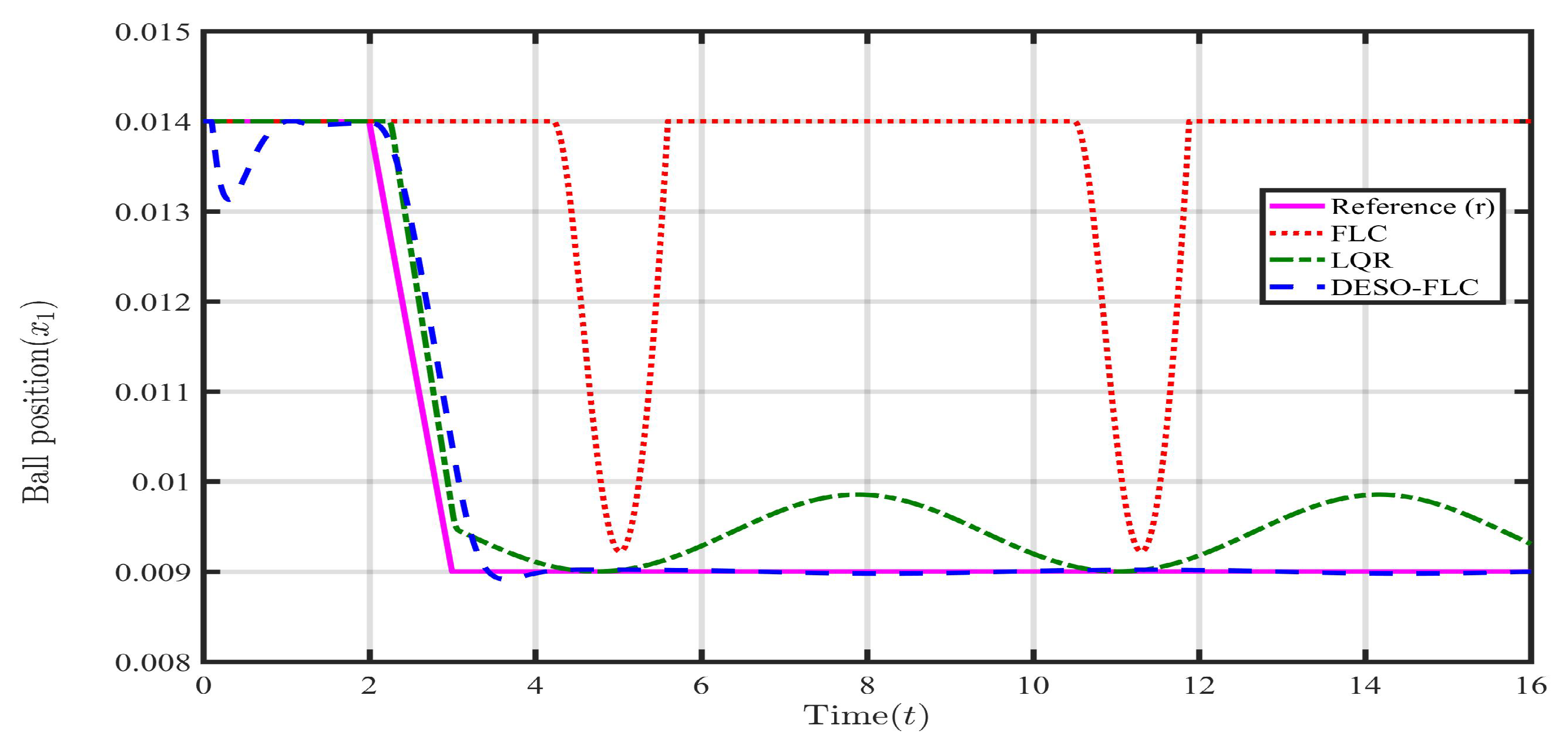
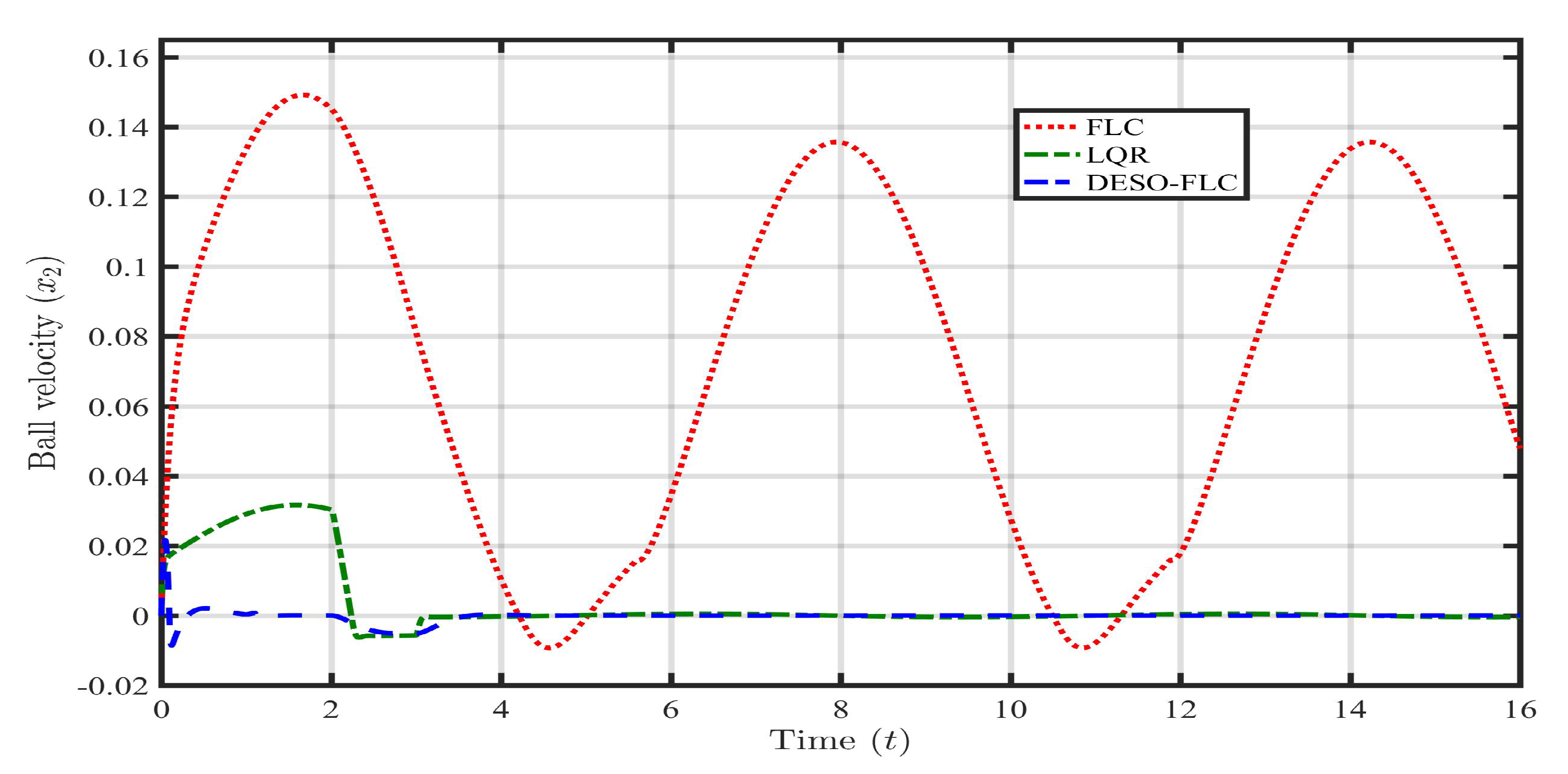
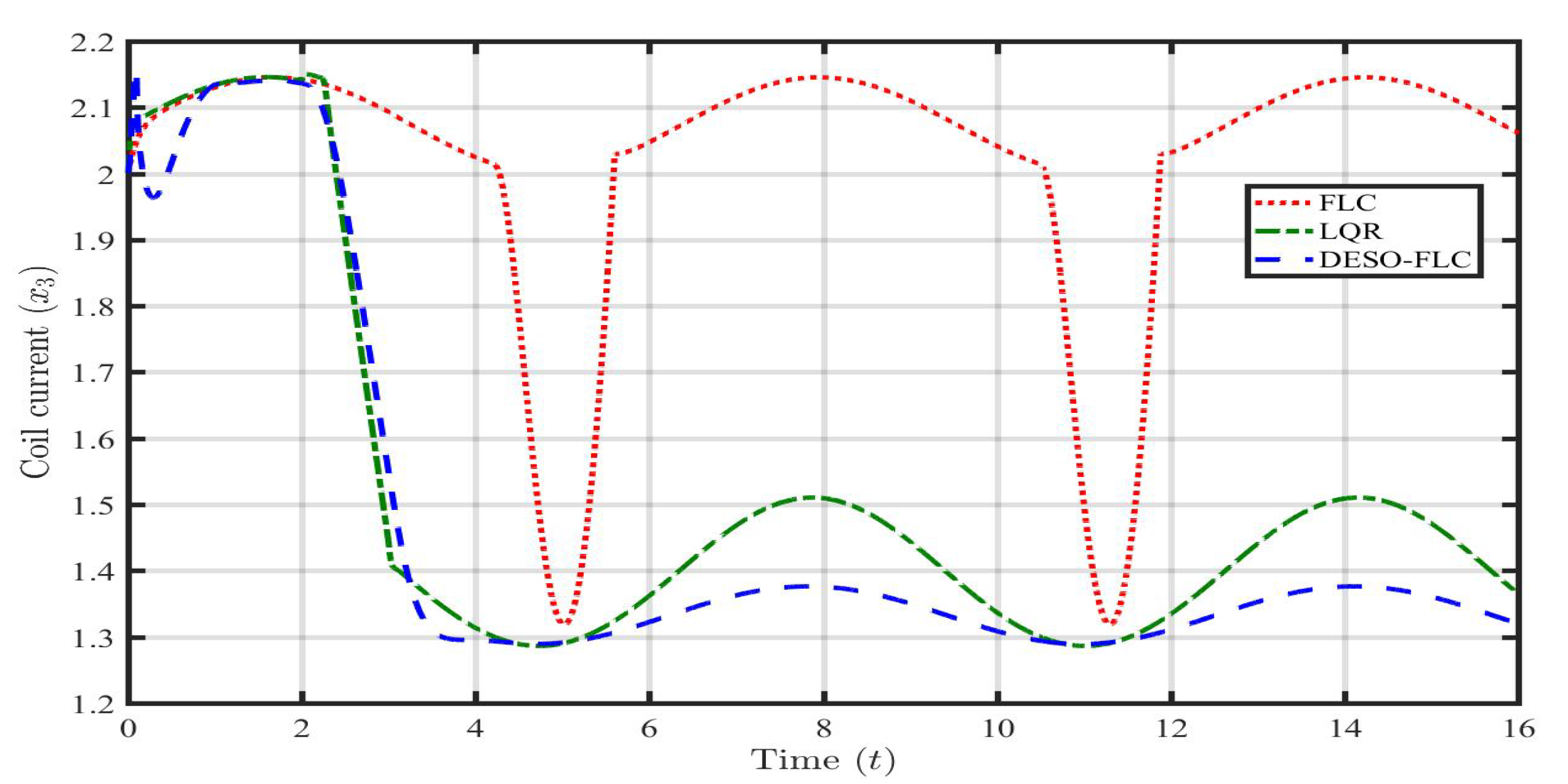
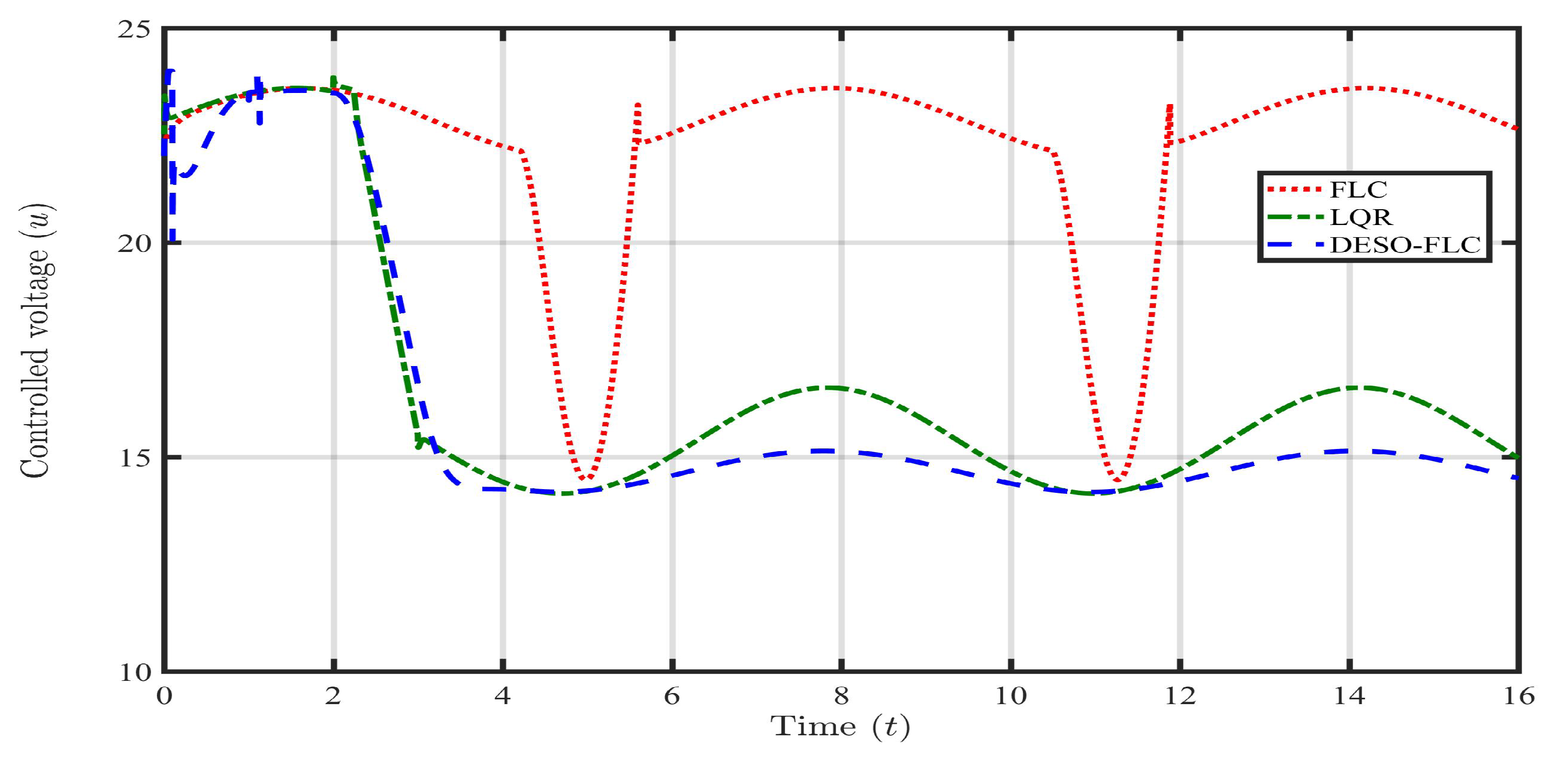
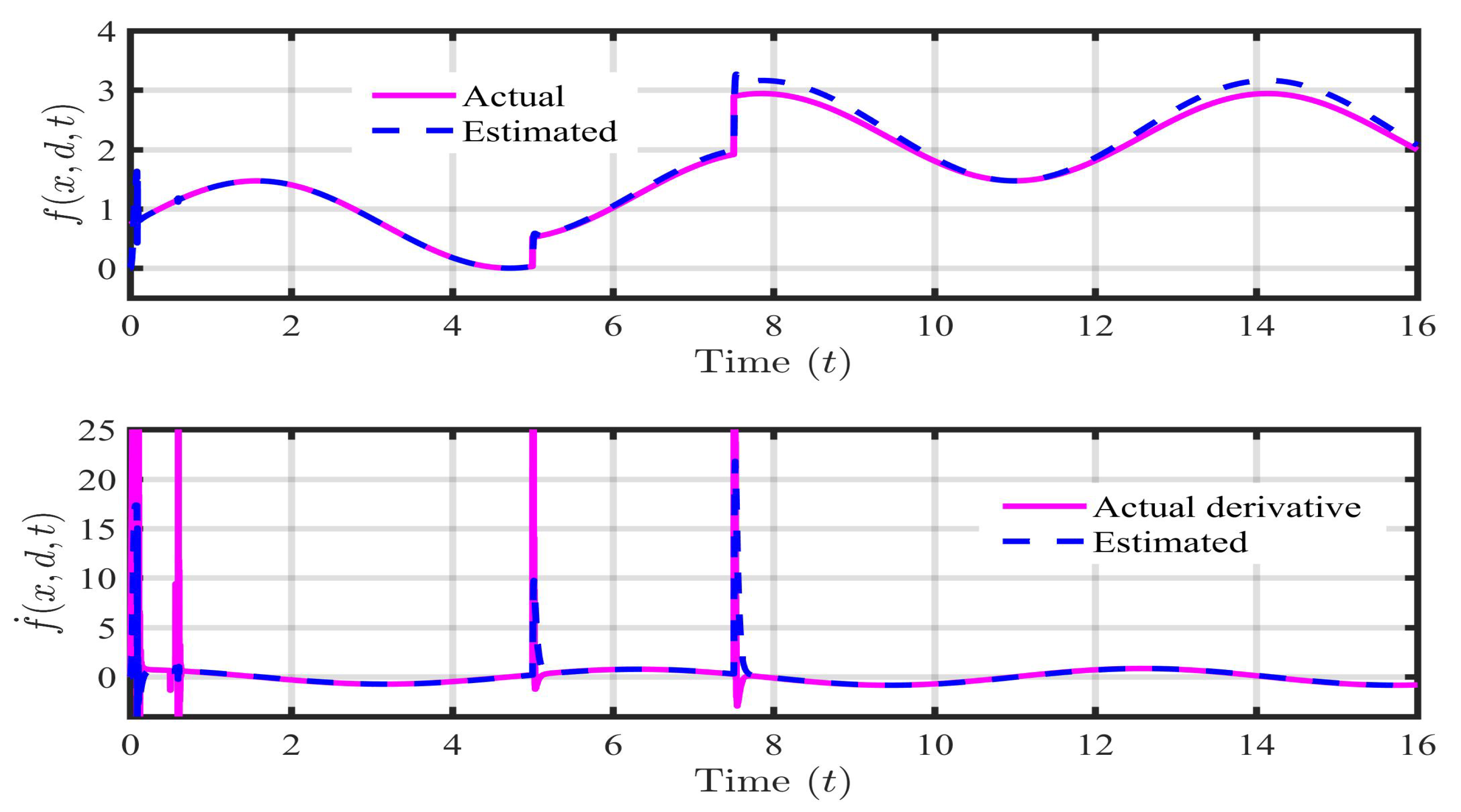
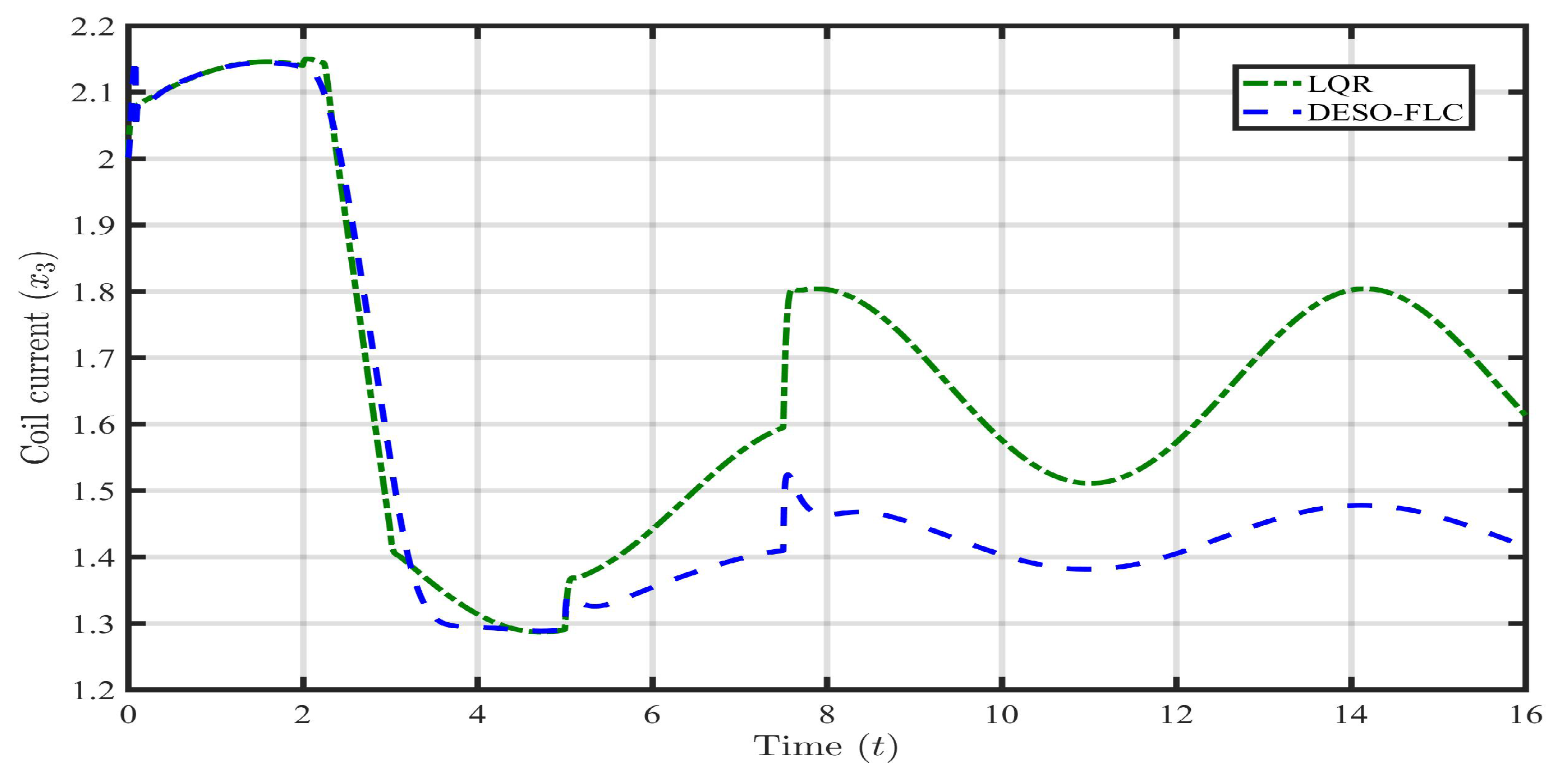
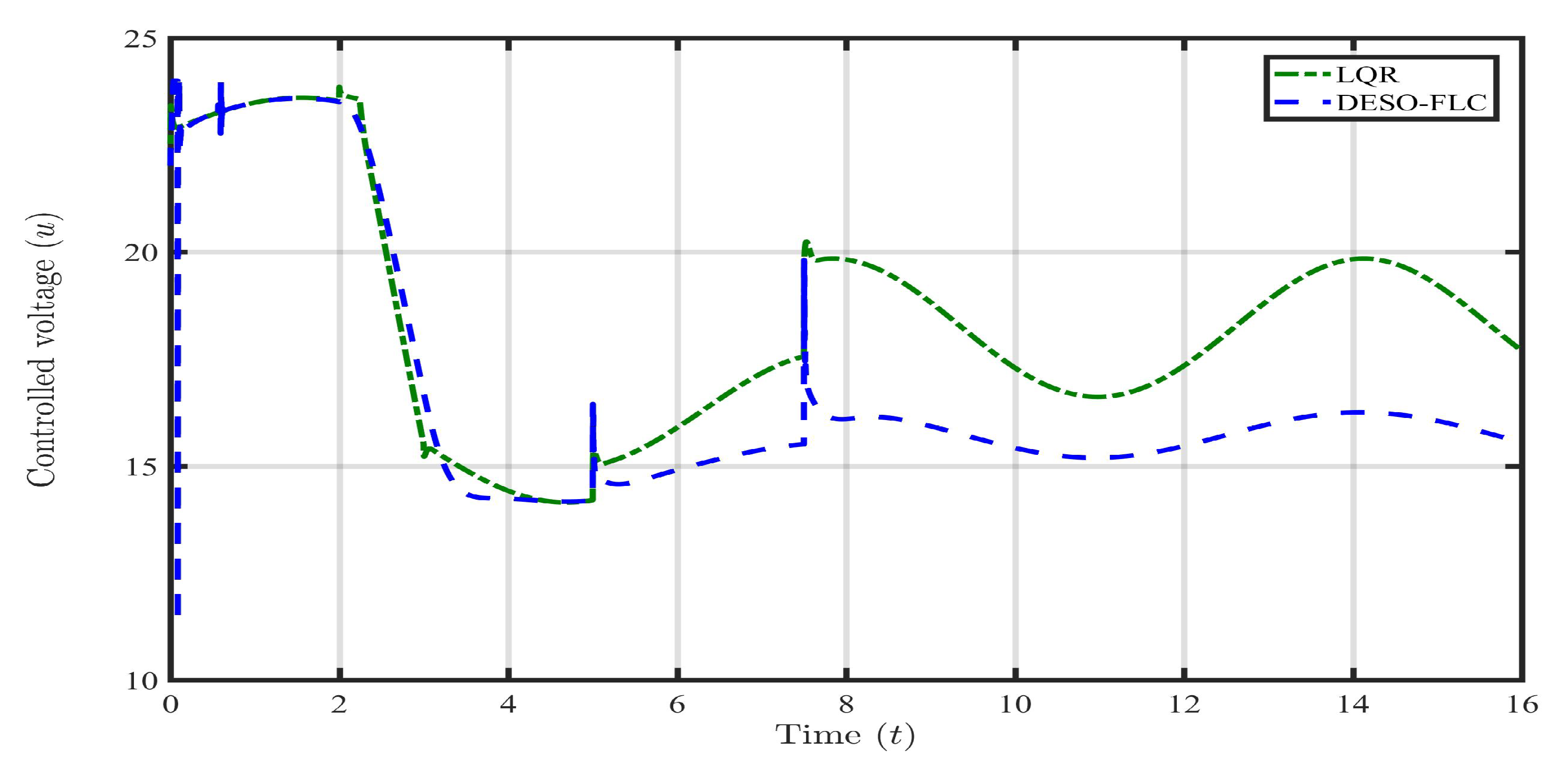
5. Practical Application and Results
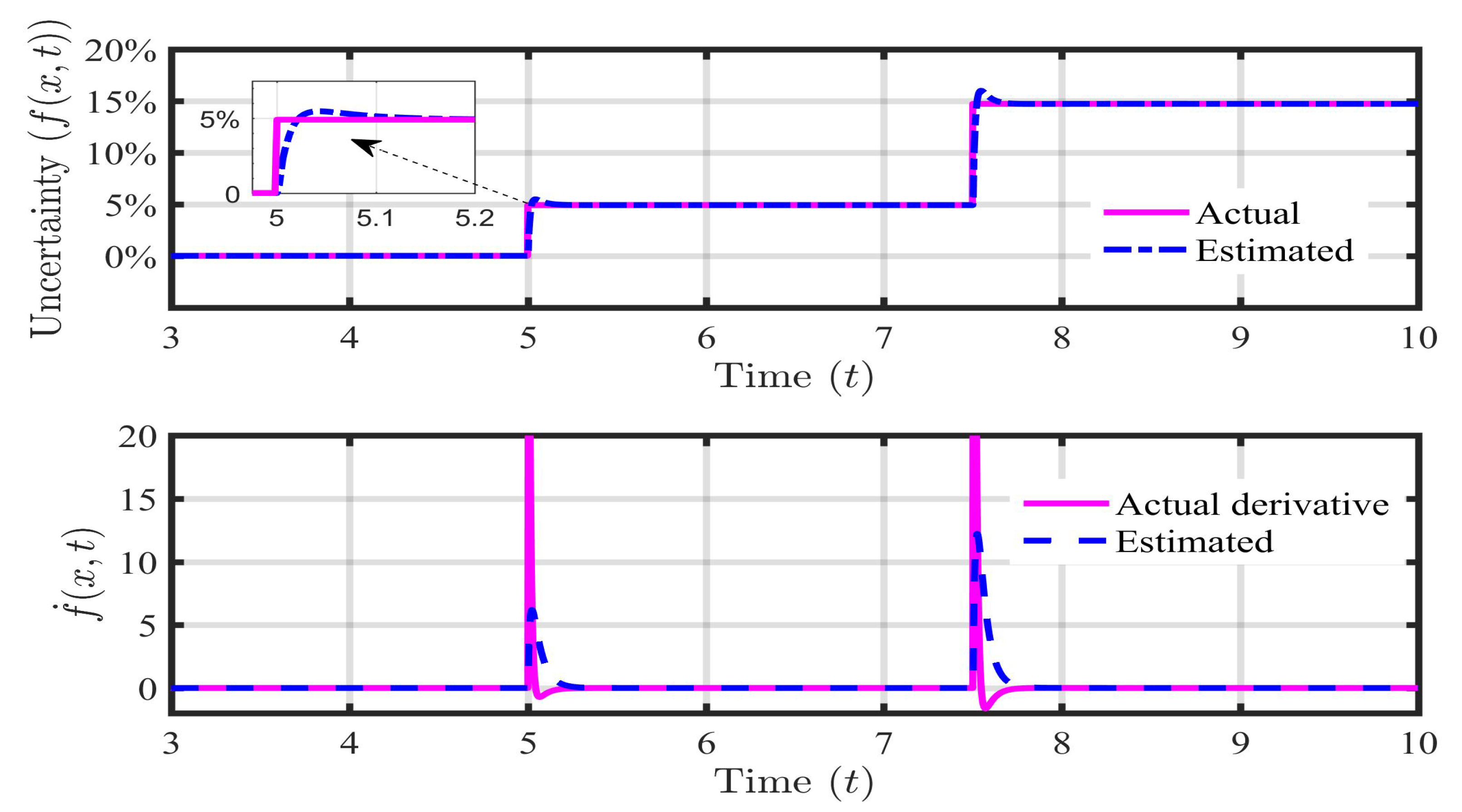
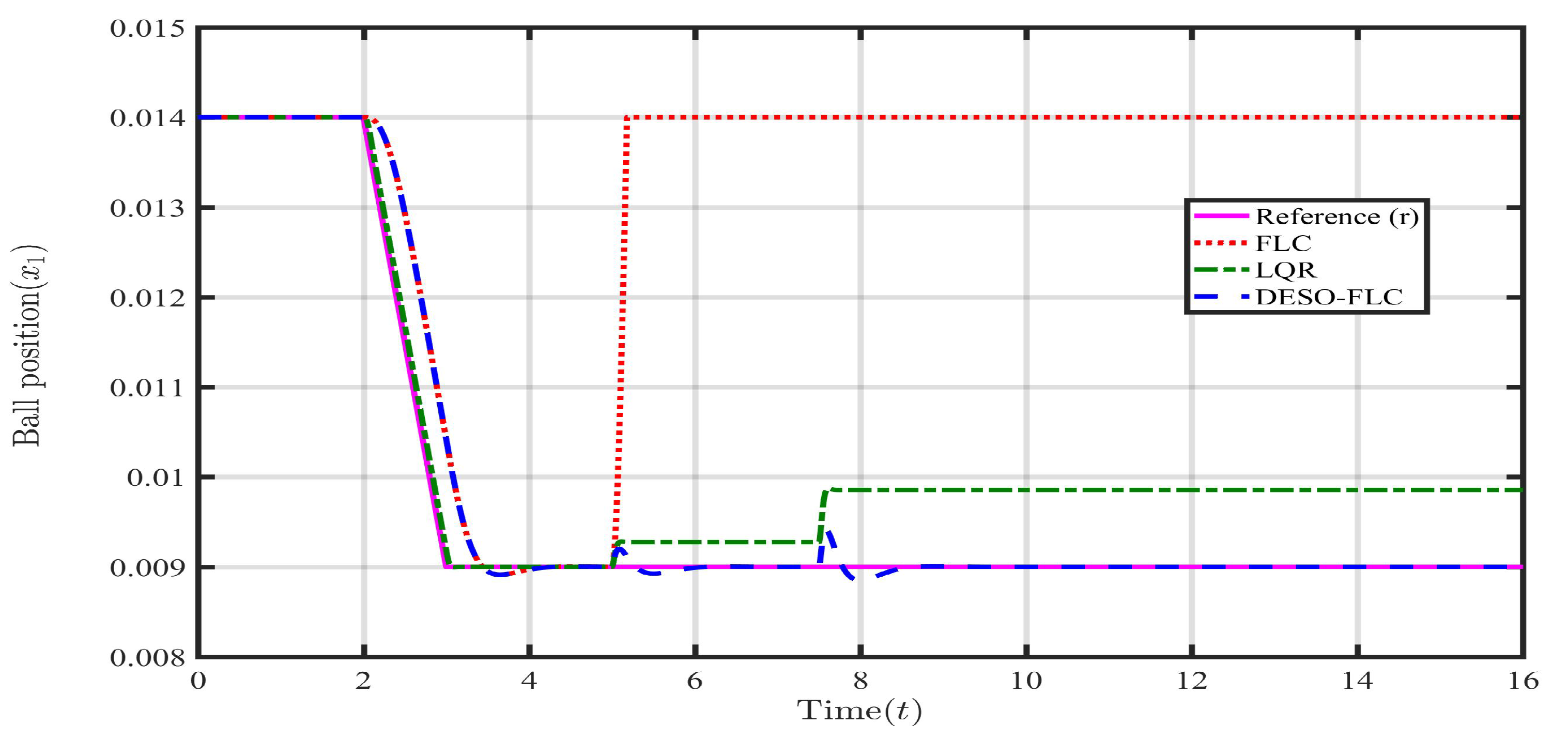
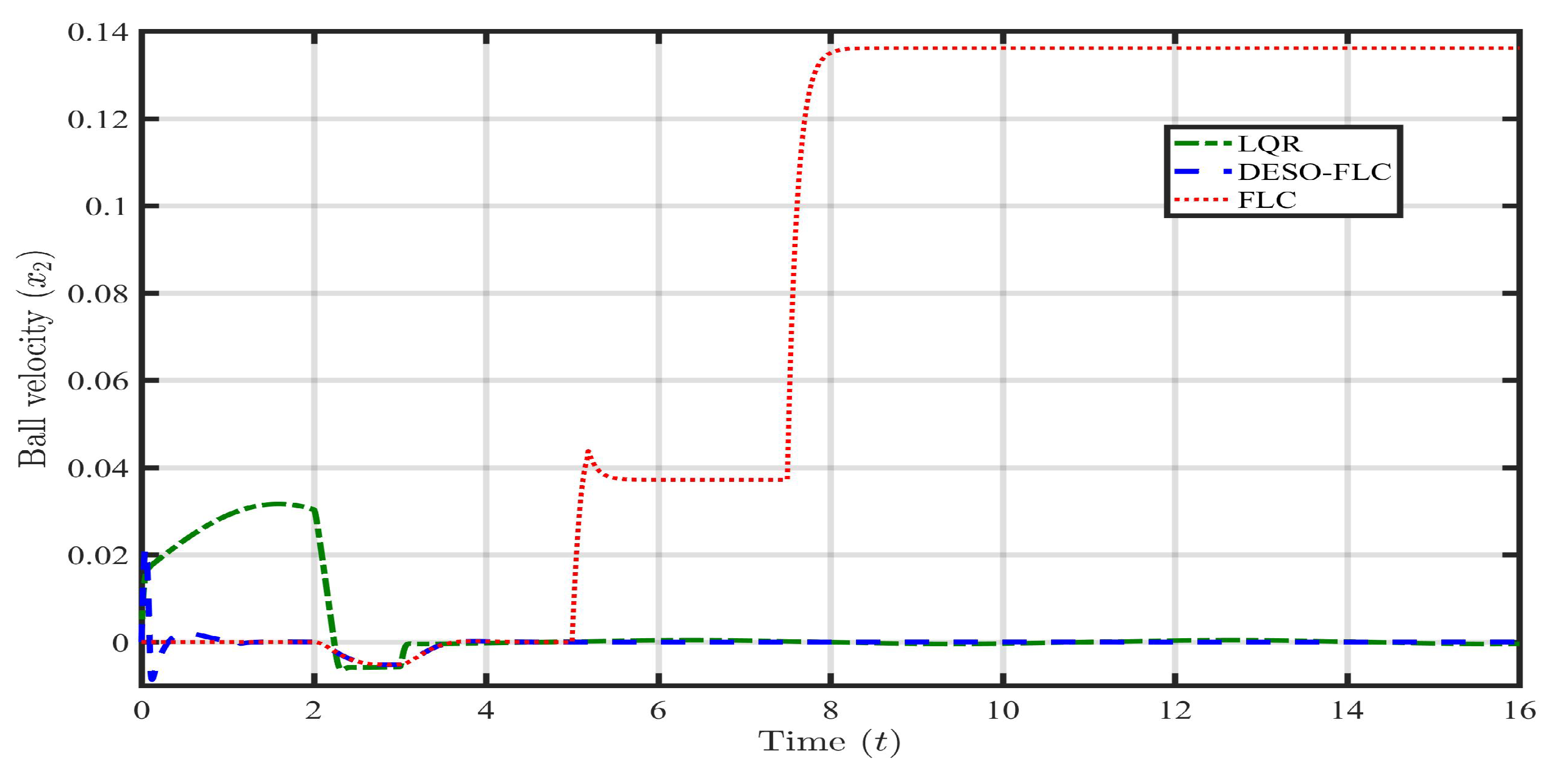
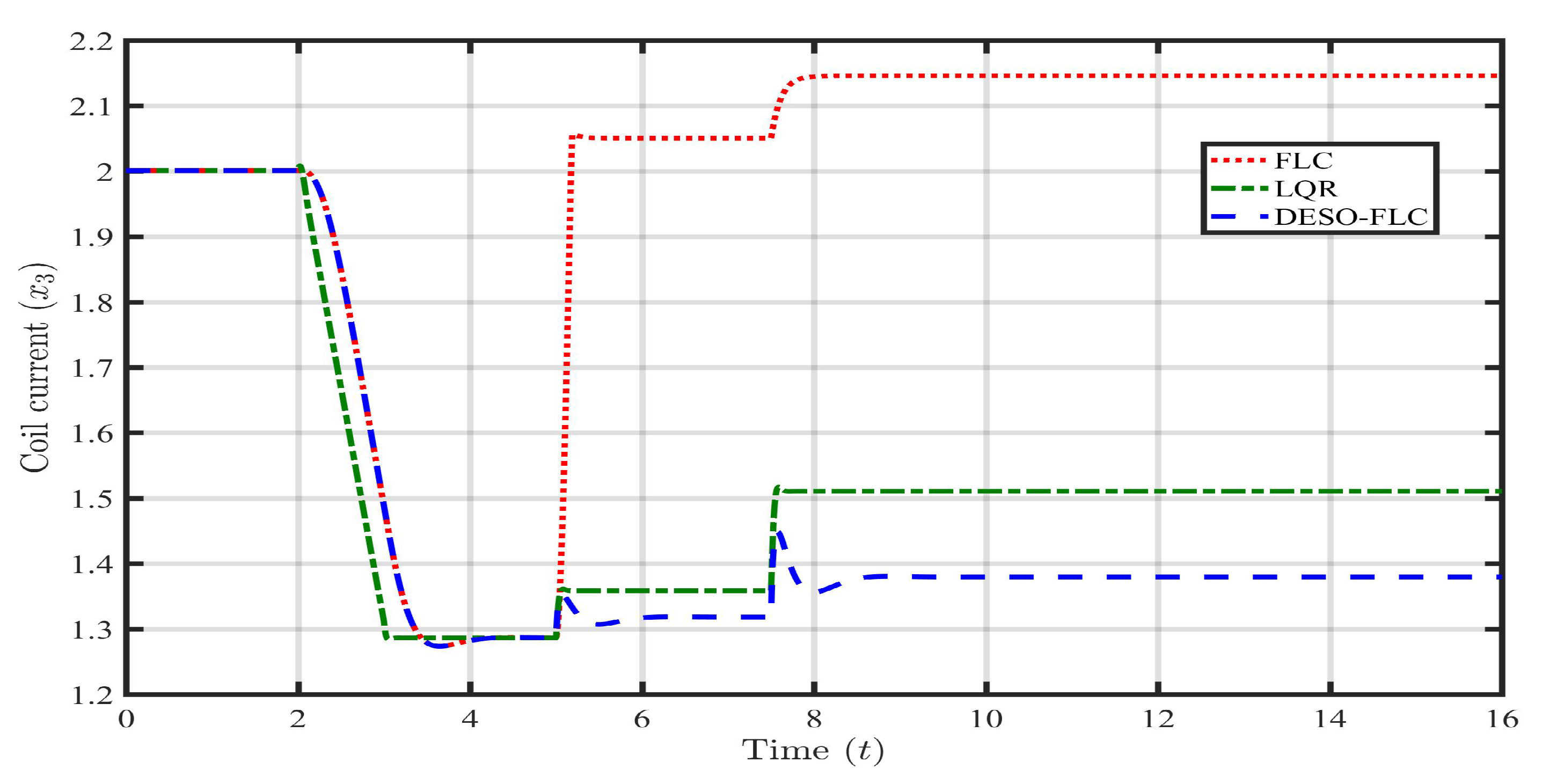
5.1. Case 1: Payload Disturbance ()
5.2. Case 2: Parametric Uncertainty (, )
5.3. Case 3: Payload disturbance with Parametric Uncertainty (, , )
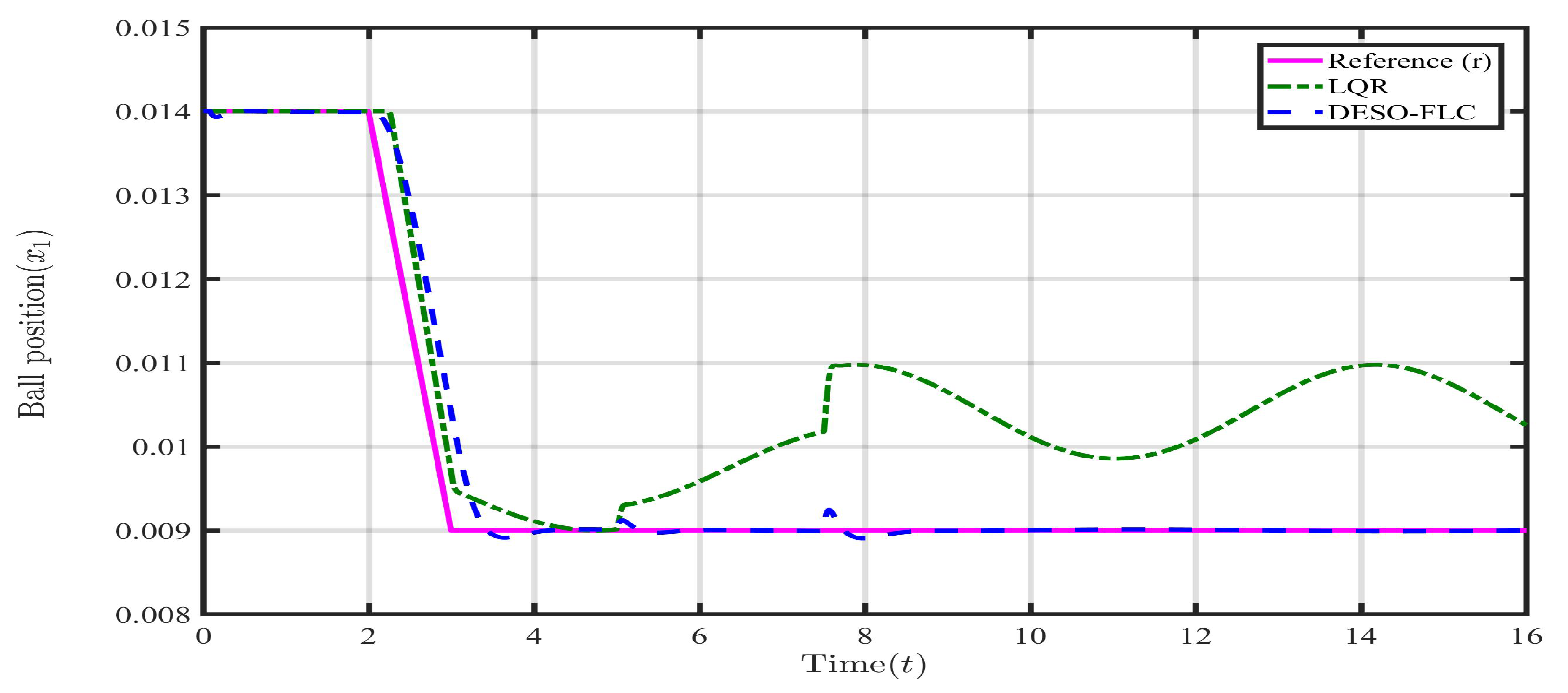
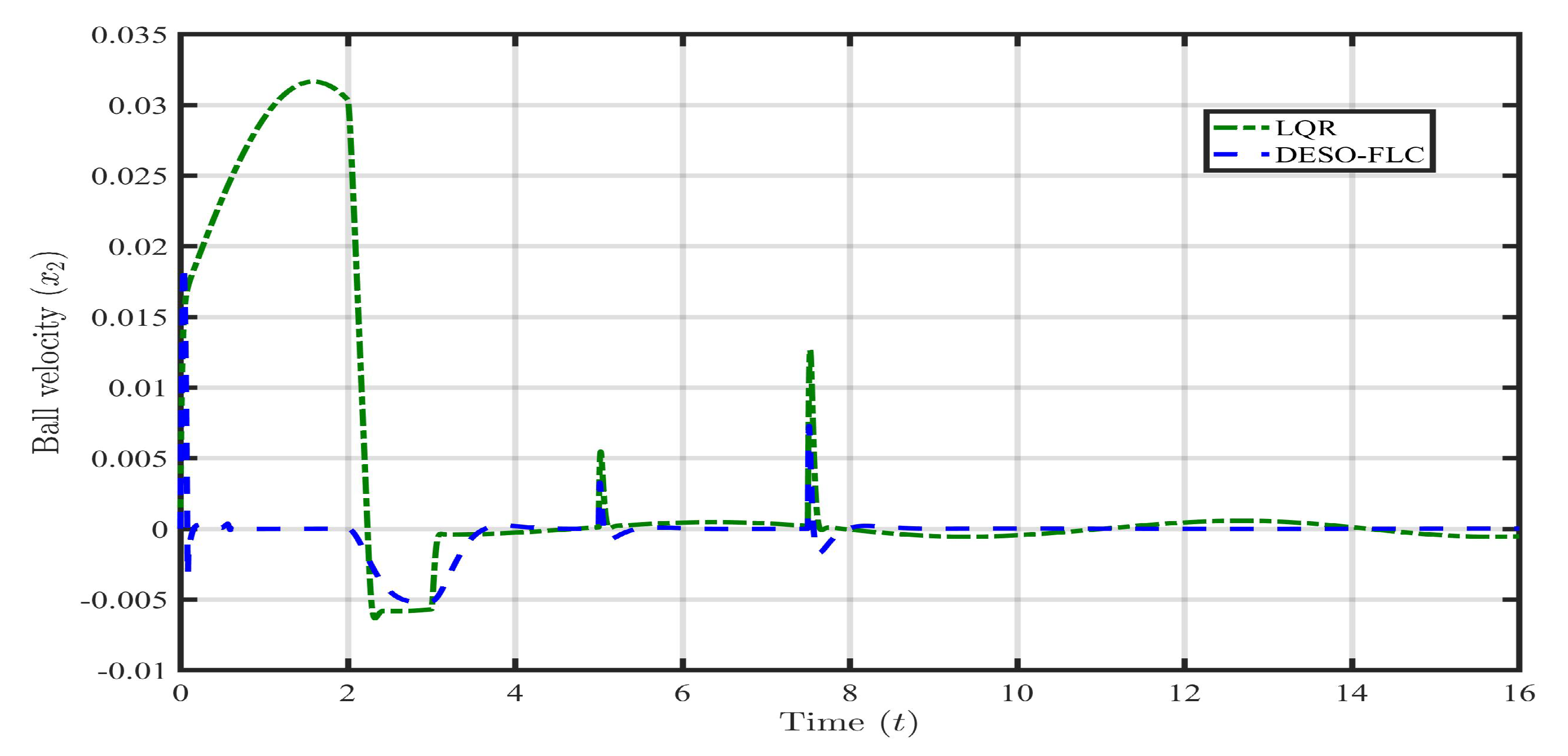
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ADRC | Active Disturbance Rejection Control |
| DOB | Disturbance Observer |
| DOBC | Disturbance Observer Based Control |
| DESO | Dual Extended State Observer |
| DESOBC | Dual Extended State Observer Based Control |
| DESO-FLC | Dual Extended State Observer Based Feedback Linearizing Control |
| ESO | Extended State Observer |
| FLC | Feedback Linearzing Control |
| ICF | Integral Chain Form |
| ISE | Integral Square Error |
| ISTE | Integral Square Time Error |
| LQR | Linear Quadratic Regulator |
| MLS | Magnetic Levitation System |
| NESO | Nonlinear Extended State Observer |
References
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods - An Overview. IEEE Transactions on Industrial Electronics 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Ran, M.; Li, J.; Xie, L. A new extended state observer for uncertain nonlinear systems. Automatica 2021, 131, 109772. [Google Scholar] [CrossRef]
- Gandhi, R.V.; Adhyaru, D.M. Hybrid extended state observer based control for systems with matched and mismatched disturbances. ISA transactions 2020, 106, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Nie, Z.; Wang, Q.; She, J.; Liu, R.; Guo, D. New results on the robust stability of control systems with a generalized disturbance observer. Asian Journal of Control 2019, Online, 1–13. [Google Scholar] [CrossRef]
- She, J.H.; Xin, X.; Yamaura, T. Analysis and design of control system with equivalent-input-disturbance estimation. Proceedings of the IEEE International Conference on Control Applications 2006, 1, 1463–1469. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Transactions 2014, 53, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.; Zhao, Z. On the convergence of an extended state observer for nonlinear systems with uncertainty. Systems & Control Letters 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Chen, W.; Guo, L. Analysis of disturbance observer based control for nonlinear systems under disturbances with bounded variation. In Proceedings of the Control 2004, 2004; Vol. 1; pp. 1–5.
- Chen, W.H.; Guo, L. Control of nonlinear systems with unknown actuator nonlinearities. In Proceedings of the IFAC Nonlinear Control Systems; 2004; pp. 1347–1352. [Google Scholar] [CrossRef]
- Chen, W.H.; Li, S.; Yang, J. Non-linear disturbance observer-based robust control for systems with mismatched disturbances/uncertainties. IET Control Theory & Applications 2011, 5, 2053–2062. [Google Scholar] [CrossRef]
- I., W.; K., I. On the active input-output feedback linearization of single-link flexible joint manipulator : an extended state observer approach. IEEE Transactions on Industrial Electronics 2018, pp. 1–9.
- Li, S.; Member, S.; Yang, J.; Chen, W.; Member, S.; Chen, X. Generalized Extended State Observer Based Control for Systems With Mismatched Uncertainties. IEEE Transactions on Industrial Electronics 2012, 59, 4792–4802. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, W.; Liu, X.; Chen, Z.; Wang, S. A novel extended state observer. ISA Transactions 2015, 58, 309–317. [Google Scholar] [CrossRef]
- Castillo, A.; García, P.; Sanz, R.; Albertos, P. Enhanced extended state observer-based control for systems with mismatched uncertainties and disturbances *. ISA Transactions 2018, 73, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Castillo, A.; Santos, T.L.; Garcia, P.; Normey-Rico, J.E. Predictive ESO-based control with guaranteed stability for uncertain MIMO constrained systems. ISA Transactions 2021, 112. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Zhang, D.; Lu, B. ESO based sliding mode control for the welding robot with backstepping. International Journal of Control 2021, 94, 3322–3331. [Google Scholar] [CrossRef]
- Xu, Z.; Qi, G.; Liu, Q.; Yao, J. ESO-based adaptive full state constraint control of uncertain systems and its application to hydraulic servo systems. Mechanical Systems and Signal Processing 2022, 167, 108560. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.; Phadke, S. State and Extended Disturbance Observer for Sliding Mode Control of Mismatched Uncertain Systems. Journal of Dynamic Systems, Measurement, and Control 2015, 137, 074502. [Google Scholar] [CrossRef]
- Hou, L.; Wang, L.; Wang, H. SMC for Systems With Matched and Mismatched Uncertainties and Disturbances Based on NDOB. ACTA AUTOMATICA SINICA 2017, 43, 1257–1264. [Google Scholar] [CrossRef]
- Fuh, C.C.; Tsai, H.H.; Yao, W.H. Combining a feedback linearization controller with a disturbance observer to control a chaotic system under external excitation. Communications in Nonlinear Science and Numerical Simulation 2012, 17, 1423–1429. [Google Scholar] [CrossRef]
- Kayacan, E.; Fossen, T. Feedback linearization control for systems with mismatched uncertainties via distrubance observers. Asian Journal of Control 2019, 21, 1–13. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Active Disturbance Rejection Control for Uncertain Nonaffine-in-Control Nonlinear Systems. IEEE Transactions on Automatic Control 2017, 62, 5830–5836. [Google Scholar] [CrossRef]
- Guo, L.; Cao, S. Anti-disturbance control theory for systems with multiple disturbances: A survey. ISA Transactions 2014, 53, 846–849. [Google Scholar] [CrossRef]
- Liu, C.; Liu, G.; Fang, J. Feedback Linearization and Extended State Observer-Based Control for Rotor-AMBs System. IEEE Transactions on Industrial Electronics 2017, 64, 1313–1322. [Google Scholar] [CrossRef]
- Kayacan, E.; Peschel, J.; Chowdhary, G. A self-learning disturbance observer for nonlinear systems in feedback-error learning scheme. Engineering Applications of Artificial Intelligence 2017, 62, 276–285. [Google Scholar] [CrossRef]
- Abdul-Adheem, W.; Ibraheem, I. Improved sliding mode nonlinear extended state observer based active disturbance rejection control for uncertain systems with unknown total disturbance. International Journal of Advanced Computer Science and Applications 2016, 7, 80–93. [Google Scholar]
- Han, J. The extended state observer of a class of uncertain systems. in Chinese, Control and Decision 1995, 10, 85–88. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, Y.; Han, J. An alternative paradigm for control system design. In Proceedings of the 40th Conference on Decision and Control; IEEE, 2001; Vol. 5, pp. 4578–4585. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.; Chen, X. Disturbance Observer-Based Control:Methods and Applications; CRC Press, Taylor & Francis Group, 2014; pp. 1–344.
- Han, J. From PID to active disturbance rejection control. 900 IEEE Transactions on Industrial Electronics 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gandhi, R.; Adhyaru, D. Novel approximation-based dynamical modelling and nonlinear control of electromagnetic levitation system. International Journal of Computational Systems Engineering 2018, 4, 224–237. [Google Scholar] [CrossRef]
- Ibraheem, I.; Abdul-Adeem, W. An Improved Active Disturbance Rejection Control for a Differential Drive Mobile Robot with Mismatched Disturbances and Uncertainties. In Proceedings of the IEEE; 2017; pp. 7–12. [Google Scholar]
- Freidovich, L.; Khalil, H. Performance recovery of feedback-linearization based designs. IEEE Transactions on Automatic Control 2008, 53, 2324–2334. [Google Scholar] [CrossRef]
- Han, H.; Chen, J.; Karimi, H.R. State and disturbance observers-based polynomial fuzzy controller. Information Sciences 2017, 382-383, 38–59. [Google Scholar] [CrossRef]
- Su, J.; Chen, W.; Li, B. High order disturbance observer design for linear and nonlinear systems. 2015 IEEE International Conference on Information and Automation, ICIA 2015 - In conjunction with 2015 IEEE International Conference on Automation and Logistics, 2015; 1893–1898. [Google Scholar] [CrossRef]
- Guo, B.; Zhao, Z. Active disturbance rejection control: Theoretical perspectives. Communications in Information and Systems 2016, 15, 361–421. [Google Scholar] [CrossRef]
- Gandhi, R.; Adhyaru, D. Modeling of current and voltage controlled electromagnetic levitation system based on novel approximation of coil inductance. In Proceedings of the 2018 4th International Conference on Control, Automation and Robotics (ICCAR); IEEE: Auckland, Newzealand; 2018; pp. 212–217. [Google Scholar] [CrossRef]
- Gandhi, R.; Adhyaru, D. Hybrid intelligent controller design for an unstable electromagnetic levitation system : a fuzzy interpolative controller approach. International Journal of Control and Automation 2019, 13, 735–754. [Google Scholar] [CrossRef]
- Gandhi, R.; Adhyaru, D. Feedback linearization based optimal controller design for electromagnetic levitation system. In Proceedings of the International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT); IEEE: Tamilnadu, India, 2016; pp. 38–43. [Google Scholar] [CrossRef]
- Gandhi, R.; Adhyaru, D. Fuzzy Tuner Based Modified Cascade Control for Electromagnetic Levitation System. In Proceedings of the 2019 Australian and New Zealand Control Conference (ANZCC 2019); 2019; pp. 1–6. [Google Scholar]
- E., J. Quanser magnetic levitation user manual. Technical report, Ontario, Canada, 2012.
- Zheng, Q.; Gao, L.Q.; Gao, Z. On Stability Analysis of Active Disturbance Rejection Control for Nonlinear Time-Varying Plants with Unknown Dynamics. In Proceedings of the 46th IEEE Conference on Decision and Control; 2007; pp. 3501–3506. [Google Scholar]
- Gandhi, R.; Adhyaru, D. Simplified Takagi-Sugeno fuzzy regulator design for stabilizing control of electromagnetic levitation system. In Proceedings of the Innovations in Infrastructure; Springer, Singapore: Ahmedabad, India, 2019; Vol. 757, pp. 1–11. [Google Scholar] [CrossRef]
- Michail, K.; Zolotas, A.; Goodall, R. Optimised sensor selection for control and fault tolerance of electromagnetic suspension systems: A robust loop shaping approach. ISA Transactions 2014, 53, 97–109. [Google Scholar] [CrossRef] [PubMed]
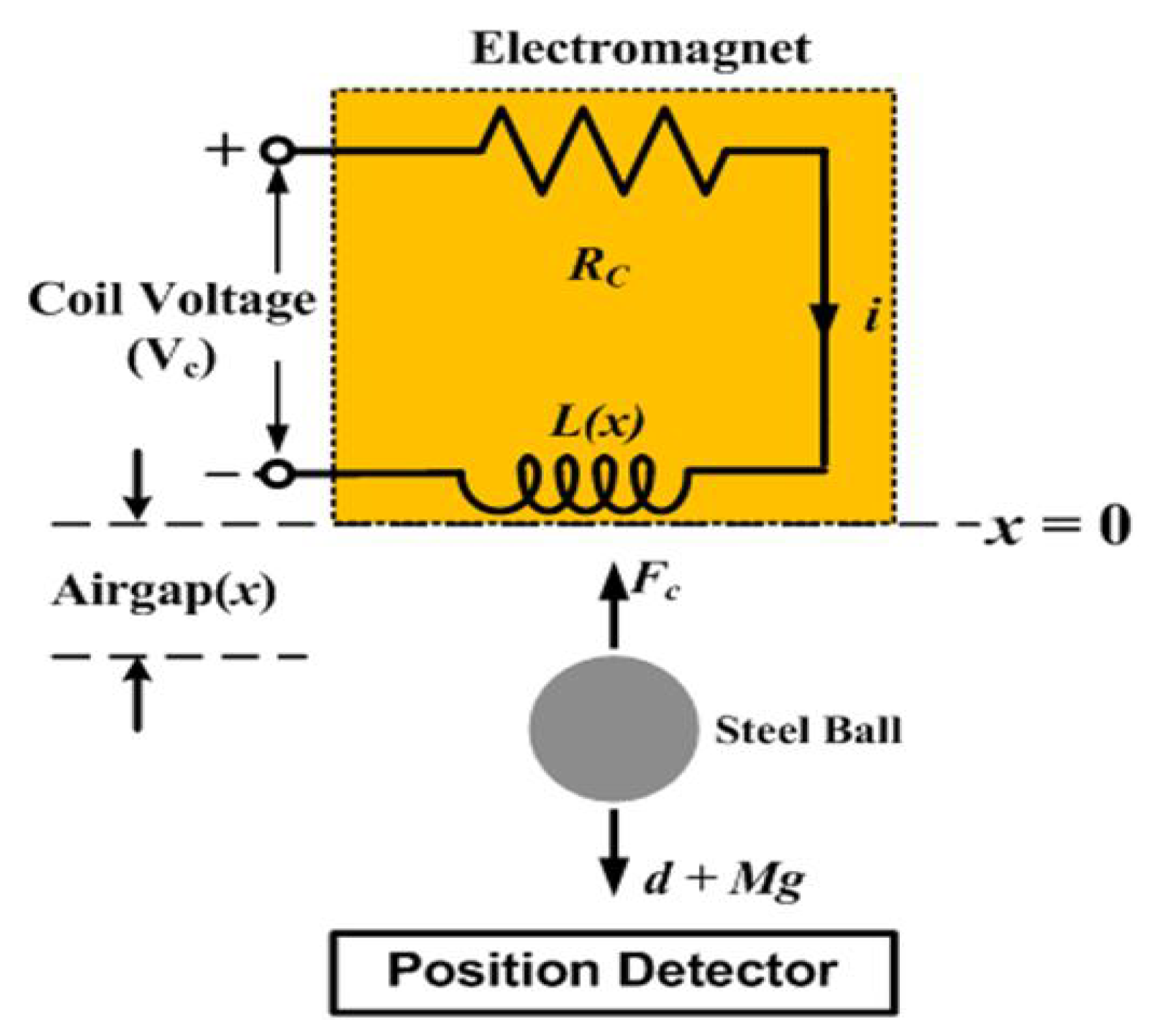
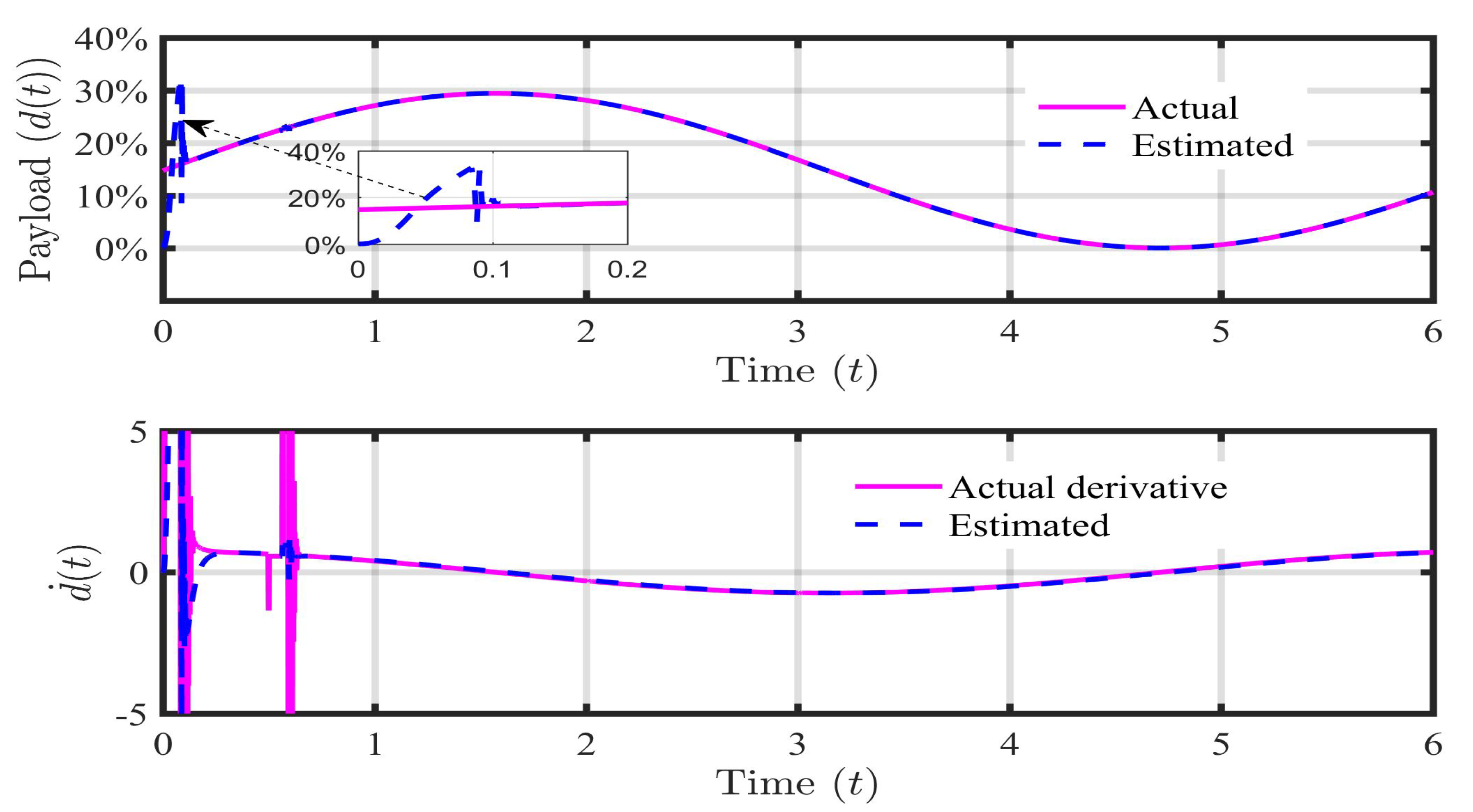

| Parameter | Description | Value |
|---|---|---|
| g | gravitational constant | 9.81 |
| electromagnetic constant | 6.5308 | |
| mass of steel ball | ||
| current sensor resistance | 1 | |
| coil resistance | 10 | |
| coil inductance | 0.4125 H |
| Control approach | ISE | ITAE |
|---|---|---|
| FLC | 3.608 | 0.8538 |
| LQR | 4.902 | 0.07994 |
| DESO-FLC | 1.991 | 0.006622 |
| Control approach | ISE | ITAE |
|---|---|---|
| FLC | 3.733 | 0.9386 |
| LQR | 9.345 | 0.1516 |
| DESO-FLC | 1.814 | 0.005375 |
| Title 1 | Title 2 | Title 3 |
|---|---|---|
| FLC | 4.178 | 0.9725 |
| LQR | 2.887 | 0.2527 |
| DESO-FLC | 1.773 | 0.005928 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





