SL(2, C) Scheme Processing of Singularities in Quantum Computing and Genetics

1. Introduction

In signal processing of a time series, the lines of the Fourier spectrum are described by discontinuities. The approach may be generalized with number theory by taking Ramanujan sums as the building blocks of the signal expansion, e.g., see [1].

A more ambitious approach is to use algebraic geometry to reveal the singularities of an object. In recent papers, we explored topics of quantum computing and DNA biology with a common algebraic geometrical tool that we now call $SL(2,\mathbb{C})$ scheme processing. The necessary ingredient is a finitely generated group $\pi$ expressing the symmetries of the investigated object. The $SL(2,\mathbb{C})$ character variety associated to $\pi$ is determined and summarized by its Groebner basis $\mathcal{G}$. The multivariate polynomials in $\mathcal{G}$ may contain isolated (or non-isolated) singularities that characterize the richness of the object. In this essay, the polynomials are reduced to surfaces living in the 3-dimensional projective space $P^3\left(\mathbb{Q}\right)$ over the rationals. In this way, we may use tools of schemes for the resolution of singularities [2] that are implemented in the software Magma [3].

Scheme theory was created by A. Grothendieck to generalize smooth manifolds to algebraic varieties possibly decorated with singularities. For our purpose, it is enough to see a scheme as a geometrical object defined by the vanishing of polynomials defined over an affine (or a projective space) like those living in $\mathcal{G}$.

In Section 2, we briefly describe the mathematical formalism used in our paper. It includes the definition of the character variety $\mathcal{V}$ representing the finitely generated group $\pi$ over the group $SL(2,\mathbb{C})$ and how a Groebner basis $\mathcal{G}$ is obtained from $\mathcal{V}$ in practice. The section mentions the distinction between simple singularities and singularities whose support is not zero dimensional. We then investigate the algebraic geometry of three types of complex objects in physics and biology. The first two objects rely on quantum computing following our previous papers [4,5]. Section 3 discusses the symmetries and related representations of the Akbulut cork W, a fundamental object in the theory of exotic 4-manifolds. Section 4 refers to the symmetries and the related representations of an hyperbolic 3-manifold found in the context of magic states in quantum computing. Section 5 investigates a third class of objects, which are a family of biological molecules called microRNAs that regulate the types and amounts of proteins [6]. In Section 6, we provide commentary on our results.

2. Theory

Details about the theory are described below. The corresponding implementation is available on the Magma software [3].

2.1. The $SL(2,\mathbb{C})$ Character Variety of a Finitely Generated Group and a Groebner Basis

Let $f_p$ be a finitely generated group, we describe the representations of $f_p$ in the (double cover alias the group extension of order two of the Lorentz group) $SL(2,\mathbb{C})$, the group of $(2\times 2)$ matrices with complex entries and determinant 1. The group $SL(2,\mathbb{C})$ may be seen simultaneously as a ‘space-time’ (a Lorentz group) and a ‘quantum’ (a spin) group.

Representations of $f_p$ in $SL(2,\mathbb{C})$ are homomorphisms $\rho :f_p\to SL(2,\mathbb{C})$ with character ${\kappa }_{\rho }\left(g\right)=\mathrm{tr}\left(\rho \left(g\right)\right)$, $g\in f_p$. The set of characters allows to define an algebraic set by taking the quotient of the set of representations $\rho$ by the group $SL(2,\mathbb{C})$, which acts by conjugation on representations [7].

Such an algebraic set is called the $SL(2,\mathbb{C})$ character variety of $f_p$. It is made of a sequence of multivariate polynomials called a scheme X. The vanishing of polynomials defines the ideal $\mathcal{I}\left(X\right)$ of the scheme X. A Groebner basis $\mathcal{G}\left(X\right)$ is a particular set of the polynomial ring $\mathcal{I}\left(X\right)$ that has to follow algorithmic rules (similar to the Euclidean division for univariate polynomials).

For the effective calculations of the character variety, we make use of a software on Sage [8]. We also need Magma [3] for the calculation of a Groebner basis, at least for 3- and 4-letter sequences.

2.2. Singularities of an Algebraic Surface

Simple Singularities

The surfaces S of interest in this case are said to be almost not singular in the sense that they have at worst simple singularities. In Magma, it is referred to a simple or A-D-E singularity if it is an isolated singularity on S which is analytically of the type $A_n$, $n\ge 1$,$D_n$, $n\ge 4$, $E_6$, $E_7$ or $E_8$.

The A-D-E type and the number of simple singularities is reflected in our notation. E. g., $S^{\left(l{A}_1\right)}$ means a surface with l singularities of type $A_1$, $S^{\left(A_2\right)}$ means a surface with a single singularity of type $A_2$ and $S^{\left(D_4\right)}$ means a surface with a single singularity of type $D_4$ . The Cayley cubic encountered in our previous paper is ${\kappa }_4^{\left(4A_1\right)}(x,y,z)=xyz+x^2+y^2+z^2-4$ [5]. The Fricke surface of type $D_4$ is $S^{\left(D_4\right)}=xyz+x^2+y^2+z^2-8(x+y+z)+28$ [9] (Figure 16). Many other examples can be found in [6].

The relevant Magma command for such simply singular surfaces is HasOnlySimpleSingularities(S).

2.3. Arbitrary Singularities

Let $X\in P^3\left(\mathbb{Q}\right)$ be a singular surface (a surface containing a non zero dimensional singular subset of points). Let $Y\in P^3\left(\mathbb{Q}\right)$ be a regular surface (devoid of singularities) above X that is, a representation (in a sense to be qualified) $\rho :Y\to X$. The set of such morphisms $\rho$ belongs to the so-called spectrum ${\mathrm{Spec}}_X\left(Y\right)$ of Y in X.

In our context, the formal desingularization of an (hyper)surface X in $P^3\left(\mathbb{Q}\right)$ is realized with a proper birational map $Y\to X$, with Y is regular. The formal desingularization is realized with the introduction of a formal prime divisor $\mathrm{Spec}\widehat{{\mathcal{O}}_{X,p}}\to X$, where $p\in X$ is a regular point of codomension 1, ${\mathcal{O}}_{X,p}$ is the structure sheaf at p of X seen as a scheme and the hat means the completion [10].

Taking the affine surface $S(x,y,z)$, the related homogeneous polynomial defines a hypersurface $X(x,y,z,w)\in P^3\left(\mathbb{Q}\right)$ so that a formal prime divisor is actually a morphism $\varphi :{\mathrm{Spec}}_{\varphi }\left[\left[t\right]\right]\to X$ defined by the $\mathbb{Q}$-algebra homomorphism ${\varphi }^{♯}:\mathbb{Q}([x,y,z,w]/<X>\to {\mathbb{F}}_{\varphi }\left[\left[t\right]\right]$ where ${\mathbb{F}}_{\varphi }=\mathbb{Q}\left(s\right)\left[\alpha \right]$, s a parameter and $\alpha$ is defined by the vanishing of a minimal polynomial.

The relevant Magma command for this case is FormallyResolveProjectiveHyperSurface(S: AdjComp := true). Thanks to the setting AdjComp := true, the command returns the number of essential singularities allowing to obtain the formal divisors needed to only compute birational invariants or adjoint spaces [10,11].

2.4. Kodaira-Enriques Classification

Given an ordinary projective surface S in the projective space $P^3$ over a number field, if S is birationally equivalent to a rational surface, the software Magma [3] determines the map to such a rational surface and returns its type within five categories. The returned type of S is $P^2$ for the projective plane, a quadric surface (for a degree 2 surface in $P^3$), a rational ruled surface, a conic bundle or a degree p Del Pezzo surface where $1\le p\le 9$.

A further classification may be obtained for S in $P^3$ if S has at most point singularities (unless the singularities may be formally resolved as we described in the previous subsection for the case of characteristic zero). Magma computes the type of S (or rather, the type of the non-singular projective surfaces in its birational equivalence class) according to the classification of Kodaira and Enriques [12]. The first returned value is the Kodaira dimension of S, which is $-\infty$, 0, 1 or 2. The second returned value further specifies the type within the Kodaira dimension $-\infty$ or 0 cases (and is irrelevant in the other two cases).

Kodaira dimension $-\infty$ corresponds to birationally ruled surfaces. The second return in this case is the irregularity $q\ge 0$ of S. So S is birationally equivalent to a ruled surface over a smooth curve of genus q and is a rational surface if and only if q is zero.

Kodaira dimension 0 corresponds to surfaces which are birationally equivalent to a $K_3$ surface, an Enriques surface, a torus or a bi-elliptic surface.

Every surface of Kodaira dimension 1 is an elliptic surface (or a quasi-elliptic surface in characteristics 2 or 3), but the converse is not true: an elliptic surface can have Kodaira dimension $-\infty$, 0 or 1.

Surfaces of Kodaira dimension 2 are algebraic surfaces of general type.

A Singular Surface

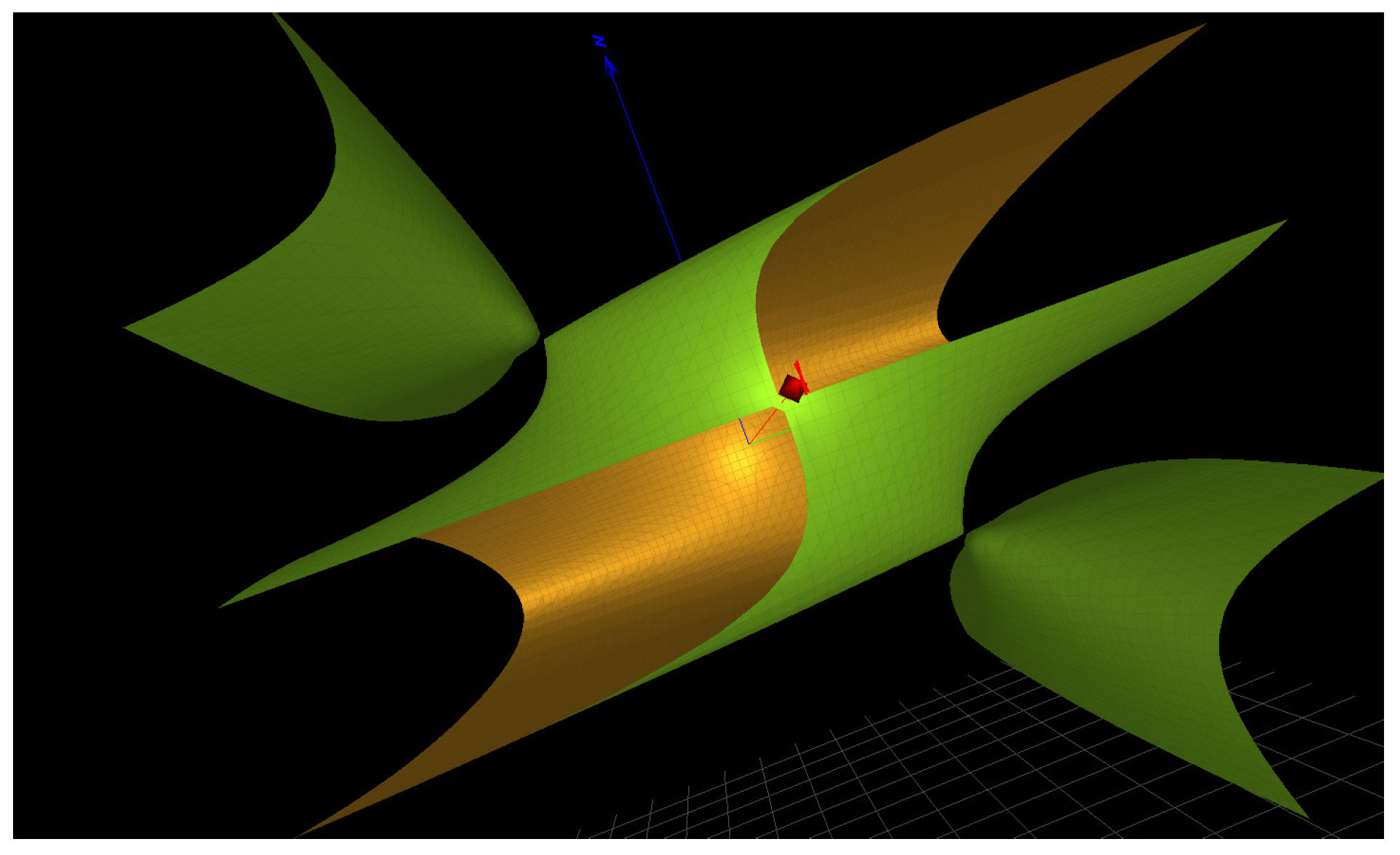
Let us illustrate our approach with a selected singular surface encountered in the context of the transcription factor Prdm1 in our recent paper [6] (Section 3.1). The affine surface under question is $S_2(x,y,z)=z^4+2y{z}^3+x^2-6yz-2x-8$. It contains 9 essential singularities in the desingularization. A 3-dimensional plot of $S_2(x,y,z)$ is in Figure 1. The surface is a conic bundle of $K_3$ type.

The projective surface is $S_2(x,y,z,w)=z^4+2y{z}^3+w^2(x^2-6yz)-2x{w}^3-8w^4$. There exists 5 distinct types of minimal polynomial. For one of the divisors, the minimal polynomial is ${\alpha }^2+2s+1$ and the prime divisor in the desingularization is the morphism $\varphi :{\mathrm{Spec}}_{\varphi }\left[\left[t\right]\right]\to X$ defined by

$$x\to 1,y\to st,z\to t,w\to \alpha t^2+0\left(t^4\right).$$

The 9 formal morphisms are used to compute the global sections (or adjoints) ${\mathrm{Hom}}_{i,j}$. For $i,j<3$, one obtains ${\mathrm{Hom}}_{1,1}={\mathrm{Hom}}_{2,1}={\mathrm{Hom}}_{2,2}={\mathrm{Hom}}_{2,3}={\mathrm{Hom}}_{3,1}={\mathrm{Hom}}_{3,2}={\mathrm{Hom}}_{3,3}=0$, ${\mathrm{Hom}}_{1,2}=[z,w]$, ${\mathrm{Hom}}_{1,3}=[xz,yz,z^2,xw,yw,zw,w^2]$.

3. $SL(2,\mathbb{C})$ Scheme Processing of an Akbulut Cork

This example belongs to the theory of 4-manifolds and was investigated by the authors in the context of magic states of quantum computing [4]. To our earlier work we add the investigation of $SL(2,\mathbb{C})$ character variety of the relevant fundamental groups. In particular, we put the central object of the exotic $R^4$ manifolds –the Akbulut cork– in a new perspective, by revealing its singularity spectrum.

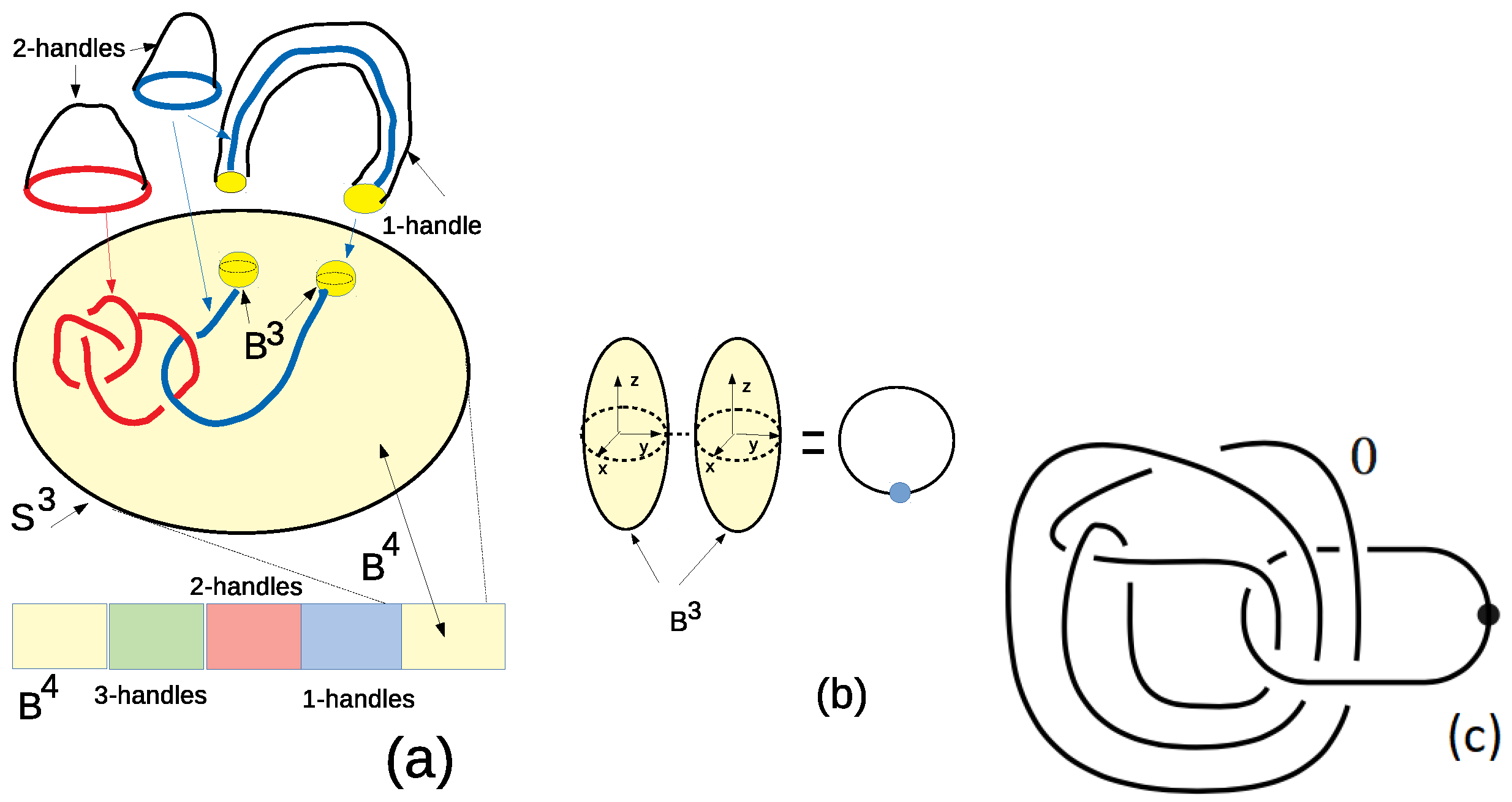
The theory of 4-manifolds is described in books [13,14,15]. Here we are interested in the decomposition of a 4-manifold into one- and two-dimensional handles as shown in Figure 2 [13] (Figure 1.1 and Figure 1.2). Let $B^n$ and $S^n$ be the n-dimensional ball and the n-dimensional sphere, respectively. An observer is placed at the boundary $\partial B^4=S^3$ of the 0-handle $B^4$ and watch the attaching regions of the 1- and 2-handles. The attaching region of 1-handle is a pair of balls $B^3$ (the yellow balls), and the attaching region of 2-handles is a framed knot (the red knotted circle) or a knot going over the 1-handle (shown in blue). For closed 4-manifolds, there is no need of visualizing a 3-handle since it can be directly attached to the 0-handle. The 1-handle can also be figured out as a dotted circle $S^1\times B^3$ obtained by squeezing together the two three-dimensional balls $B^3$ so that they become flat and close together [14] (p. 169) as shown in Figure 2b.

For the attaching region of a 2- and a 3-handle one needs to enrich our knowledge by introducing the concept of an Akbulut cork to be described in the next paragraph [4] (Figure 3).

3.1. Akbulut Cork

A Mazur manifold is a contractible, compact, smooth 4-manifold (with boundary) not diffeomorphic to the standard 4-ball $B^4$ [13]. Its boundary is a homology 3-sphere. If we restrict to Mazur manifolds that have a handle decomposition into a single 0-handle, a single 1-handle and a single 2-handle then the manifold has to be of the form of the dotted circle $S^1\times B^3$ (as in Figure 2b) (right) union a 2-handle. The simplest object of this type is the Akbulut cork shown in Figure 2c [16,17].

Given $p,q,r$ (with $p\le q\le r$), the Brieskorn 3-manifold $\mathsf{\Sigma }(p,q,r)$ is the intersection in the complex 3-space ${\mathbb{C}}^3$ of the 5-dimensional sphere $S^5$ with the surface of equation $z_1^p+z_2^q+z_3^r=0$. The smallest known Mazur manifold is the Akbulut cork W and its boundary is the Brieskorn homology sphere $\mathsf{\Sigma }(2,5,7)$. The Akbulut cork has a simple definition in terms of the framings $\pm 1$ of $(-3,3,-3)$ pretzel knot also called $K=9_{46}$ [18] (Figure 3). It has been shown that $\partial W=\mathsf{\Sigma }(2,5,7)=K(1,1)$ and $W=K(-1,1)$.

An exotic $R^4$ is a differentiable manifold that is homeomorphic but not diffeomorphic to the Euclidean space ${\mathbb{R}}^4$. An exotic $R^4$ is called small if it can be smoothly embedded as an open subset of the standard ${\mathbb{R}}^4$ and is called large otherwise. Here we are concerned with an example of a small exotic $R^4$.

According to [18], there exists an involution $f:\partial W\to \partial W$ that surgers the dotted 1-handle $S^1\times B^3$ to the 0-framed 2-handle $S^2\times B^2$ and back, in the interior of W. There exists a smooth contractible 4-manifold V with $\partial V=\partial W$, such that V is homeomorphic but not diffeomorphic to W relative to the boundary [16] (Theorem 1). This leads us to our next paragraph.

3.2. The Manifold $\overline{W}$ Mediating the Akbulut Cobordism between Exotic Manifolds V and W

A cobordism between two oriented m-manifolds M and N is any oriented $(m+1)$-manifold $W_0$ such that the boundary is $\partial W_0=\overline{M}\cup N$, where M appears with the reverse orientation. The cobordism $M\times [0,1]$ is called the trivial cobordism. Next, a cobordism $W_0$ between M and N is called an h-cobordism if $W_0$ is homotopically like the trivial cobordism. The h-cobordism due to S. Smale in 1960, states that if $M^m$ and $N^m$ are compact simply-connected oriented M-manifolds that are h-cobordant through the simply-connected $(m+1)$-manifold $W_0^{m+1}$, then M and N are diffeomorphic [15] (p. 29).

However this theorem fails in dimension 4. If M and N are cobordant 4-manifolds, then N can be obtained from M by cutting out a compact contractible submanifold W and gluing it back in by using an involution of $\partial W$.

The h-cobordism under question in our example may be described by attaching an algebraic cancelling pair of 2- and 3-handles to the interior of Akbulut cork W. The 4-manifold $\overline{W}$ mediating V and W resembles the Akbulut cork with the dot replaced by a 0-surgery The manifold under question is nothing but $L7a6(0,1)(0,1)$] (see [16] (p. 355) or [4] (Figure 3c)).

3.3. The Character Variety for an Akbulut Cork W

With Snappy, we find that the fundamental group ruling the Akbulut cork $W=9_{46}(-1,1)$ is the two-generator group

$${\pi }_1\left(W\right)=〈a,b|aBA{b}^{2}ABabaBABab,a^{3}BA{b}^{3}AB〉,A=a^{-1},B=b^{-1}.$$

(1)

With Sage software in Reference [8], we compute the corresponding character variety. Then, from Magma [3], the Groebner basis is found in the form

$$\begin{array}{cc}& {\mathcal{G}}_W(x,y,z)=z(z-2)[x+y+f_1\left(z\right)][y^2-y+f_2\left(z\right][y+f_3\left(z\right)]f_4\left(z\right),\\ & f_1\left(z\right)=-171/34z^8+913/34z^7-2429/34z^6+4733/34z^5-2443/17z^4\\ & -224/17z^3+1847/17z^2-1103/34z-1,\\ & f_2\left(z\right)=-95/34z^8+477/34z^7-1221/34z^6+2331/34z^5-1089/17\ast z^4\\ & -285/17z^3+858/17z^2-337/34z-1\\ & f_3\left(z\right)=-71/17z^7+376/17z^6-997/17z^5+1942/17z^4-1993/17z^3\\ & -188/17z^2+1477/17z-436/17,\\ & f_4\left(z\right)=z^7-5z^6+13z^5-25z^4+24z^3+4z^2-18z+5.\end{array}$$

(2)

The factor containing $f_1\left(z\right)$ in Equation (3) is the singular surface $S_W(x,y,z)$ shown in Figure 3. It is a rational scroll and a surface of a general type. The factor containing $f_2\left(z\right)$ is an hyperelliptic function of genus 7, discriminant $\approx 1.327502101$ and points at infinity $(1,0,0)$ and $(1,-95/34,0)$. The factor containing $f_3\left(z\right)$ is an ordinary curve. The factor containing $f_4\left(z\right)$ is a seventh-order polynomial.

Formal Desingularization of the Surface $S_W(x,y,z)$

The formal desingularization of a hypersurface X in the three-dimensional projective space ${\mathbb{P}}_{\mathbb{Q}}^3$ over the rationals $\mathbb{Q}$ is described in [10] and can be explicitely given with Magma [3] (Section 122.5.3).

To the surface $X=S_W(x,y,z)$ we associate the degree 8 homogeneous polynomial $S_W(x,y,z,w)=x+y+f_1(z,w)\in \mathbb{Q}(x,y,z,w)$ , with $f_1(z,w)=-171/34z^8+913/34w{z}^7+\cdots -1103/343w^{7}z-w^8$.

For the projective surface $X=S_W(x,y,z,w)$, the two essential (over the three) singular morphisms are

$$\begin{array}{cc}& x\to 1\\ & y\to st-1\\ & z\to t\\ & w\to \alpha t+O\left(t^8\right),\end{array}$$

(3)

$$\begin{array}{cc}& x\to 1\\ & y\to s\\ & z\to 34/171(s+1)t^7+O\left(t^8\right)\\ & w\to O\left(t^8\right),\end{array}$$

(4)

where $\alpha$ has minimal polynomial $-s-{\alpha }^8{f}_1\left({\alpha }^{-1}\right)$.

These formal morphisms are used to compute the global sections (or adjoints) ${\mathrm{Hom}}_{i,j}$.

For the surface $S_W(x,y,z)$ one gets

${\mathrm{Hom}}_{1,1}={\mathrm{Hom}}_{2,1}={\mathrm{Hom}}_{2,2}=0$, ${\mathrm{Hom}}_{1,2}=[z^6,z^{5}w,z^4{w}^2,z^3{w}^3,z^2{w}^4,z{w}^5,w^6]\cdots$

3.4. The Character Variety for the Mediating Manifold $\overline{W}$

The fundamental group ${\pi }_1\left(\overline{W}\right)$ of the h-cobordism $\overline{W}$ is as follows [4]

$${\pi }_1\left(\overline{W}\right)=〈a,b|a^3{b}^{2}A{B}^{3}A{b}^2,{\left(ab\right)}^{2}a{B}^{2}A{b}^{2}A{B}^2〉.$$

(5)

The cardinality structure of subgroups of this fundamental group is

$${\eta }_d\left[{\pi }_1\left(\overline{W}\right)\right]={\eta }_d\left[{\pi }_1\left(W\right)\right]=[1,0,0,0,1,1,2,0,0,\mathbf{1},0,\mathbf{5},4,\mathbf{9},\mathbf{7},1\cdots ],$$

where the bold digits refers to our investigation in [4] (Table 1) about the existence of a finite geometry obtained with a subgroup of the corresponding index. The smallest case occurs at index 10 and the geometry is the Mermin pentagram, a type of contextual geometry.

As before, with Sage software in Reference [8], we compute the corresponding character variety. Then, from Magma, the Groebner basis is found in the form

$$\begin{array}{cc}& {\mathcal{G}}_{\overline{W}}=(z-2)(z^2-z-1)[x+g_1\left(z\right)][y+g_2\left(z\right)]g_3\left(z\right),\\ & g_1\left(z\right)=-z^9+3z^8+5z^7-18z^6-10z^5+43z^4-2z^3-27z^2+3z+4,\\ & g_2\left(z\right)=-z^8+2z^7+6z^6-11z^5-15z^4+24z^3+9z^2-10z-2,\\ & g_3\left(z\right)=z^7+z^6-5z^5-6z^4+6z^3+5z^2-2z-1.\\ \hfill \end{array}$$

(6)

Although the card seq for manifolds W and $\overline{W}$ are the same, we clearly see that the character variety are distinct. In the later case, it contains two ordinary curves and polynomials of degree 1, 2 and 7.

4. $SL(2,\mathbb{C})$ Scheme Processing in Topological Quantum Computing

In this section, we are interested in the $SL(2,\mathbb{C})$ character variety of the fundamental group of (hyperbolic) 3-manifold L10n46 (alias otet${08}_{00002}$). This manifold describes the 4-fold (irregular) covering of the figure-eight knot $4_1=K4a1$ [19] (Table 2). It is connected to the magic state describing the contextual geometry of two-qubits (e.g., [19] (Figure 1) or [20] (Table 1)). The basic idea has been to put magic states and informationally complete POVMs under the same hat [21]. Thanks to the character variety and the related algebraic surfaces , we can add the topological aspect to the previous description.

The Groebner basis of the character variety for the fundamental group of 3-manifold L10n46 may be obtained with Magma. The 3-generator fundamental group is

$${\pi }_1\left(\mathrm{L}10\mathrm{n}46\right)=〈a,b,c|abAcBac,abbCBccBBBACbcbC〉.$$

(7)

The character variety ${\mathcal{G}}_{\mathrm{L}10\mathrm{n}46}(e,f,g,h)(x,y,z)$ is now seven-dimensional as in [6] and selected choices of parameters e, f, g and h allow us to determine the algebraic surfaces within the Groebner basis.

For instance, we find

$$\begin{array}{cc}& {\mathcal{G}}_{\mathrm{L}10\mathrm{n}46}(0,0,0,0)=y{S}_1(x,y,z)S_2(x,y,z)S_3(x,y,z)\cdots \\ & S_1(x,y,z)=f_{2,\left\{\right\}}^{\left(A_1\right)}(x,y,z)=xyz+x{z}^2+x^2+y^2+z^2+yz-x-6,\\ & S_2(x,y,z)=x{z}^2+yz-x-2,\\ & S_3(x,y,z)=-x^2{z}^2+2x^2+y^2+z^2+2x-4.\\ \hfill \end{array}$$

(8)

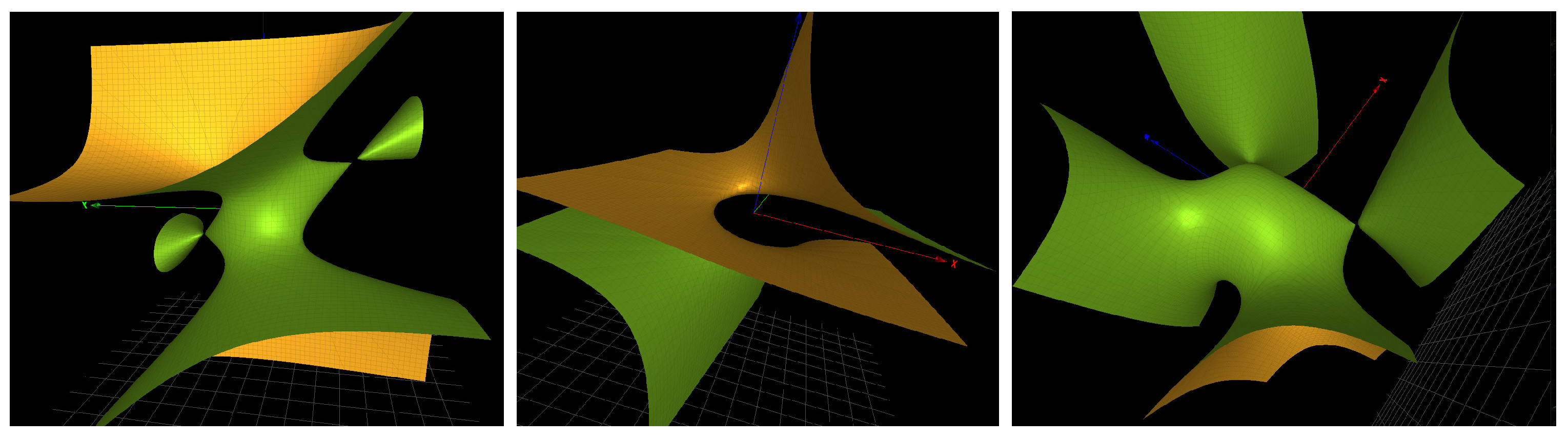
The first surface $S_1(x,y,z)=f_{2,\left\{\right\}}^{\left(A_1\right)}$ in the product (8) has a single simple singularity of type $A_1$ whose reduced singular subscheme is of degree 2 with a vanishing support.

The second surface $S_2(x,y,z)$ is a singular rational scroll with a single essential singularity. The corresponding singular morphism $\mathrm{Spec}{\mathbb{F}}_{\varphi }\left[\left[t\right]\right]\to X=S_2(x,y,z,w)$ is

$$\begin{array}{cc}& x\to 1\\ & y\to s\\ & z\to t\\ & w\to ((-2s^3-6s)/(s^2+4)\alpha +(-2s^2-4)/(s^2+4))\alpha t+O\left(t^3\right),\end{array}$$

(9)

where $\alpha$ has minimal polynomial ${\alpha }^2-s\alpha -1$.

The third surface $S_3(x,y,z)=-x^2{z}^2+2x^2+2x+y^2+z^2-4$ is a singular surface of the degree 4 del Pezzo type. There are 4 essential singularities. We retain one of the two singularities with a nontrivial minimal polynomial. The corresponding singular morphism $\mathrm{Spec}{\mathbb{F}}_{\varphi }\left[\left[t\right]\right]\to X=S_1(x,y,z,w)$ is

$$\begin{array}{cc}& x\to 1\\ & y\to s\\ & z\to t\\ & w\to \alpha t-1/(s^4+4s^2+4)t^2+(-1/2s^4+9/2)/(s^6+6s^4+12s^2+8)\alpha t^3)+O\left(t^5\right)\end{array}$$

(10)

where $\alpha$ has minimal polynomial ${\alpha }^2-1/(s^2+2)$.

All three affine surfaces are shown in Figure 4.

5. $SL(2,\mathbb{C})$ Scheme Processing in microRNAs

In this section, we focus on the $SL(2,\mathbb{C})$ character varieties attached to microRNAs (miRNAs for short). This case was already tackled in our recent paper [6].

The miRNAs are short (approximately 22 nt long) single-stranded RNA molecules playing a fundamental role in the expression and regulation of genes by targeting specific messenger RNAs (mRNAs) for degradation or translational repression. The genes encoding miRNAs are much longer than the processed mature miRNA molecule. There are pre-miRNAs comprising of approximately 70-nucleotides in length which are folded into imperfect stem-loop structures.

Each miRNA is synthesized as an miRNA duplex comprised of two strands (-5p and -3p). However, only one of the two strands becomes active, which is selectively incorporated into the RNA-induced silencing complex in a process known as miRNA strand selection [22,23]. For details about the miRNA sequences, we use the Mir database [24,25].

Disregulation of miRNAs may lead to a disease like cancer. A key microRNA known as an oncomir (involved in immunity and cancer) is mir-155 [6].

Here, we select examples of human miRNAs from the perspective of evolution. The generator of the group $\pi$ to be considered is a short (about 8-letter long) seed made of two to four distinct bases in the set {A,U,G,C}. Most of the time, $\pi$ is close to a free group of rank equal the number of distinct bases in the seed minus one. This point can be checked by the cardinality structure of conjugacy classes subgroups of $\pi$ (denoted card seq). Exceptions to this rule and the occurrence of singularities (isolated or not) in the corresponding character variety built from $\pi$, is a witness of a potential disease. Unlike the case of transcription factors, until now, singularities possibly found with microRNAs are isolated singularities.

According to Reference [26] (Table 3), the slowest evolving miRNA gene is hsa-mir-503 (the notation hsa is for the human specie). It is known that mir-503 regulates gene expression from different aspects of pathological processes of diseases, including carcinogenesis, angiogenesis, tissue fibrosis and oxidative stress [27]. The seed region for mir-503-5p is AGCAGCGG and the corresponding Groebner basis for parameters $(e,f,g,h)=(0,0,0,0)$ is very simple: ${\mathcal{G}}_{mir-503-5p}(0,0,0,0)={\kappa }_4^{\left(4A_1\right)}(x,y,z)$, as shown in Figure 5 (Left).

For $(e,f,g,h)=(1,1,0,0)$, ${\mathcal{G}}_{mir-503-5p}(1,1,0,0)=-3xyz{\kappa }_3(x,y,z)$, with ${\kappa }_3(x,y,z)$ is the Fricke surface found in [5] (Section 3.3). For $(e,f,g,h)=(1,1,1,1)$, there are many more polynomials. One of them defines the Fricke surface $xyz+x^2+y^2+z^2-2x-y-2$. The considered seed region for mir-503-3p is GGGUAUU. The surfaces in the Groebner basis are very simple in this case and not even simple singularities lie in them.

One of the fastest evolving microRNA is mir-214 [26] (Table 3). First mir-214 was reported to promote apoptosis in HeLa cells. Presently, mi-214 is implicated in an extensive range of conditions such as cardiovascular diseases, cancers, bone formation and cell differentiation [28]. For mir-214-5p and the seed sequence GCCUGU, one finds the surface $f_{1,\{1:0:0:0\}}^{\left(A2\right)}(x,y,z)=xyz+y^2+z^2-4$ within ${\mathcal{G}}_{mir-214-5p}(0,0,0,0)$, as shown in Figure 5. A surface of the same type $f_{1,\{1:0:0:0\}}^{\left(A2\right)}(x,y,z)=xyz+y^2+z^{2}y-2z-1$ is found in ${\mathcal{G}}_{mir-214-5p}(1,1,1,1)$. For a longer seed, surfaces are not found to contain singularities.

6. Conclusion

Over the last few years, the authors of this article have found that some mathematical techniques employed for quantum information processing and quantum computing may also apply to biology at the genome scale. More precisely, group theory and representations of symmetries with characters of finite groups have been used for topological quantum computing (TQC) [19] or elementary particles [29], and the the encoding of proteins [30]. Methods for dealing with infinite groups and $SL(2,\mathbb{C})$ representations of such groups in TQC papers [5,31] were similarly employed for transcription factors [6] and miRNAs [6].

Our efforts in this paper are belonging to the field of scheme processing, where the desingularization of discontinuities of algebraic surfaces is a spectrum. The scheme spectrum is a well known concept in commutative algebra. The prime spectrum of a ring is the set of prime ideals of the ring R and denoted by $\mathrm{Spec}\left(R\right)$. The sheaf of rings $\mathcal{O}$ is the relevant algebraic geometrical notion introduced by Grothendieck to develop this field [2,32]. We touched this important concept of schemes while investigating non-zero dimensional sets of singularities in surfaces belonging to the $SL(2,\mathbb{C})$ character variety of an infinite group. We are fortunate that the software Magma is designed to implement schemes in a variety of applications (curves, surfaces and more). Another computer algebra system with similar facilities is Singular [33].

We have no doubt that scheme theory will play and increasing role in our future efforts of relating quantum concepts and biology. In the future, this may be applicable to the field of ‘quantum consciousness’ [34].