1. Introduction
The analysis of the interior of the stars is fascinating to astrophysicists, mainly to the General theory of relativity (GR). For the fact that, about the late phase of stellar evolution, general relativistic effects much more important. In this direction, one of the incredible works was that of the Tolman [
1] solution (1939). Tolman extensively deliberated the stellar interior and gave us a explicit solutions for the static, spherically symmetric equilibrium fluid distribution [
2]. In different dimension, it has been tested in which include cosmology, gravitational waves, astrophysics and thermodynamics [
3] of the stellar system and it has present important contributions to the different astrophysics and cosmological issues. Many of them present collapsing of wormhole solution with static spherically symmetric geometry [
4] and non static spherically symmetric object with anisotropic fluid profile. Moraes and his co-authors [
5] studied modified Tolman-Oppenheimer-Volkoff (TOV) equation in which they illustrates the equilibrium conditions of the compact structures.
In the modifying form of gravitational action asks for lots of fundamental challenges. These models can show ghost-like behavior, instabilities, while on the other side, it has to match with experiments and observations in the low energy limit. Also in the framework of
gravity some interesting results have been found at solar system [
6], galactic and cosmological scales.
Several models exist which attempt to explain the early acceleration of the universe. The most accepted models contain a slowly varying potential and a scalar field. There are another class of models where the gravity is modified under the general relativity. One of the procedure of the modifications depended upon phenomenological considerations is provided by
theory of gravity. Indeed,
theories are conformally identical to Einstein’s theory plus a scalar degree of freedom classified the scalar in which potential is uniquely established from Ricci scalar. There are various model, in the literature, where the authors [
7] considered Einstein equation with corrections. The consistent theory of gravity, modified or classified, should be equally suitable to the strong gravity regime.
Here
is a analytic (general) function of
R (Ricci scalar). As an example, cosmological solutions gives the accelerated expansion of the universe at late times. Also it have been found that many stability conditions may lead to avoid tachyon and ghost solution. In addition, there exist viable
models satisfying both stability conditions [
8] and background cosmological constraints and results have been obtained to place constants on
cosmological model by cosmic microwave background radiation (CMBR) galaxy and anisotropic power spectrum [
9,
10]. To consider
gravity in low energy limit, it is viable to obtain accurate gravitational potentials capable of describing the flat rotational curves of the dynamics of galaxy or spiral galaxies clusters without considering large amount of dark matter [
11].
Numerous investigations [
12,
13,
14,
15,
16] have used different method to examined the stability as well as consistency of
gravity theory. There are definite form of
algebraic function which eliminated the existence of stable astrophysical form and reported unrealistic. In recent years, more research has been performed on the steadiness, dynamical unsteadiness, existence of celestial stellar system of this theory [
17,
18,
19]. Harko et.all [
20] proposed the concept of matter and curvature couplings to represent a new version of altered theory of gravity, namely
gravity. They also represented the relating field equation with the help of gravitational potential mechanism and showed the important of alternative gravity theory. Also the same authors have initiated various model for
algebraic functional for detachable compose viz.
=
+
. Houndjo [
21] investigated matter instructed age of accelerating cosmic by
gravity. Also, Baffou and his teammates [
22] examined spatially uniform cosmic in the field of
gravity.
Modified and extended models are always popular due to the potential of representation of gravitational field nature near curvature singularities accurately and as well to overcome the cosmological constant problems. Convincing confirmation for the extension of the universe has been provided by the many independent observations, some of these are supernovas Ia data [
23], cosmic microwave background radiation [
24] and baryon acoustic oscillation [
25] according to the study by the WMAP. For addressing this phenomenon, several assumption have been suggested from dark energy model to modified theories of gravity . Nowadays, dark energy model have no sufficient observational support. In particular, the dark energy idea requires an eqn. of state (EoS)
, where
represents spatially homogeneous pressure, energy density , respectively and the value of the parameter
is
. Several results have initiated for interior exact solutions of the Einstein field equation and Schwarzschild found the first interior solution. Tolman proposed an inventive method for treatment of the Einstein field equation which are known as Tolman I, II, III, IV, V, VI, VII and VIII [
26].
In this paper, we consider Tolman VI model [
27] in the class of modified gravity in which the gravitational action carries a general function
. For this model, the study of the background cosmological evolution can be simplified by performing transformation on metric. Such type of transformation maps from a frame where the resulting field equations and gravitational action are modified from general relativity (GR), called the Jordan frame, to a frame where the gravitational action for the new obtain metric is the Einstein-Hilbert one, called the Einstein frame. The
gravity theory has been related to stellar astrophysics [
28] and cosmology [
29], among other areas, giving testable and interesting results.
The present article deals with isotropic Tolman VI in modified gravity. The physical characteristics of our obtained model are studied for three compact stars PSR J1614-2230, Vela X-1 and 4U 1538-52. The paper is organized in following order of sections. Sec. II, we explain about the general formalism of gravity and in section III, the proposed model is obtained for different values of coupling parameter . At the boundary, we matched our interior space-time to the exterior space-time in section IV. Section V explains the physical properties between Einstein theory and gravity. Finally in section VI, we discuss and concludes the whole work by pointing on major findings.
2. Mathematics Behind f(R,T) Gravity
In this section we devote how the f(R,T) was introduced. The Ricci scalar is integrated over a four dimensional volume element
when Einstein’s field equation is derived from Einstein-Hilbert action as
If we replace the Ricci scalar R by f (R,T), We can get the f(R,T) field equations. Therefore, the complete action in f (R,T) formalism is
where,
T is the trace of the energy momentum tensor
. Also,
represents the Lagrangian matter dencity and
.
The energy momentum tensor is defined as
along with the trace
. Also the Lagrangian density
depends only the metric tensor component
, not its derivatives. Here, we have
By variation principle w.r.t
, Equation (
2) gives the field equation
where,
and
Here, covariant derivative
is associated with Levi-Civita connection of the metric tensor
and the box operation □ is defined as
with
The covariant derivative of the Equation (
5) gives
In
gravity, the stress-energy tensor of the matter field do not obey the conservation low due to interaction between the curvature and matter as in general relativity. With the help of the Equation (
3), we get the tensor
as follows
for the field equation, we assume the energy-momentum tensor as
provided, the
four velocity, such that
and
with
and
are matter density, radial pressure and transverse pressure, respectively. If we specify pressure as
, the Equation (
7) reduces to
3. Interior space-time and the realistic viable f(R,T) gravity models:
We will represent the model with the help of realistic f(R, T ) gravity model. Here, we consider a separable functional form of f(R, T ) given by,
in the relativistic structures to study the coupling effects of matter and curvature components in f(R, T ) gravity, where
and
representing arbitrary functions of R and T, respectively. Several viable model in f(R, T ) gravity can be generated in linear combining of different forms of
and
. In the present model, we assume
and
. Then the expression for
becomes
where,
is arbitrary constant to be evaluated depending on many physical requirements.
In curvature coordinate, we consider the static and spherically symmetric line element describing a wormhole region by the following metric:
where, both
depends on
r, i.e both are purely radial and
. In modified gravity, the field equation along the line element (
12) can be written as
where a prime (
′) denotes differentiation with respect to the radial coordinates ‘r’.
We denote
and
by,
where,
represents the density and
represents the pressure in Einstein gravity. To solve the Equations (
13)−(
15) we use the metric potential by Tolman [
1] in which the expression
where, A,B are arbitrary constant. The restriction of
is
, but this is not most general choice. Using the expression of the Equation (
13) and (
18), we obtain the Einstein density as
Similarly, using the expression of the Equations (
14), (
18) and (19), we obtain the Einstein pressure as follows
If we eliminate radius
r from (
20) and (
21), we obtain the relation between Einstein density and pressure. Also, the positivity of density profile demands the range for
n are
or
or
. So the interval of validity is
. Now, using the expression
and
from (
16) and (
21), we get the expression for matter density
and pressure
in modified
gravity as follows
where,
The square of the sound velocity for Einstein and our present model are obtained as follows
Negative sign in the sound speed index can be removed in the interval
. The profile of density and pressure are shown in
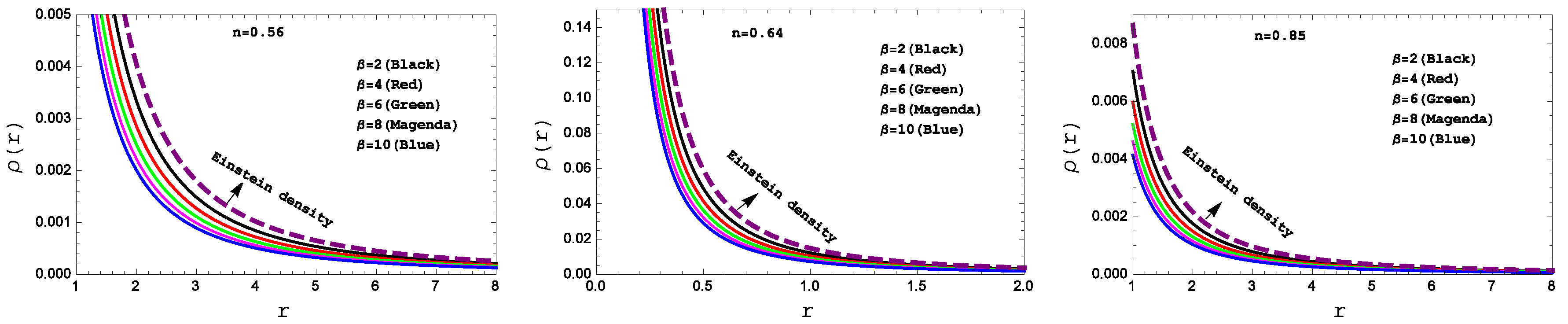
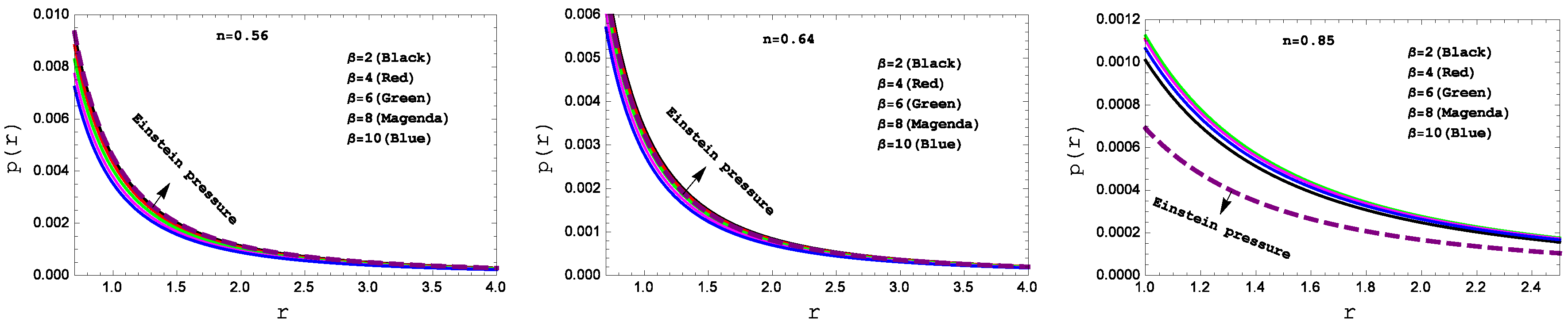
Figure 1 and
Figure 2, respectively. One can see that the density and pressure are both positive definite but at the stellar center both are infinite.
In the literature, it is well-known that the mass distributions must obey all the energy conditions in its interiors. These energy conditions are named as null, strong, week and dominant energy conditions and symbolized by NEC, SEC, WEC and DEC. All the energy conditions are satisfied for our present model if the following inequality are hold.
NEC:
, SEC:
,
, WEC:
,
, DEC:
,
.
It is clear from
Figure 3 that
, in the
Figure 4,
and
is non negative shown in the
Figure 5. So all the necessary energy conditions have been fulfilled for our
gravity model.
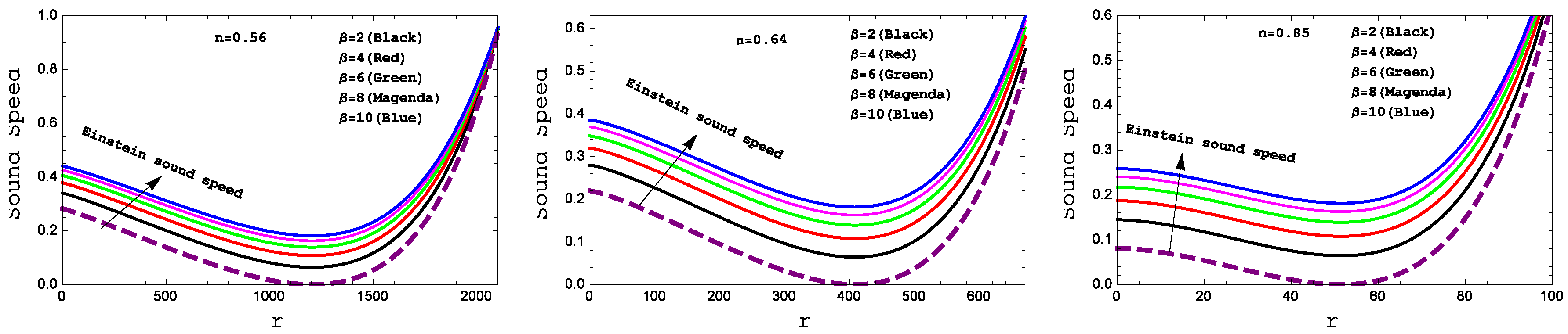
Figure 3.
Behavior of the “Speed sound” with respect to the radial coordinate “ r” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel)corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 3.
Behavior of the “Speed sound” with respect to the radial coordinate “ r” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel)corresponding to the numerical value of constants A and B from the table II and for different values of .
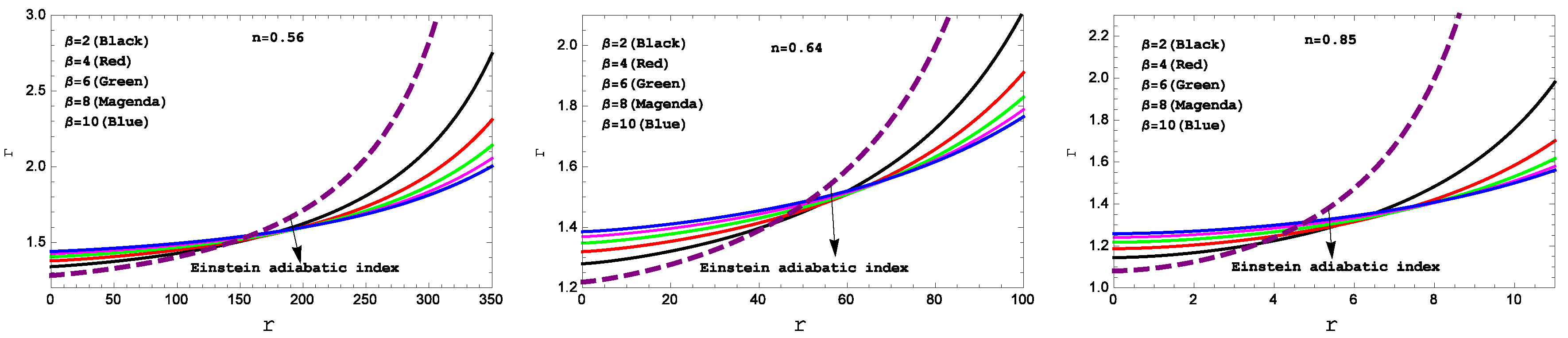
Figure 4.
Variation of “ adiabatic index” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel)corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 4.
Variation of “ adiabatic index” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel)corresponding to the numerical value of constants A and B from the table II and for different values of .
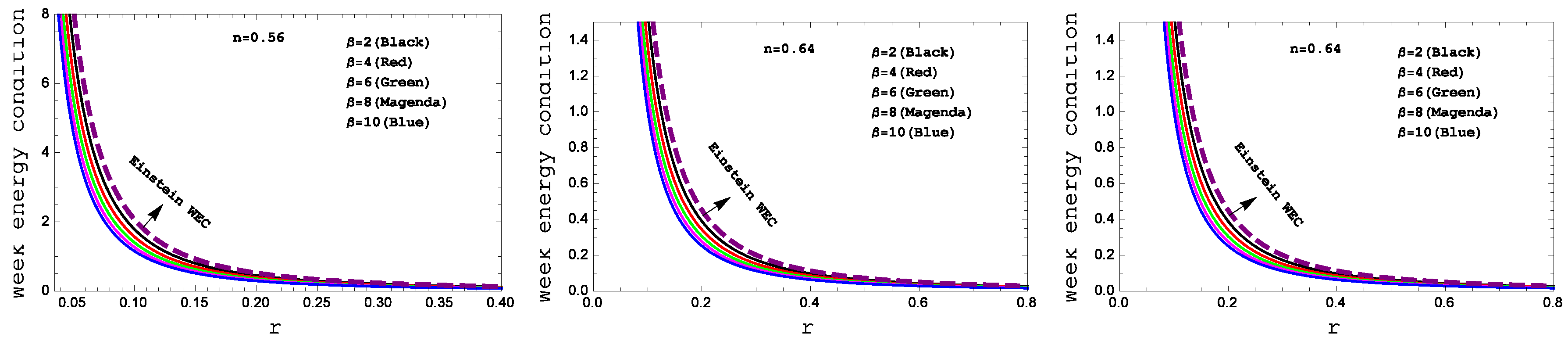
Figure 5.
Behavior of the “Week energy condition” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 5.
Behavior of the “Week energy condition” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
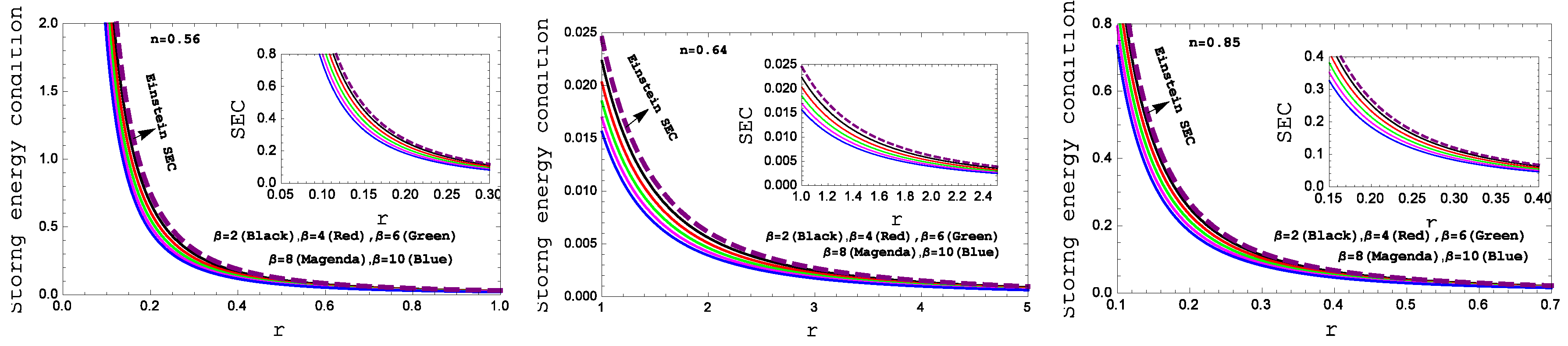
Figure 6.
Behavior of the “Strong energy condition” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 6.
Behavior of the “Strong energy condition” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
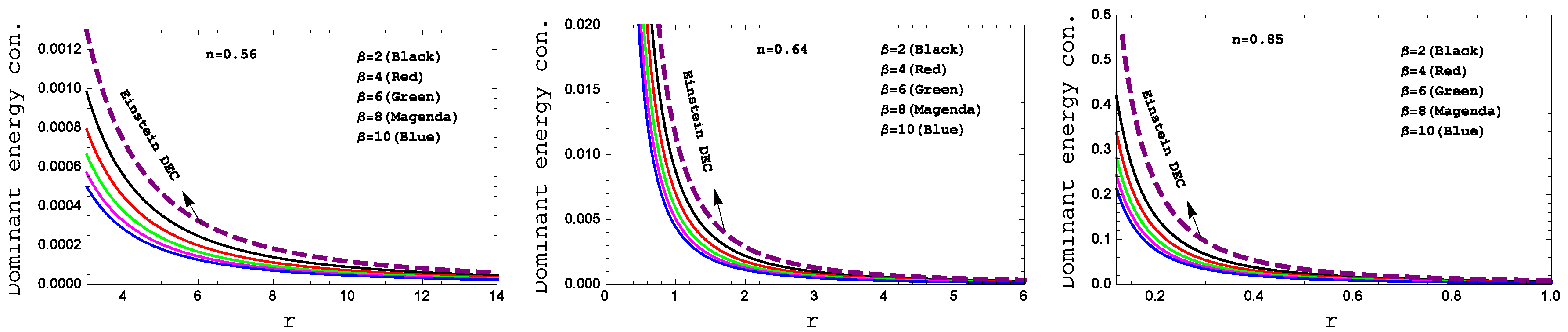
Figure 7.
Behavior of the “Dominant energy condition” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 7.
Behavior of the “Dominant energy condition” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
6. Discussion and concluding remarks
In this present work, we have investigated the behavior of Tolman VI spacetime in modified gravity. We endeavored to solve the modified field equations and investigated the physical viability according to the standard theory. We contrasted the behavior of the matter energy density, isotropic pressure, the sound speed energy, the all energy conditions (namely, weak, strong and dominated energy condition), EoS parameter, mass profile as well as gravitational redshift between the modified theory and standard Einstein theory.
For the arbitrary constant
and 10 the graphical picture have been presented in the
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10 for the compact stars
,
and
while,
gives the General relativity case.
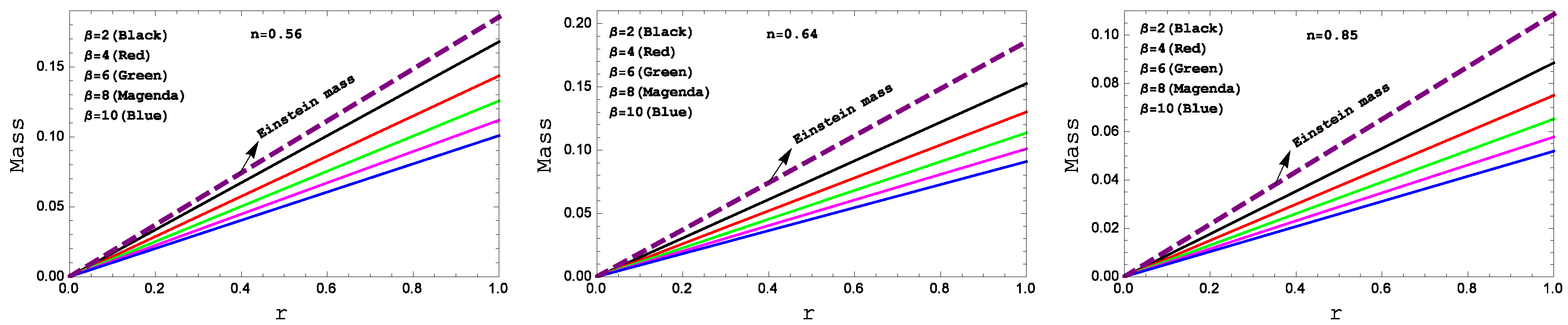
Figure 9.
Behavior of the “mass profile” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel)corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 9.
Behavior of the “mass profile” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel)corresponding to the numerical value of constants A and B from the table II and for different values of .
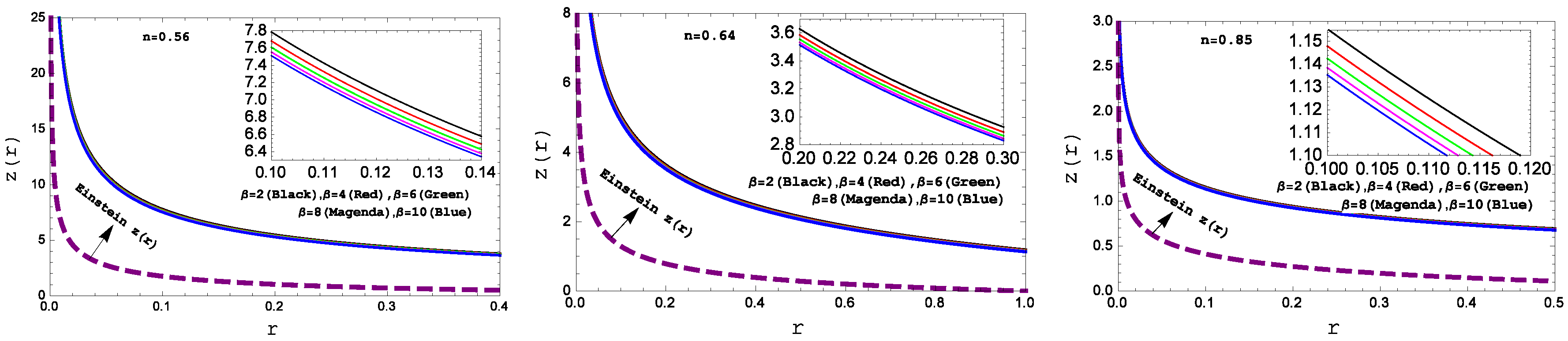
Figure 10.
Behavior of the “Gravitational red-shift” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
Figure 10.
Behavior of the “Gravitational red-shift” with respect to the radial coordinate “ r ” for the compact star PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) corresponding to the numerical value of constants A and B from the table II and for different values of .
A clear picture of energy progression has been obtained in
Figure 1. The figure shows declining nature about the surface and promises the real origination of stellar body with positive behavior at the stellar interior.
We have plotted pressure
p versus radius
r in
Figure 2 for the three compact stars PSR J1614-2230(left panel), Vela X-1(middle panel) and 4U 1538-52(right panel) for various values of
. One can see that
i.e positive, continuous and monotonically decreasing. Also, at some radial value, the pressure does vanish for both the cases.
Square of the sound speed and relativistic adiabatic index have been plotted in
Figure 3 and
Figure 4, respectively. From the
Figure 3, one can see that the square of the sound speed lies in the predicted range i.e.
throughout the fluid sphere. The
Figure 4 confirms the stability of under the adiabatic index
for our present model.
In our
gravity model, the weak energy condition (WEC) in
Figure 5, the strong energy condition (SEC) in
Figure 6 and dominant energy condition (DEC) in
Figure 7 are also met. For the complication in the expressions of density and pressure we have shown graphical presentation which certifies about the well behaved nature of the energy conditions.
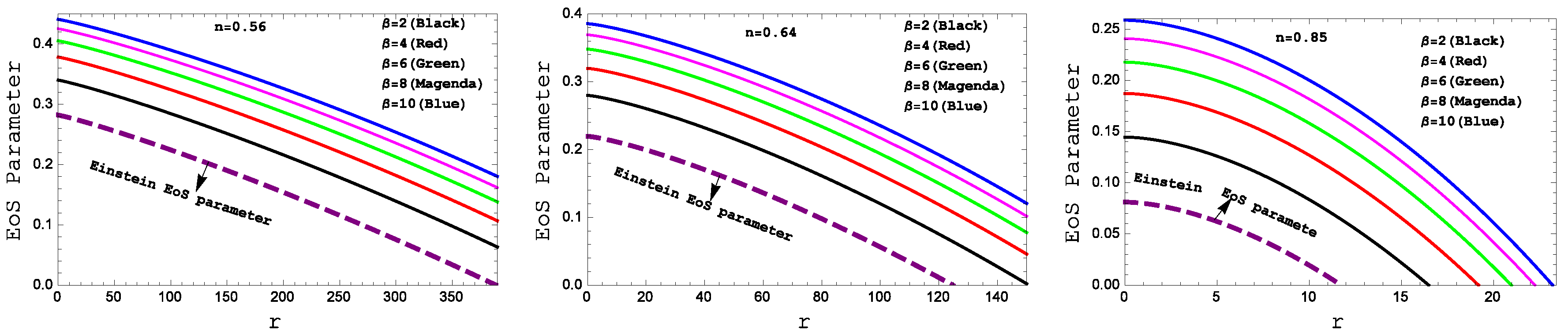
We have plotted equation of state parameter profile
in
Figure 8 for different values of
. It is clear from the figure that at the center of the star these parameter take maximum values while it decreases towards the boundary. Moreover,
lies between 0 to 1 i.e
which indicates the non-exotic behavior of matter distribution. Also, we can see that there are linear relation between isotropic pressure (p) and matter density (
).
The mass function is plotted against radius in
Figure 9. This figure shows that mass function is monotonic increasing function of radius and having no central singularity. The mass functional values are in agreement with required physical conditions as one can investigate from the figure.
We have plotted the Gravitational redshift in
Figure 10 for different values of
. One can see that Gravitational redshift is monotonic decreasing function of radius. Also, gravitational redshift is lower with higher values of coupling parameter
From all graphical illustrations and obtained results, we can conclude that our present model is regular and potentially stable. Also, detailed numerical features can be found from
Table 1 and
Table 2. The numerical values of A and B increases with increasing values of
. The surface density
, and surface red-shift
all takes lower values when coupling parameter
increases. Moreover, the central values of adiabatic index (
at
) increase with increasing values of
, which concludes that for higher values of
our model becomes more stable. Through analytical, numerical and graphical analysis, all the features of our present model are well described. Finally, we summarize our discussion that we are convinced by the calculated outcomes which shows that the system is physically reasonable and viably stable. Also, our outcomes could be useable in modeling relativistic compact objects as a real astrophysical phenomena.
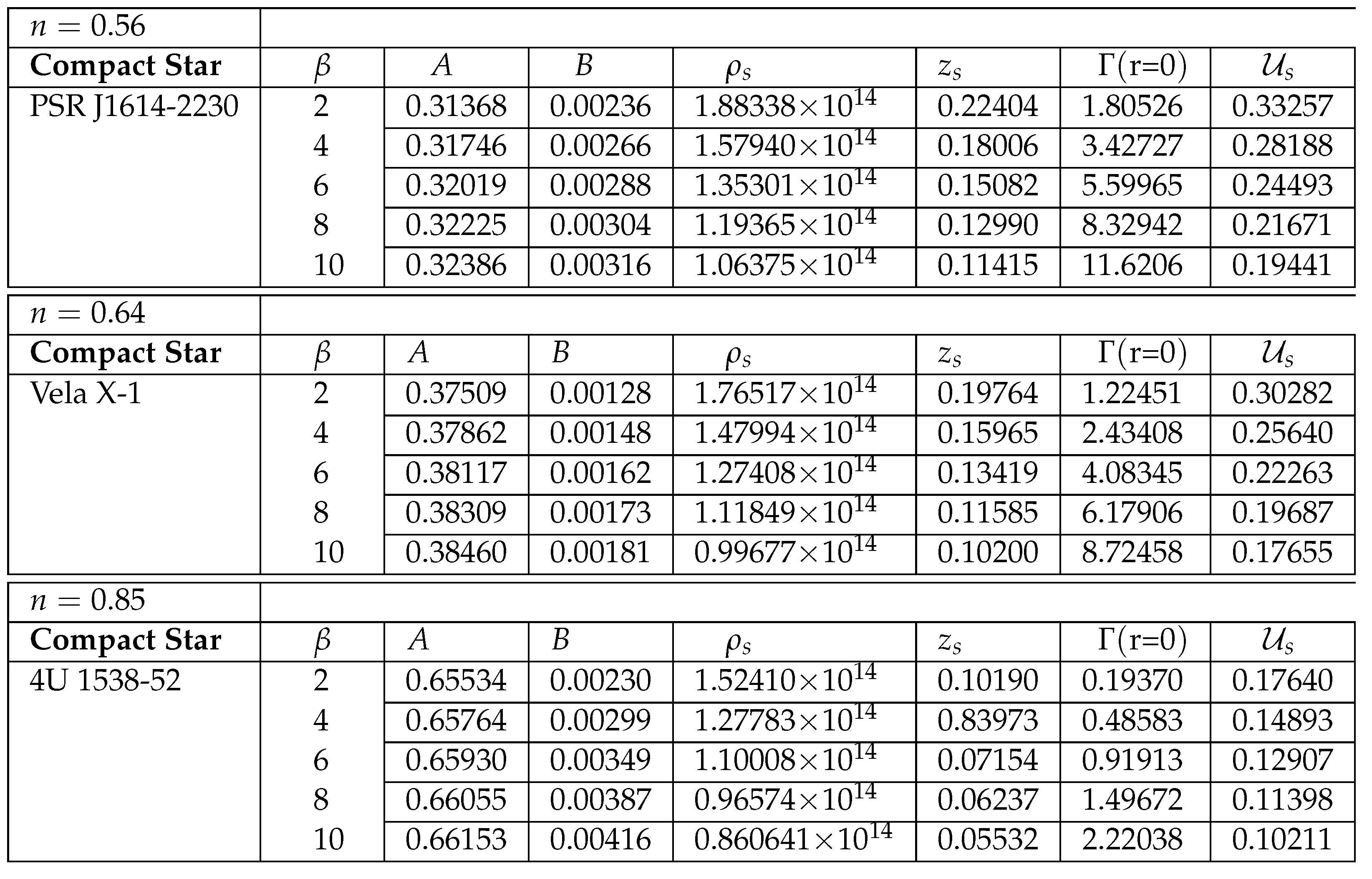
Table 1.
Numerical values of constants for three well-known celestial compact stars.
Table 1.
Numerical values of constants for three well-known celestial compact stars.
Table 2.
Numerical values of constants for three well-known celestial compact stars.
Table 2.
Numerical values of constants for three well-known celestial compact stars.