1. Introduction
Identification of systems with multiple nonlinearities studied in several papers. Parametric identification of nonlinearities [
1] based on the use of frequency response inversion based on insufficient data. Sinusoidal tests used to detect nonlinearity. The type nonlinearity determines based on the analysis of the restoring force function. The curve fitting method is the basis for estimating nonlinearity parameters. The function description method [
2] used for the parametric identification of a system with two nonlinear elements. An approach to parameters estimating of the transfer function of a second-order system suggests in [
3]. The system contains dry and quadratic friction. Harmonic linearization of nonlinearities performed beforehand. Parameter estimates define as the solution of an equations system.
Identification of nonlinear systems, especially with multiple local nonlinearities [
4] exhibiting disproportionate ratios of the degree of nonlinearity and present at a single or multiple spatial location, is a challenging inverse problem. Identification of such complex nonlinear systems cannot handle by the existing conventional restoring force or by describing function methods. Meta support vector machine approach [
4] uses for the identification of a spring mass system with several degrees of freedom. Systems identification with multiple nonlinearities considers in [
5]. The approach is based on the Hilbert–Huang transform. Application stages of this approach and the amplitude-frequency modulation procedure considered. In [
6], a nonlinear vibration system study with a known structure. Optimization method and recursive algorithm used to nonlinearity form select from a given class.
The second- and third-order system identification with dry friction nonlinearities connected in parallel studies in [
7]. The identification procedure base on application of the weighted least squares method. Identifiable conditions obtained and the parameters finding algorithm for a discrete nonlinear system [
8] with feedback proposed. Nonlinear mechanical vibrations study in [
9]. A gray box model or a model based on semi-physical principles applied. It assumed that observed nonlinearities localized in the physical space.
The system with two nonlinearities considers in [
10]. The structure one nonlinearity is a priori known. The second nonlinearity approximates by a time series. In [
11], the method presented to design mathematical models for the dynamic system on a set of local nonlinear attachments. Devices installed in the same primary construction. The identification method uses on the measurements processing, and the synthesis of the model based on physical laws. The closed system identification considered in [
12]. Frequency methods applied for estimation system. Convolution schemes use and the learning theory apply in [
13]. Voltaire and Taylor series use to design models. State space models and learning algorithms based on variational auto-coders used for nonlinear systems (NS) parameters identification [
14].
The review [
15] contains the methods analysis applied for the nonlinear process’s identification in the structure’s dynamics. Disadvantages of approaches based on linearization, harmonic balance, and the surface restoring force method note. Identification algorithms based on the Hilbert frequency transformation proposed in [
16]. The chaos theory used to identify bifurcation processes in [
17]. The systems Identification with feedback considered in [
18,
19]. The proposed approach is based on the transfer function analysis of the system. The approaches analysis of feedback systems (FS) identification consider in [
20]. The algorithm determining (AD) parameter estimates asymptotic bias in a nonlinear FS proposed in [
21]. AD based on the correlation analysis between the system input and the noise. Very often, the FS identification replaces by the open system parameters assessment [
22,
23]. A complex structure is the identification problem of nonlinear FS. A recursive identification procedure proposes in [
24]. The forward channel describes by an autoregressive model, and the reverse channel describes by a nonlinear model.
So, the review shows that most of the studies based on NS frequency identification methods. Estimating approaches to the nonlinearity structure proposing sometimes. Different procedures apply to linearization of the nonlinearity from a specified class. Approaches to NS linearization with feedback considered. The identification problem of systems with multiple nonlinearities is less studied. The complexity of such systems is the main difficulty for the identification. Identification approaches and methods of such systems base on localization of nonlinearity.
We propose an approach to adaptive identification of a system with multiple nonlinearities. This is a complex problem, and its solution boils down to: (i) the requirements formation on state variables for system parameters evaluation; (ii) conditions analysis guaranteeing the consideration system nonlinear properties (S-synchronizability); (iii) synthesis of an adaptive system. We give a solution to these problems.
2. Problem Statement
Consider the system
where
is the state vector,
is the state matrix,
,
is nonlinear vector-function,
is input (control) vector,
,
is output vector,
,
is perturbation vector (measurement errors),
is operator to obtain the vector
.
can be a differential operator.
Information set for
where
.
Assumption 1. Elements
,
are smooth, one-valued functions and belong to the class
where
is input of a nonlinear element.
The condition
may be met in some cases. We apply the model
for the parameters estimation of matrices
, where
,
,
are matrices with tuning parameters.
Problem: construct the model (5) for the system (1) based on the analysis
and assumption 1, and find the tuning laws
,
и
to
where
is the Euclidean norm.
We use the S-synchronizability concept of the system (1).
3. S-Synchronizability of System
S-synchronizability (SS) guarantees the structural identifiability for the system
. SS bases on the property’s analysis of geometric frameworks
[
26].
reflects system
nonlinear properties, and properties
depend on the parameters
. An unsuccessful choice of input can give to a so-called “insignificant” framework
[
25]. Therefore, the input (control) choice is the important problem in the identification systems design.
Let the framework
closed, and its area is not zero. Denote the
height as
, where height is the distance between two points on framework opposite sides. Then the framework
, and consequently, the system is identifiable or
-identifiable [
25] if:
- (i)
the input bounded, piecewise, continuous and constantly excited (see below);
- (ii)
exists such that .
Structural identifiability conditions of the system. Let is the domain , is diameter ; , where is acceptable inputs set for the system. The set contains representative inputs.
Definition 1. The input is S-synchronizing the system if the domain of the framework has a maximum diameter on the set .
Remark 1. We understand the system (1), (2) synchronization as the choice of such the input , which reflects all the features of the framework .
Consider a reference framework
.
is the structure
that reflects all the properties of the nonlinear function
. Let
be the diameter of the framework
.
exists for a system (1), (2) with an S-synchronizing input. If
, then
where
,
is a sign of closeness. Subset
elements have the property
Consider the framework . Denote the framework center on the set as , and the area center denote as . Let . Determine secants for fragments , where;, , , and are parameters .
Theorem 1 [
25]. Let the set
of synchronizing inputs for the system
obtain and (i)
exists such that
; (ii) the condition
is hold, where
are secant coefficients for fragments
,
. Then the system
is
-identifiable or structurally identifiable, and
.
4. On Excitation Constancy Condition
The condition excitation constant (EC) is important in parametric identification problems. If the system is nonlinear, then the EC condition may not be sufficient. The system must be S-synchronized as we consider the nonlinear properties of the system. The EC condition has the form.
Definition 2. Vector
constantly excited with level
or has property
if
for
and
at some interval
, where
is unity matrix.
The condition (9) has a different form
We use condition (9) next.
Assumption 2. The frequencies set correspond to when have expansion into the Fourier series.
Assumption 3. is the set of allowable input frequencies that ensure S-synchronizability of the system.
If
guarantees the system S-synchronizability by the variable
, then a vector
is representative and applicable for the adaptive identification. Assuming the
boundedness, we write the condition EC for
as
where
is some number.
5. Structural-Parametric Approach to System Identification
We propose a method for the system
identification based on the structural-parametric approach (SPA) [
27]. The SPA realization depends on a priori information. The system
has a complex form. Therefore, the adaptive algorithms synthesis is based on a priori information about the system structure.
Let the composition of subsystems included in be known. Knowing the output vector dimension the matrix can decompose into blocks (subsystem ). Perform the subsystems analysis and select subsystems that contain nonlinearities . Apply SPA to each element . If the subsystem does not contain nonlinearities, then apply the adaptive identification procedure.
Remark 2. The SPA based on the system S-synchronizability and the condition (9) fulfillment.
The SPA contains two procedures under uncertainty: (i) SF1 structural analysis, (ii) parametric (adaptive) identification. These stages describe in [
27].
Remark 3. The system’s structural identifiability (S-synchronizability) affects the connection of subsystems and the correlation of variables. The relationships analysis excludes influencing relationships and gives a solution to the system (nonlinearity) structural identifiability problem. The mutual influence diagram construction is possible only if the condition is true.
Remark 4. The system S-synchronizability evaluation is based on the framework
construction and analysis.
[
25,
26] reflects the nonlinearity structure of the corresponding subsystem
.
Remark 5. Obtained estimates of nonlinearities structure in are the basis for the adaptive parametric identification implementation.
Remark 6. We have information about nonlinearity. Therefore, the structural analysis stage for was not performed.
Remark 7. Structural identification and structural identifiability based on a single approach. Structural identifiability guarantees the solution of the structural identification problem for nonlinear systems.
6. Adaptive Identification of System
Consider the subsystem
,
,
is a linear operator in (2). Let the information set
be known for
.
-th order differential equation
corresponds to the equations system describing the subsystem
where
is state vector,
is the first element
;
,
and
are matrices of corresponding dimensions;
;
;
is degree
polynomial.
2 is a Hurwitz matrix.
Divide the left and right parts of (12) into a degree
polynomial
where
does not coincide with roots of the polynomial
. Then (12)
where
,
and
depend on subsystem parameters
and
, variables
satisfy the equation
Remark 8. The specificity and structure of the right part (15) define by the matrix and the polynomial .
The representation (15) allows us to estimate the parameters of
on a given set of
. Apply the adaptive model
where
;
,
,
are tuned parameters. The equation for identification error
where
,
,
,
.
Lyapunov function (LF) for the identification algorithms synthesis has the form
. Then
If
,
have the property
, then obtain from
where
,
,
are positive numbers ensuring algorithms convergence. Get algorithms to adjust model (17) parameters from (20)-(22)
So, the adaptive system for identification of subsystem parameters describe by the Equations (18) and (20)–(22). Denote it as .
Consider LF
where
is spur of matrix,
,
,
and
.
Let
and
Theorem 2. Let (i) functions
,
are positive definite and satisfy conditions
(ii)
is Hurwitz matrix; (iii) variables
,
have the property
. The all trajectories of the system
bounded belong to the domain
, and the estimate
is valid.
The Theorem 2 proof gives in Appendix A.
Let
where
,
is the sign of the matrices direct sum,
,
are minimum and maximum matrix
eigenvalues,
.
The exponential stability proof is based on ensuring the
-property for functions
,
[
29].
Definition 3 [
29]. A non-positive quadratic form
has the
-property or
if fair
for any
,
in some bounded domain
where
is the Euclidean norm of the vector
Y,
,
.
-property is the constructive completeness sign the quadratic form
. It reduces the
properties analysis to the characteristic’s evaluation of the
M-matrix [
30].
Lemma 1. has the
-property
if matrix
and
, where
are positive numbers,
.
The Lemma 1 proof gives in Appendix B.
Lemma 2. If Lemma 1 conditions satisfy, then
has the
-property
where
.
The Lemma 1 proof gives in Appendix C.
Consider the Lyapunov vector function
. Let functions
exist such that
Analysis of adaptive system properties (18), (20)–(22) based on the study of the inequalities system
Apply (31) and obtain a vector comparison system for (32)
where
,
is
M-matrix
The stability conditions for the
M-matrix
have the form [
30]
where
are diagonal minors of the matrix
.
These conditions have the form for
So, the following statement is true.
Theorem 3. Let (i) positive-definite Lyapunov functions
,
have the infinitesimal higher limit for , ; (ii) matrix and are piecewise continuous bounded and , ; (iii) the equality
is fair in area
, where
,
,
is null matrix,
is some neighborhood of the point
,
; (iv) Lemma 1, 2 conditions satisfied for
and
; (v) the estimate (26) fair for function
; (vi) the inequalities system (32) is valid for
,
; (vii) the upper solution for
satisfies equation (33) if inequality (31) is true for elements
. Then the adaptive system (18), (20)–(22) is exponentially stable with the estimate
if conditions (34) held.
Theorem 3 shows if the information matrix is constantly excited, then the adaptive system (18), (20)–(22) guarantees consistent parameters estimates for system . This statement is valid if (34) is fulfilled.
Remark 9. The EC condition () is the base for the stability proof of the adaptive system. EC indirectly consider when applying the Lyapunov function. The approach proposed above ensures the -property for the Lyapunov function. It bases on consideration the condition . The Lyapunov function analysis considers features of adaptive algorithms when the condition applies.
7. Nonlinear Correction of Nonlinear System
The system contains an amplifier with an electric motor and
a relay control described by a function
f1(u)
The correcting device is a nonlinear velocity feedback with a parabolic
characteristic
f2(x2)
where
is control,
is input,
.
Equation (13) and polynomials in (13), (14) have the form
where
,
are positive numbers that do not coincide with the roots of the equation
.
Adaptive model and algorithms for estimating system parameters (42), (43)
where
,
. Equation for error
where
,
,
.
Denote
. The vector tuning law follows from (35)
where
,
.
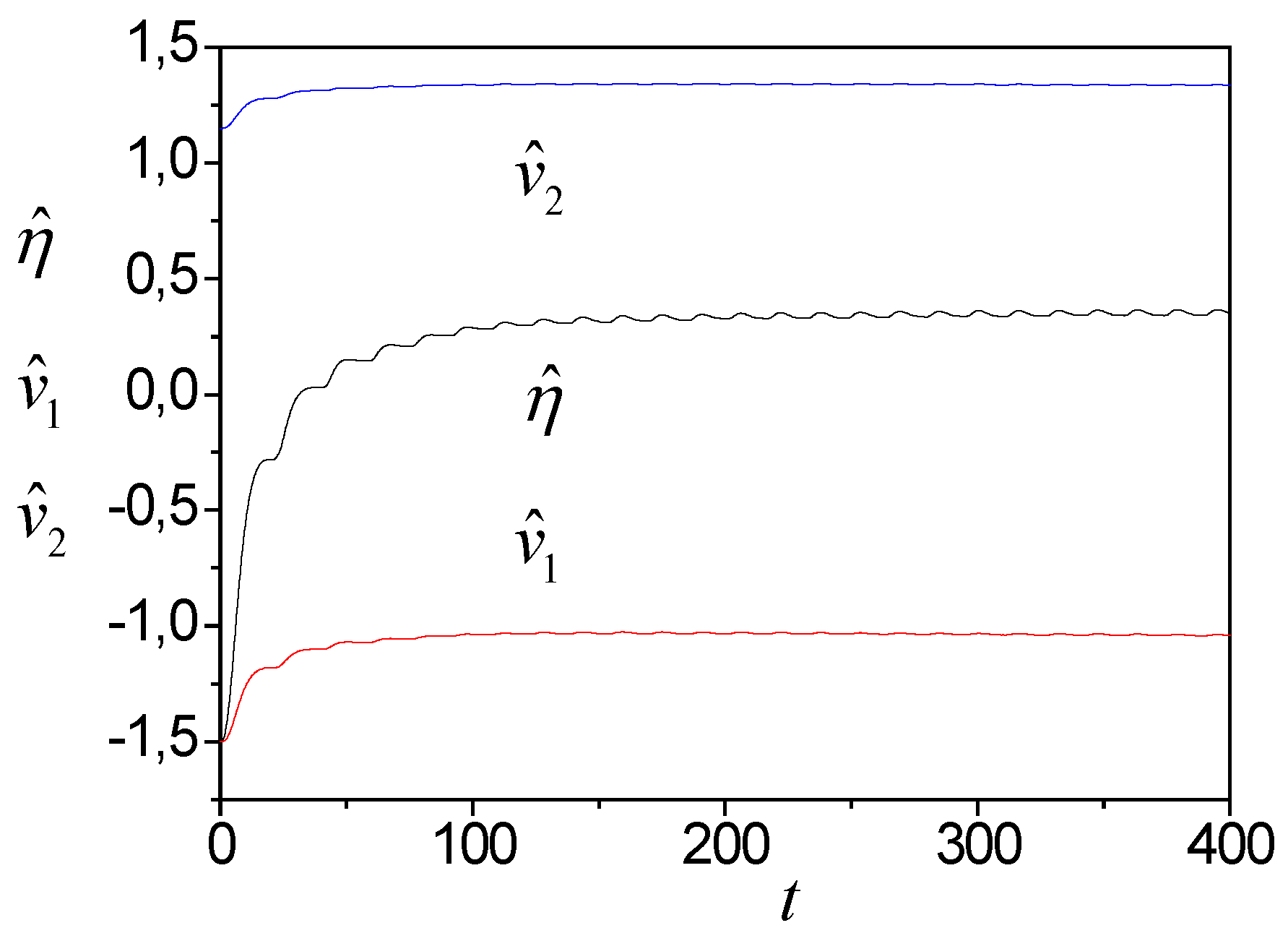
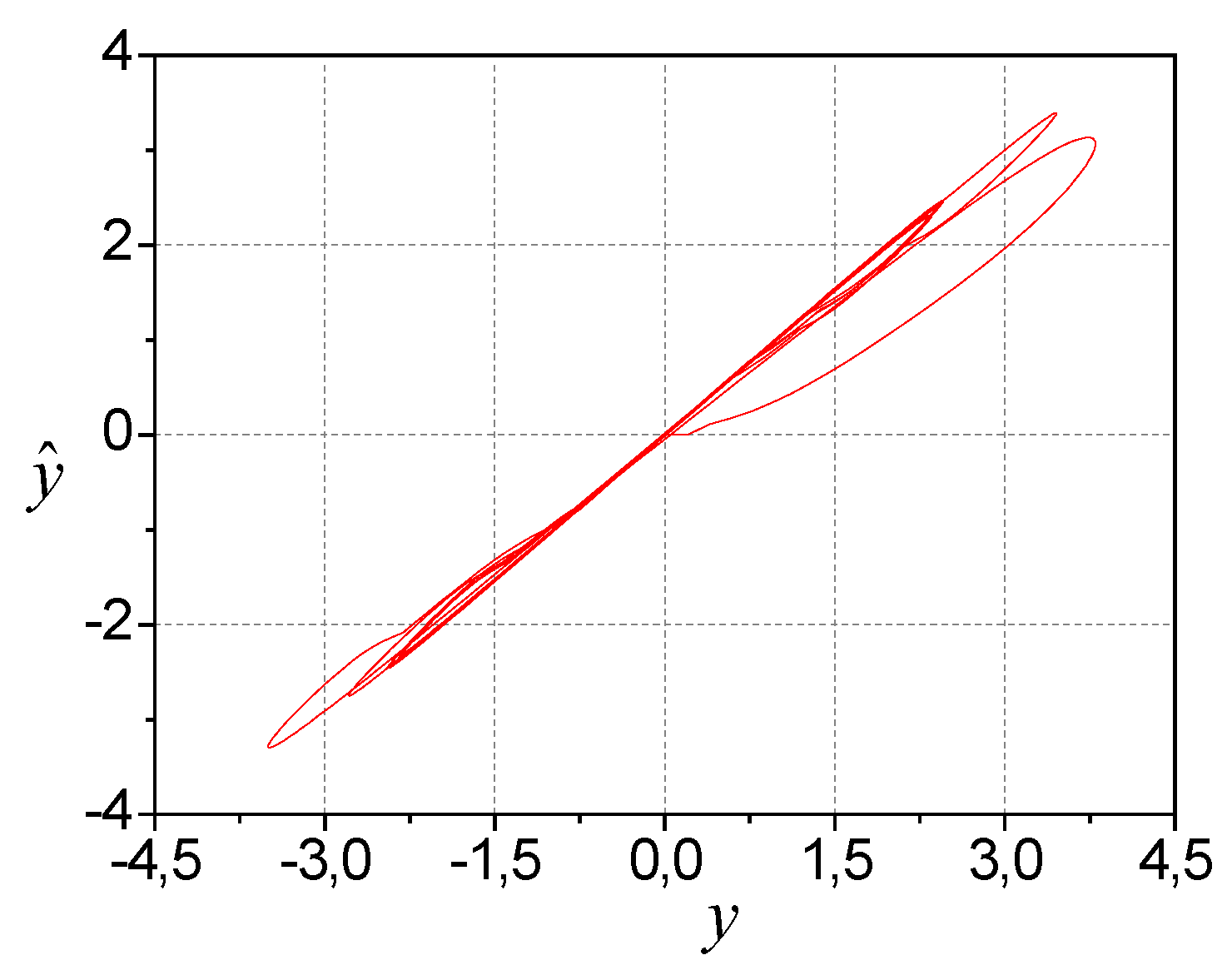
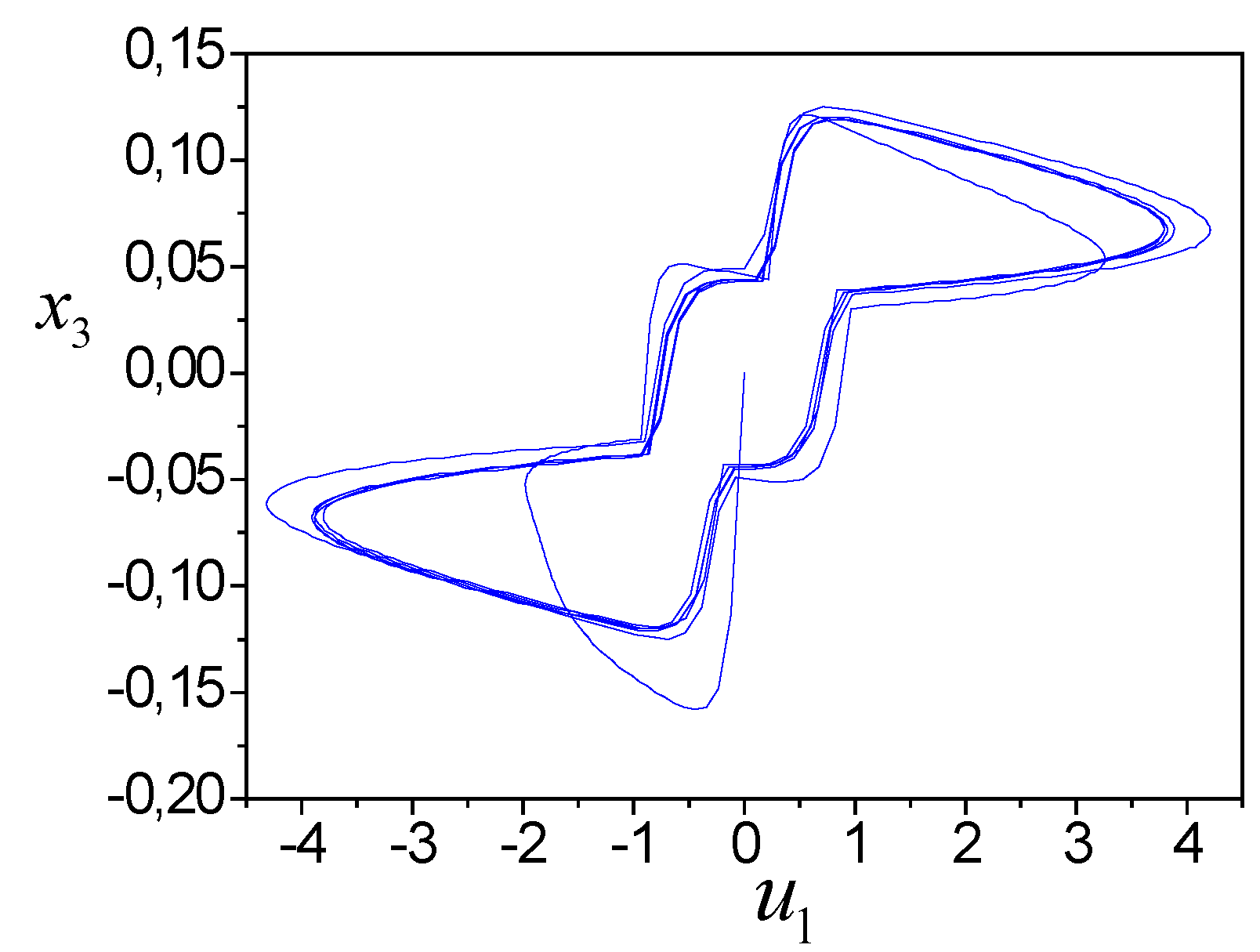
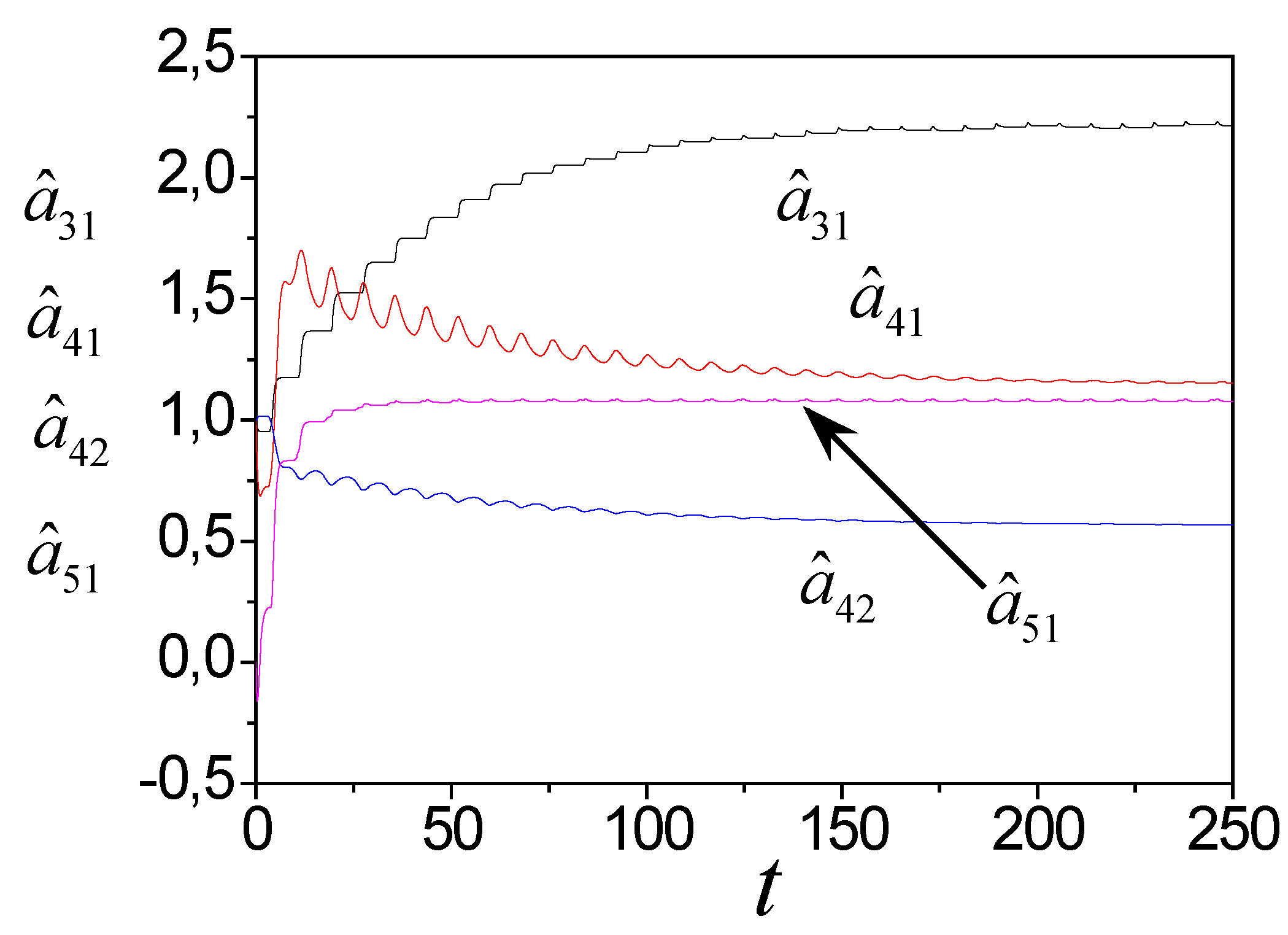
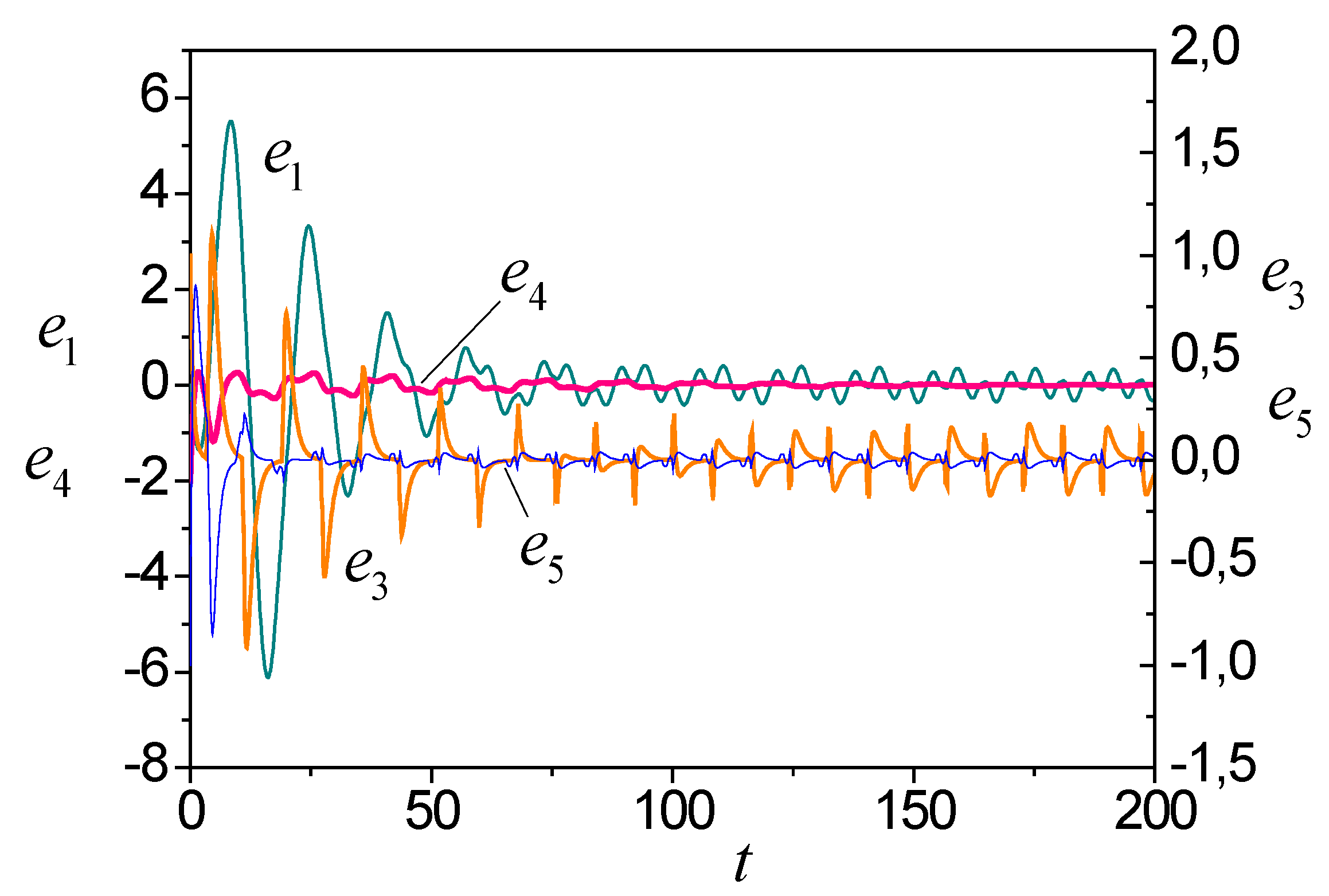
The system (44), and (46) trajectories boundedness follows from Theorem 2. The simulation results show in
Figure 1,
Figure 2,
Figure 3 and
Figure 4. Present the model (44) parameter tuning in
Figure 1 and
Figure 2.
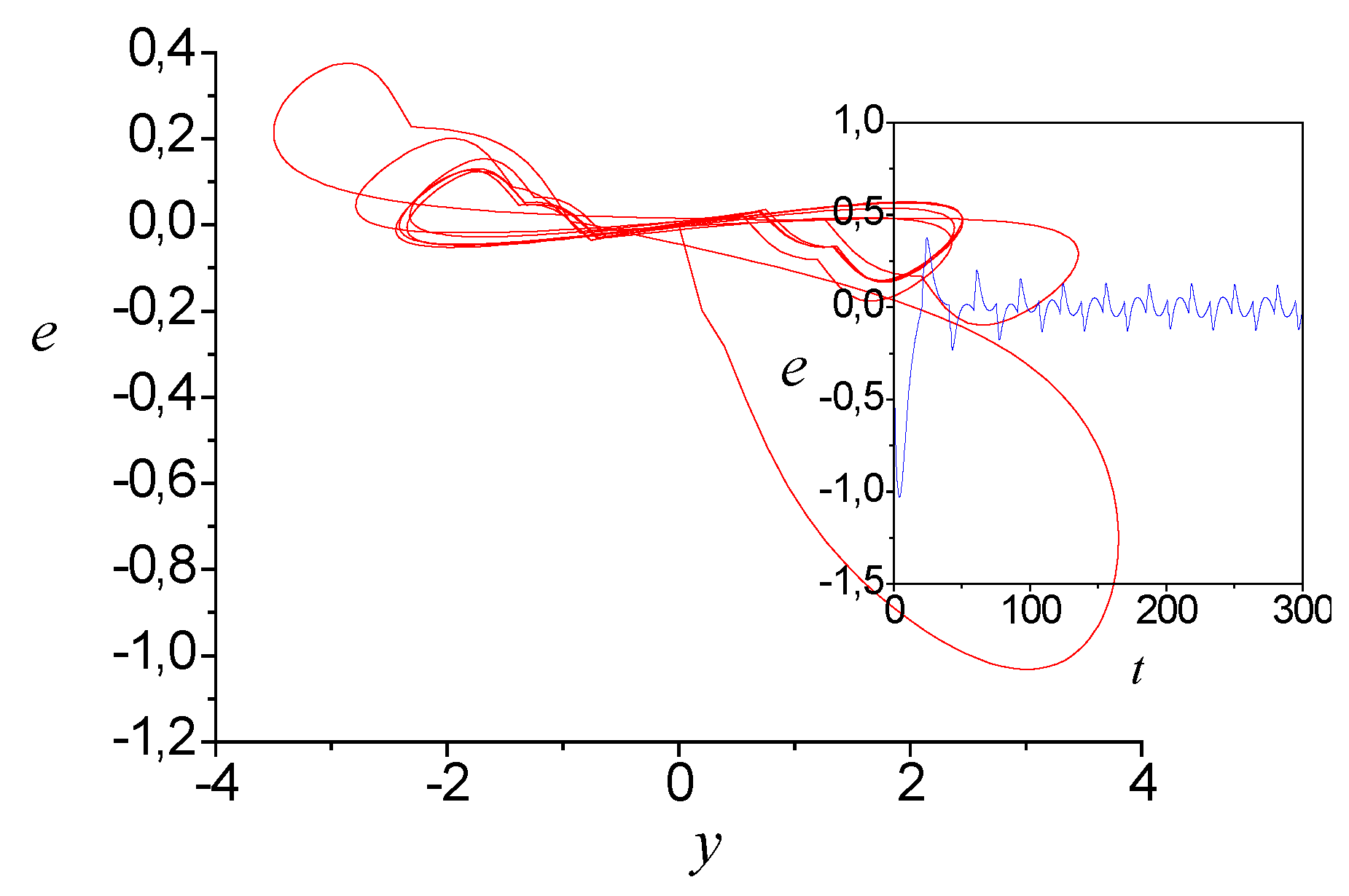
Figure 3 reflects the change in the estimation error. The output form determines the error change.
Figure 3 shows also the change in
depending on the dynamics of the system output (36). The model adequacy in the output space demonstrates in
Figure 4.
Note [
32] that the system (36), (37) is unidentifiable by the function F2 on the measurements set. In this case, we can use indirect information about the dependence of
on
. It is true since the relationship between
and
.
Consider the case when the structure of nonlinearity is a priori unknown. Use the relationship diagram (RD) [
28] for system (36). The relationship between
and
is significant. Therefore, consider the framework
described by the function
(
Figure 5).
belongs to the relay functions class with a dead zone. Replacing
with
changes the boundaries of the dead zone. This problem solves in the identification process. Construct the framework
described by the mapping
(the structure
coincides with
), and the secant
where
. Coefficient of determination is
. It indicates the presence of nonlinear properties.
Determine the discrepancy . It contains information about the function . Construction and approximate the curve on the interval . Obtain a model with a quadratic structure. The model structure coincides with . So, we have performed a structural identification of the system (36).
.
8. Self-Oscillation Generation System
The self-oscillation system contains (i) a control object (variables
), (ii) nonlinear (variable
) and linear (variable
) converters, (iii) an amplifier-converter with a nonlinear actuator (variable
)
where
is time constant,
,
is input.
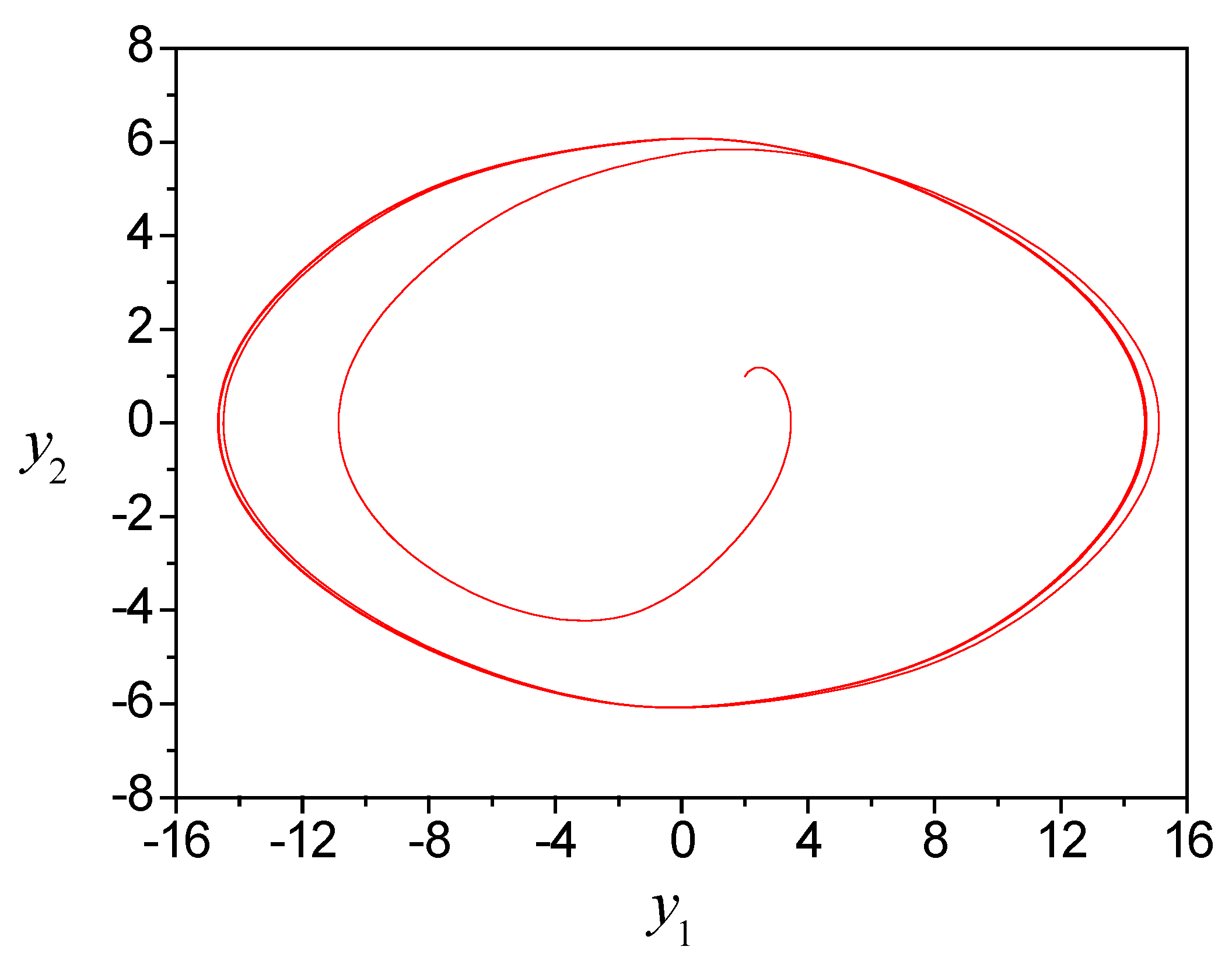
(
) is a saturation function with a dead zone
The object phase portrait shows in
Figure 6. It shows self-oscillations in the system. We transform the first two equations of the system (48) using the approach from
Section 6. Present these equations as (38) and divide (38) by
. Transform variables
and obtain the identification form
The adaptive system for evaluating system (51) parameters has the form
where
,
.
Consider the Lyapunov functions
and get adaptive algorithms for tuning system parameters (52)
where
.
Apply Theorem 2 and get the boundedness of trajectories in an adaptive system
where
.
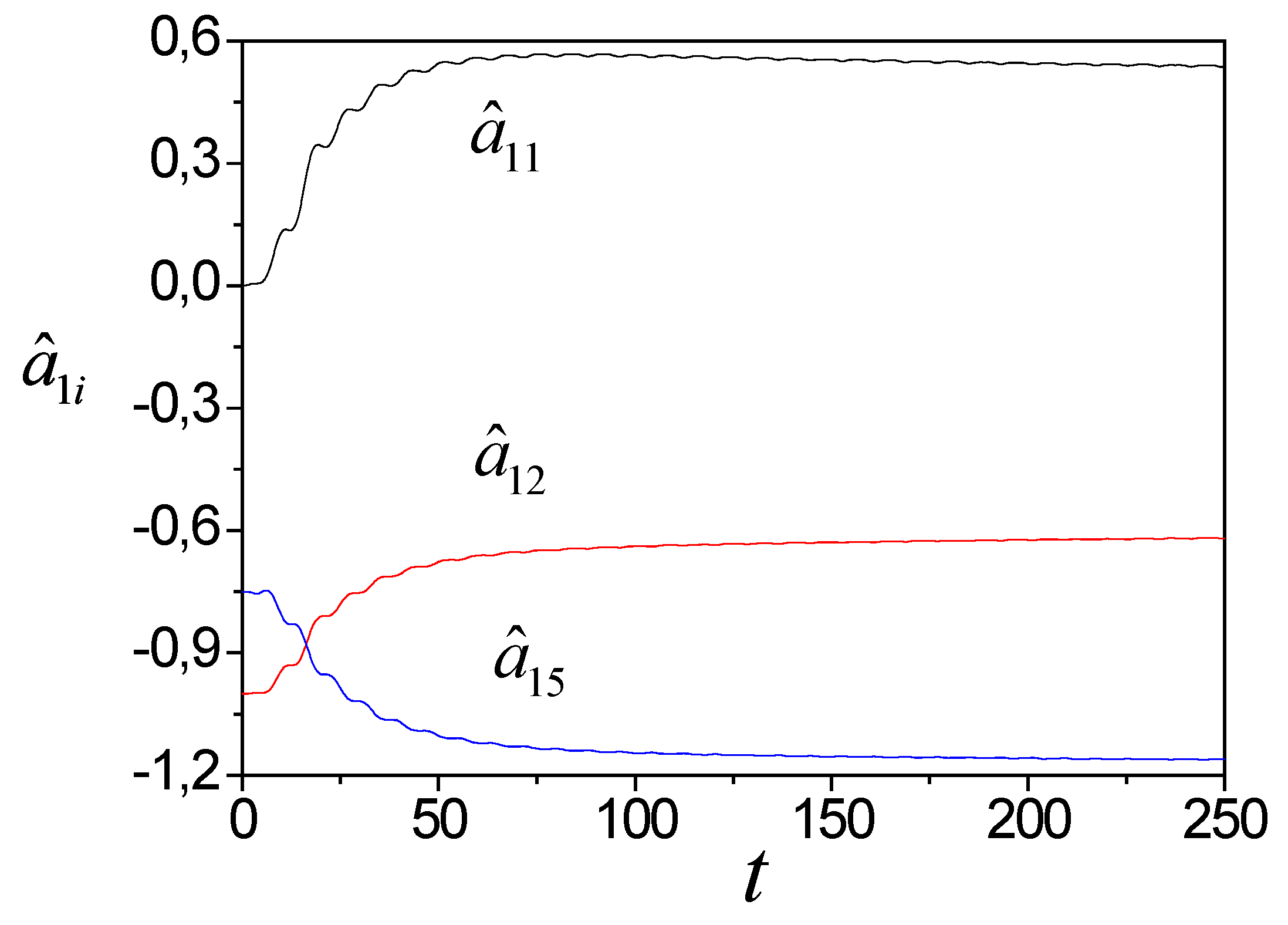
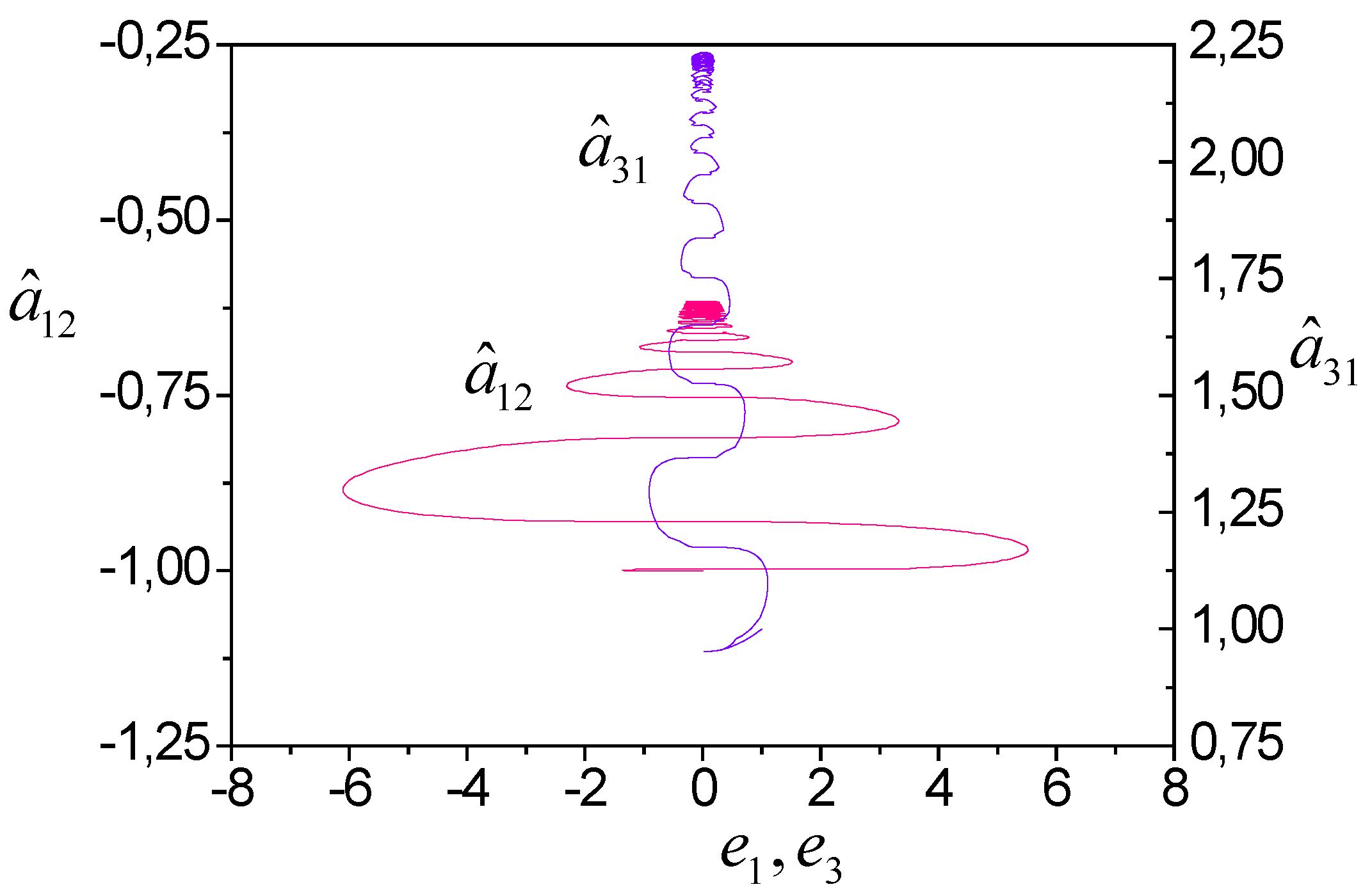
Tuning parameters in the space
shows in
Figure 10. We see that
and S-synchronizability execution does not guarantee the asymptotic stability of the system. Nonlinearity is the reason for such properties of an adaptive system.
Consider Lyapunov functions
,
Theorem 4. Let (i) positive-definite Lyapunov functions
,
,
have an infinitesimal upper limit at
,
; (ii)
,
,
,
,
,
; (iii) the inequality is fulfilled for
where
,
,
,
and
are minimum and maximum eigenvalues of the matrix
; (iv)
, where
,
; (v)
; (vi) the equality
fulfilled in the domain
, where
,
,
are zero vectors,
is number of adjustable parameters,
is some neighborhood of a point
,
; (vii) the matrix system of inequalities
is valid for
, where
block-diagonal matrix
(viii) the upper solution for
satisfies the equation
if functions
exist such that
,
, where
,
is vector
element. Then the adaptive system (54), (55) is exponentially dissipative with the estimate
if
The Theorem 4 proof gives in Appendix D.
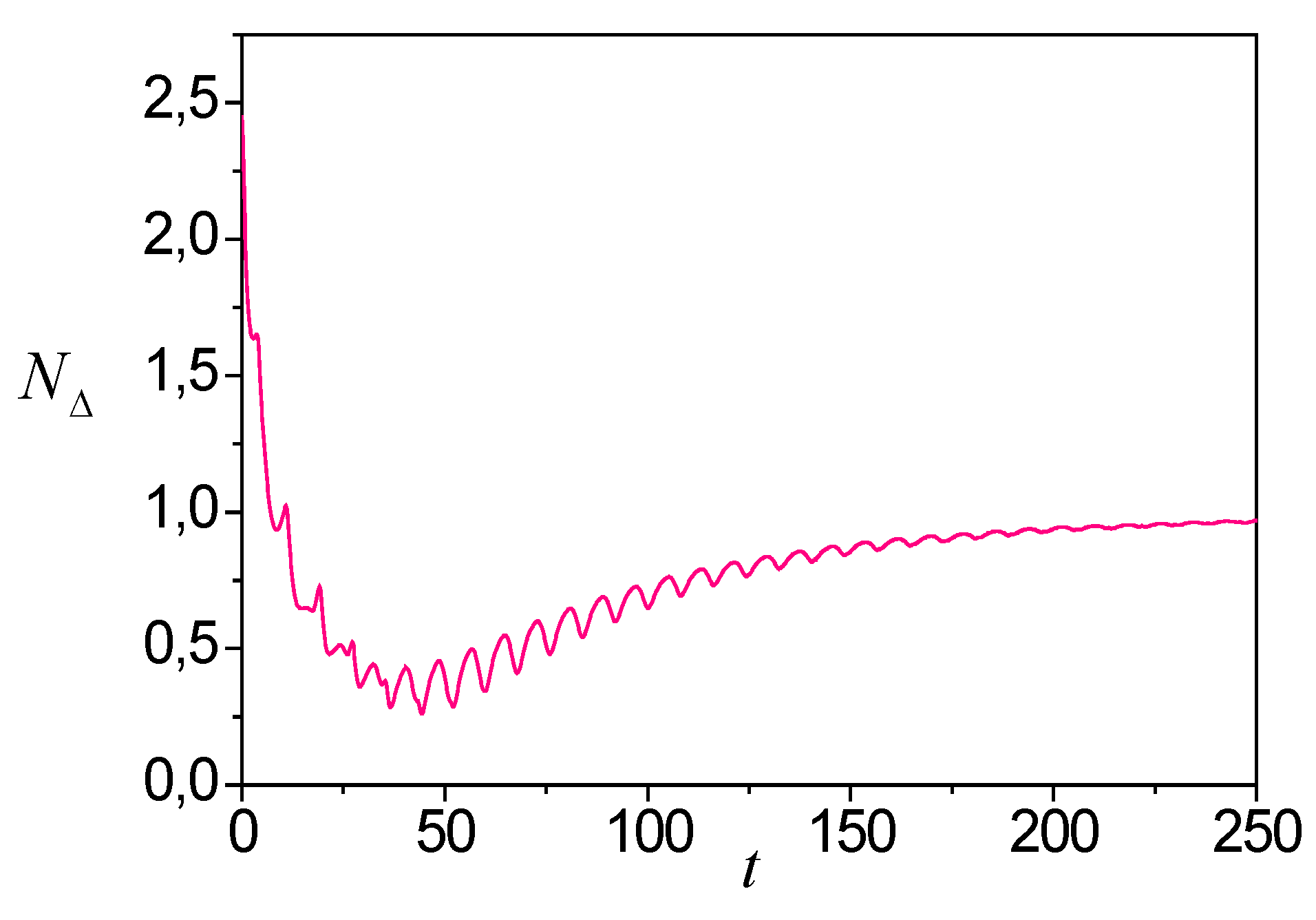
As follows from Theorem 4, system (48), (49) limiting properties depend on nonlinearity, feedback and constant excitation. In particular, this is true for block 3. The Theorem 4 statement confirms by
Figure 11. It reflects the change of parametric error norm for channels 3-5
So, the nonlinearities and feedback give biased estimates for the system parameters (48).
9. Conclusions
We propose the approach to adaptive identification for systems with multiple nonlinearities. It uses the transformation of equations based on the experimental data available set. Adaptive identification system designed. System decomposition into several subsystems is proposed for the adaptation process simplify. The trajectories boundedness in the adaptive system proved. The S-synchronizability problem of the system considers, and the excitation constancy condition modification proposes. The modification considers the requirement for nonlinear system structural identifiability. The Lyapunov vector function method applies to prove exponential stability.
Nonlinear correction of a nonlinear system considers. Adaptive algorithms obtain for estimating system parameters. The system trajectories limitation proved. A nonlinear system considers for self-oscillation generation with nonlinear feedback. The adaptive parametric identification system develops. We study the effect of feedback and nonlinearity. Simulation results confirm theoretical results.
Appendix A. Proof of Theorem 2
Consider the Lyapunov function
(24).
has the form of subsystem
motions
Apply Theorem 2 condition (i). As
, the
-subsystem is stable. Integrate
satisfies the Theorem 2 condition (1). Therefore, all trajectories of the
-subsystem belong to the domain
The desired estimate follows from (A.2). □
Appendix B. Proof of Lemma 1
Apply the inequality [30]
and (26). Then
where
is matrix with elements
and
.
Let
and
, where
are positive numbers.
-property for
obtains from (B.3)
where
. □
Appendix C. Proof of Lemma 2
Let for
where
is system equilibrium position,
is some neighborhood of a point
,
is null matrix,
,
is some number.
Let
,
. Apply (C.2) and present (C.1) as
Apply to (С.3) inequalities (B.2), (26) and obtain
where
.
So,
-property for
□
Appendix D. Proof of Theorem 4
Consider the Lyapunov vector function (56). Elements
satisfy Theorem 4 condition (i). Ensure the
-property for each component
. Apply the approach used in proving Lemmas 1 and 2. Consider the proof procedure with the example
.
has form
Apply to (D.1) inequalities (B.2) and obtain
Let
,
,
,
,
,
are minimum and maximum eigenvalues of the matrix
. Theorem 4 condition (iii) holds for
. Then (D.2)
So, the
-property obtain for
. Consider
where
,
,
.
levels the EC property, as the nonlinear properties of the system effect.
Apply Theorem 2 and get the adaptive system trajectories boundedness. Then (D.4)
where
is uncertainty appearing at
,
.
Apply the above approach and get the
- property for the remnants
where
.
Consider components
and use the approach used for Lemma 2 proving. Let the condition
for
, where
is system equilibrium position,
is some neighborhood of a point
,
,
are corresponding variables in (48). Then
where
,
. Apply (B.2) and get the
-property for
Similarly, obtain the
-property for elements
where
is the result of the violation of the EC condition. The
boundedness follows from Theorem 2.
The derivative
satisfies the matrix system of inequalities
where
,
,
The comparison system is fair for (D.10)
if functions
exist such that the comparison system is fair for (D.10)
where
,
is elements of the vector
.
Form
shows that system (48) channels are isolated at the level of stability research. Therefore, perform the analysis
for each channel.
is an
M-matrix [
30]. The major minors
positivity is the condition for the asymptotic stability of the adaptive system. Have
We see that the limiting properties (48) depend on the nonlinear properties of the system, feedback, and constant excitation. In particular, this is true for channel 3 in (D.10). □
References
- Aykan M., Özgüven H.N. (2012) Parametric Identification of Nonlinearity from Incomplete FRF Data Using Describing Function Inversion. In: Adams, D., Kerschen, G., Carrella, A. (eds) Topics in Nonlinear Dynamics, Volume 3. Conference Proceedings of the Society for Experimental Mechanics Series. Springer, New York. https://doi.org/10.1007/978-1-4614-2416-1_25.
- Zhao Z., Li C., Ahlin K., Du. H. (2016) Nonlinear system identification with the use of describing functions – a case study, Vibroengineering PROCEDIA, 8, 33-38.
- Pavlov Y.N., Nedashkovskii V.M., Tihomirova E.A. (2015) Identification of Nonlinear Dynamic Systems Possessing Some Nonlinearities, Science and Education of the Bauman MSTU, 07, 217–234.
- Prawin J., Rao A.R.M. & Sethi A. (2020) Parameter identification of systems with multiple disproportional local nonlinearities, Nonlinear Dyn, 100, 289–314.
- Pai P. F., Palazotto A. N. (2008) Detection and identification of nonlinearities by amplitude and frequency modulation analysis, Mechanical Systems and Signal Processing, 22(5), 1107-1132.
- Safari S., Monsalve J. M. L. (2021) Direct optimization based model selection and parameter estimation using time-domain data for identifying localised nonlinearities, Journal of Sound and Vibration, 501, , 116056.
- Noël J., Schoukens J. (2018) Grey-box state-space identification of nonlinear mechanical vibrations, International Journal of Control, 91(5).
- Li C. (2021) Closed-loop identification for a class of nonlinearly parameterized discrete-time systems, Automatica, 131, 109747.
- Noël J.P., and Schoukens J. (2018) Grey-box State-space Identification of Nonlinear Mechanical Vibrations, International Journal of Control, 91(5), 1118-1139.
- Binczak S., Busvelle E., Gauthier J.-P., Jacquir S. (2006) Identification of Unknown Functions in Dynamic Systems. https://pageperso.lis-lab.fr/eric.busvelle/papers/bioid.pdf.
- Singh A. and Moore K. J. (2021) Identification of multiple local nonlinear attachments using a single measurement case, Journal of Sound and Vibration, 513, 116410.
- Paul Van den Hof. (1997) Closed-loop issues in system identification. In: Y. Sawaragi and S. Sagara (Eds.), System Identification (SYSID’97), Proc. 11th IFAC Symp. System Identification, Kitakyushu, Japan, 8-11 July 1997. IFAC Proceedings Series, 3, 1547-1560.
- Andersson C., Ribeiro A. H., Tiels K., Wahlström N. and Schön T. B. (2019) Deep convolutional networks in system identification, IEEE 58th Conference on Decision and Control (CDC).
- Gedon D., Wahlström N., Schön T. B., Ljung L. (2021) Deep State Space Models for Nonlinear System Identification. arXiv:2003.14162v3 [eess.SY].
- Kerschen G., Worden K., Vakakis A. and Golinval J.-C. (2006) Past, present and future of nonlinear system identification in structural dynamics, Mechanical Systems and Signal Processing, Elsevier, 20 (3), 505-592.
- Holmes P. (1982) The dynamics of repeated impacts with a sinusoidally vibrating table, Journal of Sound and Vibration, 84, 173–189.
- Azeez M.A.F., Vakakis A.F. (1999) Numerical and experimental analysis of a continuously overhung rotor undergoing vibro-impacts, International Journal of Non-Linear Mechanics, 34, 415–435.
- Van den Hof P. (1998) Closed-loop issues in system identification. Annual Reviews in Control, 22(0), 173 – 186.
- Aljamaan, I. (2016) Nonlinear Closed-Loop System Identification in The presence of Non-stationary Noise Source (Unpublished doctoral thesis). University of Calgary, Calgary, AB.
- Forssell U., Ljung L. (1999) Closed-loop identification revisited, Automatica, 35, 1215-1241.
- Mejari M., Piga D. and Bemporad A. (2018) A bias-correction method for closed-loop identification of Linear Parameter-Varying systems, Automatica, 87, 128–141.
- Piga, D., Tуth R. (2014) A bias-corrected estimator for nonlinear systems with output-error type model structures, Automatica, 50(9), 2373–2380.
- Gilson, M. and Van den Hof, P. (2001) On the relation between a bias-eliminated leastsquares (BELS) and an IV estimator in closed-loop identification, Automatica, 37(10), 1593–1600.
- Song G., Xu L. Ding F. (2019) Recursive least squares algorithm and stochastic gradient algorithm for feedback nonlinear equation-error systems. International Journal of Modelling, Identification and Control, 32(3-4), pp. 251-257.
- Karabutov N. (2021) Introduction to the structural identifiability of nonlinear systems; URSS/ Lenand: Moscow.
- Karabutov N.N. (2020) S-synchronization Structural Identifiability and Identification of Nonlinear Dynamic Systems. Mekhatronika, Avtomatizatsiya, Upravlenie, 21(6), 323-336. (In Russ.).
- Karabutov N. (2018) Structural-parametrical design method of adaptive observers for nonlinear systems, International journal of intelligent systems and applications, 10(2), 1-16.
- Karabutov N. (2018) Geometrical frameworks in identification problem, Intelligent control and automation, 12(2), 17-43.
- Karabutov N. (2017) Adaptive observers with uncertainty in loop tuning for linear time-varying dynamical systems, International journal intelligent systems and applications, 9(4), 1-13.
- Gantmacher F.R. (2000) The Theory of Matrices; AMS Chelsea Publishing: Reprinted by American Mathematical Society.
- Karabutov N. (2022) Structural Identifiability of Feedback Systems with Nonlinear Adulterating, Contemporary Mathematics, 3(2), 257-269.
- Karabutov N. (2021) Structural Identifiability of Systems with Multiple Nonlinearities, Contemporary Mathematics, 2(2) 141-161.
- Barbashin E.A. (1970) Lyapunov function; Nauka: Moscow.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).