The Imaginary Universe

1. Introduction

The universe began with the Big Bang, which is a current prevailing scientific opinion. But this Big Bang was not an explosion of 4-dimensional spacetime, which also is a current prevailing scientific opinion, but an explosion of dimensions. More precisely, in the $-1$-dimensional void, a 0-dimensional point appeared, inducing the appearance of countably infinitely other points indistinguishable from the first one. The breach made by the first operation of the dimensional successor function of the Peano axioms inevitably continued leading to the formation of 1-dimensional, real and imaginary lines, allowing for an ordering of points using multipliers of real units (ones) or imaginary units ($a\in \mathbb{R}\iff a=1b$1, and $a\in \mathbb{I}\iff a=ib$, where $b\in \mathbb{R}$). Then out of two lines of each kind, crossing each other only at one initial point $(0,0)$, the dimensional successor function formed 2-dimensional ${\mathbb{R}}^2$, ${\mathbb{I}}^2$, and $\mathbb{R}\times \mathbb{I}$ Euclidean planes, with ${\mathbb{I}}^2$ being a mirror reflection of ${\mathbb{R}}^2$. And so on, forming n-dimensional Euclidean spaces ${\mathbb{R}}^a\times {\mathbb{I}}^b$ with $a\in \mathbb{N}$ real and $b\in \mathbb{N}$ imaginary lines, $n:=a+b$, and the scalar product defined by

$$\begin{array}{cc}\hfill \mathbf{x}·\mathbf{y}& =\left(x_1,\dots ,x_a,i{x}_1^{\prime },\dots ,i{x}_b^{\prime }\right)\left(y_1,\dots ,y_a,i{y}_1^{\prime },\dots ,i{y}_b^{\prime }\right):=\hfill \\ \hfill & :=\sum _{k=1}^a{x}_k{y}_k+\sum _{l=1}^b{x}_l^{\prime }\overline{y_l^{\prime }},\hfill \end{array}$$

(1)

where $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^a\times {\mathbb{I}}^b$. With the appearance of the first 0-dimensional point, information began to evolve [1,2,3,4,5,6].

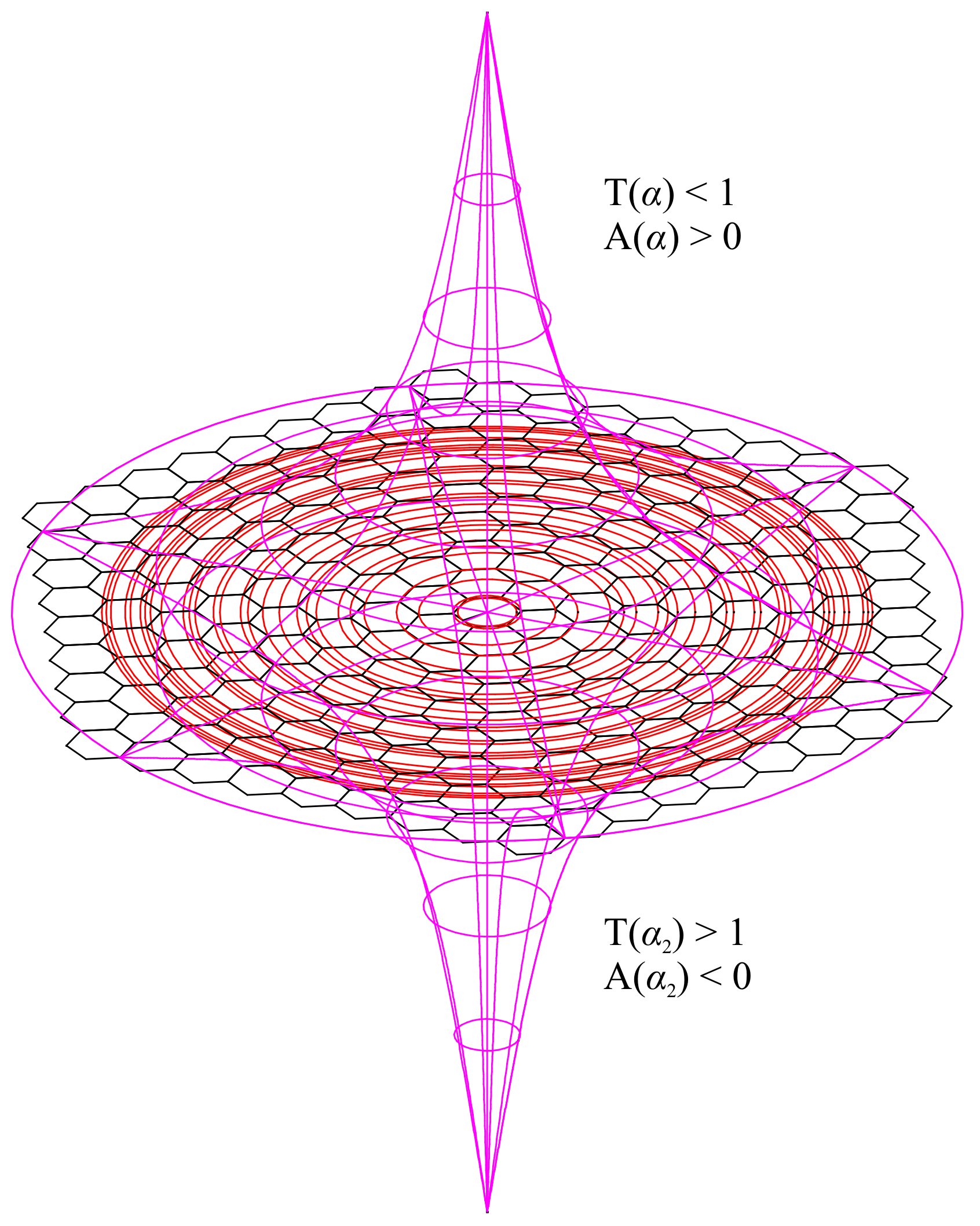
However, the dimensional properties are not uniform. Concerning regular convex n-polytopes in natural dimensions, for example, there are countably infinitely many regular convex polygons, five regular convex polyhedra (Platonic solids), six regular convex 4-polytopes and only three regular convex n-polytopes if $n>3$ [7]. In particular, 4-dimensional Euclidean space is endowed with a peculiar property known as exotic ${\mathbb{R}}^4$ [8], absent in other dimensionalities. Due to this property, ${\mathbb{R}}^3\times \mathbb{I}$ space provides a continuum of homeomorphic but non-diffeomorphic differentiable structures. Each piece of individually memorized information is homeomorphic to the corresponding piece of individually perceived information but remains nondiffeomorphic (non-smooth). This allowed the variation of phenotypic traits within individuals’ populations [9] and extended the evolution of information into biological evolution. Exotic ${\mathbb{R}}^4$ solves the problem of extra dimensions of nature, and perceived space requires a natural number of dimensions [10]. Each biological cell perceives an emergent space of three real dimensions and one imaginary (time) observer-dependently [11] and at present, when $i0=0$ is real, through a spherical Planck triangle corresponding to one bit of information in units of $-c^2$, where c is the speed of light in vacuum. This is the emergent dimensionality (ED) [5,9,12,13,14]. Appendix F presents some arguments to support the claim that perceived dimensionality sets favourable conditions for biological evolution to emerge.

Each dimension requires certain units of measure. In real dimensions, Max Planck in 1899 derived the natural units of measure as "independent of special bodies or substances, thereby necessarily retaining their meaning for all times and for all civilizations, including extraterrestrial and nonhuman ones" [15]. Planck units utilize the Planck constant h that he introduced in his black-body radiation formula. However, in 1881, George Stoney derived a system of natural units [16] based on the elementary charge e (Planck’s constant was unknown then). The ratio of Stoney units to Planck units is $\sqrt{\alpha }$, where $\alpha$ is the fine-structure constant. This study derives the complementary set of natural units applicable to imaginary dimensions, including imaginary units, based on the discovered negative fine-structure constant ${\alpha }_2$.

Imaginary and negative physical quantities are the subject of research. In particular, the subject of scientific research is thermodynamics in the complex plane. For example, Lee–Yang zeros [17,18] and photon-photon thermodynamic processes under negative optical temperature conditions [19] have been experimentally observed. Furthermore, the rendering of synthetic dimensions through space modulations has recently been suggested because it does not require any active materials or other external mechanisms to break the time-reversal symmetry [20]. However, physical quantities accessible for direct everyday observation are mostly real and positive with the negativity of distances, velocities, accelerations, etc., induced by the assumed orientation of space. Quantum measurement results, for example, are real eigenvalues of Hermitian operators. Unlike charges, negative, real masses are generally inaccessible for direct observation. However, dissipative coupling between excitons and photons in an optical microcavity leads to the formation of exciton polaritons with negative masses [21]. In Section 6 we show that negative masses also result from merging black-body objects.

Furthermore, the study introduces a model for storing the excess energy of neutron stars and white dwarfs that exceed their mass–energy equivalences in imaginary dimensions. The model results in the upper bound on the size-to-mass ratio of their cores, where the Schwarzschild radius sets the lower bound.

The paper is structured as follows. Section 2 shows that Fresnel coefficients for the normal incidence of electromagnetic radiation on monolayer graphene include the second negative fine-structure constant ${\alpha }_2$ as a fundamental constant of nature. Section 3 shows that by this second fine-structure constant nature endows us with the ${\alpha }_2$-natural units. Section 4 introduces the concept of a black-body object in thermodynamic equilibrium, emitting perfect black-body radiation, and reviews its necessary properties. Section 5 introduces complex mass and charge energies expressed in terms of real and imaginary ${\alpha }_2$-Planck units introduced in Section 3 and applies them to black-body objects. Section 6 considers observed mergers of black-body objects to show that the observed data can be explained without the need to introduce hypothetical exotic stellar objects. Section 7 discusses fluctuations of black-body objects. Section 8 defines the complex forces. The complex force between real masses and imaginary charges is used in Section 9 to derive a black-body object surface gravity and the generalized Hawking radiation temperature, and in Section 10 discussed in the context of the Bohr model of the hydrogen atom. Section 11 summarizes the findings of this study. Certain prospects for further research are given in the Appendices.

2. The Second Fine-Structure Constant

Numerous publications provide Fresnel coefficients for the normal incidence of electromagnetic radiation (EMR) on monolayer graphene (MLG), which are remarkably defined only by $\pi$ and the fine-structure constant $\alpha$

$${\alpha }^{-1}={\left(\frac{q_{\mathrm{P}}}{e}\right)}^2=\frac{4\pi {ϵ}_0\hslash c}{e^2}\approx 137.036,$$

(2)

where $q_{\mathrm{P}}$ is the Planck charge, ℏ is the reduced Planck constant, ${ϵ}_0\approx 8.8542\times {10}^{-12}[{\mathrm{kg}}^{-1}·{\mathrm{m}}^{-3}·{\mathrm{s}}^2·{\mathrm{C}}^2]$ is vacuum permittivity (the electric constant), and e is the elementary charge. Transmittance (T) of MLG

$$\mathrm{T}=\frac{1}{{\left(1+\frac{\pi \alpha }{2}\right)}^2}\approx 0.9775,$$

(3)

for normal EMR incidence was derived from the Fresnel equation in the thin-film limit [22] (Eq. 3), whereas spectrally flat absorptance (A) $\mathrm{A}\approx \pi \alpha \approx 2.3\%$ was reported [23,24] for photon energies between about $0.5$ and $2.5$ [eV]. T was related to reflectance (R) [25] (Eq. 53) as $\mathrm{R}={\pi }^2{\alpha }^2\mathrm{T}/4$, i.e,

$$\mathrm{R}=\frac{\frac{1}{4}{\pi }^2{\alpha }^2}{{\left(1+\frac{\pi \alpha }{2}\right)}^2}\approx 1.2843\times {10}^{-4},$$

(4)

The above equations for T and R, as well as the equation for the absorptance

$$\mathrm{A}=\frac{\pi \alpha }{{\left(1+\frac{\pi \alpha }{2}\right)}^2}\approx 0.0224,$$

(5)

were also derived [26] (Eqs. 29-31) based on the thin film model (setting $n_s=1$ for substrate). The sum of transmittance (3) and the reflectance (4) at normal EMR incidence on MLG was derived [27] (Eq. 4a) as

$$\begin{array}{cc}\hfill \mathrm{T}+\mathrm{R}& =1-\frac{4\sigma \eta }{4+4\sigma \eta +{\sigma }^2{\eta }^2+k^2{\chi }^2}=\hfill \\ \hfill & =\frac{1+\frac{1}{4}{\pi }^2{\alpha }^2}{{\left(1+\frac{\pi \alpha }{2}\right)}^2}\approx 0.9776,\hfill \end{array}$$

(6)

where $\eta \approx 376.73\left[\mathsf{\Omega }\right]$ is the vacuum impedance, $\sigma =e^2/(4\hslash )=\pi \alpha /\eta \approx 6.0853\times {10}^{-5}\left[{\mathsf{\Omega }}^{-1}\right]$ is the MLG conductivity [28], k is the wave vector of light in vacuum, and $\chi =0$ is the electric susceptibility of vacuum. Therefore, these coefficients are well established theoretically and experimentally [22,23,24,27,29,30].

As a consequence of the conservation of energy

$$(\mathrm{T}+\mathrm{A})+\mathrm{R}=1.$$

(7)

In other words, the transmittance in the Fresnel equation describing the reflection and transmission of EMR at normal incidence on a boundary between different optical media is, in the case of the 2-dimensional (boundary) of MLG, modified to include its absorption.

The reflectance $\mathrm{R}=0.013\%$ (4) of MLG can be expressed as the quadratic equation of $\alpha$

$$\begin{array}{cc}\hfill \mathrm{R}{\left(1+\frac{\pi \alpha }{2}\right)}^2-\frac{1}{4}{\pi }^2{\alpha }^2& =0,\hfill \\ \hfill \frac{1}{4}\left(\mathrm{R}-1\right){\pi }^2{\alpha }^2+\mathrm{R}\pi \alpha +\mathrm{R}& =0,\hfill \end{array}$$

(8)

which can be expressed in terms of the reciprocal of $\alpha$, defining $\beta :=1/\alpha$ as

$$\mathrm{R}{\beta }^2+\mathrm{R}\pi \beta +\frac{1}{4}\left(\mathrm{R}-1\right){\pi }^2=\mathrm{R}{\left(\beta +\frac{\pi }{2}\right)}^2-\frac{{\pi }^2}{4}=0.$$

(9)

The quadratic equation (9) has two roots

$$\beta ={\alpha }^{-1}=\frac{-\pi R+\pi \sqrt{\mathrm{R}}}{2R}\approx 137.036,\mathrm{and}$$

(10)

$${\beta }_2={\alpha }_2^{-1}=\frac{-\pi R-\pi \sqrt{\mathrm{R}}}{2R}\approx -140.178.$$

(11)

Therefore, the Equation (8) includes the second negative fine-structure constant ${\alpha }_2$. It turns out that the sum of the reciprocals of these fine-structure constants (10) and (11)

$$\begin{array}{cc}\hfill {\alpha }^{-1}+{\alpha }_2^{-1}& =\frac{-\pi R+\pi \sqrt{\mathrm{R}}-\pi R-\pi \sqrt{\mathrm{R}}}{2R}=\frac{-2\pi }{2}=-\pi ,\hfill \end{array}$$

(12)

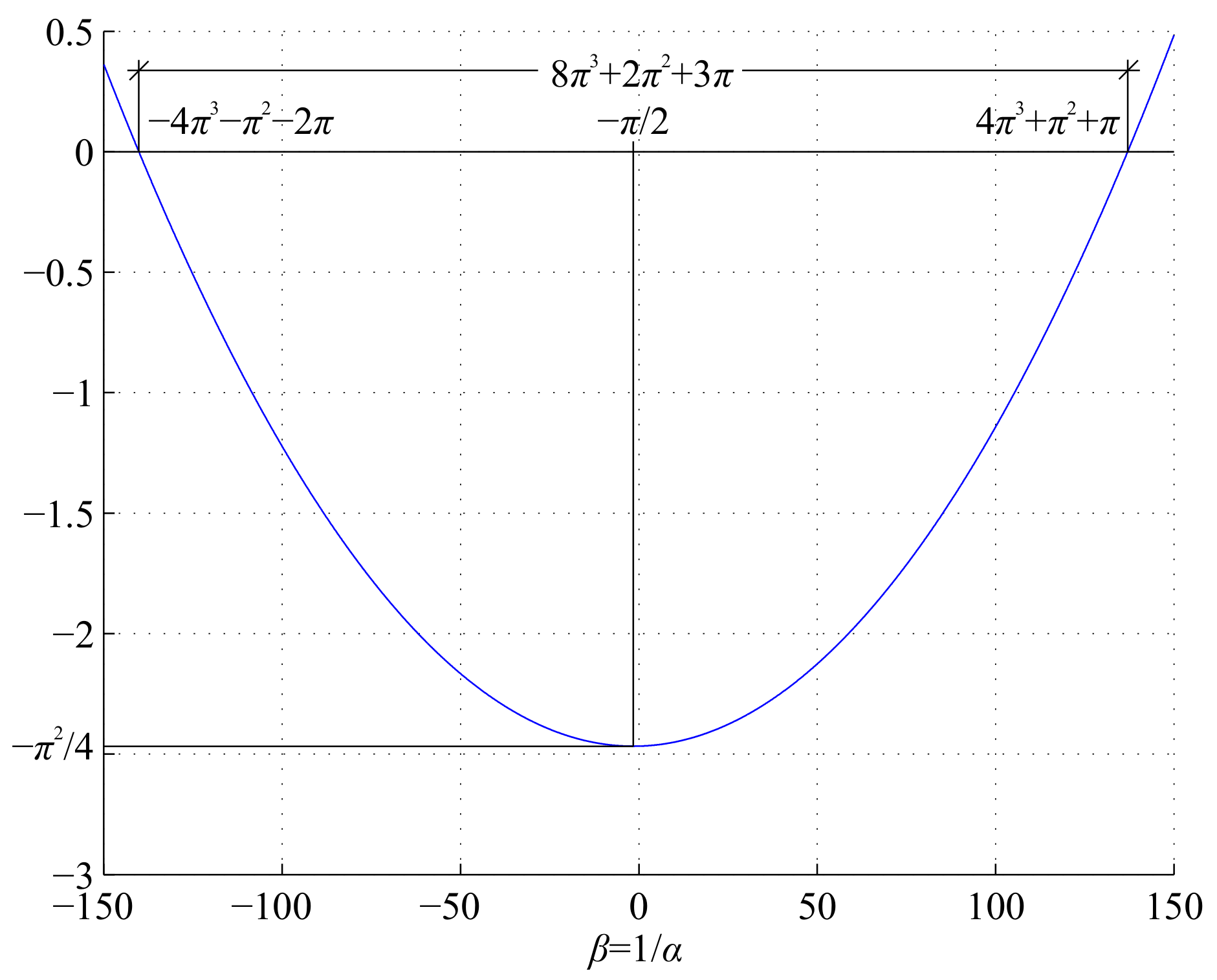
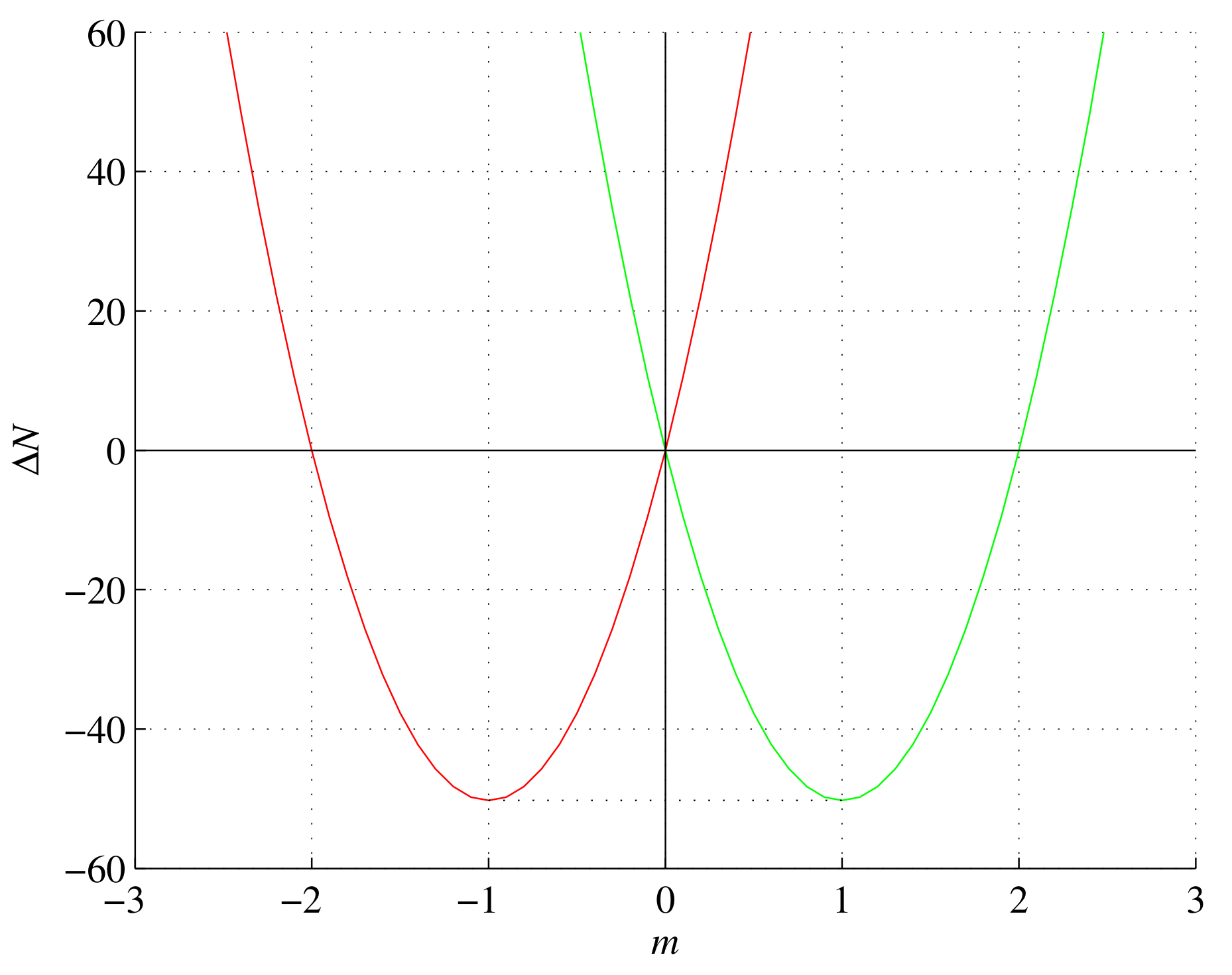
is remarkably independent of the value of the reflectance R. Furthermore, the minimum of the parabola (9) amounts $-{\pi }^2/4\approx -2.4674$ and occurs at $-\pi /2\approx -1.5708$, as shown in Figure 1. Also, these values are independent of the reflectance (4) value, and the same results can (only) be obtained for $\mathrm{T}+\mathrm{A}$ (cf. Appendix B).

We further note that the relation (12) corresponds to the following identity

$$\frac{\alpha +{\alpha }_2}{\alpha {\alpha }_2}=-\pi ,$$

(13)

between the roots (10) and (11), which is also present in the MLG Fresnel equations and the corresponding Euclid formula (cf. Appendix D).

These dependences on $\pi$ only between the fine-structure constants $\alpha$ and ${\alpha }_2$ suggest that they do not vary over time.

These results are also intriguing in the context of a peculiar algebraic expression for the fine-structure constant [31]

$${\alpha }^{-1}=4{\pi }^3+{\pi }^2+\pi \approx 137.036303776$$

(14)

that contains a free $\pi$ term and is very close to the physical definition (2) of ${\alpha }^{-1}$, which according to the CODATA 2018 value is $137.035999084$. We note in passing that CODATA values are computed by averaging the measurements.

Using relations (12) and (14), we can express the negative reciprocal of the 2^nd fine-structure constant ${\alpha }_2^{-1}$ that emerged in the quadratic equation (8) also as a function of $\pi$ only

$${\alpha }_2^{-1}=-\pi -{\alpha }_1^{-1}=-4{\pi }^3-{\pi }^2-2\pi \approx -140.177896429.$$

(15)

Using relations (14) and (15), T (3), R (4), and A (5) of MLG for normal incidence of EMR can be expressed just by $\pi$ (cf. Appendix C). Moreover, equation (8) includes two $\pi$-like constants for two surfaces with positive and negative Gaussian curvatures (cf. Appendix E).

3. Set of ${\alpha }_2$-Planck Units

In this section, we shall derive complementary Planck units based on the second fine-structure constant ${\alpha }_2$. We shall further call them ${\alpha }_2$-Planck units. Natural units can be derived from numerous starting points [5,32] (cf. Appendices Appendix G and Appendix H). The central assumption in all natural unit systems is that the quotient of the unit of length ${\ell }_{*}$ and time $t_{*}$ is a unit of speed; we call it $c={\ell }_{*}/t_{*}$. It is the speed of light in vacuum c in all systems of natural units, except for Hartree and Schrödinger units, where it is $c\alpha$, and Rydberg units, where it is $c\alpha /2$2. On the other hand, c as the velocity of the electromagnetic wave is derivable from Maxwell’s Equations in vacuum

$${\nabla }^2\mathbf{E}={\mu }_0{ϵ}_0\frac{{\partial }^2\mathbf{E}}{\partial t^2},\frac{{\partial }^{2}E}{\partial x^2}={\mu }_0{ϵ}_0\frac{{\partial }^{2}E}{\partial t^2},$$

(16)

where $\mathbf{E}$ is the electric field, and ${\mu }_0$ is vacuum permeability (the magnetic constant). Without postulating any solution to this equation but by simple substitution $\partial x:={\ell }_{*}$ and $\partial t:=t_{*}$, ${\partial }^{2}E:=E_{*}$ factors out, and we obtain well known

$$1={\mu }_0{ϵ}_0{c}^2,$$

(17)

symmetric in its electric and magnetic parts [33] from which the bivalued $c=\pm 1/\sqrt{{\mu }_0{ϵ}_0}$ can be obtained, knowing the values of ${\mu }_0$ and ${ϵ}_0$. We note that it is $c^2$, not c, present in mass-energy equivalence, the Lorentz factor, the BH potential, etc. We further note that Maxwell’s equations in vacuum are not directly dependent on the fine-structure constant(s). It is included in the magnetic constant ${\mu }_0$.

In the following, we assume the universality of the real elementary electric charge e defining both matter and antimatter, the Planck constant h, the uncertainty principle parameter, and the gravitational constant G (i.e. we assume that there are no counterparts to these physical constants in other physical dimensions in our model and that these dimensional constants are positive). The last two assumptions are probably too far-reaching, given that we do not need to know the gravitational constant G or the Planck constant h to find the product of the Planck length ${\ell }_{\mathrm{P}}$ and the speed of light in vacuum [34]. We note in passing that antimatter obeys gravity [35], which is consistent with the findings of this study.

The fine-structure constant can be defined as the quotient (2) of the squared (and thus positive) elementary charge e and the squared Planck charge $\alpha =e^2/q_{\mathrm{P}}^2$. We chose Planck units over other natural unit systems not only because they incorporate the fine-structure constant $\alpha$ and the Planck constant h. Other systems of natural units (except for Stoney units) also incorporate them. The reason is that only the Planck area defines one bit of information on a patternless black hole surface given by the Bekenstein bound (47) and the binary entropy variation [5,12].

To accommodate the negativity of the fine-structure constant discovered in the preceding section, we must introduce the imaginary Planck charge $q_{\mathrm{P}i}$ so that its square would yield a negative value of ${\alpha }_2$.

$$\begin{array}{cc}\hfill q_{\mathrm{P}}^2=\frac{e^2}{\alpha }& \ne q_{\mathrm{P}i}^2=\frac{e^2}{{\alpha }_2}\Rightarrow q_{\mathrm{P}i}=ae,a\in \mathbb{I},\hfill \\ \hfill e^2=q_{\mathrm{P}}^2\alpha & =q_{\mathrm{P}i}^2{\alpha }_2.\hfill \end{array}$$

(18)

Next, we note that an imaginary $q_{\mathrm{P}i}$, which must have a physical definition analogous to $q_{\mathrm{P}}$, requires either a real and negative speed of light or some complementary real and negative electric constant (we assume that h is positive). Let us call them $c_2$ and $\widetilde{{ϵ}_0}$

$$q_{\mathrm{P}}^2=4\pi {ϵ}_0\hslash c>0\nLeftrightarrow q_{\mathrm{P}i}^2=4\pi \widetilde{{ϵ}_0}\hslash c_2<0.$$

(19)

From this equation, we find that $\widetilde{{ϵ}_0}{c}_2<0$, as the values of the other constants are known. Next, we assume that the solution (17) of Maxwell’s equations in vacuum is also valid for other values of the constants involved. Let us call the unknown magnetic constant ${\mu }_2$, so

$${\mu }_0{ϵ}_0{c}^2={\mu }_2\widetilde{{ϵ}_0}{c}_2^2=1.$$

(20)

From that and from $\widetilde{{ϵ}_0}{c}_2<0$, we conclude that the product ${\mu }_2{c}_2<0$. We note that the quotient of the squared Planck charge and mass introduces the imaginary Planck mass $m_{\mathrm{P}i}$

$$\frac{q_{\mathrm{P}}^2}{m_{\mathrm{P}}^2}=\frac{q_{\mathrm{P}i}^2}{m_{\mathrm{P}i}^2}=4\pi {ϵ}_{0}G,$$

(21)

the value of which can be calculated, knowing the value of the imaginary Planck charge $q_{\mathrm{P}i}$ from the relation (18). From (21) we also conclude that $\widetilde{{ϵ}_0}={ϵ}_0>0$ and then by (20) that ${\mu }_2>0$ and $c_2<0$. Knowing $m_{\mathrm{P}i}$ we can determine the value of the negative nonprincipal square root of $c_2=\pm 1/\sqrt{{\mu }_2{ϵ}_0}$ of the relation (20) as

$$c_2=\frac{q_{\mathrm{P}i}^2}{4\pi {ϵ}_0\hslash }\approx -3.066653\times {10}^8[\mathrm{m}/\mathrm{s}],$$

(22)

which is greater than the speed of light in vacuum c in modulus.

The mass, length, time, and charge units can express all electrical units. Therefore, along with temperature, amount of substance, and luminous intensity, they are base units of the International System of Quantities (ISQ). We further conclude that the magnetic constant ${\mu }_2$ is lower than ${\mu }_0$

$$\begin{array}{cc}\hfill {\mu }_0& =\frac{4\pi \hslash \alpha }{c{e}^2}\approx 1.2569\times {10}^{-6}[\mathrm{kg}·\mathrm{m}·{\mathrm{C}}^{-2}],\hfill \\ \hfill {\mu }_2& =\frac{4\pi \hslash {\alpha }_2}{c_2{e}^2}\approx 1.2012\times {10}^{-6}[\mathrm{kg}·\mathrm{m}·{\mathrm{C}}^{-2}].\hfill \end{array}$$

(23)

Unlike the electric constant ${ϵ}_0$, the magnetic constants $\mu$ are independent of the unit of time. Furthermore, negative ${\alpha }_2$ and $c_2$ lead to the second, also time-dependent but negative vacuum impedance

$$\begin{array}{cc}\hfill {\eta }_2& =-\frac{4\pi {\alpha }_2\hslash }{e^2}=-\frac{1}{{ϵ}_0{c}_2}\approx \hfill \\ \hfill & \approx -368.29[\mathrm{kg}·{\mathrm{m}}^2·{\mathrm{s}}^{-1}·{\mathrm{C}}^{-2}]\left(|{\eta }_2|<|\eta |\right).\hfill \end{array}$$

(24)

Finally, combining relations (18) and (19) yields

$$e^2=4\pi {ϵ}_0\hslash c\alpha =4\pi {ϵ}_0\hslash c_2{\alpha }_2,$$

(25)

which leads to the following important relation between the speeds of light in vacuum c, $c_2$, and the fine-structure constants $\alpha$, ${\alpha }_2$

$$c\alpha =c_2{\alpha }_2,$$

(26)

valid for both principal and non-principal square roots of the relation (20). $c\alpha$ is also the electron’s velocity at the first circular orbit in the Bohr hydrogen atom model3 to which we shall return in Section 10. Furthermore, the relation (26) introduces an interesting interplay between $\alpha$ vs. ${\alpha }_2$ and c vs. $c_2$ that, as we conjecture, should be able to explain $\nu =5/2$ state in the fractional quantum Hall effect in the 2D system of electrons, as well as other fractional states with an even denominator [36] (cf. Appendix I). The relation (26) is not the only $\alpha$ to ${\alpha }_2$ relation. Along with the two $\pi$-like constants ${\pi }_1$, ${\pi }_2$ (relations (A21) and (A23), cf. Appendix E)

$$\frac{{\alpha }_2}{\alpha }=\frac{c}{c_2}=\frac{{\pi }_1}{\pi }=\frac{\pi }{{\pi }_2}=\frac{m_{\mathrm{P}}^2}{m_{\mathrm{P}i}^2}=\frac{q_{\mathrm{P}}^2}{q_{\mathrm{P}i}^2}\approx -0.9776.$$

(27)

Therefore, the non-principal square root of $c=\pm 1/\sqrt{{\mu }_0{ϵ}_0}$ and principal square root of $c_2=\pm 1/\sqrt{{\mu }_2{ϵ}_0}$ in (20) also introduce, respectively, imaginary ($-c$)-Planck units and real ($-c_2$)-Planck units. In particular, the imaginary ($-c$)-Planck time parameterizes the HSs time relations [5,12]. We conjecture that ${\alpha }_2$-Planck units is appropriate for espressing physical quantities of ${\mathbb{I}}^3\times \mathbb{R}$ Euclidean space rather than ${\mathbb{R}}^3\times \mathbb{I}$ Euclidean space that we perceive due to the minimum energy principle (cf. Appendix F). Furthermore, the speed of electromagnetic radiation is the product of its wavelength and frequency, and these quantities would be imaginary in terms of imaginary Planck units; the negative speed of light is necessary to accommodate this.

The negative speed of light $c_2$ (22) leads to the complementary Planck charge $q_{\mathrm{P}i}$, length ${\ell }_{\mathrm{P}i}$, mass $m_{\mathrm{P}i}$, time $t_{\mathrm{P}i}$, and temperature $T_{\mathrm{P}i}$ that redefined by square roots containing $c_2$ raised to odd powers (1, 3, 5) become bivalued and real-imaginary since c and $c_2$ are bivalued. In other words, both Planck and ${\alpha }_2$-Planck units have four forms equal in modulus: real positive, real negative, imaginary positive, and imaginary negative. However, here we consider mostly real, positive $\alpha$-Planck units and imaginary, positive ${\alpha }_2$-Planck units (hence the subscript i).

Principal square roots of the base ${\alpha }_2$-Planck units (for negative $c_2$) that can be expressed, using the relation (26), in terms of base Planck units $q_{\mathrm{P}}$, ${\ell }_{\mathrm{P}}$, $m_{\mathrm{P}}$, $t_{\mathrm{P}}$, and $T_{\mathrm{P}}$ are

$$\begin{array}{cc}\hfill q_{\mathrm{P}i}& =\sqrt{4\pi {ϵ}_0\hslash c_n}=q_{\mathrm{P}}\sqrt{\frac{\alpha }{{\alpha }_2}}\approx \hfill \\ \hfill & \approx i1.8969\times {10}^{-18}\left[\mathrm{C}\right]\left(|q_{\mathrm{P}i}|>|q_{\mathrm{P}}|\right),\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\ell }_{\mathrm{P}i}& =\sqrt{\frac{\hslash G}{c_n^3}}={\ell }_{\mathrm{P}}\sqrt{\frac{{\alpha }_2^3}{{\alpha }^3}}\approx \hfill \\ \hfill & \approx i1.5622\times {10}^{-35}\left[\mathrm{m}\right]\left(|{\ell }_{\mathrm{P}i}|<|{\ell }_{\mathrm{P}}|\right),\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill m_{\mathrm{P}i}& =\sqrt{\frac{\hslash c_n}{G}}=m_{\mathrm{P}}\sqrt{\frac{\alpha }{{\alpha }_2}}\approx \hfill \\ \hfill & \approx i2.2012\times {10}^{-8}\left[\mathrm{kg}\right]\left(|m_{\mathrm{P}i}|>|m_{\mathrm{P}}|\right),\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill t_{\mathrm{P}i}& =\sqrt{\frac{\hslash G}{c_n^5}}=t_{\mathrm{P}}\sqrt{\frac{{\alpha }_2^5}{{\alpha }^5}}\approx \hfill \\ \hfill & \approx i5.0942\times {10}^{-44}\left[\mathrm{s}\right]\left(|t_{\mathrm{P}i}|<|t_{\mathrm{P}}|\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill T_{\mathrm{P}i}& =\sqrt{\frac{\hslash c_n^5}{G{k}_{\mathrm{B}}^2}}=T_{\mathrm{P}}\sqrt{\frac{{\alpha }^5}{{\alpha }_2^5}}\approx \hfill \\ \hfill & \approx i1.4994\times {10}^{32}\left[\mathrm{K}\right]\left(|T_{\mathrm{P}i}|>|T_{\mathrm{P}}|\right).\hfill \end{array}$$

(32)

Most Planck units derived from the ${\alpha }_2$-Planck base units (28)-(32) are also imaginary. They include the ${\alpha }_2$ Planck volume

$$\begin{array}{cc}\hfill {\ell }_{\mathrm{P}i}^3& ={\left(\frac{\hslash G}{c_n^3}\right)}^{3/2}={\ell }_{\mathrm{P}}^3\sqrt{\frac{{\alpha }_2^9}{{\alpha }^9}}\approx \hfill \\ \hfill & \approx i3.8127\times {10}^{-105}\left[{\mathrm{m}}^3\right]\left(|{\ell }_{\mathrm{P}i}^3|<|{\ell }_{\mathrm{P}}^3|\right),\hfill \end{array}$$

(33)

the ${\alpha }_2$ Planck momentum

$$\begin{array}{cc}\hfill p_{\mathrm{P}i}& =m_{\mathrm{P}i}{c}_n=\sqrt{\frac{\hslash c_n^3}{G}}=m_{\mathrm{P}}c\sqrt{\frac{{\alpha }^3}{{\alpha }_2^3}}\approx \hfill \\ \hfill & \approx i6.7504\left[\mathrm{kg}\mathrm{m}/\mathrm{s}\right]\left(|m_{\mathrm{P}i}{c}_n|>|m_{\mathrm{P}}c|\right),\hfill \end{array}$$

(34)

the ${\alpha }_2$ Planck energy

$$\begin{array}{cc}\hfill E_{\mathrm{P}i}& =m_{\mathrm{P}i}{c}_n^2=\sqrt{\frac{\hslash c_n^5}{G}}=E_{\mathrm{P}}\sqrt{\frac{{\alpha }^5}{{\alpha }_2^5}}\approx \hfill \\ \hfill & \approx i2.0701\times {10}^9\left[\mathrm{J}\right]\left(|E_{\mathrm{P}i}|>|E_{\mathrm{P}}|\right),\hfill \end{array}$$

(35)

and the ${\alpha }_2$ Planck acceleration

$$\begin{array}{cc}\hfill a_{\mathrm{P}i}& =\frac{c_n}{t_{\mathrm{P}i}}=\sqrt{\frac{c_n^7}{\hslash G}}=a_{\mathrm{P}}\sqrt{\frac{{\alpha }^7}{{\alpha }_2^7}}\approx \hfill \\ \hfill & \approx \pm i6.0198\times {10}^{51}[\mathrm{m}/{\mathrm{s}}^2]\left(|a_{\mathrm{P}i}|>|a_{\mathrm{P}}|\right).\hfill \end{array}$$

(36)

However, the ${\alpha }_2$-Planck density

$$\begin{array}{cc}\hfill {\rho }_{\mathrm{P}2}& =\frac{m_{\mathrm{P}i}}{{\ell }_{\mathrm{P}i}^3}=\frac{c_n^5}{\hslash G^2}={\rho }_{\mathrm{P}}\frac{{\alpha }^5}{{\alpha }_2^5}\approx \hfill \\ \hfill & \approx -5.7735\times {10}^{96}[\mathrm{kg}/{\mathrm{m}}^3]\left(|{\rho }_{\mathrm{P}2}|>|{\rho }_{\mathrm{P}}|\right),\hfill \end{array}$$

(37)

and the ${\alpha }_2$-Planck area

$$\begin{array}{cc}\hfill {\ell }_{\mathrm{P}i}^2& =\frac{\hslash G}{c_n^3}={\ell }_{\mathrm{P}}^2\frac{{\alpha }_2^3}{{\alpha }^3}\approx \hfill \\ \hfill & \approx -2.4406\times {10}^{-70}\left[{\mathrm{m}}^2\right]\left(|{\ell }_{\mathrm{P}i}^2|<|{\ell }_{\mathrm{P}}^2|\right),\hfill \end{array}$$

(38)

are real and bivalued similarly to the Planck density ${\rho }_{\mathrm{P}}$ and area ${\ell }_{\mathrm{P}}^2$. Interestingly, both Planck forces $F_{\mathrm{P}}$ and

$$\begin{array}{cc}\hfill F_{\mathrm{P}2}& =\frac{c_2^4}{G}=\frac{c^4}{G}\frac{{\alpha }^4}{{\alpha }_2^4}=F_{\mathrm{P}}\frac{{\alpha }^4}{{\alpha }_2^4}\approx \hfill \\ \hfill & \approx 1.3251\times {10}^{44}\left[\mathrm{N}\right]\left(F_{\mathrm{P}2}>F_{\mathrm{P}}\right),\hfill \end{array}$$

(39)

are strictly positive.

We note that Coulomb’s law for elementary charges and Newton’s law of gravity for Planck masses define the fine-structure constants

$$\frac{1}{4\pi R_{*}^2}\frac{e^2}{{ϵ}_0}=\alpha G\frac{m_{\mathrm{P}}^2}{R_{*}^2}={\alpha }_{2}G\frac{m_{\mathrm{P}i}^2}{R_{*}^2},$$

(40)

where $R_{*}$ is some real or imaginary distance and $m_{\mathrm{P}i}$ is imaginary. The area of a sphere in the denominator of the Coulomb force invites further research.

The relations between time (31) and temperature (32) ${\alpha }_2$-Planck units are inverted, ${\alpha }^5{t}_{\mathrm{P}i}^2={\alpha }_2^5{t}_{\mathrm{P}}^2$, ${\alpha }_2^5{T}_{\mathrm{P}i}^2={\alpha }^5{T}_{\mathrm{P}}^2$, and saturate the energy-time version of Heisenberg’s uncertainty principle (HUP) taking energy from the equipartition theorem for one bit of information [5,12,37]

$$\frac{1}{2}{k}_{\mathrm{B}}{T}_{\mathrm{P}}{t}_{\mathrm{P}}=\frac{1}{2}{k}_{\mathrm{B}}{T}_{\mathrm{P}i}{t}_{\mathrm{P}i}=\frac{\hslash }{2}.$$

(41)

Furthermore, eliminating $\alpha$ and ${\alpha }_2$ from the relations (28)-(30), yields

$$\begin{array}{cc}\hfill & {\ell }_{\mathrm{P}}{m}_{\mathrm{P}}^3={\ell }_{\mathrm{P}i}{m}_{\mathrm{P}i}^3\mathrm{and}{\ell }_{\mathrm{P}}{q}_{\mathrm{P}}^3={\ell }_{\mathrm{P}i}{q}_{\mathrm{P}i}^3.\hfill \end{array}$$

(42)

Contrary to the elementary charge e (18), there is no physically meaningful elementary mass $M_e=\pm 1.8592\times {10}^{-9}\left[\mathrm{kg}\right]$ that would satisfy the relation (30)

$$M_e^2=\alpha m_{\mathrm{P}}^2={\alpha }_2{m}_{\mathrm{P}i}^2.$$

(43)

Neither is there a physically meaningful elementary (and imaginary) length $L_e\approx \pm i9.7382\times {10}^{-39}\left[\mathrm{m}\right]$ satisfying the relation (38)

$$L_e^2={\alpha }^3{\ell }_{\mathrm{P}i}^2={\alpha }_2^3{\ell }_{\mathrm{P}}^2,$$

(44)

(which in modulus is almost 1660 times smaller than the Planck length), or an elementary temperature $T_e\approx \pm 6.4450\times {10}^{26}\left[\mathrm{K}\right]$ abiding to (32)

$$T_e^2={\alpha }^5{T}_{\mathrm{P}}^2={\alpha }_2^5{T}_{\mathrm{P}i}^2,$$

(45)

and close to the Hagedorn temperature of grand unified string models.

Planck charge relation (18) and the charge conservation principle imply that the elementary charge e is the quantum of charge in real and imaginary dimensions, while masses, lengths, temperatures, and other derived quantities that can vary with time are not similarly quantized. The universal character of the charges is additionally emphasized by the real $\sqrt{\alpha }$ multiplied by i in the imaginary charge energy (58) and imaginary $\sqrt{{\alpha }_2}$ in the real charge energy (59). Furthermore, the same forms of the relations (18) and (43) reflect the same forms of Coulomb’s law and Newton’s law of gravity, which are the inverse-square laws.

In the following, where deemed appropriate, we shall express the physical quantities by Planck units

$$\begin{array}{cc}M:=m{m}_{\mathrm{P}},\hfill & M_i:=m_i{m}_{\mathrm{P}i},m,m_i\in \mathbb{R}\hfill \\ E:=m{E}_{\mathrm{P}}\hfill & E_i:=m_i{E}_{\mathrm{P}i},\hfill \\ Q:=qe,\hfill & Q_i:=iQ=iqe,q\in \mathbb{Z},\hfill \\ \lambda :=l{\ell }_{\mathrm{P}},\hfill & {\lambda }_i:=l_i{\ell }_{\mathrm{P}i},l=\frac{2\pi }{m},l_i=\frac{2\pi }{m_i},\hfill \\ \{R,D\}:=\{r,d\}{\ell }_{\mathrm{P}},\hfill & \{R_i,D_i\}:=\{r_i,d_i\}{\ell }_{\mathrm{P}i},r,d,r_i,d_i\in \mathbb{R},\hfill \end{array}$$

(46)

where uppercase letters M, E, Q, $\lambda$, R, and D denote respectively masses, energies, charges, Compton wavelengths, radii, and diameters (or lengths), lowercase letters denote multipliers of the positive real Planck units and imaginary ${\alpha }_2$-Planck units, and the subscripts i refer to the multiplication of imaginary quantities. We note that the discretization of charges by integer multipliers q of the elementary charge e seems too far-reaching, considering the fractional charges of quasiparticles, in particular in the open research problem of the fractional quantum Hall effect (cf. Appendix I), and energy-dependent fractional charges in electron pairing [38].

4. Black Body Objects

There are only three observable objects in nature that emit perfect black-body radiation: unsupported black holes (BHs, the densest), neutron stars (NSs), supported, as accepted, by neutron degeneracy pressure, and white dwarfs (WDs), supported, as accepted, by electron degeneracy pressure (the least dense). We shall collectively call them black-body objects (BBs). The spectral density in sonoluminescence, light emission by sound-induced collapsing gas bubbles in fluids, was also shown to have the same frequency dependence as black-body radiation [39,40]. Thus, the sonoluminescence, and in particular shrimpoluminescence [41], is probably emitted by collapsing micro-BBs. Micro-BH induced in glycerin by modulating acoustic waves was reported [42].

The term "black-body object" is not used in general relativity (GR) and standard cosmology, but standard cosmology scrunches under embarrassingly significant failings, not just tensions as is sometimes described, as if to somehow imply that a resolution will eventually be found [43]. Also, James Webb Space Telescope data show multiple galaxies that grew too massive too soon after the Big Bang, which is a strong discrepancy with the $\mathsf{\Lambda }$ cold dark matter model ($\Lambda$CDM) expectations on how galaxies formed at early times at both redshifts, even when considering observational uncertainties [44]. This is an important unresolved issue indicating that fundamental changes to the reigning $\Lambda$CDM model of cosmology are needed [44]. The term object as a collection of matter is a misnomer as it neglects the (quantum) nonlocality [45] that is independent of the entanglement among particles [46], as well as the Kochen-Specker contextuality [47], and increases as the number of particles grows [48,49]. Thus, we use emphasis for (perceivably indistinguishable) particle and (perceivably distinguishable) object, as well as for matter and distance. The ugly duckling theorem [50,51] asserts that every two objects we perceive are equally similar (or equally dissimilar), however ridiculous and contrary to common sense4 that may sound. These terms do not have an absolute meaning in ED. In particular, given the observation of quasiparticles in classical systems [52]. Within the framework of ED no object is enclosed in space.

Entropic gravity [37] explains the galaxy rotation curves without resorting to dark matter (which is not required to explain the rotation curves of certain galaxies, such as the massive relic galaxy NGC 1277 [53]), has been experimentally confirmed [54], and is decoherence-free [55]. It has been experimentally confirmed that the so-called accretion instability is a fundamental physical process [56]. We conjecture that this process, already recreated under laboratory conditions [57], is common for all BBs. As black-body radiation is radiation of global thermodynamic equilibrium, it is patternless [58] (thermal noise) radiation that depends only on one parameter. In the case of BHs, this is known as Hawking [59] radiation, and this parameter is the BH temperature $T_{\mathrm{BH}}=T_{\mathrm{P}}/\left(2\pi d_{\mathrm{BH}}\right)$ corresponding to the BH diameter [5] $D_{\mathrm{BH}}=d_{\mathrm{BH}}{\ell }_{\mathrm{P}}$, where $d_{\mathrm{BH}}\in \mathbb{R}$. Furthermore, BHs absorb patternless information [5,60]. Therefore, since Hawking radiation depends only on the diameter of a BH, it is the same for a given BH, even though it is momentary as the BH fluctuates (cf. Section 7).

As black-body radiation is patternless, triangulated [5] BBs contain a balanced number of Planck area triangles, each having binary potential $\delta {\phi }_k=-c^2·\{0,1\}$, as has been shown for BHs [5], based on the Bekenstein-Hawking (BH) entropy [61] $S_{\mathrm{BH}}=k_{\mathrm{B}}{N}_{\mathrm{BH}}/4$, where $N_{\mathrm{BH}}:=4\pi R_{\mathrm{BH}}^2/{\ell }_{\mathrm{P}}^2=\pi d_{\mathrm{BH}}^2$ is the information capacity of the BH surface, i.e., the $⌊N_{\mathrm{BH}}⌋\in {\mathbb{N}}_0$ Planck triangles5 corresponding to bits of information [5,12,37,61,62], and the fractional part triangle(s) having the area $\left\{N_{\mathrm{BH}}\right\}{\ell }_{\mathrm{P}}^2=(N_{\mathrm{BH}}-⌊N_{\mathrm{BH}}⌋){\ell }_{\mathrm{P}}^2$ too small to carry a single bit of information [5,12].

BH entropy can be derived from the Bekenstein bound

$$S\le \frac{2\pi k_{\mathrm{B}}RE}{\hslash c}=\pi k_{\mathrm{B}}md,$$

(47)

which defines an upper limit on the thermodynamic entropy S that can be contained within a sphere of radius R and energy E. Substituting BH (Schwarzschild) radius $R_{\mathrm{BH}}=2G{M}_{\mathrm{BH}}/c^2$ and mass-energy equivalence $E_{\mathrm{BH}}=M_{\mathrm{BH}}{c}^2$, where $M_{\mathrm{BH}}$ is the BH mass, into the bound (47), it reduces to the BH entropy. In other words, the BH entropy saturates the Bekenstein bound (47)6.

The patternless nature of perfect black-body radiation was derived [5] by comparing the BH entropy with the binary entropy variation $\delta S=k_{\mathrm{B}}{N}_1/2$ ([5] Eq. (55)), valid for any holographic sphere (HS), where $N_1\in \mathbb{N}$ denotes the number of active Planck triangles with binary potential $\delta {\phi }_k=-c^2$. Thus, the entropy of all BBs is

$$S_{\mathrm{BB}}=\frac{1}{4}{k}_{\mathrm{B}}{N}_{\mathrm{BB}}.$$

(48)

Furthermore, $N_1=N_{\mathrm{BB}}/2$ confirms the patternless thermodynamic equilibrium of BBs by maximizing Shannon entropy [5].

We shall define the generalized radius of a BB (this definition applies to all HSs) having mass $M_{\mathrm{BB}}$ as a function of $G{M}_{\mathrm{BB}}/c^2$ multiplier $k\in \mathbb{R},k\ge 2$

$$\begin{array}{c}\hfill R_{\mathrm{BB}}:=k\frac{G{M}_{\mathrm{BB}}}{c^2},d_{\mathrm{BB}}=2k{m}_{\mathrm{BB}},\end{array}$$

(49)

and the generalized BB energy $E_{\mathrm{BB}}$ as a function of $M_{\mathrm{BB}}{c}^2$ multiplier $a\in \mathbb{R}$ (this definition also applies to all HSs)

$$E_{\mathrm{BB}}:=a{M}_{\mathrm{BB}}{c}^2,E_{\mathrm{BB}}=a{m}_{\mathrm{BB}}{E}_{\mathrm{P}}.$$

(50)

Substituting $M_{\mathrm{BB}}$ from definition (49) into definition (50) and the latter into the Bekenstein bound (47), it becomes

$$S\le \frac{1}{2}{k}_{\mathrm{B}}\frac{a}{k}{N}_{\mathrm{BB}},$$

(51)

and equals the BB entropy (48) if $\frac{a}{2k}=\frac{1}{4}\Rightarrow a=\frac{k}{2}$. Thus, the energy of all BBs having a generalized radius (49) is

$$E_{\mathrm{BB}}=\frac{k}{2}{M}_{\mathrm{BB}}{c}^2=\frac{k}{2}{m}_{\mathrm{BB}}{E}_{\mathrm{P}}=\frac{d_{\mathrm{BB}}}{4}{E}_{\mathrm{P}},$$

(52)

with $k=2$ in the case of BHs, setting the lower bound for other BBs. We shall further call the coefficient k the size-to-mass ratio (STM). It is similar to the specific volume (the reciprocal of density) of the BB. We shall derive the upper STM bound in Section 5.

According to the no-hair theorem, all BHs general relativity (GR) solutions are characterized only by three parameters: mass, electric charge, and angular momentum. However, BHs are fundamentally uncharged, since the parameters of any conceivable BH, in particular, charged (Reissner–Nordström) and charged-rotating (Kerr–Newman) BH, can be arbitrarily altered, provided that the BH area does not decrease [63] using Penrose processes [64,65] to extract electrostatic and/or rotational energy of BH [66]. Thus any BH is defined by only one real parameter: its diameter, mass, temperature, energy, etc., each corresponding to the other. We note that in the complex Euclidean ${\mathbb{R}}^a\times {\mathbb{I}}^b$ space, an n-ball ($n=a+bi\in \mathbb{C}$) is spherical only for a vanishing imaginary dimension and for the radius $r=1/\sqrt{\pi }$ ($R={\ell }_{\mathrm{P}}/\sqrt{\pi }$) [12,14], resulting in its information capacity $N=4$, one unit of BH entropy [61]. This confirms the universality and applicability of the BH entropy (48) to all BBs.

Interiors of the BBs are inaccessible to an exterior observer [61], which makes them similar to interior-less mathematical points representing real numbers on a number line7. Yet, a BH can embrace this defining real number. Three points forming a Planck triangle corresponding to a bit of information on a BH surface can store this parameter, and this is intuitively comprehensible: the area of a spherical triangle is larger than that of a flat triangle defined by the same vertices, provided the curvature is nonvanishing and depends on this curvature, i.e., this additional parameter defines it. Thus, the only meaningful spatial notion is the Planck area triangle, which encodes one bit of classical information and its curvature.

However, it is accepted that in the case of NSs, electrons combine with protons to form neutrons, so that NSs are composed almost entirely of neutrons. But it is never the case that all electrons and all protons of an NS become neutrons. WDs are charged by definition, as they are accepted to be mostly composed of electron degenerate matter. But how can a charged BB store both the curvature and an additional parameter corresponding to its charge? Fortunately, the relation (18) ensures that the charges are the same in real and imaginary dimensions. Therefore, each charged Planck triangle of a BB surface is associated with at least three $\mathbb{R}\times \mathbb{I}$ Planck triangles, each sharing a vertex or two vertices with this triangle in ${\mathbb{R}}^2$. And this configuration is capable of storing both the curvature and the charge. The Planck area ${\ell }_{\mathrm{P}}^2$ (38) and the $\mathbb{R}\times \mathbb{I}$ imaginary Planck area ${\ell }_{\mathrm{P}}{\ell }_{\mathrm{P}i}={\ell }_{\mathrm{P}}^2\sqrt{{\alpha }_2^3/{\alpha }^3}\approx \pm 0.9666i{\ell }_{\mathrm{P}}^2$, which is smaller in modulus, can be considered in a polyspherical coordinate system, in which gravitation/acceleration acts in a radial direction (with the entropic gravitation acting inwardly and acceleration acting in both radial directions) [5], while electrostatics act in a tangential direction.

Contrary to the no-hair theorem, we characterize BBs only by mass and charge, neglecting the angular momentum since the latter introduces the notion of time, which we find redundant in the BB description of a patternless thermodynamical equilibrium.

Not only BBs are perfectly spherical. Also, their mergers, to which we shall return in Section 6, are perfectly spherical, as it has been experimentally confirmed [67] based on the registered gravitational event GW170817. One can hardly expect a collision of two perfectly spherical, patternless thermal noises to produce some aspherical pattern instead of another perfectly spherical patternless noise. Where would the information about this pattern come from at the moment of the collision? From the point of impact? No point of impact is distinct on a patternless surface.

The considerations previously discussed may be confusing to the reader, as the energy (52) of BBs other than BHs (i.e. for $k>2$) exceeds the mass-energy equivalence $E=M{c}^2$, which is the limit of the maximum real energy. In the following section, we will model a part of the energy of NS and WD that exceeds $M{c}^2$ as imaginary and thus unmeasurable.

5. BB Complex Energies

A complex energy formula

$$E_R:=E_{M_R}+i{E}_{Q_R}=M_R{c}^2+\frac{i{Q}_R}{2\sqrt{\pi {ϵ}_{0}G}}{c}^2,$$

(53)

where $E_{M_R}$ and $i{E}_{Q_R}$ represent respectively real and imaginary energy of an object having mass $M_R$ and charge $Q_R$8 was proposed in ref. [68]. Equation (53) considers real masses $M_R$ and charges $Q_R$. To store the surplus energy we shall modify it to a form involving real physical quantities expressed terms in Planck units and imaginary physical quantities expressed terms of the imaginary ${\alpha }_2$-Planck units using relations (26), (30), (35), (46), and (25)

$$\begin{array}{c}\hfill \frac{e}{2\sqrt{\pi {ϵ}_0}}=\sqrt{\alpha c\hslash }=\sqrt{{\alpha }_2{c}_2\hslash }.\end{array}$$

(54)

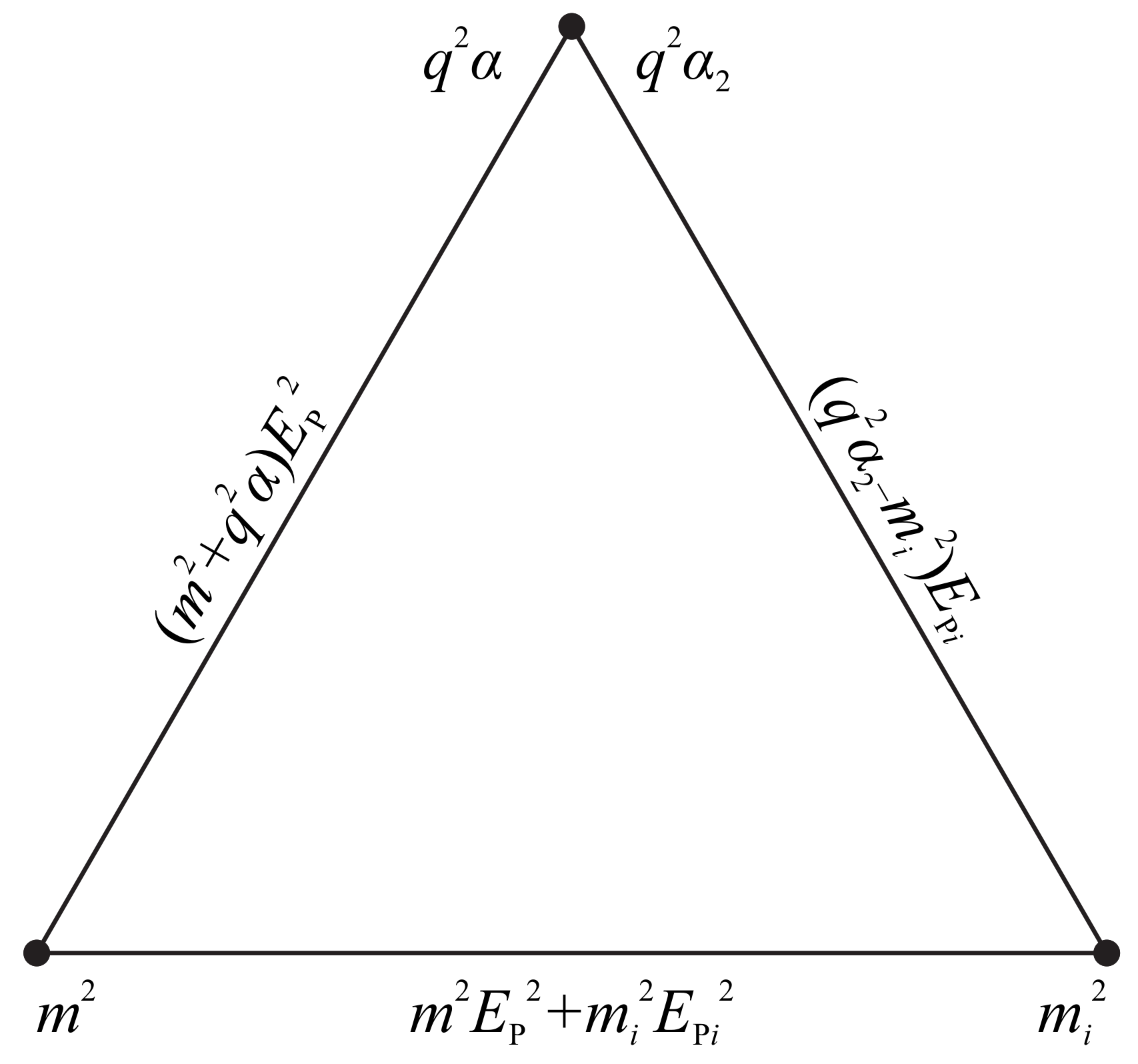
To this end, we define the following three complex energies, linking the mass, imaginary mass, and charge within the ED framework, the complex energy of real mass and imaginary charge

$$\begin{array}{cc}\hfill E_{M{Q}_i}& :=E_M+E_{Q_i}=M{c}^2+\frac{Q_i}{2\sqrt{\pi {ϵ}_{0}G}}{c}^2=\hfill \\ \hfill & =\left(m{m}_{\mathrm{P}}+iq\sqrt{\alpha }{m}_{\mathrm{P}}\right)c^2=\left(m+iq\sqrt{\alpha }\right)E_{\mathrm{P}},\hfill \end{array}$$

(55)

of real charge and imaginary mass

$$\begin{array}{cc}\hfill & E_{Q{M}_i}:=E_Q+E_{M_i}=\frac{Q}{2\sqrt{\pi {ϵ}_{0}G}}{c}_2^2+M_i{c}_2^2=\hfill \\ \hfill & =\left(q\sqrt{{\alpha }_2}{m}_{\mathrm{P}i}+m_i{m}_{\mathrm{P}i}\right)c_2^2=\frac{{\alpha }^2}{{\alpha }_2^2}\left(q\sqrt{\alpha }+\sqrt{\frac{\alpha }{{\alpha }_2}}{m}_i\right)E_{\mathrm{P}},\hfill \end{array}$$

(56)

and of real mass and imaginary mass

$$\begin{array}{cc}\hfill E_{M{M}_i}& :=M{c}^2+M_i{c}_2^2=\left(m+\sqrt{\frac{{\alpha }^5}{{\alpha }_2^5}}{m}_i\right)E_{\mathrm{P}},\hfill \end{array}$$

(57)

as illustrated in Figure 2.

We neglect the energy of real and imaginary charges $E_{Q{Q}_i}$, since by the relation (18), the unit of charge is the same in real and imaginary dimensions. The mass-energy equivalence relates the mass M or $M_i$ to the speed of light c or $c_2$.

Energies (55) and (56) yield two different charge energies corresponding to the elementary charge, the imaginary quantum

$$E_{Q_i}(q=\pm 1)=\pm i\sqrt{\alpha }{E}_{\mathrm{P}}\approx \pm i1.6710\times {10}^8\left[\mathrm{J}\right],$$

(58)

and the - larger in modulus - real quantum

$$E_Q(q=\pm 1)=\pm \sqrt{{\alpha }_2}{E}_{\mathrm{P}i}\approx \pm 1.7684\times {10}^8\left[\mathrm{J}\right].$$

(59)

Furthermore, $\forall q$, ${\alpha }^2{E}_{Qi}=i{\alpha }_2^2{E}_Q$.

The squared moduli of the complex energies (55)-(57), expressed in terms of the Planck energy, are

$$\begin{array}{c}\hfill |E_{M{Q}_i}{|}^2=\left(M^2+q^2\alpha m_{\mathrm{P}}^2\right)c^4=\left(m^2+q^2\alpha \right)E_{\mathrm{P}}^2,\end{array}$$

(60)

$$\begin{array}{c}\hfill |E_{Q{M}_i}{|}^2=\frac{{\alpha }^4}{{\alpha }_2^4}\left(q^2\alpha m_{\mathrm{P}}^2-M_i^2\right)c^4=\frac{{\alpha }^4}{{\alpha }_2^4}\left(q^2\alpha -\frac{\alpha }{{\alpha }_2}{m}_i^2\right)E_{\mathrm{P}}^2,\end{array}$$

(61)

$$\begin{array}{c}\hfill |E_{M{M}_i}{|}^2=\left(M^2-\frac{{\alpha }^4}{{\alpha }_2^4}{M}_i^2\right)c^4=\left(m^2-\frac{{\alpha }^5}{{\alpha }_2^5}{m}_i^2\right)E_{\mathrm{P}}^2.\end{array}$$

(62)

Theorem 1.

Complex energies (55)-(57) cannot simultaneously have their real and imaginary parts equal in modulus.

Proof. 

Complex energies $E_{M{Q}_i}$ and $E_{Q{M}_i}$ are real-to-imaginary balanced if their real and imaginary parts are equal in modulus. This holds for

$$q^2\alpha =m^2=-\frac{\alpha }{{\alpha }_2}{m}_i^2.$$

(63)

However, they cannot be simultaneously balanced with the energy $E_{M{M}_i}$, which is balanced for

$$m^2=-\frac{{\alpha }^5}{{\alpha }_2^5}{m}_i^2\ne -\frac{\alpha }{{\alpha }_2}{m}_i^2.$$

(64)

□

Since by the relation (18) charges are the same in real and imaginary dimensions, squared moduli of complex energies $E_{M{Q}_i}$ and $E_{Q{M}_i}$ must be equal, allowing us to obtain the value of the imaginary mass $M_i$ as a function of mass M and charge Q in this equilibrium

$$\begin{array}{cc}\hfill & m_i=\pm \sqrt{\frac{{\alpha }_2}{\alpha }\left[q^2\alpha \left(1-\frac{{\alpha }_2^4}{{\alpha }^4}\right)-\frac{{\alpha }_2^4}{{\alpha }^4}{m}^2\right]}.\hfill \end{array}$$

(65)

In particular for $q=0$ the relation (65) yields

$$m_i^2=-\frac{{\alpha }_2^5}{{\alpha }^5}{m}^2\mathrm{or}{M}_i=\pm i\frac{{\alpha }_2^2}{{\alpha }^2}M\approx \pm 0.9557iM,$$

(66)

which corresponds to the relation (64). Since the mass $m_i\in \mathbb{R}$, the square root argument must be nonnegative in relation (65)

$$\begin{array}{cc}\hfill & m\ge \left|q\right|\sqrt{\alpha \left(\frac{{\alpha }^4}{{\alpha }_2^4}-1\right)}\approx \left|q\right|0.0263.\hfill \end{array}$$

(67)

This means that the masses of uncharged micro-BHs ($q=0$) in thermodynamic equilibrium can be arbitrary. However, micro NSs and micro WDs, also in thermodynamic equilibrium, are charged. Thus, even a single elementary charge ($q=1$) of a white dwarf renders its mass $M_{\mathrm{WD}}=5.7275\times {10}^{-10}\left[\mathrm{kg}\right]$ comparable to the mass of a grain of sand.

We note here that only the masses satisfying $M<2\pi m_{\mathrm{P}}\approx 1.3675\times {10}^{-7}\left[\mathrm{kg}\right]$ have Compton wavelengths larger than Planck length [5]. We note in passing that a classical description has been ruled out on the microgram ($1\times {10}^{-9}\left[\mathrm{kg}\right]$) mass scale [69]. Comparing this bound with the bound (67) yields the charge multiplier q corresponding to an atomic number

$$Z=⌊\frac{2\pi }{\sqrt{\alpha \left(\frac{{\alpha }^4}{{\alpha }_2^4}-1\right)}}⌋=⌊238.7580⌋=238,$$

(68)

of a hypothetical element, which - as we conjecture - sets the limit on an extended periodic table and is a little higher than the accepted limit of $Z=184$ (unoctquadium). More massive elements would have Compton wavelengths smaller than the Planck length, which is physically implausible because the Planck area is the smallest area required to encode one bit of information [5,37,61,62]. From the relation (67) we can also obtain the maximum wavelength $l=2\pi /m$ corresponding to the charge q. For $q^2=1$ it is $\lambda <3.8589\times {10}^{-33}\left[\mathrm{m}\right]$ with $l<238.7580$ corresponding to the bound (68).

Theorem 2.

Complex energies (55)-(57) are equal.

$$\begin{array}{cc}\hfill & |E_{M{Q}_i}{|}^2=|E_{Q{M}_i}{|}^2={\left|E_{M{M}_i}\right|}^2=\hfill \\ \hfill & =\left(1+\frac{{\alpha }_2^4}{{\alpha }^4}\right)m^2{E}_{\mathrm{P}}^2=\left(1+\frac{{\alpha }_2^4}{{\alpha }^4}\right)q^2\alpha E_{\mathrm{P}}^2=\left(1+\frac{{\alpha }_2^4}{{\alpha }^4}\right)\frac{{\alpha }^9}{{\alpha }_2^9}{m}_i^2{E}_{\mathrm{P}}^2\hfill \end{array}$$

(69)

for

$$q^2\alpha =-\frac{{\alpha }^5}{{\alpha }_2^5}{m}_i^2=\frac{{\alpha }_2^4}{{\alpha }^4}{m}^2,m_i^2=-\frac{{\alpha }_2^9}{{\alpha }^9}{m}^2.$$

(70)

Proof. 

Direct calculation proves the relation () and if the squared moduli (60)-(62) are equal to some constant energy

$$\begin{array}{cc}\hfill & |E_{M{Q}_i}{|}^2=|E_{Q{M}_i}{|}^2={\left|E_{M{M}_i}\right|}^2:=A^2{E}_{\mathrm{P}}^2,\hfill \end{array}$$

(71)

then subtracting $|E_{M{Q}_i}{|}^2-{\left|E_{Q{M}_i}\right|}^2$ yields

$$m^2+\frac{\alpha }{{\alpha }_2}{m}_i^2=A^2\left(1-\frac{{\alpha }_2^4}{{\alpha }^4}\right);$$

(72)

subtracting this from $|E_{M{M}_i}{|}^2$ yields

$$m_i^2=-A^2\frac{{\alpha }_2^9}{{\alpha }^5({\alpha }^4+{\alpha }_2^4)},$$

(73)

which substituted into the relation (72) yields

$$m^2=A^2\frac{{\alpha }^4}{{\alpha }^4+{\alpha }_2^4},$$

(74)

and finally, substituting the relation (74) into the modulus (60) yields

$$q^2\alpha =A^2\frac{{\alpha }_2^4}{{\alpha }^4+{\alpha }_2^4}.$$

(75)

□

We can interpret the squared generalized energy of BBs (52) as the squared modulus of the complex energy of the real mass $E_{M{Q}_i}$, taking the observable real energy $E_{\mathrm{BB}}=M_{\mathrm{BB}}{c}^2$ of the BB as the real part of this energy. Thus

$$\begin{array}{c}\hfill \frac{k^4}{4}{m}_{\mathrm{BB}}^2=m_{\mathrm{BB}}^2+q_{\mathrm{BB}}^2\alpha ,q_{\mathrm{BB}}^2\alpha =m_{\mathrm{BB}}^2\left(\frac{k^2}{4}-1\right),\end{array}$$

(76)

where $q_{\mathrm{BB}}^2\alpha$ represents a charge surplus energy exceeding $M_{\mathrm{BB}}{c}^2$. Similarly, we can interpret the squared generalized energy of BBs (52) as the squared modulus of the complex energy of the imaginary mass $E_{Q{M}_i}$. Thus

$$\begin{array}{cc}\hfill & \frac{k^2}{4}{m}_{\mathrm{BB}}^2=\frac{{\alpha }^4}{{\alpha }_2^4}\left(q_{\mathrm{BB}}^2\alpha -\frac{\alpha }{{\alpha }_2}{m}_{iBB}^2\right).\hfill \end{array}$$

(77)

Substituting $q_{\mathrm{BB}}^2\alpha$ from the relation (76) into the relation (77) turns the equilibrium condition (65) into a function of the STM k instead of the charge q

$$\begin{array}{c}\hfill m_{i\mathrm{BB}}=\pm m_{\mathrm{BB}}\sqrt{\frac{{\alpha }_2}{\alpha }\left[\frac{k^2}{4}\left(1-\frac{{\alpha }_2^4}{{\alpha }^4}\right)-1\right]},\end{array}$$

(78)

which yields the imaginary mass of a BH (for $k=2$) and corresponds to the relation (66) between uncharged masses M and $M_i$, which is, notably, independent of the STM. The square root argument in the relation (78) must be non-negative, since $m_{\mathrm{BB}},m_{i\mathrm{BB}}\in \mathbb{R}$. This leads to the maximum STM bound

$$\begin{array}{c}\hfill k\le \frac{2}{\sqrt{1-\frac{{\alpha }_2^4}{{\alpha }^4}}}\approx 6.7933=k_{\max }.\end{array}$$

(79)

The relations (76) and (78) are shown in Figure 3.

Furthermore, using the relation (26), from (78) we obtain the relation between real and imaginary BH energies $E_{\mathrm{BH}i}=\pm i{E}_{\mathrm{BH}}$, which are equal in modulus. In general, the relation (78) relates BBO energies as

$$E_{\mathrm{BBI}i}^2=E_{\mathrm{BB}}^2\left[\frac{{\alpha }^4}{{\alpha }_2^4}\left(\frac{k^2}{4}-1\right)-\frac{k^2}{4}\right].$$

(80)

The maximum STM bound $k_{\max }$ (79) sets the bounds on the BB energy (52), mass, and radius (49)

$$R_{\mathrm{BH}}=\frac{2G{M}_{\mathrm{BB}}}{c^2}\le R_{\mathrm{BB}}\le \frac{k_{\max }G{M}_{\mathrm{BB}}}{c^2}.$$

(81)

In particular, using the relations (46), $2m_{\mathrm{BB}}\le r_{\mathrm{BB}}\le k_{\max }{m}_{\mathrm{BB}}$ or $r_{\mathrm{BB}}/k_{\max }\le m_{\mathrm{BB}}\le r_{\mathrm{BB}}/2$.

Furthermore, the relations (67) and (79) expresed in terms of the generalized radius (49) $k=d_{\mathrm{BB}}/\left(2m_{\mathrm{BB}}\right)$ set the bound on the minimum mass of BB if $|E_{M{Q}_i}{|}^2={\left|E_{Q{M}_i}\right|}^2$

$$\begin{array}{cc}\hfill & m_{\mathrm{BB}}>max\left\{q_{\mathrm{BB}}\sqrt{\alpha \left(\frac{{\alpha }^4}{{\alpha }_2^4}-1\right)},\frac{d_{\mathrm{BB}}}{4}\sqrt{1-\frac{{\alpha }_2^4}{{\alpha }^4}}\right\},\hfill \end{array}$$

(82)

where

$$q_{\mathrm{BB}}^2\alpha =\frac{d_{\mathrm{BB}}^2}{16}\frac{{\alpha }_2^4}{{\alpha }^4}$$

(83)

defines a condition in which neither $q_{\mathrm{BB}}$ nor $d_{\mathrm{BB}}$ can be further increased to reach its counterpart (defined, respectively, by $d_{\mathrm{BB}}$ and $q_{\mathrm{BB}}$) in the bound (82). Thus, for example, 1-bit BB ($d_{\mathrm{BB}}=1/\sqrt{\pi }$) corresponds to $q_{\mathrm{BB}}>1.5780$, $\pi$-bit BB ($d_{\mathrm{BB}}=1$) corresponds to $q_{\mathrm{BB}}>2.7969$, while the conjectured heaviest element with atomic number $q_{\mathrm{BB}}$ (68) corresponds to

$$d_{\mathrm{BB}}=\pm \frac{8\pi }{\sqrt{1-\frac{{\alpha }_2^4}{{\alpha }^4}}}\approx \pm 85.3666.$$

(84)

In the case of a BB, we obtain the equality of all three complex energies (55)-(57) substituting $A=m_{\mathrm{BB}}k/2$ from (49) into the relation (71) and comparing this with (69). This yields

$$\begin{array}{cc}\hfill & k_{\mathrm{eq}}=2\sqrt{1+\frac{{\alpha }_2^4}{{\alpha }^4}}\approx 2.7665,\hfill \end{array}$$

(85)

at which all three energies are equal. The equilibrium $k_{\mathrm{eq}}$ (85) and the maximum $k_{\max }$ (79) STMa satisfy $k_{\mathrm{eq}}^2+16/k_{\max }^2=8$.

The BB in the energy equilibrium $k_{\mathrm{eq}}$ bearing the elementary charge ($q^2=1$) would have mass $M_{{\mathrm{BB}}_{\mathrm{eq}}}\approx \pm 1.9455\times {10}^{-9}\left[\mathrm{kg}\right]$, imaginary mass $M_{i{\mathrm{BB}}_{\mathrm{eq}}}\approx \pm i1.7768\times {10}^{-9}\left[\mathrm{kg}\right]$, wavelength ${\lambda }_{{\mathrm{BB}}_{\mathrm{eq}}}\approx \pm 1.1361\times {10}^{-33}\left[\mathrm{m}\right]$, and imaginary wavelength ${\lambda }_{i{\mathrm{BB}}_{\mathrm{eq}}}\approx \pm i1.2160\times {10}^{-33}\left[\mathrm{m}\right]$. On the other hand, the relation (76) provides the BB charge in equilibrium (71) as $q_{\mathrm{BB}}\left(k_{\mathrm{eq}}\right)\approx 11.1874m_{\mathrm{BB}}$ and the limit of the BB charge $q_{\mathrm{BB}}\left(k_{\max }\right)\approx 37.9995m_{\mathrm{BB}}$

We note that BBs with STMs $2\le k\le 3$ are referred to in state of the art as ultracompact [70], where $k=3$ is a photon sphere radius9. Any object that undergoes complete gravitational collapse passes through an ultracompact stage [71], where $k<3$. Collapse can be approached by gradual accretion, increasing the mass to the maximum stable value, or by loss of angular momentum [71]. During the loss of angular momentum, the star passes through a sequence of increasingly compact configurations until it finally collapses to become a black hole. It was also pointed out [72] that for a neutron star of constant density, the pressure at the center would become infinite if $k=2.25$, a radius of the maximal sustainable density for gravitating spherical matter given by Buchdahl’s theorem. It was shown [73] that this limit applies to any well-behaved spherical star where density increases monotonically with radius. Furthermore, some observers would measure a locally negative energy density if $k<2.6\left(6\right)$ thus breaking the dominant energy condition, although this may be allowed [74]. As the surface gravity grows, photons from further behind the NS become visible. At $k\approx 3.52$ the whole NS surface becomes visible [75]. The relative increase in brightness between the maximum and minimum of a light curve are greater in the case of $k<3$ than in the case of $k>3$ [75]. Therefore the equilibrium STM ratio $k_{\mathrm{eq}}\approx 2.7665$ (85) is well within the range of radii of ultracompact objects researched in state-of-the-art within the framework of GR.

However, aside from the Schwarzschild radius, derivable from escape velocity $v_{esc}^2=2GM/R$ of mass M by setting $v_{esc}^2=c^2$, and discovered in 1783 by John Michell [76], all the remaining significant radii of GR are only approximations10. GR neglects the value of the fine-structure constants $\alpha$ and ${\alpha }_2$, which, similarly to $\pi$ or the base of the natural logarithm, are the fundamental constants of nature.

6. BB Mergers

As the entropy (Boltzmann, Gibbs, Shannon, von Neumann) of independent systems is additive, a merger of BB₁ and BB₂ having entropies11 (48) $S_1=\frac{1}{4}{k}_{\mathrm{B}}{N}_1$ and $S_2=\frac{1}{4}{k}_{\mathrm{B}}\pi d_2^2$, produces a BB_C having entropy

$$S_1+S_2=S_C\iff d_1^2+d_2^2=d_C^2,$$

(86)

which shows that the resultant information capacity is the sum of the information capacities of the merging components. Thus, a merger of two primordial BHs, each having the Planck length diameter, the reduced Planck temperature $\frac{T_{\mathrm{P}}}{2\pi }$ (the largest physically significant temperature [12]), and no tangential acceleration $a_{LL}$[5,12], produces a BH having $d_{\mathrm{BH}}=\pm \sqrt{2}$ which represents the minimum BH diameter allowing for the notion of time [12]. In comparison, a collision of the latter two BHs produces a BH having $d_{\mathrm{BH}}=\pm 2$ having the triangulation defining only one precise diameter between its poles (cf. [5] Figure 3(b)), which is also recovered from HUP (cf. Appendix G).

Substituting the generalized diameter (49) into the entropy relation (86) establishes a Pythagorean relation between the generalized energies (52) of the merging components and the merger

$$\frac{k_C^2}{4}{m}_C^2=\frac{k_1^2}{4}{m}_1^2+\frac{k_2^2}{4}{m}_2^2,\forall m_k\in \{\mathbb{R},\mathbb{I}\}.$$

(87)

It is accepted that gravitational events’ observations alone allow measuring the masses of the merging components, setting a lower limit on their compactness, but it does not exclude mergers more compact than neutron stars, such as quark stars, BHs, or more exotic objects [84]. We note in passing that describing the registered gravitational events as waves is misleading - normal modulation of the gravitational potential, registered by LIGO and Virgo interferometers, and caused by rotating (in the merger case, inspiral) objects, is wrongly interpreted as a gravitational wave understood as a carrier of gravity [85]. Furthermore, it has been hinted that outside GR, merging BHs may differ from their GR counterparts [86].

The accepted value of the Chandrasekhar WD mass limit, which prevents its collapse into a denser form, is $M_{\mathrm{Ch}}\approx 1.4M_{\odot }$[87] and the accepted value of the analogous Tolman–Oppenheimer–Volkoff NS mass limit is $M_{\mathrm{TOV}}\approx 2.9M_{\odot }$ [88,89]. There is no accepted value of the BH mass limit. The conjectured value is $5\times {10}^{10}{M}_{\odot }\approx 9.95\times {10}^{40}\mathrm{kg}$. We note in passing that a BH with a surface gravity equal to the Earth’s surface gravity (9.81 m/s²) would require a diameter of $D_{BH}\approx 9.16\times {10}^{15}\mathrm{m}$ (slightly less than one light year) [5] and mass $M_{BH}\approx 3.08\times {10}^{42}\mathrm{kg}$ exceeding the conjectured limit. The masses of most registered merging components go well beyond $M_{\mathrm{TOV}}$. Of those that do not, most of the total or final masses exceed this limit. Therefore, these mergers are classified as BH mergers. Only a few are classified otherwise, including GW170817, GW190425, GW200105, and GW200115, listed in Table 1.

The relation (87) explains the measurements of large masses of the BB mergers with at least one charged merging component without resorting to any hypothetical types of exotic stellar objects such as quark stars. Interferometric data, available online at the Gravitational Wave Open Science Center (GWOSC) portal12, indicates that the total mass of a merger is the sum of the masses of the merging components. Thus

$$\begin{array}{cc}\hfill m_C& =m_1+m_2,\hfill \\ \hfill m_C^2& =m_1^2+m_2^2+2m_1{m}_2,\hfill \\ \hfill m_C^2& \left\{\begin{array}{cc}\ge m_1^2+m_2^2\hfill & \mathrm{if}{m}_1{m}_2\ge 0\hfill \\ \le m_1^2+m_2^2\hfill & \mathrm{if}{m}_1{m}_2\le 0\hfill \end{array}\right..\hfill \end{array}$$

(88)

We can use the squared moduli $|E_{M{Q}_i}{|}^2$, $|E_{Q{M}_i}{|}^2$, and $|E_{M{M}_i}{|}^2$ to derive some information about the merger from the relation (87). We shall initially assume $m_k\ge 0\Rightarrow m_1{m}_2\ge 0$, since negative masses, similar to negative lengths, and their products with positive ones, are (in general [21]) inaccessible for direct observation, unlike charges. $|E_{M{Q}_i}{|}^2$ with the first inequality (88) yields

$$\begin{array}{cc}\hfill & |E_{M{Q}_i}{|}_C^2=|E_{M{Q}_i}{|}_1^2+{\left|E_{M{Q}_i}\right|}_2^2,\hfill \\ \hfill & m_C^2=m_1^2+m_2^2+(q_1^2+q_2^2)\alpha -q_C^2\alpha \ge m_1^2+m_2^2,\hfill \\ \hfill & q_C^2\le q_1^2+q_2^2,\hfill \end{array}$$

(89)

On the other hand, $|E_{Q{M}_i}{|}^2$ with the inequality (89) lead to (${\alpha }_2<0$), so the direction of the inequality is reversed)

$$q_C^2\le q_1^2+q_2^2\Rightarrow m_{iC}^2\ge m_{i1}^2+m_{i2}^2.$$

(90)

But $|E_{M{M}_i}{|}^2$ with the first inequality (88) lead to

$$m_C^2\ge m_1^2+m_2^2\Rightarrow m_{iC}^2\le m_{i1}^2+m_{i2}^2,$$

(91)

contradicting the inequality (90) (${\alpha }_2^5<0$), while $|E_{M{M}_i}{|}^2$ with the inequality (90) lead to

$$m_{iC}^2\ge m_{i1}^2+m_{i2}^2\Rightarrow m_C^2\le m_1^2+m_2^2,$$

(92)

contradicting the first inequality (88) and consistent with the second inequality (88) introducing the product of positive and negative masses. $|E_{Q{M}_i}{|}^2$ with the inequality (91) yields

$$m_{iC}^2\le m_{i1}^2+m_{i2}^2\Rightarrow q_C^2\ge q_1^2+q_2^2,$$

(93)

contradicting the inequality (90) and so on.

The additivity of the entropy (86) of statistically independent merging BBs, both in global thermodynamic equilibrium, defined by their generalized radii (49), introduces the energy relation (87). This relation, equality of charges in real and imaginary dimensions (18), and the BB complex energies (60)-(62) induce imaginary, negative, and mixed masses during the merger. Thus, the BB merger spreads in all dimensions, not only observable ones, as a gravitational event associated with a fast radio burst (FRB) event, as reported [90] based on the gravitational event GW1904251 and the FRB 20190425A event13. Furthermore, IXPE14 observations show that the detected polarized X-rays from 4U 0142+61 pulsar exhibit a ${90}^{\circ }$ linear polarization swing from low to high photon energies [91]. In addition, direct evidence for a magnetic field strength reversal based on the observed sign change and extreme variation of FRB 20190520B’s rotation measure, which changed from $\sim 10000[\mathrm{rad}·{\mathrm{m}}^{-2}]$ to $\sim -16000[\mathrm{rad}·{\mathrm{m}}^{-2}]$ between June 2021 and January 2022 has been reported [92]; such extreme rotation measure reversal has never been observed before in any FRB or any astronomical object.

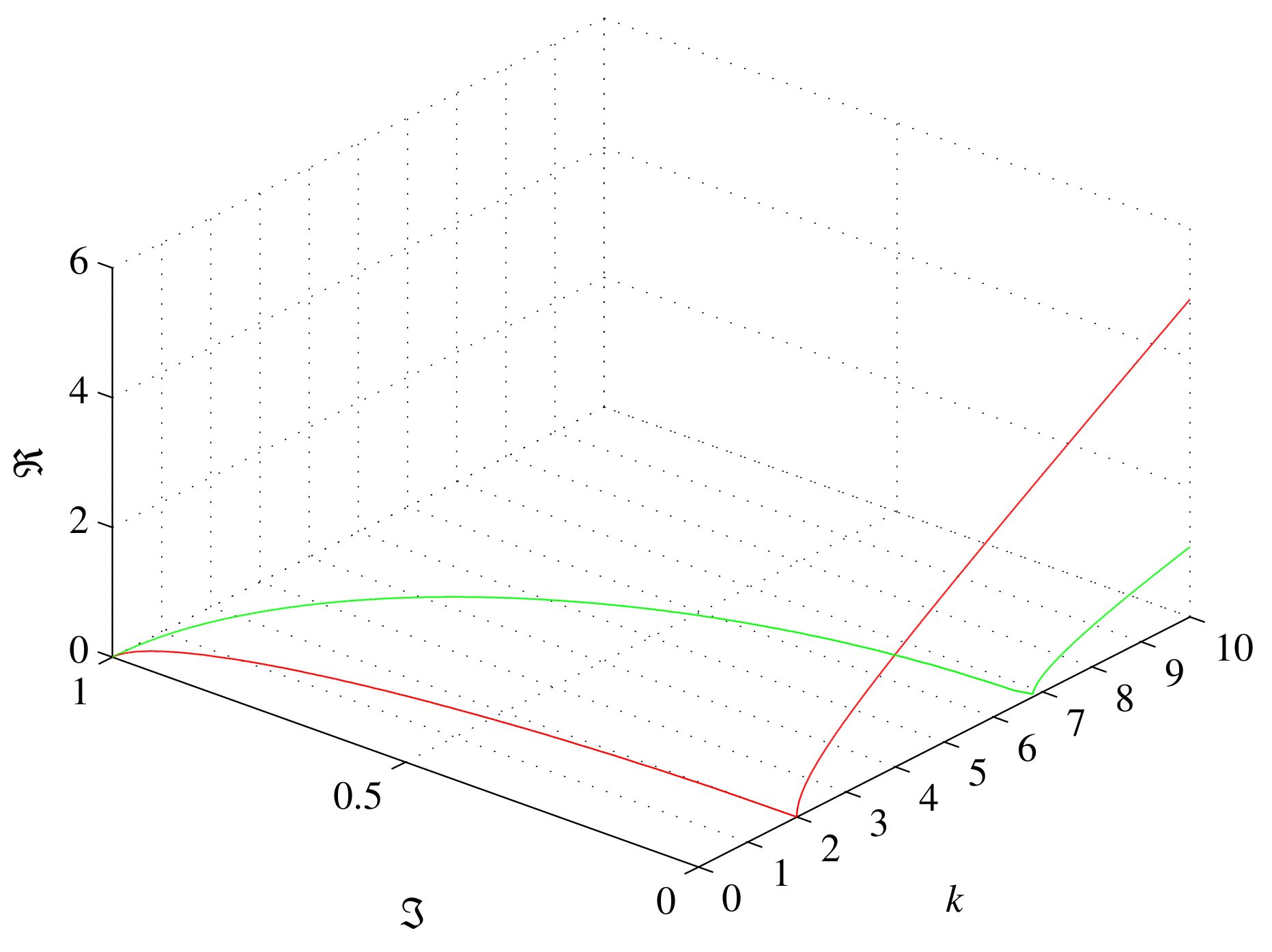
In the observable dimensions during the merger, the STM ratio $k_C$ decreases, making the BB_C denser until it becomes a BH for $k_C=2$ and no further charge reduction is possible (cf. Figure 3). From the relation (87) and the first inequality (88) we see that this holds for

$$k_C^2\left(M_1^2+M_2^2\right)\le k_1^2{M}_1^2+k_2^2{M}_2^2.$$

(94)

For two merging BHs $k_1=k_2=2$ and the relation (94) yields $k_C^2\le 4\Rightarrow k_C=2=k_{{\mathrm{BH}}_C}$.

Table 1 lists the mass-to-size ratios $k_{{\mathrm{BB}}_C}$ calculated according to the relation (87) that provide the measured mass $M_{{\mathrm{BB}}_C}$ of the merger and satisfy the inequality (94). The mass-to-size ratios $k_{{\mathrm{BB}}_1}$ and $k_{{\mathrm{BB}}_2}$ of the merging components were arbitrarily selected on the basis of their masses, taking into account the limit of mass $M_{\mathrm{TOV}}$ of the NS.

7. BB Fluctuations

A relation [93] (p.160) describing a BH information capacity, having an initial information capacity15 $N_j=4\pi R_j^2/{\ell }_{\mathrm{P}}^2$, after absorption of a particle having the Compton wavelength equal to the BH radius $R_j$

$$N_{j+1}^A=64{\pi }^3\frac{{\ell }_{\mathrm{P}}^2}{R_j^2}+32{\pi }^2+4\pi \frac{R_j^2}{{\ell }_{\mathrm{P}}^2},$$

(95)

was subsequently generalized [5] (Eq. (18)) to all Compton wavelengths $\lambda =l{\ell }_{\mathrm{P}}=\frac{2\pi }{m}{\ell }_{\mathrm{P}}$ (or frequencies $\nu =c/\lambda =1/\left(l{t}_{\mathrm{P}}\right)$) and thus to all radiated Compton energies $E=m{E}_{\mathrm{P}}$, $m\in \mathbb{R}$ absorbed (+) or emitted (−) by a BH as

$$N_{j+1}^{A/E}\left(m\right)=16\pi m^2\pm 8\pi dm+\pi d^2.$$

(96)

The relation (96) can be further generalized, using the generalized diameter $d=2k\widehat{m}$ (49), to all BBs as

$$\mathsf{\Delta }{N}^{A/E}:=N_{j+1}^{A/E}(k,m)-N_j=16\pi m\left(m\pm k\widehat{m}\right),$$

(97)

where $\widehat{m}$ represents the BB mass, and its roots are

$$\begin{array}{cc}\hfill & m^{A/E}=\{0,\mp k\widehat{m}\}=\left\{0,\mp \frac{d}{2}\right\}=\{0,\mp r\},\hfill \end{array}$$

(98)

where it vanishes.

Thus, in general, a BB changes its information capacity by

$$\begin{array}{cc}\hfill & \mathsf{\Delta }{N}^A\left\{\begin{array}{cc}>0\hfill & m\in (-\infty ,-k\widehat{m})\cap (0,\infty )\hfill \\ =0\hfill & m=\{-k\widehat{m},0\}\hfill \\ <0\hfill & m\in (-k\widehat{m},0)\hfill \end{array}\right.,\hfill \\ \hfill & \mathsf{\Delta }{N}^E\left\{\begin{array}{cc}>0\hfill & m\in (-\infty ,0)\cap (k\widehat{m},\infty )\hfill \\ =0\hfill & m=\{0,k\widehat{m}\}\hfill \\ <0\hfill & m\in (0,k\widehat{m})\hfill \end{array}\right.,\hfill \end{array}$$

(99)

absorbing or emitting energy m with $min\left(\mathsf{\Delta }N\right)=-4\pi k^2{\widehat{m}}^2$ at $m=\pm k\widehat{m}/2$, as shown in Figure 4. The relation (99) shows that, depending on its mass $\widehat{m}$, a BB can expand or contract by emitting or absorbing energy m [5]. However, expansion by emission ($\mathsf{\Delta }{N}^E>0$), for example, requires energy $m>k\widehat{m}$ exceeding the mass-energy equivalence of BB for $k>2$, which is consistent with the results presented in Section 5.

8. Complex Forces

Coulomb’s force $F_C$ between two charges is positive or negative, depending on the sign and type (real or imaginary) of the charges, as summarized below in the case of some real distance separating the charges

$$\begin{array}{ccc}\hfill & q_1{q}_2>0& q1q_2<0\\ Q_k=q_{k}e\hfill & F_C>0& F_C<0\\ Q_k=i{q}_{k}e\hfill & F_C<0& F_C>0\end{array}$$

(100)

Newton’s law of universal gravitation is also positive or negative, depending on the sign and type of masses, as summarized below

$$\begin{array}{ccc}\hfill & m_{*1}{m}_{*2}>0& m_{*1}{m}_{*2}<0\\ M_k=m_k{m}_{\mathrm{P}}\hfill & F_G>0& F_G<0\\ M_{ik}=m_{ik}{m}_{\mathrm{P}i}\hfill & F_{2G}<0& F_{2G}>0\end{array}$$

(101)

In the case of an imaginary distance, the signs of the inequalities are opposite. We do not consider mixed real or imaginary radii and mixed forces (based on real and imaginary masses/charges) as the real and imaginary dimensions are orthogonal.

Complex energies (55)-(57) define complex forces (similarly to the complex energy of real masses and charges (53), [68] Eq. (7)) acting over real and imaginary distances $R,R_i$. Using the relations (46), we obtain the following products

$$\begin{array}{cc}\hfill & E_{1m{q}_i}{E}_{2m{q}_i}:=E_{1M{Q}_i}{E}_{2M{Q}_i}/E_{\mathrm{P}}^2=\hfill \\ \hfill & =m_1{m}_2-q_1{q}_2\alpha +i\sqrt{\alpha }(m_1{q}_2+m_2{q}_1),\hfill \end{array}$$

(102)

$$\begin{array}{cc}\hfill & E_{1q{m}_i}{E}_{2q{m}_i}:=E_{1Q{M}_i}{E}_{2Q{M}_i}/E_{\mathrm{P}}^2=\hfill \\ \hfill & =\frac{{\alpha }^4}{{\alpha }_2^4}\left(\alpha q_1{q}_2+\frac{\alpha }{{\alpha }_2}{m}_{i1}{m}_{i2}+\sqrt{\frac{\alpha }{{\alpha }_2}}\sqrt{\alpha }\left(q_1{m}_{i2}+q_2{m}_{i1}\right)\right),\hfill \end{array}$$

(103)

$$\begin{array}{cc}\hfill & E_{1m{m}_i}{E}_{2m{m}_i}:=E_{1M{M}_i}{E}_{2M{M}_i}/E_{\mathrm{P}}^2\hfill \\ \hfill & =m_1{m}_2+\frac{\alpha }{{\alpha }_2}{m}_{i1}{m}_{i2}+\sqrt{\frac{{\alpha }^5}{{\alpha }_2^5}}\left(m_1{m}_{i2}+m_2{m}_{i1}\right),\hfill \end{array}$$

(104)

defining three complex forces acting over a real distance R

$$F_{A{B}_i}=\frac{G}{c^4{R}^2}{E}_{1A{B}_i}{E}_{2A{B}_i}=\frac{F_{\mathrm{P}}}{r^2}{E}_{1a{b}_i}{E}_{2a{b}_i},$$

(105)

and three complex forces acting over an imaginary distance $R_i$

$${\tilde{F}}_{A{B}_i}=\frac{G}{c_2^4{R}_i^2}{E}_{1A{B}_i}{E}_{2A{B}_i}=\frac{{\alpha }_2}{\alpha }\frac{F_{\mathrm{P}}}{r_i^2}{E}_{1a{b}_i}{E}_{2a{b}_i},$$

(106)

where $A,B\in \{M,Q\}$ and $a,b\in \{m,q\}$, and

$${\alpha }_2{r}^2{F}_{A{B}_i}=\alpha r_i^2{\tilde{F}}_{A{B}_i}.$$

(107)

With a further simplifying assumption of $r^2=r_i^2$, the forces acting on a real distanceR are stronger and opposite to the corresponding forces acting on an imaginary distance$R_i$ even though the Planck force is lower than the ${\alpha }_2$-Planck force (39). This is a strong assumption, but seemingly correct. The general radius (49) and energy (52) are the same in Planck units and in ${\alpha }_2$-Planck units; STM remains the same.

9. BB Complex Gravity and Temperature

We can use the complex force $F_{M{Q}_i}$ (105) with the product (102) (i.e., complex Newton’s law of universal gravitation) to calculate the BB surface gravity $g_{\mathrm{BB}}$, assuming an uncharged ($q_2=0$) test mass $m_2$ and comparing this force with Newton’s 2^nd law of motion

$$\begin{array}{cc}\hfill & \frac{F_{\mathrm{P}}}{r_{\mathrm{BB}}^2}\left(m_{\mathrm{BB}}{m}_2+i\sqrt{\alpha }{m}_2{q}_{\mathrm{BB}}\right)=\hfill \\ \hfill & =M_2{g}_{\mathrm{BB}}=m_2{m}_{\mathrm{P}}{\widehat{g}}_{\mathrm{BB}}{a}_{\mathrm{P}},\hfill \\ \hfill & {\widehat{g}}_{\mathrm{BB}}=\frac{1}{r_{\mathrm{BB}}^2}\left(m_{\mathrm{BB}}+i\sqrt{\alpha }{q}_{\mathrm{BB}}\right),\hfill \end{array}$$

(108)

where $g_{\mathrm{BB}}={\widehat{g}}_{\mathrm{BB}}{a}_{\mathrm{P}}$, ${\widehat{g}}_{\mathrm{BB}}\in \mathbb{R}$. Substituting $q_{\mathrm{BB}}\sqrt{\alpha }$ from the BB equilibrium relation (76) and mass taken from the generalized BB radius (49) $r_{\mathrm{BB}}=k{m}_{\mathrm{BB}}$ into the relation (108) yields

$${\widehat{g}}_{\mathrm{BB}}=\frac{1}{k{r}_{\mathrm{BB}}}\left(1\pm i\sqrt{\frac{k^2}{4}-1}\right),$$

(109)

which reduces to BH surface gravity for $k=2$ and in modulus

$${\widehat{g}}_{\mathrm{BB}}^2=\frac{1}{k^2{r}_{\mathrm{BB}}^2}\left(1+i\sqrt{\frac{k^2}{4}-1}\right)\left(1-i\sqrt{\frac{k^2}{4}-1}\right)=\frac{1}{4r_{\mathrm{BB}}^2}.$$

(110)

for all k. In particular,

$$\begin{array}{cc}\hfill & g_{\mathrm{BB}}\left(k_{\max }\right)=\pm \frac{a_{\mathrm{P}}}{d_{\mathrm{BB}}}\left(0.2944\pm 0.9557i\right),\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill & g_{\mathrm{BB}}\left(k_{\mathrm{eq}}\right)=\pm \frac{a_{\mathrm{P}}}{d_{\mathrm{BB}}}\left(0.7229\pm 0.6909i\right).\hfill \end{array}$$

(112)

The BB surface gravity (109) leads to the generalized complex Hawking blackbody-radiation equation

$$\begin{array}{c}\hfill T_{\mathrm{BB}}=\frac{\hslash }{2\pi c{k}_{\mathrm{B}}}{g}_{\mathrm{BB}}=\frac{T_{\mathrm{P}}}{k\pi d_{\mathrm{BB}}}\left(1\pm i\sqrt{\frac{k^2}{4}-1}\right),\end{array}$$

(113)

describing the BB temperature16 by including its charge in the imaginary part, which also for $k=2$ and in modulus reduces to BH temperature for all k.

In particular,

$$\begin{array}{cc}\hfill & T_{\mathrm{BB}}\left(k_{\max }\right)=\pm \frac{T_{\mathrm{P}}}{2\pi d_{\mathrm{BB}}}\left(\frac{\sqrt{{\alpha }^4-{\alpha }_2^4}}{{\alpha }^2}\pm i\frac{{\alpha }_2^2}{{\alpha }^2}\right),\hfill \\ \hfill & =\pm \frac{T_{\mathrm{P}}}{2{\pi }^3{d}_{\mathrm{BB}}}\left(\sqrt{{\pi }^4-{\pi }_1^4}\pm i{\pi }_1^2\right),\hfill \\ \hfill & =\pm \frac{T_{\mathrm{P}}}{2\pi {\pi }_2^2{d}_{\mathrm{BB}}}\left(\sqrt{{\pi }_2^4-{\pi }^4}\pm i{\pi }^2\right),\hfill \end{array}$$

(114)

$$\begin{array}{cc}\hfill & T_{\mathrm{BB}}\left(k_{\mathrm{eq}}\right)=\pm \frac{T_{\mathrm{P}}}{2\pi d_{\mathrm{BB}}}\frac{{\alpha }^2\pm i{\alpha }_2^2}{\sqrt{{\alpha }^4+{\alpha }_2^4}},\hfill \\ \hfill & =\pm \frac{T_{\mathrm{P}}}{2\pi d_{\mathrm{BB}}}\frac{{\pi }^2\pm i{\pi }_1^2}{\sqrt{{\pi }^4+{\pi }_1^4}}=\pm \frac{T_{\mathrm{P}}}{2\pi d_{\mathrm{BB}}}\frac{{\pi }_2^2\pm i{\pi }^2}{\sqrt{{\pi }_2^4+{\pi }^4}},\hfill \end{array}$$

(115)

reduce to the BH temperature for ${\alpha }_2=0$. We note that for $d_{\mathrm{BB}}=1$, $Re\left(T_{\mathrm{BB}}\left(k_{\max }\right)\right)\approx 6.6387\times {10}^{30}\left[\mathrm{K}\right]$ has the magnitude of the Hagedorn temperature of strings, while $T_{\mathrm{P}}/\left(2\pi \right)\approx 2.2549\times {10}^{31}\left[\mathrm{K}\right]$. It seems, therefore, that a universe without ${\alpha }_2$-imaginary dimensions (i.e., with ${\alpha }_2=0$) would be a black hole. Hence, the evolution of information [1,2,3,4,5,6] requires imaginary time. And we cannot zero ${\alpha }_2$ as we would have to neglect the existence of graphene.

10. Hydrogen Atom

The Bohr model of the hydrogen atom is based on three assumptions that can be conveniently expressed in terms of Planck units, using the relations (46). The assumption of a natural number of electron wavelengths ${\lambda }_e$ that fits along the circumference of the electron’s orbit of radius R becomes

$$n{\lambda }_e=2\pi R\iff n{l}_e=2\pi r,n\in \mathbb{N}.$$

(116)

De Broglie’s relation between electron mass $M_e$, velocity $V_e$ and wavelength becomes

$${\lambda }_e=\frac{h}{M_e{V}_e}=\frac{2\pi \hslash }{M_e{V}_e}\iff l_e=\frac{2\pi }{m_e{v}_e},V_e=v_{e}c,v_e\in \mathbb{R}.$$

(117)

Finally, the postulated equality between the centripetal force exerted on the electron orbiting around the proton (assuming an infinite mass of the latter) and the Coulomb force between the electron and the proton17 becomes

$$\frac{M_e{V}_e^2}{R}=\frac{1}{4\pi {ϵ}_0}\frac{e^2}{R^2}\iff m_e{v}_e^{2}r=\frac{e^2}{4\pi {ϵ}_0\hslash c}=\alpha .$$

(118)

It is remarkable that such a simple postulate expressed in terms of Planck units introduces the fine-structure constant $\alpha$. Joining the relations (116) and (117) yields

$$m_e{v}_{e}r=n,$$

(119)

which combined with (118) and using the relation (26) yields

$$V_e=v_{e}c=\frac{1}{n}\alpha c=\frac{1}{n}{\alpha }_2{c}_n\iff v_e=\frac{1}{n}\alpha ,$$

(120)

Thus, at the first circular orbit ($n=1$) in this model $v_e=\alpha$.

We shall now assume that the centripetal force acting on the electron is equal to the complex force $F_{M{Q}_i}$ (105) with the product of real mass and imaginary charge energies (102) and use the reduced mass of the proton-electron system

$$\begin{array}{cc}\hfill & \frac{m_e{m}_p}{m_e+m_p}\frac{v_e^2}{r}=\frac{m_e{m}_p+\alpha +i\sqrt{\alpha }(m_e-m_p)}{r^2},\hfill \\ \hfill v_e^2& =\frac{m_e+m_p}{r}\left(1+\frac{\alpha }{m_e{m}_p}\right)+i\frac{\sqrt{\alpha }}{r}\frac{m_e^2-m_p^2}{m_e{m}_p},\hfill \\ \hfill r& =\frac{m_e+m_p}{v_e^2}\left(1+\frac{\alpha }{m_e{m}_p}\right)+i\frac{\sqrt{\alpha }}{v_e^2}\frac{m_e^2-m_p^2}{m_e{m}_p},\hfill \end{array}$$

(121)

where $q_e=-1$ and $q_p=1$ are the electron and proton charges, and $M_p=m_p{m}_{\mathrm{P}}$, $m_p\in \mathbb{R}$ is the proton mass.

For the electron mass $M_e=9.1094\times {10}^{-31}$ [kg] and the proton mass $M_p=1.6726\times {10}^{-27}$ [kg] the equation (121) yields $v_e\approx 7.2993\times {10}^{-3}-i3.2816\times {10}^{-21}\approx \alpha$ assuming that R is equal to the Bohr radius $a_0=5.2918\times {10}^{-11}\left[\mathrm{m}\right]$ or the radius $R\approx (5.2946\times {10}^{-11}-i4.7607\times {10}^{-29})\left[\mathrm{m}\right]\approx a_0$ assuming that the Bohr model gives the velocity of the electron, that is, $v_e=\alpha$.

We note that these values correspond to the values given by the Bohr model. We further note that neglecting the opposite signs of the charges ($q_e=q_p=-1$ or $q_e=q_p=1$) in the relation (121) yields, respectively, an imaginary electron velocity $v_e\approx 3.2852\times {10}^{-21}\pm i7.2993\times {10}^{-3}\approx \pm i\alpha$ and a negative radius $R\approx (-5.2947\times {10}^{-11}\pm i4.7660\times {10}^{-29})\left[\mathrm{m}\right]\approx -a_0$. We further note that switching the signs of charges ($q_e=1$, $q_p=-1$) provides complex conjugates of the relation (121), which in this case describes the antihydrogen. Therefore, we conjecture that the energy generated during a hydrogen-antihydrogen collision is

$$E_{H-\overline{H}}=2(m_e{m}_p+\alpha )E_{\mathrm{P}}\approx 2.8549\times {10}^7\left[\mathrm{J}\right].$$

(122)

Finally, we note that the relation (121) based, as the Bohr model, on the mass of the electron provides a better agreement to the Bohr radius and the fine-structure constant since

$$\begin{array}{cc}\hfill m_e{v}_e^{2}r& =m_e{m}_p+\alpha +i\sqrt{\alpha }(m_e-m_p),\hfill \\ \hfill r& =\frac{m_p}{{\alpha }^2}+\frac{1}{m_e\alpha }+i{\alpha }^{-3/2}\left(1-\frac{m_p}{m_e}\right)\approx \frac{1}{m_e\alpha }=\frac{a_0}{{\ell }_{\mathrm{P}}},\hfill \\ \hfill v_e^2& =\alpha m_e{m}_p+{\alpha }^2+i{\alpha }^{3/2}(m_e-m_p)\approx {\alpha }^2.\hfill \end{array}$$

(123)

We note that none of the charged elementary particles that form atoms and antiatoms satisfies the complex energy equality of Theorem 2. For example, both proton ($q_p=1$) and electron ($q_e=-1$) satisfy $\alpha ={\alpha }_2^4{m}_e^2/{\alpha }^4$ and $\alpha ={\alpha }_2^4{m}_p^2/{\alpha }^4$ of the relation (70) but $m_e\ne m_p$. However, we can postulate the equality of the products of the complex energies (102)-(104), that is, for hydrogen and antihydrogen atoms

$$\begin{array}{cc}\hfill E_{epm{q}_i}& =m_e{m}_p+\alpha \pm i\sqrt{\alpha }(m_e-m_p),\hfill \\ \hfill E_{epq{m}_i}& =\frac{{\alpha }^4}{{\alpha }_2^4}\left(-\alpha +\frac{\alpha }{{\alpha }_2}{m}_{ie}{m}_{ip}\pm \sqrt{\frac{\alpha }{{\alpha }_2}}\sqrt{\alpha }\left(m_{ie}-m_{ip}\right)\right),\hfill \\ \hfill E_{epm{m}_i}& =m_e{m}_p+\frac{\alpha }{{\alpha }_2}{m}_{ie}{m}_{ip}\pm \sqrt{\frac{{\alpha }^5}{{\alpha }_2^5}}\left(m_e{m}_{ip}+m_p{m}_{ie}\right),\hfill \\ \hfill E_{epm{q}_i}& =E_{epq{m}_i}=E_{epm{m}_i}\approx \alpha ,\hfill \end{array}$$

(124)

with "+" for hydrogen and "−" for antihydrogen. Knowing the values of $m_e$ and $m_p$ the system of equations (124) resolves to

$$\begin{array}{cc}\hfill m_{ie}& =\{0\pm i0.1314,0\pm i0.0543\},\hfill \\ \hfill m_{ip}& =\{-m_{ie2},-m_{ie1}\},\hfill \end{array}$$

(125)

yielding real masses $|M_1|=1.19486\times {10}^{-09}\left[\mathrm{kg}\right]$ and $|M_2|=2.8929\times {10}^{-09}\left[\mathrm{kg}\right]$.

Expressed in terms of Planck units and the reduced mass of the proton-electron system, the Rydberg constant for hydrogen, is

$$R_{\mathrm{H}}=\frac{m_e{m}_p}{m_e+m_p}\frac{{\alpha }^2}{4\pi {\ell }_{\mathrm{P}}}\approx 1.0968\times {10}^{+07}[1/\mathrm{m}],$$

(126)

and the corresponding Rydberg formula can be expressed as

$$\frac{m_e{m}_p}{m_e+m_p}l=\frac{4\pi }{{\alpha }^2}\frac{n_1^2{n}_2^2}{n_2^2-n_1^2}=\frac{n_1^2{n}_2^2}{n_2^2-n_1^2}4{\pi }^3(16{\pi }^4+8{\pi }^3+9{\pi }^2+2\pi +1),$$

(127)

using the wavelength relation (46) and $\alpha$ algebraic expression (14). The coefficients $\{16,8,9,2,1\}$ form part of the OEIS sequence A158565 for $n=10$.

11. Discussion

The reflectance of graphene under the normal incidence of electromagnetic radiation expressed as the quadratic equation for the fine-structure constant $\alpha$ includes the 2^nd negative fine-structure constant ${\alpha }_2$. The sum of the reciprocal of this 2^nd fine-structure constant ${\alpha }_2$ with the reciprocal of the fine-structure constant $\alpha$ (2) is independent of the reflectance value R and is remarkably equal to simply $-\pi$. The particular algebraic definition of the fine-structure constant ${\alpha }^{-1}=4{\pi }^3+{\pi }^2+\pi$, containing the free term $\pi$, when introduced into this sum, yields ${\alpha }_2^{-1}=-4{\pi }^3-{\pi }^2-2\pi <0$ (15). The negative fine-structure constant ${\alpha }_2$ leads to the ${\alpha }_2$-Planck units applicable to imaginary dimensions, including imaginary ${\alpha }_2$-Planck units (28)-(36). The real and imaginary mass and charge units (21), temperature and time units (41), and length and mass units (42) are directly related to each other. Furthermore, the relation (18) shows that the elementary charge e is common for real and imaginary dimensions.

Applying ${\alpha }_2$ Planck units to a complex energy formula [68] yields complex energies (55), (56) setting the atomic number $Z=238$ as the limit on an extended periodic table. The generalized energy (52) of all perfect black-body objects (black holes, neutron stars and white dwarfs) having the generalized radius $R_{\mathrm{BB}}=k{R}_{\mathrm{BH}}/2$ exceeds the mass-energy equivalence if $k>2$. The complex energies (55)-(57) allow storage of the excess of this energy in their imaginary parts. The results show that the perfect black-body objects other than black holes cannot have masses lower than $5.7275\times {10}^{-10}\left[\mathrm{kg}\right]$ and that $k_{\max }\approx 6.7933$ $k\le 6.7933$ defined by the relation (79). In addition, it is shown that a black-body object is in the equilibrium of complex energies if its radius $R_{\mathrm{eq}}\approx 1.3833R_{\mathrm{BH}}$ (85). The proposed model explains the registered (GWOSC) high masses of the neutron star mergers without resorting to any hypothetical types of exotic stellar objects.

In the context of the results of this study, monolayer graphene, a truly 2-dimensional material with no thickness18, is a keyhole to other, unperceivable dimensionalities. The history of graphene is also instructive. Discovered in 1947 [95], graphene was long considered an academic material until it was eventually pulled from graphite in 2004 [96] by means of ordinary Scotch tape19. These fifty-seven years, along with twenty-nine years (1935-1964) between the condemnation of quantum theory as incomplete [97] and Bell’s mathematical theorem [98] asserting that it is not true, and the fifty-eight years (1964-2022) between the formulation of this theorem and 2022 Nobel Prize in Physics for its experimental loophole-free confirmation, should remind us that Max Planck, the genius who discovered Planck units, has also discovered Planck’s principle.