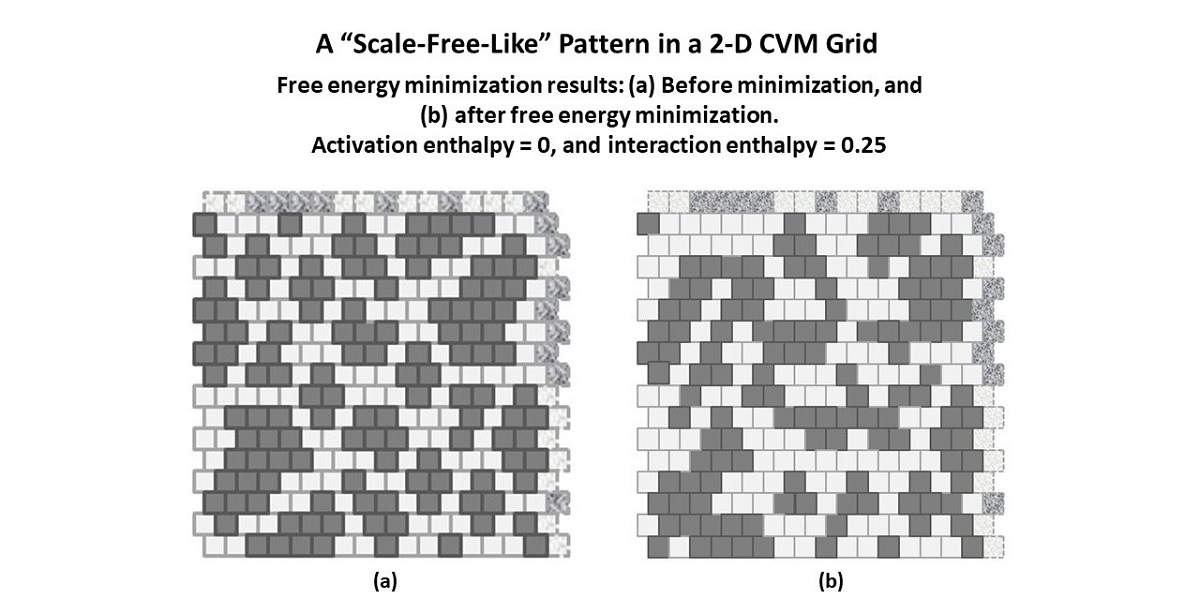
One of the biggest challenges in characterizing 2-D image topographies is finding a low-dimensional parameter set that can succinctly describe, not so much image patterns themselves, but the nature of these patterns. The 2-D Cluster Variation Method (CVM), introduced by Kikuchi in 1951, can characterize very local image pattern distributions using configuration variables, identifying nearest-neighbor, next-nearest-neighbor, and triplet configurations. Using the 2-D CVM, we can characterize 2-D topographies using just two parameters; the activation enthalpy and the interaction enthalpy. Initial investigations with two different representative topographies (``scale-free-like'' and ``rich club-like'') produce interesting results when brought to a CVM free energy minimum. Additional phase space investigations, where one of these two parameters has been set to zero, identify useful parameter ranges. Careful comparison of the analytically-predicted configuration variables versus those obtained when performing computational free energy minimization on a 2-D grid show that the computational results differ significantly from the analytic solution. The 2-D CVM can potentially function as a secondary free energy minimization within the hidden layer of a neural network, providing a basis for extending node activations over time and allowing temporal correlation of patterns.