Preprint

Article

Inflation of Universe by nonlinear electrodynamics

Altmetrics

Downloads

275

Views

165

Comments

A peer-reviewed article of this preprint also exists.

Sergey Kruglov^*

This version is not peer-reviewed

Submitted:

17 February 2024

Posted:

19 February 2024

You are already at the latest version

Alerts

Abstract

We show that Universe inflation occurs when Einstein's gravity couples to nonlinear electromagnetic fields with cosmic stochastic magnetic fields background. Nonlinear electrodynamics with two parameters is used. The strength of magnetic fields to have the Universe inflation is obtained. It is shown that singularities of the energy density and pressure are absent for any scale factors. At large scale factors one arrives at equation of state for ultra-relativistic case. It is demonstrated that the curvature invariants do not have singularities. By computing the deceleration parameter we show that graceful exit takes place with reasonable e-folding number. The duration of Universe inflation as a function of model parameters is obtained. The classical stability and causality are analyzed by calculating the speed of the sound.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

The Standard Cosmological Model (SCM) is successful but it does not solve such important problems as the initial singularity and Universe acceleration. Within the SCM there are singularities of curvature invariants at the time of the creation of Universe named Big Bang. Inflation is a rapid cosmological expansion at the initial time after Big Bang. Originally, the inflationary scenario was proposed by Guth [1] to have the initial state that required by the SCM. Universe inflation can be described by different ways: deforming general relativity [2,3,4], by the introduction of the cosmological constant, and by using quintessence (a scalar field) [5]. Here, we describe Universe inflation with the help of nonlinear electrodynamics (NED) as the source of Einstein’ gravity. Born and Infeld [6] proposed one-parameter NED which smoothes point-like charge singularity possessing self-energy finite. Also, due to quantum corrections Maxwell’s electrodynamics becomes NED (Euler–Heisenberg electrodynamics) [7,8,9]. Therefore, it is justified to consider Einstein’ gravity coupled to NED because in the inflation era electromagnetic fields were very strong. Some scenarios of Universe inflation by stochastic magnetic background were considered in [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. Here, we use NED with two parameters, which becomes Maxwell’s electrodynamics at weak fields, and it drives the Universe to accelerate for the stochastic magnetic background field. Thus, our model solves problems connected with the initial singularity and Universe acceleration.

In section 2 we consider Einstein’s gravity coupled to NED with two parameters

β

and

σ

. We find the strength of magnetic fields when the Universe inflation occurs. It is shown that singularities of the energy density and pressure are absent. For large scale factors one has equation of state for ultra-relativistic case and graceful exit takes place with reasonable e-folding number. We demonstrate that singularities of curvature invariants are absent. We calculate the deceleration parameter in section 3 which shows the evolution of universe. The duration of the universe inflation is analysed. We compute the speed of sound and study the causality and unitarity principles. Section 4 is a conclusion.

We use units with

c = ℏ = 1

and metric signature is

η = d i a g (-, +, +, +)

2. Cosmology

The Einstein–Hilbert action coupled to NED is

S = \int d^{4} x \sqrt{- g} [\frac{1}{2 κ^{2}} R + L],

(1)

where R is the Ricci scalar,

κ^{2} = 8 π G

and G is Newton’s constant. We propose the NED Lagrangian as

L = - \frac{F}{4 π {(1 + 2 β F)}^{σ}},

(2)

and

F = F^{μ ν} F_{μ ν} / 4 = (B^{2} - E^{2}) / 2

is the Lorentz invariant, E and B are the electric and magnetic fields, correspondingly. The

β

is dimensional parameter and

σ

is dimensionless parameter. When

β F \to 0

Lagrangian (2) becomes the Maxwell’s Lagrangian. We will study Universe inflation with stochastic magnetic fields background. From action (1), we obtain equations as follow:

R_{μ ν} - \frac{1}{2} g_{μ ν} R = - κ^{2} T_{μ ν},

(3)

\nabla_{μ} (L_{F} F^{μ ν}) = 0,

(4)

where

L_{F} = \frac{\partial L}{\partial F} = \frac{2 β (σ - 1) F - 1}{4 π {(1 + 2 β F)}^{σ + 1}},

(5)

and the stress-energy tensor is given by

T_{μ ν} = - F_{μ ρ} F_{ν}^{ρ} L_{F} - g_{μ ν} L (F) .

(6)

We consider the line element of homogeneous and isotropic cosmological spacetime in the form

d s^{2} = - d t^{2} + a {(t)}^{2} (d x^{2} + d y^{2} + d z^{2}),

(7)

where

a (t)

is a scale factor. The cosmic background is stochastic magnetic fields and after averaging the magnetic fields we have the isotropy of the Friedman–Robertson–Walker space-time [24]. It our approach the wavelength of electromagnetic waves is smaller than the curvature. As a result, after averaging of magnetic field we have

〈 B 〉 = 0, 〈 B_{i} B_{j} 〉 = \frac{1}{3} B^{2} g_{i j} .

(8)

Here, the brackets denote an average over a volume. In the following we omit the brackets. It is worth noting that the NED stress-energy tensor in such approach may be represented as for a perfect fluid [14]. For three dimensional flat universe the Friedmann’s equation is given by

3 \frac{\ddot{a}}{a} = - \frac{κ^{2}}{2} (ρ + 3 p),

(9)

with

\ddot{a} = \partial^{2} a / d t^{2}

. The Universe accelerates when

ρ + 3 p < 0

. By virtue of Eq. (6) we find

ρ = - L = \frac{B^{2}}{8 π {(1 + β B^{2})}^{σ}},

p = L - \frac{2 B^{2}}{3} L_{F} = \frac{B^{2} [1 - β B^{2} (4 σ - 1)]}{24 π {(1 + β B^{2})}^{σ + 1}} .

(10)

From Eq. (10) one obtains

ρ + 3 p = \frac{B^{2} [1 - β B^{2} (2 σ - 1)]]}{4 π {(1 + β B^{2})}^{σ + 1}} .

(11)

Making use of Eq. (11) and the requirement

ρ + 3 p < 0

to have the Universe acceleration, we find

\sqrt{β} B > \frac{1}{\sqrt{2 σ - 1}} .

(12)

According to Eq. (12) we have the restriction

σ > 1 / 2

. The plot of the function

\sqrt{β} B

versus

σ

is depicted in Figure 1.

The conservation of the stress-energy tensor,

\nabla^{μ} T_{μ ν} = 0

, gives the equation

\dot{ρ} + 3 \frac{\dot{a}}{a} (ρ + p) = 0 .

(13)

With the help of Eq. (10), we obtain

ρ + p = \frac{B^{2} [1 + β B^{2} (1 - σ)]}{6 π {(1 + β B^{2})}^{σ + 1}} .

(14)

Making use of Eqs. (13) and(14), one finds

B (t) = \frac{B_{0}}{a {(t)}^{2}} .

(15)

The

B_{0}

is the magnetic field when

a (t) = 1

. It was shown in Ref. [14] that Eq. (15) takes place for any NED Lagrangians. Because the scale factor increases during the inflation, the magnetic field decreases. From Eqs. (10) and (15) we obtain

lim_{a (t) \to \infty} ρ (t) = lim_{a (t) \to \infty} p (t) = 0,

lim_{a (t) \to 0} ρ (t) = lim_{a (t) \to 0} p (t) = \infty σ < 1,

lim_{a (t) \to 0} ρ (t) = lim_{a (t) \to 0} p (t) = 0 σ > 1,

lim_{a (t) \to 0} ρ (t) = - lim_{a (t) \to 0} p (t) = \frac{1}{8 π β} σ = 1 .

(16)

Thus, singularities of the energy density and pressure as

a (t) \to 0

are absent at

σ \geq 1

. At the beginning of the Universe evolution when

a \approx 0

, we have at

σ = 1

ρ = - p

that corresponds to de Sitter space-time. By virtue of Eq. (10) one finds the equation of state

w = p (t) / ρ (t) = \frac{1 - (4 σ - 1) β B^{2}}{3 (1 + β B^{2})} .

(17)

The function w versus

β B^{2}

is given in Figure 2 corresponding to

σ = 0.75, 1, 1.5

From Eq. (17) we have

lim_{B \to 0} w = \frac{1}{3},

(18)

(

a (t) \to \infty

) that corresponds to the equation of state for ultra-relativistic case [25]. At

β B^{2} = 1 / (σ - 1)

de Sitter spacetime occurs,

w = - 1

. Making use of Eqs. (3) and (6), we find the Ricci scalar

R = κ^{2} T_{μ}^{μ} = \frac{κ^{2} σ β B^{4}}{2 π {(1 + β B^{2})}^{σ + 1}} = κ^{2} (ρ - 3 p) .

(19)

We depict the function

β R / κ^{2}

versus

β B^{2}

in Figure 3.

By virtue of Eq. (19) we obtain

lim_{B \to 0} R (t) = 0,

lim_{B \to \infty} R (t) = 0 a t σ > 1,

lim_{B \to \infty} R (t) = \frac{κ^{2}}{2 π β} a t σ = 1 .

(20)

The Ricci tensor squared

R_{μ ν} R^{μ ν}

and the Kretschmann scalar

R_{μ ν α β} R^{μ ν α β}

are expressed in the form of combinations of

κ^{4} ρ^{2}

κ^{4} ρ p

, and

κ^{4} p^{2}

[17]. Therefore, in accordance with Eq. (16), they are finite as

a (t) \to 0

and

a (t) \to \infty

for

σ \geq 1

. Equations (12) and (15) show that Universe inflation takes plase at

a (t) < \sqrt[4]{β B_{0}^{2} (2 σ - 1)}

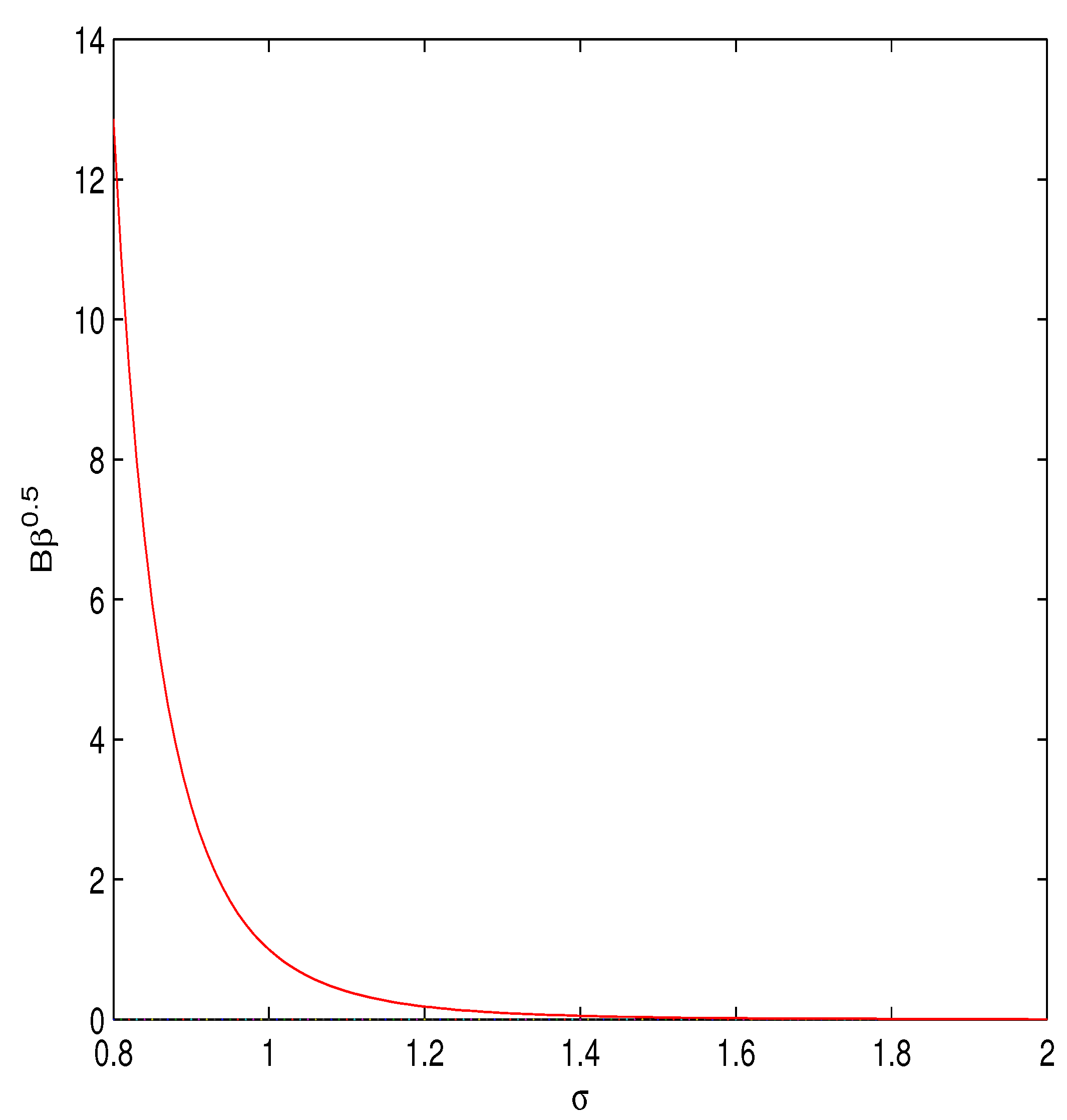
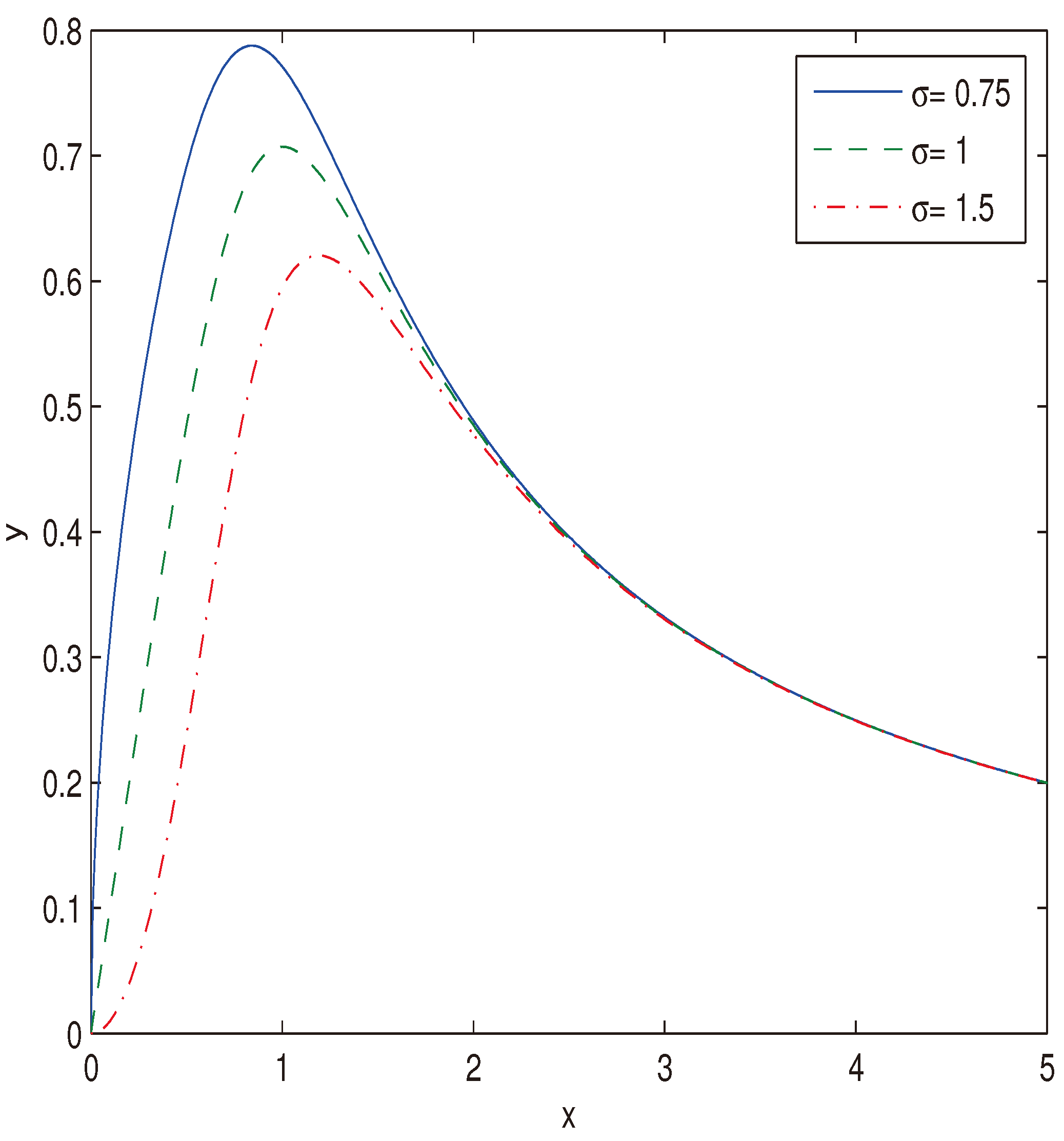
3. Universe evolution

To study the Universe evolution we consider the Friedmann equation for three dimensional flat Universe

{(\frac{\dot{a}}{a})}^{2} = \frac{κ^{2} ρ}{3} .

(21)

With the help of Eqs. (10) and (21), one finds

\dot{a} = \frac{κ B_{0} a^{2 σ - 1}}{2 \sqrt{6 π} {(a^{4} + β B_{0}^{2})}^{σ / 2}} .

(22)

Introducing the unitless variables

x = a / (β^{1 / 4} \sqrt{B_{0}})

y = 2 \sqrt{6 π β} \dot{x} / κ

Eq. (22) reads

y = \frac{x^{2 σ - 1}}{{(x^{4} + 1)}^{σ / 2}} .

(23)

We depicted the function

y (x)

in Figure 4.

Figure 4 shows that the inflation starting from Big Bang possesses the graceful exit when

\ddot{a} = 0

(

d y / d x = 0

x_{e n d} = \sqrt[4]{2 σ - 1}

. Then the universe decelerates. In accordance with Figure 4 when

σ

increases the graceful exit point

x_{e n d}

(

a_{e n d}

) also increases. Making use of Eq. (22) we obtain

\int_{a (t_{i n})}^{a (t_{e n d})} \frac{{(a^{4} + β B_{0}^{2})}^{σ / 2}}{a^{2 σ - 1}} d a = \frac{κ B_{0}}{2 \sqrt{6 π}} \int_{t_{i n}}^{t_{e n d}} d t .

(24)

Integrating Eq. (24) one arrives at the equation

\frac{a {(t_{e n d})}^{2 (1 - σ)} {(β B_{0}^{2})}^{σ / 2}}{2 (1 - σ)} F (\frac{1 - σ}{2}, - \frac{σ}{2}; \frac{3 - σ}{2}; - \frac{a {(t_{e n d})}^{4}}{β B_{0}^{2}})

- \frac{a {(t_{i n})}^{2 (1 - σ)} {(β B_{0}^{2})}^{σ / 2}}{2 (1 - σ)} F (\frac{1 - σ}{2}, - \frac{σ}{2}; \frac{3 - σ}{2}; - \frac{a {(t_{i n})}^{4}}{β B_{0}^{2}}) = \frac{κ B_{0}}{2 \sqrt{6 π}} Δ t .

(25)

The

F (a, b; c; z)

is the hypergeometric function and

▵ t = t_{e n d} - t_{i n}

is the duration of the inflation. The hypergeometric function in Eq. (25) obeys the relation

c - a = 1

, and can be expressed in the form of the incomplete B-function,

B_{z} (p, q) = p^{- 1} z^{p} F (1 - q, p; p + 1; z)

[26]. With the help of Eq. (25) we will study the Universe inflation evolution.

Making use of Eqs. (9), (10), (15) and (21) we find the deceleration parameter which describes the Universe expansion

q = - \frac{\ddot{a} a}{{(\dot{a})}^{2}} = \frac{ρ + 3 p}{2 ρ} = \frac{x^{4} + 1 - 2 σ}{x^{4} + 1} .

(26)

The deceleration parameter q versus

x = a / {(β B_{0}^{2})}^{1 / 4}

is plotted in Figure 5. The inflation occurs when

q < 0

and stops at the graceful exit

q = 0

(

x_{e n d} = \sqrt[4]{2 σ - 1}

). Then the deceleration phase starts (

q > 0

). It is worth noting that a singularity at the early epoch is absent. To evaluate the amount of the inflation we use the e-folding number [27]

N = ln \frac{a (t_{e n d})}{a (t_{i n})} .

(27)

Here,

t_{e n d}

is the inflation final time and

t_{i n}

is an initial time of the inflation. The point of graceful exit is

x_{e n d} = \sqrt[4]{2 σ - 1}

and

a (t_{e n d}) = \sqrt[4]{2 σ - 1} β^{1 / 4} \sqrt{B_{0}}

. The horizon and flatness problems may be solved if the e-folding number is

N \approx 70

[27]. By virtue of Eq. (27) one finds the scale factor which corresponds to the inflation initial time

a (t_{i n}) = \frac{\sqrt[4]{2 σ - 1} β^{1 / 4} \sqrt{B_{0}}}{exp (70)} \approx 4 \sqrt[4]{2 σ - 1} \times 10^{- 31} β^{1 / 4} \sqrt{B_{0}} .

(28)

Our model has phases of the Universe inflation, the graceful exit and deceleration. From Eq. (25) and inequality

a (t_{e n d}) ≫ a (t_{i n})

(

a (t_{e n d}) \approx 4 \times 10^{31} a (t_{i n})

), we obtain

▵ t = \frac{\sqrt{6 π} a {(t_{e n d})}^{2 (1 - σ)} β^{σ / 2} B_{0}^{σ - 1}}{(1 - σ) κ} F (\frac{1 - σ}{2}, - \frac{σ}{2}; \frac{3 - σ}{2}; - \frac{a {(t_{e n d})}^{4}}{β B_{0}^{2}}) .

(29)

a (t_{e n d}) ≫ 1

, one can use the Pfaff transformation [26]

F (a, b; c; z) = {(1 - z)}^{- a} F (a, c - b; c; \frac{z}{z - 1}) .

(30)

With the aid of Eq. (30), at

a (t_{e n d}) ≫ 1

, we find

F (\frac{1 - σ}{2}, - \frac{σ}{2}; \frac{3 - σ}{2}; - \frac{a {(t_{e n d})}^{4}}{β B_{0}^{2}}) = F (- \frac{σ}{2}, \frac{1 - σ}{2}; \frac{3 - σ}{2}; - \frac{a {(t_{e n d})}^{4}}{β B_{0}^{2}})

\approx {(1 + \frac{a {(t_{e n d})}^{4}}{β B_{0}^{2}})}^{σ / 2} F (- \frac{σ}{2}, 1; \frac{3 - σ}{2}; 1) = (1 - σ) {(1 + \frac{a {(t_{e n d})}^{4}}{β B_{0}^{2}})}^{σ / 2} .

(31)

We have used formulas [28]

F (a, b; c; 1) = Γ (c) Γ (c - a - b) / (Γ (c - a) Γ (c - b))

Γ (1 + z) = z Γ (z)

. Making use of Eqs. (29) and (31), at

a (t_{e n d}) ≫ 1

, one finds the equation

a (t_{e n d}) = \sqrt{\frac{κ B_{0} Δ t}{\sqrt{6 π}}},

(32)

corresponding to the radiation era. From Eq. (32),

a (t_{e n d}) = \sqrt[4]{(2 σ - 1) β B_{0}^{2}}

, the coupling

β

is given by

β = \frac{κ^{2} Δ t^{2}}{6 π (2 σ - 1)} .

(33)

If one takes the inflation duration

▵ t \approx 10^{- 32} s

, the values of

κ = \sqrt{8 π G}

, one can find

β

from Eq. (33). The function

y = β / (κ^{2} Δ t^{2})

versus

σ

is depicted in Figure 6.

Figure 6 shows that when parameter

σ

increases the coupling

β

decreases in order to have the same Universe inflation time.

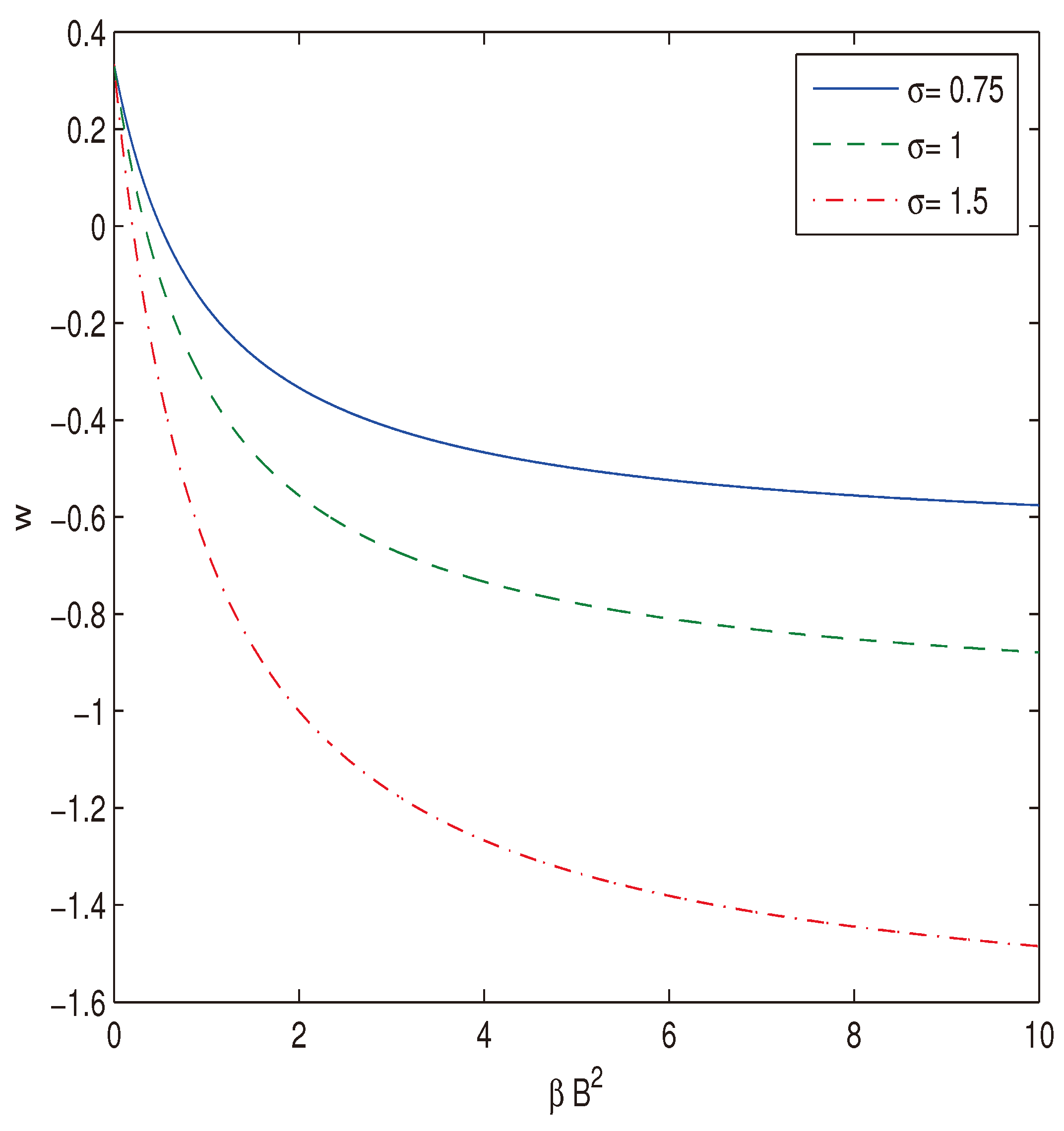
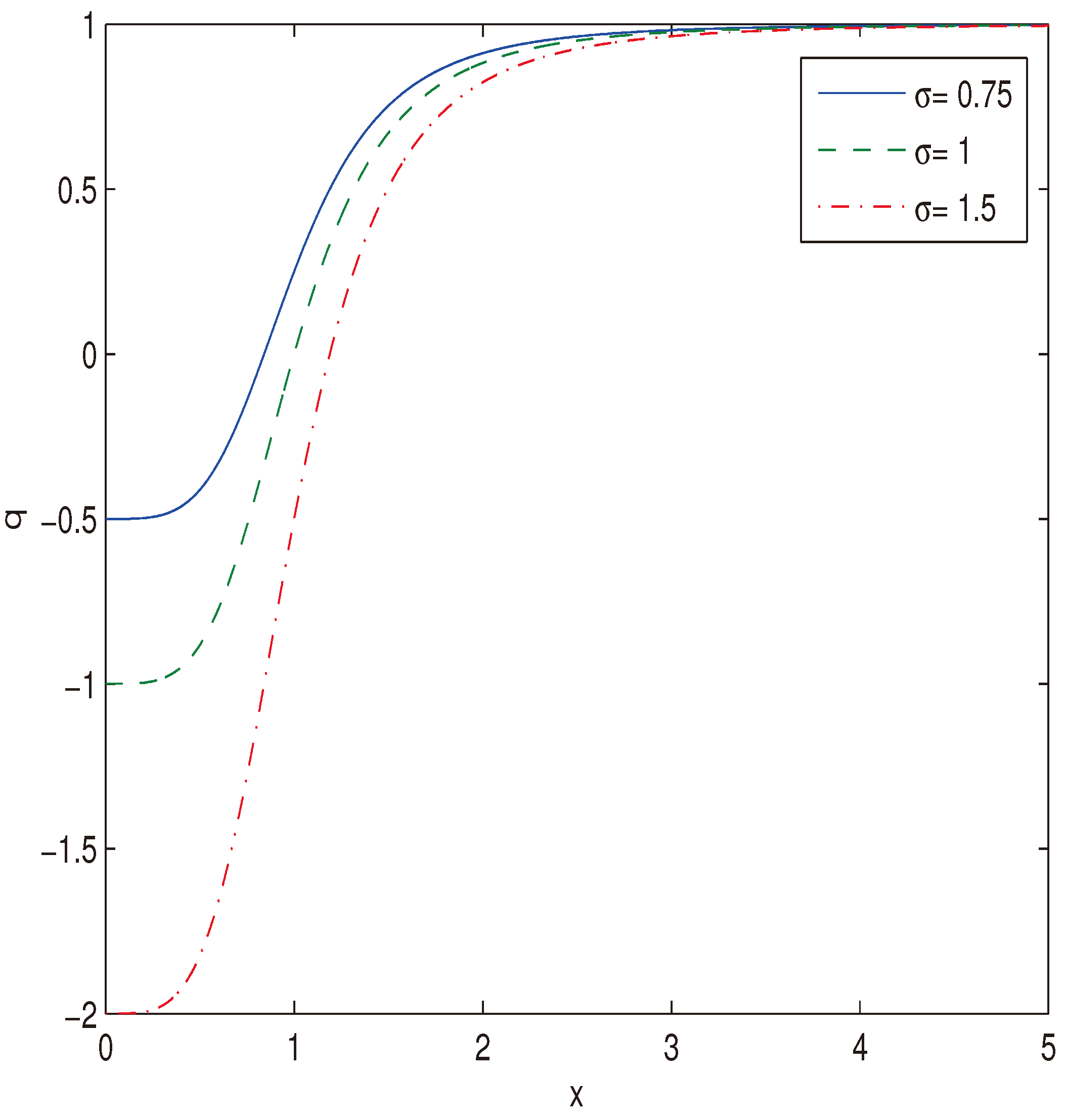
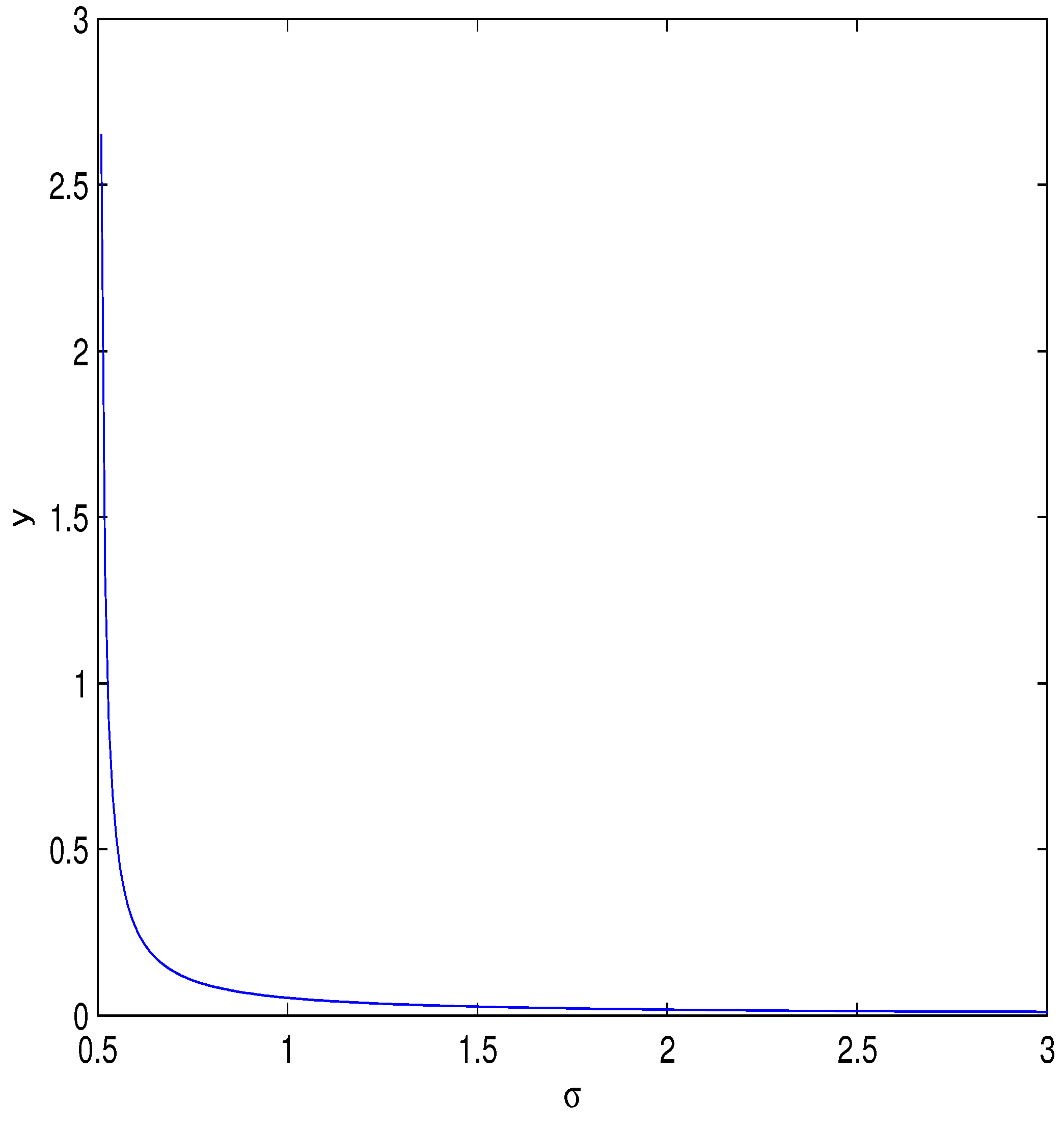
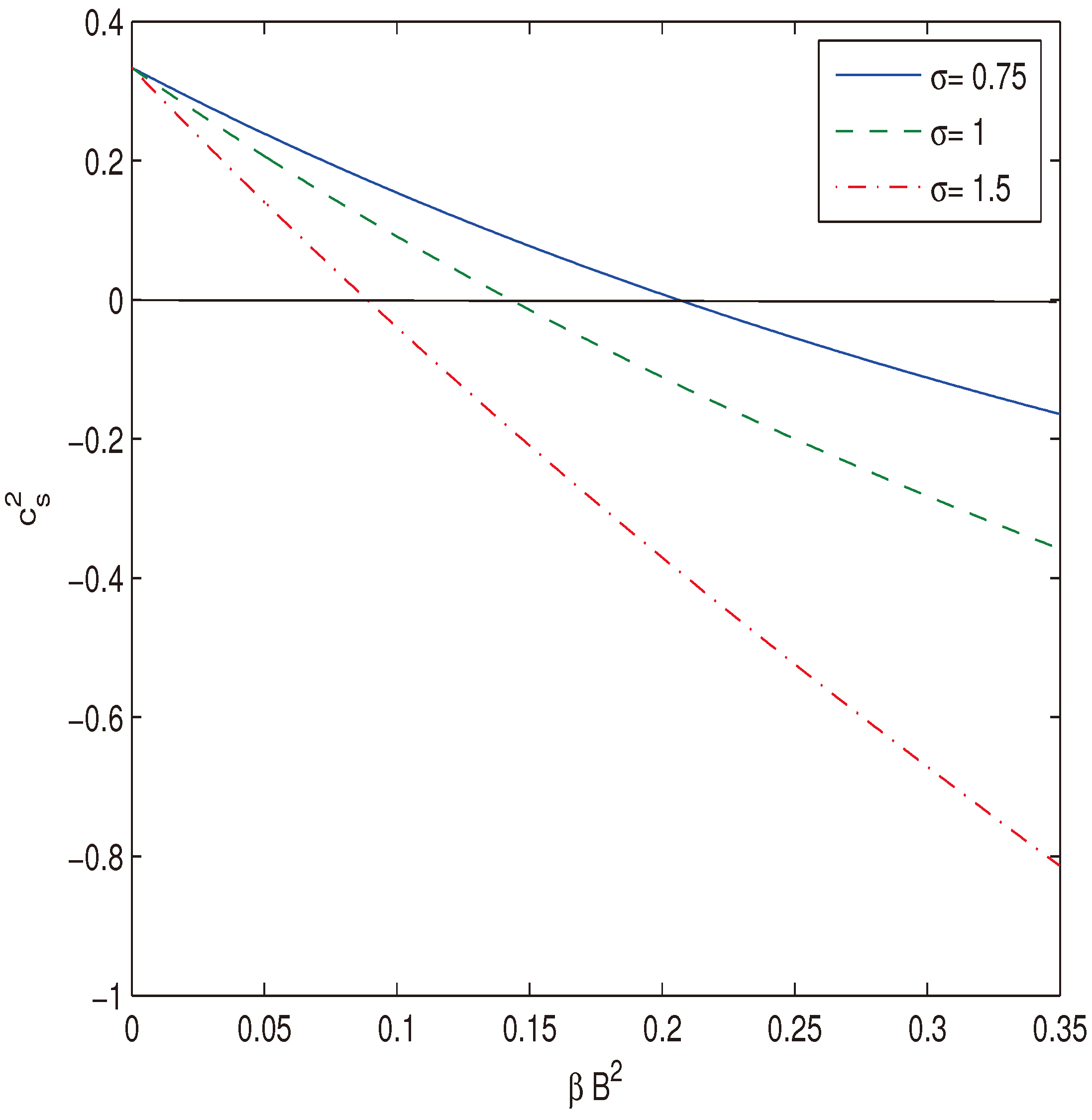
3.1. Causality and unitarity

When the sound speed is less than the light local speed (

c_{s} \leq 1

) [29] the causality takes place, and when the sound square speed is positive (

c_{s}^{2} > 0

) a classical stability holds. By virtue of Eq. (10) we obtain the speed squared of sound

c_{s}^{2} = \frac{d p}{d ρ} = \frac{{(β B^{2})}^{2} (4 σ^{2} - 5 σ + 1) + β B^{2} (2 - 9 σ) + 1}{3 (1 + β B^{2}) (1 + β B^{2} (1 - σ))} .

(34)

The function

c_{s}^{2}

versus

β B^{2}

is plotted in Figure 7.

In accordance with Figure 7 when parameter

σ

increases the causality and unitarity hold for smaller background magnetic field. From Eq. (34) we obtain that

c_{s}^{2} = 0

β B^{2} = \frac{9 σ - 2 \pm \sqrt{σ (65 σ - 16)}}{2 (4 σ^{2} - 5 σ + 1)} .

(35)

By virtue of Eqs. (12) and (35) and Figure 7, we find that at the acceleration phase, the classical stability, causality and unitarity are broken.

4. Conclusion

Einstein’s gravity coupled to NED with two parameters has been studied. We showed that the background stochastic magnetic fields, as a source of gravity, leads to Universe inflation. The magnetic fields interval when the Universe inflation occurs has been found. The singularities of the energy density and pressure are absent in our model. It was shown that at the large scale factor the equation of state corresponds to ultra-relativistic case. We have demonstrated that there are not singularities of curvature invariants. The evolution of the universe has ben described. We have obtained the function of the scale factor on the time. The deceleration parameter has been calculated to study the Universe evolution. We have analysed the amount of the inflation by considering the e-folding number. It was demonstrated that for some model parameters the reasonable e-folding number takes place. The Universe inflation duration as the function of parameters

β

and

σ

has been calculated. To study the causality and unitarity principles we computed the speed of sound. We have obtained the interval of background magnetic fields when causality and unitarity hold. There are similarities and differences of our Universe inflation model compared with models in Refs. [30,31]. The SCM problems of the initial singularity and Universe acceleration are solved in our model.

References

A. H. Guth, Phys. Rev. D 23, 347 (1981). [CrossRef]
Alexei A. Starobinsky, Phys. Lett. B 91 99-102 (1980). [CrossRef]
S. Capozziello and V. Faraoni, Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics (Springer Science+Business Media B.V., New York, 2011).
S. Nojiri and S. D. Odintsov, Phys. Rept. 505, 59 (2011).
Andrei D. Linde, Lect. Notes Phys. 738, 1-54 (2008).
M. Born and L. Infeld, Proc. Royal Soc. (London) A 144, 425 (1934). [CrossRef]
W. Heisenberg and E. Euler, Z. Physik 98, 714 (1936). [CrossRef]
J. Schwinger, Phys. Rev. 82, 664 (1951). [CrossRef]
S. L. Adler, Ann. Phys. (N.Y.) 67, 599 (1971). [CrossRef]
C. S. Camara, M. R. de Garcia Maia, J. C. Carvalho, and J. A. S. Lima, Phys. Rev. D 69, 123504 (2004). [CrossRef]
E. Elizalde, J. E. Lidsey, S. Nojiri, and S. D. Odintsov, Phys. Lett. B 574, 1 (2003). [CrossRef]
V. A. De Lorenci, R. Klippert, M. Novello, and J. S. Salim, Phys. Rev. D 65, 063501 (2002). [CrossRef]
M. Novello, S. E. Perez Bergliaffa, and J. M. Salim, Phys. Rev. D 69, 127301 (2004). [CrossRef]
M. Novello, E. Goulart, J. M. Salim, and S. E. Perez Bergliaffa, Class. Quant. Grav. 24, 3021 (2007). [CrossRef]
D. N. Vollick, Phys. Rev. D 78, 063524 (2008). [CrossRef]
R. García-Salcedo, T. Gonzalez, A. Horta-Rangel, and I. Quiros. Phys. Rev. D 90, 128301 (2014). [CrossRef]
S. I. Kruglov, Phys. Rev. D 92, 123523 (2015). [CrossRef]
S. I. Kruglov, Int. J. Mod. Phys. A 35, 2050168 (2020). [CrossRef]
S. I. Kruglov, Eur. Phys. J. Plus 135, 370 (2020). [CrossRef]
S. I. Kruglov, Int. J. Mod. Phys. D 29, 2050102 (2020). [CrossRef]
S. I. Kruglov, Int. J. Mod. Phys. A 32, 1750071 (2017). [CrossRef]
S. I. Kruglov, Int. J. Mod. Phys. A 31, 1650058 (2016). [CrossRef]
S. I. Kruglov, Int. J. Mod. Phys. D 25, 1640002 (2016). [CrossRef]
R. Tolman and P. Ehrenfest, Phys. Rev. 36, 1791 (1930). [CrossRef]
L. D. Landau and E. M. Lifshits, The Classical Theory of Fields (Pergamon Press, 1975).
H. Bateman and A. Erdelyi, Higher Transcendental Functions (MC GRAW-HILL BOOK COMPANY, INC, 1953).
A. R. Liddle and. H. Lyth, Cosmological Inflation and Large-Scale Structure (Cambrige University Press, 2000).
Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, Edit by M. Abramowitz and I. Stegun. National Bureau of Standarts, Applied Mathematics Series 55 (1972).
R. García-Salcedo, T. Gonzalez, and I. Quiros, Phys. Rev. D 89, 084047 (2014). [CrossRef]
H. B. Benaoum1, Genly Leon, A. Övgün, and H. Quevedo. Eur. Phys. J. C 83, 367 (2023). [CrossRef]
S. I. Kruglov, Eur. Phys. J. C (in Press).

Figure 1. The function

\sqrt{β} B

vs.

σ

. As

σ \to 1 / 2

B \to \infty

and when

σ \to \infty

, one has

B \to 0

Figure 1. The function

\sqrt{β} B

vs.

σ

. As

σ \to 1 / 2

B \to \infty

and when

σ \to \infty

, one has

B \to 0

Figure 2. The function w vs.

β B^{2}

for

σ = 0.75, 1, 1.5

Figure 2. The function w vs.

β B^{2}

for

σ = 0.75, 1, 1.5

Figure 3. The function

β R / κ^{2}

vs.

β B^{2}

for

σ = 0.75, 1, 1.5

. When

σ \geq 1

the Ricci scalar singularity as

B \to \infty

is absent.

Figure 3. The function

β R / κ^{2}

vs.

β B^{2}

for

σ = 0.75, 1, 1.5

. When

σ \geq 1

the Ricci scalar singularity as

B \to \infty

is absent.

Figure 4. The function

y = 2 \sqrt{6 π β} \dot{x} / κ

vs.

x = a / (β^{1 / 4} \sqrt{B_{0}})

for

σ = 0.75, 1, 1.5

Figure 4. The function

y = 2 \sqrt{6 π β} \dot{x} / κ

vs.

x = a / (β^{1 / 4} \sqrt{B_{0}})

for

σ = 0.75, 1, 1.5

Figure 5. The function q vs.

x = a / {(β B_{0}^{2})}^{1 / 4}

Figure 5. The function q vs.

x = a / {(β B_{0}^{2})}^{1 / 4}

Figure 6. The function

y = β / (κ^{2} Δ t^{2})

vs.

σ

Figure 6. The function

y = β / (κ^{2} Δ t^{2})

vs.

σ

Figure 7. The function

c_{s}^{2}

vs.

β B^{2}

Figure 7. The function

c_{s}^{2}

vs.

β B^{2}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.