Submitted:
02 December 2024
Posted:
03 December 2024
You are already at the latest version
Abstract
Often, in biology, we are faced with the problem of exploring relevant unknown biological hy-
potheses in the form of myriads of combination of factors that might be affecting the pathway under certain conditions. Currently, a major persisting problem is to cherry pick the combinations based on expert advice, literature survey or guesses for investigation. This entails investment in time, energy and expenses at various levels of research. To address these issues, a search engine design was recently published, which showed promise by revealing existing confirmatory published wet lab results. Additionally and of import, an adaptation of the published engine mined up a range of unexplored/untested/unknown combinations of genetic factors in the Wnt pathway that were affected by ETC-1922159 enantiomer, a PORCN-WNT inhibitor, after the colorectal can- cer cells were treated with the inhibitor drug. Here, the R code of the search engine is explained that will help biologists/oncologists to understand how gene combinations can be ranked. Using this engine they will be able to find combinations which they might want to test in wet lab. Further, they will not have to struggle to search for unknown/unexplored combinations of genes/protiens working in a phenomena.
Keywords:
Gene combination
; Colorectal Cancer
; ETC-1922159
; Machine learning
1. Insight, Innovation, and Integration
Which gene combination to test in wet lab? This is a fundamental problem that biologists/oncologists face in their search for potential breakthroughs that could help understand the mechanism of cell biology leading to scientific discoveries and therapeutic interventions. To address this issue, an elucidation of an adaptation of a machine learning based search engine is provided. The manuscript explains the R code using an example of static data generated from colorectal cancer cells that were treated with ETC-1922159. Thus the struggle to search for combinations will be reduced. The work might help answer many questions in cell biology.
2. Introduction
We developed a search engine to rank/prioritize unknown/unexplored combinations of genes that might be working synergistically in a signaling pathway Sinha [1]. Also, the foundation of this work is based on sensitivity indices. The use of these indices to study when, which genetic factor will be have greater influence on the pathway have recently been published in Sinha [2]. In order to understand the significance of the solution proposed to the problem of combinatorial search that the biologists face in revealing unknown biological search problem, these works are of importance.
Using the same code with modifications, it was possible to generate the rankings for 3rd order combinations. 100 genes were randomly selected from the list of down regulated genes by the pipeline and a 3rd order combination was generated from this set of genes. The total number of 3rd order gene combinations is . So for example, if we are interested in the study of hydrogen proton channel HVCN1 and involvement of V-ATPases through one of its components ATP6V0A2, we would like to know what are their combinatorial rankings in a list of randomly picked up set of genes or do they really have any synergistic influence in the Wnt pathway in colorectal cancer cases, after treatment with ETC-1922159?
This manuscript explains the sequence of the code in the pipeline that constitute the search engine. Note that the pipeline is generic in nature and can be modified, and here we present a possible solution to the combinatorial problem. This is to resolve the issue of finding potential combinations which might be working synergistically. These combinations are addressed as biological hypotheses. We will also address the issues in the paper as we move through the code and point out openning were the scientific community can work to refine the pipeline. Instead of considering these opennings as loop holes, interested parties could tune/refine the pipeline as per their requirement. Currently, the code is broadly divided into three main parts that execute the following - • preprocessing and extraction of data • genenration of sensitivity indices on measurements from the data and • ranking of the sensitivity indices. However, for a more professionalized version, the pipeline can be divided into smaller independent modules. The schematic diagram of the pipeline is represented in Figure 1. Also, the code in R is presented and the coding is explained, where necessary. Note that explanation for the working of any particular package that has been used in the pipeline will not be provided. Instead, references will be provided for these packages or executable files.
3. Source and Description of Data
Data used in this research work was released in a publication by Madan et al. [3]. The ETC-1922159 was released in Singapore in July 2015 under the flagship of the Agency for Science, Technology and Research (A*STAR) and Duke-National University of Singapore Graduate Medical School (Duke-NUS). Note that the ETC-1922159 data show numerical point measurements that is as Madan et al. [3] quote - "List of differentially expressed genes identified at three days after the start of ETC-159 treatment of colorectal tumors. Log2 fold-changes between untreated (vehicle, VEH) and ETC-159 treated (ETC) tumors are reported." The numerical point measurements of differentially expressed genes were recorded using the following formulation of fold changes in equation 1 (see Tusher et al. [4], Choe et al. [5] and Witten and Tibshirani [6]).
4. Steps of Execution via Code Elucidation
Fonts used for different constituents of the code - • variables in file and arguments in italics; • file names in sans serif; • functions in bold; • R code is in verbatim.
4.1. Preprocessing of ETC-1922159 Data
We begin with the first step of the search engine by processing the data that has been provided in Madan et al. [3]. Note that the data had to be manually preprocessed in order to store it in a desired format in a file (here a .txt file). Since the file contained a list of both down and up regulated genes, it was necessary to segregate them in two files. A snap shot of the manually preprocessed file is shown in Figure 2. In this file, the down regulated genes affected by ETC-1922159 have been stored. The orange boundary in Figure 2 contains the file header with different columns separated by a delimiter, here, "+" symbol (see the magnification in blue). The columns include the titles • GeneSymbol or name of abbreviated name of gene, • ENSEMBLgeneID (not used in this code), • GeneDescription containing a short detail of gene, • log2foldchange(VEH/ETC) which represents the numerical point measurement and BH-adjustedP-value which represents the changes in gene expression were considered significant if the Benjamini-Hochberg adjusted P-value <0.0001 (not used in this code). An instance of the tuple in orange boundary is depicted by specific recorded values for instance tuple in red boundary. So, of particular interest would be gene MCM4 and its recorded fold change value of 3.03, from the red boundary, however, before we do that, we need to put the stored information in the .txt file in a particular format for further processing. After manual processing, we stored the list of down and up regulated files in the following two files onc2015280x2-A.txt and onc2015280x2-B.txt, respectively.
4.2. Extraction of ETC-1922159 Data
Once the data has been stored in the required format after manual preprocessing, the next step involves the extraction of data from these files and storage of the information in a requisite format. This is done using the file extractETCdata.R which contains the function extractETCdata. We begin with the explanation of the code in a sequential manner below.
4.2.1. Description of extractETCdata.R
The function extractETCdata takes in the argument with the name data.type that is a numerical value. Here, if the data type then name of the file containing down(up) regulated genes is stored in the filename. The if condition is used for assigning the file name to filename with the condition as argument data.type (See lines 1-7 below).
1 extractETCdata <- function(data.type){
2 if(data.type == 1){
3 filename <- "../data/onc2015280x2-A.txt"
4 }else{
5 filename <- "../data/onc2015280x2-B.txt"
6 }
7
Next, the total number of lines needs to be known once the file to be worked on has been decided. This is required in order to know the number of entries in the file, which gives the list of genes. The processing begins with the system command which executes Unix utilities like wc or word count with an option to count lines l. We use the option of intern to capture the output of the command wc in the output (see line 9 below). The output from the command is stored in lineCnt. This output is in the form of a string and the goal is to know the line count from this string. To proceed, the strsplit function is used in order to break up string in lineCnt into the atomic elements. Further, since the output of the strsplit is in the form of a list, to simplify the data structure, unlist is used produce a vector of atomic elements with an argument strsplit(lineCnt, " "). So here the output of strsplit(lineCnt, " ") goes as argument in the function unlist. The output of unlist which is a vector is stored in x (see line 10 below). Next, to extract the numerical value of the number of lines in the file, a for command is run, were the iterator i takes in one element of vector in x at a time (see line 11 below) and tests if it is a numeric value. If a numeric value is found, the for loop breaks, else continues with the next element of x in the iterator. So, for every value of x in i, if value in i as numeric is not found to be true or is missing/not available, the iterator moves to the next element of x. Else, if the value in i as numeric is found to be true in the if condition, then this value is assigned to nLines and the execution breaks out of the for loop (see lines 11-14).
8 # find total number of lines in the file
9 lineCnt <- system(command=paste("wc -l ",
filename,sep=""),intern=TRUE)
10 x <- unlist(strsplit(lineCnt," "))
11 for(i in x){
12 if(is.na(as.numeric(i))){}
13 else{nLines <- as.numeric(i); break;}
14 }
15
Once we know the number of lines in the file, we proceed to extract the information in the file, line by line. Lines 20-84 below contain the part of code that will extract the information from the file. However, due to the length of the code, the explaination is broken up into parts. The entire code for extracting the information is contained in the block within the while loop, which starts from line 20. The while runs till a condition is no longer true. Before that, the file needs to be openned for processing. This is done using the file command which takes in filename as the argument for variable description and r to read, as the argument for variable open. This opens the connection for the file of interest and the connection to the file is stored in a variable connecTion. We also set the variable cnt to 0 as an iterator for the while loop that needs to execute as long as the condition cnt ≤ nLines as argument to the while is met (see line 20). If the condition in line 20 is not met, the execution exits the while loop block.
Once inside the condition is satisfied, the counter is incremented by 1, stating that the first line is being read. This is indicated by updated cnt value in line 21. Next, the cntth line is read from the file using the function readLines which take in as arguments the value in connecTion and n (as 1 to read only one line). The output is the cntth line that is stored in sentence. For processing purpose the sentence is concatenated with a return character. However, if the cntth line is the first line, then the loop just skips it and jumps to the next line in the file (see lines 16-24).
16 # extraction information from the file
17 connecTion <- file(description = filename,
open = "r")
18 cnt <- 0
19 #browser()
20 while(cnt <= nLines){
21 cnt <- cnt + 1
22 sentence <- readLines(con = connecTion,
n = 1)
23 cat(sentence,"\n")
24 if(cnt == 1){}
However, if the cntth line is the 2nd one in the file, then we know that it contains the information on column names. This needs to be extracted from the sentence variable in the second iteration of the while loop which extends from lines 25 to 59. Again, to explain the aspects of the code, we will break this else if(cnt ){...} block into parts. This block contains two for loop blocks. The first block is used to retrieve the names of the columns that are delimited by a "+" sign (see lines 25-45). The second block is to create corresponding variable names that match with the retreived names followed by initialization (see lines 46-58).
The else if block begins with a few initializations. The cntth sentence is split and stored in a simple format in tempSentence. The length of the sentence in terms of the number of characters is stored in tempSentenceLength. The position of the delimiter "+" within the sentence is also stored using the which function. Finally, the names of the columns need to be stored in cnames and an index indx is used as a start position at a particular location in tempSentence for processing purpose. In the first for loop, with the iterator i taking on values of the position of the delimiter (stored in delimPlusPos) one at a time in every loop, a particluar piece of code is executed depending on the value of the index position in indx. In line 31, if the location of the indx is 1, i.e the starting character of the sentence, then the first name needs to be extracted that lies between position 1 and position (i-1). Note at location i, there is a "+" symbol. To execute this, the command capture.output is used that converts the concatenated elements of tempSentence[1:(i-1)] via cat command (see line 33). capture.output coverts the input argument in a string and stores the retreived name in tempName. Next, this column name is stored in cnames in line 34. In case the indx is the position which contains the last delimiter i.e. length(delimPlusPos) then the last and the penultimate column names need to be retreived. The penultimate column name can be retreived from the characters between the penultimate delimiter and the last delimiter, i.e delimPlusPos[indx-1]+1):(i-1) (see line 36). The last column name can be retreived after the last delimiter and end of the sentence, i.e delimPlusPos[indx]+1):tempSentenceLength (see line 38). Finally, if the iterator neither points to the 1st or the last length(delimPlusPos) delimiter position, then the column name can be retrieved from characters lying between the position of the previous delimiter position and current delimiter position, i.e (delimPlusPos[indx-1]+1):(i-1) (see line 41). Each of these are ranges that are encased in the vector tempSentence and are concatenated via cat and captured in tempName and later stored in cnames. After the execution of the for loop ends, that is the iterator i has covered all the delimiter positions in delimPlusPos, cnames contains all the column names (see lines 31-45).
25 else if(cnt == 2){
26 tempSentence <- unlist(strsplit(
x = sentence, split = "+"))
27 tempSentenceLength <- length(tempSentence)
28 delimPlusPos <- which(tempSentence == "+")
29 cnames <- c()
30 indx <- 1
31 for(i in delimPlusPos){
32 if(indx == 1){
33 tempName <- capture.output(
cat(tempSentence[1:(i-1)],sep=""))
34 cnames <- c(cnames, tempName)
35 }else if(indx == length(delimPlusPos)){
36 tempName <- capture.output(cat(
tempSentence[(delimPlusPos[indx-1]+1):
(i-1)], sep=""))
37 cnames <- c(cnames, tempName)
38 tempName <- capture.output(cat(
tempSentence[(delimPlusPos[indx]+1):
tempSentenceLength], sep=""))
39 cnames <- c(cnames, tempName)
40 }else{
41 tempName <- capture.output(cat(
tempSentence[(delimPlusPos[indx-1]+1):
(i-1)], sep=""))
42 cnames <- c(cnames, tempName)
43 }
44 indx <- indx + 1
45 }
Once the names of the column has been stored, the corresponding variables need to be created and initialized. This is done in the second block as described above. The second for loop iterates through the list of column names. In each iteration of the for loop, a condition is checked which tests whether a particular pattern exists within the column name under consideration. If the condition is satisfied, as above, the corresponding variable is created and initialized. We use the grep function to find the pattern in the column name i, as i iterates through cnames in the for loop. If there is a match and the pattern exists in column name i, then the length of this match will not be equal to 0, like (length(grep(pattern = "sym", x = i)) != 0) on line 47. When this happens, the creation and initialization of a variable follows. In the above example, Genesymbol is created and initialized. Finally, the block for else if is completed, if one is dealing with the 2nd line of the file (see lines 46-58).
46 for(i in cnames){
47 if(length(grep(pattern = "sym",
x = i)) != 0){
48 Genesymbol <- c()
49 }else if(length(grep(pattern = "ID",
x = i)) != 0){
50 ENSEMBLgeneID <- c()
51 }else if(length(grep(pattern = "des",
x = i)) != 0){
52 Genedescription <- c()
53 }else if(length(grep(pattern = "fold",
x = i)) != 0){
54 logTwoFC <- c()
55 }else if(length(grep(pattern = "value",
x = i)) != 0){
56 BHadjustedPvalue <- c()
57 }
58 }
Next, for all cntth line of the file that is neither 1st or 2nd, the last part of the else block for the while loop in line 20 is executed. This block is encoded in lines 59-82. Most of the code is similar to the preceeding block with a few changes. Line 60 contains the same command to store the sentence read at cntth line of the file and line 61 is used to find the positions where the delimiter is positioned. In the next step, if there is an error in positioning of the delimiter due to manual preprocessing error, the command shows that correction needs to be done at line cnt. From lines 64 to 83, the coding is similar to the foregoing piece of code, except that if the index indx is 1, now, the name of the gene is stored in Genesymbol; if the index indx is length(delimPlusPos) then fold change values are stored in logTwoFC from the left side of the delimiter and adjusted P-values are stored in BHadjustedPvalue from the right side of the delimiter; if indx is 2, then ENSEMBLgeneID value is stored in ENSEMBLgeneID and finally, if indx is 3, then Genedescription is stored in Genedescription. Lines starting with # are commented and used only for testing purpose and do not give any value (see lines 59-84). Note that as each line is read, information is stored using rbind function that keeps attaching or binding the current value to the existing vector in a variable. For example, Genesymbol <- rbind(Genesymbol, tempName) will append Genesymbol with the current tempName thus increasing the size of the vector in Genesymbol by 1. This procedure gets repreated. Thus ends the storage of information regarding from the file in the variables.
59 }else{
60 tempSentence <- unlist(strsplit(
x = sentence, split = "+"))
61 delimPlusPos <- which(tempSentence == "+")
62 if(length(delimPlusPos) != 4){
cat("Correction needed at - ",cnt);
break
}
63 indx <- 1
64 for(i in delimPlusPos){
65 if(indx == 1){
66 tempName <- capture.output(cat(
tempSentence[1:(i-1)],sep=""))
67 Genesymbol <- rbind(Genesymbol, tempName)
68 }else if(indx == length(delimPlusPos)){
69 tempName <- capture.output(cat(
tempSentence[(delimPlusPos[indx-1]+1):
(i-1)], sep=""))
70 logTwoFC <- rbind(logTwoFC,
as.numeric(tempName))
71 # tempName <- capture.output(cat(
# tempSentence[(delimPlusPos[indx]+1):
# (tempSentenceLength-1)], sep=""))
72 tempName <- capture.output(cat(
tempSentence[delimPlusPos[indx]+(1:7)],
sep=""))
73 BHadjustedPvalue <-
rbind(BHadjustedPvalue, tempName)
74 }else if(indx == 2){
75 tempName <- capture.output(cat(
tempSentence[(delimPlusPos[indx-1]+1):
(i-1)], sep=""))
76 ENSEMBLgeneID <- rbind(ENSEMBLgeneID,
tempName)
77 }else if(indx == 3){
78 tempName <- capture.output(cat(
tempSentence[(delimPlusPos[indx-1]+1):
(i-1)], sep=""))
79 Genedescription <-
rbind(Genedescription, tempName)
80 }
81 indx <- indx + 1
82 }
83 }
84 }
Next, we close the open file using the command close with an argument connecTion. And finally, we combine the variable names in a data frame, a kind of data structure using data.frame and arguments Genesymbol, ENSEMBLgeneID, Genedescription, logTwoFC and BHadjustedPvalue. The data frame is stored in the variable oncETC. Finally, the return command returns this data frame as output using the function return and oncETC (see lines 85-89).
85 close(connecTion)
86
87 oncETC <- data.frame(Genesymbol,
ENSEMBLgeneID, Genedescription,
logTwoFC, BHadjustedPvalue)
88 return(oncETC)
89 }
Note that the preprocessing and extraction of data can have different flavours depending on the type of data and experiment one is dealing. However, the output of the extraction should be a data frame (a kind of variable in R) containing the extracted data that needs to be used in sensitivity analysis. This is explained next.
4.2.2. Exercise
As an exercise, the readers are encourged to build their own preprocessed file manually, from the data given in Madan et al. [3] and see if they can reproduce the results in the form of a data frame using the function extractETCdata.
4.3. Computing the Sensitivity Indices
We move on to the next stage of the pipeline were the sensitivity indices need to be generated. Why we are generating these indices and how it helps in ranking up a set of factors and its combinations involved in the pathway have been discussed in Sinha [7] and Sinha [8]. Here we concentrate on the implementation of the pipeline and explanation of the code only. The code has been saved in the file name manuscript-2-2.R and one of the author has been lazy enough not to change the name of the code. However, it also points to the fact that the author is not concerned with the show of expertise in nomenclature of file names and neither does he wish to earn a PhD in nomenclature of file names. Moving to the main topic, the code begins with the definitions of some functions and inclusion of packages from which specific function can be used during programming.
4.3.1. Description of Manuscript-2-2.R
Here, the library function is used to call the package "sensitivity" which has been implemented in R and goes as an argument into the function library. Details of the package can be found in Pujol et al. [9]. Next we define a function, using the function function and give this function a name new.name. The function takes in as argument, a two dimensional matrix X. k is the number of genes under consideration out of a set of genes. The new.name implements the g-function (a model) that is used to assign weights to each of the genes, with a random weight. For this, runif function is used. b is updated as each gene is considered one at a time in the for loop. At the end of the function, value in b is returned implicity. What happens is as the loop iterates length(a) times, were the expression shows the number of genes the user has selected. Note that lenght if a is computed using the value of k. This function read within lines 3-10. Also, genSampleComb is a function which returns a two dimensional matrix with the a specific number of columns defined in yCol. More about this function will be talked at a later stage. Here, definitions of the functions are provided (see lines 1-14).
1 library(sensitivity)
2 # Function definitions
3 new.fun <- function(X){
4 a <- runif(k)
5 b <- 1
6 for (j in 1:length(a)) {
7 b <- b * (abs(4 * X[, j] - 2) +
a[j])/(1 + a[j])
8 }
9 b
10 }
11
12 genSampleComb <- function(yCol){
13 return(disty[,yCol])
14 }
15
Since the code can be adapted for different data sets, a query is asked to the user regarding the generation of distribution around point measurements, if they exist in the data under consideration. To query the user, the function readline is employed. The user has to type in the option provided in the query for a particular functionality to take affect. Here, the response to the query is stored in the variable DISTRIBUTION. Next, if the response in DISTRIBUTION is a yes, that is, the user typed in "y", then the ensuing block within the if command will get executed, else it will be skipped. Again, the block under consideration, defines a new function gdfetppv which takes in arguments n and yt, were n contains the number of points which a user might want to generate for a distribution around a numerical point estimate. The measured numerical point estimates for each gene under consideration are assorted in a vector yt. The length of yt shows the number of genes involved in the study of sensitivity analysis. As the for iterates through each gene, for the corresponding numerical point estimate for a partipular gene, a distribution around the point estimate is generated with the mean value being yt[i] (i is the iterator) and a standard deviation of . Along with the distribution a minor jitter or noise is added. Thus, the whole distribution is stored in a vector. Note that the output of the jitter function is a vector and R stores vector in column format. Consequently, as the for loop iterates from one gene to another, the columns are bound together using a column binding function cbind. Thus, randyt keeps on increasing column wise, till all genes have been covered. Once out of the loop, the row vector yt is appended with the distribution matrix randyt using row binding function rbind. The output of the function is a two dimensional matrix containing the point estimate in the first row and the corresponding distribution in the rows below (see lines 20-28).
16 # Generation of distributions
17 DISTRIBUTION <- readline("Should i generate
distribution of data [y/n] - ")
19 if(DISTRIBUTION == "y"){
20 gdfetppv <- function(n,yt){
21 randyt <- c()
22 lenyt <- length(yt)
23 for(i in 1:lenyt){
24 randyt <- cbind(randyt,
jitter(rnorm(n, mean = yt[i],
sd = 0.005), factor = 1))
25 }
26 yt <- rbind(yt, randyt)
27 return(yt)
28 }
29 }
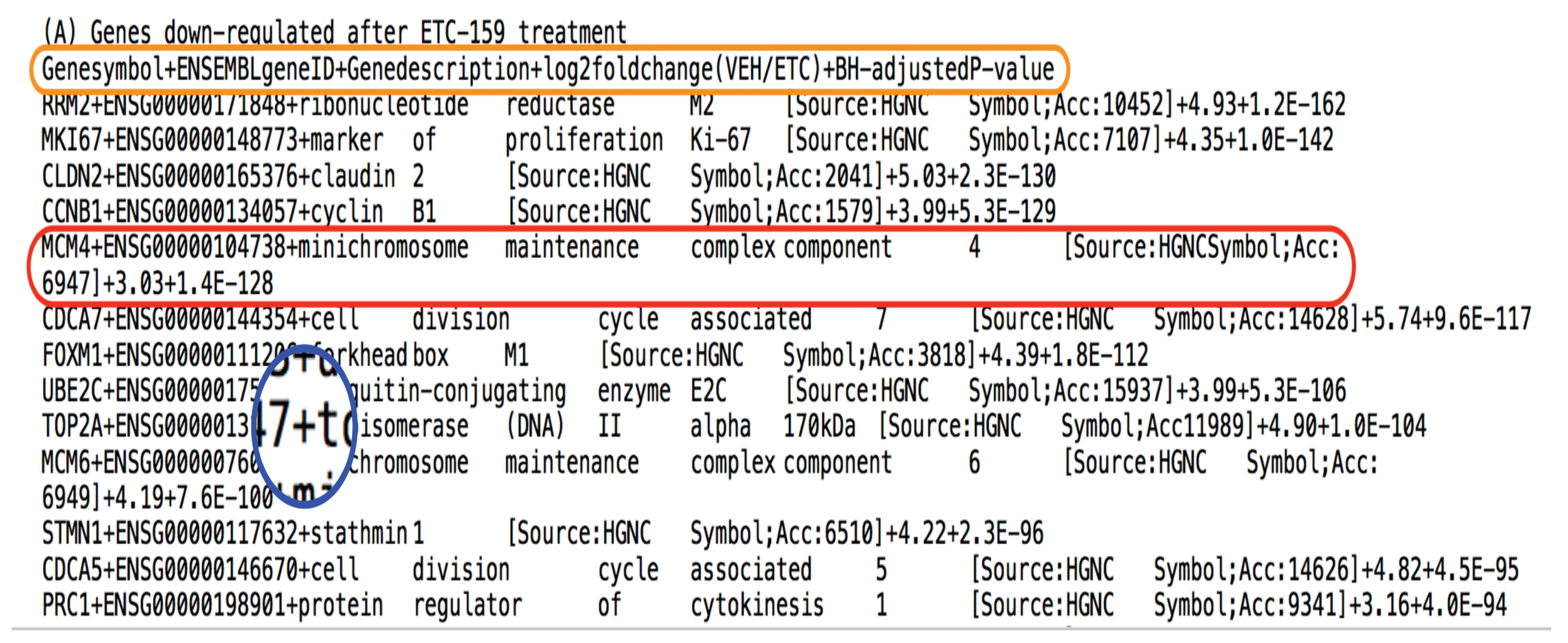
After the functions have been defined, the main execution begins. The code starts with the extraction fo the data using the readline argument and provides an option to the used to choose file that contains data regarding down regulated genes or up regulated genes. Once the respone is recorded, it is stored in the variable DATATYPE. If the user enters a wrong number, then a while loop is run which asks to enter the right response. This feedback continues till the user enters the right response (see lines 30-33). After the correct response is recorded, we use the function extractETCdata to extract the information from the particular file associated with the response in DATATYPE. This is done using the command extractETCdata(DATATYPE) and the output of the function is stored in oncETCmain. We keep a copy of the stored information in oncETCmain and make a second copy in the subsequent line in oncETC(see line 34-35). This manuscript explains the code for retrieving 2nd order combination, only so as to set a platform for many who would be reading the article. Note, before the use of the function i.e. instantiation of the function, the function needs to be defined and initialized. We defined the function and named it. After that an instance of the function is used to get a certain result. One instance is extractETCdata(1) and another instance is extractETCdata(2).
30 # Data extraction
31 DATATYPE <- readline("Choose a file to
process [1/2] \n
1 - ../data/onc2015280x2-A.txt \n
Genes down-regulated after ETC-159
treatment \n
2 - ../data/onc2015280x2-B.txt \n
Genes up-regulated after ETC-159
treatment \n
File number - ")
32 while(DATATYPE != "1" & DATATYPE != "2"){
DATATYPE <- readline("Type the kind of
data to be processed [1/2] - ")
33 }
34 oncETCmain <- extractETCdata(DATATYPE)
35 oncETC <- oncETCmain
Of interest is the column containing the fold change numerical point estimates that are stored in the variable oncETC. Since the information under this column is stored in the data frame, it needs to be converted into a matrix for further processing by sensitivity analysis package. For this, as.matrix function is used which takes in the object in x along with arguments ncol which asks for the number of columns into which the information needs to be divided and byrow being false stating that the information will not be lined up row wise, but column wise. The result of the transformation is stored in y. Next, respective column elements in y are allotted their gene names. This is acheived using oncETC$Genesymbol. The rownames of y which depict the gene names are thus assigned. We also save the names of the genes in factor.names variable. The dimension or the size of y in terms of number of rows and number of columns is recorded using the function dim and the measurements are stored in dim.y. dim.y[1] contains the number of rows which implicitly defines the number of genes (stored in no.genes). The whole list of genes can be shown on the command prompt during the execution of the code via cat(rownames(y)) (see lines 35-40).
35 y <- as.matrix(x = oncETC$logTwoFC,
ncol = 1, byrow = FALSE)
36 rownames(y) <- oncETC$Genesymbol
37 factor.names <- oncETC$Genesymbol
38 dim.y <- dim(y)
39 no.genes <- dim.y[1]
40 cat(rownames(y))
Next, the user is asked which gene the user would like to investigate and the response is stored in geneName. Also, since the pipeline is about investigating combinations, we need to input the number of combinations we are interested in. For this, a similar query is asked and the value is stored in the variable k. Since it is in the character format, it needs to be converted into a numerical format and that is done using as.numeric function. The cat function helps in displaying messages to ease the user to understand what is happening while execution of the program. The combinations that can be generated from k genes, out of the total number of genes no.genes is computed using combn. This returns a two dimensional matrix to geneComb whose number of columns represent the total number of combinations, i.e dim(geneComb[2]) (see lines 41-47).
41 geneName <- readline("\nEnter name of
gene to be evaluated - ")
42 # Regarding combinations
43 ANSWER <- readline("nCk - choosing k - ")
44 k = as.numeric(ANSWER)
45 cat("choosing ",k," out of the",
no.genes," genes!\n---\n")
46 geneComb <- combn(no.genes,k)
47 no.geneComb <- dim(geneComb)[2]
Next, initialization of the variables needs to be done for processing of the data. A series of list data structure is initialized and names are assigned to each new list as shown from lines 49 to 60. These are the variables where the sensitivity indicies will be stored. siNames contains the names of the indicies which the search engine uses and the user can pick any one of them for computation. Line 63 prompts the user to enter the name of the sensitivity index, after looking at displayed list in the command on line 62. This name is stored in the variable varName. Next, we search for the pattern (stored in varName) in some of the Sobol index names and if the user has chosen a sobol sensitivity index, then ISSOBOL is assigned to a true value. This will be used and explained later on (see lines 49-66).
48 # some initializations
49 sensiFdiv.TV <- list()
50 sensiFdiv.KL <- list()
51 sensiFdiv.Chi2 <- list()
52 sensiFdiv.Hellinger <- list()
53 sensiHSIC.rbf <- list()
54 sensiHSIC.linear <- list()
55 sensiHSIC.laplace <- list()
56 SB.jansen <- list()
57 SB.2002 <- list()
58 SB.2007 <- list()
59 SB.martinez <- list()
60 SBL <- list()
61 siNames <- c("Fdiv.TV", "Fdiv.KL",
"Fdiv.Chi2", "Fdiv.Hellinger", "HSIC.rbf",
"HSIC.linear", "HSIC.laplace", "SB.2002",
"SB.2007", "SB.jansen", "SB.martinez", "SBL")
62 cat("Types of SA - ", siNames, "\n")
63 varName <- readline("Enter a type of SA - ")
64 ISSOBOL <- FALSE
65 if(length(grep(varName, "SB.2002"))!= 0 |
length(grep(varName, "SB.2007"))!= 0 |
length(grep(varName, "SB.jansen"))!= 0 |
length(grep(varName, "SB.martinez"))!= 0
| length(grep(varName, "SBL"))!= 0){
ISSOBOL <- TRUE
66 }
Regarding the generation of distribution of numerical point measurements, it is important to specify the number of samples. The user is usually given a choice as shown in line 67 (here commented). However, for exercise purpose, we set the value of number of samples to be . Next, the function for generating distribution of size 9 per gene measurement is used and the output is converted into a data frame using the function data.frame. This data frame is then stored in variable disty or distribution of y. We again save the number of samples as an extra using the dim function, in a variable no.Samples (see lines 67-71).
67 # n <- as.numeric(readline("Enter number of
samples for distribution (odd numeric) - "))
68 n <- 9
69 disty <- data.frame(gdfetppv(n,t(y)))
70 no.Samples <- dim(disty)[1]
71 cat("generating sample combinations!\n")
The apply function is one of the important functions in R langauge and widely used for vector programming. It is important here in the sense that we need to compute the indices for combinations of factors. The arguments for apply take in a matrix, the indicator for a vector in a matrix over which a function will be applied. Here we see that geneComb is the matrix containing the combinations of genes; MARGIN with an indicator 2 means the columns of geneComb will be worked upon by the function genSampleComb in the variable FUN. Thus the function apply will apply the function genSampleComb to the columns of the matrix geneComb. The function genSampleComb in line 12, takes in a column of the matrix geneComb and returns the k distributions that are stored in the matrix disty. So, if k is 2, then the number of rows in geneComb will be 2. These 2 elements associated with a particular column in geneComb will contain the gene numbers in a list of genes. During the application of the apply function, yCol stores a column of geneComb and uses genSampleComb to generate disty[,yCol], a matrix, were n is number of samples and k is the number of elements in combination. The procedure is applied to all columns of geneComb, for this. (see line 72).
72 distyN <- apply(X = geneComb, MARGIN = 2,
FUN = genSampleComb)
Next, the combinatorial distributions stored in distyN are processed to segregate the gene combinations that contain the particular gene of interest defined by the user from a list of gene, in geneName. List variables are defined and to find combinations containing geneName, a for loop is executed were the iterator iterates through the total number of combinations. For each of the combination contained in names(distyN[i]), if geneName is found to be existing, then the distribution containing geneName and another gene in distyN[i] is stored in x.S, a list. For every such identification, a counter cnt is incremented. Finally, after all combinations have been found which contain geneName, the final is assigned to number of selected gene combinations no.slgeneComb (see lines 73-85).
73 # Sample with replicates
74 x.S <- list()
75 x.Sfh <- list()
76 x.Ssh <- list()
78 cnt <- 0
79 for(i in 1:no.geneComb){
80 if(geneName %in% names(distyN[[i]])){
81 cnt <- cnt + 1
82 x.S[[cnt]] <- distyN[[i]]
83 }
84 }
85 no.slgeneComb <- cnt
Usually a user will be asked about the total number of iterations for which the sensitivity indicies will be generated. This is done to get an average sensitivity index score which is then used for ranking of the combinations. For demonstration purpose, we set the iteration number to itrNo . The for loops the iterator for 50 iterations. Every iteration, the number of interation is displayed at the start of the for loop. The samples need to be shuffled every time in order to have variation so that the mean of the sensitivity indices can be generated. This can be done by using the function sample which take a range of values from 1 to no.Samples and the size of the sample is set to no.Samples. The shuffled samples are stored in sample.index. idx.fh and idx.sh are used to divide the sample into two halves, in case one is using Sobol method for generating sensitivity indicies. Next, if the method used is Sobol or a variant of the same, as indicated by , then shuffling of the samples in combination happens. This shuffling is done in lines 99-100, for all combinations, i.e j from 1 to no.slgeneComb. For, non Sobol based methods, the shuffling is simple as shown in line 104.
86 # itrNo <- as.numeric(readline("Number
of iterations for averaged ranking - "))
87 itrNo <- 50
88 hmean <- list()
89 for(itr in 1:itrNo){
90 # disty <- data.frame(gdfetppv(n,yt))
91 # distyN can be replaced with x.S also
92 cat("generating for sample - ", itr, "\n")
93 sample.index <- sample(x = 1:no.Samples,
size = no.Samples)
94 idx.fh <- sample.index[1:(no.Samples/2)]
95 idx.sh <- sample.index[((no.Samples/2)+1)
:no.Samples]
96 # Shuffle the samples
97 if(ISSOBOL){
98 for(j in 1:no.slgeneComb){
99 x.Sfh[[j]] <- x.S[[j]][idx.fh,]
100 x.Ssh[[j]] <- x.S[[j]][idx.sh,]
101 }
102 }else{
103 for(j in 1:no.slgeneComb){
104 x.S[[j]] <- x.S[[j]][sample.index,]
105 }
106 }
Once the samples for the combinations have been stored in x.S, it is time to generate the sensitivity indicies. To generate a sensitivity index of a particular type, the user has to specify the name of the sensitivity index. This has already been done earlier and the name is stored in varName. What follows is a series of condition tests using the if ... else to know which type of sensitivity method needs to be taken into account and necessary method to be initiated to generate the indicies. One of the approach would be to use grep function which searches for a pattern in varName. If the pattern exists, then the length of the finding would not be zero. When this condition holds, then a particular index associated with the pattern is intiated. So, if "TV" is the pattern and it found to be in the varName, then f-divergence method Csiszár et al. [10] with a Total variation distance needs to be initiated. The short explanation on the theoretical principles of density and variance based methods has been explained in Sinha [2]. Here we concentrate on the flow of the code. In line 109, we define and initialize a new variable FdivTV. After some displays on the screen, lapply is used on x.S. lapply returns a list of the same length as x.S, each element of which is the result of applying function sensiFdiv to the corresponding element of x.S. Additionally, since the sensitivity method uses a model function, we use extra arguments in the lapply function, like model = new.fun; nboot = 0 and conf = 0.95. This new.fun has earlier been defined in the beginning of the code. So, lapply generates sensitivity indices for each of the matricies containing a specific gene combination using the new.fun via sensiFdiv. The result is stored in a variable h. 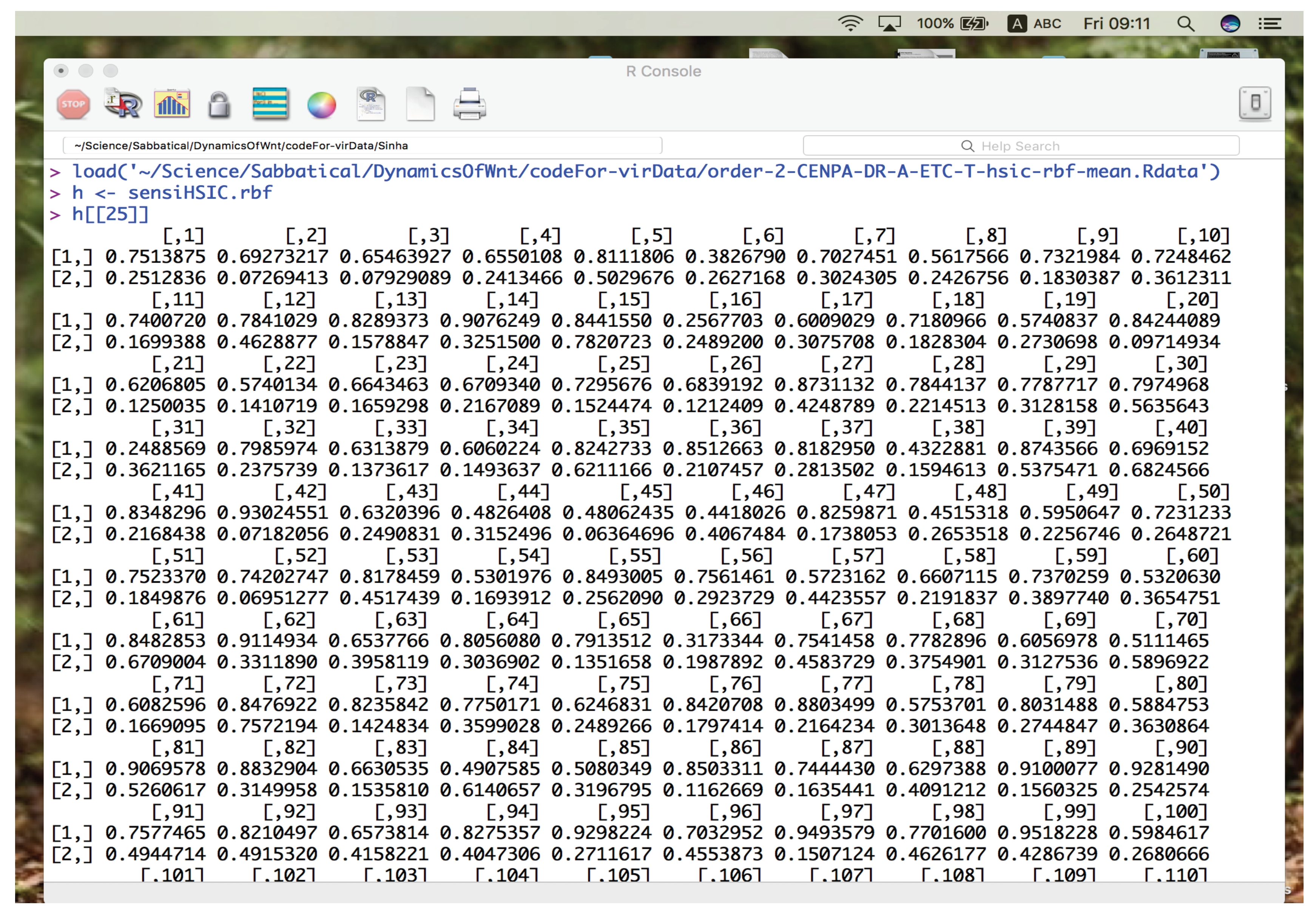Since we know that lapply will generate sensitivity indices for each of the matrices in x.S, thus each combination has an associated sensitivity that is stored in h[[p]]$S$original. We bind this to the variable FdivTV (see lines 108-113).
Next, since the for loop in line 89 works for many iterations, we need to store the sensitivity index computed in this iteration in a certain variable. This is done in sensiFdiv.TV[[itr]], definition of which was done in line 49. Also, if this is the first iteration, then we define the file name based on the data that is being used and the iteration (see lines 115-117).
107 # itr <- 1
108 if(length(grep("TV",varName))!= 0){
109 FdivTV <- c()
110 cat("computing estimate different
indices ...\n")
111 cat("Fdiv SA - TV\n")
112 h <- lapply(x.S, sensiFdiv,
model = new.fun, fdiv = "TV",
nboot = 0, conf = 0.95)
113 for(p in 1:no.slgeneComb){
FdivTV <- cbind(FdivTV,
h[[p]]$S$original)
}
114 sensiFdiv.TV[[itr]] <- FdivTV
115 if(DATATYPE == "1" & itr == 1){
filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-tv-mean.Rdata",
sep = "")
116 }else if(DATATYPE == "2" & itr == 1){
filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-tv-mean.Rdata",
sep = "")
117 }
The next series of conditions deals with the different methods in a similar manner as explained for lines 108-117. Lines 118-130 talk about f-divergence method Csiszár et al. [10] with a Kullback-Leibler divergence .
118 }else if(length(grep("KL",varName))
!= 0){
119 FdivKL <- c()
120 cat("computing estimate different
indices ...\n")
121 cat("Fdiv SA - KL\n")
122 h <- lapply(x.S, sensiFdiv,
model = new.fun, fdiv = "KL",
nboot = 0, conf = 0.95)
123 for(p in 1:no.slgeneComb){
124 FdivKL <- cbind(FdivKL,
h[[p]]$S$original)
125 }
125 sensiFdiv.KL[[itr]] <- FdivKL
126 if(DATATYPE == "1" & itr == 1){
127 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-kl-mean.Rdata",
sep = "")
128 }else if(DATATYPE == "2" & itr == 1){
129 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-kl-mean.Rdata",
sep = "")
130 }
Lines 131-144 talk about f-divergence method Csiszár et al. [10] with a distance .
131 }else if(length(grep("Chi2",varName))
!= 0){
132 FdivChi2 <- c()
133 cat("computing estimate different
indices ...\n")
134 cat("Fdiv SA - Chi2\n")
135 h <- lapply(x.S, sensiFdiv,
model = new.fun, fdiv = "Chi2",
nboot = 0, conf = 0.95)
136 for(p in 1:no.slgeneComb){
137 FdivChi2 <- cbind(FdivChi2,
h[[p]]$S$original)
138 }
139 sensiFdiv.Chi2[[itr]] <- FdivChi2
140 if(DATATYPE == "1" & itr == 1){
141 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-chi2-mean.Rdata",
sep = "")
142 }else if(DATATYPE == "2" & itr == 1){
143 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-chi2-mean.Rdata",
sep = "")
144 }
Lines 145-158 talk about f-divergence method Csiszár et al. [10] with a Hellinger distance .
145 }else if(length(grep("Hellinger",varName))
!= 0){
146 FdivHellinger <- c()
147 cat("computing estimate different
indices ...\n")
148 cat("Fdiv SA - Hellinger\n")
149 h <- lapply(x.S, sensiFdiv,
model = new.fun, fdiv = "Hellinger",
nboot = 0, conf = 0.95)
150 for(p in 1:no.slgeneComb){
151 FdivHellinger <- cbind(FdivHellinger,
h[[p]]$S$original)
152 }
153 sensiFdiv.Hellinger[[itr]]
<- FdivHellinger
154 if(DATATYPE == "1" & itr == 1){
155 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-hellinger-mean.Rdata",
sep = "")
156 }else if(DATATYPE == "2" & itr == 1){
157 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-hellinger-mean.Rdata",
sep = "")
158 }
Da Veiga [11] recently proposed a new set of dependence measures using kernel methods. These also, have been implemented in Pujol et al. [9]. The following contains variants of different kernels involved in computing the sensitvity indices. Lines 159-172 show similar execution code as above with changes insome of the arguments in the lapply function. Here, the "rbf" or radial basis function is used within sensiHSIC.
159 }else if(length(grep("rbf",varName))
!= 0){
160 HSICrbf <- c()
161 cat("computing estimate different
indices ...\n")
162 cat("HSIC SA - rbf kernel\n")
163 h <- lapply(x.S, sensiHSIC,
model = new.fun, kernelX = "rbf",
paramX = NA, kernelY = "rbf",
paramY = NA, conf = 0.95)
164 for(p in 1:no.slgeneComb){
165 HSICrbf <- cbind(HSICrbf,
h[[p]]$S$original)
166 }
167 sensiHSIC.rbf[[itr]] <- HSICrbf
168 if(DATATYPE == "1" & itr == 1){
169 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-hsic-rbf-mean.Rdata",
sep = "")
170 }else if(DATATYPE == "2" & itr == 1){
171 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-hsic-rbf-mean.Rdata",
sep = "")
172 }
Lines 173-186 show similar execution code as above with changes insome of the arguments in the lapply function. Here, the linear function is used.
173 }else if(length(grep("linear",varName))
!= 0){
174 HSIClinear <- c()
175 cat("computing estimate different
indices ...\n")
176 cat("HSIC SA - linear kernel\n")
177 h <- lapply(x.S, sensiHSIC,
model = new.fun, kernelX = "linear",
paramX = NA, kernelY = "linear",
paramY = NA, conf = 0.95)
178 for(p in 1:no.slgeneComb){
179 HSIClinear <- cbind(HSIClinear,
h[[p]]$S$original)
180 }
181 sensiHSIC.linear[[itr]] <- HSIClinear
182 if(DATATYPE == "1" & itr == 1){
183 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-hsic-linear-mean.Rdata",
sep = "")
184 }else if(DATATYPE == "2" & itr == 1){
185 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-hsic-linear-mean.Rdata",
sep = "")
186 }
Lines 187-200 show similar execution code as above with changes insome of the arguments in the lapply function. Here, the laplace function is used.
187 }else if(length(grep("laplace",varName))
!= 0){
188 HSIClaplace <- c()
189 cat("computing estimate different
indices ...\n")
190 cat("HSIC SA - laplace kernel\n")
191 h <- lapply(x.S, sensiHSIC,
model = new.fun, kernelX = "laplace",
paramX = NA, kernelY = "laplace",
paramY = NA, conf = 0.95)
192 for(p in 1:no.slgeneComb){
193 HSIClaplace <- cbind(HSIClaplace,
h[[p]]$S$original)
194 }
195 sensiHSIC.laplace[[itr]] <- HSIClaplace
196 if(DATATYPE == "1" & itr == 1){
197 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-hsic-laplace-mean.Rdata",
sep = "")
198 }else if(DATATYPE == "2" & itr == 1){
199 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-hsic-laplace-mean.Rdata",
sep = "")
200 }
Finally, we come to the section, were variants of the Sobol function have been encoded. It is here that the use of divided samples X.Sfh and X.Ssh comes to play. We do not use the lapply function. Instead, the Sobol’ [12] variants are enconded using name specific function (see below). Lines 201-214 show similar execution code as above, but using soboljansen.
201 }else if(length(grep("jansen",varName))
!= 0){
202 SBLjansen <- c()
203 cat("computing estimate different
indices ...\n")
204 cat("Sobol Jansen SA\n")
205 for(p in 1:no.slgeneComb){
206 h <- soboljansen(model = new.fun,
X1 = t(x.Sfh[[p]]),
X2 = t(x.Ssh[[p]]), conf = 0.95)
207 SBLjansen <- cbind(SBLjansen,
c(h$S$original, h$T$original))
208 }
209 SB.jansen[[itr]] <- SBLjansen
210 if(DATATYPE == "1" & itr == 1){
211 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-jansen-mean.Rdata",
sep = "")
212 }else if(DATATYPE == "2" & itr == 1){
213 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-jansen-mean.Rdata",
sep = "")
214 }
Lines 215-228 show similar execution code as above, but using sobol2002.
215 }else if(length(grep("2002",varName))
!= 0){
216 SBL2002 <- c()
217 cat("computing estimate different
indices ...\n")
218 cat("Sobol 2002 SA\n")
219 for(p in 1:no.slgeneComb){
220 h <- sobol2002(model = new.fun,
X1 = t(x.Sfh[[p]]),
X2 = t(x.Ssh[[p]]), conf = 0.95)
221 SBL2002 <- cbind(SBL2002,
c(h$S$original, h$T$original))
222 }
223 SB.2002[[itr]] <- SBL2002
224 if(DATATYPE == "1" & itr == 1){
225 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-2002-mean.Rdata",
sep = "")
226 }else if(DATATYPE == "2" & itr == 1){
227 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-2002-mean.Rdata",
sep = "")
228 }
Lines 229-242 show similar execution code as above, but using sobol2007.
229 }else if(length(grep("2007",varName))
!= 0){
230 SBL2007 <- c()
231 cat("computing estimate different
indices ...\n")
232 cat("Sobol 2007 SA\n")
233 for(p in 1:no.slgeneComb){
234 h <- sobol2007(model = new.fun,
X1 = t(x.Sfh[[p]]),
X2 = t(x.Ssh[[p]]), conf = 0.95)
235 SBL2007 <- cbind(SBL2007,
c(h$S$original, h$T$original))
236 }
237 SB.2007[[itr]] <- SBL2007
238 if(DATATYPE == "1" & itr == 1){
239 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-2007-mean.Rdata",
sep = "")
240 }else if(DATATYPE == "2" & itr == 1){
241 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-2007-mean.Rdata",
sep = "")
242 }
Lines 243-256 show similar execution code as above, but using sobolmartinez.
243 }else if(length(grep("martinez",varName))
!= 0){
244 SBLmartinez <- c()
245 cat("computing estimate different
indices ...\n")
246 cat("Sobol Martinez SA\n")
247 for(p in 1:no.slgeneComb){
248 h <- sobolmartinez(model = new.fun,
X1 = t(x.Sfh[[p]]),
X2 = t(x.Ssh[[p]]), conf = 0.95)
249 SBLmartinez <- cbind(SBLmartinez,
c(h$S$original, h$T$original))
250 }
251 SB.martinez[[itr]] <- SBLmartinez
252 if(DATATYPE == "1" & itr == 1){
253 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-martinez-mean.Rdata",
sep = "")
254 }else if(DATATYPE == "1" & itr == 1){
255 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-martinez-mean.Rdata",
sep = "")
256 }
Lines 257-272 show similar execution code as above, but using sobol.
257 }else if(length(grep("SBL",varName))
!= 0){
258 sbl <- c()
259 cat("computing estimate different
indices ...\n")
260 cat("SBL SA\n")
261 for(p in 1:no.slgeneComb){
262 h <- sobol(model = new.fun,
X1 = t(x.Sfh[[p]]),
X2 = t(x.Ssh[[p]]), order = 1,
conf = 0.95)
263 sbl <- cbind(SBL, c(h$S$original,
h$T$original))
264 }
265 SBL[[itr]] <- sbl
266 if(DATATYPE == "1" & itr == 1){
267 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sbl-mean.Rdata",
sep = "")
268 }else if(DATATYPE == "2" & itr == 1){
269 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sbl-mean.Rdata",
sep = "")
270 }
271 }
272 }
Once the indices have been generated, they need to be stored in a file for further processing. The following set of lines help in saving the work, were the function save is used and variables no.slgeneComb, x.S and the respective sensitivity indices related to varName is stored in the filename.
273 if(length(grep("TV",varName))!= 0){
274 save(no.slgeneComb, x.S,
sensiFdiv.TV, file = filename)
275 }else if(length(grep("KL",varName))
!= 0){
276 save(no.slgeneComb, x.S,
sensiFdiv.KL, file = filename)
277 }else if(length(grep("Chi2",varName))
!= 0){
276 save(no.slgeneComb, x.S,
sensiFdiv.Chi2, file = filename)
277 }else if(length(grep("Hellinger",varName))
!= 0){
278 save(no.slgeneComb, x.S,
sensiFdiv.Hellinger, file = filename)
279 }else if(length(grep("rbf",varName))
!= 0){
280 save(no.slgeneComb, x.S,
sensiHSIC.rbf, file = filename)
281 }else if(length(grep("linear",varName))
!= 0){
282 save(no.slgeneComb, x.S,
sensiHSIC.linear, file = filename)
283 }else if(length(grep("laplace",varName))
!= 0){
284 save(no.slgeneComb, x.S,
sensiHSIC.laplace, file = filename)
285 }else if(length(grep("jansen",varName))
!= 0){
286 save(no.slgeneComb, x.S,
SB.jansen, file = filename)
287 }else if(length(grep("2002",varName))
!= 0){
289 save(no.slgeneComb, x.S,
SB.2002, file = filename)
290 }else if(length(grep("2007",varName))
!= 0){
291 save(no.slgeneComb, x.S,
SB.2007, file = filename)
292 }else if(length(grep("martinez",varName))
!= 0){
293 save(no.slgeneComb, x.S,
SB.martinez, file = filename)
294 }else if(length(grep("SBL",varName))
!= 0){
295 save(no.slgeneComb, x.S,
SBL, file = filename)
296 }
This ends the coding part of estimating sensitvity indices. Once the indices are ready they can be used in various ways for evaluation of the combinations. Here, we use one of the ways to ranking these scores. However, not that there is no one definite rule to say that one has to rank in this way only. It depends on the research to decide what method one is employing for ranking. We use the algorithm by Joachims [13]. Though complex in nature, it does a fair job in ranking the scores. The use of a machine learning approach is also made available to see how the learning algorithms play critical role in revealing unknown/untested combinatorial hypotheses. Other reasons of using these will be stated later on.
4.3.2. Exercise
At this stage, it would be great to see how the two codes on extracting data and generating indices works out. The readers are requested to generate the different types of indices based on their choice and see what comparisons can be made using the different indices. Also try the following exercies -
- Generate HSIC rbf indices for 2nd order combinations for downregulated AXIN2. What does the combination of AXIN2 with another factor that has lowest score mean?
- Generate FDiv KL indices for 2nd order combinations for downregulated MYC. What does the combination of MYC with another factor that has highest score mean?
- Generate HSIC laplace indices for 2nd order combinations for downregulated NKD1. What does the combination of NKD1 with another factor that has score in the middle mean?
- Generate FDiv TV indices for 2nd order combinations for downregulated CDAN1. What does the combination of CDAN1 with another factor that has score at 100 position in ascending order mean?
- Generate Sobol indices for 2nd order combinations for downregulated MINA. How many kinds of indices can you generate? Compare them for a particular combination!
- Generate Sobol jansen indices for 2nd order combinations for downregulated MINA. How many kinds of indices can you generate? Compare them for two different combinations!
- Generate Sobol martinez indices for 2nd order combinations for downregulated MINA. How many kinds of indices can you generate? Compare them for 20 different combinations!
- Generate Sobol 2002 and 2007 indices for 2nd order combinations for downregulated MINA. How many kinds of indices can you generate? Compare Sobol 2002 vs Sobol 2007
- Compare HSIC rbf, HSIC laplace, FDiv TV, FDiv KL, Sobol, Sobol jansen, Sobol martinez, Sobol 2002 and 2007 indices for down regulated LGR5-RNF43.
4.4. Ranking & Sorting
4.4.1. Description of SVM-Results-S-mean.R
This part of the code is the last in the pipeline that works on the generated sensitivity indices. The code is in the file SVMRank-Results-S-mean.R. It ranks the sensitivity indices using a machine learning algorithm. We go through this part of the code and will then come back to why’s and why not’s. Lines 1-16 are basic data processing techniques and some formalities that need to be done befor we begin on the ranking part. So, by now, it should be expected the reader is able to work through the line and understand what is happening if a following line is being executed, at least, theoretically.
1 DATATYPE <- readline("Choose a file
to process [1/2] \n
2 1 - ../data/onc2015280x2-A.txt \n
3 Genes down-regulated after ETC-159
treatment \n
4 2 - ../data/onc2015280x2-B.txt \n
5 Genes up-regulated after ETC-159
treatment \n
6 File number - ")
7 while(DATATYPE != "1" & DATATYPE != "2"){
8 DATATYPE <- readline("Type the kind of
data to be processed - ")
9 }
10
11 CHOOSE <- as.numeric(readline("pick a
numeric for k in nCk - "))
12 k <- as.numeric(CHOOSE)
13
14 geneName <- readline("Please enter the
name of the gene to be processed - ")
15 siNames <- c("Fdiv.TV", "Fdiv.KL",
"Fdiv.Chi2", "Fdiv.Hellinger", "HSIC.rbf",
"HSIC.linear", "HSIC.laplace", "SB.2002",
"SB.2007", "SB.jansen", "SB.martinez",
"SBL")
16 sa.name <- readline("Please enter the
name of the proposed SA from above
list - ")
We stored the sensitivity indices in different files. These files need to be accessed in order for the procedure of ranking to be initiated. The following lines help retrieve the file names which can then be loaded into the R workspace from where it can be accessed easily. To retrieve the file name, the function paste is employed. Readers are encouraged to find how the paste function works. After the file name is constructed, the contents of the file are loaded using the load function, followed by the assignment of stored data into a variable h. Lines 17-113 show the code for various kinds of indicies that a user can access, after using paste and load.
17 if(length(grep(sa.name,"Fdiv.TV"))
!= 0){
18 if(DATATYPE == "1"){
19 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-tv-mean.Rdata",
sep = "")
20 }else{
21 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-tv-mean.Rdata",
sep = "")
22 }
23 load(filename)
24 h <- sensiFdiv.TV
25 }else if(length(grep(sa.name,"Fdiv.KL"))
!= 0){
26 if(DATATYPE == "1"){
27 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-kl-mean.Rdata",
sep = "")
28 }else{
29 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-kl-mean.Rdata",
sep = "")
30 }
31 load(filename)
32 h <- sensiFdiv.KL
33 }else if(length(grep(sa.name,"Fdiv.Chi2"))
!= 0){
34 if(DATATYPE == "1"){
35 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-chi2-mean.Rdata",
sep = "")
36 }else{
37 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-chi2-mean.Rdata",
sep = "")
38 }
39 load(filename)
40 h <- sensiFdiv.Chi2
41 }else if(length(grep(sa.name,"Fdiv.Hellinger"))
!= 0){
42 if(DATATYPE == "1"){
43 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-fdiv-hellinger-mean.Rdata",
sep = "")
44 }else{
45 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-fdiv-hellinger-mean.Rdata",
sep = "")
46 }
47 load(filename)
48 h <- sensiFdiv.Hellinger
49 }else if(length(grep(sa.name,"HSIC.rbf"))
!=0){
50 if(DATATYPE == "1"){
51 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-hsic-rbf-mean.Rdata",
sep = "")
52 }else{
53 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-hsic-rbf-mean.Rdata",
sep = "")
54 }
55 load(filename)
56 h <- sensiHSIC.rbf
57 }else if(length(grep(sa.name,"HSIC.linear"))
!= 0){
58 if(DATATYPE == "1"){
59 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-hsic-linear-mean.Rdata",
sep = "")
60 }else{
61 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-hsic-linear-mean.Rdata",
sep = "")
62 }
63 load(filename)
64 h <- sensiHSIC.linear
65 }else if(length(grep(sa.name,"HSIC.laplace"))
!= 0){
66 if(DATATYPE == "1"){
67 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-hsic-laplace-mean.Rdata",
sep = "")
68 }else{
69 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-hsic-laplace-mean.Rdata",
sep = "")
70 }
71 load(filename)
72 h <- sensiHSIC.laplace
73 }else if(length(grep(sa.name,"SB.2002"))
!= 0){
74 if(DATATYPE == "1"){
75 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-2002-mean.Rdata",
sep = "")
76 }else{
77 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-2002-mean.Rdata",
sep = "")
78 }
79 load(filename)
80 h <- SB.2002
81 }else if(length(grep(sa.name,"SB.2007"))
!= 0){
82 if(DATATYPE == "1"){
83 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-2007-mean.Rdata",
sep = "")
84 }else{
85 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-2007-mean.Rdata",
sep = "")
86 }
87 load(filename)
88 h <- SB.2007
89 }else if(length(grep(sa.name,"SB.jansen"))
!= 0){
90 if(DATATYPE == "1"){
91 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-jansen-mean.Rdata",
sep = "")
92 }else{
93 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-jansen-mean.Rdata",
sep = "")
94 }
95 load(filename)
96 h <- SB.jansen
97 }else if(length(grep(sa.name,"SB.martinez"))
!= 0){
98 if(DATATYPE == "1"){
99 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sb-martinez-mean.Rdata",
sep = "")
100 }else{
101 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sb-martinez-mean.Rdata",
sep = "")
102 }
103 load(filename)
104 h <- SB.martinez
105 }else if(length(grep(sa.name,"SBL"))
!= 0){
106 if(DATATYPE == "1"){
107 filename <- paste("order-",k,"-",
geneName,
"-DR-A-ETC-T-sbl-mean.Rdata",
sep = "")
108 }else{
109 filename <- paste("order-",k,"-",
geneName,
"-UR-A-ETC-T-sbl-mean.Rdata",
sep = "")
110 }
111 load(filename)
112 h <- SBL
113 }
Once the indicies that have to be worked on have been put in h, the indicies need to be averaged. For demonstration purpose, we average only 2 iterations and see how things turn out. However, we need to understand how the data is stored in h. Figure 3 shows a screen shot of how element of h looks. h[[25]] is the 25th element and is a matrix of size . 2 is the number of elements in a combination under consideration and 2743 are the total number of distinct 2nd order combinations. We exploit this view of h to compute the means of for all elements of a combination and over all distinct combinations. This is done in the for loops below in which p iterates over elements of combination and itr iterates over the total number of iterations. Thus h[[itr]][p,] between the two nested for loops considers the pth row of itrth matrix in h. Then, r binds all the h[[1]][p,], h[[2]][p,], ..., h[[itrNo]][p,], using rbind. After exiting the inner loop, we use the apply function to r matrix over the columns (i.e the distinct combinations) with a function mean. Thus we get a vector of mean values of sensitivity index for each distinct combination over all iterations, for the pth element. This process is again repeated for the next p value. Finally, the vector of means are stacked in SAmean. Lines 114-124 show this coding below.
114 # Use this for averaged ranking
115 # itrNo <- 50
116 itrNo <- 2
117 SAmean <- c()
118 for(p in 1:k){
119 r <- c()
120 for(itr in 1:itrNo){
121 r <- rbind(h[[itr]][p,])
122 }
123 SAmean <- rbind(SAmean, apply(X = r,
MARGIN = 2, mean))
124 }
Next, we format the data in the form that is suitable for the machine. The output of the next block of code can be depicted in Figure 4. Note that it is a screen shot for how the data is saved for a 3rd order combination. i invite readers to decode the following block by themselves as an exercise.
125 # y <- SA
126 y <- SAmean
127 data <- c()
128 for(i in 1:no.slgeneComb){
129 z <- c()
130 z <- cbind(z,i)
131 for(j in 1:k){
132 z <- cbind(z,
paste(j,":",y[j,i],sep=""))
133 }
134 z <- cbind(z,"\n")
135 data <- rbind(data,z)
136 }
Next the file names for traning, testing, model and predition are built using paste (see lines 137-140). And finally, data is concatenated to the training and the testing files (see lines 141-142).
137 trnfl <- paste("svr-trn-order-",k,
"-",geneName,".txt", sep = "")
138 tstfl <- paste("svr-tst-order-",k,
"-",geneName,".txt", sep = "")
139 mdlfl <- paste("svr-mdl-order-",k,
"-",geneName,".txt", sep = "")
140 predfl <- paste("svr-pred-order-",k,
"-",geneName,".txt", sep = "")
141 cat(t(data),file=trnfl)
142 cat(t(data),file=tstfl)
We now come to the main part of the code which involves using the support vector ranking algorithm. Since it is a compiled executable file, it needs to be executed using a system command. However, before that, the command that needs to be executed must be prepared in the right format. For this the paste command is used (see line 144). In the paste command takes in the C value in the form of ; to terminate svm-light QP subproblem optimization, if no progress after this number of iterations; number of new variables entering the working set in each svm-light iteration (default ) : Set to prevent zig-zagging : We set n to 9 considering the number of samples generated from distribution; the training file and the model file. Finally we use the built up command in the system function (see line 145).
143 # svm rank learn on C value - 20
144 cmd <- paste(
"./../svm_rank/svm_rank_learn
-c 20 -# 100 -n 9",trnfl,mdlfl,sep=" ")
145 system(command=cmd)
Similar format is used to classify the test file, once the model has been prepared using the . This is acheived using the . Note that when there is only one instance of each training data, then after the model is being built on it, for ranking purpose, we use the same training as testing file. This might sound strange at first view, however, the model should be able to rank the scores based of the original data. It is not a hard and fast rule to rank through SVMs but, here we show and example of the same. One can use a completely different algorithm also for the same set of training data. Ranking is done in the next lines 146-148.
146 # svm rank classify
147 cmd <- paste(
"./../svm_rank/svm_rank_classify",
tstfl,mdlfl,predfl,sep=" ")
148 system(command=cmd)
Once the ranking is done, the data in the prediction file is stored in a variable via read.table function and later stored in an appropriate file. Again the file name need to be constructed. See lines 149-156.
149 # read predictions of rankings
150 dataScore <- read.table(predfl)
151 # save it in appropriate file
152 if(DATATYPE == "1"){
153 save(dataScore,file=paste("order-",k,
"-SA-",sa.name,"-",geneName,
"-rankingScore-mean-DR.R",sep=""))
154 }else{
155 save(dataScore,file=paste("order-",k,
"-SA-",sa.name,"-",geneName,
"-rankingScore-mean-UR.R",sep=""))
156 }
4.4.2. Exercise
Please download the and as intructed on the website of Joachims [13], compile the same to get executable files.
4.4.3. Sorting
Finally, we sort the predicted results. These are expressed in the last block from lines 157-172. dataScore that contained the predictions is sorted using the sort function and the indices of the sorted values is also retured (see line 159). Next, using the for loop we arrange the names of the combinations in a sorted order using the sorted index in line 159. These sorted combinations are appended in sortedGenecomb (see lines 161-167). Finally, we store these results according to the type of data we are dealing with.
157 # sort the predicted scores
158 cat("sorting in ascending order
- top is lowest in ranking")
159 dataScore <- sort(dataScore$V1,
index.return=TRUE)
160 noCombs <- length(dataScore$ix)
161 # arrange the combinations by ranking
162 sortedGenecomb <- c()
163 for(i in 1:noCombs){
164 idx <- dataScore$ix[i]
165 z <- capture.output(cat(
names(x.S[[idx]]),sep="-"))
166 sortedGenecomb <- c(sortedGenecomb, z)
167 }
168 if(DATATYPE == "1"){
169 write.table(sortedGenecomb,
file=paste("order-",k,"-SA-",
sa.name,"-",geneName,
"-ranking-mean-DR.txt",sep=""))
170 }else{
171 write.table(sortedGenecomb,
file=paste("order-",k,"-SA-",
sa.name,"-",geneName,
"-ranking-mean-UR.txt",sep=""))
172 }
The sorted combinations look like that in Figure 5. This finishes the general framework of the pipeline.
5. Requisites to Execute the Code
(1) R statistical langauge (2) from https://www.cs.cornell.edu/people/tj/svm_light/svm_rank.html (3) Sensitivity package (4) ETC-1922159 data set.
6. Code Surgery via Browser Scalpel
R provides with a browser function which can help one to seen the contents of the variables and intermediate outputs once the execution of the code has begun. The function is like a scalpel which helps dissect the entire code as the execution proceeds one step at a time. Various functionalities exist to use browser function. These can be seen by typing ?browser at the command prompt. Briefly - • c exit the browser and continue execution at the next statement. • f finish execution of the current loop or function help print this list of commands. • n evaluate the next statement, stepping over function calls. For byte compiled functions interrupted by browser calls, n is equivalent to c. • s evaluate the next statement, stepping into function calls. Again, byte compiled functions make s equivalent to c. • where print a stack trace of all active function calls. • r invoke a "resume" restart if one is available; interpreted as an R expression otherwise. Typically "resume" restarts are established for continuing from user interrupts. • Q exit the browser and the current evaluation and return to the top-level prompt.
As a small example, using the browser function on extractETCdata function is depicted in the snap shot in Figure 6. Especially note the output of the browser function in the white patch in the above figure. What we find is that at each punch of the "return" or "enter" button on the computer, a following line appears (an instance shown here were the execution of the browser had reached in the code in extractETCdata.R)-
> source("extractETCdata.R")
> extractETCdata(1)
Called from: extractETCdata(1)
Browser[1]>
debug at extractETCdata.R#3: if (data.type == 1){
filename <- "../data/onc2015280x2-A.txt"
} else {
filename <- "../data/onc2015280x2-B.txt"
}
Browser[2]>.
.
What is happening is that we inserted a browser function in extractETCdata.R just after extractETCdata <- function(data.type){. After compiling extractETCdata.R using the source function and executing extractETCdata(1) at the R prompt >, the browser function comes into affect. This is shown with an additional Browser[]>. Evidence of this is provided by the line stating the following - "Called from: extractETCdata(1)". next, on pressing "return", the execution moves to the next command that it needs to execute. This is denoted by debug function and the line reads as "debug at extractETCdata.R#3:", meaning that the execution is waiting at command 3 in the code. Along with it, whole command that needs to be executed in one go is also presented. Here it is the if(data.type == 1) {...} else {...} command. Since the data.type == 1 is true, the command filename <- ../data/onc2015280x2-A.txt" is executed. This is shown in the next line that the browser has to execute, when the above condition holds true. See Figure 6.
6.1. Exercise
Please use browser function to inspect the values in the variables and see how the code executes for extractETCdata.R and manuscript-2-2.R.
Results from the search engine can be found in the recently unpublished preprint in Sinha [14].
7. MYC-HOXB8-EZH2
EZH2 encodes enhancer of zeste homolog 2 and is involved in transcriptional repression via epigenetic modifications. It has been found to be either mutated or over-expressed in many forms of cancer. Over expression of EZH2 leads to silencing of various tumor suppressor genes and thus implicating it for potential roles in tumorigenesis Simon and Lange [15]. EZH2 is a subunit of the highly conserved Polycomb repressive complex 2 (PRC2) which executes the methylation of the histone H3 at lysine-27 O’Meara and Simon [16]. Thus targeting EZH2 has become a major research domain for cancer therapeutics Kim and Roberts [17]. In colon cancer, it has been shown that depletion of EZH2 has led to blocking of proliferation of the cancer Fussbroich et al. [18]. This indicates the fact that tumor suppressor genes get activated and lead to subsequent blocking of the cancer. Also, EZH2 is recruited by PAF to bind with -catenin transcriptional complex for further Wnt target gene activation, independent of the EZH2 epigenetic modification activities Jung et al. [19].
Consistent with these, ETC-15922159 treatment lead to down regulation of EZH2 in colorectal cancer samples Madan et al. [3]. This would have activated a lot of tumor suppressor genes that led to subsequent suppression of regrowth in treated cancer samples. More importantly, MYC directly upregulates core components of PRC2, EZH2 being one of them, in embryonic stem cells Neri et al. [20]. Neri et al. [20] show that silencing of c-MYC and N-MYC Dardenne et al. [21] lead to reduction in the expression of PRC2 and thus EZH2. Furthermore, in colorectal cancer cases, Satoh et al. [22] show that knockdown of MYC led to decrease in EZH2 levels. Similar findings have been observed in Yamaguchi and Hung [23], Chen et al. [24] & Fluge et al. [25]. Our in silico findings show consistent results with respect to this down regulation after assigning a low rank of 54 along with MYC-HOXB8.
More specifically, our in silico pipeline is able to approximate the value of the 3rd order combination of MYC-HOXB8-EZH2 by assigning a rank that is consistent with wet lab findings of dual combinatorial behaviour of MYC-EZH2 and MYC-HOXB8. However, the since the mechanism of combination of MYC-HOXB8 is not known hitherto, it would be interesting to confirm the behaviour of MYC-HOXB8-EZH2 at 3rd order to reveal a portion of the Wnt pathway’s modus operandi in colorectal cancer. Further wet lab tests on these in silico findings will confirm the efficacy of the search engine.
8. Future Work
The ETC-1922159 was released in Singapore in July 2015 under the flagship of the Agency for Science, Technology and Research (A*STAR) and Duke-National University of Singapore Graduate Medical School (Duke-NUS). In the publication in https://www.nature.com/articles/onc2015280 , recording of regulation (up/down) of some 5000 genes were made (available online with the published paper), after the drug was tested on Colorectal cancer cells. I tested the modification of the search engine (as mentioned in Sinha [1]) and discovered various 2nd order combinations of genes that might affect various pathways, after the drug was administered. The documentation of the discoveries citet published confirmatory results of existing gene combinations. Next, based on these confirmatory results, I find appropriate rankings that the search engine points to for the ETC-1922159 data. Lastly, based on these rankings, I infer new combinations pointed out by the search engine. The results of the work were shared in the first Gordon Wnt Research Conference in 2017, in Vermont in USA. The discoveries have been segregated into 8 areas for research. These are documented in 8 different articles, unpublished preprints of which have been made available in the following links -
- Wnt related synergies in https://www.preprints.org/manuscript/202409.0453/v1
- NFB related synergies in https://www.preprints.org/manuscript/202409.0696/v1
- TNF related synergies in https://www.preprints.org/manuscript/202409.0471/v1
- DNA repair related synergies in https://www.preprints.org/manuscript/202409.0885/v1
- ABC transporter related synergies in https://www.preprints.org/manuscript/202409.0908/v1
- Interleukin related synergies in https://www.preprints.org/manuscript/202409.1353/v1
- BCL related synergies in https://www.preprints.org/manuscript/202409.0855/v1
- ANTXR2 related synergies in https://www.preprints.org/manuscript/202409.0817/v1
The adaptation of the code for the search engine published in Sinha [1] and the related unpublished research work, is available on Biorxiv at https://www.biorxiv.org/content/10.1101/180927v2. Adaptation of code for ETC-1922159 data can be found in the link in the above mentioned Biorxiv paper.
9. Code Availability
Conflicts of Interest
There are no conflicts to declare.
Acknowledgments
Special thanks to Mrs. Rita Sinha and late Mr. Prabhat Sinha for supporting the author financially, without which this work could not have been made possible.
Data Availability Statement
Data used in this research work has been released online publicaly, in a publication in Madan et al. [3]. The ETC-1922159 was released in Singapore in July 2015 under the flagship of the Agency for Science, Technology and Research (A*STAR) and Duke-National University of Singapore Graduate Medical School (Duke-NUS). This work is licensed under a Creative Commons Attribution- NonCommercial-NoDerivs 4.0 International License. To view a copy of this license, visit urlhttp://creativecommons.org/licenses/by-nc-nd/4.0/. Note, the license also states that you do not have to comply with the license for elements of the material in the public domain or where your use is permitted by an applicable exception or limitation. Further, approriate rights from the journal have been obtained to share the data.
References
- Sinha, S. Machine learning ranking of plausible (un)explored synergistic gene combinations using sensitivity indices of time series measurements of Wnt signaling pathway. Integrative Biology 2024. [Google Scholar] [CrossRef]
- Sinha, S. Hilbert-Schmidt and Sobol sensitivity indices for static and time series Wnt signaling measurements in colorectal cancer-part A. BMC systems biology 2017, 11, 120. [Google Scholar] [CrossRef]
- Madan, B.; Ke, Z.; Harmston, N.; Ho, S.Y.; Frois, A.; Alam, J.; Jeyaraj, D.A.; Pendharkar, V.; Ghosh, K.; Virshup, I.H.; others. Wnt addiction of genetically defined cancers reversed by PORCN inhibition. Oncogene 2016, 35, 2197. [Google Scholar] [CrossRef]
- Tusher, V.G.; Tibshirani, R.; Chu, G. Significance analysis of microarrays applied to the ionizing radiation response. Proceedings of the National Academy of Sciences 2001, 98, 5116–5121. [Google Scholar] [CrossRef] [PubMed]
- Choe, S.E.; Boutros, M.; Michelson, A.M.; Church, G.M.; Halfon, M.S. Preferred analysis methods for Affymetrix GeneChips revealed by a wholly defined control dataset. Genome biology 2005, 6, R16. [Google Scholar] [CrossRef] [PubMed]
- Witten, D.; Tibshirani, R. A comparison of fold-change and the t-statistic for microarray data analysis. Analysis 2007, 1776, 58–85. [Google Scholar]
- Sinha, S. Prioritizing 2nd order interactions via support vector ranking using sensitivity indices on time series Wnt measurements. bioRxiv 2017, 060228. [Google Scholar]
- Sinha, S. Sensitivity analysis based ranking reveals unknown biological hypotheses for down regulated genes in time buffer during administration of PORCN-WNT inhibitor ETC-1922159 in CRC. bioRxiv 2017, 180927. [Google Scholar]
- Pujol, G.; Iooss, B.; Janon, A.; Boumhaout, K.; Da Veiga, S.; Fruth, J.; Gilquin, L.; Guillaume, J.; Le Gratiet, L.; Lemaitre, P.; others. Sensitivity: global sensitivity analysis of model outputs. R package version 2016, 1. [Google Scholar]
- Csiszár, I.; others. Information-type measures of difference of probability distributions and indirect observations. Studia Sci. Math. Hungar. 1967, 2, 299–318. [Google Scholar]
- Da Veiga, S. Global sensitivity analysis with dependence measures. Journal of Statistical Computation and Simulation 2015, 85, 1283–1305. [Google Scholar] [CrossRef]
- Sobol’, I.M. On sensitivity estimation for nonlinear mathematical models. Matematicheskoe Modelirovanie 1990, 2, 112–118. [Google Scholar]
- Joachims, T. Training linear SVMs in linear time. Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2006, pp. 217–226.
- Sinha, S. A Glimpse of Ocean of Abundant Discoveries: Two-Way Cross Family Analysis of In-Silico Ranked 2nd Order Unexplored, ETC-1922159 Affected, Synergistic Combinations in CRC Cells. Preprints 2023. [Google Scholar] [CrossRef]
- Simon, J.A.; Lange, C.A. Roles of the EZH2 histone methyltransferase in cancer epigenetics. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis 2008, 647, 21–29. [Google Scholar] [CrossRef]
- O’Meara, M.M.; Simon, J.A. Inner workings and regulatory inputs that control Polycomb repressive complex 2. Chromosoma 2012, 121, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Roberts, C.W. Targeting EZH2 in cancer. Nature medicine 2016, 22, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Fussbroich, B.; Wagener, N.; Macher-Goeppinger, S.; Benner, A.; Fälth, M.; Sültmann, H.; Holzer, A.; Hoppe-Seyler, K.; Hoppe-Seyler, F. EZH2 depletion blocks the proliferation of colon cancer cells. PloS one 2011, 6, e21651. [Google Scholar] [CrossRef]
- Jung, H.Y.; Jun, S.; Lee, M.; Kim, H.C.; Wang, X.; Ji, H.; McCrea, P.D.; Park, J.I. PAF and EZH2 induce Wnt/β-catenin signaling hyperactivation. Molecular cell 2013, 52, 193–205. [Google Scholar] [CrossRef]
- Neri, F.; Zippo, A.; Krepelova, A.; Cherubini, A.; Rocchigiani, M.; Oliviero, S. Myc regulates the transcription of the PRC2 gene to control the expression of developmental genes in embryonic stem cells. Molecular and cellular biology 2012, 32, 840–851. [Google Scholar] [CrossRef]
- Dardenne, E.; Beltran, H.; Benelli, M.; Gayvert, K.; Berger, A.; Puca, L.; Cyrta, J.; Sboner, A.; Noorzad, Z.; MacDonald, T.; others. N-Myc induces an EZH2-mediated transcriptional program driving neuroendocrine prostate cancer. Cancer Cell 2016, 30, 563–577. [Google Scholar] [CrossRef]
- Satoh, K.; Yachida, S.; Sugimoto, M.; Oshima, M.; Nakagawa, T.; Akamoto, S.; Tabata, S.; Saitoh, K.; Kato, K.; Sato, S.; others. Global metabolic reprogramming of colorectal cancer occurs at adenoma stage and is induced by MYC. Proceedings of the National Academy of Sciences 2017, 114, E7697–E7706. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, H.; Hung, M.C. Regulation and Role of EZH2 in Cancer. Cancer research and treatment: official journal of Korean Cancer Association 2014, 46, 209. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.F.; Luo, X.; Xiang, L.S.; Li, H.T.; Zha, L.; Li, N.; He, J.M.; Xie, G.F.; Xie, X.; Liang, H.J. EZH2 promotes colorectal cancer stem-like cell expansion by activating p21cip1-Wnt/β-catenin signaling. Oncotarget 2016, 7, 41540. [Google Scholar] [CrossRef] [PubMed]
- Fluge. Ø; Gravdal, K.; Carlsen, E.; Vonen, B.; Kjellevold, K.; Refsum, S.; Lilleng, R.; Eide, T.; Halvorsen, T.; Tveit, K.; others. Expression of EZH2 and Ki-67 in colorectal cancer and associations with treatment response and prognosis. British journal of cancer 2009, 101, 1282–1289. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Schematic view of the pipeline. Execution begins with preprocessing and extraction of data, followed by generation of sensitivity indices and culminating in ranking and sorting of the indices and the associated combinations. See steps 1., 2. and 3. Figure from Sinha [1].
Figure 1.
Schematic view of the pipeline. Execution begins with preprocessing and extraction of data, followed by generation of sensitivity indices and culminating in ranking and sorting of the indices and the associated combinations. See steps 1., 2. and 3. Figure from Sinha [1].
Figure 2.
A snapshot of the manually processed file. In this file, the down regulated genes affected by ETC-1922159 have been stored. Orange boundary - contains the file header with different columns separated by a delimiter, here, "+" symbol.
Figure 2.
A snapshot of the manually processed file. In this file, the down regulated genes affected by ETC-1922159 have been stored. Orange boundary - contains the file header with different columns separated by a delimiter, here, "+" symbol.
Figure 3.
Screen shot of data loaded using load function and the assignment of the stored sensitivity indices to variable h.
Figure 3.
Screen shot of data loaded using load function and the assignment of the stored sensitivity indices to variable h.
Figure 4.
Screen shot of data after transformation in lines 125-136. This is an example of 3rd order combination.
Figure 4.
Screen shot of data after transformation in lines 125-136. This is an example of 3rd order combination.
Figure 5.
Screen shot of ranked combinations.
Figure 6.
Screen shot of browser output in the white patch in the screen shoot.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
