RADAR: Mechanistic Pathways for Detecting Data Contamination in LLM Evaluation

1. Introduction

Large Language Models (LLMs) show strong performance across tasks, but data contamination remains a major challenge in evaluation. Overlap between training and evaluation sets inflates metrics and obscures the distinction between genuine reasoning and memorization [1,2,3].

Existing detection methods typically compare evaluation data to training corpora, check n-gram overlaps, or flag verbatim outputs [4]. These approaches are limited: they require access to training data, fail with paraphrased contamination, and cannot reveal whether a model solved a task by recall or reasoning.

We propose RADAR, which instead analyzes internal computation dynamics. Leveraging mechanistic interpretability, RADAR extracts features from attention, hidden states, and activation flows [5,6]. Recall exhibits focused attention and rapid confidence convergence, while reasoning shows distributed activation and gradual stabilization.

Our contributions are: (1) We demonstrate that mechanistic features can reliably distinguish recall from reasoning with 93% accuracy, (2) We provide interpretable insights into the internal signatures of these cognitive processes, and (3) We offer a practical tool for contamination detection that works without access to training data.

2. Methodology

2.1. Framework Architecture

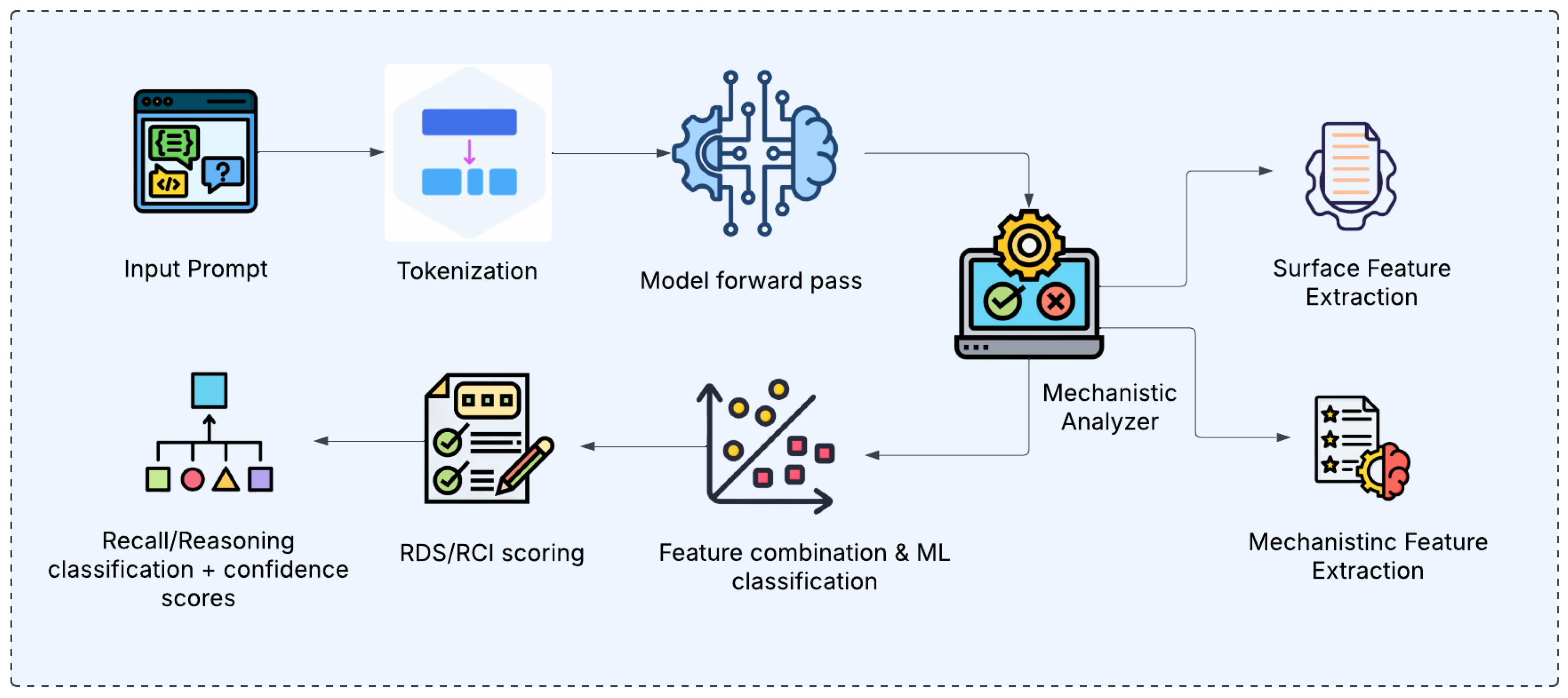
RADAR operates through three integrated components: (1) Mechanistic Analyzer that extracts internal model states, (2) Feature Extraction that computes surface and mechanistic features, and (3) Classifier that predicts recall vs. reasoning, , as illustrated in Figure 1..

The Mechanistic Analyzer interfaces with target LLMs (e.g., DialoGPT-medium) configured to output attention weights and hidden states. For each prompt, it analyzes attention patterns across all heads and layers, computing entropy and specialization metrics, and examines hidden state dynamics, including variance, norms, and effective rank.

2.2. Feature Engineering

We extract 37 features organized into two complementary categories:

Surface Features (17): Derived from the model’s output trajectory across layers, these features capture prediction dynamics through confidence statistics (mean, std, max, min, range), convergence properties (layer, speed, slope), entropy measures (mean, change, information gain), and stability metrics.

Mechanistic Features (20): Derived from attention weights and hidden states across all layers and heads, these features capture internal computational mechanisms, including attention specialization (specialized heads, specialization scores, entropy), circuit dynamics (depth, complexity, activation flow), intervention sensitivity (ablation robustness, critical components), working memory (hidden state variance, norm trajectories), and causal effects (logit attribution, mediation scores).

2.3. Classification System

The classification module employs an ensemble of four supervised learning models: Random Forest[7], Gradient Boosting[8], Support Vector Machine (SVM)[9], and Logistic Regression[10]. Each model is trained on the extracted feature vectors after normalization with StandardScaler. The scaling ensures zero mean and unit variance across features:

$$x_i^{\prime }={\displaystyle \frac{x_i-{\mu }_i}{{\sigma }_i}},$$

where ${\mu }_i$ and ${\sigma }_i$ denote the mean and standard deviation of feature i.

For prediction, each base classifier $j\in \{1,\dots ,M\}$ (with $M=4$) outputs a hard label ${\widehat{y}}_j$ and a probability estimate $p_j=P(y=1\mid x^{\prime })$, where $y=1$ corresponds to recall and $y=0$ to reasoning. The ensemble aggregates these outputs as:

$$\widehat{y}=1\left[{\displaystyle \frac{1}{M}}\sum _{j=1}^M{\widehat{y}}_j>{\displaystyle \frac{1}{2}}\right],\overline{p}={\displaystyle \frac{1}{M}}\sum _{j=1}^M{p}_j$$

The final confidence score is defined consistently with the predicted label:

$$\mathrm{conf}=\overline{p},\widehat{y}=1\left(\mathrm{recall}\right),1-\overline{p},\widehat{y}=0\left(\mathrm{reasoning}\right)$$

3. Experiments and Results

3.1. Experimental Setup and Results

We curated two datasets: a balanced training set (30 examples: 15 recall, 15 reasoning) and a diverse test set (100 examples: 20 clear recall, 20 clear reasoning, 30 challenging cases, 30 complex reasoning). The classifier achieved 96.7% cross-validation accuracy during training.

RADAR achieved an overall accuracy of 93.0% on the test set, with task-specific performance of 97.7% on recall tasks and 89.3% on reasoning tasks. A detailed breakdown of performance across different categories is shown in Table 1.

3.2. Feature Analysis

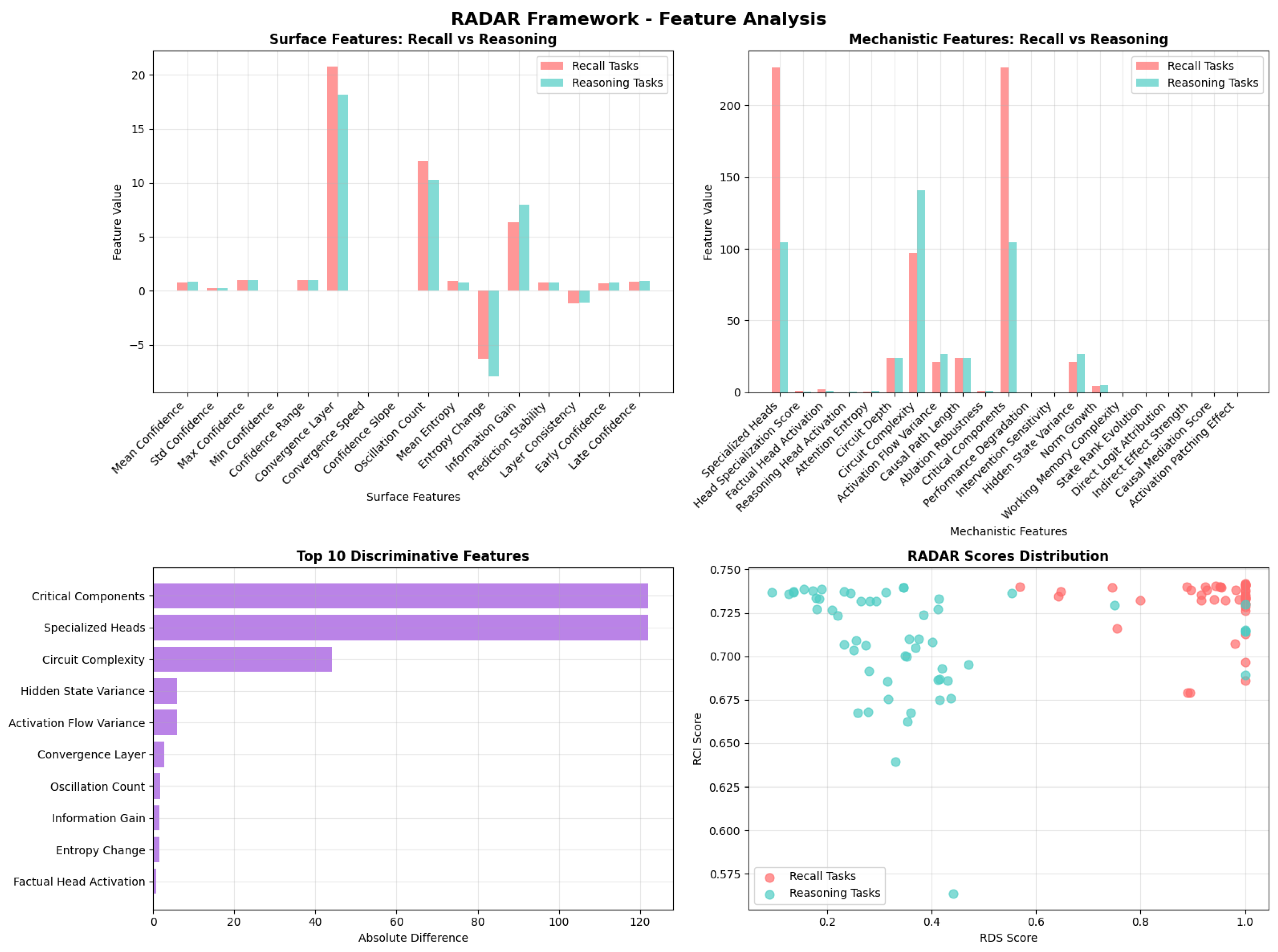
Key discriminative features include specialized attention heads (higher for recall), circuit complexity (higher for reasoning), and confidence convergence patterns (faster for recall). Recall tasks showed a mean Recall Detection Score (RDS) of 0.933 compared to 0.375 for reasoning, demonstrating clear separability, as shown in Figure 2.

Surface features revealed that recall tasks exhibit higher early confidence and faster convergence, whereas reasoning tasks show gradual confidence build-up and later stabilization. Mechanistic features highlighted that recall relies on focused attention patterns and specialized heads, while reasoning engages broader network resources with higher activation flow variance. The scatter plot visualization confirms clear separation between recall and reasoning tasks in the RDS–RCI score space.

4. Discussion and Implications

4.1. Contamination Detection Applications

RADAR’s ability to distinguish recall from reasoning has direct implications for contamination detection. When reasoning-type prompts elicit recall-like internal signatures (high confidence, fast convergence, specialized attention), this indicates potential contamination where the model "knows" rather than "computes" the answer.

Our approach offers several benefits: (1) Works without access to training data, (2) Analyzes computational processes rather than just outputs, (3) Provides interpretable features explaining classifications, (4) Complements existing external detection methods, and (5) Scales to different model architectures.

4.2. Interpretability Insights

The feature analysis confirms that recall and reasoning leave distinct mechanistic signatures. Recall processes exhibit focused attention patterns with rapid confidence convergence, suggesting direct retrieval pathways. Reasoning processes show distributed attention, gradual confidence build-up, and higher circuit complexity, indicating multi-step computational processes engaging broader network resources. Top discriminative features (Specialized Heads, Circuit Complexity, Hidden State Variance) capture fundamental differences in how the model processes information, providing interpretable insights into the underlying cognitive mechanisms.

5. Conclusion

RADAR demonstrates that mechanistic interpretability can effectively detect data contamination by analyzing internal LLM processing signatures. Our framework achieves 93% accuracy in distinguishing recall from reasoning, providing interpretable insights into the cognitive processes underlying model responses. This work opens new directions for LLM evaluation that move beyond surface-level metrics to examine computational mechanisms. The ability to detect contamination without training data access, combined with interpretable mechanistic features, makes RADAR a valuable tool for improving LLM evaluation reliability.

Future work will explore scaling to larger models, developing unsupervised detection methods, and extending to other contamination types. The integration of mechanistic interpretability with traditional evaluation methods promises more robust and trustworthy LLM assessment frameworks.

Appendix A.1. Model Configuration

The target model (microsoft/DialoGPT-medium) was configured with output_attentions=True and output_hidden_states=True. Analysis focused on input prompt tokens to capture reasoning during comprehension.

Appendix A.2. Feature Computation

Surface features tracked confidence and entropy trajectories across layers. Mechanistic features analyzed attention weight distributions using entropy measures and computed hidden state statistics including effective rank via SVD decomposition.

Appendix A.3. Training Procedure

Features were preprocessed and standardized using StandardScaler. Each ensemble model was trained with k-fold cross-validation for robust performance estimation.

Appendix B.1. Training Dataset

The training dataset was used exclusively for training the classifier. It consists of 30 examples, each containing a prompt and a corresponding label indicating whether the expected response is based on “recall” or “reasoning.” The composition is as follows:

Table A1. Composition of the training dataset.

Category	Count
Total Examples	30
Recall Examples	15
Reasoning Examples	15

Table A1. Composition of the training dataset.

Category	Count
Total Examples	30
Recall Examples	15
Reasoning Examples	15

This dataset provides the classifier with a basic representation of the internal features and patterns that distinguish factual retrieval from logical inference. Representative examples are shown below:

Table A2. Sample training dataset prompts and labels.

Prompt	Label
“The capital of France is”	recall
“If X is the capital of France, then X is”	reasoning
“2 + 2 equals”	recall
“If a triangle has angles 60, 60, and X degrees, then X equals”	reasoning

Table A2. Sample training dataset prompts and labels.

Prompt	Label
“The capital of France is”	recall
“If X is the capital of France, then X is”	reasoning
“2 + 2 equals”	recall
“If a triangle has angles 60, 60, and X degrees, then X equals”	reasoning

Appendix B.2. Test Dataset

The test dataset was used only for evaluating the trained classifier on unseen data. It comprises 100 examples, with broader coverage to assess generalization across different levels of difficulty and ambiguity:

Table A3. Composition of the test dataset.

Category	Count
Total Examples	100
Clear Recall Examples	20
Clear Reasoning Examples	20
Challenging/Ambiguous Cases	30
Complex Reasoning Cases	30

Table A3. Composition of the test dataset.

Category	Count
Total Examples	100
Clear Recall Examples	20
Clear Reasoning Examples	20
Challenging/Ambiguous Cases	30
Complex Reasoning Cases	30

The inclusion of challenging and complex reasoning cases is important for evaluating robustness, especially in detecting possible data contamination where a reasoning task could be solved by recall.

Examples from each category are shown below:

Table A4. Sample test dataset prompts by category.

Category	Example Prompt	Label
Clear Recall	“The capital of Germany is”	recall
Clear Reasoning	“If a rectangle has length 5 and width 3, its area is”	reasoning
Challenging/Ambiguous	“What is the sum of 10 and 15?”	reasoning
Complex Reasoning	“If a store has 100 items and sells 30% of them, how many items remain?”	reasoning

Table A4. Sample test dataset prompts by category.

Category	Example Prompt	Label
Clear Recall	“The capital of Germany is”	recall
Clear Reasoning	“If a rectangle has length 5 and width 3, its area is”	reasoning
Challenging/Ambiguous	“What is the sum of 10 and 15?”	reasoning
Complex Reasoning	“If a store has 100 items and sells 30% of them, how many items remain?”	reasoning

Appendix B.3. Why Challenging or Ambiguous Prompts Are Difficult

Challenging or ambiguous prompts are difficult because they blur the line between recall and reasoning.

• Some prompts may appear to require reasoning (e.g., arithmetic) but can be solved by memorized recall if the model has seen similar examples during training.
• Conversely, some factual prompts may trigger reasoning-like processing if the information is incomplete or framed indirectly.
• Ambiguity arises when the surface form of the task does not clearly signal whether the solution requires stored knowledge or active inference.

These cases are crucial for evaluation because they reveal whether the classifier is robust to subtle shifts in task framing and whether it can correctly separate recall-driven answers from reasoning-based ones.

Appendix D.1. Surface Features (16 Features)

Surface features analyze the confidence and entropy trajectories across all model layers to capture behavioral patterns without requiring deep mechanistic analysis.

Appendix D.1.1. Confidence-Based Features (8 Features)

Feature	Type	Definition & Computation
mean_confidence	float	Mean confidence across all layers: $\overline{c}={\displaystyle \frac{1}{L}}{\sum }_{l=1}^L{c}_l$ where $c_l$ is the maximum softmax probability at layer l, and L is the total number of layers.
std_confidence	float	Standard deviation of confidence trajectory: ${\sigma }_c=\sqrt{{\displaystyle \frac{1}{L-1}}{\sum }_{l=1}^L{(c_l-\overline{c})}^2}$. Higher values indicate more variable confidence across layers.
max_confidence	float	Maximum confidence achieved: $c_{max}={max}_{l\in [1,L]}{c}_l$. Indicates peak certainty reached by the model.
min_confidence	float	Minimum confidence observed: $c_{min}={min}_{l\in [1,L]}{c}_l$. Represents lowest certainty point in processing.
confidence_range	float	Range of confidence values: $\Delta c=c_{max}-c_{min}$. Measures the span of confidence variation across layers.
convergence_layer	int	Layer index where maximum confidence is achieved: $l^{*}=arg{max}_l{c}_l$. Earlier convergence may indicate simpler recall tasks.
convergence_speed	float	Inverse of convergence layer: $v_{conv}={\displaystyle \frac{1}{l^{*}+1}}$. Higher values indicate faster convergence to high confidence.
confidence_slope	float	Linear regression slope of confidence trajectory: $\beta ={\displaystyle \frac{{\sum }_{l=1}^L(l-\overline{l})(c_l-\overline{c})}{{\sum }_{l=1}^L{(l-\overline{l})}^2}}$ where $\overline{l}={\displaystyle \frac{L+1}{2}}$. Positive slopes indicate increasing confidence.

Appendix D.1.2. Trajectory Dynamics Features (4 Features)

Feature	Type	Definition & Computation
oscillation_count	int	Number of sign changes in the discrete confidence derivative. Let $\Delta c_l=c_{l+1}-c_l$ for $l=1,\dots ,L-1$. Then oscillation_count $=\#\{l\in \{1,\dots ,L-2\}:(\Delta c_l)(\Delta c_{l+1})<0\},$ i.e., consecutive derivatives with opposite sign. Zeros in $\Delta c_l$ are ignored for sign changes.
early_confidence	float	Mean confidence in the first half of layers: $$c_{\mathrm{early}}={\displaystyle \frac{1}{\lfloor L/2\rfloor }}\sum _{l=1}^{\lfloor L/2\rfloor }{c}_l.$$ Captures initial model certainty.
late_confidence	float	Mean confidence in the second half of layers: $$c_{\mathrm{late}}={\displaystyle \frac{1}{\lceil L/2\rceil }}\sum _{l=\lfloor L/2\rfloor +1}^L{c}_l.$$ Captures final model certainty.
prediction_stability	float	Inverse of confidence standard deviation: $$s_{\mathrm{pred}}=1-{\sigma }_c,{\sigma }_c=\sqrt{{\displaystyle \frac{1}{L-1}}\sum _{l=1}^L{\left(c_l-\overline{c}\right)}^2},\overline{c}={\displaystyle \frac{1}{L}}\sum _{l=1}^L{c}_l.$$ Higher values indicate more stable predictions across layers.

Appendix D.1.3. Information-Theoretic Features (4 Features)

Feature	Type	Definition & Computation
mean_entropy	float	Average entropy across layers: $$\overline{H}={\displaystyle \frac{1}{L}}\sum _{l=1}^L{H}_l,H_l=-\sum _i{p}_{l,i}log{p}_{l,i},$$ where $p_{l,i}$ is the probability of token i at layer l and log is the natural logarithm.
entropy_change	float	Change from first to last layer: $$\Delta H=H_L-H_1.$$ Negative values indicate uncertainty reduction.
information_gain	float	Negative entropy change: $$IG=-\Delta H=H_1-H_L.$$ Positive values indicate successful uncertainty reduction.
layer_consistency	float	Inverse of entropy standard deviation: $$\mathrm{consistency}=1-\sqrt{{\displaystyle \frac{1}{L-1}}\sum _{l=1}^L{\left(H_l-\overline{H}\right)}^2}.$$ Higher values indicate more consistent information processing across layers.

Appendix D.2. Mechanistic Features (21 Features)

Mechanistic features analyze internal model dynamics through attention patterns, activation flows, and causal intervention proxies to understand the computational mechanisms underlying different task types.

Appendix D.2.1. Attention Specialization Features (5 Features)

Feature	Type	Definition & Computation
num_specialized_heads	int	Total count of attention heads with entropy below a specialization threshold (typically $\tau =1.5$): $$N_{\mathrm{spec}}=\sum _{l=1}^L\sum _{h=1}^H\mathbf{1}[H_{l,h}<\tau ],$$ where $H_{l,h}$ is the entropy of head h in layer l.
head_specialization_score	float	Normalized specialization measure: $$S_{\mathrm{head}}=1-{\displaystyle \frac{{\overline{H}}_{\mathrm{attn}}}{3.0}},$$ where ${\overline{H}}_{\mathrm{attn}}$ is the mean attention entropy across all heads. Higher values indicate more specialized attention patterns.
factual_head_activation	float	Inverse relationship with attention entropy: $$A_{\mathrm{fact}}={\displaystyle \frac{1}{{\overline{H}}_{\mathrm{attn}}+ϵ}},ϵ={10}^{-8}.$$ Higher values suggest factual recall patterns (low entropy, focused attention).
reasoning_head_activation	float	Proportional to attention entropy: $$A_{\mathrm{reason}}={\displaystyle \frac{{\overline{H}}_{\mathrm{attn}}}{3.0}}.$$ Higher values suggest reasoning patterns (high entropy, distributed attention).
attention_entropy	float	Mean entropy across all attention heads: $${\overline{H}}_{\mathrm{attn}}={\displaystyle \frac{1}{LH}}\sum _{l=1}^L\sum _{h=1}^H{H}_{l,h},H_{l,h}=-\sum _{i,j}{A}_{l,h}^{(i,j)}log{A}_{l,h}^{(i,j)},$$ where $A_{l,h}^{(i,j)}$ is the attention weight from position i to j.

Appendix D.2.2. Circuit Dynamics Features (4 Features)

Feature	Type	Definition & Computation
effective_circuit_depth	float	Number of layers with significant causal effects. Equal to the number of attention layers analyzed. Represents the depth of the computational circuit.
circuit_complexity	float	Product of variance and norm growth: $$C_{\mathrm{circuit}}={\sigma }_{\mathrm{var}}^2·{\gamma }_{\mathrm{norm}},$$ where ${\sigma }_{\mathrm{var}}^2$ is activation variance growth and ${\gamma }_{\mathrm{norm}}$ is the norm growth trajectory.
activation_flow_variance	float	Variance in activation magnitudes across layers. Measures how much activation patterns change between layers, indicating computational complexity.
causal_path_length	float	Length of the causal computation path. Currently equal to circuit depth, representing the number of processing steps in the causal chain.

Appendix D.2.3. Intervention Sensitivity Features (4 Features)

Feature	Type	Definition & Computation
ablation_robustness	float	Robustness to component removal: $$R_{\mathrm{ablation}}=1-{\displaystyle \frac{{\overline{H}}_{\mathrm{attn}}}{5.0}}.$$ Higher entropy (distributed attention) leads to lower robustness.
critical_component_count	int	Number of critical components: $$N_{\mathrm{critical}}=max(1,N_{\mathrm{spec}}).$$ Uses specialized head count as a proxy for critical components.
performance_degradation_slope	float	Rate of performance degradation under intervention: $${\beta }_{\mathrm{degrad}}=\left|{\sigma }_{\mathrm{causal}}\right|,$$ where ${\sigma }_{\mathrm{causal}}$ is the standard deviation of causal effect estimates across layers.
intervention_sensitivity	float	Sensitivity to interventions: $$S_{\mathrm{interv}}=1-R_{\mathrm{ablation}}.$$ Inverse of ablation robustness; higher values indicate greater sensitivity.

Appendix D.2.4. Working Memory Features (4 Features)

Feature	Type	Definition & Computation
hidden_state_variance	float	Variance in hidden state activations. Measures variability in internal representations across layers, indicating working memory usage.
norm_growth_trajectory	float	Growth pattern of activation norms. ${\gamma }_{\mathrm{norm}}$ tracks how activation magnitudes change across layers, indicating information accumulation.
working_memory_complexity	float	Complexity of working memory usage. Currently uses rank evolution as a proxy for working memory complexity.
state_rank_evolution	float	Evolution of representation rank. $R_{\mathrm{evolution}}$ measures how the effective dimensionality of representations changes across layers.

Appendix D.2.5. Causal Effect Features (4 Features)

Feature	Type	Definition & Computation
direct_logit_attribution	float	Direct causal effect on output: $$E_{\mathrm{direct}}={\displaystyle \frac{1}{L}}\sum _{l=1}^L{\displaystyle \frac{{\overline{H}}_{\mathrm{attn},l}}{10}},$$ where ${\overline{H}}_{\mathrm{attn},l}$ is mean attention entropy at layer l. Proxy for direct causal contribution.
indirect_effect_strength	float	Strength of indirect causal effects: $$E_{\mathrm{indirect}}={\sigma }_{\mathrm{causal}},$$ where ${\sigma }_{\mathrm{causal}}$ is the standard deviation of layer-wise causal effect estimates.
causal_mediation_score	float	Mediation effect strength: $$M_{\mathrm{causal}}=E_{\mathrm{direct}}\times E_{\mathrm{indirect}}.$$ Product of direct and indirect effects, measuring causal mediation.
activation_patching_effect	float	Proxy measure for activation patching: $$P_{\mathrm{patch}}=E_{\mathrm{direct}}.$$ Note: This is computed from attention entropy, not from actual activation patching experiments.

Appendix E.1. Surface Feature Extraction

• Extract confidence trajectory:

  $${\left\{c_l\right\}}_{l=1}^L,c_l=\underset{i}{max}{p}_{l,i}$$
• Extract entropy trajectory:

  $${\left\{H_l\right\}}_{l=1}^L,H_l=-\sum _i{p}_{l,i}log{p}_{l,i}$$
• Compute statistical measures: mean, standard deviation, minimum, maximum, and range.
• Analyze trajectory dynamics: slope, oscillations, and convergence properties.
• Calculate information-theoretic measures.

Appendix E.2. Mechanistic Feature Extraction

• Analyze attention patterns across all layers and heads.
• Compute attention entropy for each head:

  $$H_{l,h}=-\sum _{i,j}{A}_{l,h}^{(i,j)}log{A}_{l,h}^{(i,j)}$$
• Identify specialized heads:

  $$N_{\mathrm{spec}}=\sum _{l,h}\mathbf{1}[H_{l,h}<1.5]$$
• Analyze activation patterns (variance, norms, and rank evolution).
• Compute proxy causal effects from attention entropy.
• Calculate intervention sensitivity measures.

Appendix F.1. Proxy Measures

Several features rely on proxy measures rather than direct computation:

• Causal effects: Derived from attention entropy instead of actual interventions.
• Activation patching: Approximated via attention entropy proxy, not true patching experiments.
• Critical components: Approximated using specialized head counts.
• Working memory: Approximated using rank evolution as a complexity proxy.

Appendix F.2. Computational Considerations

• All features can be computed in a single forward pass.
• No gradient computation is required for feature extraction.
• Attention patterns are analyzed across all layers and heads.
• Surface features require only the output probability distributions.