4.1. The Category WP
In this section, we introduce the fourth new idea in the paper – a
categorical framework for
WPMSs and accompanying operations. The idea has been touched on in [
4] and [
18], where a generalized notion of probabilistic metric spaces is introduced in the context of quantales.
The reader is referred to [
19] for general categorical notions. Let | WP | denote the family of
WPMSs. For (
S,
F) and (
T,
G) in | WP |, a
morphism [
f]: (
S,
F) → (
T,
G) is a mapping
f :
S →
T such that
Fpq ≤ Gf(p)f(q) for each
p,
q ∈
S, where
≤ denotes the point-wise order on Δ
+. The symbol WP((
S,
F), (
T,
G)) denotes the family of morphisms from (
S,
F) to (
T,
G). The composition of morphisms [
f]: (
S,
F) → (
T,
G) and [
g]: (
T,
G) → (
V,
K) is the morphism [
g ° f ]: (
S,
F) → (
V,
K). Also, [
idS] is the identity morphism for each
WPMS (
S,
F), so WP is a category.
The first result characterizes the morphisms in WP in terms of the families of distances.
Lemma 4.1.1. The following statements are equivalent for WPMSs (S, F) and (T, G) and a mapping f : S → T, where ΩF = {ωt} and ΩG = {ρt}.
- (a)
[f] : (S, F) → (T, G) is a WP-morphism [f] : (S, F) → (T, G).
- (b)
For each 0 < t < 1, f : (S, ωt) → (T, ρt) is a non-expansive mapping.
Proof ¬(b) ⇒ ¬(a): Choose t, p, and q such that ωt(p, q) < ρt(f(p), f(q)). Let ωt(p, q) < x < ρt(f(p), f(q)). Therefore, Gf(p)f(q)(x) < t ≤ Fpq(x), so ¬(a) holds.
¬(a) ⇒ ¬(b): Choose p, q, and x such that Gf(p)f(q)(x) < Fpq(x) and let Gf(p)f(q)(x) < t < Fpq(x). Then ωt(p, q) < x ≤ ρt(f(p), f(q)). Hence, ωt(p, q) < ρt(f(p), f(q)), so ¬(b) holds.
□
Corollary 4.1.1. The following statements are equivalent for WPMSs (S, F) and (T, G) and a mapping h : S → T, where ΩF = {ωt} and ΩG = {ρt}.
- (a)
[h] : (S, F) → (T, G) is a WP-isomorphism.
- (b)
h is a bijection and Fpq = Gh(p)h(q) for each p, q ∈ S.
- (c)
For each 0 < t < 1, h : (S, ωt) → (T, ρt) is a surjective isometry.
Proof The equivalence of (a) and (b) follows from the definition of a WP-isomorphism. The equivalence of (a) and (c) follows from Lemma 4.1.1.
□
We note that the notion of
isomorphic WPMS’s is the same as the idea of
isometric WPMS’s found in ([
1], 8.1.2).
The next result lists some elementary facts about the category WP. The proof is left to the reader.
Lemma 4.1.2. The following statements hold for WPMSs (S, F) and (T, G).
- (a)
The monomorphisms (resp. epimorphisms) in WP are exactly the morphisms that are injections (resp. surjections) on the base sets.
- (b)
For each t ∈ T, constt : S → T defines a WP-morphism [constt] : (S, F) → (T, G).
- (c)
Let H ⊆ S and FH = F|H×H. Then (H, FH) is a WPMS and inclH : H → S defines a WP-morphism [inclH] : (H, FH) → (S, F).
In the literature, both countable products and arbitrary products of WPMSs have been studied. In our setting, we can characterize when products exist.
For a set W = {(Si, Fi) | i ∈ I} ⊆ | WP |, let S = ΠSi and define the mapping F : S × S → F(R+, I) by F(p, q) = inf{Fi(pi, qi) | i ∈ I}. Then the following statements hold:
- (1)
For each p, q ∈ S, Fpq(0) = 0, Rng(Fpq) ⊆ I, and Fpq is non-decreasing. (This follows since each Fi(pi, qi) ∈ ρ+.)
- (2)
(S, F) satisfies (w1) – (w3). (Clearly, (w1) and (w2) hold. If Fpq(x) = Fqr(y) = 1 for some p, q, r ∈ S and x, y ∈ R+, then each Fi(pi, qi)(x) = Fi(qi, ri)(y) = 1, so Fi(pi, ri)(x + y) = 1. Hence, Fpq(x + y) = 1, so (w3) holds.)
- (3)
For each 0 < t < 1, ωt = sup{ωi,t}, where ΩF = {ωt} and each ΩF(i) = {ωi,t}.
It may not be the case that sup(Fpq) = 1 for each p, q ∈ S (Example 4.1.1), so Fpq may not belong to ρ+. To remedy this problem, we introduce the following property.
We say that W satisfies the uniform limit property (ulp) if for each ε > 0 and each {pi, qi} ⊆ Si, i ∈ I, there is x ∈ R+ such that inf{Fi(pi, qi)(x) | i ∈ I} > 1 - ε. Clearly, (ulp) holds if W is a finite family. Also, if W satisfies (ulp), then each Fpq∈ ρ+, so by (1) and (2), (S, F) is a WPMS.
Prop 4.1.1. The following statements hold for a set W = {(Si, Fi) | i ∈ I} ⊆ | WP |.
- (a)
If W satisfies (ulp), then (S, F) is the product in WP of the members of W. Hence, each finite family of WPMSs has a product in WP.
- (b)
If W satisfies (ulp) and W consists of Menger spaces, then (S, F) is a Menger space.
- (c)
If W is an infinite set and its product in WP exists, then W satisfies (ulp).
Proof (a): Based on our earlier discussion, (S, F) is a WPMS, where S = ΠSi and F : S × S → Δ+ is defined by F(p, q) = inf{Fi(pi, qi) | i ∈ I}. For each i ∈ I, let πi : S → Si be the standard projection mapping. Since F ≤ Fi, [πi] : (S, F) → (Si, Fi) is a morphism. Let (T, G) be a WPMS and assume that each [fi] : (T, G) → (Si, Fi) is a morphism. Let f : T → S be the mapping that satisfies πi ° f = fi for each i. Then G(a, b) ≤ Fi(fi(a), fi(b)) for each a, b ∈ T and i, so G(a, b) ≤ F(f(a), f(b)). Therefore, [f] : (T, G) → (S, F) is a morphism. If the morphism [g] : (T, G) → (S, F) satisfies πi ° g = fi for each i, then clearly, f = g. Hence, (S, F) is the product.
(b): We refer to (2) above. Suppose F(p, r)(x + y) < b = F(p, q)(x) ≤ c = F(q, r)(y) for p, q, r ∈ S and x, y ∈ R+. Choose i ∈ I with Fi(pi, ri)(x + y) < b. Since b ≤ Fi(pi, qi)(x) and c ≤ Fi(qi, ri)(y), Fi(pi, ri)(x + y) < min{Fi(pi, qi)(x), Fi(qi, ri)(y)}. This is a contradiction, so (S, F) is a Menger space.
(c): Assume that (T, G) is the product of the family W based on the projection mappings {[σi] : (T, G) → (Si, Fi)}. If W doesn’t satisfy (ulp), then there is 0 < ε < 1 and {pi, qi} ⊆ Si, i ∈ I, such that inf{Fi(pi, qi)(x) | i ∈ I} ≤ δ = 1 - ε for each x ∈ R+.
Let ({*}, H) be the trivial WPMS and for each i, define the morphism [fi] : ({*}, H) → (Si, Fi) by fi(*) = pi. By assumption, there is a morphism [f] : ({*}, H) → (T, G) such that σi ° f = fi for each i.
Similarly, for each i, define the morphism [gi] : ({*}, H) → (Si, Fi) by gi(*) = qi. Then there is a morphism [g] : ({*}, H) → (T, G) such that σi ° g = gi for each i. Let s = f(*) and t = g(*). Then for each i ∈ I and x ∈ R+, Gst(x) ≤ Fi(fi(*), gi(*))(x) = Fi(pi, qi)(x), so sup(Gst) ≤ inf{Fi(pi, qi)(x)} ≤ δ, which contradicts the fact that Gst ∈ Δ+. Therefore, W satisfies (ulp).
□
Many authors have studied products of
WPMSs independently of any categorical framework. For example, ([
20], Theorem 1) establishes the finite case of
Prop 4.1.1(a) and ([
21], Proposition 3) “purports” to establish a general product theorem. Here are some additional details about finite products based on the previous construction:
If (S, F) is the product of a finite family {(Si, F(i))} of WPMS’s, then ωt = max{ωi,t} for each t, where ΩF = {ωt} and ΩF(i) = {ωi,t} for each i.
The product of a finite family of Menger spaces is a Menger space. (By Prop 2.2.2, each coordinate distance is a pseudometric, so by the previous remark, each distance in the product is a pseudometric. Hence, by Prop 2.2.2, the product is a Menger space.)
The product (S, F) of a finite family {(Si, Fi)} of special WPMS’s is a special WPMS. (For each p, q ∈ S and i, choose xi such that Fi(pi, qi)(xi) = 1. Then F(p, q)(max{xi}) = 1.)
The following example shows that the (ulp) property doesn’t hold in general.
Example 4.1.1. For each n ∈ N+, define Fn : [0, n] × [0, n] → Δ+ by Fn(p, q)(x) = H(x - | p - q |).
Each ([0, n], Fn) ∈ | WPM |, but W = {([0, n] , Fn) | n ∈ N+} doesn’t satisfy (ulp). To see this, note that for each x ∈ R+, inf{Fn(0, n)(x)} = inf{H(x - n)} = 0.
By way of contrast with Prop 4.1.1, we have the following rather dramatic result.
Prop 4.1.2.
No pair of WPMSs has a coproduct in WP.
Proof Let (
S,
F) and (
T,
G) be
WPMSs and assume that (
C,
H) is their coproduct in WP based on the morphisms [
i] : (
S,
F) → (
C,
H) and [
j] : (
T,
G) → (
C,
H). Suppose Ω
H = {ρ
t}. Choose
p ∈
S and
q ∈
T and let
a =
i(
p) and
b =
j(
q). Let
r = ρ
1/2(
a,
b) + 1. Let
D = {0,
r} and let
Kr0 =
K0r :
R+ →
I be the characteristic function of (
r, +∞). Also, let
K00 =
Krr =
H. Then (
D,
K) is a
WPMS and Ω
K = {ω
t}, where each ω
t satisfies ω
t(0,
r) =
r. By
Lemma 4.1.2(b), each constant mapping defines a morphism, so there exists a morphism [
h] : (
C,
H) → (
D,
K) such that
h ° i =
const0 and
h ° j =
constr. By
Lemma 4.1.1,
h : (
C, ρ
1/2) → (
D, ω
1/2) is non-expansive, so
which is a contradiction. Hence, the coproduct doesn’t exist.
□
A result related to
Prop 4.1.2 is found in ([
22], Proposition 1) stating that the category Met (
§4.2) has no coproducts. Next, we consider limits in WP.
Prop 4.1.3. Suppose W = {(Si, Fi) | i ∈ D} ⊆ | WP |, where (D, ≤) is a directed set, and ({(Si, Fi) | i ∈ I}, {[fij] : (Sj, Fj) → (Si, Fi) | i, j ∈ D and i ≤ j}) is an inverse system in WP. If W satisfies (ulp), then the inverse system has an inverse limit in WP.
Proof Let P = ΠSi and define F : P × P → Δ+ by F(p, q) = inf{Fi(pi, qi) | i ∈ I}. By Prop 4.1.1(a), (P, F) is the product of {(Si, Fi)}. Let S = {s ∈ P | i, j ∈ D and i ≤ j ⇒ fij(sj) = si}. By Lemma 4.1.2(c), (S, FS) is also a WPMS. We claim that ((S, FS), {[πi] : (S, FS) → (Si, Fi) | i ∈ D}) is the inverse limit, where each πi is a projection mapping. If ((T, G), {[φi] : (T, G) → (Si, Fi) | i ∈ I}) is a source (fij ° φj = φi for i, j ∈ D satisfying i ≤ j), then φ : T → S defined by φ(t) = (φi(t)) is well-defined and πi ° φ= φi for each i. By assumption, for u, v ∈ T and i ∈ D, Guv ≤ Fi(φi(u), φi(v)), so Guv ≤ FS(φ(u), φ(v)). Therefore, [φ] : (T, G) → (S, FS) is a WP-morphism.
□
Prop 4.1.4. Each directed system in WP has a direct limit.
Proof Let ({(Si, Fi) | i ∈ I}, {fij : (Si, Fi) → (Sj, Fj) | i, j ∈ I and i ≤ j}) be a directed system in WP, where (I, ≤) is a directed set. For each i, j ∈ I, let I(i, j) = {k ∈ I | i ≤ k and j ≤ k}. For each i ∈ I, let S^i = Si × {i}, and let S^ = ∪{S^i | i ∈ I}. For (p, i) ∈ S^i and (q, j) ∈ S^j, define (p, i) ~ (q, j) if there is k ∈ I(i, j) such that fik(p) = fjk(q). Then ~ is an equivalence relation on S^.
Let
denote the set of equivalence classes for
~. Let
a = [(
p,
i)],
b = [(
q,
j)] ∈
S. If
a =
b, let
Fab =
H. If
a ≠
b, let
It is easy to verify that (S, F) is a WPMS. For each i ∈ I, define ψi : Si → S by ψi(p) = [(p, i)].
- (1)
Each [ψi] : (Si, Fi) → (S, F) is a morphism and {[ψi]} is a sink for the directed system.
[Let a = [(p, i)], b = [(q, i)] ∈ S, and x ∈ R+. If a = b, then Fi(p, q)(x) ≤ 1 = H(x) = Fab(x). If
a ≠ b, then Fi(p, q) ≤ sup{Fk(fik(p), fik(q)) | i ≤ k} = Fab(x). If i, j ∈ I and i ≤ j, then fij(p) = fjj(fij(p)) for each p ∈ Si, so (p, i) ~ (fij(p), j). Hence, for each p ∈ Si, ψj(fij(p)) = [(fij(p), j)] = [(p, i)] = ψi(p). Therefore, ψj ° fij = ψi for each i, j ∈ I.]
- (2)
((S, F), {[ψi] : (Si, Fi) → (S, F) | i ∈ I}) is the direct limit of the directed system.
[Let ((T, G), {[φi] : (Si, Fi) → (T, G) | i ∈ I}) be a sink for the directed system and define the mapping h : S → T by h([(p, i)]) = φi(p). If (p, i) ~ (q, j), then there exists k ∈ I(i, j) such that fik(p) = fjk(q), so φi(p) = φk(fik(p)) = φk(fjk(q)) = φj(q). Hence, h is well-defined and h ° ψi = φi for each i ∈ I.]
We claim that [
h] : (
S,
F) → (
T,
G) is a morphism. Let
a = [(
p,
i)],
b = [(
q,
j)] ∈
S. If
a =
b, then
Fab =
H =
Gh(a)h(b). Suppose
a ≠
b. If
k ∈
I(
i,
j), then since [φ
k] is a morphism,
Therefore, Fab ≤ G(h(a), h(b)).
□
Here are two useful examples that illustrate the previous results.
Example 4.1.2. Each WPMS is the direct limit of the family of finite subspace WPMSs.
Let (S, F) be a WPMS and assume that I ⊆ PF+(S) satisfies S = ∪I and (I, ≤) is a directed set, where ≤ is defined by A ≤ B if A ⊆ B. Let W = {(A, FA) | A ∈ I} be the family of subspace WPMSs (Lemma 4.1.2(c)) and let F = {[fAB] : (A, FA) → (B, FB) | A, B ∈ I and A ≤ B}, where each fAB is the inclusion mapping. Since {W, F} is a directed system, by Prop 4.1.4, {(T, G), {[ψA] : A ∈ I} is the direct limit, where T = {[(a, A)] : A ∈ I and a ∈ A} is the set of equivalence classes of ~ and each ψA : S → T is defined by ψA(a) = [(a, A)]. Since (a, A) ~ (b, B) if there exists C ∈ I(A, B) such that fAC(a) = fBC(b), we have [(a, A)] = {(a, B) : a ∈ B ∈ I}.
By Lemma 4.1.2(c), {(S, F), {[inclA] : (S, FA) → (S, F) | A ∈ I} is a sink for the directed system, so there exists a morphism [h] : (T, G) → (S, F) such that h ° ψA = inclA for each A ∈ I. It is easy to verify that h is a bijection since S = ∪I. Also, Gtt′ = Fh(a)h(b) for each t = [(a, A)] and t′ = [(b, B)], so by Corollary 4.1.1, [h] is an isomorphism. Therefore, (S, F) is the direct limit.
Example 4.1.3. Each Menger space (S, F) is the inverse limit of special Menger spaces with a finite range.
Let V = {
V ∈ P
F+(
S) | {0, 1} ⊆
V} and for
V,
W ∈ V, define
V ≤
W if
V ⊆
W. Then (V, ≤) is an down-directed set. Statement (1) in
Theorem 3.2.2 shows that for each
V ∈ V, (
S,
FV) is a
Menger space with a finite range. Also, by
Lemma 3.2.1(c), each π
V = [
idS] : (
S,
F) → (
S,
FV) is a morphism, so W = {(
S,
FV) |
V ∈ V} satisfies (
ulp). If
V,
W ∈ V and
V ≤
W, then
FWpq(
x) ≤
FVpq(
x) for each
p,
q ∈
S and
x ∈
R+. Therefore, each
fVW = [
idS] : (
S,
FW) → (
S,
FV) is a morphism, so (W, {
fVW |
V,
W ∈ V and
V ≤
W}) is an inverse system in
WP. Based on the construction in
Prop 4.1.3, the inverse limit is (ρ,
G), where ∆ = {δ ∈
SV |
V,
W ∈ V and
V ≤
W ⇒
fVW(δ
W) = δ
V} and
G(δ, ξ) =
inf{
FV(δ
V, ξ
V) |
V ∈ V} for δ, ξ ∈ ∆. Let δ ∈ ∆ and let
A,
B ∈ V. Let
V =
A ∩
B. Then
V ∈ V and δ
A =
fVA(δ
A) = δ
V =
fVB(δ
B) = δ
B, so ∆ is the diagonal in
SV, that is,
Since {(S, F), {πV | V ∈ V}) is a source for the inverse system, the bijection φ: S → ∆ defined by φ(s)V = s for each V ∈ V defines a morphism [φ] : (S, F) → (∆, G). Let p, q ∈ S and x ∈ R+. Then y = Fpq(x) ≤ z = Gφ(p)φ(q)(x) = inf{FVpq(x) | V ∈ V}. Choose A ∈ V that contains y. Then z ≤ FApq(x) = y, so Fpq = Gφ(p)φ(q). Hence, by Corollary 4.1.1, [φ] is an isomorphism.
Notice that the same conclusion holds by using the family V = {{0, 1}} ∪ {{0, r, 1} : 0 < r < 1}.
4.2. Subcategories of 𝓦𝓟
In this section, we introduce and compare several special subcategories of 𝓦𝓟. Here are the categories that we’ll be using:
𝓓𝓲𝓼𝓽 – objects are distance-spaces and morphisms are non-expansive mappings.
𝓟𝓜𝓮𝓽 (resp. 𝓜𝓮𝓽) – objects are pseudometric (resp. metric) spaces and morphisms are non-expansive mappings.
𝓦𝓟D – full subcategory of 𝓦𝓟 based on WPMSs determined by pseudometric spaces.
𝓦𝓟M – full subcategory of 𝓦𝓟 based on Menger spaces.
𝓦𝓟S – full subcategory of 𝓦𝓟 based on special WPMSs.
The following result describes some relationships between the various categories.
Theorem 4.2.1.
- (a)
𝓟𝓜𝓮𝓽 is a reflective subcategory of 𝓓𝓲𝓼𝓽.
- (b)
𝓟𝓜𝓮𝓽 and 𝓦𝓟𝓓 are isomorphic categories.
- (c)
𝓦𝓟𝓓 is a coreflective subcategory of 𝓦𝓟S and the coreflection of a special WPMS (S, F) is the WPMS determined by the pseudometric space (S, ω1).
- (d)
𝓦𝓟𝓜 is a reflective subcategory of 𝓦𝓟.
Proof (a): Let (M, ω) be a distance-space. By Prop A.2.1, there is a largest pseudometric dω such that dω ≤ ω, so r = idM : (M, ω) → (M, dω) is a non-expansive mapping. Let f : (M, ω) → (N, σ) be a non-expansive mapping to a pseudometric space and define τ by τ(x, y) = σ(f(x), f(y)). Since σis a pseudometric, τ is a pseudometric on M satisfying τ ≤ ω, so τ ≤ dω. Hence, f : (M, dω) → (N, σ) is a morphism and f ° r = f. Clearly, f is the unique mapping with this property.
(
b): For each (
S, γ) ∈ | 𝓟𝓜𝓮𝓽 |, let
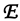
((
S, γ)) = (
S,
Gγ) (
Example 2.1.1) and for each non-expansive mapping
g : (
S, γ) → (
S′, γ′), where (
S′, γ′) ∈ | 𝓟𝓜𝓮𝓽 |, let
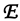
(
g) =
g. By definition, for
p,
q ∈
S,
Gpq(
x) =
H(
x - γ(
p,
q)). Hence, if
Gpq(
x) = 1, then
x > γ(
p,
q)) ≥ γ′(
g(
p),
g(
q)), so we obtain
G′
g(p)g(q)(
x) =
H(
x - γ′(
g(
p),
g(
q))) = 1. Therefore,
Gpq ≤
G′
g(p)g(q), so
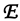
(
g) is a morphism. This defines a functor
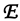
: 𝓟𝓜𝓮𝓽 → 𝓦𝓟
D.
For each (
S,
Gγ) ∈ | 𝓦𝓟
D |, let 𝓕((
S,
Gγ)) = (
S, γ) and for each morphism [
h] : (
S,
Gγ) → (
S′,
Gγ′), where (
S′, γ′) ∈ | 𝓦𝓟
D |, let 𝓕(
h) =
h. Given
p,
q ∈
S and ε > 0, choose γ(
p,
q) <
x < γ(
p,
q) + ε. Then
Gpq(
x) = 1, so
G′
h(p)h(q)(
x) = 1 since [
h] is a morphism. Therefore,
x > γ′(
h(
p),
h(
q)). Hence, γ(
p,
q) + ε > γ′(
h(
p),
h(
q)) for each ε > 0, so
h : (
S, γ) → (
S′, γ′) is a non-expansive mapping. This defines a functor 𝓕 : 𝓦𝓟
D → 𝓟𝓜𝓮𝓽. Based on the definitions,
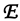 °
°𝓕 (resp. 𝓕
° 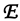
) is the identity functor on 𝓦𝓟
D (resp. 𝓟𝓜𝓮𝓽), so
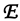
is an isomorphism.
(c): If (S, F) is a special WPMS, then by Lemma 2.2.2, γ = ω1 is a pseudometric. Let (S, Gγ) be the WPMS determined by (S, γ) which belongs to | 𝓦𝓟D |.
- (1)
[idS] : (S, Gγ) → (S, F) is a morphism.
[Let p, q ∈ S. Since Gpq(x) = H(x - ω1(p, q)), if x ≤ ω1(p, q), then Gpq(x) = 0 ≤ Fpq(x). On the other hand, if x > ω1(p, q), then Fpq(x) = 1, so Gpq(x) ≤ Fpq(x).]
- (2)
(S, Gγ) is the coreflection of (S, F) in 𝓦𝓟D.
[Suppose [g] : (M, Gγ′ = {G′ab})) → (S, F) is a 𝓦𝓟-morphism where the domain WPMS is determined by the pseudometric space (M, γ′). Let a, b ∈ M. Then G′ab ≤ Fpq, where p = g(a) and q = g(b). If γ′(a, b) < γ(p, q), choose γ′(a, b) < x < γ(p, q). Since x < γ(p, q) = ω1(p, q), Fpq(x) < 1, but G′ab(x) = H(x - γ′(a, b)) = 1, so Fpq(x) = 1, which is a contradiction. Hence, γ(p, q) ≤ γ′(a, b), so g is a non-expansive mapping. Therefore, by Lemma 4.1.1, [g] : (M, Gγ′) → (S, Gγ) is a morphism, which establishes (2).]
(d): Let (S, F) be a WPMS and ΩF = {ωt}. By Prop A.2.1, for each 0 < t < 1, the path-metric ρt based on ωt is the largest pseudometric on S satisfying ρt ≤ ωt. Since ΩF is linearly ordered, Ω = {ρt} is also linearly ordered. For each 0 < t < 1, let ρt′ = sup{ρs | 0 < s < t}. By Lemma 2.4.1, {ρt′} is a linearly ordered family of pseudometrics that satisfies (lcp), so by Theorem 3.2.1(a)(c), there is a Menger space (S, G) such that ΩG = {ρt′}. Since each ρt′ ≤ ωt, by Lemma 4.1.1, [idS] : (S, F) → (S, G) is a morphism.
- (3)
(S, G) is the reflection of (S, F) in 𝓦𝓟M.
[Let [f] : (S, F) → (S*, F*) be a 𝓦𝓟-morphism to a Menger space, where ΩF* = {ωt*}. By Lemma 4.1.1, for each t, f : (S, ωt) → (S*, ωt*) is non-expansive, so ωt*(f(p), f(q)) ≤ ωt(p, q) for p, q ∈ S. Since (S*, F*) is a Menger space, by Prop 2.2.2, ΩF* consists of pseudometrics, so for each t, the equation σt(p, q) = ωt*(f(p), f(q)) defines a pseudometric σt on S satisfying σt ≤ ωt. Hence, by Prop A.2.1, each σt ≤ ρt. By Prop 2.4.1(a), σt = sup{σs | 0 < s < t} = sup{ρs | 0 < s < t} = ρt′. Hence, by Lemma 4.1.1, [f] : (S, G) → (S*, F*) is a morphism. Therefore, [idS] : (S, F) → (S, G) is the reflection mapping associated with 𝓦𝓟M.]
□
The following example illustrates the reflection into Menger spaces.
Example 4.2.1.
- (1)
In
Example 2.1.4, (
R,
F) is
not a
Menger space and the distances have the following form: for each 0 <
t ≤ 1 and
p,
q ∈
R,
| |
⎧ 0 |
| p - q | ≤ 1 - t. |
| ωt(p, q) = |
⧼ |
| |
⎩ 1 |
otherwise. |
Let 0 < t < 1 and ε= 1 - t, and let ρ be a pseudometric satisfying ρ ≤ ωt. If | p - q | ≤ ε, then ρ(p, q) ≤ ωt(p, q) = 0, soρ (p, q) = 0. If | p - q | > ε, choose n satisfying 1/n < ε/| p - q | and let xk = (1 - k/n)p + (k/n)q for 0 ≤ k ≤ n. For each k, | xk - xk+1 | = | p - q |/n < ε, so ωt(xk, xk+1) = 0. Hence, ρ(p, q) ≤ Σρ(xk, xk+1) ≤ Σωt(xk, xk+1) = 0. Therefore, ρ is the zero pseudometric.
The construction used in the proof of Theorem 4.2.1(d) shows that the Menger space reflection of (R, F) is the trivial WPMS (R, {H}).
- (1)
In
Example 2.1.5, (
R+,
F) is
not a Menger space and the distances have the following form: for each 0 <
t ≤ 1 and
p,
q ∈
R+,
| |
⎧ e1(p, q) |
0 < t ≤ 1/2 |
| ωt(p, q) = |
⧼ |
| |
⎩ e2(p, q) |
1/2 < t ≤ 1. |
By definition,
e1(
p,
q) =
min{
a,
b} and
e2(
p,
q) =
max{
a,
b}, where
a = |
p -
q | and
b = |
p2 -
q2 |. In addition,
e2 is a pseudometric. Let
c = 1/2,
A = [0,
c], and
B = (
c, +∞). An analysis of cases shows that the largest pseudometric
d1 ≤
e1 is defined by
| |
⎧ e1(p, q) |
p, q ∈ A or p, q ∈ B
|
|
d1(p, q) = |
⧼ q - p2 - c2
|
p ∈ A and q ∈ B
|
| |
⎩ p - q2 - c2 |
q ∈ A and p ∈ B. |
The construction used in the proof of
Theorem 4.2.1(d) shows that the Menger space reflection (
R+,
G) of (
R+,
F) has the pseudometrics defined by
| |
⎧ d1
|
0 < t ≤ 1/2 |
| ρt′ = |
⧼ |
| |
⎩ e2 |
1/2 < t ≤ 1. |
The construction is the one used in the proof of
Theorem 3.2.1. One can show that if
p,
q ∈
A or
p,
q ∈
B, then
Gpq =
Fpq. However, if
p ∈
A and
q ∈
B, then
| |
⎧ 0 |
0 ≤ x ≤ d1(p, q) |
|
Gpq(x) = |
⧼ 1/2 |
d1(p, q) < x ≤ e2(p, q) |
| |
⎩ 1 |
x > e2(p, q). |
For example, if p = 1/4 and q = 1, then a = 3/4 and b = 15/16. Therefore, Fpq(x) = 0 for 0 ≤ x ≤ 3/4 and Gpq(x) = 1/2 for 11/16 < x < 3/4, so Fpq ≠ Gpq.
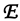 ((S, γ)) = (S, Gγ) (Example 2.1.1) and for each non-expansive mapping g : (S, γ) → (S′, γ′), where (S′, γ′) ∈ | 𝓟𝓜𝓮𝓽 |, let
((S, γ)) = (S, Gγ) (Example 2.1.1) and for each non-expansive mapping g : (S, γ) → (S′, γ′), where (S′, γ′) ∈ | 𝓟𝓜𝓮𝓽 |, let 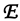 (g) = g. By definition, for p, q ∈ S, Gpq(x) = H(x - γ(p, q)). Hence, if Gpq(x) = 1, then x > γ(p, q)) ≥ γ′(g(p), g(q)), so we obtain G′g(p)g(q)(x) = H(x - γ′(g(p), g(q))) = 1. Therefore, Gpq ≤ G′g(p)g(q), so
(g) = g. By definition, for p, q ∈ S, Gpq(x) = H(x - γ(p, q)). Hence, if Gpq(x) = 1, then x > γ(p, q)) ≥ γ′(g(p), g(q)), so we obtain G′g(p)g(q)(x) = H(x - γ′(g(p), g(q))) = 1. Therefore, Gpq ≤ G′g(p)g(q), so 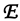 (g) is a morphism. This defines a functor
(g) is a morphism. This defines a functor 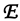 : 𝓟𝓜𝓮𝓽 → 𝓦𝓟D.
: 𝓟𝓜𝓮𝓽 → 𝓦𝓟D. 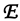 °𝓕 (resp. 𝓕 °
°𝓕 (resp. 𝓕 °  ) is the identity functor on 𝓦𝓟D (resp. 𝓟𝓜𝓮𝓽), so
) is the identity functor on 𝓦𝓟D (resp. 𝓟𝓜𝓮𝓽), so 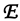 is an isomorphism.
is an isomorphism.


