On the Prime Numbers and Some Graphs Related to the Set of Number of Diagonals of Regular Polygons

1. Introduction

Prime numbers are key in number theory and they have always remained a matter fascination to the mathematicians, and many scientific and technical communities.

A polygon is a flat 2-dimensional ($2D$) shape made of straight lines. The sides connect to form a closed shape. Diagonals of a polygon are the lines that connect the alternate vertices of the polygon. The number of diagonals of a polygon with n vertices is given by ${\displaystyle \frac{n(n-3)}{2}}$.

A graph G is defined as the pair $\left(V\right(G),E(G\left)\right)$, where $V\left(G\right)$ is the set of vertices of G and $E\left(G\right)$ is the set of edges of G. For two distinct vertices a and b of $V\left(G\right)$, the notation $a-b$ means that a and b are adjacent. A graph G is said to be complete if $a-b$ for all distinct $a,b\in V\left(G\right)$, and G is said to be empty if $E\left(G\right)=\varnothing$. Note by this definition that a graph may be empty even if $V\left(G\right)\ne \varnothing$. An empty graph could also be described as totally disconnected. If $\left|V\right(G\left)\right|\ge 2$, a path from a to b is a series of adjacent vertices $a-v_1-v_2-...-v_n-b$. The length of a path is the number of edges it contains. A cycle is a path that begins and ends at the same vertex in which no edge is repeated, and all vertices other than the starting and ending vertex are distinct. If a graph G has a cycle, the girth of G (notated $g\left(G\right)$) is defined as the length of the shortest cycle of G; otherwise, $g\left(G\right)=\infty$. A graph G is connected if for every pair of distinct vertices $a,b\in V\left(G\right)$, there exists a path from a to b. If there is a path from a to b with $a,b\in V\left(G\right)$, then the distance from a to b is the length of the shortest path from a to b and is denoted by $d(a,b)$. If there is not a path between a and b, $d(a,b)=\infty$. The diameter of G is diam$\left(G\right)=Sup\left\{d\right(a,b\left)\right|a,b\in V\left(G\right)\}$. A graph is said to be planar if it can be drawn in the plane so that its edges intersect only at their ends [1].

It is well known that we can translate some properties of number theory to graph theory language and then the geometric properties of graphs help us explore some interesting results in number theory. In this regard, we will discuss the relationship between prime numbers and diagonals of polygons. In addition, we will introduce and investigate two graphs related to the the set of number of diagonals of regular polygons.

2. Main Results

Notation and Remark 2.1. We know that the number of diagonals in n-sided polygon $D_n=n(n-3)/2$. Now, consider the following set that is the set of number of diagonals in n-gon for $n=4,5,6,\dots$.

$$D=\{2,5,9,14,20,27,35,44,54,65,77,90,104,119,135,152,...\}.$$

Set $D_n=\left\{firstnelementsofD\right\}$. For example,

$$D_{41}=\{2,5,9,14,20,27,35,44,54,65,77,90,104,119,135,$$

$$152,170,189,209,230,252,275,299,324,350,377,405,434,464,495,527,560,$$

$$594,629,665,702,720,779\}.$$

Now, set

$$F=\left\{\right(2,5),(9,14),(20,27),(35,44),(54,65),(77,90),(104,119),(135,152),$$

$$(170,189),(209,230),(252,275),(299,324),(350,377),(405,434),(464,495),$$

$$(527,560),(594,629),(665,702),(720,779),...\}.$$

Then for $(x,y)\in \left\{\right(2,5),(9,14),(20,27),(35,44),(54,65),(77,90),(104,119\left)\right\}$, we have $x+y$ is a prime number. But $135+152=287$ is not a prime number.

Definition 2.2. 

The graph related to the set of number of diagonals of regular polygons, denoted by ${\Gamma }^{+}\left(D_n\right)$, is an undirected simple graph whose vertices are $D_n$ and two distinct vertices x and y are adjacent if and only if $x+y$ is a prime number.

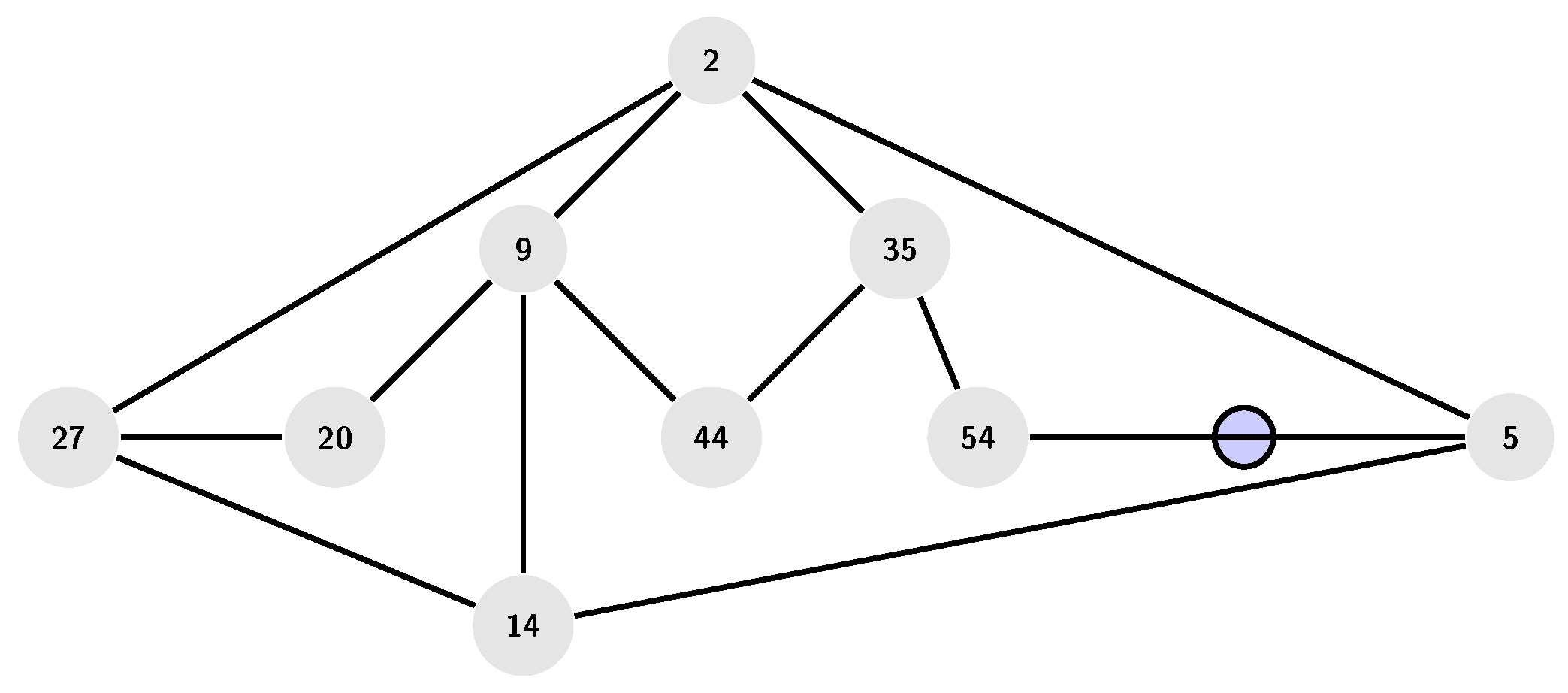
Example 2.3. 

From the Figure 1, the following can be obtained for the graph ${\Gamma }^{+}\left(D_9\right)$:

(a)

The prime numbers introduced form the graph ${\Gamma }^{+}\left(D_9\right)$ are the following set:

$$\{7,11,19,23,29,37,41,53,59,67,71,79,89\}.$$

(b)

$g\left({\Gamma }^{+}\left(D_9\right)\right)=4$.

(c)

$diam\left({\Gamma }^{+}\left(D_9\right)\right)=3$.

(d)

${\Gamma }^{+}\left(D_9\right)$ is a connected graph.

Recall that a vertex with degree zero is called an isolated vertex.

Theorem 2.4. 

Let $n\in N$. Then ${\Gamma }^{+}\left(D_n\right)$ has no isolated vertex if for each $k\in N$ there is a prime number p such that $9-4k^2+12k+8p$ is a square odd number.

Proof. 

Assume that $y\in {\Gamma }^{+}\left(D_n\right)$. Then $y={\displaystyle \frac{k(k-3)}{2}}$ for some $k\in N$. To see that ${\Gamma }^{+}\left(D_n\right)$ has no isolated vertex, we need to find $t\in N$ such that y is adjacent to $x:={\displaystyle \frac{t(t-3)}{2}}$. That is $x+y$ is a prime number p, say. So $p={\displaystyle \frac{t(t-3)}{2}}+{\displaystyle \frac{k(k-3)}{2}}$. It follows that $t^2-3t+k^2-3k-2p=0$. Set $\Delta ={(-3)}^2-4\left(1\right)(k^2-3k-2p)=9-4k^2+12k+8p$. Then $t={\displaystyle \frac{3+\sqrt{\Delta }}{2}}$ or $t={\displaystyle \frac{3-\sqrt{\Delta }}{2}}$. Therefore, $t\in N$ if we have that $\Delta =9-4k^2+12k+8p$ is a square odd number. □

Theorem 2.5. 

${\Gamma }^{+}\left(D_n\right)$ is a planar graph for each $n\le 9$.

Proof. 

This follows from the figure of the graph ${\Gamma }^{+}\left(D_9\right)$. □

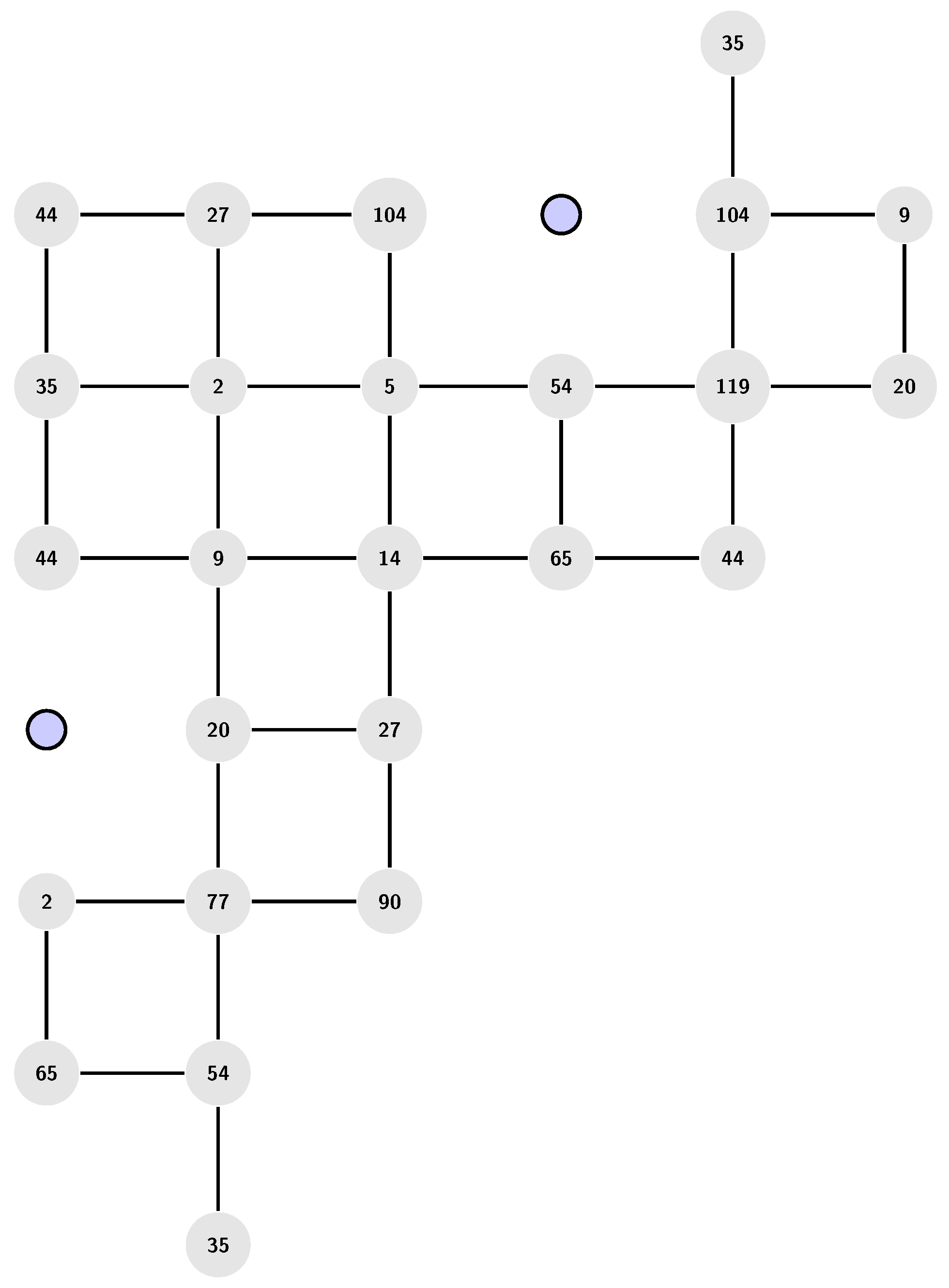
Example 2.6. 

We can deduce form the Figure 2 (that show all edges of ${\Gamma }^{+}\left(D_{17}\right)$ but some vertex are repeated) that the prime numbers introduced form the graph ${\Gamma }^{+}\left(D_{17}\right)$ are the following set:

$$\{7,11,19,23,29,37,41,53,59,67,71,79,89,97,109,113,119,131,139,163,167,178,223\}.$$

In fact, these prime number are with the form ${\displaystyle \frac{n^2+k^2-3(k+n)}{2}}$ for some positive integer $n,k$.

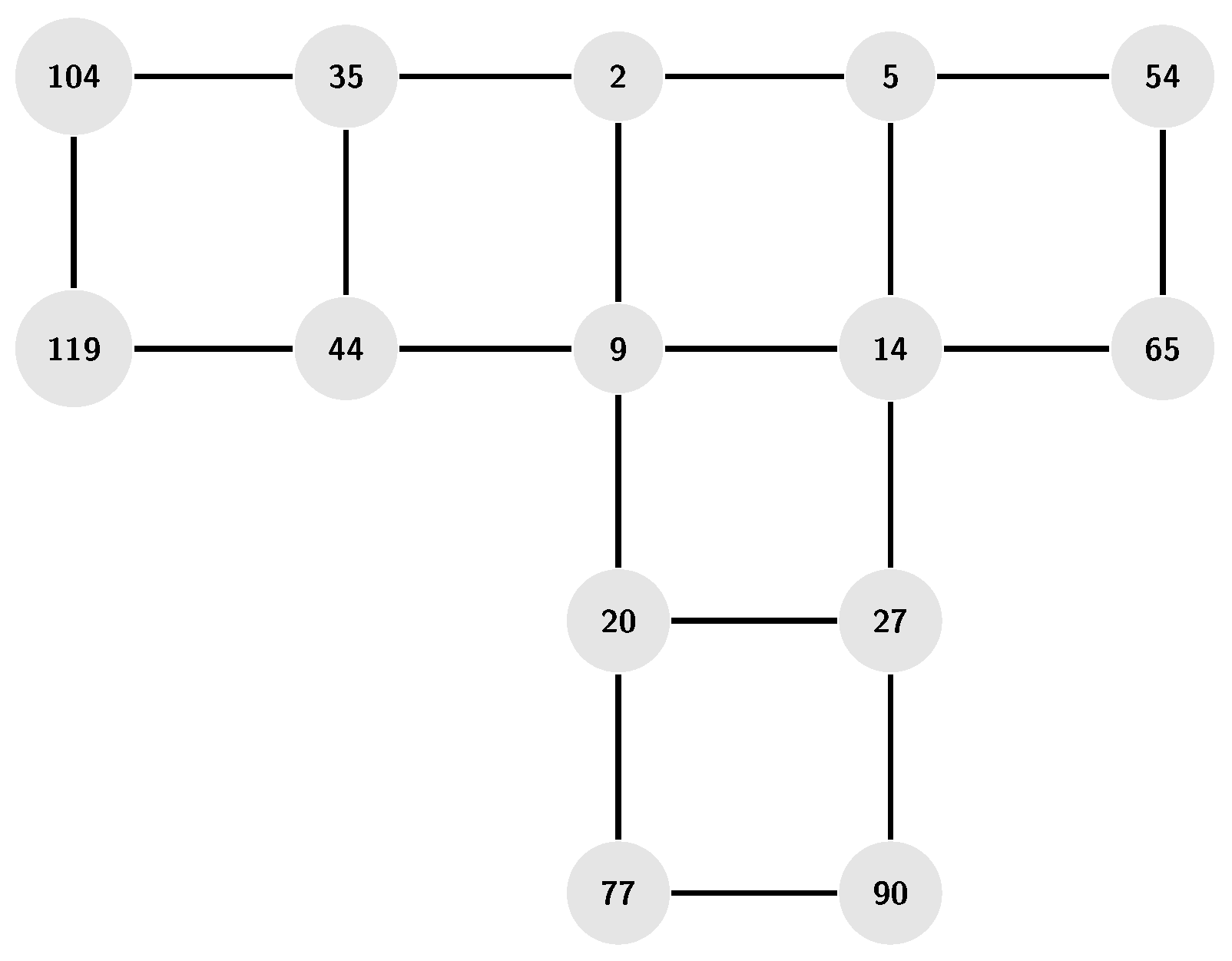
Example 2.7. 

We can deduce form the Figure 3 that (in fact, the Figure 3 is a some of the shape of the graph ${\Gamma }^{+}\left(D_{17}\right)$) the graph ${\Gamma }^{+}\left(D_n\right)$ is a connected graph for each $n\le 17$.

Theorem 2.8. 

Let p be a prime number. Then P can be written as the difference of the number of diagonals of

(a)

$p+1$-gon and $p+2$-gon, i.e. every prime number can be written as the difference of the diagonals of two consecutive polygons.

(b)

${\displaystyle \frac{p+1}{2}}$-gon and ${\displaystyle \frac{p+5}{2}}$-gon, where $P\ne 3$.

Proof. (a) Set $n=p+1$. Then

$$p=p+1-1=n-1={\displaystyle \frac{2n-2}{2}}={\displaystyle \frac{n^2-n-2-n^2+3n}{2}}=$$

$${\displaystyle \frac{(n+1)(n+1-3)}{2}}-{\displaystyle \frac{n(n-3)}{2}}.$$

Thus p is a difference of the diagonals of n-gon and $n+1$-gon.

(b) This follows from the fact that the number of diagonals of ${\displaystyle \frac{p+5}{2}}$-gon is ${\displaystyle \frac{p^2+4p-5}{8}}$ and the number of diagonals of ${\displaystyle \frac{p+1}{2}}$-gon is ${\displaystyle \frac{p^2-4p-5}{8}}$. □

Example 2.9. 

Consider $F_{41}$ (the subset of F in Notation and Remark 2.1) that is an array of set of the number of diagonals for $n=4,5,\dots ,41$, where the pairs marked in red do not have a prime difference.

$$F_{41}=\{(2,5),\begin{array}{c}\hfill (9,14)\end{array},(20,27),\begin{array}{c}\hfill (35,44)\end{array},(54,65),(77,90),(104,119),\begin{array}{c}\hfill (135,152)\end{array},$$

$$(170,189),\begin{array}{c}\hfill (209,230)\end{array},(252,275),\begin{array}{c}\hfill (299,324)\end{array},\begin{array}{c}\hfill (350,377)\end{array},(405,434),(464,495),$$

$$\begin{array}{c}\hfill (527,560)\end{array},\begin{array}{c}\hfill (594,629)\end{array},(665,702),\begin{array}{c}\hfill (720,779)\end{array}\}.$$

Then the set of prime numbers that is generated by $5-2=3$, $27-20=7$, …, $702-665=37$ is as follows:

$${\mathfrak{P}}_{41}=\{3,7,11,13,17,19,23,29,31,37\}.$$

In fact, the elements of ${\mathfrak{P}}_{41}$ are the prime numbers with the form $n-1$ for $n=4,8,12,14,18,20,24,30,32,38$. Continuing this way, we can create an infinite set of prime numbers ${\mathfrak{P}}_n$ with this form.

Example 2.10. 

Consider $F_{41}$ (the subset of F in Notation and Remark 2.1) that is an array of set of the number of diagonals for $n=4,5,\dots ,41$, where the pairs whose sum is not a prime number are highlighted in blue.

$$F_{41}=\{(2,5),(9,14),(20,27),(35,44),(54,65),(77,90),(104,119),\begin{array}{c}\hfill (135,152)\end{array},$$

$$(170,189),(209,230),\begin{array}{c}\hfill (252,275)\end{array},\begin{array}{c}\hfill (299,324)\end{array},(350,377),(405,434),\begin{array}{c}\hfill (464,495)\end{array},$$

$$(527,560),(594,629),(665,702),\begin{array}{c}\hfill (720,779)\end{array}\}.$$

Then the set of prime numbers that is generated by $5+2=7$, $9+14=23$, …, $702+665=1367$ is as follows:

$${\mathbb{P}}_{41}=\{7,23,47,79,119,167,223,359,439,727,839,1097,1223,1367\}.$$

In fact, the elements of ${\mathbb{P}}_{41}$ are the prime numbers with the form $n^2-2n-1$ for $n=$ 4, 6, 8, 10, 12, 14, 16, 20, 22, 28, 30, 34, 36, 38. Continuing this way, we can create an infinite set of prime numbers ${\mathbb{P}}_n$ with this form.

Definition 2.11. 

The another graph related to the set of number of diagonals of regular polygons, denoted by ${\Gamma }^{-}\left(D_n\right)$, is an undirected simple graph whose vertices are $D_n$ and two distinct vertices x and y are adjacent if and only if $x-y$ is a prime number.

Theorem 2.12. 

Let $n\in N$. Then ${\Gamma }^{-}\left(D_n\right)$ has no isolated vertex if for each $k\in N$ there is a prime number p such that $9+4k^2-12k+8p$ is a square odd number.

Proof. 

Assume that $y\in {\Gamma }^{-}\left(D_n\right)$. Then $y={\displaystyle \frac{k(k-3)}{2}}$ for some $k\in N$. To see that ${\Gamma }^{-}\left(D_n\right)$ has no isolated vertex, we need to find $t\in N$ such that y is adjacent to $x:={\displaystyle \frac{t(t-3)}{2}}$. That is $x-y$ is a prime number p, say. So $p={\displaystyle \frac{t(t-3)}{2}}-{\displaystyle \frac{k(k-3)}{2}}$. It follows that $t^2-3t-k^2+3k-2p=0$. Set $\Delta ={(-3)}^2-4\left(1\right)(-k^2+3k-2p)=9+4k^2-12k+8p$. Then $t={\displaystyle \frac{3+\sqrt{\Delta }}{2}}$ or $t={\displaystyle \frac{3-\sqrt{\Delta }}{2}}$. Therefore, $t\in N$ if we have that $\Delta =9-4k^2+12k+8p$ is a square odd number. □

Corollary 2.13. 

If $x={\displaystyle \frac{t(t-3)}{2}}\in {\Gamma }^{-}\left(D_n\right)$ and $y={\displaystyle \frac{k(k-3)}{2}}\in {\Gamma }^{-}\left(D_n\right)$ such that $k-1$ is a prime number, then x is adjacent to y.

Proof. 

Set $p=k-1$. By using the proof of Theorem 2.12, we get that $\Delta =9+4k^2-12k+8p={(2k-1)}^2$. Now, the result follows from Theorem 2.12. □

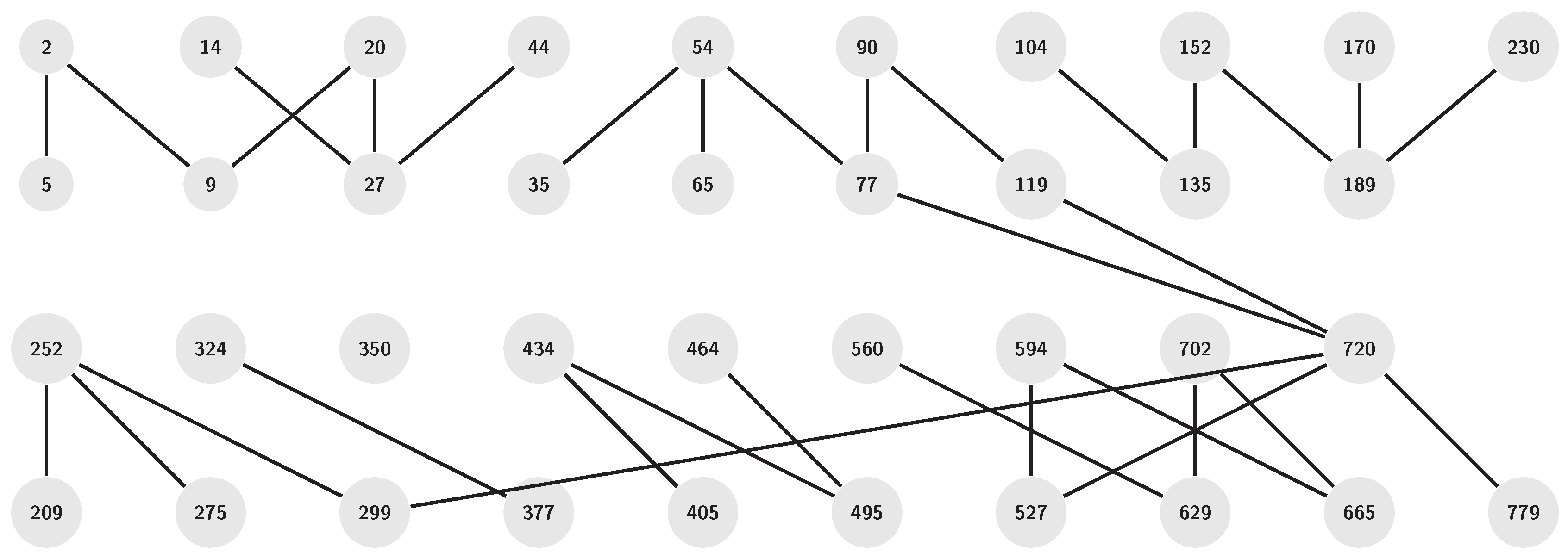
Example 2.14. 

We can see that in the Figure 4 that ${\Gamma }^{-}\left(D_n\right)$ has no cycle for e$n\le 37$. The prime numbers introduced form the graph ${\Gamma }^{-}\left(D_{19}\right)$ are the following set:

$$P=\{3,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,193,421,601,643\}.$$

Definition 2.15. 

The graph related to the set of number of diagonals of regular polygons, denoted by ${\Gamma }^{-}\left(P_n\right)$, is an undirected simple graph whose vertices are $\{4,5,6,..\}$ that is the number of gon in regular polygons for $n=4,5,\dots$ and two distinct vertices n and m are adjacent if and only if the difference of number of diagonals of n-gon and m-gon be a prime number.

Proposition 2.16. 

The graph ${\Gamma }^{-}\left(P_n\right)$ is a bipartite graph with two parts $V_1=\{4,7,8,11,12,15\dots \}$ and $V_2=\{5,6,9,10,13,14\dots \}$.

Proof. 

Clearly every element of $V_1$ is of the form $4+4n$ for $n=0,1,2,\dots$ or $3+4n$ for $n=1,2,\dots$ and every element of $V_2$ is of the form $5+4n$ or $6+4n$ for $n=0,1,2,\dots$. Now if $x,y\in V_1$, then $x=4+4n$ or $x=3+4n$ and $y=4+4n$ or $y=3+4n$. In any case, we have

$${\displaystyle \frac{x(x-3)}{2}}-{\displaystyle \frac{y(y-3)}{2}}$$

is an even and so is not prime. Thus x is not adjacent to y. Similarly, any two elements of $V_2$ are not adjacent. □

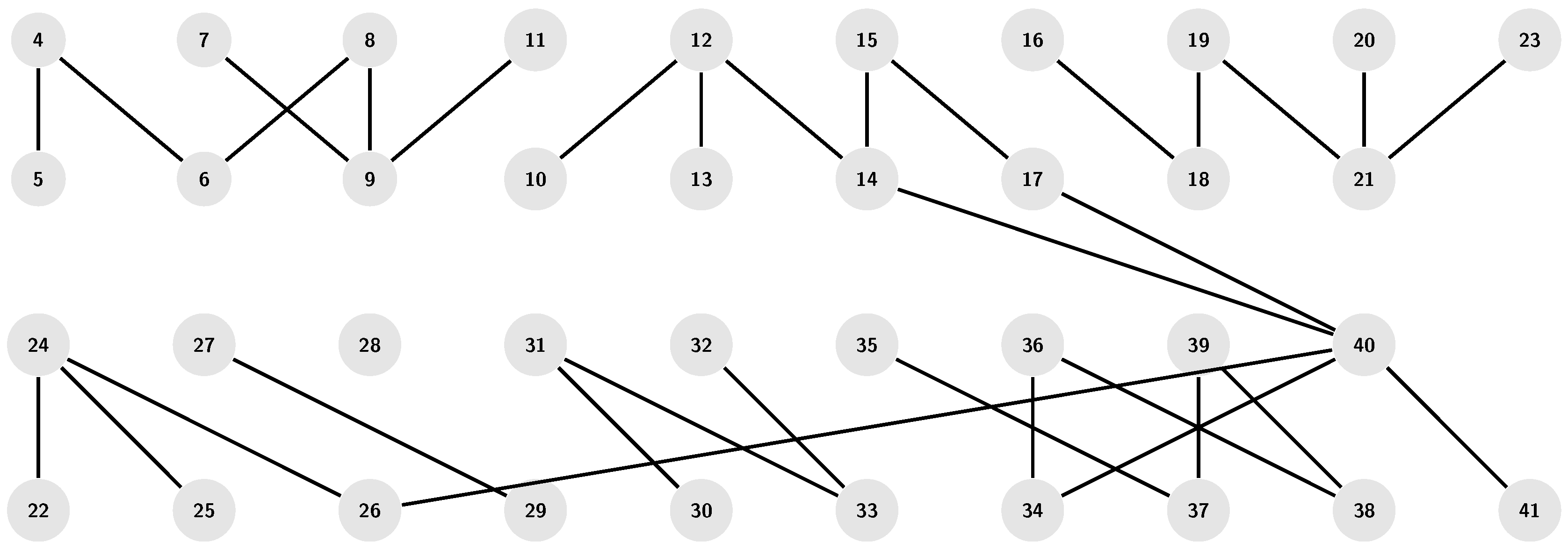
Example 2.17. 

From the Figure 5, the following can be obtained for the graph ${\Gamma }^{-}\left(P_n\right)$:

(a)

The graph ${\Gamma }^{-}\left(P_n\right)$ is not connected for $8\le n\le 41$;

(b)

28 is an isolated vertex for $28\le n\le 41$;

(c)

$g\left({\Gamma }^{-}\left(P_n\right)\right)=\infty$ for $n\le 39$ and $g\left({\Gamma }^{-}\left(P_{40}\right)\right)=4$;

(d)

$diam\left({\Gamma }^{-}\left(P_n\right)\right)=5$ for $9\le n\le 39$ and $diam\left({\Gamma }^{-}\left(P_{40}\right)\right)=9$;

(e)

If n is an odd number, then the set of prime numbers generated from ${\Gamma }^{-}\left(P_n\right)$ is ${\displaystyle \frac{n-1}{2}}$ first elements of P in Example 2.14. For example ${\Gamma }^{-}\left(P_{23}\right)$ this set is

$$\{3,7,11,13,17,19,23,29,31,37,41\}.$$