Modelling the Effectiveness of Sulphadoxine - Pyrimethamine as an Intermittent Preventative Treatment for Malaria in Pregnant Women in Malawi

1. Introduction

Malaria is a significant public health concern in many regions across the globe, particularly in tropical and sub-tropical regions where Anopheles mosquitoes are prevalent [1]. In 2023, the global estimate of malaria cases reached approximately 263 million, with an incidence rate of 60.4 cases per 1,000 individuals at risk [2]. Infants, children under the age of 5, pregnant women and girls, travellers, and people living with HIV or AIDS are at higher risk of severe infection [1]. The disease is caused by Plasmodium parasites (P. falciparum, P. vivax, P. malariae, P. ovale and P. knowlesi) transmitted to humans by female Anopheles mosquitoes [3]. The most deadly parasite among Plasmodium species is P. falciparum, which is most prevalent on the African continent [1,4]. Not all female Anopheles mosquitoes have malaria [3], but they become infectious when they bite humans carrying the parasite during a blood meal. They then transmit the parasite to other humans, continuing the malaria transmission cycle. The life cycle of malaria is depicted in Figure 1.

Despite efforts to reduce the incidence of malaria, the disease remains a major public health concern [5]. The interventions used for malaria prevention for all groups include vector control, vaccination, and preventive chemotherapies. For pregnant women, intermittent preventive treatment with sulfadoxine-pyrimethamine (IPTp-SP) is administered exclusively as a prophylactic measure during pregnancy [2,5]. When prevention fails, infected individuals are prescribed treatment based on the severity of their condition and their general health status to treatments such as artesunate and artemisinin-based combination therapy [2].

Protecting pregnant women from malarial infections has been a significant challenge in Malawi [5]. Therefore, investigating the effectiveness of sulphadoxine-pyrimethamine as an intermittent preventative treatment for malaria in pregnant women in Malawi is a plausible approach to addressing this issue. According to [5], while everyone is at risk of contracting malaria, pregnant women face a particularly high risk of its adverse consequences due to reduced immunity [6,7]. Their increased vulnerability is attributed to the immunological and physiological changes that occur during pregnancy, which can increase malaria severity and lead to complications such as maternal anaemia, preterm birth, and low birth weight [1,3,6,7]. Pregnant women are three times more likely to develop severe malaria compared to non-pregnant women in the same geographic area [4,8]. In Malawi, IPTp-SP remains a trusted intervention for preventing malaria during pregnancy.

Some studies have suggested that IPTp-SP doses effectively suppress the adverse effects of malaria during pregnancy, and their effectiveness appears to vary depending on the number of doses taken by pregnant women [9,10]. This remains true even in the presence of widespread resistance of Plasmodium species to sulphadoxine-pyrimethamine (SP) [5,11]. Three or more doses of IPTp-SP are the most effective in averting the adverse effects of malaria in pregnant women [10,11,12].

Compartmental mathematical models of malaria are widely documented in the literature [13]. The pioneering mathematical models of malaria that describe vector-host dynamics, upon which other models of malaria are based, include the Ross-Macdonald models, and the Anderson and May model [13,14,15,16]. [17] and [18] adapted these frameworks to variable population size models while trying to describe the disease dynamics of malaria. However, their models did not incorporate any interventions, but provided a framework for studying control strategies for the containment of malaria. [17] developed an SEIRS model that incorporates reinfection due to the loss of immunity in the recovered population. Through numerical simulations, they confirmed that abrupt reductions in the mosquito population may temporarily decrease malaria prevalence but do not lead to elimination in endemic regions. Using the same SEIRS framework, [18] emphasized that lowering $R_0$ below 1 may not always guarantee malaria eradication due to possible subcritical bifurcations and concluded that targeted interventions must be carefully structured to achieve effective malaria control. [19] suggested that combining effective antimalarial drugs with comprehensive control measures is essential for reducing transmission and the pool of infectious individuals. [20] developed a mathematical model that analyzed the dynamics of malaria disease transmission and evaluated control strategies for its management. [21] emphasized the importance of applying mathematical models to improve public health strategies against malaria. [22] considered a combination of intervention strategies such as effective mass drug administration and vector control (LLITNs and IRS) to combat and eventually eliminate the malaria. Although various transmission and control compartmental mathematical models of malaria are widely documented in the literature, our proposed model is seemingly new as it investigates the effectiveness of IPTp-SP as a prophylactic treatment for pregnant women.

The proposed compartmental model is not exhaustive. One limitation is that it does not specify the number of doses pregnant women are receiving. The recommended number of IPTp-SP doses during pregnancy is at least three, with the first dose administered as early as possible at the beginning of the second trimester, but not before week 13 of pregnancy [2].

In the following sections, we formulate and analyze a deterministic model incorporating IPTp-SP as an intervention strategy. Key parameters influencing transmission are identified through sensitivity analysis of the model. Finally, some parameter values are assumed within realistic ranges to support the analytical results, with the caveat that model outcomes are not compared with real data.

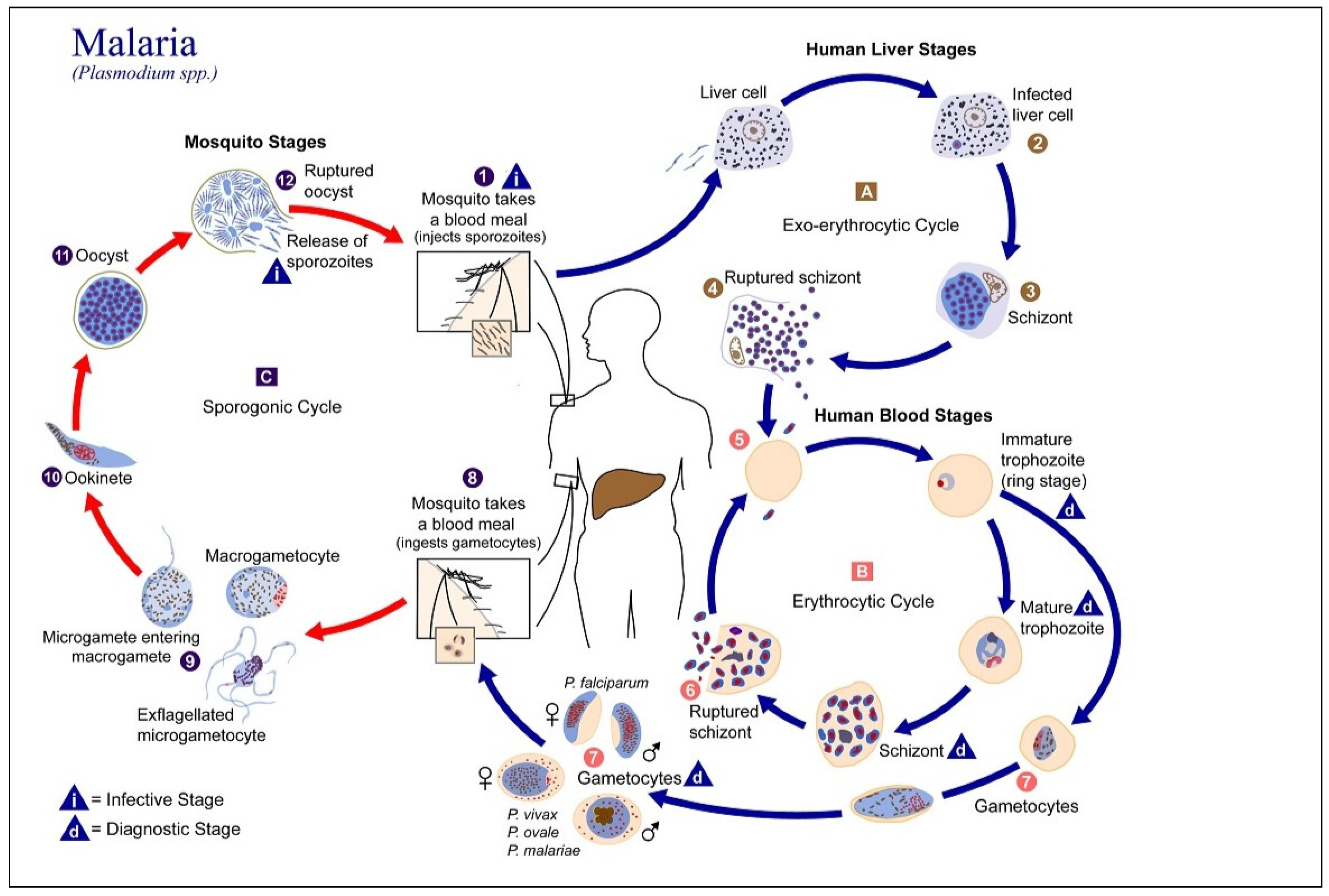
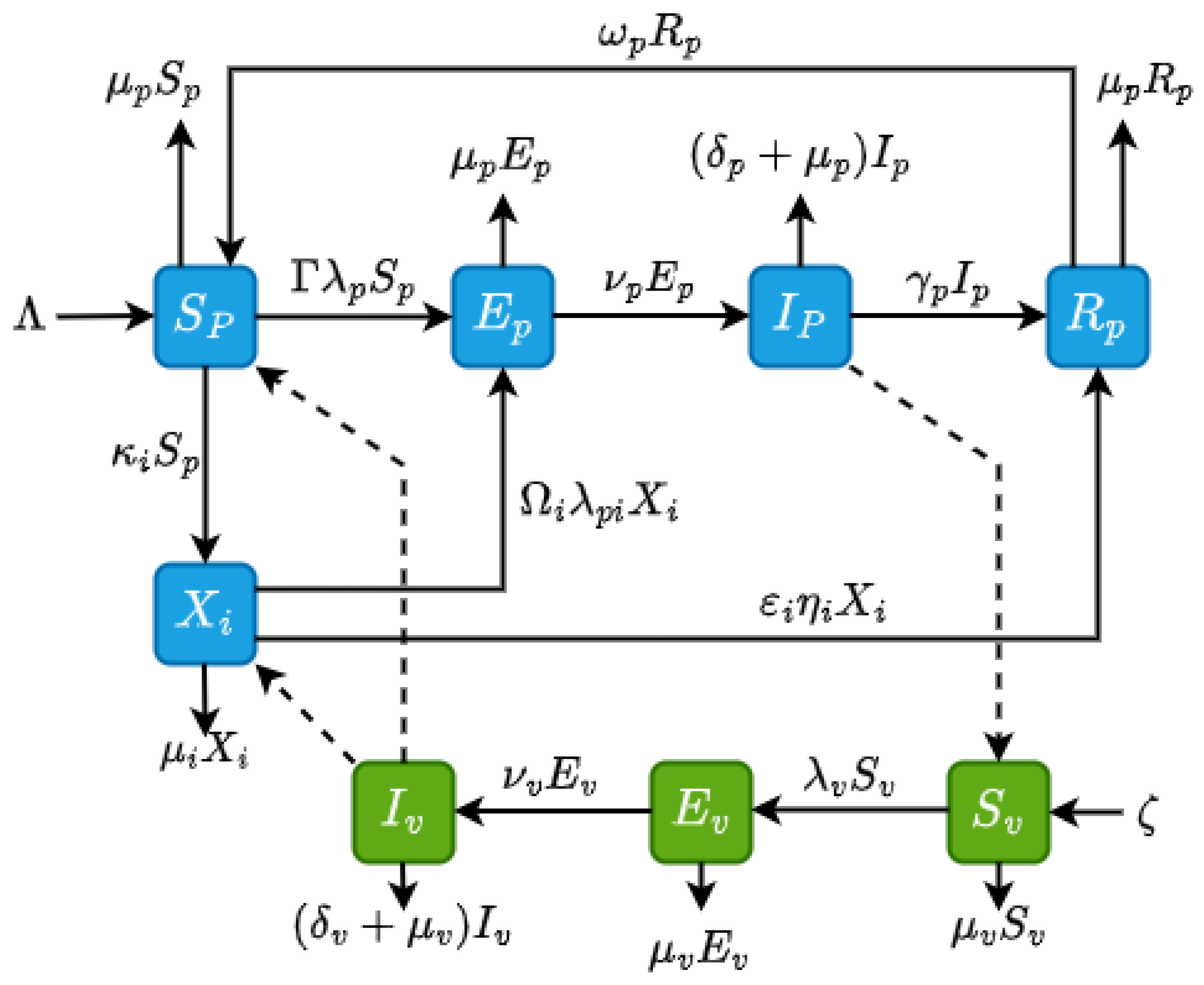
2. Methods: Model Formulation and Description

The population of pregnant women is divided based on malaria and dosing status. When malaria invades, it categorizes them into non-intersecting classes: susceptible ($S_p$), exposed ($E_p$), infected ($I_p$), and recovered ($R_p$), with $X_{i}s$ representing susceptible pregnant women who receive any number of IPTp-SP doses (one, two, or at least three). Similarly, vectors are classified based on their malaria status. When malaria spreads among vectors, it divides them into non-intersecting classes: susceptible ($S_v$), exposed ($E_v$), and infected ($I_v$). The total population of pregnant women at any time is given by:

$$N_p\left(t\right)=S_p\left(t\right)+X_i\left(t\right)+E_p\left(t\right)+I_p\left(t\right)+R_p\left(t\right).$$

(1)

And the total population of vectors at any given time is given by:

$$N_v\left(t\right)=S_v\left(t\right)+E_v\left(t\right)+I_v\left(t\right).$$

(2)

The recruitment rate of pregnant women through conception is $\Lambda$, while $\zeta$ represents the recruitment rate of the mosquitoes through birth. The natural death rates of pregnant women and mosquito populations are ${\mu }_p$ and ${\mu }_v$, respectively, with these rates being proportional to the number of individuals or mosquitoes in each class. The biting rate of mosquitoes is $\alpha$. The fraction of susceptible pregnant women taking IPTp-SP prophylaxis is denoted as $\left({\kappa }_i\right)$, while the fraction not taking IPTp-SP prophylaxis is given by $(1-\kappa )$. The fraction of pregnant women protected from malaria due to IPTp-SP effectiveness, $\left({\epsilon }_i\right)$, transitions directly to the recovered class $\left(R_p\right)$ at the treatment success rate $\left({\eta }_i\right)$. Conversely, $(1-\epsilon )$ represents the fraction of pregnant women who contract malaria at a treatment failure rate $(1-\eta )$. Male (microgametocytes) and female (macrogametocytes) gametocytes are ingested by Anopheles mosquitoes during a blood meal from an infected pregnant woman at the rate:

$${\displaystyle {\lambda }_v\left(t\right)=\frac{\alpha {\beta }_{pv}{I}_p\left(t\right)}{N_p\left(t\right)},}$$

where ${\beta }_{pv}$ is the success rate of gametocyte transmission from an infected pregnant woman to susceptible mosquitoes. Thereafter, susceptible mosquitoes enter the exposed class $E_v\left(t\right)$. During this stage, gametocytes fuse, generating zygotes that later develop into oocytes, which eventually rupture to release sporozoites. At this point, mosquitoes transition into the infected class $I_v\left(t\right)$ at the rate ${\nu }_v$. Mosquitoes may die from the disease at the rate ${\delta }_v$ in the infected class. During a subsequent blood meal, malaria-infected female Anopheles mosquitoes inoculate sporozoites into pregnant women at the rates:

$${\displaystyle {\lambda }_{pi}\left(t\right)=\frac{\alpha {\beta }_{vpi}{I}_v\left(t\right)}{N_p\left(t\right)},}$$

and

$${\displaystyle {\lambda }_p\left(t\right)=\frac{\alpha {\beta }_{vp}{I}_v\left(t\right)}{N_p\left(t\right)},}$$

where ${\beta }_{vpi}$ and ${\beta }_{vp}$ represent the success rates of sporozoite transmission from infected mosquitoes $I_v\left(t\right)$ to susceptible pregnant women taking IPTp-SP prophylaxis $\left({\kappa }_i\right)$ and those not taking IPTp-SP prophylaxis $(1-\kappa )$, respectively, during a blood meal. This transitions pregnant women into the latent stage, $E_p\left(t\right)$. Upon infection, sporozoites invade liver cells, where they mature and multiply before rupturing and releasing merozoites. These merozoites then infect red blood cells, continuing a cycle of replication. The blood-stage parasites cause the disease’s symptoms and clinical manifestations, transitioning pregnant women into the infected class $I_p\left(t\right)$ at the rate ${\nu }_p$. Infected pregnant women may die from the disease at the rate ${\delta }_p$ or move to the recovered class, $R_p$, at the rate ${\gamma }_p$. Once immunity wanes, they return to the susceptible class, $S_p$, at the rate ${\omega }_p$. Figure 2 provides a graphical interpretation of the malaria compartmental model

Based on our model description, assumptions, definitions of the state variables and parameters in Table 1, the proposed $S_p{X}_i{E}_p{I}_p{R}_p{S}_p$ malaria model satisfies the following system of non-linear ordinary differential equations:

$$\begin{array}{l}{\displaystyle \frac{d{S}_p}{dt}=\Lambda +{\omega }_p{R}_p-{\kappa }_i{S}_p-\Gamma {\lambda }_p{S}_p-{\mu }_p{S}_p}\\ {\displaystyle \frac{d{X}_i}{dt}={\kappa }_i{S}_p-{\epsilon }_i{\eta }_i{X}_i-{\Omega }_i{\lambda }_{pi}{X}_i-{\mu }_p{X}_i}\\ {\displaystyle \frac{d{E}_p}{dt}=\Gamma {\lambda }_p{S}_p+{\Omega }_i{\lambda }_{pi}{X}_i-{\nu }_p{E}_p-{\mu }_p{E}_p}\\ {\displaystyle \frac{d{I}_p}{dt}={\nu }_p{E}_p-({\gamma }_p+{\delta }_p+{\mu }_p)I_p}\\ {\displaystyle \frac{d{R}_p}{dt}={\gamma }_p{I}_p+{\epsilon }_i{\eta }_i{X}_i-{\omega }_p{R}_p-{\mu }_p{R}_p}\\ {\displaystyle \frac{d{S}_v}{dt}=\zeta -{\lambda }_v{S}_v-{\mu }_v{S}_v}\\ {\displaystyle \frac{d{E}_v}{dt}={\lambda }_v{S}_v-{\nu }_v{E}_v-{\mu }_v{E}_v}\\ {\displaystyle \frac{d{I}_v}{dt}={\nu }_v{E}_v-({\mu }_v+{\delta }_v)I_v}\end{array}\}$$

(3)

where:

$$\Gamma =(1-{\kappa }_i)$$

and

$${\Omega }_i=(1-{\epsilon }_i)(1-{\eta }_i)$$

3. Results

3.1. Invariant Region

Both the model state variables and parameters are assumed non-negative for all time $t\ge 0$. Let $(S_p,X_i,E_p,I_p,R_p,S_v,E_v,I_v)\in {\mathbb{R}}^8$ be any solution of the system with non-negative initial conditions. Applying Birkhoff and Rota’s Theorem [23] on differential inequality, from Equation (1), we have $N_p\left(t\right)\le \Lambda -{\mu }_p{N}_p$ as $t\to \infty$, and thus, $0\le N_p\left(t\right)\le {\displaystyle \frac{\Lambda }{{\mu }_p}}$. Hence the feasible solutions on the human population enter the region

$${\displaystyle {\Pi }_p=\{\left(S_p,X_i,E_p,I_p,R_p\right)\in {\mathbb{R}}_{\ge 0}^5:N_p\left(t\right)\le \frac{\Lambda }{{\mu }_p}\}.}$$

(4)

Similarly, it can be shown that the feasible solutions on the mosquito population given by Equation (2) enter the region

$${\displaystyle {\Pi }_v=\{\left(S_v,,E_v,I_v\right)\in {\mathbb{R}}_{\ge 0}^3:N_v\left(t\right)\le \frac{\zeta }{{\mu }_v}\}.}$$

(5)

Therefore, from (4) and (5), the possible solutions of model (3) will enter the the positively invariant region $\Pi ={\Pi }_p\times {\Pi }_v$.

3.2. Positivity of the State Variables

Since is a positively invariant set under the flow induced by model (3), we now show that every solution with initial condition in ${\mathbb{R}}^8$ remains in that region for $t>0$.

Theorem 1.

The solution set $\{S_p,X_i,E_p,I_p,R_p,S_v,E_v,I_v\}\left(t\right)$ of the malaria model (3) with the initial condition $\{S_p,X_i,E_p,I_p,R_p,S_v,E_v,I_v\}\left(0\right)$ is positive for all $t>0$.

Proof. 

Let $t=sup\{t>0:S_p>0,X_i>0,E_p>0,I_p>0,R_p>0,S_v>0,E_v>0,I_v>0\}\in [0,t]$, gives $t>0$. The first equation of model (3) gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{S}_p}{dt}}& =\Lambda +{\omega }_p{R}_p-{\kappa }_i{S}_p-\Gamma {\lambda }_p{S}_p-{\mu }_p{S}_p\hfill \\ \hfill {\displaystyle \frac{d{S}_p}{dt}}& \ge -S_P\left(t\right)({\kappa }_i+\Gamma {\lambda }_p+{\mu }_p)\hfill \\ \hfill {\displaystyle S_p\left(t\right)}& \ge S_p\left(0\right)e^{-\left({\int }_0^t\Gamma {\lambda }_p\left(s\right)ds+({\kappa }_i+{\mu }_p)t\right)}\ge 0\hfill \end{array}$$

The second equation of the model (3) gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{X}_i}{dt}}& ={\kappa }_i{S}_p-{\epsilon }_i{\eta }_i{X}_i-{\Omega }_i{\lambda }_{pi}{X}_i-{\mu }_p{X}_i\hfill \\ \hfill {\displaystyle \frac{d{X}_i}{dt}}& \ge -X_i({\epsilon }_i{\eta }_i+{\Omega }_i{\lambda }_{pi}+{\mu }_p)\hfill \\ \hfill X_i\left(t\right)& \ge X_i\left(0\right)e^{-\left({\int }_0^t{\Omega }_i{\lambda }_{pi}\left(s\right)ds+({\epsilon }_i{\eta }_i+{\mu }_p)t\right)}\ge 0\hfill \end{array}$$

Hence $S_p$ and $X_i$ is always positive for all $t>0$.

The third equation of model model (3) gives

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{E}_p}{dt}}& =\Gamma {\lambda }_p{S}_p+{\Omega }_i{\lambda }_{pi}{X}_i-{\nu }_p{E}_p-{\mu }_p{E}_p\hfill \\ \hfill {\displaystyle \frac{d{E}_p}{dt}}& \ge -E_p\left({\nu }_p+{\mu }_p\right)\hfill \\ \hfill E_p\left(t\right)& \ge E_p\left(0\right)e^{-\left({\nu }_p+{\mu }_p\right)t}\ge 0\hfill \end{array}$$

Similarly it can be shown that $I_p>0$, $R_p>0$, $S_v>0$, $E_v>0$, and $I_v>0$ □

3.3. Existence and Stability of Steady-State Solutions

The disease-free equilibrium (DFE) of the malaria model (3) denoted by $E_0$ is given by

$$E_0=\left(S_p^{*},X_i^{*},E_p^{*},I_p^{*},R_p^{*},S_v^{*},E_v^{*},I_v^{*}\right)$$

At equilibrium we consider the compartments $S_p^{*}$, $X_i^{*}$ and $S_v^{*}$ of the system (3) which as non-infected compartments. Therefore from equations 1,2, and 6 of the model (3) we have

$$\begin{array}{cc}\hfill \Lambda -{\kappa }_i{S}_p^{*}-{\mu }_p{S}_p& =0\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\kappa }_i{S}_p^{*}-{\epsilon }_i{\eta }_i{X}_i^{*}-{\mu }_p{X}_i^{*}& =0\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \zeta -{\mu }_v{S}_v^{*}& =0\hfill \end{array}$$

(8)

From (6) $S_p^{*}$ is given as:

$$\begin{array}{cc}\hfill S_p^{*}& ={\displaystyle \frac{\Lambda }{({\kappa }_i+{\mu }_p)}}\hfill \\ \hfill & =c_i\Lambda \hfill \end{array}$$

where

$$c_i={\displaystyle \frac{1}{({\kappa }_i+{\mu }_p)}}$$

Substituting $S_p^{*}$ in (7), we have:

$$\begin{array}{cc}\hfill X_i^{*}& =\Lambda c_i{d}_i\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill d_i& ={\displaystyle \frac{{\kappa }_i}{({\epsilon }_i{\eta }_i+{\mu }_p)}}\hfill \end{array}$$

Therefore:

$$\begin{array}{cc}\hfill X_i^{*}& ={\displaystyle \frac{{\kappa }_i\Lambda }{({\kappa }_i+{\mu }_p)({\epsilon }_i{\eta }_i+{\mu }_p)}}\hfill \end{array}$$

(9)

Equation (9) is the general form for finding the disease-free equilibrium points for the IPTp-SP intervention model.

From (8) we can solve for $S_v^{*}$ to have:

$$S_v^{*}={\displaystyle \frac{\zeta }{{\mu }_v}}.$$

Consequently, the disease-free equilibrium for the model (3) will be given by:

$$\begin{array}{c}\hfill \left({\displaystyle \frac{\Lambda }{({\kappa }_i+{\mu }_p)}},{\displaystyle \frac{{\kappa }_i\Lambda }{({\kappa }_i+{\mu }_p)({\epsilon }_i{\eta }_i+{\mu }_p)}},0,0,0,{\displaystyle \frac{\zeta }{{\mu }_v}},0,0\right)\end{array}$$

The effective reproduction number is obtained by using the next generation matrix [24]. Let

$$\mathcal{F}=\left[\begin{array}{c}\Gamma {\lambda }_p{S}_p+{\Omega }_1{\lambda }_p{X}_i\\ 0\\ {\lambda }_v{S}_v\\ 0\end{array}\right]$$

and

$$\mathcal{V}=\left[\begin{array}{c}({\nu }_p+{\mu }_p)E_p\\ ({\gamma }_p+{\delta }_p+{\mu }_p)I_p-{\nu }_p{E}_p\\ ({\nu }_v+{\mu }_v)E_v\\ ({\mu }_v+{\delta }_v)I_v-{\nu }_v{E}_v\end{array}\right]$$

The effective reproduction number is the spectral radius $\rho \left(F{V}^{-1}\right)$ and the resulting expression is given by

$$\alpha {\mu }_p\sqrt{{\displaystyle \frac{\zeta {\nu }_p{\beta }_{\mathrm{pv}}{\nu }_v\left(\Gamma {\beta }_{\mathrm{vp}}\left({\eta }_i{\epsilon }_i+{\mu }_p\right)+{\Omega }_i{\kappa }_i{\beta }_{\mathrm{vpi}}\right)}{\Lambda {\mu }_v\left({\mu }_p+{\nu }_p\right)\left({\delta }_v+{\mu }_v\right)\left({\mu }_v+{\nu }_v\right)\left({\kappa }_i+{\mu }_p\right)\left({\gamma }_p+{\delta }_p+{\mu }_p\right)\left({\eta }_i{\epsilon }_i+{\mu }_p\right)}}}$$

(10)

The effective reproduction number is defined as the number of secondary malaria infections caused by one infectious pregnant woman or mosquito during the infectious period in a completely susceptible population. This number is not only important for describing how quickly the disease could spread, but it can also provide valuable information for controlling and preventing the spread of the disease [22].

3.4. Local Stability of the Disease-Free Equilibrium

Local stability of the DFE is established from the Corollary of the theorem in [25,26].

Corollary 1.

Corollary of Gershgorin Circle Theorem: Let A be an n × n matrix with real entries. If the diagonal elements $a_{ii}$ of A satisfy

$$a_{ii}<-r_i$$

where

$$r_i=\sum _{j=1,j\ne i}^n\left|a_{ij}\right|$$

for i = 1...n, then the eigenvalues of A are negative or have negative real parts.

Lemma 1.

The DFE for the malaria model (3) is locally asymptotically stable if $R_0<1$ and unstable when $R_0>1$.

Proof. 

The Jacobian matrix for (3) at disease-free equilibrium is given as

$${\displaystyle \left[\begin{array}{cccccccc}-d_4& 0& 0& 0& {\omega }_p& 0& 0& -\frac{\Gamma \alpha {\beta }_{vp}{\mu }_p}{d_4}\\ {\kappa }_i& -h& 0& 0& 0& 0& 0& -\frac{{\Omega }_i\alpha {\beta }_{vpi}{\kappa }_i{\mu }_p}{d_{4}h}\\ 0& 0& -d_0& 0& 0& 0& 0& \frac{\Gamma \alpha {\beta }_{vp}{\mu }_p}{d_4}+\frac{{\Omega }_i\alpha {\beta }_{vpi}{\kappa }_i{\mu }_p}{d_{4}h}\\ 0& 0& {\nu }_p& -d_1& 0& 0& 0& 0\\ 0& {\eta }_i{\epsilon }_i& 0& {\gamma }_p& -g& 0& 0& 0\\ 0& 0& 0& -\frac{\alpha {\beta }_{pv}{\mu }_p\zeta }{\Lambda {\mu }_v}& 0& -{\mu }_v& 0& 0\\ 0& 0& 0& \frac{\alpha {\beta }_{pv}{\mu }_p\zeta }{\Lambda {\mu }_v}& 0& 0& -d_2& 0\\ 0& 0& 0& 0& 0& 0& {\nu }_v& -d_3\end{array}\right]}$$

where $d_0=\left({\nu }_p+{\mu }_p\right),d_1=\left({\delta }_p+{\gamma }_p+{\mu }_p\right),d_2=\left({\nu }_v+{\mu }_v\right),d_3=\left({\delta }_v+{\mu }_p\right),d_4=\left({\kappa }_i+{\mu }_p\right),g=\left({\omega }_p+{\mu }_p\right)$ and $h=\left({\epsilon }_i{\eta }_i+{\mu }_p\right)$. According to the corollary, the Jacobian matrix will have negative eigenvalues if the following inequalities are satisfied:

$$\begin{array}{cc}\hfill {\displaystyle d_4}& >{\displaystyle \frac{{\omega }_p{d}_4+\Gamma \alpha {\beta }_{vp}{\mu }_p}{d_4}}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill h& >{\displaystyle \frac{{\kappa }_i{d}_{4}h+{\Omega }_i\alpha {\beta }_{vpi}{\kappa }_i{\mu }_p}{d_{4}h}}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill d_0& >{\displaystyle \frac{h\Gamma \alpha {\beta }_{vp}{\mu }_p+{\Omega }_i\alpha {\beta }_{vpi}\kappa i{\mu }_p}{d_{4}h}}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill d_1& >{\nu }_p\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill g& >\left({\eta }_i{\epsilon }_i+{\gamma }_p\right)\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\mu }_v& >{\displaystyle \frac{\alpha {\beta }_{pv}{\mu }_p\zeta }{\Lambda {\mu }_v}}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill d_2& >{\displaystyle \frac{\alpha {\beta }_{pv}{\mu }_p\zeta }{\Lambda {\mu }_v}}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill d_3& >{\nu }_v\hfill \end{array}$$

(18)

Combining (13),(14),(17) and (18) we have:

$$1>{\displaystyle \frac{{\alpha }^2{\beta }_{pv}{\mu }_p^2\zeta {\nu }_p{\nu }_v\left(\Gamma {\beta }_{vp}h+{\Omega }_i{\beta }_{vpi}{\kappa }_i\right)}{\Lambda {\mu }_v{d}_0{d}_1{d}_2{d}_3{d}_{4}h}}=R_e^2$$

This shows that the disease disease-free equilibrium is locally asymptotically stable if $R_e<1$ and unstable if $R_e>1$. □

3.5. Existence of Endemic Equilibria

The endemic equilibrium is the equilibrium of the system (3) where the disease persists in the population. The endemic equilibrium point $E_1$ of the system (3) satisfies $S_p^{*}>0$, $X_i^{*}>0$, $E_p^{*}>0$, $I_p^{*}>0$, $R_p^{*}>0$, $S_v^{*}>0$, $E_v^{*}>0$, $I_v^{*}>0$.

If ${\displaystyle E_1=\left(S_p^{*},X_i^{*},E_p^{*},I_p^{*},R_p^{*},S_v^{*},E_v^{*},I_v^{*}\right)}$ represents any arbitrary equilibrium of the system (3). Solving the system (3) at equilibrium results into:

$$\begin{array}{cc}\hfill S_p^{*}& ={\displaystyle \frac{\Lambda +R_p^{*}{\omega }_p}{{\kappa }_i+\Gamma {\lambda }_p+{\mu }_p}}\hfill \\ \hfill X_i^{*}& ={\displaystyle \frac{{\kappa }_i\left(\Lambda +R_p^{*}{\omega }_p\right)}{\left({\kappa }_i+\Gamma {\lambda }_p+{\mu }_p\right)\left({\Omega }_i{\lambda }_{\mathrm{pi}}+{\eta }_i{ϵ}_i+{\mu }_p\right)}}\hfill \\ \hfill E_p^{*}& ={\displaystyle \frac{\left(\Lambda +R_p^{*}{\omega }_p\right)\left(\Gamma {\lambda }_p\left({\eta }_i{ϵ}_i+{\mu }_p\right)+{\Omega }_i{\lambda }_{\mathrm{pi}}\left({\kappa }_i+\Gamma {\lambda }_p\right)\right)}{\left({\mu }_p+{\nu }_p\right)\left({\kappa }_i+\Gamma {\lambda }_p+{\mu }_p\right)\left({\Omega }_i{\lambda }_{\mathrm{pi}}+{\eta }_i{ϵ}_i+{\mu }_p\right)}}\hfill \\ \hfill I_p^{*}& ={\displaystyle \frac{{\nu }_p\left(\Lambda +R_p^{*}{\omega }_p\right)\left(\Gamma {\lambda }_p\left({\eta }_i{ϵ}_i+{\mu }_p\right)+{\Omega }_i{\lambda }_{\mathrm{pi}}\left({\kappa }_i+\Gamma {\lambda }_p\right)\right)}{\left({\mu }_p+{\nu }_p\right)\left({\gamma }_p+{\delta }_p+{\mu }_p\right)\left({\kappa }_i+\Gamma {\lambda }_p+{\mu }_p\right)\left({\Omega }_i{\lambda }_{\mathrm{pi}}+{\eta }_i{ϵ}_i+{\mu }_p\right)}}\hfill \\ \hfill R_p^{*}& ={\displaystyle \frac{{\eta }_i{ϵ}_i\left({\kappa }_i\left(\Lambda +i_p{\gamma }_p\right)+i_p{\gamma }_p\left(\Gamma {\lambda }_p+{\mu }_p\right)\right)+i_p{\gamma }_p\left({\kappa }_i+\Gamma {\lambda }_p+{\mu }_p\right)\left({\Omega }_i{\lambda }_{\mathrm{pi}}+{\mu }_p\right)}{{\eta }_i{ϵ}_i\left({\kappa }_i{\mu }_p+\left({\mu }_p+{\omega }_p\right)\left(\Gamma {\lambda }_p+{\mu }_p\right)\right)+\left({\mu }_p+{\omega }_p\right)\left({\kappa }_i+\Gamma {\lambda }_p+{\mu }_p\right)\left({\Omega }_i{\lambda }_{\mathrm{pi}}+{\mu }_p\right)}}\hfill \\ \hfill S_v^{*}& ={\displaystyle \frac{\zeta }{{\lambda }_v+{\mu }_v}}\hfill \\ \hfill E_v^{*}& ={\displaystyle \frac{\zeta {\lambda }_v}{\left({\lambda }_v+{\mu }_v\right)\left({\mu }_v+{\nu }_v\right)}}\hfill \\ \hfill I_v& ={\displaystyle \frac{\zeta {\lambda }_v{\nu }_v}{\left({\delta }_v+{\mu }_v\right)\left({\lambda }_v+{\mu }_v\right)\left({\mu }_v+{\nu }_v\right)}}\hfill \end{array}$$

where the forces of infection at equilibrium are given by ${\displaystyle {\lambda }_p^{*}=\frac{\alpha {\beta }_{vp}{I}_v^{*}}{N_p^{*}}}$, ${\displaystyle {\lambda }_{pi}^{*}=\frac{\alpha {\beta }_{vpi}{I}_v^{*}}{N_p^{*}}}$, ${\displaystyle {\lambda }_v^{*}=\frac{\alpha {\beta }_{pv}{I}_p^{*}}{N_p^{*}}}$ respectively

3.6. Global Stability of the Endemic Equilibrium

The global stability of the endemic equilibrium for system(3) is analysed.

Theorem 2.

If $R_0>1$, then the endemic equilibrium point of the model is globally asymptotically stable on ℵ for

$$\begin{array}{cccc}\hfill {\displaystyle {\nu }_p}& ={\displaystyle \frac{({\nu }_p+{\mu }_p){\mu }_p}{\alpha {\beta }_{vp}{S}_p^{*}}}\hfill & \hfill {\displaystyle {\nu }_v}& ={\displaystyle \frac{({\nu }_v+{\mu }_v){\mu }_v}{\alpha {\beta }_{pv}{S}_v^{*}}}\hfill \\ \hfill {\displaystyle {\mu }_p}& ={\displaystyle \frac{\Lambda }{S_p^{*}}}\hfill & \hfill {\displaystyle {\mu }_v}& ={\displaystyle \frac{\zeta }{S_v^{*}}}\hfill \end{array}$$

Proof. 

We define a Lyapunov function:

$$\begin{array}{cc}\hfill {\displaystyle L\left(t\right)}& ={\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}}}\left(S_p-S_p^{*}log{S}_p\right)+{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}}}\left(S_v-S_v^{*}log{S}_v\right)+{\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}}}{E}_p+{\displaystyle \frac{1}{{\mu }_p}}{I}_p\hfill \\ \hfill & +{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}}}{E}_v+{\displaystyle \frac{1}{{\mu }_v}}{I}_v\hfill \end{array}$$

Getting the time derivative we have:

$$\begin{array}{cc}\hfill L^{\prime }\left(t\right)& ={\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}}}\left(1-{\displaystyle \frac{S_p^{*}}{S_p}}\right)S_p^{\prime }+{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}}}\left(1-{\displaystyle \frac{S_v^{*}}{S_v}}\right)S_v^{\prime }+{\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}}}{E}_p^{\prime }+{\displaystyle \frac{1}{{\mu }_p}}{I}_p^{\prime }\hfill \\ \hfill & +{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}}}{E}_v^{\prime }+{\displaystyle \frac{1}{{\mu }_v}}{I}_v^{\prime }\hfill \\ \hfill L^{\prime }\left(t\right)& ={\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}{S}_p}}\left(S_p-S_p^{*}\right)S_p^{\prime }+{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}{S}_v}}\left(S_v-S_v^{*}\right)S_v^{\prime }+{\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}}}{E}_p^{\prime }+{\displaystyle \frac{1}{{\mu }_p}}{I}_p^{\prime }\hfill \\ \hfill & +{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}}}{E}_v^{\prime }+{\displaystyle \frac{1}{{\mu }_v}}{I}_v^{\prime }\hfill \\ \hfill L^{\prime }\left(t\right)& ={\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}{S}_p}}\left(S_p-S_p^{*}\right)\left(\Lambda -{\displaystyle \frac{{\beta }_{vp}\alpha I_v}{N_p}}{S}_p-{\mu }_p{S}_p\right)\hfill \\ & +{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}{S}_v}}\left(S_v-S_v^{*}\right)\left(\zeta -{\displaystyle \frac{{\beta }_{pv}\alpha I_p}{N_p}}{S}_v-{\mu }_v{S}_v\right)\hfill \\ & +{\displaystyle \frac{1}{\alpha {\beta }_{vp}{S}_p^{*}}}\left({\displaystyle \frac{{\beta }_{vp}\alpha I_v}{N_p}}{S}_p-{\nu }_p{E}_P-{\mu }_p{E}_p\right)+{\displaystyle \frac{1}{{\mu }_p}}\left({\nu }_p{E}_p-{\gamma }_p{I}_p-{\delta }_p{I}_p-{\mu }_p{I}_p\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\alpha {\beta }_{pv}{S}_v^{*}}}\left({\displaystyle \frac{{\beta }_{pv}\alpha I_p}{N_p}}{S}_v-{\nu }_v{E}_v-{\mu }_v{E}_v\right)+{\displaystyle \frac{1}{{\mu }_v}}\left({\nu }_v{E}_v-{\delta }_v{I}_v-{\mu }_v{I}_v\right)\hfill \end{array}$$

After some algebraic manipulations, we have:

$$\begin{array}{cc}\hfill L^{\prime }\left(t\right)& =-{\displaystyle \frac{\Lambda }{\alpha {\beta }_{vp}{S}_p^{*}}}\left({\displaystyle \frac{S_p}{S_p^{*}}}+{\displaystyle \frac{S_p^{*}}{S_p}}-2\right)-{\displaystyle \frac{\zeta }{\alpha {\beta }_{pv}{S}_v^{*}}}\left({\displaystyle \frac{S_v}{S_v^{*}}}+{\displaystyle \frac{S_v^{*}}{S_v}}-2\right)-\left(I_p-{\displaystyle \frac{I_p}{N_p}}\right)\hfill \\ \hfill & -\left(I_v-{\displaystyle \frac{I_v}{N_v}}\right)-{\displaystyle \frac{{\gamma }_p{I}_p}{{\mu }_p}}-{\displaystyle \frac{{\delta }_p{I}_p}{{\mu }_p}}-{\displaystyle \frac{{\delta }_v{I}_v}{{\mu }_v}}\hfill \end{array}$$

Clearly, $\left(I_p-{\displaystyle \frac{I_p}{N_p}}\right)\le 0$ and $\left(I_v-{\displaystyle \frac{I_v}{N_v}}\right)\le 0$ And since the arithmetic mean is greater than or equal to the arithmetic mean we have:

$$\begin{array}{c}\hfill \left({\displaystyle \frac{S_p}{S_p^{*}}}+{\displaystyle \frac{S_p^{*}}{S_p}}\right)\ge 2\end{array}$$

and

$$\begin{array}{c}\hfill \left({\displaystyle \frac{S_v}{S_v^{*}}}+{\displaystyle \frac{S_v^{*}}{S_v}}\right)\ge 2\end{array}$$

Thus, $L^{\prime }\left(t\right)\le 0$ for all $\left(S_p,E_p,I_p,R_p,S_v,E_v,I_v\right)\in \aleph$. Thus, by the asymptotic stability theorem [27], the positive endemic equilibrium state E₁ is globally asymptotically stable in ℵ. □

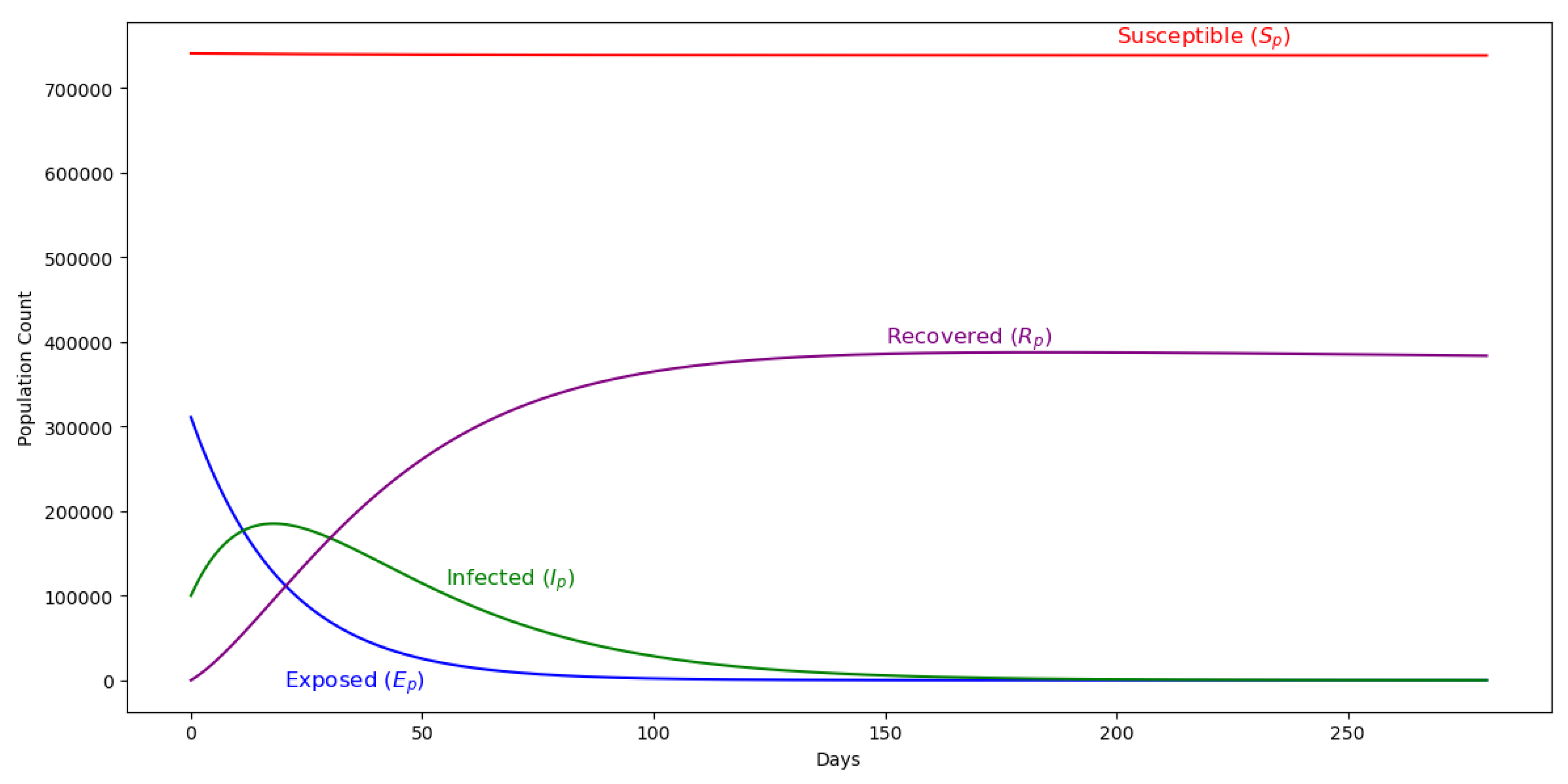
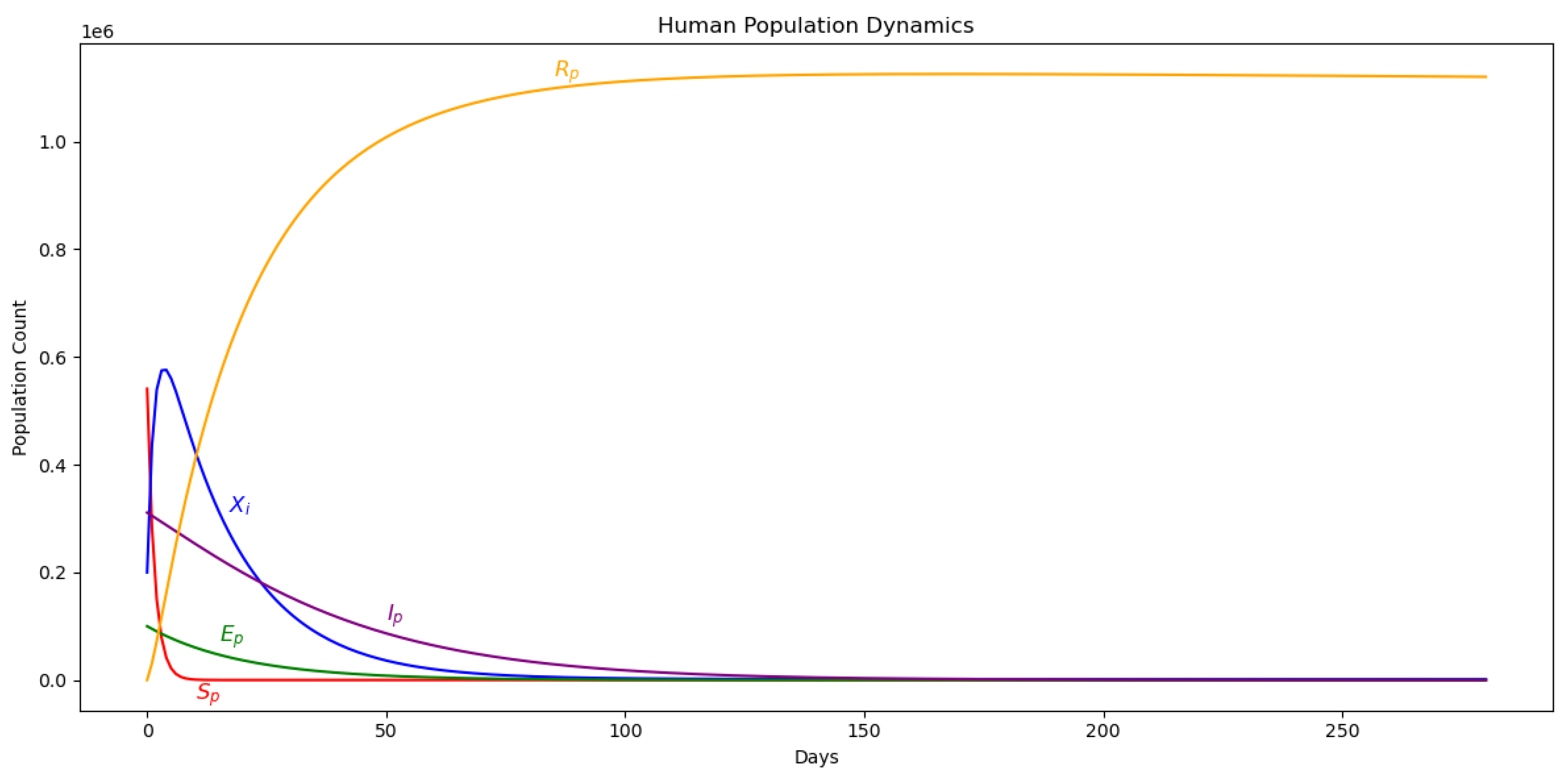
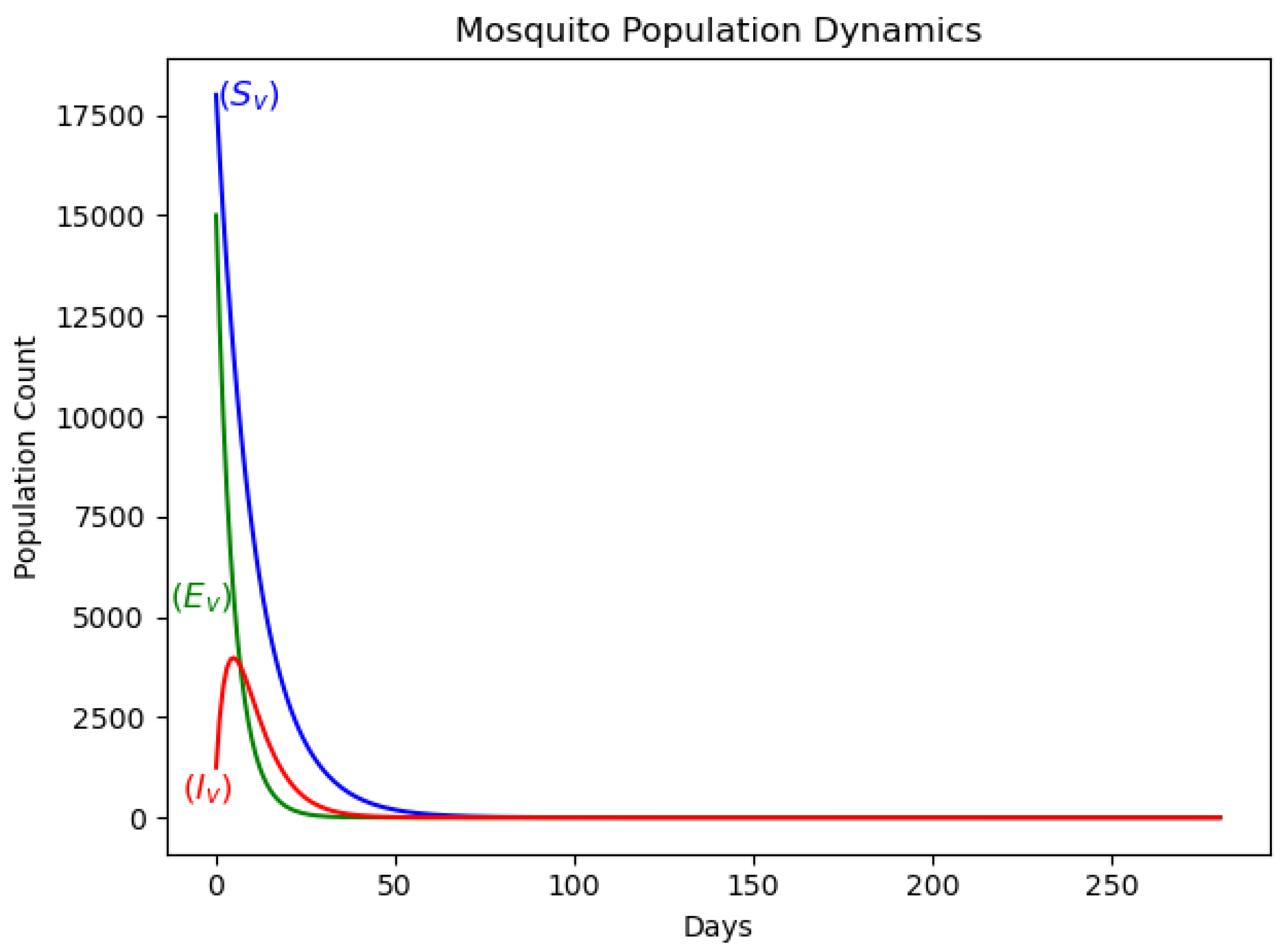
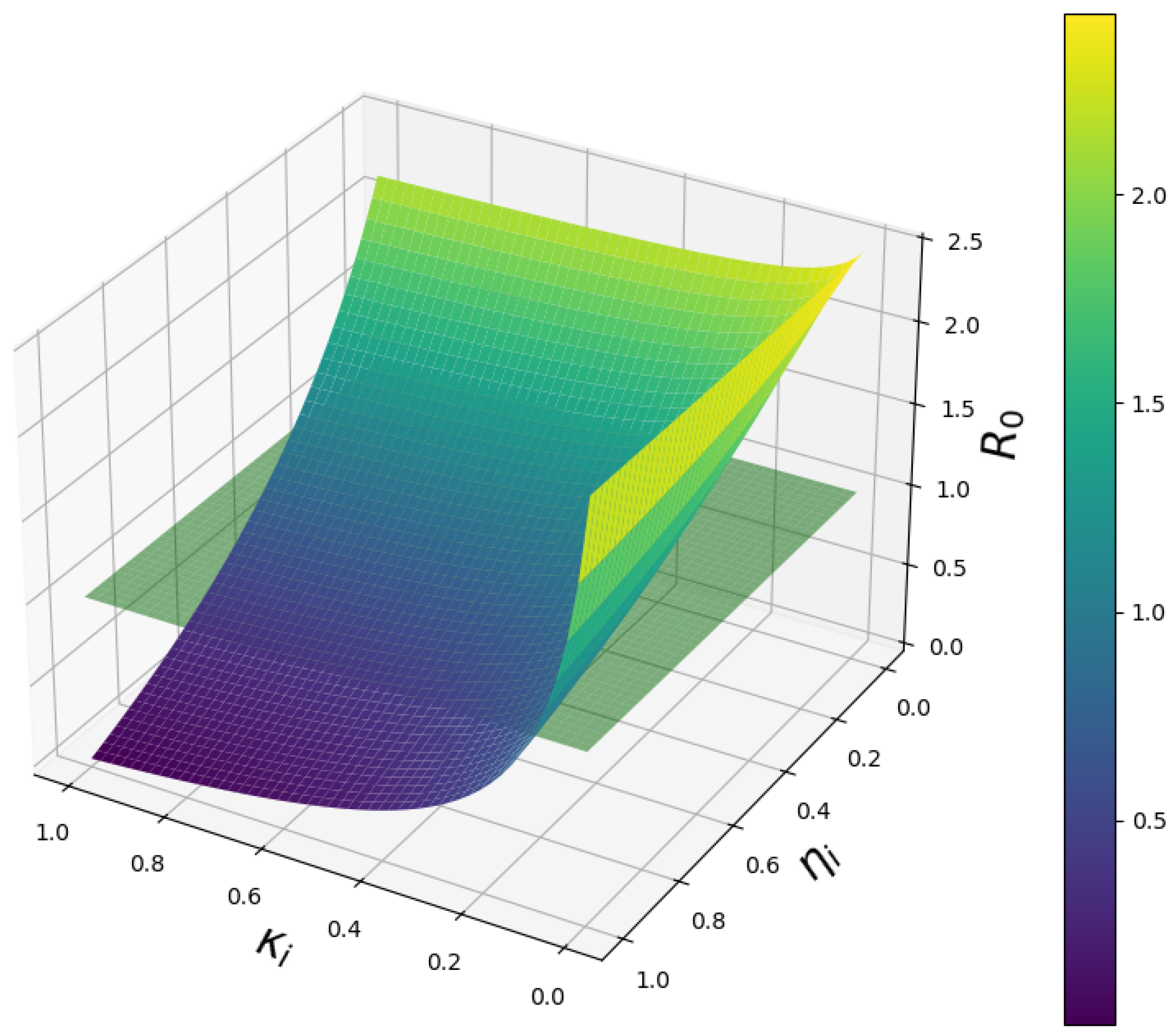
4. Model simulations and Discussions

Numerical simulations of the model system (3) are carried out using python to illustrate some of the analytical results. Parameters values for the model simulation are provided in Table 2, some of these parameters were obtained from literature [5,28,29,30,31] while others were assumed (within realistic range) for the purpose of simulations.

The dynamics of the population of pregnant women without treatment are depicted in Figure 3, while those with treatment are shown in Figure 4. The dynamics of the mosquito population are presented in Figure 5.

The impact of administering IPTp-SP dosage within a population of pregnant women is investigated under the assumption that infection occurs exclusively via bites from infectious mosquitoes. The initial condition introduces 100,000 individuals in the latent compartment. Parameter values are drawn from Table 2. Figure 3 and Figure 5 illustrate the dynamics of the pregnant women and mosquito populations, respectively, in the absence of IPTp-SP treatment (${\kappa }_i=0$). The corresponding basic reproduction number is estimated at 0.91, indicating that malaria transmission would subside over time even without intervention. For comparison, Figure 4 presents the system dynamics under the implementation of IPTp-SP. A comparative analysis reveals that the intervention significantly enhances disease suppression, supporting its role as an effective strategy for reducing malaria burden among pregnant women.

Introducing a treated proportion of pregnant women, defined by ${\kappa }_i\in (0,1)$, clearly changes the system dynamics. Notably, there is a substantial increase in transitions to the recovered class among pregnant women, surpassing all other demographic compartments. This effect is likely driven by the reduced incidence of malaria infections under the IPTp-SP intervention, facilitating a more direct pathway to recovery. Moreover, the susceptible population declines to zero in the presence of treatment—contrasting with the no-intervention scenario, where susceptibility remained persistently high.

A mesh plot was employed to generate a three-dimensional representation of the influence of two critical parameters: the proportion of pregnant women receiving IPTp-SP treatment (${\kappa }_i$) and the treatment success rate (${\eta }_i$). As shown in Figure 6, the color gradient highlights a marked decline in the basic reproduction number, $R_0$, as both ${\kappa }_i$ and ${\eta }_i$ approach 1. This trend emphasizes the combined effect of high treatment coverage and efficacy, with $R_0$ values falling below unity when both parameters attain near-optimal levels—indicating the potential for disease elimination under effective intervention strategies.

5. Discussion and Conclusions

A compartmental model describing malaria transmission dynamics among pregnant women was developed, integrating both the human host and mosquito vector populations. The stability properties of the equilibrium points were analytically assessed, and numerical simulations were carried out to support and illustrate the theoretical results. Control of infection was examined through the implementation of an IPTp-SP intervention strategy. Analytical investigation demonstrated global stability of the disease-free equilibrium, and the basic reproduction number, $R_0$, was shown to fall below unity under the intervention, suggesting the potential for malaria elimination within the pregnant population. While the model provides valuable insights, it remains a simplification of real-world dynamics and offers several avenues for refinement. For example, the current framework treats the intervention as one, yet stratification into discrete treatment levels—such as single-dose, double-dose, and three or more doses—could provide a more accurate understanding. Ultimately, an integrated model encompassing all treatment levels may offer a more robust depiction of the intervention. Furthermore, the assumption of constant treatment efficacy could be relaxed by incorporating the pharmacokinetics and pharmacodynamics (PK/PD) of IPTp-SP to reflect varying drug concentrations and biological response over time. These improvements could be explored through targeted numerical simulations to evaluate the impact of differential dosing and treatment dynamics on malaria control outcomes.