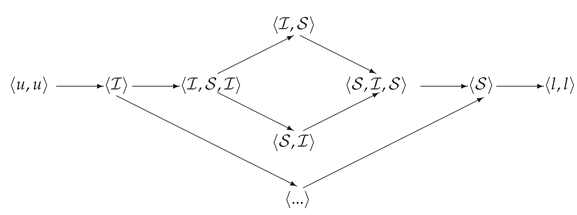
The associativity of the operation ⊙ can be shown in the same manner as in the proof of Lemma 8. So, the set forms a monoid.
In this chapter, we will consider the question of how many convergence operators are there. An application of the lemma below significantly narrows down the search area.
Below, we will indicate all possible convergence operators and present them in the form of multiplications of members of the collection .
Proof. For a given function and , the composition is a function from X to . So, we can consider the cluster functions in the sense of Definition 1, of type . Thus, any cluster operator designates the function
defined by
for all .
In the first step, we will prove that for any convergence operator
, the following equality holds true:
=
.
Indeed, by definition, for any , we have
=.
According to Lemma 13 we have
{...:
:...}:::
: ...}: ::
:...}:
{...:
:...}:::
:...}: ::
:...}:
:
:...}:::
:...}: ::
:...}:
::...}:
:
:...}:::
:...}: ::
:...}:
::...}:
:
:...}:
::
:...}:
::
:...}:
, where in the last two equations, we have used the property noted in Remark 11 and the fact that .
So, and consequently, the value described in is equal to
which proves the equality .
According to Theorem 1, one can use at most the following six non-neutral cluster operators in the formula :
, , , , and .
So, as a consequence of , for any convergence operator
, where ,
there exist at most the following six convergence operators of the type
, namely:
,
,
,
,
and
.
Now, let us observe that any convergence function
is a function from X to . So, any convergence function of the type
is a cluster function in the sense of Definition 1, and consequently, according to Theorem 1, for any convergence operator
, where , we can obtain at most the following convergence operators of the type
:
,
,
,
,
and
.
Now, considering the convergence operators of the type , for a given function and , we define the function by
, for all .
Then, for each point we have
.
But, because of Theorem 1, we know that must be equal to , , , , , or .
So, all possible non-neutral operators of the type are listed in part (i) of the theorem as , , , , and , respectively.
For this reason, we can obtain the following seven types of operators of the form
:
(C1) ,
(C2) ,
(C3) ,
(C4) ,
(C5) ,
(C6) ,
(C7) ,
The alternating application of the operations and on the operator , allows for the determination of all convergence operators of the type (C7), i.e., specified by for an even natural number s, listed in part (ii) of the theorem.
Below, in the same way, using the operators listed in part (i) instead of , we will determine all operators of the type (C1),...,(C6), i.e., specified by , or , for an even natural number s. We will consider all possible cases. Next, by applying Lemma 7, and the equalities (d) stated in the proof of Theorem 1 without reference to them and using Lemma 17, we will show that some of the descriptions designate the same operator. As a result, we will indicate all possible operators of this type mentioned in parts (iii), (iv), and (v) of the theorem.
In the case (C1).
• Type :
−
i.e., ,
−
i.e., ,
− = =
i.e., ,
− =
i.e., .
• Type :
− = =
= i.e., ,
− =
i.e., ,
− = =
i.e., ,
− =
i.e., .
• Type :
− =
= i.e., ,
−
i.e., ,
− =
i.e., ,
−
i.e., .
• Type :
− = =
= i.e., ,
− =
i.e., ,
− =
i.e., ,
−
i.e., .
In the case (C2).
• Type :
− i.e., ,
−
i.e., ,
− = =
i.e., ,
− i.e., ,
− =
i.e., ,
− = =
i.e., .
• Type
− i.e.,
−
i.e., ,
− i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
• Type
− i.e., ,
−
i.e., ,
−
i.e., ,
−
,
i.e., ,
−
i.e., ,
−
i.e., .
• Type
−
i.e., .
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
In the case (C3).
• Type :
− i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
−
i.e., ,
−
i.e.,
−
i.e., ,
−
i.e., .
In the case (C4).
• Type :
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
• Type :
− i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
In the case (C5).
• Type :
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
In the case (C6).
• Type
:
− i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
− i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
Finally, we will prove that the alternating application of the operations and on the operator , leads to the determination of all convergence operators specified by for an odd natural number s, listed in part (vi) of the theorem.
• Type :
− i.e., ,
−
i.e., ,
−
i.e., ,
− i.e., ,
−
i.e., ,
− i.e., .
• Type :
− i.e., ,
−
i.e., ,
− i.e., ,
−
i.e., ,
−
i.e., ,
− i.e., .
• Type :
− i.e., ,
−
,
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
• Type
:
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., ,
−
i.e., .
The proof is finished. □
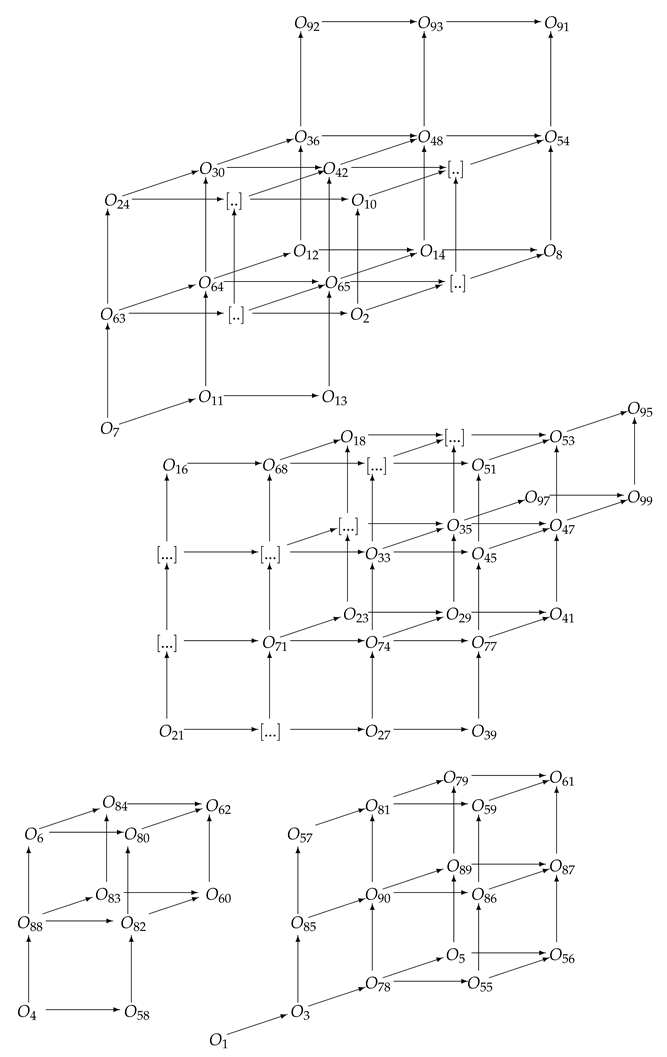
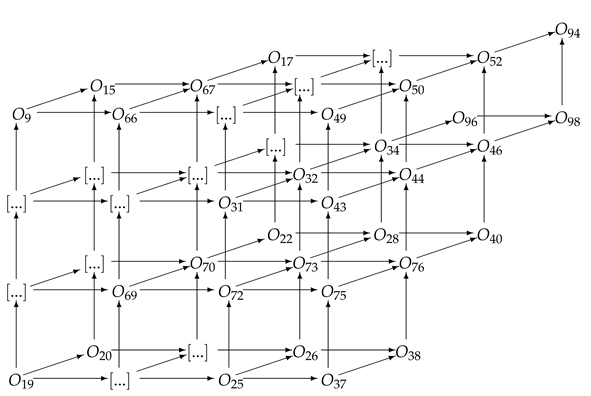
Finally, in the diagrams below, we present the relationships between the studied here operators, where we will use only the numbers used in the denotations of the operators listed in the last theorem.