On Constructing H-Irregularity Labeling with Minimum Label for Certain Balloon Graphs

1. Introduction

Wilson (see [11]) defines a graph $\varrho$ as $\left(V\right(\varrho ),E(\varrho \left)\right)$, where $V\left(\varrho \right)$ represents a finite set of nonempty vertices and $E\left(\varrho \right)$ is a finite set of unordered pairs of distinct elements from $V\left(\varrho \right)$, known as edges.

Wallis in [10] describes a labeling on $\varrho$ as a function whose domain is either $V\left(\varrho \right)$, $E\left(\varrho \right)$, or $V\left(\varrho \right)\cup E\left(\varrho \right)$, and its codomain is a set of positive or nonnegative integers. When the domain is $V\left(\varrho \right)$, it is called vertex labeling; when it is $E\left(\varrho \right)$, it is edge labeling; and when it is $V\left(\varrho \right)\cup E\left(\varrho \right)$, it is total labeling. Various labeling techniques can be employed, one of which is irregular labeling with the domain $V\left(\varrho \right)\cup E\left(\varrho \right)$ mapping to a set of positive integers. This labeling is discussed in this paper.

Gallian in [4] states that there are about 200 types of labeling techniques, evolving in approximately 3000 papers. These techniques include irregular labeling, introduced by Chartrand et al. (see [3]). In irregular labeling, the weight of a vertex $v\in V\left(\varrho \right)$ relative to a total labeling is defined as the sum of the label of v and all labels of edges incident to v. From some types of irregular labeling on a graph $\varrho$, the concepts of total edge irregularity strength ($tes$) and total vertex irregularity strength ($tvs$) arise.

Ashraf et al. (see [2]) introduced the strength of irregularity-H, an extension of $tes$ and $tvs$. A graph $\varrho$ with an H-covering means that for any edge of $\varrho$, there exists a subgraph of $\varrho$ isomorphic to H that includes the edge. Let $\phi :V\left(\varrho \right)\cup E\left(\varrho \right)\to \{1,2,\dots ,p\}$ be any total p-labeling on $\varrho$. For any subgraph K of $\varrho$ isomorphic to H, the H-weight of K with respect to $\phi$, denoted by $w{t}_{\phi }\left(K\right)$, is defined as $w{t}_{\phi }\left(K\right)={\sum }_{v\in V\left(K\right)}\phi \left(v\right)+{\sum }_{e\in E\left(K\right)}\phi \left(e\right)$. A total p-labeling on $\varrho$ is called H-irregular if $w{t}_{\phi }\left(K^{\prime }\right)\ne w{t}_{\phi }\left(K^{\prime \prime }\right)$ for every two distinct subgraphs $K^{\prime }$ and $K^{\prime \prime }$ isomorphic to H. The smallest integer p such that $\varrho$ can be labeled with an H-irregular total p-labeling is called the total H-irregularity strength of $\varrho$, denoted by $tHs(\varrho ,H)$.

Recently, $tHs(\varrho ,H)$ has been extensively studied. Agustin et al. in [1] obtained results on $tHs(\varrho ,H)$ for shackles and amalgamation graphs. Nisviasari et al. in [7] researched $tHs(\varrho ,H)$ for triangular ladder and grid graphs. Hidayatul et al. (see [5]) obtained results on $tHs(\varrho ,H)$ for grid, butterfly, hexagonal, and diamond graphs. Suni et al. in [9] investigated diamond ladder, circular triple ladder, and prism graphs. Wahyujati et al. (see [12]) studied the total H-irregularity strength of edge comb product graphs. Shulhany et al. (see [8]) examined the same parameter for some classes of graphs, while Labane et al. (see [6]) have done so for cycles and diamond graphs. In this work, we introduce a new type of graph that has not been previously studied by other researchers, which involves applying specific graph operations. These results not only provide fresh insights but also extend the applicability of $tHs(\varrho ,H)$ to a broader spectrum of graph types. The use of graph operations in the investigation further highlights the structural complexity and versatility of the studied graphs. This finding will significantly enrich the theory of $tHs(\varrho ,H)$ by deepening our understanding of its behavior in diverse graph classes and paving the way for future studies in this area.

Theorem 1. 

[2]. Let ϱ be a graph admitting an $H-$covering and have w subgraphs isomorphic to H. Then

$$tHs(\varrho ,H)\ge ⌈1+{\displaystyle \frac{w-1}{\left|V\right(H\left)\right|+\left|E\right(H\left)\right|}}⌉.$$

2. Main Results

Our research findings will be presented in this section. First, we begin with the following definition.

Definition 1. 

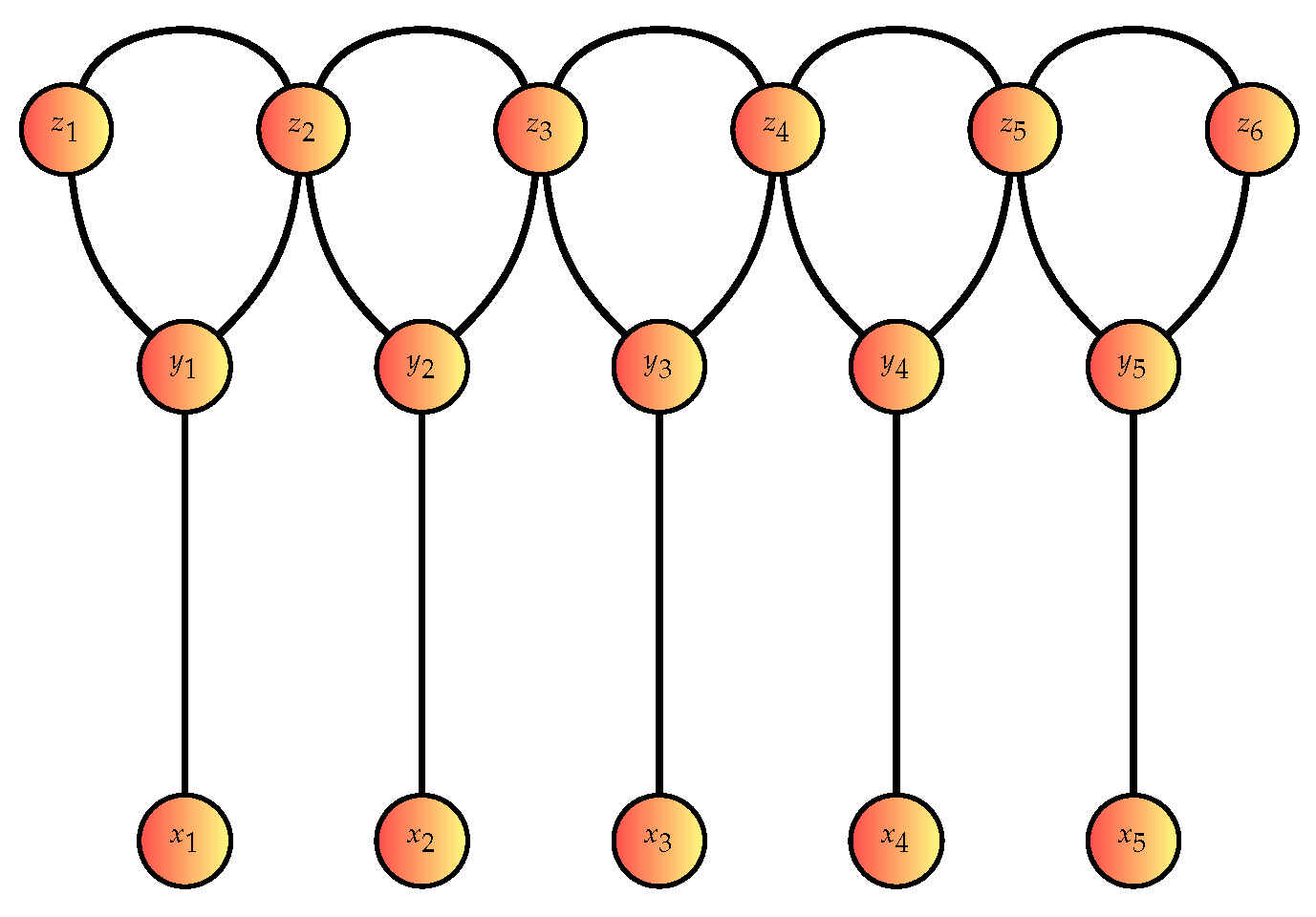
The balloon graph $B{l}_{\eta }$, $\eta \ge 1$, is a graph with

$$V\left(B{l}_{\eta }\right)=\{x_q,y_q:q=1,2,\dots ,\eta \}\cup \{z_q:q=1,2,\dots ,\eta +1\}$$

and

$$E\left(B{l}_{\eta }\right)=\{x_q{y}_q,y_q{z}_q,y_q{z}_{q+1},z_q{z}_{q+1}:q=1,2,\dots ,\eta \}.$$

The following is provided as an example of balloon graph.

Figure 1. Balloon Graph $B{l}_5$

Figure 1. Balloon Graph $B{l}_5$

Theorem 2. 

Given $B{l}_{\eta },\eta \ge 1$ with $B{l}_{\zeta }-$covering. Then, for $1\le \zeta \le \eta$,

$$tHs(B{l}_{\eta },B{l}_{\zeta })=⌈{\displaystyle \frac{6\zeta +\eta +1}{7\zeta +1}}⌉.$$

Proof. The balloon $B{l}_{\eta }$, $\eta \ge 1$ admits $B{l}_{\zeta }-$covering with exactly $\eta -\zeta +1$ balloons $B{l}_{\zeta }$, $1\le \zeta \le \eta$ and $\eta$ is a positive integer. From Theorem 1, it holds

$$tHs(B{l}_{\eta },B{l}_{\zeta })\ge ⌈1+{\displaystyle \frac{(\eta -\zeta +1)-1}{7\zeta +1}}⌉=⌈{\displaystyle \frac{6\zeta +\eta +1}{7\zeta +1}}⌉.$$

Next, put $p=⌈{\displaystyle \frac{6\zeta +\eta +1}{7\zeta +1}}⌉$, $tHs(B{l}_{\eta },B{l}_{\zeta })\le p$ will be proven. On balloon graph $B{l}_{\eta }$ with $B{l}_{\zeta }-$covering, $1\le \zeta \le \eta$, we define

$${\Psi }_{\eta ,\zeta }:V\left(B{l}_{\eta }\right)\cup E\left(B{l}_{\eta }\right)\to \{1,2,\dots ,p\},$$

for $\zeta =1,2,\dots ,\eta$, in this manner:

for $q=1,2,\dots ,\eta$,

$${\Psi }_{\eta ,\zeta }\left(x_q\right)=⌈{\displaystyle \frac{q}{7\zeta +1}}⌉,{\Psi }_{\eta ,\zeta }\left(y_q\right)=⌈{\displaystyle \frac{q+2\zeta }{7\zeta +1}}⌉,{\Psi }_{\eta ,\zeta }\left(x_q{y}_q\right)=⌈{\displaystyle \frac{q+\zeta }{7\zeta +1}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(y_q{z}_q\right)=⌈{\displaystyle \frac{q+3\zeta }{7\zeta +1}}⌉,{\Psi }_{\eta ,\zeta }\left(y_q{z}_{q+1}\right)=⌈{\displaystyle \frac{q+4\zeta }{7\zeta +1}}⌉,{\Psi }_{\eta ,\zeta }\left(z_q{z}_{q+1}\right)=⌈{\displaystyle \frac{q+5\zeta }{7\zeta +1}}⌉.$$

for $q=1,2,\dots ,\eta +1$,

$${\Psi }_{\eta ,\zeta }\left(z_q\right)=⌈{\displaystyle \frac{q+6\zeta }{7\zeta +1}}⌉.$$

The largest label is reached when $q=\eta +1$, that is, ${\Psi }_{\eta ,\zeta }\left(z_q\right)=⌈{\displaystyle \frac{6\zeta +\eta +1}{7\zeta +1}}⌉.$

For every $r=1,2,3,\dots ,\eta -\zeta +1$, the vertex set is

$$V\left(B{l}_{\zeta }\right)=\{x_{r+q},y_{r+q}:q=0,1,2,\dots ,\zeta -1\}\cup \{z_{r+q}:q=0,1,2,\dots ,\zeta \}$$

and edge set is

$$E\left(B{l}_{\zeta }\right)=\{x_{r+q}{y}_{r+q},y_{r+q}{z}_{r+q},y_{r+q}{z}_{r+q+1},z_{r+q}{z}_{r+q+1}:q=0,1,2,\dots ,\zeta -1\}.$$

Furthermore, for every subgraph $B{l}_{\zeta }^r$ in $B{l}_{\zeta }$ the weight of $B{l}_{\zeta }^r,r=1,2,\dots ,\eta -\zeta +1$, with respect to ${\Psi }_{\eta ,\zeta }:V\left(B{l}_{\zeta }\right)\cup E\left(B{l}_{\zeta }\right)\to \{1,2,\dots ,p\}$ is

$$w{t}_{{\Psi }_{\eta ,\zeta }}\left(B{l}_{\zeta }^r\right)=\sum _{v\in V\left(B{l}_{\zeta }^r\right)}{\Psi }_{\eta ,\zeta }\left(v\right)+\sum _{e\in E\left(B{l}_{\zeta }^r\right)}{\Psi }_{\eta ,\zeta }\left(e\right).$$

Then, for $r=1,2,\dots ,\eta -\zeta$,

$$\begin{array}{cc}\hfill w{t}_{{\Psi }_{\eta ,\zeta }}B{l}_{\zeta }^{r+1}-w{t}_{{\Psi }_{\eta ,\zeta }}B{l}_{\zeta }^r=& {\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(z_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{y}_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }{z}_{r+\zeta }\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }{z}_{r+\zeta +1}\right)+{\Psi }_{\eta ,\zeta }\left(z_{r+\zeta }{z}_{r+\zeta +1}\right)-{\Psi }_{\eta ,\zeta }\left(x_r\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(y_r\right)-{\Psi }_{\eta ,\zeta }\left(z_r\right)-{\Psi }_{\eta ,\zeta }\left(x_r{y}_r\right)-{\Psi }_{\eta ,\zeta }\left(y_r{z}_r\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(y_r{z}_{r+1}\right)-{\Psi }_{\eta ,\zeta }\left(z_r{z}_{r+1}\right)\hfill \\ \hfill =& ⌈{\displaystyle \frac{r+\zeta }{7\zeta +1}}⌉+⌈{\displaystyle \frac{r+3\zeta }{7\zeta +1}}⌉+⌈{\displaystyle \frac{r+7\zeta +1}{7\zeta +1}}⌉+⌈{\displaystyle \frac{r+2\zeta }{7\zeta +1}}⌉\hfill \\ \hfill & +⌈{\displaystyle \frac{r+4\zeta }{7\zeta +1}}⌉+⌈{\displaystyle \frac{r+5\zeta }{7\zeta +1}}⌉+⌈{\displaystyle \frac{r+6\zeta }{7\zeta +1}}⌉-⌈{\displaystyle \frac{r}{7\zeta +1}}⌉\hfill \\ \hfill & -⌈{\displaystyle \frac{r+2\zeta }{7\zeta +1}}⌉-⌈{\displaystyle \frac{r+6\zeta }{7\zeta +1}}⌉-⌈{\displaystyle \frac{r+\zeta }{7\zeta +1}}⌉-⌈{\displaystyle \frac{r+3\zeta }{7\zeta +1}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+4\zeta }{7\zeta +1}}⌉-⌈{\displaystyle \frac{r+5\zeta }{7\zeta +1}}⌉\hfill \\ \hfill & =1.\hfill \end{array}$$

For every $r=1,2,\dots ,\eta -\zeta$ we get $w{t}_{{\Psi }_{\eta ,\zeta }}\left(B{l}_{\zeta }^r\right)<w{t}_{{\Psi }_{\eta ,\zeta }}\left(B{l}_{\zeta }^{r+1}\right)$. Hence, $w{t}_{{\Psi }_{\eta ,\zeta }}\left(B{l}_{\zeta }^{r+1}\right)=1+w{t}_{{\Psi }_{\eta ,\zeta }}\left(B{l}_{\zeta }^r\right)$. Moreover, all $DB{L}_{\zeta }-$weights are distinct. Therefore, ${\Psi }_{\eta ,\zeta }$ is total $B{l}_{\zeta }-$irregular labeling of $B{l}_{\eta }$.

Since $tHs(B{l}_{\eta },B{l}_{\zeta })\ge p$ and $tHs(B{l}_{\eta },B{l}_{\zeta })\le p$, we have $tHs(B{l}_{\eta },B{l}_{\zeta })=p$, which can be expressed as

$$tHs(B{l}_{\eta },B{l}_{\zeta })=⌈{\displaystyle \frac{6\zeta +\eta +1}{7\zeta +1}}⌉.$$

□

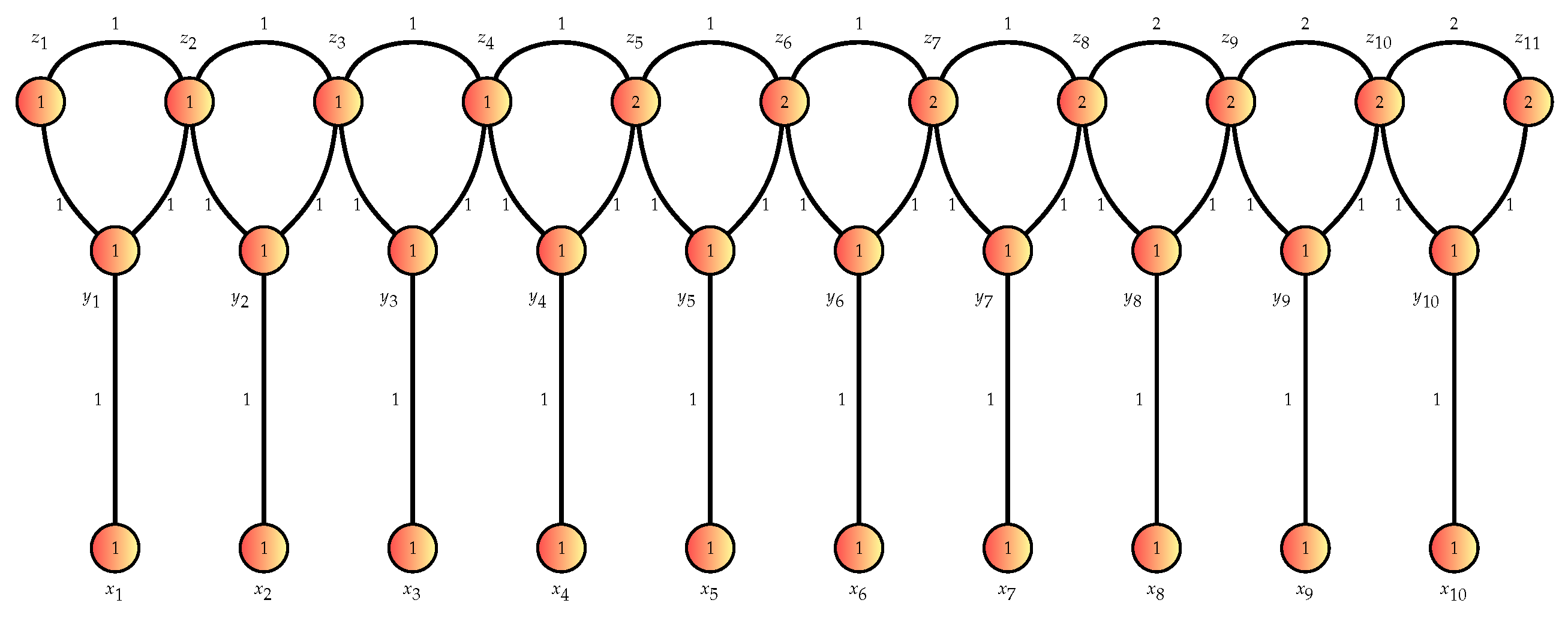
The following on Figure 2 is an example of $B{l}_{10}$ with $B{l}_3-$covering and we have $tHs(B{l}_{10},B{l}_3)=2.$

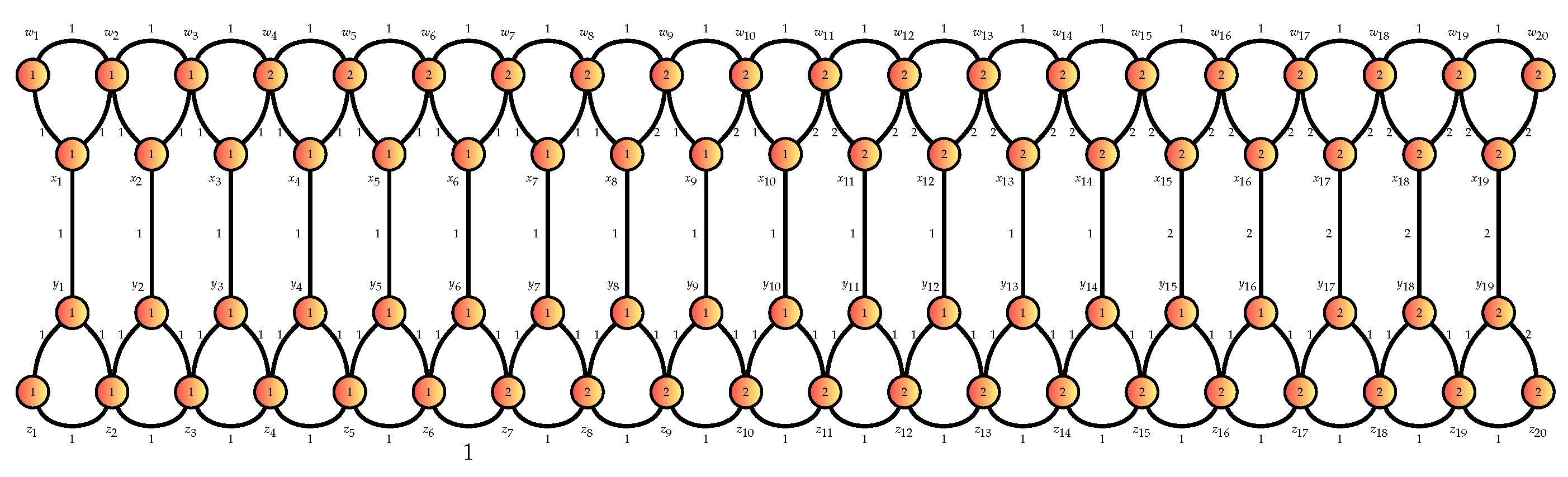
Now, by double balloon graph, we mean the graph defined in Definition 2 as follows.

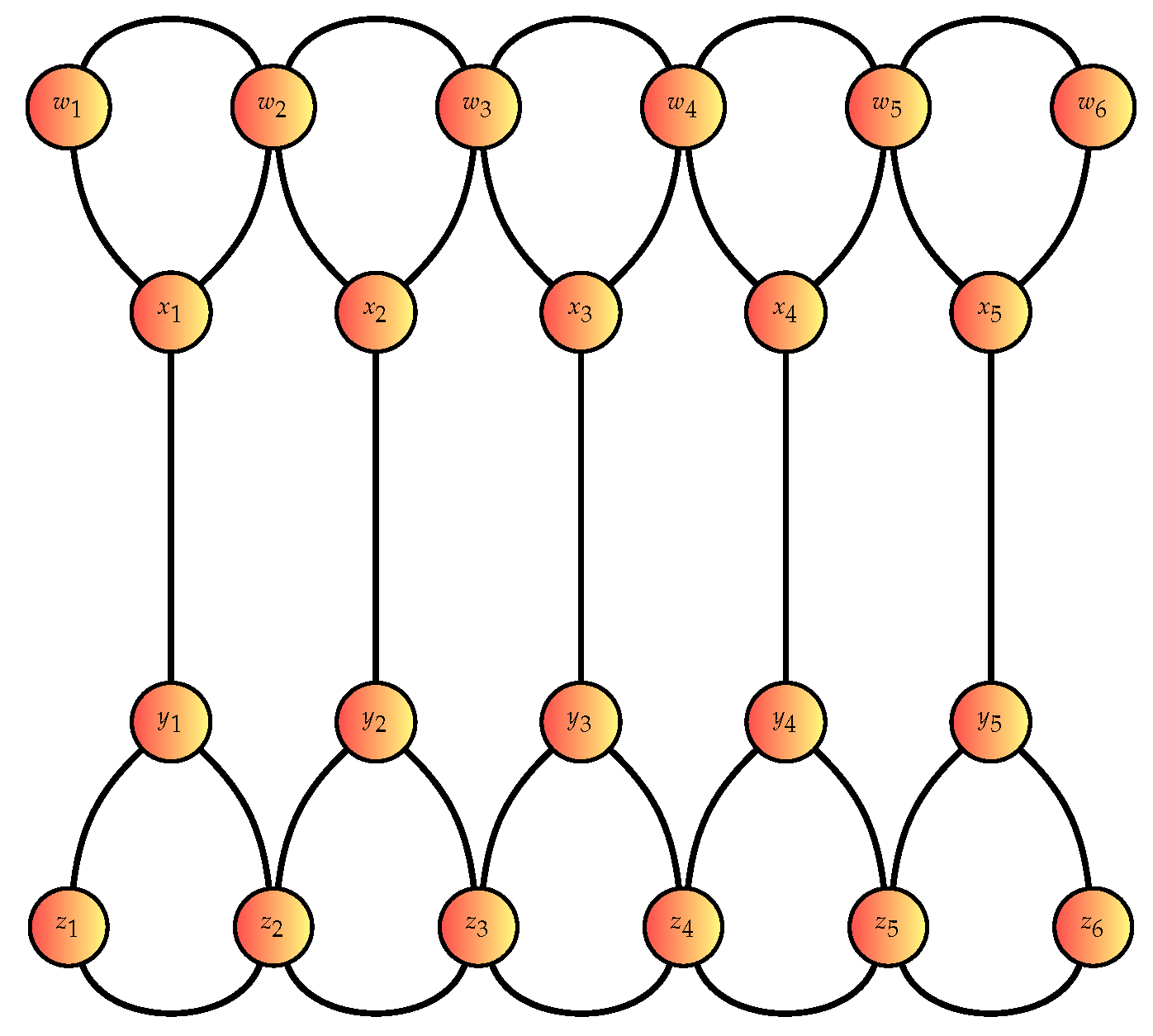
Definition 2. 

A double ballon graph $DB{l}_{\eta }$, $\eta \ge 1$, is a graph with

$$V\left(DB{l}_{\eta }\right)=\{x_q,y_q:q=1,2,\dots ,\eta \}\cup \{w_q,z_q:q=1,2,\dots ,\eta +1\}$$

and

$$E\left(DB{l}_{\eta }\right)=\{w_q{w}_{q+1},x_q{w}_q,x_q{w}_{q+1},x_q{y}_q,y_q{z}_q,y_q{z}_{q+1},z_q{z}_{q+1}:q=1,2,\dots ,\eta \}.$$

The following figure is provided as an example of double balloon graph.

Figure 3. Double Balloon Graph $DB{l}_5$

Figure 3. Double Balloon Graph $DB{l}_5$

Theorem 3. 

Given $DB{l}_{\eta },\eta \ge 1$ with $DB{l}_{\zeta }-$covering. Then, for $1\le \zeta \le \eta$,

$$tHs(DB{l}_{\eta },DB{l}_{\zeta })=⌈{\displaystyle \frac{10\zeta +\eta +2}{11\zeta +2}}⌉.$$

Proof. The double balloon graph, $DB{l}_{\eta }$, $\eta \ge 1$ admits $DB{l}_{\zeta }-$covering with exactly $\eta -\zeta +1$ double balloon $DB{l}_{\zeta }$, $1\le \zeta \le \eta$ and $\eta$ is a positive integer. From Theorem 1, we obtain

$$tHs(DB{l}_{\eta },DB{l}_{\zeta })\ge ⌈1+{\displaystyle \frac{(\eta -\zeta +1)-1}{11\zeta +2}}⌉=⌈{\displaystyle \frac{10\zeta +\eta +2}{11\zeta +2}}⌉.$$

Next, put $p=⌈{\displaystyle \frac{10\zeta +\eta +2}{11\zeta +2}}⌉$, $tHs(DB{l}_{\eta },DB{l}_{\zeta })\le p$ will be proven. On double balloon graph $DB{l}_{\eta }$ with $DB{l}_{\zeta }-$covering, $1\le \zeta \le \eta$, we define

$${\Psi }_{\eta ,\zeta }:V\left(DB{l}_{\eta }\right)\cup E\left(DB{l}_{\eta }\right)\to \{1,2,\dots ,p\},$$

for $\zeta =1,2,\dots ,\eta$, as follows:

for $q=1,2,\dots ,\eta$,

$${\Psi }_{\eta ,\zeta }\left(x_q\right)=⌈{\displaystyle \frac{q+7\zeta }{11\zeta +2}}⌉,{\Psi }_{\eta ,\zeta }\left(y_q\right)=⌈{\displaystyle \frac{q+4\zeta }{11\zeta +2}}⌉,{\Psi }_{\eta ,\zeta }\left(x_q{y}_q\right)=⌈{\displaystyle \frac{q+5\zeta }{11\zeta +2}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(y_q{z}_q\right)=⌈{\displaystyle \frac{q+2\zeta }{11\zeta +2}}⌉,{\Psi }_{\eta ,\zeta }\left(y_q{z}_{q+1}\right)=⌈{\displaystyle \frac{q+3\zeta }{11\zeta +2}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(z_q{z}_{q+1}\right)=⌈{\displaystyle \frac{q}{11\zeta +2}}⌉,{\Psi }_{\eta ,\zeta }\left(w_q{w}_{q+1}\right)=⌈{\displaystyle \frac{q+\zeta }{11\zeta +2}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(x_q{w}_q\right)=⌈{\displaystyle \frac{q+6\zeta }{11\zeta +2}}⌉,{\Psi }_{\eta ,\zeta }\left(x_q{w}_{q+1}\right)=⌈{\displaystyle \frac{q+8\zeta }{11\zeta +2}}⌉.$$

for $q=1,2,\dots ,\eta +1$,

$${\Psi }_{\eta ,\zeta }\left(w_q\right)=⌈{\displaystyle \frac{q+10\zeta +1}{11\zeta +2}}⌉,{\Psi }_{\eta ,\zeta }\left(z_q\right)=⌈{\displaystyle \frac{q+9\zeta }{11\zeta +2}}⌉.$$

The largest label is reached when $q=\eta +1$, that is ${\Psi }_{\eta ,\zeta }\left(w_q\right)=⌈{\displaystyle \frac{10\zeta +\eta +2}{11\zeta +2}}⌉.$

For every $r=1,2,3,\dots ,\eta -\zeta +1$, the vertex set is

$$V\left(DB{l}_{\zeta }\right)=\{x_{r+q},y_{r+q}:q=0,1,2,\dots ,\zeta -1\}\cup \{w_{r+q},z_{r+q}:q=0,1,2,\dots ,\zeta \}$$

and the edge set is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill E\left(DB{l}_{\zeta }\right)=& \{w_{r+q}{w}_{r+q+1},x_{r+q}{w}_{r+q},x_{r+q}{w}_{r+q+1},x_{r+q}{y}_{r+q},y_{r+q}{z}_{r+q},\hfill \\ & y_{r+q}{z}_{r+q+1},z_{r+q}{z}_{r+q+1}:q=0,1,2,\dots ,\zeta -1\}.\hfill \end{array}\end{array}$$

Furthermore, for every subgraph $DB{l}_{\zeta }^r$ in $DB{l}_{\zeta }$, the weight of $DB{l}_{\zeta }^r,r=1,2,\dots ,\eta -\zeta +1$, with respect to ${\Psi }_{\eta ,\zeta }:V\left(DB{l}_{\zeta }\right)\cup E\left(DB{l}_{\zeta }\right)\to \{1,2,\dots ,p\}$ is

$$w{t}_{{\Psi }_{\eta ,\zeta }}\left(DB{l}_{\zeta }^r\right)=\sum _{v\in V\left(DB{l}_{\zeta }^r\right)}{\Psi }_{\eta ,\zeta }\left(v\right)+\sum _{e\in E\left(DB{l}_{\zeta }^r\right)}{\Psi }_{\eta ,\zeta }\left(e\right).$$

Then, for $r=1,2,\dots ,\eta -\zeta$, we have

$$\begin{array}{cc}\hfill w{t}_{{\Psi }_{\eta ,\zeta }}DB{l}_{\zeta }^{r+1}-w{t}_{{\Psi }_{\eta ,\zeta }}DB{l}_{\zeta }^r=& {\Psi }_{\eta ,\zeta }\left(w_{r+\zeta +1}\right)+{\Psi }_{\eta ,\zeta }\left(w_{r+\zeta }{w}_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{w}_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{w}_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(z_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{y}_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }{z}_{r+\zeta }\right)\hfill \\ \hfill & +{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }{z}_{r+\zeta +1}\right)+{\Psi }_{\eta ,\zeta }\left(z_{r+\zeta }{z}_{r+\zeta +1}\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(x_r\right)-{\Psi }_{\eta ,\zeta }\left(y_r\right)-{\Psi }_{\eta ,\zeta }\left(z_r\right)-{\Psi }_{\eta ,\zeta }\left(w_r\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(w_r{w}_{r+1}\right)-{\Psi }_{\eta ,\zeta }\left(x_r{w}_r\right)-{\Psi }_{\eta ,\zeta }\left(x_r{w}_{r+1}\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(x_r{y}_r\right)-{\Psi }_{\eta ,\zeta }\left(y_r{z}_r\right)-{\Psi }_{\eta ,\zeta }\left(y_r{z}_{r+1}\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(z_r{z}_{r+1}\right)\hfill \\ \hfill =& ⌈{\displaystyle \frac{r+11\zeta +2}{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+2\zeta }{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+7\zeta }{11\zeta +2}}⌉\hfill \\ & +⌈{\displaystyle \frac{r+9\zeta }{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+8\zeta }{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+5\zeta }{11\zeta +2}}⌉\hfill \\ & +⌈{\displaystyle \frac{r+10\zeta +1}{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+6\zeta }{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+3\zeta }{11\zeta +2}}⌉\hfill \\ & +⌈{\displaystyle \frac{r+4\zeta }{11\zeta +2}}⌉+⌈{\displaystyle \frac{r+\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+7\zeta }{11\zeta +2}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+4\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+9\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+10\zeta +1}{11\zeta +2}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+6\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+8\zeta }{11\zeta +2}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+5\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+2\zeta }{11\zeta +2}}⌉-⌈{\displaystyle \frac{r+3\zeta }{11\zeta +2}}⌉\hfill \\ & -⌈{\displaystyle \frac{r}{11\zeta +2}}⌉\hfill \\ \hfill & =1.\hfill \end{array}$$

For every $r=1,2,\dots ,\eta -\zeta$ we get $w{t}_{{\Psi }_{\eta ,\zeta }}\left(DB{l}_{\zeta }^r\right)<w{t}_{{\Psi }_{\eta ,\zeta }}\left(DB{l}_{\zeta }^{r+1}\right)$. Hence, $w{t}_{{\Psi }_{\eta ,\zeta }}\left(DB{l}_{\zeta }^{r+1}\right)=1+w{t}_{{\Psi }_{\eta ,\zeta }}\left(DB{l}_{\zeta }^r\right)$. Furthermore, all $DB{L}_{\zeta }-$weights are distinct. Thus, ${\Psi }_{\eta ,\zeta }$ is total $DB{l}_{\zeta }-$irregular labeling of $DB{l}_{\eta }$.

Since $tHs(DB{l}_{\eta },DB{l}_{\zeta })\ge p$ and $tHs(DB{l}_{\eta },DB{l}_{\zeta })\le p$, we have

$$tHs(DB{l}_{\eta },DB{l}_{\zeta })=p,$$

which can be expressed as

$$tHs(DB{l}_{\eta },DB{l}_{\zeta })=⌈{\displaystyle \frac{10\zeta +\eta +2}{11\zeta +2}}⌉.$$

□

Figure 4 is given as an example of $DB{l}_{19}$ with $DB{l}_2-$covering, and with $tHs(DB{l}_{19},DB{l}_2)=2.$

Subsequently, Definition 3 furnishes the definition of a double balloon ladder graph.

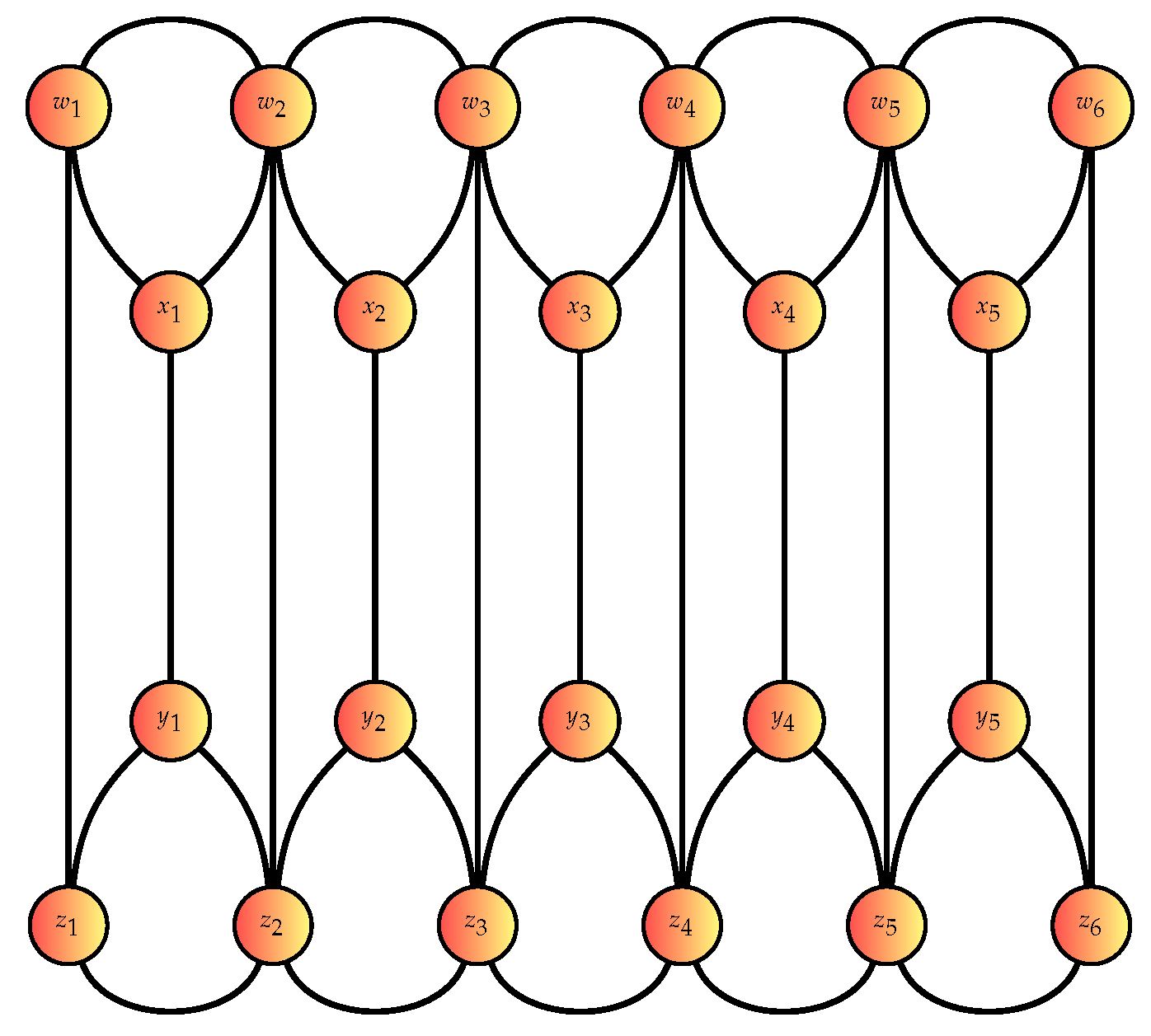
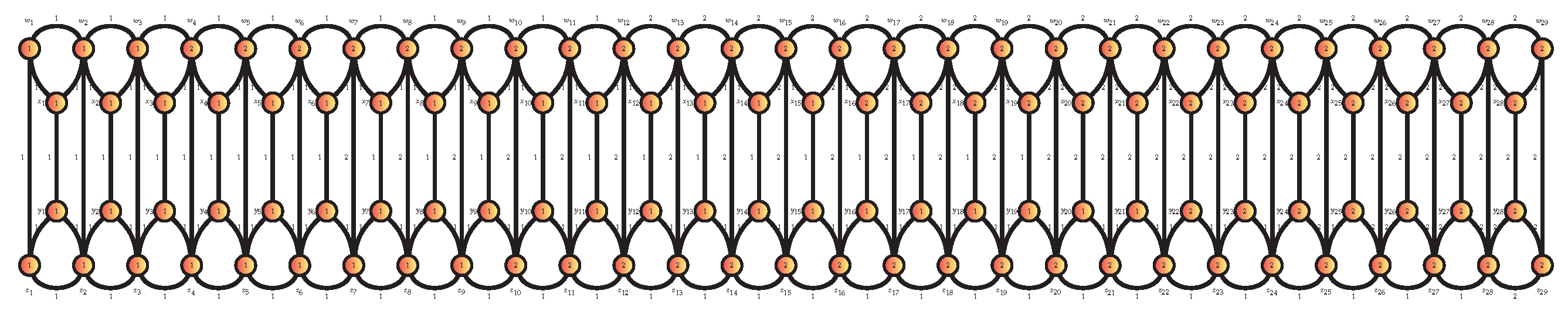
Definition 3. 

A double balloon ladder graph $DBl{L}_{\eta }$, $\eta \ge 1$, is a graph with

$$V\left(DBl{L}_{\eta }\right)=\{x_q,y_q:q=1,2,\dots ,\eta \}\cup \{w_q,z_q:q=1,2,\dots ,\eta +1\}$$

and

$$E\left(DBl{L}_{\eta }\right)=\{w_q{w}_{q+1},x_q{w}_q,x_q{w}_{q+1},x_q{y}_q,y_q{z}_q,y_q{z}_{q+1},z_q{z}_{q+1}:q=1,2,\dots ,\eta \}$$

$$\cup \{w_q{z}_q:q=1,2,\dots ,\eta +1\}.$$

The following is provided as an example of double balloon ladder graph.

Figure 5. Double Balloon Ladder Graph $DBl{L}_5$

Figure 5. Double Balloon Ladder Graph $DBl{L}_5$

Theorem 4. 

Given $DBl{L}_{\eta },\eta \ge 1$ with $DB{l}_{\zeta }-$covering. Then, for $1\le \zeta \le \eta$,

$$tHs(DBl{L}_{\eta },DBl{L}_{\zeta })=⌈{\displaystyle \frac{11\zeta +\eta +3}{12\zeta +3}}⌉.$$

Proof. 

The balloon $DBl{L}_{\eta }$, $\eta \ge 1$ admits $DBl{L}_{\zeta }-$covering with exactly $\eta -\zeta +1$ double balloon ladder $DBl{L}_{\zeta }$, $1\le \zeta \le \eta$ and $\eta$ is a positive integer. By Theorem 1,

$$tHs(DBl{L}_{\eta },DBl{L}_{\zeta })\ge ⌈1+{\displaystyle \frac{(\eta -\zeta +1)-1}{12\zeta +3}}⌉=⌈{\displaystyle \frac{11\zeta +\eta +3}{12\zeta +3}}⌉.$$

Next, put $p=⌈{\displaystyle \frac{11\zeta +\eta +3}{12\zeta +3}}⌉$, $tHs(DBl{L}_{\eta },DBl{L}_{\zeta })\le p$ will be proven. On double balloon ladder $DBl{L}_{\eta }$ with $DBl{L}_{\zeta }-$covering, $1\le \zeta \le \eta$, we define

$${\Psi }_{\eta ,\zeta }:V\left(DBl{L}_{\eta }\right)\cup E\left(DBl{L}_{\eta }\right)\to \{1,2,\dots ,p\},$$

for $\zeta =1,2,\dots ,\eta$, in this way:

for $q=1,2,\dots ,\eta$,

$${\Psi }_{\eta ,\zeta }\left(x_q\right)=⌈{\displaystyle \frac{q+6\zeta }{12\zeta +3}}⌉,{\Psi }_{\eta ,\zeta }\left(y_q\right)=⌈{\displaystyle \frac{q+3\zeta }{12\zeta +3}}⌉,{\Psi }_{\eta ,\zeta }\left(x_q{y}_q\right)=⌈{\displaystyle \frac{q+4\zeta }{12\zeta +3}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(y_q{z}_q\right)=⌈{\displaystyle \frac{q+\zeta }{11\zeta +3}}⌉,{\Psi }_{\eta ,\zeta }\left(y_q{z}_{q+1}\right)=⌈{\displaystyle \frac{q+2\zeta }{12\zeta +3}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(z_q{z}_{q+1}\right)=⌈{\displaystyle \frac{q}{12\zeta +3}}⌉,{\Psi }_{\eta ,\zeta }\left(w_q{w}_{q+1}\right)=⌈{\displaystyle \frac{q}{12\zeta +3}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(x_q{w}_q\right)=⌈{\displaystyle \frac{q+5\zeta }{12\zeta +3}}⌉,{\Psi }_{\eta ,\zeta }\left(x_q{w}_{q+1}\right)=⌈{\displaystyle \frac{q+7\zeta }{12\zeta +3}}⌉.$$

for $q=1,2,\dots ,\eta +1$,

$${\Psi }_{\eta ,\zeta }\left(w_q\right)=⌈{\displaystyle \frac{q+11\zeta +2}{12\zeta +3}}⌉,{\Psi }_{\eta ,\zeta }\left(z_q\right)=⌈{\displaystyle \frac{q+9\zeta }{12\zeta +3}}⌉,$$

$${\Psi }_{\eta ,\zeta }\left(w_q{z}_q\right)=⌈{\displaystyle \frac{q+10\zeta +1}{12\zeta +3}}⌉.$$

The largest label is obtained when $q=\eta +1$, that is ${\Psi }_{\eta ,\zeta }\left(w_q\right)=⌈{\displaystyle \frac{11\zeta +\eta +3}{12\zeta +3}}⌉.$

For every $r=1,2,3,\dots ,\eta -\zeta +1$, the vertex set is

$$V\left(DBl{L}_{\zeta }\right)=\{x_{r+q},y_{r+q}:q=0,1,2,\dots ,\zeta -1\}\cup \{w_{r+q},z_{r+q}:q=0,1,2,\dots ,\zeta \}$$

and the edge set

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill E\left(DBl{L}_{\zeta }\right)=& \{w_{r+q}{w}_{r+q+1},x_{r+q}{w}_{r+q},x_{r+q}{w}_{r+q+1},x_{r+q}{y}_{r+q},y_{r+q}{z}_{r+q},\hfill \\ & y_{r+q}{z}_{r+q+1},z_{r+q}{z}_{r+q+1},w_q{z}_q:q=0,1,2,\dots ,\zeta -1\}.\hfill \end{array}\end{array}$$

Furthermore, for every subgraph $DBl{L}_{\zeta }^r$ in $DB{l}_{\zeta }$ we have weight $DBl{L}_{\zeta }^r,r=1,2,\dots ,\eta -\zeta +1$, with respect to ${\Psi }_{\eta ,\zeta }:V\left(DBl{L}_{\zeta }\right)\cup E\left(DBl{L}_{\zeta }\right)\to \{1,2,\dots ,p\}$ is

$$w{t}_{{\Psi }_{\eta ,\zeta }}\left(DB{l}_{\zeta }^r\right)=\sum _{v\in V\left(DBl{L}_{\zeta }^r\right)}{\Psi }_{\eta ,\zeta }\left(v\right)+\sum _{e\in E\left(DBl{L}_{\zeta }^r\right)}{\Psi }_{\eta ,\zeta }\left(e\right).$$

Then, for $r=1,2,\dots ,\eta -\zeta$, we have

$$\begin{array}{cc}\hfill w{t}_{{\Psi }_{\eta ,\zeta }}DB{l}_{\zeta }^{r+1}-w{t}_{{\Psi }_{\eta ,\zeta }}DB{l}_{\zeta }^r=& {\Psi }_{\eta ,\zeta }\left(w_{r+\zeta +1}\right)+{\Psi }_{\eta ,\zeta }\left(w_{r+\zeta }{w}_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{w}_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{w}_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(z_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(x_{r+\zeta }{y}_{r+\zeta }\right)+{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }{z}_{r+\zeta }\right)\hfill \\ \hfill & +{\Psi }_{\eta ,\zeta }\left(y_{r+\zeta }{z}_{r+\zeta +1}\right)+{\Psi }_{\eta ,\zeta }\left(z_{r+\zeta }{z}_{r+\zeta +1}\right)\hfill \\ & +{\Psi }_{\eta ,\zeta }\left(w_{r+\zeta +1}{z}_{r+\zeta +1}\right)-{\Psi }_{\eta ,\zeta }\left(x_r\right)-{\Psi }_{\eta ,\zeta }\left(y_r\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(z_r\right)-{\Psi }_{\eta ,\zeta }\left(w_r\right)-{\Psi }_{\eta ,\zeta }\left(w_r{w}_{r+1}\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(x_r{w}_r\right)-{\Psi }_{\eta ,\zeta }\left(x_r{w}_{r+1}\right)-{\Psi }_{\eta ,\zeta }\left(x_r{y}_r\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(y_r{z}_r\right)-{\Psi }_{\eta ,\zeta }\left(y_r{z}_{r+1}\right)-{\Psi }_{\eta ,\zeta }\left(z_r{z}_{r+1}\right)\hfill \\ & -{\Psi }_{\eta ,\zeta }\left(w_r{z}_r\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill =& ⌈{\displaystyle \frac{r+12\zeta +3}{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+9\zeta }{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+6\zeta }{12\zeta +3}}⌉\hfill \\ & +⌈{\displaystyle \frac{r+8\zeta }{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+7\zeta }{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+4\zeta }{12\zeta +3}}⌉\hfill \\ & +⌈{\displaystyle \frac{r+10\zeta +1}{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+5\zeta }{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+2\zeta }{12\zeta +3}}⌉\hfill \\ & +⌈{\displaystyle \frac{r+3\zeta }{12\zeta +3}}⌉+⌈{\displaystyle \frac{r+\zeta }{13\zeta +2}}⌉+⌈{\displaystyle \frac{r+11\zeta +2}{12\zeta +3}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+6\zeta }{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+3\zeta }{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+9\zeta }{12\zeta +3}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+11\zeta +2}{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+8\zeta }{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+5\zeta }{12\zeta +3}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+7\zeta }{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+4\zeta }{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+\zeta }{12\zeta +3}}⌉\hfill \\ & -⌈{\displaystyle \frac{r+2\zeta }{12\zeta +3}}⌉-⌈{\displaystyle \frac{r}{12\zeta +3}}⌉-⌈{\displaystyle \frac{r+10\zeta +1}{12\zeta +3}}⌉\hfill \\ \hfill =& 1.\hfill \end{array}$$

For every $r=1,2,\dots ,\eta -\zeta$ we get $w{t}_{{\Psi }_{\eta ,\zeta }}\left(DBl{L}_{\zeta }^r\right)<w{t}_{{\Psi }_{\eta ,\zeta }}\left(DBl{L}_{\zeta }^{r+1}\right)$. Hence, $w{t}_{{\Psi }_{\eta ,\zeta }}\left(DBl{L}_{\zeta }^{r+1}\right)=1+w{t}_{{\Psi }_{\eta ,\zeta }}\left(DBl{L}_{\zeta }^r\right)$. Furthermore, all $DB{L}_{\zeta }-$weights are distinct. Thus, ${\Psi }_{\eta ,\zeta }$ is total $DBl{L}_{\zeta }-$irregular labeling of $DBl{L}_{\eta }$.

Since $tHs(DBl{L}_{\eta },DBl{L}_{\zeta })\ge p$ and $tHs(DBl{L}_{\eta },DBl{L}_{\zeta })\le p$ we have

$$tHs(DBl{L}_{\eta },DBl{L}_{\zeta })=p,$$

which can be expressed as

$$tHs(DBl{L}_{\eta },DBl{L}_{\zeta })=⌈{\displaystyle \frac{11\zeta +\eta +3}{12\zeta +3}}⌉.$$

□

The following on Figure 6 is an example of $DBl{L}_{28}$ with $DBl{L}_2-$covering, and we get $tHs(DBl{L}_{28},DBl{L}_2)=2.$

3. Concluding Remarks

This research focuses on the total $H-$irregularity strength of balloon graph $B{l}_{\eta }$ with $B{l}_{\zeta }-$covering, double balloon graph $DB{l}_{\eta }$, and double balloon ladder graph $DBl{L}_{\eta }$ with $DB{l}_{\zeta }-$covering. We found that the lower bound given in Theorem 1 is sharp for all these graphs.