Translution: Unifying Transformer and Convolution for Adaptive and Relative Modeling

1. Introduction

When employing deep neural networks to model a specific type of data (e.g., images or text), it can be decoupled into two steps: 1) identifying relevant data elements (e.g., patches in images or words in text) or regions, and 2) encoding these elements into effective representations.

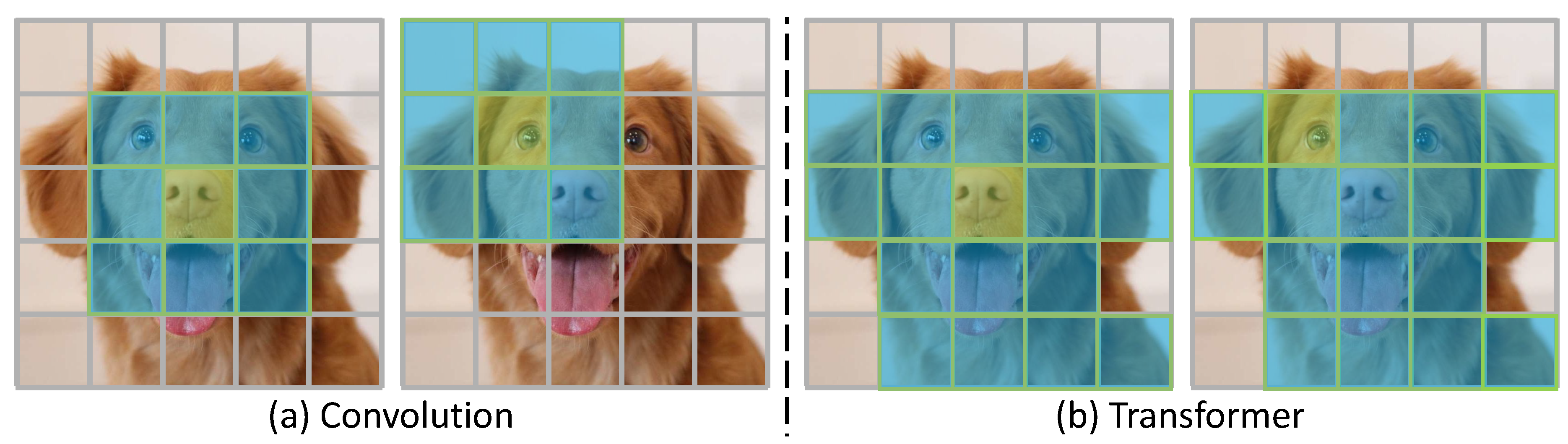
In Convolution [1,2,3,4,5], as shown in Figure 1a, the relevant region identification step is handled by convolutional filters with a fixed local receptive field (kernel). This fixed kernel defines a neighborhood of elements considered relevant. For visual data like images, such local focus is often effective because spatially adjacent pixels or patches tend to be related (e.g., forming parts of the same object). However, the rigid nature of a fixed-size kernel makes Convolution inevitably covers some irrelevant pixels or regions — especially near object boundaries or in background areas that fall inside the window. 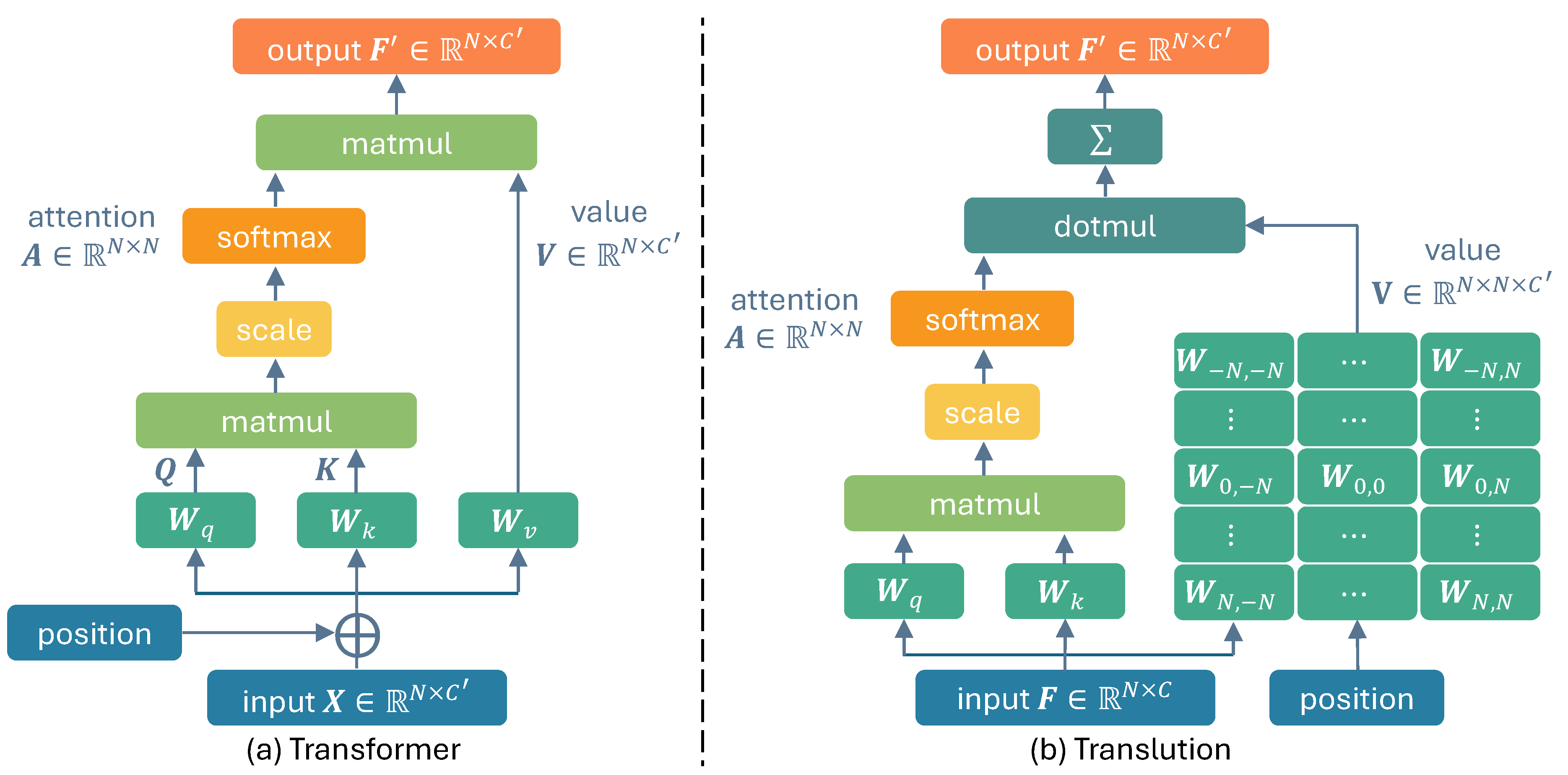In contrast, as shown in Figure 1b, Transformer [6,7,8,9,10] uses a self-attention mechanism to adaptively identify relevant regions. Instead of being limited to a predetermined locality, self-attention allows the model to dynamically attend to relevant regions. This means a Transformer can focus on important features regardless of their distance, potentially ignoring irrelevant context more flexibly than a Convolution’s fixed receptive field, which makes it highly suitable for processing long texts.

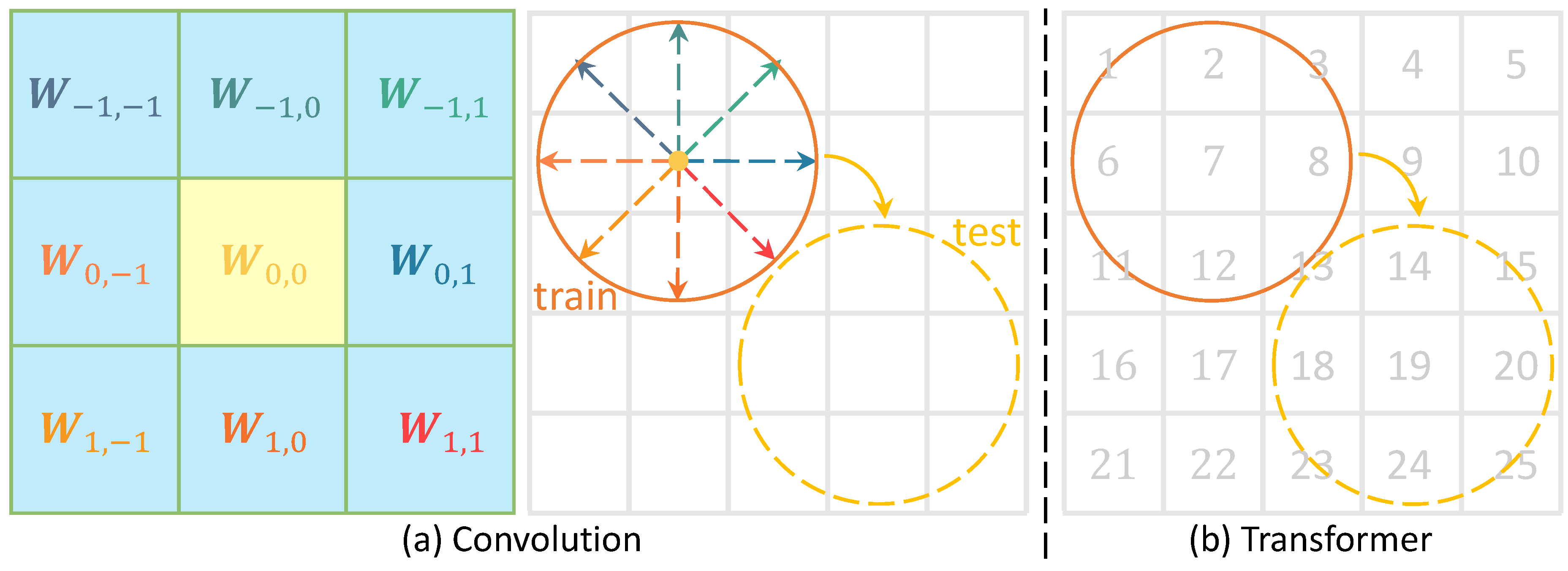
When it comes to encoding the structure from these relevant regions, Convolution and Transformer employ different strategies. As shown in Figure 2a, a convolutional kernel learns distinct weights for each relative position within its receptive field. In other words, the filter has separate parameters for each offset (direction and distance) from the center. This design enables Convolution to encode local structure relatively — capturing orientation and distance relationships. On the other hand, as shown in Figure 2b, Transformer uses a shared set of weights to process inputs from all positions. The same value-projection weights are applied universally across positions. Consequently, the Value of Transformer does not encode whether one patch is to the left or right of another. To introduce positional information, Transformer incorporates absolute positional embeddings (either fixed sinusoidal or learned positional vectors) into the input features at the outset. Although these embeddings enable Transformer to infer order or spatial relationships, they introduce noise into each token’s representation. The absolute position information becomes part of the input features. Consequently, when the same object moves to a different location, Transformer may struggle to recognize it. Note that as the dataset scale increases, Transformer will become effective because the data might include scenarios where the object appears in different locations.

In summary, Convolution encodes structure through fixed local filters with position-specific weights, whereas Transformer relies on adaptive global attention and requires absolute positional encoding to capture order or spatial patterns. In this article, we introduce Translution, a new neural network module that combines the adaptive identification capabilities of the Transformer with the relative encoding advantages of Convolution. Translution retains the self-attention mechanism of Transformer but utilizes separate parameters to compute Value. This design enables Translution to effectively encode relative structures. However, this integration leads to a significant increase in the number of parameters and memory consumption. Specifically, for an input with N tokens, Transformer requires only 1 set of shared parameters to calculate Value, whereas Translution consumes ${(2N-1)}^2$ sets of parameters. This exceeds our available computational resources for high-resolution datasets. Consequently, we restricted our evaluation of Translution to low-resolution datasets, specifically MNIST and CIFAR. Experiments demonstrate that Translution outperforms Transformer in terms of accuracy. However, these experiments are not comprehensive. We encourage the community to further evaluate Translution on larger-scale datasets in a variety of scenarios and to develop optimized versions for wider applicability.

2. Related Work

Transformer [6] eschews recurrence and kernel size, relying on self-attention for relevant regin identification. Because it has no built-in notion of order, Transformer layers add explicit positional encodings to token embeddings so the model can use sequence order. Transformer employs sinusoidal (fixed) position vectors and note that learned embeddings produce nearly identical performance, with the fixed sinusoidal encodings chosen because they may allow better extrapolation to longer sequences. Subsequent work has explored “relative attention” [11,12,13,14,15,16,17]. For example, Shaw et al.enhanced Transformer by adding learnable relative positional vectors into the key and value computation for language modeling [11]. Bello et al.expanded this approach to two dimensions for image processing [18]. HaloNet employs learnable relative positional vectors to modify the query, making it aware of relative positions [19]. CoAtNet [17] adds a learnable scalar for each direction and distance into attention. ConViT also incorporates relative position embedding into the attention mechanism, employing a more complex strategy [20]. Unlike these existing relative attention methods, Translution divides the modeling process into two distinct phases: relevant region identification and relative structure encoding. In the first phase, Translution utilizes attention to only identify related regions. In the second phase, it employs a convolution-style method that uses separate weights (matrices) for each relative position within its receptive field to encode the relative structure.

Convolutional neural networks (CNNs) [1,2] have been the backbone of vision and sequence models for years. By using small, shared kernels and pooling, CNNs efficiently capture local spatial or temporal patterns with translation-invariant filters. Recent architectural developments increasingly seek to integrate self-attention with convolution. A prevalent strategy, particularly in vision applications, involves combining convolutional modules and Transformer-like blocks. For instance, BoTNet substitutes the spatial convolutions with global self-attention in the final three bottleneck blocks of ResNet [18], while CeiT combines convolutions for extracting low-level features with Transformers to manage long-range dependencies [21]. In contrast to these approaches, Translution functions at the module or layer level, blending the the advantages of Transformer and Convolution into a fundamental and unified operation.

3. Proposed Method

3.1. Convolution

Suppose ${\mathit{F}}_{x,y}\in {\mathbb{R}}^{1\times C}$ represents the feature or representation at location $(x,y)$ in an image with dimensions $H\times W$, where C is the number of feature channels, H is the height, and W is the width. Convolution is designed to capture the local structure centered at $(x,y)$ with a fixed kernel size $h\times w$,

$${\mathit{F}}_{x,y}^{\prime }=\sum _{{\delta }_x=-\lfloor h/2\rfloor }^{\lfloor h/2\rfloor }\sum _{{\delta }_y=-\lfloor w/2\rfloor }^{\lfloor w/2\rfloor }{\mathit{F}}_{x+{\delta }_x,y+{\delta }_y}·{\mathit{W}}_{{\delta }_x,{\delta }_y},$$

(1)

where ${\mathit{W}}_{{\delta }_x,{\delta }_y}\in {\mathbb{R}}^{C\times C^{\prime }}$ represents the learnable weights for displacement $({\delta }_x,{\delta }_y)$, $C^{\prime }$ represents the output feature dimension, and · is matrix multiplication.

By assigning a set of weights for each offset within the receptive field, Convolution is able to discern direction and distance, and capture the local structure relatively. This means that when the absolute location of an object changes, it can still capture the same structure. However, Convolution employs a rigid method to identify relevant regions, using a fixed-size window, making it inevitably include irrelevant pixels or regions — particularly near object boundaries or in background areas within the window.

3.2. Transformer

Suppose ${\mathit{X}}_i\in {\mathbb{R}}^{1\times C}$ represents the feature or representation of the i-th patch at location $(x_i,y_i)$. Transformer first incorporates the embedding of absolute position into the input ${\mathit{X}}_i$, as follows,

$${\mathit{F}}_i={\mathit{X}}_i+\mathrm{Embed}\left(i\right),$$

(2)

and then performs two separate linear projections on the feature map to generate queries $\mathit{Q}\in {\mathbb{R}}^{N\times C^{″}}$ and keys $\mathit{K}\in {\mathbb{R}}^{N\times C^{″}}$, where $C^{″}$ is the dimension for queries or keys. Subsequently, scaled dot-product attention $\mathit{A}\in {\mathbb{R}}^{N\times N}$ (where $N=H\times W$) is computed for each query, and a softmax function is applied to normalize the attention weights for a query across all tokens,

$$\mathit{Q}=\mathit{F}·{\mathit{W}}_q,\mathit{K}=\mathit{F}·{\mathit{W}}_k,\mathit{A}={\displaystyle \frac{\mathit{Q}·{\mathit{K}}^T}{\sqrt{C^{″}}}},{\alpha }_{i,j}={\displaystyle \frac{e^{A_{i,j}}}{{\sum }_{n=1}^N{e}^{A_{i,n}}}},$$

(3)

where ${\mathit{W}}_q,{\mathit{W}}_k\in {\mathbb{R}}^{C\times C^{″}}$. Next, Transformer conducts another feature encoding on the input feature map to generate values $\mathit{V}\in {\mathbb{R}}^{N\times C^{\prime }}$, where $C^{\prime }$ is the value dimension. Finally, the output is computed as a weighted sum of the values,

$$\mathit{V}=\mathit{F}·{\mathit{W}}_v,{\mathit{F}}_i^{\prime }=\sum _{j=1}^N{\alpha }_{i,j}\times {\mathit{V}}_j,$$

(4)

where ${\mathit{W}}_v\in {\mathbb{R}}^{C\times C^{\prime }}$ and $\mathit{F}\in {\mathbb{R}}^{N\times C^{\prime }}$. With self-attention, Transformer can adaptively search for related regions, providing greater flexibility than methods that use local fixed-size windows. However, unlike Convolution, which learns a feature encoding for every direction and distance, Transformer does not encode the structure in a relative manner.

3.3. Translution

Translution is designed to integrate the adaptive relative region identification capabilities of Transformer with the relative encoding strengths of Convolution. Specifically, Translution maintains the self-attention mechanism of Transformer but employs distinct parameters to compute Value,

$$\begin{array}{cc}\hfill & \mathrm{self}-\mathrm{attention}:\mathit{Q}=\mathit{F}·{\mathit{W}}_q,\mathit{K}=\mathit{F}·{\mathit{W}}_k,\mathit{A}={\displaystyle \frac{\mathit{Q}·{\mathit{K}}^T}{\sqrt{C^{\prime }}}},{\alpha }_{i,j}={\displaystyle \frac{e^{A_{i,j}}}{{\sum }_{n=1}^N{e}^{A_{i,n}}}},\hfill \\ \hfill & \mathrm{relative}\mathrm{encoding}:\begin{array}{c}\hfill {\mathit{V}}_{i,j}={\mathit{F}}_j·{\mathit{W}}_{{\delta }_x,{\delta }_y},\end{array}\mathrm{where}{\delta }_x=x_i-x_j,{\delta }_y=y_i-y_j,\hfill \\ \hfill & \mathrm{weighted}\mathrm{sum}:{\mathit{F}}_i^{\prime }=\sum _{j=1}^N{\alpha }_{i,j}\times {\mathit{V}}_{i,j},\hfill \end{array}$$

(5)

where ${\mathit{W}}_{{\delta }_x,{\delta }_y}\in {\mathbb{R}}^{C\times C^{\prime }}$ denotes the learnable weights for displacement $({\delta }_x,{\delta }_y)$.

Figure 3. Comparison of Transformer and Translution in computing Value. 1) Transformer uses a shared set of weights, i.e., ${\mathit{W}}_v$, across all patches for computing Value. 2) Translution employs separate parameters for each offset (direction and distance), i.e., $\{{\mathit{W}}_{-N,-N},\dots ,{\mathit{W}}_{0,0},\dots ,{\mathit{W}}_{N,N}\}$, to encode relative structures. Suppose there are N tokens, Translution consumes ${(2N-1)}^2$ more parameters than Transformer. This may be one of the major issues with Translution. However, with the upgrading of computational resources and the increase in GPU memory, this will not be a problem in the near future.

Figure 3. Comparison of Transformer and Translution in computing Value. 1) Transformer uses a shared set of weights, i.e., ${\mathit{W}}_v$, across all patches for computing Value. 2) Translution employs separate parameters for each offset (direction and distance), i.e., $\{{\mathit{W}}_{-N,-N},\dots ,{\mathit{W}}_{0,0},\dots ,{\mathit{W}}_{N,N}\}$, to encode relative structures. Suppose there are N tokens, Translution consumes ${(2N-1)}^2$ more parameters than Transformer. This may be one of the major issues with Translution. However, with the upgrading of computational resources and the increase in GPU memory, this will not be a problem in the near future.

4. Discussion

4.1. Translution Unifies Transformer and Convolution

The fixed receptive field in Convolution can be viewed as a form of attention, where the weight is set to 1 within the receptive field and 0 elsewhere. The weights ${\mathit{W}}_v$ for computing Value in Transformer act as a shared linear projection across all directions and distances. Consequently, Translution represents an operation that integrates the functionalities of Convolution and Transformer, as follows,

$$\begin{array}{ccc}\mathrm{Convolution}:\hfill & {\mathit{F}}_i^{\prime }=\sum _{j=1}^N{\alpha }_{i,j}\times {\mathit{F}}_j·{\mathit{W}}_{{\delta }_x,{\delta }_y},\hfill & \mathrm{where}{\alpha }_{i,j}=\left\{\begin{array}{cc}1,\hfill & ({\delta }_i,{\delta }_j)\in \mathrm{kernel},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ \mathrm{Transformer}:\hfill & {\mathit{F}}_i^{\prime }=\sum _{j=1}^N{\alpha }_{i,j}\times {\mathit{F}}_j·{\mathit{W}}_v,\hfill & \mathrm{where}{\alpha }_{i,j}={\displaystyle \frac{e^{A_{i,j}}}{{\sum }_{n=1}^N{e}^{A_{i,n}}}}.\hfill \\ \mathrm{Translution}:\hfill & {\mathit{F}}_i^{\prime }=\sum _{j=1}^N{\alpha }_{i,j}\times {\mathit{F}}_j·{\mathit{W}}_{{\delta }_x,{\delta }_y},\hfill & \mathrm{where}{\alpha }_{i,j}={\displaystyle \frac{e^{A_{i,j}}}{{\sum }_{n=1}^N{e}^{A_{i,n}}}}.\hfill \end{array}$$

In other words, Convolution and Transformer can be viewed as specific instances of Translution, where Convolution simplifies the attention mechanism and Transformer omits the encoding of direction and distance.

4.2. Why Not Integrate Relative Encoding into Self-Attention Rather than into the Computation of Value?

The attention weight ${\alpha }_{i,j}$ between two tokens is a scalar ranging from 0 to 1. As a scalar, it cannot convey extensive information such as displacement. However, being a scalar within the (0,1) range, it effectively reflects relationships. If two tokens are highly related, the attention weight tends towards 1. Conversely, if two tokens are unrelated, the attention weight approaches 0. In contrast, the computation of Value involves vectors, which can encapsulate sufficient information to represent direction and distance. This aligns with the motivation to decouple modeling into identification and encoding of relevant regions. Here, self-attention is responsible for identifying relevant regions, while the computation of Value handles the encoding of these regions.

4.3. General Translution: A More General Version of Translution

The calculation of the Value in Translution, i.e., Eq. (5), assumes that positions in the data (e.g., images or text) are discrete. In this setting, it is feasible to assign a different set of weights for each direction and distance. However, if the positions are continuous variables, e.g., in point clouds, it becomes impractical to assign individual weights for each direction and distance, as there are infinitely many possible variations in continuous space. In this case, it may be necessary to design new functions for the relative encoding of relevant regions.

Suppose ${\mathit{p}}_i$ denotes the position of the i-th token. For language, ${\mathit{p}}_i$ can represent the index of the i-th word in the text. For images, ${\mathit{p}}_i$ corresponds to the row and column indices of the i-th patch. For point clouds, ${\mathit{p}}_i$ refers to the 3D coordinates of the i-th point. A more general version of Translution can be formulated as follows,

$$\mathrm{General}\mathrm{Translution}:{\mathit{F}}_i^{\prime }=\sum _{j=1}^L{\alpha }_{i,j}\times f({\mathit{p}}_i-{\mathit{p}}_j,{\mathit{F}}_j),$$

(6)

where ${\alpha }_{i,j}\in [0,1]$ denotes the attention weight measuring the relevance of the j-th token to the i-th token, and $f:{\mathbb{R}}^{d+C}\to {\mathbb{R}}^{C^{\prime }}$ is a function that encodes relative positional information into the token features (d denotes the dimensionality of the position, C is the number of input feature channels, and $C^{\prime }$ is the number of output feature channels). When applying Translution to a new type of data, the key is to develop an effective attention mechanism $\alpha$ and structure encoding function f. Point Spatio-Temporal Transformer [22] can be viewed as a specific instance of general Translution, which has been demonstrated to be effective for 3D point cloud video classification tasks, particularly on small-scale datasets.

5. Experiment

We compare Translution and Transformer using the same Vision Transformer (ViT)1 [9] architecture. For our method, we substitute the Transformer component in ViT with Translution, while maintaining the remaining architecture unchanged.

5.1. MNIST, CIFAR-10 and CIFAR-100

For MNIST images of size $28\times 28$, we set the patch size to 7, resulting in ${\displaystyle \frac{28}{7}}\times {\displaystyle \frac{28}{7}}+1=17$ input tokens (the ‘1’ represents the additional CLS token). For CIFAR images of size $32\times 32$, we set the patch size to 8, also yielding ${\displaystyle \frac{32}{8}}\times {\displaystyle \frac{32}{8}}+1=17$ input tokens. The dimension of the embedding vectors is set to 64, the MLP hidden layer dimension is set to 128, the number of head is set to 1 and the head dimension is 64. All training starts from scratch.

As shown in Figure 4, Translution outperforms Transformer in terms of accuracy. Moreover, the advantage is more pronounced in shallower networks, e.g., at a depth of 1. As the network depth increases, the differences diminish. This may indicate that as the network becomes deeper, the influence of absolute positioning embedding decreases because it is only used once at the initial input stage.

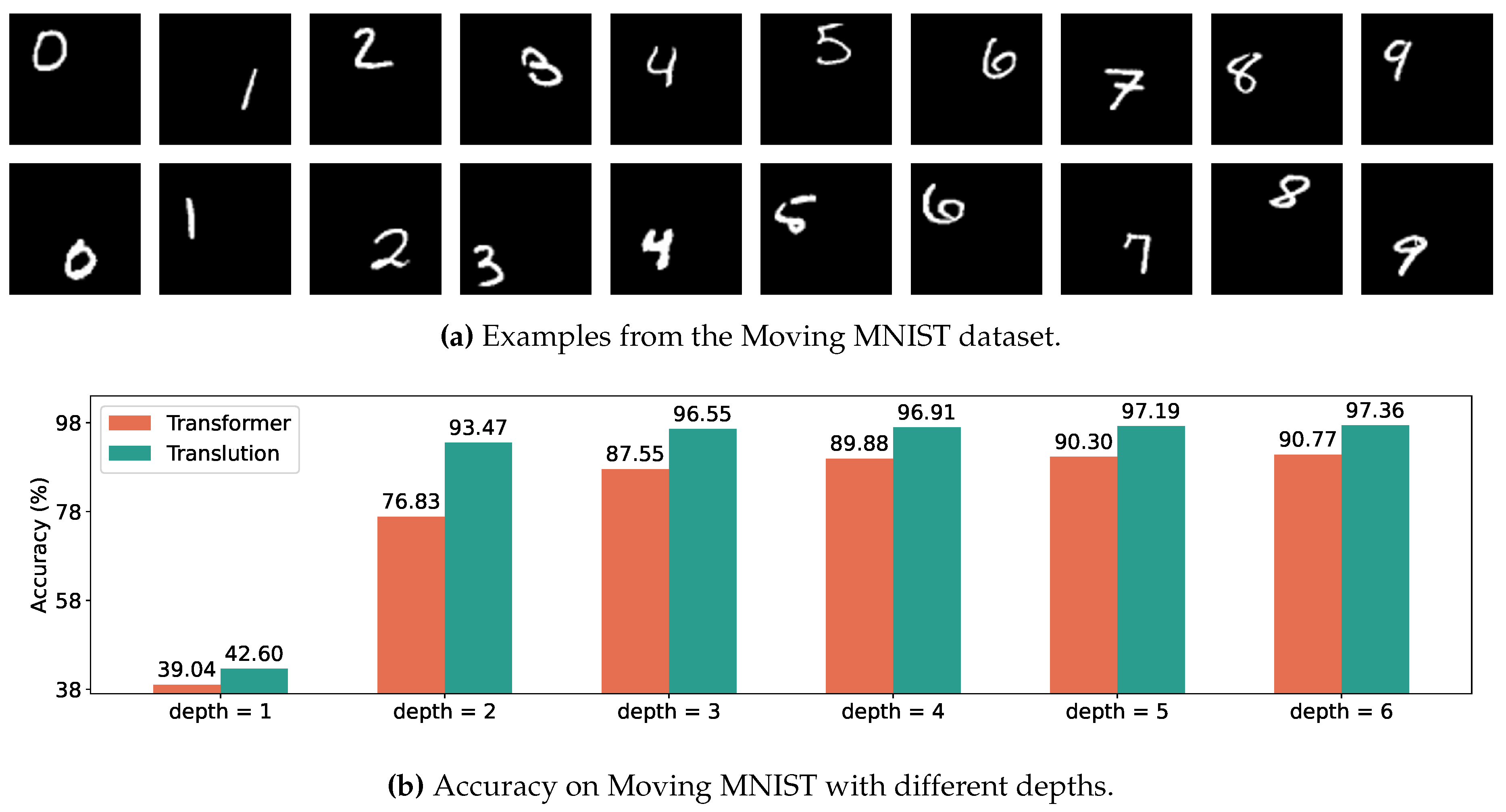
5.2. Moving MNIST

The location of digits in MNIST and objects in CIFAR is typically centered within the images. To assess the capability of modeling relative structures, we synthesize a Moving MNIST dataset [23,24] featuring MNIST digits that move within a $64\times 64$ area, as shown in Figure 5a. We set the patch size to 8, resulting in ${\displaystyle \frac{64}{8}}\times {\displaystyle \frac{64}{8}}+1=65$ input tokens.

As shown in Figure 5b, the relative modeling of Translution effectively improves accuracy on the Moving MNIST dataset. Furthermore, comparing Figure 4a with Figure 5b, it is evident that changes in absolute location in Moving MNIST significantly affect Transformer. In contrast, when the depth of the network increases, it does not significantly impact Translution.

6. Conclusion

In this article, we propose Translution, a novel neural network module that integrates the adaptive identification capabilities of Transformer with the advantageous relative encoding properties of Convolution. Preliminary experimental results demonstrate the effectiveness of the method. Nevertheless, further validation using larger-scale datasets across diverse scenarios is required to comprehensively assess its performance. Additionally, the increasing number of parameters involved in the relative Value computation poses potential learning challenges, suggesting that optimized variants should be explored in future work.