1. Introduction
In the era of big data, graphs are widely used to represent real-world data, such as social networks, road networks, and web networks, in an efficient and structured manner. Through vertices and edges, graphs visually depict complex relationships and structures among entities. These graph datasets are often vast in scale and intricate in structure. Graphs can be classified as either static or dynamic: static graphs remain unchanged over time, whereas dynamic graphs continuously evolve as vertices and edges are added or removed [
1,
2,
3,
4,
5,
6,
7]. Real-world graph data are typically large-scale and dynamic. For instance, on Facebook, an average of six new accounts are registered every second; the World Wide Web sees approximately three new accounts created per second; Twitter users generate about 10,000 tweets per second; and Alibaba's e-commerce platform processes over 20,000 transactions per second [
8].
Dynamic graphs play a crucial role in various real-world applications. For instance, they are employed in real-time financial fraud detection to identify abnormal transaction patterns in financial networks, in social network analysis to track changes in user relationships and activities for enhanced information diffusion modeling, and in recommendation systems to generate personalized suggestions by dynamically reflecting user behavior.[
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24]
Despite significant advancements in efficiently processing large-scale graph data, handling dynamic graphs remains considerably more complex than managing static ones[
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39]. Unlike static graphs, which represent a single point in time, dynamic graphs require continuous tracking and management of changes. These graphs often necessitate real-time or near-real-time updates, demanding high computational efficiency. The real-time tracking and analysis of dynamic graphs pose substantial challenges in terms of computational resources and processing time. Traditional approaches based on central processing units (CPUs) were initially developed to handle rapidly changing dynamic graphs. As general-purpose processors, CPUs are designed for a wide range of computations. For instance, Tornado [
9] introduced mechanisms to reduce unnecessary computations in dynamic graphs, while GraPU [
20] accelerated processing through precomputations in buffered updates. Graphtinker [
21] proposed scalable data structures for dynamic graphs, and DZiG [
22] developed a processing system optimized for sparse graphs. However, the inherent limitations in CPU parallelism restrict their ability to achieve high performance in large-scale graph processing.
Recently, research has increasingly focused on leveraging the parallel processing capabilities of GPUs for graph data processing. With support for thousands of concurrent threads, GPUs excel in parallel computations, making them highly efficient for handling the complex calculations involved in large-scale graph data processing. Their computational power enables real-time analysis of evolving graph structures. Several GPU-based dynamic graph update systems have been developed to process continuously changing graphs, including cuSTINGER [
1], Hornet [
2], GPMA [
3], LPMA [
4], aimGraph [
5], and faimGraph [
6]. cuSTINGER and Hornet utilize array-based memory management systems, while GPMA and LPMA are based on the Compressed Sparse Row (CSR) format. In contrast, aimGraph and faimGraph employ chain-based memory management systems. Among these, cuSTINGER and GPMA represent notable adaptations of the CPU-based systems STINGER [
23] and PMA [
24] to GPU platforms, optimizing GPU computational performance and memory access efficiency.
Most traditional systems assume that the input graph can be entirely stored in GPU memory [
1,
2,
3,
4,
5]. In other words, these systems are constrained by the requirement that the input graph must fit within the limited global memory capacity of the GPU. To address this limitation, out-of-memory graph processing systems have been proposed [
7]. For example, EGraph [
7] integrates Subway [
31], a GPU-based static graph processing system, with GPMA's dynamic graph update mechanism, enabling the processing of graphs that exceed GPU memory capacity. Despite the rapid parallel processing capabilities of GPUs, their memory constraints remain a significant challenge, particularly for real-time dynamic graph processing.
In this paper, we propose an efficient scheme for processing large-scale dynamic graphs based on subgraph scheduling and operation reduction. First, the structure and dynamic change patterns of the graph are analyzed on the host to determine the optimal partition loading order using priority scores. These scores consider not only active vertices within a partition but also those that may potentially become active, optimizing data processing on GPUs and maximizing memory utilization. Additionally, since the structure of dynamic graphs evolves over time, snapshots are generated at specific intervals to capture the graph’s state and collect relevant information. These snapshots help identify instances where identical vertices or edges are repeatedly inserted and deleted, enabling an operation reduction method to minimize unnecessary computations. This approach effectively reduces resource usage and enhances graph processing speed.
The structure of this paper is as follows.
Section 2 analyzes existing research on large-scale graph processing using GPUs and examines the associated challenges.
Section 3 presents the proposed scheduling and operation reduction methods for efficient dynamic graph processing on GPUs.
Section 4 evaluates the effectiveness of the proposed method through performance assessments using various graph algorithms. Finally,
Section 5 concludes the paper and outlines potential directions for future research.
2. Related Works
With the rapid growth of graph sizes, research on graph processing using both CPUs and GPUs has been actively pursued. CPUs offer abundant memory and computational capabilities, facilitating the efficient execution of complex graph algorithms. In contrast, GPUs provide massive parallel processing power, enabling the simultaneous execution of numerous threads to efficiently parallelize graph algorithms[
26,
27,
28,
29,
30]. Several GPU-based graph processing methods have been developed to enhance performance. GTS [
25] introduces a fast and scalable approach based on streaming topology, while CuSha [
26] develops a novel graph representation optimized for GPU utilization. Gunrock [
27] employs a frontier-based synchronous execution model specifically designed for GPUs. Additionally, Totem [
28], Garaph [
29], and Scaph [
30] integrate the strengths of both CPUs and GPUs to accelerate graph processing in heterogeneous systems. Totem partitions large-scale graphs for concurrent processing on CPUs and GPUs; Garaph optimizes GPU-accelerated graph processing using a scheduling algorithm based on the proportion of active vertices, and Scaph enhances scalability through value-centric differential scheduling. Subway focuses on minimizing data transfer in out-of-memory scenarios, providing a robust foundation for processing complex static graph datasets. Since real-world data is inherently dynamic and its structure evolves over time, studying dynamic graph processing is essential. Numerous CPU-based systems for efficient dynamic graph processing have been proposed in recent years [
17,
18,
19,
20,
21,
22,
23,
24]. Unlike static graphs, dynamic graph processing requires tracking and recording changes in the graph over time, introducing additional computational challenges.
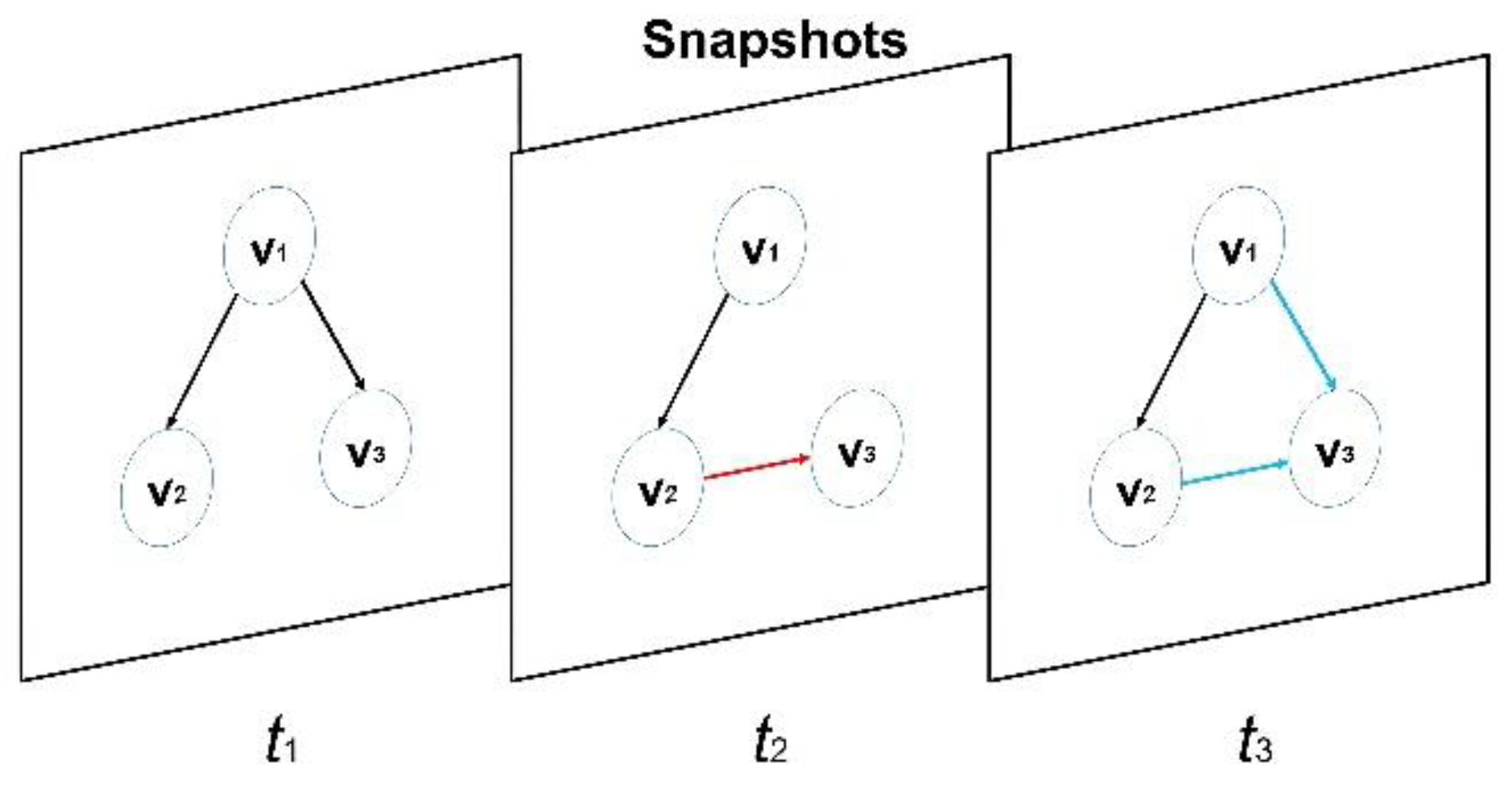
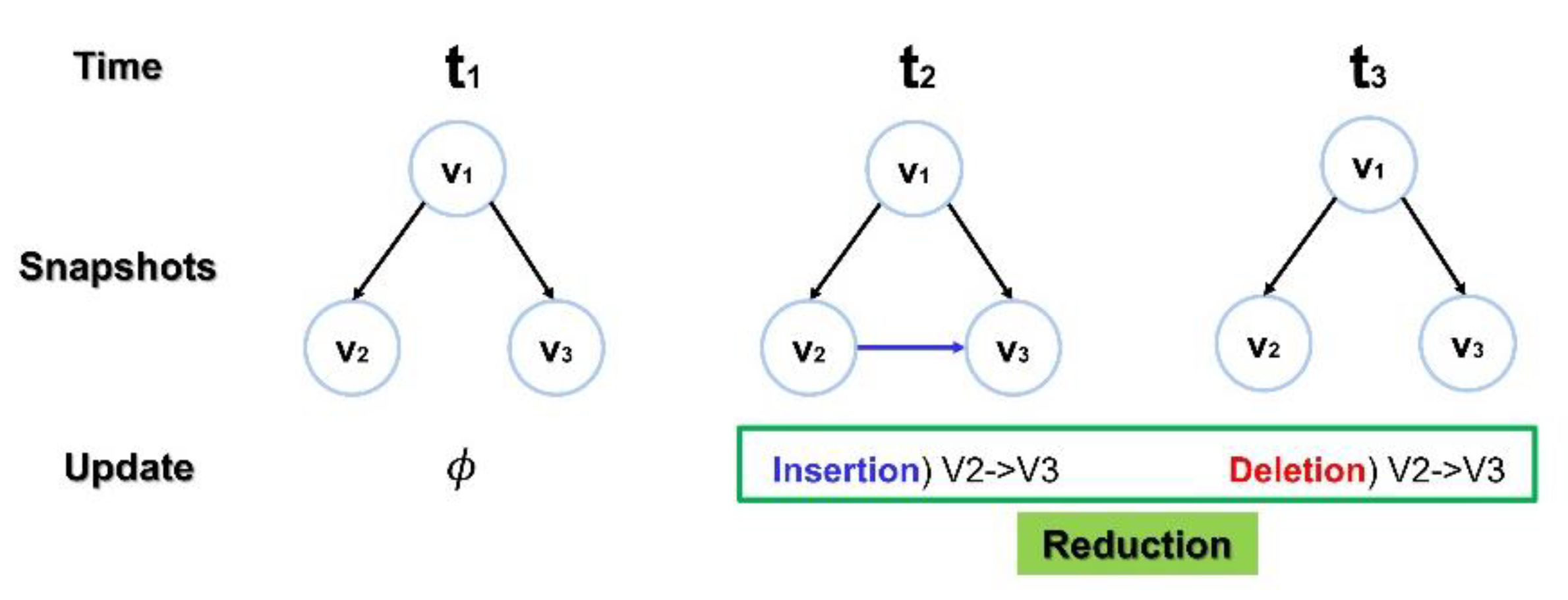
Figure 1 illustrates snapshots that represent the state of a dynamic graph at specific points in time. These snapshots capture the current structure of the graph and are used to track changes over time. Detecting changes in dynamic graphs involves identifying and recording events such as the addition or deletion of edges and the creation or removal of vertices. STINGER is a data structure and API suite designed for efficiently handling large-scale dynamic graphs. It supports rapid edge additions, deletions, and other graph modifications in CPU-based systems. Similarly, PMA is a data structure optimized for dynamic graph processing, enabling efficient management of graph changes. However, CPU-based systems face inherent limitations due to the restricted parallelism and memory bandwidth of CPUs, which hinder their scalability for large-scale dynamic graph processing.
Various studies have explored GPU-based dynamic graph processing [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. EGraph is a representative system designed to efficiently handle dynamic graphs on GPUs. It partitions graphs into subgraphs and processes them in parallel to optimize GPU resource utilization. To reduce data transfer overhead between the CPU and GPU, EGraph employs the Loading-Processing-Switching (LPS) execution model. However, EGraph has certain limitations. It does not account for preliminary active vertices during scheduling, which can prevent the graph from achieving an optimal processing order during repeated executions. Additionally, it does not effectively address the redundant processing of overlapping snapshot sections, leading to inefficiencies in dynamic graph updates.
This paper proposes a priority-based scheduling and computation reduction method to overcome the limitations of existing approaches. By prioritizing both active and preliminary active vertices, the proposed method enhances GPU resource utilization and minimizes redundant computations caused by dynamic graph updates, thereby improving processing performance.
3. Proposed Dynamic Graph Processing Scheme
3.1. Overall Architecture
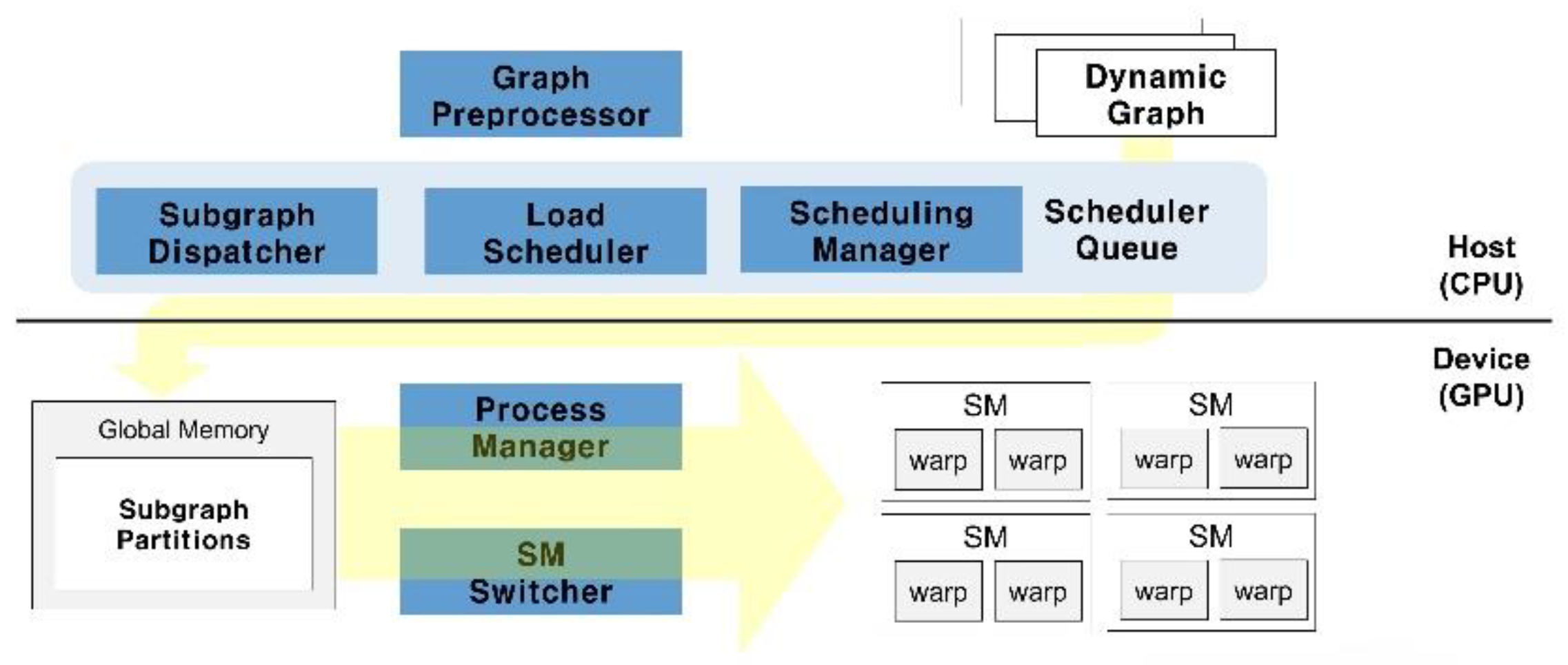
This paper presents a system architecture that integrates the capabilities of both CPUs and GPUs to efficiently process large-scale dynamic graphs. By leveraging the parallel processing power of GPUs alongside the management and scheduling capabilities of CPUs, the proposed system accelerates dynamic graph processing. The architecture maximizes GPU parallelism to expedite graph computations while utilizing the CPU for preprocessing, management, and task scheduling. This integrated approach reduces computational complexity and workload, thereby enhancing overall processing performance.
Figure 2 illustrates the overall structure of the proposed scheme for dynamic graph processing, comprising a host and a device. The host consists of the Graph Preprocessor, Scheduling Manager, Operation Reduction Module, and Partitions Dispatcher, while the device includes the Process Manager and streaming multiprocessors (SM) Switcher. On the host side, key tasks include preprocessing the original graph, maintaining snapshots that capture the evolving structure of the dynamic graph, scheduling graph partitions, and transferring them to the GPU for processing. The device side is responsible for receiving graph data, executing computations on the GPU, and ensuring load balancing to optimize performance.
3.2. Graph Preprocessor
For an input graph to be processed by the GPU, it must first undergo preprocessing to fit within the GPU’s limited memory. Since the size of the input graph often exceeds the capacity of the GPU’s global memory, the Graph Preprocessor divides the input graph into fine-grained partitions that can fit within this memory constraint. During partitioning, a vertex-cut method is employed to segment the graph into sizes optimized for GPU memory usage. This approach ensures that each partition remains within the available memory capacity while maintaining computational efficiency. Equation (1) calculates the size of each partition, ensuring that the total size of N partitions,|Partition|x N does not exceed the size of the global memory capacity, |Global|.
The resulting partitions are assigned to the GPU’s SMs for parallel processing. The vertex-cut method is designed to preserve the graph’s structural integrity while optimizing memory utilization. Through this process, the Graph Preprocessor ensures that the input graph is efficiently prepared for GPU-based processing. The graph partitioning approach ensures that the input graph is properly divided to maximize GPU efficiency. In the event of graph updates (e.g., edge or vertex additions and deletions), only the affected portions of the graph are processed. This selective update mechanism minimizes CPU-GPU data transfer costs by moving only the necessary data for graph updates, thereby reducing redundant data transfers and improving overall processing efficiency.
3.3. Scheduling Method
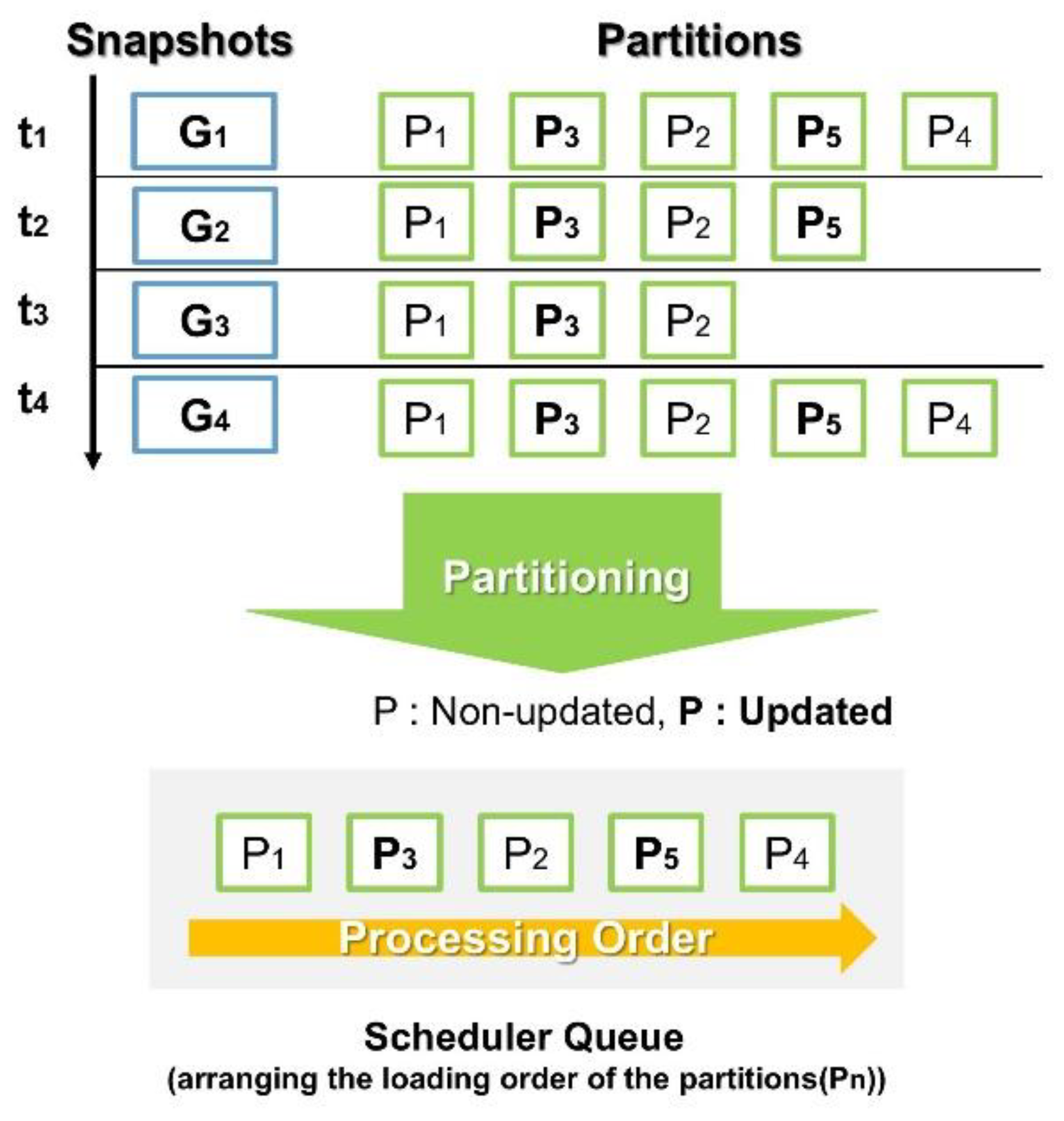
Before transmitting the divided graph partitions to the GPU, it is essential to determine their loading order, a process referred to as scheduling. The Scheduling Manager efficiently organizes and coordinates operations for each partition of the subdivided graph. This involves prioritizing partitions and determining the optimal sequence for loading them onto the GPU. Additionally, the scheduler considers the dynamic nature of graphs to establish and manage schedules that adapt to graph changes in real time.
Figure 3 illustrates the process of partitioning and scheduling snapshots of a dynamic graph. Over time intervals t1 to t4, snapshots G1, G2, G3, and G4 are generated. If a snapshot exceeds the GPU’s global memory capacity, it is further divided into multiple partitions. These partitions are then enqueued in the Scheduler Queue based on their priority, ensuring efficient processing on the GPU.
This paper proposes an optimized method for determining the loading order to enhance the efficiency of dynamic graph processing on GPUs. Partitions generated through graph partitioning are assigned priorities to ensure optimal scheduling. Updated partitions are prioritized for processing first, while partitions that appear in multiple snapshots are also loaded into the GPU’s global memory earlier to minimize redundant computations. Additionally, this study considers not only active vertices but also potentially active vertices that may become active in subsequent processing. By incorporating these factors into priority assignment, the proposed method improves GPU resource utilization and enhances overall processing efficiency.
Equation (2) represents N(Pi), which refers to the number of snapshots required to process Pi when an update occurs. Active(Pi) denotes the number of active vertices within the partition, and Potential(Pi) refers to the potential active vertices, i.e., the tentative active vertices within the partition. K varies depending on whether an update has occurred. If an update occurs in the partition, K is set to 1; if no update occurs, it is set to 0, and the priority is adjusted accordingly.
α and β are scaling factors set during preprocessing to emphasize the impact of certain values. This priority formula ensures that partitions are efficiently loaded into the GPU.
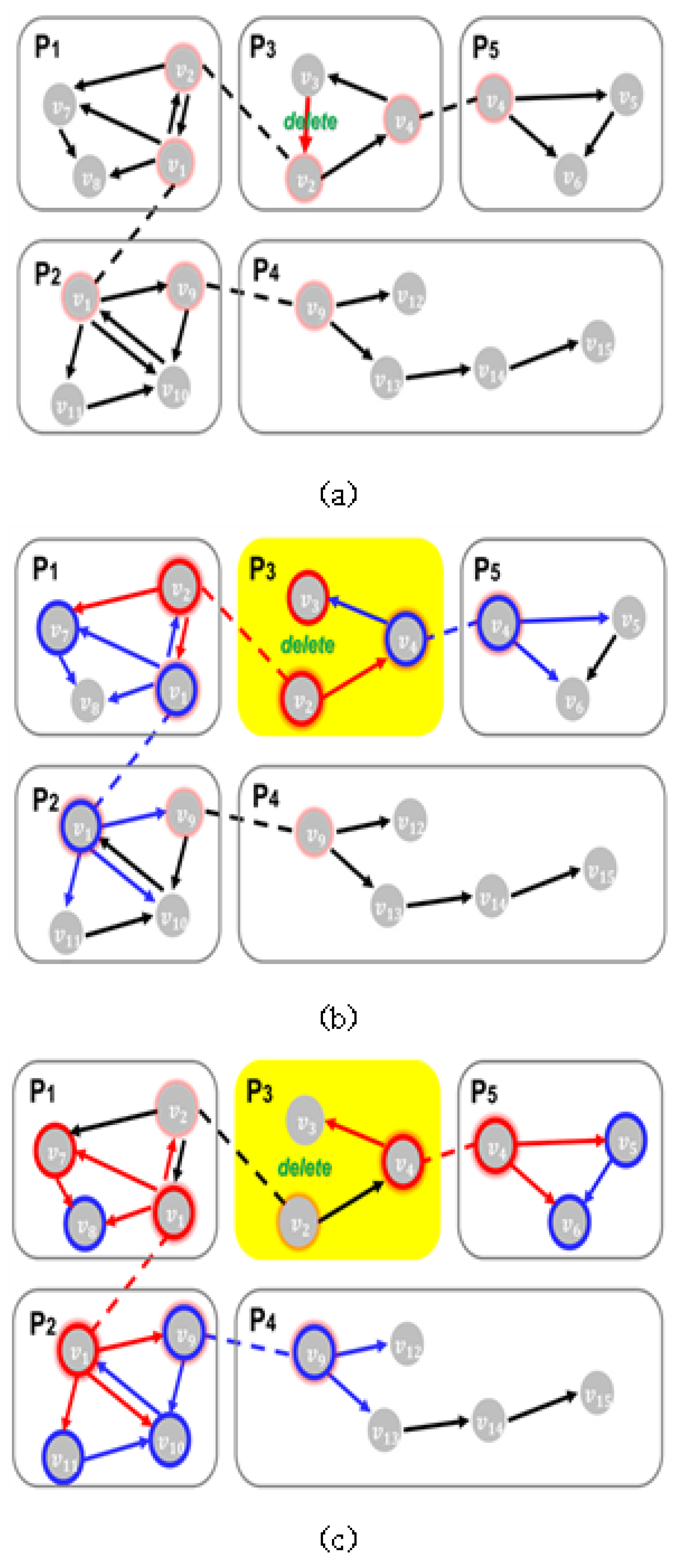
Figure 4 illustrates an example of active and potentially active vertices during dynamic graph processing when an edge between two vertices V2 and V3 is deleted.
Figure 4a shows a scenario where the edge between vertices V2 and V3 in partition P3 is deleted.
Figure 4b depicts the activation process, where V2 and V3 become active vertices due to the edge deletion. Additionally, vertices connected to these active vertices, which are likely to become active in subsequent steps, are marked as potentially active vertices (highlighted in blue). In this example, V1, V3 and V7 are identified as potentially active vertices.
Figure 4c demonstrates the transition where active vertices are processed, and potentially active vertices from
Figure 4b V1, V3 and V7 transition into active vertices and are subsequently processed.
3.4. Operation Reduction Method
The Operation Reduction Module implements techniques to minimize computational overhead before transmitting graph snapshots to the GPU. These techniques account for the dynamic nature of graphs by analyzing the characteristics of snapshots that evolve over time. As snapshots are generated at different time points, the module efficiently preprocesses them to reduce redundant operations before execution on the GPU. This preprocessing step optimizes GPU resource utilization and improves overall processing efficiency.
The core of the operation reduction method lies in efficiently tracking changes in the graph at each time step and eliminating redundant computations on identical edges or vertices. To achieve this, the Operation Reduction Module stores graph snapshots and compares them with previous states, identifying unchanged partitions and skipping their processing. This significantly reduces the overall computational load. This approach is particularly beneficial in scenarios where edges are frequently added or removed, as it prevents unnecessary operations on unaffected vertices. Additionally, only the modified portions of the graph are transmitted to the GPU, rather than reprocessing the entire dataset. By focusing solely on the necessary updates, this method minimizes memory transfer costs, reducing both computational overhead and resource waste during data transmission. Therefore, the proposed optimization enhances the overall efficiency and performance of dynamic graph processing.
Figure 5 illustrates an example of operation reduction for redundant computations on the same edge. As shown in the figure, dynamic graph snapshots are generated at time points t1, t2 and t3. At t2, an edge is added between V2 and V3, and at t3, the same edge is removed. Consequently, the snapshot at t1 becomes identical to the snapshot at t3. In such scenarios, the module avoids unnecessary update operations, thereby reducing the computational workload on the GPU. This optimization minimizes redundant operations, conserves resources, and enhances the efficiency of dynamic graph processing.
3.5. Processing Loaded Partitions
After the preprocessed partitions are prioritized by the Scheduling Manager, the Partitions Dispatcher transfers them from host memory to GPU memory. Each partition, optimized for parallel processing, is transferred according to the determined loading order and stored in the GPU’s global memory. The Process Manager then ensures that these partitions, loaded via the Partitions Dispatcher, are efficiently processed simultaneously on the SMs. SMs, being the core components of the GPU, are responsible for executing parallel tasks. The Process Manager coordinates tasks within the SMs, ensuring that each operates as efficiently as possible to maximize GPU resource utilization.
When processing partitions, the computational loads of different tasks may vary, leading to load imbalance. To address this, an SM Switcher is employed to ensure load balancing by evenly distributing workloads across the SMs.
The SM Switcher continuously monitors the workload of each SM and redistributes unprocessed tasks from heavily loaded SMs to idle ones. This process involves temporarily pausing tasks assigned to overloaded SMs, dividing the unprocessed portions into smaller subsets, and reallocating these subsets to idle SMs. By dynamically balancing workloads, the SM Switcher optimizes resource utilization and enhances the overall efficiency of dynamic graph processing.
4. Performance Evaluation
4.1. Performance Evaluation Environment
A performance evaluation was conducted to demonstrate the effectiveness of the proposed scheme for dynamic graph processing on GPUs. This evaluation compares the proposed scheme with existing approaches to highlight its advantages.
Table 1 outlines the performance evaluation environment. For the experiments, an integrated CPU-GPU environment was established. The CPU environment consisted of an AMD Ryzen Threadripper PRO 5955WX processor with 16 cores running at 2.7 GHz and 32 GB of memory. The GPU environment utilized an NVIDIA GeForce RTX 4090 with 24 GB of memory. The proposed method was implemented and tested on a Linux (Ubuntu 23.04 LTS) operating system, using GCC 11.4.0 and CUDA 12.2.
Table 2 presents the datasets used for the evaluation. The following datasets consist of directed graph data provided by the SuiteSparse Matrix Collection [
40]. The soc-LiveJournal1 dataset was collected from the LiveJournal online social network. The twitter7 dataset represents the Twitter follower network, while the sk-2005 dataset is based on web crawl data from the .sk domain.
4.2. Self-Performance Evaluation
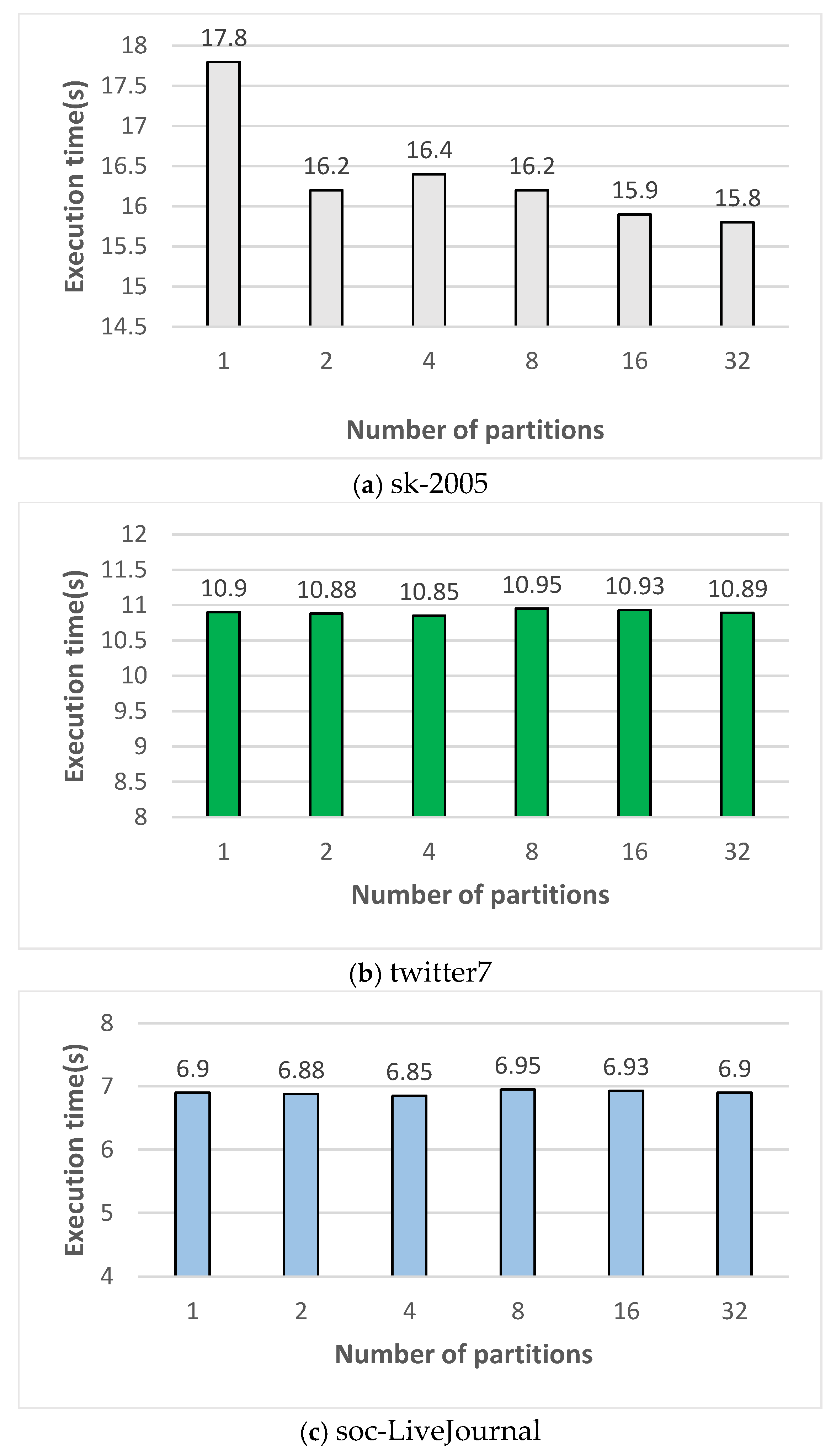
This performance evaluation compares graph processing execution times to determine the optimal partition size for the proposed scheme. The evaluation employed the Single Source Shortest Path (SSSP) algorithm with the sk-2005, twitter7, and soc-LiveJournal1 datasets.
Figure 6 presents the execution times for each dataset. The x-axis represents the number of partitions, ranging from 2, 4, 8, 16, to 32. For the sk-2005 dataset, the fastest execution time was achieved with 32 partitions, while the slowest occurred with only 1 partition. For the twitter7 dataset, the fastest execution time was recorded with 2 partitions, and the slowest with 8 partitions. Similarly, for the soc-LiveJournal1 dataset, the fastest execution time was also observed with 2 partitions, while the slowest occurred with 8 partitions. The optimal number of partitions for the proposed scheme depends on both the dataset size and the capacity of the GPU’s global memory.
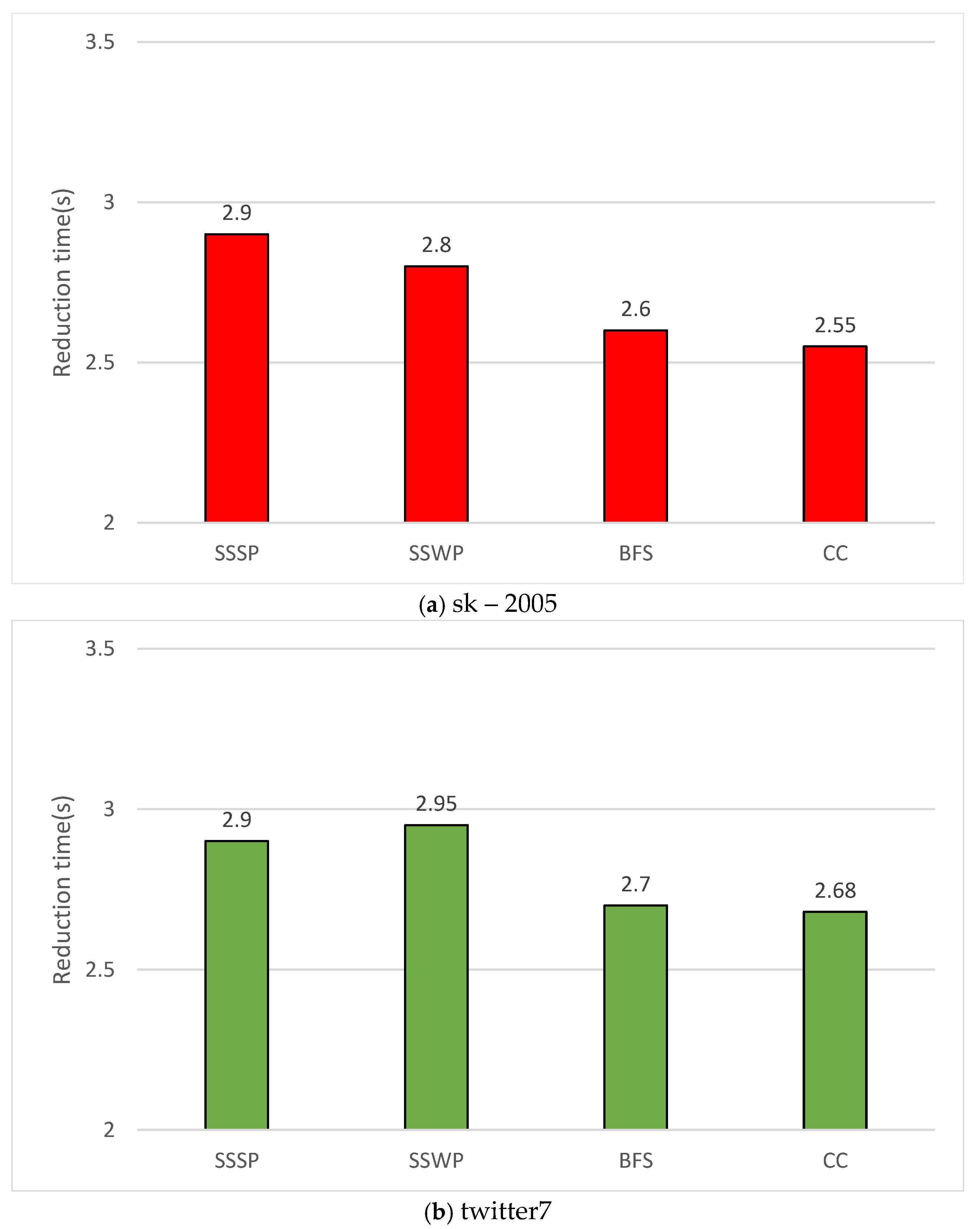
This performance evaluation also examines graph processing execution times for each algorithm when applying the operation reduction method. The GPU processing times are compared with and without operation reduction to assess its impact.
Figure 7 presents the processing times, including the preprocessing time required to apply the operation reduction method and the resulting reduction in execution times. The evaluation was conducted using the sk-2005 and twitter7 datasets, with the graph modification rate set to 1%. Both preprocessing time and operation reduction time were measured. The x-axis of
Figure 7 represents the algorithms being compared, listed in the following order: Single Source Shortest Path (SSSP), Single Source Widest Path (SSWP), Breadth-First Search (BFS), and CC. The y-axis of
Figure 8 represents the net benefit time, calculated as the reduced execution time achieved through operation reduction minus the preprocessing time. The results confirm that the time savings from operation reduction significantly outweighed the preprocessing time. This performance evaluation demonstrates the superior efficiency of the proposed operation reduction method.
4.3. Performance Evaluation Results
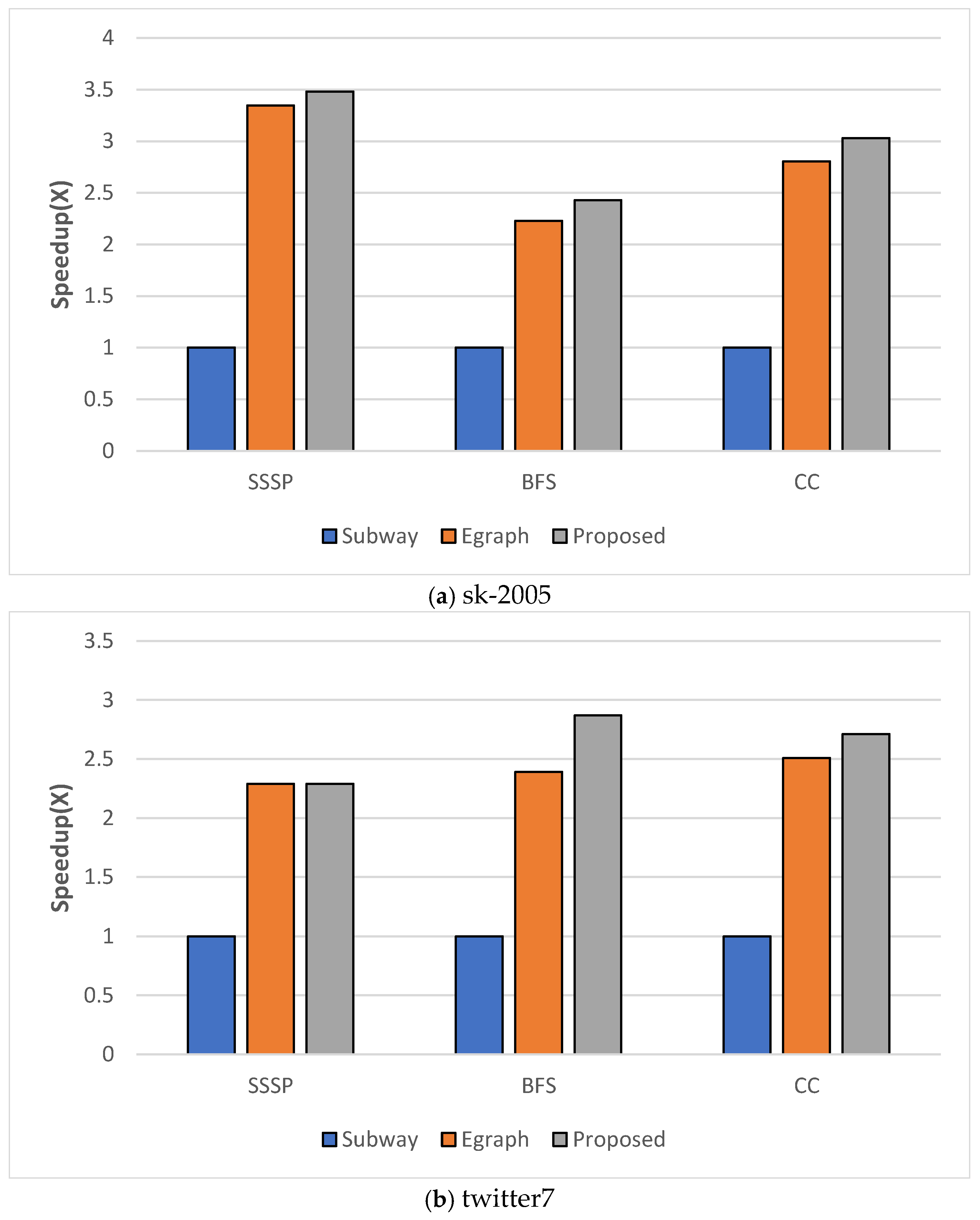
The performance evaluation compared the proposed scheme with a modified version of Subway, a static graph processing scheme adapted for dynamic graph processing, and EGraph, a dynamic graph processing scheme. This comparison assessed the performance differences between the proposed scheme and existing approaches, demonstrating the efficiency of the proposed scheme in dynamic graph processing. The experiments were conducted using the sk-2005 and twitter7 datasets, with the data modification rate set to 0.01%. The evaluation employed the Connected Components (CC), SSSP, and BFS algorithms. The x-axis of
Figure 8 represents the algorithms being compared.
In
Figure 8, the x-axis represents the algorithms under comparison, while the y-axis indicates the performance improvement ratios of EGraph and the proposed scheme relative to Subway (baseline set at 1). In
Figure 8(a), the proposed scheme achieved 348%, 243%, and 303% faster processing speeds compared to Subway, and 104%, 109%, and 108% improvements over EGraph. In
Figure 8(b), the proposed scheme demonstrated 229%, 287%, and 271% faster speeds than Subway, and 100%, 120%, and 108% faster than EGraph.
The performance differences arise from the distinct processing approaches of each scheme. Subway processes only one snapshot at a time, resulting in relatively slower execution. EGraph supports dynamic graph processing but does not consider tentative active vertices during scheduling and lacks an operation reduction method, leading to unnecessary computations and suboptimal performance. The proposed scheme overcomes these limitations through priority-based scheduling, which accounts for tentative active vertices to efficiently determine the GPU processing order, and operation reduction techniques, which eliminate duplicate computations across snapshots. This enables more efficient partition processing in response to dynamic graph changes. Therefore, the proposed scheme achieved up to 348% faster speeds than Subway and 120% faster speeds than EGraph, maximizing resource utilization and computational efficiency in dynamic graph processing.
5. Conclusions
In this paper, we proposed a novel scheme for efficiently processing dynamic graphs in GPU environments with limited memory. The proposed scheme integrates dynamic scheduling and operation reduction techniques, effectively reducing data transfers between the CPU and GPU while minimizing the overall computational load. The dynamic scheduling technique considers both active and tentative active vertices to efficiently determine the GPU load order for each partition. The operation reduction technique adapts to dynamic graph changes, eliminating unnecessary computations and proving particularly effective in environments with frequent vertex and edge insertions or deletions.
Future research will focus on expanding the proposed scheme to distributed platforms to evaluate performance on larger-scale graph processing tasks. The applicability of the scheme across various graph algorithms will be explored, and optimized techniques will be developed for real-time dynamic graph processing environments. Through these advancements, the proposed scheme can address more complex and large-scale dynamic graph processing challenges.
Supplementary Materials
Not applicable.
Author Contributions
Conceptualization, S.S., J.C., D.C, H.L., D.C., J.L., K.B., and J.Y.; methodology, S.S., J.C., D.C., K.B., and J.Y.; software, S.S., J.C.,; validation, S.S., J.C., D.C, H.L., D.C., J.L., K.B., and J.Y.; formal analysis, S.S., J.C., K.B., and J.Y..; data curation, S.S., J.C., D.C.; writing—original draft preparation, , S.S., J.C.; writing—review and editing, J.Y.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT). (No. 2022R1A2B5B02002456, 50%) and by "the MSIT(Ministry of Science and ICT), Korea, under the Grand Information Technology Research Center support program(IITP-2025-2020-0-01462, 50%) supervised by the IITP(Institute for Information & communications Technology Planning & Evaluation).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in [SuiteSparse Matrix Collection] at [
https://sparse.tamu.edu], reference number [
40]..
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:.
| BFS |
Breadth-First Search |
| CC |
Connected Component |
| CPU |
Central processing units |
| CSR |
Compressed Sparse Row |
| DOI |
Digital object identifier |
| LPS |
Loading-Processing-Switching |
| SM |
Streaming multiprocessors |
| SSSP |
Single Source Shortest Path |
References
- Green, O.; Bader, D.A. CuSTINGER: Supporting Dynamic Graph Algorithms for GPUs. IEEE High Performance Extreme Computing Conference (HPEC) 2016, 1–6. [Google Scholar] [CrossRef]
- Busato, F.; Green, O.; Bombieri, N.; Bader, D.A. Hornet: An Efficient Data Structure for Dynamic Sparse Graphs and Matrices on GPUs. In Proceedings of the 2018 IEEE High Performance extreme Computing Conference (HPEC); 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Sha, M.; Li, Y.; He, B.; Tan, K.-L. Accelerating Dynamic Graph Analytics on GPUs. Proc. VLDB Endow. 2017, 11, 107–120. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, F.; Lin, Y.; Yu, Y. An Efficient Data Structure for Dynamic Graph on GPUs. IEEE Trans. Knowl. Data Eng. 2023, 35, 11051–11066. [Google Scholar] [CrossRef]
- Winter, M.; Zayer, R.; Steinberger, M. Autonomous, Independent Management of Dynamic Graphs on GPUs. In Proceedings of the 2017 IEEE High Performance Extreme Computing Conference (HPEC); 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Winter, M.; Mlakar, D.; Zayer, R.; Seidel, H.-P.; Steinberger, M. FaimGraph: High Performance Management of Fully-Dynamic Graphs under Tight Memory Constraints on the GPU. In Proceedings of the Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis; IEEE Press, 2018. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, Y.; Zhao, J.; Mao, F.; Gu, L.; Liao, X.; Jin, H.; Liu, H.; Guo, S.; Zeng, Y.; et al. EGraph: Efficient Concurrent GPU-Based Dynamic Graph Processing. IEEE Trans. Knowl. Data Eng. 2023, 35, 5823–5836. [Google Scholar] [CrossRef]
- Gao, H.; Liao, X.; Shao, Z.; Li, K.; Chen, J.; Jin, H. A Survey on Dynamic Graph Processing on GPUs: Concepts, Terminologies, and Systems. Front. Comput. Sci. 2023, 18, 184106. [Google Scholar] [CrossRef]
- Mao, F.; Liu, X.; Zhang, Y.; et al. PMGraph: Accelerating Concurrent Graph Queries Over Streaming Graphs. ACM Trans. Archit. Code Optim. 2024, 1–6. [Google Scholar] [CrossRef]
- Hanauer, K.; Henzinger, M.; Schulz, C. Recent Advances in Fully Dynamic Graph Algorithms—A Quick Reference Guide. ACM J. Exp. Algorithmics 2022, 27, 1–6. [Google Scholar] [CrossRef]
- Pandey, P.; Wheatman, B.; Xu, H.; Buluc, A. Terrace: A Hierarchical Graph Container for Skewed Dynamic Graphs. Proc. ACM SIGMOD Int. Conf. Manag. Data 2021, 1372–1385. [Google Scholar] [CrossRef]
- Vaziri, P.; Vora, K. Controlling Memory Footprint of Stateful Streaming Graph Processing. In Proceedings of the 2021 USENIX Annual Technical Conference (USENIX ATC 21); USENIX Association, 2021; pp. 269–283. Available online: https://www.usenix.org/conference/atc21/presentation/vaziri.
- Jiang, Z.; Mao, F.; Guo, Y.; Liu, X.; Liu, H.; Liao, X.; Jin, H.; Zhang, W. ACGraph: Accelerating Streaming Graph Processing via Dependence Hierarchy. Proc. Design Autom. Conf. 2023, 1–6. [Google Scholar] [CrossRef]
- Sun, G.; Zhou, J.; Li, B.; Gu, X.; Wang, W.; He, S. FTGraph: A Flexible Tree-Based Graph Store on Persistent Memory for Large-Scale Dynamic Graphs. Proc. IEEE Int. Conf. Cluster Comput. 2024, 39–50. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Cheng, J.; Wu, Y.; Ye, C.; Yu, H.; Huang, Z.; Jin, H.; Liao, X.; Gu, L.; et al. SaGraph: A Similarity-Aware Hardware Accelerator for Temporal Graph Processing. In Proceedings of the 2023 60th ACM/IEEE Design Automation Conference (DAC); 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Concessao, K.J.; Cheramangalath, U.; Dev, R.; Nasre, R. Meerkat: A Framework for Dynamic Graph Algorithms on GPUs. Int. J. Parallel Program. 2024, 52, 400–453. [Google Scholar] [CrossRef]
- Cheng, R.; Hong, J.; Kyrola, A.; Miao, Y.; Weng, X.; Wu, M.; Yang, F.; Zhou, L.; Zhao, F.; Chen, E. Kineograph: Taking the Pulse of a Fast-Changing and Connected World. In Proceedings of the Proceedings of the 7th ACM European Conference on Computer Systems; Association for Computing Machinery: New York, NY, USA, 2012; pp. 85–98. [Google Scholar] [CrossRef]
- Han, W.; Miao, Y.; Li, K.; Wu, M.; Yang, F.; Zhou, L.; Prabhakaran, V.; Chen, W.; Chen, E. Chronos: A Graph Engine for Temporal Graph Analysis. In Proceedings of the Proceedings of the Ninth European Conference on Computer Systems; Association for Computing Machinery: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Shi, X.; Cui, B.; Shao, Y.; Tong, Y. Tornado: A System for Real-Time Iterative Analysis over Evolving Data. Proc. ACM SIGMOD Int. Conf. Manag. Data 2016, 417–430. [Google Scholar] [CrossRef]
- Sheng, F.; Cao, Q.; Cai, H.; Yao, J.; Xie, C. GraPU: Accelerate Streaming Graph Analysis through Preprocessing Buffered Updates. In Proceedings of the Proceedings of the ACM Symposium on Cloud Computing; Association for Computing Machinery: New York, NY, USA, 2018; pp. 301–312. [Google Scholar] [CrossRef]
- Jaiyeoba, W.; Skadron, K. GraphTinker: A High-Performance Data Structure for Dynamic Graph Processing. Proc. IEEE Int. Parallel Distrib. Process. Symp. (IPDPS) 2019, 1030–1041. [Google Scholar] [CrossRef]
- Mariappan, M.; Che, J.; Vora, K. DZiG: Sparsity-Aware Incremental Processing of Streaming Graphs. Proc. Sixteenth Eur. Conf. Comput. Syst. 2021, 83–98. [Google Scholar] [CrossRef]
- Ediger, D.; McColl, R.; Riedy, J.; Bader, D.A. STINGER: High Performance Data Structure for Streaming Graphs. In Proceedings of the 2012 IEEE Conference on High Performance Extreme Computing; 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Bender, M.A.; Hu, H. An Adaptive Packed-Memory Array. ACM Trans. Database Syst. 2007, 32, 26. [Google Scholar] [CrossRef]
- Kim, M.-S.; An, K.; Park, H.; Seo, H.; Kim, J. GTS: A Fast and Scalable Graph Processing Method Based on Streaming Topology to GPUs. In Proceedings of the Proceedings of the 2016 International Conference on Management of Data; Association for Computing Machinery: New York, NY, USA, 2016; pp. 447–461. [Google Scholar] [CrossRef]
- Khorasani, F.; Vora, K.; Gupta, R.; Bhuyan, L.N. CuSha: Vertex-Centric Graph Processing on GPUs. Proc. Int. Symp. High Perform. Parallel Distrib. Comput. (HPDC) 2014, 239–251. [Google Scholar] [CrossRef]
- Wang, Y.; Davidson, A.; Pan, Y.; Wu, Y.; Riffel, A.; Owens, J.D. Gunrock: A High-Performance Graph Processing Library on the GPU. Proc. ACM SIGPLAN Symp. Principles Pract. Parallel Program. (PPoPP) 2016, 1–6. [Google Scholar] [CrossRef]
- Gharaibeh, A.; Beltrão Costa, L.; Santos-Neto, E.; Ripeanu, M. A Yoke of Oxen and a Thousand Chickens for Heavy Lifting Graph Processing. In Proceedings of the Proceedings of the 21st International Conference on Parallel Architectures and Compilation Techniques; Association for Computing Machinery: New York, NY, USA, 2012; pp. 345–354. [Google Scholar] [CrossRef]
- Ma, L.; Yang, Z.; Chen, H.; Xue, J.; Dai, Y. Garaph: Efficient {GPU-Accelerated} Graph Processing on a Single Machine with Balanced Replication. In Proceedings of the 2017 USENIX Annual Technical Conference (USENIX ATC 17); USENIX Association: Santa Clara, CA, 2017; pp. 195–207. [Google Scholar]
- Zheng, L.; Li, X.; Zheng, Y.; Huang, Y.; Liao, X.; Jin, H.; Xue, J.; Shao, Z.; Hua, Q.-S. Scaph: Scalable GPU-Accelerated Graph Processing with Value-Driven Differential Scheduling. In Proceedings of the Proceedings of the 2020 USENIX Conference on Usenix Annual Technical Conference; USENIX Association: USA, 2020. [Google Scholar]
- Sabet, A.H.N.; Zhao, Z.; Gupta, R. Subway: Minimizing Data Transfer During Out-of-GPU-Memory Graph Processing. Proc. Eur. Conf. Comput. Syst. (EuroSys) 2020, 1–6. [Google Scholar] [CrossRef]
- Han, W.; Mawhirter, D.; Wu, B.; Buland, M. Graphie: Large-Scale Asynchronous Graph Traversals on Just a GPU. Proc. Parallel Archit. Compil. Tech. (PACT) 2017, 233–245. [Google Scholar] [CrossRef]
- Wang, Q.; Ai, X.; Zhang, Y.; Chen, J.; Yu, G. HyTGraph: GPU-Accelerated Graph Processing with Hybrid Transfer Management. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE); IEEE Computer Society: Los Alamitos, CA, USA, 2023; pp. 558–571. [Google Scholar]
- Song, S.; Lee, H.; Kim, Y.; Lim, J.; Choi, D.; Bok, K.; Yoo, J. Graph Processing Scheme Using GPU With Value-Driven Differential Scheduling. IEEE Access 2024, 12, 41590–41600. [Google Scholar] [CrossRef]
- Low, Y.; Gonzalez, J.; Kyrola, A.; Bickson, D.; Guestrin, C.; Hellerstein, J.M. Distributed GraphLab: A Framework for Machine Learning in the Cloud. 2012. [CrossRef]
- Gonzalez, J.E.; Low, Y.; Gu, H.; Bickson, D.; Guestrin, C. {PowerGraph}: Distributed {Graph-Parallel} Computation on Natural Graphs. In Proceedings of the 10th USENIX Symposium on Operating Systems Design and Implementation (OSDI 12); USENIX Association: Hollywood, CA, 2012; pp. 17–30, https://www.usenix.org/conference/osdi12/technical-sessions/presentation/gonzalez. [Google Scholar]
- Zhang, Y.; Liao, X.; Jin, H.; Gu, L.; Tan, G.; Zhou, B.B. HotGraph: Efficient Asynchronous Processing for Real-World Graphs. IEEE Trans. Comput. 2017, 66, 799–809. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Y.; Zhuo, Y.; Qian, X.; Huan, C.; Chen, K. Wonderland: A Novel Abstraction-Based Out-of-Core Graph Processing System. ACM SIGPLAN Notices 2018, 53, 608–621. [Google Scholar] [CrossRef]
- Malewicz, G.; Austern, M.H.; Bik, A.J.C.; Dehnert, J.C.; Horn, I.; Leiser, N.; Czajkowski, G. Pregel: A System for Large-Scale Graph Processing. In Proceedings of the Proceedings of the ACM SIGMOD International Conference on Management of Data; Association for Computing Machinery: New York, NY, USA, 2010; pp. 135–145. [Google Scholar] [CrossRef]
- https://sparse.tamu.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).