Submitted:
03 February 2025
Posted:
04 February 2025
You are already at the latest version
Abstract
Keywords:
1. Premise
2. Preliminaries
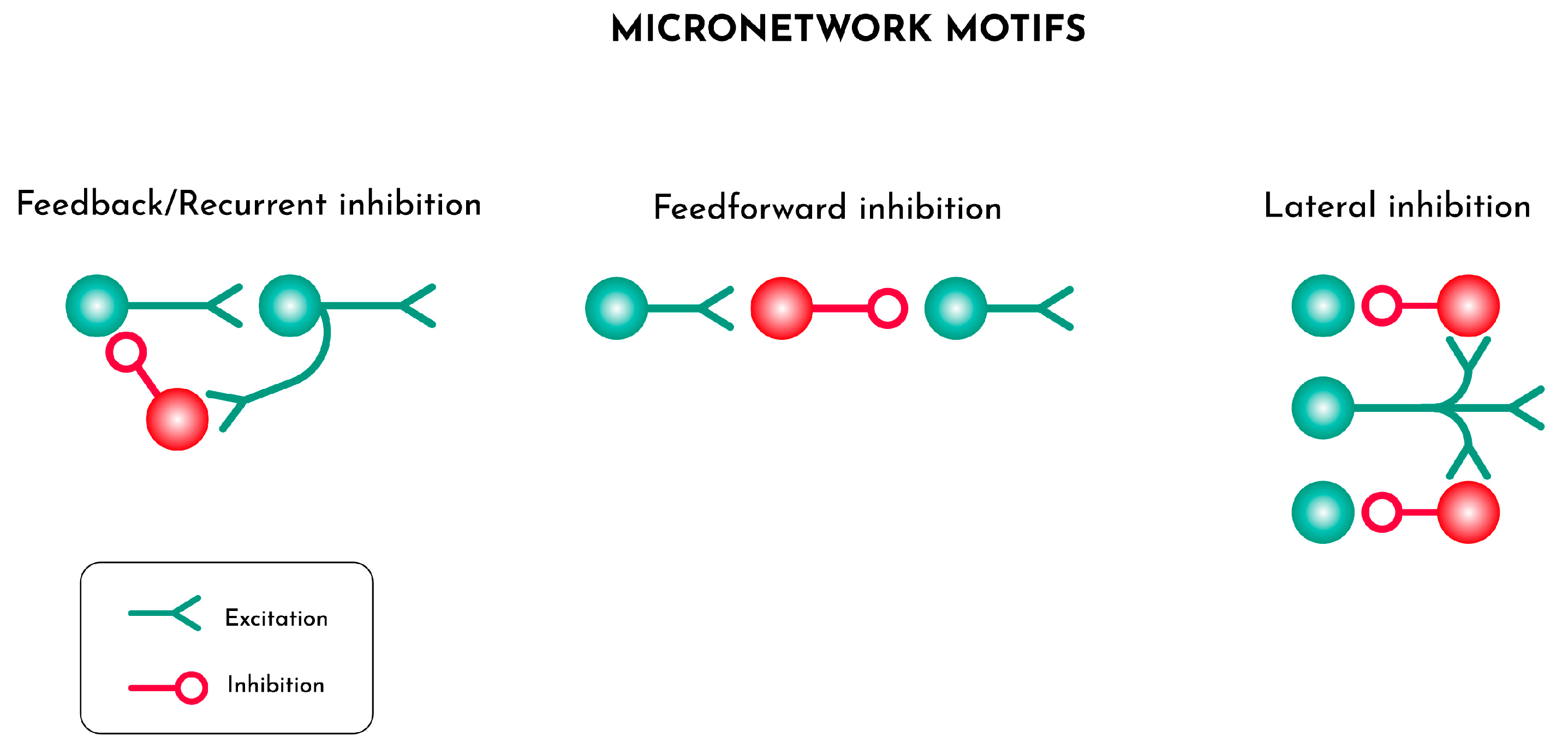
2.1. Populations and Networks
2.2. Excitation-Inhibition Balance
2.3. From Small-World and E/I Balanced Networks to Metastability
3. The Complexity of the Determinants of Brain Dynamics
- The development of small-world neural networks can be understood in the context of their interactions with the development of vascular networks.
- Homeostasis, and specifically a tight E/I balance, relies heavily on the role of glia, and particularly astrocytes.
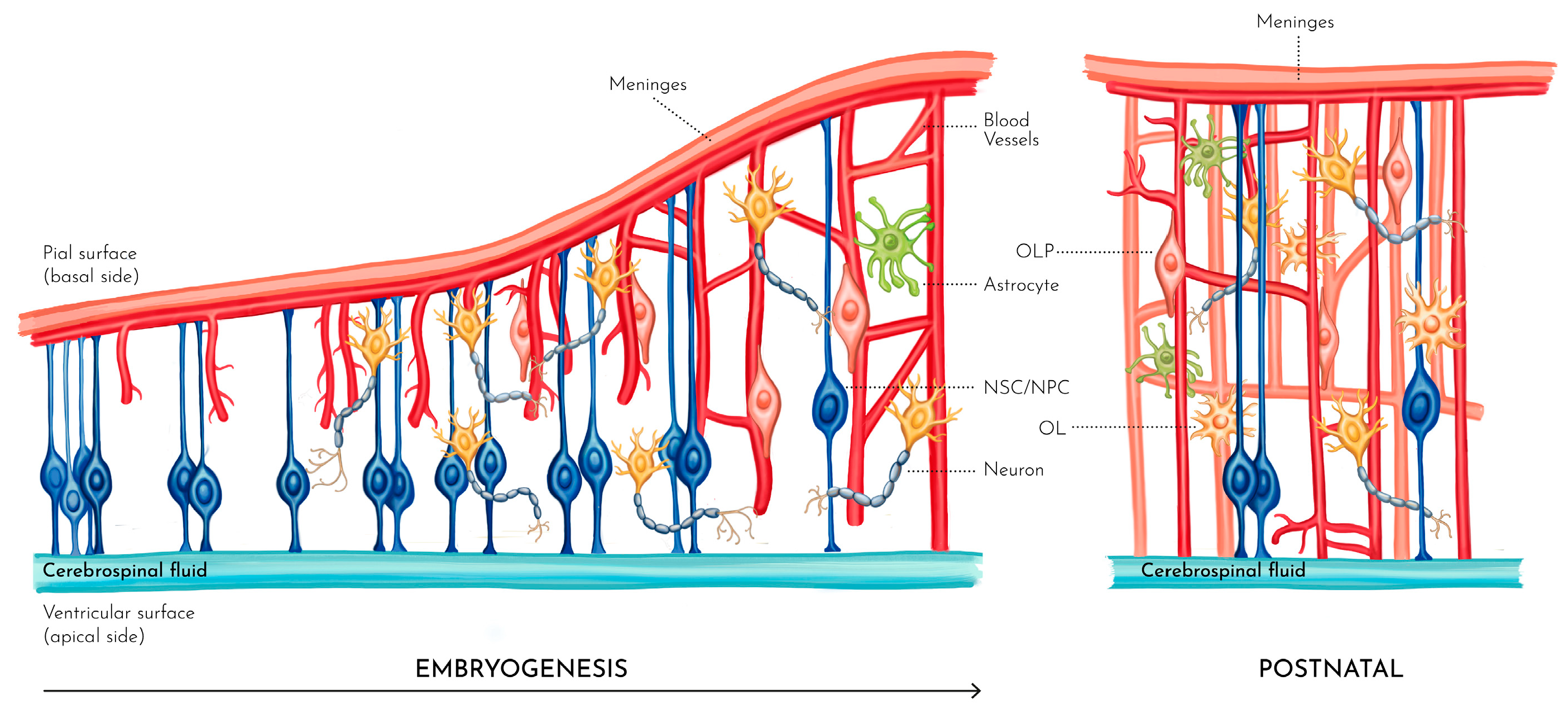
3.1. The Development of Neural Networks
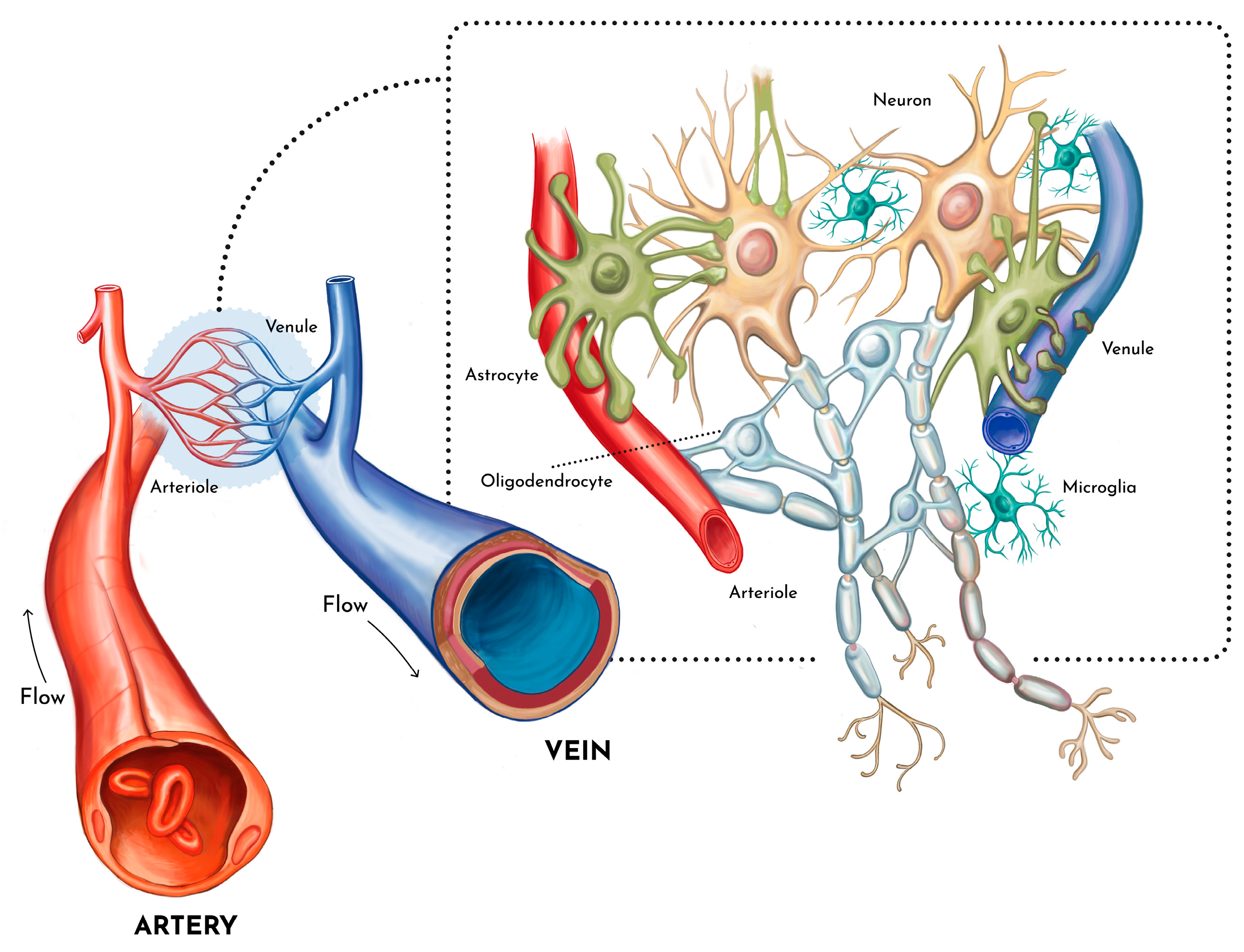
3.2. The Development and Cross-Talk of Vascular Networks
3.3. The Control of Excitation-Inhibition Ratio Balance
4. The Relevance of the Neurogliovascular Unit to Psychiatric Disorders
5. Conclusions
Acknowledgments
References
- Agnes, E.J.; Vogels, T.P. Co-dependent excitatory and inhibitory plasticity accounts for quick, stable and long-lasting memories in biological networks. Nat. Neurosci. 2024, 27, 964–974. [Google Scholar] [CrossRef] [PubMed]
- Akarca, D.; Vértes, P.E.; Bullmore, E.T.; Astle, D.E. A generative network model of neurodevelopmental diversity in structural brain organization. Nat Commun 2021, 12, 4216. [Google Scholar] [PubMed]
- Araque, A.; Parpura, V.; Sanzgiri, R.P.; Haydon, P.G. Glutamate-dependent astrocyte modulation of synaptic transmission between cultured hippocampal neurons. Eur. J. Neurosci. 1998, 10, 2129–2142. [Google Scholar] [CrossRef] [PubMed]
- Arnatkeviciute, A.; Fulcher, B.D.; Oldham, S.; Tiego, J.; Paquola, C.; Gerring, Z.; Aquino, K.; Hawi, Z.; Johnson, B.; Ball, G.; et al. Genetic influences on hub connectivity of the human connectome. Nat. Commun. 2021, 12, 1–14. [Google Scholar] [CrossRef]
- Azmitia, E.C.; Saccomano, Z.T.; Alzoobaee, M.F.; Boldrini, M.; Whitaker-Azmitia, P.M. Persistent Angiogenesis in the Autism Brain: An Immunocytochemical Study of Postmortem Cortex, Brainstem and Cerebellum. J. Autism Dev. Disord. 2015, 46, 1307–1318. [Google Scholar] [CrossRef]
- Balchandani, P.; Naidich, T.P. Ultra-High-Field MR Neuroimaging. AJNR Am J Neuroradiol 2015, 36, 1204–15. [Google Scholar] [CrossRef]
- Barabási, D.L.; Bianconi, G.; Bullmore, E.; Burgess, M.; Chung, S.; Eliassi-Rad, T.; George, D.; Kovács, I.A.; Makse, H.; Nichols, T.E.; et al. Neuroscience Needs Network Science. J. Neurosci. 2023, 43, 5989–5995. [Google Scholar] [CrossRef]
- Bassett, D.S.; Bullmore, E.T. Small-World Brain Networks Revisited. Neuroscientist 2017, 23, 499–516. [Google Scholar]
- Bassett, D.S.; Meyer-Lindenberg, A.; Achard, S.; Duke, T.; Bullmore, E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proc. Natl. Acad. Sci. 2006, 103, 19518–19523. [Google Scholar] [CrossRef]
- Bassett, D.S.; Zurn, P.; Gold, J.I. On the nature and use of models in network neuroscience. Nat. Rev. Neurosci. 2018, 19, 566–578. [Google Scholar] [CrossRef]
- Bassingthwaighte, J.B. Fractal Vascular Growth Patterns. Acta Stereol 1992, 11 (Suppl. 1), 305–319. [Google Scholar] [PubMed]
- Beaulieu, C. Numerical data on neocortical neurons in adult rat, with special reference to the GABA population. Brain Res. 1993, 609, 284–292. [Google Scholar] [CrossRef] [PubMed]
- Belan, P.; Kostyuk, P. Glutamate-receptor-induced modulation of GABAergic synaptic transmission in the hippocampus. Pfl?gers Arch. Eur. J. Physiol. 2002, 444, 26–37. [Google Scholar] [CrossRef] [PubMed]
- Börgers, C.; Kopell, N. Synchronization in Networks of Excitatory and Inhibitory Neurons with Sparse, Random Connectivity. Neural Comput. 2003, 15, 509–538. [Google Scholar] [CrossRef]
- Brambilla, P.; Cerini, R.; Fabene, P.F.; Andreone, N.; Rambaldelli, G.; Farace, P.; Versace, A.; Perlini, C.; Pelizza, L.; Gasparini, A.; et al. Assessment of cerebral blood volume in schizophrenia: A magnetic resonance imaging study. J. Psychiatr. Res. 2007, 41, 502–510. [Google Scholar] [CrossRef]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef]
- Brembs, B. The brain as a dynamically active organ. Biochem Biophys Res Commun 2020, 564, 55–69. [Google Scholar] [CrossRef]
- Bremermann, H.J. Limits of Genetic Control. IEEE Transactions on Military Electronics 1963, MIL-7, 200–205. [Google Scholar] [CrossRef]
- Brynildsen, J.K.; Rajan, K.; Henderson, M.X.; Bassett, D.S. Network models to enhance the translational impact of cross-species studies. Nat. Rev. Neurosci. 2023, 24, 575–588. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. The economy of brain network organization. Nat. Rev. Neurosci. 2012, 13, 336–349. [Google Scholar] [CrossRef]
- Buzsáki, G.; Wang, X.-J. Mechanisms of Gamma Oscillations. Annu. Rev. Neurosci. 2012, 35, 203–225. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Hugues, E.; Sporns, O.; Deco, G. Role of local network oscillations in resting-state functional connectivity. NeuroImage 2011, 57, 130–139. [Google Scholar] [CrossRef] [PubMed]
- Calzavarini, F.; Cevolani, G. Abductive reasoning in cognitive neuroscience: weak and strong reverse inference. Synthese 2022, 200, 1–26. [Google Scholar] [CrossRef]
- Captur, G.; Karperien, A.L.; Hughes, A.D.; Francis, D.P.; Moon, J.C. The fractal heart — embracing mathematics in the cardiology clinic. Nat. Rev. Cardiol. 2016, 14, 56–64. [Google Scholar] [CrossRef]
- Cardy, J.; Täuber, U.C. Theory of Branching and Annihilating Random Walks. Phys. Rev. Lett. 1996, 77, 4780–4783. [Google Scholar] [CrossRef]
- Carmeliet, P.; Tessier-Lavigne, M. Common mechanisms of nerve and blood vessel wiring. Nature 2005, 436, 193–200. [Google Scholar] [CrossRef]
- Caserta, F.; Eldred, W.; Fernandez, E.; Hausman, R.; Stanford, L.; Bulderev, S.; Schwarzer, S.; Stanley, H. Determination of fractal dimension of physiologically characterized neurons in two and three dimensions. J. Neurosci. Methods 1995, 56, 133–144. [Google Scholar] [CrossRef]
- Castaldo, F.; dos Santos, F.P.; Timms, R.C.; Cabral, J.; Vohryzek, J.; Deco, G.; Woolrich, M.; Friston, K.; Verschure, P.; Litvak, V. Multi-modal and multi-model interrogation of large-scale functional brain networks. NeuroImage 2023, 277, 120236. [Google Scholar] [CrossRef]
- Clark-Raymond, A.; Halaris, A. VEGF and depression: A comprehensive assessment of clinical data. J. Psychiatr. Res. 2013, 47, 1080–1087. [Google Scholar] [CrossRef]
- Collignon, A.; Dion-Albert, L.; Ménard, C.; Coelho-Santos, V. Sex, hormones and cerebrovascular function: from development to disorder. Fluids Barriers CNS 2024, 21, 1–19. [Google Scholar] [CrossRef]
- Colombo, M.A.; Napolitani, M.; Boly, M.; Gosseries, O.; Casarotto, S.; Rosanova, M.; Brichant, J.-F.; Boveroux, P.; Rex, S.; Laureys, S.; et al. The spectral exponent of the resting EEG indexes the presence of consciousness during unresponsiveness induced by propofol, xenon, and ketamine. 2019, 189, 631–644. [Google Scholar] [CrossRef] [PubMed]
- D’amour, J.A.; Froemke, R.C. Inhibitory and Excitatory Spike-Timing-Dependent Plasticity in the Auditory Cortex. Neuron 2015, 86, 514–528. [Google Scholar] [CrossRef] [PubMed]
- Deco G, Jirsa V, McIntosh AR, Sporns O, Kotter R. 2009. Key role of coupling, delay, and noise in resting brain fluctuations. Proc Natl Acad Sci U S A 2009, 106, 10302-7.
- Deco, G.; Kringelbach, M.L.; Arnatkeviciute, A.; Oldham, S.; Sabaroedin, K.; Rogasch, N.C.; Aquino, K.M.; Fornito, A. Dynamical consequences of regional heterogeneity in the brain’s transcriptional landscape. Sci. Adv. 2021, 7, eabf4752. [Google Scholar] [CrossRef]
- Deco, G.; Ponce-Alvarez, A.; Hagmann, P.; Romani, G.L.; Mantini, D.; Corbetta, M. How Local Excitation-Inhibition Ratio Impacts the Whole Brain Dynamics. J. Neurosci. 2014, 34, 7886–7898. [Google Scholar] [CrossRef]
- Demirtaş, M.; Burt, J.B.; Helmer, M.; Ji, J.L.; Adkinson, B.D.; Glasser, M.F.; Van Essen, D.C.; Sotiropoulos, S.N.; Anticevic, A.; Murray, J.D. Hierarchical Heterogeneity across Human Cortex Shapes Large-Scale Neural Dynamics. Neuron 2019, 101, 1181–1194.e13. [Google Scholar] [CrossRef]
- Duclos, K.K.; Hendrikse, J.L.; Jamniczky, H.A. Investigating the evolution and development of biological complexity under the framework of epigenetics. Evol. Dev. 2019, 21, 276–293. [Google Scholar] [CrossRef]
- Eichmann, A.; Thomas, J.-L. Molecular Parallels between Neural and Vascular Development. Cold Spring Harb. Perspect. Med. 2013, 3, a006551. [Google Scholar] [CrossRef]
- Fields, R.D.; Araque, A.; Johansen-Berg, H.; Lim, S.-S.; Lynch, G.; Nave, K.-A.; Nedergaard, M.; Perez, R.; Sejnowski, T.; Wake, H. Glial Biology in Learning and Cognition. Neurosci. 2013, 20, 426–431. [Google Scholar] [CrossRef]
- Flanagan, B.; McDaid, L.; Wade, J.J.; Toman, M.; Wong-Lin, K.; Harkin, J. A Computational Study of Astrocytic GABA Release at the Glutamatergic Synapse: EAAT-2 and GAT-3 Coupled Dynamics. Front. Cell. Neurosci. 2021, 15, 682460. [Google Scholar] [CrossRef]
- Fornito, A.; Zalesky, A.; Breakspear, M. The connectomics of brain disorders. Nat. Rev. Neurosci. 2015, 16, 159–172. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Transients, metastability, and neuronal dynamics. Neuroimage 1997, 5, 164–71. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Peterson, E.J.; Voytek, B. Inferring synaptic excitation/inhibition balance from field potentials. NeuroImage 2017, 158, 70–78. [Google Scholar] [CrossRef]
- Gerhardt, H.; Golding, M.; Fruttiger, M.; Ruhrberg, C.; Lundkvist, A.; Abramsson, A.; Jeltsch, M.; Mitchell, C.; Alitalo, K.; Shima, D.; et al. VEGF guides angiogenic sprouting utilizing endothelial tip cell filopodia. J. Cell Biol. 2003, 161, 1163–1177. [Google Scholar] [CrossRef] [PubMed]
- Gollo, L.L.; Breakspear, M. The frustrated brain: from dynamics on motifs to communities and networks. Philos. Trans. R. Soc. B: Biol. Sci. 2014, 369, 20130532. [Google Scholar] [CrossRef] [PubMed]
- Goulas, A.; Changeux, J.-P.; Wagstyl, K.; Amunts, K.; Palomero-Gallagher, N.; Hilgetag, C.C. The natural axis of transmitter receptor distribution in the human cerebral cortex. Proc. Natl. Acad. Sci. 2021, 118. [Google Scholar] [CrossRef]
- Guidolin, D.; Fede, C.; Tortorella, C. Nerve cells developmental processes and the dynamic role of cytokine signaling. Int. J. Dev. Neurosci. 2018, 77, 3–17. [Google Scholar] [CrossRef]
- Han, J.; Kesner, P.; Metna-Laurent, M.; Duan, T.; Xu, L.; Georges, F.; Koehl, M.; Abrous, D.N.; Mendizabal-Zubiaga, J.; Grandes, P.; et al. Acute Cannabinoids Impair Working Memory through Astroglial CB1 Receptor Modulation of Hippocampal LTD. Cell 2012, 148, 1039–1050. [Google Scholar] [CrossRef]
- Hancock, F.; Rosas, F.E.; Luppi, A.I.; Zhang, M.; Mediano, P.A.M.; Cabral, J. Metastability demystified - the foundational past, the pragmatic present and the promising future. Nat Rev Neurosci. 2024. [CrossRef]
- Hancock, F.; Rosas, F.E.; Mediano, P.A.M.; Luppi, A.I.; Cabral, J.; Dipasquale, O. May the 4C's be with you: an overview of complexity-inspired frameworks for analysing resting-state neuroimaging data. J R Soc Interface 2022, 19, 20220214. [Google Scholar] [CrossRef]
- Hannezo, E.; Scheele, C.L.G.J.; Moad, M.; Drogo, N.; Heer, R.; Sampogna, R.V.; van Rheenen, J.; Simons, B.D. A Unifying Theory of Branching Morphogenesis. Cell 2017, 171, 242–255.e27. [Google Scholar] [CrossRef] [PubMed]
- Hanson, D.R.; I Gottesman, I. Theories of schizophrenia: a genetic-inflammatory-vascular synthesis. BMC Med Genet. 2005, 6, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Hellyer, P.J.; Scott, G.; Shanahan, M.; Sharp, D.J.; Leech, R. Cognitive Flexibility through Metastable Neural Dynamics Is Disrupted by Damage to the Structural Connectome. J. Neurosci. 2015, 35, 9050–9063. [Google Scholar] [CrossRef]
- Helmstaedter, M.; Sakmann, B.; Feldmeyer, D. Neuronal Correlates of Local, Lateral, and Translaminar Inhibition with Reference to Cortical Columns. Cereb. Cortex 2008, 19, 926–937. [Google Scholar] [CrossRef] [PubMed]
- Hevner, R.; Daza, R.; Englund, C.; Kohtz, J.; Fink, A. Postnatal shifts of interneuron position in the neocortex of normal and reeler mice: evidence for inward radial migration. Neuroscience 2004, 124, 605–618. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. Bull Math Biol 1990, 52, 25–71; discussion 5. [Google Scholar] [CrossRef]
- Hollestein, V.; Poelmans, G.; Forde, N.J.; Beckmann, C.F.; Ecker, C.; Mann, C.; Schäfer, T.; Moessnang, C.; Baumeister, S.; Banaschewski, T.; et al. Excitatory/inhibitory imbalance in autism: the role of glutamate and GABA gene-sets in symptoms and cortical brain structure. Transl. Psychiatry 2023, 13, 1–9. [Google Scholar] [CrossRef]
- Honey, C.J.; Sporns, O.; Cammoun, L.; Gigandet, X.; Thiran, J.P.; Meuli, R.; Hagmann, P. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. 2009, 106, 2035–2040. [Google Scholar] [CrossRef]
- Hoseth, E.Z.; Krull, F.; Dieset, I.; Mørch, R.H.; Hope, S.; Gardsjord, E.S.; Steen, N.E.; Melle, I.; Brattbakk, H.-R.; Steen, V.M.; et al. Attenuated Notch signaling in schizophrenia and bipolar disorder. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Howarth, C.; Gleeson, P.; Attwell, D. Updated Energy Budgets for Neural Computation in the Neocortex and Cerebellum. J. Cereb. Blood Flow Metab. 2012, 32, 1222–1232. [Google Scholar] [CrossRef]
- Howarth, C.; Peppiatt-Wildman, C.M.; Attwell, D. The Energy Use Associated with Neural Computation in the Cerebellum. J. Cereb. Blood Flow Metab. 2009, 30, 403–414. [Google Scholar] [CrossRef] [PubMed]
- Hua, J.; Brandt, A.S.; Lee, S.; Blair, N.I.S.; Wu, Y.; Lui, S.; Patel, J.; Faria, A.V.; Lim, I.A.L.; Unschuld, P.G.; et al. Abnormal Grey Matter Arteriolar Cerebral Blood Volume in Schizophrenia Measured With 3D Inflow-Based Vascular-Space-Occupancy MRI at 7T. Schizophr. Bull. 2016, 43, 620–632. [Google Scholar] [CrossRef]
- Hua, J.; Qin, Q.; Donahue, M.J.; Zhou, J.; Pekar, J.J.; van Zijl, P.C. Inflow-based vascular-space-occupancy (iVASO) MRI. Magn Reson Med 2011, 66, 40–56. [Google Scholar] [PubMed]
- Hunter, P.J.; Borg, T.K. Integration from proteins to organs: the Physiome Project. Nat. Rev. Mol. Cell Biol. 2003, 4, 237–243. [Google Scholar] [CrossRef]
- Iadecola, C. The Neurovascular Unit Coming of Age: A Journey through Neurovascular Coupling in Health and Disease. Neuron 2017, 96, 17–42. [Google Scholar] [CrossRef]
- Ii, S.; Kitade, H.; Ishida, S.; Imai, Y.; Watanabe, Y.; Wada, S. Multiscale modeling of human cerebrovasculature: A hybrid approach using image-based geometry and a mathematical algorithm. PLOS Comput. Biol. 2020, 16, e1007943. [Google Scholar] [CrossRef]
- Isaacson, J.S.; Scanziani, M. How Inhibition Shapes Cortical Activity. Neuron 2011, 72, 231–243. [Google Scholar] [CrossRef]
- Izhikevich, E.M.; Edelman, G.M. Large-scale model of mammalian thalamocortical systems. Proc. Natl. Acad. Sci. 2008, 105, 3593–3598. [Google Scholar] [CrossRef]
- A Jelen, L.; King, S.; Mullins, P.G.; Stone, J.M. Beyond static measures: A review of functional magnetic resonance spectroscopy and its potential to investigate dynamic glutamatergic abnormalities in schizophrenia. J. Psychopharmacol. 2018, 32, 497–508. [Google Scholar] [CrossRef]
- A Jones, C.; Li, D.Y. Common cues regulate neural and vascular patterning. Curr. Opin. Genet. Dev. 2007, 17, 332–336. [Google Scholar] [CrossRef]
- Jourdain, P.; Bergersen, L.H.; Bhaukaurally, K.; Bezzi, P.; Santello, M.; Domercq, M.; Matute, C.; Tonello, F.; Gundersen, V.; Volterra, A. Glutamate exocytosis from astrocytes controls synaptic strength. Nat. Neurosci. 2007, 10, 331–339. [Google Scholar] [CrossRef] [PubMed]
- Kalil, K.; Dent, E.W. Branch management: mechanisms of axon branching in the developing vertebrate CNS. Nat. Rev. Neurosci. 2013, 15, 7–18. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Jiang, L.; Goldman, S.A.; Nedergaard, M. Astrocyte-mediated potentiation of inhibitory synaptic transmission. Nat. Neurosci. 1998, 1, 683–692. [Google Scholar] [CrossRef] [PubMed]
- Karch, R.; Neumann, F.; Neumann, M.; Schreiner, W. A three-dimensional model for arterial tree representation, generated by constrained constructive optimization. Comput. Biol. Med. 1999, 29, 19–38. [Google Scholar] [CrossRef]
- Katsel, P.; Roussos, P.; Pletnikov, M.; Haroutunian, V. Microvascular anomaly conditions in psychiatric disease. Schizophrenia – angiogenesis connection. Neurosci. Biobehav. Rev. 2017, 77, 327–339. [Google Scholar] [CrossRef]
- Kauffman, S.A. Antichaos and Adaptation. Sci. Am. 1991, 265, 78–84. [Google Scholar] [CrossRef]
- Kersanté, F.; Rowley, S.C.S.; Pavlov, I.; Gutièrrez-Mecinas, M.; Semyanov, A.; Reul, J.M.H.M.; Walker, M.C.; Linthorst, A.C.E. A functional role for both γ-aminobutyric acid (GABA) transporter-1 and GABA transporter-3 in the modulation of extracellular GABA and GABAergic tonic conductances in the rat hippocampus. J. Physiol. 2013, 591, 2429–2441. [Google Scholar] [CrossRef]
- Kim, J.; Kwon, N.; Chang, S.; Kim, K.-T.; Lee, D.; Kim, S.; Yun, S.J.; Hwang, D.; Kim, J.W.; Hwu, Y.; et al. Altered branching patterns of Purkinje cells in mouse model for cortical development disorder. Sci. Rep. 2011, 1, 122. [Google Scholar] [CrossRef]
- Kirchner, J.H.; Gjorgjieva, J. Emergence of local and global synaptic organization on cortical dendrites. Nat. Commun. 2021, 12, 1–18. [Google Scholar] [CrossRef]
- Kong, X.; Kong, R.; Orban, C.; Wang, P.; Zhang, S.; Anderson, K.; Holmes, A.; Murray, J.D.; Deco, G.; Heuvel, M.v.D.; et al. Sensory-motor cortices shape functional connectivity dynamics in the human brain. Nat. Commun. 2021, 12, 1–15. [Google Scholar] [CrossRef]
- Kumar, B.S.; Menon, S.C.; Gayathri, S.R.; Chakravarthy, V.S. The Influence of Neural Activity and Neural Cytoarchitecture on Cerebrovascular Arborization: A Computational Model. Front. Neurosci. 2022, 16, 917196. [Google Scholar] [CrossRef] [PubMed]
- Lawn, T.; Howard, M.A.; Turkheimer, F.; Misic, B.; Deco, G.; Martins, D.; Dipasquale, O. From neurotransmitters to networks: Transcending organisational hierarchies with molecular-informed functional imaging. Neurosci. Biobehav. Rev. 2023, 150, 105193. [Google Scholar] [CrossRef] [PubMed]
- Lea-Carnall, C.A.; El-Deredy, W.; Stagg, C.J.; Williams, S.R.; Trujillo-Barreto, N.J. A mean-field model of glutamate and GABA synaptic dynamics for functional MRS. NeuroImage 2022, 266, 119813–119813. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.-H.; Kim, Y.-K. Increased plasma VEGF levels in major depressive or manic episodes in patients with mood disorders. J. Affect. Disord. 2012, 136, 181–184. [Google Scholar] [CrossRef]
- Libby, J.; Marghoub, A.; Johnson, D.; Khonsari, R.H.; Fagan, M.J.; Moazen, M. Modelling human skull growth: a validated computational model. J. R. Soc. Interface 2017, 14, 20170202. [Google Scholar] [CrossRef]
- Lim, L.; Mi, D.; Llorca, A.; Marín, O. Development and functional diversification of cortical interneurons. Neuron 2018, 100, 294–313. [Google Scholar] [CrossRef]
- Lindenmayer, A. Mathematical models for cellular interactions in development. I. Filaments with one-sided inputs. J Theor Biol 1968, 18, 280–99. [Google Scholar]
- Litwin-Kumar, A.; Doiron, B. Formation and maintenance of neuronal assemblies through synaptic plasticity. Nat. Commun. 2014, 5, 5319–5319. [Google Scholar] [CrossRef]
- Liu, Q.-S.; Xu, Q.; Arcuino, G.; Kang, J.; Nedergaard, M. Astrocyte-mediated activation of neuronal kainate receptors. Proc. Natl. Acad. Sci. 2004, 101, 3172–3177. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, M.; Zhou, Y.; He, Y.; Hao, Y.; Song, M.; Yu, C.; Liu, H.; Liu, Z.; Jiang, T. Disrupted small-world networks in schizophrenia. Brain 2008, 131, 945–961. [Google Scholar] [CrossRef]
- Liu, Y.; Ouyang, P.; Zheng, Y.; Mi, L.; Zhao, J.; Ning, Y.; Guo, W. A Selective Review of the Excitatory-Inhibitory Imbalance in Schizophrenia: Underlying Biology, Genetics, Microcircuits, and Symptoms. Front. Cell Dev. Biol. 2021, 9. [Google Scholar] [CrossRef] [PubMed]
- Lodato, S.; Rouaux, C.; Quast, K.B.; Jantrachotechatchawan, C.; Studer, M.; Hensch, T.K.; Arlotta, P. Excitatory Projection Neuron Subtypes Control the Distribution of Local Inhibitory Interneurons in the Cerebral Cortex. Neuron 2011, 69, 763–779. [Google Scholar] [CrossRef] [PubMed]
- Lord, L.-D.; Expert, P.; Huckins, J.F.; E Turkheimer, F.E. Cerebral Energy Metabolism and the Brain’s Functional Network Architecture: An Integrative Review. Br. J. Pharmacol. 2013, 33, 1347–1354. [Google Scholar] [CrossRef]
- Lord, L.-D.; Stevner, A.B.; Deco, G.; Kringelbach, M.L. Understanding principles of integration and segregation using whole-brain computational connectomics: implications for neuropsychiatric disorders. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2017, 375, 20160283. [Google Scholar] [CrossRef]
- Luppi, A.I.; Rosas, F.E.; Mediano, P.A.; Menon, D.K.; Stamatakis, E.A. Information decomposition and the informational architecture of the brain. Trends Cogn. Sci. 2024, 28, 352–368. [Google Scholar] [CrossRef]
- Mapelli, J.; Gandolfi, D.; Vilella, A.; Zoli, M.; Bigiani, A. Heterosynaptic GABAergic plasticity bidirectionally driven by the activity of pre- and postsynaptic NMDA receptors. Proc. Natl. Acad. Sci. 2016, 113, 9898–9903. [Google Scholar] [CrossRef]
- Marcaggi, P.; Attwell, D. Role of glial amino acid transporters in synaptic transmission and brain energetics. Glia 2004, 47, 217–225. [Google Scholar] [CrossRef]
- Markello, R.D.; Hansen, J.Y.; Liu, Z.-Q.; Bazinet, V.; Shafiei, G.; Suárez, L.E.; Blostein, N.; Seidlitz, J.; Baillet, S.; Satterthwaite, T.D.; et al. neuromaps: structural and functional interpretation of brain maps. Nat. Methods 2022, 19, 1472–1479. [Google Scholar] [CrossRef]
- Meier, M.H.; Shalev, I.; Moffitt, T.E.; Kapur, S.; Keefe, R.S.; Wong, T.Y.; Belsky, D.W.; Harrington, H.; Hogan, S.; Houts, R.; et al. Microvascular Abnormality in Schizophrenia as Shown by Retinal Imaging. Am. J. Psychiatry 2013, 170, 1451–1459. [Google Scholar] [CrossRef]
- Menassa, D.A.; Gomez-Nicola, D. Microglial Dynamics During Human Brain Development. Front. Immunol. 2018, 9, 1014. [Google Scholar] [CrossRef]
- Meyer, H.S.; Schwarz, D.; Wimmer, V.C.; Schmitt, A.C.; Kerr, J.N.D.; Sakmann, B.; Helmstaedter, M. Inhibitory interneurons in a cortical column form hot zones of inhibition in layers 2 and 5A. Proc. Natl. Acad. Sci. 2011, 108, 16807–16812. [Google Scholar] [CrossRef] [PubMed]
- Milošević, N.T.; Ristanović, D. Fractality of dendritic arborization of spinal cord neurons. Neurosci. Lett. 2006, 396, 172–176. [Google Scholar] [CrossRef] [PubMed]
- Min, R.; Nevian, T. Astrocyte signaling controls spike timing–dependent depression at neocortical synapses. Nat. Neurosci. 2012, 15, 746–753. [Google Scholar] [CrossRef] [PubMed]
- Miyoshi, G.; Hjerling-Leffler, J.; Karayannis, T.; Sousa, V.H.; Butt, S.J.B.; Battiste, J.; Johnson, J.E.; Machold, R.P.; Fishell, G. Genetic Fate Mapping Reveals That the Caudal Ganglionic Eminence Produces a Large and Diverse Population of Superficial Cortical Interneurons. J. Neurosci. 2010, 30, 1582–1594. [Google Scholar] [CrossRef]
- Morigiwa, K.; Tauchi, M.; Fukuda, Y. Fractal analysis of ganglion cell dendritic branching patterns of the rat and cat retinae. Neurosci. Res. Suppl. 1989, 10, S131–S139. [Google Scholar] [CrossRef]
- Muldoon, S.F.; Bridgeford, E.W.; Bassett, D.S. Small-World Propensity and Weighted Brain Networks. Sci. Rep. 2016, 6, 22057. [Google Scholar] [CrossRef]
- Navarrete, M.; Perea, G.; de Sevilla, D.F.; Gómez-Gonzalo, M.; Núñez, A.; Martín, E.D.; Araque, A. Astrocytes Mediate In Vivo Cholinergic-Induced Synaptic Plasticity. PLOS Biol. 2012, 10, e1001259. [Google Scholar] [CrossRef]
- Nunes, F.D.D.; Ferezin, L.P.; Pereira, S.C.; Figaro-Drumond, F.V.; Pinheiro, L.C.; Menezes, I.C.; Baes, C.v.W.; Coeli-Lacchini, F.B.; Tanus-Santos, J.E.; Juruena, M.F.; et al. The Association of Biochemical and Genetic Biomarkers in VEGF Pathway with Depression. Pharmaceutics 2022, 14, 2757. [Google Scholar] [CrossRef]
- Ofer, N.; Shefi, O.; Yaari, G. Branching morphology determines signal propagation dynamics in neurons. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Okun, M.; Lampl, I. Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities. Nat. Neurosci. 2008, 11, 535–537. [Google Scholar] [CrossRef]
- Oldham, S.; Fulcher, B.D.; Aquino, K.; Arnatkevičiūtė, A.; Paquola, C.; Shishegar, R.; Fornito, A. Modeling spatial, developmental, physiological, and topological constraints on human brain connectivity. Sci. Adv. 2022, 8, eabm6127. [Google Scholar] [CrossRef] [PubMed]
- Öz, G.; Seaquist, E.R.; Kumar, A.; Criego, A.B.; Benedict, L.E.; Rao, J.P.; Henry, P.-G.; Van De Moortele, P.-F.; Gruetter, R.; Heinonen, I.; et al. Human brain glycogen content and metabolism: implications on its role in brain energy metabolism. Am. J. Physiol. Metab. 2007, 292, E946–E951. [Google Scholar] [CrossRef]
- Palmer, T.D.; Willhoite, A.R.; Gage, F.H. Vascular niche for adult hippocampal neurogenesis. J Comp Neurol 2000, 425, 479–94. [Google Scholar] [CrossRef] [PubMed]
- Pandit, A.S.; Expert, P.; Lambiotte, R.; Bonnelle, V.; Leech, R.; Turkheimer, F.E.; Sharp, D.J. Traumatic brain injury impairs small-world topology. Neurology 2013, 80, 1826–1833. [Google Scholar] [CrossRef] [PubMed]
- Papo, D.; Buldú, J. Does the brain behave like a (complex) network? I. Dynamics. Phys. Life Rev. 2023, 48, 47–98. [Google Scholar] [CrossRef]
- Páscoa dos Santos F, Verschure PF. 2024. Metastable Dynamics Emerge from Local Excitatory-Inhibitory Homeostasis in the Cortex at Rest. bioRxiv:2024.08.24.609501.
- Peyrounette, M.; Davit, Y.; Quintard, M.; Lorthois, S. Multiscale modelling of blood flow in cerebral microcirculation: Details at capillary scale control accuracy at the level of the cortex. PLOS ONE 2018, 13, e0189474. [Google Scholar] [CrossRef]
- Pla, R.; Stanco, A.; Howard, M.A.; Rubin, A.N.; Vogt, D.; Mortimer, N. Dlx1 and Dlx2 Promote Interneuron GABA Synthesis, Synaptogenesis, and Dendritogenesis. Cereb Cortex 2018, 28, 3797–3815. [Google Scholar] [CrossRef]
- Podvalny, E.; Noy, N.; Harel, M.; Bickel, S.; Chechik, G.; Schroeder, C.E.; Mehta, A.D.; Tsodyks, M.; Malach, R. A unifying principle underlying the extracellular field potential spectral responses in the human cortex. J. Neurophysiol. 2015, 114, 505–519. [Google Scholar] [CrossRef]
- Poil, S.S.; Hardstone, R.; Mansvelder, H.D.; Linkenkaer-Hansen, K. Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks. J Neurosci 2012, 32, 9817–23. [Google Scholar] [CrossRef]
- Pope, M.; Fukushima, M.; Betzel, R.F.; Sporns, O. Modular origins of high-amplitude cofluctuations in fine-scale functional connectivity dynamics. Proc. Natl. Acad. Sci. 2021, 118. [Google Scholar] [CrossRef]
- Pulvermüller, F.; Tomasello, R.; Henningsen-Schomers, M.R.; Wennekers, T. Biological constraints on neural network models of cognitive function. Nat. Rev. Neurosci. 2021, 22, 488–502. [Google Scholar] [CrossRef] [PubMed]
- Rae, C.D. A Guide to the Metabolic Pathways and Function of Metabolites Observed in Human Brain 1H Magnetic Resonance Spectra. Neurochem. Res. 2013, 39, 1–36. [Google Scholar] [CrossRef] [PubMed]
- Ramezanian-Panahi, M.; Abrevaya, G.; Gagnon-Audet, J.-C.; Voleti, V.; Rish, I.; Dumas, G. Generative Models of Brain Dynamics. Front. Artif. Intell. 2022, 5, 807406. [Google Scholar] [CrossRef]
- Ramón y Cajal, S. Textura del sistema nervioso del hombre y de los vertebrados : estudios sobre el plan estructural y composición histológica de los centros nerviosos adicionados de consideraciones fisiológicas fundadas en los nuevos descubrimientos: Madrid : N. Moya, 1899; 1899-1904.
- Roca, C.; Adams, R.H. Regulation of vascular morphogenesis by Notch signaling. Genes Dev. 2007, 21, 2511–2524. [Google Scholar] [CrossRef]
- Rothman, D.L.; Behar, K.L.; Hyder, F.; Shulman, R.G. In vivo NMR Studies of the Glutamate Neurotransmitter Flux and Neuroenergetics: Implications for Brain Function. Annu. Rev. Physiol. 2003, 65, 401–427. [Google Scholar] [CrossRef]
- Rowitch, D.H.; Kriegstein, A.R. Developmental genetics of vertebrate glial–cell specification. Nature 2010, 468, 214–222. [Google Scholar] [CrossRef]
- Rubinov, M. Distinctions between brain structure, complexity, and function. Comment on “Does the brain behave like a (complex) network? I. Dynamics” by Papo and Buldú. Physics of Life Reviews 2024, 50, 30–31. [Google Scholar]
- Sahara, S.; Yanagawa, Y.; O'Leary, D.D.M.; Stevens, C.F. The Fraction of Cortical GABAergic Neurons Is Constant from Near the Start of Cortical Neurogenesis to Adulthood. J. Neurosci. 2012, 32, 4755–4761. [Google Scholar] [CrossRef]
- Santello, M.; Bezzi, P. ; VolterraA. TNFalpha controls glutamatergic gliotransmission in the hippocampal dentate gyrus. Neuron 2011, 69, 988–1001. [Google Scholar]
- Santello, M.; Cali, C.; Bezzi, P. Gliotransmission and the tripartite synapse. Adv Exp Med Biol 2012, 970, 307–31. [Google Scholar]
- Shanahan, M. Metastable chimera states in community-structured oscillator networks. Chaos: Interdiscip. J. Nonlinear Sci. 2010, 20, 013108–013108. [Google Scholar] [CrossRef] [PubMed]
- Shipley, R.J.; Smith, A.F.; Sweeney, P.W.; Pries, A.R.; Secomb, T.W. A hybrid discrete–continuum approach for modelling microcirculatory blood flow. Math. Med. Biol. A J. IMA 2019, 37, 40–57. [Google Scholar] [CrossRef] [PubMed]
- Shonkoff JP, Phillips DA, National Research Council (U.S.). Committee on Integrating the Science of Early Childhood Development. 2000. From neurons to neighborhoods : the science of early child development. Washington, D.C.: National Academy Press. xviii, 588 p. p.
- Shu, Y.; Hasenstaub, A.; McCormick, D.A. Turning on and off recurrent balanced cortical activity. Nature 2003, 423, 288–293. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.L.; Trachtenberg, J.T. Experience-dependent binocular competition in the visual cortex begins at eye opening. Nat. Neurosci. 2007, 10, 370–375. [Google Scholar] [CrossRef]
- Smith, T.G., Jr.; Lange, G.D.; Marks, W.B. Fractal methods and results in cellular morphology--dimensions, lacunarity and multifractals. J Neurosci Methods 1996, 69, 123–36. [Google Scholar] [CrossRef]
- Southwell, D.G.; Paredes, M.F.; Galvao, R.P.; Jones, D.L.; Froemke, R.C.; Sebe, J.Y.; Alfaro-Cervello, C.; Tang, Y.; Garcia-Verdugo, J.M.; Rubenstein, J.L.; et al. Intrinsically determined cell death of developing cortical interneurons. Nature 2012, 491, 109–113. [Google Scholar] [CrossRef]
- Sporns, O. The complex brain: connectivity, dynamics, information. Trends Cogn Sci 2022, 26, 1066–1067. [Google Scholar] [CrossRef]
- Sporns, O.; Kötter, R. Motifs in Brain Networks. PLOS Biol. 2004, 2, e369–e369. [Google Scholar] [CrossRef]
- Stam, C.J.; Jones, B.F.; Nolte, G.; Breakspear, M.; Scheltens, P. Small-world networks and functional connectivity in Alzheimer's disease. Cereb Cortex 2007, 17, 92–9. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Takeda, T.; Ishikawa, A.; Ohtomo, K.; Kobayashi, Y.; Matsuoka, T. Fractal dimension of dendritic tree of cerebellar Purkinje cell during onto- and phylogenetic development. Neurosci. Res. 1992, 13, 19–31. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Edelman, G.M.; Sporns, O. Complexity and coherency: integrating information in the brain. Trends in Cognitive Sciences 1998, 2, 474–484. [Google Scholar] [CrossRef] [PubMed]
- Touboul, J.; Wendling, F.; Chauvel, P.; Faugeras, O. Neural mass activity, bifurcations, and epilepsy. Neural Comput 2011, 23, 3232–86. [Google Scholar] [CrossRef]
- Turkheimer, F.E.; Leech, R.; Expert, P.; Lord, L.-D.; Vernon, A.C. The brain's code and its canonical computational motifs. From sensory cortex to the default mode network: A multi-scale model of brain function in health and disease. Neurosci. Biobehav. Rev. 2015, 55, 211–222. [Google Scholar] [CrossRef] [PubMed]
- Turkheimer, F.E.; Rosas, F.E.; Dipasquale, O.; Martins, D.; Fagerholm, E.D.; Expert, P.; Váša, F.; Lord, L.-D.; Leech, R. A Complex Systems Perspective on Neuroimaging Studies of Behavior and Its Disorders. Neurosci. 2021, 28, 382–399. [Google Scholar] [CrossRef]
- van Vreeswijk, C.; Sompolinsky, H. Chaos in Neuronal Networks with Balanced Excitatory and Inhibitory Activity. Science 1996, 274, 1724–1726. [Google Scholar] [CrossRef]
- van Vreeswijk, C.; Sompolinsky, H. Chaotic Balanced State in a Model of Cortical Circuits. Neural Comput. 1998, 10, 1321–1371. [Google Scholar] [CrossRef]
- Váša, F.; Shanahan, M.; Hellyer, P.J.; Scott, G.; Cabral, J.; Leech, R. Effects of lesions on synchrony and metastability in cortical networks. NeuroImage 2015, 118, 456–467. [Google Scholar] [CrossRef]
- Verkhratsky, A.; Nedergaard, M. Astroglial cradle in the life of the synapse. Philos Trans R Soc Lond B Biol Sci 2014, 369, 20130595. [Google Scholar] [CrossRef]
- Verkhratsky, A.; Nedergaard, M. Physiology of Astroglia. Physiol Rev 2018, 98, 239–389. [Google Scholar] [CrossRef]
- Vértes, P.E.; Alexander-Bloch, A.F.; Gogtay, N.; Giedd, J.N.; Rapoport, J.L.; Bullmore, E.T. Simple models of human brain functional networks. Proc. Natl. Acad. Sci. 2012, 109, 5868–5873. [Google Scholar] [CrossRef] [PubMed]
- Vogels, T.P.; Sprekeler, H.; Zenke, F.; Clopath, C.; Gerstner, W. Inhibitory Plasticity Balances Excitation and Inhibition in Sensory Pathways and Memory Networks. Science 2011, 334, 1569–1573. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-J.; Buzsáki, G. Gamma Oscillation by Synaptic Inhibition in a Hippocampal Interneuronal Network Model. J. Neurosci. 1996, 16, 6402–6413. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yu, S.; Li, M. Neurovascular crosstalk and cerebrovascular alterations: an underestimated therapeutic target in autism spectrum disorders. Front. Cell. Neurosci. 2023, 17, 1226580. [Google Scholar] [CrossRef]
- Wang, Z.; Ying, Z.; Bosy-Westphal, A.; Zhang, J.; Schautz, B.; Later, W.; Heymsfield, S.B.; Müller, M.J. Specific metabolic rates of major organs and tissues across adulthood: evaluation by mechanistic model of resting energy expenditure. Am. J. Clin. Nutr. 2010, 92, 1369–1377. [Google Scholar] [CrossRef]
- Waschke, L.; Donoghue, T.; Fiedler, L.; Smith, S.; Garrett, D.D.; Voytek, B.; Obleser, J. Modality-specific tracking of attention and sensory statistics in the human electrophysiological spectral exponent. eLife 2021, 10. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Wearne, S.; Rodriguez, A.; Ehlenberger, D.; Rocher, A.; Henderson, S.; Hof, P. New techniques for imaging, digitization and analysis of three-dimensional neural morphology on multiple scales. 2005, 136, 661–680. [Google Scholar] [CrossRef]
- Wigström, H.; Gustafsson, B. Facilitation of hippocampal long-lasting potentiation by GABA antagonists. Acta Physiol. Scand. 1985, 125, 159–172. [Google Scholar] [CrossRef]
- Wu, G.K.; Tao, H.W.; Zhang, L.I. From elementary synaptic circuits to information processing in primary auditory cortex. Neurosci. Biobehav. Rev. 2011, 35, 2094–2104. [Google Scholar] [CrossRef]
- Wu, M.W.; Kourdougli, N.; Portera-Cailliau, C. Network state transitions during cortical development. Nat. Rev. Neurosci. 2024, 25, 535–552. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.; Stathopoulou, M.G.; de Andrés, F.; Siest, G.; Murray, H.; Martin, M.; Cobaleda, J.; Delgado, A.; Lamont, J.; Peñas-Liedó, E.; et al. VEGF-related polymorphisms identified by GWAS and risk for major depression. Transl. Psychiatry 2017, 7, e1055. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.C.; Vest, R.T.; Kern, F.; Lee, D.P.; Agam, M.; Maat, C.A.; Losada, P.M.; Chen, M.B.; Schaum, N.; Khoury, N.; et al. A human brain vascular atlas reveals diverse mediators of Alzheimer’s risk. Nature 2022, 603, 885–892. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; La Camera, G. Co-existence of synaptic plasticity and metastable dynamics in a spiking model of cortical circuits. PLoS Comput Biol 2024, 20, e1012220. [Google Scholar]
- Yang, Y.; Guan, W.; Sheng, X.-M.; Gu, H.-J. Role of Semaphorin 3A in common psychiatric illnesses such as schizophrenia, depression, and anxiety. Biochem. Pharmacol. 2024, 226, 116358. [Google Scholar] [CrossRef]
- Yarkoni, T.; A Poldrack, R.; E Nichols, T.; Van Essen, D.C.; Wager, T.D. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods 2011, 8, 665–670. [Google Scholar] [CrossRef]
- Ye, Z.; Mostajo-Radji, M.A.; Brown, J.R.; Rouaux, C.; Tomassy, G.S.; Hensch, T.K. Instructing Perisomatic Inhibition by Direct Lineage Reprogramming of Neocortical Projection Neurons. Neuron 2015, 88, 475–83. [Google Scholar]
- Zang, Y.; Chaudhari, K.; Bashaw, G.J. New insights into the molecular mechanisms of axon guidance receptor regulation and signaling. Curr Top Dev Biol 2021, 142, 147–196. [Google Scholar]
- Zhang S, Larsen B, Sydnor VJ, Zeng T, An L, Yan X and others. 2023. In-vivo whole-cortex estimation of excitation-inhibition ratio indexes cortical maturation and cognitive ability in youth. bioRxiv:2023.06.22.546023.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




