1. Introduction
Knowledge graph is a kind of graph-structured data for representing knowledge, which supports knowledge reasoning. Knowledge graphs are widely used in various applications such as information retrieval, recommendation, and natural language processing. However, most existing knowledge graphs are incomplete and need to be reasoned and completed. Regarding this purpose, Knowledge Graph Embedding (KGE) transforms knowledge into low-dimensional vector space, to obtain the form of quantifiable, computable and reasonable knowledge for knowledge graph completion. Existing KGE methods can be classified into two categories: static KGE and temporal KGE. Static knowledge embedding considers the representation of static triples without considering changes in entities and relations along with time. Temporal knowledge embedding focuses on modeling the dynamic evolutionary properties of knowledge.
There are two main categories of approaches to modeling temporal knowledge: timestamp transformation-based models and snapshot-based models.
Timestamp transformation-based models represent timestamps within text. They incorporates timestamps into embedding vectors of entities or relations, or model time using hyperplane projections.
Snapshot-based models represent temporal knowledge as a sequence of graphs, and using
time-and-graph or
time-then-graph to model graph structures [
1].
Figure 1 is a temporal knowledge graph example, and some of its knowledge is represented in quadruple displayed in
Table 1. The relation between entities consistently vary with time. The difficulty in complete temporal knowledge graph is modeling temporal information accurately to help complete historical knowledge or predict future fact.
LLMs have demonstrated remarkable success in natural language processing tasks. This leads to numerous research efforts in knowledge extraction, fusion, representation, and completion using pre-trained language models. However, there are the following challenges in directly applying large models to temporal knowledge graphs: 1) Calculation threshold: Training and fine-tuning large models require a significant amount of computational resources; 2) Prompt requirement: The use of large models requires the design of high-quality prompts; 3) Adaptation problem: The graph is generally sparse, and using large models can easily cause overfitting.
Recently, researchers have explored the design and application of small pre-trained language models (SLMs), and various small model architectures have emerged [
2]. The performance of small models in certain tasks is not inferior to that of large models, indicating that the task of completing temporal knowledge graphs may be relatively effective through simplified language model architecture.
Driven by this motivation, we explored the application of BERT, the most basic pre-trained language model (PLM) architecture whose parameter number is far less than LLM, in tasks related to temporal knowledge graphs. We propose TKG-BERT (Temporal Knowledge Graph by Bidirectional Encoder Representations from Transformers). Our approach extends the capabilities of pre-trained language models to capture temporal aspects by introducing three methods for modeling temporal knowledge: vanilla knowledge embedding, explicit time modeling and implicit time modeling. These methods leverage the pre-trained representations learned by BERT and aim to enhance the understanding and completion of TKGs. We conduct experiments with various temporal models and explore the capacity of TKG-BERT to model temporal knowledge. The contributions of this paper are summarized as follows:
Application of pre-trained language models to temporal knowledge graphs. This work explores the utilization of PLMs, specifically BERT, for temporal knowledge graph completion. It extends the application of PLMs beyond static KGs and investigates their effectiveness in capturing and modeling temporal aspects.
Three ways for temporal knowledge embedding. We introduce three methods: vanilla knowledge embedding, explicit time modeling and implicit time modeling for embedding temporal knowledge. Main fine-tuning tasks includes masked entity modeling, masked relation modeling, and tuple classification modeling.
Evaluation of PLM capacity for temporal knowledge modeling. We conducts experiments on two temporal KG datasets to assess the capacity of TKG-BERT in temporal knowledge completion. It evaluates the ability of TKG-BERT to conduct knowledge reasoning under different time modeling ways.
The rest of this paper is organized as follows:
Section 2 provides an overview of related work in temporal knowledge graph embedding and pre-trained language models for KGE.
Section 3 gives the notations and problem definition.
Section 4 presents the model architecture, and three time modeling methods of our proposed approach TKG-BERT.
Section 5 describes the experimental setup and presents the results and analysis. Finally,
Section 6 gives the discussions and conclusions of this research.
2. Related Work
In this section, we first introduce related research of temporal knowledge embedding, and then introduce some work of pre-trained language model for KGE.
2.1. Temporal KGE
Temporal knowledge graph embedding (TKGE) methods usually extends static KGE methods to model the information of temporal feature interactions, so as to learn the accurate knowledge embedding. TKGE has become the focus and attracted numerous scholars to explore in recent years.
Timestamp-based models includes tensor decomposition models and timestamp transformation-based models. Tensor decomposition models [
3,
4,
5,
6] decompose the tensor into low-dimensional matrices and consider timestamps as an additional mode of tensor, and then low-dimensional representations for timestamps are learned for the score measurement. Timestamp transformation-based models [
7,
8,
9,
10] regards timestamps as a transformation to learn the embedding for entity and/or relation corresponding to the specific time.
Dynamic-based embedding models [
6,
11,
12,
13,
14] aim at capturing the objective occurrence sequence or evolved mechanisms by encoding the dynamic relations. For example, flowering usually occurs before fruiting. Such sequential characteristics of such events can be modeled by these models. Snapshot-based models [
15,
16,
17,
18] divide the original knowledge graphs into a series of snapshots or subgraphs, so that the evolving subgraph that has varying relation connections can be learned. Historical context-based models [
10,
16,
17,
19,
20] rely on historical information to enhance the representation of dynamic knowledge.
The above embedding models are all designed for temporal knowledge graph, and they are inadequate in capturing the global information of knowledge graph. Moreover, the existing TKGE models are easy to lose the potential temporal semantic information.
2.2. PLM for KGE
Pre-trained language model [
21,
22,
23,
24,
25] have been studied to encode KG. These methods mainly extend self-attention to learn long-range pairwise relations in common graph, and learn rich structural and semantic information. In addition, some works attempt to change the input form of transformer or improve the architecture of transformer to form a unified model.
With the further application of pre-trained language model in graph, especially transformers-based models, various efforts for static knowledge graph embedding have been explored. Among them, KG-BERT [
26] takes triples in knowledge graph as textual sequences as the input of pre-trained language models such as BERT [
27]. PKGC [
28] converts each triple and relevant attributes into prompt sentences, and further fed into PLM. HittER [
29] designs a hierarchical Transformer for KGE, and uses entity and context information as key additional information. KGTransformer [
30] uses masked pretraining and fine-tuning strategies based on transformer. SimKGC [
31] applies contrastive learning to KGE. The proposed method include three types of negatives: in-batch negatives, pre-batch negatives, and self-negatives which act as a simple form of hard negatives, which improves the performance of PLMs in KGE. Relphormer [
32] uses Triple2Seq and uniformly regards entities and relations as nodes. In addition, the proposed structure-enhanced mechanism effectively preserve the important structural information in the context subgraph, which is particularly beneficial in handling complex structure knowledge.
For temporal knowledge graph, TEMT [
33] predicts time intervals of facts by fusing their textual and temporal information. It also supports inductive inference by utilizing PLMs. PPT [
34] converts a series of sampled quadruples into pre-trained language model inputs and convert intervals between timestamps into different prompts to make coherent sentences with implicit semantic information. However, these method all involve the design of prompt to achieve a slight improvement.
3. Notations and Problem Definition
We first list the general notations used in model description in
Table 2, and define the problem of temporal knowledge graph.
A temporal knowledge graph
can be formalized by quadruple
(
s,
r,
o,
t), which is a triple with timestamp
t. The quadruple denote an fact that happen at timestamp
t, where
.
and
are subject entity and object entity, respectively.
denote a relationship fact between
s and
o. The notations used in this seciton are listed in
Table 2.
There are three common tasks of temporal knowledge embedding: entity prediction, relation prediction, and tuple classification. Entity prediction is to predict the missing subject entity s in the incomplete quadruple (?, r, o, t) or the missing object entity o in (s, r, ?, t). Relation prediction is to predict the missing relation r in (s, ?, o, t). Tuple classification is to determine whether the given tuple (s, r, o, t) is correct or incorrect.
For ease of reading, the abbreviations and meanings of the three models proposed in this study are listed in
Table 3, as well as the abbreviations and explanations of the knowledge graph completion tasks that were adopted.
4. Methodology
This section introduce our proposed temporal knowledge graph embedding approach: TKG-BERT. We illustrate model architecture of TKG-BERT in
Section 4.1. Then, we introduced three temporal knowledge modeling methods based on TKG-BERT in sequence, including vanilla, explicit, and implicit modeling. We provide a detailed introduction on how to design and perform input-output tasks for each of these three different modeling approaches.
4.1. Overview of Temporal Knowledge Graph BERT
BERT (Bidirectional Encoder Representations from Transformers) [
27] is a pre-trained language model based on multi-layer Transformer encoder [
35]. BERT learns deep bidirectional representations from unlabeled text by jointly conditioning on both the left and right context in all layers. The same as other language model, BERT consists of two steps: pre-training and fine-tuning. During pre-training, BERT is trained on large scale unlabeled general domain corpus. In fine-tuning phase, BERT is initialized with pre-traind parameters, and then is fine-tuned on specific domain corpus and tasks such as named entity recognition, question answering, and sentence pair classification.
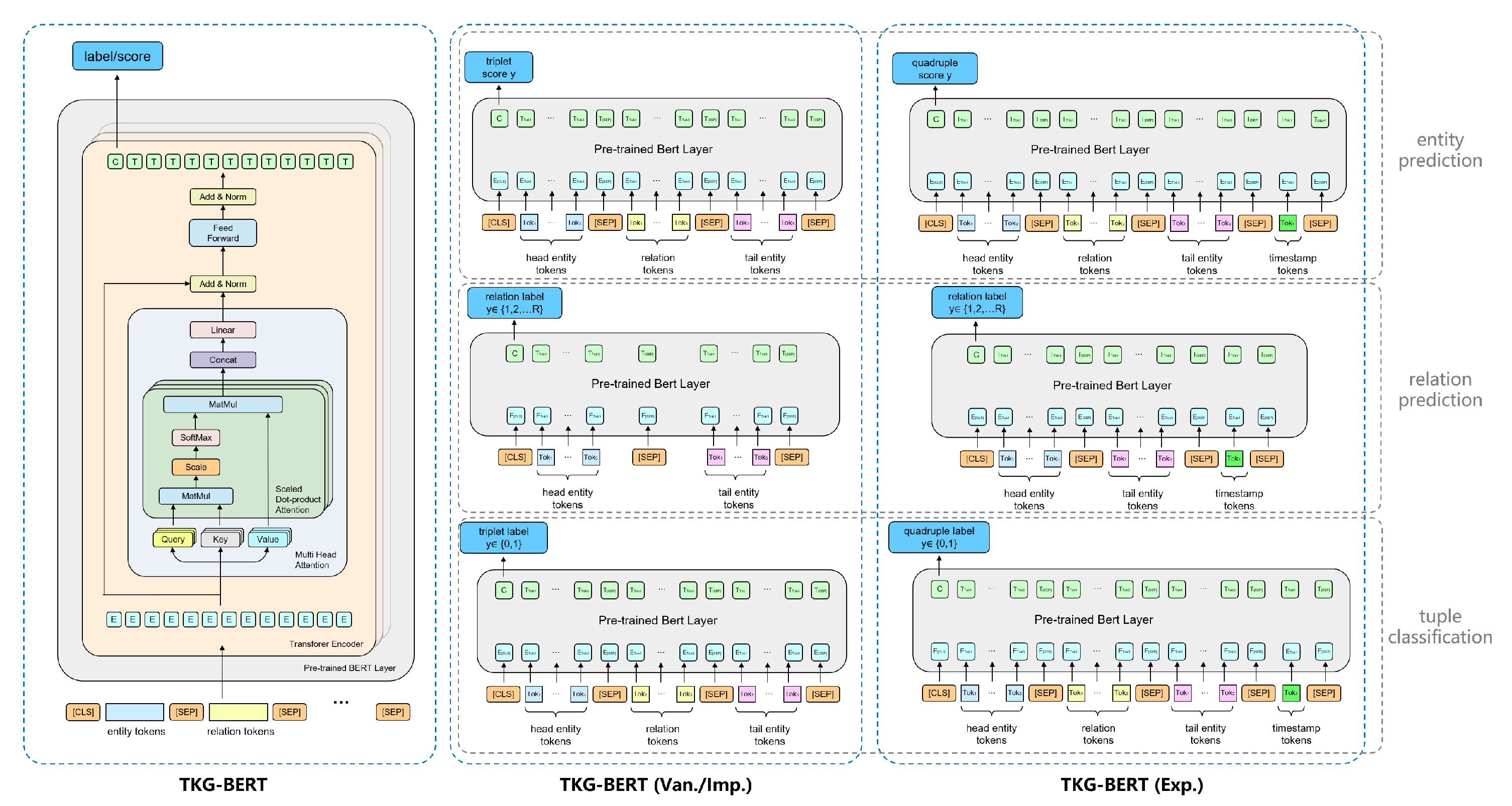
To leverage the rich language patterns and contextual representations effectively, we fine-tune the pre-trained BERT model for temporal knowledge completion tasks. We concatenate the entity tokens, relation tokens, and timestamp tokens as word sequences into BERT for fine-tuning. Such architecture is called TKG-BERT (Temporal Knowledge Graph based on BERT). TKG-BERT utilize pre-trained BERT (BERT_base), and are fine-tuned on sequence classification with temporal knowldge graph corpus.
The left part of
Figure 2 shows the architecture of TKG-BERT for modeling knowledge represented by tuple (triple or quadruple). For each tuple, we represent the entities and relation as their text word sequences. TKG-BERT take entity and relation word sequences as the input sentence for fine-tuning. As shown in
Figure 2, we concatenate the word sequences of (
s,
r,
o) as a single input sequence, i.e., the input token sequence to BERT. This is the general universal architecture, because the inpput tokens and the output labels maybe different according to different modeling modes. For example, there is an temporal quadruple:
(
Islamic Rebirth Party,
Make a visit,
Tatarstan,
2014-03-21),
Figure 2.
Illustrations of fine-tuning TKG-BERT with different time moedling ways on various tasks.
Figure 2.
Illustrations of fine-tuning TKG-BERT with different time moedling ways on various tasks.
KG-BERT takes the following token sequences as an input:
([CLS], Islamic, Rebirth, Party, [SEP], Make, visit, [SEP], Tatarstan, [SEP], 2014-03-21, [SEP]).
In original BERT, [CLS] is the special symbol for classification output, and [SEP] is the special symbol to separate non-consecutive token sequences. In our TKG-BERT, the first token of each input sequence is always [CLS], denoting the tuple representation is fed into an output layer for classification. The word sequences of entities and relations are seperated by [SEP].
Token sequences of knowledge are input into pre-trained BERT to generate embeddings (blue blocks marked with
E in
Figure 2). The embedding of each given token is generated by summing token embedding, segment embedding, and position embedding. Token embedding is the original word embedding of current token. Segment embedding is the embedding to distinguish the tokens in different segment. The tokens seperated by
[SEP] have different segment embeddings, whereas tokens within one same entity or relation have the same segment embedding. Position embedding aims to fuse position information, so different tokens at the same position have the same position embedding. The token embeddings are fed into BERT, generate the final hidden vectors (green blocks marked with "
C" and "
T" in
Figure 2) after Transformer encoding. The final hidden vector "
C" is used for aggregating sequence representation for computing the final label. Other hidden vectors marked "
T" corresponds to entity tokens, relation tokens, and
[SEP] tokens. Label denotes the final output given input triple, which is different due to different training task and mode.
The pre-trained BERT layer consists of 12 bidirectional Transformer encoders. Each bidirectional Transformer encoder implements a multi-head self-attention. The multi-head attention generate multiple sets of (
Q,
K,
V) according to different weight matrices.
Q,
K,
V refers to query, key, and value in multi-head self-attention. Transformer calculate attention according to Equation (
1). The output of Multi-head attention is Equation (
2). The final hidden vector
T are calculated by Equation (
3), wherein
is the output of normalized multi-head after residual, calculated by Equation (
4).
Building on the above, we designed three approaches for fine-tuning TKG-BERT on temporal knowledge graph reasoning tasks. This enables us to investigate whether temporal information plays a role when using language models for knowledge graph reasoning, as well as the extent to which different temporal modeling methods affect the reasoning outcomes.
4.2. Vanilla Knowledge Embedding of TKG-BERT
The vanilla knowledge embedding design of TKG-BERT (Abbreviated as TKG-BERT (Van.)) intends to investigate its performance on temporal knowledge graph tasks without incorporating temporal information. The task modeling approach for TKG-BERT (Van.) is illustrated in the middle section of
Figure 2. Under this configuration, TKG-BERT does not model the temporal information present in the temporal knowledge graph but instead trains and predicts using only the static triple components of the temporal quadruples: (
s,
r,
o). The tasks are identical to those performed on static knowledge graphs.
Original BERT randomly masks some tokens of the input sequences and then predict those masked token. Inspired by this masked language modeling, TKG-BERT adopts masking entity or relation in triple to learning their embeddings. As depicted, the three tasks include entity prediction, relation prediction, and triple classification. For the entity prediction task, masked entity modeling is employed, while for the relation prediction task, masked relation modeling is used.
Masked entity modeling is to construct positive and negative tuple samples by randomly corrupt the subject entity s or the object entity o. TKG-BERT will learning the optimal embeddings to make the triple scores of positive and negative samples seperated as far as possible. Then during the test phase, the masked entity would be predicted towards the correct scoring.
Masked relaiton modeling is to delete the relation in input tuple sequence. Only the subject entity and object entity are input into fine-tuning. The relations are regarded as labels. TKG-BERT learns to embedding the entities towards fitting the relation label representations.
The architecture of TKG-BERT(Van.) for triple classification mode is shown in
Figure 2. On this task, TKG-BERT also take the concatenation of word sequences of entities and relation as token sequence input, whereas the output label denotes the quadruple is true or false.
4.3. Explicit Time Modeling of TKG-BERT
Explicit Temporal Modeling of TKG-BERT (Abbreviated as TKG-BERT (Exp.)) refers to the process of explicitly incorporating time-related information into models designed for handling data that has a temporal component. This modeling method typically involves the explicit representation and utilization of timestamps or other temporal features in the learning and inference mechanisms of the model.
Temporal knowledge graph is usually formally represented as quadruple: (
s,
r,
o,
t), wherein
t is the time that the triple fact happens. Explicit time modeling is to treat the timestamp as individual elements as entity and relaiton, and learn the embedding of the timestamp. Compared to TKG-BERT(Van.) with no temporal modeling, TKG-BERT(Exp.) embeds timestamps alongside entities and relations, appending the timestamp token after the entity-relation triple, thereby inputting the temporal quadruples into the model. Tasks under explicit temporal modeling include entity prediction with timestamps, relation prediction with timestamps, and quadruple classification. The inputs and outputs for these three tasks are illustrated in the right part of
Figure 2.
TKG-BERT(Exp.) for predicting entity takes the concatenation of subject entity, relation, object entity, and timestamp in quadruple as token sequence input. Embedded by the pre-trained BERT layer, the token embeddings are transformed to final hidden vectors. The hidden vector C of the special token [CLS] aggregates the sequence representation, then calculate the quadruple score as the model output.
TKG-BERT(Exp.) for predicting relation only use the tokens of subject entity
s, the object entity
o, and timestamp
t to predict the relation
r between them. In preliminary of KG-BERT [
36], predicting with two entities directly is better than using entity prediction mode with relation corruption. So we adopt the same way for predicting relation. After encoding and final hidden vector generating, the model output the relation label
of given entity pair.
TKG-BERT(Exp.) for quadruple classification takes the quadruple as token sequence input. The only difference between quadruple classification and triple classification is the addition of the timestamp. Quadruple classification also adopt binary classification, distinguish positive and negative quadruple samples.
4.4. Implicit Time Modeling of TKG-BERT
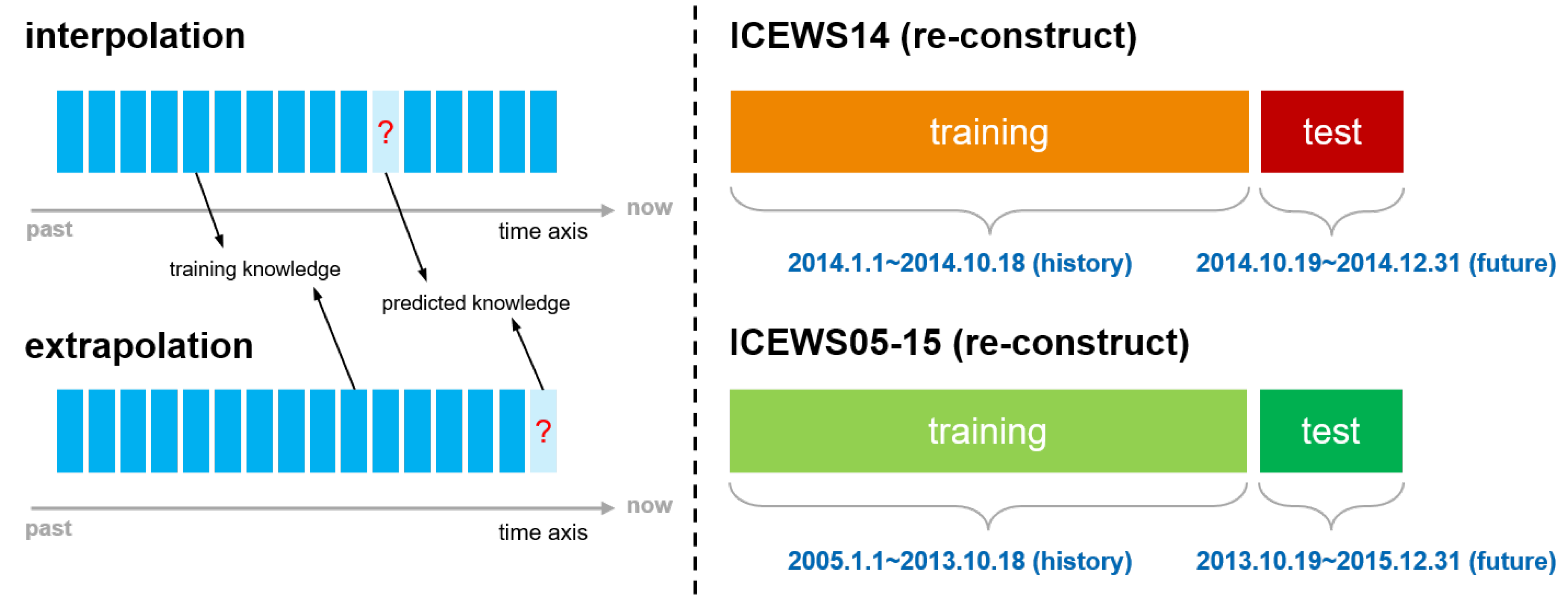
In previous research on temporal knowledge graphs, the modes of knowledge prediction include interpolation and extrapolation. As shown in the left part of
Figure 3, "interpolation" involves randomly selecting a portion of the knowledge for model training and speculating on the missing knowledge. In this mode, the model may infer missing historical knowledge based on knowledge from future time points. "Interpolation" mode corresponds to vanilla knowledge modeling of TKG-BERT. "Extrapolation", on the other hand, involves training the model using historical data and then reasoning or predicting knowledge at future time points. In the previous subsection on explicit temporal modeling, we adopted the interpolation setting. However, in practice, the extrapolation mode is more aligned with practical applications. Therefore, we designed a time modeling approach under the extrapolation setting, which is the implicit temporal modeling (Abbreviated as TKG-BERT (Imp.)).
As illustrated in the right part of
Figure 3, we restructured the two datasets used in this study according to their temporal order, selecting 80% of the historical data for the training set and the more recent data for the test set. Under this setting, similar to the TKG-BERT(Van.), we do not explicitly embed temporal information such as timestamps. Instead, we implicitly model time through the restructuring of the dataset , learning from history to predict the future.
TKG-BERT(Imp.) captures temporal dynamics within a KG without explicitly encoding or representing time-related information. In this method, the model learns to infer temporal patterns and dependencies from the input data itself, rather than relying on explicit timestamps or time intervals. For the given temporal knowledge graph, we reconstruct the graph, create training set by selecting the fact quadruples that occurred relatively earlier, and conduct entity or relation prediction of the fact quadruples which occurr in a relatively future time.
4.5. Training Loss
The three modeling ways of TKG-BERT use different training objectives. For entity prediction tasks and tuple classification tasks, we train the model by learning the scores of tuples, so that the scores of positive samples are much higher than those of negative samples. The acquisition of negative samples is generated through negative sampling.
The scoring function for a quadruple (
s,
r,
o,
t) is
, where
W is the classification layer weights and, "
C" is the output embedding of token
[CLS]. Given the positive quadruple set
and a negative triple set
, constructed accordingly, we calculate cross-entropy loss with
and triple labels:
where
is the label (negative or positive) of that quadruple. The negative quadruple set
is simply generated by replacing subject entity
s or object entity
r in a positive quadruple
with a randomly entity
or
.
where
is the set of entities. A quadruple will not be treated as a negative example if it is already in positive set
. The pre-trained parameter weights and new weights
W can be updated via gradient descent.
For relation prediction task, the final hidden state "C" corresponding to [CLS] is used as the representation of the two entities. The only new parameters introduced in relation prediction fine-tuning are classification layer weights , where R is the number of relations in a KG. The scoring function for a quadruple is .
We compute the following cross-entropy loss with
and relation labels:
where
is an observed positive triple,
is the relation indicator for the triple
when
and
when
5. Experiments
We conduct abundant experiments to evaluate the performance of TKG-BERT on public temporal KG datasets. In the following sections, we first introduce experiment settings, including dataset selection, evaluation tasks and metrics, and hyperparameter settings. Then we present each part of the experiment results, analyze the role of time and temporal information in knowledge reasoning tasks.
5.1. Experimental Settings
This section introduces the temporal knowledge graph dataset used in this research, the experimental tasks, and the evaluation metrics, as well as the of hyperparameter settings during model training.
5.1.1. Datasets
We evaluate TKG-BERT on two temporal KG dataset: ICEWS14 and ICEWS05-15. They are constructed from ICEWS (Integrated Crisis Early Warning System) [
37], an periodic updated event graph. ICEWS consists of events that represent interactions between the socio-political actors (for instance, cooperative or hostile actions between individuals, groups, sectors and nation states). ICEWS has been discontinued, changed to POLECAT
1. POLECAT contains event data from 2018 to the present, updated weekly, and previously events of terminated years stored monthly. Event knowledge are stored in fields according to an event standard. However, as most of the research and experiments on temporal knowledge graphs are based on the ICEWS dataset, we also used this series of datasets for research purposes in order to facilitate performance comparison with baseline models.
ICEWS14 and ICEWS05-15 used in this work are subsets of the data present in the ICEWS repository as created by Garcia-Duran et al. [
38]. The statistics of the 2 datasets are listed in
Table 4. ICEWS14 is a short-range dataset consisting of the events that occurred in 2014. ICEWS05-15 is a long-range dataset consisting of the events that occurred between 2005 to 2015. We take the same partition proportion for training/validation/test set as DE [
39], which is a classic temporal KGE model.
5.1.2. Tasks and Metrics
Four kinds of tasks are adopted to evaluate different time modeling way of TKG-BERT, including
sop,
rp,
tc, and
qc, as listed in
Table 5. The most principal task for temporal knowledge graph completion (TKGC) is
sop, namely entity prediction. It aims to forecast the absent entity within a test quadruple (
s, r, o, t). Specifically, it means predicting the missing
s when presented with (
?, r, o, t), or predicting the missing
o when given (
s, r, ?, t). For each test quadruple, we substitute the unknown entity with every candidate entity from the entity set
, thereby creating a collection of corrupted quadruples. We then evaluate these corrupted quadruples using temporal KG embedding models to assign scores.
A superior model should position the genuine quadruple ahead of the corrupted ones in its ranking. Consequently, we ascertain the rank of the genuine quadruple among the corrupted set. The mean rank across all test quadruples is denoted as MR, while the mean reciprocal rank is referred to as MRR. Hits@n measures the percentage of correctly predicted entities that appear within the top n ranks. Lower MR values, higher MRR values, and increased Hits@n percentages all indicate enhanced model performance. To conduct a quantitative comparison of different models, we utilize the widely accepted evaluation metrics: Mean Rank (MR), Mean Reciprocal Rank (MRR), and Hits@n (where the value of n is 1, 3, and 10).
5.1.3. Hyper-Parameter Setting
TKG-BERT are implemented with deep learning framework PyTorch and is trained on GPU of NVIDIA GeForce RTX 4090. Unless otherwise specified, we take the default setting for all hyper-parameters, which are listed as follows: learning rate is , training batch size is 32, evaluation batch size is 135, the max token sequence is limited to 15, the training epochs are 5.0, negative ratio is 2, embedding size is 50, output embedding dimension is 100; we use multi-head attention in fine-tuning, and set the number of head to 2, the margin of hinge loss is 5. We use pre-trained BERT word embeddings bert-base-uncased.
5.2. Temporal Knowledge Graph Completion
This section is the main experimental part of TKGC, which includes three temporal knowledge modeling methods for subject entity and object entity prediction, relation prediction, and tuple classification tasks.
5.2.1. Comparison on Entity Prediction
For entity prediction task, we compare TKG-BERT with two categories of models: static KGE model and temporal KGE model. We compare TKG-BERT (Van.) with static KGE models to explore their completion capabilities without temporal modeling. Meanwhile, TKG-BERT(Exp.) and TKG-BERT(Imp.) are contrasted with temporal models to investigate the performance gains achieved through time-aware information modeling.
Compared static models: DistMult [
40], ComplEx [
41], R-GCN [
42], ConvE [
43], ConvTransE [
44], RotatE [
45].
Compared temporal models under the interpolation setting: HyTE [
46], TTransE [
47], TA-DistMult [
38], and DE [
39]. The interpolation setting is appropriate for the comparison of TKG-BERT(Exp.).
Compared temporal models under the extrapolation setting: RG-CRN [
48], CyGNet [
49], RE-NET [
50], RE-GCN [
19]. The extrapolation setting is appropriate for comparison of TKG-BERT(Imp.).
Table 6 present the entity prediction results on the test sets of ICEWS14 and ICEWS05-15. The results of baseline models are from RE-GCN [
20]. As demonstrated in the table, the three time modeling approaches of TKG-BERT consistently outperform the baselines across most metrics, showing significant improvements.
Specifically, for static knowledge graph embedding, which there is no time information modeling, TKG-BERT(Van.) far exceed all baselines. On ICEWS14, TKG-BERT(Van.) achieves the improvements of 20.42%(51.92-31.50) on MRR, 14.0% (36.26-22.46) on Hits@1, 27.9% (62.88-34.98) on Hits@3, 28.17% (78.20-50.03) on Hits@10, compared with suboptimal model (ConvTransE). On ICEWS05-15, TKG-BERT(Van.) achieves the improvements of 35.06%(85.34-30.28) on MRR, 37.51% (59.07-21.56) on Hits@1, 32.36% (68.06-35.70) on Hits@3, 21.73% (72.69-50.96) on Hits@10 compared with suboptimal model (ConvTransE). There is a huge improvement in both ICEWS14 and ICEWS05-15, and the improvement in ICEWS05-15 is greater than that in ICEWS14.
For temporal knowledge graph embedding under interpolation setting, corresponding to explicit time modeling, TKG-BERT(Exp.) also show superiority on entity prediction. On ICEWS14, TKG-BERT(Exp.) achieves the improvements of 2.07%(52.17-50.10) on MRR, 0.92% (40.12-39.20) on Hits@1, 1.37% (58.27-56.90) on Hits@3, 0.11% (70.91-70.80) on Hits@10 compared with suboptimal model (DE-DistMult). On ICEWS05-15, TKG-BERT(Exp.) achieves the improvements of 5.18%(53.58-48.40) on MRR, 1.94% (38.54-36.60) on Hits@1, 8.77% (63.37-54.60) on Hits@3, 4.19% (75.99-71.80) on Hits@10 compared with suboptimal model (DE-DistMult). The effect improvement of TKG-BERT(Exp.) is relatively small compared to TKG-BERT(Van.), and the improvement on ICEWS05-15 is slightly higher than that on ICEWS14.
For temporal knowledge graph embedding under extrapolation setting, corresponding to implicit time modeling. TKG-BERT(Imp.) also show superiority on entity prediction. On ICEWS14, TKG-BERT(Imp.) achieves the improvements of 11.57%(49.35-37.78) on MRR, 8.47% (35.64-27.17) on Hits@1, 14.83% (57.33-42.50) on Hits@3, 16.92% (75.76-58.84) on Hits@10 compared with suboptimal model (RE-GCN). On ICEWS05-15, TKG-BERT(Exp.) achieves the improvements of 12.3%(50.57-38.27) on MRR, 12% (39.43-27.43) on Hits@1, 11.91% (54.97-43.06) on Hits@3, 9.32% (69.25-59.93) on Hits@10 compared with suboptimal model (RE-GCN). The effect improvement of TKG-BERT(Imp.) is relatively significant compared to TKG-BERT(Exp.), whereas the improvement on ICEWS14 and that on ICEWS05-15 is almost equivalent.
The excellent performance of TKG-BERT shows the powerful contextual prediction capability of BERT. According to the statistics of three datasets in
Table 4, ICEWS05-15 has more complicated graph structure than ICEWS14. Correspondingly, the entity prediction results on ICEWS05-15 is better compared with ICEWS14. These results indicates that TKG-BERT take good advantage of BERT because it is expert in dealing with complex graph structure. Futhermore, From the comparative results of the three types of KGE models, it can be seen that without utilizing time information, the entity prediction capability of TKG-BERT far exceeds that of static models. However, under conditions where time modeling is employed, the improvement in TKG-BERT’s performance is limited. TKG-BERT with implicit time modeling (TKG-BERT(Imp.)) has a slight advantage over TKG-BERT with explicit time modeling (TKG-BERT(Exp.)) in entity prediction. This is because implicit time modeling and explicit time modeling are equivalent to different tasks, with implicit modeling being more difficult and therefore performing worse.
5.2.2. Relation Prediction and Tuple Classification
In addition to entity prediction, relation prediction and tuple classification are also common tasks used to evaluate the effectiveness of knowledge graph embedding and completion. We conducted comparisons of the three time modeling approaches of TKG-BERT on the ICEWS14 and ICEWS05-15 datasets. For relation prediction and triple classification, we do not find baseline models on these two datasets. The analysis for TKG-BERT on these two tasks is conducted by self-comparing.
The results of relation prediction and tuple classification are listed in
Table 7 and
Table 8. From the table, we can see that the overall performance ranking of the three modeling approaches of TKG-BERT is: TKG-BERT (Exp.) > TKG-BERT (Van.) > TKG-BERT (Imp.). Comparing them pairwise, TKG-BERT (Exp.) includes timestamp information in addition to what TKG-BERT (Van.) does, resulting in a slight improvement in performance. Compared to TKG-BERT (Van.), TKG-BERT (Imp.) does not utilize timestamp information either, but it reconstructs the dataset according to chronological order, training on historical data and predicting future data, which falls under the ’extrapolation’ setting for model evaluation. In contrast, TKG-BERT (Van.) operates under the ’interpolation’ setting, which is relatively easier as it does not strictly adhere to chronological data division, allowing the model to infer answers for historical test samples from future data. This may contribute to its seemingly better performance. When comparing TKG-BERT (Exp.) and TKG-BERT (Imp.), TKG-BERT (Exp.) performs interpolation tasks with the assistance of timestamps, while TKG-BERT (Imp.) performs extrapolation tasks without timestamps, thus TKG-BERT (Exp.) achieves better results than TKG-BERT (Imp.).
The relation predict accuracy is about 0.4. Hits@1, Hits@3, and Hits@10 are about 0.4, 0.6, and 0.8, respectively. For tuple classification, the F1, precision, recall and accuracy are basically between 0.8 and 0.9. The overall performance of tuple classification tasks is better than that of entity prediction and relation prediction tasks, because the difficulty of binary classification tasks for tuples is lower than that of multi classification tasks for entity or relation prediction. In practical applications, entity and relation classification are suitable for more refined predictions and require greater computational complexity.
5.2.3. Mean Rank of Entity and Relation
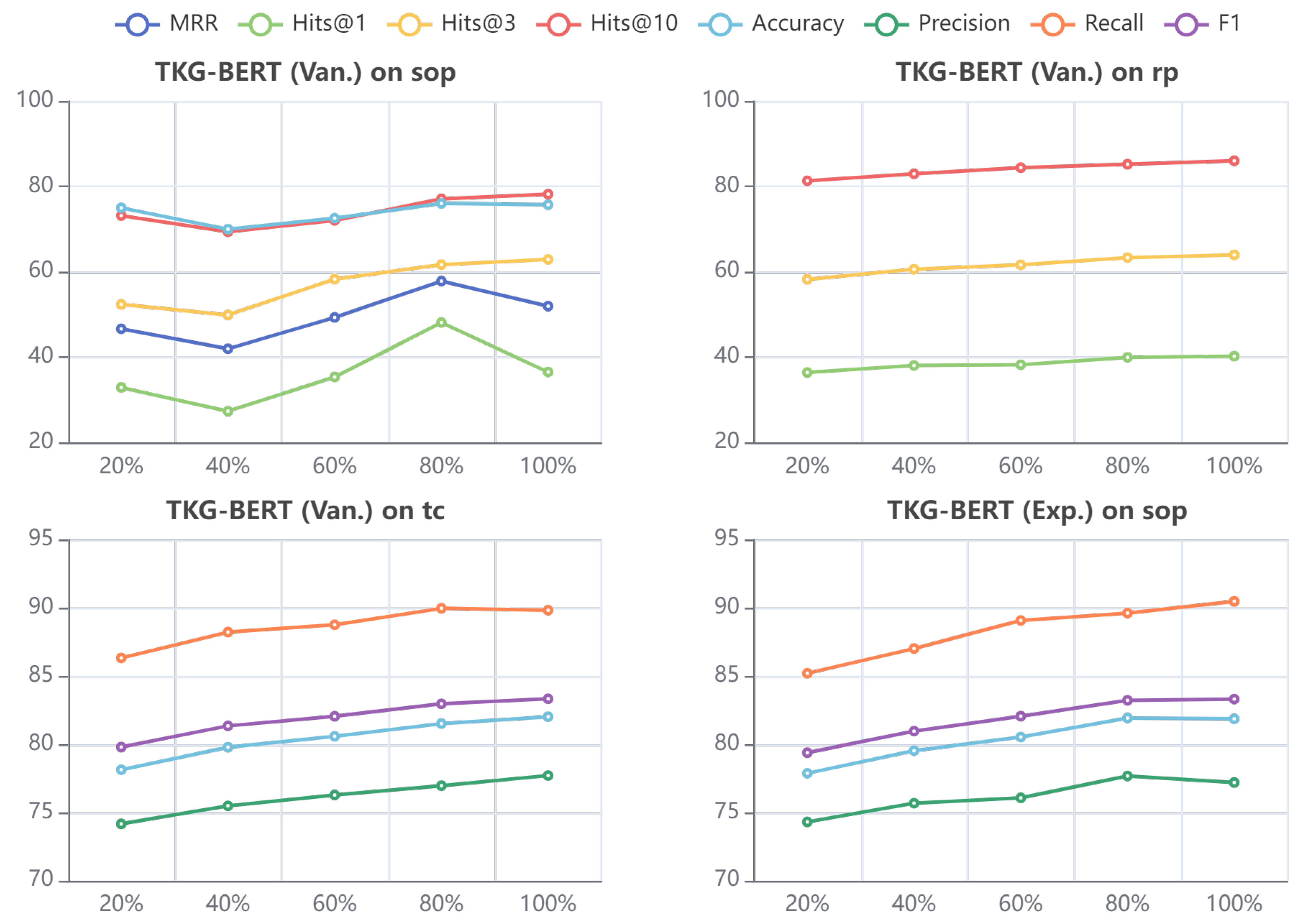
We have visualized the Mean Rank (MR) values for entities and relations in our entity prediction and relation prediction experiments, and the results are shown in
Figure 4. It can be seen from the figure that, TKG-BERT reduces the entity MR of entity prediction task for both datasets to 6 and 7 respectively. This means that the vast majority of entities are trained to have ranked mean values of about 6 and 7 in entity prediction task. Since other research works usually do not focus on this metric, the baseline under this metric is not found for comparison in this study. It is known that the MR of entities in static knowledge graphs is generally reduced to a few hundred to a few thousand after training
2. Given the entity number of these two temporal datasets in this study (7,128 entities in ICEWS14 and 10,488 entities in ICEWS05-15), reducing the MR of entities to less than 10 proves the strong entity semantic learning and reasoning capability of TKG-BERT.
The lower part of
Figure 4 represents the Mean Rank (MR) on ICEWS14 using different proportions of the training set. As the size of the training set increases, TKG-BERT (Van.) consistently reduces the overall MR value, lowering the rank of the correct entities and relations. This demonstrates that, without time modeling, continuously increasing the training set helps improve TKG-BERT’s overall predictive performance for both entities and relations.
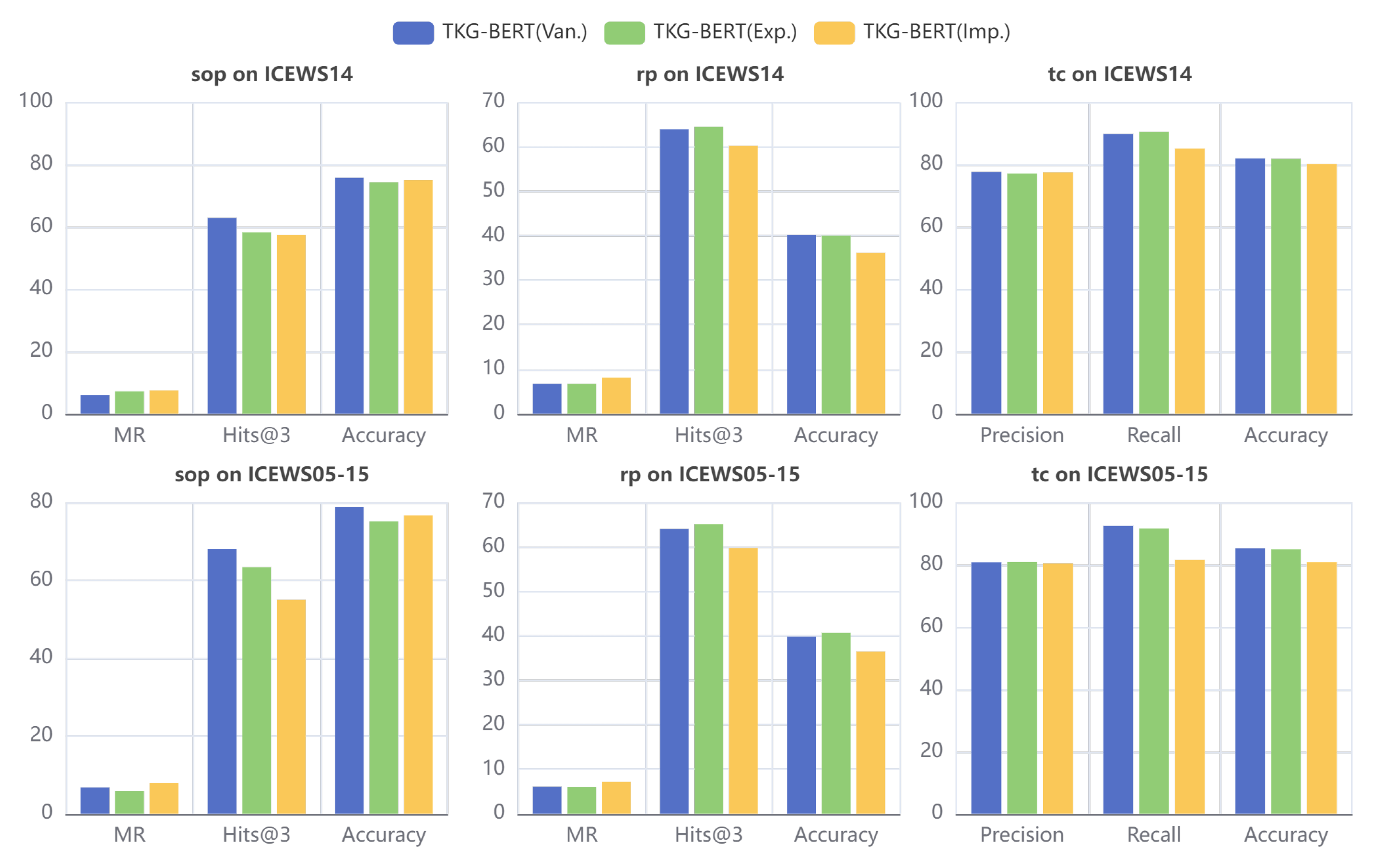
5.3. Explicit Time Modeling v.s. Implicit Time Modeling
We compared the performance of TKG-BERT on different tasks under different time modeling settings, including TKG-BERT(Van.), TKG-BERT(Exp.) and TKG-BERT(Imp.). The results are in
Figure 5. Horizontal coordinates represent the metrics for the tasks, including MR, Hits@3, precision, recall, f1, and accuracy. Vertical coordinates represent the results of TKG-BERT on corresponding metric. The metric values except MR are in percentage. The histograms show following findings:
On a fixed dataset, whether or not time information is embedded does not significantly affect the performance of reasoning tasks.
For the sop task, the model performance ranking is: TKG-BERT(Van.) > TKG-BERT(Exp.) > TKG-BERT(Imp.). For rp and tc tasks, there is almost no difference between TKG-BERT(Van.) and TKG-BERT(Exp.), both performing slightly better than TKG-BERT(Imp.).
The differences in the various time modeling approaches of TKG-BERT are more pronounced on ICEWS05-15.
We re-construct ICEWS14 to model temporal information implicitly. Specifically, the fact quadruples that happens in relatively previous time are used for training, those happens later are used for testing. The proportion of the training, validating, and test set is the same as original dataset. This setting increases the difficulty of the model in performing prediction tasks, so the results show worse. Besides, there are some other reasons for the above phenomena:
BERT uses pre-trained word vectors, which do not capture the implicit temporal information in digital text. TKG-BERT(Exp.) embeds timestamp information directly, has little contribution compared with conventional no-temporal modeling approach.
We use reconstructed dataset for implicit temporal modeling. In original dataset, there is a situation where some event knowledge with later timestamp is introduced into the training set (test leakage), while knowledge with former timestamp is classified into test set, due to data randomization. However, implicit temporal modeling, on the other hand, divides the training set and the test set according to the chronological order, so it does not suffer from such problem . Correspondingly, TKG-BERT (Imp.) performs slightly worse under, which is more realistic.
The inclusion of timestamp information had a weakening effect on the model’s performance in entity prediction tasks, while it provided a slight improvement in relation prediction tasks. This might be due to the large time span covered by the ICEWS05-15 dataset, making TKG-BERT more sensitive to changes in the textual information of timestamps.
5.4. Performance on Different Training Proportion
Figure 6 reports the performance of TKG-BERT on four tasks of ICEWS14 dataset with various proportion of training set. The horizontal axis represents the training set proportion we selected: 20%, 40%, 60%, 80%, 100%. The color of the fold line represents each metric on that task. We note that the model effectiveness on each metric does not change much with different training set ratios. Along with the training set ratio increases, the accuracy improves slowly, but with diminishing marginal benefits. The most affected by training set ratio is entity prediction, with the best results at a training set of 80%. Taking the metric of accuracy on entity prediction as an example, the model performance varies within 10% between the best (on 80% training set) and the worst (on 40% training set) cases.
The metrics for TKG-BERT in the rp and tc tasks gradually increase with the expansion of the training set, indicating that the model’s performance on these two tasks is affected by the training set in a relatively stable manner. Specifically, for the tuc task (triple classification for TKG-BERT (Van.) and quadruple classification for TKG-BERT (Exp.)), the improvement in metrics becomes more pronounced as the size of the training set increases.
For tasks less influenced by the training set (such as rp), they are suitable for predictions in small-sample scenarios; for tasks with more stable influence from the training set (such as tc), they are applicable in scenarios with larger training samples; and for tasks with greater fluctuations (such as spp), optimal model settings need to be explored based on the actual situation.
6. Conclusions
This paper proposes a novel approach called TKG-BERT for temporal knowledge graph embedding. The paper investigates the role of temporal information in knowledge completion tasks. TKG-BERT utilizes pre-trained language models, specifically BERT, to model temporal knowledge in three different ways: vanilla static knowledge modeling, explicit time modeling, and implicit time modeling. The proposed approach is evaluated through various KG completion task to explore the capacity of pre-trained language models to handle temporal knowledge. Experimental results suggest the following conclusions:
The entity prediction task is the most complex, leading to the least stable model performance. In contrast, the model shows relatively stable performance in the tuple classification task.
Temporal information is necessary, and explicitly incorporating temporal information can lead to a slight improvement in performance. But there is a need to find more effective ways of modeling timing, in order to effectively utilize temporal information.
When temporal information is lacking, the model can choose to mine existing knowledge information, thereby improving the inference of unknown knowledge.
Explicit temporal modeling is suitable for interpolation scenarios where timestamps are available, while implicit temporal modeling is more applicable to stream data and extrapolation scenarios where timestamps are not accessible, making it more aligned with practical needs.
Overall, the TKG-BERT approach presented in this paper fills the gap in the research on temporal knowledge graph completion using pre-trained language models. The experimental results demonstrate the effectiveness and potential of TKG-BERT in temporal knowledge graph representation.
Author Contributions
For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, W.F. and J.L.; methodology, W.F.; software, Z.Z.; validation, A.Z.; formal analysis, J.L.; investigation, W.F.; resources, Z.G.; data curation, Z.Z.; writing—original draft preparation, W.F.; writing—review and editing, Y.J.; visualization, A.Z.; supervision, Z.G.; project administration, W.F.; funding acquisition, Y.J. and Z.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Major Key Project of PCL (Grant No. PCL2024A05), the Shenzhen Science and Technology Program (No. KJZD20231023094701003), and the National Natural Science Foundation of China (Grant No. 62372137).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Acknowledgments
We reference the code provided by exBERT
3 to implement our model.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| LLM |
Large Language Model |
| KG |
Knowledge Graph |
| TKG |
Tmploral Knowledge Graph |
| TKGC |
Tmploral Knowledge Graph Completion |
| KGE |
Knowledge Graph Embedding |
| TKGE |
Temporal Knowledge Graph Embedding |
| PLM |
Pre-trained Language Model |
| BERT |
Bidirectional Encoder Representations from Transformers |
| ICEWS |
Integrated Crisis Early Warning System |
| MR |
Mean Rank |
| MRR |
Mean Reciprocal Rank |
References
- Gao, J.; Ribeiro, B. On the equivalence between temporal and static equivariant graph representations. International Conference on Machine Learning. PMLR, 2022, pp. 7052–7076.
- Nguyen, C.V.; Shen, X.; Aponte, R.; Xia, Y.; Basu, S.; Hu, Z.; Chen, J.; Parmar, M.; Kunapuli, S.; Barrow, J.; Wu, J.; Singh, A.; Wang, Y.; Gu, J.; Dernoncourt, F.; Ahmed, N.K.; Lipka, N.; Zhang, R.; Chen, X.; Yu, T.; Kim, S.; Deilamsalehy, H.; Park, N.; Rimer, M.; Zhang, Z.; Yang, H.; Rossi, R.A.; Nguyen, T.H. A Survey of Small Language Models. 2024.
- Hitchcock, F.L. The Expression of a Tensor or a Polyadic as a Sum of Products. Journal of Mathematics and Physics. [CrossRef]
- Kipf, T.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv: Learning,arXiv: Learning.
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika. [CrossRef]
- Xu, C.; Chen, Y.Y.; Nayyeri, M.; Lehmann, J. Temporal Knowledge Graph Completion using a Linear Temporal Regularizer and Multivector Embeddings. Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2021. [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowledge and Information Systems. [CrossRef]
- Garcia-Duran, A.; Dumancic, S.; Niepert, M. Learning Sequence Encoders for Temporal Knowledge Graph Completion. arXiv: Artificial Intelligence,arXiv: Artificial Intelligence. 2018. [Google Scholar]
- Wang, Z.; Li, X. Hybrid-TE: Hybrid Translation-Based Temporal Knowledge Graph Embedding. IEEE Conference Proceedings,IEEE Conference Proceedings.
- Cao, Y.; Wang, X.; He, X.; Hu, Z.; Chua, T.S. Unifying Knowledge Graph Learning and Recommendation: Towards a Better Understanding of User Preferences. The World Wide Web Conference, 2019. [CrossRef]
- Liu, Y.; Hua, W.; Xin, K.; Zhou, X. Context-aware temporal knowledge graph embedding. International Conference on Web Information Systems Engineering. Springer, 2020, pp. 583–598.
- Han, Z.; Chen, P.; Ma, Y.; Tresp, V. DyERNIE: Dynamic Evolution of Riemannian Manifold Embeddings for Temporal Knowledge Graph Completion. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), 2020. [CrossRef]
- Goel, R.; Kazemi, S.M.; Brubaker, M.; Poupart, P. Diachronic embedding for temporal knowledge graph completion. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, Vol. 34, pp. 3988–3995.
- Zhao, A.; Gu, Z.; Jia, Y.; Feng, W.; Zhang, Y. TSEE: a novel knowledge embedding framework for cyberspace security 2023.
- Jin, W.; Qu, M.; Jin, X.; Ren, X. Recurrent Event Network: Autoregressive Structure Inference over Temporal Knowledge Graphs. Cornell University - arXiv,Cornell University - arXiv. 2019. [Google Scholar]
- Tang, X.; Yuan, R.; Li, Q.; Wang, T.; Yang, H.; Cai, Y.; Song, H. Timespan-Aware Dynamic Knowledge Graph Embedding by Incorporating Temporal Evolution. IEEE Access, 6849. [Google Scholar] [CrossRef]
- Jung, J.; Jung, J.; Kang, U. Learning to Walk across Time for Interpretable Temporal Knowledge Graph Completion. Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2021. [CrossRef]
- Li, Z.; Jin, X.; Li, W.; Guan, S.; Guo, J.; Shen, H.; Wang, Y.; Cheng, X. Temporal Knowledge Graph Reasoning Based on Evolutional Representation Learning. Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, 2021. [CrossRef]
- Jin, W.; Qu, M.; Jin, X.; Ren, X. Recurrent event network: Autoregressive structure inference over temporal knowledge graphs. arXiv preprint arXiv:1904.05530. 2019; arXiv:1904.05530 2019. [Google Scholar]
- Li, Z.; Jin, X.; Li, W.; Guan, S.; Guo, J.; Shen, H.; Wang, Y.; Cheng, X. Temporal knowledge graph reasoning based on evolutional representation learning. Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, 2021, pp. 408–417.
- Wu, Z.; Jain, P.; Wright, M.; Mirhoseini, A.; Gonzalez, J.E.; Stoica, I. Representing long-range context for graph neural networks with global attention. Advances in Neural Information Processing Systems 2021, 34, 13266–13279. [Google Scholar]
- Rong, Y.; Bian, Y.; Xu, T.; Xie, W.; Wei, Y.; Huang, W.; Huang, J. Self-supervised graph transformer on large-scale molecular data. Advances in Neural Information Processing Systems 2020, 33, 12559–12571. [Google Scholar]
- Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; Liu, T.Y. Do transformers really perform badly for graph representation? Advances in Neural Information Processing Systems 2021, 34, 28877–28888. [Google Scholar]
- Jin, B.; Zhang, Y.; Zhu, Q.; Han, J. Heterformer: Transformer-based deep node representation learning on heterogeneous text-rich networks. Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2023, pp. 1020–1031.
- Mialon, G.; Chen, D.; Selosse, M.; Mairal, J. Graphit: Encoding graph structure in transformers. arXiv preprint arXiv:2106.05667. arXiv:2106.05667 2021.
- Yao, L.; Mao, C.; Luo, Y. KG-BERT: BERT for knowledge graph completion. arXiv preprint arXiv:1909.03193. arXiv:1909.03193 2019.
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, arXiv:1810.04805 2018.
- Lv, X.; Lin, Y.; Cao, Y.; Hou, L.; Li, J.; Liu, Z.; Li, P.; Zhou, J. Do pre-trained models benefit knowledge graph completion? a reliable evaluation and a reasonable approach. Association for Computational Linguistics, 2022.
- Chen, S.; Liu, X.; Gao, J.; Jiao, J.; Zhang, R.; Ji, Y. Hitter: Hierarchical transformers for knowledge graph embeddings. arXiv preprint arXiv:2008.12813. 2020; arXiv:2008.12813 2020. [Google Scholar]
- Liu, X.; Zhao, S.; Su, K.; Cen, Y.; Qiu, J.; Zhang, M.; Wu, W.; Dong, Y.; Tang, J. Mask and reason: Pre-training knowledge graph transformers for complex logical queries. Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2022, pp. 1120–1130.
- Wang, L.; Zhao, W.; Wei, Z.; Liu, J. SimKGC: Simple contrastive knowledge graph completion with pre-trained language models. arXiv preprint arXiv:2203.02167. arXiv:2203.02167 2022.
- Bi, Z.; Cheng, S.; Chen, J.; Liang, X.; Xiong, F.; Zhang, N. Relphormer: Relational Graph Transformer for Knowledge Graph Representations. Neurocomputing 2024, 566, 127044. [Google Scholar] [CrossRef]
- Islakoglu, D.S.; Chekol, M.W.; Velegrakis, Y. Leveraging Pre-trained Language Models for Time Interval Prediction in Text-Enhanced Temporal Knowledge Graphs. The Semantic Web: 21st International Conference, ESWC 2024, Hersonissos, Crete, Greece, May 26–30, 2024, Proceedings, Part I; Springer-Verlag: Berlin, Heidelberg, 2024; p. 59–78. [CrossRef]
- Xu, W.; Liu, B.; Peng, M.; Jia, X.; Peng, M. Pre-trained Language Model with Prompts for Temporal Knowledge Graph Completion. Annual Meeting of the Association for Computational Linguistics, 2023.
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, .; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30.
- Yao, L.; Mao, C.; Luo, Y. KG-BERT: BERT for knowledge graph completion. arXiv preprint arXiv:1909.03193. 2019; arXiv:1909.03193 2019. [Google Scholar]
- Boschee, E.; Lautenschlager, J.; O’Brien, S.; Shellman, S.; Starz, J.; Ward, M. ICEWS coded event data. Harvard Dataverse 2015, 12. [Google Scholar]
- García-Durán, A.; Dumančić, S.; Niepert, M. Learning sequence encoders for temporal knowledge graph completion. arXiv preprint arXiv:1809.03202. 2018; arXiv:1809.03202 2018. [Google Scholar]
- Goel, R.; Kazemi, S.M.; Brubaker, M.; Poupart, P. Diachronic embedding for temporal knowledge graph completion. Proceedings of the AAAI conference on artificial intelligence, 2020, Vol. 34, pp. 3988–3995.
- Yang, B.; Yih, W.t.; He, X.; Gao, J.; Deng, L. Learning sequence encoders for temporal knowledge graph completion. arXiv preprint arXiv:1809.03202. arXiv:1412.6575 2014.
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. International conference on machine learning. PMLR, 2016, pp. 2071–2080.
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. The Semantic Web: 15th International Conference, ESWC 2018, Heraklion, Crete, Greece, June 3–7, 2018, Proceedings 15. Springer, 2018, pp. 593–607.
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. Proceedings of the AAAI conference on artificial intelligence, 2018, Vol. 32.
- Shang, C.; Tang, Y.; Huang, J.; Bi, J.; He, X.; Zhou, B. End-to-end structure-aware convolutional networks for knowledge base completion. Proceedings of the AAAI conference on artificial intelligence, 2019, Vol. 33, pp. 3060–3067.
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv preprint arXiv:1902.10197. 2019; arXiv:1902.10197 2019. [Google Scholar]
- Dasgupta, S.S.; Ray, S.N.; Talukdar, P. Hyte: Hyperplane-based temporally aware knowledge graph embedding. Proceedings of the 2018 conference on empirical methods in natural language processing, 2018, pp. 2001–2011.
- Jiang, T.; Liu, T.; Ge, T.; Sha, L.; Chang, B.; Li, S.; Sui, Z. Towards time-aware knowledge graph completion. Proceedings of COLING 2016, the 26th International Conference on Computational Linguistics: Technical Papers, 2016, pp. 1715–1724.
- Seo, Y.; Defferrard, M.; Vandergheynst, P.; Bresson, X. Structured sequence modeling with graph convolutional recurrent networks. Neural Information Processing: 25th International Conference, ICONIP 2018, Siem Reap, Cambodia, -16, 2018, Proceedings, Part I 25. Springer, 2018, pp. 362–373.
- Zhu, C.; Chen, M.; Fan, C.; Cheng, G.; Zhang, Y. Learning from history: Modeling temporal knowledge graphs with sequential copy-generation networks. Proceedings of the AAAI conference on artificial intelligence, 2021, Vol. 35, pp. 4732–4740.
- Jin, W.; Qu, M.; Jin, X.; Ren, X. Recurrent Event Network: Autoregressive Structure Inferenceover Temporal Knowledge Graphs. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), 2020, pp. 6669–6683.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).