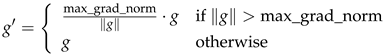HTIM: A Hybrid Deep Learning Approach For Pedestrian Trajectory Imputation

1. Introduction

Pedestrian trajectory unpredictability has presented a formidable challenge for autonomous vehicles, necessitating sophisticated trajectory imputation techniques. The erratic and dynamic nature of pedestrian movement makes it challenging to accurately predict their future paths. Factors such as sudden changes in direction, varying speeds, and unexpected interactions with the environment contribute to this unpredictability. Bearing this unpredictability in mind, autonomous vehicles have transformed transportation by utilizing state-of-the-art technologies like artificial intelligence, sensor fusion, and machine learning to navigate safely and independently. Central to their operation is the ability to efficiently plan and follow trajectories while adapting to changing environments. In this context, a trajectory refers to the path a entity takes over time, including its spatial coordinates, velocity, and orientation. Mathematically, a trajectory $X\left(t\right)=\left(x\right(t),y(t),v(t),\theta (t\left)\right)$ describes the vehicle’s state in a specific coordinate system where $\left(x\right(t),y(t\left)\right)$ denotes its position, $v\left(t\right)$ represents its velocity, and $\theta \left(t\right)$ indicates its heading at time t. Trajectory imputation is a critical aspect of motion prediction, focusing on filling in missing points within incomplete trajectories to create a comprehensive representation of an object’s movement. Essentially, trajectory imputation involves using existing trajectory data to interpolate or extrapolate missing segments, compensating for factors like sensor errors, occlusions, or data loss. By integrating predictive models with historical trajectory information, trajectory imputation facilitates the reconstruction of a coherent and uninterrupted trajectory, vital for applications such as autonomous navigation and activity recognition. The primary objective of trajectory imputation is to estimate the missing points inside the incomplete trajectory to yield a complete trajectory represnted as following: ${\mathit{T}}_{\mathbf{complete}}=\{(x_1,y_1,t_1),(x_2,y_2,t_2)\dots (x_n,y_n,t_n)\}$ and

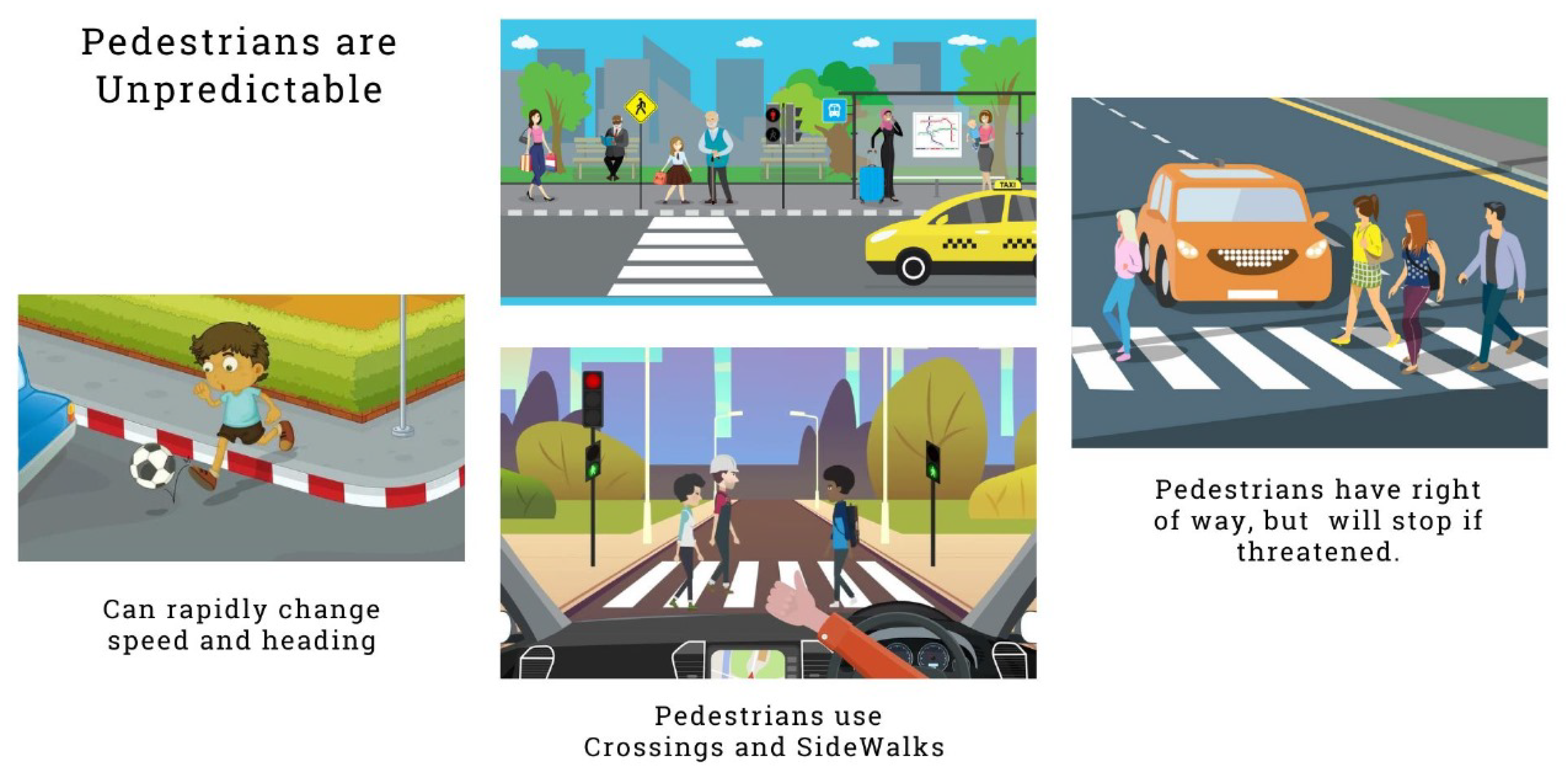
Figure 1. Humans are unpredictable, a critical security concern for autonomous vehicles, Image Courtesy: coursera.org.

Figure 1. Humans are unpredictable, a critical security concern for autonomous vehicles, Image Courtesy: coursera.org.

$$\begin{array}{cc}\hfill {\mathit{T}}_{\mathbf{incomplete}}=\{& (x_1,y_1,t_1),(x_2,y_2,t_2)\dots \hfill \\ \hfill & (x_{n-m-1},y_{n-m-1},t_{n-m-1}),\hfill \\ \hfill & (x_{n-m},y_{n-m},t_{n-m}),\hfill \\ \hfill & (x_{n-m+p},y_{n-m+p},t_{n-m+p})\dots \hfill \\ \hfill & (x_n,y_n,t_n)\}\hfill \end{array}$$

where $p-1$ represents the number of missing points to be imputed.

Since the early days, several techniques have been employed for trajectory imputation each with its advantages and limitations. These techniques include Kalman Filtering [1], which is widely used for state estimation and trajectory prediction in autonomous vehicles. They provide a recursive solution for predicting the phase of a dynamic system dependent on noisy sensor measurements. Kalman filters are particularly effective in scenarios with linear dynamics and Gaussian noise distributions. Particle filters, also known as Monte Carlo localization [2], are probabilistic algorithms used for non-linear and non-Gaussian state estimation. They represent the posterior distribution of the vehicle’s state using a set of weighted particles. These particles are sampled and propagated based on motion models and sensor measurements. Bayesian inference provides a principled framework for updating beliefs about the vehicle’s state based on observed data and prior knowledge. It allows for the incorporation of uncertainty into trajectory prediction and facilitates decision-making under uncertainty.

In recent times, machine learning methodologies, like support vector machines [3], neural networks and Gaussian processes, have been increasingly employed for trajectory imputation in autonomous vehicles. These approaches learn complex relationships from data and can capture intricate patterns in vehicle motion and environmental interactions. The advancement of deep learning [4] fields has significantly influenced trajectory imputation in autonomous vehicle systems. Deep learning techniques have demonstrated remarkable capabilities in capturing intricate patterns and dependencies within trajectory data, leading to enhanced prediction accuracy and robustness. Several key techniques have emerged that harness the strength of deep learning models. Recurrent Neural Networks (RNN), particularly Gated Recurrent Unit(GRU) and Long short-term Memory(LSTM), and several of LSTM’s variants like Bi-directional LSTM (Bi-LSTM) [5], Attention-based LSTM (AttLSTM) [6], Stacked LSTM [7], Convolutional LSTM (ConvLSTM) [8], LSTM with Temporal Convolutional Networks (TCN) [9] and Peephole LSTM [10] have gained prominence in trajectory imputation tasks.

Our research has made the following noteworthy contributions:

• We have explored the challenges and requirements specific to trajectory interpolation for autonomous vehicles, considering the real-time nature and safety criticality of autonomous driving systems.
• We have examined the use of the LSTM and GRU in the travel path restoration of pedestrians, taking into consideration their propensity for managing temporal dependencies and contextual interactions.
• We have designed an encoder-decoder imputation model comprising LSTM blocks for the encoder and GRU blocks for the decoder.
• Our model evaluation has been conducted on the inD dataset, marking one of the earliest instances of research on this dataset for the trajectory imputation task.

Section 2 provides an overview of existing related literature. Section 3 identifies gaps in previous researches. The dataset description and preprocessing methods are outlined in Section 4. Section 5 elaborates on the proposed methodology. Experimental results and discussions are presented in Section 6. Finally, Section 7 offers a conclusion for the study and proposes avenues for future research. Moreover, Table 1 presents the symbols used in this paper.

2. Related Work

Missing value handling is one of the most difficult problems in the field of time series data. A wide variety of approaches from complex convolutional recurrent encoder-decoder architectures to recurrent dynamical systems have been thoroughly explored by researchers. By studying various literatures, we have examined different approaches used to fill the gaps in the workings related to time series datasets, exposing the advantages and disadvantages of each.

Using a bidirectional recurrent dynamical system, Cao et al. [11] described a technique for inferring time series data that can directly estimate the missing value. There was no significant presumption about the underlying data generation method. The majority of other current systems, according to the paper, made significant assumptions about the data-generating process. According to Kreindler et al.  [12] there was no abrupt spike in the data and the data were smoothable while generating the missing data. Therefore, smoothing the surrounding data could produce missing values. Some current methods have used interpolation to infer the missing values; however, local interpolation has generated the missing values without taking into account the relationship between the variables over time. The model BRITS, deviced in this literature, has outperformed all baseline models in terms of mean absolute error and mean relative error.

Nawaz et al. [13] have introduced a deep learning-based convolutional recurrent encoder-decoder architecture to address the GPS trajectory imputation problems. There have been temporal and spatial components to GPS trajectory data. While recurrent neural networks such as LSTM have been effective in predicting consecutive time series, convolutional neural networks have excelled at extracting the spatial aspect from data. They have been used by the suggested ConvLSTM to get better results on trajectory imputation tasks. It has used the GPS trajectories with transportation mode labels from the Microsoft Geolife trajectory dataset ( [14]) and employed the Average Displacement Error (ADE) as an evaluation metric.

Ma et al. [15] have proposed a novel deep neural network approach to address the human trajectory imputation problem, which is a crucial step in the COVID-19 contact tracing process. The representation process using graph embedding has been the first component of the solution and the transformer model has been the second. The formation of the human trajectory sequence has occurred in a high-dimensional environment, making it difficult to extract significant information. The nodes have been mapped from high-dimensional to low-dimensional vector space using the graph embedding model to remove the challenges. It aided in capturing the sequential aspect of human trajectory as well as geo-spatial aspects. A deep CNN decoder, a softmax classifier, and a transformer encoder-based feature extractor make up the deep learning model. Because it can understand linkages and dependencies, the transformer’s main feature, the Multi-head Self-Attention, has confirmed good performance for a sequence-to-sequence model. The CRAWDAD unm/blebeacon [16] dataset, an open-source human mobility dataset, has been used for the study.

The problem of trajectory prediction from partial observations owing to the miss-detection of dynamic agents (cars, pedestrians, etc.) which can be brought on by poor image quality or occlusion by other dynamic agents, has been studied by Fujii et al.  [17]. The standard method for handling the incomplete trajectory problem has been to consider the miss detection cases as anomalies and remove them from the dataset. Because such a strategy has eliminated the possibility of coordination with the agents that are excluded, there has been a higher chance of major mishaps. Traditional methods for trajectory prediction have included those based on Bayesian filters. Their fundamental structure has made them unreliable for long-term prediction. RNN, most notably the LSTM, has now been widely used in modeling to anticipate human motions. The study has proposed a two-block RNN for trajectory prediction from partial trajectory due to miss-detection, which has learned the inference step of Bayesian filters. Two publicly accessible datasets, ETH [18] and UCY [19] have been used in the experiment.

Almolegi et al.  [20] have introduced a novel model called Move, Attend, and Predict (MAP) which forecasts a person’s next location based on motions previously captured by a mobile device. The model has used a deep neural network to identify the important components of the mobility history for each location. The program also has used an approach called embedding representation learning to extract relevant properties from the movement data. The model has been tested on two big datasets and demonstrates that it has outperformed other models for location prediction. The study solely has taken into account two types of input data: locations and timings. It has ignored other elements that may impact people’s movements, such as preferences, social networks, weather, traffic, and so on. The model has been tested on two datasets: Geolife and Foursquare [21].

Wang et al. [22] have introduced a novel deep learning approach to address the prevalent problem of missing trajectory data in GPS applications. Their proposed method has leveraged an RNN with an encoder-decoder architecture and an attention mechanism [23]. To enhance data reconstruction quality, they have introduced a new loss function based on the R2 coefficient and implemented a smoothing technique using a moving average and Savitzky-Golay filter [24]. Evaluating their model on a real-world GPS dataset from the Geolife project, comprising 17,621 trajectories collected over five years from 182 users, they have demonstrated its superiority over several baseline methods, including linear interpolation, cubic spline interpolation, Kalman filter, LSTM and Bi-LSTM in terms of recovery accuracy and result stability across various missing rates and patterns. Additionally, through ablation tests and parameter sensitivity analysis, they have validated the effectiveness of their model components and design choices, underscoring the potential of their deep learning approach for robust trajectory data reconstruction.

3. Gap Analysis

Table 2 has provided a comprehensive analysis of the limitations found in previous research. The gap analysis of the reviewed literature underscores several notable limitations encountered in prior research. Notably, Nawaz et al. demonstrated effectiveness in identifying patterns in common scenarios, but their method may struggle with complex, crowded trajectory movements.

Additionally, Cao et al. approach, despite enhancing predictive accuracy, introduces uncertainty and noise by treating missing values as variables. The transformer-based model by Ma et al. exhibits promise with Bluetooth low energy data but lacks exploration on other trajectory data types. Almolegi et al. MAP model faces constraints in handling new or unseen locations, while Fujii et al. Bayesian filter framework adds complexity potentially impacting scalability. Moreover, Wang et al. model, leveraging an RNN with encoder-decoder architecture, may overlook comprehensive performance assessment due to limited evaluation metrics. These findings underscore the necessity for further research to address these limitations comprehensively.

4. Dataset Observation and Prepossessing

In this section, we have explored the dataset collection, observation and prepossessing carried out as part of the research, providing a detailed overview of the steps taken to collect and prepare those data.

4.1. Dataset Observation

Various trajectory datasets have existed for road users, but very few have met the needs of autonomous driving research. Examples include BIWI Walking Pedestrians [25], Stanford Drone [26],CITR and DUT [27], highD [28], Interaction [29] and Ko-PER [30]. Most lack sufficient data or public road scenarios. The inD dataset [31] is a new and unique dataset of naturalistic vehicle trajectories recorded at German intersections using a drone. The dataset includes more than 11,500 road users consisting of vehicles, bicyclists and pedestrians at four different locations(Braunschweig, Frankfurt, Lindau, Wurzburg) with varying traffic density and complexity. Table has shown its comparison with other datasets.

The inD dataset surpasses other datasets in capturing naturalistic road user behavior due to its strategic design principles:

• Preserving naturalistic behavior: By avoiding visible sensors resembling traffic surveillance cameras, the inD dataset ensures road users are not impacted by the measurement method.
• Having satisfactory size: The inclusion of trajectories from thousands of road users provides the necessary size and variety for robust data-driven algorithms.
• Differentiating recording locations and times: The inD dataset captures measurements from multiple sites and diverse times of day, including public roads, ensuring coverage of different road layouts, densities and traffic rules for enhanced signifance in automated driving scenarios.
• Detecting and tracking all road user types: Unlike datasets that limit themselves to specific categories, the inD dataset tracks all road users, recognizes the vital importance of capturing interactions across diverse user types.
• Tracking road users with top accuracy: The inD dataset guarantees trajectories with a positioning inaccuracy of less than 0.1 meters, regardless of road user type, ensuring precision in capturing the intricacies of user movement.
• Including infrastructure details: With the precise recording of road layouts and local traffic rules, the inD dataset acknowledges the dependency of road user behavior on these factors, providing comprehensive information within the dataset.

Table 3. Overview of Trajectory Data and Characteristics. 

Title	Location	# Trajectories	# Locations	Road User Types	Data Frequency	Method
BIWI ETH	University building entry	360	1	pedestrian	2.5 Hz	stat. sensor
Interaction	Urban intersection	18642	4	vehicles	10 Hz	drone/cam.
Ko-PER	Urban intersection	350	1	pedestrian, bicycle, car,truck	25 Hz	stat. sensor
Crowds UCY/ Zara	Campus, urban street	909	3	pedestrian	2.5 Hz	stat. sensor
Stanford Drone	Campus	10240	8	pedestrian, bicycle, car, skateboard, cart, bus	25 Hz	drone
BIWI	Hotel sidewalk, hotel entry	389	1	pedestrian	2.5 Hz	stat. sensor
VRU Trajectory	Urban intersection	3278	1	pedestrian, bicycle	25 Hz	stat. sensor
DUT	Campus	1862	2	pedestrian, vehicles	23.98 Hz	drone
CITR	Designed experiment	340	1	pedestrian, golf-cart	29.97 Hz	drone
inD	Urban intersection	13599	4	pedestrian, bicycle, car, truck, bus	25 Hz	drone

Table 3. Overview of Trajectory Data and Characteristics. 

Title	Location	# Trajectories	# Locations	Road User Types	Data Frequency	Method
BIWI ETH	University building entry	360	1	pedestrian	2.5 Hz	stat. sensor
Interaction	Urban intersection	18642	4	vehicles	10 Hz	drone/cam.
Ko-PER	Urban intersection	350	1	pedestrian, bicycle, car,truck	25 Hz	stat. sensor
Crowds UCY/ Zara	Campus, urban street	909	3	pedestrian	2.5 Hz	stat. sensor
Stanford Drone	Campus	10240	8	pedestrian, bicycle, car, skateboard, cart, bus	25 Hz	drone
BIWI	Hotel sidewalk, hotel entry	389	1	pedestrian	2.5 Hz	stat. sensor
VRU Trajectory	Urban intersection	3278	1	pedestrian, bicycle	25 Hz	stat. sensor
DUT	Campus	1862	2	pedestrian, vehicles	23.98 Hz	drone
CITR	Designed experiment	340	1	pedestrian, golf-cart	29.97 Hz	drone
inD	Urban intersection	13599	4	pedestrian, bicycle, car, truck, bus	25 Hz	drone

4.2. Point of Interest Dataset Generation

The main dataset has pedestrian and vehicle trajectories. Here, the first task is to extract the pedestrians’ trajectories that cross the road and truncate their trajectories to meet the area of focus shown in Figure 2 [32].

Muktadir et al. [32,33] have dealt with human trajectories while keeping the concerns of autonomous vehicles in mind. The pedestrians walking by the side of each road should not be our concern. The road crossing pedestrians’ trajectories should be our focal point, as only then the factor of autonomous vehicles comes into play. Only by incorporating the trajectories of road-crossing pedestrians, they have created a curated dataset, which we have used [33]. 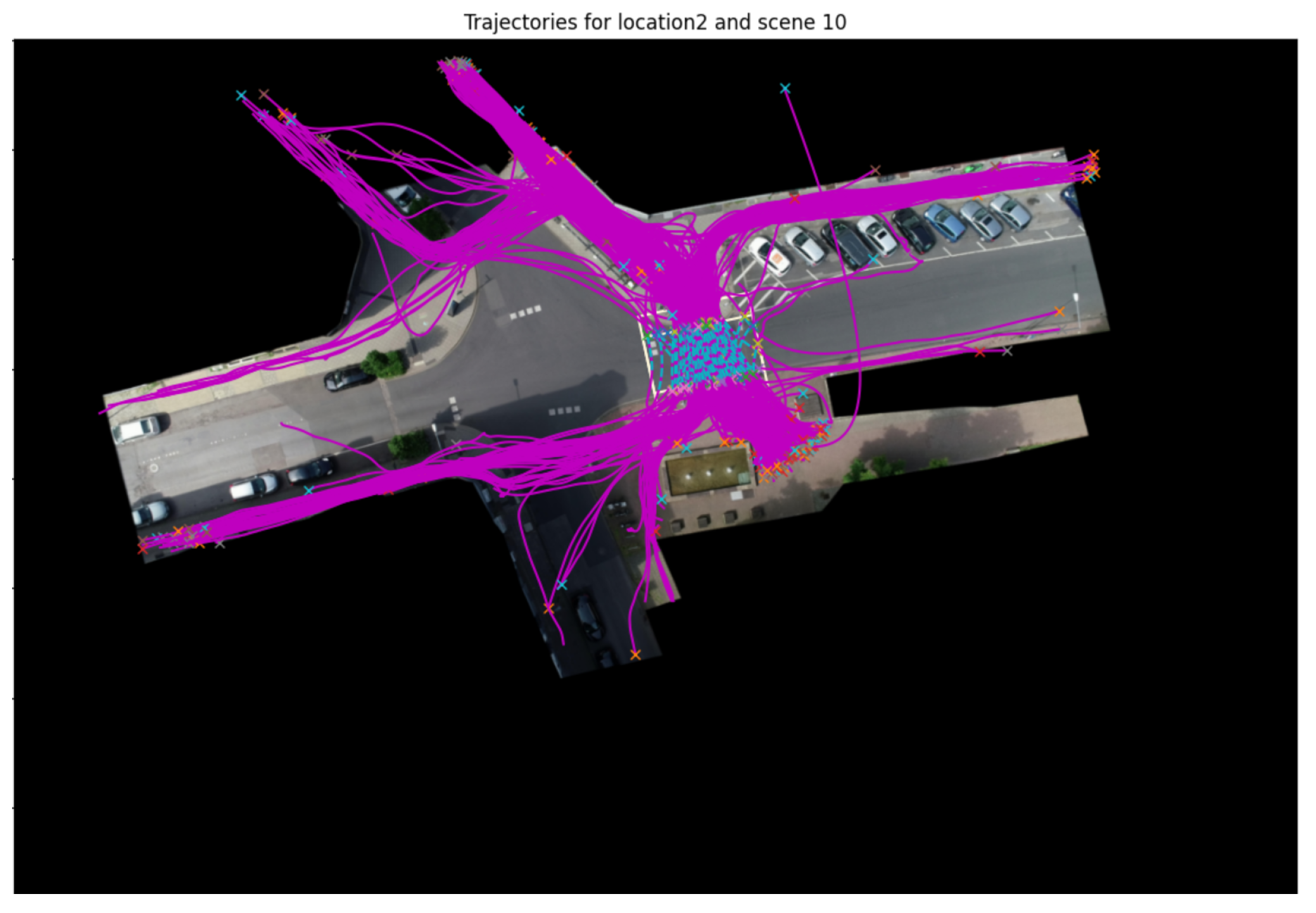Figure 3 [32] depicts all trajectories in purple color and trajectories of pedestrians in blue color.

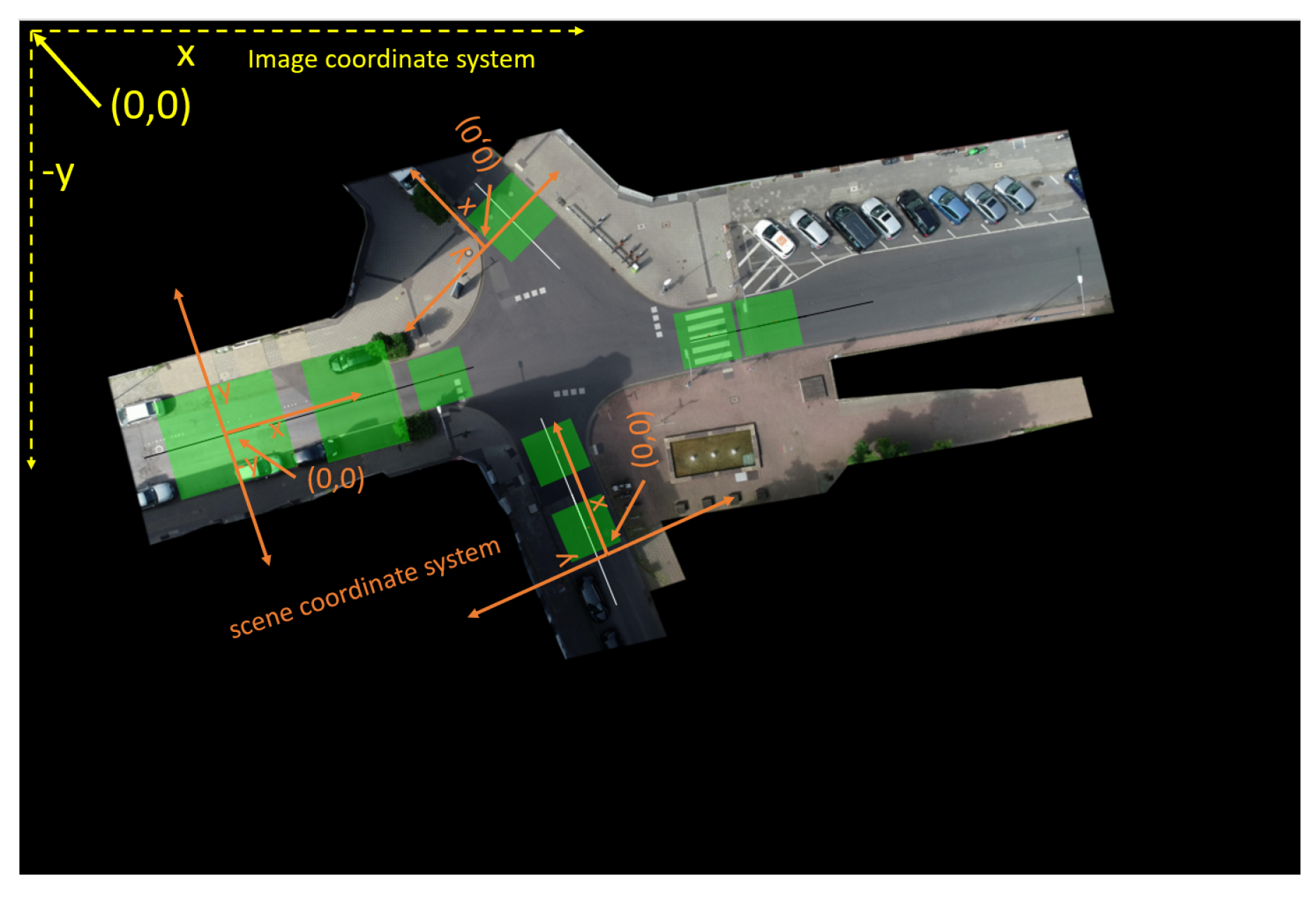
The original inD dataset follows the image coordinate system where the origin lies in the top-left corner of the background image. The curated dataset has involved trajectories with a scene coordinate system where the origin has been located at the center of the scene bounding box(Figure 2) and the x-axis has been adjusted to align with the road reference line in Figure 4 [32].

4.3. Making Incomplete Trajectories

In this section, we have presented our approach to creating incomplete trajectories through a masking strategy. We aim to simulate missing data in the trajectory sequences, which will be used during training.

4.3.1. Masking Strategy

To simulate missing data in the trajectory sequences, we employ a masking strategy that involves randomly selecting segments of the trajectory and marking them as missing. Let $\mathit{X}$ represent a complete trajectory with T data points, where $x_t$ denotes the data point at time step t. We have defined the masking strategy as follows:

• Masking Ratio ($\alpha$): We have introduced a hyperparameter $\alpha$ which represents the percentage of data points we want to mask in each trajectory. The value of $\alpha$ has been determined during training and can be fine-tuned for optimal performance.
• Random Selection: We have randomly selected segments of the trajectory, with a length proportional to $\alpha ·T$, to be marked as missing. These segments will have to be replaced with a special token denoted as [MASK], indicating the presence of missing data.

4.3.2. Creating Incomplete Trajectories

Using the aforementioned masking strategy, we have generated incomplete trajectories from complete ones. Let ${\mathit{X}}_{\mathrm{incomplete}}$ represent the resulting incomplete trajectory. We have defined the process mathematically as follows:

$${\mathit{X}}_{\mathit{incomplete}}=\mathit{Mask}(\mathit{X},\alpha )$$

(1)

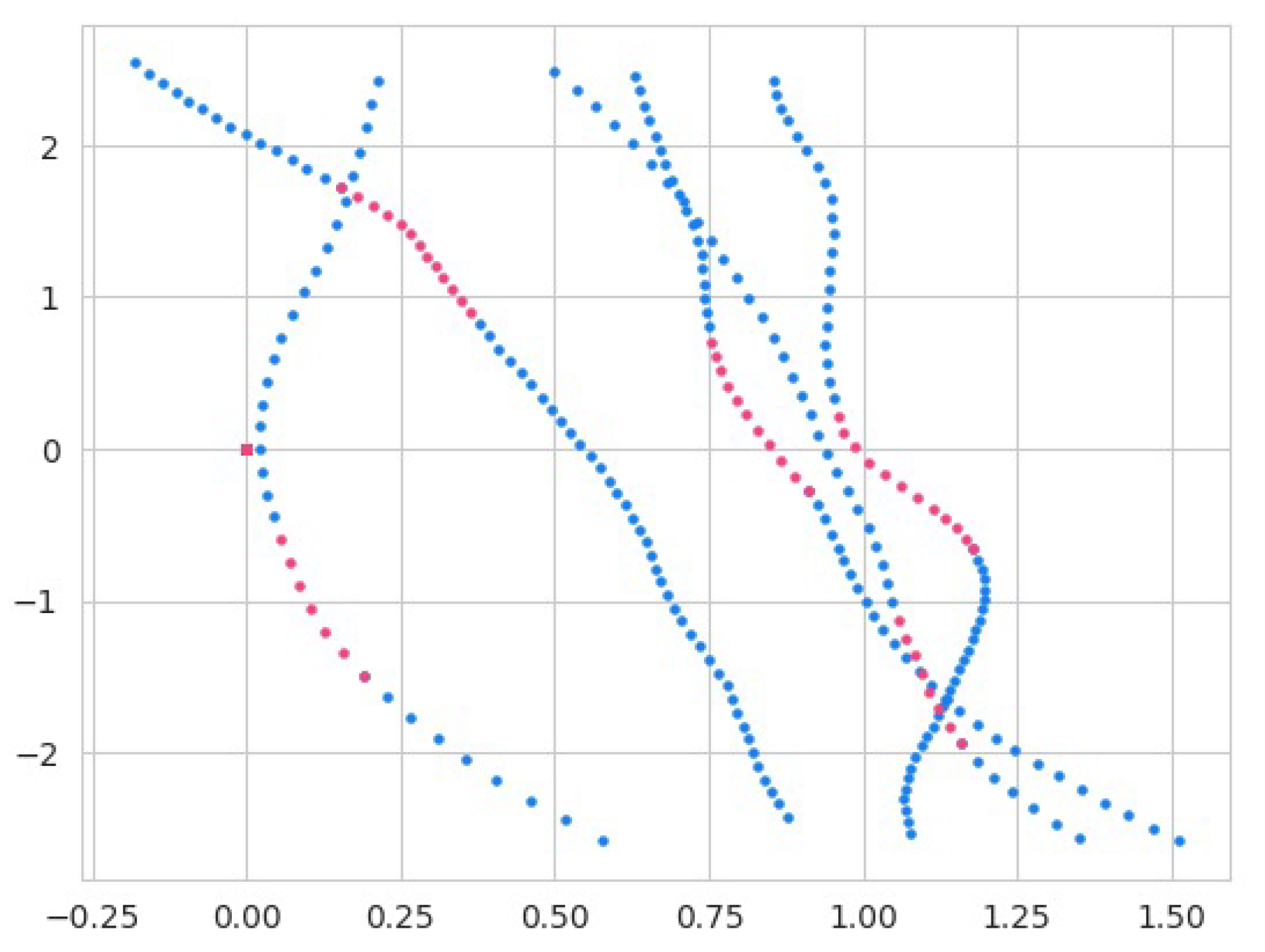
Where $\mathrm{Mask}(·)$ is a function that applies the masking strategy to the complete trajectory $\mathit{X}$ with a masking ratio of $\alpha$. In Figure 5 the complete trajectories have been presented in green color and the incomplete trajectories have been represented by red color.

4.4. Padding and Binary Masking

Trajectories in the training dataset have been padded to the maximum length across different trajectories from all four locations. This has been a crucial step for efficient batch processing during training. Let $X_i$ represent the trajectory of the i-th example, and $T_i$ be its original length. Trajectories have been padded to length $T_{\max }$, where $T_{\max }={max}_i{T}_i$.

Additionally, a binary mask has been created for each trajectory to indicate the presence of observed points (1) and missing points (0) in the incomplete trajectories. The binary mask has been denoted as $M_i$, where $M_{i,t}=1$ if the point at time step t is observed and $M_{i,t}=0$ if it is missing.

5. Methodology

This section has explored the complex structural characteristics of the methodology, providing a thorough comprehension of the design elements and organizational components that are the basis of the approach.

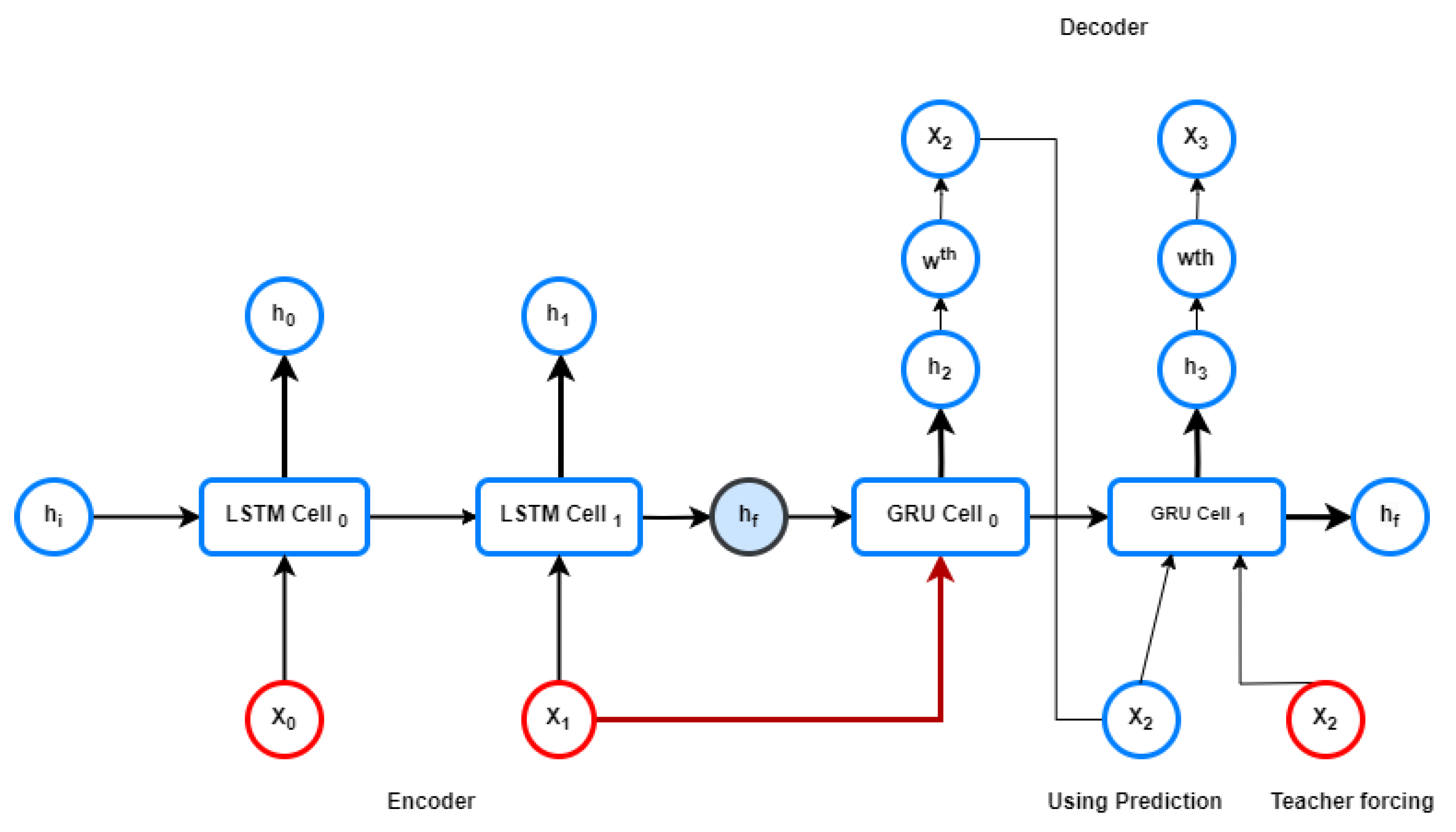
5.1. LSTM Encoder-GRU Decoder Architecture with Teacher Forcing

The LSTM-GRU (Gated Recurrent Unit) based Encoder-Decoder is a sequence-to-sequence model commonly used in various natural language processing and sequence generation tasks. As the name suggests, it consists of two main components, Encoder and Decoder. We picked LSTM for the Encoder part and GRU for the Decoder after thorough experimentation.

5.1.1. LSTM Encoder

The LSTM Encoder, a crucial component of sequence-to-sequence models, analyzes input sequences to capture their temporal dependencies. For an input sequence $X=\{x_1,x_2...x_T\}$ of length T, the encoder produces a hidden state sequence $H^{\mathrm{enc}}=\{h_1^{\mathrm{e}},h_2^{\mathrm{e}}...h_T^{\mathrm{e}}\}$.

The LSTM encoder updates its hidden states by the following equations:

$$\begin{array}{cc}\hfill i_t& =\sigma ({\mathit{W}}_{\mathit{ii}}{x}_t+{\mathit{b}}_{\mathit{ii}}+{\mathit{W}}_{\mathit{hi}}{h}_{t-1}^{\mathrm{e}}+{\mathit{b}}_{\mathit{hi}})\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill f_t& =\sigma ({\mathit{W}}_{\mathit{if}}{x}_t+{\mathit{b}}_{\mathit{if}}+{\mathit{W}}_{\mathit{hf}}{h}_{t-1}^{\mathrm{e}}+{\mathit{b}}_{\mathit{hf}})\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill g_t& =tanh({\mathit{W}}_{\mathit{ig}}{x}_t+{\mathit{b}}_{\mathit{ig}}+{\mathit{W}}_{\mathit{hg}}{h}_{t-1}^{\mathrm{e}}+{\mathit{b}}_{\mathit{hg}})\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill o_t& =\sigma ({\mathit{W}}_{\mathit{io}}{x}_t+{\mathit{b}}_{\mathit{io}}+{\mathit{W}}_{\mathit{ho}}{h}_{t-1}^{\mathrm{e}}+{\mathit{b}}_{\mathit{ho}})\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill c_t& =f_t\odot c_{t-1}+i_t\odot g_t\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill h_t^{\mathrm{e}}& =o_t\odot tanh\left(c_t\right)\hfill \end{array}$$

(7)

where: $\sigma$ denotes the sigmoid function, ⊙ represents element-wise multiplication, $x_t$ stands for the input at time step t, $h_t^{\mathrm{e}}$ represents the hidden state at time step t, $i_t$, $f_t$, $g_t$, and $o_t$ denote the input, forget, cell, and output gates at time step t respectively, and W and b represent the weight and bias matrices for different gates. $c_t$ represents the cell state at time step t.The LSTM’s unusual architecture, comprising input, forget, cell, and output gates has allowed it to successfully capture long-range relationships in sequential data, making it well-suited for jobs requiring memory retention over longer periods. The LSTM encoder is renowned for its ability to alleviate the vanishing gradient problem commonly encountered in traditional RNNs. This is achieved through its sophisticated gating mechanisms, which regulate the flow of information across time steps. The input gate $i_t$ controls the influx of fresh information into the cell state $c_t$, while the forget gate $f_t$ regulates the confinement of former cell state information. The output gate $o_t$ governs the flow of information from the cell state to the hidden state, ensuring that relevant information is propagated forward while irrelevant information is suppressed.

5.1.2. GRU Decoder with Teacher Forcing

The GRU Decoder with Teacher Forcing is responsible for generating an output sequence based on the hidden states obtained from the encoder. Given the hidden state sequence $H^{\mathrm{enc}}$ and an input sequence $Y=\{y_1,y_2\dots y_U\}$ of length U, the decoder computes an output sequence $Y^{\prime }=\{y_1^{\prime },y_2^{\prime }\dots y_U^{\prime }\}$.

The GRU decoder updates its hidden states and produces the output using the following equations, incorporating the concept of teacher forcing:

$$\begin{array}{cc}\hfill h_t^{\mathrm{d}}& =\mathrm{GRU}(y_t,h_{t-1}^{\mathrm{d}})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill r_t& =\sigma (W_{yr}{y}_t+U_{hr}{h}_{t-1}^{\mathrm{d}}+b_r)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill z_t& =\sigma (W_{yz}{y}_t+U_{hz}{h}_{t-1}^{\mathrm{d}}+b_z)\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\tilde{h}}_t& =tanh(W_{y\tilde{h}}{y}_t+r_t\odot \left(U_{h\tilde{h}}{h}_{t-1}^{\mathrm{d}}\right)+b_{\tilde{h}})\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill h_t^{\mathrm{d}}& =(1-z_t)\odot h_{t-1}^{\mathrm{d}}+z_t\odot {\tilde{h}}_t\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill y_t^{\prime }& =\mathrm{Regressor}\left(h_t^{\mathrm{d}}\right)\hfill \end{array}$$

(13)

where GRU represents the operation of a Gated Recurrent Unit, $\sigma$ denotes the sigmoid function, ⊙ represents element-wise multiplication, $y_t$ is the input at time step t, $h_t^{\mathrm{d}}$ represents the hidden state at time step t, $r_t$ and $z_t$ denote the reset and update gates respectively, ${\tilde{h}}_t$ is the candidate hidden state, W and U are weight matrices, and b are bias vectors. Regressor is a function that maps the hidden state to the output space.

The GRU Decoder with Teacher Forcing employs the use of teacher forcing, a technique where the decoder receives the true values of the previous time steps as inputs during training instead of its predictions. This technique facilitates learning by providing more accurate guidance to the model during training. The probability of using teacher forcing at each time step can be controlled by a parameter $\alpha \in [0,1]$, where $\alpha =1$ indicates full teacher forcing (always using true values), and $\alpha =0$ indicates no teacher forcing (always using model predictions). The probability of using teacher forcing at time step t can be expressed as:

$$P\left(\mathrm{teacher}\mathrm{forcing}\mathrm{at}t\right)=\alpha$$

Thus, the input $y_t$ to the decoder is determined by whether teacher forcing is applied or not:

$$y_t=\left\{\begin{array}{cc}{y}_{t-1}\hfill & \mathrm{with}\mathrm{probability}\alpha \hfill \\ y_{t-1}^{\prime }\hfill & \mathrm{with}\mathrm{probability}1-\alpha \hfill \end{array}\right.$$

where $y_{t-1}^{\prime }$ represents the predicted output of the decoder at time step $t-1$.

Figure 6. Encoder-Decoder Architecture.

Figure 6. Encoder-Decoder Architecture.

5.1.3. Justification for Using GRU

(1)

Sequential Modeling: Because each point in a trajectory depends on the ones before it, trajectory data is inherently sequential. GRUs excel at sequential modeling as they maintain a hidden state that evolves, allowing them to capture dependencies in sequential data.

(2)

Memory Cells with Gates: GRUs are equipped with memory cells and gating mechanisms, enabling them to reset and update their internal state dynamically. The reset gate allows the model to choose which historical data to disregard, while the update gate determines which fresh data to incorporate. This flexibility mitigates the vanishing gradient issue and facilitates the capture of long-term interdependencies.

(3)

Efficient Training: GRUs are designed for computational efficiency, making them suitable for handling lengthy sequences often encountered in trajectory data. The efficiency of GRUs may contribute to quicker convergence during training.

(4)

Parameter Efficiency: Compared to LSTM networks, GRUs have fewer parameters, enhancing their parameter efficiency. This characteristic is particularly beneficial when working with trajectory data that may have limited samples. The reduced number of parameters helps prevent overfitting and may lead to better generalization for new trajectories.

5.2. Training

Training the trajectory imputation model has involved several key components that contribute to its overall performance. In this subsection, we have elaborated on some crucial parts of training phase, like optimization strategy, gradient clipping and learning rate scheduler.

• Optimization
  To update the model parameters, the Adam optimizer has been utilized. The Adam optimization algorithm has computed adaptive learning rates for each parameter based on their first-order moment estimate (mean) and the second-order moment estimate (uncentered variance). The update rule for the parameters $\theta$ has been given by:

  $${\theta }_{t+1}={\theta }_t-\frac{\mathrm{lr}}{\sqrt{{\widehat{v}}_t}+ϵ}{\widehat{m}}_t$$

  (14)

  where ${\widehat{m}}_t$ and ${\widehat{v}}_t$ are the biased first and second-moment estimates, $ϵ$ is a small constant to prevent division by zero, and lr is the learning rate.
• Gradient Clipping
  Gradient clipping has been employed to prevent exploding gradients during backpropagation. This technique involves scaling the gradients if their norm exceeds a predefined threshold (max_grad_norm). The scaled gradient $g^{\prime }$ has been computed as follows:

  

  (1)
• Learning Rate Scheduler
  The learning rate has been scheduled using the ReduceLROnPlateau(a PyTorch library function which decreases learning rate when a metric has ceased improving) scheduler. This scheduler has adjusted the learning rate if the validation losses plateaus, enabling the model to fine-tune its parameters more effectively. The learning rate update rule has been given by:

  $${\mathit{lr}}_{\mathit{new}}=\mathit{factor}\times {\mathit{lr}}_{\mathit{old}}$$

  (16)

  where ${\mathrm{lr}}_{\mathrm{old}}$ is the previous learning rate, and factor is a user-defined factor (default is 0.3).

5.3. Hyperparameters

In this subsection, we have defined and elaborated on the hyperparameters used in the trajectory imputation model. Hyperparameters are essential for influencing how the model behaves and performs during training. The hyperparameters have been divided into two categories: model parameters, which have defined the model’s architecture, and training parameters, which have affected how the model learns.

5.3.1. Model Parameters

• Dimensionality of input trajectories: This parameter has represented the number of features or dimensions in the input data.
• Number of hidden units: The hidden size has determined the ability of the model to grasp and represent temporal dependencies.
• Dimensionality of output trajectories: Similar to input size, this parameter has defined the number of features in the output predictions.
• Number of layers: This parameter has controlled the depth of the recurrent neural network, influencing its ability to model complex patterns.

5.3.2. Training Parameters

• Gradient clipping threshold: For gradients during backpropagation, this value has established the highest permitted norm. It has improved training stability and helped stop gradients from blowing up.
• Maximum gradient norm for scaling gradients: Gradient clipping has been applied to limit the norm of gradients. If the computed norm exceeds, the gradients have been scaled to meet this threshold.

Together, these hyperparameters have formed the trajectory imputation model’s design and training behavior. To achieve best performance and robustness during training, these variables must be fine-tuned.

6. Experimental Results and Discussion

The "Results and Discussion" section has dived into the model’s performance, highlighting significant metrics such as L1 loss and ADE. Graphical representations, including trend plots and a table of training results, provide a thorough picture. Table 4 has showcase the minimum values for different metrics. Figure 14 has clearly illustrated the model’s ability to predict and finish trajectories.

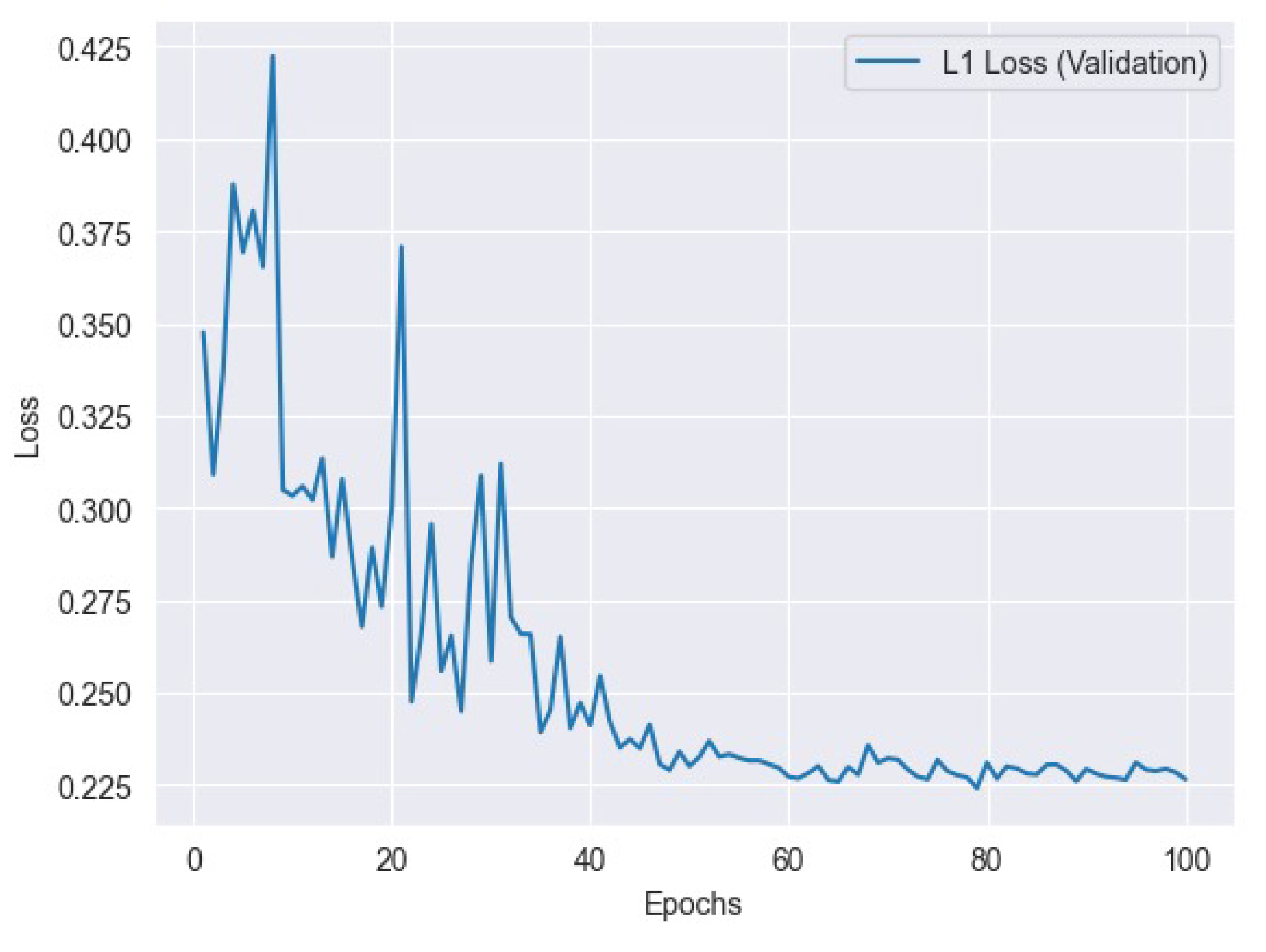
6.1. L1 Loss

The L1 loss, sometimes referred to as the mean absolute error (MAE) or L1 norm loss, is a commonly employed loss function in the fields of machine learning and optimization, specifically in regression problems. The metric measures the absolute disparities between the anticipated values ${\widehat{y}}_i$ and the actual target values $y_i$ for a total of n data points. The L1 loss has been calculated by taking the absolute difference between the predicted value (${\widehat{y}}_i$) and the actual value ($y_i$) for each data point, and then averaging these differences across the total number of data points (n). The inclusion of the absolute value in this formula has ensured that both overestimates and underestimates have an equal impact on the loss. The L1 loss has exhibited lower sensitivity to outliers in comparison to the L2 loss (mean squared error), rendering it appropriate for situations where the influence of outliers on the total loss should be constrained. 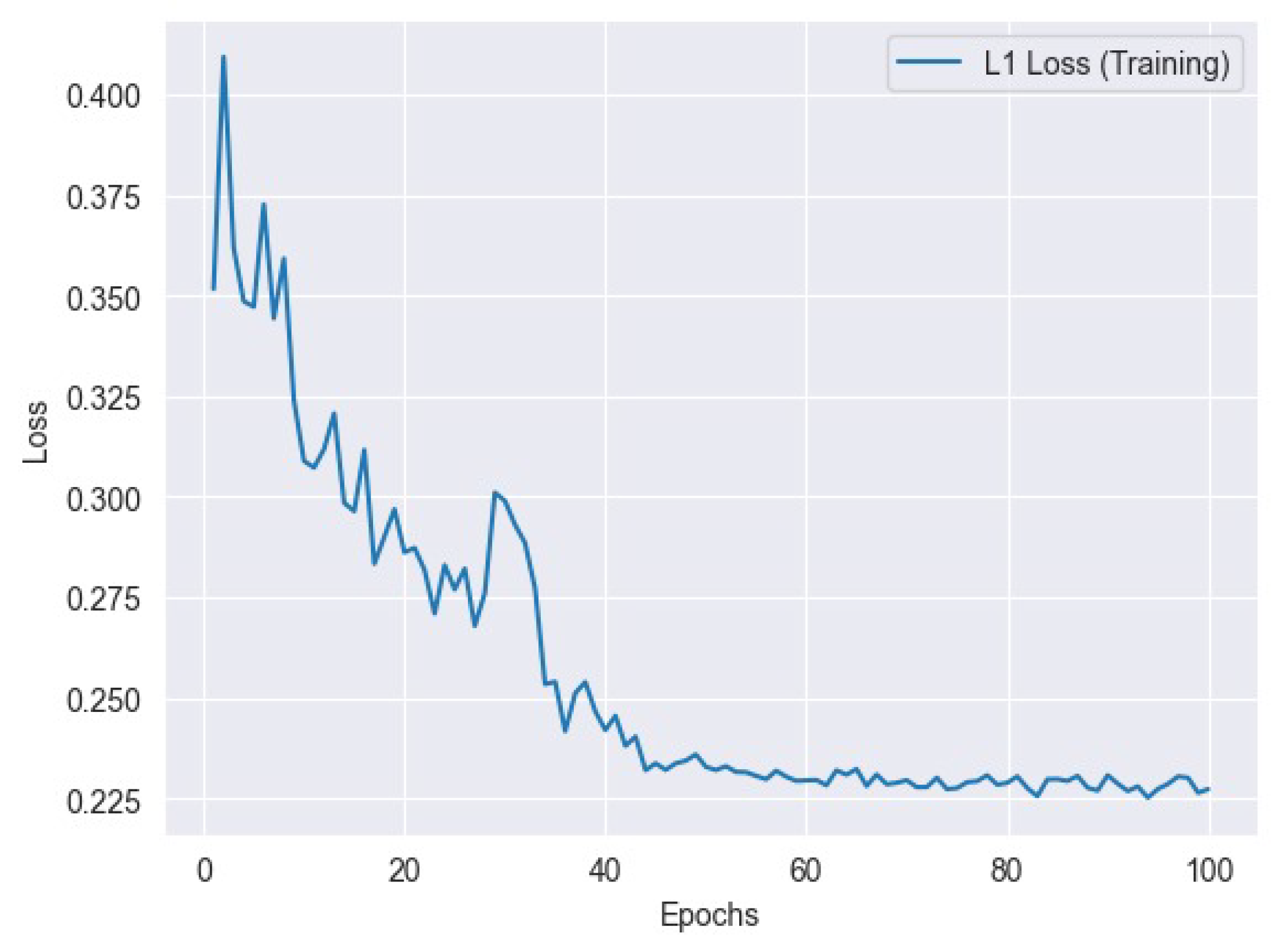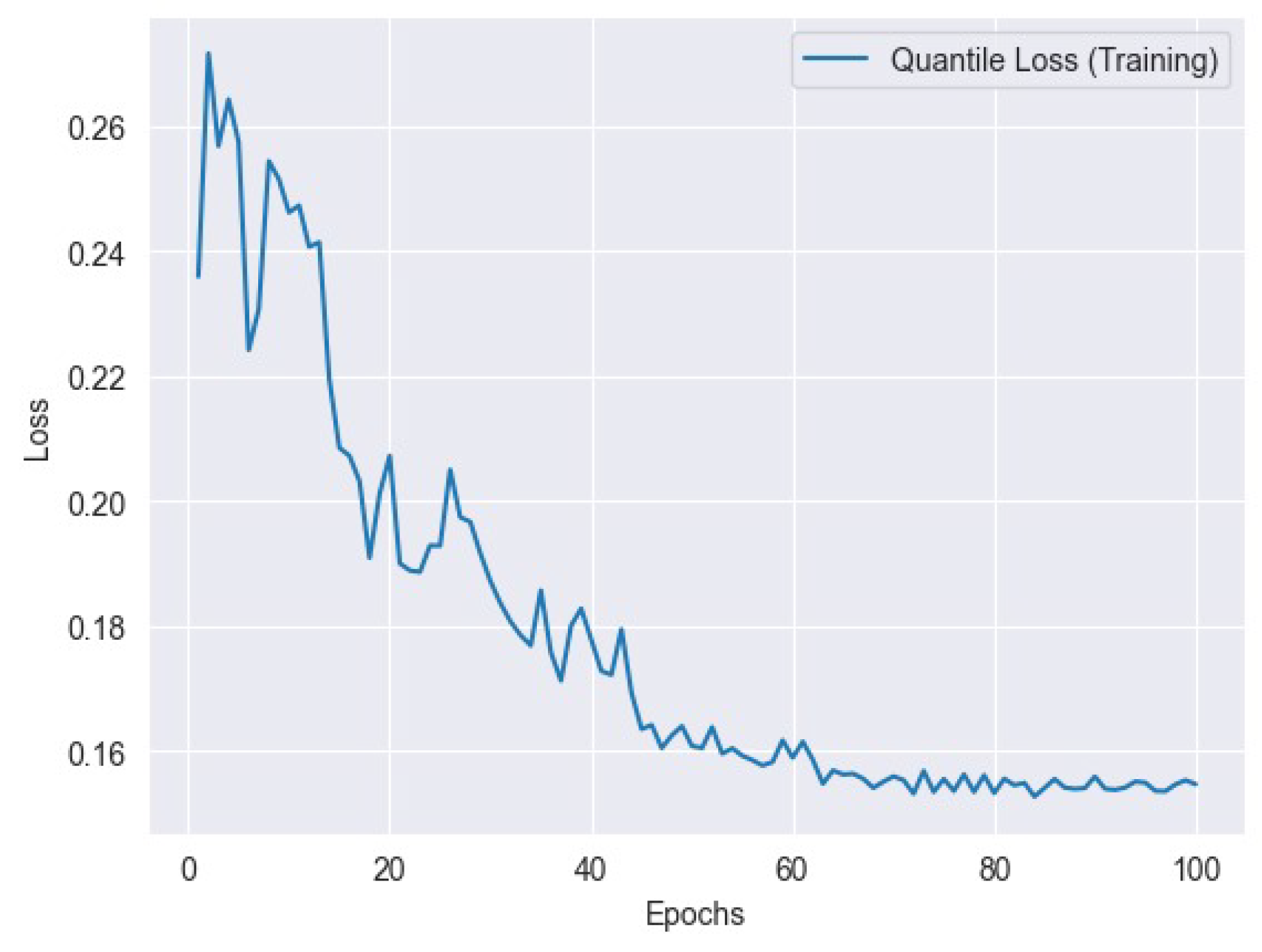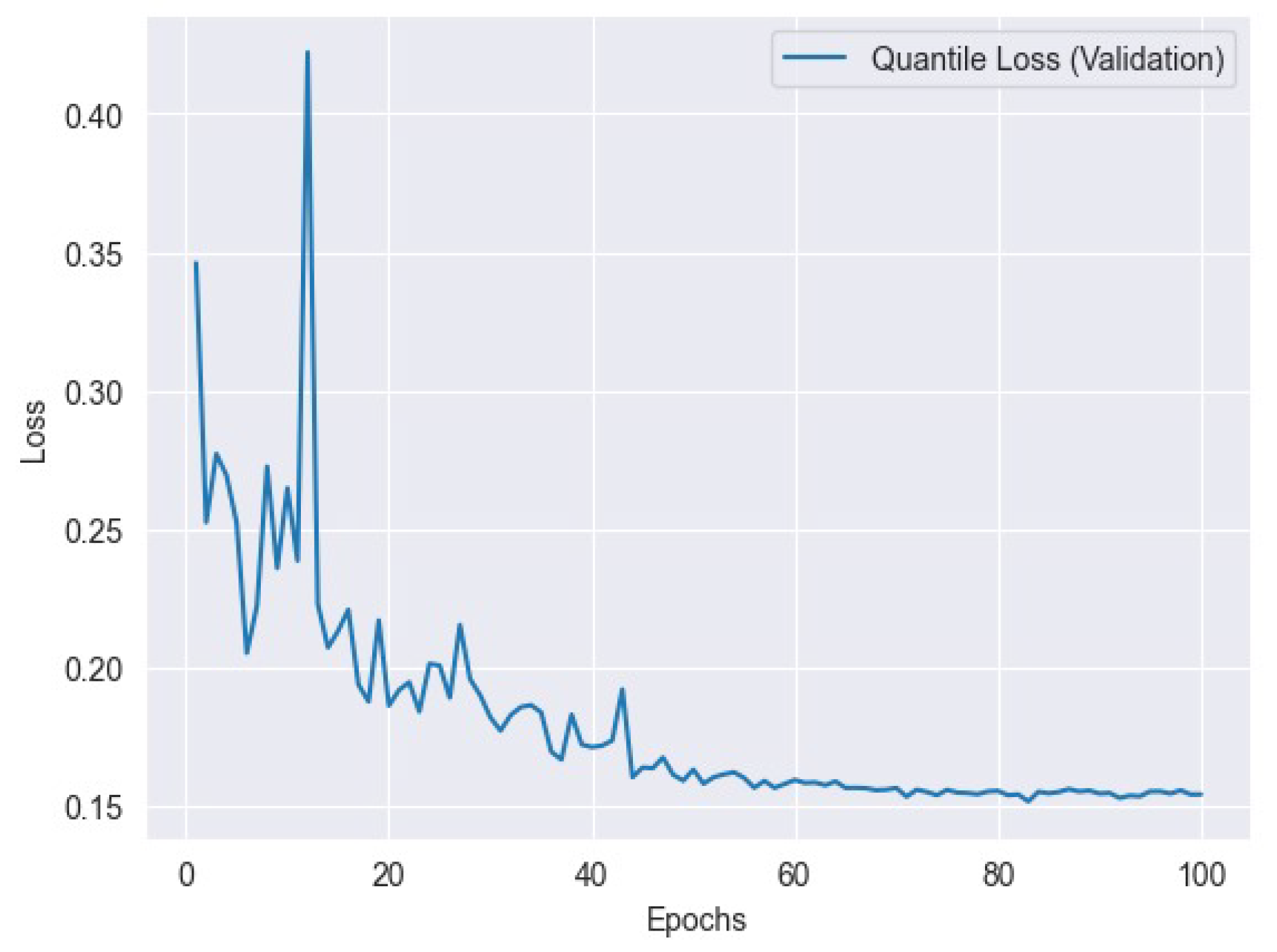Figure 7 represents the l1 training loss and Figure 8 represents the l1 validation loss.

The L1 loss formula is given by:

$$\mathit{L}\mathit{1}\_\mathit{Loss}=\frac{1}{n}\sum _{i=1}^n|{\widehat{y}}_i-y_i|$$

(17)

6.2. MSE Loss

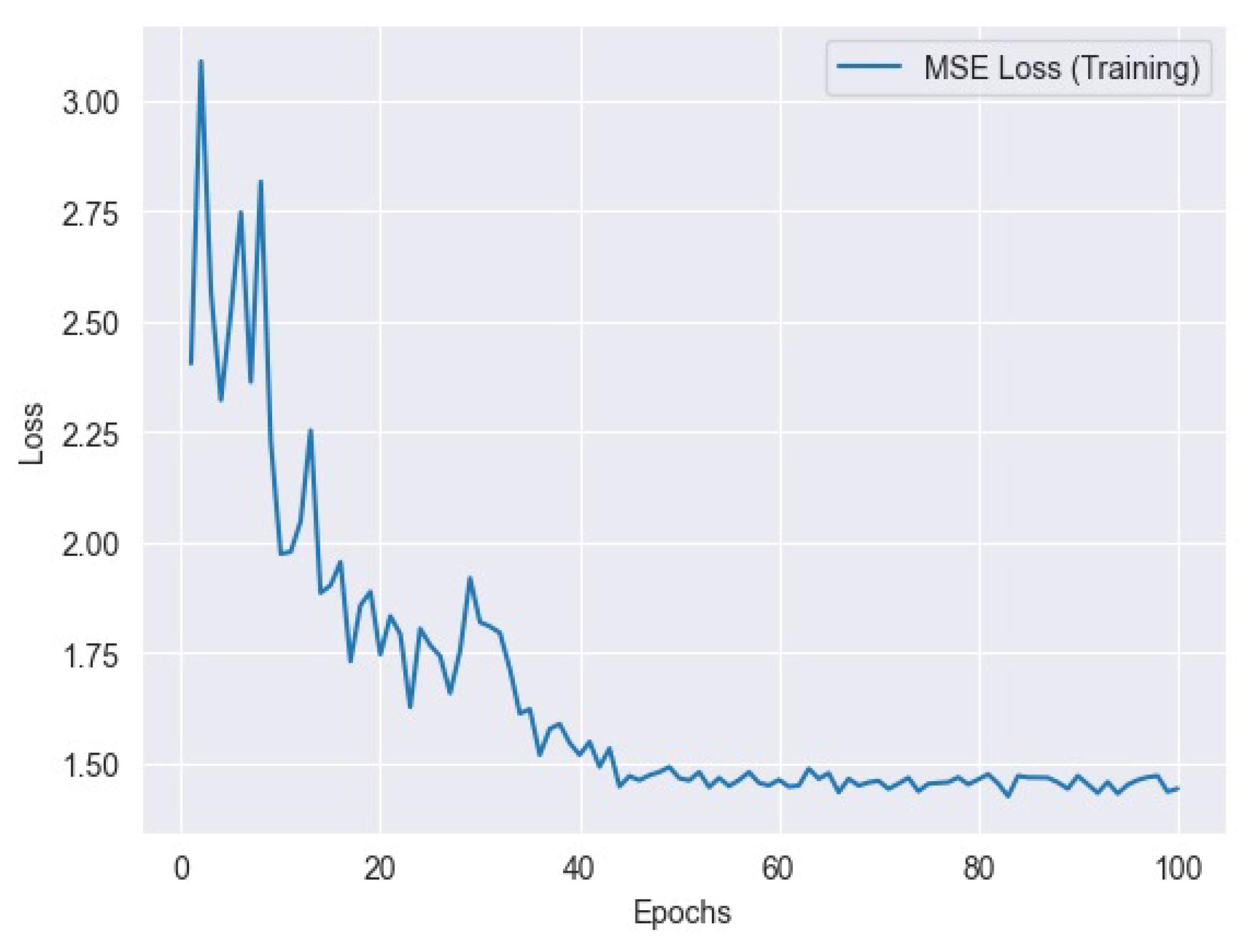
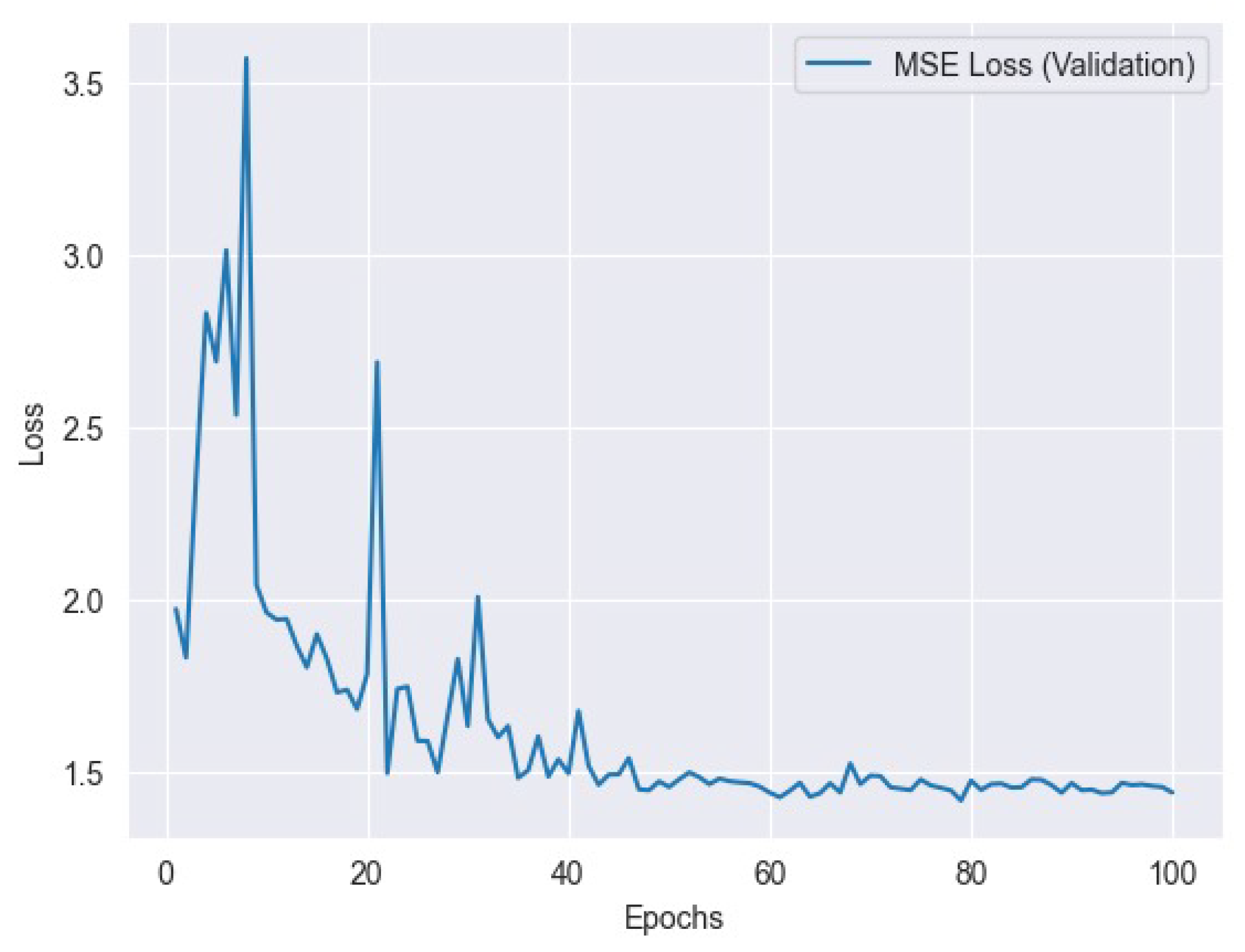
Mean Squared Error (MSE) is a common metric used in regression analysis to measure the average squared difference between predicted values and actual values. The Mse loss can be represented as follows:

$$\mathit{MSE}=\frac{1}{n}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(18)

where $y_i$ represents the actual value, ${\widehat{y}}_i$ represents the predicted value, and n is the number of data points. Figure 9 represents the MSE training loss and Figure 10 represents the MSE validation loss.

6.3. ADE loss

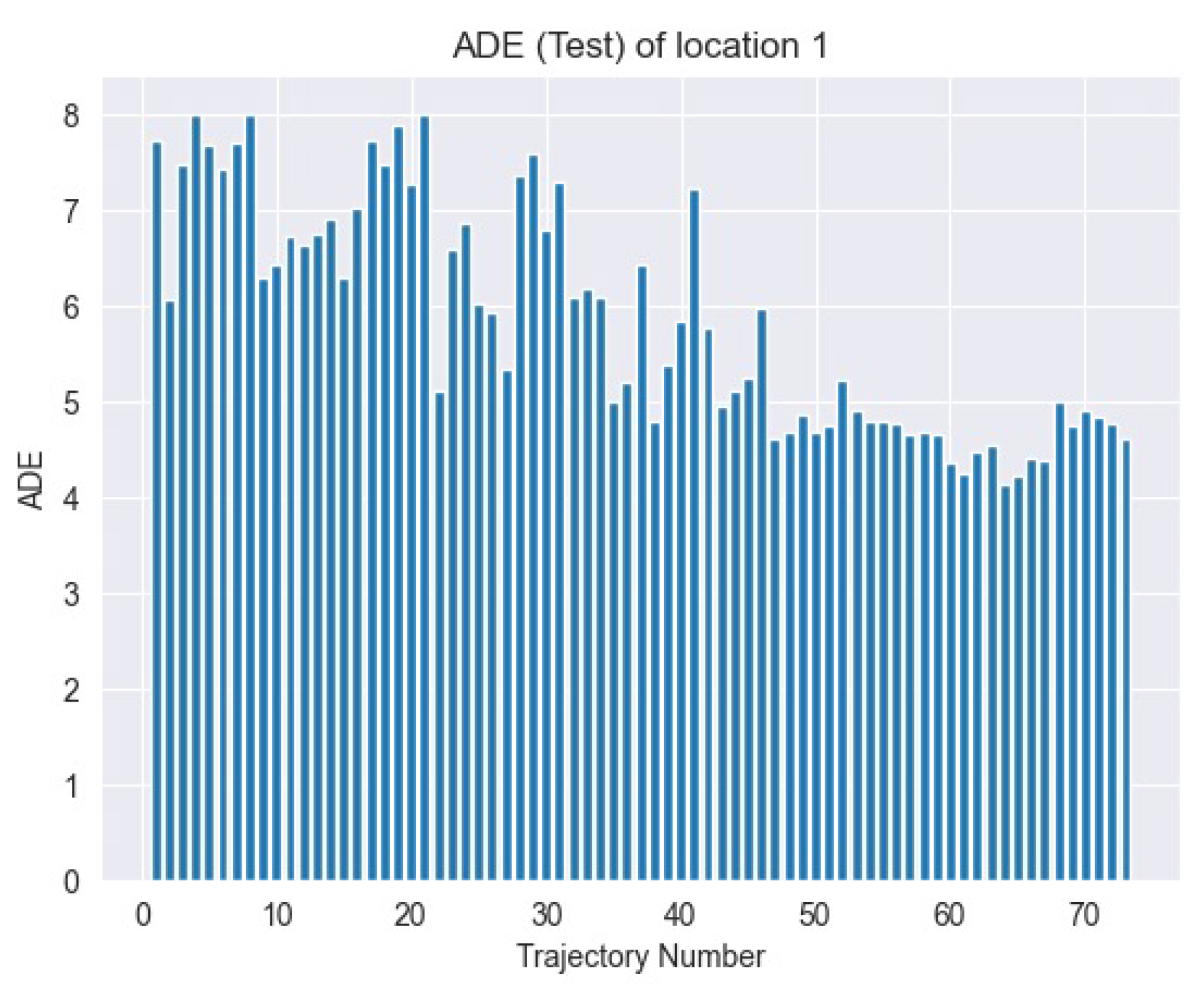
The Average Displacement Error (ADE) loss is a widely utilized statistic in trajectory prediction applications. The metric calculates the average Euclidean distance between anticipated points and their associated ground truth points throughout a series of frames. The ADE loss has been computed using the following formula:

$$ADE=\frac{1}{N}\sum _{i=1}^N\parallel {\widehat{y}}_i-y_i\parallel ,$$

(19)

where N is the total number of points in the sequence, ${\widehat{y}}_i$ represents the predicted position, and $y_i$ is the ground truth position. Figure 11 has shown the ADE loss over time.

6.4. Quantile Loss

Quantile Loss is a loss function used in quantile regression to measure the difference between predicted quantiles and actual quantiles of the target distribution. It is particularly useful when modeling non-normally distributed data or when different quantiles are of interest. The Quantile Loss is defined as:

$$\begin{array}{c}\mathit{Quantile}\mathit{Loss}=\sum _{i=1}^n\left(\tau ·max(y_i-{\widehat{y}}_i,0)\right.\hfill \\ \hfill \left.+(1-\tau )·max({\widehat{y}}_i-y_i,0)\right)\end{array}$$

(20)

where $y_i$ represents the actual value, ${\widehat{y}}_i$ represents the predicted value, $\tau$ is the desired quantile level, and n is the number of data points. Figure 12 represents the Quantile training loss, and Figure 13 represents the Quantile validation loss.

As shown in Table 4, the table summarizes the minimum losses obtained from training, validation, and testing across various metrics. These minimum values provide insight into the performance achieved by the model in different evaluation stages.

6.5. Graph Representations of Predicted Trajectory and Ground Truth Trajectory

In this subsection, we present a visual contrast between the predicted trajectory and the baseline trajectory. Figure 14 illustrates the trajectories plotted on a graph, with velocity values indicated. The x-axis represents the horizontal position, while the y-axis represents the vertical position. The blue line denotes the ground truth trajectory, while the red line represents the generated trajectory. Additionally, velocity values are annotated along the trajectories, providing insights into the speed variations throughout the movement. Arrows indicating the direction of movement are also included to enhance the visualization. This comparison allows for a qualitative assessment of the model’s performance in predicting trajectories and provides valuable insights into the dynamics of the system under study.

Figure 14. Comparison of generated and ground truth trajectories with velocity values.

Figure 14. Comparison of generated and ground truth trajectories with velocity values.

6.6. Comparison with Other Models

In this subsection, we have conducted a comprehensive comparison of four models: Two block RNN, Brits, GRU Encoder-Decoder, and our LSTM-GRU Encoder-Decoder model. The evaluation was primarily based on their respective L1 loss values, providing a quantitative measure of their performance.

As depicted in Table 5, the L1 loss values for each model are presented. The Two block RNN model yielded an L1 loss of 0.363, followed by Brits with a loss of 0.312. The GRU-based Encoder-Decoder model exhibited an L1 loss of 0.306. Notably, our proposed LSTM-GRU Encoder-Decoder model outperformed the others with an impressively low L1 loss of 0.2264.

7. Conclusion

In this research, we have designed a novel machine-learning model for imputing missing trajectory data for autonomous cars. Trajectory data is vital for the planning, navigation, and safety of autonomous cars, but it can be damaged or lost due to many circumstances, such as sensor failures, occlusions, noise, etc. Existing methods for trajectory imputation are either too straightforward, such as linear interpolation, or too complicated, such as generative adversarial networks. We have proposed a hybrid model that incorporates LSTM and GRU to capture the temporal, spatial, and contextual characteristics of the trajectory data. Our model can handle different sorts of missing patterns and impute trajectories with excellent accuracy and efficiency. In future research endeavors, an intriguing avenue for enhancement involves experimenting with Transformer models in the context of trajectory imputation for autonomous cars. Also, we can experiment by adding different types of embedding, like positional embedding, graph embedding with Attention mechanism to our proposed architecture, and observe the outcomes in these cases.